Abstract
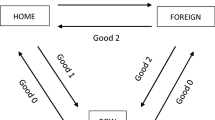
We build a model of cross-border pollution between two large open economies, one importing the polluting good and the other exporting it, and derive their non-cooperative trade and environmental tax policies. We show among other things, that (1) in response to a bilateral reduction in trade taxes by both countries, the former country’s optimal policy is to lower its Nash emissions tax while the latter’s is to raise it, and (2) in response to an increase in emissions tax rates by both countries, the former country’s optimal reaction is to raise its Nash import tariff, while the latter’s is to reduce its Nash export tax. That is, in the present context, freer trade leads the exporting country to adopt stricter while the importing country laxer environmental tax policies.
Similar content being viewed by others
Notes
Recent empirical contributions to this literature include, among others, Antweiler et al. (2001), Ederington et al. (2005). Copeland and Taylor (2004) provide a comprehensive review of the theoretical and empirical studies on the environmental consequences of economic growth and international trade.
For example, Markusen (1975) shows that the large countries set the emissions tax equal to the domestic external cost per unit of output, while the optimal import tariff is higher than then standard optimal tariff. This is because a tariff by improving an importing country’s terms of trade leads to lower polluting production abroad, thus fewer cross-border emissions and cleaner environment in the tariff country.
This is because a higher emissions tax by one country improves the other country’s terms of trade, thus expanding dirty production abroad and cross-border pollution.
In the context of the so called “strategic environmental policy” literature, among others, Conrad (1993) concludes that imperfect competition and cross-border pollution when countries are restricted from using trade taxes they set environmental taxes below the Pigouvian level. This, and other related studies, does not examine the optimal adjustments in one country’s Nash emissions tax rate when another country changes its own tax rate.
It is also unrelated to the literature on the linkage between trade and environmental agreements.
Beghin et al. (1997) note that it is rather difficult to categorize this relationship a priori, and thus it is by and large a matter of empirical assessment. Recent studies in the related literature assume quasi-linear utility functions which lead to \(E_{qr} =0\), i.e., goods and clean environment are independent in consumption, e.g., see Chao et al. (2012), Vlassis (2012). Furthermore, among others, Copeland and Taylor (2004), Hatzipanayotou et al. (2008) discuss the (non-) separability between private goods and clean environment in consumption.
The assumption of perfectly transboundary pollution, i.e., \(\theta =\theta ^{*}=1\), is widely used in the relevant literature, e.g., see Vlassis (2012), Keen and Kotsogiannis (2011). A more general specification of cross-border pollution would be \(r=z+\theta z^{*}\) and \(r^{*}=z^{*}+\theta ^{*}z\), where \(\theta >0(\theta ^{*}>0)\) is the fraction of pollution transmitted from Foreign (Home) to Home (Foreign).
Note that since \(\tau ^{*}(<0)\) is an export tax, then increasing (reducing) its rate implies that \(d\tau ^{*}{<} \ 0(>0)\).
Solving \(\Omega _t +\Phi _t =0\) and \(\Omega _\tau +\Phi _\tau =0\) for Home, and \(\Omega _{t^{*}} +\Phi _{t^{*}} =0\) and \(\Omega _{\tau ^{*}} +\Phi _{\tau ^{*}} =0\) for Foreign, the cooperative emissions taxes are \(t^{c}=t^{*c}=E_r +E_{r^{*}}^*\), and the cooperative trade policy requires that \(\left( {\tau -\tau ^{*}} \right) =0\). Since \(\tau >0\) and \(\tau ^{*}<0, \left( {\tau -\tau ^{*}} \right) =0\) is satisfied only when \(\tau ^{c}=\tau ^{*^{c}}=0\), that is, the cooperative trade policy is free trade.
Uniform demand and supply reactions means, e.g., \(E_{qq} =E_{q^{*}q^{*}}^*, E_{qr} =E_{q^{*}r^{*}}^*, R_{pp} =R_{p^{*}p^{*}}^*\). The assumption that supply and demand responses are identical in two countries is often made in the tax harmonization literature, e.g., Keen (1989), and recently Vlassis (2012).
We can call the right-hand-side expression of \(t^{N}\) in Eq. (9), smaller than \(E_r \), effective marginal willingness to pay for reducing pollution accounting for induced changes in the terms of trade, and the relationship between the non-numeraire good and clean environment in consumption.
In the absence of terms of trade effects, Eqs. (9) and (10) indicate that the corresponding Nash trade policy is free-trade for both countries. This result is easily verifiable considering a special case model of two small open economies under constant terms of trade. Thus, letting \({ dP}=0\) in Eqs. (17) and (18) in the Appendix, it can be shown that at Nash equilibrium for Home \(t^{N}=E_r \) and \(\tau ^{N}=0\), and similarly for Foreign \(t^{*^{N}}=E_{r^{*}}^*\) and \(\tau ^{*^{N}}=0\).
From Appendix (22), \(\partial t^{N}/\partial \tau =-\Omega _{tt}^{-1} \Omega _{t\tau } =-\left( {3/4} \right) \Omega _{tt}^{-1} R_{pp} >0\).
These induced world price and pollution effects of Foreign’s higher \(t^{*N}\) on \(t^{N}\) are given by expression \(\Omega _{tt^{*}} \) in Appendix (21). Because of the algebraic complexity of this expression, it helps to interpret the results letting \(E_{qr} =0\). Then, \(\Omega _{tt^{*}} =-R_{pp}^2 (4E_{rr} +E_{qq}^2 M_{pp} )/4M_{pp}^2 >(<)0\). The first term captures the required decrease in \(t^{N}\) due to lower pollution in Home, and the second term captures the required increase in \(t^{N}\) due to Home’s increased production and lower imports.
Limão (2005) concludes that in the absence of political economy considerations the two instruments are always strategic complements, while in the presence of such considerations they can also be strategic substitutes or even independent of each other. Our \(\Omega _{t\tau }\) term corresponds in Limão’s (2005) \(W_{\tau e} \) term (p. 190), where \(\tau \) is the import tariff and \(e\) is the emissions tax. Without political economy considerations \(W_{\tau e}\) is positive for both countries.
For example, \(\frac{dt^{N}}{d\tau }+\frac{dt^{N}}{d\tau ^{*}}=\Omega _1^{-1} H^{-2}R_{pp}^2 \left\{ {2M_{pp}^2 +8E_{qr}^2 R_{pp}^2 +8E_{qr} R_{pp} E_{qq} -8E_{qr} R_{pp}^2 } \right\} >0\).
The sign of the term \(\Omega _{\tau \tau ^{*}} \) determines the strategic relationship between the import tariff and the export tax. Here, the sign of this term is positive, i.e., \(\frac{\partial \tau ^{N}}{\partial \tau ^{*}}=-\Omega _{\tau \tau ^{*}} \Omega _{\tau \tau }^{-1} >0\), which means that the two trade taxes are strategic substitutes: an increase in \(\tau ^{*}\), which being negative, is a reduction in export tax, induces Home to increase \(\tau \). Similarly, an increase in Home’s import tariff, induce Foreign to reduce its export tax. Intuitively, as one country increases its trade tax towards the prohibitive level, the other country’s optimal reaction is to lower its trade tax towards zero, as there are no terms of trade gains at zero trade. The result that trade taxes are strategic substitutes is in line with the relevant literature on strategic trade policy and tariff games (see footnote 16 in Lahiri et al. 2002).
For example,\(\frac{d\tau ^{N}}{dt}+\frac{d\tau ^{N}}{dt^{*}}=-\frac{1}{2}R_{pp} M_{pp}>0\).
References
Antweiler W, Copeland B, Taylor MS (2001) Is free trade good for the environment? Am Econ Rev 91:877–908
Bagwell K, Staiger RW (2001) Domestic policies, national sovereignty, and international economic institutions. Q J Econ 116:519–562
Beghin J, Holst D, Van der Mensbrugghe D (1997) Trade and pollution linkages: piecemeal reform and optimal intervention. Can J Econ 30:442–455
Burguet R, Sempere J (2003) Trade liberalization, environmental policy and welfare. J Environ Econ Manag 46:25–37
Chao CC, Laffargue J, Yu E (2012) Tariff and environmental policies with product standards. Can J Econ 45:978–995
Conconi P (2003) Green lobbies and transboundary pollution in large open economies. J Int Econ 59:399–422
Conrad K (1993) Taxes and subsidies for pollution intensive industries as trade policy. J Environ Econ Manag 25:121–135
Copeland B (1996) Pollution content tariffs, environmental rent shifting, and the control of cross-border pollution. J Int Econ 40:459–476
Copeland B (2000) Trade and environment: policy linkages. Environ Dev Econ 5:405–432
Copeland B, Taylor MS (2004) Trade, growth, and the environment. J Econ Lit 42:7–71
Copeland B, Taylor MS (2005) Free trade and global warming: a trade theory view of the Kyoto protocol. J Environ Econ Manag 49:205–234
Ederington J (2002) Trade and domestic policies linkage in international agreements. Int Econ Rev 43:1347–1367
Ederington J, Levinson M, Minier J (2005) Footloose and pollution free. Rev Econ Stat 87:92–99
Hatzipanayotou P, Lahiri S, Michael M (2008) Cross-border pollution, terms of trade, and welfare. Environ Res Econ 41:327–345
Keen M, Kotsogiannis C (2011) Coordinating Climate and Trade Policies: Pareto Efficiency and the Role of Border Tax Adjustments, CESifo Working Paper No. 3494
Keen M (1989) Pareto-improving indirect tax harmonization. Eur Econ Rev 33:1–12
Lahiri S, Raimondos-Møller P, Wong K-Y, Woodland A (2002) Optimal foreign aid and tariffs. J Dev Econ 67:79–99
Limão N (2005) Trade policy, cross-border externalities and lobbies: do linked agreements enforce more cooperative outcomes? J Int Econ 67:175–199
Ludema RD, Wooton I (1994) Cross border externalities and trade liberalization: the strategic control of pollution. Can J Econ 27:950–966
Markusen J (1975) International externalities and optimal tax structure. J Int Econ 5:15–29
Panagariya A, Palmer K, Oates W, Krupnick W (2004) Towards an integrated theory of open economy environmental and trade policy. In: Environmental policy and fiscal federalism: selected essays of Wallace E. Edward Elgar, Oates, pp 100–125
Rauscher M (1997) International trade, factor movements and the environment. Claredon Press, Oxford
Vlassis N (2012) The welfare consequences of pollution-tax harmonization, Environmental and Resource Economics, forthcoming
Walz U, Wellisch D (1997) Is free trade in the interest of exporting countries when there is ecological dumping? J Public Econ 66:261–275
Acknowledgments
We thank an Associate Editor and two anonymous referees of the Journal, participants in the 10th Annual ASSET Conference, the 12th Annual ETSG Conference, and the 66th Annual IIPF Congress, for their constructive comments and suggestions. The authors graciously acknowledge the co-funding of this research by the European Social Fund (ESF) and the Greek NSRF—Research Funding Program: THALIS. The authors are solely responsible for possible shortcomings of the paper.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Derivation of Equation (5)
Differentiating Eq. (4) we obtain:
Differentiating Eq. (1) we obtain:
Substituting Eq. (16) into (15) gives Eq. (5) in the text.
1.2 Derivations of Equations (7) and (8), and Definitions of \(\Omega ^{\prime }s\) and \(\Phi ^{\prime }s\)
1.2.1 Equations (7) and (8)
Differentiating Eqs. (2) and (3), respectively, accounting for cross-border pollution and endogenous terms of trade we obtain:
Equivalently we define the expressions for \(B_P ,B_t ,B_\tau ,B_{t^{*}}\) and \(B_{\tau ^{*}} \). Substituting changes of terms of trade from Eq. (5) into Eqs. (17) and (18), we obtain Eqs. (7) and (8) in the text.
1.2.2 The Complete Definitions of \(\Omega ^{\prime }s\) and \(\Phi ^{\prime }s\)
Equivalently we define the expressions for \(\Phi _\tau ,\Phi _t ,\Phi _{\tau ^{*}} ,\Phi _{t^{*}} \).
1.3 Optimal Adjustments in Emissions and Trade Taxes
Given that demand and supply reactions in the two countries are uniform, the definitions for \(\Omega ^{\prime }s\) and \(\Phi ^{\prime }s\) are as follows:
Equivalently we define the expressions for \(\Phi _{t^{*}} ,\Phi _t ,\Phi _{\tau ^{*}}\) and \(\Phi _\tau \). Also note that in this case:
1.3.1 Optimal Adjustments in Emissions Taxes When Trade Taxes Change
Totally differentiating the best-response functions \(\Omega _t =0\) and \(\Phi _{t^{*}} =0\), treating \((t,t^{*})\) as endogenous and \((\tau ,\tau ^{*})\) as exogenous gives the following matrix system:
where the determinant of the left-hand-side coefficients matrix of the unknown, \(\Omega _1 \left( {{=}\Omega _{tt} \left( {\Omega _{tt} -\Omega _{tt^{*}} \Omega _{tt}^{-1} \Omega _{tt^{*}} } \right) } \right) \), is positive for stability. Also, because of the assumed uniform reactions, \(\Omega _{t\tau ^{*}} =\Phi _{t^{*}\tau } \) and \(\Omega _{t\tau } =\Phi _{t^{*}\tau ^{*}} \). Then, for changes in Home’s Nash tariff we obtain:
where now \(H=2(M_{pp} +2E_{qr} R_{pp} )<0\). Equivalently, from Eq. (21) we obtain \(\left( {dt^{*N}/d\tau ^{*}} \right) >0\) and \(\left( {dt^{N}/d\tau ^{*}} \right) <0\). In Eqs. (22) and (23):
For the expressions above and for the rest of this section it is assumed that third order derivatives are zero, e.g., \(E_{qqq} =0, R_{ppp} =0\). Also, use was made of Eqs. (19) and (20).
1.3.2 Optimal Adjustments in Trade Taxes When Emissions Taxes Change
Totally differentiating the best-response functions \(\Omega _\tau =0\) and \(\Phi _{\tau ^{*}} =0\), treating \((\tau ,\tau ^{*})\) as endogenous and \((t,t^{*})\) as exogenous we obtain the following matrix system:
Assuming uniform demand and supply reactions in the two countries, \(\Omega _{\tau \tau } \left( {{=}\Phi _{\tau ^{*}\tau ^{*}} } \right) {=} (3/4)M_{pp} <0, \Omega _{\tau t^{*}} \left( {{=}\Phi _{\tau ^{*}t} } \right) =-(1/4)R_{pp} <0, \Omega _{\tau \tau ^{*}} \left( {{=}\Phi _{\tau ^{*}\tau } } \right) =-(1/4)M_{pp} >0\), and \(\Omega _{\tau t} \left( {=\Phi _{\tau ^{*}t^{*}} } \right) =(3/4)R_{pp} >0\). The determinant of the left-hand-side coefficients matrix of the unknown, \(\Omega _2 \left( {=\Omega _{\tau \tau } \left( {\Omega _{\tau \tau } -\Omega _{\tau \tau ^{*}} \Omega _{tt}^{-1} \Omega _{\tau \tau ^{*}} } \right) } \right) \), is positive for stability. Then, for changes in Home’s emissions tax we obtain:
Equivalently we obtain \(\left( {d\tau ^{*N}/dt^{*}} \right) >0\) and \(\left( {d\tau ^{N}/dt^{*}} \right) =0\). In Eqs. (25)–(26):
Rights and permissions
About this article
Cite this article
Tsakiris, N., Michael, M.S. & Hatzipanayotou, P. Asymmetric Tax Policy Responses in Large Economies With Cross-Border Pollution. Environ Resource Econ 58, 563–578 (2014). https://doi.org/10.1007/s10640-013-9710-7
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10640-013-9710-7