1 Introduction

Augmented Reality (AR) technologies allow for holograms to be layered over the real-world, “augmenting” human vision by adding technical information or illustrations onto 3D space. This placement of virtual objects in one’s actual physical environment distinguishes AR from Virtual Reality (VR), where the entire visual environment is computer-generated. AR and VR are members of a class of eXtended Reality technologies (XR) that are rapidly reshaping education (Johnson-Glenberg, 2018), often without rigorous empirical support of their efficacy or impact on learning and teaching.

AR technologies can be used by holding up the camera of a cell phone or tablet and looking at augmentations on the camera feed (e.g., Pokémon Go). Additionally, head‐mounted displays (HMDs) now exist for hands-free layering of AR holograms over real-world environments. This technological advance is significant because learners’ hands are free to gesture and manipulate virtual objects, and learners can directly see and interact with their environment and collaborators. There are several meta-analyses of educational interventions that estimate the effects of AR. These meta-analyses estimate the positive effect of AR on student outcomes to be anywhere from d = 0.64 (Garzón & Acevedo, 2019), to g = 0.65–0.75 (Chang et al., 2022).

Dynamic geometry software (DGS; Hollebrands, 2007) allows students to manipulate mathematical objects through dragging motions and see measurements updated in real time. DGS is ubiquitous in the mathematics education literature (Juandi et al., 2021) and is integrated into major curricula in the United States (Sherman et al., 2020). But little research has examined AR-based DGS, with even less known about AR-based DGS that are collaborative in nature – where multiple students can manipulate the same shapes at the same time while in the same physical location. This new class of DGS allows students to interact with shapes in 3D – a profound affordance of XR (Johnson-Glenberg, 2018). In the present study, we conducted an experiment where 120 high school students were assigned to either solve geometry simulations collaboratively on a tablet-based DGS or using a head-mounted display (HMD) AR-based DGS. We look at students’ learning and how it was impacted by the dimensionality (2D or 3D) of the geometric shapes, as well as how they engaged with gestures and epistemic actions on virtual objects.

1.1 Theoretical framework

1.1.1 Embodied cognition, gesture, and action

Contemporary AR systems allow students to interact with virtual objects using their bodies to manipulate and move around the objects–interactions not supported by print media and 2D displays. This capitalizes on embodied views of the nature of cognition (Lakoff & Núñez, 2000; Nathan, 2021), which posit that all conceptual knowledge is understood and experienced through the body and is action-based in nature. Embodied views of cognition often give rise to learning pedagogies where students engage in perceptual, sensorial, and motor activities to deepen their understanding of mathematical ideas (e.g., Abrahamson & Sánchez-García, 2016; Dimmel & Bock, 2019; Smith et al., 2014), including through gestures.

Gestures are the spontaneous or purposeful arm and hand movements that people produce when reasoning or communicating (McNeill, 1992). Gestures are an important way in which mathematical ideas are embodied, as they allow students to depict, transform, and even become mathematical objects (Alibali & Nathan, 2012; Gerofsky, 2011). Gestures can be classified into several categories; the most relevant categorizations for the present study includes pointing gestures, where people use their hands to indicate or draw attention to some position in their environment (McNeill, 1992) and dynamic gestures (Nathan et al., 2014) which depict the transformation of a mathematical object through multiple states (e.g., making a triangle with your hands and showing it grow larger). In mathematics education, pointing gestures can serve to ground mathematical cognition in the environment (Alibali & Nathan, 2012), while dynamic gestures can allow learners to enact hypothetical transformations of mathematical figures to explore relationships (Pier et al., 2019). These kinds of gestures can impact both the gesturer’s cognition (Novack & Goldin-Meadow, 2015) as well as the cognition of collaborators (Walkington et al., 2019).

Here we differentiate gestures from epistemic actions performed on objects. An epistemic action involves actively manipulating a real or virtual dynamic object in your environment to obtain new information, usually with your hands (Kirsh & Maglio, 1994), such as pulling on the vertex of a virtual cube to make it larger or rotating a square by spinning it around. Kirsh and Maglio (1994) theorized epistemic actions: “We have found that some of the translations and rotations made by players… are best understood as actions that use the world to improve cognition” (p. 513; emphasis added). Epistemic actions are physical actions that leverage objects in the environment to support the enactor’s cognition by making their problem-solving faster, easier, and more reliable (Kirsh & Maglio, 1994). These are contrasted with pragmatic actions that are the actions performed to actually achieve a task.

1.1.2 Dynamic geometry software

DGS is a class of digital tools that allows students to dynamically view and interact with invariant properties of objects that reflect geometric relations. DGS can take precise measurements, which instantaneously update as the object is dragged (Hollebrands, 2007). AR-based DGS brings together the affordances of physical and virtual learning experiences (Bujak et al., 2013) because it has the dynamicity and immediate feedback of a traditional DGS, combined with a three-dimensionality for embodied interactions with objects in real-world spaces. AR-based DGS platforms offer new possibilities for collaboration, as physical interplay occurs between learners as they work in 3D space together and embody concepts in coordinated ways to solve problems (Lindgren & Johnson-Glenberg, 2013).

DGS allows students to engage in mathematical justification practices through interactions with objects. Generalization is a cornerstone of mathematics because it provides the basis for claims that are true or false for an entire class of objects. Justifications are critical to generalization because they are “the process of supporting your mathematical claims and choices when solving problems or explaining why your claim makes sense” (Bieda & Staples, 2020, p. 103) and “explain or provide insight into the underlying mathematics” (Staples et al., 2017, p. 24). Students’ justifications may stem from students’ intuition (i.e., snap judgments) about whether conjectures seem true or false, and from their insights about geometric shapes – their ideas about how a specific geometric shape “works,” that is not necessarily backed up by a formal chain of reasoning (Zhang et al., 2016). We consider these three outcomes – intuition, insight, and generalization – in the present study. We define a “conjecture” as a mathematical statement that students are asked to justify the truth of (e.g., The sum of the lengths of two sides of a triangle are greater than the remaining side).

1.1.3 Affordances of augmented reality

Affordances of AR identified in the literature include the ability of AR to (1) allow for visualizations of concepts, (2) allow students to experience concepts in three dimensions, (3) give opportunities for collaboration among students to reach a learning goal, and (4) allow for immersion where holograms fit into the real world (Wu et al., 2013). AR allows students to change perspectives by moving their bodies (Dimmel et al., 2021), seeing how shapes change when looked on from different angles (Bock & Dimmel, 2021). In AR, learners also have direct access to three-dimensional figures rather than two-dimensional projections of three-dimensional figures. This could reduce cognitive load (Dimmel & Bock, 2019) and improve learning (Jacobson, 2011); this is an especially important affordance of XR (Johnson-Glenberg, 2018; Wu et al., 2013). Finally, in AR-based DGS, students can manipulate the scale of objects (Dimmel & Bock, 2019), making them very small to room-sized or bigger.

While dimensionality is identified as an affordance of AR, the most recent and comprehensive meta-analysis of AR in education challenges its utility. Chang et al. (2022) found that “the expected mean effect size for studies incorporating 3-D visualization in the AR learning environment is 0.71 points lower than the expected mean for studies that did not incorporate 3-D visualization in the AR learning environment” (p. 13). The authors argued that 3D visualizations can cause deceptive clarity where students overestimate their understanding. Krüger et al. (2022) in a study of 2D versus 3D visualizations of the human heart found that the 3D visualizations increased germane cognitive load and spatial relations knowledge, but that this was only the case for learners with higher mental rotation ability. The issue of dimensionality is particularly relevant to geometry education, where students must learn about 3D shapes like prisms and pyramids, and 3D concepts like volume and nets. In the present study, we will contrast using AR to learn about 2D geometry objects like squares and triangles, to using AR to learn about 3D geometry objects like prisms and cones.

1.2 Literature review of mathematics learning with augmented reality

1.2.1 Meta-analyses of the effect of augmented reality in mathematics education

There are four recent meta-analyses looking at the effectiveness of AR in mathematics education. Chang et al. (2022) included mathematics studies that involved 17 different comparisons and found a negative learning outcome meta-regression coefficient for the subject area of mathematics (g = -0.34), while finding positive effects for language and social studies. They also found that AR studies that involved 3D visualizations tended to have smaller effect sizes than those that did not. Zhang et al. (2022) included only three studies of mathematics, finding g = 0.578. Garzón and Acevedo (2019) grouped mathematics with natural sciences, and thus included 32 studies in this category in their meta-analysis, finding an effect size of d = 0.62. This was similar to the findings from the fourth meta-analysis (Garzón et al., 2019). These meta-analyses leave us with an unclear idea of the effectiveness of AR in mathematics education, so we turn to recent systematic reviews.

1.2.2 Systematic reviews on augmented reality in mathematics education

There are five recent systematic reviews of AR in mathematics education. Pahmi et al. (2023) included 23 publications, finding that the majority of studies focused on junior high school, the topic of geometry, and involved researcher-developed AR tools; they concluded from the literature base that AR supports mathematics learning. Jabar et al. (2022) included 20 articles focusing on secondary school and found again that geometry was the most common topic, and that measuring outcomes in the cognitive domain (focusing on conceptual learning) occurred in the majority of articles. Korkmaz and Morali (2022) included 24 mixed methods or qualitative articles, finding most had small sample sizes, involved adults, and focused on developing spatial skills. Palancı and Turan (2021) included 86 studies, with the majority being qualitative. They again found geometry and the secondary school level to be common and stated that 34 of the included studies suggested that AR supports learning in mathematics education. However, only 16 of these studies included a control group. Ahmad and Junaini’s (2020) review included 19 quantitative studies and 19 qualitative studies, finding algebra to be the most popular topic for AR, and concluding that AR was promising for supporting math learning. While all of the systematic reviews painted a positive picture of AR in mathematics education, none of them examined the methodological quality of the studies being used to conclude that AR was effective. For this reason, we turn to examining individual experimental studies.

1.2.3 Prior experimental studies on the effect of augmented reality in mathematics education

We used the references sections of the meta-analyses and systematic reviews to extract 50 quantitative studies of AR in mathematics education, of which we found 23 that both had a control group and measured mathematics learning outcomes. Nineteen of the 23 studies concluded AR was superior to the control condition in terms of mathematics learning gains, while 4 found no significant differences (Alves et al., 2017; Bhagat et al., 2021; Conley et al., 2020; Rebollo et al., 2022). We looked critically at this evidence base, noting several issues. Some studies had very small sample sizes (30 students or less being assigned to 2 + conditions). Demitriadou et al. (2020) had a sample size of 20, Alves et al. (2017) had a sample size of 24, Bhagat et al. (2021) had a sample size of 27, Cheng et al (2018) had a sample size of 30, and Flores-Bascuñana et al. (2019) had a sample size of 30. Others had larger sample sizes, but assignment to conditions was done at the classroom level (usually with one classroom in the experimental and another in the control; Chao & Chang, 2018; Elsayed & Al-Najrani, 2021; Sun & Chen, 2019; Cerro Velázquez and Morales Méndez, 2021; Wu et al., 2019). Such designs fail to take into account the strong impact classroom-level assignment has on statistical power and validity of results, compared to student-level assignment. Others had issues with their analyses, such as only comparing means without taking into account variance (e.g., de Ravé, et al., 2016; Flores-Bascuñana et al., 2019).

But the largest and most consistent issue we saw in all 23 experimental studies was a lack of equivalence between the experimental group (AR) and the control group, on factors unrelated to AR. Most of the studies did not describe their control condition at all, referring to it as simply “traditional instruction” or “paper-based instruction” (e.g., Ahmad, 2021; Cai et al., 2020; Conley et al., 2020), while other studies simply said they used manipulatives as their control condition (e.g., Andrea et al., 2019; Flores-Bascuñana et al., 2019). Notably, there are many differences between traditional instruction, manipulatives, and AR-based instruction that are not related to the specific elements of AR and are not relevant to the studies’ research questions. For example, perhaps the fact that the AR was presented digitally (rather than via pencil/paper or manipulatives) drove the significant findings, and any digital intervention (even one that did not involve AR, like using a computer and mouse) would have yielded similar effects. It is also not clear from the articles if the wording of the tasks, all visual images seen by students, all mathematical instructions given to students, the quantity and types of feedback received by students, etc. were matched across conditions – there are a plethora of differences that may be driving effects in any of these studies. None were designed to isolate the effects of AR specifically, let alone investigate the unique elements AR offers. Only 6 of the 23 studies showed their control conditions in their reporting (Demitriadou et al., 2020; Gecu-Parmaksiz & Delialioglu, 2019; Ibáñez et al., 2020; Sommerauer & Müller, 2014; Sun & Chen, 2019, 2020), and often the images they provided raised more questions. For example, Demitriadou et al. (2020) showed images of completely different tasks for the “first activity” in their study, where the control condition was identifying shapes like a dice and a tennis ball in a set of ten 3D shapes, while in the AR condition there were only seven shapes, and none were contextualized as real-world objects. None of the 23 studies gave enough information to conclude that their comparison conditions were equivalent on key non-AR-related factors.

Further, only one study (Bhagat et al., 2021) measured process variables. Process variables measure what the students were actually doing as they engaged with the AR or control condition. Bhagat et al. (2021) looked at eye movements during the AR and non-AR tasks to measure visual attention, finding that learners in the AR condition attended more to complex 3D objects than learners in the control condition, but that this did not result in better achievement. Finally, although many studies related to geometry (18 of the 23), few allowed students to interact dynamically with geometric objects. This is a unique affordance of AR versus physical manipulatives.

1.3 Research purpose and research questions

Although AR-based applications for mathematics education show positive effects in reviews and meta-analyses, well-designed, rigorous studies with strong control conditions are lacking. Further, nearly all of the current studies lack process data to illuminate what is happening as students engage with AR materials. In addition, in mathematics education few studies have looked at AR-based DGS where mathematical figures are dynamically manipulable, despite that this is an important affordance of AR technology. There is some evidence that dimensionality – i.e., whether students are able to interact with 3D objects in three dimensions – is important, but findings question whether this is helpful (Chang et al., 2022). In the present study, we address the following research questions:

  1. 1)

    Is interacting with geometry simulations on tablets more or less effective than interacting with the same simulation using AR HMDs?

  2. 2)

    Is this treatment effect moderated by whether the shape is two-dimensional or three-dimensional?

  3. 3)

    How does process-level data on gestures and actions performed on virtual objects vary across AR HMD and tablet conditions?

  4. 4)

    Are process-level differences moderated by whether the shape is two-dimensional or three-dimensional?

2 Materials and methods

2.1 Participants and procedure

Participants included 120 high school students (71 female, 45 male, 4 chose not to identify) who were either enrolled in outreach programs at a local university or were students at a local urban high school. Participants had parental consent, gave their assent, and were given $25 gift cards for their participation. All students enrolled in the outreach programs were recruited to participate through contacting their parents with parental consent forms during in-person orientation events or via email. In addition, all students who were in the high school Geometry classrooms of the two participating teachers were recruited to participate by handing out parental consent forms during their math class. Students who participated in the study were selected arbitrarily from the students who were present on data collection days and who had parental consent, until our pre-registered sample size of 120 was reached.

The average age was 15.1 years (SD = 1.1 years). The majority of students in the outreach programs qualified for their programs because of socioeconomic need, and the high school had approximately 45% students qualifying for free/reduced lunch. Participants were racially and ethnically diverse, with 43 students identifying as Black, 42 as Hispanic, 29 as White, 11 as Asian, 1 as Native American, and 4 as Other/Missing (participants could select multiple categories). Twenty-eight percent of students reported speaking a language other than English at home. Sessions took approximately 1–1.25 h, with students doing the AR/tablet activities for 30–45 min of this time.

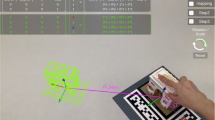
Participants were placed into pairs, with the only criteria for pairs being whether the other student in the pair had class or outreach programs at the same time as the first student. Then pairs were assigned to either the tablet condition or the AR HMD condition (order of pair assignment to conditions was alternated). Students in both conditions would first do a short tutorial (matched across conditions) where they learned to control the geometry simulations, which were designed in the GeoGebra 3D software (Hohenwarter & Fuchs, 2004; all simulations can be viewed at https://sites.google.com/view/flatlandxr/access-sims). Then, one of the simulations in Table 1 was opened, and pairs would have 60 s to play with the simulation before seeing the accompanying geometric conjecture. Each GeoGebra simulation was identical across conditions; the only difference is whether it was displayed on an iPad and manipulated through touch of the fingers on the flat screen or displayed through an AR HMD in 3D space near the student and manipulated with hand grasping motions detected via hand-tracking (i.e., without controllers). In the AR HMD condition, both students wore their own Microsoft HoloLens2 AR HMDs, but the simulation was “synched” such that they both saw the same geometry hologram in the same physical location and could see when their partner modified the simulation. The simulation did not use markers, offering control of where to place and move content. Due to these features (marker-less, dynamic, collaborative, locationally synched, controlled via hand-tracking), ours is the most technically advanced implementation of AR for mathematics education that we are aware of in the research literature. In the tablet condition, the two students worked on a single iPad (Fig. 1). After 60 s, in both conditions, the accompanying geometry conjecture was projected onto a screen in front of the pair, and students were asked to determine whether the conjecture was true or false and to give a reason why. Students would cycle through 6 of the 8 conjectures in Table 1 this way, with conjectures ordered via a Latin Square. Students would take a paper-based post-test and a Qualtrics survey individually at the end of the session.

Table 1 Eight simulations and accompanying conjectures given to students
Full size table
Fig. 1
figure 1

Tablet condition (left) versus AR HMD condition (right)

Full size image

This study was pre-registered on the Open Science Framework website (https://osf.io/6tgwd). The sample size was determined by an apriori power analysis, using a simulation approach. To generate the data for the power simulations, we used the parameter estimates of the logistic multilevel models estimated from past empirical data. The standardized minimum detectable effect sizes in terms of the logistic data-generating model (Chinn, 2000) were chosen to be a total effect of d = 0.6, based on prior meta-analyses. We had three pre-registered hypotheses, of which we explore two in this paper (the third, related to student talk moves, is beyond our scope). Our first pre-registered hypothesis focuses on student performance outcomes: We hypothesize that AR HMDs will be significantly more effective than tablets, but only for the 3D shapes. They will be comparable for 2D shapes. Our second pre-registered hypothesis focuses on process-level data: We hypothesize that students will perform more actions on the objects and gestures relating to the objects in AR when the shapes are three-dimensional, compared to when working with the shapes on the tablet. Actions and gestures will be comparable for 2D shapes across tablet and AR HMD.

2.2 Measures

We look at outcomes while students are solving geometry conjectures at two time points: (1) while students were collaboratively justifying the conjectures within the AR HMD or tablet simulation, and (2) while students were individually justifying the conjectures on a pencil-and-paper post-test, after the experience is over. Our pre-registration stated we would look at three outcomes to define “effectiveness”: (1) whether students were correct in deciding whether each conjecture was true or false (called “intuition”), (2) whether students were able to articulate relevant and valid mathematical ideas related to why the conjecture was true or false (called “insight”), and (3) whether students’ insights had elements of generalization – of applying across multiple different cases (called “proof” in the pre-registration, but “generalization” here). See Appendix 1 Table 5 for criteria for these outcomes across our 8 conjectures. Inter-rater reliability was obtained on a randomly-selected 10% subset (37 of the 370 instances of students justifying a conjecture collaboratively during the learning activity were double-coded; Cohen’s kappas were: Insight: 0.73 and Generalization: 0.80; 73 of the 726 instances of students justifying a conjecture individually on the post-test were double-coded; Cohen’s kappas were: Insight: 0.74 and Generalization: 0.75). Gestures (pointing gestures and dynamic gestures) and epistemic actions (manipulation of the figure using the hands or fingers) were coded using the criteria in Appendix 2 Table 6, and a randomly-selected 10% subset of the videos were double-coded (Cohen’s kappas were: Pointing Gestures: 0.75; Dynamic Gestures: 0.72; Manipulation/Epistemic action: 0.94).

We also had three covariates that we used as controls, as stated in our pre-registration; these were given via Qualtrics at the end of the session so that students would not be fatigued when doing the AR/tablet activities. We used a condensed version of the Spatial Reasoning Instrument (SRI; α = 0.74; Ramful et al., 2017) to measure spatial ability in terms of three subscales: mental rotation (5 items), spatial visualization (5 items, e.g., mental folding), and spatial orientation (5 items, e.g., navigation and point of view). We used a condensed version of the Diagnostic Geometry Assessment (DGA; α = 0.77; Masters, 2010) to provide a covariate for students’ geometry knowledge. The test has 11 items across three sections – shapes, transformations, and measurement. We also used the Linnenbrink-Garcia et al. (2010) mathematics individual interest scale, which includes 8 interest items rated on a 1–5 Likert scale (α = 0. 92). There were two students in the sample who had complete SRI but partial DGA data, and who were missing interest data and some other demographic data.

2.3 Methods of analysis

Datasets are openly available on https://osf.io/b5cj2/files/osfstorage. Data were modelled using mixed effects logistic regression models (Snijders & Bosker, 1999), where repeated observations of conjectures were nested within students or pairs. Logistic regression is typically used in educational research specifically in the form of item response theory models (Wu & Zombo, 2007), where repeated observations of students answering items as correct or incorrect are nested within students. Here random intercepts for students provide an estimate of student ability, while random intercepts for items provide an estimate of item difficulty. These models have been increasingly applied to other kinds of item-level analysis in mathematics education specifically, where interventions or important comparisons occur within-subjects (Walkington et al., 2022), and when student variables like gesture (Nathan et al., 2021) or language usage (Pier et al., 2019), or item features like readability (Walkington et al., 2018) are most sensibly coded at the student-item level.

Data were analyzed using the lme4 package (Bates et al., 2015) in R (R Core Team, 2022). Random effects were used for student or pair ID and conjecture ID. We first ran the models for the first time point which was when students were engaged in the activity in pairs. The outcome variables of intuition, insight, and generalization were coded at the level of the pair (i.e., both students in the pair got the same code for their collective reasoning), since separating one student’s reasoning from their partner’s reasoning when giving their answer was usually impossible. Gestures and actions originally coded at the student level were transformed for the pair level. Gesture/action variables were 0 if neither student in the pair made the gesture or action, and 1 if either student in the pair made the gesture or action. As analyses were run at the pair level and we would expect to have 60 pairs × 6 conjectures = 360 data points. We had 354 data points, as 2 pairs solved fewer than 6 conjectures due to time limitations and technical issues.

We then ran the models for the second time point when students individually took the post-test. We would expect to have 120 students × 6 conjectures = 720 data points for this analysis, but we had 704 data points, due to the issues described above (which lost 12 data points due to technical/time issues), plus 4 additional instances where a student left a post-test question blank because they ran out of time. For this analysis, we were able to use the gesture and action data that was at the student level (1 = student performed gesture or action for that conjecture; 0 = student did not), as the other outcomes (Intuition, Insight, Generalization) were also at the student level (e.g., 1 = student correct on post-test, 0 = student incorrect on post-test).

Predictors in the models included whether the conjecture was 2D or 3D, whether the pair was assigned to tablet or AR HMD condition, and the interaction of these two variables. Controls included the students’ gender, whether they had taken high school geometry, language spoken at home, geometry interest, DGA score, SRI score, and age; only controls that significantly improved model fit were retained. The three outcomes (Intuition, Insight, Generalization) were modelled as 0/1 variables, as were the three gesture/action categories (Pointing Gesture, Dynamic Gesture, Epistemic Action/Manipulation) thus necessitating the logistic models. d-type effect sizes were calculated from logistic regression coefficients using the method from Chinn (2000).

In our results, we give the raw unstandardized coefficient from the logistic regression model (“B”), which does not have a direct interpretation. We also provide this coefficient converted into an Odds Ratio (this is done by exponentiating the raw B coefficient; “OR”), which gives the ratio of the probability of a favorable outcome to the probability of a non-favorable outcome; this value being greater than 1 implies the favorable outcome is more likely. We additionally provide the d-type (standardized mean difference) effect size (“d”) which is obtained by dividing the raw B coefficient by 1.81 (Chinn, 2000).

3 Results

Descriptive statistics for the quantitative variables are shown in Table 2. The descriptive statistics for the three different outcome variables, two different conditions, and two different dimensionalities are shown in Appendix 3, as are descriptive statistics for individual conjectures (Tables 7, 8, and 9). In Table 2, intuition is consistently the easiest outcome to achieve (around 75% correct), followed by insight (55–65% correct), and generalization (30–40% correct). We further investigated these trends in the regression models (Tables 3 and 4). In the student-level data (Table 4), we note that DGA and SRI scores are predictive of some of the outcome variables, with positive associations; none of the other demographic variables we tested (including gender) were ever significant.

Table 2 Descriptive statistics
Full size table
Table 3 Logistic mixed effects regression results: During activity (pair-level data)
Full size table
Table 4 Logistic mixed effects regression results: Post-test (student-level data)
Full size table

3.1 Predicting intuition

For pair-level data, Model 1 (Table 3) shows that when predicting intuition, there is a significant interaction between condition (tablet vs. AR) and dimension (2D vs. 3D; χ2(1) = 4.33, p = 0.0374). Looking at the pair-level model for intuition (Model 1 in Table 3), we see that AR HMDs are significantly less effective for the reference dimension category (2D shapes), compared to tablet (B = -0.84, OR = 0.43, d = 0.46, p = 0.0302). We also see that for the reference condition category (tablet), 3D shapes are more difficult than 2D shapes (B = -1.17, OR = 0.31, d = -0.65, p < 0.001). However, for AR, the negative effect for 3D shapes is reduced and is no longer significantly different from zero (B = -1.17 + 0.79 = -0.38, OR = 1.46, d = -0.21, p = 0.2814).

The student-level data, Model 7 (Table 4), shows the intuition outcome has a similar result. There is again a significant interaction between condition (tablet vs. AR) and dimension (2D vs. 3D; χ2(1) = 4.91, p = 0.02678). Looking at the values in the table, we see that for the reference category (tablet), 3D shapes are more difficult than 2D shapes (B = -1.02, OR = 0.36, d = -0.56, p = 0.0066). However, for AR, this negative effect for 3D shapes is completely cancelled and is no longer significantly different from zero (B = -1.02 + 1.10 = 0.0097, OR = 1.01, d = 0.005, p = 0.8078). Thus, it appears that AR is most beneficial for supporting participants’ 3D intuitions.

3.2 Predicting insight and generalization

The pair-level and student-level models for insight (Models 2 and 8, Tables 3 and 4) and generalization (Models 3 and 9, Tables 3 and 4) all show that 3D conjectures are more difficult for students to solve than 2D conjectures (pair-level insight: B = -1.04, OR = 0.35, d = -0.58, p < 0.001; pair-level generalization: B = -1.39, OR = 0.25, d = -0.77, p < 0.001; student-level insight: B = -0.66, OR = 0.52, d = -0.36, p < 0.001; student-level generalization: B = -0.97, OR = 0.38, d = -0.54, p < 0.001). However, in none of these models was the interaction between condition and dimension significant (pair-level insight: χ2(1) = 2.82, p = 0.09285; pair-level generalization: χ2(1) = 0.00, p = 0.9792; student-level insight: χ2(1) = 1.05, p = 0.3053; student-level generalization: χ2(1) = 0.270, p = 0.6034).

We also do not see main effects for condition (tablet versus AR) reach significance in any of these models. However, it is notable that in the pair-level data, in the model predicting generalization (Model 3, Table 3), the main effect for AR (compared to tablet) is B = -0.73, OR = 0.48, d = -0.41, and p = 0.0518. Overall, although we do not see statistically significant results suggesting AR is worse than tablet for predicting insight and generalization, we note that the consistency of the directionally negative effects for AR should warrant further scrutiny.

3.3 Predicting gestures and actions

With respect to pointing gestures, we found in both the pair-level data (Model 4 in Table 3) and the student-level data (Model 10 in Table 4) that students were less likely to use pointing gestures when confronted with 3D shapes (pair-level: B = -0.89, OR = 0.41, d = -0.49, p = 0.0398; student-level: B = -0.88, OR = 0.41, d = -0.48, p = 0.0014), compared to 2D shapes. As can be seen from the tables, condition was not a significant predictor of pointing gestures in either model. The interaction of condition and dimension was also not significant in either model (pair-level: χ2(1) = 2.06, p = 0.1508; student-level: χ2(1) = 1.63, p = 0.2018).

With respect to dynamic gestures, we found that in both the pair-level data (Model 5 in Table 3) and the student-level data (Model 11 in Table 4) that students were more likely to use dynamic gestures when using AR (pair level: B = 0.91, OR = 2.48, d = 0.50; p = 0.0028; student-level: B = 0.70, OR = 2.01, d = 0.39, p = 0.012), compared to tablet. As can be seen from the tables, dimension was not significant in either model. The interaction between dimension and condition was also not significant in either model (pair-level: χ2(1) = 0.46, p = 0.4891; student-level: χ2(1) = 0.68, p = 0.4097).

With respect to actions manipulating the shapes, we found that in both the pair-level data (Model 6 in Table 3) and the student-level data (Model 12 in Table 4) that students were less likely to manipulate the shape when using AR (pair level: B = -2.28, OR = 0.10, d = -1.26, p < 0.001; student-level: B = -1.63, OR = 0.20, d = -0.90, p < 0.001), compared to tablet. As can be seen from the tables, dimension was not significant in either model. The interaction between dimension and condition was not significant in either model (pair-level: χ2(1) = 1.26, p = 0.2613; student-level: χ2(1) = 2.92, p = 0.0875).

3.4 Supplementary analyses

Although our pre-registration did not directly address hypotheses related to a mediation model, where condition (tablet versus AR) led to particular gestures/actions, which in turn enhanced particular outcomes, we did some exploratory analyses. Although we had found effects of condition on intuition (depending on dimension), neither of our gesture variables, nor our manipulation/epistemic actions variable, was significantly predictive of intuition. This held both in models that included and did not include condition.

Adding dynamic gestures to the student-level models for insight and generalization, both with and without condition, also did not yield significant effects. However, in the pair-level models, dynamic gestures had a significantly positive association with generalization, both when controlling for condition (B = 1.30, OR = 3.67, d = 0.64, p = 0.0121) and when not controlling for condition (B = 1.14, OR = 3.13, d = 0.63, p = 0.0259).

We also consistently found significant positive associations between manipulation/epistemic action and both insight and generalization in pair-level models, and generalization and insight in student-level models (pair-level insight: B = 0.83, OR = 2.29, d = 0.46, p = 0.0108; pair-level generalization: B = 1.89, OR = 6.62, d = 1.04, p < 0.001; student-level insight: B = 0.41, OR = 1.51, d = 0.23, p = 0.0370; student-level generalization: B = 0.74, OR = 2.10, d = 0.41, p < 0.001). These results held even when condition was included as a predictor (pair-level insight: B = 0.78, OR = 2.18, d = 0.43, p = 0.0209; pair-level generalization: B = 1.81, OR = 6.11, d = 1.00, p < 0.001; student-level insight: B = 0.43, OR = 1.54, d = 0.24, p = 0.0358; student-level generalization: B = 0.72, OR = 2.05, d = 0.40, p = 0.0012). Thus, epistemic actions performed to manipulate geometric objects were associated with valid forms of reasoning and were also more likely to happen with AR HMDs compared to tablets. However, we note that we did not find that condition (AR HMD vs. tablet) significantly predicted insight or generalization outcomes, so moving forwards with mediation would not be appropriate.

4 Discussion

4.1 Interpretation of results

Many past studies have found positive effects for using AR, compared to traditional forms of instruction. In the present study, we compared dynamically interacting with identical geometry simulations on a tablet versus using AR HMDs, examining differences when reasoning about 2D and 3D figures. We looked across three different outcomes – intuition, insight, and generalization – and overall found little evidence that AR simulations were more effective than tablet simulations.

4.1.1 Intuition

Intuition – students’ initial sense of whether mathematical statements were true or false – was the outcome with the most promising results for AR. Our first pre-registered hypothesis stated: We hypothesize that AR HMDs will be significantly more effective than tablets, but only for the 3D shapes. They will be comparable for 2D shapes. This hypothesis was partially validated. For 3D shapes, we found evidence that AR might be preferable – that the increased difficulty of processing 3D shapes might be ameliorated when using AR compared to tablets. This is in contrast to Chang et al. (2022), who found lower effect sizes when AR integrated 3D visualization. However, we also found that for intuition, students perform worse in AR than on tablet for 2D shapes. Although some prior studies obtained null effects (Alves et al., 2017; Conley et al., 2020; Rebollo et al., 2022), we are not aware of any showing significantly negative effects for AR.

From this, we conclude that AR might be especially effective in getting an initial sense of the properties of 3D shapes This is consistent with past research that has used AR to help students learn about basic geometrical elements of 3D shapes (Andrea et al., 2019; Arvanitaki & Zaranis, 2020; Demitriadou et al., 2020; Gecu-Parmaksiz & Delialioglu, 2019). This also supports theories suggesting that being able to interact with shapes in three dimensions is an important affordance of XR (Dimmel & Bock, 2019; Jacobson, 2011; Johnson-Glenberg, 2018; Wu et al., 2013). There is less to be enthusiastic about when it comes to AR for reasoning about 2D shapes, based on our results. Two-dimensional objects do not activate the unique affordances that AR has – in fact, placing a 2D shape in three dimensions might increase confusion. For example, when looked upon from certain angles in AR, 2D shapes can appear skewed or as a line (Bock & Dimmel, 2021).

4.1.2 Insight and generalization

While our first hypothesis was partially validated for the intuition outcome, it was not validated for the insight and generalization outcomes. There were no significant interactions between dimension and condition for these outcomes. We also see no main effect for condition in any of the models, although in one of the generalization models, there was a non-significant negative effect size of d = -0.4 for AR compared to tablet. Overall, we do not see any evidence that AR can support more advanced forms of mathematical reasoning than those supported by traditional tablet DGS (Hollebrands, 2007). This novel finding likely arises, in part, because past controlled experiments rarely compare AR to other comparable forms.

We see further reasons to be cautious that AR might be detrimental compared to tablet, particularly with respect to justification practices (Bieda & Staples, 2020; Staples et al., 2017) involving generalization. This is not consistent with prior research suggesting the effectiveness of AR (Ahmad and Junaini, 2020; Jabar et al., 2022; Korkmaz & Morali, 2022; Pahmi et al., 2023; Palancı and Turan, 2021), and prior meta-analyses (Chang et al., 2022; Garzón & Acevedo, 2019; Garzón et al., 2019; Zhang et al., 2022). However, our focus on insight and generalization relating to geometric conjectures may be cognitively distinct from prior studies, which focused on tasks like calculating volume or slicing 3D shapes.

4.1.3 Gestures and actions

Our second pre-registered hypothesis was: We hypothesize that students will perform more actions on the objects and gestures relating to the objects in AR HMD when the shapes are three-dimensional, compared to when working with the shapes on the tablet. Actions and gestures will be comparable for 2D shapes across tablet and AR HMD. This hypothesis was not validated – we did not see a significant interaction between dimension and condition in any of our models where gesture/action was the outcome.

However, we found evidence that when using AR HMDs (compared to tablets), students use more dynamic gestures (hand movements that show the transformation of a mathematical object through multiple states; Nathan et al., 2021) and fewer manipulations of virtual objects (using your hands to resize, change the shape of, or move a virtual object; authors, date). In other words, in the AR environment, rather than actually dynamically transforming the shape and observing the result, students would make hand gestures showing how they imagined the object would react when transformed. And while dynamic gestures have been shown in many prior studies (Nathan et al., 2021; Pier et al., 2019; Walkington et al., 2022), and in this study, to have strong associations with generalization practices in mathematics, one could imagine that actually manipulating the object to enact the simulation (rather than imagining it) might in some cases be less error-prone and more precise.

We also found that epistemic actions students performed to manipulate mathematical objects were associated with higher levels of insight and generalization. Although research has in general suggested the effectiveness of DGS where shapes can be dynamically manipulated by learners (Chan & Leung, 2014; Juandi et al., 2021), here we extend this work by showing how this manipulability is associated with learning in an AR context, where students are exploring mathematical conjectures. This also extends theories of embodied cognition. We replicated previous results (from studies where students did not have access to virtual objects) about the importance of dynamic gestures to mathematical generalization. We now also show how epistemic actions are an important mechanism of embodied reasoning when virtual objects are present. Our data showing differences in actions between tablet and AR is consistent with the epistemic action hypothesis (Kirsh & Maglio, 1994)—that people perform some actions that are not functionally necessary in order to benefit their cognitive processes.

4.2 Limitations

We report some limitations of our study. First, the duration of our activities was short (30–45 min), as using the AR HMDs for longer than this becomes extremely taxing on the person and on the technology. We might see greater effects from a longer AR intervention; however, a recent meta-analysis suggests that as duration increases by 1 h, the effect size (g) increases by only 0.03 (Chang et al., 2022). The second issue is that with such a short intervention, both the positive effects related to the novelty of AR (e.g., Huang, 2020), as well as negative effects related to initial difficulty using the AR interface (e.g., Radu, 2014), may mask effects that would otherwise be observed. The technical challenges of implementing a collaborative, dynamic, wireless, hands-free, head-mounted AR system were large, and this technology may not yet be ready for studies of extended duration. But as technology advances, these kinds of studies will be important.

4.3 Significance

We next highlight what makes this study significant for the field of technology in education, as we found substantially different results from the majority of prior studies. First, our control group was especially strong compared to prior studies, as it isolated the primary characteristic that makes AR unique – projecting holograms into 3D space and manipulating these holograms with 3D hand motions – while holding other technology affordances constant. The affordances that were held constant included a movement-based digital interface, the dynamicity of the objects, updated numerical measurements of objects, the exact look of the objects and the instructions and feedback given to students, and the problem tasks themselves. Our study was also one of few with a pre-registered design and hypotheses, as well as an apriori power analysis used to strictly determine sample size. And, according to our review of experimental studies, this study had a larger sample size than all except two prior studies in this area (Chen, 2019; Conley et al., 2020), and we note that one of these two studies (Conley et al., 2020) found null effects for AR. We also had student-level (rather than class-level) assignment to condition, and we looked at both collaborative (students in pairs) and individual learning outcomes. Our sample was racially, ethnically, and linguistically diverse. We also were one of the very few studies in this area to examine process data (see also Bhagat et al., 2021) – looking at gesture and actions as students engaged with the AR and with tablets.

4.4 Implications

We offer several implications from this work. First, coming out of this study, we have the sense that collaborative, dynamic, markerless forms of AR using HMDs may not yet be ready to improve mathematics learning writ large. This might be particularly true for more complex kinds of reasoning involved in secondary-level mathematical generalization. There might, however, be important opportunities to use these technologies for introductory lessons on 3D concepts. Second, we recommend that future studies and AR designs should consider the dimensionality of the objects that are represented in AR. Many designers and researchers seem to operate from an intuition that 3D objects are the most fertile ground for developing AR applications, but this is the first study we know of that has explicitly tested the role of dimensionality. And third, having access to process data can help us improve AR’s capabilities and give us insights into design. For example, in the present study, an important question is why were students in the experimental condition less likely to directly manipulate the shapes? Would manipulating the shapes more have led to greater performance? Correlations suggest this is the case, but causal designs and models exploring these kinds of questions will be essential. Indeed, students may have manipulated the objects more in the tablet condition because it is easier to swipe your finger a few inches on a small screen, compared to using your arm and hand to successfully grab and drag a control point in 3D space. These kinds of usability differences between modalities should be critically considered by AR designers.

4.5 Conclusion

We encourage future researchers and designers to move beyond the question “Is AR better?” to consider more nuanced questions, such as “For what instructional content, when targeting what instructional outcomes, should AR be leveraged?” The vision of all instructional materials eventually being AR-based seems unlikely or at least quite far in the future, so for now we should consider the most high-leverage, high-reward areas for AR development. Using AR to model and interact with phenomena that have inherently 3D properties and relationships, to gain initial intuitions about how systems act (which can later be built upon outside of AR), is a promising area for development. Yet our findings indicate that it ultimately depends on the forms of interactions that students have with the objects and the concepts they are interacting with for determining the depth and validity of their mathematical reasoning. Designs that do not critically consider the circumstances under which AR is being used may risk having significantly negative effects on learning, compared to a strong alternative form of instruction.