1 Introduction

In the past two decades, the remarkable growth of digital technology has transformed the landscape of mathematics education (Hoyles, 2018), with widespread adoption of computers, the Internet, mobile devices, and Artificial Intelligence (AI) revolutionizing everyday pedagogical practices (Selwyn, 2021). Mathematics educators are thus confronted with the imperative to harness the potential of such advancement as a powerful tool for enhancing their teaching (Blannin, 2022). For instance, the emergence of mathematics software affords educators to visualise intricate mathematical ideas (Martinovic & Karadag, 2012), and online platforms have enabled real-time communication and interactive teaching, as shown during the COVID-19 pandemic online education (Li, 2022; Mella-Norambuena et al., 2021; Mukuka et al., 2021). Schools have started implementing sophisticated tools such as interactive whiteboards (Shi et al., 2021), electronic classrooms, and digital textbooks to augment effectiveness and engagement in mathematics education (Rezat, 2021). These developments have been particularly significant in the post-pandemic era, when global prominence has been given to incorporating digital technology into classrooms, with AI playing an increasingly integral role in personalized learning approaches that provide immediate feedback and enhance overall mathematics education experiences (Huang et al., 2023; Moore et al., 2023).

In the Chinese educational context, while the crucial role of digital technology in enhancing the effectiveness of student learning and teacher instruction is underscored by China’s Mathematics Curriculum Standards for Compulsory Education (2011 version) (Gao, 2021), and significant investments have been made to foster digital advancements in education (Wang et al., 2017), research into how educators are harnessing these digital technologies in alignment with TPACK components, particularly XK, is sparse. For instance, while interactive whiteboards and educational software are increasingly commonplace in Chinese classrooms, there is limited empirical evidence on how mathematics teachers’ understanding of XK affects the use of these digital technologies to enhance the teaching of complex mathematical concepts. This gap is particularly evident when considering the diverse educational backgrounds of teachers and the varying levels of technology implementation across urban and rural schools (Zhao, 2024). Hence, a nuanced understanding of how XK influences the deployment of digital tools within the classroom settings remains a considerable gap, especially against the backdrop of China’s unique educational settings. In recent years, the integration of AI into educational practice adds a layer of complexity that has not been thoroughly dissected in the context of TPACK’s application in China. This evolving landscape necessitates a re-evaluation of the professional development needs of educators (Mishra et al., 2023; Selwyn, 2021), particularly as they are tasked with the integration of cutting-edge technologies in pedagogically sound ways. Nevertheless, how this integration occurs within the framework of TPACK, and its influence on the effectiveness of technology integration in mathematics education, still requires deeper investigation, particularly considering China’s distinctive cultural and educational parameters.

This study aims to provide an in-depth examination of technology integration and the influence of contextual factors in this process. By adopting the theory of TPACK (Mishra & Koehler, 2006; Mishra et al., 2023), we seek to illuminate the intricacies of how secondary mathematics teachers incorporate digital technology. Specifically, the study explores how fundamental knowledge, particularly contextual knowledge, incrementally shapes and influences teachers’ integration efforts. Through this lens, this study offers insights and a nuanced understanding of the challenges and opportunities that context presents in the effective use of technology in secondary mathematics education. Based on the discussion, two research questions are formulated.

  1. 1.

    What are the interrelationships among the components within the TPACK framework?

  2. 2.

    How do they collectively contribute to the development of effective technology integration in mathematics education?

By examining these research questions, the study makes meaningful strides in elucidating the intricate interplay between XK and other pivotal components of TPACK including Content Knowledge (CK), PK, Technology Knowledge (TK), PCK, TPK, TCK, and TPACK. The study presents a fresh viewpoint on how a deep understanding of context can guide the effective incorporation of technology in mathematics education, thereby enhancing the understanding of TPACK’s multifaceted nature. The research underscores the importance of further exploring these interrelationships in a more comprehensive manner. Ultimately, such explorations can greatly benefit educators and students in the continually evolving realm of mathematics education by fostering a more comprehensive grasp of the key components in the TPACK framework. In the following sections, the study discusses existing research on the TPACK model, presents the assumptions and methodologies of our study, and then delves into the findings and engages in a thoughtful discussion.

2 Literature review

2.1 TPACK model

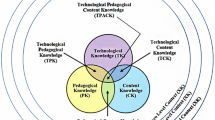
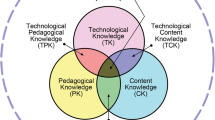
The TPACK model, developed from the Pedagogical Content Knowledge theory (Shulman, 1986), has gained widespread recognition as a fundamental framework for understanding and examining teachers’ knowledge for effectively integrating digital technology into teaching and learning (Abubakir & Alshaboul, 2023; Mishra & Koehler, 2006; Voogt et al., 2013; Willermark, 2018). It delineates seven essential knowledge (see Fig. 1) that teachers should possess to seamlessly incorporate digital technology into their instructional practices while providing insights into how teachers can acquire this knowledge (Harris & Hofer, 2011; Koh et al., 2010; Voogt et al., 2013). Table 1 describes seven essential knowledge and competencies required (Koehler & Mishra, 2009; Mishra & Koehler, 2006). Three fundamental knowledge domains, CK, PK, and TK and their synthesised constituents, interweave to capture the complexities of integrating technology into teaching.

Fig. 1
figure 1

Self-created diagram based on the TPACK theory

Full size image
Table 1 The components of the TPACK framework (Koehler & Mishra, 2009; Mishra & Koehler, 2006)
Full size table

2.2 Interconnected of TPACK components

The synergy and interconnectedness of its components within the TPACK framework are crucial for understanding how teachers effectively integrate technology into mathematics education (Archambault & Barnett, 2010; Schmid et al., 2020). This framework suggests that successful technology integration is not solely dependent on individual knowledge domains but arises from their interplay, and comprehending the interactions and mutual influences among these components enables educators to make well-informed decisions regarding the integration of technology into their teaching practices (Angeli & Valanides, 2009; Mishra & Koehler, 2006). Additionally, it also equips educators with a roadmap to bridge the digital technology proficiency gap, leverage available resources efficiently, and unlock the full potential of digital technology in subject teaching, such as in mathematics education (Bueno & Niess, 2023). This profound understanding empowers them to create immersive and efficacious learning experiences for students, fostering the acquisition of mathematical knowledge and cultivating digital literacy (Bueno & Niess, 2023).

Investigations into the interplay of these components in mathematics education have revealed intriguing dynamics. In Angeli and Valanides’s (2009) study exploring the interconnectedness of the seven components of TPACK, it was found that effective technology integration relies on the seamless interplay among these knowledge domains rather than their isolated existence. Yang et al. (2021) combined the TPACK and Technology Accepted Model to find how teachers’ TPACK impacted their acceptance of e-Schoolbag. They argued that found that while TK, PK, and CK did not directly predict TPACK, they mediated TPACK through TCK and TPK. Moreover, empirical studies have demonstrated a significant impact of TCK experiences on TPACK, underscoring the crucial role of teachers’ technological expertise in shaping their instructional practices (Dong et al., 2015; Pamuk et al., 2013). It can be noticed that previous research has notably emphasized the interdependencies among various components of the TPACK framework (Chai et al., 2013; Koh et al., 2013; Pamuk et al., 2013). These studies have examined the relationships among TK, PK, and CK and their collective influence on teachers’ TPACK. While these investigations have enriched the understanding of the complex interplay within the TPACK framework, a notable research gap persists in considering the contextual aspect of knowledge.

2.3 A missing XK

With the deepening of research on the TPACK framework, researchers have emphasized the crucial role of XK in technological integration, which was previously overlooked in the original TPACK framework (Li et al., 2023; Mishra, 2019; Porras-Hernández & Salinas-Amescua, 2013; Rosenberg & Koehler, 2015). XK encompasses an understanding of the factors that influence the integration of digital technology in teaching and learning environments; this understanding encompasses school, district, state, or national policies and perspectives on technology integration (Mishra, 2019). Consequently, Porras-Hernández and Salinas-Amescua (2013) proposed an expanded model incorporating XK, delineating three distinct contextual levels: micro, meso, and macro.

  • Micro-level context refers to factors directly related to classroom teaching and learning, encompassing elements like teachers’ familiarity with classroom norms and the presence of digital devices.

  • Meso-level context comprises factors associated with school and community support, including the school’s culture, administrative backing, the availability of educational infrastructure, and engagement with the wider community.

  • Macro-level context encompasses broader contextual elements, including national and international policies, cultural influences, economic factors, educational backgrounds, national curriculum standards and overarching education policies.

By redefining XK within these levels, the model provided a more context-sensitive perspective on the factors impacting technology integration in education while contributing to ongoing development and refinement of the TPACK framework (Mishra, 2019; Porras-Hernández & Salinas-Amescua, 2013). Accordingly, following Porras-Hernández and Salinas-Amescua (2013), Mishra expanded the existing TPACK framework to include XK as the eighth factor in 2019 to provide a more comprehensive elucidation of teachers’ knowledge for effectively integrating digital technology into teaching and learning (Mishra, 2019), as shown in Fig. 1.

2.4 Interplay between TPACK and XK

While extensive studies (Schmid et al., 2020; Susanti et al., 2022; Yang et al., 2021) have investigated the interplay among the core components of the TPACK framework, there remains a notable gap in understanding the role of XK within this context. Previous studies, predominantly conducted in Western contexts, have made significant contributions by elucidating the complex relationships between PK, CK, and TK within TPACK (Ozudogru & Ozudogru, 2019; Schmid et al., 2020). However, XK has received considerably less attention in TPACK literature (Li et al., 2024; Mishra, 2019). The limited exploration of the intricate interplay between XK and the core components of TPACK across diverse cultural contexts underscores a significant research gap. It highlights the need for more comprehensive investigations into the role of XK and its interface with TPACK components to uncover their potential interrelationships, which is one of the study’s aims.

The absence of comprehensive studies investigating the impact of XK within TPACK is a critical research limitation, given its role as an external force influencing technology integration. Understanding how XK interacts with PK, CK, and TK and their intersections is essential to shaping the effectiveness of technology-enhanced mathematics instruction. This knowledge can provide valuable insights for educators, curriculum designers, and policymakers in creating an environment conducive to seamless technology integration while considering the broader educational context (Mishra, 2019; Mishra et al., 2023; Porras-Hernández & Salinas-Amescua, 2013). Therefore, it becomes evident that this research gap significantly amplifies the significance of this investigation, specifically regarding XK. Simultaneously, it underscores the untapped potential and necessity to explore the intricate dynamics of how XK interacts with the core components of TPACK in mathematics education. This understanding holds immense promise for informing teacher preparation programs, curriculum design, and professional development initiatives by fostering a comprehensive perspective on leveraging technology’s potential in effective pedagogy.

In summary, the existing literature on TPACK has demonstrated remarkable progress in elucidating the relationships among its core components. However, the insufficient attention devoted to XK highlights a critical research gap the study aims to address. Gaining a deep understanding of the interplay between XK and the other components within the context of mathematics education is pivotal and imperative for advancing the field, informing pedagogical practices, and facilitating technology integration across diverse educational settings. This research seeks to bridge this gap and contribute to the ongoing discourse on TPACK, XK, and their interplay in mathematics education, aiming to enhance teaching and learning outcomes through effective technology integration.

3 Research model and hypotheses

In order to answer the research questions and fill the gaps in understanding the influences and interactions among TPACK components, this study hypothesised a network of sixteen specific relationships using SEM. These relationships capture the effects of one component on another within the TPACK framework and enable the evaluation of the impacts of various components on one another (see Fig. 2). By paralleling XK as an equally important core constituent alongside CK, PK, and TK, the proposed relationships within these hypotheses encompass the effects of these four primary components on their corresponding higher-level components and the broader influences of these components on the overall TPACK construct. This SEM model design allows researchers to examine the intricate relationships and interdependencies among TPACK components, offering insights into the critical role of XK within the TPACK framework. By examining how these components affect each other, the study aims to enhance the understanding of TPACK and contribute to developing effective strategies for technology integration in mathematics education.

3.1 Research model

Fig. 2
figure 2

The proposed SEM model

Full size image

3.2 Hypotheses

H1. TK has a positive effect on TCK.

H2. TK has a positive effect on TPK.

H3. TK has a positive effect on TPACK.

H4. CK has a positive effect on TCK.

H5. CK has a positive effect on PCK.

H6. CK has a positive effect on TPACK.

H7. PK has a positive effect on PCK.

H8. PK has a positive effect on TPK.

H9. PK has a positive effect on TPACK.

H10. XK has a positive effect on TCK.

H11. XK has a positive effect on PCK.

H12. XK has a positive effect on TPK.

H13. XK has a positive effect on TPACK.

H14. TCK has a positive effect on TPACK.

H15. PCK has a positive effect on TPACK.

H16. TPK has a positive effect on TPACK.

4 Method

4.1 Research design

To thoroughly explore the interrelationships among the components of TPACK in mathematics education, the present study adopted a cross-sectional survey design, which is particularly suited to studies aimed at capturing the current state and interrelations of variables at a specific point in time. This design choice is reinforced by the guidelines posited by Cohen et al. (2018), emphasizing its suitability for observational studies that seek to infer relationships rather than causality. The decision to employ a cross-sectional survey was primarily driven by the study’s analytical needs, specifically the application of SEM. SEM was chosen for its robust capability in examining complex models that involve multiple interdependent variables (Hair et al., 2018). This methodological approach allows for a simultaneous examination of the relationships within the TPACK framework, assessing direct and indirect effects and mediating factors between constructs (Byrne, 2016).

The variables included in the SEM were selected based on the TPACK framework’s theoretical underpinnings and its relevance to the research questions. Each variable corresponds to a component of the TPACK framework: CK, PK, TK, PCK, TCK, TPK, TPACK, and XK. The inclusion of XK, particularly, reflects a unique aspect of the model tailored to the Chinese educational context, where local educational policies, cultural norms, and technological infrastructure influence the integration of technology in teaching. Additionally, the application of SEM in this study mirrors the analytical techniques employed in seminal TPACK research, such as those conducted by Koh et al. (2013) and Pamuk et al. (2013), providing a methodological bridge that connects this study to established scholarly discourse. The use of this advanced statistical technique is intended to yield a comprehensive understanding of the relationships within the TPACK framework, offering insights that are not only theoretically sound but also pragmatically applicable to the challenges and opportunities of technology integration in mathematics education.

4.2 Participants

Within the educational landscape of China, there are five distinct levels of education: early childhood education, primary school education (grades one through six), middle school education (grades seven to nine), high school education (grades ten to twelve), and tertiary education. This research focuses on in-service mathematics teachers within the middle schools of Chongqing, located in the southwest region of China. The participant pool exhibited gender balance, with 31.3% (n = 141) being female mathematics teachers and 68.7% (n = 310) being male mathematics teachers. Additionally, participants were evenly distributed across all three grades: grade seven (35.0%, n = 158), grade eight (32.2%, n = 145), and grade nine (32.8%, n = 148). Apart from gender and grade distribution, this study also collected comprehensive data on the educational backgrounds of the mathematics teachers as presented in Table 2. A significant proportion of participants held bachelor’s degrees (51.0%, n = 230), while only a limited number possessed doctoral degrees (4.0%, n = 18). Notably, there was substantial representation of secondary mathematics teachers from non-mathematics educational backgrounds, accounting for approximately 35.3% (n = 159) of the total participant pool. This comprehensive description of participant demographics provides a thorough understanding of the composition and diversity of the mathematics teacher sample, ensuring the study’s relevance and generalizability to the middle school context in Chongqing, China.

Table 2 Participants demographic information
Full size table

4.3 Instrument

In this study, the research team employed the Secondary Mathematics Teachers’ TPACK Scale (SMTTS), developed by Li et al. (2023), to gather data. The scale was explicitly devised for assessing mathematics teachers’ TPACK and its associated components, rendering it a well-suited instrument for accomplishing the research objectives. The SMTTS instrument consisted of 32 items specifically designed to capture distinct dimensions within the TPACK framework. These dimensions encompass CK, PK, TK, PCK, TCK, TPK, TPACK and XK. To illustrate, two sample items from the SMTTS are presented here: one evaluating XK, ‘I understand the policies and measures to improve mathematics teachers’ ICT capacity in my school’; and another assessing the integrated TPACK, ‘I can design inquiry activities to guide students to make sense of mathematics content knowledge with appropriate technology tools (e.g., facilitating students’ use of an iPad to learn the surface area of a cuboid during group discussions)’. The complete SMTTS instrument is detailed in the work of Li et al. (2023).

To create a Chinese version of the questionnaires, a careful translation process was implemented, adhering to the guidelines suggested by Cohen et al. (2018). Initially, a bilingual panel, consisting of a mathematics teacher from China and a colleague based in Australia, was formed to ensure a faithful translation. Both individuals, proficient in Mandarin and English, engaged in collaborative translation sessions via Zoom to guarantee that the language nuances and educational terminologies were preserved accurately. Subsequently, the preliminary Chinese translation of the questionnaire was subjected to a pilot test with a group of 65 mathematics teachers, representative of the target population for the study. The feedback obtained from these educators was systematically analysed, facilitating iterative modifications to the questionnaire (Bryman, 2016). This process was instrumental in not only confirming the reliability of the translated instrument but also in fine-tuning its content to ensure cultural relevance and clarity in the context of Chinese mathematics education. The careful attention to translation detail and subsequent pilot testing were critical in validating the questionnaire’s used in this study. As a result, the translated questionnaire was deemed to exhibit both reliability and validity, providing a robust tool for assessing the TPACK knowledge of secondary mathematics teachers in China.

4.3.1 Reliability and validity of the SMTTS

Several key statistical analyses were conducted to ensure the instrument’s reliability and validity during the formal questionnaire. The suitability of the data for factor analysis was assessed using the Kaiser-Meyer-Olkin (KMO) measure, which yielded a high value of 0.916, and Bartlett’s Test (p < 0.01). The cumulative variance explained accounted for 71.5% of the total variance, indicating that the factors extracted from the analysis collectively explained a substantial portion of the data’s variability. Principal component analysis was employed to extract eight distinct factors within the scale, with factor loading values ranging from 0.754 to 0.892 (see Table 3). These robust and distinctive factors underscored the instrument’s effectiveness in measuring targeted constructs. Additionally, the internal consistency of the items within the SMTTS was evaluated using Cronbach’s alpha test. The results revealed high Cronbach’s alpha coefficients ranging from 0.820 to 0.889 (see Table 3), indicating strong internal consistency among the instrument’s items. This level of consistency aligns with the criteria proposed by Cohen et al. (2018) and further enhances the reliability of the SMTTS. The discriminant validity was rigorously assessed to ensure the accurate measurement of distinct constructs, reduction of methodological bias, and enhancement of construct validity in the instrument. Following the guidelines outlined by Hair et al. (2010), a comprehensive evaluation process was conducted across seven key dimensions: χ2/df = 1.295, Root Mean Square Error of Approximation (RMSEA = 0.026), Goodness of Fit Index (GFI = 0.928), Adjusted Goodness-of-fit Index (AGFI = 0.913), Normed Fit Index (NFI = 0.929), Comparative Fit Index (CFI = 0.983), and Tucker-Lewis Index (TLI = 0.980). This thorough assessment demonstrated the robustness of the scale and its ability to provide precise and distinct measurements essential for achieving the research objectives. By carefully selecting the SMTTS instrument and conducting a rigorous assessment of its reliability and validity, this study ensured that the data collected was high quality and accurately measured the intended TPACK and related constructs. This process is crucial for achieving our research goals and contributing to theoretical advancements.

Table 3 EFA and Cronbach Alpha (Li et al., 2023)
Full size table

4.3.2 Convergent validity

Assessing convergent validity is a crucial step in validating a measurement instrument, as it substantiates its construct validity and reliability. This process enhances the comprehension of the investigated constructs and facilitates meaningful comparisons with existing literature (DeVellis, 2017). Two established formulas (refer to Table 4) were utilized to calculate the Average Variance Extracted (AVE) and Composite Reliability (CR) coefficients (Henseler et al., 2015). As depicted in Table 4, AVE values ranging from 0.580 to 0.659 were observed, all surpassing the common threshold of 0.50. These results provide substantial evidence for excellent convergent validity of the instrument, aligning with Hair et al. (2010). Simultaneously, each construct exhibited CR values spanning from 0.820 to 0.901, exceeding the generally accepted threshold of 0.70. This indicates that the instrument demonstrates commendable internal consistency reliability, as Hair et al. (2010) advocated. These findings affirm that the instrument possesses high reliability and convergent validity while effectively measuring CK, PK, TK, XK, TPK, TCK, PCK, and TPACK within this research study’s scope.

Table 4 Convergent validity (Li et al., 2023)
Full size table

4.4 Recruitment

The survey distribution process was efficiently conducted through Qualtrics, a widely acknowledged survey tool, and WeChat, a popular and convenient platform for surveys among the Chinese population. This method ensured a streamlined and accessible approach to data collection, tailored to the preferences and familiarity of the target audience. The research team collaborated with the Chongqing Teacher Education Training Centre administrator, who facilitated the data collection process. To enhance response rates and encourage participation, the research team designed an engaging poster that effectively conveyed essential study details, including its objectives, participation significance, and involvement instructions. Over a four-week period, participants were invited to fill out the questionnaire using QR codes and links. A remarkable 451 mathematics teachers completed the questionnaire, yielding an impressive response rate of approximately 30.1%.

4.5 Data collection

A random sampling method was employed to ensure a representative sample of secondary mathematics teachers, aligning with established practices in educational research (Punch & Oancea, 2014). The data were collected using a web-based questionnaire that utilized a 5-point Likert scale to measure responses, facilitating the standardized assessment of perceptions regarding the integration of technology in mathematics education (Fowler Jr, 2013). Throughout the study, stringent measures were implemented to safeguard participant anonymity and autonomy, as emphasized in Bryman’s ethical research guidelines (Bryman, 2016). An informed consent form, coupled with an explanatory statement, was integrated into the web-based questionnaire, facilitating a transparent process where participants could willingly decide their involvement without any external pressure. To further protect participant privacy, all data collected were anonymized by using Qualtrics before analysis, ensuring that individual responses could not be traced back to specific educators. This measure not only respected participants’ confidentiality but also aligned with the ethical standards prescribed by the Institutional Review Board. Additionally, the anonymized data were securely stored on a personal Google Drive, accessible only to the research team. Data will be retained for a period of five years after the completion of the study, after which it will be permanently deleted to ensure further privacy protection. The survey was made available for one month, providing ample time for participants to respond at their convenience, which contributed to a reasonable response rate and a diverse data set. These methodological decisions underscored our commitment to ethical research practices, prioritizing participant rights and data integrity, and adhering to established ethical standards in educational research (Cohen et al., 2018).

4.6 Data analysis

The data analysis in this study was conducted using a multifaceted approach, integrating quantitative and statistical methods to address the research questions effectively. This comprehensive strategy was essential for thoroughly exploring the relationships among the components of TPACK. All data analyses were performed using SPSS (Version 28) and AMOS (Version 28), two widely recognized statistical software programs. The study employed two essential statistical methods to comprehensively understand the research data, particularly in the context of middle school education in Chongqing, China. First, descriptive statistics were utilized, including mean scores and frequency distributions. These statistics provided a succinct summary of the sample’s characteristics and offered an overview of the response distribution (Cohen et al., 2018). This initial step was crucial for clearly understanding the participant group’s composition, thereby establishing the study’s relevance and applicability within the Chinese context. Secondly, SEM was used to examine the complex relationships among the TPACK components. SEM is a robust statistical technique renowned for its ability to simultaneously analyse intricate interactions among multiple variables (Byrne, 2016; Hair et al., 2010). In this study, SEM was instrumental in revealing the complex dynamics and mutual influences of the TPACK components in mathematics education. It provided a comprehensive view of how these components interconnect, highlighting the multifaceted nature of TPACK and its implications for mathematics teachers. By utilizing these analytical approaches, the research offered a nuanced and comprehensive perspective on the relationships within TPACK and their significance in middle school mathematics education.

5 Finding

5.1 Discriminant validity

The discriminant validity analysis findings (see Table 5) demonstrate that the square root of the AVE for each construct exceeds the correlation coefficients between constructs, thus supporting the fulfillment of discriminant validity criteria (Fornell & Larcker, 1981). The square root of AVE values for each construct, indicated in parentheses in the table, are all higher than their corresponding correlation coefficients, indicating sufficient differentiation among constructs. This suggests that the measurement model employed effectively distinguishes between different constructs and minimizes overlap or redundancy. The results confirm that the instruments utilized in this research provide precise and distinct measurements for assessing constructs, thereby enhancing the overall validity of our study’s measurement model (Hair et al., 2010). The robustness of these findings in capturing distinct dimensions within the TPACK framework is underscored, thereby demonstrating the sufficient uniqueness of the constructs in the context of this study. Consequently, this strengthens the reliability of measurements and enhances the overall quality of data analysis. The confirmation of discriminant validity ensures that there is no significant overlap among these constructs, which is crucial for accurate measurement and drawing meaningful conclusions about their relationships.

Table 5 Results of discriminant validity
Full size table

5.2 Test of the model

Researchers have yet to reach a consensus on the ideal fit indices for reporting (Byrne, 2016). However, several indices have been recommended and used in previous studies, including \({x}^{2}/df\), RMSEA, GFI, AGFI, NFI, CFI, and TLI (Özgür, 2020; Teo et al., 2019; Yang et al., 2021). In alignment with these recommendations, the present study utilized these indices to assess the model’s goodness of fit (as shown in Table 6). Based on the criteria outlined by (Hair et al., 2018), the model’s goodness of fit was evaluated across seven dimensions, yielding the following values: \({x}^{2}/df\) = 1.435, RMSEA = 0.031, GFI = 0.920, AGFI = 0.905, NFI = 0.921, CFI = 0.974, and TLI = 0.971. These analyses offer valuable insights into how well the path model aligns with the collected data. The reported values of these fit indices indicate that the path model achieved an accepted level of fit. In essence, based on the assessment of these fit indices, the proposed SEM model demonstrates an excellent fit with the data. This suggests that the model successfully captures the relationships among the various components of TPACK and provides valuable insights into how these components jointly impact technology integration in mathematics education.

Table 6 Fit indices of the proposed model
Full size table

5.3 The outcome of the hypotheses

The study examined 16 hypotheses to delve into the intricate relationships between the various components within the TPACK framework and how these components jointly facilitate effective technology integration in mathematics education (see Table 7). Figure 3 visually represents the connections between the elements of the TPACK framework. According to the SEM analysis, 12 out of the 16 hypotheses received support. Below is a concise summary of the hypothesis testing results.

5.3.1 Supported hypotheses

H1. TK→TCK: The path coefficient is 0.381 (p < 0.001), indicating a positive effect of TK on TCK.

H2. TK→TPK: The path coefficient is 0.231 (p < 0.001), confirming a positive effect of TK on TPK.

H4. CK→TCK: The path coefficient is 0.210 (p < 0.001), supporting a positive influence of CK on TCK.

H5. CK→PCK: The path coefficient is 0.235 (p < 0.001), suggesting a positive effect of CK on PCK.

H7. PK→PCK: The path coefficient is 0.192 (p = 0.001), indicating a positive influence of PK on PCK.

H8. PK→TPK: The path coefficient is 0.201 (p < 0.001), supporting a positive effect of PK on TPK.

H9. PK→TPACK: The path coefficient is 0.181 (p = 0.002), confirming a positive impact of PK on TPACK.

H11. XK→PCK: The path coefficient is 0.260 (p < 0.001), suggesting a positive effect of XK on PCK.

H12. XK→TPK: The path coefficient is 0.267 (p < 0.001), supporting a positive influence of XK on TPK.

H13. XK→TPACK: The path coefficient is 0.221 (p < 0.001), indicating a positive effect of XK on TPACK.

H14. TCK→TPACK: The path coefficient is 0.333 (p < 0.001), confirming a positive influence of TCK on TPACK.

H15. PCK→TPACK: The path coefficient is 0.126 (p = 0.023), suggesting a positive effect of PCK on TPACK.

5.3.2 Not supported hypotheses

H3. TK→TPACK: The path coefficient is 0.001 (p = 0.986), indicating no significant effect of TK on TPACK.

H6. CK→TPACK: The path coefficient is 0.067 (p = 0.261), suggesting no significant influence of CK on TPACK.

H10. XK→TCK: The path coefficient is 0.109 (p = 0.057), indicating no significant effect of XK on TCK.

H16. TPK→TPACK: The path coefficient is -0.029 (p = 0.577), suggesting no significant effect of TPK on TPACK.

The study revealed robust support for multiple hypotheses, demonstrating significant positive relationships among various components within the TPACK framework. These findings contribute to a more comprehensive understanding of how these components collectively influence technology integration in mathematics education. However, certain hypotheses did not receive statistically significant support, thereby highlighting areas where these relationships may have limited impact. These results offer valuable insights for educators and policymakers aiming to enhance technology integration in mathematics education.

Table 7 Hypotheses testing results
Full size table
Fig. 3
figure 3

The proposed model of TPACK

Full size image

5.4 The SEM model path analysis

Utilizing path analysis, this study examined the direct, indirect, and total effects that each exogenous variable exerts on the endogenous variables within the SEM model. The direct effect represents a straightforward connection between constructs, visualized by a direct arrow in the model. On the other hand, the indirect effect quantifies how a specific variable influences another variable through mediating variables within the model (Byrne, 2016). Notably, the total effect encompasses both direct and indirect effects, accounting for their combined influence on a given factor. In alignment with Cohen’s (2018) guidelines, effect sizes were assessed using standardized values, where effect sizes less than 0.1 were deemed small, those around 0.3 were considered medium, and values equal to or exceeding 0.5 were classified as large. Table 8 presents the standardized effect size values for direct, indirect, and total effects. This thorough analysis fosters a deeper understanding of the interactions among various variables within the SEM model and sheds light on their differing levels of influence on the endogenous variables. The study’s findings offer an encompassing view of the relationships between the components within the TPACK framework and their collective impact on the effective integration of technology in mathematics education. By analysing Table 8, several noteworthy insights can be gleaned from this examination.

Table 8 Direct indirect and total effects of determinants on variables
Full size table

5.4.1 TPACK

Four critical components, namely XK, PK, PCK, and TCK, significantly impact mathematics teachers’ TPACK. Collectively, these factors account for 34.6% of the observed variability in the TPACK component. Notably, TCK has a substantial positive influence on TPACK, with a significant direct effect size of 0.333, which is considered moderate. This finding emphasizes the crucial role of teachers’ TCK in enhancing their overall TPACK, highlighting the importance of integrating technological and pedagogical knowledge in mathematics education.

5.4.2 TCK

Within the TPACK framework, the endogenous factor, TCK, is significantly influenced by TK. TK demonstrates a noteworthy and positive direct impact on TCK, with a standardized effect size of 0.381. This result underscores the importance of teachers’ TK in the development of TCK. However, no significant relationship was found between XK and TCK. It is important to note that CK and TK together account for only 19.8% of the variance observed in TCK. This suggests that other factors may also contribute to shaping this component.

5.4.3 TPK

The endogenous variable TPK is significantly influenced by TK, PK, and XK. Collectively, these three factors account for 22.2% of the variance in TPK. However, the effect sizes for TK, PK, and XK on TPK are relatively modest, ranging from 0.201 to 0.267. While these factors are contributory to the development of TPK, their individual impacts are moderate, indicating that other elements might also play a significant role in shaping TPK.

5.4.4 PCK

PCK is significantly explained by PK, CK, and XK, which collectively contribute to 20.1% of the variance in PCK. These three factors, while significant, have small effect sizes on PCK, ranging between 0.192 and 0.260. This indicates that while they play a role in the development of PCK, other factors may also be instrumental in providing a more comprehensive understanding.

These findings provide valuable insights into the complex interplay among the components of the TPACK framework and their combined influence on the effective integration of technology in mathematics education. Comprehending these relationships is vital for the development of effective teacher training programs and strategies that are geared towards bolstering technology integration in educational environments, thereby ultimately enhancing the quality of mathematics education in modern classrooms.

6 Discussion

The findings of this study provide valuable insights into the intricate interrelationships among the components within the TPACK framework and their collective impact on the effective integration of technology in mathematics education. The primary objective of this research was to explore these relationships and their profound implications for mathematics education. Understanding how these components interact and influence one another is crucial for advancing the quality of mathematics education through technology integration (Li, 2023; Rakes et al., 2022; Susanti et al., 2022). Importantly, this study’s findings offer a comprehensive understanding of the interrelationships among TPACK framework components, specifically focusing on the significant influence of XK. This investigation represents a substantial contribution to academia and practical mathematics education.

The results of this study underscore the multifaceted interplay of TPACK components, with a particular focus on the substantial influence of XK. While past research has explored the relationships among various TPACK components (Angeli & Valanides, 2009; Koh et al., 2013; Schmid et al., 2020; Yang et al., 2021), XK’s role has, until now, remained largely unexplored. Some researchers highlighted the significance of XK (Mishra, 2019; Mishra et al., 2023; Porras-Hernández & Salinas-Amescua, 2013; Swallow & Olofson, 2017). For instance, Swallow and Olofson (2017) found that micro-level contextual factors such as teachers’ backgrounds, attitudes, and personal conceptualization of contemporary education significantly influenced technology integration. However, these studies did not empirically analyse the relationship between XK and other components of TPACK. This research, utilizing SEM, is the first to examine the extensive impact of XK on the relationships within the TPACK framework, specifically emphasizing its significant influence on three key TPACK components: TPK, PCK, and the overall TPACK construct. Moreover, these findings have significant implications for mathematics education, highlighting the crucial need to acknowledge and integrate XK within TPACK. It can be said that this study has shed light on the critical role that XK plays in shaping the landscape of technology integration in mathematics education. Additionally, previous studies (Niess et al., 2009; Schmid et al., 2020) have extensively examined the intricate relationships among various components of TPACK. However, including XK as a significant factor in our study represents a novel and valuable contribution to the existing body of knowledge. This research has the potential to advance the understanding of the multifaceted nature of TPACK and emphasizes the imperative for further investigation into the specific mechanisms through which XK influences these components.

Furthermore, in this exploration of the TPACK framework, it becomes evident that three other key components, namely PK, PCK, and TCK, exert substantial influences on teachers’ TPACK. Collectively, these components account for a significant portion of the observed variability in the TPACK component. Among these, TCK emerges as a critical factor, exerting a substantial positive influence on TPACK with a medium effect size of 0.333. This finding aligns with prior research (Dong et al., 2015; Koh et al., 2013; Pamuk et al., 2013) and supports the well-established notion of the pivotal role of mathematics teachers in enhancing their overall TPACK (Mishra & Koehler, 2006). However, this result deviates slightly from studies such as Yang et al. (2021), which claimed no significant influence of PK and PCK on teachers’ TPACK. The contrasting results between these studies highlight the complex nature of these relationships and suggest that the influence of specific TPACK components may vary based on context and other contributing factors. Additionally, TCK is significantly influenced by TK, as evidenced by a substantial and positive direct impact with a standardized effect size of 0.381. This finding aligns with the study conducted by Pamuk et al. (2013), which emphasized the crucial role of teachers’ TK in fostering the development of TCK. Moreover, the combined influence of CK and TK accounts for 19.8% of the observed variations in TCK, underscoring the intricate and multifaceted nature of factors influencing this aspect. However, it is important to acknowledge that our analysis did not reveal a significant relationship between XK and TCK. This finding indicates that there may be other influential factors contributing to the development of this crucial component within the TPACK framework. Therefore, future research efforts could be directed towards exploring these potential factors and their impact on the formation of TCK, aiming to provide a more comprehensive understanding of this aspect of technology integration in mathematics education.

Additionally, the study reveals the substantial influence of TK, PK, and XK on TPK development, collectively accounting for 22.2% of the variance in TPK. This underscores the significance of these factors in shaping teachers’ TPK. These findings align with previous research highlighting the interconnected nature of these components (Pamuk et al., 2013; Yang et al., 2021). However, it is important to acknowledge that the effect sizes of these factors on TPK are relatively moderate, indicating their moderate individual contributions. While these components significantly influence TPK, their impact is not overwhelmingly strong. This suggests that factors beyond the scope of this study, such as contextual elements or individual teaching practices, may also contribute to shaping teachers’ TPK. These nuances underscore the intricate nature of this aspect within the realm of TPACK. Similarly, PCK is significantly influenced by PK, CK, and XK, collectively accounting for 20.1% of the variance in PCK. These findings provide further empirical support for the intricate interplay among these components within the broader TPACK framework. Simultaneously, identifying these influences aligns with existing literature that underscores the interdependence of pedagogical and content knowledge in effective teaching (Qiu et al., 2022; Shulman, 1986). However, it is essential to note that although statistically significant, the effect sizes of these factors on PCK are relatively small. This highlights their contribution to PCK development while acknowledging the presence of other influential factors that may contribute to its effective cultivation.

6.1 Implications for mathematics education

By shedding light on the complex interplay among the components within the TPACK framework, this research underscores the criticality of acknowledging the multifaceted nature of mathematics instruction. Notably, the study reveals the substantial influence of XK on various TPACK components, such as TPK and PCK, emphasizing the imperative to recognize and integrate XK within the TPACK paradigm. One of the primary implications is the essential role of XK in shaping the landscape of technology integration in mathematics education. This research, groundbreaking in its focus on the Chinese education context, demonstrates the extensive impact of XK on the TPACK framework, with a particular emphasis on its significant influence on three key components: TPK, PCK, and the overarching TPACK construct. Consequently, mathematics educators and curriculum developers need to recognize the importance of XK and consider its integration into educational strategies. Such recognition can pave the way for more holistic approaches to mathematics instruction incorporating diverse knowledge domains, thereby enhancing technology integration. Moreover, in alignment with previous research, these findings underscore the need for a nuanced understanding of TPACK, highlighting its multifaceted nature and the intricate relationships among its components (Chai et al., 2013; Koh et al., 2013; Pamuk et al., 2013). A mere conceptualization of TPACK as a simple combination of technological, pedagogical, and content knowledge is no longer adequate. Instead, educators and policymakers must embrace the intricate interplay of factors within this framework, acknowledging that the effectiveness of technology integration in mathematics education is determined by more than just individual components in isolation (Li et al., 2024). By adopting an integrated approach, policy directives can facilitate the creation of comprehensive teacher training programs and curriculum reforms. Such initiatives should aim not only to equip educators with technological skills but also to deepen their understanding of how these tools can be woven into pedagogically sound practices (Drijvers et al., 2018; Khong et al., 2023). This holistic perspective is crucial for developing educational strategies that prepare teachers to effectively navigate and utilize the complexities of the TPACK framework in enhancing student learning outcomes.

Furthermore, the elucidation of XK’s critical interplay within the TPACK framework, as presented in this study, marks a distinctive contribution to the discourse on technology integration in the Chinese educational context. The delineation of XK’s impact on TPACK provides empirical grounding for educational practices, advocating for the adoption of culturally sensitive pedagogical strategies that are cognizant of the local educational ethos (Li et al., 2023; Mishra et al., 2023). This research distinctly informs policy-making, suggesting that policy directives should underscore the enhancement of teachers’ TPACK not in isolation but in synergy with contextual variables that reflect the unique Chinese educational context (Zhao, 2024). For educational practice, this study advances the imperative for curricula that integrate digital technologies with an acute awareness of local educational traditions and values. In this regard, the findings actuate a reformulation of teacher professional development agendas, underpinning the necessity for training that transcends mere technical skill acquisition to encompass comprehensive, context-driven pedagogical methodologies. In essence, the ramifications of this research for educational policy are profound, beckoning a paradigm shift towards contextually rich, technology-infused educational frameworks. These frameworks should facilitate teacher agency in technologically enriched environments while anchored in the particularities of the Chinese educational context, thereby resonating with global educational innovation movements.

While this study provides a detailed examination of how XK influences the application of the TPACK framework within Chinese mathematics education, the findings also invite broader considerations of how these dynamics might manifest differently in other educational systems. Globally, educational contexts vary significantly due to diverse cultural values, technological readiness, and policy environments. For instance, in more technologically advanced educational systems, the integration of technology might be more focused on enhancing collaborative learning environments rather than on addressing fundamental access issues. Conversely, in developing regions where technology access remains a significant barrier, the focus might be on how XK can facilitate basic digital literacy before it can influence pedagogical and content knowledge integration. Additionally, cultural factors such as the societal value placed on education, the role of teachers, and traditional teaching methods can significantly alter the interplay and impact of the TPACK components. By comparing these variations, researchers can further refine the TPACK model to account for such differences, potentially leading to a more nuanced understanding of technology integration that respects and responds to local conditions and cultures. This comparative approach not only validates the robustness of the TPACK framework across diverse settings but also highlights the need for flexible, culturally-adaptive educational technology policies and practices that can cater to a wide range of educational challenges and aspirations globally.

6.2 Limitation and future research

The research was conducted within a specific Chinese educational context, raising questions about the generalizability of our findings to other regions or educational settings. The study’s context-specific nature may limit the direct applicability of the results to systems with different educational policies, cultural expectations, or technological infrastructure. Moreover, within our TPACK model, variables such as TCK and TPK exhibited relatively small effect sizes. These findings suggest that additional factors, possibly cultural or institutional, may significantly influence the effectiveness of technology integration strategies. Such variations could stem from differences in how digital technology is perceived and utilized in educational practices across different cultural or institutional settings.

Given these considerations, future research should address several critical areas to enhance our understanding of TPACK in diverse educational environments. First, future studies should investigate how TPACK components interact in varied educational settings, such as online platforms or blended learning environments. This exploration could reveal how different contextual factors influence technology integration and help in developing tailored teacher training programs that are sensitive to these contextual nuances. Second, as AI continues to play a growing role in educational practices, research should explore how AI tools can be incorporated within the TPACK framework to enhance pedagogical effectiveness and student learning outcomes (Mishra et al., 2023). Studies could focus on specific AI applications that assist in bridging gaps in technological and pedagogical knowledge among teachers. Finally, recognizing the significance of XK, further research is needed to dissect which aspects of XK (miro, meso, or macro) are most influential on the components of TPACK. Understanding these dynamics can enable educational leaders and curriculum developers to prioritize essential XK areas in mathematics teacher education programs.

7 Conclusion

In the rapidly evolving field of mathematics education, the effective integration of digital technology presents significant challenges and vital opportunities. This comprehensive study offers an in-depth examination of the TPACK framework, particularly emphasising the pivotal role played by XK across its various components. The research findings underscore XK’s substantial influence on critical aspects of TPACK, encompassing TPK, PCK, and the overarching TPACK construct. These insights advocate for an integrated approach in teacher training programs, prioritising the seamless blending of content, pedagogy, technology, and contextual knowledge. Concurrently, the study underscores the importance of fostering teachers’ mastery in PK, PCK, TCK, and XK to enhance the meaningful integration of technology in mathematics education. It underscores the need for holistic training initiatives that cultivate technological proficiency and deepen pedagogical understanding, ensuring that educators can effectively integrate digital technologies into their teaching practices. In conclusion, this research makes a substantial contribution to understanding the intricate dynamics of TPACK and its practical implications, thereby paving the way for enhanced mathematics instruction in the digital era.