A tropical-algebraic method for the control of timed event graphs with partial synchronization

Abstract

This paper studies a scenario in which the occurrence of one or more events in a discrete event system is subject to external restrictions which may change unexpectedly during run-time. The system is modeled as a timed event graph (TEG) and, in this context, the presence of the aforementioned external restrictions has become known as partial synchronization (PS). This phenomenon arises naturally in several applications, from manufacturing to transportation systems. We develop a formal and systematic method to compute optimal control signals for TEGs in the presence of PS, where the control objective is tracking a given output reference as closely as possible and optimality is understood in the widely-adopted just-in-time sense. The approach is based on the formalism of tropical semirings — in particular, the min-plus algebra and derived semiring of counters. We claim that our method expands modeling and control capabilities with respect to previously existing ones by tackling the case of time-varying PS restrictions, which, to the best of our knowledge, has not been dealt with before in this context.

1 Introduction

In this paper, we consider a scenario where the occurrence of one or more events in a discrete event system is subject to restrictions imposed by external signals, and where such external signals may change unexpectedly during run-time. We employ the modeling formalism of timed event graphs (TEGs), a subclass of timed Petri nets characterized by the fact that each place has precisely one upstream and one downstream transition and all arcs have weight one. In particular, the former restriction implies that TEGs are not suitable for modeling conflict or choice. They can, however, model certain synchronization and delay phenomena, which are central in, e. g., manufacturing and transportation systems. One advantage of TEGs is the well-known fact that in a suitable mathematical framework, namely an idempotent semiring (or dioid) setting such as the max-plus or the min-plus algebra, their evolution can be described by linear equations (see Baccelli et al. 1992 for a thorough coverage). Based on such linear dioid models, an elaborate control theory has become available, mostly focusing on optimality in a just-in-time sense: the aim is to fire all input transitions as late as possible while guaranteeing that the firing of output transitions is not later than specified by a reference signal. In a manufacturing context, for example, the firing of an input and an output transition could correspond respectively to the provisioning of raw material and the completion of a workpiece. In general, a just-in-time policy aims at satisfying customer demands while minimizing internal stocks. For a tutorial introduction to this control framework, the reader may refer to Hardouin et al. (2018).

The conditions for transition firings in TEGs are classically modeled by standard synchronization, i.e., a transition can only fire after the firing of certain other transitions, possibly with some delay, and the firing of one transition never disables another. In some applications, however, different forms of synchronization arise. In this paper, we consider partial synchronization (or PS, for short), which consists in the existence of external signals that limit the time instants at which certain transitions in the system are allowed to fire. This captures phenomena that arise in several scenarios of practical relevance. In manufacturing, for instance, the occurrence of events corresponding to turning on different high-power demanding machines may be restricted to not occur simultaneously in order to avoid spikes in the energy consumption, or there may be time windows within which some equipment is scheduled for maintenance and, therefore, cannot operate. In transportation networks, the use of shared track segments by lower-priority lines can be thought of as being restricted according to the predetermined schedules of higher-priority lines. Building on preliminary results introduced in Schafaschek et al. (2022), we propose an original approach to tackle the modeling and control of TEGs under such PS restrictions.

In the above examples, it is reasonable to suppose that the external signals restricting the occurrence of certain events may vary over time. In the manufacturing cases, the plans for utilizing heavy machinery or for performing equipment maintenance may be updated, whereas in transportation networks the availability of shared track segments to lower-priority lines may be altered due, e.g., to delays in higher-priority ones. Thereby motivated, as the chief novelty with respect to Schafaschek et al. (2022) and the main contribution of this paper, we additionally study the case in which partial-synchronization signals may change during the operation of the system. To the best of what our literature research could reveal, this problem has not been dealt with before in this context.

TEGs with PS were originally studied in David-Henriet et al. (2013, 2014, 2016), where they are modeled by recursive equations with additional constraints over the max-plus and the min-plus algebra; the authors develop a method for optimal feedforward control and MPC for this class of systems. In Trunk et al. (2020), a specific semiring of operators is introduced to model the subclass of TEGs under periodic PS, where PS restrictions are determined by periodic signals. An advantage of the operatorial representation is the possibility to obtain a direct input-output relation (i.e., a transfer function or transfer matrix) for the system, which allows to efficiently compute the response to periodic inputs over an infinite horizon and solve output-reference and model-reference control problems. In this contribution, we make no periodicity assumption on the PS signals and propose a method entirely based on the well-established semiring of counters (i.e., nonincreasing formal power series over the min-plus algebra). We believe this makes our model more intuitive and easier to interpret than that in Trunk et al. (2020) and, most importantly, it allows us to harness the benefits of having a transfer relation for the system while encompassing the general class of TEGs under (not necessarily periodic) PS treated in David-Henriet et al. (2013, 2014, 2016).

Other classes of systems somewhat related to TEGs with PS have been investigated in the past decades. Katz (2007) and Maia et al. (2011a, 2011b) consider (A, B)-invariant and semimodule subspaces in order to compute a control enforcing certain restrictions on the state of the system. This can be applied, for instance, to ensure that the sojourn time of tokens through the system belongs to a given interval. Note that this models a different phenomenon from that of TEGs with PS, where the permission to fire certain transitions is successively granted and revoked according to external signals but no upper bound for their firing times is directly imposed. In De Schutter and van den Boom (2003), the authors study TEGs with soft synchronization, where the synchronization between certain transitions in the system can be broken at a cost. For example, an operation may be allowed to start without waiting for the conclusion of delayed predecessor operations, hence preventing the propagation of delays but incurring penalty costs. Dually to PS, where external signals impose additional restrictions, in this case external decisions can overrule standard synchronization constraints based on a trade-off between performance criteria and penalty costs. Finally, it is worth mentioning that a phenomenon analogous to PS has been studied by the scheduling community, where the external restrictions for the occurrence of certain events are often referred to as availability constraints (see, e.g., Pinedo 2008 and references therein). A closer comparison of our results with such scheduling methods is beyond the scope of this paper and remains as an interesting subject for future work.

The paper is organized as follows. Section 2 summarizes relevant facts on idempotent semirings. In Section 3, a method for the modeling and optimal control of TEGs with PS is discussed. As the main novelty of this paper, the method is enhanced in Section 4 in order to handle TEGs with varying PS restrictions. Section 5 provides a step-by-step summary of the method, serving as a guide to facilitate its application, which is illustrated with an example in Section 6. Our conclusions and final remarks are presented in Section 7.

2 Preliminaries

The purpose of this section is to make the paper largely self-contained. We present a summary of some basic definitions and results on idempotent semirings and timed event graphs — for a more exhaustive discussion, the reader may refer to Baccelli et al. (1992) — and touch on some topics from residuation theory and control of TEGs (see Blyth and Janowitz 1972 and Hardouin et al. 2018).

2.1 Idempotent semirings

An idempotent semiring (or dioid) $\mathcal {D}$ is a set endowed with two binary operations, denoted $\oplus$ (sum) and $\otimes$ (product), such that: $\oplus$ is associative, commutative, idempotent (i.e., $(\forall a \in \mathcal {D})\, a \oplus a = a$), and has a neutral (zero) element, denoted $\varepsilon$; $\otimes$ is associative, distributes over $\oplus$, and has a neutral (unit) element, denoted e; the element $\varepsilon$ is absorbing for $\otimes$ (i.e., $(\forall a \in \mathcal {D})\, a \otimes \varepsilon = \varepsilon \otimes a =\varepsilon$).

As in conventional algebra, the product symbol $\otimes$ is often omitted. Throughout this paper, we assume that the product has precedence over all other operations in a dioid. More precisely, for any operator $\circledast$ on $\mathcal {D}$ and for all $a,b,c,d\in \mathcal {D}$, an expression like $ab \circledast cd$ is to be read $(a\otimes b) \circledast (c\otimes d)$.

A canonical order relation can be defined over $\mathcal {D}$ by

$$\begin{aligned} (\forall a,b \in \mathcal {D})\ a\preceq b\, \Leftrightarrow \, a\oplus b=b\,. \end{aligned}$$

(1)

Note that $\varepsilon$ is the bottom element of $\mathcal {D}$, as $(\forall a \in \mathcal {D})\,\varepsilon \preceq a$.

An idempotent semiring $\mathcal {D}$ is complete if it is closed for infinite sums and if the product distributes over infinite sums. For a complete idempotent semiring, the top element is defined as $\top = \bigoplus _{x\in \mathcal {D}}x$, and the greatest lower bound operation, denoted $\wedge$, by

$$\begin{aligned} (\forall a,b\in \mathcal {D})\ \, a\wedge b\, = \bigoplus _{x\preceq a,x\preceq b} x\ . \end{aligned}$$

Operation $\wedge$ is associative, commutative, and idempotent, and the following equivalences hold:

$$\begin{aligned} (\forall a,b\in \mathcal {D})\ \, a\oplus b = b\, \Leftrightarrow \, {a\preceq b}\, \Leftrightarrow \, a\wedge b = a\, . \end{aligned}$$

The set $\overline{\mathbb {Z}}\,\, {\overset{\tiny def }{=}}\,\, \mathbb {Z}\cup \{-\infty ,+\infty \}$, with the minimum operation as $\oplus$ and conventional addition as $\otimes$, forms a complete idempotent semiring called min-plus algebra, denoted $\overline{\mathbb {Z}}_{min }$, in which $\varepsilon = +\infty$, $e = 0$, and $\top = -\infty$. Note that in $\overline{\mathbb {Z}}_{min }$ we have, e.g., $2\oplus 5 = 2$, so $5\preceq 2$; the order is reversed with respect to the conventional order over $\mathbb {Z}$.¹

Remark 1

(Baccelli et al. 1992) The set of $n\!\times \!n$-matrices with entries in a complete idempotent semiring $\mathcal {D}$, endowed with sum and product operations defined by

$$\begin{aligned} (A \oplus B)_{ij}&= A_{ij} \oplus B_{ij}\,, \\ (A \otimes B)_{ij}&= \bigoplus _{k=1}^{n}\, (A_{ik} \otimes B_{kj})\,, \end{aligned}$$

for all $i,j \in \{1,\ldots ,n\}$, forms a complete idempotent semiring denoted $\mathcal {D}^{n \times n}$. Its unit element (or identity matrix) is the $n\!\times \!n$-matrix with entries equal to e on the diagonal and $\varepsilon$ elsewhere; the zero (resp. top) element is the $n\!\times \!n$-matrix with all entries equal to $\varepsilon$ (resp. $\top$). The definition of order Eq. 1 implies, for any $A,B \in \mathcal {D}^{n \times n}$,

$$\begin{aligned} A \preceq B\ \Leftrightarrow \ {(\forall \, i,j \in \{1,\ldots ,n\})}\, A_{ij} \preceq B_{ij}\,. \end{aligned}$$

It is possible to deal with nonsquare matrices in this context by suitably padding them with $\varepsilon$-rows or columns; this is done only implicitly, as it does not interfere with the relevant parts of the results of operations between matrices.

In this paper, we shall denote the $i^{\text {th}}$ row and the $j^{\text {th}}$ column of a matrix A by $A_{[i\varvec{\cdot }]}$ and $A_{[\varvec{\cdot }j]}$, respectively. In the case of row or column vectors, i.e., $a\in \mathcal {D}^{1\times n}$ or $a\in \mathcal {D}^{n\times 1}$ with $n\ge 2$, we denote the $i^{\text {th}}$ entry simply by $a_i$.

A mapping $\Pi : \mathcal {D} \rightarrow \mathcal {C}$, with $\mathcal {D}$ and $\mathcal {C}$ two idempotent semirings, is isotone if $(\forall a,b \in \mathcal {D})\,a\preceq b \Rightarrow \Pi (a) \preceq \Pi (b)$.

Remark 2

The composition of two isotone mappings is isotone.

Remark 3

Let $\Pi$ be an isotone mapping over a complete idempotent semiring $\mathcal {D}$, and let $\mathcal {Y} = \{x \in \mathcal {D}\,\vert \, \Pi (x)=x\}$ be the set of fixed points of $\Pi$. It follows that $\bigwedge _{y\in \mathcal {Y}} y$ (resp. $\bigoplus _{y\in \mathcal {Y}} y$) is the least (resp. greatest) fixed point of $\Pi$.

Algorithms exist which allow to compute the least and greatest fixed points of isotone mappings over complete idempotent semirings. In particular, the algorithm presented in Hardouin et al. (2018) is applicable to the relevant mappings considered in this paper.

In a complete idempotent semiring $\mathcal {D}$, the Kleene star operator on $a\in \mathcal {D}$ is defined as $a^* = \bigoplus _{i\ge 0}a^i$, with $a^0=e$ and $a^i=a^{i-1}\otimes a$ for $i>0$.

Remark 4

(Baccelli et al. 1992) The implicit equation $x=ax\oplus b$ over a complete idempotent semiring admits $x=a^*b$ as least solution. This applies, in particular, in the case $x,b \in \mathcal {D}^n$ and $a\in \mathcal {D}^{n \times n}$ (cf. Remark 1). Moreover, if x is a solution of $x=ax\oplus b$, then $x=a^*x$.

2.2 Semirings of formal power series

Let $s=\{s(t)\}_{t\in \overline{\mathbb {Z}}}$ be a sequence over $\overline{\mathbb {Z}}_{min }$. The $\delta$-transform of s is a formal power series in $\delta$ with coefficients in $\overline{\mathbb {Z}}_{min }$ and exponents in $\overline{\mathbb {Z}}$, defined by

$$\begin{aligned} s = \bigoplus _{t\in \overline{\mathbb {Z}}}s(t)\delta ^t\,. \end{aligned}$$

We denote both the sequence and its $\delta$-transform by the same symbol, as no ambiguity will occur.

In this paper, each term s(t) of a sequence will refer to the accumulated number of firings of a certain transition up to time t. Naturally, this interpretation carries over to the terms of a series corresponding to the $\delta$-transform of such a sequence. A series s thus obtained is clearly nonincreasing (in the order of $\overline{\mathbb {Z}}_{min }$, which, as pointed out before, is the reverse of the standard order of $\mathbb {Z}$), meaning $s(t-1)\succeq s(t)$ for all t. We will henceforth refer to such series as counters.

The set of counters (i.e., nonincreasing power series), with addition and multiplication defined by

$$\begin{aligned} s\oplus s'&= \bigoplus _{t\in \overline{\mathbb {Z}}}(s(t)\oplus s'(t))\delta ^t\,,\\ s\otimes s'&= \bigoplus _{t\in \overline{\mathbb {Z}}}\Big (\bigoplus _{\tau \in \overline{\mathbb {Z}}}(s(\tau )\otimes s'(t-\tau ))\Big )\delta ^t\,, \end{aligned}$$

is a complete idempotent semiring, which we denote by $\Sigma$. It has zero element $s_{\varepsilon }$ given by $s_{\varepsilon }(t)=\varepsilon$ for all t, unit element $s_e$ given by $s_e(t)=e$ for $t\le 0$ and $s_e(t)=\varepsilon$ for $t>0$, and top element $s_{\top }$ given by $s_{\top }(t)=\top$ for all t. In fact, it is easy to see that $s_{\varepsilon }$, $s_{e}$, respectively $s_{\top }$ are indeed the zero, unit, respectively top elements in $\Sigma$: $\forall s\in \Sigma$, $\forall t\in \overline{\mathbb {Z}}$,

$$\begin{aligned} (s \oplus s_{\varepsilon })(t)&= s(t) \oplus s_{\varepsilon }(t) = s(t)\,;\\ (s \otimes s_{e})(t)&= \bigoplus _{\tau \in \overline{\mathbb {Z}}}\, s(\tau )\otimes s_{e}(t-\tau )\\&= \bigoplus _{\tau \ge t} s(\tau )\\&= s(t)\qquad \text {(as { s} is nonincreasing)}\,;\\ (s \oplus s_{\top })(t)&= s(t) \oplus s_{\top }(t) = \top \,. \end{aligned}$$

The definition of order Eq. 1, together with the addition operation on counters defined above, imply that the order in $\Sigma$ is taken coefficient-wise, i.e., for any $s,s'\in \Sigma$, $s\preceq s' \Leftrightarrow (\forall t\in \overline{\mathbb {Z}}) s(t)\preceq s'(t)$.

Fig. 1

Counter $s=e\delta ^3 \oplus 1\delta ^7 \oplus 3\delta ^{10} \oplus 4\delta ^{+\infty }$

Counters can be represented compactly by omitting terms $s(t)\delta ^t$ whenever $s(t)=s(t+1)$. For example, a counter s with $s(t)=e$ for $t\le 3$, $s(t)=1$ for $3< t\le 7$, $s(t)=3$ for $7< t\le 10$, and $s(t)=4$ for $t> 10$ can be written $s=e\delta ^3 \oplus 1\delta ^7 \oplus 3\delta ^{10} \oplus 4\delta ^{+\infty }$. If associated with the firings of a transition in a TEG, counter s would encode a first firing occurring at time 3, then two more firings at time 7, and the fourth and last firing at time 10. This is graphically illustrated in Fig. 1, where the squares indicate the terms appearing in the compact notation. It is also common to omit terms with $\varepsilon$-coefficients. For instance, for any $\tau \in \overline{\mathbb {Z}}$, the counter with coefficients equal to e for $t\le \tau$ and $\varepsilon$ for $t>\tau$ is simply denoted by $e\delta ^{\tau }$; in particular, with $\tau >0$, for any $s\in \Sigma$ we have

$$\begin{aligned} (s\otimes e\delta ^{\tau })(t)&= \bigoplus _{t' \ge t-\tau }s(t')\otimes e\ \, \oplus \ \, \bigoplus _{t' < t-\tau }s(t')\otimes \varepsilon \\&= \bigoplus _{t'\ge t-\tau }s(t')\\&= s(t-\tau )\qquad \text {(as { s} is nonincreasing)} \end{aligned}$$

for all $t\in \overline{\mathbb {Z}}$, i.e., multiplication by $e\delta ^{\tau }$ can be seen as a backward shift operation by $\tau$ time units.

2.3 Residuation theory

Residuation theory provides, under certain conditions, greatest (resp. least) solutions to inequalities such as $f(x)\preceq b$ (resp. $f(x)\succeq b$).

Definition 1

An isotone mapping $f : \mathcal {D} \rightarrow \mathcal {C}$, with $\mathcal {D}$ and $\mathcal {C}$ complete idempotent semirings, is said to be residuated if for all $y\in \mathcal {C}$ there exists a greatest solution to the inequality $f(x)\preceq y$. This greatest solution is denoted $f^{\sharp }(y)$, and the mapping $f^{\sharp } : \mathcal {C} \rightarrow \mathcal {D}$, $y \mapsto \bigoplus \{x\in \mathcal {D}\,\vert \,f(x)\preceq y\}$, is called the residual of f.

Mapping f is said to be dually residuated if for all $y\in \mathcal {C}$ there exists a least solution to the inequality $f(x)\succeq y$. This least solution is denoted $f^{\flat }(y)$, and the mapping $f^{\flat } : \mathcal {C} \rightarrow \mathcal {D}$, $y \mapsto \bigwedge \{x\in \mathcal {D}\,\vert \,f(x)\succeq y\}$, is called the dual residual of f.

Note that, if equality $f(x)=y$ is solvable, $f^{\sharp }(y)$ yields its greatest solution (as long as mapping f is residuated, understood). Similarly, provided f is dually residuated, the least solution is given by $f^{\flat }(y)$.

Theorem 1

(Blyth and Janowitz 1972) Mapping f as in Def. 1 is residuated if and only if there exists a unique isotone mapping $f^{\sharp } : \mathcal {C} \rightarrow \mathcal {D}$ such that ${(\forall y\in \mathcal {C})}\, {f\big (f^{\sharp }(y)\big ) \preceq y}$ and $(\forall x\in \mathcal {D})\, f^{\sharp }\big (f(x)\big ) \succeq x$.

Remark 5

For $a \in \mathcal {D}$, mapping $L_a : \mathcal {D} \rightarrow \mathcal {D}$, $x\mapsto a \otimes x$, is residuated; its residual is denoted by $L_a^{\sharp }(y) = a\circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} y$ ($\circ {\hspace{-5.0pt}}\backslash {\hspace{-0.2pt}}$ is the “left-division” operator). More generally, for $A \in \mathcal {D}^{n{\times }m}$, mapping $L_A : \mathcal {D}^{m{\times }p} \rightarrow \mathcal {D}^{n{\times }p}$, $X\mapsto A \otimes X$, is residuated; $L_A^{\sharp }(Y) = A\circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} Y \in \mathcal {D}^{m{\times }p}$ can be computed as follows: for all $1\le i\le m$ and $1\le j\le p$, $(A\circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} Y)_{ij} = \bigwedge _{k=1}^n A_{ki}\circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} Y_{kj}$ .

2.4 The Hadamard product of counters

Definition 2

(Hardouin et al. 2008) The Hadamard product of $s_1,s_2 \in \Sigma$, written $s_1 \odot s_2$, is the counter defined as follows:

$$\begin{aligned} (\forall t \in \overline{\mathbb {Z}})\ \, (s_1 \odot s_2)(t)=s_1(t)\otimes s_2(t)\,. \end{aligned}$$

The Hadamard product is associative, commutative, distributes over $\oplus$ and $\wedge$, has neutral element $e\delta ^{+\infty }$, and $s_\varepsilon$ is absorbing for it (i.e., ${(\forall s\in \Sigma )}$ ${s\odot s_\varepsilon = s_\varepsilon }$).

Proposition 2

(Hardouin et al. 2008) For any $a\in \Sigma$, the mapping $\Pi _a : \Sigma \rightarrow \Sigma$, $x \mapsto a \odot x$, is residuated. For any $b \in \Sigma$, $\Pi _a^{\sharp }(b)$, denoted $b \odot ^{\sharp } a$, is the greatest $x \in \Sigma$ such that $a \odot x \preceq b$.

Proposition 3

(Zorzenon et al. 2022) For $a\in \Sigma$, let $\mathcal {D}_a = \{x\in \Sigma \, \vert \, x = s_\varepsilon \ \text {if}\ \exists t\in \mathbb {Z} \text { with }{a(t) = -\infty \}}$, and $\mathcal {C}_a = \{y\in \Sigma \,\vert \, (\forall t\in \mathbb {Z})\, a(t) \in \{-\infty ,+\infty \}\Rightarrow y(t) = +\infty \}$. The mapping $\Pi _a:\mathcal {D}_a\rightarrow \mathcal {C}_a$, $x\mapsto a\odot x$ is dually residuated for any $a\in \Sigma$. Its dual residual is denoted by $\Pi _a^\flat (y) = y\odot ^\flat a$ and corresponds to the least $x\in \Sigma$ that satisfies $a\odot x\succeq y$.

Given two counters $s_1,s_2 \in \Sigma$, the series s defined by ${(\forall t \in \overline{\mathbb {Z}})}\, s(t)=s_1(t)-s_2(t)$ is not necessarily a counter; $s_1 \odot ^{\sharp } s_2$ is the greatest counter less than or equal to s (in the sense of a coefficient-wise order like that of $\Sigma$). Similarly, provided the conditions from Prop. 3 are met, $s_1 \odot ^{\flat } s_2$ is the least counter greater than or equal to s. These ideas are graphically illustrated in Fig. 2.

Fig. 2

Graphical illustration of $s =$ “$s_1-s_2$” $\notin \Sigma$ ($\bigcirc$) in comparison with $s_1 \odot ^{\sharp } s_2$ ( ) and $s_1 \odot ^{\flat } s_2$ ( ), where $s_1=1\delta ^{1}\oplus 3\delta ^4\oplus 5\delta ^{+\infty }$ and $s_2=e\delta ^0\oplus 1\delta ^2 \oplus 2\delta ^6\oplus 3\delta ^{+\infty }$. One can see that $s_1 \odot ^{\sharp } s_2$ is the closest counter approximation of s from below in the sense of a coefficient-wise order like that of $\Sigma$ (or from above, in the graphical sense); similarly, $s_1 \odot ^{\flat } s_2$ is the closest counter approximation of s from above in the sense of a coefficient-wise order like that of $\Sigma$ (or from below, in the graphical sense)

2.5 TEG models in idempotent semirings

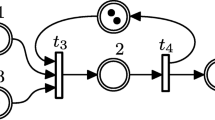
Timed event graphs (TEGs) are timed Petri nets in which each place has exactly one upstream and one downstream transition and all arcs have weight 1. With each place p is associated a holding time, representing the minimum time every token needs to spend in p before it can contribute to the firing of its downstream transition. In a TEG, we can distinguish input transitions (those that are not affected by the firing of other transitions), output transitions (those that do not affect the firing of other transitions), and internal transitions (those that are neither input nor output transitions). In this paper, for simplicity we shall limit our discussion to TEGs with a single output transition, which we denote y; input and internal transitions are denoted by $u_j$ and $x_i$, respectively. Figure 3 shows an example of a TEG, with input transitions $u_1$ and $u_2$, output transition y, and internal transitions $x_1$, $x_2$, and $x_3$.

Fig. 3

A TEG with two inputs $u_1$ and $u_2$, a single output y, and three internal transitions $x_1$, $x_2$, and $x_3$

A TEG is said to be operating under the earliest firing rule if every internal and output transition fires as soon as it is enabled.

With each transition $x_i$, we associate a sequence $\{x_i(t)\}_{t\in \overline{\mathbb {Z}}}$, for simplicity denoted by the same symbol, where $x_i(t)$ represents the accumulated number of firings of $x_i$ up to time t. Similarly, we associate sequences $\{u_j(t)\}_{t\in \overline{\mathbb {Z}}}$ and $\{y(t)\}_{t\in \overline{\mathbb {Z}}}$ with transitions $u_j$ and y, respectively. By inspection of Fig. 3, one can see that, at any time t, $x_1(t)$ cannot exceed the minimum between $u_1(t)$ and $x_2(t-1)+2$. This can be expressed in $\overline{\mathbb {Z}}_{min }$ as

$$\begin{aligned} (\forall t \in \overline{\mathbb {Z}})\ \ x_1(t) \succeq u_1(t) \oplus 2x_2(t -1)\,. \end{aligned}$$

(2)

Under the earliest firing rule, Eq. 2 turns into equality and, through the $\delta$-transform, can be written in $\Sigma$ as

$$\begin{aligned} x_1 = u_1 \oplus 2\delta ^1 x_2\,. \end{aligned}$$

We can obtain similar relations for $x_2$, $x_3$, and y; then, defining the vectors

$$\begin{aligned} u\,=\,\begin{bmatrix}u_1\\ u_2 \end{bmatrix},\qquad \quad x\,=\,\begin{bmatrix}x_1\\ x_2\\ x_3 \end{bmatrix}, \end{aligned}$$

we can write

$$\begin{aligned} x\,&= \begin{bmatrix} s_{\varepsilon } &{} 2\delta ^1 &{} s_{\varepsilon }\\ e\delta ^3 &{} s_{\varepsilon } &{} 1\delta ^2\\ s_{\varepsilon } &{} e\delta ^4 &{} s_{\varepsilon } \end{bmatrix}\!x\, \oplus \, \begin{bmatrix} e\delta ^0 &{} s_{\varepsilon }\\ s_{\varepsilon } &{} e\delta ^0\\ s_{\varepsilon } &{} s_{\varepsilon } \end{bmatrix}\!u\,,\\ y\,&=\, \begin{bmatrix}s_{\varepsilon }\ {}&s_{\varepsilon }\ {}&e\delta ^0 \end{bmatrix} x\,. \end{aligned}$$

In general, a TEG can be described by implicit equations over $\Sigma$ of the form

$$\begin{aligned} \begin{aligned} x&= Ax \oplus Bu\,,\\ y&= Cx\,. \end{aligned} \end{aligned}$$

(3)

From Remark 4, the least solution of Eq. 3 is given by

$$\begin{aligned} x = A^*Bu \qquad \text {and}\qquad y = CA^*Bu\,. \end{aligned}$$

(4)

We denote

$$\begin{aligned} \mathcal {F}=A^*B\qquad \text {and}\qquad \mathcal {G}=CA^*B\,, \end{aligned}$$

(5)

where $\mathcal {G}$ is often called the transfer matrix (or, in the case of a single input and a single output, transfer function) of the system. For instance, for the system from Fig. 3, we obtain

$$\begin{aligned} \mathcal {F}= \begin{bmatrix} e\delta ^0\oplus 2\delta ^4(1\delta ^6)^*\ {} &{} 2\delta ^1(1\delta ^6)^*\\ e\delta ^3(1\delta ^{6})^* &{} (1\delta ^{6})^*\\ e\delta ^{7}(1\delta ^{6})^* &{} e\delta ^{4}(1\delta ^{6})^* \end{bmatrix}\quad \text {and}\quad \mathcal {G}= \begin{bmatrix} e\delta ^{7}(1\delta ^{6})^*\ {}&e\delta ^{4}(1\delta ^{6})^* \end{bmatrix}.\ \ \end{aligned}$$

(6)

These computations can be performed with the aid of the toolbox introduced in Cottenceau et al. (2020).

2.6 Optimal control of TEGs

Assume that a TEG to be controlled is modeled by equations 3 and that an output-reference $z \in \Sigma$ is given. Under the just-in-time paradigm, we aim at firing the input transitions the least possible number of times while guaranteeing that the output transition fires, by each time instant, at least as many times as specified by z. In other words, we seek the greatest (in the order of $\overline{\mathbb {Z}}_{min }$) input (vector) u such that $y=\mathcal {G} u\preceq z$. Based on Eq. 4 and Remark 5, the solution is directly obtained by

$$\begin{aligned} u_{\text {opt}} = \mathcal {G}\circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} z\,. \end{aligned}$$

(7)

Example 1

For the TEG from Fig. 3, suppose it is required that the accumulated number of firings of y be e ($=0$) for $t<14$, 1 for $14\le t<23$, 3 for $23\le t< 29$, and 4 for $t\ge 29$. In other words, one firing is required by time 14, then two more by time 23, and finally one more by time 29. This can be represented by the output-reference

$$\begin{aligned} z=e\delta ^{14} \oplus 1\delta ^{23} \oplus 3\delta ^{29} \oplus 4\delta ^{+\infty }\,. \end{aligned}$$

Applying Eq. 7, we obtain the just-in-time input

$$\begin{aligned} u_{\text {opt}}\, = \begin{bmatrix}u_{1_{\text {opt}}}\\ u_{2_{\text {opt}}} \end{bmatrix} = \begin{bmatrix} e\delta ^{4} \oplus 1\delta ^{10} \oplus 2\delta ^{16} \oplus 3\delta ^{22} \oplus 4\delta ^{+\infty }\\ e\delta ^{7} \oplus 1\delta ^{13} \oplus 2\delta ^{19} \oplus 3\delta ^{25} \oplus 4\delta ^{+\infty } \end{bmatrix}\,, \end{aligned}$$

and the corresponding optimal output is

$$\begin{aligned} y_{\text {opt}}\, =\, \mathcal {G} u_{\text {opt}}\, =\, e\delta ^{11} \oplus 1\delta ^{17} \oplus 2\delta ^{23} \oplus 3\delta ^{29} \oplus 4\delta ^{+\infty }\,. \end{aligned}$$

One can easily verify that indeed $y_{\text {opt}} \preceq z$, as illustrated in Fig. 4.

Fig. 4

Tracking of reference z ($\triangle$) by the optimal output $y_{\text {opt}}$ ($\,\bullet \,$) obtained in Example 1

3 Modeling and optimal control of TEGs under fixed partial synchronization

The behavior of TEGs with partial synchronization (PS) cannot be modeled solely by equations like Eq. 3. In this section, we propose a way to express PS in the context of counters and to obtain optimal (just-in-time) inputs for TEGs with partially-synchronized transitions.

3.1 The concept of partial synchronization

A general way of characterizing the partial synchronization phenomenon is the following: the firings of a TEG’s partially-synchronized (internal) transition $x_{\iota }$ are subject to a predefined synchronizing signal ${\mathcal {S} : \overline{\mathbb {Z}}\rightarrow \mathbb {Z}_{\text {min}}^+}$, where

$$\begin{aligned} \mathbb {Z}_{\text {min}}^{+} = \{a \in \overline{\mathbb {Z}}_{min }\,\vert \, \varepsilon \prec a\preceq e\} \subset \overline{\mathbb {Z}}_{min }\end{aligned}$$

is the set of finite nonnegative (in the standard sense) elements of $\overline{\mathbb {Z}}_{min }$. More precisely, an additional condition for the firing of $x_{\iota }$ — besides the ones from standard synchronization as expressed in Eq. 3 — is imposed; namely, at any time $t\in \overline{\mathbb {Z}}$, $x_{\iota }$ can only fire if $\mathcal {S}(t)\ne e$, in which case it can fire at most $\mathcal {S}(t)$ times. If $\mathcal {S}(t)=e$, $x_{\iota }$ is not allowed to fire at time t. Note that limiting $\mathcal {S}$ to only assume finite values is not restrictive, as they can be arbitrarily large. In $\overline{\mathbb {Z}}_{min }$, this condition on $x_{\iota }$ reads as

$$\begin{aligned} (\forall t \in \overline{\mathbb {Z}})\ \ x_{\iota }(t) \succeq \mathcal {S}(t) \otimes x_{\iota }(t-1)\,. \end{aligned}$$

(8)

Signal $\mathcal {S}$ as above defines a sequence $\{\mathcal {S}(t)\}_{t\in \overline{\mathbb {Z}}}$ over $\overline{\mathbb {Z}}_{min }$. It should be clear, however, that this sequence is not necessarily nonincreasing (in the order of $\overline{\mathbb {Z}}_{min }$), and thus its $\delta$-transform may, in general, not be a counter. In the sequel, we present a way to capture the effects of PS within the domain of $\Sigma$.

3.2 Modeling of TEGs under partial synchronization

We now propose an alternative perspective to model PS in TEGs. The method consists in appending to any partially-synchronized transition $x_{\iota }$ the structure shown in Fig. 5. At any given time t, the number of tokens in place $p_r$ corresponds to how many firings PS allows for $x_{\iota }$ at t. For this to correctly represent the restrictions on $x_{\iota }$ due to PS, the number of tokens in $p_r$ needs to be managed accordingly, which is made possible by assigning appropriate firing schedules to transitions $\rho$ and $\alpha$. Suppose $x_{\iota }$ is to be conceded k firings at time t. Then, $\rho$ will fire k times at t, inserting k tokens in $p_r$. These will remain available for only one time unit, during which they enable up to k firings of $x_{\iota }$. Note that the number of tokens inserted in $p_r$ provides only an upper bound to the number of times $x_{\iota }$ can fire at time t, but it is not known a priori how many firings (if any) $x_{\iota }$ will actually perform. The role of transition $\xi$ is to make the mechanism independent of how often $x_{\iota }$ fires by returning to $p_r$ at time $t+1$ all the tokens consumed by $x_{\iota }$ at t. In fact, as the earliest firing rule is assumed, based on Fig. 5 we have $\xi (t)=x_{\iota }(t-1)$ for all $t\in \overline{\mathbb {Z}}$ (or simply $\xi = e\delta ^1 x_{\iota }$). Then, at time $t+1$, $x_{\iota }$’s “right to fire” is revoked, which is carried out by scheduling k firings for $\alpha$ so that $p_r$ becomes empty. Formally, $\alpha = e\delta ^1\rho$. In order to avoid any (nondeterministic) dispute between $\alpha$ and $x_{\iota }$ for the tokens residing in $p_r$ at $t+1$, the final touch is to assume that $\alpha$ has higher priority than $x_{\iota }$, meaning the firing schedule of $x_{\iota }$ must be determined under the hard restriction that it cannot interfere with that of $\alpha$. The described mechanism is initialized as follows: if $x_{\iota }$ is first granted the right to fire at time $\tau$, define $\rho (t) =e$ for all $t\le \tau$.

Fig. 5

Appended structure (in gray) to represent PS of internal transition $x_{\iota }$ in a TEG

Example 2

Consider the TEG from Fig. 3 and suppose transition $x_2$ is partially synchronized, with the following restrictions: it may only fire at times

$$\begin{aligned} t\in \mathcal {T}=\big \{[4,6] \cup [10,12] \cup [18,19] \cup [24,27]\cup [31,32]\big \}\subset \mathbb {Z}\,, \end{aligned}$$

and at most once at each $t\in \mathcal {T}$. This PS is modeled through the structure described above, as shown in Fig. 6, with

$$\begin{aligned} \rho (t) = {\left\{ \begin{array}{ll} e &{} \text {if}\ t\le 4\,; \\ 1\otimes \rho (t-1) &{} \text {if}\ t-1\in \mathcal {T}\,;\\ \rho (t-1) &{} \text {if}\ t-1\notin \mathcal {T}\ \text {and}\ t>4\,. \end{array}\right. } \end{aligned}$$

Explicitly, we have

$$\begin{aligned} \rho \, =\&e\delta ^4\oplus 1\delta ^5\oplus 2\delta ^6\oplus 3\delta ^{10}\oplus 4\delta ^{11}\oplus 5\delta ^{12}\oplus 6\delta ^{18}\oplus 7\delta ^{19}\oplus 8\delta ^{24}\\ {}&\oplus 9\delta ^{25} \oplus 10\delta ^{26}\oplus 11\delta ^{27}\oplus 12\delta ^{31}\oplus 13\delta ^{32}\oplus 14\delta ^{+\infty }\,. \end{aligned}$$

Recall that the schedule for $\alpha$ is then determined as $\alpha = e\delta ^1\rho$, i.e., by shifting that of $\rho$ backwards by one time unit.

Fig. 6

TEG from Fig. 3 with internal transition $x_2$ under PS

It should be clear that the overall system resulting from the method described above is no longer a TEG, as place $p_r$ has two upstream and two downstream transitions. As a consequence, it cannot be modeled solely by linear equations such as Eq. 3. In order to capture the restrictions imposed by PS on a transition $x_{\iota }$, we need to be able to express the relationship among transitions (and corresponding counters) $\rho$, $\alpha$, $x_{\iota }$, and $\xi$. For this, the Hadamard product of counters is used.

Recall from Def. 2 that the Hadamard product amounts to the coefficient-wise standard sum of counters. From the structure of Fig. 5 one can see that, at any time instant t, the combined accumulated number of firings of $\alpha$ and $x_{\iota }$ cannot exceed (in the conventional sense) that of $\rho$ and $\xi$. The Hadamard product allows us to translate this into the following condition:

$$\begin{aligned} \rho \odot \xi \, \preceq \, \alpha \odot x_{\iota }\,. \end{aligned}$$

(9)

With $\rho$, $\alpha$, and $\xi$ defined as described in this section, inequality Eq. 9 fully captures the restrictions imposed by PS on a transition $x_{\iota }$.

Remark 6

The formulation presented in this section does not entail any loss of generality with respect to that of Section 3.1. If transition $x_{\iota }$ is partially synchronized based on a synchronizing signal $\mathcal {S}$, the structure of Fig. 5 can be adopted to implement the same PS for $x_{\iota }$ by defining, for all $t\in \overline{\mathbb {Z}}$, $\rho (t)=\bigotimes _{\tau \le t} \mathcal {S}(\tau )$. Hence, the accumulated number of firings of $\rho$ by any time t is equal to the total number of firings of $x_{\iota }$ allowed by $\mathcal {S}$ up to t — naturally, not all such firings are necessarily performed by $x_\iota$, i.e., in general we have $x_\iota \succeq \rho$. Recall that $\alpha$ is then automatically defined as $\alpha =e\delta ^1\rho$.

Fig. 7

Illustration of the assumption that there is an input transition $u_\eta$ directly connected to partially-synchronized transition $x_{\iota }$ (cf. Remark 7)

Remark 7

We shall henceforth assume that the firings of a partially-synchronized transition $x_\iota$ can be allowed or prevented in real time, i.e., that there is a control input transition $u_\eta$ with a single downstream place which is initially empty, has zero holding time, and is an upstream place of $x_\iota$. This is illustrated in Fig. 7 for a general TEG, and it is the case, in particular, for the system from Example 2 (see input $u_2$ in Fig. 6). Note that this assumption is compatible with the real-world examples mentioned in the introduction; it is natural to assume that one is capable of deciding (through a direct control signal) whether or not a machine or piece of equipment should be turned on, the same being true about granting permission for a train/vehicle to enter a shared track segment.

We should emphasize that, even though from the point of view of the model structure and the description of TEGs from Section 2.5 both transitions $\rho$ and $u_\eta$ characterize “inputs” connected to $x_\iota$, their roles are conceptually very different. Whereas $u_\eta$ is indeed a control input whose firing schedule can be freely assigned, the firings of $\rho$ are assumed to be predetermined based on external factors, thus enforcing the restrictions from PS, as explained above.

Remark 8

The modeling method presented in this section naturally applies to the case of TEGs with multiple transitions under PS. Suppose that, in a given TEG, out of the n internal transitions, I are partially synchronized, with $I\le n$. PS is modeled by appending an independent structure like the one from Fig. 5 to each partially-synchronized transition $x_\iota$, accordingly adding subscripts to transitions — and corresponding counters — $\rho _\iota$, $\xi _\iota$, and $\alpha _\iota$. It is then straightforward to generalize the previous discussion leading to condition Eq. 9, namely every $x_\iota$ must obey

$$\begin{aligned} \rho _\iota \odot \xi _\iota \, \preceq \, \alpha _\iota \odot x_\iota \,. \end{aligned}$$

(10)

Based on Remark 7, we assume there is an input transition $u_\eta$ connected to each partially-synchronized transition $x_\iota$ via a place with zero holding time and no initial tokens.

3.3 Optimal control of TEGs with a single partially-synchronized transition

Consider a TEG modeled by linear equations 3, and suppose one of its internal transitions, $x_{\iota }$, is partially synchronized. We represent the PS phenomenon through the structure shown in Fig. 7, as discussed in Section 3.2, including input transition $u_\eta$ according to Remark 7. Recall that counters $\rho$ and $\alpha =e\delta ^1 \rho$ are predetermined. Given an output reference z, our objective is to obtain the optimal input ${u}_{\text {opt}}$ which leads to tracking the reference as closely as possible while respecting the partial synchronization of $x_{\iota }$ described by $\rho$, i.e., we seek the largest counter u such that $y=\mathcal {G} u \preceq z$ and such that Eq. 9 holds.

Let us start by noting that, as Eq. 4 describes the behavior of the TEG operating under the earliest firing rule, for an arbitrary input $u\in \Sigma ^{m\times 1}$ leading to a schedule of $x_\iota$ that respects Eq. 9, the schedule of all internal transitions can be uniquely determined through matrix $\mathcal {F}=A^*B \in \Sigma ^{n \times m}$, where n is the number of internal transitions and m the number of inputs in the TEG. Denoting the $\iota ^{\text {th}}$ row of $\mathcal {F}$ by $\mathcal {F}_{[\iota \varvec{\cdot }]}$ , we have $x_{\iota }=\mathcal {F}_{[\iota \varvec{\cdot }]}u$ . Applying this to Eq. 9, together with the fact that $\xi = e\delta ^1 x_{\iota }$ and $\alpha = e\delta ^1\rho$ (cf. Section 3.2), we can write

$$\begin{aligned} \rho \odot e\delta ^1 \mathcal {F}_{[\iota \varvec{\cdot }]} u\, \preceq \, e\delta ^1\rho \odot \mathcal {F}_{[\iota \varvec{\cdot }]} u\ . \end{aligned}$$

(11)

Recalling Proposition 2, inequality Eq. 11 is equivalent to

$$\begin{aligned}e\delta ^1 \mathcal {F}_{[\iota \varvec{\cdot }]} u\, \preceq \, (e\delta ^1\rho \odot \mathcal {F}_{[\iota \varvec{\cdot }]} u) \odot ^{\sharp } \rho \,, \end{aligned}$$

which, in turn, is equivalent to (cf. Remark 5)

$$\begin{aligned} u\, \preceq \, e\delta ^1 \mathcal {F}_{[\iota \varvec{\cdot }]} \circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} \big [(e\delta ^1\rho \odot \mathcal {F}_{[\iota \varvec{\cdot }]} u) \odot ^{\sharp } \rho \big ]\,.\end{aligned}$$

(12)

Finding an input which leads to tracking the reference while respecting Eq. 9 thus amounts to simultaneously solving $u\preceq \mathcal {G}\circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} z$ and Eq. 12, i.e., solving

$$\begin{aligned}u\, \preceq \, e\delta ^1 \mathcal {F}_{[\iota \varvec{\cdot }]} \circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} \big [(e\delta ^1\rho \odot \mathcal {F}_{[\iota \varvec{\cdot }]} u) \odot ^{\sharp } \rho \big ]\ \wedge \ \mathcal {G}\circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} z\,, \end{aligned}$$

which is equivalent to

$$\begin{aligned}u\, =\, e\delta ^1 \mathcal {F}_{[\iota \varvec{\cdot }]} \circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} \big [(e\delta ^1\rho \odot \mathcal {F}_{[\iota \varvec{\cdot }]} u) \odot ^{\sharp } \rho \big ]\ \wedge \ \mathcal {G}\circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} z\ \wedge \ u\,. \end{aligned}$$

The optimal input ${u}_{\text {opt}}$ is, therefore, the greatest fixed point of mapping ${\Phi : \Sigma ^{m\times 1} \rightarrow \Sigma ^{m\times 1}}$,

$$\begin{aligned} \Phi (u)\, =\, e\delta ^1 \mathcal {F}_{[\iota \varvec{\cdot }]} \circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} \big [(e\delta ^1\rho \odot \mathcal {F}_{[\iota \varvec{\cdot }]} u) \odot ^{\sharp } \rho \big ]\ \wedge \ \mathcal {G}\circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} z\ \wedge \ u\,. \end{aligned}$$

(13)

Notice that $\Phi$ consists in a succession of order-preserving operations (product $\otimes$, Hadamard product $\odot$ and its residual $\odot ^{\sharp }$, left-division $\circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}}$, and infimum $\wedge$), which, in turn, can be seen as the composition of corresponding isotone mappings (for instance, following the notation of Prop. 2, $s_1 \odot s_2$ corresponds to $\Pi _{s_1}\!(s_2)$, and similarly for the other operations). Therefore, according to Remark 2, $\Phi$ is also isotone; Remark 3 then ensures the existence of its greatest fixed point.

Fig. 8

Tracking of the reference z ($\triangle$) by the optimal output $y^{}_{opt }$ ($\,\bullet \,$) obtained in Example 3

Example 3

Let us revisit Example 1, only now with transition $x_2$ partially synchronized as in Example 2. For the TEG from Fig. 3, from Eq. 6 we have $\mathcal {F}_{[2\varvec{\cdot }]}= \begin{bmatrix} e\delta ^3(1\delta ^{6})^*\ {}&(1\delta ^{6})^* \end{bmatrix}$. With $\rho$ and $\alpha$ defined as in Example 2, we compute the greatest fixed point of mapping $\Phi$ to get

$$\begin{aligned} u_{\text {opt}}\, = \begin{bmatrix}u_{1_{\text {opt}}}\\ u_{2_{\text {opt}}} \end{bmatrix} = \begin{bmatrix} e\delta ^{3} \oplus 1\delta ^{9} \oplus 2\delta ^{15} \oplus 3\delta ^{22} \oplus 4\delta ^{+\infty }\\ e\delta ^{6} \oplus 1\delta ^{12} \oplus 2\delta ^{19} \oplus 3\delta ^{25} \oplus 4\delta ^{+\infty } \end{bmatrix}\,. \end{aligned}$$

The corresponding optimal output (see Remark 9, below) is

$$\begin{aligned} y_{\text {opt}}\, =\, \mathcal {G} u_{\text {opt}}\, =\, e\delta ^{10} \oplus 1\delta ^{16} \oplus 2\delta ^{23} \oplus 3\delta ^{29} \oplus 4\delta ^{+\infty }\,. \end{aligned}$$

The resulting reference tracking is illustrated in Fig. 8; as expected, performance is clearly degraded due to the additional restrictions imposed by PS, meaning the reference cannot be tracked as closely as in the case without PS (compare with Fig. 4).

Remark 9

Due to the additional restrictions for the firing of a partially-synchronized transition, in general it may be the case that a TEG under PS does not behave purely according to Eq. 3, and hence $y\ne \mathcal {G} u$. Nonetheless, since in the presented method the firing schedules of all input transitions are computed so as to respect condition Eq. 9 and to be just-in-time, a partially-synchronized transition $x_\iota$ is only going to be enabled when PS indeed allows it to fire. That is to say, the additional restrictions are dealt with offline in the computation phase, and the obtained optimal inputs guarantee that the evolution of the system will follow Eq. 3, as if unaffected by PS constraints. To put it in a formal way, as $x_{\iota _{opt }}=\mathcal {F}_{[\iota \varvec{\cdot }]}u_{\text {opt}}$ and as $x_{\iota _{opt }}$ satisfies Eq. 9, we have $x_{\text {opt}}=\mathcal {F} u_{\text {opt}}$ and hence $y_{\text {opt}}=\mathcal {G} u_{\text {opt}}$. Naturally, the same reasoning carries over to the case of multiple partially-synchronized transitions, to be discussed in Section 3.4.

Remark 10

For the just-in-time input $u_{\text {opt}}$ obtained through the method presented in this section, it holds that $\mathcal {F}_{[\iota \varvec{\cdot }]} u_{\text {opt}}=u_{\eta _\text {opt}}$. Intuitively, as $u_{\text {opt}}$ is computed so that $x_{\iota _{opt }}=\mathcal {F}_{[\iota \varvec{\cdot }]}u_{\text {opt}}$ respects condition Eq. 9, this means the control input $u_\eta$ enabling $x_\iota$ to fire is always provided exactly within the time windows in which PS allows $x_\iota$ to fire.

To show this, first note that, since $\mathcal {F}_{[\iota \varvec{\cdot }]} u_{opt }\, =\, x_{\iota _{opt }}\,\succeq \,u_{\eta _opt }$, it suffices to prove that $\mathcal {F}_{[\iota \varvec{\cdot }]} u_{opt }\preceq u_{\eta _opt }$. The proof goes by contradiction. Assume $\mathcal {F}_{[\iota \varvec{\cdot }]} u_{opt }\npreceq u_{\eta _opt }$, and consider the input $\widetilde{u}\in \Sigma ^{m\times 1}$ with

$$\begin{aligned} \widetilde{u}_\kappa \ =\ {\left\{ \begin{array}{ll} u_{\eta _opt }\oplus \mathcal {F}_{[\iota \varvec{\cdot }]} u_{opt }\,, &{}\text {for}\ \kappa = \eta \,,\\ u_{\kappa _{\text {opt}}} \,, &{}\text {for}\ \kappa \ne \eta \,. \end{array}\right. } \end{aligned}$$

Because input transition $u_{\eta }$ is connected to $x_\iota$ via a place with no initial tokens and zero holding time (see Remark 7 and Fig. 7), for matrix $B\in \Sigma ^{n\times m}$ as in Eq. 3 it follows that, for all $\mu \in \{1,\ldots ,n\}$,

$$\begin{aligned} B_{\mu \eta }\ =\ {\left\{ \begin{array}{ll} s_e \,, &{}\text {for}\ \mu = \iota \,,\\ s_{\varepsilon } \,, &{}\text {for}\ \mu \ne \iota \,. \end{array}\right. } \end{aligned}$$

(14)

So, denoting the $\eta ^{\text {th}}$ column of B by $B_{[\varvec{\cdot }\eta ]}$, for any $j\in \{1,\ldots ,n\}$ we have

$$\begin{aligned} \mathcal {F}_{j\eta }\, =\, [A^*B]_{j\eta }\, =\, [A^*]_{[j\varvec{\cdot }]} B_{[\varvec{\cdot }\eta ]}\, =\, [A^*]_{j\iota }\,. \end{aligned}$$

(15)

Moreover, as $x_{opt }$ is a solution of Eq. 3 and, therefore, $x_{opt }=A^*x_{opt }$ (cf. Remark 4), we have

$$\begin{aligned} x_{j_{\text {opt}}}\,=\,[A^*]_{[j\varvec{\cdot }]}x_{opt }\, =\,\bigoplus _{\mu =1}^{n} [A^*]_{j\mu }x_{\mu _{\text {opt}}}\, \succeq \, [A^*]_{j\iota }x_{\iota _{opt }}\,. \end{aligned}$$

Combined with Eq. 15, this means

$$\begin{aligned} x_{j_{\text {opt}}}\,\succeq \, \mathcal {F}_{j\eta }x_{\iota _{opt }}\ \end{aligned}$$

(16)

for all $j\in \{1,\ldots ,n\}$. Then,

$$\begin{aligned} \mathcal {F}_{[j\varvec{\cdot }]}\widetilde{u}\&=\ \bigoplus _{\begin{array}{c} \kappa =1\\ \kappa \ne \eta \end{array}}^m \mathcal {F}_{j\kappa } u_{\kappa _{\text {opt}}}\ \, \oplus \ \mathcal {F}_{j\eta } (u_{\eta _opt }\oplus \mathcal {F}_{[\iota \varvec{\cdot }]}u_{opt })\\&=\ \bigoplus _{\begin{array}{c} \kappa =1\\ \kappa \ne \eta \end{array}}^m \mathcal {F}_{j\kappa } u_{\kappa _{\text {opt}}}\ \, \oplus \ \mathcal {F}_{j\eta }u_{\eta _opt }\ \oplus \ \mathcal {F}_{j\eta }\mathcal {F}_{[\iota \varvec{\cdot }]}u_{opt }\\&=\, \bigoplus _{\kappa =1}^m \mathcal {F}_{j\kappa } u_{\kappa _{\text {opt}}}\ \, \oplus \ \mathcal {F}_{j\eta } \mathcal {F}_{[\iota \varvec{\cdot }]}u_{opt }\\&=\, \mathcal {F}_{[j\varvec{\cdot }]}u_{opt }\ \oplus \ \mathcal {F}_{j\eta } \mathcal {F}_{[\iota \varvec{\cdot }]}u_{opt }\\&=\, \mathcal {F}_{[j\varvec{\cdot }]}u_{opt }\,,\end{aligned}$$

where the last equality follows from Eq. 16 and the fact that ${\mathcal {F}_{[j\varvec{\cdot }]}u_{opt }=x_{j_{\text {opt}}}}$ for all $j\in \{1,\ldots ,n\}$ (which includes, of course, the case $j=\iota$). This implies $\mathcal {F}\widetilde{u}=\mathcal {F}u_{opt }$ and thus, recalling from Eq. 5 that $\mathcal {G}=C\mathcal {F}$, also ${\mathcal {G}\widetilde{u}=\mathcal {G}u_{opt }\preceq z}$, so $\widetilde{u}\preceq \mathcal {G}\circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} z$.

Furthermore, the fact that $\mathcal {F}_{[\iota \varvec{\cdot }]}\widetilde{u}=\mathcal {F}_{[\iota \varvec{\cdot }]}u_{opt }$ as shown above implies $\widetilde{u}$ satisfies Eq. 12, so we conclude that $\widetilde{u}$ is a fixed point of mapping $\Phi$. But $\widetilde{u} \succeq u_{\text {opt}}$ and $\widetilde{u} \ne u_{\text {opt}}$, contradicting the fact that $u_{\text {opt}}$ is the greatest fixed point of $\Phi$.

3.4 Optimal control of TEGs with multiple partially-synchronized transitions

Consider a TEG modeled by linear equations 3, and suppose I out of its n internal transitions are partially synchronized. We assume, for ease of discussion and without loss of generality, that the corresponding counters $x_\iota$ are the first I entries of vector $x\in \Sigma ^{n\times 1}$. The PS of each partially-synchronized transition $x_{\iota }$, $\iota \in \{1,\ldots ,I\}$, is again represented by a structure like the one from Fig. 7, accordingly adding subscripts to transitions — and corresponding counters — $\rho _\iota$, $\xi _\iota$, and $\alpha _\iota$. The assumptions from Remark 8 concerning input transitions $u_\eta$ connected to each $x_{\iota }$ are in place.

Besides tracking a given reference z as closely as possible, the optimal input must now be computed ensuring that Eq. 10 holds for every $\iota \in \{1,\ldots ,I\}$. Following the same arguments as in Section 3.3, one can see that inequality Eq. 10 is equivalent to

$$\begin{aligned} u\, \preceq \, e\delta ^1 \mathcal {F}_{[\iota \varvec{\cdot }]} \circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} \big [(e\delta ^1\rho _\iota \odot \mathcal {F}_{[\iota \varvec{\cdot }]} u) \odot ^{\sharp } \rho _\iota \big ]\,. \end{aligned}$$

(17)

Recall that $\mathcal {F}_{[\iota \varvec{\cdot }]}$ is the $\iota ^{\text {th}}$ row of $\mathcal {F}=A^*B$ as in Eq. 4, i.e., for an input u that leads to respecting Eq. 9 for every $\iota \in \{1,\ldots ,I\}$ we have $x_\iota =\mathcal {F}_{[\iota \varvec{\cdot }]}u$.

Defining the collection of mappings $\Phi _\iota : \Sigma ^{m\times 1} \rightarrow \Sigma ^{m\times 1}$,

$$\begin{aligned} \Phi _\iota (u)\, =\, e\delta ^1 \mathcal {F}_{[\iota \varvec{\cdot }]} \circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} \big [(e\delta ^1\rho _\iota \odot \mathcal {F}_{[\iota \varvec{\cdot }]} u) \odot ^{\sharp } \rho _\iota \big ]\,, \end{aligned}$$

where m is the number of input transitions in the system, an input $u\in \Sigma ^{m\times 1}$ satisfying Eq. 17 simultaneously for all $\iota \in \{1,\ldots ,I\}$ while respecting reference z is such that

$$\begin{aligned} u\preceq \bigwedge _{\iota =1}^I\! \Phi _\iota (u)\qquad \text {and}\qquad u \preceq \mathcal {G}\circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} z \end{aligned}$$

or, again through a reasoning similar to the one put forth in Section 3.3,

$$\begin{aligned} u\, = \bigwedge _{\iota =1}^I\! \Phi _\iota (u)\ \wedge \ \mathcal {G}\circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} z\ \wedge \ u\,. \end{aligned}$$

Hence, the input ${u}_{\text {opt}}$ which optimally tracks the reference while respecting Eq. 17 for all $\iota \in \{1,\ldots ,I\}$ is the greatest fixed point of the (isotone) mapping $\overline{\Phi } : \Sigma ^{m\times 1} \rightarrow \Sigma ^{m\times 1}$,

$$\begin{aligned} \overline{\Phi }(u)\, =\, \bigwedge _{\iota =1}^I\! \Phi _\iota (u)\ \wedge \ \mathcal {G}\circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} z\ \wedge \ u\,. \end{aligned}$$

(18)

Remark 11

Similarly to Remark 10, the method presented in this section yields a just-in-time input $u_{\text {opt}}$ such that $\mathcal {F}_{[\iota \varvec{\cdot }]} u_{\text {opt}}=u_{\iota _\text {opt}}$ for every $\iota \in \{1,\ldots ,I\}$. Again the intuition behind this fact is that, as the method guarantees that $x_{\iota _{opt }}=\mathcal {F}_{[\iota \varvec{\cdot }]}u_{\text {opt}}$ obeys Eq. 10 for all $\iota \in \{1,\ldots ,I\}$, no partially-synchronized transition $x_\iota$ is ever enabled to fire by the corresponding control input $u_\iota$ unless it is also allowed to fire by the PS restrictions.

To show this, let us first recall from Remark 8 that we can assume, without loss of generality, that $\eta =\iota$ whenever $u_\eta$ is connected to $x_{\iota }$. As ${\mathcal {F}_{[\iota \varvec{\cdot }]} u_{opt }\, =\, x_{\iota _{opt }}\succeq \,u_{\iota _\text {opt}}}$ for every $\iota \in \{1,\ldots ,I\}$, all that needs to be proved is that $\mathcal {F}_{[\iota \varvec{\cdot }]} u_{opt }\preceq u_{\iota _\text {opt}}$ for all $\iota$. The proof is again done by contradiction. Note that negating the claim “${\mathcal {F}_{[\iota \varvec{\cdot }]} u_{opt }\preceq u_{\iota _\text {opt}}}$ for all $\iota \in \{1,\ldots ,I\}$” implies assuming there exists $\widetilde{\iota }\in \{1,\ldots ,I\}$ such that $\mathcal {F}_{[\widetilde{\iota }\varvec{\cdot }]} u_{opt }\npreceq u_{\widetilde{\iota }_\text {opt}}$. Now, seeing as the arguments from Remark 10 are valid for an arbitrary $\iota$, the remainder of the proof proceeds identically to the referred remark, only replacing $\iota$ and $\eta$ with $\widetilde{\iota }$.

4 Optimal control of TEGs under varying PS

In this section, as the main contribution of this paper, we extend the results presented in Section 3 to the case of varying PS, i.e., where the restrictions on partially-synchronized transitions may change during run-time. We start with the simpler case of TEGs with a single partially-synchronized transition (Sections 4.1 and 4.2) and then proceed to generalize to the case of multiple partially-synchronized transitions (Section 4.3). In order to avoid breaking the flow and improve readability, some proofs are postponed to the appendix.

4.1 Problem formulation — the case of a single partially-synchronized transition

Consider a system modeled as a TEG with n internal transitions — one of which, $x_\iota$, is partially synchronized — and m input transitions — one of which, $u_\eta$, is connected to $x_\iota$ via a place with no initial tokens and zero holding time, according to Remark 7. Assume the system is operating optimally with respect to a given output-reference z, with optimal input $u_{\text {opt}}$ obtained according to the method presented in Section 3.

Now, suppose that at a certain time T the restrictions due to PS are altered, which, in terms of the modeling technique introduced in Section 3.2, means the firing schedule of transition $\rho$ is updated to a new one, $\rho '$. Naturally, as past firings cannot be altered, it must be the case that $\rho '(t)=\rho (t)$ for all $t\le T$. Define, inspired by Menguy et al. (2000), the mapping $r_T^{\ }: \Sigma \rightarrow \Sigma$ such that, for any $s\in \Sigma$, $r_T^{\ }(s)$ is the counter defined by

$$\begin{aligned}{}[r_T^{\ }(s)](t) = {\left\{ \begin{array}{ll} s(t) \,, &{}\text {if}\ t \le T\,,\\ \varepsilon \,, &{}\text {if}\ t > T\,. \end{array}\right. } \end{aligned}$$

(19)

We then have $r_T^{\ }(\rho ')=r_T^{\ }(\rho )$ — and thus, recalling that $\alpha = e\delta ^1\rho$, the schedule of transition $\alpha$ is also updated to $\alpha '$ with $r_{\!(T+1)}^{\ }(\alpha ')=r_{\!(T+1)}^{\ }(\alpha )$. Based on Eq. 9, the new restrictions imposed by PS on $x_\iota$ can be expressed by

$$\begin{aligned} \rho ' \odot \xi \, \preceq \, \alpha ' \odot x_\iota \,. \end{aligned}$$

(20)

Our goal is to determine the input $u_{\text {opt}}'$ which preserves $u_{\text {opt}}$ up to time T and which results in an output that tracks reference z as closely as possible, while guaranteeing that the resulting firing schedule for $x_\iota$, denoted $x_{\iota _{opt }}'$, observes the restrictions from PS expressed by Eq. 20. Recall, as argued in Section 3.3, that we can express the firing schedule of $x_\iota$ in terms of u as $x_\iota =\mathcal {F}_{[\iota \varvec{\cdot }]}u$, where $\mathcal {F}_{[\iota \varvec{\cdot }]}$ is the $\iota ^{\text {th}}$ row of $\mathcal {F}=A^*B$ as in Eq. 4. Combined with the fact that $\xi = e\delta ^1 x_\iota$ and $\alpha ' = e\delta ^1\rho '$ (cf. Section 3.2), this means we can write Eq. 20 as

$$\begin{aligned} \rho ' \odot e\delta ^1 \mathcal {F}_{[\iota \varvec{\cdot }]} u\, \preceq \, e\delta ^1\rho ' \odot \mathcal {F}_{[\iota \varvec{\cdot }]} u\,. \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \,\,(\star ) \end{aligned}$$

Let us now extend the definition Eq. 19 of mapping $r_T^{\ }$ to matrices, for simplicity using the same notation: for $A\in \Sigma ^{p\times q}$, $r_T^{\ }$ is applied entry-wise, i.e., $\big [r_T^{\ }(A)\big ]_{ij}=r_T^{\ }\big ([A]_{ij}\big )$ for any $i\in \{1,\ldots ,p\}$ and $j\in \{1,\ldots ,q\}$. The problem described above can then be stated as follows: find the greatest element of the set

$$\begin{aligned} \mathcal {Q}=\big \{u \in \Sigma ^{m\times 1}\ \vert \ \mathcal {G} u \preceq z\ \text {and}\ (\star )\ \text {and}\ r_T^{\ }(u) = r_T^{\ }(u_{opt })\big \}. \end{aligned}$$

(21)

4.2 Optimal update of the inputs — the case of a single partially-synchronized transition

As a first step towards determining the greatest element of set $\mathcal {Q}$ defined in Eq. 21, let us state the following result, which is an adaptation of Theorem 1 from Menguy et al. (2000).

Proposition 4

Let $\mathcal {D}$ be a complete idempotent semiring, $f : \mathcal {D} \rightarrow \mathcal {D}$ a residuated mapping, $\psi : \mathcal {D} \rightarrow \mathcal {D}$, and $c \in \mathcal {D}$. Consider the set

$$\begin{aligned} \mathcal {S}_{\psi } = \{x \in \mathcal {D}\,\vert \, x \preceq \psi (x)\ \text {and}\ f(x) = c\}\,\end{aligned}$$

and the isotone mapping $\Omega : \mathcal {D} \rightarrow \mathcal {D}$,

$$\begin{aligned} \Omega (x)\, =\, x \wedge \psi (x) \wedge f^{\sharp }(c)\,. \end{aligned}$$

If $\mathcal {S}_{\psi } \ne \emptyset$, we have $\bigoplus _{x\in \mathcal {S}_{\psi }}x\, =\, \bigoplus \{x\in \mathcal {D}\,\vert \, \Omega (x) = x\}$.

Now, notice that

$$\begin{aligned} (\star )&\Leftrightarrow \ e\delta ^1 \mathcal {F}_{[\iota \varvec{\cdot }]} u\, \preceq \, (e\delta ^1\rho ' \odot \mathcal {F}_{[\iota \varvec{\cdot }]} u) \odot ^{\sharp } \rho '\\&\Leftrightarrow \ u\, \preceq \, e\delta ^1 \mathcal {F}_{[\iota \varvec{\cdot }]} \circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} \big [(e\delta ^1\rho ' \odot \mathcal {F}_{[\iota \varvec{\cdot }]} u) \odot ^{\sharp } \rho '\big ]\,. \end{aligned}$$

So, defining the mapping $\Psi : \Sigma ^{m\times 1} \rightarrow \Sigma ^{m\times 1}$,

$$\begin{aligned} \Psi (u)\,=\, \mathcal {G}\circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} z\, \wedge \, e\delta ^1 \mathcal {F}_{[\iota \varvec{\cdot }]} \circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} \big [(e\delta ^1\rho ' \odot \mathcal {F}_{[\iota \varvec{\cdot }]} u) \odot ^{\sharp } \rho '\big ]\,, \end{aligned}$$

(22)

set $\mathcal {Q}$ can be equivalently written as

$$\begin{aligned} \mathcal {Q}=\big \{u \in \Sigma ^{m\times 1}\ \vert \ u \preceq \Psi (u)\ \text {and}\ r_T^{\ }(u) = r_T^{\ }(u_{\text {opt}})\big \}. \end{aligned}$$

Moreover, consider the following fact.

Remark 12

Mapping $r_T^{\ }$ as defined in Eq. 19 is residuated. Its residual is the mapping $r_T^{\,\sharp }: \Sigma \rightarrow \Sigma$ such that, for any $s\in \Sigma$, $r_T^{\,\sharp }(s)$ is the counter defined by

$$\begin{aligned}{}[r_T^{\,\sharp }(s)](t) = {\left\{ \begin{array}{ll} s(t) \,, &{}\text {if}\ t \le T\,,\\ s(T) \,, &{}\text {if}\ t > T\,. \end{array}\right. } \end{aligned}$$

In fact, $r_T^{\,\sharp }$ is clearly isotone and we have, for any $s\in \Sigma$, $r_T^{\ }\big (r_T^{\,\sharp }(s)\big ) = r_T^{\ }(s) \preceq s$ and $r_T^{\,\sharp }\big (r_T^{\ }(s)\big ) = r_T^{\,\sharp }(s) \succeq s$, so the conditions from Theorem 1 are fulfilled. Mapping $r_T^{\,\sharp }$ is applied to matrices entry-wise, the same way as $r_T^{\ }$.

A correspondence between set $\mathcal {Q}$ and set $\mathcal {S}_{\psi }$ from Prop. 4 is thus revealed: take $\mathcal {D}$ as $\Sigma ^{m\times 1}$, $\psi$ as $\Psi$, f as $r_T^{\ }$, and c as $r_T^{\ }(u_{\text {opt}})$. Therefore, as long as set $\mathcal {Q}$ is nonempty, recalling that mapping $r_T^{\ }$ is residuated (cf. Remark 12) and $r_T^{\,\sharp }\circ r_T^{\ }= r_T^{\,\sharp }$, we can apply the proposition to conclude that the sought optimal update of the input, $u_{\text {opt}}'$, is the greatest fixed point of mapping ${\Gamma : \Sigma ^{m\times 1} \rightarrow \Sigma ^{m\times 1}}$,

$$\begin{aligned} \Gamma (u)\,=\, u\, \wedge \, \Psi (u)\,\wedge \, r_T^{\,\sharp }(u_{\text {opt}})\,. \end{aligned}$$

(23)

The next step is to investigate whether set $\mathcal {Q}$ is nonempty. With that in mind, let us define the set

$$\begin{aligned} \widetilde{\mathcal {Q}}=\big \{u \in \Sigma ^{m\times 1}\ \vert \ (\star )\ \text {and}\ r_T^{\ }(u) = r_T^{\ }(u_{\text {opt}})\big \} \supseteq \mathcal {Q}\,. \end{aligned}$$

(24)

We look for an element $\underline{u}$ of $\widetilde{\mathcal {Q}}$ that leads to the fastest possible behavior of the system, i.e., to the least (in the order of $\Sigma$) possible counter $\underline{y}=\mathcal {G}\underline{u}$. If such an input does not lead to respecting reference z, then, since multiplication by $\mathcal {G}$ is order-preserving, clearly no input satisfying $(\star )$ and $r_T^{\ }(u) = r_T^{\ }(u_{\text {opt}})$ will. Formally, as shall be concluded in Corollary 7, $\mathcal {Q}\ne \emptyset \, \Leftrightarrow \, \mathcal {G}\underline{u}\preceq z$.

Even though $\widetilde{\mathcal {Q}}$ may not possess a least element, any input in $\widetilde{\mathcal {Q}}$ which leads to the fastest possible schedule of the internal transitions while guaranteeing that the restrictions due to PS are respected will result in the least possible schedule for the output y.

In the quest for such an input, we observe that a bound for the firing schedule of $x_\iota$ can be obtained² from Eq. 20, as, recalling from Section 3.2 that $\alpha '=e\delta ^1\rho '$ and $\xi = e\delta ^1 x_\iota$,

$$\begin{aligned} (20) \Leftrightarrow \ (\rho ' \odot e\delta ^1 x_\iota ) \odot ^{\flat } e\delta ^1\rho '\, \preceq \,x_\iota \,.\, \end{aligned}$$

The left-hand side of the latter inequality provides a bound for how small (in the sense of the order of $\Sigma$) $x_\iota$ can be. It represents the maximal number of firings allowed for $x_\iota$ under the PS-restrictions.

Furthermore, naturally no internal transition can fire more often than enabled by the inputs. Considering that input firings that have occurred before time T cannot be changed, the most often each input $u_\kappa$ can possibly fire from time T onward is encoded by the counter $r_T^{\ }(u_{\kappa _{\text {opt}}})$, which represents the preservation of past firings and then an infinite number of firings at time T. Thus, $\mathcal {F} r_T^{\ }(u_{\text {opt}})$ imposes a bound for x, limiting how often each internal transition can fire, i.e., we must have $x\succeq \mathcal {F} r_T^{\ }(u_{\text {opt}})$; in particular, this implies $x_\iota \succeq \mathcal {F}_{[\iota \varvec{\cdot }]} r_T^{\ }(u_{\text {opt}})$.

We also require x to be a solution of Eq. 3, which, according to Remark 4, implies $x=A^*x$. In particular, this means we must have $x_\iota =[A^*]_{[\iota \varvec{\cdot }]} x \succeq [A^*]_{\iota \iota } x_\iota$. But recall from Eq. 15 that $[A^*]_{\iota \iota }=\mathcal {F}_{\iota \eta }$, so the above condition can be written as $x_\iota \succeq \mathcal {F}_{\iota \eta }x_\iota$.

Based on the foregoing discussion, any schedule for $x_\iota$ must obey

$$\begin{aligned} x_\iota \,\succeq \,\big [(\rho ' \odot e\delta ^1 x_\iota ) \odot ^{\flat } e\delta ^1\rho '\big ]\, \oplus \, \mathcal {F}_{[\iota \varvec{\cdot }]} r_T^{\ }(u_{\text {opt}})\,\oplus \, \mathcal {F}_{\iota \eta } x_\iota \,, \end{aligned}$$

which is equivalent to saying $x_\iota$ must be a fixed point of the (isotone) mapping ${\Lambda : \Sigma \rightarrow \Sigma }$,

$$\begin{aligned} \Lambda (\chi )\,=\,\big [(\rho ' \odot e\delta ^1 \chi ) \odot ^{\flat } e\delta ^1\rho '\big ]\, \oplus \, \mathcal {F}_{[\iota \varvec{\cdot }]} r_T^{\ }(u_{\text {opt}})\,\oplus \, \mathcal {F}_{\iota \eta } \chi \,\oplus \,\chi \,. \end{aligned}$$

(25)

Remark 13

One can easily see that, for any $\widetilde{u}\in \widetilde{\mathcal {Q}}$, $\mathcal {F}_{[\iota \varvec{\cdot }]}\widetilde{u}$ is a fixed point of $\Lambda$, because

• $\widetilde{u}$ satisfies ($\star$), which is equivalent to

  $$\begin{aligned} (\rho ' \odot e\delta ^1 \mathcal {F}_{[\iota \varvec{\cdot }]} u) \odot ^{\flat } e\delta ^1\rho '\, \preceq \, \mathcal {F}_{[\iota \varvec{\cdot }]} u\,; \end{aligned}$$

  (26)

• $\mathcal {F}_{[\iota \varvec{\cdot }]}\widetilde{u}\, \succeq \, \mathcal {F}_{[\iota \varvec{\cdot }]} r_T^{\ }(\widetilde{u})\, =\, \mathcal {F}_{[\iota \varvec{\cdot }]} r_T^{\ }(u_{\text {opt}})$;

• $\widetilde{x}=\mathcal {F}\widetilde{u}$ is a solution of Eq. 3, so $\mathcal {F}_{[\iota \varvec{\cdot }]}\widetilde{u}\,=\,\widetilde{x}_\iota \,=\,[A^*]_{[\iota \varvec{\cdot }]}\widetilde{x}\,\succeq \, [A^*]_{\iota \iota }\widetilde{x}_\iota \, =\, \mathcal {F}_{\iota \eta } \widetilde{x}_\iota$ .

Remark 13 implies that any firing schedule of $x_\iota$ which is reachable from the inputs and which is compatible with the restrictions due to PS and with past input firings is in fact a fixed point of mapping $\Lambda$. What remains to be investigated then is whether the least fixed point of $\Lambda$ — which we shall denote $\underline{x}_\iota$ — is indeed feasible, i.e., whether there exists an input $\underline{u}$ which is an element of $\widetilde{\mathcal {Q}}$ and such that $\mathcal {F}_{[\iota \varvec{\cdot }]} \underline{u} = \underline{x}_\iota$ . In the following, we present a constructive proof that the answer is positive.

Define the vector $\theta \in \Sigma ^{m\times 1}$ such that, for all $\mu \in \{1,\ldots ,m\}$,

$$\begin{aligned} \theta _{\mu }={\left\{ \begin{array}{ll} \underline{x}_\iota \,, &{}\text {if}\ \mu = \eta \,,\\ s_{\varepsilon }\,, &{}\text {if}\ \mu \ne \eta \,, \end{array}\right. } \end{aligned}$$

and consider the input

$$\begin{aligned} \underline{u}\ =\ r_T^{\ }(u_{\text {opt}})\oplus \theta \ =\ \begin{bmatrix} r_T^{\ }(u_{1_{\tiny opt }})\\[1mm] \vdots \\ [-0.25mm] r_T^{\ }(u_{\eta _{\tiny opt }}) \oplus \underline{x}_\iota \\[1mm] \vdots \\ [-0.25mm] r_T^{\ }(u_{m_{\tiny opt }}) \end{bmatrix}. \end{aligned}$$

(27)

In order to show that $\mathcal {F}_{[\iota \varvec{\cdot }]} \underline{u} = \underline{x}_\iota$, first note that, as

$$\begin{aligned} A^*\,=\,\bigoplus _{\kappa \ge 0} A^{\kappa }\,=\, \mathcal {I}^{n\times n}\, \oplus \, \bigoplus _{\kappa \ge 1} A^{\kappa }\, \succeq \, \mathcal {I}^{n\times n}\,, \end{aligned}$$

(28)

where $A^0=\mathcal {I}^{n\times n}$ is the identity matrix in $\Sigma ^{n\times n}$ (see Remark 1), it follows that $\big [A^*\big ]_{\iota \iota }\succeq \big [\mathcal {I}^{n\times n}\big ]_{\iota \iota } = s_e$, so $\mathcal {F}_{\iota \eta }\underline{x}_\iota = \big [A^*\big ]_{\iota \iota }\underline{x}_\iota \succeq \underline{x}_\iota$. On the other hand, the fact that $\underline{x}_\iota$ is a fixed point of $\Lambda$ implies $\underline{x}_\iota \succeq \mathcal {F}_{\iota \eta }\underline{x}_\iota$, and hence

$$\begin{aligned} \ \mathcal {F}_{\iota \eta }\underline{x}_\iota \,=\,\underline{x}_\iota \,.\ \end{aligned}$$

(29)

Then, we have

$$\begin{aligned} \mathcal {F}_{[\iota \varvec{\cdot }]} \underline{u}\&=\ \bigoplus _{\begin{array}{c} \mu =1\\ \mu \ne \eta \end{array}}^m \mathcal {F}_{\iota \mu }r_T^{\ }(u_{\mu _{\tiny opt }})\ \, \oplus \, \mathcal {F}_{\iota \eta }\big (r_T^{\ }(u_{\eta _{\tiny opt }}) \oplus \underline{x}_\iota \big )\\&=\ \bigoplus _{\begin{array}{c} \mu =1\\ \mu \ne \eta \end{array}}^m \mathcal {F}_{\iota \mu }r_T^{\ }(u_{\mu _{\tiny opt }})\ \, \oplus \, \mathcal {F}_{\iota \eta }r_T^{\ }(u_{\eta _{\tiny opt }})\, \oplus \, \mathcal {F}_{\iota \eta }\underline{x}_\iota \\&=\ \bigoplus _{\mu =1}^m \mathcal {F}_{\iota \mu }r_T^{\ }(u_{\mu _{\tiny opt }})\ \, \oplus \, \mathcal {F}_{\iota \eta }\underline{x}_\iota \\&=\ \mathcal {F}_{[\iota \varvec{\cdot }]} r_T^{\ }(u_{opt })\,\oplus \, \underline{x}_\iota \hspace{1.2cm}\text {(because of (A3))}\\&=\ \underline{x}_\iota \hspace{3.65cm}\text {(as}\, \underline{x}_\iota \, \text {is a fixed point of}\, \Lambda ). \end{aligned}$$

Now, to prove that $\underline{u}\in \widetilde{\mathcal {Q}}$, we begin by noticing that, because $\underline{x}_\iota$ is a fixed point of $\Lambda$,

$$\begin{aligned}(\rho ' \odot e\delta ^1 \underline{x}_\iota ) \odot ^{\flat } e\delta ^1\rho '\, \preceq \, \underline{x}_\iota \,. \end{aligned}$$

Combined with the fact that $\mathcal {F}_{[\iota \varvec{\cdot }]}\underline{u} = \underline{x}_\iota$ as shown above, this implies taking $u=\underline{u}$ satisfies Eq. 26, which is equivalent to $(\star )$.

It remains to show that $r_T^{\ }(\underline{u}) = r_T^{\ }(u_{\text {opt}})$. Note that, as $r_T^{\ }\circ r_T^{\ }=r_T^{\ }$, for $\mu \ne \eta$ it trivially holds that $r_T^{\ }(\underline{u}_{\mu }) = r_T^{\ }(u_{\mu _{\tiny opt }})$. The problem is then reduced to showing that $r_T^{\ }(\underline{u}_{\eta }) =r_T^{\ }\big (r_T^{\ }(u_{\eta _{\tiny opt }}) \oplus \underline{x}_\iota \big ) = r_T^{\ }(u_{\eta _{\tiny opt }})$, which, in turn, as $r_T^{\ }$ distributes over $\oplus$, is equivalent to $r_T^{\ }(u_{\eta _{\tiny opt }}) \oplus r_T^{\ }(\underline{x}_\iota ) = r_T^{\ }(u_{\eta _{\tiny opt }})$, or $r_T^{\ }(\underline{x}_\iota )\preceq r_T^{\ }(u_{\eta _{\tiny opt }})$. Our argument will be based on the following result.

Proposition 5

$r_T^{\,\sharp }(x_{\iota _{opt }})$ is a fixed point of mapping $\Lambda$.

A consequence of Prop. 5 is that $\underline{x}_\iota \preceq r_T^{\,\sharp }(x_{\iota _{opt }}) = r_T^{\,\sharp }(\mathcal {F}_{[\iota \varvec{\cdot }]} u_{\text {opt}})$. We also know from Remark 10 that $\mathcal {F}_{[\iota \varvec{\cdot }]} u_{\text {opt}}=u_{\eta _{\tiny opt }}$. Thus, as $r_T^{\ }$ is isotone and recalling that $r_T^{\ }\circ r_T^{\,\sharp }= r_T^{\ }$,

$$\begin{aligned} r_T^{\ }(\underline{x}_\iota )\, \preceq \, r_T^{\ }\big (r_T^{\,\sharp }(u_{\eta _{\tiny opt }})\big )\,=\, r_T^{\ }(u_{\eta _{\tiny opt }})\,, \end{aligned}$$

concluding the proof that $\underline{u}\in \widetilde{\mathcal {Q}}$.

This does not guarantee, however, that $\mathcal {Q}\ne \emptyset$, as it is possible that $\mathcal {G} \underline{u} \npreceq z$ and hence $\underline{u}\notin \mathcal {Q}$. Intuitively, if the new restrictions from PS on $x_\iota$ are more stringent than the original ones, since up to time T we implemented just-in-time inputs based on the original restrictions, it may be impossible to respect both reference z and the new restrictions after T. As we assume PS-restrictions to be hard ones, this means we have no choice but to relax z, i.e., look for a new reference $z'\succeq z$ for which a solution exists. In fact, we seek the least possible such $z'$, in order to remain as close as possible to the original reference. A natural choice is then to take $z'=z\oplus \mathcal {G} \underline{u}$; as $\oplus$ is performed coefficient-wise on counters, this amounts to preserving the terms of z that can still be achieved if $\underline{u}$ is taken as input, and relaxing those that cannot only as much as necessary to be matched by the resulting output $y=\mathcal {G} \underline{u}$. The following proposition establishes that this is indeed the optimal way of relaxing z.

Proposition 6

Let $\mathcal {Q}'$ denote the set defined as $\mathcal {Q}$ in Eq. 21, only replacing z with $z'$, and let $\underline{u}$ be defined as in Eq. 27. The least $z'\succeq z$ such that $\mathcal {Q}'\ne \emptyset$ is $z'=z\oplus \mathcal {G} \underline{u}$.

Prop. 6 also provides a simple way to check whether set $\mathcal {Q}$ is nonempty.

Corollary 7

Let $\mathcal {Q}$ be defined as in Eq. 21 and $\underline{u}$ as in Eq. 27. Then, $\mathcal {Q}\ne \emptyset \, \Leftrightarrow \, \mathcal {G}\underline{u}\preceq z$.

In the case $\mathcal {Q}$ turns out to be empty, define the mapping ${\Psi ' : \Sigma ^{m\times 1} \rightarrow \Sigma ^{m\times 1}}$ as $\Psi$ in Eq. 22, only replacing z with $z'=z\oplus \mathcal {G} \underline{u}$. Following the same procedure as before, we can apply Prop. 4 — only now taking $\psi$ as $\Psi '$ instead of $\Psi$ — to conclude that $u_{\text {opt}}'$ is the greatest fixed point of mapping $\Gamma ' : \Sigma ^{m\times 1} \rightarrow \Sigma ^{m\times 1}$,

$$\begin{aligned} \Gamma '(u)\, =\, u\, \wedge \, \Psi '(u)\, \wedge \, r_T^{\,\sharp }(u_{\text {opt}})\,. \end{aligned}$$

(30)

Example 4

Consider, once more, the system from Example 1, with transition $x_2$ partially synchronized as in Example 2, and assume it is operating optimally according to the input obtained in Example 3. Now, suppose that at time $T=14$ the restrictions from PS are updated as follows: transition $x_2$ is no longer allowed to fire at times 18 and 19. This means that now $x_2$ may only fire at times

$$\begin{aligned} t\in \mathcal {T}' =\big \{[4,6] \cup [10,12] \cup [24,27]\cup [31,32]\big \}\subset \mathbb {Z}\,. \end{aligned}$$

The new schedule $\rho '$ for transition $\rho$ is defined similarly as in Example 2:

$$\begin{aligned} \rho '(t) = {\left\{ \begin{array}{ll} e &{} \text {if}\ t\le 4\,; \\ 1\otimes \rho '(t-1) &{} \text {if}\ t-1\in \mathcal {T}'\,;\\ \rho '(t-1) &{} \text {if}\ t-1\notin \mathcal {T}'\ \text {and}\ t>4\,. \end{array}\right. } \end{aligned}$$

The explicit counter thus obtained is

$$\begin{aligned} \rho '\, =\&e\delta ^4\oplus 1\delta ^5\oplus 2\delta ^6\oplus 3\delta ^{10}\oplus 4\delta ^{11}\oplus 5\delta ^{12}\oplus 6\delta ^{24} \oplus 7\delta ^{25} \oplus 8\delta ^{26}\\ {}&\oplus 9\delta ^{27}\oplus 10\delta ^{31}\oplus 11\delta ^{32}\oplus 12\delta ^{+\infty }\,. \end{aligned}$$

According to the discussion following Prop. 6, in order to check whether reference z is still achievable — i.e., whether $\mathcal {Q}\ne \emptyset$ — we compute input $\underline{u}$ as indicated in Eq. 27; for that, we first need to compute $\underline{x}_2$, which is the least fixed point of mapping $\Lambda$ defined in Eq. 25. Note that, as the total number of output firings required by reference z is 4, we know the computed just-in-time inputs will not fire more than 4 times in total, and consequently the same is true for transition $x_2$. Thus, in order to simplify computations, the initial counter $\chi$ for computing the least fixed point of $\Lambda$ may be chosen such that $\chi (t)\succeq 4$ for all t. As we also know that the obtained least fixed point $\underline{x}_2$ will be such that $\underline{x}_2\succeq \mathcal {F}_{[2\varvec{\cdot }]} r_T^{\ }(u_{\text {opt}})$, a natural choice for the starting point of the fixed point algorithm is $\chi \,=\,\mathcal {F}_{[2\varvec{\cdot }]} r_T^{\ }(u_{\text {opt}})\oplus 4\delta ^{+\infty }$; the first term in the sum represents the maximal (in the standard sense) possible number of firings of $x_2$, and the second truncates counter $\chi$ so that the total number of firings does not exceed 4. We obtain

$$\begin{aligned} \underline{x}_2\,=\, e\delta ^{6} \oplus 1\delta ^{12} \oplus 2\delta ^{24} \oplus 3\delta ^{31} \oplus 4\delta ^{+\infty } \end{aligned}$$

and then

$$\begin{aligned} \underline{u}\,=\, \begin{bmatrix} e\delta ^{3} \oplus 1\delta ^{9} \oplus 2\delta ^{14} \oplus \varepsilon \delta ^{+\infty }\\ e\delta ^{6} \oplus 1\delta ^{12} \oplus 2\delta ^{24} \oplus 3\delta ^{31} \oplus 4\delta ^{+\infty } \end{bmatrix}\,. \end{aligned}$$

This yields

$$\begin{aligned} \mathcal {G}\underline{u}\,=\, e\delta ^{10} \oplus 1\delta ^{16} \oplus 2\delta ^{28} \oplus 3\delta ^{35} \oplus 4\delta ^{+\infty }\,\npreceq \,z\,, \end{aligned}$$

implying $\mathcal {Q}= \emptyset$. Thus, we need to relax reference z according to Prop. 6, which gives

$$\begin{aligned} z' \,=\, e\delta ^{14} \oplus 1\delta ^{23} \oplus 2\delta ^{28} \oplus 3\delta ^{35} \oplus 4\delta ^{+\infty }\,. \end{aligned}$$

Finally, the updated optimal input $u_{\text {opt}}'$ is obtained by computing the greatest fixed point of mapping $\overline{\Gamma }$, resulting in

$$\begin{aligned} u_{\text {opt}}'\,=\, \begin{bmatrix} e\delta ^{3} \oplus 1\delta ^{9} \oplus 2\delta ^{21} \oplus 3\delta ^{28}\oplus 4\delta ^{+\infty }\\ e\delta ^{6} \oplus 1\delta ^{12} \oplus 2\delta ^{24} \oplus 3\delta ^{31} \oplus 4\delta ^{+\infty } \end{bmatrix} \end{aligned}$$

and

$$\begin{aligned} y_{\text {opt}}'\,=\,\mathcal {G}u_{\text {opt}}'\,=\, e\delta ^{10} \oplus 1\delta ^{16} \oplus 2\delta ^{28} \oplus 3\delta ^{35} \oplus 4\delta ^{+\infty }\,. \end{aligned}$$

The tracking of the new reference $z'$ by the updated output $y_{\text {opt}}'$ is shown in Fig. 9.

Fig. 9

Tracking of the new reference $z'$ ($\triangle$) by the updated optimal output $y_{\text {opt}}'$ ($\,\bullet \,$) obtained in Example 4

4.3 Problem formulation and optimal update of the inputs — the case of multiple partially-synchronized transitions

Consider a system modeled as a TEG with n internal transitions — I of which are partially synchronized — and m input transitions. As in Section 3.4, for ease of discussion and without loss of generality let us assume that the corresponding counters $x_\iota$ are the first I entries of vector $x\in \Sigma ^{n\times 1}$. Based on Remark 8, we also assume there is an input transition $u_\eta$ connected to each partially-synchronized transition $x_\iota$ via a place with zero holding time and no initial tokens. Moreover, again to facilitate the discussion and without loss of generality, let these inputs be the first I entries of the input vector $u\in \Sigma ^{m\times 1}$, and let $\eta =\iota$ whenever $u_\eta$ is connected to $x_\iota$. Suppose the system is operating optimally with respect to a given output-reference z, with optimal input $u_{\text {opt}}$ obtained according to the method presented in Section 3.

Now, suppose that at a certain time T the restrictions due to PS are altered for some (possibly all) $x_\iota$, $\iota \in \{1,\ldots ,I\}$. In terms of the modeling technique introduced in Section 3.2, this means that, for each $\iota \in \{1,\ldots ,I\}$, the firing schedule of transition $\rho _\iota$ is updated to a new one, $\rho _\iota '$, with $r_T^{\ }(\rho _\iota ')=r_T^{\ }(\rho _\iota )$ (and with the possibility that $\rho _\iota '=\rho _\iota$). Recalling that we have $\alpha _\iota = e\delta ^1\rho _\iota$, the schedule of transition $\alpha _\iota$ is thus also updated to $\alpha _\iota '$ with $r_{\!(T+1)}^{\ }(\alpha _\iota ')=r_{\!(T+1)}^{\ }(\alpha _\iota )$. Based on Eq. 10, the new restrictions imposed by PS on each partially-synchronized transition $x_\iota$ can be expressed by

$$\begin{aligned} \rho _\iota ' \odot \xi _\iota \, \preceq \, \alpha _\iota ' \odot x_\iota \,. \end{aligned}$$

(31)

Our goal is to determine the input $u_{\text {opt}}'$ which preserves $u_{\text {opt}}$ up to time T and which results in an output that tracks reference z as closely as possible, while guaranteeing, for every $\iota \in \{1,\ldots ,I\}$, that the resulting firing schedule for $x_\iota$, denoted $x_{\iota _{opt }}'$, observes the restrictions from PS expressed by Eq. 31.

Recall that we can express the firing schedule of each $x_\iota$ in terms of u as $x_\iota =\mathcal {F}_{[\iota \varvec{\cdot }]}u$, where $\mathcal {F}_{[\iota \varvec{\cdot }]}$ is the $\iota ^{\text {th}}$ row of $\mathcal {F}=A^*B$ as in Eq. 4. Combined with the fact that $\xi _\iota = e\delta ^1 x_\iota$ and $\alpha _\iota ' = e\delta ^1\rho _\iota '$ (cf. Section 3.2), this means we can write Eq. 31 as

$$\begin{aligned} \rho _\iota ' \odot e\delta ^1 \mathcal {F}_{[\iota \varvec{\cdot }]} u\, \preceq \, e\delta ^1\rho _\iota ' \odot \mathcal {F}_{[\iota \varvec{\cdot }]} u\,.\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (\star \star ) \end{aligned}$$

The problem described above can then be stated as follows: find the greatest element of the set

$$\begin{aligned} \begin{aligned} \mathcal {V}\,=\,\big \{u \in \Sigma ^{m\times 1}\ \vert \ {}&\mathcal {G} u \preceq z\ \text {and}\ r_T^{\ }(u) = r_T^{\ }(u_{\text {opt}})\\&\ \ \text {and}\, (\star \star )\, \text {holds for all}\ \iota \in \{1,\ldots ,I\}\big \}. \end{aligned} \end{aligned}$$

(32)

Along the lines of Section 4.2, we set out to look for the greatest element of set $\mathcal {V}$ defined in Eq. 32 by noticing that

$$\begin{aligned} (\star \star )&\Leftrightarrow \ e\delta ^1 \mathcal {F}_{[\iota \varvec{\cdot }]} u\, \preceq \, (e\delta ^1\rho _\iota ' \odot \mathcal {F}_{[\iota \varvec{\cdot }]} u) \odot ^{\sharp } \rho _\iota '\\&\Leftrightarrow \ u\, \preceq \, e\delta ^1 \mathcal {F}_{[\iota \varvec{\cdot }]} \circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} \big [(e\delta ^1\rho _\iota ' \odot \mathcal {F}_{[\iota \varvec{\cdot }]} u) \odot ^{\sharp } \rho _\iota '\big ]\,. \end{aligned}$$

Let us define, for each $\iota \in \{1,\ldots ,I\}$, the mapping $\Psi _\iota : \Sigma ^{m\times 1} \rightarrow \Sigma ^{m\times 1}$,

$$\begin{aligned} \Psi _\iota (u)\,=\, e\delta ^1 \mathcal {F}_{[\iota \varvec{\cdot }]} \circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} \big [(e\delta ^1\rho _\iota ' \odot \mathcal {F}_{[\iota \varvec{\cdot }]} u) \odot ^{\sharp } \rho _\iota '\big ]\,, \end{aligned}$$

and also the mapping $\overline{\Psi } : \Sigma ^{m\times 1} \rightarrow \Sigma ^{m\times 1}$,

$$\begin{aligned} \overline{\Psi }(u)\,=\, \mathcal {G}\circ {\hspace{-7.0pt}}\backslash {\hspace{-0.1pt}} z\, \wedge \, \bigwedge _{\iota =1}^{I}\Psi _\iota (u)\,. \end{aligned}$$

(33)

Note that u satisfying ($\star \star$) is equivalent to $u\preceq \Psi _\iota (u)$, so we can write set $\mathcal {V}$ equivalently as

$$\begin{aligned} \mathcal {V}=\big \{u \in \Sigma ^{m\times 1}\ \vert \ u \preceq \overline{\Psi }(u)\ \text {and}\ r_T^{\ }(u) = r_T^{\ }(u_{\text {opt}})\big \}. \end{aligned}$$

The problem stated above can then be solved by applying Prop. 4, taking $\mathcal {D}$ as $\Sigma ^{m\times 1}$, $\psi$ as $\overline{\Psi }$, f as $r_T^{\ }$, and c as $r_T^{\ }(u_{\text {opt}})$. Thus, as long as set $\mathcal {V}$ is nonempty, recalling that mapping $r_T^{\ }$ is residuated (cf. Remark 12) and $r_T^{\,\sharp }\circ r_T^{\ }= r_T^{\,\sharp }$, the sought optimal update of the input, $u_{\text {opt}}'$, is the greatest fixed point of mapping ${\overline{\Gamma } : \Sigma ^{m\times 1} \rightarrow \Sigma ^{m\times 1}}$,

$$\begin{aligned} \overline{\Gamma }(u)\,=\, u\, \wedge \, \overline{\Psi }(u)\,\wedge \, r_T^{\,\sharp }(u_{\text {opt}})\,. \end{aligned}$$

(34)

Next, we must investigate whether set $\mathcal {V}$ is nonempty. To that end, let us define the set

$$\begin{aligned} \begin{aligned} \widetilde{\mathcal {V}}=\big \{u \in \Sigma ^{m\times 1}\ \vert \ (\star \star )\, \text {holds for all}\ {}&\iota \in \{1,\ldots ,I\}\\ {}&\!\!\!\text {and}\ r_T^{\ }(u) = r_T^{\ }(u_{\text {opt}})\big \}\,. \end{aligned} \end{aligned}$$

(35)

We look for an element $\underline{u}$ of $\widetilde{\mathcal {V}}$ that leads to the fastest possible behavior of the system, i.e., to the least (in the order of $\Sigma$) possible firing schedule of y. If such an input does not ensure that reference z is respected, then clearly there does not exist any input that does so while satisfying ($\star \star$) for all $\iota \in \{1,\ldots ,I\}$ and $r_T^{\ }(u) = r_T^{\ }(u_{\text {opt}})$. This means, as shall be concluded formally in Corollary 11, $\mathcal {V}\ne \emptyset \, \Leftrightarrow \, \mathcal {G}\underline{u}\preceq z$.

In general, set $\widetilde{\mathcal {V}}$ may not possess a least element. Nevertheless, our goal is to find an input in $\widetilde{\mathcal {V}}$, not necessarily least or unique, which leads to the fastest possible schedule of the internal transitions while guaranteeing that the restrictions on all partially-synchronized transitions are respected, as this will result in the least possible schedule for the output y.

Note that, for any $\iota \in \{1,\ldots ,I\}$, a bound for the firing schedule of $x_\iota$ can be obtained from Eq. 31, as, recalling from Section 3.2 that $\alpha _\iota '=e\delta ^1\rho _\iota '$ and $\xi _\iota = e\delta ^1 x_\iota$,

$$\begin{aligned} (31) \Leftrightarrow \ (\rho _\iota ' \odot e\delta ^1 x_\iota ) \odot ^{\flat } e\delta ^1\rho _\iota '\, \preceq \,x_\iota \,. \end{aligned}$$

In the latter inequality, the left-hand side establishes a bound for how small (in the sense of the order of $\Sigma$) $x_\iota$ can be, representing the maximal number of firings allowed for $x_\iota$ under the PS-restrictions.

Additionally, as no internal transition can fire more often than enabled by the inputs and as the most often each input $u_\kappa$ can possibly fire from time T onward is encoded by the counter $r_T^{\ }(u_{\kappa _{\text {opt}}})$ (because past firings must be preserved), one can see that $\mathcal {F} r_T^{\ }(u_{\text {opt}})$ imposes a bound for x, i.e., it must hold that $x\succeq \mathcal {F} r_T^{\ }(u_{\text {opt}})$. In particular, for each $\iota \in \{1,\ldots ,I\}$, this implies $x_\iota \succeq \mathcal {F}_{[\iota \varvec{\cdot }]} r_T^{\ }(u_{\text {opt}})$.

It is also natural to require that x be a solution of Eq. 3, which, according to Remark 4, implies $x=A^*x$. In particular, for each ${\iota \in \{1,\ldots ,I\}}$, this means we must have ${x_\iota =[A^*]_{[\iota \varvec{\cdot }]} x \succeq [A^*]_{\iota j} x_j}$ for all ${j\in \{1,\ldots ,I\}}$. But note that Eq. 15 implies ${[A^*]_{\iota j}=\mathcal {F}_{\iota j}}$ for any ${\iota ,j\in \{1,\ldots ,I\}}$; hence, we can rewrite the above condition as ${x_\iota \succeq \mathcal {F}_{\iota j}x_j}$.

In conclusion, for every $\iota \in \{1,\ldots ,I\}$, any schedule for $x_\iota$ must obey

$$\begin{aligned} x_\iota \,\succeq \,\big [(\rho _\iota ' \odot e\delta ^1 x_\iota ) \odot ^{\flat } e\delta ^1\rho _\iota '\big ]\, \oplus \, \mathcal {F}_{[\iota \varvec{\cdot }]} r_T^{\ }(u_{\text {opt}})\,\oplus \, \bigoplus _{j=1}^I \mathcal {F}_{\iota j} x_j\,. \end{aligned}$$

(36)

Note that the inequality above — in particular, its last term — implies the schedules of all partially-synchronized transitions are interdependent. Therefore, we must look for the fastest feasible schedule of all such transitions simultaneously. With that in mind, define, for each $\iota \in \{1,\ldots ,I\}$, the mapping ${\Lambda _\iota : \Sigma ^{n\times 1} \rightarrow \Sigma }$,

$$\begin{aligned} \Lambda _\iota (x)\,=\,\big [(\rho _\iota ' \odot e\delta ^1 x_\iota ) \odot ^{\flat } e\delta ^1\rho _\iota '\big ]\, \oplus \, \mathcal {F}_{[\iota \varvec{\cdot }]} r_T^{\ }(u_{\text {opt}})\,\oplus \, \bigoplus _{j=1}^I \mathcal {F}_{\iota j} x_j\ \,\oplus \,x_\iota \,, \end{aligned}$$

and then define the mapping ${\overline{\Lambda } : \Sigma ^{n\times 1} \rightarrow \Sigma ^{n\times 1}}$,

$$\begin{aligned} \Big [\overline{\Lambda }(x)\Big ]_\kappa \ =\ {\left\{ \begin{array}{ll} \Lambda _\kappa (x) \,, &{}\text {if}\ 1\le \kappa \le I\,,\\ x_\kappa \oplus \mathcal {F}_{[\kappa \varvec{\cdot }]} r_T^{\ }(u_{\text {opt}}) \,, &{}\text {if}\ I+1\le \kappa \le n\,. \end{array}\right. } \end{aligned}$$

(37)

Based on the foregoing discussion, it is clear that any vector $x\in \Sigma ^{n\times 1}$ whose entries are feasible schedules for the internal transitions $x_\kappa$, ${\kappa \in \{1,\ldots ,n\}}$, must be a fixed point of mapping $\overline{\Lambda }$. The following remark formalizes the idea.

Remark 14

For any $\widetilde{u}\in \widetilde{\mathcal {V}}$, it follows that $\mathcal {F}\widetilde{u}\in \Sigma ^{n\times 1}$ is a fixed point of mapping $\overline{\Lambda }$. To show this, first note that, for any ${\iota \in \{1,\ldots ,I\}}$, $\widetilde{u}$ satisfies ($\star \star$), which is equivalent to

$$\begin{aligned} (\rho _\iota ' \odot e\delta ^1 \mathcal {F}_{[\iota \varvec{\cdot }]} u) \odot ^{\flat } e\delta ^1\rho _\iota '\, \preceq \, \mathcal {F}_{[\iota \varvec{\cdot }]} u\,. \end{aligned}$$

(38)

Moreover, $\widetilde{x}=\mathcal {F}\widetilde{u}$ is a solution of Eq. 3, so from Remark 4 it follows that $\widetilde{x}=A^*\widetilde{x}$ and hence

$$\begin{aligned} \widetilde{x}_\iota \,=\,[A^*]_{[\iota \varvec{\cdot }]}\widetilde{x}\,\succeq \, [A^*]_{\iota j}\widetilde{x}_j\, =\, \mathcal {F}_{\iota j} \widetilde{x}_j \end{aligned}$$

for all ${j\in \{1,\ldots ,I\}}$. Finally, for all ${\kappa \in \{1,\ldots ,n\}}$, we have

$$\begin{aligned} \mathcal {F}_{[\kappa \varvec{\cdot }]}\widetilde{u}\, \succeq \, \mathcal {F}_{[\kappa \varvec{\cdot }]} r_T^{\ }(\widetilde{u})\, =\, \mathcal {F}_{[\kappa \varvec{\cdot }]} r_T^{\ }(u_{\text {opt}})\,. \end{aligned}$$

Remark 14 implies that, if any $x\in \Sigma ^{n\times 1}$ comprises firing schedules of internal transitions which are compatible with past input firings and such that the schedules $x_\iota$ of partially-synchronized transitions are reachable from the inputs and are compatible with the restrictions due to PS, then such x is in fact a fixed point of mapping $\overline{\Lambda }$. Thus, what remains to be checked is whether the least fixed point of $\overline{\Lambda }$ — which we shall denote $\underline{x}$ — is indeed feasible, i.e., whether there exists an input $\underline{u}$ which is an element of $\widetilde{\mathcal {V}}$ and such that $\mathcal {F}\underline{u} = \underline{x}$. Similarly to Section 4.2, we prove constructively that the answer is affirmative. As the proof is analogous to the corresponding discussion in Section 4.2, we state the two key facts as propositions and omit their proofs from the present discussion. The interested reader can find the proofs in Appendix A.2.

Let us denote the $\mu ^\text {th}$ entry of $\underline{x}$ by $\underline{x}_\mu$, and define the vector ${\theta \in \Sigma ^{m\times 1}}$ such that, for all $\mu \in \{1,\ldots ,m\}$,

$$\begin{aligned} \theta _{\mu }={\left\{ \begin{array}{ll} \underline{x}_\mu \,, &{}\text {if}\ 1\le \mu \le I\,,\\ s_{\varepsilon } \,, &{}\text {if}\ I+1\le \mu \le m\,. \end{array}\right. } \end{aligned}$$

Now, consider the input

$$\begin{aligned} \underline{u}\ =\ r_T^{\ }(u_{\text {opt}})\oplus \theta \ =\ \begin{bmatrix} r_T^{\ }(u_{1_{\text {opt}}}) \oplus \underline{x}_1\\[1mm] \vdots \\ [-0.25mm] r_T^{\ }(u_{I_{\text {opt}}}) \oplus \underline{x}_I\\[0.5mm] r_T^{\ }(u_{(I+1)_{\text {opt}}})\\[1mm] \vdots \\ [-0.25mm] r_T^{\ }(u_{m_{\text {opt}}}) \end{bmatrix}. \end{aligned}$$

(39)

Proposition 8

Let $\underline{u}$ be defined as in Eq. 39, $\underline{x}$ the least fixed point of mapping $\overline{\Lambda }$ defined in Eq. 37, and $\mathcal {F}=A^*B$ as in Eq. 4. Then, it holds that $\mathcal {F}\underline{u} = \underline{x}$.

Proposition 9

Vector $\underline{u}$ defined as in Eq. 39 is an element of set $\widetilde{\mathcal {V}}$ defined in Eq. 35.

This does not guarantee, however, that $\mathcal {V}\ne \emptyset$, as it is possible that $\mathcal {G} \underline{u} \npreceq z$ and hence $\underline{u}\notin \mathcal {V}$. Intuitively, if the updated restrictions from PS on some partially-synchronized transitions are more stringent than the original ones, since up to time T we implemented just-in-time inputs based on the original restrictions, it may be impossible to respect both reference z and the new restrictions after T. As we assume PS-restrictions to be hard ones, this means we have no choice but to relax z, i.e., look for a new reference $z'\succeq z$ for which a solution exists. In fact, we seek the least possible such $z'$, in order to remain as close as possible to the original reference. A natural choice is then to take $z'=z\oplus \mathcal {G} \underline{u}$; as $\oplus$ is performed coefficient-wise on counters, this amounts to preserving the terms of z that can still be achieved by taking $\underline{u}$ as input, and relaxing those that cannot only as much as necessary to be matched by the resulting output $y=\mathcal {G} \underline{u}$. The following proposition establishes that this is indeed the optimal way of relaxing z.

Proposition 10

Let $\mathcal {V}'$ denote the set defined as $\mathcal {V}$ in Eq. 32, only replacing z with $z'$, and let $\underline{u}$ be defined as in Eq. 39. The least $z'\succeq z$ such that $\mathcal {V}'\ne \emptyset$ is $z'=z\oplus \mathcal {G} \underline{u}$.

Prop. 10 also provides a simple way to check whether set $\mathcal {V}$ is nonempty.

Corollary 11

Let $\mathcal {V}$ be defined as in Eq. 32 and $\underline{u}$ as in Eq. 39. Then, $\mathcal {V}\ne \emptyset \, \Leftrightarrow \, \mathcal {G}\underline{u}\preceq z$.

If $\mathcal {V}$ turns out to be empty, define the mapping ${\overline{\Psi }{'} : \Sigma ^{m\times 1} \rightarrow \Sigma ^{m\times 1}}$ as $\overline{\Psi }$ in Eq. 33, only replacing z with $z'=z\oplus \mathcal {G} \underline{u}$. Following the same procedure as before, we can apply Prop. 4 — only now taking $\psi$ as $\overline{\Psi }{'}$ instead of $\overline{\Psi }$ — to conclude that $u_{\text {opt}}'$ is the greatest fixed point of mapping $\overline{\Gamma }{'} : \Sigma ^{m\times 1} \rightarrow \Sigma ^{m\times 1}$,

$$\begin{aligned} \overline{\Gamma }{'}(u)\, =\, u\, \wedge \, \overline{\Psi }{'}(u)\, \wedge \, r_T^{\,\sharp }(u_{\text {opt}})\,. \end{aligned}$$

(40)

5 Summary of the method

Let us now provide a step-by-step overview of how to apply the method discussed in the previous sections. We assume that a TEG modeling the system to be controlled is given, as are the external signals describing PS restrictions on some of its internal transitions. Assume also the transfer relations $\mathcal {F}$ and $\mathcal {G}$ (see Eq. 5, Section 2.5) to have been precomputed and an output-reference to be provided in the form of a counter z. To make the description as general as possible, we consider the case of multiple transitions under PS (a single partially-synchronized transition can be seen as a particular case).

• i. Model the PS restrictions by appending to each partially-synchronized transition $x_\iota$ a structure like the one shown in Fig. 5, and obtain the counters $\rho _\iota$ according to the given external signals, as described in Section 3.2. Recall that this implicitly provides counters $\alpha _\iota =e\delta ^1\rho _\iota$.

• ii. Obtain the optimal input $u_{\text {opt}}$ by computing the greatest fixed point of mapping $\overline{\Phi }$ defined as in Eq. 18, according to Section 3.4.

• iii. If, at a certain time T, the PS restrictions on one or more of the partially-synchronized transitions are altered, update the corresponding counters $\rho _\iota$ and $\alpha _\iota$ to $\rho _\iota '$ and $\alpha _\iota '$.

• iv. Obtain the input $\underline{u}$ defined as in Eq. 39. As a prerequisite, compute $\underline{x}$, the least fixed point of mapping $\overline{\Lambda }$ defined in Eq. 37.

• v. Based on Corollary 11, check whether set $\mathcal {V}$ — defined as in Eq. 32 — is nonempty by checking if the inequality $\mathcal {G}\underline{u}\preceq z$ holds.

• vi. In the case $\mathcal {V}\ne \emptyset$, obtain the optimal updated input $u_{\text {opt}}'$ by computing the greatest fixed point of mapping $\overline{\Gamma }$ defined in Eq. 34.

• vii. If $\mathcal {V}=\emptyset$, obtain the least feasible reference $z'$ according to Prop. 10 and then obtain the optimal updated input $u_{\text {opt}}'$ by computing the greatest fixed point of mapping $\overline{\Gamma }{'}$ defined in Eq. 40.

6 Application Example

In order to help elucidating the method presented in this paper and illustrate its applicability, we now employ it to solve a reference-tracking control problem for a system consisting in a simple manufacturing workcell, schematically represented in Fig. 10. Two types of unprocessed workpieces are supplied to the system, each of which is transported by a dedicated robot from the respective input buffer to a corresponding machine for processing. The processed workpieces output by the two machines are then assembled together by a third machine, resulting in the final product which then leaves the system. Machine 1 is highly demanding in terms of power consumption and, therefore, can only be turned on at certain time instants, determined according to the operation of other heavy machinery in the shop floor and here considered to be given as external constraints. In turn, the assembly performed by Machine 3 is a high-precision operation and hence regular maintenance is required in order to guarantee the quality of the final products; the maintenance schedule for Machine 3 is also considered to be externally stipulated.

Fig. 10

Schematic representation of the manufacturing workcell

Fig. 11

TEG (in black) modeling the manufacturing workcell from Fig. 10, with PS (gray structures) on transitions $x_2$ and $x_7$

The system can be modeled by the TEG shown in Fig. 11. The firing of input transitions $u_1$ and $u_3$ represents the arrival of unprocessed workpieces of the respective types at the input buffers (for simplicity, the buffers are assumed to have unlimited capacity). Transition $x_1$ models Robot 1 collecting an unprocessed workpiece from the first input buffer, whereas $x_2$ represents the workpiece being fed to Machine 1 for processing; analogously for transitions $x_4$ and $x_5$ with respect to Robot 2 and Machine 2. The processing of each workpiece in Machine 1 takes 3 time units and there is a cooldown time of 1 time unit between two consecutive operations; Machine 2 takes 5 time units to process each workpiece and its cooldown time is of 2 time units. Both robots as well as machines 1 and 2 have capacity for one workpiece at a time. Once workpieces from machines 1 and 2 are ready (transitions $x_3$ and $x_6$, respectively), they are transported via conveyor belts and take 2 time units to reach Machine 3, where assembly starts (transition $x_7$) and takes 8 time units to be concluded (transition $x_8$). Machine 3 can perform up to two assembly operations in parallel and has a cooldown time of 2 time units. Finally, transition y represents final products being sent out of the system. The transfer relations $\mathcal {F}$ and $\mathcal {G}$ (cf. Eq. 5) for the described system are

$$\begin{aligned} \mathcal {F}\ {}&=\ \begin{bmatrix} e\delta ^0\oplus 1\delta ^2(1\delta ^4)^*\ \ {} &{} 1\delta ^1(1\delta ^4)^*\ {} &{} s_\varepsilon &{} s_\varepsilon \\[2pt] e\delta ^1(1\delta ^{4})^*\ \ {} &{} (1\delta ^{4})^*\ {} &{} s_\varepsilon &{} s_\varepsilon \\[2pt] e\delta ^{4}(1\delta ^{4})^*\ \ {} &{} e\delta ^{3}(1\delta ^{4})^*\ {} &{} s_\varepsilon &{} s_\varepsilon \\[2pt] s_\varepsilon \ \ {} &{} s_\varepsilon \ {} &{} e\delta ^0\oplus 1\delta ^2(1\delta ^7)^*\ {} &{} s_\varepsilon \\[2pt] s_\varepsilon \ \ {} &{} s_\varepsilon \ {} &{} e\delta ^1(1\delta ^7)^*\ {} &{} s_\varepsilon \\[2pt] s_\varepsilon \ \ {} &{} s_\varepsilon \ {} &{} e\delta ^6(1\delta ^7)^*\ {} &{} s_\varepsilon \\[2pt] e\delta ^6(1\delta ^4\oplus 2\delta ^{10})^*\ \ {} &{} e\delta ^5(1\delta ^4\oplus 2\delta ^{10})^*\ {} &{} e\delta ^8(1\delta ^7)^*\ {} &{} (2\delta ^{10})^*\\[2pt] e\delta ^{14}(1\delta ^4 \oplus 2\delta ^{10})^*\ \ {} &{} e\delta ^{13}(1\delta ^4 \oplus 2\delta ^{10})^*\ {} &{} e\delta ^{16}(1\delta ^7)^*\ {} &{} e\delta ^8(2\delta ^{10})^* \end{bmatrix}\,,\\ \mathcal {G}\ {}&=\ \begin{bmatrix} e\delta ^{14}(1\delta ^4 \oplus 2\delta ^{10})^*\ \ {}&e\delta ^{13}(1\delta ^4 \oplus 2\delta ^{10})^*\ \ {}&e\delta ^{16}(1\delta ^7)^*\ \ {}&e\delta ^8(2\delta ^{10})^* \end{bmatrix}\,. \end{aligned}$$

PS restrictions are imposed over transition $x_2$ to capture the external constraints for turning on Machine 1. These constraints are provided before the beginning of each work period, determined according to a global plan for the whole shop floor (and, in particular, for the other high-power demanding machines). For the period considered in this example, the instants at which Machine 1 is allowed to be turned on (i.e., at which $x_2$ may fire) are those in the set

$$\begin{aligned} \mathcal {T}_2=\big \{[5,12] \cup [18,22]\cup [27,38]\cup [46,50]\cup [55,62]\big \}\subset \mathbb {Z}\,. \end{aligned}$$

Similarly, transition $x_7$ is partially synchronized to account for the times Machine 3 cannot operate due to scheduled maintenance. Suppose the maintenance takes place periodically at all time intervals $[20n+1,20n+4]$ for $n\in \mathbb {N}_0=\{0,1,2,\ldots \}$, and suppose Machine 3 is first allowed to be turned on at time 5. This means it can only be turned on at the intervals $\big [20n+5,20(n+1)\big ]$ for $n\in \mathbb {N}_0$, i.e., $x_7$ can only fire at time instants belonging to

$$\begin{aligned} \mathcal {T}_7=\big \{[5,20] \cup [25,40]\cup [45,60]\cup [65,80]\cup \ldots \big \}\subset \mathbb {Z}\,. \end{aligned}$$

Starting with step i from Section 5, these PS phenomena are modeled according to Section 3.2, as shown in Fig. 11, and we obtain the corresponding schedules for transitions $\rho _\iota$, $\iota \in \{2,7\}$, as

$$\begin{aligned} \rho _\iota (t)\ =\ {\left\{ \begin{array}{ll} e &{} \text {if}\ t\le 5\,; \\ 1\otimes \rho _\iota (t-1) &{} \text {if}\ t-1\in \mathcal {T}_\iota \,;\\ \rho _\iota (t-1) &{} \text {if}\ t-1\notin \mathcal {T}_\iota \ \text {and}\ t>5\,. \end{array}\right. } \end{aligned}$$

(41)

Consider the following specification, given based on the demand for products in the considered period: a total of 2 finished products are required by time 36, plus 1 product by time 50, and finally 3 more products by time 70. This can be encoded as the following output-reference for the system:

$$\begin{aligned} z = e\delta ^{36} \oplus 2\delta ^{50} \oplus 3\delta ^{70} \oplus 6\delta ^{+\infty }\,. \end{aligned}$$

Following step ii, we obtain the optimal (just-in-time) input

$$\begin{aligned} u_{\text {opt}}\, = \begin{bmatrix}u_{1_{\text {opt}}}\\[2pt] u_{2_{\text {opt}}}\\[2pt] u_{3_{\text {opt}}}\\[2pt] u_{4_{\text {opt}}} \end{bmatrix} = \begin{bmatrix} e\delta ^{11} \oplus 1\delta ^{20} \oplus 2\delta ^{27} \oplus 3\delta ^{34} \oplus 4\delta ^{47} \oplus 5\delta ^{54} \oplus 6\delta ^{+\infty }\\[2pt] e\delta ^{12} \oplus 1\delta ^{21} \oplus 2\delta ^{28} \oplus 3\delta ^{35} \oplus 4\delta ^{48} \oplus 5\delta ^{55} \oplus 6\delta ^{+\infty }\\[2pt] e\delta ^{9} \oplus 1\delta ^{18} \oplus 2\delta ^{25} \oplus 3\delta ^{32} \oplus 4\delta ^{45} \oplus 5\delta ^{52} \oplus 6\delta ^{+\infty }\\[2pt] e\delta ^{17} \oplus 1\delta ^{26} \oplus 2\delta ^{33} \oplus 3\delta ^{40} \oplus 4\delta ^{53} \oplus 5\delta ^{60} \oplus 6\delta ^{+\infty } \end{bmatrix} \end{aligned}$$

and the corresponding output

$$\begin{aligned} y_{\text {opt}} = \mathcal {G}u_{\text {opt}} = e\delta ^{25} \oplus 1\delta ^{34} \oplus 2\delta ^{41} \oplus 3\delta ^{48} \oplus 4\delta ^{61} \oplus 5\delta ^{68} \oplus 6\delta ^{+\infty } \,. \end{aligned}$$

As an illustration of Remark 11, one can verify that indeed $x_{2_\text {opt}}=\mathcal {F}_{[2\varvec{\cdot }]} u_{\text {opt}}=u_{2_\text {opt}}$ and $x_{7_\text {opt}}=\mathcal {F}_{[7\varvec{\cdot }]} u_{\text {opt}}=u_{4_\text {opt}}$.

Now, suppose that at time $T=40$ the operation schedule of other (external) machines is changed, so that Machine 1 is no longer allowed to be turned on in the interval [46, 50]. This results in the new set of allowed firing times

$$\begin{aligned} \mathcal {T}_2' =\big \{[5,12] \cup [18,22]\cup [27,38]\cup [55,62]\big \}\subset \mathbb {Z}\,. \end{aligned}$$

As indicated in step iii, we update counter $\rho _2$ to $\rho _2'$, defined as in Eq. 41 only replacing $\mathcal {T}_2$ with $\mathcal {T}_2'$ (whereas $\rho _7'=\rho _7$). Proceeding to step iv, we compute the input leading to the fastest possible behavior of the system while guaranteeing that the updated PS restrictions are observed, given by $\underline{u}$ defined in Eq. 39. Similarly to what was argued in Example 4, note that we can limit the total number of firings of each input transition by the total number of desired output firings — in this case, 6 — as each firing of transition y depends on exactly one firing from each $u_i$, $i\in \{1,2,3,4\}$. Truncating the counters in $\underline{u}$ accordingly, we obtain

$$\begin{aligned} \underline{u}\, = \begin{bmatrix} e\delta ^{11} \oplus 1\delta ^{20} \oplus 2\delta ^{27} \oplus 3\delta ^{34} \oplus 4\delta ^{40} \oplus 6\delta ^{+\infty }\\[2pt] e\delta ^{12} \oplus 1\delta ^{21} \oplus 2\delta ^{28} \oplus 3\delta ^{35} \oplus 4\delta ^{55} \oplus 5\delta ^{59} \oplus 6\delta ^{+\infty }\\[2pt] e\delta ^{9} \oplus 1\delta ^{18} \oplus 2\delta ^{25} \oplus 3\delta ^{32} \oplus 4\delta ^{40} \oplus 6\delta ^{+\infty }\\[2pt] e\delta ^{17} \oplus 1\delta ^{26} \oplus 2\delta ^{33} \oplus 3\delta ^{40} \oplus 4\delta ^{60} \oplus 5\delta ^{65} \oplus 6\delta ^{+\infty } \end{bmatrix}\,, \end{aligned}$$

leading to (according to step v)

$$\begin{aligned} \mathcal {G}\underline{u}\, =\, e\delta ^{25} \oplus 1\delta ^{34} \oplus 2\delta ^{41} \oplus 3\delta ^{48} \oplus 4\delta ^{68} \oplus 5\delta ^{73} \oplus 6\delta ^{+\infty }\, \npreceq \,z \,. \end{aligned}$$

This implies $\mathcal {V}=\emptyset$ as reference z is no longer achievable; in fact, by inspection of the counter above one can see that it is no longer possible to provide the last required firing before time 70, as specified in z. Therefore, we move to step vii and apply Prop. 10 to relax z and obtain the new reference

$$\begin{aligned} z'\,=\, z\oplus \mathcal {G}\underline{u}\, =\, e\delta ^{36} \oplus 2\delta ^{50} \oplus 3\delta ^{70} \oplus 5\delta ^{73} \oplus 6\delta ^{+\infty }\,. \end{aligned}$$

The updated optimal input schedules are then

$$\begin{aligned} u_{\text {opt}}' \, = \begin{bmatrix} e\delta ^{11} \oplus 1\delta ^{20} \oplus 2\delta ^{27} \oplus 3\delta ^{34} \oplus 4\delta ^{55} \oplus 5\delta ^{59} \oplus 6\delta ^{+\infty }\\[2pt] e\delta ^{12} \oplus 1\delta ^{21} \oplus 2\delta ^{28} \oplus 3\delta ^{35} \oplus 4\delta ^{56} \oplus 5\delta ^{60} \oplus 6\delta ^{+\infty }\\[2pt] e\delta ^{9} \oplus 1\delta ^{18} \oplus 2\delta ^{25} \oplus 3\delta ^{32} \oplus 4\delta ^{50} \oplus 5\delta ^{57} \oplus 6\delta ^{+\infty }\\[2pt] e\delta ^{17} \oplus 1\delta ^{26} \oplus 2\delta ^{33} \oplus 3\delta ^{40} \oplus 4\delta ^{60} \oplus 5\delta ^{65} \oplus 6\delta ^{+\infty } \end{bmatrix}\,. \end{aligned}$$

and the resulting output is

$$\begin{aligned} y_{\text {opt}}' = \mathcal {G}u_{\text {opt}}' = e\delta ^{25} \oplus 1\delta ^{34} \oplus 2\delta ^{41} \oplus 3\delta ^{48} \oplus 4\delta ^{68} \oplus 5\delta ^{73} \oplus 6\delta ^{+\infty } \,. \end{aligned}$$

7 Conclusion

In this paper, a formal and systematic method is provided for the optimal (just-in-time) control of timed event graphs with partial synchronization, i.e., TEGs in which one or more transitions may be restricted to fire within certain time windows specified by external signals. We propose a way to model PS entirely within the domain of the semiring of counters. Based on such models, we obtain just-in-time control inputs that lead to tracking a given output reference as closely as possible while respecting PS restrictions. The main contribution of this work is making it possible to tackle scenarios in which PS restrictions may vary over time, which, as we argue, is a phenomenon naturally arising in many practical applications and not dealt with before in this context. It is possible that unexpected changes in PS restrictions render the original reference unachievable; our method provides a way to relax the reference as little as possible and to update the input control signals so that the ultimately obtained output is as close as possible to the original reference and PS restrictions are never violated. Another advantage of the presented approach, as shown in Schafaschek et al. (2022), is that it can be readily combined with other recent results and applied to systems exhibiting not only PS but also resource-sharing phenomena, which is not the case for previous related work. Solving a more comprehensive case study and comparing our method with other methods (from, e.g., the scheduling community) addressing similar problems are subjects for future work.

Appendix A Proofs

1.1 A.1 Proofs from Section 4.2

Proof of Proposition 4

Define the set

$$\begin{aligned} \widetilde{\mathcal {S}}_{\psi } = \{x \in \mathcal {D}\,\vert \, x \preceq \psi (x)\ \text {and}\ f(x) \preceq c\} \end{aligned}$$

and denote $\chi = \bigoplus _{x\in \mathcal {S}_{\psi }}x$ and $\widetilde{\chi } = \bigoplus _{x\in \widetilde{\mathcal {S}}_{\psi }}x$. Note that

$$\begin{aligned} x \preceq \psi (x)\ \text {and}\ f(x) \preceq c\&\Leftrightarrow \ x \preceq \psi (x)\ \text {and}\ x \preceq f^{\sharp }(c)\qquad \small (see Def.~1) \\&\Leftrightarrow \ x \preceq \psi (x) \wedge f^{\sharp }(c)\\&\Leftrightarrow \ x = x \wedge \psi (x) \wedge f^{\sharp }(c) = \Omega (x)\,. \end{aligned}$$

So, set $\widetilde{\mathcal {S}}_{\psi }$ can be equivalently defined as $\widetilde{\mathcal {S}}_{\psi } = \{x \in \mathcal {D}\,\vert \, x = \Omega (x)\}$, clearly implying ${\widetilde{\chi } = \bigoplus \{x\in \mathcal {D}\,\vert \, \Omega (x) = x\}}$. Then, it also follows from Remark 3 that $\widetilde{\chi } \in \widetilde{\mathcal {S}}_{\psi }$.

Now, assume $\mathcal {S}_{\psi } \ne \emptyset$. As $\mathcal {S}_{\psi } \subseteq \widetilde{\mathcal {S}}_{\psi }$, this implies ${(\exists \widetilde{x} \in \widetilde{\mathcal {S}}_{\psi })\, f(\widetilde{x}) = c}$. Taking such an $\widetilde{x}$, we have $\widetilde{x} \preceq \widetilde{\chi }$ and so $c = f(\widetilde{x}) \preceq f(\widetilde{\chi })$ (as f is isotone). But we saw above that $\widetilde{\chi } \in \widetilde{\mathcal {S}}_{\psi }$, meaning $f(\widetilde{\chi }) \preceq c$, so $f(\widetilde{\chi }) = c$. Therefore, $\widetilde{\chi } \in \mathcal {S}_{\psi }$ and hence $\widetilde{\chi } \preceq \chi$. On the other hand, $\mathcal {S}_{\psi } \subseteq \widetilde{\mathcal {S}}_{\psi }$ implies $\chi \preceq \widetilde{\chi }$, showing that $\chi = \widetilde{\chi }$. $\square$

Proof of Proposition 5

For any $t\le T$, we have

$$\begin{aligned} \big [\rho '\, \odot \, e\delta ^1 r_T^{\,\sharp }(x_{\iota _{opt }})\big ](t)\&=\ \rho '(t)\, \otimes \, \big [e\delta ^1 r_T^{\,\sharp }(x_{\iota _{opt }})\big ](t)&\\&=\ \rho (t)\, \otimes \, \big [r_T^{\,\sharp }(x_{\iota _{opt }})\big ](t-1)&\\&=\ \rho (t)\, \otimes \, x_{\iota _{opt }}(t-1)\qquad \quad&\text {(because}\, t-1<T)\\&=\ \rho (t)\, \otimes \, \big [e\delta ^1 x_{\iota _{opt }}\big ](t)&\\&=\ \big [\rho (t)\, \odot \, e\delta ^1 x_{\iota _{opt }}\big ](t)&\\&\preceq \ \big [e\delta ^1\rho \, \odot \, x_{\iota _{opt }}\big ](t)&\text {(as}\, x_{\iota _{opt }}\text {satisfies Eq. 9)}\\&=\ \big [e\delta ^1\rho \big ](t)\, \otimes \, x_{\iota _{opt }}(t)&\\&=\ \big [e\delta ^1\rho '\big ](t)\, \otimes \, \big [r_T^{\,\sharp }(x_{\iota _{opt }})\big ](t)&\text {(again as}\, t-1<T)\\&=\ \big [e\delta ^1\rho '\, \odot \, r_T^{\,\sharp }(x_{\iota _{opt }})\big ](t)\,.&\end{aligned}$$

Moreover, for $t>T$,

$$\begin{aligned} \big [\rho '\, \odot \, e\delta ^1 r_T^{\,\sharp }(x_{\iota _{opt }})\big ](t)\&=\ \rho '(t)\, \otimes \, \big [e\delta ^1 r_T^{\,\sharp }(x_{\iota _{opt }})\big ](t)&\\&=\ \rho '(t)\, \otimes \, \big [r_T^{\,\sharp }(x_{\iota _{opt }})\big ](t-1)&\\&=\ \rho '(t)\, \otimes \, \big [r_T^{\,\sharp }(x_{\iota _{opt }})\big ](T)&\text {(because}\, t-1\ge T)\\&=\ \rho '(t)\, \otimes \, \big [r_T^{\,\sharp }(x_{\iota _{opt }})\big ](t)&\text {(because}\, t> T)\\&\preceq \ \big [e\delta ^1\rho '\big ](t)\, \otimes \, \big [r_T^{\,\sharp }(x_{\iota _{opt }})\big ](t)&\\&=\ \big [e\delta ^1\rho '\, \odot \, r_T^{\,\sharp }(x_{\iota _{opt }})\big ](t)\,.&\end{aligned}$$

This shows that $\rho '\, \odot \, e\delta ^1 r_T^{\,\sharp }(x_{\iota _{opt }})\,\preceq \,e\delta ^1\rho '\, \odot \, r_T^{\,\sharp }(x_{\iota _{opt }})$ or, equivalently,

$$\begin{aligned} \big (\rho ' \odot e\delta ^1 r_T^{\,\sharp }(x_{\iota _{opt }})\big )\, \odot ^{\flat }\, e\delta ^1\rho '\, \preceq \, r_T^{\,\sharp }(x_{\iota _{opt }})\,. \end{aligned}$$

We also have

$$\begin{aligned} r_T^{\,\sharp }(x_{\iota _{opt }})\,=\,r_T^{\,\sharp }\big (\mathcal {F}_{[\iota \varvec{\cdot }]}u_{opt }\big )\, \succeq \, \mathcal {F}_{[\iota \varvec{\cdot }]}u_{opt }\,\succeq \,\mathcal {F}_{[\iota \varvec{\cdot }]}r_T^{\ }(u_{opt })\,. \end{aligned}$$

Finally, as $x_{\iota _{opt }}$ is a solution of Eq. 3, we have

$$\begin{aligned} x_{\iota _{opt }}\,=\,[A^*]_{[\iota \varvec{\cdot }]}x_{opt }\,\succeq \,[A^*]_{\iota \iota }x_{\iota _{opt }}\,=\,\mathcal {F}_{\iota \eta }x_{\iota _{opt }}\,, \end{aligned}$$

which implies $r_T^{\,\sharp }(x_{\iota _{opt }})\,\succeq \,r_T^{\,\sharp }\big (\mathcal {F}_{\iota \eta }x_{\iota _{opt }}\big )\,\succeq \,\mathcal {F}_{\iota \eta }r_T^{\,\sharp }(x_{\iota _{opt }})$. $\square$

Proof of Proposition 6

Taking $z'=z\oplus \mathcal {G} \underline{u}$ implies $\mathcal {G}\underline{u}\preceq z'$ and, as $\underline{u}\in \widetilde{\mathcal {Q}}$, it follows that $\underline{u}\in \mathcal {Q}'$ and hence $\mathcal {Q}'\ne \emptyset$. Now, take $\zeta \succeq z$ such that $\mathcal {Q}_{\zeta }\ne \emptyset$ (where $\mathcal {Q}_{\zeta }$ is defined like $\mathcal {Q}$, only replacing z with $\zeta$), and take ${v\in \mathcal {Q}_{\zeta }}$. As $\mathcal {F}v$ is a solution of Eq. 3, from Remark 4 is follows that $\mathcal {F}v=A^*\mathcal {F}v$, which implies

$$\begin{aligned} \mathcal {F}_{[j\varvec{\cdot }]}v\,=\,[A^*]_{[j\varvec{\cdot }]}\mathcal {F}v\,=\,\bigoplus _{\kappa =1}^n [A^*]_{j\kappa }[\mathcal {F}v]_\kappa \,\succeq \,[A^*]_{j\iota }[\mathcal {F}v]_\iota \,=\,[A^*]_{j\iota }\mathcal {F}_{[\iota \varvec{\cdot }]} v \end{aligned}$$

for all $j\in \{1,\ldots ,n\}$. Moreover, as $v \in \widetilde{\mathcal {Q}}$, we know from Remark 13 that $\mathcal {F}_{[\iota \varvec{\cdot }]} v$ is a fixed point of mapping $\Lambda$, which implies $\mathcal {F}_{[\iota \varvec{\cdot }]} v\succeq \underline{x}_\iota$. Hence, recalling from Eq. 15 that $\mathcal {F}_{j\eta }=[A^*]_{j\iota }$ for any $j\in \{1,\ldots ,n\}$, we have

$$\begin{aligned} \mathcal {F}_{[j\varvec{\cdot }]}v\,\succeq \,[A^*]_{j\iota }\mathcal {F}_{[\iota \varvec{\cdot }]} v\,=\,\mathcal {F}_{j\eta }\mathcal {F}_{[\iota \varvec{\cdot }]} v \,\succeq \,\mathcal {F}_{j\eta }\underline{x}_\iota \,. \end{aligned}$$

(A1)

The fact that $v \in \widetilde{\mathcal {Q}}$ also implies $r_T^{\ }(v)=r_T^{\ }(u_{opt })$, so $v\succeq r_T^{\ }(u_{opt })$ and hence

$$\begin{aligned} (\forall j\in \{1,\ldots ,n\})\ \,\mathcal {F}_{[j\varvec{\cdot }]}v\,\succeq \,\mathcal {F}_{[j\varvec{\cdot }]}r_T^{\ }(u_{opt })\,. \end{aligned}$$

(A2)

Thus, for every $j\in \{1,\ldots ,n\}$ we have

$$\begin{aligned} \mathcal {F}_{[j\varvec{\cdot }]}\underline{u}\&=\ \bigoplus _{\begin{array}{c} \mu =1\\ \mu \ne \eta \end{array}}^m \mathcal {F}_{j\mu }r_T^{\ }(u_{\mu _{\text {opt}}})\ \, \oplus \, \mathcal {F}_{j\eta }\big (r_T^{\ }(u_{\mu _{\text {opt}}})\oplus \underline{x}_\iota \big )\\&=\, \bigoplus _{\begin{array}{c} \mu =1\\ \mu \ne \eta \end{array}}^m \mathcal {F}_{j\mu }r_T^{\ }(u_{\mu _{\text {opt}}})\ \, \oplus \, \mathcal {F}_{j\eta }r_T^{\ }(u_{\mu _{\text {opt}}})\,\oplus \,\mathcal {F}_{j\eta }\underline{x}_\iota \\&=\, \bigoplus _{\mu =1}^m \mathcal {F}_{j\mu }r_T^{\ }(u_{\mu _{\text {opt}}})\ \, \oplus \, \mathcal {F}_{j\eta }\underline{x}_\iota \\&=\, \mathcal {F}_{[j\varvec{\cdot }]}r_T^{\ }(u_{opt })\,\oplus \,\mathcal {F}_{j\eta }\underline{x}_\iota \\&\preceq \, \mathcal {F}_{[j\varvec{\cdot }]}v\,, \end{aligned}$$

where the last inequality is a consequence of Eqs. A1 and A2. This means $\mathcal {F}\underline{u}\preceq \mathcal {F}v$. But, recalling from Eq. 5 that $\mathcal {G}=C\mathcal {F}$, we then have $\mathcal {G}\underline{u} = C\mathcal {F}\underline{u} \preceq C\mathcal {F} v = \mathcal {G} v \preceq \zeta$, so ${z'=z\oplus \mathcal {G} \underline{u} \preceq z\oplus \zeta = \zeta }$. $\square$

Proof of Corollary 7

First note that, if $\mathcal {G}\underline{u}\preceq z$, then $\underline{u}\in \mathcal {Q}$ and hence $\mathcal {Q}\ne \emptyset$. Conversely, if ${\mathcal {Q}\ne \emptyset }$, then obviously the least $z'\succeq z$ such that $\mathcal {Q}'\ne \emptyset$ is z itself; Prop. 6 then implies $z=z\oplus \mathcal {G} \underline{u}$ or, equivalently, $z\succeq \mathcal {G} \underline{u}$. $\square$

1.2 A.2 Proofs from Section 4.3

Proof of Proposition 8

We want to show that $\mathcal {F}_{[\iota \varvec{\cdot }]} \underline{u}=\underline{x}_\iota$ for all $\iota \in \{1,\ldots ,I\}$. First, from Eq. 28 it follows, for all $\iota \in \{1,\ldots ,I\}$, that $[A^*]_{\iota \iota }\succeq \big [\mathcal {I}^{n\times n}\big ]_{\iota \iota } = s_e$, so $\mathcal {F}_{\iota \iota }\underline{x}_\iota = [A^*]_{\iota \iota }\underline{x}_\iota \succeq \underline{x}_\iota$. On the other hand, the fact that $\underline{x}$ is a fixed point of $\overline{\Lambda }$ implies $\underline{x}_\iota \succeq \mathcal {F}_{\iota \iota }\underline{x}_\iota$, and hence

$$\begin{aligned} \mathcal {F}_{\iota \iota }\underline{x}_\iota \,=\,\underline{x}_\iota \,; \end{aligned}$$

(A3)

it further implies that

$$\begin{aligned} \underline{x}_\iota \,\succeq \, \bigoplus _{\begin{array}{c} j=1\\ j\ne \iota \end{array}}^I \mathcal {F}_{\iota j}\underline{x}_j\qquad \text {and}\qquad \underline{x}_\iota \,\succeq \,\mathcal {F}_{[\iota \varvec{\cdot }]}r_T^{\ }(u_{\text {opt}})\,. \end{aligned}$$

(A4)

Then, for any $\iota \in \{1,\ldots ,I\}$, we have

$$\begin{aligned} \mathcal {F}_{[\iota \varvec{\cdot }]} \underline{u}\&=\ \bigoplus _{\mu =I+1}^m \mathcal {F}_{\iota \mu }r_T^{\ }(u_{\mu _{\tiny opt }})\ \, \oplus \, \bigoplus _{j=1}^I\mathcal {F}_{\iota j}\big (r_T^{\ }(u_{j_{\tiny opt }}) \oplus \underline{x}_j\big )\\&=\ \bigoplus _{\mu =I+1}^m \mathcal {F}_{\iota \mu }r_T^{\ }(u_{\mu _{\tiny opt }})\ \, \oplus \, \bigoplus _{j=1}^I\mathcal {F}_{\iota j}r_T^{\ }(u_{j_{\tiny opt }})\, \oplus \ \, \bigoplus _{j=1}^I\mathcal {F}_{\iota j}\underline{x}_j\\&=\ \bigoplus _{\mu =1}^m \mathcal {F}_{\iota \mu }r_T^{\ }(u_{\mu _{\tiny opt }})\ \, \oplus \, \bigoplus _{j=1}^I\mathcal {F}_{\iota j}\underline{x}_j\\&=\ \mathcal {F}_{[\iota \varvec{\cdot }]}r_T^{\ }(u_{\text {opt}})\, \oplus \, \bigoplus _{\begin{array}{c} j=1\\ j\ne \iota \end{array}}^I\mathcal {F}_{\iota j}\underline{x}_j\ \, \oplus \, \mathcal {F}_{\iota \iota }\underline{x}_\iota \\&=\ \mathcal {F}_{[\iota \varvec{\cdot }]}r_T^{\ }(u_{\text {opt}})\, \oplus \, \bigoplus _{\begin{array}{c} j=1\\ j\ne \iota \end{array}}^I\mathcal {F}_{\iota j}\underline{x}_j\ \, \oplus \, \underline{x}_\iota \qquad \qquad \text {(because of Eq. A3)}\\&=\ \underline{x}_\iota \qquad \qquad \text {(due to Eq. A4)}\,. \end{aligned}$$

$\square$

Lemma 12

(of Proposition 9) $r_T^{\,\sharp }(x_{\text {opt}})$ is a fixed point of mapping $\overline{\Lambda }$.

Proof

It follows as a straightforward generalization of the proof of Prop. 5. $\square$

Proof of Proposition 9

Because $\underline{x}$ is a fixed point of $\overline{\Lambda }$, for all $\iota \in \{1,\ldots ,I\}$ it follows that

$$\begin{aligned}(\rho ' \odot e\delta ^1 \underline{x}_\iota ) \odot ^{\flat } e\delta ^1\rho '\, \preceq \, \underline{x}_\iota \,. \end{aligned}$$

Combined with the fact that $\mathcal {F}_{[\iota \varvec{\cdot }]}\underline{u} = \underline{x}_\iota$ for all such $\iota$, as shown in Prop. 8, this implies taking $u=\underline{u}$ satisfies Eq. 38, which is equivalent to ($\star \star$).

It remains to show that $r_T^{\ }(\underline{u}) = r_T^{\ }(u_{\text {opt}})$. Note that, as $r_T^{\ }\circ r_T^{\ }=r_T^{\ }$, for ${\mu \in \{I+1,\ldots ,m\}}$ it trivially holds that $r_T^{\ }(\underline{u}_{\mu }) = r_T^{\ }(u_{\mu _{\tiny opt }})$. The problem is then reduced to showing that, for all $\iota \in \{1,\ldots ,I\}$, $r_T^{\ }(\underline{u}_\iota ) =r_T^{\ }\big (r_T^{\ }(u_{\iota _{\tiny opt }}) \oplus \underline{x}_\iota \big ) = r_T^{\ }(u_{\iota _{\tiny opt }})$, which, in turn, as $r_T^{\ }$ distributes over $\oplus$, is equivalent to $r_T^{\ }(u_{\iota _{\tiny opt }}) \oplus r_T^{\ }(\underline{x}_\iota ) = r_T^{\ }(u_{\iota _{\tiny opt }})$, or $r_T^{\ }(\underline{x}_\iota )\preceq r_T^{\ }(u_{\iota _{\tiny opt }})$. From Prop. 12 we know that $\underline{x}_\iota \preceq r_T^{\,\sharp }(x_{\iota _{\text {opt}}}) = r_T^{\,\sharp }(\mathcal {F}_{[\iota \varvec{\cdot }]} u_{\text {opt}})$ for every $\iota$. We also know from Remark 11 that $\mathcal {F}_{[\iota \varvec{\cdot }]} u_{\text {opt}}=u_{\iota _{\tiny opt }}$. Thus, as $r_T^{\ }$ is isotone and recalling that $r_T^{\ }\circ r_T^{\,\sharp }= r_T^{\ }$, for all $\iota \in \{1,\ldots ,I\}$ we have

$$\begin{aligned} r_T^{\ }(\underline{x}_\iota )\, \preceq \, r_T^{\ }\big (r_T^{\,\sharp }(u_{\iota _{\tiny opt }})\big )\,=\, r_T^{\ }(u_{\iota _{\tiny opt }})\,. \end{aligned}$$

$\square$

Proof of Proposition 10

It follows by direct analogy with the proof of Prop. 6. $\square$

Proof of Corollary 11

It follows by direct analogy with the proof of Corollary 7. $\square$