Modeling and analysis of switching max-plus linear systems with discrete-event feedback

Abstract

Switching max-plus linear system (SMPLS) models are an apt formalism for performance analysis of discrete-event systems. SMPLS analysis is more scalable than analysis through other formalisms such as timed automata, because SMPLS abstract pieces of determinate concurrent system behavior into atomic modes with fixed timing. We consider discrete-event systems that are decomposed into a plant and a Supervisory Controller (SC) that controls the plant. The SC needs to react to events, concerning e.g. the successful completion or failure of an action, to determine the future behavior of the system, for example, to initiate a retrial of the action. To specify and analyze such system behavior and the impact of feedback on timing properties, we introduce an extension to SMPLS with discrete-event feedback. In this extension, we model the plant behavior with system modes and capture the timing of discrete-event feedback emission from plant to SC in the mode matrices. Furthermore, we use I/O automata to capture how the SC responds to discrete-event feedback with corresponding mode sequences of the SMPLS. We define the semantics of SMPLS with events using new state-space equations that are akin to classical SMPLS with dynamic state-vector sizes. To analyze the extended models, we formulate a transformation from SMPLS with events to classical SMPLS with equivalent semantics and properties such that performance properties can be analyzed using existing techniques. Our approach enables the specification of discrete-event feedback from the plant to the SC and its performance analysis. We demonstrate our approach by specifying and analyzing the makespan of a flexible manufacturing system.

1 Introduction

Model-based design is an approach in which systems are designed using models that are both understandable by engineers and amenable to mathematical analysis. The system implemented by this approach should behave as predicted by the mathematical model, and therefore can be analyzed and improved using this model. Examples of such modeling formalisms are Petri Nets (Peterson 1981), Synchronous Dataflow (Lee and Messerschmitt 1987), Timed Automata (Alur and Dill 1994) (TA), and Max-Plus Linear Systems (Baccelli et al. 1992).

Max-Plus Linear Systems (MPLS) are used to model a wide variety of discrete-event systems (DES) (Geilen and Stuijk 2010; Geilen 2010; De Schutter and De Moor 1998; De Schutter and van den Boom 2001). They offer performance analysis methods through linear max-plus operators, which contributes to the scalability of the analysis. An extension to MPLS is the class of Switching Max-Plus Linear Systems (SMPLS) (van den Boom and De Schutter 2006). This extension is used to model and analyze systems that switch between different modes of operation. In each mode, the system is described by a Max-Plus Linear (MPL) state-space model.

(S)MPLS have scalability advantages over alternative performance-oriented models such as Timed Petri Nets or TA for the analysis of DES. SMPLS allow modeling and analysis of concurrent system behavior that would lead to state-space explosion in other formalisms. For instance, comparisons between TA and MPLS-based analysis were made in van der Sanden et al. (2016); Skelin et al. (2015). SMPLS models reduce state-space explosion by aggregating concurrent, but determinate pieces of behavior into atomic modes with a fixed timing captured in matrices. In Skelin et al. (2015), the authors use MPLS and TA models to analyze a realistic case study from the multimedia domain, and compare their analysis times. For similar analysis types (maximum response delay and maximum inter-firing latency) MPLS analysis methods are significantly faster than their TA counterparts and require noticeably fewer resources. The tools used were SDF3 (Stuijk et al. 2006) for MPLS analysis and UPPAAL (Behrmann et al. 2006) for TA analysis.

SMPLS are used to specify and analyze a variety of DES such as synchronous dataflow graphs (Geilen and Stuijk 2010; Geilen 2010) and flexible manufacturing systems (FMS) (van der Sanden et al. 2016). To demonstrate our approach, in this article we use an FMS as our running example. An FMS is defined as “an integrated, computer-controlled, complex of automated material handling devices and machine tools that can simultaneously process multiple types of parts while reducing the overhead time, effort, and cost of changing production line configurations in response to changing requirements” (Stecke 1983). These features that are required in FMS, result in more complex systems, making the design process more difficult (ElMaraghy 2005). Therefore, it is necessary to automate the design process to handle the complexity of design. SMPLS provides a mathematical framework to model all the parts of an FMS in a formal way so that they can be analyzed and reasoned about. System operations are abstracted into a set of modes and their effect on the system is captured using max-plus matrices while the state of the system is captured in a vector. The overall behavior of the system is modeled as switching between the modes. Analysis of the system is then performed using max-plus-linear matrix-vector multiplications. Modeling and timing analysis of these systems is an important step toward performance optimization and automated design.

Although SMPLS are a powerful formalism for timing analysis and performance optimization, SMPLS abstract from discrete-event feedback that is sent from plant to SC (Ramadge and Wonham 1987). This concerns, on the one hand, the information about the feedback, for instance, acknowledgment of completion of an action, confirmation of success or indication of failure. On the other hand, it also concerns the impact of this feedback on the flow and timing of future operations that depend on it. SMPLS traditionally deal with a different type of feedback in the form of observed variations in system timing as perturbations recorded in the state vector. In contrast, this article focuses on discrete-event feedback from plant to SC and the interactions between these control layers. We introduce an extension to SMPLS to specify such discrete-event feedback and capture the interactions between SC and plant, including their timing. We show how these SMPLS with events can be analyzed by a reduction to classical SMPLS without discrete-event feedback, but with equivalent performance. We focus on the domain of FMS to demonstrate and evaluate our approach, but it is applicable in other domains as well in which systems are modelled and analyzed using SMPLS.

Fig. 1

Overview of our approach, where the green parts indicate our contributions presented in this article

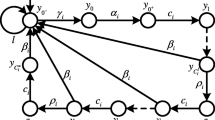
Figure 1 shows an overview of our contributions (colored green) next to the state of the art (colored blue). In classical SMPLS, a system is specified using a set of modes, matrices with a fixed size corresponding to each mode, and a mode automaton that specifies the possible sequences of modes. The corresponding SMPLS state-space equations then give the semantics of the system, in the form of the set of possible state-vector sequences. On the semantics, we define the properties of interest for the system (in this article, makespan). Max-plus automata (Gaubert 1995), constructed from the SMPLS specifications, are used for analysis.

Our contributions in this article are summarized as follows (Fig. 1, green colored):

• We introduce an extension of SMPLS, with events, to capture discrete-event feedback. We use I/O automata to succinctly specify the SC that captures the allowed mode sequences including the emission and processing of events. Each mode is characterized by a max-plus matrix that captures the timing of mode execution on the system state and the timing of event emission.

• We introduce the semantics of SMPLS with events by transforming a specification consisting of an I/O automaton with mode matrices to state-space equations with dynamic state-vector sizes to capture the timing of event emission and processing.

• We introduce a transformation from SMPLS with events to classical SMPLS, to facilitate re-use of existing performance analysis techniques.

• We prove that the transformed SMPLS has the same set of state-vector sequences as the SMPLS with events. The transformed SMPLS can therefore be used to analyze the performance properties of the SMPLS with events.

• We show how the maximum makespan of an SMPLS can be analyzed using max-plus automata.

The remainder of the article is organized as follows. Section 2 presents our running example. In Section 3, we demonstrate how to model and analyze this example using a baseline SMPLS approach. In Section 4, we extend the example with discrete events and we demonstrate our approach. In Section 5, we evaluate the approach on a realistic FMS example. In Section 6, we examine related literature and compare the state of the art to our approach. In Section 7, we conclude this article.

2 Running example

We introduce our work using a running example in the application domain of lithography scanners (Jonk et al. 2019). Lithography scanners are highly complex cyber-physical systems used to manufacture integrated circuits (Butler 2011). These machines use an optical system to project an image of a pattern onto a photosensitive layer deposited on a substrate, called a wafer. A single pattern is repeatedly projected many times on a wafer. The wafer needs to be repositioned each time. Figure 2 (redrawn from Butler 2011) shows two types of operations executed to expose one wafer. The Scan operation exposes one field of the wafer to light, while the Step operation adjusts the wafer to Scan the next field. We aggregate each Step operation and its subsequent Scan operation into a Step/Scan operation. A full wafer exposure is defined as a series of Step/Scan operations which are to be tracked with nanometer positional accuracy. While performing these Step/Scans, the system can experience physical disturbances. System-wide sensor data from previous scans are therefore collected to adjust the setpoints for each Step/Scan operation. AdjustSetpoint is an operation that computes these setpoint adjustments. The Step/Scan operations have a functional dependency on the AdjustSetpoint operations. Operations are executed on resources. In our running example, a Stage resource executes the Step/Scan operations and a Compute resource executes the AdjustSetpoint operations.

To minimize the wafer exposure time, the AdjustSetpoint and Step/Scan operations must be executed in a pipeline. In our running example, the pipeline depth is assumed to be two. The result of a Step/Scan operation is used to make decisions to either continue performing a next AdjustSetpoint and Step/Scan operation or to execute a Calibrate operation¹. The Calibrate operation simultaneously uses the Stage and Compute resources.

This system is modeled using two approaches. In the baseline approach, the system is specified and analyzed based solely on a feed-forward mechanism. Step/Scans are assumed to execute with sufficient accuracy so that no feedback is required and operations can be queued in a fully feed-forward fashion. We present this approach in Section 3 to provide the theoretical preliminaries and establish the basis for our feedback approach. The feedback approach is presented in Section 4.

Fig. 2

A schematic overview of a wafer being exposed. Redrawn from Fig. 15 in Butler (2011)

3 Feed-forward modeling and analysis

In this section, we present the baseline analysis technique, and illustrate it with the running example (van der Sanden et al. 2016). We introduce the background material and literature used in our research as a baseline to which we compare our modeling and analysis technique. We introduce the concepts of max-plus algebra used to reason about the timing of systems. Then we model and analyze our running example in subsections concerning specification, semantics and analysis (in line with the breakdown in Fig. 1). This feed-forward approach lacks the necessary concepts and mechanisms to succinctly specify discrete-event feedback from the plant to the SC and the SC’s reaction to such feedback. We introduce the extension in the next section.

3.1 Max-plus algebra

The approaches that we present in this article use max-plus algebra and the theory of max-plus linear systems to specify and analyze FMS. In this subsection, we introduce the required max-plus concepts. The max-plus semiring $\mathbb {R}_{max}$ is the set $T=\mathbb {R} \cup \{{-\infty {}}\}$, called the max-plus time domain, equipped with the operators addition ($a\oplus b=max(a,b)$) and multiplication ($a \otimes b = a+b$) (Akian et al. 2006). Both operators are commutative and associative. Multiplication binds stronger than addition in the notation of expressions. The zero element is ${-\infty {}}$, meaning that for all $x \in T$, $x\oplus {-\infty {}}= x$ and $x \otimes {-\infty {}}= {-\infty {}}$. The unit element for multiplication is 0, meaning $x \otimes 0 = x$ for all x. The sum over an empty set is considered to be equal to the unit element of addition, i.e., ${-\infty {}}$.

A max-plus matrix is a matrix over time domain T. For a max-plus matrix $A \in T^{n\times n}$, we let $A_{ij}$ denote the element in the ith row and the jth column. $\bar{0}$ denotes a zero matrix of appropriate size in the context where it is used. $\bar{0}^{u,v}$ denotes a zero matrix of size $u\times v$. A max-plus (column) vector is a max-plus matrix with a single column. We denote the ith element in vector $\bar{x}$ by $\bar{x}_i$. The norm of vector $\bar{x}$, denoted by $\vert \bar{x}\vert$, is defined as: $\vert \bar{x}\vert = \bigoplus _i \bar{x}_i$. I is the max-plus version of the identity matrix, having 0 elements on the diagonal and ${-\infty {}}$ elements elsewhere. For matrix A of size $m \times l$ and matrix B of size $l \times n$, the max-plus matrix product $C=A \otimes B$ with size $m \times n$ is defined as $C_{ik} = \bigoplus _{j}^{} A_{ij} \otimes B_{jk}$.

For notational convenience and to avoid case distinctions, we allow vectors to be of length zero, and we allow matrices to have zero rows and/or zero columns with the following convention. A matrix of zero rows, when multiplied with another matrix yields a matrix which has again zero rows and hence, when multiplied with a vector yields a vector of length zero. A matrix with zero columns can be multiplied with a matrix with zero rows. The result is a matrix containing the value ${-\infty {}}$, as ${-\infty {}}$ is the result of the ‘empty’ inner product that is computed, i.e., the max-plus sum of an empty set.

Fig. 3

Interaction between plant and SC modeled in the feed-forward approach

3.2 Feed-forward specification

Figure 3 illustrates the feed-forward approach in modeling an FMS where an SC executes modes on a plant and does not receive discrete-event feedback from the plant. We specify the system behavior of our running example as an SMPLS.

Definition 1

An SMPLS is a tuple (M, A, Y, n), with

• a finite set M of modes;

• a function $A:M \rightarrow T^{n\times n}$ that maps each mode to an n-by-n max-plus matrix;

• a finite state automaton $Y=( Q,S, \Delta ,M,F )$ that specifies the possible sequences of modes, where Q is a finite set of states, $S \subseteq Q$ is a set of initial states, $\Delta \subseteq Q\times M \times Q$ is a mode-labelled transition relation, and $F\subseteq Q$ is a set of final states;

• and the state-vector size n.

We model the feed-forward case for our running example as our Reference System $RS = ( M_{RS} , A_{RS} ,$ $Y_ RS , n_{RS} )$. We model each ‘AdjustSetpoint followed by Step/Scan’ pattern by a mode that we call $Scan$. We also define a $Calibrate$ mode that performs the $Calibrate$ operation of the system. We assume that after executing the $Scan$ mode twice, the system may either calibrate the stage or continue scanning without calibration. The system halts after having executed four $Scan$ modes. We thus have $M_{RS} = \{ Scan,Calibrate \}$ and automaton $Y_ RS$ as depicted in Fig. 4, where $q_0$ is the initial state (marked by an arrow) and $q_4$ is the final state (marked by a double-walled circle). The mapping $A_{RS}$ of modes to mode matrices of size $n_{RS}$ is presented below after we have discussed the modes.

Fig. 4

Mode automaton of a batch of four scans ($Y_ RS$)

In SMPLS, a mode matrix captures the effect of executing the mode on a state vector. In our context, we are interested in availability times of the system resources. Hence, the elements of the state vector capture resource availability times. An execution of the $Scan$ mode in $RS$ claims the Compute resource to perform the AdjustSetpoint operation, releases the Compute resource and claims the Stage resource, performs the $Step/Scan$ operation, and finally releases the Stage resource. Each mode of $RS$ is mapped to a mode matrix (by function $A_{RS}$) of size $n_{RS} =2$ that describes how the availability times of the resources change by executing the mode. Each mode matrix captures the timing dependencies between resource claims and releases, and the max-plus multiplication of state vectors and matrices determines the resource availability times after executing the mode. We assume that $AdjustSetpoint$, $Step/Scan$, and $Calibrate$ operations take 2, 3, and 4 time units, respectively. The matrices associated with the $Scan$ and $Calibrate$ modes of $RS$ are then as follows:

$$\begin{aligned} A( Scan ) = \begin{bmatrix} 2 &{} {-\infty {}}\\ 5 &{} 3 \\ \end{bmatrix} , A( Calibrate ) = \begin{bmatrix} 4 &{} 4 \\ 4 &{} 4 \\ \end{bmatrix} \end{aligned}$$

Because the system has two resources, we have state vectors and mode matrices of size 2. In a mode matrix, the indices of rows and columns correspond to resource numbers. Each element $A_{ij}$ corresponds to the minimum time that the mode takes between claiming resource j and releasing resource i. As an example, consider $A( Scan )$. Index 1 refers to resource Compute and index 2 refers to resource Stage. The value 2 in the matrix denotes that resource 1 is claimed and that it takes at least 2 time units before it is released. The value ${-\infty {}}$ implies the absence of a timing dependency between claiming resource 2 and releasing resource 1. Value 5 means that it takes at least 5 time units to release resource 2 after claiming resource 1, due to a dependency between the operations $AdjustSetpoint$ and $Step/Scan$. This value corresponds to the summed durations of the individual operations.

Figure 5 shows the Gantt charts of executing the two possible mode sequences specified by the automaton in Fig. 4. The execution of operations is pipelined, based on the availability of the system resources that they use and their timings. Figure 5(a) corresponds to mode sequence $Scan,Scan,Scan,Scan$, and Fig. 5(b) corresponds to mode sequence $Scan,Scan,Calibrate,$ $Scan,Scan$. The arrows show functional dependencies between the $AdjustSetpoint$ and the $Step/Scan$ operations that are respected when executing a $Scan$ mode. Each row in the chart represents a system resource. On top of each chart, the resource availability state vectors are shown.

Fig. 5

Gantt charts of a batch of four pipelined $Scan$ modes, without (a) and with (b) calibration

3.3 Feed-forward semantics

The semantics of an SMPLS is defined as the set of possible sequences of state vectors. Such a sequence is denoted by $\bar{x}(k)$. For the running example, there are two sequences, which are shown in Fig. 5. Formally, the semantics of an SMPLS is defined as follows.

Definition 2

A word in an SMPLS (M, A, Y, n) with $Y=(Q,S, \Delta ,M,F)$ is a finite sequence of modes. A word $w = m_1,m_2,...,m_j \in M^*$ is accepted by automaton Y if and only if there exists a sequence $q_0,q_1,... ,q_j \in Q^*$ of states such that $q_0 \in S$, $(q_k,m_{k+1},q_{k+1}) \in \Delta$ for all $0 \le k < j$, and $q_j \in F$. The language $\mathcal {L}(Y)$ of an automaton Y is the set of all words that are accepted by the automaton Y.

Definition 3

Given a word $w = m_1,m_2,...,m_j\in M^*$, we define the corresponding sequence of state vectors $\bar{x}(k)$ for $0\le k\le j$ using the following equation:

$$\begin{aligned} \bar{x}(k+1) = A(m_{k+1}) \otimes \bar{x}(k) \end{aligned}$$

(1)

where initial state vector $\bar{x}(0) = \bar{0}$. For the example, this means that all resources are assumed to be initially available at time 0.

Equation 1 provides the basis for the semantics of SMPLS (see Fig. 1).

Definition 4

The semantics of an SMPLS is the set of sequences of state vectors defined by Eq. 1 corresponding to the words in $\mathcal {L}(Y)$.

We apply worst-case makespan analysis to demonstrate one type of performance analysis that can be performed on SMPLS. To define the makespan of an SMPLS, we first define the makespan of a mode sequence.

Definition 5

Let $w \in M^*$ be a word. We let $\bar{x}(w)$ denote the state vector after execution of the sequence w of modes. The makespan of a word w is then defined as $\mu (w) = \vert \bar{x}(w)\vert$. The makespan of SMPLS (M, A, Y, n) is defined as $\mu (M, A, Y, n) = \sup _{w\in {\mathcal {L}}(Y)} \mu (w)$.

The makespan of w equals the time at which the last mode in w has completed execution. For example, the makespans of the sequences in Fig. 5(a) and (b) are 14 and 20, respectively. We define the makespan of an SMPLS as the worst-case makespan of all of its mode sequences. Hence, the makespan of the system in Fig. 5 is 20. Note that the makespan over an infinite language may be infinite.

3.4 Max-plus automata

For the running example, we can find the makespan by enumerating all mode sequences. In general, this is not feasible, because it does not scale well, and infinitely many of them may exist. To obtain a generic analysis method, we transform an SMPLS to a max-plus automaton to analyze its timing properties. A max-plus automaton is a generalization of a finite state automaton that not only defines a set of accepted words, but also assigns weights to those words. It assigns a weight to each transition, so that by adding the weights of the transitions of a word, we obtain the weight of that word.

Definition 6

A max-plus automaton (Gaubert 1995) is a five-tuple $\mathcal {A}=(Q,\Sigma ,\alpha ,\beta ,D)$, with

• a finite set Q of states;

• a finite alphabet $\Sigma$;

• a function $\alpha : Q \rightarrow T$ that assigns an initial weight to every state;

• a function $\beta : Q \rightarrow T$ that assigns a final weight to every state;

• a function $D: Q \times \Sigma \times Q \rightarrow T$ that assigns a weight to every transition.

A max-plus automaton defines transitions for all pairs of states and all symbols. It therefore may be non-deterministic. It rules out unwanted transitions (and hence unwanted words) by assigning the weight ${-\infty {}}$ to them. Transitions are further labeled with a symbol of the alphabet.

Definition 7

Let path $p=q_0,q_1,...,q_{j} \in Q^{j+1}$ and let $w=a_1,a_2,...,a_j \in \Sigma ^j$. The weight of word w on path p is defined as $weight(w,p) = \alpha (q_0) + D(q_0,a_1,q_1) + ... +D(q_{j-1},a_j,q_j) + \beta (q_{j})$.

Since max-plus automata are non-deterministic, they generally have multiple paths corresponding to a given word, which may have different weights. The weight of a word is the maximum weight of all paths corresponding to that word.

Definition 8

The weight of a word $w\in \Sigma ^*$ is

$$\begin{aligned} weight (w) = \bigoplus _{p\in Q^{\vert w \vert +1}} weight(w,p) \end{aligned}$$

Definition 9

A word w in a max-plus automaton is accepted if $weight (w) \ne {-\infty {}}$. The language of a max-plus automaton $\mathcal {A}$ is the set of all accepted words and is denoted by $\mathcal {L(A)}$.

We use the product of two max-plus automata for timing analysis of SMPLS. The product of two max-plus automata is defined for automata with equal alphabets.

Definition 10

The product ${\mathcal {A}} \odot {\mathcal {B}}$ of max-plus automata (defined in Gaubert (1995)) $\mathcal {A} = (Q_{\mathcal {A}},\Sigma ,\alpha _{\mathcal {A}},\beta _{\mathcal {A}}, D_{\mathcal {A}})$ and ${\mathcal {B}} = (Q_{\mathcal {B}},\Sigma ,\alpha _{\mathcal {B}},\beta _{\mathcal {B}},$ $D_{\mathcal {B}})$ is a max-plus automaton $(Q,\Sigma ,\alpha ,\beta ,D)$ with:

• the set $Q = Q_{\mathcal {A}} \times Q_{\mathcal {B}}$ of states;

• the alphabet $\Sigma$;

• the function $\alpha : Q \rightarrow T$ that assigns an initial weight $\alpha _{\mathcal {A}}(q_1) \otimes \alpha _{\mathcal {B}}(q_2)$ to every state $(q_1,q_2) \in Q$;

• the function $\beta : Q \rightarrow T$ that assigns a final weight $\beta _{\mathcal {A}}(q_1) \otimes \beta _{\mathcal {B}}(q_2)$ to every state $(q_1,q_2) \in Q$;

• the function $D: Q \times \Sigma \times Q \rightarrow T$ that maps a weight $D_{\mathcal {A}}(q_1, a, q_1') \otimes D_{\mathcal {B}}(q_2, a, q_2')$ to every transition $((q_1,q_2), a, (q_1',q_2'))$.

Hence, the product of two max-plus automata is a max-plus automaton with the product of the states, where a state has initial weight $>{-\infty {}}$ iff it is the product of two states with initial weight $>{-\infty {}}$. The same rule applies to final weights of states. The transition weights are the max-plus product of the transition weights of the two automata. Therefore, we only assign a weight $> {-\infty {}}$ to those transitions that have weight $> {-\infty {}}$ in both automata. The product automaton only accepts words that are accepted by both automata. The weight of any word in the product automaton is the sum of the weights of this word in the constituent automata.

In line with Definition 5, and analogous to the worst-case analysis in Section IV of Gaubert (1995), we define the makespan of a max-plus automaton as the largest weight of any word. Only accepted words have a weight larger than ${-\infty {}}$.

Definition 11

The makespan of a max-plus automaton $\mathcal {A}$ is defined as

$$\begin{aligned} \mu ({\mathcal {A}})= \sup _{w \in {\mathcal {L}}({\mathcal {A}})} \mu (w) \end{aligned}$$

As an example, Fig. 6 shows a graphical representation of a max-plus automaton. By convention, transitions with weight ${-\infty {}}$ are not drawn. In this max-plus automaton, $Q=\{1,2\}$ and $\Sigma = \{S,C\}$. States 1 and 2 have initial weight 0, indicated by the incoming labelled arrows. States 1 and 2 have final weight 0, denoted by the outgoing labelled arrows. Transitions are $D=\{((1,S,1),2), ((1,S,2),5),((2,C,2),4),...\}$. By definition, there exists a transition between any pair of states for any symbol in a max-plus automaton. Some have weight ${-\infty {}}$, for instance $D(2,S,1)={-\infty {}}$ (and hence are not drawn). An example of a path in this automaton is $p_1 = 1,1,2,1$ having weight 13 for word $CSC$. There are other paths for the word $CSC$, for example $p_2 = 2,2,2,2$ with weight 11.

Fig. 6

Max-plus automaton (representing the mode matrices of RS)

3.5 Feed-forward analysis

To analyze a system, we use the specified mode automaton of the system and the mode matrices associated with each mode as input. We then generate a max-plus automaton that represents the behavior of the system. This way, we reduce the makespan analysis problem of our SMPLS to the makespan analysis of a max-plus automaton and use the existing analysis methods for such systems (van der Sanden et al. 2016; Gaubert 1995; Singh and Judd 2014).

Fig. 7

Transformation of system specification into a max-plus automaton

The transformation that we perform is analogous to the construction described in Section VI of Gaubert (1995), and is depicted in Fig. 7. The transformation for an SMPLS (M, A, Y, n) is defined as the product of two max-plus automata H(Y) and $G(M,A)$. The max-plus automaton H(Y) captures the possible sequences of modes and restricts the behavior of the system to the specified behavior, without any timing information. On the other hand, the max-plus automaton $G(M,A)$ specifies all the timing information of the modes, but it does not restrict the sequences of modes, allowing all possible mode sequences. The product of these two max-plus automata restricts the language of the system to the specified mode sequences and contains all timing information of sequences of that language. This max-plus automaton therefore has all the necessary information to analyze the timing behavior of the system.

Definition 12

H(Y) is max-plus automaton $(Q,\Sigma ,\alpha ,\beta ,D)$ with:

• the set $Q = Q(Y)$;

• the alphabet $\Sigma = M(Y)$;

• the function $\alpha$ that assigns an initial weight 0 to every state $q \in S(Y)$ and ${-\infty {}}$ otherwise;

• the function $\beta$ that assigns a final weight 0 to every state $q \in F(Y)$ and ${-\infty {}}$ otherwise;

• the function D that maps a weight 0 to every transition in $\Delta (Y)$ and a weight ${-\infty {}}$ to every transition not in $\Delta (Y)$.

Figure 8 depicts the max-plus automaton H(Y) for $RS$. For simplicity, $Scan$ and $Calibrate$ are depicted by the symbols S and C, respectively. This max-plus automaton accepts all the sequences of modes that the system may execute. All transitions have either weight 0 or ${-\infty {}}$ so that it assigns weight 0 to all words accepted by Y and ${-\infty {}}$ to all other words.

Fig. 8

Max-plus automaton of the mode automaton of RS

$G(M,A)$ is a max-plus automaton capturing the timing information of the mode matrices.

Definition 13

$G(M,A)$ is max-plus automaton $(Q,\Sigma ,\alpha ,\beta ,D)$ with:

• the set $Q=\{q_1,q_2, ..., q_n\}$ of states, where n is the size of the matrices of A (from Definition 1);

• the alphabet $\Sigma = M$;

• the function $\alpha$ that assigns an initial weight 0 to every state;

• the function $\beta$ that assigns a final weight 0 to every state;

• the function D that assigns a weight $A(m)_{ji}$ to every transition (i, m, j).

Figure 6 depicts the max-plus automaton $G(M,A)$ for RS. Through the weights, this automaton represents the timing (makespan) of any mode sequence, not restricted to the language of Y. Figure 9 shows the product of the automata in Figs. 6 and 8, where each state labeled $q_{i,j} \in Q$ is the product of $q_i \in Q(G(M,A))$ and $q_j \in Q(H(Y))$.

Using the product max-plus automaton of Fig. 9, we can compute the makespan of the system. The makespan is the maximum of all the path weights from any initial state (state with initial weight $\ne {-\infty {}}$) to any final state (state with final weight $\ne {-\infty {}}$). We prove that this makespan is equal to the makespan of the corresponding SMPLS. To this end, we first prove Lemma 1. Lemma 1 is a known result about max-plus automata. Since we are not aware of an explicit statement of it in literature, it is given here, including a proof, for the sake of completeness.

Fig. 9

Max-plus automaton representing the behavior of RS

Lemma 1

Let M be a set of modes and let A be a function that maps every mode $m\in M$ to a matrix A(m). Let $w = m_1,m_2,...,m_k \in M^k$ for some $k\ge 0$. Further, let $\bar{x}(w)$ be defined as:

$$\begin{aligned} \bar{x}(w) = \bigotimes _{0\le j < k} (A(m_{k-j}) \otimes \bar{0}) \end{aligned}$$

Then for all i, $\bar{x}{(w)}_i$ is equal to the longest w-path to state i in G(M, A).

Proof

The proof proceeds by induction on the length of w. For length 0, we have $\bar{x}(\epsilon ) = \bar{0}$ (where $\epsilon$ denotes the empty word). Every state i in G(M, A) has initial weight 0, so the assertion holds. Now assume that $\bar{x}(w)_i$ is equal to the weight of the longest path to state i in G(M, A) for word $w=m_1, m_2, ... ,m_k$ of length k. For word $w'=m_1,...,m_k,m_{k+1}$, we have $\bar{x}(w')_i = \bigoplus _j A(m_{k+1})_{ij} \otimes \bar{x}(w)_j$. By Definition 13, element $A(m_{k+1})_{ij}$ is equal to the weight of the edge from state j to state i, labelled $m_{k+1}$. All $w'$ paths to state i are w paths to some state j, followed by an edge labelled $m_{k+1}$ from j to i. So the longest $w'$ path to i is equal to the maximum over all j of the longest w path to j plus the weight of the $m_{k+1}$-edge from j to i. Therefore, by induction $\bar{x}(w')_i$ is equal to the weight of the longest path to state i in G(M, A) over the word $w'$. So the assertion holds for words of length $k+1$ as well. $\square$

Theorem 1

Let SMPLS $S=(M, A, Y, n)$. Then, $\mu (M, A, Y, n) = \mu (G(M,A)\odot H(Y))$.

Proof

Let $G=G(M,A)$ and $H = H(Y)$. $G\odot H$ only accepts words that are accepted by both G and H and it assigns a weight to those words which is the sum of their weights in G and H. Any state in H has initial weight 0 iff it is an initial state in Y. Otherwise, it has initial weight ${-\infty {}}$. Further any transition in H has weight 0, iff it is a transition in Y. Furthermore, any state in H has final weight 0 iff it is a final state in Y. Otherwise it has final weight ${-\infty {}}$. Therefore, H accepts exactly all words accepted by Y, and thus $\mathcal {L}(H)= \mathcal {L}(Y)$. Because H only has weights of 0 and ${-\infty {}}$, it restricts the words that are accepted in $G\odot H$. On the other hand, G accepts all words by assigning weights $\ne {-\infty {}}$ to every word. Consequently, the words accepted by $G\odot H$ are the words accepted by Y, i.e. $\mathcal {L}(G\odot H)= \mathcal {L}(Y)$. Therefore, the weight in $G\odot H$ of an accepted word in Y is equal to its weight in G, and ${-\infty {}}$ for a word not accepted by Y.

Lemma 1 proves that $\bar{x}(w)_i$ is the longest path to state i corresponding to the word w in G. Then $\vert \bar{x}(w)\vert$ is equal to the weight of the longest path for the word w to any state in G. Therefore, if w is accepted by H, then $\vert \bar{x}(w)\vert$ equals the weight of the longest path corresponding to w in $G\odot H$. Words not accepted by H do not follow this rule but their weight in $G\odot H$ is ${-\infty {}}$ because their weight in H is ${-\infty {}}$. And since they are not in $\mathcal {L}(Y)$, they do not affect the makespan. Since $\mu (M, A, Y, n)$ is equal to the largest makespan of any word in $\mathcal {L}(Y)$, $\mu (M, A, Y, n)$ is equal to the weight of the longest path in $G\odot H$. $\square$

For the max-plus automaton of Fig. 9, $\mu (M, A, Y, n) = 20$ for the path indicated in green. This path also gives us the accepted word $w_1 = SSCSS$ which determines the makespan of the system. We have multiple paths that correspond to $w_1$ but because the makespan of a word is the longest path for that word, $\mu (w_1)$ corresponds to path $q_{01}, q_{12}, q_{22}, q_{51}, q_{32}, q_{42}$. We also have another accepted word $w_2 = SSSS$. Similarly, we compute $\mu (w_2) = 14$, corresponding to path $q_{01}, q_{12}, q_{22}, q_{32}, q_{42}$. These results conform to the Gantt charts shown in Fig. 5.

4 Modeling and analysis of systems with discrete-event feedback

The baseline method explained in the previous section can model and analyze SMPLS that do not require discrete-event feedback from the system to the SC. SMPLS in general may require such mechanisms and the existing methods cannot succinctly specify discrete-event feedback and its impact on system timing and mode sequences that the system executes. This section introduces a method to model the behavior of such systems. For the purpose of analysis, we then introduce a transformation to a classical SMPLS such that system properties can be analyzed using existing analysis methods. We augment the running example by adding a feedback mechanism and use it to demonstrate our extension.

A key aspect of our approach is that we specify discrete-event feedback from system to SC in a way that allows analysis using the existing max-plus techniques. We introduce a model that includes events received back from the system and the possibility to react on them. Similar to the previous section, we distinguish specification, semantics and analysis aspects to model and analyze an FMS with feedback (in line with the breakdown in Fig. 1). Figure 10 illustrates our approach in modeling and analyzing an FMS that includes discrete-event feedback from the plant to the SC.

Fig. 10

Interaction between plant and SC modeled and analyzed in our approach

4.1 Augmented running example

We use the example of the previous section and add information about discrete-event feedback. We call this system the System With Events (SWE). Each $Scan$ operation emits an event $ScanResult$ after it is executed. The event $ScanResult$ models the feedback that is received, which contains information about the $Success$ or $Failure$ of the $Scan$ operation. The outcome of $ScanResult$ is $Success$ if the system executes that $Scan$ operation with sufficient accuracy, without the need to $Calibrate$. In that case, the system continues scanning. The outcome of $ScanResult$ is $Failure$ if the system accuracy is compromised after which the system will execute a $Calibrate$ operation. The calibration operation involves processing sensor data and making mechanical setpoint adjustments. We assume that the calibration process itself does not fail. Moreover, failed scans are not repeated, implying that a failed scan cannot be repaired. The data obtained from a failed scan can be used to adjust the setpoints.

The system works with a pipeline depth of two scans. Since it does not have any results from previous scans at the start, it performs two initial scans. The subsequent scans need to wait for the feedback from the previous ones. The reason to wait is that the system needs to use the result of the scans to determine either to continue scanning or to calibrate before executing the next scans. The feedback dependencies between scans is such that every $Scan _k$ waits for the result of $Scan _{k-2}$, for all $k>2$. After having executed four scans, two emitted events remain. These events are processed after which the machine halts. These events will not result in a calibration because there are no more scans to perform.

4.2 System specification with discrete events

We define SMPLS with events to specify a system with feedback dependencies. In this specification, the mode matrices are expanded to incorporate the timing of events and their impact on the timing of future modes. We define sets of events and event outcomes. Furthermore, we use I/O automata instead of ordinary automata to specify how event outcomes determine the possible mode sequences. By using event outcomes as input actions of the I/O automaton, and modes as output actions, we define system behavior in response to event outcomes.

Definition 14

An SMPLS with events is a nine-tuple ($M, E, U, \sigma , \gamma , A_c,A_e,Y, n$) with

• a finite set M of modes;

• a finite set E of events;

• a finite set U of event outcomes;

• a relation $\sigma \subseteq M \times E$ relating events to the modes that emit them;

• an injective relation $\gamma \subseteq E \times U$ relating event to their possible event outcomes;

• a function $A_c:M \rightarrow T^{n\times n}$ that maps each mode to a max-plus matrix of size $n\times n$;

• a function $A_e:M \rightarrow T^{p\times n}$ that maps each mode $m\in M$ to a max-plus matrix of size $p\times n$ with $p =\vert \sigma \cap (\{m\}\times E)\vert$ the number of events emitted by m;

• an I/O automaton Y with a set $I=U\cup \{\lambda \}$ of input actions representing event outcomes or the absence of such an outcome (action $\lambda$), and a set $O=M \cup \{\epsilon \}$ of output actions representing modes or the absence of a mode (action $\epsilon$);

• n the size of the core state vectors.

The number of events emitted by a mode m is determined by the number of pairs $(m,e)\in \sigma$ for some $e\in E$, , i.e., $\vert \sigma \cap (\{m\}\times E)\vert$. An I/O automaton is defined as follows.

Definition 15

An I/O automaton (Lynch and Tuttle 1988) is a seven-tuple (Q, S, $\Sigma$, I, O, $\Delta$, F) with

• a finite set $Q$ of states;

• a set $S \subseteq Q$ of initial states;

• a finite set $\Sigma$ of actions and disjoint sets I, O of input and output actions, such that $I \cup O = \Sigma$;

• a transition relation $\Delta \subseteq Q \times I \times O \times Q$;

• a set $F \subseteq Q$ of final states.

Figure 11 shows the I/O automaton of SWE, where transitions are labeled as (input action, output action), denoting that the automaton receives an input action on a transition and produces the output action of that transition. The empty input action $\lambda$, denotes that the transition does not process any event outcome. The empty output action $\epsilon$, means that no mode is executed in that transition. We specify SWE as an SMPLS with events in the following way:

• $M = \{ Scan,Calibrate \}$;

• $A_c( Scan ) = \begin{bmatrix} 2 &{} {-\infty {}}\\ 5 &{} 3 \\ \end{bmatrix}$, $A_c( Calibrate ) = \begin{bmatrix} 4 &{} 4 \\ 4 &{} 4 \\ \end{bmatrix}$

• $A_e( Scan ) = \begin{bmatrix} 5&3 \end{bmatrix}$, $A_e( Calibrate ) = [\;\;]\ \text {(denoting a matrix with 0 rows)}$

• $E = \{ ScanResult \}$;

• $U = \{ Success,Failure \}$;

• $\sigma = \{( Scan ,ScanResult)\}$;

• $\gamma = \{(ScanResult, Success ) , (ScanResult, Failure )\}$;

• the I/O automaton of Fig. 11;

• $n=2$.

Fig. 11

I/O automaton of a batch of four scans with choices based on discrete-event feedback(SWE)

Figure 11 shows choices of the system based on the outcome of the $ScanResult$ event, emitted by the $Scan$ modes. The outcome can either be $Success$ or $Failure$. Compared to the case without feedback, all modes have a matrix $A_e$ that captures the timing of event emission. The mode $Scan$ has $A_e( Scan )=\begin{bmatrix} 5&3 \end{bmatrix}$. $Scan$ emits one event, therefore, this matrix has one row representing the timing of this event relative to the availability times of system resources. These times are given by the state vector at the beginning of the mode execution. The mode $Calibrate$ emits no events so $A_e( Calibrate )$ is the $0 \times 2$ matrix that has no rows.

Because the pipeline depth of $Scans$ is two, the number of events in the system that have not yet been processed is at most two. Multiple instances of the same event are processed in FIFO order. For instance, the event that is processed in the transition from $q_3$ to $q_4$ in the automaton of Fig. 11 is the one that is emitted on the transition from $q_0$ to $q_2$.

Note that the I/O automaton (Fig. 11) captures the SC’s decision based on the outcome of events, leading to a calibration in case of failure. How the timing of the events affects timing of future modes is captured in the event matrices specified by $A_e$. Without capturing this timing dependency, the model would show acausal behavior, with a Gantt chart similar to Fig. 5a (for the case with four success outcomes). In that Gantt chart, we see that the AdjustSetpoint operation of the third Scan mode is executed (at time 4) before the Step/Scan operation of the second Scan mode has emitted its event (at time 5), because the Compute resource is available. This violates the timing causality of the decision to execute another Scan mode (instead of Calibrate). The information about the success or failure of the first Scan mode is only available at time 5. By introducing the event matrix for events, we can capture the timing dependencies for modes that depend on the outcome of the event, and ensure that they do not execute before the outcome of that event is known.

Figure 12 shows the Gantt charts of different mode sequences, depending on the outcomes of events emitted by Scan modes. The blue arrows indicate the ScanResult event being emitted and its outcome being processed by one of the next modes. Figure 12(a) differs from Fig. 5(a) in the sense that the last two scans cannot be executed before the system receives the outcome of previous scans. Therefore, the AdjustSetpoint operation of the third Scan cannot use the Compute resource before the outcome of the event emitted by the first Scan is known. Figure 12(b) corresponds to mode sequence $Scan,Scan,Calibrate,Scan,Scan$, and Fig. 12(c) corresponds to mode sequence $Scan,Scan,Scan,Calibrate,Scan$.

Fig. 12

Gantt charts of a batch of four pipelined $Scan$ actions

Our method requires the emission and processing of events in a system to be consistent. This means that events are only processed after they are emitted, and that events that are emitted must be processed before the system reaches a final state. To define the notion of a consistent I/O automaton, we first define the language of an I/O automaton.

Definition 16

A word in an I/O automaton Y=(Q, S, $\Sigma$, I, O, $\Delta$, F) is a finite sequence of pairs $(i,o) \in I\times O$. The word $w = (i_1,o_1), (i_2,o_2),...,(i_y,o_y) \in (I\times O)^*$ is accepted by Y if there exists a sequence $q_0, q_1, ... q_y \in Q^*$ of states such that $q_0 \in S$ and $(q_{j}, i_{j+1},o_{j+1},q_{j+1}) \in \Delta$, for all $0\le j < y$, and $q_y \in F$. The language $\mathcal {L}(Y)$ is the set of all words accepted by Y.

Definition 17

Given an accepted word $w=(i_1,o_1), (i_2,o_2), ..., (i_n,o_n)$ and an event $e \in E$, the number of times event e is emitted in w is defined as $\#^e(e,w) = \vert \{ 1\le j \le n \mid (o_j,e) \in \sigma \}\vert$. Moreover, the number of times event e is processed in w is defined as $\#^p(e,w) = \vert \{ 1\le j \le n \mid (e,i_j) \in \gamma \}\vert$.

In Definition 17, $\#^e(e,w)$ denotes the number of transitions in w where the output action $o_j$ is a mode that emits event e as specified in $\sigma$. Similarly, to compute the number of times event e is processed, $\#^p(e,w)$ denotes the number of transitions in w where the input action $i_j$ is an outcome of e, as defined by relation $\gamma$.

Definition 18

An I/O automaton is called consistent iff for any accepted word $w= (i_1,o_1), (i_2,o_2) ,$ $...,(i_n,o_n)$ and any event $e \in E$, $\#^e(e,w)=\#^p(e,w)$, and for all $k \le \vert w \vert$, if $u= (i_1,o_1), (i_2,o_2) ,...,$ $(i_k,o_k)$ then $\#^e(e,u) \ge \#^p(e,u)$.

4.3 System semantics with discrete events

Similar to the feed-forward semantics, we introduce an MPL representation, in which the behavior is the set of possible sequences of state vectors. In our feed-forward example, a state vector contains the availability times of resources in each state of the system. Our proposed approach introduces new information to the state of the system, which is the time at which the outcome of an event is produced, and hence available to future modes that depend on it. To this end, we introduce the notion of event vector $\bar{e}$. Each element of this vector corresponds to a point in time at which the outcome of an event is produced.

We concatenate the event vector to the state vector, and call it the augmented state vector, to record all the necessary information of the system in each state. We refer to the original part of the state vector, i.e., the part excluding the events, as the core state vector, and denote it by $\bar{x}_c$. The size of the augmented state vector will vary because the event vector may have different sizes in different states of the system, depending on the difference between the number of events emitted and processed prior to that state. Event vector $\bar{e}(k)$ contains the timestamps of the events that are emitted by modes in the system prior to reaching state k, and are not yet processed.

In the SMPLS equation of the system with events, we distinguish three categories of events, that together form the event vector. The part of the event vector that is being processed in the current mode execution is referred to as $\bar{e}_p$. This is defined by an outcome of that event being the input action of the transition of the I/O automaton that triggers the state update corresponding to the equation. Note that this means that $e_p$ has size 0 or 1, because at most one event outcome is processed in a transition. The part of the event vector that is untouched, i.e., conveyed without change to the next state vector, is referred to as $\bar{e}_c$. The part corresponding to events being newly emitted in the transition is referred to as $\bar{e}_e$.

Fig. 13

Events in the augmented state vector, corresponding to the fragment $q_0,q_2,q_3,q_4$ of Fig. 15

Figure 13 shows four augmented state vectors corresponding to three subsequent transitions following the path $q_0,q_2,q_3,q_4$ of Fig. 15 (the matrices in Figs. 13 and 15 are explained later). The first state vector $\bar{x}(0)$ has no event timing, so $\bar{e}(0)$ is empty. The state vector only consists of the core state vector, which has size two in all states. On the first transition $k=1$, we emit one event to the state vector with a time stamp of 5, so $\bar{e}_e(1) = [5]$, which resides at the bottom of the augmented state vector $\bar{x}(1)$. $\bar{e}_c(1)$ and $\bar{e}_p(1)$ in transition 1 are empty because we are not conveying or processing any events in transition 1. Note that the indices of event vectors $e_c$, $e_p$ and $e_e$ correspond to transitions and not states. On the second transition $k=2$, we convey the event to the next vector, so $\bar{e}_c(2) = [5]$. We also emit a new event to the next state vector, so $\bar{e}_e(2) = [8]$. On the third transition $k=3$, we process the first event that was emitted, so $\bar{e}_p(3) = [5]$.

In the model with feedback, we use mode matrices $A_c(m)$ and $A_e(m)$ (Definition 14) to capture the update of the impacted part of the augmented state vector, i.e., the core and the emitted events. We call $A_c(m)$ the core part and $A_e(m)$ the event part. The core part captures the relation between the current core state vector $\bar{x}_c$, and the next one, while the event part represents how the emitted events in the next vector depend on the current core state vector. In the example, Scan emits one event and $A_{e}( Scan ) = \begin{bmatrix} 5 &{} 3\\ \end{bmatrix}$.

Our specification of the mode I/O automaton includes transitions with the empty output action $\epsilon$, meaning that the transition does not execute any modes. For convenience, we extend the domain of the functions $A_c$ and $A_e$ to include this empty output action $\epsilon$. We let $A_c(\epsilon ) = I$ (the max-plus identity matrix), and $A_e(\epsilon )$ be equal to a matrix with zero rows because the empty mode is assumed to emit no events.

Consider an accepted word $w=(i_1,o_1),(i_2,o_2),$ $...,(i_j,o_j)$. We denote $q_k$ as the source state of the kth transition of the I/O automaton for word w. We let $\#^c(q_k,i_k)$ denote the number of events being conveyed in the kth transition, i.e., the number of events present in state $q_k$ that are not processed in $i_k$. This is equal to the size of the vector $\bar{e}_c(k)$.

Similar to $A_c$ and $A_e$, we introduce matrices $B_c$ and $B_e$, collectively called B, to capture the relation between the processed events in a transition and the core state vector and emitted events of the next state. $B_c$ captures the relation between $\bar{e}_p$ and $\bar{x}_c$, while $B_e$ relates the processed events $\bar{e}_p$ to the emitted events $\bar{e}_e$. A mode that processes events does not start until the event outcome is available, i.e., the mode execution is according to starting core state vector $\bar{x}_c \oplus \bar{0}^{n,v} \otimes \bar{e}_p$, with n equal to the size of $\bar{x}_c$ and v equal to the size of $\bar{e}_p$. Recall that v is either 0 (for input action $\lambda$) or 1 if the input action is an event outcome. The execution of the mode itself from this starting vector is captured by matrices $A_c$ and $A_e$, as far as the core state vector and the emitted events are concerned, respectively. Therefore, the matrices $B_c$ and $B_e$ that describe how the core state vector and the emitted events depend on the processed events are given by $B_c = A_c \otimes \bar{0}^{n,v}$, and $B_e = A_e \otimes \bar{0}^{n,v}$.

An example of $A_c$, $A_e$, $B_c$, and $B_e$ is found in Fig. 14 on the left. The matrix corresponds to the transition from $q_3$ to $q_4$ in Fig. 15. For every state of the automaton, we know what events are emitted and not yet processed when we arrive in that state and in what order they have been emitted. The consistency requirement (Definition 18) ensures that the different paths from any initial state to that state result in the same set of events emitted and not yet processed in that state. In state $q_3$, we have one event (ScanResult) being processed in that transition, so the size of $\bar{e}_p$, v, is equal to 1. The size of $A_c$ is equal to $2\times 2$ and $A_e$ has 2 columns. $B_c$ and $B_e$ are 2-by-1 and 1-by-1 matrices, respectively, given by $B_c = \begin{bmatrix} 2&5\end{bmatrix}^T$ and $B_e = [5]$. The matrix on the right side of Fig. 14 is explained later in this section.

Fig. 14

Parts of an example matrix ($N^r_{q_3, Success , Scan }$ of Fig. 15) and matrix reordering

With the introduced $A_c$, $A_e$, $B_c$ and $B_e$ matrices, we can now formulate the SMPLS equations as follows:

$$\begin{aligned} \bar{x}_c(k)= & {} A_c(o_k) \otimes \bar{x}_c(k-1) \oplus B_c(i_k,o_k) \otimes \bar{e}_p(k) \end{aligned}$$

(2)

$$\begin{aligned} \bar{e}_e(k)= & {} A_e(o_k) \otimes \bar{x}_c(k-1) \oplus B_e(i_k,o_k) \otimes \bar{e}_p(k) \end{aligned}$$

(3)

$$\begin{aligned} \bar{e}(k-1)= & {} \begin{pmatrix} \bar{e}_p\\ \bar{e}_c \end{pmatrix} (k) \end{aligned}$$

(4)

$$\begin{aligned} \bar{e}(k)= & {} \begin{pmatrix} \bar{e}_e\\ \bar{e}_c \end{pmatrix} (k) \end{aligned}$$

(5)

Equation 2 shows how processed events and the starting core state vector $\bar{x}_c$ of a mode affect the next core state vector. Equation 3 shows how they affect the timing of the events emitted by the mode. Equations 4 and 5 show conveying of outcome timings to the next augmented state vector to be processed in a later mode execution. The conveyed outcome timings remain unchanged by this operation. We combine (Eqs. 2–5) into a single matrix-vector equation:

$$\begin{aligned} \begin{pmatrix} \bar{x}_c \\ \bar{e} \end{pmatrix} (k) = N_{q_k,i_k,o_k} \otimes \begin{pmatrix} \bar{x}_c \\ \bar{e} \end{pmatrix} (k-1) \end{aligned}$$

(6)

where for any $q \in Q, i \in I, o \in O$,

$$\begin{aligned} N_{q,i,o} = \begin{pmatrix} A_c(o) &{} B_c(i,o) &{} {-\infty {}}\\ A_e(o) &{} B_e(i,o) &{} {-\infty {}}\\ {-\infty {}}&{} {-\infty {}}&{} I_{\#^c(q,i)} \end{pmatrix}, \end{aligned}$$

$I_{\#^c(q,i)}$ is the identity matrix of size ${\#^c(q,i)}$, the number of events conveyed in the transition, and the ${-\infty {}}$ symbols represent matrices of appropriate sizes filled with ${-\infty {}}$.

Note that the matrix depends on the state q, because q determines the events that are emitted leading up to state q. It further depends on the label of the transition (i, o) that is taken by the I/O automaton, which indicates what event is being processed (as determined by event outcome i) and what event is being emitted (determined by mode o) in the transition.

The set of events present in a state of the I/O automaton is independent of the path that is taken to reach that state. However, the order in which they are emitted may be different. To make the event timings inside an augmented state vector consistent in each state, independent of the path taken to reach that state, we impose a canonical ordering on them. We order them alphabetically using event names, but any other canonical order could have been chosen as well. When the same event is emitted multiple times along a path, we order their outcomes and time stamps in accordance to the order of emission, having the timing of the event emitted during an earlier transition at the top. To maintain this canonical order, we have to reorder the rows and columns of matrices $N_{q,i,o}$ such that they are consistent with the canonical order. We denote these reordered matrices by $N^r_{q,i,o}$ and present the equations of SMPLS with events as:

$$\begin{aligned} \bar{x}(k) = N^{r}_{q_{k},i_{k},o_{k}} \otimes \bar{x}(k-1) \end{aligned}$$

(7)

We illustrate the matrix $N^r_{q_3, Success , Scan }$ as an example in Fig. 14. This is the matrix for the transition from $q_3$ to $q_4$ in Fig. 11. The transition has an input action Success, which is an outcome of the event ScanResult. Therefore, $B_c(i,o)$ and $B_e(i,o)$ are not empty. The timestamp we are processing is from the ScanResult event emitted on the transition from state $q_0$ to $q_2$ and, being the first ScanResult emitted, is the third element on the augmented state vector. So $B_c(i,o)$ and $B_e(i,o)$ are ordered in the third column of $N^r_{q_3, Success , Scan }$. Furthermore, we are conveying one event timestamp (the one emitted in $(q_2,(\lambda , Scan ), q_3)$) to the next vector. So $I_{\#^c(q,i)}$ has size 1. The conveyed event timestamp is in the fourth element of the augmented state vector. So $I_{\#^c(q,i)}$ is the fourth column of $N^r_{q,i,o}$. Finally, we emit an event to the next vector. We also want to order the events on the next augmented state vector, so we have $I_{\#^c(q,i)}$ on the third row, and $A_e$ on the fourth. This puts the earlier emitted event timestamp higher in the next augmented state vector in accordance with the selected canonical order. The emitted event must also be recorded orderly (alphabetically, then order of emission) in the next state vector, so it goes at the bottom (because it is emitted later). The target state is not needed to determine $N^r_{q,i,o}$, because on any transition of the I/O automaton, knowing the set and canonical order of events in the starting state and the input and output action of the transition, the set and canonical order of events in the target state can be determined.

Fig. 15

The automaton of SWE with the result of $N^r_{q,i,o}$ on each transition

Figure 15 shows the correctly ordered matrices for SWE on each transition. With these matrices, we can compute the state vector $\bar{x}(k)$ for a given word by matrix-vector multiplication along any path of the automaton for that word leading to state k. Because of the reordering applied to the state matrices, and the consistency of Y, for any path leading to a selected state, $\bar{x}(w)$ will contain the same events in the same order. Consider state $q_5$ as an example. Any path to it yields an augmented state vector with availability timings of the two resources at the top and two events emitted by the third and fourth Scan, ordered by order of emission from top to bottom.

4.4 System analysis with discrete events

In this section, we show how an SMPLS with events can be transformed into a classical SMPLS, while retaining all the timing information of the added interactions. This means that all the interactions, including the additional discrete-event interactions, can be analyzed using existing methods for classical SMPLS.

In a classical SMPLS, the state of the system is updated by mode execution, and the mode matrices capture the relation between the current state and the next. A key difference between the SMPLS semantics for systems with events and classical SMPLS is that the former have state vectors with a dynamically changing size, whereas the latter have fixed-size state vectors. In an SMPLS with events, the next state of the system depends on the mode, the current state, the history of events emitted and not yet processed, the ones being conveyed to the next state, and the ones being processed in the transition. This history can be retrieved for every state of the mode automaton. In our transformation, we use system modes that capture this dependency, so that the resulting SMPLS only depends on its modes for state updates. Our mode I/O automaton has input actions and output actions (event outcomes and mode, respectively) as transition labels. Therefore, the state in the automaton and the labels together, constitute a mode of our classical SMPLS. We capture these in a set of modes, each pertaining to a transition going out of a state in the I/O automaton.

The envisioned approach reduces the analysis of an SMPLS with events to the analysis of its corresponding classical SMPLS (Fig. 1). We use the notation $S'(M', A', Y', n')$ to denote the classical SMPLS that is the result of the transformation from the SMPLS $S=(M, A_c, A_e, E, U, \sigma , \gamma , Y, n)$ with events.

First, we describe $M '$. We capture how the next state vector depends on the current state vector as a mode that is executed on the transition. We remove the dependency on the history of a state in Y, by combining this history and the transition label into one mode. Then, we present that mode as the one being executed on that transition in the classical SMPLS. $M'$ contains a triple (q, i, o) for every transition (i, o) out of every state q in Y. For example, we have $(q_0,\lambda , Scan )$ as one mode for $S'$ in our SWE example.

Second, mode automaton $Y'$ is the finite state automaton derived from Y, with modes $M'$ as follows.

Definition 19

The finite state automaton $Y'$ equals $(Q_{Y}, S_{Y}, \Delta ', M', F_{Y})$ with $\Delta ' = \{ (q_1,(q_1,i, {} o),q_2) \mid (q_1,(i,o),q_2) \in \Delta _{Y} \}$, and $M'=\{(q_1,i,o)\mid (q_1,(i,o),q_2) \in \Delta _{Y}\}$.

Using the semantics described in Section 4.3, for each transition in Y we have a matrix ($N^r_{q,i,o}$). These matrices typically are not of the same size. However, a classical SMPLS requires all mode matrices to be of the same size. To address the issue, we find the largest dimension in any matrix $N^r_{q,i,o}$, denoted by l, and enlarge all the $N^r_{q,i,o}$ matrices such that they become square matrices of size l by padding the extra rows and columns of the matrices with ${-\infty {}}$. We denote the enlarged matrix by $N^R_{q,i,o}$. We obtain $l_{ SWE }=4$. Padding $N^r_{q_0,\lambda , Scan }$ gives matrix $N^R_{q_0, \lambda , Scan }$:

$$\begin{aligned} N^R_{q_0,\lambda , Scan } =\begin{bmatrix} 2 &{} {-\infty {}}&{} {-\infty {}}&{} {-\infty {}}\\ 5 &{} 3 &{} {-\infty {}}&{} {-\infty {}}\\ 5 &{} 3 &{} {-\infty {}}&{} {-\infty {}}\\ {-\infty {}}&{} {-\infty {}}&{} {-\infty {}}&{} {-\infty {}}\end{bmatrix} \end{aligned}$$

We define a function $N^R(q, i, o)= N^R_{q,i,o}$ that is analogous to the function A of Section 3.5. $N^R$ corresponds to $A'$ of our classical SMPLS $S'$. As a result, the state vectors of $S'$ all have the core state vector and the event vector of the augmented state vector of the SMPLS with events, and are padded with ${-\infty {}}$ to size l. Now we have $n' = l$. For example, the state vector $\begin{bmatrix} 2 &{}5 &{} 5\\ \end{bmatrix} ^T$ in Fig. 13 corresponds to the state vector $\begin{bmatrix} 2 &{}5 &{} 5 &{} {-\infty {}}\\ \end{bmatrix} ^T$ in the transformed SMPLS.

With this transformation, we have obtained a classical SMPLS $S'=(M', A', Y', n')$ that is equivalent to the SMPLS with events S in terms of the sequences of state vectors that it allows, and can be analyzed with the same analysis method as used in Section 3.5.

Definition 20

Given SMPLS with events $S=(M, A_c, A_e, E, U, \sigma , \gamma , Y, n)$, its equivalent classical SMPLS is defined as $S'(M', A', Y', n')$ where $M'$ and $Y'$ are as defined in Definition 19, where $A'=N^R$ and $n'$ is the size of the $N^R$ matrices.

The equivalence between an SMPLS with events and its corresponding classical SMPLS is characterized by the following proposition.

Proposition 1

Let SMPLS $S=(M, A_c, A_e, E, U, \sigma , \gamma , Y,n)$. Let SMPLS $S'=(M', A', Y',$$n')$ be the transformed classical equivalent of S. For every state vector sequence $\bar{x}(k)$ in S, there is a state vector sequence $\bar{x}'(k)$ in $S'$ such that for all $k>0$, $\bar{x}'(k)_u = \bar{x}(k)_u$, for all $u \le p_k$, and $\bar{x}'(k)_u = {-\infty {}}$, for all $p_k < u \le n'$, where $p_k$ is the state vector size of $\bar{x}(k)$ and $n'$ is the state vector size of $S'$, and vice versa.

Proof

Let $\bar{x}(k)$ be a state vector sequence in S corresponding to the word $w = (i_1,o_1), (i_2,o_2),...,(i_k,o_k) \!\in \! \mathcal {L}(Y)$, accepted with the path going through states $q_0,q_1,\!...\!,q_{k}$. Consider the word $w' = (q_0,i_1,o_1), (q_1,i_2,o_2),...,(q_{k-1},i_k,o_k)$, being the corresponding word in $S'$. By Definition 19, all initial states of Y and $Y'$ are equal, and all final states of Y and $Y'$ are equal. Also every transition of Y is present in $Y'$ between the same states, with the source state label inserted in the transition label. Therefore, $w'$ is going through the same states and ends up in the final state $q_{k}$, thus, $w' \in \mathcal {L}(Y')$.

Let $\bar{x}'(k)$ be the state vector sequence corresponding to $w'$.

The proof proceeds by induction on k. Note that we start with $k=1$ as the base case, because Proposition 1 holds for $k>0$ and the initial state vector is by definition the zero vector. After the transition $(q_0,(i_1,o_1),q_1)$ in S, we have:

$$\begin{aligned} \bar{x}(1)_u= & {} \bigoplus _v N^r_{{q_{0},i_1,o_1}_{uv}} \otimes \bar{x}(0)_v \\= & {} \bigoplus _v N^r_{{q_{0},i_1,o_1}_{uv} } \\ \bar{x}'(1)_u= & {} \bigoplus _v A'(q_{0},i_1,o_1)_{uv} \otimes \bar{x}'(0)_v \\= & {} {\left\{ \begin{array}{ll} \bigoplus _v A'(q_{0},i_1,o_1)_{uv}, &{} \text {if } u \le p_1 \\ {-\infty {}}, &{} u > p_1 \end{array}\right. } \end{aligned}$$

where $p_1$ is the size of $\bar{x}(1)$. Because $A'(q_{0},i_1,o_1)$ is $N^r_{q_{0},i_1,o_1}$ padded by ${-\infty {}}$ to size $n'$, we have for all $u \le p_1, v \le n, A'(q_{0},i_1,o_1)_{uv} = N^r_{{q_{0},i_1,o_1}_{uv}}$ and $A'(q_{0},i_1,o_1)_{uv}={-\infty {}}$ otherwise. Therefore, the proposition holds for $k=1$. For the induction step, we assume that it holds for k. For case $k+1$, we have $\bar{x}(k) = \begin{bmatrix}a_1,...,a_{p_k}\end{bmatrix}^T$, and $\bar{x}'(k) = \begin{bmatrix}a_1,...,a_{p_k},...,a_n'\end{bmatrix}^T$. After the transition $(q_k,(i_{k+1},o_{k+1}),q_{k+1})$, we have:

$$\begin{aligned} \bar{x}(k+1)_u= & {} \bigoplus _v N^r_{{q_{k},i_{k+1},o_{k+1}}_{uv}} \otimes \bar{x}(k)_v \\= & {} \bigoplus _v N^r_{{q_{k},i_{k+1},o_{k+1}}_{uv}} \otimes a_v \\ \bar{x}'(k+1)_u= & {} \bigoplus _v A'(q_{k},i_{k+1},o_{k+1})_{uv} \otimes \bar{x}'(k)_v \\= & {} {\left\{ \begin{array}{ll} \bigoplus _v A'(q_{k},i_{k+1},o_{k+1})_{uv} \otimes a_v &{} \text {if } u \le p_{k+1}\\ {-\infty {}}&{} u > p_{k+1} \end{array}\right. } \end{aligned}$$

again, because $A'(q_{k},i_{k+1},o_{k+1})$ is $N^r_{q_{k},i_{k+1},o_{k+1}}$ padded by ${-\infty {}}$ to size $n'$. The proof for the other direction (from $S'$ to S) follows the same identities. $\square$

Theorem 2

Let SMPLS $S\!=\!(M, A_c, A_e, E, U, \sigma , \gamma , Y, n)$. Let SMPLS $S'\!=\!(M', A', Y', n')$ be the transformed classical equivalent of S. Then, the makespan of S equals the makespan of $S'$.

Proof

From Proposition 1 and Definition 5, we conclude that Theorem 2 holds for non-zero-length accepted words. For accepted words of length zero, we have $\vert \bar{x}(0)\vert = \vert \bar{x}'(0)\vert = 0$. Therefore, Theorem 2 holds for all accepted words. $\square$

For SWE, (7) gives the state vectors for its SMPLS S with feedback. For this SMPLS, $\mu (S) = 20$. The weight of the longest path in the corresponding max-plus automaton of $S'$ is also 20. Both results correspond to the word ($\lambda$, Scan), ($\lambda$, Scan), (Failure, Calibrate), ($\lambda$, Scan), (Failure, Scan), (Success, $\epsilon$), (Success, $\epsilon$) of S. There are other words with makespan 20 as well, and the weight of the longest path corresponding to those words in the max-plus automaton of $S'$ is also 20.

The equivalence between the state vectors of the SMPLS with events and those in the derived classical representation as stated in Proposition 1 implies that other analyses using SMPLS which are invariant under the equivalence between the semantics, like the throughput analysis of van der Sanden et al. (2016), also carry over to our setting with discrete-event feedback. Other analysis techniques besides worst-case makespan, such as latency analysis (Basten et al. 2020), reachability analysis (Adzkiya et al. 2015), and stability analysis (Goverde 2007) can be performed on the derived classical representation. Building upon the work of van der Sanden et al. (2016) and Basten et al. (2020), the semantics of the SMPLS with events can also be used to generate a state space that allows best-case makespan and throughput analysis with events.

Although the analysis is performed on the equivalent classical SMPLS of the SWE, specifying SWE using a classical SMPLS would be a very difficult task. A system designer would have to manually write the $N^R$ matrices for SWE for every transition in the automaton, ordering the events in every state while making sure the emission and processing of events are consistent. Our succinct specification method enables automated synthesis of the $N^r_{q,i,o}$ matrices of Fig. 15 (demonstrated in Section 5) as well as the padded matrices. The designer would only need to specify the matrices $A_c( Scan ),A_e( Scan ),$ and $A_c( Calibrate )$ (or, in turn, derive them through some other modeling formalism). Our approach also provides an automated consistency check to make sure events are not ignored and also not processed when they are not emitted yet in the system. A designer using our approach could then focus their effort on defining the sets and their relations and specifying the behavior of the SC in a concise way.

5 Evaluation

In this section, we evaluate our approach on an FMS that needs discrete-event feedback to be taken into account in the performance analysis. The eXplore Cyber Physical Systems (xCPS Adyanthaya et al. 2017, Fig. 16) platform, is a small-scale production line that captures the features and behavior of FMS present in the industry. The machine assembles complementary circular pieces. These are named top pieces and bottom pieces, and the machine assembles tops on bottoms and outputs the assembled products.

The pieces go through several processing steps in the machine: first, they are collected by a gantry arm and put onto the input belt (Belt 1). They are then moved to the turner station where all tops are turned upside-down. The bottoms pass through this station since they are assumed to not need orientation correction. The turner has a robotic grip that goes down, picks up the piece, moves up, rotates, and finally goes down and releases the piece. If a piece is too wide, the turner cannot grab it. It cannot be turned to its appropriate orientation in this case. After the turner station, the pieces go two separate ways, depending on their type. The bottoms are pushed to an indexing table, and the tops move to the assembler. The proper routing of pieces is managed through a number of sensors, stoppers, and switches. When a correctly oriented top arrives at the assembler, the assembler picks up the top and puts it on the bottom. Afterward the assembled product is pushed to the output belt and is removed from the assembly line. Incorrectly oriented tops are not used for assembly.

Fig. 16

The xCPS

We model the system as an SMPLS with events with 27 system resources ($n=27$). The resources include the belts, stoppers, sensors, switches, the indexing table, the turner, and the assembler. We assume an order of entry for the pieces. They arrive in the system in pairs of tops and bottoms. The system has 17 modes that capture its full behavior. The modes of the system correspond to movement of the pieces between different stations and the operations being performed on them. These modes abstract a number of system operations into a single piece of behavior.

Fig. 17

The internal operations of mode TurnerGoDown

We define an event that is emitted in the system as feedback. The event E1, emitted by the mode TurnerGoDown, is the result of the turner robot going down to try to grab a top. It may either succeed or fail, which are the two possible outcomes of the event. If the turner fails to go down, we assume that the piece is too wide and unfit for assembly. We use this information when the top piece is under the assembler robot to activate the right sequence of modes to refrain from picking it and to reject it. Figure 17 shows mode TurnerGoDown and its internal operations. It first claims the system resources that it needs (indicated by the blue boxes on the left). Then, it stops Belt 1 (the belt before the turner) to prevent other pieces from going to the turner station. After that, the turner begins going down, which is represented by the operation TurnerDown. At the end of this operation, the mode emits the event E1 with success or failure outcome, and releases the resources that it claimed. After this mode, we have branches in the I/O automaton that capture system behavior based on the outcome of this event. If the turner succeeds going down, we execute the mode that turns the top piece. Otherwise, we lift the turner and move the out-of-spec top piece down the line until it can be rejected.

There are 27 resources in the model, so we have $A_c$ matrices of 27 by 27 for modes and core state vectors of size 27. The mode TurnerGoDown has $A_e$ matrix of 1 by 27, since it emits one event ($p=1$). Other modes do not emit any events. We model the system in two variations. For one case, we consider a batch of two products being processed by the system, and for the other case a batch of three products. The statistics of the mode automata (two versions) of xCPS are given in Table 1. The makespan of this system is analyzed with the method explained in Section 4. The analysis is implemented within SDF3 (Stuijk et al. 2006), using and extending its max-plus analysis algorithms.

Our implementation traverses the automaton $Y$ and computes and stores (reordered and padded) matrices for each transition. The complexity of this operation is proportional to the number of transitions in $Y$, $\mathcal {O}(\vert \Delta _Y \vert \times l^2)$, where l is the size of the padded matrices. Then it transforms $Y$ and the computed matrices into a max-plus automaton using the method depicted in Fig. 7. The complexity of this operation is $\mathcal {O}(\vert \Delta _Y \vert \times l^2)$ (we compute an edge for each element of the matrices, hence, $l^2$). Hence, the complexity of computing the max-plus automaton is $\mathcal {O}( \vert \Delta _Y \vert \times l^2)$. We now have a max-plus automaton $\mathcal {A}=(Q_A,\Sigma _A,\alpha _A,\beta _A,D_A)$. Then we use the Bellman-Ford algorithm (Bellman 1958) to compute the maximum weight path from any starting state to a final state. The complexity of the Bellman-Ford algorithm is $\mathcal {O}(Q_A\times D_A)$. From our max-plus automaton construction, we know that $\vert Q_A \vert = l \times \vert Q_Y \vert$, where $Q_Y$ is the set of states of Y, and $D_A = \vert \Delta _Y \vert \times l^2$. Therefore, the complexity of our analysis function is $\mathcal {O}( \vert Q_Y \vert \times \vert \Delta _Y \vert \times l^3 )$.

Table 1 Analysis results of the xCPS

For a batch of two products, it takes about 0.38 seconds to construct the max-plus automaton ($G \odot H$), and the analysis takes about 0.15 seconds, giving the worst-case makespan of 31.67 seconds. It corresponds to the scenario in which the first top is out of spec and rejected, while the second one is successfully turned and assembled on the first bottom. This means that if the first top fails, it is more efficient to assemble the second top on the second bottom than to assemble it on the first bottom. The designers of xCPS may use this information to exclude this behavior from the SC, leading to a more efficient way of handling failure, which is to reject the corresponding bottom of a failed top.

Another way the designers could use this information is to find out what component contributes the most to this worst-case timing and try to improve it to achieve better performance. One of the key components that determines the scenario with the worst-case makespan is the indexing table. The reason is that, after we assemble the second top on the first bottom, the second bottom has to go through the system; this has the largest impact when the bottom is going through the indexing table while other resources are idle. Assume the designers of xCPS has a limited budget to spend to improve system timing in the most effective way. They could speed up the indexing table to achieve faster timing. After changing the alignment timing of the indexing table from 0.3 to 0.28, we observe that the successful assembly of two products becomes the worst-case makespan (31.58 seconds). Since assembly takes more time than failure, this is the desired situation. So we can improve system behavior by speeding up the indexing table.

The experiment with three products is more challenging because it has more behaviors and more concurrency that increases the size of the I/O automaton. Computing the max-plus automaton for three products takes 20 seconds. The analysis takes 1.45 seconds and shows that the worst-case makespan of the system is 55.13 seconds. It corresponds to the scenario in which the turner succeeds once, then fails, and again succeeds in grabbing the top piece. Although at first glance we would expect three successes to take the longest time, since assembly takes longer than rejection, in reality, a failure in between successes disrupts the flow of operations. In this particular scenario, the failed top moves to the assembler station and waits to be rejected. After it is rejected, the second bottom waits for the third top. This disrupts the flow, because this waiting means that the third bottom has to go through the system while no other operation is being performed. If we reject the second bottom, we do so in parallel to other necessary operations, so it does not take more time. But the second bottom waiting for the third top implies taking more time at the end of assembly to let the last bottom pass through.

With this information, the designers of the xCPS can again improve the SC excluding the worst performing behavior from the options allowed by the automaton. In this case, one can specify that the system rejects the corresponding bottom of a failed top to handle failures more efficiently, in line with the earlier observation for two products. We do so and perform the analysis again. This shows three successes to be the worst-case makespan (55.04 seconds). This scenario cannot be removed but may be used to identify the component in the system that is the best candidate to improve (or replace) to have the greatest impact on the overall system performance.

6 Related work

In this section, we discuss the literature relevant to our work. We focus on specification and analysis of interactions between the SC and plant in the form of discrete-event feedback and modes in SMPLS. We first briefly introduce a state-of-the-art approach to model and analyze a system using SMPLS. Then, we discuss feedback in loop control with a few examples and the key difference to our approach. Next, we discuss how our work is related to SC synthesis and the extensions of SC synthesis to max-plus linear systems. We further discuss two methods that model discrete events as uncontrollable actions, one in supervisory control theory and the other in timed automata, and present the key advantages of our work compared to that work. We finalize the discussion with a method that encodes information in the state vector of SMPLS resulting in dynamic state-vector sizes for the purpose of analysis.

A method similar to the one we use to create a max-plus automaton from timing matrices of modes is introduced in van der Sanden et al. (2016). The authors specify modular automata with modes as transition labels and compute the product automaton. By assigning matrices to the modes on those transitions, a max-plus automaton is created. The work proposes timing analysis on the state space of the monolithic product automaton to find the best-case mode sequence to be executed for best performance. The method takes a feed-forward approach and does not capture or take into account discrete-event feedback from plant to SC. Therefore, the SC is free to choose any mode sequence. As a result, the model cannot capture future behavior and timing that depends on events and their outcomes. We have shown in this article how this approach can be extended to specify and analyze performance of systems with discrete-event feedback and have illustrated it with worst-case makespan analysis.

Feedback from plant to controller is well investigated in the control domain. Control approaches building on (S)MPLS plant models that take into account feedback from the plant are, for instance, van den Boom De Schutter (2006); Brunsch et al. (2012); Fusco et al. (2018); van Amstel (2014); van den Boom et al. (2020). All these approaches obtain feedback by observing the state and outputs (i.e., the states in the (S)MPLS model) during system execution. For instance, van Amstel (2014) focuses on selecting the appropriate mode of operation as a function of the measured disturbances in the environment of the MPL system. This leads to an optimization problem to select what mode the system should execute next. The solution to this optimization problem yields an optimal controller. Another example is van den Boom De Schutter (2006) where a model-predictive control (MPC) problem is defined to address this optimization challenge. A controller is designed to optimize system timing based on a prediction horizon, the current state of the system, and the output. Our approach enables the SC to react to discrete-event feedback from the plant in the form of event outcomes with their timing captured in the augmented state vector.

The mode automaton of our approach could be the outcome of a SC synthesis procedure (Ramadge and Wonham 1987). In such a setting, the modes would be considered controllable actions and the event outcomes would be considered uncontrollable actions. The synthesis approach could be used to prune a controller so that it is guaranteed to satisfy desirable logical properties, such as non-blockingness, or any properties defined with additional automata. Extensions of SCS theory have been defined for max-plus automata (Lahaye et al. 2015; Komenda et al. 2009). These techniques can likely be applied in our setting to additionally guarantee that the controlled system satisfies performance properties. The mode automaton of our approach may be synthesized from modular automata making the approach more scalable (van der Sanden et al. 2016). The partial order reduction method of van der Sanden et al. (2018) may be applied to reduce the complexity of sthe controller before analysis while preserving its timing properties.

An approach to model and analyze systems with discrete-event feedback was proposed in van Putten et al. (2020). The authors position their work within the framework of SC synthesis of Ramadge and Wonham (1987), and define modes, where disturbances that affect system performance are considered feedback, modeled as uncontrollable modes. The chosen model is an extended finite automaton with variables, guards and update functions to capture the effect of untimed feedback on mode execution. Since the notion of feedback is not timed, this automaton does not capture timing information of feedback. Feedback is not provided through timed events, but instead is captured as variables referring to resource availability times, which allows decisions based on those variables to enable or disable the corresponding transitions. Because feedback is not timed, the approach cannot model timing dependencies between modes that are due to the fact that decisions based on event outcomes can only be made at the moment these outcomes become available. For instance, if we model the augmented running example of this article (SWE) in the approach of van Putten et al. (2020), the resulting Gantt chart would be Fig. 5a for the case with four successes. The approach does not consider the timing dependency between $Scans$ that requires a successful $Scans$ to be confirmed before starting another, and therefore, the cases covered in this article cannot be modeled and analyzed. Further, van Putten et al. (2020) does not give semantics in the form of an SMPLS, but uses a state-space approach for performance analysis, instead of the max-plus automaton analysis that we use. Analysis through max-plus automata is generally faster than state-space analysis (Geilen and Stuijk 2010), although it is also restricted to worst-case analysis, whereas the state-space approach is suitable for best-case analysis as well (Geilen et al. 2020). Our model can be used to generate a state space with event timing information though, in line with the proposal of van Putten et al. (2020), which is an interesting topic for future work.

Timed Automata extended with concepts of game theory, timed games (Behrmann et al. 2007), allow synthesis of a controller ensuring safe behavior and eventually reaching a final state avoiding deadlocks. A timed game automaton is introduced in which the set of actions is partitioned into controllable and uncontrollable actions. Similar to van Putten et al. (2020), feedback is modeled as uncontrollable actions that may occur and affect the system in terms of timing and behavior. Compared to TA, SMPLS provide more efficient analysis (faster, better scalable, using less resources) for systems with highly concurrent determinate behavior. TA do not support max-plus mode matrices to capture timing of high-level functionalities. So to model the systems of this article, all the detailed information of low-level actions and their durations needs to be encoded explicitly. An example system was investigated in van der Sanden et al. (2016) and found to be much harder to analyze in TA than with SMPLS. A similar conclusion can be found in Skelin et al. (2015) where MPLS analysis methods were found to be significantly faster than their TA counterparts and require noticeably fewer resources for similar analysis types (maximum response delay and maximum inter-firing latency).

SMPLS are used in literature as a semantic framework for dataflow models (Geilen 2010; de Groote et al. 2012). One such study can be found in Geilen et al. (2017) which uses SMPLS to analyze the performance of Scenario-Aware Dataflow Graphs. The use of SMPLS involves state vectors of varying sizes and correspondingly, non-square matrices in the analysis in a way that is similar to our approach. The work focuses on throughput analysis by means of a direct construction of a max-plus automaton from the SMPLS with varying state sizes. Instead of transforming SMPLS with events to classical SMPLS for analysis, we could have adapted the method of throughput analysis of Geilen et al. (2017) to perform makespan analysis. The methods are similar, in that they use dynamically-sized state vectors, and equally complex; by choosing the transformation method, we show that our framework can encode events in a classical SMPLS that can be analyzed without the need for a special analysis method.

7 Conclusion

In this article, we introduced SMPLS with events, as an extension of SMPLS, as a novel way to succinctly specify feedback in the form of discrete events and to analyze the impact of feedback on timing properties. In this extension, we modeled the plant behavior with system modes and captured the timing of discrete-event feedback emission from plant to SC in the mode matrices. We used I/O automata to capture how the SC responds to discrete-event feedback with corresponding mode sequences of the SMPLS. We defined the semantics of an SMPLS with events based on its modes, an I/O automaton, and adapted state-space equations. We showed how our model specifies emission of an event by a mode, and how other modes can use the outcome of an event that they rely on. We showed that the new state-space equations define an SMPLS with a dynamic state-vector size. To analyze the system, we introduced a transformation from SMPLS with events to classical SMPLS with equivalent semantics and properties, so that performance properties can be analyzed using existing methods, and proved its correctness. We demonstrated our approach for worst-case makespan analysis on a prototype production system. Our framework can be used for analysis of other properties than worst-case makespan, such as latency analysis, best-case makespan, reachability analysis, and stability analysis. We focused on the domain of FMS to demonstrate and evaluate our approach, but it is also applicable to other areas where systems are modelled and analyzed using SMPLS.