Abstract
Timed Event Graphs (TEGs) are a graphical model for decision free and time-invariant Discrete Event Systems (DESs). To express systems with time-variant behaviors, a new form of synchronization, called partial synchronization (PS), has been introduced for TEGs. Unlike exact synchronization, where two transitions t1,t2 can only fire if both transitions are simultaneously enabled, PS of transition t1 by transition t2 means that t1 can fire only when transition t2 fires, but t1 does not influence the firing of t2. This, for example can describe the synchronization between a local train and a long distance train. Of course it is reasonable to synchronize the departure of a local train by the arrival of long distance train in order to guarantee a smooth connection for passengers. In contrast, the long distance train should not be delayed due to the late arrival of a local train. Under the assumption that PS is periodic, we can show that the dynamic behavior of a TEG under PS can be decomposed into a time-variant and a time-invariant part. It is shown that the time-variant part is invertible and that the time-invariant part can be modeled by a matrix with entries in the dioid \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\), i.e. the time-invariant part can be interpreted as a standard TEG. Therefore, the tools introduced for standard TEGs can be used to analyze and to control the overall system. In particular, in this paper output reference control for TEGs under PS is addressed. This control strategy determines the optimal input for a predefined reference output. In this case optimality is in the sense of the ”just-in-time” criterion, i.e., the input events are chosen as late as possible under the constraint that the output events do not occur later than required by the reference output.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and motivation
TEGs are a subclass of timed Petri nets where each place has exactly one input and one output transition and all arcs have weight 1. Timed Event Graphs under Partial Synchronization (TEGsPS) are an extension of TEGs introduced in David-Henriet et al. (2014). A similar extension was introduced in De Schutter and van den Boom (2003), where TEGs with hard and soft synchronization are studied. TEGsPS can express some time-variant phenomena which cannot be expressed by standard TEGs. For instance, partial synchronization (PS) is useful to model systems where particular events can only occur in a specific time window. E.g., at an intersection, a vehicle can only cross when the traffic light is green. Clearly this describes a time-variant behavior, since the vehicle is delayed by a time that depends on its time of arrival at the intersection. If an earliest functioning rule is adopted, the behavior of a TEG can be modeled by linear equations in a specific algebraic structure called dioid. Based on such dioids, a general theory has been developed for performance evaluation and control of TEGs, e.g. Baccelli et al. (1992) and Heidergott et al. (2005). In particular, the problem of output reference control for TEGs was studied in Baccelli et al. (1992); Cohen et al. (1989); Menguy et al. (1998, 2000). Recently, in David-Henriet et al. (2014, 2015, 2016), dioid theory has been applied to TEGsPS and first results have been obtained for performance evaluation and controller synthesis for TEGsPS. In David-Henriet et al. (2014) output reference control was introduced for TEGsPS. There, the earliest evolution of a Timed Event Graph under Partial Synchronization (TEGPS) is modeled as a (max,+)-system with additional constraints. The control problem is then solved for a finite reference output by solving the backward equation for this (max,+)-system. In Hamaci et al. (2006) and Trunk et al. (2017b) output reference control was studied for TEGs with positive integer weights on the arcs. These TEGs exhibit event-variant behavior and can therefore be seen as the counter-part to TEGsPS.
In this paper we investigate TEGsPS where partial synchronization is periodic. To consider only periodic partial synchronization is not overly restrictive as periodic schedules are common in many applications. E.g. in transportation networks: many public transportation system as well as freight railway services work with a periodic schedule. Similarly in manufacturing systems: there are many production processes, where a resource is shared between several machines on the basis of a periodic schedule. We show that for TEGsPS with periodic PS the dynamic behavior can be modeled in a specific dioid called \(\mathcal {T}_{per} [\![ \gamma ]\!]\). A specific time-variant operator is introduced to take PS into account. Similar to transfer functions for standard TEGs in the dioid \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\), the transfer behavior of TEGsPS is described by ultimately cyclic series in the dioid \(\mathcal {T}_{per} [\![ \gamma ]\!]\). These transfer functions are useful, for instance, for computing the output for a given input of a system, for system composition and for control synthesis.
This paper is organized as follows: Section 2 summarizes the necessary facts on TEGsPS and dioid theory. In Section 3, modeling of TEGsPS in the dioid \(\mathcal {T}_{per} [\![ \gamma ]\!]\) is introduced. Section 4 discusses a decomposition method for elements in \(\mathcal {T}_{per} [\![ \gamma ]\!]\) and provides tools to handle operations on ultimately cyclic series in \(\mathcal {T}_{per} [\![ \gamma ]\!]\). In particular, we show that basic operations on ultimately cyclic series in \(\mathcal {T}_{per} [\![ \gamma ]\!]\) can be reduced to operations between matrices in \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\). In Section 5, transfer functions for TEGsPS in \(\mathcal {T}_{per} [\![ \gamma ]\!]\) are used to solve the optimal output reference control problem for this system class.
A preliminary version of this work has been reported in Trunk et al. (2018), where the modeling process of a TEGPS in the dioid \(\mathcal {T}_{per} [\![ \gamma ]\!]\) was established and a decomposition into an invertible time-variant and a time-invariant part was discussed. The purpose of this paper is to introduce optimal output reference control for TEGsPS based on the model in the dioid \(\mathcal {T}_{per} [\![ \gamma ]\!]\). As a prerequisite, results on the residuation of the product in the dioid \(\mathcal {T}_{per} [\![ \gamma ]\!]\) are obtained.
2 Timed event graphs and dioids
2.1 Timed event graphs
In the following, we briefly recall the necessary facts on TEGs. For details, see Baccelli et al. (1992) and Heidergott et al. (2005). A TEG consists of a set of places P = {p1,⋯,pn}, a set of transitions T = {t1,⋯,tm} and a set of arcs \(A\subseteq (P\times T)\cup (T \times P)\), all with weight 1. Place pi is an upstream place of transition tj (and transition tj is a downstream transition of place pi), if (pi,tj) ∈ A. Conversely, pi is a downstream place of transition tj (and tj is an upstream transition of place pi), if (tj,pi) ∈ A. For TEGs, each place pi has exactly one upstream transition and exactly one downstream transition. Moreover, each place pi exhibits an initial marking \((\boldsymbol {{\mathcal{M}}}_{0})_{i} \in \mathbb {N}_{0}\) and a holding time \((\boldsymbol {\phi })_{i} \in \mathbb {N}_{0}\). A transition tj is said to be enabled, if the marking in every upstream place is at least 1. When tj fires, the marking \((\boldsymbol {{\mathcal{M}}})_{i}\) in every upstream place pi is reduced by 1 and the marking \((\boldsymbol {{\mathcal{M}}})_{o}\) in every downstream place po is increased by 1. The holding time (ϕ)i is the time a token must remain in place pi before it contributes to the firing of the downstream transition of pi. The set T of transitions is partitioned into input transitions, i.e., transitions without upstream places, output transitions, i.e., transitions without downstream places and internal transitions, i.e., transitions with both upstream and downstream places. We say that a TEG is operating under the earliest functioning rule, if all internal and output transitions are fired as soon as they are enabled.
2.2 Timed event graphs under partial synchronization
TEGsPS provide a suitable model for some time-variant discrete event systems. In the following, we give a brief introduction. For further information the reader is invited to consult (David-Henriet et al. 2014). Considering the TEG in Fig. 1a, assuming the earliest functioning rule, incoming tokens in place p1 are immediately transferred to place p2 by the firing of transition t2, as the holding time of place p1 is zero. Note that zero holding times are, by convention, not indicated in visual illustrations of TEGs. In contrast, Fig. 1b illustrates a TEG with PS of transition t2 by transition ta. This means that t2 can only fire if ta fires, but the firing of ta does not depend on t2.
In this example, place p3 (equipped with a holding time of ω) and transition ta, together with the corresponding arcs, constitute an autonomous TEG. Under the earliest functioning rule, the firings of transition ta generate a periodic signal \(\mathcal {S}_{\omega }\) with a period \(\omega \in \mathbb {N}\). Therefore, the PS of t2 by ta can also be described by a predefined signal \(\mathcal {S}_{\omega }\): \(\mathbb {Z} \rightarrow \{0,1\}\), enabling the firing of t2 at times t where \(\mathcal {S}_{\omega }(t)= 1\). In particular, \(\mathcal {S}_{\omega }(t) = 1 \text { if } t \in \{j\omega \ \text {with } j\in \mathbb {Z}\}\) and 0 otherwise.
Definition 1
A periodic signal \(\mathcal {S}:\mathbb {Z} \rightarrow \{0,1\}\) is defined by a string 〈n0,n1,⋯,nI〉, with \(n_{i} \in \mathbb {N}_{0}, 0\leq i\leq I\) and a period \(\omega \in \mathbb {N}\), such that \(\forall j\in \mathbb {Z}\)
where the string 〈n0,n1,⋯,nI〉 is strictly increasing, i.e., ∀i ∈{1,⋯,I}, ni− 1 < ni, and nI < ω.
Example 1
The signal
is a periodic signal with a period ω = 4 and a string 〈0,1〉. Therefore \(\forall j \in \mathbb {Z}\),
Definition 2
A Timed Event Graph under periodic partial synchronization is a TEG where the firings of some internal and output transitions are synchronized with periodic signals.
Note that the assumption that only internal and output transitions are subject to PS is not restrictive since we can always add new input transitions and extend the set of internal transitions by the former input transitions. In David-Henriet et al. (2015), ultimately periodic signals are considered for PS of transitions. It was shown that the behavior of a TEGPS with such synchronization signals can be described by recursive equations in state space form. In this work, we focus on (immediately) periodic signals for PS of transitions. To consider only periodic PS allows us to define a dioid of operators to describe the behavior of TEGsPS. In particular, we can show that the transfer behavior of a TEGPS is described by a rational power series of an ultimately cyclic form. Let us note that focusing on periodic signals for a PS of a transition is not overly restrictive as periodic schedules are common in many applications.
Example 2
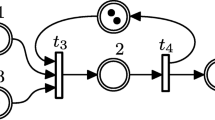
Let us consider a simple supply chain between two factories. Factory 1 is a supplier for factory 2. The products of factory 1 are transported via a train connection to factory 2. This simple supply chain is modelled by the TEG under periodic PS shown in Fig. 2, with periodic PS of transition t2 by the signal, \(\forall j\in \mathbb {Z}\)
Transition t1 models the issue of the goods at factory 1 and transition t4 the receipt of goods at factory 2. Transition t2,t3 and places p2,p3 model the train line between the factories. The holding time of 10 time units of place p3 models the travel time of trains between the factories. The 2 initial tokens in place p2 describe the maximal capacity of the trains. The schedule of the trains is modelled by the signal \(\mathcal {S}_{2}\), hence every 20 time units there is a train leaving from factory 1. We will recall this example again in Section 5 and demonstrate how ”just-in-time” control for this supply chain can be computed using the methods developed in this paper.
2.3 Dioids
A dioid \(\mathcal {D}\) is an algebraic structure with two binary operations, ⊕ (addition) and ⊗ (multiplication). Addition is commutative, associative and idempotent (i.e. \(\forall a \in \mathcal {D},\ a \oplus a = a\)). The neutral element for addition, denoted by ε, is absorbing for multiplication (i.e., \(\forall a \in \mathcal {D},\ a \otimes \varepsilon = \varepsilon \otimes a = \varepsilon \)). Multiplication is associative, distributive over addition and has a neutral element denoted by e. The element e (resp, ε) is called unit (resp. zero) element of the dioid.
Note that, as in conventional algebra, the multiplication symbol ⊗ is often omitted. A dioid \(\mathcal {D}\) is said to be complete if it is closed for infinite sums and if multiplication distributes over infinite sums. A complete dioid is a partially ordered set, with a canonical order ≽ defined by a ⊕ b = a ⇔ a ≽ b. The infimum operator can then be defined by \(a,b \in \mathcal {D}\), \(a \wedge b = \bigoplus \{ x \in \mathcal {D} \ | x\oplus a\preceq a, x\oplus b \preceq b \}\). Moreover, in a complete dioid, the Kleene star of an element \(a \in \mathcal {D}\), denoted a∗, is defined by \(a^{*} = {\bigoplus }_{i= 0}^{\infty }a^{i}\) with a0 = e and ai+ 1 = a ⊗ ai. Let \(\mathcal {C}\subseteq \mathcal {D}\) then \(\mathcal {C}\) is a subdioid of \(\mathcal {D}\) if e and ε are in \(\mathcal {C}\) and \(\mathcal {C}\) is closed for ⊕ and ⊗.
Theorem 1
(Baccelli et al. 1992) In a complete dioid \(\mathcal {D}\), x = a∗b is the least solution of the implicit equation x = ax ⊕ b.
Here, the adjective ”least” refers to the canonical order in the dioid described above.
Both multiplication and addition on a (complete) dioid \(\mathcal {D}\) can be readily extended to the matrix case: for matrices \(\boldsymbol {A},\boldsymbol {B} \in \mathcal {D}^{m\times n},\ \boldsymbol {C} \in \mathcal {D}^{n\times q}\) and a scalar \(\lambda \in \mathcal {D}\), matrix addition and multiplication are defined by
Moreover, the order relation on matrices of the same dimension is understood elementwise, i.e. A ≽B iff (A)i,j ≽ (B)i,j,∀i,j. The identity matrix, denoted by I, is a square matrix with elements e on the diagonal and ε otherwise.
2.4 Complete dioids and residuation theory
Residuation theory is a formalism to address the problem of approximate mapping inversion over ordered sets (Baccelli et al. 1992). It applies to complete dioids, since a complete dioid \(\mathcal {D}\) is a partially ordered set.
Definition 3
(Baccelli et al. 1992) A mapping \(f:\mathcal {D}\rightarrow {\mathcal{L}}\), with \(\mathcal {D}\) and \({\mathcal{L}}\) complete dioids, is residuated if \(\forall b \in {\mathcal{L}}\) the inequality f(x) ≼ b has a greatest solution in \(\mathcal {D}\), denoted f♯(b). The mapping \(f^{\sharp } :{\mathcal{L}}\rightarrow \mathcal {D}\), is called the residual of f.
Theorem 2
(Baccelli et al. 1992) A mapping \(f:\mathcal {D}\rightarrow {\mathcal{L}}\), with \(\mathcal {D}\) and \({\mathcal{L}}\) complete dioids, is residuated iff f(ε) = ε and f is lower-semicontinuous, that is
for every (finite or infinite) subset X of \(\mathcal {D}\).
On a complete dioid the mapping Ra : x↦xa, (right multiplication by a) resp. La : x↦ax (left multiplication by a), is lower-semicontinuous and therefore residuated. The residual mappings are denoted  (right division by a) and
(right division by a) and  (left division by a). Left and right division can be extended to the matrix case. For matrices \(\boldsymbol {A}\in \mathcal {D}^{m\times n} ,\boldsymbol {B} \in \mathcal {D}^{m\times q},\ \boldsymbol {C} \in \mathcal {D}^{n\times q}\)
(left division by a). Left and right division can be extended to the matrix case. For matrices \(\boldsymbol {A}\in \mathcal {D}^{m\times n} ,\boldsymbol {B} \in \mathcal {D}^{m\times q},\ \boldsymbol {C} \in \mathcal {D}^{n\times q}\)

In the following some useful properties of left and right division are summarized, for a proof see Baccelli et al. (1992) or the recent summary paper (Hardouin et al. 2018). For \(a,b,x \in \mathcal {D}\) and \(\mathcal {D}\) a complete dioid,

3 Modeling of TEGs under PS in the Dioid \(\mathcal {T} [\![ \gamma ]\!]\)
To model TEGsPS, a dater function \(x_{i}: \mathbb {Z}\rightarrow \mathbb {Z}_{max}:= \{\mathbb {Z} \}\cup \{ \infty \}\cup \{ -\infty \} \) is associated to each transition ti. The value xi(k) gives the date (time) when transition ti fires the (k + 1)st time. Naturally, dater functions are nondecreasing functions, i.e., xi(k + 1) ≥ xi(k). The set of dater functions is denoted by Σ. On Σ, addition and multiplication by a constant are defined as follows:
The zero element \(\tilde {\varepsilon }\) on Σ is defined by \(\tilde {\varepsilon }(k) = - \infty ,\ \forall k \in \mathbb {Z}\). The \(\tilde {\oplus }\) operation induces an order relation on Σ, i.e., for \(x,y \in {\Sigma },\ x\preceq y \Leftrightarrow x \tilde {\oplus } y = y\). In this order, the top element \(\tilde {\top }\) is defined by \(\tilde {\top }(k) = +\infty ,\ \forall k \in \mathbb {Z}\). An operator, i.e., a map, \(o:{\Sigma } \rightarrow {\Sigma }\) is linear if (a) \(\forall x,y \in {\Sigma } : o(x \tilde {\oplus } y)= o(x)\tilde {\oplus } o(y)\) and (b) \(\lambda \tilde {\otimes } o(x)\ = o(\lambda \tilde {\otimes } x)\). An operator is additive if (a) is satisfied. Let \(\mathcal {O}\) denote the set of all operators \(o:{\Sigma } \rightarrow {\Sigma } \). Moreover, let \(\mathcal {O}_{a}\) denote the subset of all additive operators in \(\mathcal {O}\).
Proposition 1
(Cottenceau et al. 2014) The set \(\mathcal {O}_{a}\) equipped with addition and multiplication: \(x \in {\Sigma }, \forall o_{1},o_{2} \in \mathcal {O}_{a}\),
is a noncommutative complete dioid. The identity operator (unit element) is denoted by e: ∀x ∈Σ, e(x) = x, the zero operator (zero element) is denoted by ε: \(\forall x \in {\Sigma }, \ \varepsilon (x) = \tilde {\varepsilon }\) and the top operator (top element) is denoted by ⊤: \(\forall x \in {\Sigma } \backslash \{\tilde {\varepsilon } \}, \ \top (x) = \tilde {\top }\).
To simplify notation, we write ox instead of o(x) wherever clear from the context.
Definition 4 (Basic operators in \(\mathcal {O}\))
Dynamic phenomena arising in TEGsPS can be described by the following basic operators in \(\mathcal {O}\):
where ⌈a⌉ is the smallest integer greater than or equal to a.
It can be easily checked that all these operators are additive, i.e., \( {\delta }^{\tau },{\gamma }^{\eta },{\varDelta }_{\omega |\varpi }\in \mathcal {O}_{a}\). The time- and event-shift operator δ and γ are used to model the dynamic behavior of standard TEGs, e.g., Baccelli et al. (1992). In addition we introduce the Δω|ϖ operator to consider phenomena caused by PS.
Proposition 2
(Trunk et al. 2018) The basic operators satisfy the following relations
Remark 1
Equation 12 implies that for − b < τ ≤ 0, \({\varDelta }_{\omega |b} {\delta }^{\tau } {\varDelta }_{b|\varpi } ={\varDelta }_{\omega |\varpi }\), since,
3.1 Dioid of time operators \(\mathcal {T}\)
In the following, we introduce a dioid of specific time operators in order to model the time-variant behavior of periodic PS.
Definition 5 (Dioid of T-operators \(\mathcal {T}\))
We denote by \(\mathcal {T}\) the dioid of operators obtained by addition and composition of operators in \((\varepsilon , \mathrm {e}, {\delta }^{\varsigma },{\varDelta }_{\omega |\varpi }, \top )\) with \(\varsigma \in \mathbb {Z}\), and \(\omega ,\varpi \in \mathbb {N}\). The elements of \(\mathcal {T}\) are called T-operators (T is for time).
For example, \({\delta }^{3}{\varDelta }_{4|4}{\delta }^{1}{\varDelta }_{3|2} \in \mathcal {T}\). Since a T-operator only describes a time relation in a system, e.g., a delay, we can associate a function \(\mathcal {R}_{v}: \mathbb {Z}_{max}\rightarrow \mathbb {Z}_{max}\) to a T-operator v. This function, when evaluated on t, is obtained by replacing x(k) by t in the expression of v(x)(k). For example, \((({\varDelta }_{3|4}{\delta }^{1}\oplus {\delta }^{2}{\varDelta }_{3|3})x)(k) = {\max \limits } (\lceil (x(k)+1)/4 \rceil 3, 2+\lceil x(k)/3 \rceil 3)\) and therefore \(\mathcal {R}_{{\varDelta }_{3|4}{\delta }^{1}\oplus {\delta }^{2}{\varDelta }_{3|3}}(t) = \max \limits (\lceil (t+1)/4 \rceil 3, 2+\lceil t/3 \rceil 3)\). The interpretation of \(\mathcal {R}_{v}\) is as follows. Let x1, respectively x2, be the dater functions associated with transitions t1, respectively t2. If v maps x1 to x2, then \(\mathcal {R}_{v}\) maps the time of the (k + 1)st firing of t1 into the time of the (k + 1)st firing of t2. \(\mathcal {R}_{v}\) is therefore called the release-time function associated to the T-operator v. We denote by \({\mathcal{R}}\) the set of functions \(\mathcal {R}_{v}\) generated by all operators v in \(\mathcal {T}\). Clearly, there is an isomorphism between the set of T-operators and the set \({\mathcal{R}}\). The order relation over the dioid \(\mathcal {T}\) corresponds to the order induced by the \(\max \limits \) operation on \({\mathcal{R}}\).
For \(v_{1}, v_{2} \in \mathcal {T}\),
Definition 6 (Periodic T-operators)
A T-operator \(v\in \mathcal {T}\) is said to be ω-periodic if its corresponding function \(\mathcal {R}_{v}\) is quasi-ω-periodic, i.e., \(\exists \omega \in \mathbb {N}\) such that \(\forall t \in \mathbb {Z}_{max},\ \mathcal {R}_{v}(t+\omega ) = \omega +\mathcal {R}_{v}(t)\). The set of ω-periodic T-operators is denoted by \(\mathcal {T}_{\omega }\). Moreover the set of periodic operators is defined by \(\mathcal {T}_{per} = \bigcup _{\omega \in \mathbb {N}} \mathcal {T}_{\omega }\).
Example 3
The operator Δ4|4 is 4-periodic and the operator \({\varDelta }_{3|3}{\delta }^{2}\) is 3-periodic as \(\mathcal {R}_{{\varDelta }_{4|4}}(t) = \lceil t/4 \rceil 4 \) and \(\mathcal {R}_{{\varDelta }_{3|3}{\delta }^{2}}(t) = \lceil (t +2)/3 \rceil 3 \). Therefore \({\varDelta }_{4|4} \in \mathcal {T}_{4}\), \({\varDelta }_{3|3}{\delta }^{2} \in \mathcal {T}_{3}\). Evidently, both operators are also 12-periodic and therefore \({\varDelta }_{4|4},{\varDelta }_{3|3}{\delta }^{2} \in \mathcal {T}_{12}\).
Proposition 3
(Trunk et al. 2018) An ω-periodic T-operator \(v\in \mathcal {T}_{\omega }\) has an ω-periodic canonical form given by a finite sum \({\bigoplus }_{i=1}^{I}{\delta }^{\tau _{i}}{\varDelta }_{\omega |\omega }{\delta }^{\tau _{i}^{\prime }}\), where τi < τi+ 1∀i ∈{1,⋯,I − 1}, I ≤ ω and \(-\omega < \tau _{i}^{\prime } \leq 0, \forall i \in \{1, {\cdots } ,I\}\).
Remark 2
Clearly each ω-periodic operator \(v\in \mathcal {T}_{per}\) is also nω-periodic with n ≥ 1 and can be represented as \({\bigoplus }_{i=1}^{I}{\delta }^{\tau _{i}}{\varDelta }_{n\omega |n\omega }{\delta }^{\tau _{i}^{\prime }}\) and I ≤ nω.
Proposition 4
The 1-periodic identity operator e = Δ1|1 can be represented in the specific form,
Proof
Recall the isomorphism between T-operators and the set \({\mathcal{R}}\). Hence it is sufficient to show that \(\mathcal {R}_{\mathrm {e}} =\mathcal {R}_{{\bigoplus }_{i=0}^{\omega -1} {\delta }^{-i} {\varDelta }_{\omega |\omega }{\delta }^{1+i-\omega }} \). Moreover, since \(\forall t \in \mathbb {Z}_{max}, \mathcal {R}_{\mathrm {e}}(t) = t\), it remains to show that \(\forall t \in \mathbb {Z}_{max}, \mathcal {R}_{{\bigoplus }_{i=0}^{\omega -1} {\delta }^{-i} {\varDelta }_{\omega |\omega }{\delta }^{1+i-\omega }}(t) = t\).
Because \(\mathcal {R}_{{\bigoplus }_{i=0}^{\omega -1} {\delta }^{-i} {\varDelta }_{\omega |\omega }{\delta }^{1+i-\omega }}(t)\) is a quasi ω-periodic function, Definition 6, it is sufficient to evaluate Eq. 15 for t = {1 − ω,⋯ ,0}. This leads to,
□
Example 4
The identity operator e = Δ1|1 can be represented as \(\mathrm {e} = {\varDelta }_{3|3}{\delta }^{-2} \oplus {\delta }^{-1}{\varDelta }_{3|3}{\delta }^{-1} \oplus {\delta }^{-2}{\varDelta }_{3|3}\). Figure 3 illustrates that indeed \(\mathcal {R}_{\mathrm {e}}(t)= \mathcal {R}_{{\varDelta }_{3|3}{\delta }^{-2} \oplus {\delta }^{-1}{\varDelta }_{3|3}{\delta }^{-1} \oplus {\delta }^{-2}{\varDelta }_{3|3}}(t) = \max \limits (\mathcal {R}_{{\varDelta }_{3|3}{\delta }^{-2}}(t),\mathcal {R}_{{\delta }^{-1}{\varDelta }_{3|3}{\delta }^{-1}}(t),\mathcal {R}_{{\delta }^{-2}{\varDelta }_{3|3}}(t))\).
The time-variant behavior caused by a periodic PS of a transition can be conveniently modeled in the dioid \(\mathcal {T}\).
For this, recall the definition of a periodic signal \(\mathcal {S}\) (Definition 1). We associate with a periodic signal \(\mathcal {S}:\mathbb {Z}\rightarrow \{0,1\}\) characterized by 〈n0,⋯nI〉 and period ω a function \(\mathcal {R}_{S}: \mathbb {Z}_{max}\rightarrow \mathbb {Z}_{max}\). This function \(\mathcal {R}_{S}(t)\) is defined by, \(\forall j\in \mathbb {Z}\),
Example 5
The function \(\mathcal {R}_{S_{1}}(t)\) (Fig. 4b) associated to the signal S1 (Fig. 4) given in Example 1 is
The value of \(\mathcal {R}_{S}(t)\) can be interpreted as the next time when the signal \(\mathcal {S}\) enables the firing of the corresponding transition. Clearly, an ω-periodic signal \(\mathcal {S}\) leads to a corresponding function \(\mathcal {R}_{S}(t)\) which satisfies \(\forall t \in \mathbb {Z}_{max}, \mathcal {R}_{S}(t+\omega ) = \omega + \mathcal {R}_{S}(t)\).
To prove that a periodic PS of a transition (i.e., the PS is specified by a periodic signal \(\mathcal {S}\)) admits an operator representation in the dioid \(\mathcal {T}\), we must show the existence of an operator \(v\in \mathcal {T}\) such that \(\mathcal {R}_{v} = \mathcal {R}_{S}\).
Proposition 5
(Trunk et al. 2018) A periodic partial synchronization of a transition by the signal \(\mathcal {S}\) in Definition 1 has an operator representation given by
Example 6
Consider the TEGPS shown in Fig. 5, where the signal \(\mathcal {S}_{1}\) is given in Eq. 1 (Example 1) and dater function x1(k) (resp. x2(k)) is associated with transition t1 (resp. t2). According to Proposition 5, the behavior of the periodic PS of transition t2 is modeled by the following operator:
where the latter equality holds as δ0 = e.
Since the holding time of place p1 is 0 and there are no initial tokens in the place p1 this operator describes the firing relation between t1 and t2, i.e., \(x_{2} = ({\delta }^{-3}{\varDelta }_{4|4} \oplus {\varDelta }_{4|4}{\delta }^{-1})x_{1}\). Therefore, \(x_{2}(k) = \max \limits (-3+\lceil x_{1}(k)/4\rceil 4, \lceil (x_{1}(k)-1)/4\rceil 4 )\).
Remark 3
Due to the influence of the PS, this firing relation between t1 and t2 is time-variant. For instance, if the (k + 1)st firing of t1 is at time instant x1(k) = 1, then the (k + 1)st firing of t2 is at x2(k) = 1, i.e., we have no delay. In contrast, if the (k + 1)st firing of t1 is at time instant x1(k) = 2, then the (k + 1)st firing of t2 is at x2(k) = 4, and the delay is 2.
3.2 Dioid \(\mathcal {T} [\![ \gamma ]\!]\)
Since the γ operator commutes with all T-operators, i.e., \(\forall v\in \mathcal {T},\ v\gamma = \gamma v\), we can define the dioid \(\mathcal {T} [\![ \gamma ]\!]\) as follows.
Definition 7
(Dioid \( \mathcal {T} [\![ \gamma ]\!] \)) We denote by \(\mathcal {T} [\![ \gamma ]\!] \) the quotient dioid in the set of formal power series in one variable γ with exponents in \(\mathbb {Z}\) and coefficients in the noncommutative complete dioid \(\mathcal {T}\) induced by the equivalence relation, \(\forall s \in \mathcal {T}\),
Hence we identify two series s1, s2 with the same equivalence class, if \(s_{1}{\gamma }^{*} = \ s_{2}{\gamma }^{*}\). It is helpful to think of sγ∗ as the representative of the equivalence class of s. Note that we can interpret elements in \(\mathcal {T} [\![ \gamma ]\!]\) as nondecreasing functions \(s: \mathbb {Z}\rightarrow \mathcal {T}\), where s(η) refers to the coefficient of γη. Hence, \(\forall \eta \in \mathbb {Z}, s(\eta ) \preceq s(\eta +1) \). For a fundamental mathematical background on quotient dioids, the reader is invited to consult (Baccelli et al. 1992). Moreover, in Hardouin et al. (2018) quotient dioids are studied from a didactic point of view.
Definition 8
Let \(s_{1},s_{2}\in \mathcal {T} [\![ \gamma ]\!]\), then addition and multiplication are defined by
We denote by \(\mathcal {T}_{per} [\![ \gamma ]\!]\) the subdioid of \(\mathcal {T} [\![ \gamma ]\!]\), obtained by restricting the coefficients v to periodic operators, i.e., \(v\in \mathcal {T}_{per}\). As before, ⊕ defines an order on \(\mathcal {T} [\![ \gamma ]\!]\), i.e., \(a,b\in \mathcal {T} [\![ \gamma ]\!]:\ a\oplus b = b \Leftrightarrow a \preceq b\). Hence \(\forall s_{1},s_{2} \in \mathcal {T} [\![ \gamma ]\!],\ s_{1} \preceq s_{2} \Leftrightarrow s_{1}(\eta ) \preceq s_{2}(\eta ),\ \eta \in \mathbb {Z} \). A monomial in \(\mathcal {T} [\![ \gamma ]\!]\) is defined by vγη, where \(v \in \mathcal {T}\) and \(\eta \in \mathbb {Z}\). The ordering of two monomials \(v_{1}{\gamma }^{\eta _{1}}, v_{2}{\gamma }^{\eta _{2}} \in \mathcal {T} [\![ \gamma ]\!]\) can be checked as follows,
A polynomial is a finite sum of monomials, i.e., \({\bigoplus }_{i=1}^{I} v_{i}{\gamma }^{\eta _{i}}\).
Proposition 6
Let \(p \in \mathcal {T}_{per} [\![ \gamma ]\!]\) be a polynomial, then p has a canonical form \(p = {\bigoplus }_{j=1}^{J}v_{j}^{\prime }{\gamma }^{\eta _{j}^{\prime }}\) such that ∀j ∈{1,⋯ ,J}, the ω-periodic T-operator \(v_{j}^{\prime }\) is in the canonical form of Proposition 3, and coefficients and exponents are strictly ordered, i.e., for \(j\in \{1,{\cdots } ,J-1 \},\ \eta _{j}^{\prime }< \eta _{j+1}^{\prime }\) and \(v_{j}^{\prime } \prec v_{j+1}^{\prime }\).
Proof
Without loss of generality we can assume that \(p = {\bigoplus }_{i=1}^{I}v_{i}{\gamma }^{\eta _{i}}\), with ηi < ηi+ 1, i = 1,⋯I − 1. In \(\mathcal {T}_{per} [\![ \gamma ]\!]\), we identify all elements s with sγ∗, hence can also identify p and
as \(p{\gamma }^{*} =p^{\prime }{\gamma }^{*} \). Hence, \(v_{i}^{\prime } \preceq v_{i+1}^{\prime }\). If \(v_{i}^{\prime } = v_{i+1}^{\prime }\) we can write \(v_{i}^{\prime }{\gamma }^{\eta _{i}} \oplus v_{i+1}^{\prime }{\gamma }^{\eta _{i+1}} = v_{i}^{\prime }({\gamma }^{\eta _{i}} \oplus {\gamma }^{\eta _{i+1}})= v_{i}^{\prime }{\gamma }^{\eta _{i}}. \) Therefore, we can write \(p^{\prime }\) as \({\bigoplus }_{j=1}^{J} v_{j}^{\prime }{\gamma }^{\eta _{j}^{\prime }}\) with vj ≺ vj+ 1 and J ≤ I. □
Definition 9
(Ultimately Cyclic Series in \(\mathcal {T}_{per} [\![ \gamma ]\!]\) ): A series \(s \in \mathcal {T}_{per} [\![ \gamma ]\!]\) is said to be ultimately cyclic if it can be written as s = p ⊕ q(γηδτ)∗, where \(\eta ,\tau \in \mathbb {N}\) and p,q are polynomials in \(\mathcal {T}_{per} [\![ \gamma ]\!]\).
An element \(s \in \mathcal {T} [\![ \gamma ]\!]\) has a three dimensional graphical representation in \(\mathbb {Z}_{max}\times \mathbb {Z}_{max} \times \mathbb {Z}\). Given a series \(s = {\bigoplus }_{i} v_{i} {\gamma }^{i} \in \mathcal {T} [\![ \gamma ]\!]\), this graphical representation is obtained by depicting for every i the release-time function \(\mathcal {R}_{v_{i}}:\mathbb {Z}_{max}\rightarrow \mathbb {Z}_{max} \) of the coefficient vi in the (input-time × output-time)-plane of i.
Example 7
For the graphical representation of the polynomial \(p = ({\delta }^{1}{\varDelta }_{4|4}{\delta }^{-1} \oplus {\delta }^{-2}{\varDelta }_{4|4}){\gamma }^{0} \oplus ({\delta }^{5}{\varDelta }_{4|4}{\delta }^{-1} \oplus {\delta }^{2}{\varDelta }_{4|4}){\gamma }^{2} \oplus ({\delta }^{5}{\varDelta }_{4|4} \oplus {\delta }^{6}{\varDelta }_{4|4}{\delta }^{-1}){\gamma }^{4} \in \mathcal {T}_{per} [\![ \gamma ]\!]\), respectively its representative
see Fig. 6. The slices in the (I/O-time)-plane for the event-shift values k = 0,1 are illustrated in Fig. 7a. These slices correspond to the release-time function \(\mathcal {R}_{{\delta }^{1}{\varDelta }_{4|4}{\delta }^{-1} \oplus {\delta }^{-2}{\varDelta }_{4|4}}\) of the coefficient \({\delta }^{1}{\varDelta }_{4|4}{\delta }^{-1} \oplus {\delta }^{-2}{\varDelta }_{4|4}\) for γ0 (resp. γ1) in p. The slices for k = 2,3 and k ≥ 4 are shown in Fig. 7b and c. To improve readability, the graphical representation for elements \(s\in \mathcal {T} [\![ \gamma ]\!]\) has been truncated to non-negative values in Figs. 6 and 7.
3D representation of polynomial \(p = ({\delta }^{1}{\varDelta }_{4|4}{\delta }^{-1} \oplus {\delta }^{-2}{\varDelta }_{4|4}){\gamma }^{0}\oplus ({\delta }^{5}{\varDelta }_{4|4}{\delta }^{-1} \oplus {\delta }^{2}{\varDelta }_{4|4}){\gamma }^{2} \oplus ({\delta }^{5}{\varDelta }_{4|4} \oplus {\delta }^{6}{\varDelta }_{4|4}{\delta }^{-1}){\gamma }^{4}\).
Slices of the coefficients of p in the (I/O-time)-plane. a \(\mathcal {R}_{{\delta }^{1}{\varDelta }_{4|4}{\delta }^{-1} \oplus {\delta }^{-2}{\varDelta }_{4|4}}\), b \(\mathcal {R}_{{\delta }^{5}{\varDelta }_{4|4}{\delta }^{-1} \oplus {\delta }^{2}{\varDelta }_{4|4}}\) and c \(\mathcal {R}_{{\delta }^{5}{\varDelta }_{4|4} \oplus {\delta }^{6}{\varDelta }_{4|4}{\delta }^{-1}}\)
An important subdioid of \(\mathcal {T} [\![ \gamma ]\!]\) is the dioid \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\). This dioid is obtained by restricting the coefficients v to the set {ε,δτ} of T-operators, i.e., an element in \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) is written as \({\bigoplus }_{i}{\delta }^{\tau _{i}}{\gamma }^{n_{i}}\) with \(\tau _{i},n_{i}\in \mathbb {Z}\). This dioid has been extensively studied, e.g. Gaubert and Klimann (1991) and Baccelli et al. (1992). The product of two monomials \({\gamma }^{n_{1}}{\delta }^{t_{1}},{\gamma }^{n_{2}}{\delta }^{t_{2}} \in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) is obtained by, \({\gamma }^{n_{1}}{\delta }^{t_{1}}\otimes {\gamma }^{n_{2}}{\delta }^{t_{2}} = {\gamma }^{n_{1}+n_{2} }{\delta }^{t_{1} +t_{2}}\). Moreover, Eq. 19 is simplified to \({\gamma }^{n_{1}}{\delta }^{t_{1}} \preceq {\gamma }^{n_{2}}{\delta }^{t_{2}} \Leftrightarrow (n_{1} \geq n_{2} \text { and } t_{1} \leq t_{2})\), and as a consequence of Eq. 10,
A comprehensive description of calculations with series in \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) can be found in Baccelli et al. (1992). It is well known that the input-output behavior of a standard TEG can be described by a transfer function matrix composed of ultimately cyclic series in \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\). Moreover, based on \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\), methods for performance evaluation and controller synthesis have been introduced for TEGs, e.g. Gaubert and Klimann (1991), Maia et al. (2003), and Hardouin et al. (2017). In (Hardouin et al. 2009), software tools have been made available for computations in \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\). The dioid \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) plays a key role in this paper. In particular, in Section 4, we show that all relevant operations on ultimately cyclic series \(s\in \mathcal {T}_{per} [\![ \gamma ]\!]\) can be reduced to operations on matrices in \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\). We can therefore use the existing tools for \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) to study TEGs under periodic PS.
3.3 Modeling of TEGsPS in \(\mathcal {T}_{per} [\![ \gamma ]\!]\)
A TEG under periodic PS operating under the earliest functioning rule admits a representation in \(\mathcal {T}_{per} [\![ \gamma ]\!]\) of the form
This is reminiscent of the state space form in ”classical” systems theory. In the sequel, we will therefore refer to this representation as a state space model. x (resp. u,y) refers to the vector of dater functions of internal (resp. input, output) transitions. The matrices \(\boldsymbol {A} \in \mathcal {T}_{per} [\![ \gamma ]\!]^{n\times n},\ \boldsymbol {B} \in \mathcal {T}_{per} [\![ \gamma ]\!]^{n \times g}\) and \(\boldsymbol {C} \in \mathcal {T}_{per} [\![ \gamma ]\!]^{p\times n}\) describe the influence of transitions on each other, encoded by operators in \(\mathcal {T}_{per} [\![ \gamma ]\!]\). Hence, n refers to the number of internal transitions of the TEGPS, while p and q are the number of output and input transitions. Let us consider a path constituted by the arcs (tj,pi) and (pi,to) with a synchronization of transition to by a periodic signal \(\mathcal {S}_{o}\). The influence of transition tj on transition to is coded as an operator
where \(v_{t_{o}}\) is the operator representation of the signal \(\mathcal {S}_{o}\) corresponding to the PS of to (see Example 6), (ϕ)i is the holding time of place pi and \((\boldsymbol {{\mathcal{M}}}_{0})_{i}\) is the initial marking of pi.
Example 8
Recall the TEGPS in Fig. 2 with PS of transition t2 by the signal, \(\forall j\in \mathbb {Z}\)
As ω = 20, I = 0, n0 = 1, according to Proposition 5, \(v_{S_{2}} = {\delta }^{1}{\varDelta }_{20|20}{\delta }^{-1}\). The influence of t3 on transition t2 via the path (t3,p2)(p2,t2), is coded by the operator \(v_{S_{2}}{\delta }^{0}{\gamma }^{2} = v_{S_{2}}{\gamma }^{2}= {\delta }^{1}{\varDelta }_{20|20}{\delta }^{-1}{\gamma }^{2}\). Moreover, by assigning a dater function u (resp. x1,x2,y) to transition t1 (resp. t2,t3,t4), the earliest functioning of the TEGPS is described in state space form x = Ax ⊕Bu; y = Cx, where
According to Theorem 1, the least solution of equation x = Ax ⊕Bu is x = A∗Bu. Therefore, the transfer function matrix H of a TEGPS can be obtained by y = Hu = CA∗Bu. In Trunk et al. (2018) it was shown that the entries of the transfer function matrix are ultimately cyclic series in \(\mathcal {T}_{per} [\![ \gamma ]\!]\). In order to compute this transfer function matrix, to compute system compositions, and to obtain control, we have to perform addition, multiplication and the Kleene star operation of series in \(\mathcal {T}_{per} [\![ \gamma ]\!]\). In the next section, we show how these operations between series in \(\mathcal {T}_{per} [\![ \gamma ]\!]\) can be reduced to operations between matrices in \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\).
4 Core representation of a series in \(\mathcal {T}_{per} [\![ \gamma ]\!]\)
In this section, we propose a specific decomposition of ultimately cyclic series in \(\mathcal {T}_{per} [\![ \gamma ]\!]\). We show that such series \(s\in \mathcal {T}_{per} [\![ \gamma ]\!]\) with period ω can always be represented as s = mωQbω where Q is a square matrix in \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) of size ω × ω, mω is a row vector defined as
and bω is a column vector defined as
This representation is called core representation with core matrix Q. We first demonstrate how to obtain this form on a small example and then provide a formal proof.
Example 9
Consider the following series in \(\mathcal {T}_{per} [\![ \gamma ]\!]\),
Because of Δω|ϖ = Δω|bΔb|ϖ (Remark 1) and \({\delta }^{\omega }{\varDelta }_{\omega |\varpi } = {\varDelta }_{\omega |\varpi }{\delta }^{\varpi } \), see Eq. 12, and as γ commutes with all T-operators, this series can be rewritten as
Clearly M1,M2 and S1 are elements in \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\). We now can rewrite s in the core representation,
which is in the required form.
Proposition 7
Let \(s= {\bigoplus }_{i}v_{i}{\gamma }^{i}\in \mathcal {T}_{per} [\![ \gamma ]\!]\) be an ω-periodic series, then s can be written as s = mωQbω, where \(\boldsymbol {\mathsf {Q}}\in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]^{\omega \times \omega }\) and mω, bω have the form Eqs. 22 and 23.
Proof
s being an ω-periodic series implies that all coefficients vi of s are ω-periodic T-operators. Then, due to Proposition 3, all coefficients can be expressed in canonical form \(v_{i} = {\bigoplus }_{j=1}^{J_{i}} {\delta }^{\tau _{i_{j}}}{\varDelta }_{\omega |\omega }{\delta }^{\tau _{i_{j}}^{\prime }}\) with Ji ≤ ω and \(-\omega < \tau _{i_{j}}^{\prime }\leq 0\). Then s can be rewritten as
By using Δω|ω = Δω|1Δ1|ω (Remark 1), \({\delta }^{\omega }{\varDelta }_{\omega |1} = {\varDelta }_{\omega |1}{\delta }^{1}\) Eq. 12 and \(v\gamma = \gamma v,\ \forall v\in \mathcal {T}\), the series s is written as
where \(-\omega <\tilde {\tau }_{i_{j}}= \tau _{i_{j}}-\lceil \tau _{i_{j}}/\omega \rceil \omega \leq 0\) and \(\hat {\tau }_{i_{j}} =\lceil \tau _{i_{j}}/\omega \rceil \). Observe that \(-\omega <\tilde {\tau }_{i_{j}}, \tau _{i_{j}}^{\prime } \leq 0\) hence we can express s by
where the entry \((\boldsymbol {\mathsf {Q}}_{i_{j}})_{1-\tilde {\tau }_{i_{j}},\omega +\tau _{i_{j}}^{\prime }} = {\delta }^{\hat {\tau }_{i_{j}}}{\gamma }^{i}\) and all other entries of \(\boldsymbol {\mathsf {Q}}_{i_{j}}\) are equal to ε. Hence, s is in the required form s = mωQbω, where \(\boldsymbol {\mathsf {Q}} = {\bigoplus }_{i} \left ({\bigoplus }_{j=1}^{J_{i}} \boldsymbol {\mathsf {Q}}_{i_{j}} \right )\). □
Let us note that the core Q of a series \(s\in \mathcal {T}_{per} [\![ \gamma ]\!]\) is not unique. In other words, we can express the same series with different cores, i.e., we may have \(s= \boldsymbol {\mathsf {m}}_{\omega } \boldsymbol {\mathsf {Q}} \boldsymbol {\mathsf {b}}_{\omega } = \boldsymbol {\mathsf {m}}_{\omega } \tilde {\boldsymbol {\mathsf {Q}}} \boldsymbol {\mathsf {b}}_{\omega }\) with \(\boldsymbol {\mathsf {Q}}, \tilde {\boldsymbol {\mathsf {Q}}} \in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]^{\omega \times \omega }\) but \(\boldsymbol {\mathsf {Q}} \neq \tilde {\boldsymbol {\mathsf {Q}}}\). We illustrate this in the following example.
Example 10
Recall the series \(s = {\varDelta }_{2|2} \oplus {\delta }^{1}{\varDelta }_{2|2}{\delta }^{-1} \oplus {\delta }^{2}{\gamma }^{2}({\delta }^{2}{\gamma }^{2})^{*}{\varDelta }_{2|2}\) given in Example 9. The series s can be expressed by \(\boldsymbol {\mathsf {m}}_{2}\tilde {\boldsymbol {\mathsf {Q}}}\boldsymbol {\mathsf {b}}_{2}\) where,
Clearly \(\tilde {\boldsymbol {\mathsf {Q}}}\neq \boldsymbol {\mathsf {Q}}\) see Example 9. However, \(\tilde {\boldsymbol {\mathsf {Q}}}\) is a valid core of s since
Because of Eq. 10\({\varDelta }_{1|2}{\delta }^{-1} \oplus {\varDelta }_{1|2} ={\varDelta }_{1|2}({\delta }^{-1} \oplus {\delta }^{0})= {\varDelta }_{1|2}\), and therefore
To show how the core form can be used to perform basic operations between ultimately cyclic series in \(\mathcal {T}_{per} [\![ \gamma ]\!]\) we first elaborate some properties of the mω-vector and bω-vector. The scalar product mωbω of these two vectors is the identity e:
where the latter equality holds because of Proposition 4. The dyadic product bω ⊗mω is a square matrix in \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) denoted by N. For i,j ∈{1,⋯,ω}, the entry (bω ⊗mω)i,j is given by,
Then, because of \({\varDelta }_{1|\omega }{\delta }^{-\omega } = {\delta }^{-1}{\varDelta }_{1|\omega }\) and \({\varDelta }_{1|\omega }{\delta }^{n} {\varDelta }_{\omega |1} = {\varDelta }_{1|1} = \mathrm {e}\) for − ω < n ≤ 0, see Remark 1,
i.e.,
Proposition 8
(Trunk et al. 2018) The following relations hold:
4.1 Greatest core matrix
From Example 10 it is clear that a series \(s \in \mathcal {T}_{per} [\![ \gamma ]\!]\) may have several core representations. In the following, we show that a series \(s \in \mathcal {T}_{per} [\![ \gamma ]\!]\) admits a unique greatest core, denoted \(\boldsymbol {\hat {\mathsf {Q}}}\), i.e, \(s = \boldsymbol {\mathsf {m}}_{\omega }\boldsymbol {\hat {\mathsf {Q}}} \boldsymbol {\mathsf {b}}_{\omega } \) and \(\boldsymbol {\hat {\mathsf {Q}}} \succeq \boldsymbol {\mathsf {Q}}\) for all core matrices Q such that s = mωQbω. Note that, the inequality is in the sense of the dioid \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\). This decomposition \(s = \boldsymbol {\mathsf {m}}_{\omega }\boldsymbol {\hat {\mathsf {Q}}} \boldsymbol {\mathsf {b}}_{\omega }\) is particularly useful to compute residuation of series in \(\mathcal {T}_{per} [\![ \gamma ]\!]\).
Proposition 9
For \(\boldsymbol {D}\in {\mathcal {T} [\![ \gamma ]\!]}^{1 \times \omega }\) and \(\boldsymbol {P} \in { \mathcal {T} [\![ \gamma ]\!]}^{\omega \times 1}\) one has:

For \(\boldsymbol {O}\in { \mathcal {T} [\![ \gamma ]\!]}^{n \times \omega }\) and \(\boldsymbol {G}\in { \mathcal {T} [\![ \gamma ]\!]}^{\omega \times n}\) one has:

Proof
By definition,  is the greatest solution of inequality
is the greatest solution of inequality
Clearly since mωbω = e, bωD satisfies Eq. 30 with equality. It remains to be shown that bωD is the greatest solution of Eq. 30. For this, assume that there exists \(\boldsymbol {X^{\prime }} \succeq \boldsymbol {\mathsf {b}}_{\omega }\boldsymbol {D}\) solving Eq. 30, i.e., \(\boldsymbol {\mathsf {m}}_{\omega }\boldsymbol {X^{\prime }} \preceq \boldsymbol {D}\). Multiplication is order preserving, hence left multiplication by bω results in
Furthermore, \(\boldsymbol {X^{\prime }} \preceq \boldsymbol {\mathsf {N}} \otimes \boldsymbol {X^{\prime }} \) as N = I ⊕N. Hence, \(\boldsymbol {X^{\prime }} \preceq \boldsymbol {\mathsf {b}}_{\omega } \boldsymbol {D}\) and therefore \(\boldsymbol {X^{\prime }} = \boldsymbol {\mathsf {b}}_{\omega } \boldsymbol {D}\). This proves that bωD is indeed the greatest solution of Eq. 30. Similarly, X = Pmω solves Xbω ≼P with equality. Suppose \(\boldsymbol {X^{\prime }} \succeq \boldsymbol {P} \boldsymbol {\mathsf {m}}_{\omega }\) is a solution, i.e., \(\boldsymbol {X^{\prime }}\otimes \boldsymbol {\mathsf {b}}_{\omega } \preceq \boldsymbol {P}\). Right multiplication by mω gives
Therefore \(\boldsymbol {X^{\prime }} = \boldsymbol {P}\otimes \boldsymbol {\mathsf {m}}_{\omega }\) and P ⊗mω is indeed the greatest solution, and hence  . To prove Eq. 28, note that by Proposition 8 ON ⊗bω ⊗mω = ON. Therefore ON ⊗bω is a solution of X ⊗mω ≼ON. Assume that \(\boldsymbol {X^{\prime }} \succeq \boldsymbol {O} \boldsymbol {\mathsf {N}} \otimes \boldsymbol {\mathsf {b}}_{\omega }\) is another solution, i.e., \(\boldsymbol {X^{\prime }}\boldsymbol {\mathsf {m}}_{\omega } \preceq \boldsymbol {O} \boldsymbol {\mathsf {N}} \). Right multiplication by bω results in \(\boldsymbol {X^{\prime }} \preceq \boldsymbol {O}\boldsymbol {\mathsf {N}} \otimes \boldsymbol {\mathsf {b}}_{\omega }\). Hence, ON ⊗bω is the greatest solution of
. To prove Eq. 28, note that by Proposition 8 ON ⊗bω ⊗mω = ON. Therefore ON ⊗bω is a solution of X ⊗mω ≼ON. Assume that \(\boldsymbol {X^{\prime }} \succeq \boldsymbol {O} \boldsymbol {\mathsf {N}} \otimes \boldsymbol {\mathsf {b}}_{\omega }\) is another solution, i.e., \(\boldsymbol {X^{\prime }}\boldsymbol {\mathsf {m}}_{\omega } \preceq \boldsymbol {O} \boldsymbol {\mathsf {N}} \). Right multiplication by bω results in \(\boldsymbol {X^{\prime }} \preceq \boldsymbol {O}\boldsymbol {\mathsf {N}} \otimes \boldsymbol {\mathsf {b}}_{\omega }\). Hence, ON ⊗bω is the greatest solution of  . Equation 29 is shown analogously. □
. Equation 29 is shown analogously. □
Proposition 10
Let \( \boldsymbol {\mathsf {m}}_{\omega } \boldsymbol {\mathsf {Q}} \boldsymbol {\mathsf {b}}_{\omega } \in \mathcal {T}_{per} [\![ \gamma ]\!]\) be a decomposition of \(s \in \mathcal {T}_{per} [\![ \gamma ]\!]\). The greatest core matrix is given by \(\boldsymbol {\hat {\mathsf {Q}}} = \boldsymbol {\mathsf {N}}\boldsymbol {\mathsf {Q}}\boldsymbol {\mathsf {N}}\).
Proof
Consider the inequality \(\boldsymbol {\mathsf {m}}_{\omega } \boldsymbol {\tilde {X}}\boldsymbol {\mathsf {b}}_{\omega } \preceq s\). Because of Proposition 9, its greatest solution  is given by
is given by
Moreover, because of (Proposition 8)
□
4.2 Operations between core matrices
To perform addition and multiplication of two ultimately cyclic series \(s_{1} = \boldsymbol {\mathsf {m}}_{\omega _{1}} \boldsymbol {\mathsf {Q}}_{1}\boldsymbol {\mathsf {b}}_{\omega _{1}},\ s_{2} = \boldsymbol {\mathsf {m}}_{\omega _{2}} \boldsymbol {\mathsf {Q}}_{2}\boldsymbol {\mathsf {b}}_{\omega _{2}} \in \mathcal {T}_{per} [\![ \gamma ]\!]\) in core form, it is necessary to express the core matrices \(\boldsymbol {\mathsf {Q}}_{1} \in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]^{\omega _{1} \times \omega _{1}}\) and \(\boldsymbol {\mathsf {Q}}_{2} \in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]^{\omega _{2} \times \omega _{2}}\) with identical dimensions. This is possible by expressing both series with their least common period ω = lcm(ω1,ω2).
Proposition 11
(Trunk et al. 2018)
A series \(s = \boldsymbol {\mathsf {m}}_{\omega } \boldsymbol {\mathsf {Q}}\boldsymbol {\mathsf {b}}_{\omega } \in \mathcal {T}_{per} [\![ \gamma ]\!]\) can be expressed with a multiple period nω by extending the core matrix Q, i.e., \(s = \boldsymbol {\mathsf {m}}_{\omega } \boldsymbol {\mathsf {Q}}\boldsymbol {\mathsf {b}}_{\omega } = \boldsymbol {\mathsf {m}}_{n\omega }\boldsymbol {\mathsf {Q}}^{\prime }\boldsymbol {\mathsf {b}}_{n\omega } \), where \(\boldsymbol {\mathsf {Q}}^{\prime } \in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]^{n\omega \times n\omega }\) is given by
Proposition 12 (Sum of series 2018)
Let s = mωQbω, \(s^{\prime } = \boldsymbol {\mathsf {m}}_{\omega }\boldsymbol {\mathsf {Q}}^{\prime } \boldsymbol {\mathsf {b}}_{\omega } \in \mathcal {T}_{per} [\![ \gamma ]\!]\). Then \(s \oplus s^{\prime } = \boldsymbol {\mathsf {m}}_{\omega }\boldsymbol {\mathsf {Q}}^{\prime \prime }\boldsymbol {\mathsf {b}}_{\omega } \), where \(\boldsymbol {\mathsf {Q}}^{\prime \prime } = \boldsymbol {\mathsf {Q}}\oplus \boldsymbol {\mathsf {Q}}^{\prime }\).
Proposition 13 (Product of series 2018)
Let \(s = \boldsymbol {\mathsf {m}}_{\omega }\boldsymbol {\mathsf {Q}}\boldsymbol {\mathsf {b}}_{\omega },\ s^{\prime } = \boldsymbol {\mathsf {m}}_{\omega }\boldsymbol {\mathsf {Q}}^{\prime }\boldsymbol {\mathsf {b}}_{\omega } \in \mathcal {T}_{per} [\![ \gamma ]\!]\). Then \(s\otimes s^{\prime } = \boldsymbol {\mathsf {m}}_{\omega }\boldsymbol {\mathsf {Q}}^{\prime \prime }\boldsymbol {\mathsf {b}}_{\omega }\), where \(\boldsymbol {\mathsf {Q}}^{\prime \prime } = \boldsymbol {\mathsf {Q}}\boldsymbol {\mathsf {N}}\boldsymbol {\mathsf {Q}}^{\prime }\).
Proposition 14 (Kleene star of series 2018)
Let \(s= \boldsymbol {\mathsf {m}}_{\omega } \boldsymbol {\mathsf {Q}}\boldsymbol {\mathsf {b}}_{\omega } \in \mathcal {T}_{per} [\![ \gamma ]\!]\). Then,
Proposition 15
Let \(s = \boldsymbol {\mathsf {m}}_{\omega } \boldsymbol {\hat {\mathsf {Q}}}\boldsymbol {\mathsf {b}}_{\omega },\ s^{\prime }= \boldsymbol {\mathsf {m}}_{\omega } \boldsymbol {\hat {\mathsf {Q}}}^{\prime }\boldsymbol {\mathsf {b}}_{\omega }\) be ultimately cyclic series in \(\mathcal {T}_{per} [\![ \gamma ]\!]\) with \(\boldsymbol {\hat {\mathsf {Q}}}\), respectively \(\boldsymbol {\hat {\mathsf {Q}}}^{\prime }\), their greatest core matrices. Then,

Proof

The proof of the second part of Proposition 15 is analogous. □
Due to Propositions 12, 13, 14 and 15, it is clear that computation of the sum and product, Kleene star operation and product residuation of ultimately cyclic series in \(\mathcal {T}_{per} [\![ \gamma ]\!]\) can be done based on the core of the series, i.e. in the dioid \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\). Finally, let us note that this core form of series \(s \in \mathcal {T}_{per} [\![ \gamma ]\!]\) is similar to the core form of series \(s \in \mathcal {E} [\![ \delta ]\!]\), see (Trunk et al. 2017a). More generally the dioid \(\mathcal {T}_{per} [\![ \gamma ]\!]\) with periodic time-operators can be seen as the counter part of the dioid \(\mathcal {E} [\![ \delta ]\!]\), introduced in Cottenceau et al. (2014), with periodic event-operators. The dioid \(\mathcal {E} [\![ \delta ]\!]\) is useful to obtain transfer function matrices for WBTEG.
5 Output reference control
In this section, we address the following control problem for TEGs under periodic PS. A reference dater function \(\bar {z}\) is given for the output \(\bar {y}\). We want to determine the greatest input dater function \(\bar {u}\) that leads to an output \(\bar {y}\preceq \bar {z}\). The reference dater specifies that the firings of the output transition (which in a manufacturing context, may for example correspond to completion of workpieces) should occur no latter than given instants of time. This has to be achieved by firing the input transition as late as possible. In a manufacturing context, this may correspond to feeding raw material as late as possible. This kind of optimal output reference control is often called ”just-in-time” control. For standard TEGs the problem of output reference control was studied in Baccelli et al. (1992), Cohen et al. (1989), Menguy et al. (1998), and Menguy et al. (2000). It is well known for standard TEGs, that the output to an arbitrary input dater function can simply be computed by using the transfer function model \(h \in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) of the TEG and expressing the input dater as a series \(u \in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\). Then y = h ⊗ u. Hence, the optimal control problem for standard TEGs simply amounts computing  , see Baccelli et al. (1992) and Cohen et al. (1989) for a detailed description. In the following, we show how the earliest response of a TEG under periodic PS can be computed based on its transfer function \(h\in \mathcal {T}_{per} [\![ \gamma ]\!]\) and then how the optimal just-in-time control problem for a TEG under periodic PS can be addressed. For this, we first need to provide some additional algebraic background.
, see Baccelli et al. (1992) and Cohen et al. (1989) for a detailed description. In the following, we show how the earliest response of a TEG under periodic PS can be computed based on its transfer function \(h\in \mathcal {T}_{per} [\![ \gamma ]\!]\) and then how the optimal just-in-time control problem for a TEG under periodic PS can be addressed. For this, we first need to provide some additional algebraic background.
5.1 Subdioids of \(\mathcal {T}_{per} [\![ \gamma ]\!]\)
Recall that an operator \(v\in \mathcal {T}\) is called ω-periodic if \(\exists \omega \in \mathbb {N}\) such that \(\forall k \in \mathbb {Z}_{max},\ \mathcal {R}_{v}(k+\omega ) = \omega +\mathcal {R}_{v}(k)\) (Definition 6) and that the set of ω-periodic T-operators is denoted by \(\mathcal {T}_{\omega }\). Analogously we say \(s{\bigoplus }_{i} v_{i}{\gamma }^{i} \in \mathcal {T}_{per} [\![ \gamma ]\!]\) is an ω-periodic series, iff all coefficients are ω-periodic T-operators, i.e., \(\forall i, v_{i} \in \mathcal {T}_{\omega }\). The set of ω-periodic series is denoted by \(\mathcal {T}_{\omega } [\![ \gamma ]\!]\).
Proposition 16
The sest of ω-periodic series \(\mathcal {T}_{\omega } [\![ \gamma ]\!]\) with addition and multiplication given in Definition 8 is a complete subdioid of the dioid \(\mathcal {T}_{per} [\![ \gamma ]\!]\).
Proof
According to Propositions 12 and 13, \(\mathcal {T}_{\omega } [\![ \gamma ]\!]\) is closed under (infinite) addition and multiplication. □
Remark 4
The subdioid \(\mathcal {T}_{1} [\![ \gamma ]\!]\) of \(\mathcal {T}_{per} [\![ \gamma ]\!]\), i.e. the set of 1-periodic series, is the dioid \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\). Moreover, as any 1-periodic series is also ω-periodic (\(\omega \in \mathbb {N}\)), \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) is subdioid of \(\mathcal {T}_{\omega } [\![ \gamma ]\!]\) for any \(\omega \in \mathbb {N}\).
Due to the subdioid structure of \(\mathcal {T}_{per} [\![ \gamma ]\!]\), one can define the canonical injection \(\text {Inj}: {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ] \rightarrow \mathcal {T}_{per} [\![ \gamma ]\!]\), with Inj(x) = x. For a graphical illustration of this canonical injection see the following example.
Example 11
Let us consider the series \(s = {\gamma }^{1}{\delta }^{2} \oplus \left ({\gamma }^{3}{\delta }^{3}\oplus {\gamma }^{5}{\delta }^{4}\right )({\gamma }^{3}{\delta }^{2})^{*} \in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\), with a graphical representation given in Fig. 8a. The graphical representation of the canonical injection \(\text {Inj}(s)\in \mathcal {T}_{per} [\![ \gamma ]\!]\) is shown in Fig. 8b. The series \(s\in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) (Fig. 8a) corresponds to the event-shift/output-time plane for the input-time value 0 of the 3D representation of the series \(\text {Inj}(s)\in \mathcal {T}_{per} [\![ \gamma ]\!]\) (Fig. 8b). Moreover, the canonical injection \(\text {Inj}(s)\in \mathcal {T}_{per} [\![ \gamma ]\!]\) is 1-periodic, this means the coefficients vi of γi are 1-periodic, i.e., \(\mathcal {R}_{v_{i}}(t)\) are quasi 1-periodic. Therefore, the event-shift/output-time plane for the input-time value 1 corresponds to the series \({\delta }^{1}s\in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) and for the input-time value 2 to the series \({\delta }^{2}s\in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\), etc.
Illustration of the canonical injection \(\text {Inj}:{\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ] \rightarrow \mathcal {T}_{per} [\![ \gamma ]\!]\) of the series \(s = {\gamma }^{1}{\delta }^{2} \oplus \left ({\gamma }^{3}{\delta }^{3}\oplus {\gamma }^{5}{\delta }^{4}\right )({\gamma }^{3}{\delta }^{2})^{*}\in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\)
Lemma 1
Let \(v{\gamma }^{n}\in \mathcal {T}_{\omega } [\![ \gamma ]\!]\) be an ω-periodic monomial. Then the residual Inj♯(vγn) is given by
Proof
By definition, Inj♯(vγn) is the greatest solution \(x\in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) of the following inequality:
Clearly, the least ηi such that inequality Eq. 33 holds are n and thus,
where the latter equality holds for \(\tau = \max \limits _{i}(\zeta _{i})\), because of Eq. 20. Since the inequality vγn ≽ γnδτ in \(\mathcal {T}_{\omega } [\![ \gamma ]\!]\) holds iff the inequality v ≽ δτ in \(\mathcal {T}_{\omega }\) holds, it remains to find the greatest τ such that v ≽ δτ holds. By considering the isomorphism between T-operators and release-time functions, see Eq. 13, this is equivalent to \(\mathcal {R}_{v}(t) \geq \mathcal {R}_{{\delta }^{\tau }}(t),\ \forall t \in \mathbb {Z}_{max}\).
By using \(\mathcal {R}_{{\delta }^{\tau }}(t)= \tau + t\), see Eq. 7, one obtains
Since \(\mathcal {R}_{v}\) is a quasi ω-periodic function it is sufficient to evaluate the function for ∀t ∈{0,⋯,ω − 1}. Therefore the greatest τ such that Eq. 35 (resp. Eq. 34) holds is
□
Lemma 1 can be extended to arbitrary series in \(\mathcal {T}_{\omega } [\![ \gamma ]\!]\). To do this, note that the canonical representation in Proposition 6 can be generalized to infinite sums.
Proposition 17
Let \(s = {\bigoplus }_{i}v_{i}{\gamma }^{n_{i}}\in \mathcal {T}_{\omega } [\![ \gamma ]\!]\) be an ω-periodic series in canonical representation. Then
Proof
Consider \(s = {\bigoplus }_{i}v_{i}{\gamma }^{n_{i}}\) in the canonical form, i.e., ni < ni+ 1 and vi ≺ vi+ 1 and let \(\mathcal {R}_{v_{i}}\) be the release-time function associated with vi. Recall that Inj♯(s) is the greatest solution x in \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) of inequality Inj(x) ≼ s. This is given by \({\bigoplus }_{i} {\delta }^{\tau _{i}}{\gamma }^{n_{i}}\) where τi is the greatest integer such that \({\delta }^{\tau _{i}} \preceq v_{i}\). Repeating the first step of the proof of Lemma 1, this is given by \(\tau _{i} = \min \limits _{t=0,\cdots \omega -1}(\mathcal {R}_{v_{i}}(t)-t)\). □
5.1.1 Zero slice mapping \({\varPsi }_{\omega }: \mathcal {T}_{\omega } [\![ \gamma ]\!] \rightarrow {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\)
Recall that \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) is a subdioid of \(\mathcal {T}_{\omega } [\![ \gamma ]\!]\), hence we can define a specific projection from \(\mathcal {T}_{\omega } [\![ \gamma ]\!]\) into \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) as follows.
Definition 10
Let \(s = {\bigoplus }_{i} v_{i}{\gamma }^{n_{i}} \in \mathcal {T}_{\omega } [\![ \gamma ]\!]\) be an ω-periodic series, then
This projection Ψω has an intuitive graphical interpretation. For a given \(s\in \mathcal {T}_{\omega } [\![ \gamma ]\!]\) the series \( {\varPsi }_{\omega }(s) \in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ] \) corresponds to the slice in the event/output-time plane of the 3D representation of \(s\in \mathcal {T}_{\omega } [\![ \gamma ]\!]\) at the input-time value 0. Thus, this projection is also called zero-slice mapping.
Example 12
Consider the polynomial \(p = ({\delta }^{1}{\varDelta }_{4|4}{\delta }^{-1} \oplus {\delta }^{-2}{\varDelta }_{4|4}){\gamma }^{0} \oplus ({\delta }^{5}{\varDelta }_{4|4}{\delta }^{-1} \oplus {\delta }^{2}{\varDelta }_{4|4}){\gamma }^{2} \oplus ({\delta }^{5}{\varDelta }_{4|4} \oplus {\delta }^{6}{\varDelta }_{4|4}{\delta }^{-1}){\gamma }^{4} \in \mathcal {T}_{per} [\![ \gamma ]\!]\) from Example 7 with graphical representation given in Fig. 6. Then,
The series Ψ4(p) corresponds to the slice in the (event-shift/output-time)-plane for the input-time value t = 0 in the 3D representation of p, see Fig. 9a and b.
The projection Ψω is by definition lower-semicontinuous, therefore Ψω is residuated.
Proposition 18
Let \(s = {\bigoplus }_{i} {\gamma }^{n_{i}}{\delta }^{\tau _{i}}\in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\). The residual \({\varPsi }_{\omega }^{\sharp } (s) \in \mathcal {T}_{\omega } [\![ \gamma ]\!]\) of s is
Proof
By definition of the residuated mapping, \({\varPsi }_{\omega }^{\sharp } (s) \in \mathcal {T}_{\omega } [\![ \gamma ]\!]\) is the greatest solution of inequality
We first show that Eq. 38 satisfies Eq. 39 with equality.
since \(\mathcal {R}_{{\delta }^{\tau _{i}}{\varDelta }_{\omega |\omega }}(0) = \tau _{i}+\lceil 0/\omega \rceil \omega = \tau _{i}\), see Eqs. 7 and 9. Taking into account that Ψω is isotone, it remains to show that \({\bigoplus }_{i} {\gamma }^{n_{i}}{\delta }^{\tau _{i}}{\varDelta }_{\omega |\omega }\) is the greatest solution of
For this, let \(x= {\bigoplus }_{j} v_{j}{\gamma }^{n_{j}}\) be an arbitrary series in \(\mathcal {T}_{\omega } [\![ \gamma ]\!]\). Then \({\varPsi }_{\omega }(x)= {\bigoplus }_{j} {\gamma }^{n_{j}}{\delta }^{\mathcal {R}_{v_{j}}(0)}\). Clearly, to achieve equality we need ηj = ni and \( \mathcal {R}_{v_{j}}(0)= \tau _{i}\). Furthermore, we are looking for the greatest \(v_{j} \in \mathcal {T}_{\omega }\), such that \(\tau _{i} = \mathcal {R}_{v_{j}}(0)\). Due to the canonical form (Proposition 3) we can write an ω-periodic T-operator vj as \({\bigoplus }_{i=1}^{\omega }{\delta }^{\zeta _{i}}{\varDelta }_{\omega |\omega }{\gamma }^{\zeta _{i}^{\prime }}\) with \(-\omega < \zeta _{i}^{\prime } \leq 0\). This operator corresponds to the release-time function
Now we examine \(\mathcal {R}_{v_{j}}(t)\) for t = 0, thus
Recall that \(-\omega < \zeta _{i}^{\prime } \leq 0\), hence \(\mathcal {R}_{v_{j}}(t) = \tau _{i}+\lceil (0+t)/\omega \rceil \omega \) is the greatest quasi ω-periodic release-time function such that \(\mathcal {R}_{v_{j}}(0) = \tau _{i}\). The corresponding greatest T-operator is accordingly \({\delta }^{\tau _{i}}{\varDelta }_{\omega |\omega }\). □
5.1.2 Dater functions and series in \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\)
A convenient way to compute the output of a TEG under periodic PS is to express its input and output dater functions as series in \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\). The following proposition gives a link between dater functions and series in \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\).
Proposition 19
(Baccelli et al. 1992) A dater function \(\bar {d}:\mathbb {Z}\rightarrow \mathbb {Z}_{max}\) can be expressed as a series \(d \in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\), such that,
For a more detailed description of the link between dater functions and the associated series in \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\), see e.g. Baccelli et al. (1992) and Cohen et al. (1991). The impulse is a specific dater function, namely \(\mathcal {I}(k) = -\infty \) if k < 0 and 0 otherwise. Hence, an impulse as the input of a TEG corresponds to an infinity of firings of its input transition at time 0. The \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) series corresponding to an impulse is the unit element \(\mathrm {e} \in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\), see Baccelli et al. (1992) and Cohen et al. (1991).
Moreover, a dater function \(\bar {d}\) and its series representation \(d\in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) are related by
The impulse response of a TEG can be readily expressed via the TEG transfer function \(h \in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\). The dater function \(\bar {y}_{\mathcal {I}}\) is the impulse response is characterized by
while the corresponding series is obtained by
Similarly, the response to an arbitrary input series u (with dater function \(\bar {u}\)) is
respectively
In contrast, the transfer function \(h\in \mathcal {T}_{per} [\![ \gamma ]\!]\) of a TEG under periodic PS is not entirely characterized by the impulse response. As the impulse corresponds to an infinity of firings at time 0, the impulse response of a TEG under periodic PS is characterized by the slice in the (event-shift/output-time)-plane at the input-time value 0 of the 3D representation of its transfer function \(h \in \mathcal {T}_{per} [\![ \gamma ]\!]\), see e.g., Example 12. Hence, for a TEG under periodic PS with transfer function h, the impulse response \(\overline {y}=(h\mathcal {I})\) corresponds to the series \(y={\varPsi }_{\omega }(h) \in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\), see Definition 10 and Example 12. It should be clear that in contrast to standard TEGs, the impulse response of a TEG under periodic PS only provides partial information of its transfer function. For TEGs under periodic PS, the above duality between representing the output as dater function and series in \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) reads as follows. Let \(h \in \mathcal {T}_{per} [\![ \gamma ]\!]\) be the transfer function of the TEG under periodic PS and \(\overline {u} \in {\Sigma }\), respectively \(u \in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\), be the input. Then we obtain the output dater function \(\overline {y} \in {\Sigma }\) by
and the corresponding output series \(y \in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) by
Example 13
Recall the simple supply chain in Example 2 with the TEGPS model shown in Fig. 2. The transfer function is \(h={\delta }^{11}({\gamma }^{2}{\delta }^{20})^{*}{\varDelta }_{20|20}{\delta }^{-1}\). This transfer function was computed with the ETVO toolbox (Cottenceau et al. 2019) available online at: http://perso-laris.univ-angers.fr/~cottenceau/etvo.html, this toolbox implements the algorithms given in this section. Moreover, consider the following input dater function:
This dater function is interpreted as follows: the first product available for transport from factory 1 to factory 2 is ready at time instant 0. The second and third at time instant 5. The 4th, 5th, 6th and 7th at time instant 35. According to Eq. 41, the series \(u \in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) corresponding to this dater function is u = γ0δ0 ⊕ γ1δ5 ⊕ γ3δ35 ⊕ γ7δ∗. The output \(y\in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) of the system is computed as
with associated dater function \(\overline {y}\)
Hence, this implies that the first product is available at factory 2 at time instant 11, the second and third at time instant 31, the 4th and 5th at time instant 51, and the 6th and 7th at time instant 71.
5.2 Optimal Output Reference Control
The optimal output reference control problem for a TEG under periodic PS with a transfer function \(h \in \mathcal {T}_{per} [\![ \gamma ]\!]\) is to find the greatest input dater \(\overline {u}\) such that, \(\forall k \in \mathbb {Z}\)
where \(\bar {z}\) is a given reference dater.
If, instead, we represent the unknown input and the reference as series in \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\), Eq. 44 is rephrased as
where the series \(z,u \in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) correspond to the dater functions \(\bar {z}\) and \(\overline {u}\).
Theorem 3
Let \(h\in \mathcal {T}_{per} [\![ \gamma ]\!]\) be the transfer function of a single-input single-output (SISO) TEG under periodic PS and \(z \in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) a given output reference for the system, then the optimal input uopt, i.e., the greatest solution of Eq. 45, is

Proof
As Ψω is a residuated mapping (see Proposition 18), Eq. 46 is equivalent to \(h \otimes \text {Inj}(u) \preceq {\varPsi }_{\omega }^{\sharp }(z)\). This, in turn, is equivalent to  as left multiplication in \(\mathcal {T}_{per} [\![ \gamma ]\!]\) is residuated. Finally as Inj is residuated (Proposition 17), the greatest solution of the latter inequality is Eq. 46. □
as left multiplication in \(\mathcal {T}_{per} [\![ \gamma ]\!]\) is residuated. Finally as Inj is residuated (Proposition 17), the greatest solution of the latter inequality is Eq. 46. □
Equation 46 is often referred to as the just-in-time solution. Note that the notation of greatest is in the sense of the order ≽ in the dioid \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\).
Example 14
Recall the supply chain of Example 2, which is modelled by the TEG under periodic PS given in Fig. 2 and has transfer function
Let us consider the following dater function (see Fig. 10), which describes at which instants of time goods from factory 1 need to be available at factory 2 at the latest.
The control problem is now, to compute \(\bar {u}\), i.e. the maximal time when goods from factory 1 are ready to be shipped to factory 2, such that Eq. 44 respectively Eq. 45, holds. To apply Eq. 46, the dater function \(\bar {z}\) is expressed by the series \(z = {\delta }^{25}\oplus {\gamma }^{2}{\delta }^{45}({\gamma }^{1}{\delta }^{15})^{*}\in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\). Then according to Proposition 18, \({\varPsi }_{20}^{\sharp }(z) = z{\varDelta }_{20|20} = {\delta }^{25}{\varDelta }_{20|20}\oplus ({\gamma }^{1}{\delta }^{15})^{*} ({\gamma }^{2}{\delta }^{45}{\varDelta }_{20|20})\) and

where the latter equality has been computed using ETVO toolbox (Cottenceau et al. 2019). The response y of the TEGPS to the optimal input uopt is
This series corresponds to the dater function,
Figure 10 illustrates the output reference \(\bar {z}\) and \(\bar {y}\) resulting from the optimal input \(\bar {u}_{opt}\). Clearly, as required, \(\bar {z} \succeq \bar {y}\). This means, the goods are shipped from factory 1 as late as possible, but arrive in factory 2 in time to meet the production deadlines there.
Remark 5
Output reference control can be readily extended to multiple-input multiple-output (MIMO) TEGs under periodic PS. In this case the earliest behaviour of a TEG under periodic PS is modeled by a transfer function matrix \(\boldsymbol {H} \in \mathcal {T}_{per} [\![ \gamma ]\!]^{p\times g}\). Then the optimal output reference control problem is, for all j = 1,⋯p,
where \(z_{j} \in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) represents the reference for the jth output and \(u_{i} \in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\) is ith input of the system. As Ψω is a lower semi-continuous mapping we can write Eq. 47 as, for j = 1,⋯p,
The latter set of p inequalities, can be written as a set of p ∗ q simpler inequalities, i.e., ∀j ∈{1,⋯p} and ∀i ∈{1,⋯g},
Observe that each of these inequalities has the form of Eq. 45. Hence, the optimal ith input \(u_{i,opt} \in {\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\), i.e., the greatest ui that satisfies Eq. 49 for j = 1,⋯p, is

Hence, the only difference to the SISO case is an additional infimum operation between series in \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\).
6 Conclusion
In this paper, we have introduced algebraic tools to obtain transfer function matrices for a subclass of Timed Event Graphs under Partial Synchronization, namely the case where partial synchronization of transitions is characterized by periodic signals. We have introduced the dioid \(\mathcal {T}_{per} [\![ \gamma ]\!]\), which is a quotient dioid of formal power series in γ with coefficients that are periodic time-operators. We have shown that all relevant operations on ultimately cyclic series s in this dioid can be reduced to operations on matrices in the subdioid \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\). An advantage of this approach is that existing software tools for standard TEGs in the dioid \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\), e.g. Hardouin et al. (2009) can be applied to the more general class of TEGsPS with periodic PS. The more recent toolbox (Cottenceau et al. 2019), based also on Hardouin et al. (2009), implements the ”translation process” from \(\mathcal {T}_{per} [\![ \gamma ]\!]\) to \({\mathcal{M}}_{in}^{ax}\left [\!\left [\gamma ,\delta \right ]\!\right ]\). Moreover, based on transfer functions for this class of TEGsPS we have solved the corresponding optimal output reference control problem. In particular, the proposed control method provides the optimal control input under the ”just-in-time” criterion. One possible extension of this work is to modify the control strategy such that online updates of the reference trajectory can be considered. This would allow the system to react to a change in customer demands, and will be considered in future work.
References
Baccelli F, Cohen G, Olsder G, Quadrat J (1992) Synchronization and linearity: An algebra for discrete event systems. Wiley, New York
Cohen G, Moller P, Quadrat JP, Viot M (1989) Algebraic tools for the performance evaluation of discrete event systems. Proc IEEE 77(1):39–58
Cohen G, Gaubert S, Nikoukhah R, Quadrat JP (1991) Second order theory of min-linear systems and its application to discrete event systems. In: Proceedings of the 30th IEEE conference on decision and control, pp 1511–1516 vol 2. https://doi.org/10.1109/CDC.1991.261654
Cottenceau B, Hardouin L, Boimond JL (2014) Modeling and control of weight-balanced timed event graphs in dioids. IEEE Trans Autom Control 59 (5):1219–1231. https://doi.org/10.1109/TAC.2013.2294822
Cottenceau B, Hardouin L, Trunk J (2019) Event and time variant operators. http://perso-laris.univ-angers.fr/cottenceau/etvo.html
David-Henriet X, Raisch J, Hardouin L, Cottenceau B (2014) Modeling and control for max-plus systems with partial synchronization. In: Proceedings of the 12th IFAC-IEEE international workshop on discrete event systems (WODES). France, Paris, pp 105–110
David-Henriet X, Raisch J, Hardouin L, Cottenceau B (2015) Modeling and control for (max, +)-linear systems with set-based constraints. In: IEEE international conference on automation science and engineering (CASE), pp 1369–1374. https://doi.org/10.1109/CoASE.2015.7294289
David-Henriet X, Hardouin L, Raisch J, Cottenceau B (2016) Model predictive control for discrete event systems with partial synchronization. Automatica 70:9–13
De Schutter B, van den Boom TJJ (2003) MPC for discrete-event systems with soft and hard synchronization constraints. Int J Control 76(1):82–94. https://doi.org/10.1080/0020717021000049188
Gaubert S, Klimann C (1991) Rational computation in dioid algebra and its application to performance evaluation of discrete event systems. In: Algebraic computing in control, Springer, pp 241–252
Hamaci S, Boimond JL, Lahaye S (2006) On modeling and control of discrete timed event graphs with multipliers using (min,+) algebra
Hardouin L, Le Corronc E, Cottenceau B (2009) Minmaxgd a software tools to handle series in (max, +) algebra In: SIAM conference on computational science and engineering, Miami. USA
Hardouin L, Shang Y, Maia CA, Cottenceau B (2017) Observer-based controllers for max-plus linear systems. IEEE Trans Autom Control 62(5):2153–2165. https://doi.org/10.1109/TAC.2016.2604562
Hardouin L, Cottenceau B, Shang Y, Raisch J (2018) Control and state estimation for max-plus linear systems. Foundations Trends® Syst Control 6(1):1–116. https://doi.org/10.1561/2600000013
Heidergott B, Olsder G, van der Woude J (2005) Max plus at work : Modeling and analysis of synchronized systems: A course on max-plus algebra and its applications (Princeton series in applied mathematics). Princeton University Press, Princeton
Maia CA, Hardouin L, Santos-Mendes R, Cottenceau B (2003) Optimal closed-loop control of timed event graphs in dioids. IEEE Trans Autom Control 48 (12):2284–2287
Menguy E, Boimond JL, Hardouin L (1998) Optimal control of discrete event systems in case of updated reference input. In: IFAC conference on system structure and control, pp 601–607
Menguy E, Boimond J L, Hardouin L, Ferrier J L (2000) Just-in-time control of timed event graphs: update of reference input, presence of uncontrollable input. IEEE Trans Autom Control 45(11):2155–2159. https://doi.org/10.1109/9.887652
Trunk J, Cottenceau B, Hardouin L, Raisch J (2017a) Model decomposition of weight-balanced timed event graphs in dioids: Application to control synthesis. In: 20th IFAC world congress 2017, Toulouse, pp 13995–14002
Trunk J, Cottenceau B, Hardouin L, Raisch J (2017b) Output reference control for weight-balanced timed event graphs. IEEE, 4839–4846. https://doi.org/10.1109/CDC.2017.8264374
Trunk J, Cottenceau B, Hardouin L, Raisch J (2018) Model Decomposition of Timed Event Graphs under Partial Synchronization. In: 14th Workshop on Discrete Event Systems, vol 2018. Sorrento Coast, Italy, pp 209–216
Funding
Open access funding provided by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article belongs to the Topical Collection: on Theory-2020
Guest Editors: Francesco Basile, Jan Komenda, and Christoforos Hadjicostis
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Trunk, J., Cottenceau, B., Hardouin, L. et al. Model decomposition of timed event graphs under periodic partial synchronization: application to output reference control. Discrete Event Dyn Syst 30, 605–634 (2020). https://doi.org/10.1007/s10626-020-00316-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10626-020-00316-y