Skip to main content
SpringerLink
Log in

Optimal flow control in acyclic networks with uncontrollable routings and precedence constraints

  • Published:
Discrete Event Dynamic Systems Aims and scope Submit manuscript

Abstract

This paper introduces a novel optimal flow control problem that seeks to convey a specified amount of fluid to each of the nodes of an acyclic digraph with a single source node, while minimizing the total amount of fluid inducted into the network. Two factors complicating the aforementioned task are (i) the presence of nodes with uncontrollable routing of the traversing flow and (ii) a set of precedence constraints regarding the satisfaction of the nodal fluid requirements. It is shown that the considered problem can be naturally formulated as a continuous-time optimal control problem that can be reduced to a hybrid optimal control problem with controlled switching. This property subsequently enables the solution of the considered problem through a Mixed Integer Programming formulation. Additional results in the paper establish the NP-hardness of the considered problem, highlight its affinity to some well known scheduling problems, and offer guidelines that can alleviate the increased problem complexity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Notes

  1. These distributions are determined by the consumer behavior with respect to the considered product, which is an uncontrollable and unobservable part of the entire process.

  2. Or a sampling schedule.

  3. The assumption | ∙  V| = 1 can also be satisfied for problem instances with | ∙  V| > 1 through the addition of a new dummy node; the details are left to the reader.

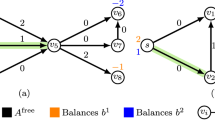
  4. We also notice that when the network of Fig. 1 is perceived in the context of the stochastic DP problem that motivated this work, the controllable (white) nodes correspond to decision nodes, and the arcs emanating from them are the available decisions. On the other hand, the uncontrollable (black) nodes model the impact of the randomness that might determine the outcome of some of the applied decisions. Obviously, in the context of such an interpretation of the considered problem and its flow dynamics, uncontrollable nodes should have a zero fluid requirement (since the sampling process takes place only at the decision nodes).

  5. An explanation of this effect can be found in the discussion provided at the end of the following section.

  6. This time is known as the schedule makespan in the relevant theory.

  7. Furthermore, it is easy to see that when defined on such a flat graph structure, the optimal control problem of Eqs. 1–6 has a very simple optimal solution, and therefore, there is no need to resort to the solution of the MIP formulation of Section 3 and the deployment of the mode graph \({\cal G}\).

  8. The insignificance of the nodes with zero fluid requirements for the determination of the optimal solution of the MIP formulation developed in Section 3, is manifested in the numerical example provided in that section, by the fact that modes ν 13, ν 24 and ν 33 correspond to zero total flows. These three modes correspond respectively to the completion of the (zero) fluid requirements for nodes 9, 5 and 3 in the graph G of Fig. 1.

References

  • Ahuja RK, Magnanti TL, Orlin JB (1993) Network flows: theory, algorithms and applications. Prentice Hall, Englewood Cliffs, NJ

    MATH  Google Scholar 

  • Aronson JE (1989) A survey of dynamic network flows. Ann Oper Res 20:1–66

    Article  MathSciNet  MATH  Google Scholar 

  • Bertsimas D, Gamarnik D (1999) Asymptotically optimal algorithms for job shop scheduling and packet switching. J Algorithms 33:296–318

    Article  MathSciNet  MATH  Google Scholar 

  • Bertsimas D, Sethuraman J (2002) From fluid relaxations to practical algorithms for job shop scheduling: the makespan objective. Math Program 92:61–102

    Article  MathSciNet  MATH  Google Scholar 

  • Bertsimas D, Gamarnik D, Tsitsiklis J (1996) Stability conditions for multi-class queueing networks. IEEE Trans Automat Contr 41:1618–1631

    Article  MathSciNet  MATH  Google Scholar 

  • Bountourelis T, Reveliotis S (2008) Optimal node visitation in stochastic digraphs. IEEE Trans Automat Contr 53:2558–2570

    Article  MathSciNet  Google Scholar 

  • Bountourelis T, Reveliotis S (2009) Optimal node visitation in acyclic stochastic digraphs with multi-threaded traversals and internal visitation requirements. Discrete Event Dyn Syst 19:347–376

    Article  MathSciNet  MATH  Google Scholar 

  • Branicky MS, Borkar VS, Mitter SK (1998) A unified framework for hybrid control: model and optimal control theory. IEEE Trans Automat Contr 43:31–45

    Article  MathSciNet  MATH  Google Scholar 

  • Dai JG (1995) On positive harris recurrence of multiclass queueing networks: a unified approach via fluid limit models. Ann Appl Probab 5:49–77

    Article  MathSciNet  MATH  Google Scholar 

  • Garey MR, Johnson DS (1979) Computers and intractability: a guide to the theory of NP-completeness. W. H. Freeman and Co., New York, NY

    MATH  Google Scholar 

  • Kotnyek B (2003) An annotated overview of dynamic network flows. INRIA, Tech. Rep. 4936

  • Lovetskii SE, Melamed II (1987) Dynamic flows in networks. Autom Remote Control 48:7–29

    MathSciNet  Google Scholar 

  • Maglaras C (2000) Discrete-review policies for scheduling stochastic networks: trajectory tracking and fluid-scale asymptotic optimality. Ann Appl Prob 10:897–929

    Article  MathSciNet  MATH  Google Scholar 

  • Meyn S (2008) Control techniques for complex networks. Cambridge University Press, Cambridge, UK

    MATH  Google Scholar 

  • Pinedo M (2002) Scheduling. Prentice Hall, Upper Saddle River, NJ

    MATH  Google Scholar 

  • Powell WB, Jaillet P, Odoni A (1995) Stochastic and dynamic networks and routing. In: Ball MO, et al (eds) Handbook in operations research and management science – network routings, Elsevier Science

  • Reveliotis SA (2007) Uncertainty management in optimal disassembly planning through learning-based strategies. IIE Trans 39:645–658

    Article  Google Scholar 

  • Reveliotis SA, Bountourelis T (2007) Efficient PAC learning for episodic tasks with acyclic state spaces. Discrete Event Dyn Syst 17:307–327

    Article  MathSciNet  MATH  Google Scholar 

  • Rybko AN, Stolyar AL (1992) Ergodicity of stochastic processes describing the operation of open queueing networks. Probl Inf Transm 28:199–220

    MathSciNet  MATH  Google Scholar 

  • Weiss G (1994) On the optimal draining of re-entrant fluid lines. Georgia Tech and Technion, Tech. Rep.

  • Winston WL (1995) Introduction To mathematical programming: applications and algorithms, 2nd edn. Duxbury Press, Belmont, CA

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Industrial & Systems Engineering, Georgia Institute of Technology, Atlanta, GA, USA

    Spyros Reveliotis

  2. Department of Industrial Engineering, University of Pittsburgh, Pittsburgh, USA

    Theologos Bountourelis

Authors
  1. Spyros Reveliotis
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Theologos Bountourelis
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Spyros Reveliotis.

Additional information

This work was partially supported by the NSF grant CMMI-0619978.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Reveliotis, S., Bountourelis, T. Optimal flow control in acyclic networks with uncontrollable routings and precedence constraints. Discrete Event Dyn Syst 21, 499–518 (2011). https://doi.org/10.1007/s10626-011-0112-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10626-011-0112-0

Keywords

Search

Navigation