On maximal partial Latin hypercubes

Abstract

A lower bound is presented for the minimal number of filled cells in a maximal partial Latin hypercube of dimension d and order n. The result generalises and extends previous results for $d=2$ (Latin squares) and $d=3$ (Latin cubes). Explicit constructions show that this bound is near-optimal for large $n> d$. For $d>n$, a connection with Hamming codes shows that this lower bound gives a related upper bound for the same quantity. The results can be interpreted in terms of independent dominating sets in certain graphs, and in terms of codes that have covering radius 1 and minimum distance at least 2.

1 Introduction

As the title indicates, the focus in this paper is on Latin hypercubes. However, the topic can be viewed in terms of design theory, graph theory, and coding theory. Previous results appear in several guises and these are reviewed in Sect. 2. We start with some basic definitions.

A Latin square of order n, denoted by LS(n), is a (2-dimensional) $n\times n$ array $L=[L(i,j)]$, with entries from an n-element set N, such that each element of N occurs once in each row and once in each column of L. The rows and columns of L are indexed by an n-element set, which we will always take to be the same as the entry set N. Unless we say otherwise, we will take $N={\mathbb {Z}}_n= \{0,1,2,\ldots ,n-1\}$.

A Latin hypercube is a generalisation of a Latin square to higher dimensions. To explain the definition, consider a d-dimensional array $H=[H(i_1,i_2,\ldots ,i_d)]$, with each coordinate indexed by an n-element set N. A line in this array is a 1-dimensional array formed from H by holding all but one coordinate fixed and allowing the remaining coordinate to vary through the elements of N. Thus a line in H generalises the notion of a row or a column in a square array of dimension 2. If it is the $j^{\textrm{th}}$ coordinate that is variable, then we will say that the line is in the j direction. The set of all lines in the j direction will be denoted by ${\mathcal {L}}_j$. Clearly there will be exactly $n^{d-1}$ lines in each of the d possible directions, and so $dn^{d-1}$ lines altogether. Given any cell C in the array there will be d lines through that cell, and we will denote the set of such lines by ${\mathcal {L}}(C)$.

Having the notion of a line, we can define a Latin hypercube of dimension d and order n, denoted by LH(d, n), to be a d-dimensional array $H=[H(i_1,i_2,\ldots ,i_d)]$, with each coordinate indexed by an n-element set N, and entries from the same set N, such that each element of N occurs once in each line of H. As with Latin squares, we will often take $N={\mathbb {Z}}_n$. A Latin square LS(n) is a particular case of a Latin hypercube LH(d, n) corresponding to dimension $d=2$. An example of an LH(d, n) with coordinates indexed by, and entries from, ${\mathbb {Z}}_n$ is given by taking the entry in cell $(x_1,x_2,\ldots ,x_d)$ to be $\sum _{i=1}^d x_i$, with addition in ${\mathbb {Z}}_n$.

An alternative view of an LH(d, n), which may be easier to visualise, is as a type of group divisible design, where the groups are the n-element sets representing the d coordinates and the entry set itself. So if H is an LH(d, n) then H consists of $d+1$ disjoint sets (the groups), where each group is an n-element set, each block of the design has precisely one entry from each group, and each d-tuple from distinct groups lies in precisely one block.

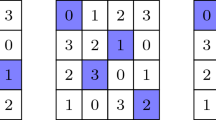
Figure 1 shows a Latin hypercube of dimension 3 and order 4 represented as 4 levels of rows and columns. The reader should visualise the 4 levels being placed on top of one another.

Fig. 1

An LH(3,4)

The same Latin hypercube can be viewed as a design, where the groups are the rows, the columns, the levels and the entries. If the rows are designated as $i_r$, the columns as $i_c$, the levels as $i_{\ell }$, and the entries as $i_e$, each for $i=0,1,2,3$, then the blocks in this case are formed as $(w_r,x_c,y_l,z_e)$ where $w,x,y,z\in {\mathbb {Z}}_4$, and $w=x+y+z$ in ${\mathbb {Z}}_4$. For example, in the 0th row, 1st column, 2nd level, the entry is 3 as highlighted in the table.

A partial Latin square of order n, denoted PLS(n), is defined in the same manner as a Latin square of order n except that some of the cells may be empty, in other words, each element of the entry set occurs at most once in each row and at most once in each column. Similarly, a partial Latin hypercube of dimension d and order n, denoted PLH(d, n) is defined in the same manner LH(d, n) except that some of the cells may be empty, in other words, each element of the entry set occurs at most once in each line.

A maximal PLH(d, n) is a PLH(d, n) that cannot be extended to another PLH(d, n) by inserting any element of the entry set N into any empty cell. We denote a maximal PLH(d, n) as an MPLH(d, n). This is analogous to a maximal PLS(n), which is a partial Latin square of order n that cannot be extended to another PLS(n) by inserting any entry into any empty cell. A maximal PLS(n) is denoted MPLS(n); it is of course the same thing as an MPLH(2, n). We will denote by f(d, n) the minimal cardinality of an MPLH(d, n), i.e.

$$\begin{aligned} f(d,n)=\min (F: \text {there exists an} \text { MPLH}(d,n) \ \text {with precisely} \ F \ \text {filled cells}). \end{aligned}$$

In the next section we review what is already known about maximum partial Latin hypercubes.

2 Previous results

Our first comment is that it is difficult to recognise what is already known because the problem can be reformulated in so many different forms. We start by reviewing results that explicitly refer to Latin squares ($d=2$) and Latin cubes ($d=3$) of variable order n.

Theorem 2.1

(Horak and Rosa [4]) If L is a partial Latin square of order n (i.e. a PLS(n)) with less than $n^2/2$ entries, then it cannot be maximal. Hence $f(2,n) \ge \lceil n^2/2\rceil$.

It will help our subsequent discussion to give a proof of this result, essentially that given in [6]. In Sect. 3, this proof is adapted and extended to deal with the case of higher dimensional hypercubes.

Proof

Let F denote the number of filled cells in the partial Latin square L of order n. We assume that $F<n^2/2$ and denote by E the number of empty cells, so that $E=n^2-F>n^2/2$. The set of all empty cells will be denoted by ${\mathcal {E}}$. We can assume that the rows and columns of L are indexed by ${\mathbb {Z}}_n$. Define $e_1(i)$ to be the number of empty cells in row i, and $e_2(j)$ to be the number of empty cells in column j. Then $\sum _{i=0}^{n-1} e_1(i)= \sum _{j=0}^{n-1} e_2(j)=E$.

If an empty cell (i, j) has less than n filled cells in the union of its row and column then there exists x in the entry set which does not appear in row i or in column j. The number of filled cells in the union of row i and column j is at most $(n-e_1(i))+$ $(n-e_2(j))$. Consequently if there is an empty cell (i, j) with $e_1(i)+e_2(j)-n>0$, then L may be extended to a PLS(n) $L'$ with $F+1$ filled cells by inserting an appropriate entry into cell (i, j).

To prove that there is such an empty cell, consider the sum

$$\begin{aligned} S=\sum _{(i,j)\in {\mathcal {E}}} (e_1(i)+e_2(j)-n). \end{aligned}$$

Here the summation is over all empty cells (i, j). Each $e_1(i)$ will appear in the summation precisely $e_1(i)$ times, and each $e_2(j)$ will appear precisely $e_2(j)$ times. Consequently

$$\begin{aligned} S=\left[ \sum _{i=0}^{n-1} (e_1(i))^2\right] + \left[ \sum _{j=0}^{n-1} (e_2(j))^2\right] -nE. \end{aligned}$$

By Cauchy’s inequality,

$$\begin{aligned} \sum _{i=0}^{n-1} (e_1(i))^2\ge \frac{1}{n} \left[ \sum _{i=0}^{n-1} e_1(i)\right] ^2=\frac{E^2}{n}, \,\text {and}\\ \sum _{j=0}^{n-1} (e_2(j))^2\ge \frac{1}{n} \left[ \sum _{j=0}^{n-1} e_2(j)\right] ^2=\frac{E^2}{n}. \end{aligned}$$

Hence $S\ge E(\frac{2E}{n}-n)>0$. Since $S>0$, at least one term in the summation must be strictly positive, i.e. there exists an empty cell (i, j) with $e_1(i)+e_2(j)-n>0$. The result follows.

$\square$

For each positive integer n there is an MPLS(n) with the number of filled cells equal to $\lceil n^2/2 \rceil$. As examples, in Fig. 2 we show squares of orders $n=6$ and $n=7$. It is easy to see how these generalise. So $f(2,n)=\lceil n^2/2 \rceil$.

Horak and Rosa [4] also proved the following result about the spectrum of MPLS(n)s, in other words the values of F for which it is possible to construct an MPLS(n) having exactly F filled cells.

Theorem 2.2

(Horak and Rosa [4]) Let $S_n$ be defined as

And suppose that the integer $F\not \in S_n$, $\frac{n^2}{2} \le F \le n^2$, and $F\ne n^2-1$. Then there exists an MPLS(n) having precisely F filled cells.

They went on to conjecture that the values of F covered by Theorem 2.2 form the spectrum of MPLS(n). They eliminated most of the values of F not covered by this Theorem, leaving undetermined the following cases:

• 1. $F=\frac{n^2}{2}+k, ~k \ \text {odd}, \ \frac{n}{2}<k\le n-1$, when n is even, and

• 2. $F=\frac{n^2+1}{2}+k, ~k \ \text {odd}, \ \frac{n-1}{2}\le k\le n-2$, when n is odd.

As far as we are aware this conjecture remains open.

Next we review what is known about MPLH(3, n)s. A Latin hypercube of dimension 3 and order n is usually called a Latin cube and denoted by LC(n) with associated notations PLC (partial) and MPLC (maximal partial). In [2] Britz, Cavenagh and Sørensen prove the following result.

Fig. 2

MPLS(6) and MPLS(7)

Theorem 2.3

If C is a partial Latin cube of order n (i.e. a PLC(n)) with less than $\left( 1-\frac{1}{\sqrt{2}}\right) n^3 \approx 0.29289\,n^3$ entries, then it cannot be maximal.

It is also shown that the bound can be improved slightly by the addition of an $O(n^2)$ term. The same paper goes on to construct MPLC(n) with $n^3/3$ filled cells when n is divisible by 3, and with $n^3/3+O(n^2)$ filled cells when n is not divisible by 3.

As regards the spectrum of values of F (the number of filled cells) for which a MPLC(n) exists the following results are also established in [2].

Theorem 2.4

There exists an MPLC(n) having precisely F filled cells if

• 1. $n\ge 10$ is even and $\frac{n^3}{2}\le F \le n^3-3$, or

• 2. $n\ge 21$ is odd and $\frac{n^3}{2}+\frac{n}{2}\le F \le n^3-3$.

Moreover, there is no MPLC(n) having precisely $n^3-1$ or $n^3-2$ filled cells.

Open questions remain about the spectrum below approximately $F=n^3/2$.

The results of [4] and [2] deal with fixed dimensions ($d=2$ and $d=3$ respectively) and variable order n. In [5] and in [1] the authors (respectively Jha, and Arumugam and Kala) obtain results covering fixed order $n=2$ and variable dimension d. These results are obtained in the context of graph domination numbers.

If $G = (V, E)$ is a finite simple connected graph then $S \subseteq V$ is called a dominating set if every vertex in $V{\setminus } S$ is adjacent to at least one vertex in S. A dominating set S is called an independent dominating set if no two vertices of S are adjacent. A survey of results on independent dominating sets is given in [3]. The minimum cardinality of an independent dominating set of a graph G is called the independent domination number of G and is denoted by i(G). The d-cube $Q_d$ is the graph whose vertex set is the set of all d-dimensional boolean vectors, i.e. $({\mathbb {Z}}_2)^d$, two vertices being joined by an edge if and only if they differ in exactly one coordinate. In [5] the following result is established.

Theorem 2.5

(Jha [5]) For d a positive integer, the independent domination number of the d-cube satisfies the inequalities

$$\begin{aligned} \frac{2^d}{d+1}\le i(Q_d) \le \frac{2^d}{2^{\lfloor \log _2(d+1) \rfloor }}. \end{aligned}$$

In particular, if $d+1$ is an integer power of 2, i.e. if $d+1=2^k$ for some integer k, then $i(Q_d)=2^d/(d+1)=2^{d-k}$.

In [1] the authors establish the values of $i(Q_d)$ for $d\le 6$ as shown in Table 1.

Table 1 Independent domination numbers for $Q_d$

There is a strong connection between independent dominating sets and maximum partial Latin hypercubes. Let G(d, n) denote the graph with vertex set $({\mathbb {Z}}_n)^{d+1}$ in which vertices are joined by an edge if and only if they differ in precisely one coordinate.

Theorem 2.6

An independent dominating set for G(d, n) is equivalent to an MPLH(d, n).

Proof

Suppose first that S is an independent dominating set for G(d, n). A PLH(d, n), say H, may be formed by taking each $(x_1,x_2,\ldots ,x_{d},x_{d+1})\in S$ and placing the entry $x_{d+1}$ in the cell $(x_1,x_2,\ldots ,x_{d})$ of H. The independence property of S ensures that no cell receives more than one entry. That H has the Latin property also follows from the independence property: if H had two cells in the same line with the same entry then the corresponding points of S would be adjacent, a contradiction. To see that H is maximal, suppose that $C=(x_1,x_2,\ldots ,x_{d})$ is an empty cell of H, so that ${\textbf{c}}_k=(x_1,x_2,\ldots ,x_{d},k)\not \in S$ for any $k\in {\mathbb {Z}}_n$. Since S is a dominating set, for each $k\in {\mathbb {Z}}_n$ there exists ${\textbf{c}}'_k=(x'_1,x'_2,\ldots ,x'_{d},k)\in S$, where $x'_i=x_i$ except for one value j where $x'_j\ne x_j$. But then cell $C'_k=(x'_1,x'_2,\ldots ,x'_{d})$ is a filled cell of H containing the entry k and it differs in only one coordinate from cell C. So, for any $k\in {\mathbb {Z}}_n$, entry k cannot be placed in cell C because this would give two cells in line j with the same entry. We deduce that no further entries can be added to H without violating the Latin condition, and so H is an MPLH(d, n).

Conversely suppose that H is an MPLH(d, n). We may assume that its coordinates and entries are from ${\mathbb {Z}}_n$. Define $S\subseteq ({\mathbb {Z}}_n)^{d+1}$ to be the set of points:

$$\begin{aligned} \{(x_1,x_2,\ldots ,x_{d},x_{d+1}): \ \text {cell} \ (x_1,x_2,\ldots ,x_{d}) \ \text {of} \ H\,\, \text {contains entry}\,\, x_{d+1}\}. \end{aligned}$$

The Latin property of H ensures that no two points from S are adjacent in G(d, n). To see that S is a dominating set for G(d, n), suppose that ${\textbf{c}}_k=(x_1,x_2,\ldots ,x_{d},k)\not \in S$. If ${\textbf{c}}_{\ell }=(x_1,x_2,\ldots ,x_{d},\ell )\in S$ for some $\ell \ne k$ then ${\textbf{c}}_k$ is adjacent to a vertex of S. If ${\textbf{c}}_{\ell }=(x_1,x_2,\ldots ,x_{d},\ell )\not \in S$ for any $\ell \in {\mathbb {Z}}_n$ then cell $C=(x_1,x_2,\ldots ,x_{d})$ of H is empty. Since H is maximal, entry k cannot be placed in cell C, and so there is a filled cell of H, $C'=(x'_1,x'_2,\ldots ,x'_{d})$ containing entry k, where $x'_i=x_i$ except for one value j where $x'_j\ne x_j$. But then ${\textbf{c}}'_k=(x'_1,x'_2,\ldots ,x'_{d},k)\in S$ and is adjacent to ${\textbf{c}}_k$ in G(d, n). It follows that S is an independent dominating set for G(d, n). $\square$

Combining this result with those of Theorem 2.5 and Table 1, gives the following results.

Corollary 2.7

$f(d,2)=i(Q_{d+1})$, and so

$$\begin{aligned} \frac{2^{d+1}}{d+2}\le f(d,2) \le \frac{2^{d+1}}{2^{\lfloor \log _2(d+2) \rfloor }}. \end{aligned}$$

In particular, if $d+2$ is an integer power of 2 then $f(d,2)=2^{d+1}/(d+2)$. For $2\le d\le 6$ values of f(d, 2) are as in Table 2.

Table 2 Minimum number of filled cells in an MPLH(d, 2)

In Sect. 3 we will generalise Corollary 2.7 to orders $n>2$.

Next we examine connections with coding theory. Results of Quistorff [10] are particularly relevant to Latin hypercubes. For background information on coding theory, see [7]. An n-ary code C of length l over ${\mathbb {Z}}_n$ is said to have covering radius r if r is the smallest integer such that every vector in ${\mathbb {Z}}_n^l$ is within Hamming distance r of a codeword of C. It is easy to see that the minimum distance of such a code can be at most $2r+1$.

Theorem 2.8

An MPLH(d, n) is equivalent to a n-ary code C of length $d+1$ over ${\mathbb {Z}}_n$ with minimum distance at least 2 and covering radius 1.

Proof

A code C of length $d+1$ over ${\mathbb {Z}}_n$ can be viewed as a set S of vertices in the graph G(d, n), and vice-versa. The set S is a dominating set if and only if the corresponding code C has covering radius 1, and it is an independent set (meaning that no two vertices of S are adjacent) if and only if C has minimum distance at least 2. The result then follows from Theorem 2.6. $\square$

Quistorff [10] uses $K_n(l,r)$ to denote the minimal cardinality of an n-ary code of length l with covering radius at most r. A covering radius of zero implies that the code has every vector as a codeword and hence $n^l$ codewords. Apart from the trivial case $n=1$, a code with cardinality $K_n(l,1)$ must therefore have covering radius 1. However, such codes may have minimum distance 1. Consequently f(d, n) may not equal $K_n(d+1,1)$, but we certainly have $f(d,n)\ge K_n(d+1,1)$. Rodemich [11] gives the bound $K_n(d+1,1)\ge \lceil n^d/d\rceil$, and this gives the bound

$$\begin{aligned} f(d,n)\ge \lceil n^d/d\rceil . \end{aligned}$$

For $d=3$ this is a better bound than the one given in [2] which we described above. But Theorem 1 of [10] improves on this in certain cases by giving the following lower bound for $K_n(d+1,1)$.

Theorem 2.9

(Quistorff [10]) If $2\le d<n\le 2d$ and $b=2d-n$, then

$$\begin{aligned}K_n(d+1,1)\ge \Big \lceil n^{d-1}\frac{2n(n-1)-b}{2d(n-1)-b}\Big \rceil . \end{aligned}$$

The bound given in [11] gives $f(4,5)\ge 157,~f(4,6)\ge 324$, and $f(4,7)\ge 601$. Theorem 2.9 improves these to give: $f(4,5)\ge 160,~f(4,6)\ge 330$, and $f(4,7)\ge 606$. We give a further improvement covering a wider range of cases in Theorem 3.1 below.

Theorem 2 of [10] shows that an n-ary code of length l with minimum distance at least 2, covering radius 1, and having M codewords gives rise to an n-ary code of length $l+1$ with minimum distance 2, covering radius 1, and having nM codewords. Recast in the language of Latin hypercubes this can be expressed as follows.

Theorem 2.10

(Quistorff [10]) Suppose that $H_d$ is an MPLH(d, n) with exactly F filled cells. Then there exists an MPLH$(d+1,n)$, $H_{d+1}$ with exactly nF filled cells.

The basis of the proof is as follows. We may assume that $H_d$ is expressed over ${\mathbb {Z}}_n$. Suppose that $C=(x_1,x_2,\ldots ,x_d)$ is any cell of $H_d$. If C is empty, then leave all n cells of the form $C^i=(x_1,x_2,\ldots ,x_d,i)$ empty in $H_{d+1}$, for $i\in {\mathbb {Z}}_n$. On the other hand, if C contains the entry z in $H_d$, then in cell $C^i=(x_1,x_2,\ldots ,x_d,i)$ of $H_{d+1}$ place the entry $z+i$ (addition in ${\mathbb {Z}}_n$), and do this for each $i\in {\mathbb {Z}}_n$. It is easy to check that $H_{d+1}$ has the desired properties. As a consequence, we have

Corollary 2.11

$f(d+1,n)\le nf(d,n)$.

3 A lower bound

The bound presented in this section is a generalisation of the result in [4] to Latin hypercubes. It improves the bound in [2], the bound that follows from [11], and the bound that follows from Theorem 1 of [10]. It also extends the bound given by [5] to a wider range of cases.

Theorem 3.1

Suppose that H is a partial Latin hypercube of dimension d and order n. To avoid trivialities, assume that $d,n\ge 2$ and that $(d,n)\ne (2,2)$. Let $n=qd+r$ where $0\le r\le d-1$. Put $k=n-q-1$ and

$$\begin{aligned}\delta =n^{d-1}\frac{r(d-r)}{d(kd+r)}.\end{aligned}$$

Let F denote the number of filled cells in H. Then if $F<\frac{n^d}{d}+\delta$, H cannot be maximal. In other words, $f(d,n)\ge \lceil \frac{n^d}{d}+\delta \rceil$.

Proof

The non-triviality conditions on d and n ensure that $k\ge 1$. Let E denote the number of empty cells in H, so that $E=n^d-F$, and assume that $F<\frac{n^d}{d}+\delta$.

Case (a): $r\ne 0$. Then $1\le r\le d-1$, so

$$\begin{aligned} E&>n^d-\frac{n^d}{d}-\delta =n^{d-1}\Big (n-\frac{n}{d}-\frac{r(d-r)}{d(kd+r)}\Big )\nonumber \\&=n^{d-1}\Big (n-q-\frac{r}{d}-\frac{r(d-r)}{d(kd+r)}\Big )\nonumber \\&=n^{d-1}\Big (n-q-\frac{kr+r}{kd+r}\Big ). \end{aligned}$$

(1)

Because $r<d$ it follows that $\displaystyle \Big \lfloor \frac{E}{n^{d-1}}\Big \rfloor \ge n-q-1=k$.

Case (b): $r=0$. Then $\delta =0$, so

$$\begin{aligned} E&>n^d-\frac{n^d}{d}\nonumber \\&=n^{d-1}\Big (n-\frac{n}{d}\Big )\nonumber \\&=n^{d-1}(n-q)\nonumber \\&=n^{d-1}(k+1). \end{aligned}$$

(2)

Hence $\displaystyle \Big \lfloor \frac{E}{n^{d-1}}\Big \rfloor \ge k+1$.

In both cases (a) and (b), put $l=\displaystyle \Big \lfloor \frac{E}{n^{d-1}}\Big \rfloor$. Then $l\ge k+1$ except possibly when $r>0$ and $l=k$.

Define e(L) to be the number of empty cells in line L. If we sum e(L) over all lines in a given direction, say the j direction, we get $\sum _{L\in {\mathcal {L}}_j} e(L)= E$.

Let $L_j(C)$ denote the line in direction j passing through the cell C. If an empty cell C has less than n filled cells in the union of all d lines through it, then there exists x in the entry set which does not appear in any of these lines. The number of filled cells in a given line L is $n-e(L)$, so the union of all the lines through a cell C has at most $\sum _{j=1}^d (n-e(L_j(C)))$ filled cells, where the summation is over all the d lines $L_j(C)$ that contain cell C. Consequently, if there is an empty cell C with $\sum _{j=1}^d(n-e(L_j(C)))<n$ then H may be extended to a PLH(d, n) $H'$ with $F+1$ filled cells by inserting an appropriate entry into cell C. Note that the inequality is equivalent to $s(C)=\left[ \sum _{j=1}^d e(L_j(C))\right] -(d-1)n>0$.

To prove that there is such an empty cell, consider the sum S of s(C) over all empty cells C. If ${\mathcal {E}}$ denotes the set of all empty cells in H then

$$\begin{aligned}S&=\sum _{C\in {\mathcal {E}}}\left\{ \left[ \sum _{j=1}^d e(L_j(C))\right] -(d-1)n\right\} \\&=\sum _{j=1}^d \sum _{C\in {\mathcal {E}}}e(L_j(C))-\sum _{C\in {\mathcal {E}}}(d-1)n\\&=\left[ \sum _{j=1}^d \sum _{C\in {\mathcal {E}}}e(L_j(C))\right] -(d-1)nE. \end{aligned}$$

The aim is to prove that $S>0$, thereby showing that at least one of the empty cells can be filled.

For an empty cell C there will be d lines through C. Consider lines in a single fixed direction, say the j direction. There will be one such line, namely $L_j(C)$, through each empty cell C and in the summation $\sum _{C\in {\mathcal {E}}} e(L_j(C))$, each term will be counted $e(L_j(C))$ times. So

$$\begin{aligned} \sum _{C\in {\mathcal {E}}} e(L_j(C))=\sum _{L\in {\mathcal {L}}_j} (e(L))^2,\end{aligned}$$

where the summation on the right-hand side is over all $n^{d-1}$ lines in the j direction.

The minimum possible value of $T_j=\sum _{L\in {\mathcal {L}}_j} (e(L))^2$ subject to $\sum _{L\in {\mathcal {L}}_j} e(L)= E$ is obtained by distributing the total value E as evenly as possible amongst the $n^{d-1}$ lines $L\in {\mathcal {L}}_j$. The average value per line is $E/n^{d-1}$. But $l=\lfloor E/n^{d-1}\rfloor$, so $l\le E/n^{d-1}<l+1$. Hence $T_j$ will be minimised if $e(L)=l$ for $\lambda$ lines, and $e(L)=l+1$ for $\mu$ lines, where $\lambda +\mu =n^{d-1}$ and $l\lambda +(l+1)\mu =E$. These equations for $\lambda$ and $\mu$ give $\lambda =(l+1)n^{d-1}-E$ and $\mu =E-ln^{d-1}$. As a consequence

$$\begin{aligned} T_j&\ge \lambda l^2 +\mu (l+1)^2\\&=n^{d-1}l^2(l+1)-n^{d-1}l(l+1)^2+E((l+1)^2-l^2)\\&=E(2l+1)-n^{d-1}l(l+1). \end{aligned}$$

It follows that

$$\begin{aligned} S&\ge dE(2l+1)-dn^{d-1}l(l+1)-(d-1)nE \nonumber \\&=E(2ld+d-nd+n)-dn^{d-1}l(l+1)\nonumber \\&=E(2ld+d-nd+qd+r)-dn^{d-1}l(l+1)\nonumber \\&=E(2ld-d(n-1-q)+r)-dn^{d-1}l(l+1)\nonumber \\&=E(2ld-kd+r)-dn^{d-1}l(l+1). \end{aligned}$$

(3)

We consider four possibilities, namely: (i) $l=k$;  (ii) $l=k+1,r=0$; (iii) $l=k+1,r>0$;  (iv) $l\ge k+2$.

• (i) If $l=k$, inequality (3) gives $S\ge E(kd+r)-dn^{d-1}k(k+1)$, but this can only happen in case (a) when $r>0$ and then from inequality (1), $E>n^{d-1}\Big (n-q-\frac{kr+r}{kd+r}\Big )$. So, if $l=k$ we have

  $$\begin{aligned} S&>n^{d-1}\Big (n-q-\frac{kr+r}{kd+r}\Big )(kd+r)-dn^{d-1}k(k+1)\\&=n^{d-1}\Big ((k+1)(kd+r)-(kr+r)\Big )-dn^{d-1}k(k+1)\\&=n^{d-1}\Big (dk(k+1)-dk(k+1)\Big )=0. \end{aligned}$$

• (ii) If $l=k+1$ and $r=0$ then inequality (3) gives $S\ge E(ld+d)-dn^{d-1}l(l+1)$, but this can only happen in case (b) and then inequality (2) gives $E>n^{d-1}(k+1)=ln^{d-1}$. Hence

  $$\begin{aligned} S> n^{d-1}(dl(l+1)-dl(l+1))=0.\end{aligned}$$

• (iii) If $l=k+1$ and $r>0$ then inequality (3) gives

  $$\begin{aligned}S\ge E(ld+d+r)-dn^{d-1}l(l+1).\end{aligned}$$

  But $E\ge ln^{d-1}$ and so

  $$\begin{aligned} S\ge n^{d-1}(dl(l+1)+rl-dl(l+1))=rln^{d-1}>0.\end{aligned}$$

• (iv) Finally, if $l\ge k+2$ then inequality (3) gives

  $$\begin{aligned}S\ge E(ld+2d+r)-dn^{d-1}l(l+1).\end{aligned}$$

  Again using $E\ge ln^{d-1}$, we obtain

  $$\begin{aligned} S\ge n^{d-1}(dl(l+2)+rl-dl(l+1))\ge dln^{d-1}>0.\end{aligned}$$

In conclusion, $S>0$ in all cases under consideration and the result follows. $\square$

We remark that for $d=2$ (squares) this result coincides with the $n^2/2$ result of [4]. For $d=3$ (cubes) it improves the result of [2], and brings it into line with the MPLC(n)s constructed in that paper that have precisely $n^3/3$ filled cells. Some rather tedious arithmetic shows that the bound of Theorem 3.1 is always at least as good as that provided by Theorem 1 of [10] (Theorem 2.9 above). In particular, $f(4,5)\ge 164, ~f(4,6)\ge 336$, and $f(4,7)\ge 612$. Theorem 3.1 also applies to a much wider range of the parameters d and n than Theorem 1 of [10].

When $n\le d$, in the terminology of Theorem 3.1, we have $q=0, r=n$ and $k=n-1$, and the bound reduces to $f(d,n)\ge \frac{n^{d+1}}{d(n-1)+n}$.

If $n>d$ then

$$\begin{aligned} \frac{n^{d+1}}{d(n-1)+n}<\frac{n^{d+1}}{d(n-1)+d}=\frac{n^d}{d}\le f(d,n) \ \text {by Theorem} \ 3.1. \end{aligned}$$

Hence, even when $n> d$, the bound implies the same inequality, although this inequality is then weaker than the bound. So in all cases we have $f(d,n)\ge \frac{n^{d+1}}{d(n-1)+n}$. For $n=2$ this coincides with the lower bound of Corollary 2.7 that came from the results of Jha [5]. So the bound of Theorem 3.1 extends that of [5].

In the next two sections we examine how close the bound is to optimality.

4 Constructing MPLH(d, n) for fixed d

The focus in this section is primarily on the case $n\ge d$. An examination of the proof of Theorem 3.1 suggests that it is likely that any MPLH(d, n) with precisely $n^d/d$ filled cells will have the property that for any empty cell, the entries in the lines through that cell are distinct and cover the entire entry set. Furthermore, if n is divisible by d, each line through an empty cell will (most likely) have n/d entries in such a minimal MPLH. The results below go some way to support this conjecture by producing designs with these properties.

Theorem 4.1

Suppose that $d\ge 2$ and that q is a prime or prime power less than or equal to d. Then there exists an MPLH(d, q) with precisely $q^{d-1}$ filled cells.

Proof

The proof is by direct construction of an MPLH(d, q) denoted by H. All arithmetic is in a finite field $F_q$ with q elements; we denote the elements of the field in some fixed order as $\lambda _1, \lambda _2,\ldots , \lambda _q$. The coordinates of H will be indexed by, and its entries taken from, $F_q$.

The filled cells of H are those with coordinates $(x_1,x_2,\ldots ,x_d)$ where $\sum _{i=1}^d x_i=0$. The remaining cells of H are empty. Clearly there are precisely $q^{d-1}$ filled cells and only one filled cell in each line. The entry in a filled cell $(x_1,x_2,\ldots ,x_d)$ is $e=\sum _{i=1}^q \lambda _i x_i$. Note that this entry does not depend on $x_j$ for the value j such that $\lambda _j=0$, and if $q<d$, this entry does not depend on $x_{q+1},x_{q+2},\ldots , x_d$.

Take an empty cell $C=(y_1,y_2,\ldots ,y_d)$. Then $S=\sum _{i=1}^d y_i \ne 0$. We show that the d lines through C collectively contain as entries all the elements of $F_q$. Put $T=\sum _{i=1}^q \lambda _i y_i$. Consider any coordinate position j where $1\le j\le q$. Put $x_j=y_j-S$ so that the cell $D_j=(y_1,y_2,\ldots ,y_{j-1},x_j,y_{j+1},\ldots ,y_d)$ is the unique filled cell of H that lies on the line through C in the j direction. The entry in cell $D_j$ is $e_j=T+\lambda _j(x_j-y_j)=T-\lambda _j S$.

If we take two distinct lines through the empty cell C, say in the j and k directions where $j\ne k$ and $1\le j,k\le q$, then the entries in these lines are $e_j=T-\lambda _j S$ and $e_k=T-\lambda _k S$, so that $e_j-e_k=(\lambda _k-\lambda _j)S \ne 0$. Hence $e_j\ne e_k$. Since there are q such lines through each empty cell C, no new entry may be placed into any such cell C, and so H is an MPLH(d, q). $\square$

As a simple consequence of Theorem 4.1 we have the following corollary.

Corollary 4.2

Suppose that d is a prime or prime power. Then there exists an MPLH(d, d) with precisely $d^{d-1}$ filled cells.

Our next result will enable us to meet the bound of Theorem 3.1 in more cases.

Theorem 4.3

Suppose that H is an MPLH(d, n) with exactly F filled cells and that k is a positive integer. Then there exists an MPLH(d, kn), $H'$, with exactly $k^dF$ filled cells.

Proof

We can assume that $k>1$. Take H to be an MPLH(d, n) with entry set ${\mathbb {Z}}_n$ and precisely F filled cells. Replace each filled cell of H containing the entry i by a Latin hypercube of dimension d and order k with entry set $\{ik,ik+1,\ldots , ik+(k-1)\}$. Each empty cell of H is replaced by an empty d-dimensional array of order k. In the representation of H as a group divisible design, this means that each point of H is inflated by a factor k, i.e. replaced by k new points, and each block of H is replaced by a Latin hypercube of type LH(d, k). The resulting design $H'$ still has $d+1$ groups, but these now have cardinality kn and each empty cell has all kn entries in the union of lines through that cell. So $H'$ is an MPLH(d, n) having precisely $k^dF$ filled cells. $\square$

Corollary 4.4

Suppose that d is a prime or prime power, and that n is divisible by d. Then there exists an MPLH(d, n) with precisely $n^d/d$ filled cells.

Proof

By Corollary 4.2, there exists an MPLH(d, d) with precisely $d^{d-1}=d^d/d$ filled cells. Put $k=n/d$ and apply Theorem 4.3 to obtain an MPLH(d, n) with precisely $k^d\times (d^d/d)=n^d/d$ filled cells. $\square$

A rather messier argument deals with the situation when n is not divisible by d.

Theorem 4.5

If d is a prime or prime power then, for large n, there exists an MPLH(d, n) that has at most $n^d/d + O(n^{d-1})$ filled cells.

Proof

Suppose that $n=dk+r$, where $1\le r\le d-1$. Take H to be an MPLH(d, d) with precisely $d^{d-1}$ filled cells. Inflate H by the factor k as described in the proof of Theorem 4.3 to form an MPLH(d, m), say $H_m$, where $m=dk$. Then $H_m$ has precisely $m^d/d$ filled cells. We may assume that the coordinates of $H_m$ are indexed by ${\mathbb {Z}}_m$ and that the entries are from the same set. We wish to add r extra possibilities for each of the d coordinates and r extra entries from the set $Y=\{m,m+1,\ldots ,m+r-1\}$ to extend $H_m$ to an MPLH($d,m+r$), $H'$. This is done by adding entries greedily in two stages.

In the first stage, take the existing lines of $H_m$ in a single fixed direction, say the first. There are $m^{d-1}$ such lines. Every empty cell of $H_m$ will lie in one of these lines. For each such line, insert new entries from Y into empty cells in that line until no further entries can be inserted without violating the Latin condition (i.e., that no line in any direction has a repeated entry). At most r entries can be placed in each line in the first direction, and so the maximum number of new entries that can be added in this way is $rm^{d-1}$. Once this process is complete, none of the original cells of $H_m$ that remain empty can have any entry from ${\mathbb {Z}}_{m+r}$ inserted without violating the Latin condition.

In the second stage, note that $H'$ will have $(m+r)^{d}$ cells, so the number of new cells added to $H_m$ to form $H'$ is $(m+r)^{d}-m^d\le dr(m+r)^{d-1}$. Insert entries from ${\mathbb {Z}}_{m+r}$ into these new cells until no further entries can be inserted without violating the Latin condition. At most $dr(m+r)^{d-1}$ new entries are made in this process.

The partial Latin hypercube $H'$ that results from the two stages cannot be extended by inserting any entry from ${\mathbb {Z}}_{m+r}$ into any empty cell, and so $H'$ is an MPLH($d,m+r$). The total number of entries in $H'$ is at most the sum of the number of entries in $H_m$ plus the number added in stages one and two above. So $H'$ has at most $m^d/d+rm^{d-1}+dr(m+r)^{d-1}\le n^d/d+(d+1)rn^{d-1}$. Thus, for large n, the constructed MPLH(d, n) has $n^d/d +O(n^{d-1})$ entries. $\square$

Finally in this section we construct MPLH(d, n) designs when d is neither a prime nor a prime power. These designs come close to meeting a lower bound of $n^d/d$ filled cells.

By applying Theorem 4.3, the MPLH(d, q) constructed in Theorem 4.1 can be inflated by a factor k to give an MPLH(d, qk) with precisely $q^{d-1}\times k^d=(qk)^d/q$ filled cells. So when n is a multiple of q we have an MPLH(d, n) with $n^d/q$ filled cells. When n is not a multiple of q we may again proceed as in Theorem 4.5 by adding extra possibilities for each of the d coordinates and extra entries to obtain an MPLH(d, n) having, for large n, $n^d/q+O(n^{d-1})$ filled cells. This result is stated in the following theorem.

Theorem 4.6

If d is neither a prime nor a prime power then, for large n, there exists an MPLH(d, n) that has at most $n^d/q + O(n^{d-1})$ filled cells, where q is the largest prime or prime power less than d.

How close $n^d/q$ is to $n^d/d$ obviously depends on d. There are many results concerning gaps between primes. As an example, we cite Nagura [8] who proved that for $m\ge 25$, there exists a prime p satisfying $m\le p\le 6m/5$. As a consequence it follows that for any d that is not a prime or prime power, there is a prime or prime power q satisfying $5d/6 \le q \le d$. So in all cases we have the following corollary of Theorem 4.6.

Corollary 4.7

If d is neither a prime nor a prime power then, for large n, there exists an MPLH(d, n) that has at most $6n^d/5d + O(n^{d-1})$ filled cells.

More recent results about gaps between primes improve the factor 6/5, taking it down to arbitrarily close to 1 for larger values of d.

5 Constructing MPLH(d, n) for fixed n

The focus in this section is on the case $d\ge n$. We will show that the bound of Theorem 3.1 can sometimes be achieved, and that it is possible to get close in other cases. Our first theorem would be vacuous if codes with such parameters did not exist. But the parameters are those of Hamming codes Ham(r, n), which exist whenever n is a prime or prime power (see [7]).

Theorem 5.1

Suppose that $r,n>1$ are integers and that ${\mathcal {C}}$ is a code over ${\mathbb {Z}}_n$ of length $(n^r-1)/(n-1)$ ($=d+1$, say) that has $n^{d+1-r}$ codewords and minimum distance 3. Then ${\mathcal {C}}$ is equivalent to an MPLH(d, n) with precisely $\displaystyle \frac{n^{d+1}}{d(n-1)+n}$ filled cells (the bound of Theorem 3.1).

Proof

The parameters of ${\mathcal {C}}$ ensure that ${\mathcal {C}}$ is a perfect code, and so has covering radius 1. Applying Theorem 2.8, ${\mathcal {C}}$ is therefore equivalent to an MPLH(d, n) with $n^{d+1-r}$ filled cells. However, $n^r=d(n-1)+n$, so the number of filled cells is $\displaystyle \frac{n^{d+1}}{d(n-1)+n}$. $\square$

Non-trivial perfect n-ary codes are only known for n a prime or prime power. It is conjectured that none exist when n is not a prime or prime power. Moreover, when n is a prime or prime power, any non-trivial perfect code ${\mathcal {C}}$ must have the parameters of Ham(r, n) for some $r\ge 2$, or it is one of the Golay codes $G_{23}$ and $G_{11}$. The code $G_{23}$ is a binary code with minimum distance 7 and covering radius 3. The code $G_{11}$ is a ternary code with minimum distance 5 and covering radius 2. So Theorem 5.1 cannot be applied directly to either of these codes.

When the parameters of an MPLH(d, n) do not correspond to those of a Hamming code, some progress can be made as a result of Theorem 2.10 that shows how to increment the dimension of an existing MPLH. To see how this works consider the code Ham(4, 2) which generates an MPLH(14, 2) having $2^{11}$ filled cells. The “‘next” Hamming code Ham(5, 2) generates an MPLH(30, 2) having $2^{26}$ filled cells. By repeated use of Theorem 2.10, we can (for examples) obtain an MPLH(22, 2) that has $2^{11+8}=2^{19}$ filled cells and an MPLH(29, 2) that has $2^{11+15}=2^{26}$ filled cells. These numbers of filled cells correspond to the values of the upper bound given in Corollary 2.7. Indeed, we can generalise that bound as follows.

Corollary 5.2

If n is a prime or prime power then, for $d\ge n$,

$$\begin{aligned}\frac{n^{d+1}}{d(n-1)+n}\le f(d,n) \le \frac{n^{d+1}}{n^{\lfloor \log _n((n-1)d+n) \rfloor }}. \end{aligned}$$

Proof

Theorem 3.1 established the lower bound in all cases. By Theorem 5.1 and the existence of Hamming codes, $\displaystyle f(d,n)=\frac{n^{d+1}}{d(n-1)+n}$ whenever d has the form $\displaystyle d=d(r)=\frac{n^r-1}{n-1}-1$ for $r>1$. The lowest such value of d is n, which corresponds to $r=2$. To establish the result it is necessary to “fill the gap” between d(r) and $d(r+1)$ for $r\ge 2$. It is easy to see that $d(r+1)-d(r)=n^r$, so the gap contains $n^r-1$ values of d. Now take an arbitrary $d^*$ in the gap so that $d^*=d(r)+k$ where $0<k<n^r$. Starting with an MPLH(d(r), n) that has the minimum number of filled cells f(d(r), n), apply Theorem 2.10k times to produce an MPLH($d(r)+k,n$) having $n^k f(d(r),n)$ filled cells. This is an MPLH($d^*,n$) with precisely F filled cells, where

$$\begin{aligned} F&=n^k \frac{n^{d(r)+1}}{d(r)(n-1)+n}\\&= \frac{n^{d(r)+k+1}}{d(r)(n-1)+n}\\&= \frac{n^{d^*+1}}{d(r)(n-1)+n} \end{aligned}$$

To complete the proof we show that

$$\begin{aligned} d(r)(n-1)+n=n^{\lfloor \log _n((n-1)d^*+n)\rfloor }.\end{aligned}$$

(4)

We have $d(r)(n-1)+n=n^r$, which gives

$$\begin{aligned}(n-1)d^*+n=(n-1)d(r)+n+(n-1)k=n^r+(n-1)k.\end{aligned}$$

The latter expression lies strictly between $n^r$ and $n^{r+1}$, so

$$\begin{aligned}\lfloor \log _n((n-1)d^*+n)\rfloor =r,\end{aligned}$$

and consequently Eq. 4 is established. $\square$

6 Concluding remarks

In many cases the bound given in Theorem 3.1 can either be achieved or approached asymptotically for large n. However, this bound is certainly not best possible. For example, f(3, 4) is bounded below by 22 using the bounds of both [11] and Theorem 2.9, and by 23 using Theorem 3.1. But a result of [12] establishes that $f(3,4)\ge 24$, and in [9] the authors prove that $f(3,4)=28$ after an extensive computer search.

Nevertheless, the constructions presented enable us to produce MPLH(d, n) designs having relatively small excess numbers of filled cells above the lower bound of Theorem 3.1. It is not always obvious which route leads to the best result. As a concluding example, consider the formation of an MPLH(6, 6). Theorem 3.1 gives the lower bound for the number of filled cells in such a design as $6^5$. Since 6 is neither a prime nor a prime power, consider the following alternative strategies.

• 1. Start with an MPLH(6, 2) with 16 filled cells, obtained from Ham(3, 2) using Theorem 5.1. Inflate by a factor 3 using Theorem 4.3 to obtain an MPLH(6, 6) with $3^6\times 16=\frac{3}{2}\times 6^5$ filled cells.

• 2. Start with the MPLH(2, 6) with 18 filled cells shown in Fig. 2. Increment the dimension 4 times using Theorem 2.10 to obtain an MPLH(6, 6) with $6^4\times 18=3\times 6^5$ filled cells.

• 3. Since 3 is a prime less than 6, Theorem 4.1 gives an MPLH(6, 3) with $3^5$ filled cells. This can be inflated by a factor 2 (Theorem 4.3) to obtain an MPLH(6, 6) with $2^6\times 3^5=2\times 6^5$ filled cells.

• 4. Start with an MPLH(3, 3) with 9 filled cells given by Theorem 4.2. Then follow either (a) or (b).

  • (a) Increment the dimension 3 times (Theorem 2.10) to obtain an MPLH(6, 3) with $3^3\times 9=3^5$ filled cells. Then proceed as in case (3) above.

  • (b) Inflate by a factor 2 (Theorem 4.3) to obtain an MPLH(3, 6) with $2^3\times 9$ filled cells. Then increment the dimension of this design 3 times (Theorem 2.10) to produce an MPLH(6, 6) with $6^3\times 2^3\times 9=2\times 6^5$ filled cells.

Of these strategies, number (1) produces an MPLH(6, 6) with the smallest number of filled cells, 50% more than the lower bound.

It is unlikely that there is a precise general formula for the minimum number of filled cells in an MPLH(d, n). But it may be possible to tighten the upper bound for this quantity and to improve the lower bound.