Abstract
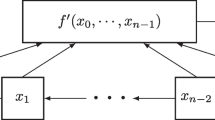
The cascade connection of two NFSRs is an important class of NFSRs which has been used in the design of many recently proposed stream ciphers, such as Grain v1, Grain-128a, Fruit and Sprout. In this paper, we consider the decomposition of an NFSR into the cascade connection of two smaller NFSRs, which is equivalent to the factorization of a characteristic function h into \(f*g\) where f and g are both characteristic functions. Inspired by the problem of factoring a large integer, we firstly consider a special case—that is, factoring h into the form \(h=g*g\). Based on the idea of “finding derivatives”, we completely solve this case in theory, and present an algorithm to compute g from h. Moreover, if the characteristic function f is “close” to g, then one can also use the same algorithm to determine g and then get f by the existing method. For the general case, the idea of “finding derivatives” can also be used and some interesting results can be derived.


Similar content being viewed by others
References
Armknecht F., Mikhalev V.: On lightweight stream ciphers with shorter internal states. In: Fast Software Encryption, pp. 451–470. Springer, Berlin (2015).
Aumasson J., Henzen L., Meier W., Nayaplasencia M.: QUARK: a lightweight hash. J. Cryptol. 26(4), 313–339 (2013).
Cannière C., Preneel B.: Trivium, vol. 4986, pp. 244–266. Lecture Notes in Computer Science. Springer, Berlin (2008).
Cannière C., Dunkelman O., Knežević M.: KATAN and KATANTAN—A Family of Small and Efficient Hardware-Oriented Block Ciphers, vol. 5747, pp. 272–288. Lecture Notes in Computer Science. Springer, Berlin (2009).
Courtois N., Meier W.: Algebraic Attacks on Stream Ciphers with Linear Feedback, vol. 2656, pp. 346–359. Lecture Notes in Computer Science. Springer, Berlin (2003).
Coven E.M., Hedlund G.A., Rhodes F.: The commuting block maps problem. Trans. Am. Math. Soc. 249(1), 113–138 (1979).
Golomb S.: Shift Register Sequences. Aegean Park Press, Laguna Hills (1982).
Green D.H., Dimond K.R.: Nonlinear product-feedback shift registers. Proc. Inst. Electr. Eng. 117(4), 681–686 (1970).
Hamann M., Krause M., Meier M.: LIZARD—a lightweight stream cipher for power-constrained devices. IACR Trans. Symmetric Cryptol. 2017(1), 45–79 (2017).
Hell M., Johansson T., Meier W.: The Grain Family of Stream Ciphers, vol. 4986, pp. 179–190. Lecture Notes in Computer Science. Springer, Berlin (2008).
Ma Z., Qi W.F., Tian T.: On the decomposition of an NFSR into the cascade connection of an NFSR into an LFSR. J. Complex. 29(2), 173–181 (2013).
Meier W., Staffelbach O.: Fast correlation attacks on certain stream ciphers. J. Cryptol. 1(3), 159–176 (1989).
Mykkeltveit J., Siu M.K., Tong P.: On the cycle structure of some nonlinear shift register sequences. Inf. Control 43, 202–215 (1979).
Tian T., Zhang J.M., Ye C.D., Qi W.F.: A survey and new results on the decomposition of an NFSR into a cascade connection of two smaller NFSRs. Cryptology ePrint Archive 536 (2014). https://eprint.iacr.org/2014/536.
Tian T., Zhang J.M., Qi W.F.: On the uniqueness of a type of cascade connection representations for NFSRs. Des. Codes Cryptogr. 87(10), 2267–2294 (2019).
Weger B.: Cryptanalysis of RSA with small prime difference. Appl. Algebra Eng. Commun. Comput. 13(1), 17–28 (2002).
Zhang J.M., Qi W.F., Tian T., Wang Z.X.: Further results on the decomposition of an NFSR into the cascade connection of an NFSR into an LFSR. IEEE Trans. Inf. Theory 61(1), 645–654 (2015).
Acknowledgements
This work was supported by the Natural Science Foundation of China (Grant Nos. 62202494, 61872383, 61602510, 61502524 and 61521003).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by T. Helleseth.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
In this section, we review the result that how to factor a Boolean function h into \(h=l*f\) where l is a linear function, see [15] for details.
Definition 31
For a term \(t=x_{i_{1}}x_{i_{2}}\cdots x_{i_{d}}\) with \(d\ge 1\) and \( i_{1}<i_{2}<\cdots <i_{d}\), the index distance tuple of t is defined as \( D(t)=(0,i_{2}-i_{1},i_{3}-i_{1},\ldots ,i_{d}-i_{1})\).
Let t be a term with the index distance tuple \(D=(0,u_{1},u_{2},\ldots ,u_{r}),r\ge 1\). Then it can be written uniquely as \(t=x_{i_{1}}*(x_{0}x_{u_{1}}\cdots x_{u_{r}})\). Let us denote the set of all terms containing the variable \(x_{0}\) by \(T_{0}\). By classifying the terms with the same index distance tuple, we have the following result.
Lemma 32
A Boolean function h which is not a constant can be written uniquely as
where \(l_{1},l_{2},\ldots ,l_{k}\) are linear functions and \( t_{1},t_{2},\ldots ,t_{k}\) are in \(T_{0}\) with pairwise distinct index distance tuples.
The representation given by Lemma 32 is called the \(*\)-product normal form of h.
Example 33
Let \(h=x_{0}\oplus x_{1}\oplus x_{3}\oplus x_{1}x_{3}\oplus x_{2}x_{3}\oplus x_{2}x_{4}\oplus x_{3}x_{4}\). Then the \(*\)-product normal form of h is given by
For a linear function \(l=c_{0}x_{0}\oplus c_{1}x_{1}\oplus \cdots \oplus c_{n-1}x_{n-1}\), define
The function \(\phi (\cdot )\) maps a linear function to a univariate polynomial over \( {\mathbb {F}}_{2}\), which is a one to one correspondence.
The uniqueness of the \(*\)-product normal form could yield the following result.
Theorem 34
Let h be a nonconstant Boolean function with \( *\)-product normal form given by (7). Then \(h=l*f\) for some Boolean functions l and f where l is a linear function if and only if \( \phi (l)\) is a divisor of \(\gcd (\phi (l_{1}),\phi (l_{2}),\ldots ,\phi (l_{k}))\).
It follows immediately from Theorem 34 that the linear left \(*\)-factor of h with the maximal \({{\,\textrm{maxsub}\,}}\) is unique. For the problem of factoring h into the form \(h=l*f\), although it is discussed clearly in theory, the authors do not present an algorithm in [15]. Here, we give an algorithm and its rough complexity analysis. Considering the simplicity in notation, for a linear function l, we make no distinction between l and \(\phi (l)\) in the following algorithm.

Remark 35
For a special case that l is known, then f can be determined directly by \(f=\frac{p}{l}*g\).
Let N be the number of terms in the ANF of h. Then the memory complexity of lines 1–4 of Algorithm 2 is bounded by O(N) and that of line 5 is bounded by \(O(N^{2})\). Thus, the memory complexity of Algorithm 2 is \( O(N^{2})\). For the time complexity, note that lines 2 and 4 is bounded by O(N), lines 3 and 5 is bounded by \(O(N^{2})\). Hence the time complexity of Algorithm 2 is \(O(N^{2})\).
Appendix B
In this section, a simple example is presented to show the process of Algorithm 1. Let \(g=x_{0}\oplus x_{1}x_{4}\oplus x_{2}x_{3}x_{4}\oplus x_{5}\) and \(h=g*g\) where \(d=\deg (g)=3.\) Then
According to (3), we have
and
where \(\deg (h_{2})=\deg (g)=3\). Thus, \(s=2\) and it follows from Theorem 18 that
It follows from Theorem 11 that
and
In this case, it means that we can get \(R(g)=x_{1}x_{2}x_{3}\oplus x_{1}x_{4}\oplus x_{5}\oplus x_{0}\) easily by Algorithm 2. Moreover, we have \(g=R^{2}(g)=x_{0}\oplus x_{1}x_{4}\oplus x_{2}x_{3}x_{4}\oplus x_{5}\).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Wang, Z., Zhao, X., Zheng, Q. et al. The decomposition of an NFSR into the cascade connection of two smaller NFSRs revisited. Des. Codes Cryptogr. 91, 1889–1910 (2023). https://doi.org/10.1007/s10623-023-01182-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10623-023-01182-z