Abstract
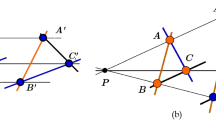
As the finite Hall planes are Non-Desarguesian, the Pappus Theorem does not hold in them. In this paper we state and prove some weaker versions of Pappus’s Theorem in Hall planes.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Burn R.P.: Bol quasi-fields and Pappus’ theorem. Math. Z. 105(5), 351–364 (1968).
Caliskan C., Moorhouse G.E.: Subplanes of order \(3\) in hughes planes. Electron. J. Comb. 18(1)P2 (2011).
Caliskan C., Petrak B.: Subplanes of order 3 in Figueroa planes. Finite Fields Appl. 20, 24–29 (2013).
Erdős P.: Some old and new problems in various branches of combinatorics. In: Proceedings of the Tenth Southeastern Conference on Combinatorics, Graph Theory and Computing Florida Atlantic University, Boca Raton, pp. 19–37 (1979).
Hall M. Jr.: Projective planes. Trans. Am. Math. Soc. 54(2), 229–277 (1943).
Hall M. Jr.: Combinatorial Theory, 2nd edn Wiley, New York (1986).
Hall M. Jr.: The Theory of Groups. Courier Dover Publications, New York (2018).
Hughes D.: A note on some partially transitive projective planes. Proc. Am. Math. Soc. 8(5), 978–981 (1957).
Hughes D.: Collineation groups of non-desarguesian planes, I: the Hall Veblen-Wedderburn systems. Am. J. Math. 81(4), 921–938 (1959).
Kallaher M.: Translation planes. In: Handbook of Incidence Geometry. North-Holland, Haarlem, pp 137–192 (1995).
Lazebnik F., Mellinger K.E., Vega O.: Embedding cycles in finite planes. Electron. J. Comb. 20(3)P24, 1–17 (2013).
Leshock L: Pappus configurations in finite Hall affine planes. Ph.D. Thesis, University of Delaware, pp. 1–84 (2020). https://sites.google.com/view/lleshock/research.
Metsch K.: Linear Spaces with Few Lines. Lecture Notes in Mathematics. Springer, New York (1991).
Moorhouse G.E.: http://www.ericmoorhouse.org/pub/index.html#planes. Accessed Feb 16 (2020).
Moorhouse G.E., Williford J.: Embedding finite partial linear spaces in finite translation nets. J. Geom. 91(1–2), 73–83 (2009).
Ostrom T.: Transitivities in projective planes. Can. J. Math. 9, 389–399 (1957).
Ostrom T.: Translation planes and configurations in Desarguesian planes. Archiv. Math. 111(1), 457–464 (1960).
Petrak B.: Fano subplanes in finite Figueroa planes. J. Geom. 99(1–2), 101–106 (2010).
Petrak B.: Finite Figueroa Planes. University of Delaware, Newark (2012).
Pickert G.: Der Satz von Pappos mit Festelementen. Archiv. Math. 10(1), 56–61 (1959).
Tait M.: On a problem of Neumann. Discret. Math. 342(10), 2843–2845 (2019).
Welsh D.J.A.: Matroid Theory. Dover Publications, New York (2010).
Wolfram Research, Inc. Mathematica, 12.0. Champaign (2019).
Acknowledgements
This work was partially supported by the Simons Foundation Award ID: 426092 and the National Science Foundation Grant: 1855723. The authors are thankful to Eric Moorhouse for sharing his knowledge on Hall planes and, in particular, for correcting an error in the original description of the action of the collineation group on pairs of lines of the Hall plane. We are also thankful to Stefaan DeWinter, Bill Kantor, and Jason Williford for useful discussions on the topics of this paper. Finally, we are thankful to the anonymous referees for their useful comments, and, in particular, for suggesting the references [1, 20, 22].
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Y. Zhou.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Lazebnik, F., Leshock, L. On Pappus configurations in Hall planes. Des. Codes Cryptogr. 90, 1203–1219 (2022). https://doi.org/10.1007/s10623-022-01036-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10623-022-01036-0