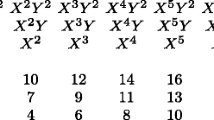Skip to main content
SpringerLink
Log in

From primary to dual affine variety codes over the Klein quartic

  • Published:
Designs, Codes and Cryptography Aims and scope Submit manuscript

Abstract

In Geil and Özbudak (Cryptogr Commun 11(2):237–257, 2019) a novel method was established to estimate the minimum distance of primary affine variety codes and a thorough treatment of the Klein quartic led to the discovery of a family of primary codes with good parameters, the duals of which were originally treated in Kolluru et al (Appl Algebra Eng Commun Comput 10(6):433-464, 2000)[Ex. 3.2, Ex. 4.1]. In the present work we translate the method from Geil and Özbudak (Cryptogr Commun 11(2):237–257, 2019) into a method for also dealing with dual codes and we demonstrate that for the considered family of dual affine variety codes from the Klein quartic our method produces much more accurate information than what was found in Kolluru et al (Appl Algebra Eng Commun Comput 10(6):433-464, 2000). Combining then our knowledge on both primary and dual codes we determine asymmetric quantum codes with desirable parameters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Notes

  1. We remark that in cases where for a given index i there exists an \(s \in {\mathbb {F}}_q\) such that for no \(P_j\) the ith coordinate is s we may leave out this value in the ith product of (6) simplifying the calculations.

References

  1. Aly S.A., Klappenecker A., Sarvepalli P.K.: Remarkable degenerate quantum stabilizer codes derived from duadic codes. In: 2006 IEEE International Symposium on Information Theory, pp. 1105–1108 (2006).

  2. Beelen P.: The order bound for general algebraic geometric codes. Finite Fields Appl. 13(3), 665–680 (2007).

    Article  MathSciNet  Google Scholar 

  3. Beelen P., Datta M.: Generalized Hamming weights of affine Cartesian codes. Finite Fields Appl. 51, 130–145 (2018).

    Article  MathSciNet  Google Scholar 

  4. Carvalho C., Chara M., Quoos L.: On evaluation codes coming from a tower of function fields. J. Symbolic Comput. 89, 121–128 (2018).

    Article  MathSciNet  Google Scholar 

  5. Cox D.A., Little J., O’Shea D.: Ideals, Varieties, and Algorithms: An Introduction to Computational Algebraic Geometry and Commutative Algebra, vol. 10. Springer, New York (1997).

    Book  Google Scholar 

  6. Duursma I.M., Kirov R.: An extension of the order bound for AG codes. In: Applied Algebra, Algebraic Algorithms, and Error-Correcting Codes. Lecture Notes in Comput. Sci., vol. 5527, pp. 11–22. Springer, Berlin (2009).

  7. Duursma I.M., Kirov R., Park S.: Distance bounds for algebraic geometric codes. J. Pure Appl. Algebra 215(8), 1863–1878 (2011).

    Article  MathSciNet  Google Scholar 

  8. Duursma I.M., Park S.: Coset bounds for algebraic geometric codes. Finite Fields Appl. 16(1), 36–55 (2010).

    Article  MathSciNet  Google Scholar 

  9. Ezerman M.F.: Quantum error-control codes. arxiv:2009.05735 (2020).

  10. Ezerman M.F., Jitman S., Solé P.: Xing-Ling codes, duals of their subcodes, and good asymmetric quantum codes. Des. Codes Cryptogr. 75(1), 21–42 (2015).

    Article  MathSciNet  Google Scholar 

  11. Feng G.L., Rao T.R.N.: Decoding algebraic-geometric codes up to the designed minimum distance. IEEE Trans. Inf. Theory 39(1), 37–45 (1993).

    Article  MathSciNet  Google Scholar 

  12. Feng G.L., Rao T.R.N.: A simple approach for construction of algebraic-geometric codes from affine plane curves. IEEE Trans. Inf. Theory 40(4), 1003–1012 (1994).

    Article  MathSciNet  Google Scholar 

  13. Feng G.L., Rao T.R.N.: Improved geometric Goppa codes part I: basic theory. IEEE Trans. Inf. Theory 41(6), 1678–1693 (1995).

    Article  Google Scholar 

  14. Fitzgerald J., Lax R.F.: Decoding affine variety codes using Gröbner bases. Des. Codes Cryptogr. 13(2), 147–158 (1998).

    Article  MathSciNet  Google Scholar 

  15. García-Marco I., Márquez-Corbella I., Ruano D.: High dimensional affine codes whose square has a designed minimum distance. Des. Codes Cryptogr. 88(8), 1653–1672 (2020).

    Article  MathSciNet  Google Scholar 

  16. Geil O.: Evaluation codes from an affine variety code perspective. In: Advances in Algebraic Geometry Codes, Ser. Coding Theory Cryptol., vol. 5, pp. 153–180. World Sci. Publ., Hackensack (2008).

  17. Geil O., Martin S.: Further improvements on the Feng-Rao bound for dual codes. Finite Fields Appl. 30, 33–48 (2014).

    Article  MathSciNet  Google Scholar 

  18. Geil O., Martin S.: An improvement of the Feng-Rao bound for primary codes. Des. Codes Cryptogr. 76(1), 49–79 (2015).

    Article  MathSciNet  Google Scholar 

  19. Geil O., Matsumoto R., Ruano D.: Feng-Rao decoding of primary codes. Finite Fields Appl. 23, 35–52 (2013).

    Article  MathSciNet  Google Scholar 

  20. Geil O., Özbudak F.: On affine variety codes from the Klein quartic. Cryptogr. Commun. 11(2), 237–257 (2019).

    Article  MathSciNet  Google Scholar 

  21. Grassl M.: Bounds on the minimum distance of linear codes and quantum codes. http://www.codetables.de (2018). Accessed July 15 2021.

  22. Grassl M., Lu S., Zeng B.: Codes for simultaneous transmission of quantum and classical information. In: 2017 IEEE International Symposium on Information Theory (ISIT), pp. 1718–1722 (2017).

  23. Høholdt T.: On (or in) Dick Blahut’s’ footprint’. Codes, Curves and Signals, pp. 3–9 (1998).

  24. Høholdt T., van Lint J.H., Pellikaan R.: Algebraic geometry codes. In: Pless V.S., Huffman W.C. (eds.) Handbook of Coding Theory, vol. 1, pp. 871–961. Elsevier, Amsterdam (1998).

    Google Scholar 

  25. Ioffe L., Mézard M.: Asymmetric quantum error-correcting codes. Phys. Rev. A 75(3), 032345 (2007).

    Article  MathSciNet  Google Scholar 

  26. Kolluru M.S., Feng G.L., Rao T.R.N.: Construction of improved geometric Goppa codes om Klein curves and Klein-like curves. Appl. Algebra Eng. Commun. Comput. 10(6), 433–464 (2000).

    Article  Google Scholar 

  27. López H.H., Soprunov I., Villarreal R.H.: The dual of an evaluation code. Des. Codes Cryptogr. 89(7), 1367–1403 (2021).

    Article  MathSciNet  Google Scholar 

  28. Matsumoto R.: Two Gilbert-Varshamov-type existential bounds for asymmetric quantum error-correcting codes. Quantum Inf. Process. 16(12), 285 (2017).

    Article  MathSciNet  Google Scholar 

  29. Matsumoto R., Miura S.: On the Feng-Rao bound for the \({\cal{L}}\)-construction of algebraic geometry codes. IEICE Trans. Fundam. 5, 926–930 (2000) E83-A.

    Google Scholar 

  30. Miura S.: Linear codes on affine algebraic curves. Trans. IEICE 10, 1398–1421 (1998) J81-A.

    Google Scholar 

  31. Patanker N., Singh S.K.: Affine variety codes over a hyperelliptic curve. Probl. Inf. Transm. 57, 84–97 (2021).

    Article  Google Scholar 

  32. Pellikaan R.: On the efficient decoding of algebraic-geometric codes. In: Eurocode ’92 (Udine, 1992), CISM Courses and Lect., vol. 339, pp. 231–253. Springer, Vienna (1993).

  33. Salazar G., Dunn D., Graham S.B.: An improvement of the Feng-Rao bound on minimum distance. Finite Fields Appl. 12, 313–335 (2006).

    Article  MathSciNet  Google Scholar 

  34. Sarvepalli P.K., Klappenecker A., Rötteler M.: Asymmetric quantum codes: constructions, bounds and performance. In: Proc. R. Soc. Lond. Ser. A: Math. Phys. Eng. Sci., vol. 465, pp. 1645–1672. The Royal Society (2009).

Download references

Acknowledgements

The author is grateful to Diego Ruano and Ryutaroh Matsumoto for many fruitful discussions, also in connection with the present paper.

Author information

Authors and Affiliations

  1. Department of Mathematical Sciences, Aalborg University, Aalborg, Denmark

    Olav Geil

Authors
  1. Olav Geil
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Olav Geil.

Additional information

Communicated by A. Winterhof.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Geil, O. From primary to dual affine variety codes over the Klein quartic. Des. Codes Cryptogr. 90, 523–543 (2022). https://doi.org/10.1007/s10623-021-00990-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10623-021-00990-5

Keywords

Mathematics Subject Classification

Search

Navigation