Greedy weights for matroids

Abstract

We introduce greedy weights of matroids, inspired by those for linear codes. We show that a Wei duality holds for two of these types of greedy weights for matroids. Moreover we show that in the cases where the matroids involved are associated to linear codes, our definitions coincide with those for codes. Thus our Wei duality is a generalization of that for linear codes given by Schaathun. In the last part of the paper we show how some important chains of cycles of the matroids appearing, correspond to chains of component maps of minimal resolutions of the independence complex of the corresponding matroids. We also relate properties of these resolutions to chainedness and greedy weights of the matroids, and in many cases codes, that appear.

Introduction

For a linear code C over a finite field $\mathbb {F}_q$ an important way to characterize the code is to decribe its parameters, the word length n, the dimension k, and the minimum distance d. A refinement of the minimum distance is the ordered set of the generalized Hammimg weights $d_1,\ldots ,d_k,$ where $d_i$ is the smallest support of any i-dimensional linear subcode of C, for $i=1,\ldots ,k$. In particular $d_1=d$. In the 1990’s (and early 2000’s) several authors (see e.g. [4,5,6,7, 18,19,20]) became interested not only in the individual subcodes of each dimension that where optimal with respect to (small) support size, but also in chains of codes that where somehow optimal, in a similar way. This gave rise to various definitions of greedy weights, which we will recall in Sect. 2.1. These weights are similar to, but in general different from, the generalized Hamming weights $d_i$. The topic has attracted new interest in recent years [1, 13].

In [9] we described how the $d_i$ are determined by certain properties of the matroid coming from any parity check matrix of the linear code. In the present paper we will describe how also the various greedy weights are determined by the matroids associated to the code. Since this description can be done for any finite matroid , we will define and describe greedy weights for finite matroids in general, and show that they coincide with those of linear codes when the matroids come from such codes. We will show a form of Wei duality relating certain weights of a matroid and its dual, inspired by a corresponding result for linear codes [19] or for (demi-)matroids [2, 12].

The spirit of the paper is the following: there is a poset of cycles of the matroid coming from any parity check matrix of the code, where a cycle is an inclusion minimal set among those subsets of $E=\{1,\ldots ,n\}$ having a fixed nullity for the rank function in question. This is dual to (the upside down version of) the poset of flats of the matroid coming from any generator matrix of the code. We will show that the greedy weights correspond to optimal ways to traverse the nodes of this poset through maximal chains of it. We define a lexicographical and a rev-lexicographical order on these chains in order to make it precise in what sense they are optimal.

In the last part we relate our results to a more concrete way to traverse maximal chains via non-zero component maps in a minimal resolution of a certain Stanley–Reisner ring, where the components in each fixed step corresponds to the nodes of a corresponding fixed rank of the poset of cycles.

This paper is organized as follows. In Sect. 2 we will give some necessary definitions relating to codes and matroids. In Sect. 3 we will describe the greedy weights for matroids, relate to those of codes, and show our form of Wei duality, which is inspired by the corresponding Wei duality for codes, proven in [19]. In Sect. 4 we discuss the connection between resolutions of the Stanley–Reisner ring associated to the matroid or the code, and the greedy weights. We also discuss the notion of chained codes and chained matroids.

The main results are Theorems 2, 3 and 4.

Definitions and notation

Generalized Hamming weights and greedy weights of codes

Definition 1

Let C be a [n, k] linear code over $\mathbb {F}_q$. Let $\varvec{c} = (c_1,\ldots ,c_n) \in C$. The Support of $\varvec{c}$ is the set

$$\begin{aligned} \mathrm {Supp}(\varvec{c}) = \{ i \in \{1,\ldots ,n\}: c_i \ne 0\}. \end{aligned}$$

Its weight is

$$\begin{aligned} wt(\varvec{c}) = |\mathrm {Supp}(\varvec{c})|. \end{aligned}$$

Similarly, if $T \subset C$, then its support and weight are

$$\begin{aligned} \mathrm {Supp}(T) = \bigcup _{\varvec{c} \in T} \mathrm {Supp}(\varvec{c}) \text { and } wt(T) = |\mathrm {Supp}(T)|. \end{aligned}$$

In [3] and [1] one describes and treats greedy weights of linear codes C over finite fields. First we recall the definitions of the generalized Hamming weights introduced by Wei [22]:

Definition 2

Let C be a [n, k]-linear code. For $1 \leqslant r \leqslant k$, the rth generalized Hamming weight is

$$\begin{aligned} d_{r}= \min \{wt(D) | D\text { is a subcode of }C\text { with }\dim D=r\}. \end{aligned}$$

A subcode $D \subset C$ computes $d_r$ if it is of dimension r and weight $d_r$.

Then, following the terminology of [18] or [20], we have the (bottom-up) greedy weights of a code:

Definition 3

Let C be a [n, k]-linear code. A (bottom-up) greedy 1-subcode is a subcode of dimension 1 of minimal weight. For $r\geqslant 2$, a (bottom-up) greedy r-subcode is a subcode of dimension r containing a (bottom-up) greedy $(r-1)$-subcode, and such that no other such subcode has lower weight.

Definition 4

Let C be a [n, k]-linear code. For $1 \leqslant r \leqslant k$, the rth (bottom-up) greedy weight $e_r$ of C is the weight of any (bottom-up) greedy r-subcode.

Remark 1

We have $e_1=d_1$.

Also introduced by Schaathun [18, Definition 6] are the top down greedy weights:

Definition 5

Let C be a [n, k]-linear code. A top-down greedy k-subcode is C itself. For $r\leqslant k-1$, a top-down greedy r-subcode is a subcode of dimension r contained in a top-down greedy $(r+1)$-subcode, and such that no other such subcode has lower weight.

Definition 6

Let C be a [n, k]-linear code. For $1 \leqslant r \leqslant k$, the rth top-down greedy weight $\tilde{e}_r$ of C is the weight of any top-down greedy r-subcode.

Remark 2

We have $\tilde{e}_k=d_k$ and $\tilde{e}_{k-1}=d_{k-1}$.

Remark 3

Let $\mathcal {F}$ be the set of towers of subcodes $D_1\subset \cdots \subset D_k$ of C satisfying $\dim D_i=i$. Alternative definitions for the bottom-up and top-down greedy weights would be

$$\begin{aligned} (e_1,\ldots ,e_k) = \min _{\mathrm {lex}}\left\{ (wt(D_1),\ldots ,wt(D_k)),\ D_1\subset \cdots \subset D_k \in \mathcal {F}\right\} \end{aligned}$$

and

$$\begin{aligned} (\tilde{e}_1,\ldots ,\tilde{e}_k) = \min _{\mathrm {revlex}}\left\{ (wt(D_1),\ldots ,wt(D_k)),\ D_1\subset \cdots \subset D_k \in \mathcal {F}\right\} , \end{aligned}$$

where lex and revlex are the lexicographic and reverse lexicographic orders respectively.

There is also another definition, used e.g by [1], essentially introduced in [7]:

Definition 7

Let C be a [n, k]-linear code. A CEZ greedy 1-subcode is a subcode of dimension 1 of minimal weight. For $r\geqslant 2$, a CEZ greedy r-subcode is a subcode of dimension r containing a subcode that computes $d_{r-1}$, and such that no other such subcode has lower weight.

Definition 8

Let C be a [n, k]-linear code. For $1 \leqslant r \leqslant k$, the rth CEZ greedy weight $g_r$ of C is the weight of any CEZ greedy r-subcode.

Remark 4

We have $g_1=e_1=d_1$ and $g_2=e_2$

For more interesting material on this topic, see [4,5,6, 13, 18].

Matroids

A matroid is a combinatorial object that capture the essence of independence. Codewords of linear codes being dependence relations between the column vectors of any parity check matrix of the code, it is natural to look at the matroid associated to a linear code. In [9], we describe how important characteristics of the code can be given a matroidal interpretation. It turns out that matroid theory has important applications in, among other, graph theory, network theory, combinatorial optimization, topology, ...

There are many equivalent definitions of a matroid. We refer to [17] for a deeper study of the theory of matroids.

Definition 9

A matroid is a pair $M=(E,r)$ where E is a finite set and $r: 2^E \rightarrow \mathbb {N}$ is a function, called the rank function, satisfying

($R_1$):

If $X \subset E$, then

$$\begin{aligned}0 \leqslant r(X) \leqslant |X|, \end{aligned}$$

($R_2$):

If $X \subset Y \subset E$ then

$$\begin{aligned} r(X) \leqslant r(Y), \end{aligned}$$

($R_3$):

If X, Y are subsets of E, then

$$\begin{aligned} r(X \cap Y) + r(X \cup Y) \leqslant r(X) + r(Y). \end{aligned}$$

The rank of the matroid is $r(M)=r(E)$.

It is a well known fact the rank function of a matroid is unit rank increase, that is, if $X \subset E$ and $x \in E$, then

$$\begin{aligned} r(X) \leqslant r(X \cup \{x\}) \leqslant r(X)+1. \end{aligned}$$

Definition 10

The nullity function of the matroid (E, r) is the function defined on $2^E$ by: for $X \subset E$,

$$\begin{aligned} n(X)=|X| - r(X).\end{aligned}$$

The nullity function of a matroid is also unit rank increase. Moreover, it satisfies $(R_1)$, $(R_2)$ as well as

($N_3$):

If X, Y are subsets of E, then $n(X \cap Y) + n(X \cup Y) \geqslant n(X) + n(Y)$

for X, Y subsets of E.

Definition 11

Let $M=(E,r)$ be a matroid. Then its dual matroid is the matroid $\overline{M}=(E,\overline{r})$ where $\overline{r}$ is defined by

$$\begin{aligned} \overline{r}(X) = |X| + r(E \backslash X) - r(E) \end{aligned}$$

for $X \subset E$.

Some subsets of the ground set of a matroid will be of special interest in this paper:

Definition 12

Let (E, r) be a matroid. A subset $X \subset E$ is dependent if

$$\begin{aligned} n(X)>0 \end{aligned}$$

and independent if

$$\begin{aligned} n(X)=0. \end{aligned}$$

A circuit is a inclusion minimal dependent set. We denote by $\mathcal {I}$ and $\mathcal {C}$ the sets of independent sets and circuits respectively.

For $1 \leqslant i \leqslant |E|-r(M)$ will denote by $\mathcal {N}_i$ the set

$$\begin{aligned} \mathcal {N}_i = \{X \subset E,\ n(X)=i\} \end{aligned}$$

and by $N_i$ the inclusion minimal elements of $\mathcal {N}_i$. It is clear that

$$\begin{aligned} \mathcal {C} = N_1. \end{aligned}$$

A cycle is an element of $N_i$ for some i. Cycles can also be described as unions of circuits, and the nullity of the cycle is equal to the maximal number of non-redundant circuits in the cycle [9].

If C is a [n, k]-linear code given by a $(n-k) \times n$ parity check matrix H, then we can associate to it a matroid $M_C=(E,r)$, where $E=\{1,\ldots ,n\}$ and if $X \subset E$, then

$$\begin{aligned} r(X)={{\,\mathrm{rk}\,}}(H_X), \end{aligned}$$

where $H_X$ is the column submatrix of H indexed by X. It can be shown that this matroid is independent of the choice of the parity check matrix of the code, and we may thus call it the matroid of C.

Resolutions

If $M=(E,r)$ is a matroid, then $(E,\mathcal {I})$ is naturally a simplicial complex (that is, $\mathcal {I}\ne \emptyset$ and is closed under taking subsets). Let $\mathbb {K}$ be a field. We can associate to M a monomial ideal $I_M$ in $S=\mathbb {K}[\{X_e\}_{e \in E}]$ defined by

$$\begin{aligned} I_M =< \varvec{X}^\sigma : \sigma \in \mathcal {C}> \end{aligned}$$

where $\varvec{X}^\sigma$ is the monomial product of all $X_e$ for $e \in \sigma$. This ideal is called the Stanley–Reisner ideal of M and the quotient $S_M=S/I_M$ the Stanley–Reisner ring associated to M. We refer to [8] for the study of such objects. As described in [9] the Stanley–Reisner ring has minimal $\mathbb {N}$ and $\mathbb {N}^n$-graded free resolutions

$$\begin{aligned} 0 \leftarrow S_M \leftarrow S \leftarrow \bigoplus _{j \in \mathbb {N}}S(-j)^{\beta _{1,j}} \leftarrow \cdots \leftarrow \bigoplus _{j \in \mathbb {N}}S(-j)^{\beta _{|E|-r(M),j}} \leftarrow 0 \end{aligned}$$

and

$$\begin{aligned} 0 \leftarrow S_M \leftarrow S \leftarrow \bigoplus _{\alpha \in \mathbb {N}^n}S(-\alpha )^{\beta _{1,\alpha }} \leftarrow \cdots \leftarrow \bigoplus _{\alpha \in \mathbb {N}^n}S(-\alpha )^{\beta _{|E|-r(M),\alpha }} \leftarrow 0.\end{aligned}$$

In particular the numbers $\beta _{i,j}$ and $\beta _{i,\alpha }$ are independent of the minimal free resolution, (and for a matroid also of the field $\mathbb {K}$) and are called respectively the $\mathbb {N}$-graded and $\mathbb {N}^n$-graded Betti numbers of the matroid. Note also that if $\alpha \not \in \{0,1\}^n$, then $\beta _{i,\sigma }=0$ [15, Corollary 1.40]. We have

$$\begin{aligned} \beta _{i,j} = \sum _{wt(\alpha )=j}\beta _{i,\alpha }. \end{aligned}$$

We also note that $\beta _{0,0}=1$.

We will also frequently use ([9, Theorem 1], first part):

Theorem 1

Let C be a [n, k]-code over $\mathbb {F}_q$. The $\mathbb {N}$-graded Betti numbers of the matroid $M_C$ satisfy: $\beta _{i,j} \ne 0$ if and only if there exists a member in $N_i$ of cardinality j. In particular, $\beta _{i,X} \ne 0$ if and only $X \in N_i$. Furthermore

$$\begin{aligned} d_i = \min \{j: \beta _{i,j} \ne 0\}. \end{aligned}$$

Remark 5

The fact that $\beta _{i,X} \ne 0$ if and only $X \in N_i$ is a consequence of the considerations on [21, p. 59], where one also relates these Betti numbers to Möbius numbers of related lattices of cycles.

Greedy weights for matroids

We will now give definitions for greedy weights for matroids, and later show that greedy weights for linear codes and their associated matroids coincide. First, recall the definition for generalized Hamming weights for matroids, given in [12]:

Definition 13

Let M be a matroid of rank $n-k$ on a set of cardinality n. For $1 \leqslant r \leqslant n-k,$

$$\begin{aligned} d_r= \min \{|\sigma |:\ \sigma \in \mathcal {N}_r\} = \min \{|\sigma |:\ \sigma \in N_r\}. \end{aligned}$$

Definition 14

Let M be a matroid on n elements of rank $n-k$. Let $\Sigma$ be the set

$$\begin{aligned} \Sigma =\left\{ (\sigma _1,\ldots ,\sigma _k) \in \mathcal {N}_1\times \cdots \times \mathcal {N}_k\vert \ \sigma _1 \subsetneq \cdots \subsetneq \sigma _k\right\} . \end{aligned}$$

Let $\overline{\Sigma }$ be the set

$$\begin{aligned} \overline{\Sigma } = \left\{ e(S)=(|\sigma _1|,\ldots ,|\sigma _k|):\ S=(\sigma _1,\ldots ,\sigma _k) \in \Sigma \right\} . \end{aligned}$$

Then the (bottom-up) greedy weights $(e_1,\ldots ,e_k)$ of M are the

$$\begin{aligned} (e_1,\ldots ,e_k) = \min _{\mathrm {lex}} \overline{\Sigma } \end{aligned}$$

while the top-down greedy weights $(\tilde{e}_1,\ldots ,\tilde{e}_k)$ of M are

$$\begin{aligned} (\tilde{e}_1,\ldots ,\tilde{e}_k) = \min _{\mathrm {revlex}} \overline{\Sigma }. \end{aligned}$$

If $S=(\sigma _1,\ldots ,\sigma _k) \in \mathcal {N}_1\times \cdots \times \mathcal {N}_k$ is such that $e(S)=(e_1,\ldots ,e_k)$ (resp. $(\tilde{e}_1,\ldots ,\tilde{e}_k)$), we say that $\sigma _i$ computes $e_i$ (resp. $\tilde{e}_i$).

Definition 15

Let M be a matroid of rank $n-k$ on a set of cardinality n, and let $(d_1,\ldots ,d_k)$ be its generalized Hamming weights. The CEZ greedy weights $(g_1,\ldots ,g_k)$ are defined as follows:

$$\begin{aligned} g_1=d_1 \end{aligned}$$

and for $2\leqslant r \leqslant k$,

$$\begin{aligned} g_r = \min \{|\sigma |:\ \sigma \in \mathcal {N}_r \text { and } \exists \tau \in \mathcal {N}_{r-1} \text { such that } \tau \subset \sigma \text { and }|\tau | = d_{r-1}\}. \end{aligned}$$

We say that $\sigma \in \mathcal {N}_i$ computes $g_i$ if it satisfies the conditions in the definition.

Example 1

Let C be the [8, 4]-linear code over $\mathbb {F}_3$ defined by the generator matrix

$$\begin{aligned} G=\begin{bmatrix} 1&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 2&{}\quad 0&{}\quad 1 \end{bmatrix}. \end{aligned}$$

Its weights are

$$\begin{aligned} (d_1,d_2,d_3,d_4)= & {} (2,4,6,8),\\ (e_1,e_2,e_3,e_4)= & {} (g_1,g_2,g_3,g_4) = (2,4,7,8) \end{aligned}$$

and

$$\begin{aligned} (\tilde{e}_1,\tilde{e}_2,\tilde{e}_3,\tilde{e}_4)=(3,4,6,8). \end{aligned}$$

As a consequence of the unique rank increase of the nullity function, both the bottom up and the top down greedy weights are strictly increasing sequences. The CEZ greedy weights $g_i$ are not necessary monotonous, as the following example shows.

Example 2

Let M on $E=\{1,\ldots ,23\}$ whose circuits are the following: all the subsets of $\{13,\ldots ,23\}$ of cardinality 9 together with $\{1,\ldots ,8\}$, $\{5,\ldots ,12\}$ and $\{1,2,3,4,9,10,11,12\}$. This is a matroid of rank 18. Then,

$$\begin{aligned} (d_1,d_2,d_3,d_4,d_5)= & {} (8,10,11,19,23),\\ (e_1,e_2,e_3,e_4,e_5)= & {} (8,12,21,12,23),\\ (\tilde{e}_1,\tilde{e}_2,\tilde{e}_3,\tilde{e}_4,\tilde{e}_5)= & {} (10,11,12,19,23),\\ (g_1,g_2,g_3,g_4,g_5)= & {} (8,12,11,19,23). \end{aligned}$$

Example 3

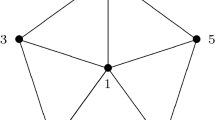
Consider the following graph:

Its associated matroid, that is, the matroid whose circuits correspond to cycles of the graph, is a matroid on the set of its 25 edges, and rank 21. The generalized Hamming weights of the matroid are

$$\begin{aligned} (d_1, d_2, d_3, d_4)=(6,12,18,25). \end{aligned}$$

The greedy weights are

$$\begin{aligned} (e_1,e_2,e_3,e_4)= & {} (6,13,21,25),\\ (\tilde{e}_1,\tilde{e}_2,\tilde{e}_3,\tilde{e}_4)= & {} (8,12,18,25),\\ (g_1,g_2,g_3,g_4)= & {} (6,13,18,25). \end{aligned}$$

The weight $d_2$ corresponds to the minimum support of the union of two different cycles (the right part of the graph), while the weight $e_2$ corresponds to the minimum cardinality of the support of the union of two different cycles, where one of the cycles is a cycle of minimal length (the left part of the graph, since the only cycle of minimal length is the hexagon on the left part). See also [14] for the computation of generalized Hamming weights of (signed) graphs.

In Definitions 14 and  15, we could actually have asked the subsets to be in $N_i$, not just $\mathcal {N}_i$, as the following proposition shows:

Proposition 1

Let M be a matroid of rank $n-k$ on a set of cardinality n. Let $\Sigma '$ be the set

$$\begin{aligned} \Sigma ' =\left\{ (\sigma _1,\ldots ,\sigma _k):\ \sigma _1 \subsetneq \cdots \subsetneq \sigma _k \text { and }\sigma _i \in N_i\text {, }\ \forall i\right\} . \end{aligned}$$

Then we have the following:

$$\begin{aligned} (e_1,\ldots ,e_k)=\min _{\mathrm {lex}}\{e(S):\ S \in \Sigma '\},\\(\tilde{e}_1,\ldots ,\tilde{e}_k)=\min _{\mathrm {revlex}}\{e(S):\ S \in \Sigma '\}, \end{aligned}$$

and for all $2\leqslant i \leqslant k$,

$$\begin{aligned} g_i=\min \{|\sigma |:\ \sigma \in N_i \text { and } \exists \tau \in N_{i-1} \text { such that } \tau \subset \sigma \text { and }|\tau | = d_{i-1}\}. \end{aligned}$$

Proof

The first and third assertions rely on the same observation. We will thus only treat the first assertion. It is clear that

$$\begin{aligned} \min _{\mathrm {lex}}\{e(S):\ S \in \Sigma '\} \geqslant _{\mathrm {lex}} (e_1,\ldots ,e_k). \end{aligned}$$

Now, let $S=(\sigma _1,\ldots ,\sigma _k) \in \Sigma$ such that

$$\begin{aligned} e(S)=(e_1,\ldots ,e_k)=\min _{\mathrm {lex}}\{e(S):\ S \in \Sigma \}. \end{aligned}$$

We will show that $\sigma _i \in N_i$ for all i. If not, let i be the smallest index for which this is not true. By definition of $N_1$ and the lexicographic order, $i >1$. Since $\sigma _i \not \in N_i$, this means that there exists $\tau \subsetneq \sigma _i$ such that $n(\tau )=i$. Obviously, $\sigma _{i-1} \not \subset \tau$ otherwise, replacing $\sigma _i$ by $\tau$ in the sequence S, we would get a chain of sets that would contradict the minimality of e(S) for the lex ordering. Thus, we can find $x \in \sigma _{i-1} - \tau$. Without loss of generality, we can suppose that $\tau =\sigma _i-\{x\}$. Consider then $\rho =\sigma _{i-1}-\{x\}$. By minimality of $\sigma _{i-1}$ in the set of subsets with nullity $i-1$, and by the unique rank increase property of n, $n(\rho ) = i-2$. Then, by ($N_3$):

$$\begin{aligned} 2i-2= n(\rho ) + n(\sigma _i) = n(\sigma _{i-1}\cap \tau ) + n(\sigma _{i-1} \cup \tau ) \geqslant n(\sigma _{i-1}) + n(\tau ) = 2i-1, \end{aligned}$$

which is absurd. Thus, all elements in S are in $N_i$, and the first assertion is proved.

The second assertion is easier to prove since we don’t have any bottom constraints. Again, it is clear that

$$\begin{aligned} \min _{\mathrm {revlex}}\{e(S):\ S \in \Sigma '\} \geqslant _{\mathrm {lex}} (\tilde{e}_1,\ldots ,\tilde{e}_k). \end{aligned}$$

For the contrary, let $S=(\sigma _1,\ldots ,\sigma _k) \in \Sigma$ such that

$$\begin{aligned} e(S)=(\tilde{e}_1,\ldots ,\tilde{e}_k)=\min _{\mathrm {revlex}}\{e(S):\ S \in \Sigma \}. \end{aligned}$$

Assume that there exists an index i such that $\sigma _i \not \in N_i$. Let $\tau _i \subsetneq \sigma _i$ such that $\tau _i \in N_i$, and take recursively for $j<i$ any $\tau _j \subset \tau _{j+1}$ such that $n(\tau _j)=j$. This can always be done by the unique rank increase property of n. Then the sequence $S'=(\tau _1,\ldots ,\tau _i,\sigma _{i+1},\ldots ,\sigma _k) \in \Sigma$, and by construction,

$$\begin{aligned} e(S') <_{\mathrm {revlex}} e(S), \end{aligned}$$

which is absurd. This in turn shows that

$$\begin{aligned} \min _{\mathrm {revlex}}\{e(S):\ S \in \Sigma '\} \leqslant _{\mathrm {lex}} (\tilde{e}_1,\ldots ,\tilde{e}_k). \end{aligned}$$

$\square$

Remark 6

The set $\Sigma '$ appearing in Proposition 1 is the set of maximal chains in the poset of cycles for the matroid. Taking complements, this is the poset of flats of the dual matroid. If $d^{\perp } \ge 3,$ then this poset is a geometric lattice with atoms of cardinality 1. Then the cardinalities $c_f$ of the flats, and hence all the cardinalities $n-c_f$ of the cycles $\sigma$ of the matroid, can be given a purely lattice-theoretical interpretation in terms of atoms. Hence it is possible to reformulate Proposition 1 by lattice-theoretical invariants.

Corollary 1

Let M be a matroid of rank $n-k$ on a set of cardinality n. For $1 \leqslant i \leqslant k$,

$$\begin{aligned} X \subset E \text { is a (top-down, bottom-up, CEZ) }i\text {-greedy subcode} \Rightarrow \beta _{i,X} \ne 0 \end{aligned}$$

and

$$\begin{aligned} g_i, e_i,\tilde{e}_i \in \{j \vert \beta _{i,j} \ne 0\}. \end{aligned}$$

Proof

In the proof above, we showed that any subset that computes a greedy-weight is a cycle. This is then a direct consequence of Theorem 1. $\square$

Wei duality of greedy weights

If M is a matroid, then it is proved in [12] that the weight hierarchy of the matroid and its dual satisfy Wei duality, that is

$$\begin{aligned} \{d_1,\ldots ,d_k\} \cup \{n+1-\overline{d}_1,\ldots ,n+1-\overline{d}_{n-k}\} = \{1,\ldots ,n\}, \end{aligned}$$

where $\overline{d}_i$ denotes the ith generalized Hamming weight of $\overline{M}$. This result is a generalization of duality for linear codes proved by Wei [22]. In his doctoral thesis [19], Schaathun proves a Wei duality for greedy weights for linear codes, namely that

$$\begin{aligned} \{e_1,\ldots ,e_k\} \cup \{n+1-\overline{\tilde{e}}_1,\ldots ,n+1-\overline{\tilde{e}}_{n-k}\} = \{1,\ldots ,n\}. \end{aligned}$$

In this section, we will prove that his result extends to matroids. As opposed to [12], our proof is constructive, in the sense that we exhibit an element in $\Sigma '(\overline{M})$ that computes the greedy weights of the dual matroid. Before doing so, if $S=(\sigma _1,\ldots ,\sigma _k) \in \Sigma$, we define $\delta (S)$ in the following (not unique) way: consider a maximal chain

$$\begin{aligned}\emptyset \subsetneq \rho _1 \subsetneq \cdots \subsetneq \rho _n=E\end{aligned}$$

that contains all the $E-\sigma _i$ for $1\leqslant i\leqslant k$. Obviously, we have $|\rho _i|=i$ for every $1\leqslant i\leqslant n$. Then $\delta (S)$ is the chain $\tau _1\subsetneq \cdots \subsetneq \tau _{n-k}$ obtained by removing all the subsets of cardinality $n-|\sigma _i|+1$. Even if this is not uniquely defined, the set $\overline{\delta }(S) = \{|\tau _1|,\ldots ,|\tau _{n-k}|\}$ is, since we have

$$\begin{aligned} \overline{\delta }(S) = \{1,\ldots ,|E|\}-\{n+1-|\sigma _i|: \ 1\leqslant i \leqslant k\}. \end{aligned}$$

In particular, we have, with a slight abuse of notation,

$$\begin{aligned} \overline{\delta }\delta S = e(S)=\{|\sigma _1|,\ldots ,|\sigma _k|\}. \end{aligned}$$

Denote by $\overline{n}$ the nullity function of $\overline{M}$.

Lemma 1

Let $S=(\sigma _1,\ldots ,\sigma _k)$ be a tower that computes the bottom up greedy weights of M, and let $\delta (S)=(\tau _1\ldots ,\tau _{n-k})$. Then for all $1\leqslant i \leqslant n-k$,

$$\begin{aligned} \overline{n}(\tau _i)=i. \end{aligned}$$

Proof

Using the notation from the definition of $\delta (S)$, we have for every i the chain

$$\begin{aligned} E- \sigma _{i+1}= \rho _j \subsetneq \cdots \subsetneq \rho _{j+s} = E-\sigma _i \end{aligned}$$

where $j= n-|\sigma _{i+1}|$ and $s=|\sigma _{i+1}|-|\sigma _i|$. From the duality formula for the rank functions and nullity functions, we get that, since $n(\sigma _t)=t$,

$$\begin{aligned} \overline{n}(E-\sigma _{i+1}) = k+i+1-|\sigma _{i+1}| \end{aligned}$$

while

$$\begin{aligned} \overline{n}(E-\sigma _i)=k+i-|\sigma _i|. \end{aligned}$$

Since $\overline{n}$ is unit rank increase, this means that all $\overline{n}(\rho _{j+t})$ are distinct, except for 2 of them, and that they span the set $\{k+i+1-|\sigma _{i+1}|,\ldots ,k+i-|\sigma _i|\}.$ We show now that $\overline{n}(\rho _j)=\overline{n}(\rho _{j+1})$. Since both set differ by just 1 element, we have either $\overline{n}(\rho _j)=\overline{n}(\rho _{j+1})$ or $\overline{n}(\rho _j)=\overline{n}(\rho _{j+1})-1$. Suppose the latter occurs. Then,

$$\begin{aligned} n(\sigma _{i+1})=n(E-\rho _j) = n-k-|\rho _j|+\overline{n}(\rho _j) = n(E-\rho _{j+1}). \end{aligned}$$

Since

$$\begin{aligned} \sigma _i \subsetneq E-\rho _{j+1} \subsetneq E-\rho _j = \sigma _{i+1} \end{aligned}$$

(the first strict inclusion coming from the fact that $n(\sigma _i)=n(\sigma _{i+1})-1 = n(E-\rho _{j+1})-1$), the tower

$$\begin{aligned} \sigma _1\subsetneq \cdots \subsetneq \sigma _i \subsetneq E-\rho _{j+1} \subsetneq \sigma _{i+2} \cdots \subsetneq \sigma _k \in \Sigma \end{aligned}$$

and the k-tuple formed by the cardinalities of the elements of the tower is strictly lower for the lex order than $(e_1,\ldots ,e_k)$ which is absurd. $\square$

Lemma 2

Let $S,S' \in \Sigma$. Then

$$\begin{aligned} e(S)<_{\mathrm {lex}} e(S') \Leftrightarrow e(\delta (S))<_{\mathrm {revlex}} e(\delta (S')). \end{aligned}$$

Proof

Write $S=(\sigma _1,\ldots ,\sigma _k)$, $S'=(\sigma '_1,\ldots ,\sigma '_k)$, $\delta (S)=(\tau _1,\ldots ,\tau _{n-k})$ and $\delta (S')=(\tau '_1,\ldots ,\tau '_{n-k})$. By hypothesis, there exists an $1\leqslant i \leqslant k$ such that for all $1\leqslant j <i$, $|\sigma _j|=|\sigma '_j|$ while $|\sigma _i|<|\sigma '_i|$. In our definition of $\delta$ above (and we keep the notation, using $\rho _s$ and $\rho '_s$ for S and $S'$ respectively) this means that for $l\geqslant n-|\sigma _i|-k+i+1$,

$$\begin{aligned} |\tau _l|=|\tau '_l| \end{aligned}$$

while

$$\begin{aligned} \left| \tau _{n-|\sigma _i|-k+i}\right| <\left| \tau '_{n-|\sigma _i|-k+i}\right| =n-|\sigma _i|+1, \end{aligned}$$

that is

$$\begin{aligned} e(\delta (S))<_{\mathrm {revlex}} e(\delta (S')) \end{aligned}$$

The other way is done in a similar way, noticing that $e\delta \delta (S)=\overline{\delta }\delta (S) = e(S)$. $\square$

We then obtain the following analogue of [19, Theorem 10.2], where one showed Wei duality for greedy weights of linear codes:

Theorem 2

Let M be a matroid of rank k on a ground set E of cardinality n. Then

$$\begin{aligned} \{e_1,\ldots ,e_k\} \cup \{n+1-\overline{\tilde{e}}_1,\ldots ,n+1-\overline{\tilde{e}}_{n-k}\} = \{1,\ldots ,n\}. \end{aligned}$$

Proof

Let $S\in \Sigma$ such that $e(S)=(e_1,\ldots ,e_k)$. Consider $T=\delta (S)$. By Lemma 1, we know that $T \in \Sigma (\overline{M})$, and thus

$$\begin{aligned} e(T) \geqslant _{\mathrm {revlex}} (\overline{\tilde{e}}_1,\ldots ,\overline{\tilde{e}}_{n-k}). \end{aligned}$$

If this is not an equality, let $T' \in \Sigma (\overline{M})$ such that $e(T')=(\overline{\tilde{e}}_1,\ldots ,\overline{\tilde{e}}_{n-k})$. Then by Lemma 2 and the fact that $e\delta \delta (T)=e(T)$, we get that

$$\begin{aligned} e(S) >_{\mathrm {lex}} e(\delta (T)) \geqslant _{\mathrm {lex}} (e_1,\ldots ,e_k)=e(S) \end{aligned}$$

which is absurd. $\square$

Greedy weights of codes and matroids

In for example [1, 3,4,5,6,7, 18,19,20] one describes and treats greedy weights of linear codes C over finite fields in various ways. In this part, we will show that the greedy weights for codes and their associated matroids coincide. We start with some lemmas:

Lemma 3

Let C be a [n, k]-code, M its associated matroid and $X \subset \{1,\ldots ,n\}$. Consider the subcode

$$\begin{aligned} C(X) = \left\{ w \in C\vert \ \mathrm {Supp}(w) \subset X\right\} \subset C. \end{aligned}$$

Then

$$\begin{aligned} \dim C(X)=n(X)=n(\mathrm {Supp}(C(X))). \end{aligned}$$

Proof

The first equality is an easy consequence from the fact that $C(X) = \ker G_{E-X}$, and a rewriting of the rank-nullity theorem using the relation between the rank of the matroid and its dual. Moreover, the dimension of the relations between the columns of H indexed $\mathrm {Supp}(C(X))$ is n(X), that is,

$$\begin{aligned} n(\mathrm {Supp}(C(X))) = n(X). \end{aligned}$$

$\square$

Theorem 3

The greedy weights of a [n, k]-linear code C and those of its associated matroid M coincide.

Proof

Let first $S=\sigma _1\subset \cdots \subset \sigma _k \in \Sigma$ be such that $e(S)=(e_1(M),\ldots ,e_k(M))$, and let $D_i=C(\sigma _i)$. Then $\dim D_i= n(\sigma _i)=i$ and $D_1 \subset \cdots \subset D_k$. We always have $\mathrm {Supp}(D_i) \subset \sigma _i$, which shows that

$$\begin{aligned} (e_1(C), \ldots ,e_k(C)) \leqslant _{\mathrm {lex}} (e_1(M),\ldots ,e_k(M)). \end{aligned}$$

For the converse, let $D_1\subset \cdots \subset D_k$ be subcodes of C with $\dim D_i=i$ and $wt(D_i) = e_i(C)$. Let $\sigma _i=\mathrm {Supp}(D_i)$. Of course

$$\begin{aligned} \sigma _1\subset \cdots \subset \sigma _k, \end{aligned}$$

and since $D_i \subset C(\sigma _i)$, we always have

$$\begin{aligned} n(\sigma _i) = \dim C(\sigma _i) \geqslant \dim D_i=i. \end{aligned}$$

We claim that there is equality. If not, let i be minimal such that $n(\sigma _i)>i$. Then, there exists $\tau$ with $n(\tau )=i$ such that $\sigma _{i-1} \subsetneq \tau \subsetneq \sigma _i$ (take $\sigma _0=\emptyset$ in the case $i=1$), and let $D'_i=C(\tau )$. Clearly

$$\begin{aligned} D_1\subset \cdots D_{i-1} \subset D_i' \end{aligned}$$

and $\dim D'_i = n(\tau )=i$. This would give rise to a tower of subcodes

$$\begin{aligned} D_1\subset \cdots D_{i-1} \subset D_i'\subset \cdots \subset D'_k \end{aligned}$$

with $\dim D_j' =j$ for $i \leqslant j\leqslant k$ that would contradict the minimality of $(e_1(C),\ldots ,e_k(C))$ for the lexicographic order. This shows that

$$\begin{aligned} (e_1(C), \ldots ,e_k(C)) \geqslant _{\mathrm {lex}} (e_1(M),\ldots ,e_k(M)). \end{aligned}$$

The proofs for top-down and CEZ greedy weights are done in a similar way. $\square$

Theorem 3 is a generalization of Wei duality for linear codes as presented in [19]. From [17, Theorem 2.2.8], the matroid associated to the dual of linear code is precisely the dual of the matroid of the linear code in question

Greedy weights and resolutions of Stanley–Reisner rings

Let M be a matroid of rank $n-k$ over a finite set E of cardinality n (for example the matroid associated to a [n, k]-linear code). As seen in Corollary 1, the sets that compute the different greedy weights are to be found in the sets that have non-zero Betti numbers. Together with the main result from [9], this suggests that all information about various kinds of greedy weights might be encoded in minimal free resolutions of the associated Stanley–Reisner ring. This is what we will look into in the first part of this section. In the second part, we will look into the concept of chained codes and matroids.

Greedy weights from strands

In the rest of this section, if M is a matroid on the finite set E of cardinality n, then S denotes the polynomial ring $\mathbb {K}[e,\ e \in E]$. This ring is naturally $\mathbb {N}^{n}$ and $\mathbb {N}$ graded.

Definition 16

Let

$$\begin{aligned} f: \bigoplus _{\sigma \in \mathbb {N}^n} S(-\sigma )^{a_\sigma } \rightarrow \bigoplus _{\sigma \in \mathbb {N}^n}S(-\sigma )^{b_\sigma } \end{aligned}$$

and $\rho ,\mu \in \mathbb {N}^n$. Then

$$\begin{aligned} f_{\rho ,\mu } : S(-\rho )^{a_\rho } \hookrightarrow \bigoplus _{\sigma \in \mathbb {N}^n} S(-\sigma )^{a_\sigma } \rightarrow \bigoplus _{\sigma \in \mathbb {N}^n}S(-\sigma )^{b_\sigma } \twoheadrightarrow S(-\mu )^{b_\mu }. \end{aligned}$$

Similarly, in the $\mathbb {N}$-graded context, let

$$\begin{aligned} g: \bigoplus _{i \in \mathbb {N}} S(-i)^{a_i} \rightarrow \bigoplus _{i \in \mathbb {N}}S(-i)^{b_i} \end{aligned}$$

and $p,q \in \mathbb {N}$. Then

$$\begin{aligned} g_{p,q} : S(-p)^{a_p} \hookrightarrow \bigoplus _{i \in \mathbb {N}} S(-i)^{a_i} \rightarrow \bigoplus _{i \in \mathbb {N}}S(-i)^{b_i} \twoheadrightarrow S(-q)^{b_q}. \end{aligned}$$

In both cases, the leftmost map is the inclusion map, while the rightmost map is the natural projection.

We are now able to define the strands of a resolution.

Definition 17

Let M be a matroid of rank $n-k$ on a finite set of cardinality n. If

$$\begin{aligned} 0 \leftarrow S_M \overset{f_0}{\leftarrow }S \overset{f_1}{\leftarrow }\bigoplus _{j \in \mathbb {N}}S(-j)^{\beta _{1,j}} \overset{f_2}{\leftarrow }\cdots \overset{f_k}{\leftarrow }\bigoplus _{j \in \mathbb {N}}S(-j)^{\beta _{k,j}} \leftarrow 0 \end{aligned}$$

is a $\mathbb {N}$-graded resolution, and if $\varvec{h}=(h_1,\ldots ,h_k) \in \mathbb {N}^k$, the $\varvec{h}$-strand of the resolution is the sequence

$$\begin{aligned} (f_{1,0,h_1},f_{2,h_1,h_2},\ldots ,f_{k,h_{k-1},h_k}). \end{aligned}$$

The strand of the resolution is the $\varvec{h}$-strand with $\varvec{h}=(d_1\ldots ,d_k)$.

If

$$\begin{aligned} 0 \leftarrow S_M \overset{\phi _0}{\leftarrow }S \overset{\phi _1}{\leftarrow }\bigoplus _{\sigma \in \mathbb {N}^n}S(-j)^{\beta _{1,\sigma }} \overset{\phi _2}{\leftarrow }\cdots \overset{\phi _k}{\leftarrow }\bigoplus _{\sigma \in \mathbb {N}^n}S(-j)^{\beta _{k,\sigma }} \leftarrow 0 \end{aligned}$$

is a $\mathbb {N}^n$-graded resolution, and if $\varvec{\sigma }=(\sigma _1,\ldots ,\sigma _k) \in (\mathbb {N}^n)^k$, the $\varvec{\sigma }$-strand of the resolution is the sequence

$$\begin{aligned} (\phi _{1,(0\ldots ,0),\sigma _1},\phi _{2,\sigma _1,\sigma _2},\ldots ,\phi _{k,\sigma _{k-1},\sigma _k}). \end{aligned}$$

We have already mentioned that $\beta _{i,\sigma } \ne 0 \Rightarrow \sigma \in \{0,1\}^n$. In the sequel, we will therefore identify elements of $\{0,1\}^n$ with subsets of $E=\{1,\ldots ,n\}$. The main theorem of this section, will be a consequence of the following lemma.

Lemma 4

Let M be a matroid of rank $n-k$ on a set E of cardinality n. Let

$$\begin{aligned} 0 \leftarrow S_M \overset{\phi _0}{\leftarrow }S \overset{\phi _1}{\leftarrow }\bigoplus _{\alpha \in \mathbb {N}^n}S(-\alpha )^{\beta _{1,\alpha }} \overset{\phi _2}{\leftarrow }\cdots \overset{\phi _k}{\leftarrow }\bigoplus _{\alpha \in \mathbb {N}^n}S(-\alpha )^{\beta _{k,\alpha }} \leftarrow 0 \end{aligned}$$

be any minimal $\mathbb {N}^n$ graded resolution of its Stanley–Reisner ring. Let $\rho ,\mu$ be two subsets of E. Then

$$\begin{aligned} \phi _{l,\rho ,\mu } \ne 0 \Leftrightarrow \rho \in N_{l-1},\ \mu \in N_{l} \text { and } \rho \subset \mu . \end{aligned}$$

Proof

Any minimal resolution differs from the Taylor resolution (see [8, Section 7.1] by adding trivial resolutions of the form

$$\begin{aligned} 0 \leftarrow \cdots \leftarrow 0 \leftarrow S(-\sigma ) \overset{\psi _j}{\leftarrow }S(-\sigma ) \leftarrow 0 \leftarrow \cdots \leftarrow 0. \end{aligned}$$

For $\rho ,\mu \subset E$, it is easy to see that if $f=g \oplus h$, then $f_{\rho ,\mu } = g_{\rho _\mu } \oplus h_{\rho ,\mu }$. In particular, if $\rho \ne \mu$, then

$$\begin{aligned} \psi _{i,\rho ,\mu }=0 \end{aligned}$$

for every i, so that

$$\begin{aligned} \phi _{l,\rho ,\mu } \ne 0 \Leftrightarrow \Phi _{l,\rho ,\mu } \ne 0 \end{aligned}$$

where $\Psi _*$ are the maps in the Taylor resolution. In any minimal free resolution, we have

$$\begin{aligned} \beta _{l,X} \ne 0 \Leftrightarrow X \in N_l, \end{aligned}$$

so we might assume that $\rho \in N_{l-1}$ and $\mu \in N_l$, otherwise $\phi _{l,\rho ,\mu } = 0$. In particular, this means that $\rho \ne \mu$.

In a first step, we prove that

$$\begin{aligned} \rho \subset \mu \Leftrightarrow \exists \tau \in \mathcal {C},\ \mu = \tau \cup \rho . \end{aligned}$$

One way is obvious. For the other way, let $y \in \mu \backslash \rho$. Since $\mu$ is a cycle, there exists $\tau \in \mathcal {C}$ with $y \in \tau \subset \mu$. Then we have

$$\begin{aligned} n(\mu ) \geqslant n(\rho \cup \tau ) \geqslant n(\rho ) + n(\tau ) - n(\rho \cap \tau ) = l-1 \end{aligned}$$

the equality coming from the fact that $n(\rho \cap \tau )=0$ since $\rho \cap \tau \subsetneq \tau$ is strictly included in a circuit and has thus nullity 0. Since $n(\mu )=l$ and $\mu$ is minimal, we have equality

$$\begin{aligned} \rho \cup \tau = \mu . \end{aligned}$$

Now, if $\rho \cup \tau =\mu$ and $\rho \in N_{l-1}$, by [9, Proposition 1], we can write $\rho = \bigcup _{i=1}^{l-1} \sigma _i$ for some distinct circuits $\sigma _i$, and by construction of the differential of the Taylor complex,

$$\begin{aligned} \Phi _{l,\rho ,\mu } \ne 0. \end{aligned}$$

Conversely, if $\Psi _{l,\rho ,\mu } \ne 0$, then again by construction of the differential of the Taylor complex, $\mu$ is the union of l circuits, and we obtain $\rho$ by taking the union of all these circuits but 1. $\square$

We then have:

Theorem 4

Let M be a matroid of rank $n-k$ on a set of cardinality n. Let

$$\begin{aligned} 0 \leftarrow S_M \overset{f_0}{\leftarrow }S \overset{f_1}{\leftarrow }\bigoplus _{j \in \mathbb {N}}S(-j)^{\beta _{1,j}} \overset{f_2}{\leftarrow }\cdots \overset{f_k}{\leftarrow }\bigoplus _{j \in \mathbb {N}}S(-j)^{\beta _{k,j}} \leftarrow 0 \end{aligned}$$

and

$$\begin{aligned} 0 \leftarrow S_M \overset{\phi _0}{\leftarrow }S \overset{\phi _1}{\leftarrow }\bigoplus _{\sigma \in \mathbb {N}^n}S(-j)^{\beta _{1,\sigma }} \overset{\phi _2}{\leftarrow }\cdots \overset{\phi _k}{\leftarrow }\bigoplus _{\sigma \in \mathbb {N}^n}S(-j)^{\beta _{k,\sigma }} \leftarrow 0 \end{aligned}$$

be $\mathbb {N}$ and $\mathbb {N}^n$-graded resolutions respectively. Then

• 1. $e_1=g_1=d_e= \min \{j, \ \beta _{1,j} \ne 0\}$ and $\tilde{e}_k = \min \{j,\ \beta _{k,j} \ne 0\}.$

• 2. For $2\leqslant l \leqslant k$, the greedy weight $e_l$ is

  $$\begin{aligned} e_l=\min \{|\sigma |,\ \exists \tau \text { that computes }e_{l-1},\ \phi _{l,\tau ,\sigma } \ne 0\}. \end{aligned}$$

• 3. For $1\leqslant l \leqslant k-1$, the top down greedy weight $\tilde{e}_l$ is

  $$\begin{aligned} e_l=\min \{|\sigma |,\ \exists \tau \text { that computes }\tilde{e}_{l+1},\ \phi _{l,\sigma ,\tau } \ne 0\}. \end{aligned}$$

• 4. For $2 \leqslant l \leqslant k$, the CEZ greedy weight $g_l$ is

  $$\begin{aligned} g_l = \min \{j,\ f_{l,d_{l-1},j} \ne 0\}. \end{aligned}$$
• 5.
  $$\begin{aligned} (e_1,\ldots ,e_k)= \min _{\mathrm {lex}} \{e(\varvec{\sigma }),\ \varvec{\sigma } \in (2^E)^n, \text { the }\varvec{\sigma }\text {-strand consists of non-zero maps}\}. \end{aligned}$$
• 6.
  $$\begin{aligned} (\tilde{e}_1,\ldots ,\tilde{e}_k)= \min _{\mathrm {revlex}} \{e(\varvec{\sigma }),\ \varvec{\sigma } \in (2^E)^n, \text { the }\varvec{\sigma }\text {-strand consists of non-zero maps}\}. \end{aligned}$$

Proof

The first point is just the definition. The second and third point are consequences of the previous lemma. The fourth point is also a consequence of the previous lemma. Here, we can take the $\mathbb {N}$-graded resolution, since any subset of cardinality $d_{l-1}$ with non-zero Betti number computes $d_{l-1}$. The two last points follow from the second and third point, as well as Proposition 1. $\square$

Example 4

Using for example [16], we are able to compute the $\mathbb {N}^n$-graded resolution of the code of Example 1.

$$\begin{aligned}&\begin{bmatrix}{6}{7}{8}&{5}{7}{8}&{5}{6}{8}&{5}{6}{7}&{2}{3}{4}&{1}{3}{4}&{1}{2} \end{bmatrix}\\&S \longleftarrow \begin{array}{c}S(-{6}{7}{8}) \bigoplus S(-{5}{7}{8}) \bigoplus S(-{5}{6}{8})\bigoplus S(-{5}{6}{7})\\ \bigoplus S(-{2}{3}{4}) \bigoplus S(-{1}{3}{4}) \bigoplus S(-{1}{2})\end{array}\\&\left[ \begin{array}{ccccccccccccccccc} -{2}{3}{4} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -{1}{3}{4} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -{1}{2} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -{5} &{}\quad -{5} &{}\quad -{5} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -{2}{3}{4} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -{1}{3}{4} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -{1}{2} &{}\quad 0 &{}\quad 0 &{}\quad {6} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -{2}{3}{4} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -{1}{3}{4} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -{1}{2} &{}\quad 0 &{}\quad 0 &{}\quad {7} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -{2}{3}{4} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -{1}{3}{4} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -{1}{2} &{}\quad 0 &{}\quad 0 &{}\quad {8} &{}\quad 0 &{}\quad 0 \\ {6}{7}{8} &{}\quad {5}{7}{8} &{}\quad {5}{6}{8} &{}\quad {5}{6}{7} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -{1} &{}\quad -{1} \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {6}{7}{8} &{}\quad {5}{7}{8} &{}\quad {5}{6}{8} &{}\quad {5}{6}{7} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {2} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {6}{7}{8} &{}\quad {5}{7}{8} &{}\quad {5}{6}{8} &{}\quad {5}{6}{7} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {3}{4} \end{array}\right] \\&\begin{array}{c}S(-{6}{7}{8}) \bigoplus S(-{5}{7}{8}) \bigoplus S(-{5}{6}{8}) \\ \bigoplus S(-{5}{6}{7}) \bigoplus S(-{2}{3}{4})\\ \bigoplus S(-{1}{3}{4}) \bigoplus S(-{1}{2})\end{array} \longleftarrow \begin{array}{c}S(-{2}{3}{4}{6}{7}{8}) \bigoplus S(-{2}{3}{4}{5}{7}{8}) \bigoplus S(-{2}{3}{4}{5}{6}{8})\\ \bigoplus S(-{2}{3}{4}{5}{6}{7}) \bigoplus S(-{1}{3}{4}{6}{7}{8}) \bigoplus S(-{1}{3}{4}{5}{7}{8})\\ \bigoplus S(-{1}{3}{4}{5}{6}{8}) \bigoplus S(-{1}{3}{4}{5}{6}{7}) \bigoplus S(-{1}{2}{6}{7}{8}) \\ \bigoplus S(-{1}{2}{5}{7}{8}) \bigoplus S(-{1}{2}{5}{6}{8}) \bigoplus S(-{1}{2}{5}{6}{7}) \\ \bigoplus S(-{5}{6}{7}{8})^{3} \bigoplus S(-{1}{2}{3}{4})^{2}\end{array}\\&\left[ \begin{array}{ccccccccccccccccc} -{5} &{}\quad -{5} &{}\quad -{5} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {1} &{}\quad {1} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ {6} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {1} &{}\quad {1} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad {7} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {1} &{}\quad {1} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad {8} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {1} &{}\quad {1} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -{5} &{}\quad -{5} &{}\quad -{5} &{}\quad -{2} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad {6} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -{2} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {7} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -{2} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {8} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -{2} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -{3}{4} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -{5} &{}\quad -{5} &{}\quad -{5} \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -{3}{4} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {6} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -{3}{4} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {7} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad -{3}{4} &{}\quad 0 &{}\quad 0 &{}\quad {8} \\ {2}{3}{4} &{}\quad 0 &{}\quad 0 &{}\quad {1}{3}{4} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {1}{2} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad {2}{3}{4} &{}\quad 0 &{}\quad 0 &{}\quad {1}{3}{4} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {1}{2} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad {2}{3}{4} &{}\quad 0 &{}\quad 0 &{}\quad {1}{3}{4} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {1}{2} \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {6}{7}{8} &{}\quad 0 &{}\quad {5}{7}{8} &{}\quad 0 &{}\quad {5}{6}{8} &{}\quad 0 &{}\quad {5}{6}{7} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {6}{7}{8} &{}\quad 0 &{}\quad {5}{7}{8} &{}\quad 0 &{}\quad {5}{6}{8} &{}\quad 0 &{}\quad {5}{6}{7} &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{array}\right] \end{aligned}$$

$$\begin{aligned}&\begin{array}{c}S(-{2}{3}{4}{6}{7}{8}) \bigoplus S(-{2}{3}{4}{5}{7}{8}) \bigoplus S(-{2}{3}{4}{5}{6}{8}) \\ \bigoplus S(-{2}{3}{4}{5}{6}{7}) \bigoplus S(-{1}{3}{4}{6}{7}{8}) \bigoplus S(-{1}{3}{4}{5}{7}{8})\\ \bigoplus S(-{1}{3}{4}{5}{6}{8}) \bigoplus S(-{1}{3}{4}{5}{6}{7}) \bigoplus S(-{1}{2}{6}{7}{8})\\ \bigoplus S(-{1}{2}{5}{7}{8}) \bigoplus S(-{1}{2}{5}{6}{8}) \bigoplus S(-{1}{2}{5}{6}{7}) \\ \bigoplus S(-{5}{6}{7}{8})^{3} \bigoplus S(-{1}{2}{3}{4})^{2} \end{array} \longleftarrow \begin{array}{c}S(-{2}{3}{4}{5}{6}{7}{8})^{3} \bigoplus S(-{1}{3}{4}{5}{6}{7}{8})^{3} \\ \bigoplus S(-{1}{2}{3}{4}{6}{7}{8})^{2} \bigoplus S(-{1}{2}{3}{4}{5}{7}{8})^{2} \\ \bigoplus S(-{1}{2}{3}{4}{5}{6}{8})^{2} \bigoplus S(-{1}{2}{3}{4}{5}{6}{7})^{2} \\ \bigoplus S(-{1}{2}{5}{6}{7}{8})^{3} \end{array} \end{aligned}$$

$$\begin{aligned}&\begin{bmatrix}-{1} &{}\quad 0 &{}\quad 0 &{}\quad -{1} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -{1} &{}\quad 0 &{}\quad 0 &{}\quad -{1} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -{1} &{}\quad 0 &{}\quad 0 &{}\quad -{1} \\ {2} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad {2} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad {2} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ -{5} &{}\quad -{5} &{}\quad -{5} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -{5} &{}\quad -{5} &{}\quad -{5} \\ {6} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad {6} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad {7} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {7} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad {8} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {8} \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad {3}{4} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {3}{4} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {3}{4} \end{bmatrix}\\&\begin{array}{c}S(-{2}{3}{4}{5}{6}{7}{8})^{3} \bigoplus S(-{1}{3}{4}{5}{6}{7}{8})^{3} \bigoplus S(-{1}{2}{3}{4}{6}{7}{8})^{2} \\ \bigoplus S(-{1}{2}{3}{4}{5}{7}{8})^{2} \bigoplus S(-{1}{2}{3}{4}{5}{6}{8})^{2} \bigoplus S(-{1}{2}{3}{4}{5}{6}{7})^{2}\\ \bigoplus S(-{1}{2}{5}{6}{7}{8})^{3} \end{array} \longleftarrow S(-{1}{2}{3}{4}{5}{6}{7}{8})^{6} \end{aligned}$$

where, for compactifying the notation, the number $a_1\cdots a_t$ represents the monomial $X_{a_1}\cdots X_{a_t}$. Here the $(\{1,2\},\{1,2,3,4\},\{1,2,3,4,6,7,8\},E)$-strand is

$$\begin{aligned} \left( \begin{bmatrix}12\end{bmatrix}, \begin{bmatrix} 0&\quad 34\end{bmatrix}, \begin{bmatrix} 678 &{}\quad 0 \\ 0 &{}\quad 678 \end{bmatrix} , \begin{bmatrix} -5&{}\quad -5&{}\quad -5&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad -5&{}\quad -5&{}\quad -5\end{bmatrix}\right) , \end{aligned}$$

thus

$$\begin{aligned} (e_1,e_2,e_3,e_4) \leqslant _{\mathrm {lex}} (2,4,7,8) \end{aligned}$$

and there is actually equality here.

Chained codes and matroids

Definition 18

Let C be a linear code of dimension k. It is called chained if there is a chain

$$\begin{aligned} D_1 \subset D_2 \subset \cdots \ \subset D_k \end{aligned}$$

of linear subcodes, such that $D_i$ computes $d_i$, for $1 \leqslant i \leqslant k$.

Then we have:

Proposition 2

Let C be a linear code of dimension k. Then the following assertions are equivalent:

• The code C is chained,

• $(d_1,\ldots ,d_k)=(e_1,\ldots ,e_k)$,

• $(d_1,\ldots ,d_k)=(\tilde{e}_1,\ldots ,\tilde{e}_k)$,

• $(d_1,\ldots ,d_k)=(g_1,\ldots ,g_k)$.

Proof

This is obvious from the definitions. $\square$

This can be generalized to matroids:

Definition 19

A matroid of rank $n-k$ on a set of cardinality n is chained if there exists a chain

$$\begin{aligned} \sigma _1\subset \cdots \subset \sigma _k \end{aligned}$$

where $\sigma _i \in N_i$ computes $d_i$.

Proposition 3

Let M be a matroid of rank $n-k$ on a set of cardinality n. then the following assertions are equivalent:

• The matroid M is chained,

• $(d_1,\ldots ,d_k)=(e_1,\ldots ,e_k)$,

• $(d_1,\ldots ,d_k)=(\tilde{e}_1,\ldots ,\tilde{e}_k)$,

• $(d_1,\ldots ,d_k)=(g_1,\ldots ,g_k)$.

Proof

This follows from the definitions. $\square$

Moreover, we have the following:

Proposition 4

A linear code is chained if and only if its associated matroid is chained.

Proof

This is a direct consequence of Theorem 3. 3. $\square$

We will end this article with commenting on the connection between chainedness of a code or matroid, and properties of minimal resolutions of their Stanley–Reisner rings.

Definition 20

Let M be a matroid of rank $n-k$ on a set of cardinality n. It has a pure resolution if the $\mathbb {N}$-graded resolution satisfies:

$$\begin{aligned} \forall 1 \leqslant i \leqslant k,\ \exists ! j_i,\ \beta _{i,j_i}\ne 0. \end{aligned}$$

Furthermore, we say that the pure resolution is linear if

$$\begin{aligned} \forall 1\leqslant i <k,\ j_{i+1} = j_i. \end{aligned}$$

A linear code has pure resolution (resp. linear resolution) if its associated matroid has.

Proposition 5

Linear codes and matroids with pure resolutions are chained.

Proof

This follows from the fact that $\beta _{i,X} \ne 0 \Leftrightarrow X \in N_i$ and the definitions. $\square$

MDS codes and uniform matroids have linear resolutions, and as such are chained. On the other hand, we have some codes that do not have linear resolutions, but pure resolutions. Examples of such codes are Reed–Müller of the first order and constant weight codes [10, Theroem 2.1]. These codes are thus also chained. In the case of constant weight codes, we have in addition that any chain of subcodes of dimension i actually compute $e_i=d_i$. In general, chained codes do not need to have pure resolutions. For example, non-binary Veronese codes studied in [11] are such codes. These codes are defined through the Veronese embedding $\mathbb {P}_2 \rightarrow \mathbb {P}_5$. Elements of $N_i$ correspond to complements of geometrical configurations, and it follows easily from [11, Theorem 21] that the code is chained but does not have pure resolution.

The set of codes/matroids with pure/linear resolutions is not closed under taking duals. However, we have:

Proposition 6

A matroid (resp. linear code) is chained if and only if its dual (resp. orthogonal complement) is chained.

Proof

This follows from Wei duality for greedy weights and Hamming weights. $\square$