Matrix theory for minimal trellises

Abstract

Trellises provide a graphical representation for the row space of a matrix. The product construction of Kschischang and Sorokine builds minimal conventional trellises from matrices in minimal span form. Koetter and Vardy showed that minimal tail-biting trellises can be obtained by applying the product construction to submatrices of a characteristic matrix. We introduce the unique reduced minimal span form of a matrix and we obtain an expression for the unique reduced characteristic matrix. Among new properties of characteristic matrices we prove that characteristic matrices are in duality if and only if they have orthogonal column spaces, and that the transpose of a characteristic matrix is again a characteristic matrix if and only if the characteristic matrix is reduced. These properties have clear interpretations for the unwrapped unit memory convolutional code of a tail-biting trellis, they explain the duality for the class of Koetter and Vardy trellises, and they give a natural relation between the characteristic matrix based Koetter–Vardy construction and the displacement matrix based Nori–Shankar construction. For a pair of reduced characteristic matrices in duality, one is lexicographically first in a forward direction and the other is lexicographically first in the reverse direction. This confirms a conjecture by Koetter and Vardy after taking into account the different directions for the lexicographical ordering.

Appendices

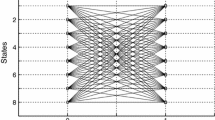
Appendix A: A dual pair of reduced characteristic matrices

Reduced characteristic matrices X and Y for a pair of binary orthogonal matrices G and H (Figs. 3, 4, 5).

$$\begin{aligned}&X = \left[ \begin{array}{ccccc} 1&{}1&{}1&{}0&{}0\\ \cdot &{}1&{}1&{}0&{}1\\ \cdot &{}\cdot &{}1&{}1&{}0\\ \cdot &{}\cdot &{}\cdot &{}1&{}1\\ \cdot &{}\cdot &{}\cdot &{}\cdot &{}1 \end{array} \right] + \left[ \begin{array}{ccccc} \cdot &{}\cdot &{}\cdot &{}\cdot &{}\cdot \\ 0&{}\cdot &{}\cdot &{}\cdot &{}\cdot \\ 0&{}0&{}\cdot &{}\cdot &{}\cdot \\ 0&{}1&{}0&{}\cdot &{}\cdot \\ 1&{}0&{}0&{}0&{}\cdot \end{array} \right] = \left[ \begin{array}{ccccc} 1&{}1&{}1&{}0&{}0\\ 0&{}1&{}1&{}0&{}1\\ 0&{}0&{}1&{}1&{}0\\ 0&{}1&{}0&{}1&{}1\\ 1&{}0&{}0&{}0&{}1\end{array} \right] ~~\begin{array}{ccccc} (0,2] \\ (1,4] \\ (2,3] \\ (3,1] \\ (4,0], \end{array}\\&Y = \left[ \begin{array}{ccccc} \cdot &{}0&{}1&{}1&{}1\\ \cdot &{}\cdot &{}0&{}0&{}1\\ \cdot &{}\cdot &{}\cdot &{}1&{}0\\ \cdot &{}\cdot &{}\cdot &{}\cdot &{}0\\ \cdot &{}\cdot &{}\cdot &{}\cdot &{}\cdot \end{array} \right] + \left[ \begin{array}{ccccc} 1&{}\cdot &{}\cdot &{}\cdot &{}\cdot \\ 1&{}1&{}\cdot &{}\cdot &{}\cdot \\ 0&{}1&{}1&{}\cdot &{}\cdot \\ 0&{}1&{}1&{}1&{}\cdot \\ 1&{}0&{}1&{}1&{}1\end{array} \right] = \left[ \begin{array}{ccccc} 1&{}0&{}1&{}1&{}1\\ 1&{}1&{}0&{}0&{}1\\ 0&{}1&{}1&{}1&{}0\\ 0&{}1&{}1&{}1&{}0\\ 1&{}0&{}1&{}1&{}1\end{array} \right] ~~\begin{array}{ccccc} (2,0] \\ (4,1] \\ (3,2] \\ (1,3] \\ (0,4]. \end{array} \end{aligned}$$

Fig. 3

Three different labelings for the minimal conventional trellises of the row space of G: vertex labeling by information symbols (top), by codeword symbols (middle), and by syndromes (bottom)

Fig. 4

A pair of dual conventional trellises, based on rows $X_{1,2,3}$ and $Y_{4,5}$

Fig. 5

A pair of dual tailbiting trellises, based on rows $X_{1,5,3}$ and $Y_{4,2}$

Label codes for KV-trellises constructed from X and Y using the span based BCJR construction.

$$\begin{aligned}&Y^T = \left[ \begin{array}{ccccc} 1&{}1&{}0&{}0&{}1\\ 0&{}1&{}1&{}1&{}0\\ 1&{}0&{}1&{}1&{}1\\ 1&{}0&{}1&{}1&{}1\\ 1&{}1&{}0&{}0&{}1\end{array} \right] \quad X= \left[ \begin{array}{ccccc} 1&{}1&{}1&{}0&{}0\\ 0&{}1&{}1&{}0&{}1\\ 0&{}0&{}1&{}1&{}0\\ 0&{}1&{}0&{}1&{}1\\ 1&{}0&{}0&{}0&{}1\end{array} \right] ,\\&X^T = \left[ \begin{array}{ccccc} 1&{}0&{}0&{}0&{}1\\ 1&{}1&{}0&{}1&{}0\\ 1&{}1&{}1&{}0&{}0\\ 0&{}0&{}1&{}1&{}0\\ 0&{}1&{}0&{}1&{}1\end{array} \right] \quad Y = \left[ \begin{array}{ccccc} 1&{}0&{}1&{}1&{}1\\ 1&{}1&{}0&{}0&{}1\\ 0&{}1&{}1&{}1&{}0\\ 0&{}1&{}1&{}1&{}0 \\ 1&{}0&{}1&{}1&{}1\end{array} \right] ,\\&S(Y^T|X) = \left[ \begin{array}{c|c|c|c|c|c|c|c|c|c|c} 0~0~0~0~0 &{}1 &{}1~1~0~0~1 &{}1 &{}1~0~1~1~1 &{}1 &{}0~0~0~0~0 &{}0 &{}0~0~0~0~0 &{}0 &{}0~0~0~0~0 \\ 0~0~0~0~0 &{}0 &{}0~0~0~0~0 &{}1 &{}0~1~1~1~0 &{}1 &{}1~1~0~0~1 &{}0 &{}1~1~0~0~1 &{}1 &{}0~0~0~0~0 \\ 0~0~0~0~0 &{}0 &{}0~0~0~0~0 &{}0 &{}0~0~0~0~0 &{}1 &{}1~0~1~1~1 &{}1 &{}0~0~0~0~0 &{}0 &{}0~0~0~0~0 \\ 0~1~1~1~0 &{}0 &{}0~1~1~1~0 &{}1 &{}0~0~0~0~0 &{}0 &{}0~0~0~0~0 &{}1 &{}1~0~1~1~1 &{}1 &{}0~1~1~1~0 \\ 1~1~0~0~1 &{}1 &{}0~0~0~0~0 &{}0 &{}0~0~0~0~0 &{}0 &{}0~0~0~0~0 &{}0 &{}0~0~0~0~0 &{}1 &{}1~1~0~0~1 \end{array} \right] ,\\&S(X^T|Y) = \left[ \begin{array}{c|c|c|c|c|c|c|c|c|c|c} 1~0~0~0~1 &{}1 &{}0~0~0~0~0 &{}0 &{}0~0~0~0~0 &{}1 &{}1~1~1~0~0 &{}1 &{}1~1~0~1~0 &{}1 &{}1~0~0~0~1 \\ 0~1~0~1~1 &{}1 &{}1~1~0~1~0 &{}1 &{}0~0~0~0~0 &{}0 &{}0~0~0~0~0 &{}0 &{}0~0~0~0~0 &{}1 &{}0~1~0~1~1 \\ 0~0~1~1~0 &{}0 &{}0~0~1~1~0 &{}1 &{}1~1~1~0~0 &{}1 &{}0~0~0~0~0 &{}1 &{}0~0~1~1~0 &{}0 &{}0~0~1~1~0 \\ 0~0~0~0~0 &{}0 &{}0~0~0~0~0 &{}1 &{}1~1~0~1~0 &{}1 &{}0~0~1~1~0 &{}1 &{}0~0~0~0~0 &{}0 &{}0~0~0~0~0 \\ 0~0~0~0~0 &{}1 &{}1~0~0~0~1 &{}0 &{}1~0~0~0~1 &{}1 &{}0~1~1~0~1 &{}1 &{}0~1~0~1~1 &{}1 &{}0~0~0~0~0 \end{array} \right] . \end{aligned}$$

Label codes for the dual trellises defined with rows 1, 3, 5 of X and rows 2, 4 of Y.

$$\begin{aligned} S(Y_{2,4}^T|X_{1,3,5})&= \left[ \begin{array}{c|c|c|c|c|c|c|c|c|c|c} \,{\cdot \,}~0~{\cdot \,}~0~{\cdot \,}&{}1 &{}{\cdot \,}~1~{\cdot \,}~0~{\cdot \,}&{}1 &{}{\cdot \,}~0~{\cdot \,}~1~{\cdot \,}&{}1 &{}{\cdot \,}~0~{\cdot \,}~0~{\cdot \,}&{}0 &{}{\cdot \,}~0~{\cdot \,}~0~{\cdot \,}&{}0 &{}{\cdot \,}~0~{\cdot \,}~0~{\cdot \,}\, \\ \,{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}\, \\ \,{\cdot \,}~0~{\cdot \,}~0~{\cdot \,}&{}0 &{}{\cdot \,}~0~{\cdot \,}~0~{\cdot \,}&{}0 &{}{\cdot \,}~0~{\cdot \,}~0~{\cdot \,}&{}1 &{}{\cdot \,}~0~{\cdot \,}~1~{\cdot \,}&{}1 &{}{\cdot \,}~0~{\cdot \,}~0~{\cdot \,}&{}0 &{}{\cdot \,}~0~{\cdot \,}~0~{\cdot \,}\, \\ \,{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}\, \\ \,{\cdot \,}~1~{\cdot \,}~0~{\cdot \,}&{}1 &{}{\cdot \,}~0~{\cdot \,}~0~{\cdot \,}&{}0 &{}{\cdot \,}~0~{\cdot \,}~0~{\cdot \,}&{}0 &{}{\cdot \,}~0~{\cdot \,}~0~{\cdot \,}&{}0 &{}{\cdot \,}~0~{\cdot \,}~0~{\cdot \,}&{}1 &{}{\cdot \,}~1~{\cdot \,}~0~{\cdot \,}\, \end{array} \right] , \\ S(X_{1,3,5}^T|Y_{2,4})&= \left[ \begin{array}{c|c|c|c|c|c|c|c|c|c|c} {\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}\\ 0~{\cdot \,}~0~{\cdot \,}~1 &{}1 &{}1~{\cdot \,}~0~{\cdot \,}~0 &{}1 &{}0~{\cdot \,}~0~{\cdot \,}~0 &{}0 &{}0~{\cdot \,}~0~{\cdot \,}~0 &{}0 &{}0~{\cdot \,}~0~{\cdot \,}~0 &{}1 &{}0~{\cdot \,}~0~{\cdot \,}~1 \\ {\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}\\ 0~{\cdot \,}~0~{\cdot \,}~0 &{}0 &{}0~{\cdot \,}~0~{\cdot \,}~0 &{}1 &{}1~{\cdot \,}~0~{\cdot \,}~0 &{}1 &{}0~{\cdot \,}~1~{\cdot \,}~0 &{}1 &{}0~{\cdot \,}~0~{\cdot \,}~0 &{}0 &{}0~{\cdot \,}~0~{\cdot \,}~0 \\ {\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}&{}{\cdot \,}&{}{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}~{\cdot \,}\end{array} \right] . \end{aligned}$$

Appendix B: A reduced characteristic matrix for the Golay code

The binary Golay code of length 24 is generated by the following twelve row vectors over $GF(4) = \{ 0,1,a,b \}$ after the concatenation $0 \mapsto 00, 1 \mapsto 11, a \mapsto 01, b \mapsto 10.$

$$\begin{aligned} \left[ \begin{array}{cccccccccccc} 1 &{}\quad a &{}\quad b &{}\quad 1 &{}\quad b &{}\quad a &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot \\ a &{}\quad b &{}\quad 1 &{}\quad a &{}\quad 1 &{}\quad b &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot \\ \cdot &{}\quad \cdot &{}\quad b &{}\quad 1 &{}\quad a &{}\quad 1 &{}\quad b &{}\quad a &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot \\ \cdot &{}\quad \cdot &{}\quad a &{}\quad b &{}\quad 1 &{}\quad b &{}\quad a &{}\quad 1 &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot \\ \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad 1 &{}\quad a &{}\quad b &{}\quad 1 &{}\quad b &{}\quad a &{}\quad \cdot &{}\quad \cdot \\ \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad a &{}\quad b &{}\quad 1 &{}\quad a &{}\quad 1 &{}\quad b &{}\quad \cdot &{}\quad \cdot \\ \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad b &{}\quad 1 &{}\quad a &{}\quad 1 &{}\quad b &{}\quad a \\ \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad a &{}\quad b &{}\quad 1 &{}\quad b &{}\quad a &{}\quad 1 \\ b &{}\quad a &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad 1 &{}\quad a &{}\quad b &{}\quad 1 \\ 1 &{}\quad b &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad a &{}\quad b &{}\quad 1 &{}\quad a \\ a &{}\quad 1 &{}\quad b &{}\quad a &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad b &{}\quad 1 \\ 1 &{}\quad b &{}\quad a &{}\quad 1 &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad \cdot &{}\quad a &{}\quad b \end{array} \right] . \end{aligned}$$

Every even row is a scalar multiple of the preceding odd row and every odd row is obtained with an obvious symmetry from the preceding even row. If we apply the concatenation in combination with a transposition of symbols $4k+2$ and $4k+4,$ i.e.,

$$\begin{aligned}&ab \mapsto 0110 \mapsto 0011,\quad b1 \mapsto 1011 \mapsto 1110,\quad 1a \mapsto 1101 \mapsto 1101, \\&ba \mapsto 1001 \mapsto 1100, \quad 1b \mapsto 1110 \mapsto 1011,\quad a1 \mapsto 0111 \mapsto 0111, \end{aligned}$$

then the result is a generator matrix G for the Golay code with optimal minimal span length $108 = 12 \cdot 9.$ The generator matrix is of the form (1) in [2] and agrees with the generator matrix in (4) of that paper after a permutation $(1\;2)(7\;8)(9\;10)(15\;16)(17\;18)(23\;24).$ The reduced characteristic matrix X for G is of the form

$$\begin{aligned} X = \left[ \begin{array}{ccc} A &{}B &{}C \\ C &{}A &{}B \\ B &{}C &{}A \end{array} \right] \end{aligned}$$

with (A|B|C) equal to

$$\begin{aligned} \left[ \begin{array}{cccccccc|cccccccc|cccccccc} 1&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 1&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 1&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 0 \end{array} \right] . \end{aligned}$$

The odd rows have span length 9 and the even rows have span length 15.

Appendix C: Non-attacking rooks for function fields

Minimal spans for characteristic generators have an analogue in discrepancies for function fields.

Given a field K of algebraic functions and two rational points (places), a function in K has span (i, j) if it has a pole of order j at the first point, no other poles, and a zero of order i at the second point. For each $j \in \mathbb {Z},$ let $\sigma (j) \in \mathbb {Z}$ be maximal such that there exists a function with span (i, j). This defines a pair $(\sigma (j),j).$ The pairs fill the plane with an infinite set of non-attacking rooks. Let $n > 0$ be minimal such that there exists a function with $(i,j)=(n,n).$ Then the pattern is periodic with period n.

For the function field F(x, y),  defined with equation $y^8+y = x^{10}+x^3$ over the field of eight elements, $n=13.$ There exist functions with minimal spans [6]

$$\begin{aligned}&(i,j) \in \{ (0,0), (1,8), (2,16), (3,10), (4,18), (5,12), (6,20),\\&\quad (7,28), (8,22), (9,30),(10,24),(11,32),(12,40) \}. \end{aligned}$$

Figure 6 pictures the minimal spans as non-attacking rooks on a chess board of size 13 with labeling $\{ 0, 1, \ldots , 11, 12 \} \times \{ 1, 2, \ldots , 12, 0 \}$ modulo 13.

Fig. 6

Non-attacking rooks for the Suzuki curve over the field of eight elements