Abstract
Time-lock encryption is a method to encrypt a message such that it can only be decrypted after a certain deadline has passed. We propose a novel time-lock encryption scheme, whose main advantage over prior constructions is that even receivers with relatively weak computational resources should immediately be able to decrypt after the deadline, without any interaction with the sender, other receivers, or a trusted third party. We build our time-lock encryption on top of the new concept of computational reference clocks and an extractable witness encryption scheme. We explain how to construct a computational reference clock based on Bitcoin. We show how to achieve constant level of multilinearity for witness encryption by using SNARKs. We propose a new construction of a witness encryption scheme which is of independent interest: our scheme, based on Subset-Sum, achieves extractable security without relying on obfuscation. The scheme employs multilinear maps of arbitrary order and is independent of the implementations of multilinear maps.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Alice has a document that she wants to make public in, say, a couple of days, but she is not willing to hand it out to anybody before this deadline. Therefore she puts the document into a box and attaches a “time-lock”. The lock keeps the box securely sealed, and thus the document stays confidential, for the determined period of time. It will unlock automatically when the deadline has passed, which makes it possible for everyone to access the document easily, without any further interaction with Alice. Time-lock encryption is a digital equivalent of such time-locked boxes. It allows to encrypt data for a period of time, up to a certain deadline, such that even a computationally powerful adversary is not able to learn any non-trivial information about the data before the deadline. However, when the time is over, even parties with relatively weak computational resources should immediately be able to decrypt easily. Essentially, time-lock encryption allows to send a message “into the future”. The key novelty of time-lock encryption is that it achieves the following properties simultaneously:
-
(1)
Non-interactive The sender Alice is not required to be available for decryption.
-
(2)
No trusted setup Time-lock encryption does not rely on trusted third parties. Thus, the sender is not required to trust any (set of) third parties to keep decryption keys (or shares of decryption keys) secret until the deadline has passed.
-
(3)
No resource restrictions Parties interested in decrypting a ciphertext are not forced to perform expensive computations until decryption succeeds. This means that a party which simply waits till the decryption deadline has passed will be able to decrypt the ciphertext at about the same time as another party who attempts to decrypt the ciphertext earlier by performing a large (but reasonably bounded) number of computations. Thus, all reasonably bounded parties will be able to decrypt a ciphertext at essentially the same time, regardless of their computational resources.
These features are achieved simultaneously which makes time-lock encryption a fascinating primitive, which enables applications that seem impossible to achieve with classical encryption schemes.
Efficient decryption without trusted third parties Time-lock encryption is related to timed-release encryption, investigated by Rivest et al. [66]. However, timed-release encryption has some drawbacks. One line of research [15, 17, 27, 66] realizes timed-release encryption by assuming a trusted third party (TTP), which reveals decryption keys at the right time. Therefore security relies crucially on the assumption that the TTP is trustworthy. In particular, it must not use its ability to allow decryption of ciphertexts earlier than desired by the sender in any malicious way, for instance by revealing a decryption key before the deadline.
The other line of research [17, 66, 69] considers constructions that require the receiver of a ciphertext to perform a feasible, but computationally expensive search for a decryption key. This puts a considerable computational overhead on the receiver. It is particularly challenging when the ciphertext is made public and there are many different receivers, some of whom may be unknown to the sender. It seems impossible to encrypt with any known timed-release encryption scheme in a way, such that all receivers are able to decrypt at the same time, unless one relies on trusted third parties, or tight synchronicity. We think it an interesting theoretical question in its own to ask if it is possible to avoid this.
1.1 Contributions
We introduce a new primitive called computational reference clocks as an extension of the standard computational model, which provide a novel and very realistic method to “emulate” real-world time in a computational model. We show that the widely-used cryptocurrency Bitcoin provides a practical example of such a reference clock, which shows that the assumption that these objects exist in practice is reasonable.
As a first application of this extended computational model, we construct time-lock encryption schemes, a primitive which exhibits many interesting features that are impossible to achieve in a plain standard computational model. We give a proof-of-concept construction of encryption schemes, where a sender is able to encrypt a ciphertext, such that not even a computationally powerful (but reasonably bounded) adversary is able to learn any non-trivial information about the message before the deadline. Once the deadline has passed, even receivers with relatively limited computational resources are immediately able to decrypt. Decryption is non-interactive, in the sense that there is no communication between the sender and receivers except for the initial, unidirectional transmission of the ciphertext, or among receivers. We call encryption schemes with these properties time-lock encryption schemes.
Our time-lock encryption scheme is built on top of the computational reference clock and a generic witness encryption (WE) scheme that is extractable. We propose a new witness encryption scheme, which achieves extractable security without using obfuscation and which is more efficient than previously known schemes. The size of the ciphertext and running time for encryption and decryption of witness encryption is linear in terms of the size of witness. Usually the linear complexity is very natural and efficient. Unfortunately, this is not good enough for witness encryption because all the instantiations of witness encryption are based on multilinear maps [18]. The current instantiations of multilinear maps [31, 32, 40, 54] are not yet practical regardless of recent lines of attacks. To mitigate this issue, we use SNARKs [12,13,14, 44, 49, 55, 56, 62] to reduce the complexity of our time-lock encryption. We show that using SNARKs can achieve short ciphertext on witness encryption and constant multilinearity level regardless of the instance and witness.
1.1.1 Time-lock encryption
Computational reference clocks A first challenge in constructing time-lock encryption is to find a reasonable equivalent of real-world time in a computational model. Real-world time is usually determined by some physical reference, like the current state of atomic reference clocks. We do not see any reasonable way to mimic this notion of time in a computational model without trusted third parties.
Our main idea is to use the current state of an iterative, public computation as what we call a computational reference clock. The abstract notion of computational reference clocks stems from the concrete idea of using the popular digital cryptocurrency Bitcoin [61] as a reference clock. To clarify what we mean by this, consider the following concrete example. The Bitcoin system performs an iterative, very large-scale, public computation, where so-called miners are contributing significant computational resources to the gradual extension of the Bitcoin block chain. Essentially, this block chain consists of a sequence of hash values \(B_1,\ldots ,B_\tau \) that satisfy certain conditions.Footnote 1 These conditions determine the difficulty of finding new blocks in the chain. The Bitcoin system adjusts the difficulty, depending on the computational resources currently contributing to the Bitcoin network, such that about every 10 minutes a new block \(B_{\tau +1}\) is appended to the chain. Thus, the block chain can serve as a reference clock, where the current length \(\tau \) of the chain tells the current “time”, and there are about 10 minutes between each “clock tick”.
Witness encryption In order to be able to sketch our construction of time-lock encryption from computational reference clocks, let us briefly recap witness encryption [43]. Witness encryption for all NP-relations was introduced by Garg et al. [43]. Known constructions [7, 21, 41, 43, 46] are based on multilinear maps [18, 40], or obfuscation [5, 6, 41].
A witness encryption scheme is associated with an NP-relation R (cf. Definition 1). For \((x,w) \in R\) we say that x is a “statement” and w is a “witness”. A witness encryption scheme for relation R allows to encrypt a message m with respect to statement x as  . Any witness w which satisfies \((x,w) \in R\) can be used to decrypt this ciphertext c as
. Any witness w which satisfies \((x,w) \in R\) can be used to decrypt this ciphertext c as  . Intuitively, one may think of a statement x as a “public key”, such that any witness w with \((x,w) \in R\) can be used as a corresponding “secret key”.
. Intuitively, one may think of a statement x as a “public key”, such that any witness w with \((x,w) \in R\) can be used as a corresponding “secret key”.
A secure witness encryption scheme essentially guarantees that no adversary is able to learn any non-trivial information about a message encrypted for statement x, unless it already “knows” a witness w for \((x,w) \in R\). Witness encryption schemes with this property are called extractable [7, 21, 48]. The notion of extractable security was first proposed in [48], along with a candidate construction, but there are no known constructions with a mathematical proof of extractable security. Zhandry constructs an extractable witness PRF in [71], but extractability is directly assumed. To the best of our knowledge, existing WE schemes [43, 46, 48, 71] do not have efficient extraction methods (since extractors for these schemes appear to be super-polynomial). An exception is the scheme of Bellare and Hoang [8] which defers the issue of extractability to its underlying obfuscation scheme.
Construction of time-lock encryption The key idea behind our construction of time-lock encryption is to combine a computational reference clock with witness encryption. For this introduction, let us consider time-lock encryption based on Bitcoin as one specific instantiation of a reference clock (we will consider more general constructions in the body of the paper). We define an NP-relation R such that
-
(1)
For \(x \in \mathbb {N} \), statements have the form \(1^x\), that is, x in unary representation.
-
(2)
Any valid Bitcoin block chain \(w = (B_1,\ldots ,B_x)\) of length at least x is a witness for statement \(1^x\), that is \((1^x,w) \in R\).
Let  be a witness encryption scheme for this particular relation R. Suppose the current state of the Bitcoin blockchain is \(B_1,\ldots ,B_\tau \). Then the block chain contains a witness w for \((1^x,w) \in R\) for all \(x \le \tau \). The Bitcoin blockchain is public. Therefore everybody is immediately able to decrypt any ciphertext
be a witness encryption scheme for this particular relation R. Suppose the current state of the Bitcoin blockchain is \(B_1,\ldots ,B_\tau \). Then the block chain contains a witness w for \((1^x,w) \in R\) for all \(x \le \tau \). The Bitcoin blockchain is public. Therefore everybody is immediately able to decrypt any ciphertext  with \(x \le \tau \), by using the witness from the public block chain as the “decryption key”.
with \(x \le \tau \), by using the witness from the public block chain as the “decryption key”.
It is worth pointing out that the reference clock does not have to start with the genesis block of Bitcoin. We can set the clock’s initial state \(w_0\) to be the latest block and ignore older parts of the blockchain. In addition, the witness does not have to include all transaction data of the blockchain, as the hash chain of the block headers is sufficient for decryption. A block header is an 80-byte digest for each block. Our model can be viewed as a pruned and simplified version of the blockchain.
Security of this construction Let  be a ciphertext with \(x > \tau \). Under the assumption that the witness encryption scheme is secure, we will show that an adversary has only two possibilities to learn any non-trivial information about m.
be a ciphertext with \(x > \tau \). Under the assumption that the witness encryption scheme is secure, we will show that an adversary has only two possibilities to learn any non-trivial information about m.
-
(1)
The adversary waits until the public Bitcoin block chain has reached length x. Then the chain contains a witness w for \((1^x,w) \in R\), which immediately allows to decrypt. However, note that then not only the adversary, but also everybody else is able to decrypt, by reading w from the public Bitcoin block chain and computing
 . Speaking figuratively, “the time-lock has opened”.
. Speaking figuratively, “the time-lock has opened”. -
(2)
The adversary tries to “put forward” the computational reference clock provided by the Bitcoin block chain, by computing the missing blocks \(B_{\tau +1},\ldots ,B_x\) of the chain secretly on its own, faster than the public computation performed by the collection of all Bitcoin miners. Note that this means that the adversary would have to outperform the huge computational resources gathered in Bitcoin, which currently (August 2017) perform more than \(6.6 \times 10^{18} \approx 2^{62}\) hash computations per second. Assuming that no adversary is able to perform this large amount of computation to learn the encrypted message earlier, the scheme is secure.
A particularly interesting case is when the value of learning the message earlier than others is below the value of the computations an adversary would have to perform. For instance, in our Bitcoin-based instantiation, an adversary would earn Bitcoin for contributing its resources to the network. Then security is provided simply by the fact that there is no incentive for the adversary to attack the time-lock encryption.
The above description is slightly simplified. The actual Bitcoin block chain (described in Sect. 5.1) and our construction (in Sect. 5.3) are more complex, but the underlying principle is the same. In particular, we will have to describe slightly more complex relations, because of the variable difficulty parameter in Bitcoin.
We stress that we do not have to put any form of trust in Bitcoin miners. The intermediate states of their computations can be completely public, and they do not have to store any secrets.
Using SNARKs to reduce multilinearity level for witness encryption The size of the ciphertext and the running time for encryption and decryption is linear in terms of the size of witness. Usually the linear complexity is very natural and efficient. Unfortunately, this is not good enough for witness encryption because all the instantiations of witness encryption are based on multilinear maps [18]. The research on multilinear maps is still in its infancy [31, 32, 40, 54] and is not yet practical regardless of recent lines of attacks. Most importantly, the existing implementations for multilinear maps are not compact, that is, the size of the group elements is polynomial in the multilinearity level (i.e., the maximum number of pairings). The multilinearity level is polynomial in the length of the witness. To mitigate this issue, we propose our second construction of time-lock encryption by using SNARKs [12,13,14, 44, 49, 55, 56, 62] together with witness encryption. Instead of directly encrypting with an instance x in witness encryption, the idea is to encrypt with SNARKs verification procedure for the statement \((x,w)\in R\). This idea of using SNARKs to gain efficiency is not new [48, 71]. However, we show that using SNARKs can achieve constant multilinearity level regardless of the instance and witness, rather than the previous linear complexity in [48, 71].
1.1.2 Extractable witness encryption
Construction of extractable witness encryption We propose a new extractable witness encryption scheme based on a special Subset-Sum (described below). To encrypt with any NP language, we present a reduction from the NP-complete CNF-SAT to our special Subset-Sum problem. We prove the extractable security of this construction in the Idealised Graded Encoding Model [4, 22, 72]. To the best of our knowledge, this is the first construction of witness encryption to achieve extractable security, without the use of obfuscation.
We use a variant of multilinear maps where the groups are indexed by the integer vectors [4, 19, 40, 72], which allows us to efficiently encode an instance of the special Subset-Sum problem. Suppose a \({\mathbf u}\)-linear map on groups \({\left\{ \mathbb {G}_{{\mathbf w}} \right\} }_{{\mathbf w}}\) with \({\mathbf w}\le {\mathbf u}\) (component-wise comparison). The pairing operation \(\mathsf{e}_{{\mathbf w},{\mathbf w^\prime }}\) maps \(\mathbb {G}_{{\mathbf w}}\times \mathbb {G}_{{\mathbf w^\prime }}\) into \(\mathbb {G}_{{\mathbf w} + {\mathbf w^\prime }}\) with \({\mathbf w} + {\mathbf w^\prime }\le {\mathbf u}\) by computing \(\mathsf{e}_{{\mathbf w},{\mathbf w^\prime }}{\left( g_{{\mathbf w}}^a, g_{{\mathbf w^\prime }}^b \right) } = g_{{\mathbf w}+{\mathbf w^\prime }}^{ab}\).
The special Subset-Sum problem is: given a multi-set of positive integer vectors \(\varDelta = {\left\{ {\left( {\mathbf v}_i: \ell _i \right) } \right\} }_{i\in I}\) where \({\left( {\mathbf v}_i : \ell _i \right) }\) means \({\mathbf v}_i\) occurs \(\ell _i\) times in the multiset and a target sum-vector \({\mathbf s}\) such that \((\ell _i+1) {\mathbf v}_i\not \le {\mathbf s}\) and \({\mathbf v}_i\) are pairwise-distinct, to decide whether there exists a subset of \(\varDelta \) that can sum up to \({\mathbf s}\). The side condition \((\ell _i+1) {\mathbf v}_i\not \le {\mathbf s}\) is to guarantee the encoding of each integer vector \({\mathbf v}_i\) can only be used for at most \(\ell _i\) times, in order to keep consistency between the encoding of the Subset-Sum and the original Subset-Sum problem. In multilinear maps, the vectors in \(\varDelta = {\left\{ {\left( {\mathbf v}_i : \ell _i \right) } \right\} }_{i\in I}\) are encoded as \({\left\{ {{g}_{{{\mathbf v}_i}}^{\alpha ^{{\mathbf v}_i}}} \right\} }_{i\in I}\) and the target vector is encoded as \({{g}_{{{\mathbf s}}}^{\alpha ^{{\mathbf s}}}}\). Suppose the subset-sum exists, that is \(\sum _{i\in I} b_i {\mathbf v}_i = {\mathbf s}\) with \(b_i\) positive integers and \(b_i\le \ell _i\). Then we compute the encoding of the target sum as below
In this way, each vector \({\mathbf v}_i\) only needs to be encoded once and the multiplication of the same encoding is in logarithm time which gains efficiency. To encrypt with any NP language, we present a reduction from CNF-SAT to our special Subset-Sum problem.
We prove that our encoding achieves extractability in the generic model of multilinear maps. The main technical detail is to construct an efficient extractor to extract a witness from the adversary’s group operations. Constructing a witness extractor for the existing witness encryption schemes [43, 48, 71] appears to be super-polynomial because of the expansion of adversary’s query-polynomial. Soundness security [43] is a special case of the extractable security; for sanity of this work, we also give full discussion about the soundness security of our scheme in Appendix G.
Interestingly extractable witness encryption with arbitrary auxiliary inputs might be unattainable [42]. A simple counter example is the following: suppose the sampler has \((x,w)\in R\), then the sampler obfuscates the decryption algorithm of witness encryption \(z=\mathcal{O}(\mathsf{WE.Dec}{\left( w,\cdot \right) })\) and gives z to the adversary; the adversary can decrypt \(\mathsf{WE.Enc}{\left( x,m \right) }\) by using the backdoor z and does not have to know w.
To circumvent this issue, we define extractable security in an oracle model. The oracle is used to model the Bitcoin blockchain. The extractability is possible to achieve for most of the non-artificial oracles. In particular, when the oracle is instantiated with a decentralised cryptocurrency such as Bitcoin, this kind of backdoor is unlikely to exist since it is believed that no one can have a witness w in advance for each instance x.
Efficiency comparison Assume a CNF formula has n variables and k clauses, and m literals. The ciphertext size of our witness encryption scheme is \(2n+2k+1\) group elements. The evaluation time is \(n+\mathcal{O}{\left( k\mathsf{log}\frac{m}{2k} \right) }\). The multilinearity level is \(n+m-k\) and can be optimised to \(n+\mathcal{O}{\left( k\mathsf{log}\frac{m}{2k} \right) }\).
The efficiency of encoding CNF-SAT in [43] depends on the reduction which is unspecified in [43]. As far as we know, the best reductions from CNF-SAT to Exact-Cover is CNF-SAT \(\rightarrow \) 3-CNF-SAT \(\rightarrow \) Exact-Cover (The details of the second reduction can be found in Appendix H). However, the reduction from CNF-SAT to 3-CNF-SAT increases the number of variables and clauses by the size of the original CNF formula, that is \(n^\prime = \mathcal{O}(m)\) and \(k^\prime = \mathcal{O}(m)\) while m is \(n\cdot k\) in the worst case. The reduction from 3-CNF-SAT to Exact-Cover generates an instance of size \(2n^\prime +7k^\prime +1\). Hence the encoding produces \(\mathcal{O}{\left( m \right) }\) group elements and the evaluation time and multilinearity level are also \(\mathcal{O}{\left( m \right) }\) with \(m=n\cdot k\) in the worst case. There are three instantiations of witness encryption for CNF formulas in [46]. Two of them are specific to the composite order multilinear groups. The prime-order groups are usually more natural and result in simpler security assumptions. The conversion from composite-order construction to prime-order multilinear groups (or more generally, groups of arbitrary order) is very expensive [46] and results in a ciphertext of \(O(n^5 k^2)\) group elements.
A direct encoding for Subset-Sum is given in [71] which encodes every integer vector in a different group. As a result, the encoding of the CNF formula is of the size of \(n+m-k\) group elements which is \(O(n\cdot k)\) in the worst case. The multilinearity level and the evaluation time are both \(n+m-k\). In comparison, our encoding for Subset-Sum only encodes the same integer vector once which results in \(2n+2k+1\) group elements. Although subgroups of multilinear maps used in [71] are indexed by numbers \(G_1,\ldots , G_n\), they have to be instantiated with integer vectors (Sect. 7 in [71]). In fact, subgroups indexed by integer vectors or integers do not affect the size of the group in the current instantiations of multilinear maps [31, 32, 40, 54]. Our witness encryption scheme has the same level of mulitilinearity as [71], i.e., \(n+m-k\), but we can further optimise this as stated above. Another main difference of our witness encryption scheme and the one in [71] is that we prove our scheme is extractable while [71] simply assumes its scheme is extractable.
1.2 Related work and further applications of time-lock encryption
Timed-release encryption was introduced by Rivest et al. [66] and considered in many follow-up works, including [15, 23, 27, 69]. Our approach is fundamentally different from theirs. In particular, we neither need trusted third parties, nor have a considerable computational overhead for decryption. Time-lock puzzles and proofs of (sequential) work [24, 29, 34, 35, 58, 59, 65, 66] are computational problems that can not be solved without running a computer continuously for a certain time. In a sense, our computational reference clocks can be seen as algorithms that continuously and publicly solve publicly verifiable [59] instances of an infinite sequence of time-lock puzzles. Essentially, we show how this computational effort, performed independently of any time-lock encryption scheme, can be “reused” to construct time-lock encryption with efficient decryption.
Time-lock encryption can be used to construct the first timed commitment scheme in the sense of Boneh and Naor [17] that does not require an inefficient forced opening. A clever idea to use Bitcoin deposits to facilitate fairness in multiparty computation was presented by Andrychowicz et al. [1, 1, 2]. Very recently, Azar et al. [3] construct “timed-delay” multi-party computation (MPC) protocols, where participating parties obtain the result of the computation only after a certain time, possibly some parties earlier than others. This is similar to the timed-release schemes of [17, 66, 69], in particular it inherits the drawback of inefficient decryption and the assumption that all parties are able to solve the puzzles in about the same time.
Garay et al. [39] analyze the Bitcoin “backbone” protocol, and show how to realize Byzantine agreement on top of this protocol in a synchronous network. Pass et al. [64] formalises the blockchain consensus mechanism in an asynchronous network. Another recent work, which shows how to construct useful cryptographic primitives under the assumption that no adversary is able to outperform the huge computational resources of the collection of all Bitcoin miners, is due to Katz et al. [53], who show how to obtain secure computation and so-called pseudonymous authenticated communication from time-lock puzzles.
Formal computational models capturing “real-world time” were described for instance by Cathalo et al. [23], who gave a security model for timed-release encryption with a “time oracle” that sequentially releases specific information, and recently by Schwenk [67], who described a security model for time-based key exchange protocols. Both works [23, 67] may assume that the party implementing the clock is honest. In contrast, we will have to deal with adversaries that may want to “put the clock forward”, therefore we need to model the computational hardness of doing so in our setting.
Independent work The idea of combining Bitcoin with witness encryption to construct time-lock encryption was described independently in [51, 57]. This paper is a merged version of these works. In March 2015, Andrew Miller sketched the basic idea of combining witness encryption with Bitcoin to get time-lock encryption in a public chat room [60]. The drafts of both [51, 57] have been done before the end of 2014 and are independent of [60].
2 Preliminaries
Definition 1
Let R be a relation. We say that R is an NP-relation, if there exists a deterministic polynomial-time (in |x|) algorithm that, on input (x, w), outputs 1 if and only if \((x,w) \in R\).
2.1 Witness encryption
Syntax Witness encryption was originally proposed by Garg et al. [43]. It provides a means to encrypt to an instance, x, of an NP language and to decrypt by a witness w that x is in the language.
Definition 2
(Witness encryption (WE) [43]) A witness encryption scheme for an NP relation R consists of the following two polynomial-time algorithms:
-
\(\mathsf{WE.Enc}{\left( 1^\lambda , x, m \right) }\) is an encryption algorithm that takes as input a security parameter \(1^\lambda \), an unbounded-length string x, and a message
 , and outputs a ciphertext c.
, and outputs a ciphertext c. -
\(\mathsf{WE.Dec}{\left( c, {w} \right) }\) is a decryption algorithm that takes as input a ciphertext c and a bit-vector w, and outputs a message m or the symbol \(\perp \).
-
Correctness. For any \({\left( x,w \right) }\in R\), we have that
$$\begin{aligned} \Pr {\left[ \mathsf{WE.Dec}{\left( \mathsf{WE.Enc}{\left( 1^{\lambda }, x, m \right) }, w \right) } = m \right] } = 1 \end{aligned}$$
Security A strong security notion for witness encryption is called extractable security which is originally proposed in [48]. The extractability says that when the adversary can distinguish two ciphertext encrypting different messages by using the same instance, then it must know a witness of the instance. Below we give a variant of extractable security in an oracle model. Intuitively, the oracle models the Bitcoin blockchain and will be instantiated with a computational reference clock defined in the next Sect. 3 when modelling our time-lock encryption. The extractability is possible to achieve for most of the non-artificial oracles. We will show that this definition is sufficient for our application of time-lock encryption. In Sect. 6, we propose a novel witness encryption scheme and we prove our new scheme achieves this form of extractable security.
Definition 3
(Extractable security) Let R be an NP relation,  be a witness encryption scheme for R, and
be a witness encryption scheme for R, and  be the following security experiment.
be the following security experiment.

We say that  is \((t,t^\prime ,q,q^\prime ,\varepsilon ,\varepsilon ^\prime )\)-secure w.r.t. an oracle
is \((t,t^\prime ,q,q^\prime ,\varepsilon ,\varepsilon ^\prime )\)-secure w.r.t. an oracle  , if for any adversary \(\mathcal{A}= (\mathcal{A}_0, \mathcal{A}_1)\) that performs at most t operations and queries the oracle for at most q times, there exists an extractor E that performs at most \(t^\prime \) operations and queries the oracle for at most \(q^\prime \) times, such that for all \(x\in {\left\{ 0,1 \right\} }^*\), the following holds:
, if for any adversary \(\mathcal{A}= (\mathcal{A}_0, \mathcal{A}_1)\) that performs at most t operations and queries the oracle for at most q times, there exists an extractor E that performs at most \(t^\prime \) operations and queries the oracle for at most \(q^\prime \) times, such that for all \(x\in {\left\{ 0,1 \right\} }^*\), the following holds:

The above definition states that if an adversary that runs in time t and queries the oracle for at most q times can break the encryption scheme with probability more than \(\varepsilon \), then there exists an extractor E that runs in time \(t^\prime \) and extracts a witness with probability more than \(\varepsilon ^\prime \). In the above definition, we give the adversary access to an oracle  . We do not yet specify what the oracle does. In the next section, we shall prove the extractable security w.r.t. an oracle in the generic model of multilinear maps. This is due to the fact that we have our proof in an idealised model, which allows us to circumvent the impossibility result [42].
. We do not yet specify what the oracle does. In the next section, we shall prove the extractable security w.r.t. an oracle in the generic model of multilinear maps. This is due to the fact that we have our proof in an idealised model, which allows us to circumvent the impossibility result [42].
2.2 SNARKs
Definition 4
(SNARKs [12, 13, 44, 56]) A SNARK for a relation R is a triple of polynomial-time algorithms  :
:
-
 takes as input a security parameter \(\lambda \) and an instance x. It computes and outputs a public evaluation key ek and public verification key vk.
takes as input a security parameter \(\lambda \) and an instance x. It computes and outputs a public evaluation key ek and public verification key vk. -
 : on input \((x,w)\in R\), the prover outputs a non-interactive proof \(\pi \)
: on input \((x,w)\in R\), the prover outputs a non-interactive proof \(\pi \) -
 : on input a verification key vk, an input x, and a proof \(\pi \), the verifier outputs \(b=1\) if he is convinced that \((x,w)\in R\).
: on input a verification key vk, an input x, and a proof \(\pi \), the verifier outputs \(b=1\) if he is convinced that \((x,w)\in R\).
A SNARK satisfies the following properties.
-
Completeness For every security parameter \(\lambda \), any instance x and its witness w such that \((x,w)\in R\), the hones prover can convince the verifier:

-
Succinctness An honestly-generated proof \(\pi \) has \(O_{\lambda }(1)\) bits and
 runs in time \(O_{\lambda }(\left| x \right| )\)
runs in time \(O_{\lambda }(\left| x \right| )\) -
Proof of knowledge If the verifier accepts a proof output by a bounded prover, then the prover “knows” a witness for the given instance. Similarly as above, we consider the security definition in an oracle model. We say a SNARK is \((t,t^\prime ,q,q^\prime ,\varepsilon , \varepsilon ^\prime )\)-secure w.r.t. an oracle
 if for every adversary \(\mathcal{A}\) that performs at most t operations and queries the oracle for at most q times, there exists an extractor E that performs at most \(t^\prime \) operations and queries the oracle for at most \(q^\prime \) times, such that for all \(x\in {\left\{ 0,1 \right\} }^*\), the following holds:
if for every adversary \(\mathcal{A}\) that performs at most t operations and queries the oracle for at most q times, there exists an extractor E that performs at most \(t^\prime \) operations and queries the oracle for at most \(q^\prime \) times, such that for all \(x\in {\left\{ 0,1 \right\} }^*\), the following holds: 
3 Definitions of time-lock encryption
In this section we will formally define secure time-lock encryption, computational reference clocks, and their associated relations.
On formally defining time-lock encryption Defining security of time-lock encryption schemes will require a slightly more fine-grained notion of “computational hardness” than most other cryptographic primitives. We will consider two Turing machines
 and
and
 , which both attempt to solve the same super-polynomial-time computational problem. Although the computational problem is super-polynomial, its instances we consider are with a relatively small difficulty parameter which makes the problem solvable within a reasonable and practical time. We will assume that
, which both attempt to solve the same super-polynomial-time computational problem. Although the computational problem is super-polynomial, its instances we consider are with a relatively small difficulty parameter which makes the problem solvable within a reasonable and practical time. We will assume that
 has access to significantly more computational resources than
has access to significantly more computational resources than
 , such that it is infeasible for
, such that it is infeasible for
 to solve the problem faster than
to solve the problem faster than
 . Clearly, modeling both
. Clearly, modeling both
 and
and
 simply as polynomial-time algorithms is not useful here. We will overcome this by making the concrete bounds on the running times of algorithms
simply as polynomial-time algorithms is not useful here. We will overcome this by making the concrete bounds on the running times of algorithms
 and
and
 explicit.
explicit.
A remark on nomenclature We will have to deal with two different notions of “time”. First, the running time of algorithms, usually measured in the number of computational steps an algorithm performs. Second, our computational equivalent of physical time, measured in some abstract discrete time unit. To avoid ambiguity, we will use the word “time” only for our computational equivalent of physical time. Rather than specifying the “running time” of an algorithm, we will specify the “number of operations” performed by the algorithm, assuming that all algorithms are executed on universal Turing machines with identical instruction sets. For example, we will write “algorithm
 performs t operations” instead of “algorithm
performs t operations” instead of “algorithm
 runs in time t”.
runs in time t”.
Computational reference clocks (CRCs) The concepts of computational reference clocks and their associated relations will be necessary to define time-lock encryption.
Definition 5
A computational reference clock (CRC) is a stateful probabilistic machine  that takes input a difficulty parameter \(\kappa \) and outputs an infinite sequence \(w_1, w_2,\ldots \) in the following way. The initial state of
that takes input a difficulty parameter \(\kappa \) and outputs an infinite sequence \(w_1, w_2,\ldots \) in the following way. The initial state of
 is \(w_0\). It runs a probabilistic algorithm
is \(w_0\). It runs a probabilistic algorithm  which computes
which computes  and outputs \(w_\tau \).
and outputs \(w_\tau \).
We write  for \(\tau \in \mathbb {N} \) to abbreviate the process of executing the clock \(\tau \) times in a row, starting from initial state \(w_0\), and outputting the state \(w_\tau \) of
for \(\tau \in \mathbb {N} \) to abbreviate the process of executing the clock \(\tau \) times in a row, starting from initial state \(w_0\), and outputting the state \(w_\tau \) of
 after \(\tau \) executions.
after \(\tau \) executions.
Intuition for Definition 5 The intuition behind this definition is that the machine
 performs an iterative, public computation, which iteratively computes
performs an iterative, public computation, which iteratively computes  . It takes super-polynomial time \(T(\kappa )\) to compute each
. It takes super-polynomial time \(T(\kappa )\) to compute each  .
.
 outputs its complete internal state after each execution, therefore no secret keys or other secret values can be hidden inside
outputs its complete internal state after each execution, therefore no secret keys or other secret values can be hidden inside
 . Algorithm
. Algorithm  is public, too. When executed for the \(\tau \)-th time, the machine responds with the current state of the computation at “time” \(\tau \). Intuitively, \(w_\tau \) serves as a “witness” that the current time is “at least \(\tau \)”.
is public, too. When executed for the \(\tau \)-th time, the machine responds with the current state of the computation at “time” \(\tau \). Intuitively, \(w_\tau \) serves as a “witness” that the current time is “at least \(\tau \)”.
Definition 5 will be useful for the construction of secure time-lock encryption, whenever it is computationally very hard, but not completely infeasible (e.g., when \(\kappa \) is relatively small), to compute \(w_\tau \) from \(w_{\tau -1}\). Think of
 as a very fast machine that works on solving an infinite sequence of computational puzzles. Jumping slightly ahead, we will later instantiate
as a very fast machine that works on solving an infinite sequence of computational puzzles. Jumping slightly ahead, we will later instantiate
 with the collection of all Bitcoin miners that contribute to expanding the publicly known Bitcoin blockchain. When executed for the \(\tau \)-th time, the machine returns the blockchain of length \(\tau \).
with the collection of all Bitcoin miners that contribute to expanding the publicly known Bitcoin blockchain. When executed for the \(\tau \)-th time, the machine returns the blockchain of length \(\tau \).
Definition 6
We say that relation R is associated to
 , if R is an NP-relation, and for all \(x \le \tau \) holds that
, if R is an NP-relation, and for all \(x \le \tau \) holds that

Intuition for Definition 6 The purpose of the relation is to describe which values \(w_\tau \) are acceptable as a “witness for time \(\tau \)”. Note that it makes sense to accept a witness \(w_\tau \) with “for time \(\tau \)” also as a witness for any “earlier time” x with \(x \le \tau \). Hence we require that \((1^{x},w_\tau ) \in R\) holds for all \(x \le \tau \).
Definition 7
Let
 be a computational reference clock. We say that an adversary
be a computational reference clock. We say that an adversary
 \((t,\tau ,\varepsilon )\)-breaks the security of
\((t,\tau ,\varepsilon )\)-breaks the security of
 with respect to R, if it performs at most t operations and \(\tau \in \mathbb {N}\) such that
with respect to R, if it performs at most t operations and \(\tau \in \mathbb {N}\) such that  , where
, where  is the following experiment.
is the following experiment.

The adversary is allowed to make at most \(\tau -1\) times queries to
 in total.
in total.
Intuition for Definition 7 Definition 7 essentially requires a lower bound on the number of operations that have to be performed in order to compute the witness \(w_\tau \) for \(\tau \in \mathbb {N} \). Even given witness \(w_{\tau -1}\) for \(\tau -1\), it should be unlikely for any adversary to output \(w_\tau \) by performing significantly less than t additional operations.
Time-lock encryption Based on the notion of computational reference clocks, we can now define time-lock encryption schemes and their security.
Definition 8
A time-lock encryption scheme for computational reference clock  with message space
with message space
 consists of two polynomial-time algorithms
consists of two polynomial-time algorithms  .
.
-
Encryption
The encryption algorithm
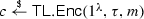 takes as input the security parameter
takes as input the security parameter 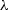 , an integer \(\tau \in \mathbb {N} \), and a message
, an integer \(\tau \in \mathbb {N} \), and a message 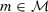 . It computes and outputs a ciphertext c.
. It computes and outputs a ciphertext c. -
Decryption
The decryption algorithm
 takes as input
takes as input  and ciphertext c, and outputs a message
and ciphertext c, and outputs a message 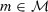 or a distinguished error symbol \(\bot \).
or a distinguished error symbol \(\bot \). -
Correctness
For correctness we require that
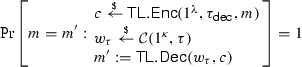
for all
 , all \(\tau \in \mathbb {N} \) with
, all \(\tau \in \mathbb {N} \) with 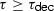 , and all
, and all 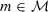 .
.
Remark 1
One may relax the correctness requirement from “perfect correctness” (as above) to correctness up to a negligible error term. We will work with the above perfect correctness condition for simplicity.
Definition 9
We say an adversary  \((t,\tau ,\varepsilon )\)-breaks time-lock encryption scheme
\((t,\tau ,\varepsilon )\)-breaks time-lock encryption scheme  for a clock
for a clock  , if \(\mathcal{A}\) performs at most t operations and \(\tau \in \mathbb {N} \) such that
, if \(\mathcal{A}\) performs at most t operations and \(\tau \in \mathbb {N} \) such that  , where
, where  is the following experiment.
is the following experiment.

We require that \(|m_0| = |m_1|\). The adversary is allowed to make at most \(\tau -1\) queries to  in total.
in total.
Intuition for Definition 9 The intuition behind this security definition is essentially that no adversary should be able to distinguish an encryption of \(m_0\) from an encryption of \(m_1\) by performing significantly less operations than the number of operations required to compute w with \((1^{\tau },w) \in R\). At a first glance it might appear that security in this sense is impossible to achieve, because
 computes such values and it is a polynomial-time algorithm. Thus, the adversary is a polynomial-time algorithm, too, then it could simply perform the same computations as
computes such values and it is a polynomial-time algorithm. Thus, the adversary is a polynomial-time algorithm, too, then it could simply perform the same computations as
 . Therefore we put an explicit bound t on the number of operations that
. Therefore we put an explicit bound t on the number of operations that
 may perform. This makes this definition useful when it is reasonable to assume that the number of operations t that can be performed within a certain time by the adversary is much smaller than the (also polynomially bounded, but much larger) number of operations \(t^\prime \) performed by
may perform. This makes this definition useful when it is reasonable to assume that the number of operations t that can be performed within a certain time by the adversary is much smaller than the (also polynomially bounded, but much larger) number of operations \(t^\prime \) performed by
 to compute w with \((1^\tau ,w) \in R\).
to compute w with \((1^\tau ,w) \in R\).
4 Constructing time-lock encryption
We first construct a time-lock encryption using witness encryption, then we show how to reduce ciphertext size and multilinearity level using SNARKs.
4.1 Constructing time-lock encryption from witness encryption
Construction 1
Let  be a computational reference clock and let R be an NP-relation, such that R is associated to
be a computational reference clock and let R be an NP-relation, such that R is associated to  . Let
. Let  be a witness encryption scheme for R. Define algorithms
be a witness encryption scheme for R. Define algorithms  of a time-lock encryption scheme as
of a time-lock encryption scheme as

Let us first prove correctness. We have to show that

holds for all  , all
, all  , and all
, and all  . The correctness of the witness encryption scheme guarantees that
. The correctness of the witness encryption scheme guarantees that

for all  , all w with
, all w with  , and all
, and all  . Thus, it remains only to show that
. Thus, it remains only to show that

holds for all  . Since R is associated to
. Since R is associated to  , this follows by Definition 5.
, this follows by Definition 5.
Remark 2
If we use a witness encryption scheme and/or a computational reference with negligible correctness error in the same construction as above, then we obtain a time-lock encryption scheme with negligible correctness error.
Remark 3
When the CRCs are instantiated with Bitcoin, the size of witnesses grows linearly with \(\tau \). However, the Bitcoin blockchain generation time is \(O(\tau \cdot T(\kappa ))\) with \(T(\kappa )\) a super-polynomial, while the computational time of our witness encryption is \(O(\tau )\). In our time-lock encryption, the super-polynomial \(T(\kappa )\) computational work is done by the Bitcoin community which possesses the huge computational resources. The current block mining difficulty is about \(\kappa \approx 71\) which means the Bitcoin community needs to hash \(2^{71}\) (\(\approx 10^{21}\)) times on average to find a nonce for a new block. It is worth pointing out that size of witnesses growing linearly holds for Bitcoin, but not necessarily for any other instantiation of CRCs. Bitcoin is just one practical example that illustrates that the concept of CRCs indeed makes sense.
Moreover, we choose the concrete setting as the “right” setting for time-lock encryption, because it simplifies the treatment of “difficult, but not too difficult to compute functions” (such as computational reference clocks) very significantly, which would be much more difficult to express precisely with traditional asymptotic formulations.
Theorem 1
For each adversary
 that \((t_\mathsf {tl},\tau ,\varepsilon _\mathsf {tl})\)-breaks
that \((t_\mathsf {tl},\tau ,\varepsilon _\mathsf {tl})\)-breaks  , we can construct an adversary
, we can construct an adversary
 that \((t^\prime ,\tau ,\varepsilon ^\prime )\)-breaks computational reference clock
that \((t^\prime ,\tau ,\varepsilon ^\prime )\)-breaks computational reference clock  , provided that the witness encryption scheme is \((t_\mathsf {tl},t^\prime ,\tau -1,\tau -1,\varepsilon _\mathsf {tl},\varepsilon ^\prime )\)-secure w.r.t.
, provided that the witness encryption scheme is \((t_\mathsf {tl},t^\prime ,\tau -1,\tau -1,\varepsilon _\mathsf {tl},\varepsilon ^\prime )\)-secure w.r.t.  .
.
Proof
Consider the following adversary  against
against  , which runs
, which runs  as a subroutine.
as a subroutine.  defines
defines  by setting
by setting  and
and  . Then it runs the extractor algorithm E for
. Then it runs the extractor algorithm E for  on
on  , and outputs whatever E outputs.
, and outputs whatever E outputs.
By construction of
 and the definition of experiments
and the definition of experiments  and
and  we have
we have

Thus, by the \((t_\mathsf {tl},t^\prime ,\tau -1,\tau -1,\varepsilon _\mathsf {tl},\varepsilon ^\prime )\)-security of  , the extractor E (and therefore also
, the extractor E (and therefore also
 ) issues at most \(\tau -1\) queries to
) issues at most \(\tau -1\) queries to  . It runs in time \(t^\prime \), and computes a witness w with \((1^\tau , w) \in R\) with probability at least \(\varepsilon ^\prime \). Thus,
. It runs in time \(t^\prime \), and computes a witness w with \((1^\tau , w) \in R\) with probability at least \(\varepsilon ^\prime \). Thus,
 \((t^\prime ,\tau ,\varepsilon ^\prime )\)-breaks
\((t^\prime ,\tau ,\varepsilon ^\prime )\)-breaks
 . \(\square \)
. \(\square \)
4.2 Reducing multilinearity level using SNARKs
For the existing constructions of witness encryption [7, 21, 41, 43, 46], as well as our proposed scheme in the following Sect. 6, the size of the ciphertext and the running time for encryption and decryption is linear in terms of the length of witness. Usually the linear complexity is very natural and efficient. Unfortunately, this is not good enough for witness encryption because all the instantiations of witness encryption are based on multilinear maps [18] of which the research is still in its infancy [31, 32, 40, 54] and is not yet practical regardless of recent lines of attacks. Furthermore, the existing implementations for multilinear maps are not compact, that is, the size of the group elements is polynomial in the multilinearity level (i.e., the maximum number of pairings). The multilinearity level is polynomial in the length of the witness. To mitigate this issue, we propose our second construction of time-lock encryption by using SNARKs [12,13,14, 44, 49, 55, 56, 62] together with witness encryption. The idea is to encrypt with SNARKs verification procedure for the statement \((x,w)\in R\), instead of directly encrypting with an instance x. This idea of using SNARKs to gain efficiency is not new [48, 71]. However, we show that using SNARKs can achieve constant multilinearity level regardless of the instance and witness, rather than the previous linear complexity stated in [48, 71].
Construction 2
Let  be a computational reference clock and let R be an NP-relation that is associated to
be a computational reference clock and let R be an NP-relation that is associated to  . Let
. Let  be a witness encryption scheme for R and
be a witness encryption scheme for R and  for R. Algorithms
for R. Algorithms  of a time-lock encryption scheme are defined as
of a time-lock encryption scheme are defined as
-
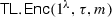 :
:-
(1)
Run the SNARK generator to get
 .
. -
(2)
Let
 and define a relation \(R^* = {\left\{ (x^*,w^*): x^*(w^*) = 1 \right\} }\). Compute
and define a relation \(R^* = {\left\{ (x^*,w^*): x^*(w^*) = 1 \right\} }\). Compute 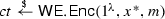 for the relation \(R^*\).
for the relation \(R^*\). -
(3)
Output \(c := (\tau , ek,ct)\).
-
(1)
-
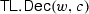 where \(c= (\tau , ek,ct)\):
where \(c= (\tau , ek,ct)\):-
(1)
Run the SNARK prover to get

-
(2)
Let \(w^* = \pi \). Compute and output

-
(1)
For correctness, we will show that

holds for all  , all
, all  , and all
, and all  . By Definition 2, we know that
. By Definition 2, we know that  . By the completeness of SNARK, we have
. By the completeness of SNARK, we have

Let  and \(w^* = \pi \). Then \((x^*,w^*)\in R^*\) as defined above. The correctness of the witness encryption scheme guarantees that
and \(w^* = \pi \). Then \((x^*,w^*)\in R^*\) as defined above. The correctness of the witness encryption scheme guarantees that

Hence we can easily see the correctness holds.
Theorem 2
For each adversary
 that \((t_\mathsf {tl},\tau ,\varepsilon _\mathsf {tl})\)-breaks
that \((t_\mathsf {tl},\tau ,\varepsilon _\mathsf {tl})\)-breaks  , we can construct an adversary
, we can construct an adversary
 that \((t_\mathsf{c},\tau ,\varepsilon _\mathsf{c})\)-breaks computational reference clock
that \((t_\mathsf{c},\tau ,\varepsilon _\mathsf{c})\)-breaks computational reference clock  , provided that the witness encryption scheme is \((t_\mathsf {tl}, t_\mathsf{e}, \tau -1, \tau -1,\varepsilon _\mathsf {tl},\varepsilon _\mathsf{e})\)-secure w.r.t.
, provided that the witness encryption scheme is \((t_\mathsf {tl}, t_\mathsf{e}, \tau -1, \tau -1,\varepsilon _\mathsf {tl},\varepsilon _\mathsf{e})\)-secure w.r.t.  and SNARK is \((t_\mathsf{e}, t_\mathsf{c}, \tau -1, \tau -1, \varepsilon _\mathsf{e}, \varepsilon _\mathsf{c})\)-secure w.r.t.
and SNARK is \((t_\mathsf{e}, t_\mathsf{c}, \tau -1, \tau -1, \varepsilon _\mathsf{e}, \varepsilon _\mathsf{c})\)-secure w.r.t.  .
.
Proof
Suppose an adversary  \((t_\mathsf {tl},\tau ,\varepsilon _\mathsf {tl})\)-breaks time-lock encryption by querying the clock for at most \(\tau -1\) times. The basic idea of the proof is: we construct a witness encryption adversary \(\mathcal{A}_\mathsf{we}\) who uses
\((t_\mathsf {tl},\tau ,\varepsilon _\mathsf {tl})\)-breaks time-lock encryption by querying the clock for at most \(\tau -1\) times. The basic idea of the proof is: we construct a witness encryption adversary \(\mathcal{A}_\mathsf{we}\) who uses  as a subroutine to break witness encryption and triggers the witness extractor to extract a valid SNARK proof. This extractor breaks the SNARK security and triggers the SNARK extractor to extract a witness for \(1^\tau \) which breaks the security of the computational reference clock.
as a subroutine to break witness encryption and triggers the witness extractor to extract a valid SNARK proof. This extractor breaks the SNARK security and triggers the SNARK extractor to extract a witness for \(1^\tau \) which breaks the security of the computational reference clock.
First the SNARK challenger runs  and gives (ek, vk, x) to a SNARK adversary \(\mathcal{A}_\mathsf{s}\). Then \(\mathcal{A}_s\) constructs a new instance
and gives (ek, vk, x) to a SNARK adversary \(\mathcal{A}_\mathsf{s}\). Then \(\mathcal{A}_s\) constructs a new instance  and a challenge ciphertext
and a challenge ciphertext  of witness encryption and give them to a witness encryption adversary \(\mathcal{A}_\mathsf{we}\). Then \(\mathcal{A}_\mathsf{we}\) forwards \(c^*\) to
of witness encryption and give them to a witness encryption adversary \(\mathcal{A}_\mathsf{we}\). Then \(\mathcal{A}_\mathsf{we}\) forwards \(c^*\) to  . \(\mathcal{A}_\mathsf{s}\) queries to
. \(\mathcal{A}_\mathsf{s}\) queries to
 and forwards the answers to \(\mathcal{A}_\mathsf{we}\) and then \(\mathcal{A}_\mathsf{we}\) forwards them to
and forwards the answers to \(\mathcal{A}_\mathsf{we}\) and then \(\mathcal{A}_\mathsf{we}\) forwards them to  . \(\mathcal{A}_\mathsf{we}\) outputs whatever
. \(\mathcal{A}_\mathsf{we}\) outputs whatever  outputs. By assumption, we know witness encryption scheme is \((t_\mathsf {tl},t_\mathsf{e},\tau -1,\tau -1,\varepsilon _\mathsf {tl},\varepsilon _\mathsf{e})\)-secure. Therefore, there exists an extractor E that performs at most \(t_\mathsf{e}\) operations, queries to the oracle at most \(\tau -1\) times and outputs a witness \(w^*\) for \(x^*\) with probability more than \(\varepsilon _\mathsf{e}\). Recall that
outputs. By assumption, we know witness encryption scheme is \((t_\mathsf {tl},t_\mathsf{e},\tau -1,\tau -1,\varepsilon _\mathsf {tl},\varepsilon _\mathsf{e})\)-secure. Therefore, there exists an extractor E that performs at most \(t_\mathsf{e}\) operations, queries to the oracle at most \(\tau -1\) times and outputs a witness \(w^*\) for \(x^*\) with probability more than \(\varepsilon _\mathsf{e}\). Recall that  . This means the extractor outputs a valid proof \(\pi \) such that
. This means the extractor outputs a valid proof \(\pi \) such that  . This extractor is clearly a SNARK adversary with at most \(\tau -1\) times queries from the oracle. Since the SNARK is \((t_\mathsf{e}, t_\mathsf{c}, \tau -1,\tau -1, \varepsilon _\mathsf{e}, \varepsilon _\mathsf{c})\)-secure, this gives us another extractor \(E^\prime \) that performs at most \(t_\mathsf{c}\) operations and queries the oracle at most \(\tau -1\) times and outputs a witness w such that \((1^\tau , w)\in R\) with probability more than \(\varepsilon _\mathsf{c}\). Therefore can see \(E^\prime \) is in fact a clock adversary who \((t_\mathsf{c}, \tau , \varepsilon _\mathsf{c})\)- breaks the clock
. This extractor is clearly a SNARK adversary with at most \(\tau -1\) times queries from the oracle. Since the SNARK is \((t_\mathsf{e}, t_\mathsf{c}, \tau -1,\tau -1, \varepsilon _\mathsf{e}, \varepsilon _\mathsf{c})\)-secure, this gives us another extractor \(E^\prime \) that performs at most \(t_\mathsf{c}\) operations and queries the oracle at most \(\tau -1\) times and outputs a witness w such that \((1^\tau , w)\in R\) with probability more than \(\varepsilon _\mathsf{c}\). Therefore can see \(E^\prime \) is in fact a clock adversary who \((t_\mathsf{c}, \tau , \varepsilon _\mathsf{c})\)- breaks the clock
 . \(\square \)
. \(\square \)
Constant level of multilinearity for witness encryption In Construction 2, the witness encryption encrypts to an instance  which is the verification procedure of a SNARK proof. The only input of \(x^*\) is a SNARK proof \(\pi \) which is succinct, i.e., a constant number of group elements. The original verification procedure
which is the verification procedure of a SNARK proof. The only input of \(x^*\) is a SNARK proof \(\pi \) which is succinct, i.e., a constant number of group elements. The original verification procedure  takes as input the verification key and the instance which means its size and computing time is at least linear in the description of the instance. Intuitively, \(x^*\) has already been initialised with the verification key and the instance, and thus its size and running time can be constant.
takes as input the verification key and the instance which means its size and computing time is at least linear in the description of the instance. Intuitively, \(x^*\) has already been initialised with the verification key and the instance, and thus its size and running time can be constant.
We shall explain how the constant complexity can be achieved with the most recent implementations of SNARKs [12,13,14, 16, 44, 56]. We first consider the SNARKs based on quadratic span programs [12, 13, 44, 56] and we use the general notations from [44]. To verify a SNARK proof, the verifier processes the instance to obtain coefficients \({\left\{ a_i \right\} }_{i\in \mathcal{I}}\) such that \(v_\mathsf{in}(x) = \sum _{i\in \mathcal{I}} a_i v_i(x)\) and then computes an encoding \(E(v_\mathsf{in}(s))\) of \(v_\mathsf{in}(s) = \sum _{k\in \mathcal{I}_\mathsf{in}} a_k \cdot v_k(s)\) by using the verification key. This is the only part of the verification that is linear in the instance and the rest of the verification can be done in a constant number of steps. Notice that verifying the instance becomes unnecessary when encrypting with witness encryption. This is because the verification of the instance can be pre-computed and hard-coded into the ciphertext of witness encryption. More specifically, when encrypting with the SNARK verification procedure with witness encryption, we can pre-compute those coefficients \({\left\{ a_i \right\} }_{i\in I}\) and the encoding \(E(v_\mathsf{in}(s))\), then directly hard-code \(E(v_\mathsf{in}(s))\) into the verification procedure and obtain  . This reduces the size and computing time of \(x^*\) into a constant, therefore the computing complexity of the ciphertext of witness encryption and the underlying multilinearity level become constant. The constant multilinearity level can also be achieved when using SNARKs from PCPs and linear-only encryption [14, 16]. In this case,
. This reduces the size and computing time of \(x^*\) into a constant, therefore the computing complexity of the ciphertext of witness encryption and the underlying multilinearity level become constant. The constant multilinearity level can also be achieved when using SNARKs from PCPs and linear-only encryption [14, 16]. In this case,  consists of a decryption algorithm of linear-only encryption and an LPCP verification decision algorithm for the instance \(1^\tau \). To discuss the complexity of the SNARK verification, we use the notations from Construction 4.5 from [16]. For an \(\ell \)-query LPCP, the complexity of the decryption of the linear-only encryption is linear in \(\ell \), and the complexity of the LPCP verification decision algorithm depends on the size of the instance x. For boolean circuit and arithmetic circuit satisfaction, 3-query LPCPs are given in Appendix A in [14], where the computation on instance x in the LPCP decision algorithm can be easily pre-computed and removed when encrypting with witness encryption. Since \(\ell = 3\) and x is removed, the witness encryption for encrypting the SNARK verification is of constant complexity.
consists of a decryption algorithm of linear-only encryption and an LPCP verification decision algorithm for the instance \(1^\tau \). To discuss the complexity of the SNARK verification, we use the notations from Construction 4.5 from [16]. For an \(\ell \)-query LPCP, the complexity of the decryption of the linear-only encryption is linear in \(\ell \), and the complexity of the LPCP verification decision algorithm depends on the size of the instance x. For boolean circuit and arithmetic circuit satisfaction, 3-query LPCPs are given in Appendix A in [14], where the computation on instance x in the LPCP decision algorithm can be easily pre-computed and removed when encrypting with witness encryption. Since \(\ell = 3\) and x is removed, the witness encryption for encrypting the SNARK verification is of constant complexity.
We note that using a third party to set up SNARK parameters is not necessary for our time-lock encryption scheme. The party who produces the ciphertext can generate the SNARK parameters itself. This party can be assumed to be trusted, since it is the owner of the plaintext. The receiver of the ciphertext can outsource the computation of generating a SNARK proof from a blockchain to a third party, but this party does not have to be trusted either since the proof can be verified. The receiver can also do this computation himself, of course. There are practical implementations of SNARKs [13, 63] and used in real-world applications, such as [11, 33], in contrast to current multilinear maps. Introducing a third party to set up public parameters for using SNARK can further improve efficiency. One can generate these parameters e.g. by using multi-party protocols [10, 20] that are tailored to support state-of-art SNARK constructions [13, 63]. These multi-party protocols guarantee that even a party controlling all but one of the parties cannot construct fraudulent proofs. One has to run the set-up protocol only once and re-use the parameters across many ciphertexts.
4.3 Extension to adaptively-secure computational reference clocks
In our Bitcoin-based instantiation of a computational reference clock
 described below, the adversary will also be able to modify the state of
described below, the adversary will also be able to modify the state of
 to a certain degree (for instance, by executing Bitcoin transactions). This is not yet captured by Definitions 5 and 7 and the proof of Theorem 1. In this section, we extend the definitions and the security proof from the Sect. 3 to this case.
to a certain degree (for instance, by executing Bitcoin transactions). This is not yet captured by Definitions 5 and 7 and the proof of Theorem 1. In this section, we extend the definitions and the security proof from the Sect. 3 to this case.
Definition 10
A computational reference clock with auxiliary input is a stateful probabilistic machine
 that outputs an infinite sequence \(w_1, w_2,\ldots \) in the following way. The initial state of
that outputs an infinite sequence \(w_1, w_2,\ldots \) in the following way. The initial state of
 is \(w_0\). On input a string
is \(w_0\). On input a string  , it runs a probabilistic algorithm
, it runs a probabilistic algorithm  which computes
which computes  and outputs \(w_\tau \).
and outputs \(w_\tau \).
Intuition for Definition 10 The main difference to Definition 5 is that now we allow the output \(w_\tau \) to depend on some auxiliary input  , which is motivated by the specific computational reference clock given by the Bitcoin blockchain. In Bitcoin the auxiliary input will consist of a list of Bitcoin transactions broadcasted by Bitcoin users in the network. An adversary may influence this list of transactions to some degree, by performing and broadcasting transactions. We will reflect this in the security definition given below, by letting the adversary choose the entire auxiliary input for each iteration of the
, which is motivated by the specific computational reference clock given by the Bitcoin blockchain. In Bitcoin the auxiliary input will consist of a list of Bitcoin transactions broadcasted by Bitcoin users in the network. An adversary may influence this list of transactions to some degree, by performing and broadcasting transactions. We will reflect this in the security definition given below, by letting the adversary choose the entire auxiliary input for each iteration of the  -function.
-function.
Definition 11
We say that an adversary  adaptively \((t,\tau ,\varepsilon )\)-breaks a computational reference clock
adaptively \((t,\tau ,\varepsilon )\)-breaks a computational reference clock  w.r.t. R , if \(\mathcal{A}\) performs at most t operations and it holds that
w.r.t. R , if \(\mathcal{A}\) performs at most t operations and it holds that  and \(\tau \in \mathbb {N}\), where
and \(\tau \in \mathbb {N}\), where  is the following experiment.
is the following experiment.

 may query
may query
 at most \(\tau -1\) times.
at most \(\tau -1\) times.
Intuition for Definition 11 The main difference to Definition 7 is that now the adversary has access to a stateful oracle  , which takes as input
, which takes as input  chosen by the adversary (possibly adaptively and depending on previous oracle responses). The initial state of the oracle is equal to the initial state \(w_0\) of reference clock
chosen by the adversary (possibly adaptively and depending on previous oracle responses). The initial state of the oracle is equal to the initial state \(w_0\) of reference clock  . When queried on input
. When queried on input
 , the oracle computes
, the oracle computes  , using its internal state w and the adversarially-provided input
, using its internal state w and the adversarially-provided input  . It updates its internal state by assigning
. It updates its internal state by assigning  , and returns w.
, and returns w.
Remark 4
Note that we do not have to adapt the security definition for time-lock encryption (Definition 9) to adaptive computational reference clocks, because Definition 9 already fits to the adaptive setting. Technically, we would have to adopt the correctness requirement in Definition 8 by adding the additional auxiliary inputs  of each clock iteration. However, this is straightforward and therefore omitted. We only note that correctness should hold for all possible auxiliary inputs, of course.
of each clock iteration. However, this is straightforward and therefore omitted. We only note that correctness should hold for all possible auxiliary inputs, of course.
Theorem 3
From each adversary
 that \((t_\mathsf {tl},\tau ,\varepsilon _\mathsf {tl})\)-breaks
that \((t_\mathsf {tl},\tau ,\varepsilon _\mathsf {tl})\)-breaks  in Construction 1 by querying
in Construction 1 by querying
 , we can construct an adversary
, we can construct an adversary
 that adaptively \((t^\prime ,\tau ,\varepsilon ^\prime )\)-breaks
that adaptively \((t^\prime ,\tau ,\varepsilon ^\prime )\)-breaks
 , provided that the witness encryption scheme is \((t_\mathsf {tl},t^\prime ,\tau -1,\tau -1,\varepsilon _\mathsf {tl},\varepsilon ^\prime )\)-secure w.r.t.
, provided that the witness encryption scheme is \((t_\mathsf {tl},t^\prime ,\tau -1,\tau -1,\varepsilon _\mathsf {tl},\varepsilon ^\prime )\)-secure w.r.t.
 .
.
The proof is identical to the proof of Theorem 1 and therefore omitted.
Theorem 4
For each adversary
 that \((t_\mathsf {tl},\varepsilon _\mathsf {tl})\)-breaks
that \((t_\mathsf {tl},\varepsilon _\mathsf {tl})\)-breaks  in Construction 2, we can construct an adversary
in Construction 2, we can construct an adversary
 that adaptively \((t^\prime ,\tau ,\varepsilon ^\prime )\)-breaks
that adaptively \((t^\prime ,\tau ,\varepsilon ^\prime )\)-breaks
 , provided that the witness encryption scheme is \((t_\mathsf {tl},t_\mathsf{e},\tau -1, \tau -1,\varepsilon _\mathsf {tl},\varepsilon _\mathsf{e})\)-secure w.r.t.
, provided that the witness encryption scheme is \((t_\mathsf {tl},t_\mathsf{e},\tau -1, \tau -1,\varepsilon _\mathsf {tl},\varepsilon _\mathsf{e})\)-secure w.r.t.
 and SNARKs is \((t_e, t^\prime , \tau -1, \tau -1,\varepsilon _\mathsf {e},\varepsilon ^\prime )\)-secure w.r.t.
and SNARKs is \((t_e, t^\prime , \tau -1, \tau -1,\varepsilon _\mathsf {e},\varepsilon ^\prime )\)-secure w.r.t.
 .
.
The proof follows the same pattern as the proof of Theorem 2 and is therefore omitted.
5 Time-lock encryption based on bitcoin
In this section, we will first describe the necessary background on Bitcoin. Then we explain how the scheme from Sect. 4 can be instantiated based on Bitcoin. Finally, we discuss some engineering tasks that arise in the context of Bitcoin-based time-lock encryption.
5.1 The bitcoin blockchain
Cryptocurrencies are a cryptographic equivalent of regular currencies. The concept of decentralized cryptocurrencies has recently received a lot of attention, mostly motivated by the tremendous success of the most prominent decentralized cryptocurrency Bitcoin [61] and the emerge of a large number of alternative decentralized cryptocurrencies.Footnote 2
Using Bitcoin as an example, we will show how decentralized cryptocurrencies can be used as a concrete instantiation of the abstract concept of computational reference clocks. We stress, however, that Bitcoin serves merely as one concrete example. For instance, other decentralized cryptocurrencies also provide mechanisms that may be used to instantiate such reference clocks.
A complete description of the full Bitcoin system is out of scope of this paper. In particular, we omit all details about Bitcoin transactions, and give only a simplified description that captures the relevant features of Bitcoin. In the sequel we focus on one central building block of Bitcoin, the so-called Bitcoin blockchain. We refer to [61] for a description of the full system.
The Bitcoin blockchain The blockchain is used in Bitcoin to prevent double-spending of Bitcoin (cf. Appendix B). It is a sequence of tuples
that satisfies
where H is a cryptographic hash function based on SHA-256 and \(B_1,\ldots , B_s\) are called blocks. \(B_0\) is a distinguished value, called the genesis block, which is a hard-coded constant in the Bitcoin software. The values \(T_i,r_i,D_i\) are described below.
Bitcoin users may attempt to find the next block \(B_{s+1}\) in the chain, which is a computationally expensive (but feasible) task, because \(B_{s+1}\) must meet certain conditions that we will describe below. Users contributing to this search are called miners. The main incentive to contribute significant computational resources to the progress of the blockchain is that for each new block the respective miner is rewarded with a certain amount of Bitcoin.Footnote 3
Each miner keeps a full local copy of the blockchain, and collects all recent transactions broadcasted by other Bitcoin peers. For each transaction, the miner first checks if it is “malicious”, that is, if it contains any coins that, according to the transaction ledger, are not in possession of the spending party. These transactions are discarded. \(T_{s+1}\) denotes the list of new transactions which are not discarded. The miner now attempts to approve these transactions, by finding that a new block \(B_{s+1}\) in the blockchain which includes these transactions. To this end, the miner increments a counter value \(r_{s+1}\), until the hash
satisfies \(B_{s+1} \le D_{s+1}\), where the binary string \(B_{s+1}\) is interpreted canonically as an integer, and \(D_{s+1}\) is the current value of a variable public system parameter called the target. The size of the target determines the computational hardness of finding new blocks. It is related to the Bitcoin difficulty by the definition
where \(\sigma = (2^{16}-1)\times 2^{208}\) is a constant, called the Bitcoin maximum target. Each new block \(B_{s+1}\) serves as a proof of work for the computational resources contributed by the miner that found \(B_{s+1}\). New blocks are broadcasted to all other Bitcoin peers, along with their associated data \((T_{s+1},r_{s+1},D_{s+1},B_{s})\). All miners receiving the new block \(B_{s+1}\) will then turn to searching for the next block \(B_{s+2}\).
It may happen that at some point the blockchain forks (for instance, if it happens that two miners simultaneously find a new block \(B_{s+1}\)), such that different miners continue their work on different branches of the fork. This problem is resolved in Bitcoin by considering only these transactions as valid, which correspond to the longest branch of the fork. Only newly mined blocks that correspond to the longest branch are rewarded. This provides an incentive for miners to contribute only to the longest branch.
Remark 5
Actually, the “length” of a chain in Bitcoin is not determined by the number of blocks, but by sum of the difficulty of all blocks in the chain. This is done to prevent that an adversary forks the chain by appending some low-difficulty blocks.Footnote 4 This distinction is not relevant for our paper. As in [1], we will therefore assume that the longest chain also corresponds to the chain with the largest sum of difficulties. When referring to the Bitcoin blockchain” in the sequel, we will mean the longest chain.
Note that the complexity of the problem of finding a new block \(B_{s+1}\) with \(B_{s+1} \le D_{s+1}\) grows with decreasing \(D_{s+1}\).Footnote 5 This allows to dynamically modify the complexity of finding a new block by modifying the difficulty. The Bitcoin system frequently adjusts the difficulty, depending on the computational power contributed by miners to the progress of the Bitcoin blockchain,Footnote 6 such that about every 10 minutes a new block is appended to the blockchain.
Important properties of the Bitcoin Blockchain The Bitcoin blockchain has the following two properties, which are particularly relevant to our work.
-
Bitcoin miners have an incentive to contribute significant computational resources to the progress of the blockchain, and to publish their solutions in order to get rewarded for their effort.
The total computing power contributed to the Bitcoin blockchain is huge, as of August 2017 the network computes more than \(6.6 \times 10^{18} \approx 2^{62}\) hashes per second.
-
The Bitcoin blockchain grows constantly and with predictable progress. The difficulty, and thus the size of the target, is frequently adjusted (about every two weeks) to the computational power currently available in the Bitcoin network, such that about every 10 minutes on average a new block is appended to the chain.
5.2 NP-relations based on hash blockchains
Let  be a hash function for some constant d. Let
be a hash function for some constant d. Let  , and let \(\delta : \mathbb {N} \rightarrow [0,2^d-1]\) be a function with polynomially-bounded description. We will call \(\beta \) the starting block and \(\delta \) the target bound function.
, and let \(\delta : \mathbb {N} \rightarrow [0,2^d-1]\) be a function with polynomially-bounded description. We will call \(\beta \) the starting block and \(\delta \) the target bound function.
Definition 12
Let  be the relation where
be the relation where  if and only if
if and only if
and w satisfies all the following properties:
-
\(|T_i|\) and \(|r_i|\) are polynomially bounded, and \(D_i \in [0,2^d-1]\)
-
w contains at least x tuples \((T_i,r_i,D_i,B_i)\)
-
\(B_1 = H(T_1,r_1,D_1,\beta )\)
-
\(B_i = H(T_i,r_i,D_i,B_{i-1})\) for all \(i \in [2,x]\)
-
\(\delta (i) \ge B_i\) for all \(i \in [1,x]\), where we interpret bit strings \(B_1,\ldots ,B_x\) canonically as integers.
Note that
 is an NP-relation, because there is an efficient deterministic algorithm that, given \((1^x,w)\), \(\beta \), and \(\delta \), verifies that
is an NP-relation, because there is an efficient deterministic algorithm that, given \((1^x,w)\), \(\beta \), and \(\delta \), verifies that  by checking the conditions from Definition 12. Note also that the problem of finding a witness w for a given statement \(1^x\) corresponds to the problem of finding a valid blockchain w of length x with respect to \((\beta ,\delta )\), which gets increasingly difficult with decreasing \(\delta \).
by checking the conditions from Definition 12. Note also that the problem of finding a witness w for a given statement \(1^x\) corresponds to the problem of finding a valid blockchain w of length x with respect to \((\beta ,\delta )\), which gets increasingly difficult with decreasing \(\delta \).
5.3 Time-lock encryption from bitcoin
We will now describe the Bitcoin-based computational reference clock
 along with a suitable associated relation
along with a suitable associated relation  . As described in Sect. 3, we can then combine these building blocks with witness encryption, to obtain a Bitcoin-based time-lock encryption scheme.
. As described in Sect. 3, we can then combine these building blocks with witness encryption, to obtain a Bitcoin-based time-lock encryption scheme.
NP-relations based on the Bitcoin blockchain Let  be the hash function used in Bitcoin. Let
be the hash function used in Bitcoin. Let
 be the relation from Definition 12, instantiated with H and the following parameters \(\beta \) and \(\delta \).
be the relation from Definition 12, instantiated with H and the following parameters \(\beta \) and \(\delta \).
-
Set \(\beta := B_0\), where \(B_0\) is the Bitcoin genesis block.
-
Fix a target bound function \(\delta : \mathbb {N} \rightarrow [0,2^{256}-1]\).
Bitcoin-based computational reference clock Let  be the function that expands the Bitcoin blockchain. That is, on input
be the function that expands the Bitcoin blockchain. That is, on input
and auxiliary input  , it computes and outputs the new state \(w_\tau \) such that \(w_{\tau } = (T_1,r_1,D_1,B_1),\ldots ,(T_{\tau },r_{\tau },D_{\tau },B_{\tau })\) with \(H(T_{\tau },r_{\tau },D_{\tau },B_{\tau -1}) = B_{\tau } \le D_\tau \), where \(D_\tau \) is the current Bitcoin target.
, it computes and outputs the new state \(w_\tau \) such that \(w_{\tau } = (T_1,r_1,D_1,B_1),\ldots ,(T_{\tau },r_{\tau },D_{\tau },B_{\tau })\) with \(H(T_{\tau },r_{\tau },D_{\tau },B_{\tau -1}) = B_{\tau } \le D_\tau \), where \(D_\tau \) is the current Bitcoin target.
Let  denote the computational reference clock that computes
denote the computational reference clock that computes  . Then the state of
. Then the state of
 at “time” \(\tau \) consists of the first \(\tau \) tuples of the Bitcoin blockchain. Recall that the progress of the chain is relatively predictable. Assuming that the current length of the chain is \(\tau \) tuples, and that new blocks will continuously be found at a rate of approximately one block every 10 minutes, then we know that in approximately \(10 \cdot x\) minutes the blockchain will contain \(\tau +x\) tuples.
at “time” \(\tau \) consists of the first \(\tau \) tuples of the Bitcoin blockchain. Recall that the progress of the chain is relatively predictable. Assuming that the current length of the chain is \(\tau \) tuples, and that new blocks will continuously be found at a rate of approximately one block every 10 minutes, then we know that in approximately \(10 \cdot x\) minutes the blockchain will contain \(\tau +x\) tuples.
Note that the relations
 from Definition 12 are associated to
from Definition 12 are associated to
 in the sense of Definition 6, provided that \(\beta = B_0\) and \(\delta \) satisfies \(\delta (i) \ge B_i\) for all \(i \in \mathbb {N} \). Unfortunately, the latter is not guaranteed, as it depends on the choice of the target bound function \(\delta \) and the future development of the size of the Bitcoin target. Therefore \(\delta \) must be chosen carefully.
in the sense of Definition 6, provided that \(\beta = B_0\) and \(\delta \) satisfies \(\delta (i) \ge B_i\) for all \(i \in \mathbb {N} \). Unfortunately, the latter is not guaranteed, as it depends on the choice of the target bound function \(\delta \) and the future development of the size of the Bitcoin target. Therefore \(\delta \) must be chosen carefully.
Choosing \(\delta \) carefully. Let x such that \(x > \tau \), that is, no witness w for  is yet contained in the Bitcoin blockchain. We note that any sequence
is yet contained in the Bitcoin blockchain. We note that any sequence
computed by the Bitcoin network in the future is only a potential witness for  . This is because relation
. This is because relation
 depends on the target bound function \(\delta \). By definition, w will only be a witness for
depends on the target bound function \(\delta \). By definition, w will only be a witness for  , if \(B_i \le \delta (i)\) holds for all \(i \in [1,x]\). It might happen that at some point \(\gamma \in [\tau +1,x]\) in the future the Bitcoin target increases to a value \(D_{\gamma }\) such that \(D_{\gamma } \ge \delta (\gamma )\). In this case we will have
, if \(B_i \le \delta (i)\) holds for all \(i \in [1,x]\). It might happen that at some point \(\gamma \in [\tau +1,x]\) in the future the Bitcoin target increases to a value \(D_{\gamma }\) such that \(D_{\gamma } \ge \delta (\gamma )\). In this case we will have  .
.
It is possible to overcome this by choosing \(\delta \) carefully. To this end, consider the following observations.
-
First, note that we must not choose \(\delta \) too small More precisely, we must not choose \(\delta \) such that there exists \(i\in \mathbb {N} \) with \(\delta (i) < B_i\). This is because then our reference clock
 would not provide suitable witness \(w_i\) for
would not provide suitable witness \(w_i\) for 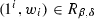 . Thus, the time-lock encryption scheme would not be correct.
. Thus, the time-lock encryption scheme would not be correct. -
Observe also that \(\delta \) must not be too large For instance, recall that
 . Thus, we could try to simply set \(\delta \) such that \(\delta (i) = 2^d\) for all \(i \in \mathbb {N} \). Then \(\delta (i) > B_i\) holds trivially for all \(i \in \mathbb {N} \).
. Thus, we could try to simply set \(\delta \) such that \(\delta (i) = 2^d\) for all \(i \in \mathbb {N} \). Then \(\delta (i) > B_i\) holds trivially for all \(i \in \mathbb {N} \).However, then it becomes very easy to compute witnesses \(w_i\) for
 , by simply evaluating the hash function H i-times to build a chain of length i. Essentially, we have eliminated the size restriction on the \(B_i\) values, such that breaking the security of clock
, by simply evaluating the hash function H i-times to build a chain of length i. Essentially, we have eliminated the size restriction on the \(B_i\) values, such that breaking the security of clock
 is clearly not hard for any such relation
is clearly not hard for any such relation
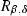 and any reasonable t. The resulting time-lock encryption scheme would be trivially insecure.
and any reasonable t. The resulting time-lock encryption scheme would be trivially insecure.
Ideally, \(\delta \) is chosen such that \(\delta (i) = D_i\) matches the Bitcoin target parameter \(D_i\) for all future \(i > \tau \). However, since \(D_i\) depends on the computational resources that currently contribute to the Bitcoin network, this would require to predict the amount of these resources. Therefore it seems impossible to predict \(D_i\) exactly. But we can try to approximate \(D_i\) with \(\delta \) as closely as possible, such that it always holds that \(\delta (i) = D_i - \varepsilon _i\) for small values \(\varepsilon _i\).
Dependence on the sender’s preferences Note that the “right” choice of \(\delta \) depends on the preference of the sender, which one of the following options is more desirable for the encrypted message.
-
If \(\delta \) is chosen too small, then the witness required to decrypt the message may never be contained in the public Bitcoin blockchain. This may happens if the Bitcoin difficulty decreases faster than expected by the encrypting party choosing \(\delta \). Thus, it may be infeasible to decrypt the ciphertext in reasonable time, such that nobody will ever learn the message (at least not within close time distance to the desired deadline).
-
If \(\delta \) is chosen too large, then an adversary that is able to perform a very large number of computations within a short time may be able to decrypt the message before the deadline, even though its computational resources are significantly below the resources of all Bitcoin miners.
Since it is not clear which of the above options is preferable in general, we think it makes most sense to let the sender choose \(\delta \) application-dependent, or possibly even individually for each encrypted message. If it is more desirable that an encrypted message remains secret (possibly for a much longer time than originally desired by the sender), rather than being decrypted before the deadline, then one would choose a very small target bound function \(\delta \). If it is preferred that the message is rather decrypted earlier than possibly never, then one would choose \(\delta \) larger. The substantial computational resources currently contributed to the Bitcoin network provide a generous margin of error for the choice of \(\delta \).
We consider the “right” choice of \(\delta \) as an application-dependent engineering problem, which we will discuss in Appendix C, along with other engineering questions arising from the Bitcoin-based instantiation of time-lock encryption.
Correctness of the Bitcoin-based time-lock encryption scheme In order to argue correctness of the Bitcoin-based time-lock encryption scheme, we assume that  is associated to
is associated to  in the sense of Definition 6. Note that this is implied by the assumption that Bitcoin is correct.
in the sense of Definition 6. Note that this is implied by the assumption that Bitcoin is correct.
Security of the Bitcoin-based time-lock encryption scheme The following theorem follows from Theorem 3.
Theorem 5
Let  be the time-lock encryption scheme obtained from combining computational reference clock
be the time-lock encryption scheme obtained from combining computational reference clock
 with a witness encryption scheme for relations
with a witness encryption scheme for relations
 by applying the construction from Sect. 4. For each adversary
by applying the construction from Sect. 4. For each adversary
 that \((t_\mathsf {tl},\varepsilon _\mathsf {tl})\)-breaks
that \((t_\mathsf {tl},\varepsilon _\mathsf {tl})\)-breaks  by querying
by querying
 at most q times, we can construct an adversary
at most q times, we can construct an adversary
 that adaptively \((t^\prime ,\varepsilon ^\prime )\)-breaks
that adaptively \((t^\prime ,\varepsilon ^\prime )\)-breaks
 with at most \(q^\prime \) queries with \(q^\prime \le q\), provided that the witness encryption scheme is \((t_\mathsf {tl},t^\prime ,q,q^\prime ,\varepsilon _\mathsf {tl},\varepsilon ^\prime )\)-secure.
with at most \(q^\prime \) queries with \(q^\prime \le q\), provided that the witness encryption scheme is \((t_\mathsf {tl},t^\prime ,q,q^\prime ,\varepsilon _\mathsf {tl},\varepsilon ^\prime )\)-secure.
The assumption that \((t^\prime ,\varepsilon ^\prime )\)-breaking the security of
 with respect to
with respect to
 and reasonable values of \(t^\prime \) and \(\varepsilon '\), can be analyzed in the Random Oracle Model [9]. To this end, consider the following lemma.
and reasonable values of \(t^\prime \) and \(\varepsilon '\), can be analyzed in the Random Oracle Model [9]. To this end, consider the following lemma.
Lemma 1
Let
 be a relation according to Definition 12, instantiated with a random oracle
be a relation according to Definition 12, instantiated with a random oracle  . Let
. Let  be an adversary, which receives as input \((\beta ,\delta )\) and \((1^\tau ,w_\tau )\) with
be an adversary, which receives as input \((\beta ,\delta )\) and \((1^\tau ,w_\tau )\) with  , and issues at most t random oracle queries. Then for all \(x \in \mathbb {N} \) holds that
, and issues at most t random oracle queries. Then for all \(x \in \mathbb {N} \) holds that

where e is Euler’s number and \(\delta _\mathsf {max} := \max _{i \in \{1,\ldots ,x\}}\{\delta (\tau +i)\}\).
The Proof of this lemma can be found in Appendix D
Further game-theoretic aspects Ideally, the target bound function \(\delta \) is chosen such that decrypting the ciphertext earlier would require so many computational resources, that from a game-theoretic perspective it is more reasonable to use these resources to perform a different computation. This is always the case when the value of learning the encrypted message before the deadline is below the revenue obtainable from the different computation.
In particular, an adversary might gain more revenue from mining Bitcoin directly than from trying to learn the time-lock encrypted message earlier than others. The revenue obtainable from Bitcoin mining is easily quantifiable, we think this is a very nice aspect of the Bitcoin-based instantiation of time-lock encryption.
Time-lock encryption beyond Bitcoin In order to obtain a stable and robust time-lock encryption scheme from Bitcoin, it is required that Bitcoin miners will continue to contribute significant computational resources to the progress of the Bitcoin blockchain. It is conceivable that Bitcoin will be discontinued at some point in the future. This may happen, for instance, due to a market crash making Bitcoin worthless, or simply because its popularity decreases over time, possibly replaced by a different cryptocurrency. This is of course unpredictable.
Currently, there are several alternate cryptocurrencies, which are colloquially referred to as “altcoins”, any of which could be used in place of Bitcoin in our construction. Of particular interest is the fact that a large number of these are either Bitcoin derivatives or are built using the same techniques. This means that our construction can be used almost directly for these “altcoins”. Of course we can also replace Bitcoin with any other cryptocurrency.
In particular, one alternative is Ethereum [37, 38], which is the most popular cryptocurrency after Bitcoin, at the time of writing. One particular advantage of Ethereum over Bitcoin is that the average block time is significantly shorter, with a new block every 25 seconds on average (September 2017). However on the other side, we do have a lower hashrate of approximately \(9 \times 10^4 \approx 2^{16.5}\). As with Bitcoin, these figures are liable to change and would then affect the final construction.
We stress that the approach for constructing time-lock encryption described in Sect. 3 is generic. That is, it is motivated by, but not reliant on Bitcoin, nor on any other cryptocurrency for that matter. In principle, our approach can be used with completely different types of iterative, public, large-scale computations. For instance, time-lock encryption could be based on other decentralized cryptocurrencies, or even on completely different types of public computations. The construction from Sect. 5.3 is only one concrete application of the techniques developed in Sect. 3, motivated by the fact that Bitcoin currently seem to be the most interesting candidate instantiation, in particular due to their wide adoption and the significant computational resources contributed to the Bitcoin network.
6 Extractable witness encryption
6.1 Extractable witness encryption from Subset-Sum
In this section, we propose a construction for extractable witness encryption from a special Subset-Sum problem and we prove the extractable security in the generic model of multilinear maps. We will show that the CNF-SAT can be reduced to this special Subset-Sum problem in the next section.
We use notations \({\mathbf u}, {\mathbf v}, {\mathbf w}\) to represent integer vectors. We call a vector of n elements the n-vector. We define \({\mathbf u}\le {\mathbf v}\) as the component-wise comparison. We denote by \({\left\{ {\left( {\mathbf v}_i : \ell _i \right) } \right\} }_{i\in I}\) a multi-set in which the element \({\mathbf v}_i\) occurs \(\ell _i\) times and \({\mathbf v}_1,\ldots , {\mathbf v}_{{\left| I \right| }}\) are pairwise-distinct. Let \({\alpha } := {\left( \alpha _1, \ldots , \alpha _d \right) }\) and \({\mathbf v} := {\left( v_1,\ldots ,v_d \right) }\). We write \(\alpha ^{{\mathbf v}}\) for \(\alpha _1^{v_{1}} \alpha _2^{v_{2}}\ldots \alpha _d^{v_{d}}\).
Our witness encryption scheme makes use of asymmetric multilinear maps in which groups are indexed by integer vectors [19, 40, 72]. Suppose we have a \({\mathbf s}\)-multilinear group family consisting of groups \({\left\{ G_{{\mathbf v}} \right\} }_{\mathbf v}\) of the same order p and \({\mathbf v}\le {\mathbf s}\), where \({\mathbf s}, {\mathbf v}\in \mathbb {Z}^\ell \) are positive integer vectors and the comparison between the vectors holds component-wise. The groups are equipped with a set of multilinear maps, \(\mathsf{e}_{{\mathbf u}, {\mathbf v}}: G_{{\mathbf u}} \times G_{{\mathbf v}} \rightarrow G_{{\mathbf u} + {\mathbf v}}\) for \({\mathbf u} + {\mathbf v} \le {\mathbf s}\), satisfying \(\mathsf{e}_{\scriptscriptstyle {{\mathbf u}, {\mathbf v}}}{\left( {{g}_{{{\mathbf u}}}^{\alpha }},{{g}_{{{\mathbf v}}}^{\beta }} \right) } = {{g}_{{{\mathbf u}+ {\mathbf v}}}^{\alpha \beta }}\). We often omit the subscripts and just write \(\mathsf{e}\).
The original Subset-Sum problem is: given a (multi)set of integer vectors and a target integer vector \({\mathbf s}\), does there exist a subset of the integer vectors such that the sum of its elements is equal to \({\mathbf s}\)? To achieve extractability in witness encryption, our encoding will be performed on a special Subset-Sum problem defined as below:
-
Instance given a multi-set of d-vectors \(\varDelta = {\left\{ {\left( {\mathbf v}_i : \ell _i \right) } \right\} }_{i\in I}\) of positive integers, and a sum d-vector \({\mathbf s}\) of positive integers such that \((\ell _i +1) {\mathbf v}_i \not \le {\mathbf s}\) for each \(i\in I\).
-
Decide is \(\sum _{i\in I} b_i {\mathbf v}_i = {\mathbf s}\) for some integers \(0\le b_i\le \ell _i\) with \(i\in I\)?
Construction 1
(Extractable witness encryption) Suppose x is an instance of the above special Subset-Sum problem and we use the above notations in the following discussion. We construct a witness encryption scheme as below:
-
\(\mathsf{WE.Enc}{\left( 1^\lambda , x, m \right) }\): run
 to get the description of a set of multilinear maps \(\mathsf{e}_{{\mathbf u}, {\mathbf v}}: G_{{\mathbf u}} \times G_{{\mathbf v}} \rightarrow G_{{\mathbf u} + {\mathbf v}}\) for \({\mathbf u} + {\mathbf v} \le {\mathbf s}\), together with group generators \({\left\{ g_{{\mathbf v}} \right\} }_{{\mathbf v}\le {\mathbf s}}\). Choose a random vector \({\alpha } := \langle \alpha _1,\ldots ,\alpha _d \rangle \). The ciphertext is \(c:= {\left( \mathsf{param}, {\left\{ g_{{\mathbf v}_i}^{\alpha ^{{\mathbf v}_i}} \right\} }_{i\in I}, m\cdot g_{{\mathbf s}}^{\alpha ^{{\mathbf s}}} \right) }\).
to get the description of a set of multilinear maps \(\mathsf{e}_{{\mathbf u}, {\mathbf v}}: G_{{\mathbf u}} \times G_{{\mathbf v}} \rightarrow G_{{\mathbf u} + {\mathbf v}}\) for \({\mathbf u} + {\mathbf v} \le {\mathbf s}\), together with group generators \({\left\{ g_{{\mathbf v}} \right\} }_{{\mathbf v}\le {\mathbf s}}\). Choose a random vector \({\alpha } := \langle \alpha _1,\ldots ,\alpha _d \rangle \). The ciphertext is \(c:= {\left( \mathsf{param}, {\left\{ g_{{\mathbf v}_i}^{\alpha ^{{\mathbf v}_i}} \right\} }_{i\in I}, m\cdot g_{{\mathbf s}}^{\alpha ^{{\mathbf s}}} \right) }\). -
\(\mathsf{WE.Dec}{\left( c, {\mathbf w} \right) }\): let \({\mathbf w} := (b_1, b_2,\ldots , b_{{\left| I \right| }})\). Compute the decryption key by

If \(\sum _{i\in I} b_i {\mathbf v}_i = {\mathbf s}\), then \(K = g_{\sum _{i\in I} b_i {\mathbf v}_i}^{\alpha ^{\sum _{i\in I} b_i {\mathbf v}_i}} = g_{{\mathbf s}}^{\alpha ^{{\mathbf s}}}\).
In the above construction, each vector \({\mathbf v}_i\) is only encoded once as a group element \(g_{{\mathbf v}_i}^{\alpha ^{{\mathbf v}_i}}\). The multiple usage of \({\mathbf v}_i\) corresponds to the multiple pairing of \(g_{{\mathbf v}_i}^{\alpha ^{{\mathbf v}_i}}\). However, we cannot allow the encoded element to be used for more than \(\ell _i\) times. This is why we have the side condition \((\ell _i+1){\mathbf v}_i\not \le {\mathbf s}\). If \(g_{{\mathbf v}_i}^{\alpha ^{{\mathbf v}_i}}\) is paired for more than \(\ell _i\) times, then the group index will be no longer smaller than the index of the target group \({\mathbf s}\). Note that the encoding described above does not directly work for the general Subset-Sum problem. For example, given \({\left\{ 1 \right\} }\), there is no subset-sum for 3, but we can obtain the encoding \({{g}_{{3}}^{\alpha ^3}}\) for the sum by computing \(\mathsf{e}{\left( {{g}_{{1}}^{\alpha ^1}}, {{g}_{{1}}^{\alpha ^1}}, {{g}_{{1}}^{\alpha ^1}} \right) }\). The problem is caused by the fact that the encoding \({{g}_{{1}}^{\alpha ^1}}\) can be used for multiple times but the element 1 can only be used for at most once in the Subset-Sum instance.
Theorem 6
Our Construction 1 of witness encryption achieves extractable security with \(t^\prime =\mathsf{poly}(t\cdot \lambda )\) and \(\varepsilon ^\prime = \varepsilon \) and \(q^\prime \le q\) in the generic model of multilinear maps.
A proof of this theorem can be found in Appendix F
Our special Subset-Sum problem can directly encode the Exact-Cover problem by representing each set of the instance of Exact-Cover as a vector and the side condition holds because each set can be used for at most once. This encoding converts the witness encryption scheme [43] into an extractable witness encryption scheme.
A weaker security guarantee for witness encryption is the soundness security. The soundness security states that if \(x\notin L\) then no polynomial-time algorithm can decrypt. An alternative definition for soundness security called adaptive soundness is given in [8]. In fact, the extractable security implies the soundness security since the probability that the extractor can extract a witness is 0 when \(x\notin L\). We also give a discussion about the soundness security of our witness encryption scheme in the Appendix G.
Since the breakthrough construction of Garg et al. [40] in 2013, multilinear maps [31, 32, 40, 45, 54] becomes a very active research area, as well as its cryptanalysis [25, 26, 28, 30, 52, 70]. Our design of witness encryption is independent of the underlying implementations of multilinear maps. In particular, our scheme seems not susceptible to the zeroising attacks since constructing top-level encodings of zeroes is difficult and requires the knowledge of a sufficient number of witnesses. We leave it as a future work to formally investigate the security of our scheme when instantiated with the current approximate multilinear maps.
6.2 Reducing CNF-SAT to Subset-Sum
In this section, we show how to construct an extractable witness encryption for any NP language. This is achieved by constructing an intuitive reduction from an instance of CNF-SAT to an instance of our special Subset-Sum. This results in a more efficient encoding for CNF formulas compared to the encoding in the existing witness encryption schemes.
The Boolean satisfiability problem (SAT) is, given a formula, to check whether it is satisfiable. Let B be a Boolean formula. A literal is either a variable x or the negation of a variable \({\overline{x}}\). A clause is a disjunction of literals, e.g., \(C = x_1\vee {\overline{x_2}} \vee {\overline{x_3}} \vee x_4\). The formula B is said to be in conjunctive normal form (CNF) if it is a conjunction of clauses \(C_1\wedge C_2 \wedge \cdots \wedge C_m\). The SAT problem for CNF formulas is called CNF-SAT.
Definition 13
(Reduction from CNF-SAT to special Subset-Sum) Assume a CNF formula has n variables \(x_1, x_2,\ldots ,x_n\), and k clauses \(C_1, C_2,\ldots ,C_k\), each clause \(C_j\) contains \(m_j\) literals. The reduction to an instance of special Subset-Sum is performed as below:
-
(1)
For each variable \(x_i\) with \(1\le i\le n\), construct two vectors \({\mathbf u}_{i,0}\) and \({\mathbf u}_{i,1}\) of \((n + 2k)\) integers as follows:
-
The i-th element of \({\mathbf u}_{i,0}\) and \({\mathbf u}_{i,1}\) is 1
-
For \(1 \le j \le k\), the \((n+j)\)-th element of \({\mathbf u}_{i,0}\) is 1 if \({\overline{x_i}}\) is in clause \(C_{j}\)
-
For \(1 \le j \le k\), the \((n+j)\)-th element of \({\mathbf u}_{i,1}\) is 1 if \(x_i\) is in clause \(C_{j}\)
-
All other elements of \({\mathbf u}_{i,0}\) and \({\mathbf u}_{i,1}\) are 0
-
-
(2)
For each clause \(C_j\) with \(1\le j\le k\), assume there are \(m_j\) literals in the clause \(C_j\), construct vectors \({\mathbf v}_{j,1}, {\mathbf v}_{j,2},\ldots ,{\mathbf v}_{j,m_j-1}\) of \(n + 2k\) integers:
-
The \({\left( n + j \right) }\)-th element and the \({\left( n+k+j \right) }\)-th element of \({\mathbf v}_{j,1}, {\mathbf v}_{j,2},\ldots ,{\mathbf v}_{j,m_j-1}\) are equal to 1
-
All other elements of \({\mathbf v}_{j,1}, {\mathbf v}_{j,2},\ldots , {\mathbf v}_{j,m_j-1}\) are 0
-
-
(3)
For each clause \(C_j\), we construct vectors \({\mathbf z}_{j,1}, {\mathbf z}_{j,2},\ldots ,{\mathbf z}_{j,m_{j-1}}\) of \(n+2k\) integers as counters:
-
The \({\left( n + k + j \right) }\)-th element of \({\mathbf z}_{j,1}, {\mathbf z}_{j,2},\ldots ,{\mathbf z}_{j,m_{j-1}}\) is equal to 1
-
All other elements of \({\mathbf z}_{j}\) is 0
-
-
(4)
Finally, construct a target sum vector \({\mathbf s}\) of \(n + 2k\) integers:
-
For \(1 \le j \le n\), the j-th element of \({\mathbf s}\) is equal to 1
-
For \(1 \le j \le k\), the \({\left( n+j \right) }\)-th element of \({\mathbf s}\) is equal to \(m_j\).
-
For \(1 \le j \le k\), the \({\left( n+k+j \right) }\)-th element of \({\mathbf s}\) is equal to \(m_j-1\).
-
Intuitively, the vector \({\mathbf u}_{i,0}\) corresponds to the negative occurrences of variable \(x_i\) in the formula while the vector \({\mathbf u}_{i,1}\) corresponds to its positive occurrences. The vectors \({\mathbf v}_{j,1}, {\mathbf v}_{j,2},\ldots ,{\mathbf v}_{j,m_j-1}\) for each clause \(C_j\) will sum to \(m_j-1\) at most, but to complete the sum \(m_j\) at least one will have to come from one of the \({\mathbf u}_{i,0}\) or \({\mathbf u}_{i,1}\) for \(1\le i\le n\), which means the clause has to be satisfied by some literals. An example for explaining this reduction is given in the following example. Notice that when adding these integer vectors, there is no “carry” between adjacent columns.
Example 1
\({\left( x_1\vee {\overline{x_2}} \right) }\wedge {\left( {\overline{x_1}} \vee {\overline{x_2}} \vee x_3 \vee {\overline{x_4}} \right) } \wedge {\left( x_1 \vee x_2\vee x_3 \right) }\) is encoded in Figure 1. The assignment \(x_1= 1, x_2 = 0, x_3 = 1, x_4 =0\) evaluates the formula to true, and it corresponds to the subset sum \({\mathbf u}_{1,1} + {\mathbf u}_{2,0} + {\mathbf u}_{3,1} + {\mathbf u}_{4,0} + {\mathbf v}_{2,1} + {\mathbf v}_{2,2} + {\mathbf v}_{3,1} + {\mathbf z}_{1,1} + {\mathbf z}_{2,1} + {\mathbf z}_{2,2} + {\mathbf z}_{3,1} = {\mathbf s}\).
We shall analyse that the above reduction transforms an instance of CNF-SAT into an instance of our special Subset-Sum, that is the side-condition \((\ell _i+1){\mathbf v}_i\not \le {\mathbf s}\) is satisfied. Each vector \({\mathbf u}_{i,b}\) can occur for at most once in the sum, otherwise the i-th element of the sum will be bigger than 1. The vectors \({\mathbf v}_{j,1},\ldots ,{\mathbf v}_{j,m_j-1}\) are the same vectors and at most \(m_j-1\) of them can occur in the sum, otherwise the \(n+k+j\)-th element of the sum will be bigger than \(m_j-1\). Similarly the vectors \({\mathbf z}_{j,1},\ldots ,{\mathbf z}_{j,m_j-1}\) are the same and at most \(m_j-1\) of them can be used in the sum otherwise the \(n+k+j\)-th element of the sum will be bigger than \(m_j-1\).
Theorem 7
The CNF formula is satisfiable iff subset sum exists.
Proof
If there is a subsequence of integer vectors summing to the sum vector \({\mathbf s}\), this must use exactly one of each of the pairs \({\left( {\mathbf u}_{i,0}, {\mathbf u}_{i,1} \right) }\) (corresponding to each variable \(x_i\) being either false or true but not both) to make the first n elements of the sum correct. Also, each clause of \(C_j\) must have been satisfied by at least one variable, or the next k elements of the sum cannot be big enough. The last k elements of the vectors are the auxiliary counters that will be used for encoding.
When the CNF formula is satisfiable with assignment \(x_1,x_2,\ldots ,x_n\), then we can construct a sub-set sum. We first choose \({\mathbf u}_{1, x_1}, {\mathbf u}_{2, x_2},\ldots ,{\mathbf u}_{n, x_n}\). Then for each \(1\le j\le k\), we compute the number of literals that evaluate to true in \(C_j\) and denote it by \(\ell _j\). For each \(1\le j\le k\), we choose vectors \({\mathbf v}_{j,1},\ldots ,{\mathbf v}_{j,m_j-1-\ell _j}\) and \({\mathbf z}_{j,1},{\mathbf z}_{j,2},\ldots ,{\mathbf z}_{j,\ell _j-1}\). It is easy to see that these vectors add up to the sum vector \({\mathbf s}\).
Therefore, there is a satisfying assignment to \(C_1\wedge C_2 \wedge \cdots \wedge C_k\) if and only if there is a subsequence of the numbers that sums to \({\mathbf s}\). \(\square \)
The reduction of the CNF formula to an instance of the special Subset-Sum consists of \(2n+m\) vectors. However, when we encrypt with Construction 1, the vectors \({\mathbf v}_{j,1},\ldots ,{\mathbf v}_{j,m_{j}-1}\) are encoded as one group element \(g_{{\mathbf v}_{j,1}}^{\alpha ^{{\mathbf v}_{j,1}}}\) since they are the same vectors. Similarly, the vectors \({\mathbf z}_{j,1},\ldots ,{\mathbf z}_{j,m_{j}-1}\) are encoded as \(g_{{\mathbf z}_{j,1}}^{\alpha ^{{\mathbf z}_{j,1}}}\). The ciphertext for encrypting a message m is
Hence the size of the ciphertext for the CNF formula is of \(2n+2k+1\) group elements. The decryption involves \(n+m-k\) mapping operations, that is the n maps to compute \(g_{\sum _{i=1}^n {\mathbf u}_{i,x_i}}^{\alpha ^{\sum _{i=1}^n {\mathbf u}_{i,x_i}}}\), and \(m-k\) maps for \(g_{\delta _j{\mathbf v}_{j,1}}^{\alpha ^{\delta _j{\mathbf v}_{j,1}}}, g_{(m_j - \delta _j){\mathbf z}_{j,1}}^{\alpha ^{(m_j - \delta _j){\mathbf z}_{j,1}}}\) for \(1\le j\le k\) which can be done in time \(O{\left( \sum _{j=1}^k {\left( \mathsf{log}{\left( \delta _i \right) } + \mathsf{log}{\left( m_j-\delta _i \right) } \right) } \right) }\le O{\left( k\mathsf{log}\frac{m}{2k} \right) }\). Hence the decryption has time complexity \(n+O{\left( k\mathsf{log}\frac{m}{2k} \right) }\). where m is the total number of literals occurred in the CNF formula. The multilinearity level is \(n+m-k\) and can be optimised to \(n+\mathcal{O}{\left( k\mathsf{log}\frac{m}{2k} \right) }\) as follows. Instead of encoding \({\mathbf v}_{j,1}\) as \({{g}_{{{\mathbf v}_{j,1}}}^{\alpha ^{{\mathbf v}_{j,1}}}}\), we can encode \({\mathbf v}_{j,1}\) as \(2\lfloor \mathsf{log}{\left( m_j \right) }\rfloor \) elements:
where \(d = 2^{\lfloor \mathsf{log}{\left( m_j \right) }\rfloor }\). As a result, this will keep the multilinearity as \(n+\sum ^k_{j=1} \mathsf{log}{\left( m_j \right) }\), instead of \(n+\sum ^k_{j=1} {\left( m_j-1 \right) }\), while the size of the encoding is of \(2n+2\sum _{i=1}^k \lfloor \mathsf{log}{\left( m_j \right) }\rfloor \) group elements. This optimisation is helpful when the size of elements in the groups depends on the multilinearity in the instantiation of multilinear maps.
7 Conclusions and future work
We have proposed our novel time-lock encryption scheme, which in contrast to previous works requires neither a trusted third party, nor a large computation on the side of the receiver. Our construction leverages any large public computations, such as those involved in Bitcoin, to realise a computational reference clock. We then couple this with an extractable witness encryption to get our final time-lock encryption scheme. However, there is scope for improvement.
As this scheme is essentially the first of its kind, it is more of a proof of concept than a concrete proposal. The current parameters would make an implementation of this scheme quite cumbersome. Thus the first avenue for future work would be to try and find a more practical scheme based on our construction, or indeed a more practical specific construction. Additionally, we get immediate gains from any improvements to our underlying building blocks, or indeed from any new, more efficient building blocks.
This leads us to the first avenue for improvement, which lies in the primitives themselves. As immediate improvement could be realised if we could use a more efficient extractable witness encryption scheme. It would be of particular interest to see if one could realise witness encryption without the use of multilinear maps. Alternatively, one could consider witness encryptions for other languages and see if there are any gains to be made there.
Another potential for improvement would be investigating the possibility of other methods of realising our computational reference clock from other forms large public computations. Or indeed, one may consider what kinds of computation, if carried out on a large distributed scale would allow us a computational reference clock.
Notes
Section 5.1 contains a more detailed background on Bitcoin.
See http://altcoins.com/ for an overview of Bitcoin alternatives.
12.5 bitcoins per block, at a value of approximately 2378 US-$ per Bitcoin, in July 2017.
Under the assumption that H is a sufficiently secure hash function.
See https://bitcoinwisdom.com/bitcoin/difficulty for a chart depicting the recent development of the difficulty in Bitcoin.
Obtained from the classical formulation \(\Pr [X \ge (1+\ell )\mu ] \le e^{\ell \mu } / (1+\ell )^{\mu (1+\ell )}\) by substituting \(x := (1+\ell )\mu \) and \(\ell := x/\mu -1\).
References
Andrychowicz M., Dziembowski S., Malinowski D., Mazurek L.: Secure multiparty computations on Bitcoin. In: 2014 IEEE Symposium on Security and Privacy, pp. 443–458, Berkeley, May 18–21, IEEE Computer Society Press (2014).
Andrychowicz M., Dziembowski S., Malinowski D., Mazurek Ł.: Fair two-party computations via Bitcoin deposits. Cryptology ePrint Archive, Report 2013/837, http://eprint.iacr.org/ (2013).
Azar P., Goldwasser S., Park S.: On time and order in multiparty computation. Cryptology ePrint Archive, Report 2015/178, http://eprint.iacr.org/ (2015).
Barak B., Garg S., Kalai Y.T., Paneth O., Sahai A.: Protecting obfuscation against algebraic attacks. In: EUROCRYPT, pp. 221–238 (2014).
Barak B., Goldreich O., Impagliazzo R., Rudich S., Sahai A., Vadhan S.P., Yang K.: On the (im)possibility of obfuscating programs. In: Kilian J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 1–18. Springer, Berlin (2001).
Barak B., Goldreich O., Impagliazzo R., Rudich S., Sahai A., Vadhan S.P., Yang K.: On the (im)possibility of obfuscating programs. J. ACM 59(2), 6 (2012).
Bellare M., Hoang V.T.: Adaptive witness encryption and asymmetric password-based cryptography. Cryptology ePrint Archive, Report 2013/704, http://eprint.iacr.org/ (2013).
Bellare M., Hoang V.T.: Adaptive witness encryption and asymmetric password-based cryptography. In: PKC, pp. 308–331 (2015).
Bellare M., Rogaway P.: Random oracles are practical: a paradigm for designing efficient protocols. In: Ashby V. (ed). ACM CCS 93, pp. 62–73, Fairfax, November 3–5, ACM Press (1993).
Sasson E.B., Chiesa A., Green M., Tromer E., Virza M.: Secure sampling of public parameters for succinct zero knowledge proofs. In: 2015 IEEE Symposium on Security and Privacy, pp 287–304 (2015).
Ben-Sasson E., Chiesa A., Garman C., Green, M., Miers I., Tromer E., Virza M.: Zerocash: danonymous payments from Bitcoin. In: IEEE Symposium on Security and Privacy, pp. 459–474 (2014).
Ben-Sasson E., Chiesa A., Genkin D., Tromer E., Virza M.: Snarks for C: verifying program executions succinctly and in zero knowledge. CRYPTO 2, 90–108 (2013).
Ben-Sasson E., Chiesa A., Tromer E., Virza M.: Succinct non-interactive zero knowledge for a von neumann architecture. In: 23rd USENIX Security Symposium (USENIX Security 14), pp. 781–796 (2014).
Bitansky N., Chiesa A., Ishai Y., Ostrovsky R., Paneth O.: Succinct non-interactive arguments via linear interactive proofs. In: TCC, pp. 315–333 (2013).
Boneh D., Boyen X., Goh E.-J.: Hierarchical identity based encryption with constant size ciphertext. In: Cramer R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 440–456. Springer, Berlin (2005).
Boneh D., Ishai Y., Sahai A., Wu D.J.: Lattice-based SNARGs and their application to more efficient obfuscation, pp. 247–277. Cham (2017).
Boneh D., Naor M.: Timed commitments. In: Bellare M. (ed). CRYPTO 2000. LNCS, vol. 1880, pp. 236–254. Springer, Berlin (2000).
Boneh D., Silverberg A.: Applications of multilinear forms to cryptography. Contemp. Math. 324, 71–90 (2003).
Boneh D., Waters B., Zhandry M.: Low overhead broadcast encryption from multilinear maps. In: CRYPTO, pp. 206–223 (2014).
Bowe S., Gabizon A., Green M.D.: A multi-party protocol for constructing the public parameters of the pinocchio zk-snark. The 5th Workshop on Bitcoin and Blockchain Research (BITCOIN’18) (2018).
Boyle E., Chung K.-M., Pass R.: On extractability obfuscation. In: Lindell, Yehuda (ed)., TCC 2014. LNCS, vol. 8349, pp. 52–73. Springer, Berlin (2014).
Brakerski Z., Rothblum G.N.: Virtual black-box obfuscation for all circuits via generic graded encoding. IACR Cryptology ePrint Archive, vol. 2013, p. 563 (2013).
Cathalo J., Libert B., Quisquater J.-J.: Efficient and non-interactive timed-release encryption. In: Qing S., Mao W., López J., Wang G. (eds). ICICS 05. LNCS, vol. 3783, pp. 291–303. Springer, Berlin (2005).
Chalkias K., Hristu-Varsakelis D., Stephanides G.: Improved anonymous timed-release encryption. Comput. Secur. 2007, 311–326 (2007).
Chen Y., Gentry C., Halevi S.: Cryptanalyses of zcandidate branching program obfuscators, pp. 278–307 (2017).
Cheon J.H., Han K., Lee C., Ryu H., Stehlé D.: Cryptanalysis of the multilinear map over the integers. In: EUROCRYPT, pp. 3–12 (2015).
Cheon J.H., Hopper N., Kim Y., Osipkov I.: Provably secure timed-release public key encryption. ACM Trans. Inf. Syst. Secur. 11(2), 4 (2008).
Cheon J.H., Lee C., Ryu H.: Cryptanalysis of the new clt multilinear maps. Cryptology ePrint Archive, Report 2015/934, http://eprint.iacr.org/ (2015)
Sherman S.M., Chow V.R., Rieffel E.G.: General certificateless encryption and timed-release encryption, In: SCN, pp. 126–143.
Coron J.-S., Gentry C., Halevi S., Lepoint T., Maji H.K., Miles E., Raykova M., Sahai A., Tibouchi M.: Zeroizing without low-level zeroes: new MMAP attacks and their limitations, pp. 247–266 (2015).
Coron J.-S., Lepoint T., Tibouchi M.: Practical multilinear maps over the integers. In: CRYPTO, pp. 476–493 (2013).
Coron J.-S., Lepoint T., Tibouchi M.: New multilinear maps over the integers. In: CRYPTO, pp. 267–286 (2015).
Danezis G., Fournet C., Kohlweiss M., Parno B.: Pinocchio coin: building zerocoin from a succinct pairing-based proof system. In: PETShop, pp. 27–30 (2013).
Dwork C., Naor M.: Pricing via processing or combatting junk mail. In: Brickell E.(ed.) CRYPTO’92. LNCS, vol. 740, pp. 139–147. Springer, Berlin (1993).
Dwork C., Naor M., Wee H.: Pebbling and proofs of work. In: Shoup V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 37–54. Springer, Berlin (2005).
Eyal I., Sirer E.G.: Majority is not enough: Bitcoin mining is vulnerable. In: Christin N., Safavi-Naini R. (eds.) FC 2014. LNCS, vol. 8437, pp. 436–454. Springer, Berlin (2014).
Ethereum Foundation. Ethereum documentation. http://www.ethdocs.org/en/latest Retrieved (2017).
Ethereum Foundation. Ethereum white paper. http://www.ethdocs.org/en/latest Retrieved (2017).
Garay J., Kiayias A., Leonardos, N.: The Bitcoin backbone protocol: analysis and applications. Cryptology ePrint Archive, Report 2014/765, http://eprint.iacr.org/, accepted to EUROCRYPT 2015 (2014).
Garg S., Gentry C., Halevi S.: Candidate multilinear maps from ideal lattices. In: EUROCRYPT. pp. 1–17 (2013).
Garg S., Gentry C., Halevi S., Raykova M., Sahai A., Waters B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: 54th FOCS, pp. 40–49. IEEE Computer Society Press (2013)
Garg S., Gentry C., Halevi S., Wichs D.: On the implausibility of differing-inputs obfuscation and extractable witness encryption with auxiliary input. In: CRYPTO, pp. 518–535 (2014).
Garg S., Gentry C., Sahai A., Waters B.: Witness encryption and its applications. STOC ’13, pp. 467–476 (2013).
Gennaro R., Gentry C., Parno B., Raykova M.: Quadratic span programs and succinct NIZKs without PCPs. In: EUROCRYPT, pp. 626–645 (2013).
Gentry C., Gorbunov S., Halevi S.: Graph-induced multilinear maps from lattices, pp. 498–527 (2015).
Gentry C., Lewko A.B., Waters B.: Witness encryption from instance independent assumptions. In: CRYPTO, pp. 426–443 (2014).
Gmaxwell. Gmaxwell/alt ideas. https://en.bitcoin.it/wiki/User:Gmaxwell/alt_ideas (2014).
Goldwasser S., Kalai Y.T., Popa R.A., Vaikuntanathan V., Zeldovich N.: How to run turing machines on encrypted data. In: CRYPTO, pp. 536–553 (2013).
Groth J.: Short pairing-based non-interactive zero-knowledge arguments. In: ASIACRYPT, pp. 321–340 (2010).
gwern.net. Time-lock encryption. http://www.gwern.net/Self-decrypting (2015).
Jager T.: How to build time-lock encryption. Cryptology ePrint Archive, Report 2015/478. http://eprint.iacr.org/ (2015).
Coron J.-S., Lepoint T., Tibouchi M.: Cryptanalysis of two candidate fixes of multilinear maps over the integers. https://eprint.iacr.org/2014/975.pdf.
Katz J., Miller A., Shi E.: Pseudonymous secure computation from time-lock puzzles. Cryptology ePrint Archive, Report 2014/857, http://eprint.iacr.org/ (2014)
Langlois A., Stehlé D., Steinfeld R.: GGHLite: more efficient multilinear maps from ideal lattices. In: EUROCRYPT, pp. 239–256 (2014).
Lipmaa H.: Progression-free sets and sublinear pairing-based non-interactive zero-knowledge arguments. In: TCC, pp. 169–189 (2012).
Lipmaa H.: Succinct non-interactive zero knowledge arguments from span programs and linear error-correcting codes. ASIACRYPT 1, 41–60 (2013).
Liu J., Kakvi S.A., Warinschi B.: Time-release protocol from Bitcoin and witness encryption for sat. Cryptology ePrint Archive, Report 2015/482, http://eprint.iacr.org/ (2015)
Mahmoody M., Moran T., Vadhan S.P.: Time-lock puzzles in the random oracle model. In: Rogaway P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 39–50, Springer, Berlin (2011).
Mahmoody M., Moran T., Vadhan S.P.: Publicly verifiable proofs of sequential work. In: Kleinberg, R.D. (ed), ITCS 2013, pp. 373–388. ACM, Berkeley (2013)
Miller A.: #bitcoin-wizards chat forum. 2015. https://botbot.me/freenode/bitcoin-wizards/2015-03-13/?msg=34092097&page=3.
Nakamoto S.: Bitcoin: a peer-to-peer electronic cash system. http://www.bitcoin.org/bitcoin.pdf (2009).
Parno B., Howell J., Gentry C., Raykova M.: Pinocchio: nearly practical verifiable computation. In: IEEE Symposium on Security and Privacy, pp. 238–252 (2013).
Parno B., Howell J., Gentry C., Raykova M.: Pinocchio: nearly practical verifiable computation. In: Proceedings of the 2013 IEEE Symposium on Security and Privacy, SP ’13, pp. 238–252 (2013).
Pass R., Seeman L., Shelat A.: Analysis of the blockchain protocol in asynchronous networks, pp. 643–673. Cham (2017).
Paterson K.G., Quaglia E.A.: Time-specific encryption. In: Proceedings of the 7th International Conference on Security and Cryptography for Networks, SCN’10, pp. 1–16 (2010).
Rivest, Ronald L., Shamir A., Wagner D.A .: Time-lock puzzles and timed-release crypto. Technical report, Massachusetts Institute of Technology (1996).
Schwenk J.: Modelling time for authenticated key exchange protocols. In: Kutylowski M., Vaidya J. (eds.) ESORICS 2014, Part II. LNCS, vol. 8713, pp. 277–294, Springer, Berlin (2014).
Todd, P.: Timelock encryption incentivised by Bitcoin. https://github.com/petertodd/timelock (2014).
Unruh D.: Revocable quantum timed-release encryption. In: Nguyen P.Q., Oswald E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 129–146, Springer, Berlin (2014).
Hu Y., Jia H.: Cryptanalysis of GGH map. https://eprint.iacr.org/2015/301.pdf.
Zhandry M.: How to avoid obfuscation using witness PRFs. In: Proceedings of TCC (2016).
Zimmerman J.: How to obfuscate programs directly. EUROCRYPT Part 9057, 439–467 (2015).
Acknowledgements
Jia Liu’s work has been funded by the UK EPSRC as part of the PETRAS IoT Research Hub Cybersecurity of the Internet of Things grant no: EP/N02334X/1. Tibor Jager and Saqib A. Kakvi were supported by the Federal Ministry of Education and Research, Germany, project REZEIVER, funding code 16K1S0711. Part of this work was done while Jia Liu and Saqib A. Kakvi were employed at the University of Bristol.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by C. Boyd.
Appendices
Appendix A: Other approaches for time-lock encryption
A software published at Github [68] presents the idea of Bitcoin-incentivized timed-release encryption. The scheme in [68] is called “time-lock encryption”, but it is not a time-lock encryption in our sense because it requires expensive exhaustive-search computations for both encryption and decryption, where encryption can be parallelized, but decryption (most likely) not. Moreover, their scheme essentially encrypts the message along with a secret key, which allows to retrieve Bitcoin published in a public deposit. The first party which successfully decrypts the ciphertext is able to collect the deposited coins, which serves as an additional incentive to perform expensive computations to decrypt the message. Therefore, in our terminology, the scheme from [68] is a timed-release encryption scheme in the classical sense of Rivest etr al. [66], where decryption is additionally incentivized by a Bitcoin deposit, but not a time-lock encryption scheme in our sense, where ciphertexts essentially decrypt “automatically” (given the public computational reference clock) and the plaintext becomes publicly available.
Among many examples of timed-release encryption schemes in the sense of Rivest et al. [66], the survey in [50] (referring to [47]) describes the idea to combine “public keys”, which are generated from a public seed with a pseudorandom number generator, with a special-purpose cryptocurrency where “mining” of coins corresponds to computing the corresponding secret keys. As already mentioned in [47], we do not know how to make this idea work. The reason is that cryptocurrencies and time-lock encryption inherently require that progress in the underlying computations can be made only sequentially (in [47] this is called “progress-free”). For example, Bitcoin achieves sequentiality by making each block in the blockchain dependent on all previous blocks. Thus, the approach of [47] requires the existence of “progress-free sequences of public keys”. We are not aware of any proof-of-concept construction of such sequences, and it is unclear whether these objects exists. Moreover, in order to encrypt with the approach described in [47, 50] for “time \(\tau \)”, one would already need to know at least the \(\tau \)-th public key in the sequence, which clearly contradicts sequentiality.
Appendix B: The double-spending problem in cryptocurrencies
A central problem that a secure digital currency has to solve is to prevent double-spending of digital coins. It seems that this is only achievable by somehow keeping track of all previous transactions, in order to be able to determine whether a malicious party tries to spend the same digital coin more than once. There are essentially two approaches to prohibit double-spending:
-
(1)
A central trusted third party (“the bank”) keeps a ledger, which contains all transactions executed in the past. This allows the trusted third party to keep track of which party is in possession of which coin. Coins can only be transferred from one party to another if the trusted third party approves the transaction. Note that this approach is inherently centralized, as it requires a central trustworthy instance that keeps track of all transactions.
-
(2)
The approach used by decentralized cryptocurrencies, like Bitcoin, is somewhat similar, however, the trusted third party is implemented by all (or most) parties simultaneously. Instead of a centralized ledger, the transaction ledger is distributed among all (or many) parties. Essentially, all transactions are broadcasted to all other parties and stored in the ledger, such that each party is able to check whether a given coin already appeared in a previous transaction, and if the claimed owner of a coin is still in possession of this coin. Thus, all parties jointly implement “the bank”. All the recently successful cryptocurrencies, in particular Bitcoin, are decentralized.
The decentralized approach requires a mechanism that allows to find a mutual agreement on the sequence of approved transactions. In Bitcoin, this mechanism is implemented by the Bitcoin blockchain.
Appendix C: Variants and further analysis
In this section, we will discuss several ideas for solving the engineering tasks and further questions related to the Bitcoin-based instantiation of time-lock encryption.
Choosing \(\delta \) for short time periods Let
 for some particular choice of \(\delta \), and let
for some particular choice of \(\delta \), and let

be a time-lock encryption with a witness encryption scheme for  . Observe that for this particular ciphertext we do not need \(\delta (i) \ge B_i\) for all \(i \in \mathbb {N} \) in order to be able to use a witnesses provided by
. Observe that for this particular ciphertext we do not need \(\delta (i) \ge B_i\) for all \(i \in \mathbb {N} \) in order to be able to use a witnesses provided by
 to decrypt c. It suffices if \(\delta (i) \ge B_i\) holds for all
to decrypt c. It suffices if \(\delta (i) \ge B_i\) holds for all  .
.
Given that the computational resources available in the Bitcoin network were relatively predictable in the past, and that the huge computational power gathered in the network provides a generous margin of error, we think that it is relatively easy to determine a suitable target bound function \(\delta \) for all ciphertexts which should be decrypted within a short period of time. By “short” we mean hours, days, or a few weeks.
More robust relations and time-lock encryption for long time periods The longer the time between encryption and decryption of a ciphertext is, the more difficult it becomes to find a suitable target bound function \(\delta \). One could, however, instead use relations which are more “robust” than the ones described in Definition 12. For example, a sender may choose a relation  , which is defined almost identical to the relations
, which is defined almost identical to the relations
 defined above, with the exception that
defined above, with the exception that  accepts
accepts
as a witness for  , even if \(\delta (i) \le B_i\) holds at most \(\omega \) times for \(i \in \{1,\ldots ,\tau \}\). More generally, if a witness encryption scheme for all NP-relations is used as a building block, then a sender could in principle choose any NP-relation it considers reasonable here.
, even if \(\delta (i) \le B_i\) holds at most \(\omega \) times for \(i \in \{1,\ldots ,\tau \}\). More generally, if a witness encryption scheme for all NP-relations is used as a building block, then a sender could in principle choose any NP-relation it considers reasonable here.
On the difficulty of advancing the Bitcoin blockchain faster Note that an adversary
 has two options to advance the Bitcoin blockchain faster than one block every ten minutes.
has two options to advance the Bitcoin blockchain faster than one block every ten minutes.
The first option is that
 performs all its computations secretly. This means that it does not contribute any blocks to the public Bitcoin blockchain, but instead keeps all newly found block secret. This is the approach of an adversary which wants to be exclusively able to decrypt the ciphertext before the deadline. Note that in this case the adversary would have to compute all missing blocks to decrypt a ciphertext on its own. If the target bound function \(\delta \) is chosen well, such that it closely approximates the actual Bitcoin target, then this essentially means that the adversary would have to perform about the same amount of computations as all Bitcoin miners together (unless it finds a better algorithm for solving the computational problem processed by the miners). Assuming that no single adversary is capable of performing this large amount of computations, this is infeasible.
performs all its computations secretly. This means that it does not contribute any blocks to the public Bitcoin blockchain, but instead keeps all newly found block secret. This is the approach of an adversary which wants to be exclusively able to decrypt the ciphertext before the deadline. Note that in this case the adversary would have to compute all missing blocks to decrypt a ciphertext on its own. If the target bound function \(\delta \) is chosen well, such that it closely approximates the actual Bitcoin target, then this essentially means that the adversary would have to perform about the same amount of computations as all Bitcoin miners together (unless it finds a better algorithm for solving the computational problem processed by the miners). Assuming that no single adversary is capable of performing this large amount of computations, this is infeasible.
Alternatively, an adversary might not be interested in being exclusively able to decrypt the ciphertext before the deadline. Instead, it might simply want that the ciphertext can be publicly decrypted earlier than desired by the sender. In this case, the adversary could contribute its computational resources to the public Bitcoin blockchain. Even though the Bitcoin system adjusts the difficulty of advancing the blockchain frequently by modifying the size of the target, note that this happens only relatively slowly, every 2016 blocks. Therefore the difficulty adjustment in Bitcoin is not able to completely prevent such attacks, it may only cushion its effectiveness. However, an adversary that aims at a speed-up by, say, 10% would have to contribute additional resources in the order of 10% of the resources of all other Bitcoin miners together. Thus, the larger the speedup desired by the adversary, the larger are the computational resources it would have to contribute. Moreover, the incentive of other Bitcoin miners to contribute their resources depends on the current difficulty. If this difficulty is too high, then the cost of contributing resources to Bitcoin mining exceeds the revenue obtainable from Bitcoin mining. This would deter other Bitcoin miners from further contributing to the Bitcoin blockchain, which cushions the effectiveness of the resources contributed by the adversary further.
A detailed analysis of adversarial strategies to advance the Bitcoin blockchain significantly faster than one block every ten minutes therefore needs to take such game-theoretic aspects into account, it is therefore out of scope of this paper. See [36] for a related work.
Appendix D: Proof of Lemma 1
Proof
We have to bound the probability that  outputs
outputs
such that w satisfies all conditions of Definition 12. Note that
 receives as input \((1^\tau ,w_\tau )\) with
receives as input \((1^\tau ,w_\tau )\) with  , which corresponds to a chain
, which corresponds to a chain
 has to find at least the remaining x tuples \((T_{\tau +i},r_{\tau +i},D_{\tau +i},B_{\tau +i})\), such that
has to find at least the remaining x tuples \((T_{\tau +i},r_{\tau +i},D_{\tau +i},B_{\tau +i})\), such that
holds for all \(i \in \{1,\ldots ,x\}\). A necessary condition for this is that
 outputs at least x values whose random oracle hash is smaller than or equal to \(\delta _\mathsf {max}\), where \(\delta _\mathsf {max} = \max _{i \in \{1,\ldots ,x\}}\{\delta (\tau +i)\}\). Note also that
outputs at least x values whose random oracle hash is smaller than or equal to \(\delta _\mathsf {max}\), where \(\delta _\mathsf {max} = \max _{i \in \{1,\ldots ,x\}}\{\delta (\tau +i)\}\). Note also that
 is able to output at most \(t+x\), namely the at most t queries \(h_1,\ldots ,h_{t}\) to the random oracle, plus the values \(h_{t+1},\ldots ,h_{t+x}\) returned by
is able to output at most \(t+x\), namely the at most t queries \(h_1,\ldots ,h_{t}\) to the random oracle, plus the values \(h_{t+1},\ldots ,h_{t+x}\) returned by
 , where
, where
We will bound the probability that at least x of these \(t+x\) values satisfy \(H(h_j) \le \delta _\mathsf {max}\), \(j \in \{1,\ldots ,t+x\}\).
Each output \(h_j\) corresponds to an independent Bernoulli experiment, which evaluates to 1 if and only if \(H(h_j) \le \delta _\mathsf {max}\). Let
be random variables, and let X denote the random variable \(X := \sum _{j=1}^{t+x} X_j\). In order to bound the probability that \(X \ge x\), we will apply the Chernoff bound. Note that the the probability that a single Bernoulli experiment outputs 1 is at most \(\delta _\mathsf {max}/2^d\), and the expected number X of experiments that output 1 after \((t+x)\) trials is \(\mu := (t+x) \cdot \delta _\mathsf {max}/2^d\). Then we have
where e is Euler’s number, the first inequality is the Chernoff bound,Footnote 7 and the second inequality uses that \(\mu > 0\). \(\square \)
Appendix E: Generic multilinear map model
We will make use of asymmetric multilinear maps in which groups are indexed by integer vectors [19, 40, 72].
Given a ring R and a universe multi-set U, an element is \({\left[ x \right] }_{S}\) where \(x\in R\) is the value of the element and \(S\subseteq U\) is the index of the element. The binary operations over elements are defined as follows:
-
For two elements \(e_1:= {\left[ x_1 \right] }_{S}\) and \(e_2:= {\left[ x_2 \right] }_{T}\) such that \(S = T\), \(e_1 + e_2\) is defined as \({\left[ x_1 + x_2 \right] }_{S}\), and \(e_1 - e_2\) is defined as \({\left[ x_1 - x_2 \right] }_{S}\).
-
For two elements \(e_1:= {\left[ x_1 \right] }_{S}\) and \(e_2:= {\left[ x_2 \right] }_{T}\), \(e_1 \cdot e_2\) is defined as \({\left( x_1 x_2, S\uplus T \right) }\) for \(S\uplus T\subseteq U\) where \(\uplus \) is the multi-set union.
A generic multilinear map oracle [4, 72] is a stateful oracle \(\mathcal M\) that responds to queries as follows:
-
Initialization \(\mathcal M\) will be initialized with a ring R, a universe set U, and a list L of initial elements. For every \({\left[ x \right] }_{S}\in L\), \(\mathcal M\) generates a handle h. The value of the handles are chosen to be independent of the elements being encoded, and the handles are distinct. \(\mathcal M\) outputs the handles generated for all the elements in L. After the initialisation, all subsequent calls to initialization queries fail.
-
Algebraic operations Given two input handles \(h_1, h_2\) and an operation \(\circ \in {\left( +,-,\cdot \right) }\), \(\mathcal M\) first locates the relevant elements \(e_1, e_2\) in the handle table. If any of the input handles does not appear in the handle table, the call to \(\mathcal M\) fails. Then \(\mathcal M\) computes \(e_1\circ e_2\); the call fails if \(e_1\circ e_2\) is undefined. \(\mathcal M\) generates a new handle for \(e_1\circ e_2\), saves this element and the new handle in the handle table, and returns the new handle.
-
Zero-test Given an input handle h, \(\mathcal M\) first locates the relevant element \({\left[ x \right] }_{S}\) in the handle table. If h does not appear in the handle table, the call fails. If \(S \ne U\) the call fails. Then \(\mathcal M\) returns 1 if \(x = 0\), otherwise returns 0.
The zero-test is only available on the top-level index. The zeros on different index levels are different.
Appendix F: Extractability security
Theorem 6
Our Construction 1 of witness encryption achieves extractable security with \(t^\prime =\mathsf{poly}(t\cdot \lambda )\) and \(\varepsilon ^\prime = \varepsilon \) and \(q^\prime \le q\) in the generic model of multilinear maps.
Proof of Theorem 6
Assume an adversary \(\mathcal{A}= (\mathcal{A}_0, \mathcal{A}_1)\) that run in time t, and an instance \(x\in {\left\{ 0,1 \right\} }^*\)

Then we shall prove there exists an extractor E that run in time \(\varTheta (t\cdot \lambda ^2)\) such that

To ease the discussion, we consider the instances of the special Subset-Sum problem defined in Definition 15, rather than the original SAT problem.
We construct an extractor E by using \(\mathcal{A}\) as subroutine to extract a witness. E queries to the oracle  and forwards the responses to the adversary whenever the adversary queries to
and forwards the responses to the adversary whenever the adversary queries to  . E gives x to \(\mathcal{A}\). \(\mathcal{A}\) chooses \((m_0,m_1)\) and sends them to E. Let x be the instance of special Subset-Sum: given a multi-set of d-vectors \(\varDelta = {\left\{ {\left( {\mathbf v}_i : \ell _i \right) } \right\} }_{i\in I}\) of positive integers and a target sum vector \({\mathbf s}\) of positive integers such that \((\ell _i +1) {\mathbf v}_i \not \le {\mathbf s}\) for each \(i\in I\).
. E gives x to \(\mathcal{A}\). \(\mathcal{A}\) chooses \((m_0,m_1)\) and sends them to E. Let x be the instance of special Subset-Sum: given a multi-set of d-vectors \(\varDelta = {\left\{ {\left( {\mathbf v}_i : \ell _i \right) } \right\} }_{i\in I}\) of positive integers and a target sum vector \({\mathbf s}\) of positive integers such that \((\ell _i +1) {\mathbf v}_i \not \le {\mathbf s}\) for each \(i\in I\).
E chooses  uniformly at random. E encodes the instance x according to our witness encryption scheme as \({\left\{ {{g}_{{{\mathbf v}_i}}^{\alpha ^{{\mathbf v}_i}}} \right\} }_{i\in I} \cup {\left\{ {{g}_{{{\mathbf s}}}^{\alpha ^{{\mathbf s}}}} \right\} }\) where \(\alpha \) is chosen uniformly at random. E chooses d fresh formal symbols \(\mathcal{X}= {\left( X_1,\ldots ,X_d \right) }\) and creates an initial list \(L := {\left\{ h_i\mapsto {\left[ y_i \right] }_{V_i} \right\} }_{i\in I}\cup {\left\{ h\mapsto {\left[ y \right] }_{T}, h^\prime \mapsto {\left[ y^\prime \right] }_{T}, h^{\prime \prime } \mapsto {\left[ y^{\prime \prime } \right] }_{T} \right\} }\) where
uniformly at random. E encodes the instance x according to our witness encryption scheme as \({\left\{ {{g}_{{{\mathbf v}_i}}^{\alpha ^{{\mathbf v}_i}}} \right\} }_{i\in I} \cup {\left\{ {{g}_{{{\mathbf s}}}^{\alpha ^{{\mathbf s}}}} \right\} }\) where \(\alpha \) is chosen uniformly at random. E chooses d fresh formal symbols \(\mathcal{X}= {\left( X_1,\ldots ,X_d \right) }\) and creates an initial list \(L := {\left\{ h_i\mapsto {\left[ y_i \right] }_{V_i} \right\} }_{i\in I}\cup {\left\{ h\mapsto {\left[ y \right] }_{T}, h^\prime \mapsto {\left[ y^\prime \right] }_{T}, h^{\prime \prime } \mapsto {\left[ y^{\prime \prime } \right] }_{T} \right\} }\) where
-
\(V_i := \mathcal{X}^{{\mathbf v}_i}\) and \(T := \mathcal{X}^{{\mathbf s}}\).
-
The handles \(h_i, h\) are chosen uniformly at random.
-
\(y_i,y\) are fresh variables.
Intuitively, \(y_i\) represents \(\alpha ^{{\mathbf v}_i}\), y represents \(m_b + \alpha ^{{\mathbf s}}\), \(y^\prime \) represents \(m_0\) and \(y^{\prime \prime }\) represents \(m_1\). Those variables are used to keep track of adversary’s computation. E gives those handles \({\left\{ h_i \right\} }_{i\in I}\cup {\left\{ h, h^\prime , h^{\prime \prime } \right\} }\) to \(\mathcal{A}\). E answers the multilinear maps oracle queries for addition, subtraction and multiplication as defined in Appendix E. To answer the zero-test queries, E instantiates those variables with its real values and test whether the results are zeros.
Note that our proof also works when the handles for group generators \(\widehat{h}\mapsto {\left[ 1 \right] }_T\) and \(\widehat{h}_i\mapsto {\left[ 1 \right] }_{V_i})\) for \(i\in I\) are given to the adversary, although our scheme itself does not need to give the group generators. The elements of the other index level are hidden.
We define an extraction function \(\mathsf{ext}\) over the polynomials z produced by the adversary. The \(\mathsf{ext}(z)\) returns an \(\left| I \right| \)-vector of integers as follows:

\(\square \)
Apparently this extraction function can be efficiently computed for any polynomial z.
Lemma 2
For any formal polynomials z produced by \(\mathcal{A}\) at an index level \(U := \mathcal{X}^{{\mathbf u}}\) with \(U\subseteq T\) for some d-vector \({\mathbf u}\) (\({\mathbf u}\le {\mathbf s}\)). Let \(\mathsf{ext}{\left( z \right) } = {\left( \delta _1,\ldots ,\delta _{\left| I \right| } \right) }\).
-
(1)
\(\mathsf{ext}(z) = \mathbf{0}\) iff z is constructed by only using variable \(y,y^\prime ,y^{\prime \prime }\).
-
(2)
If \(\mathsf{ext}(z)\ne \mathbf{0}\), then \(\sum _{i\in I} \delta _i {\mathbf v}_i = {\mathbf u}\) and \(0\le \delta _i\le \ell _i\) for each \(i\in I\).
Proof
The proof of the two results goes by induction on the structure of z.
-
(1)
if \(z = y_i\), its index level is \(\mathcal{X}^{{\mathbf v}_i}\) and \(\mathsf{ext}(z) = (\delta _1,\ldots ,\delta _{\left| I \right| })\) with \(\delta _i = 1\) and \(\delta _j = 0\) for \(j\ne i\). Clearly we have \(\sum _{j\in I} \delta _j {\mathbf v}_j = {\mathbf v}_i\).
-
(2)
if z is \(y, y^\prime , \text{ or } y^{\prime \prime }\), we have \(\mathsf{ext}(z)={\mathbf 0}\).
-
(3)
if \(z = z_{1} + z_{2}\), according to the definition of \(\mathcal M\), we know \(z_{1}, z_{2}\) are both the polynomials of the same index level \(\mathcal{X}^{\mathbf u}\). By induction hypothesis, \(\mathsf{ext}(z_1) = {\mathbf 0}\) (\(\mathsf{ext}(z_2) = {\mathbf 0}\)) iff \(z_1\) (\(z_2\)) is constructed by only using y. By definition of \(\mathsf{ext}\), for \(\mathsf{ext}{\left( z \right) }\) to be \({\mathbf 0}\), it must be \(\mathsf{ext}{\left( z_1 \right) }\) and \(\mathsf{ext}{\left( z_2 \right) }\) are both \({\mathbf 0}\), i.e., both \(z_1\) and \(z_2\) are constructed by only using \(y,y^\prime ,y^{\prime \prime }\). That is to say \(\mathsf{ext}(z) = {\mathbf 0}\) iff z is constructed by only using \(y,y^\prime ,y^{\prime \prime }\). Hence the first result holds.
W.l.o.g., assume \(\mathsf{ext}{\left( z_1 \right) }\ne {\mathbf 0}\). Let \(\mathsf{ext}{\left( z_{1} \right) } = {\left( \delta _{1},\ldots ,\delta _{\left| I \right| } \right) }\). By induction hypothesis, we have \(\sum _{i\in I} \delta _i {\mathbf v}_i = {\mathbf u}\), and \(\delta _i\le \ell _i\) for each \(i\in I\). By definition, \(\mathsf{ext}(z) = (\delta _1,\ldots ,\delta _{\left| I \right| })\), and hence the second result holds.
-
(4)
if \(z = z_{1} - z_{2}\), simiar as above.
-
(5)
if \(z = z_{1} \cdot z_{2}\), by definition of \(\mathsf{ext}\), for \(\mathsf{ext}{\left( z \right) }\) to be \({\mathbf 0}\), it must be \(\mathsf{ext}{\left( z_1 \right) }\) and \(\mathsf{ext}{\left( z_2 \right) }\) are both \({\mathbf 0}\), i.e., both \(z_1\) and \(z_2\) are constructed by only using \(y,y^\prime ,y^{\prime \prime }\). That is to say \(\mathsf{ext}(z) = {\mathbf 0}\) iff z is constructed by only using \(y,y^\prime ,y^{\prime \prime }\). Hence the first result holds.
Let \(\mathsf{ext}{\left( z_{1} \right) } = {\left( \delta ^\prime _{1},\ldots ,\delta ^\prime _{\left| I \right| } \right) }\) and \(\mathsf{ext}{\left( z_{2} \right) } = {\left( \delta ^{\prime \prime }_{1},\ldots ,\delta ^{\prime \prime }_{\left| I \right| } \right) }\). Assume \(z_1\) is a polynomial on index level \(\mathcal{X}^{{\mathbf u}}\) and \(z_2\) is a polynomial on index level \(\mathcal{X}^{{\mathbf w}}\). Then z is a polynomial on index level \(\mathcal{X}^{{\mathbf u}+{\mathbf w}}\). By induction hypothesis, we know that \(\sum _{i\in I} \delta ^\prime _i {\mathbf v}_i = {\mathbf u}\) and \(\delta ^\prime _i\le \ell _i\) for each \(i\in I\), and \(\sum _{i\in I} \delta ^{\prime \prime }_i {\mathbf v}_i = {\mathbf w}\) and \(\delta ^{\prime \prime }_i\le \ell _i\) for each \(i\in I\). Since \(\mathsf{ext}{\left( z \right) } = {\left( \delta ^\prime _1+\delta ^{\prime \prime }_1,\ldots ,\delta ^\prime _{\left| I \right| } + \delta ^{\prime \prime }_{\left| I \right| } \right) }\), we have \(\sum _{i\in I}(\delta ^\prime _i+\delta ^{\prime \prime }_i){\mathbf v}_i = {\mathbf u} + {\mathbf w}\).
We are now left to show that for any \(i\in I\), \(\delta ^\prime _i+\delta ^{\prime \prime }_i\le \ell _i\). Assume for some \(i\in I\), \(\delta ^\prime _i+\delta ^{\prime \prime }_i>\ell _i\). We shall show that \(U\not \subseteq T\). From the condition \(\ell _i {\mathbf v}_i\not \le {\mathbf s}\), we know that \((u_1,\ldots ,u_d)\not \le {\mathbf s}\). But this multiplication will be rejected by the multilinear map oracle. This contradicts the assumption.\(\square \)
Lemma 3
A formal polynomial z produced by the adversary \(\mathcal{A}\) on the top index level \({\mathbf s}\) can be rewritten into \(z = f(y_1,\ldots ,y_{\left| I \right| }) + a\cdot y + a^\prime \cdot y^\prime + a^{\prime \prime }\cdot y^{\prime \prime }\) for some integers \(a, a^\prime , a^{\prime \prime }\) by only collecting the like terms of \(y, y^\prime , y^{\prime \prime }\). Moreover the polynomial \(f(y_1,\ldots ,y_{\left| I \right| })\) is on the top index level and does not contain \(y, y^\prime , y^{\prime \prime }\) and can also be computed by the adversary.
Proof
The initial top index level elements \(h\mapsto {\left[ y \right] }_{T}, h^\prime \mapsto {\left[ y^\prime \right] }_{T}, h^{\prime \prime }\mapsto {\left[ y^{\prime \prime } \right] }_{T}\) can only be added and subtracted. No multiplication is allowed on the top level. Even if the polynomial only contains \(z^\prime -z^\prime \) with \(z^\prime \) on the top index level, this polynomial cannot be multiplied since \(z^\prime -z^\prime \) is a zero on the top index level. That is to say \(y,y^\prime ,y^{\prime \prime }\) do not occur inside of any multiplication operations. Hence we can separate \(y,y^\prime ,y^{\prime \prime }\) by using communicative and associative rules on \(+\). After collecting the like terms of y (no expansion or cancellation of the other terms), z can be rewritten as \(z = f(y_1,\ldots ,y_{\left| I \right| }) + a y + a^\prime y^\prime + a^{\prime \prime } y^{\prime \prime }\) for some polynomial f (which does not contain \(y,y^\prime ,y^{\prime \prime }\)) and some integers \(a,a^\prime ,a^{\prime \prime }\). Clearly for any polynomial produced by \(\mathcal{A}\), its communicative and associative equivalence can also be computed efficiently by \(\mathcal{A}\) by simply changing the order of addition and subtraction on the top level. \(\square \)
Let \(\mathsf{Good}\) be an event that the adversary can construct such a \(z= f(y_1,\ldots ,y_{\left| I \right| }) + a y + a^\prime y^\prime + a^{\prime \prime } y^{\prime \prime }\) with \(f(y_1,\ldots ,y_{\left| I \right| })\ne 0\) (note that we didn’t cancel terms in f. So \(f(y_1,\ldots ,y_{\left| I \right| })\) can only be 0 when it does not exist at all. Even if f only contains terms like \(z^\prime -z^\prime \), f is not 0). If \(\mathsf{Good}\) occurs, by definition \(\mathsf{ext}{\left( f(y_1,\ldots ,y_{\left| I \right| }) \right) }\ne {\mathbf 0}\). Assume \(\mathsf{ext}{\left( f(y_1,\ldots ,y_{\left| I \right| }) \right) } = (\delta _1,\ldots ,\delta _{\left| I \right| })\), then from Lemma 2, we have \(\sum _{i\in I} \delta _i {\mathbf v}_i = {\mathbf s}\) and \(0\le \delta _i\le \ell _i\) for \(i\in I\). In other words, we get a subset sum for \({\mathbf s}\). If Good does not occur, this means the adversary is not able to construct any polynomial that contains elements from both \({\left\{ y_1,\ldots ,y_{\left| I \right| } \right\} }\) and \({\left\{ y,y^\prime ,y^{\prime \prime } \right\} }\), hence the adversary can only constructs the polynomial of the form \(f_1{\left( y_1,\ldots ,y_{{\left| I \right| }} \right) }\) and \(f_2{\left( y,y^\prime ,y^{\prime \prime } \right) }\). Recall that y represents \(m_b + \alpha ^{{\mathbf s}}\), \(y^\prime \) represents \(m_0\) and \(y^{\prime \prime }\) represents \(m_1\). In any polynomial \(f_2{\left( m_b + \alpha ^{{\mathbf s}}, m_0, m_1 \right) }\), the distribution of \(m_b + \alpha ^{{\mathbf s}}\) is exactly the same as any uniform random in the ring because \(\alpha \) is chosen uniformly at random. Hence the adversary can only guess the value of b and we have
Since \(2\cdot { Pr}{\left[ b=b^\prime \right] } - 1 > \varepsilon \), we have \({ Pr}{\left[ \mathsf{Good} \right] }> 2\varepsilon -1\). And the event Good is in fact the event the extractor can extract a witness for the instance of Subset-Sum.
The extractor initialises the multilinear map oracle and it takes time \(\mathsf{poly}(\lambda )\). The extractor performs the group operations of addition, subtraction, multiplication and zero-testing queried by the adversary and it takes \(t\cdot \mathsf{poly}(\lambda )\) time since the addition, subtraction and multiplication take time \(\mathsf{poly}(\lambda )\) and zero-testing is in time \(t\cdot \mathsf{poly}(\lambda )\) since polynomial produced by the adversary is of depth at most \(\varTheta (t)\). The extraction algorithm is in time \(\varTheta (t)\). Hence it takes the extractor \(\mathsf{poly}(t\cdot \lambda )\) times in total. This concludes the proof.
Appendix G: Soundness security
Definition 14
(Soundness security [43] for WE) A witness encryption scheme for a NP language L is \((t,\varepsilon )\)-secure if for any adversary \(\mathcal{A}\) that runs in time t, for any \(x \not \in L\), we have:
The soundness security states that if \(x\notin L\) then no adversary that runs in time t can break the scheme with probability more than \(\varepsilon \). An alternative definition for soundness security called adaptive soundness is given in [8].
The soundness security of our scheme will be based on the following multilinear counting subset-sum Diffie-Hellman (mCSDH) assumption:
Definition 15
(\((t,\varepsilon )\)-secure mCSDH Assumption) Given a multi-set of d-vectors \(\varDelta = {\left\{ {\left( {\mathbf v}_i : \ell _i \right) } \right\} }_{i\in I}\) of positive integers and a sum d-vector \({\mathbf s}\) of positive integers such that \((\ell _i+1){\mathbf v}_i\not \le {\mathbf s}\) for each \(i\in I\).
Let  be a description of a multilinear group family with a set of multilinear maps \(\mathsf{e}_{{\mathbf u}, {\mathbf v}}: G_{{\mathbf u}} \times G_{{\mathbf v}} \rightarrow G_{{\mathbf u} + {\mathbf v}}\) for \({\mathbf u} + {\mathbf v} \le {\mathbf s}\), together with group generators \({\left\{ g_{{\mathbf v}} \right\} }_{{\mathbf v}\le {\mathbf s}}\). Choose a vector of randoms \({\alpha } := \langle \alpha _1,\ldots ,\alpha _d \rangle \) and a random r. If \({\mathbf s}\) cannot be represented as a subset-sum of elements from set \(\varDelta \), then for any distinguisher D that runs in time t,
be a description of a multilinear group family with a set of multilinear maps \(\mathsf{e}_{{\mathbf u}, {\mathbf v}}: G_{{\mathbf u}} \times G_{{\mathbf v}} \rightarrow G_{{\mathbf u} + {\mathbf v}}\) for \({\mathbf u} + {\mathbf v} \le {\mathbf s}\), together with group generators \({\left\{ g_{{\mathbf v}} \right\} }_{{\mathbf v}\le {\mathbf s}}\). Choose a vector of randoms \({\alpha } := \langle \alpha _1,\ldots ,\alpha _d \rangle \) and a random r. If \({\mathbf s}\) cannot be represented as a subset-sum of elements from set \(\varDelta \), then for any distinguisher D that runs in time t,
Theorem 8
Our Construction 1 for witness encryption is \((t,\varepsilon )\)-secure scheme under \((t^\prime ,\varepsilon )\)-mCSDH assumption where \(t^\prime = t + \mathsf{poly}(\lambda )\) where \(\mathsf{poly}(\lambda )\) is the time for setting up the game and computing the challenge ciphertext.
Proof
Let x be an instance of our special Subset-Sum: given a multi-set of d-vectors \(\varDelta = {\left\{ {\left( {\mathbf v}_i : \ell _i \right) } \right\} }_{i\in I}\) of positive integers and a target sum d-vector \({\mathbf s}\) of positive integers such that \(\ell _i{\mathbf v}_i\not \le {\mathbf s}\) for each \(i\in I\).
Suppose an adversary \(\mathcal{A}\) breaks the \((t,\varepsilon )\)-security on x, then we can construct a distingusher to break Assumption 15. Let  be a description of a multilinear group family. Choose a vector of randoms \({\alpha } := \langle \alpha _1,\ldots ,\alpha _d \rangle \). D is given \(U_0:={\left( \mathsf{param}, {\left\{ {{g}_{{{\mathbf v}_i}}^{\alpha ^{{\mathbf v}_{i}}}} \right\} }_{i\in I}, {{g}_{{{\mathbf s}}}^{\alpha ^{{\mathbf s}}}} \right) }\) or \(U_1:={\left( \mathsf{param}, {\left\{ {{g}_{{{\mathbf v}_i}}^{\alpha ^{{\mathbf v}_{i}}}} \right\} }_{i\in I}, {{g}_{{{\mathbf s}}}^{r}} \right) }\) as input. We denote this input by \({\left( \mathsf{param}, {\left\{ {{g}_{{{\mathbf v}_i}}^{\alpha ^{{\mathbf v}_{i}}}} \right\} }_{i\in I}, K \right) }\) where \(K = {{g}_{{{\mathbf s}}}^{\alpha ^{{\mathbf s}}}}\) or \({{g}_{{{\mathbf s}}}^{r}}\). D chooses
be a description of a multilinear group family. Choose a vector of randoms \({\alpha } := \langle \alpha _1,\ldots ,\alpha _d \rangle \). D is given \(U_0:={\left( \mathsf{param}, {\left\{ {{g}_{{{\mathbf v}_i}}^{\alpha ^{{\mathbf v}_{i}}}} \right\} }_{i\in I}, {{g}_{{{\mathbf s}}}^{\alpha ^{{\mathbf s}}}} \right) }\) or \(U_1:={\left( \mathsf{param}, {\left\{ {{g}_{{{\mathbf v}_i}}^{\alpha ^{{\mathbf v}_{i}}}} \right\} }_{i\in I}, {{g}_{{{\mathbf s}}}^{r}} \right) }\) as input. We denote this input by \({\left( \mathsf{param}, {\left\{ {{g}_{{{\mathbf v}_i}}^{\alpha ^{{\mathbf v}_{i}}}} \right\} }_{i\in I}, K \right) }\) where \(K = {{g}_{{{\mathbf s}}}^{\alpha ^{{\mathbf s}}}}\) or \({{g}_{{{\mathbf s}}}^{r}}\). D chooses  and encrypts as \(c_b = {\left( \mathsf{param}, {\left\{ {{g}_{{{\mathbf v}_i}}^{\alpha ^{{\mathbf v}_{i}}}} \right\} }_{i\in I}, {{g}_{{{\mathbf s}}}^{b}}\cdot K \right) }\). D gives \(c_b\) to \(\mathcal{A}\). \(\mathcal{A}\) outputs its guess \(b^\prime \) for b. If \(b = b^\prime \) then D outputs 1; otherwise outputs 0. When D gets \(U_1\), K is uniformly at random and hence c contains no information about b. In this case, \(\mathcal{A}\) can only guess. That is \({ Pr}{\left[ D(U_1) = 1 \right] } = 1/2\). When D gets \(U_0\), from \(\mathcal{A}\)’s view, \(\mathcal{A}\) is playing the perfect soundness security game. Hence \({ Pr}{\left[ D(U_0) = 1 \right] } = \frac{1}{2} \cdot { Pr}{\left[ \mathcal{A}{\left( c_0 \right) } = 0 \right] } + \frac{1}{2} \cdot { Pr}{\left[ \mathcal{A}{\left( c_1 \right) } = 1 \right] } = \frac{1}{2}- \frac{1}{2}\cdot {\left( { Pr}{\left[ \mathcal{A}{\left( c_0 \right) } = 1 \right] } - { Pr}{\left[ \mathcal{A}{\left( c_1 \right) } = 1 \right] } \right) }\). We have \(\left| { Pr}{\left[ D(U_0) = 1 \right] } - { Pr}{\left[ D(U_1) = 1 \right] } \right| = \frac{1}{2}\left| {{ Pr}{\left[ \mathcal{A}{\left( c_0 \right) } = 1 \right] } - { Pr}{\left[ \mathcal{A}{\left( c_1 \right) } = 1 \right] }} \right| \). Hence if \(\mathcal{A}\) breaks the \((t,\varepsilon )\)-security, then D breaks the \((t^\prime ,\varepsilon )\)-mCSDH assumption, where \(t^\prime = t + \mathsf{poly}(\lambda )\) and \(\mathsf{poly}(\lambda )\) denotes a constant number of steps used for computing the challenge ciphertext. \(\square \)
and encrypts as \(c_b = {\left( \mathsf{param}, {\left\{ {{g}_{{{\mathbf v}_i}}^{\alpha ^{{\mathbf v}_{i}}}} \right\} }_{i\in I}, {{g}_{{{\mathbf s}}}^{b}}\cdot K \right) }\). D gives \(c_b\) to \(\mathcal{A}\). \(\mathcal{A}\) outputs its guess \(b^\prime \) for b. If \(b = b^\prime \) then D outputs 1; otherwise outputs 0. When D gets \(U_1\), K is uniformly at random and hence c contains no information about b. In this case, \(\mathcal{A}\) can only guess. That is \({ Pr}{\left[ D(U_1) = 1 \right] } = 1/2\). When D gets \(U_0\), from \(\mathcal{A}\)’s view, \(\mathcal{A}\) is playing the perfect soundness security game. Hence \({ Pr}{\left[ D(U_0) = 1 \right] } = \frac{1}{2} \cdot { Pr}{\left[ \mathcal{A}{\left( c_0 \right) } = 0 \right] } + \frac{1}{2} \cdot { Pr}{\left[ \mathcal{A}{\left( c_1 \right) } = 1 \right] } = \frac{1}{2}- \frac{1}{2}\cdot {\left( { Pr}{\left[ \mathcal{A}{\left( c_0 \right) } = 1 \right] } - { Pr}{\left[ \mathcal{A}{\left( c_1 \right) } = 1 \right] } \right) }\). We have \(\left| { Pr}{\left[ D(U_0) = 1 \right] } - { Pr}{\left[ D(U_1) = 1 \right] } \right| = \frac{1}{2}\left| {{ Pr}{\left[ \mathcal{A}{\left( c_0 \right) } = 1 \right] } - { Pr}{\left[ \mathcal{A}{\left( c_1 \right) } = 1 \right] }} \right| \). Hence if \(\mathcal{A}\) breaks the \((t,\varepsilon )\)-security, then D breaks the \((t^\prime ,\varepsilon )\)-mCSDH assumption, where \(t^\prime = t + \mathsf{poly}(\lambda )\) and \(\mathsf{poly}(\lambda )\) denotes a constant number of steps used for computing the challenge ciphertext. \(\square \)
Theorem 9
The mCSDH assumption achieves \((t,\varepsilon )\)-security with \(t=\mathsf{poly}(\lambda )\) and \(\varepsilon = 0\) in the generic model of multilinear maps.
Proof
The proof is similar to the analysis in Appendix F. In fact, the extractable security implies the soundness security since the probability that the extractor can extract a witness is 0 when the subset sum does not exist. The main difference is that if the target encoding \({{g}_{{{\mathbf s}}}^{\alpha ^{{\mathbf s}}}}\) can be constructed then the subset-sum for \({\mathbf s}\) exists which contradicts with the fact that \(x\notin L\). We can easily see that \({ Pr}{\left[ D{\left( \mathsf{param}, {\left\{ {{g}_{{{\mathbf v}_i}}^{\alpha ^{{\mathbf v}_{i}}}} \right\} }_{i\in I}, {{g}_{{{\mathbf s}}}^{\alpha ^{{\mathbf s}}}} \right) } = 1 \right] } = { Pr}{\left[ D{\left( \mathsf{param}, {\left\{ {{g}_{{{\mathbf v}_i}}^{\alpha ^{{\mathbf v}_{i}}}} \right\} }_{i\in I}, {{g}_{{{\mathbf s}}}^{r}} \right) } = 1 \right] }\). \(\square \)
Appendix H: 3SAT to exact-cover
We give the textbook reduction from 3SAT to Exact-Cover (the best reduction we can find) for the convenience of reader.
Definition 16
(Exact-Cover)
-
Instance A set X and a family \(\mathcal{A}\) of subsets of X
-
Decide Is there an exact cover of X by \(\mathcal{A}\)?
Reducing 3SAT to Exact-Cover Let f be an instance of 3SAT, with variables \(x_1,\ldots ,x_n\) and clauses \(f_1,\ldots ,f_k\). We first construct a graph G from f by setting:
where the notation \(x_i\in f_j\) (resp. \({\overline{x}}_i \in f_j\)) signifies that \(x_i\) (resp. \({\overline{x}}_i\)) is a literal of the clause \(f_j\). We then obtain an instance \((X, \mathcal{A})\) of the Exact-Cover problem from this graph G by setting:
where E(x) denotes the set of edges incident to vertex x in the graph G.
It can be verified that the formula f is satisfiable if and only if the set X has an exact cover by the familiy of \(\mathcal{A}\).
Remark
Although the above reduction does not explicitly refer to 3SAT, for a clause of length \(\ell \), the reduction would generate \(2^\ell \) sets. Hence, the CNF formula has to be reduced into 3CNF first to keep it as an polynomial reduction. Clearly, the number of sets in \(\mathcal{A}\) is \(2n+7k\).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Liu, J., Jager, T., Kakvi, S.A. et al. How to build time-lock encryption. Des. Codes Cryptogr. 86, 2549–2586 (2018). https://doi.org/10.1007/s10623-018-0461-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10623-018-0461-x
Keywords
- Time-lock encryption
- Timed-release encryption
- Bitcoin
- Witness encryption
- SNARKs
- Time-lock puzzles
- Timed commitments





 . Speaking figuratively, “the time-lock has opened”.
. Speaking figuratively, “the time-lock has opened”. , and outputs a ciphertext c.
, and outputs a ciphertext c. takes as input a security parameter
takes as input a security parameter  : on input
: on input  : on input a verification key vk, an input x, and a proof
: on input a verification key vk, an input x, and a proof 
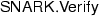 runs in time
runs in time  if for every adversary
if for every adversary 
 takes as input the security parameter
takes as input the security parameter 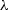 , an integer
, an integer  . It computes and outputs a ciphertext c.
. It computes and outputs a ciphertext c. takes as input
takes as input  and ciphertext c, and outputs a message
and ciphertext c, and outputs a message  or a distinguished error symbol
or a distinguished error symbol 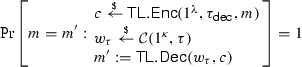
 , all
, all 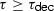 , and all
, and all  .
.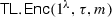 :
: .
. and define a relation
and define a relation 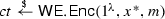 for the relation
for the relation 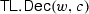 where
where 

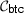 would not provide suitable witness
would not provide suitable witness  . Thus, the time-lock encryption scheme would not be correct.
. Thus, the time-lock encryption scheme would not be correct. . Thus, we could try to simply set
. Thus, we could try to simply set  , by simply evaluating the hash function H i-times to build a chain of length i. Essentially, we have eliminated the size restriction on the
, by simply evaluating the hash function H i-times to build a chain of length i. Essentially, we have eliminated the size restriction on the 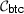 is clearly not hard for any such relation
is clearly not hard for any such relation
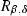 and any reasonable t. The resulting time-lock encryption scheme would be trivially insecure.
and any reasonable t. The resulting time-lock encryption scheme would be trivially insecure. to get the description of a set of multilinear maps
to get the description of a set of multilinear maps 
