Abstract
Secure multi-party computation (MPC) enables multiple players to cooperatively evaluate various functions in the presence of adversaries. In this paper, we consider non-interactive MPC (NIMPC) against honest-but-curious adversaries in the information-theoretic setting, which was introduced by Beimel et al. at CRYPTO 2014. Their main focus is to realize stronger security while completely avoiding interaction, and succeeded to show that every function admits a fully robust NIMPC protocol. In this paper, we further develop the study of NIMPC. We first present a simple lower bound on the communication complexity derived from the correctness requirement of NIMPC. Secondly, we present an efficient NIMPC protocol for indicator functions, which is an important building block of NIMPC protocols. An NIMPC protocol for arbitrary functions is also constructed from the proposed NIMPC for indicator functions by using the generic compiler introduced by Beimel et al. in CRYPTO 2014. The communication complexities of NIMPC protocols presented in this paper are much more efficient than the previous ones. In fact, the gap between the lower and upper bounds of the communication complexity is reduced from exponential in the input length to quadratic. Finally, we show some improvements on the efficiency in the so-called offline-online model. Specifically, for some sets of functions, the exponential amount of offline communication reduces the online communication to almost optimum amount in the standard model.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Secure multi-party computation (MPC) aims to enable multiple players to cooperatively compute various functions in the presence of adversaries. MPC was first introduced by Yao [15] and because of its importance in cryptography, there have been presented many variants so far [6,7,8, 10,11,12,13,14]. At CRYPTO 2014 [2] (and its full version [3]), Beimel et al. have introduced a novel type of MPC, called non-interactive MPC (NIMPC), against honest-but-curious adversaries in the information theoretical setting, which completely avoids interaction while realizing as strong security as possible:
an NIMPC protocol for a function \(f(x_1,\ldots ,x_n)\) is defined by a joint probability distribution \(R=(R_1,\ldots ,R_n)\) and local encoding functions \(\mathsf{ENC}_i(x_i,\,R_i),\) where \(1\le i\le n;\) for a set \(T \subseteq [n]=\{1,\ldots ,n\},\) the protocol is said to be T-it robust (with respect to f) if revealing the messages \((\mathsf{ENC}_i(x_i,\,R_i))_{i\not \in T}\) together with the randomness \((R_i)_{i\in T},\) where \((R_1,\ldots ,R_n)\) is sampled from R, gives the same information about \((x_i)_{i\not \in T}\) as an oracle access to the function f restricted to these input values; for \(0\le t\le n,\) the protocol is said to be t-robust if it is T-robust for every T of size at most t, and it is said to be fully robust if it is n-robust.
In [2, 3], Beimel et al. have succeeded to obtain unconditional positive results for some special cases of interest. In particular, they have presented fully robust NIMPC protocols for various classes of functions including the class of arbitrary functions. However, except for special functions like the summation in an abelian group, the communication complexity is not less than polynomial in the size of the input domain (i.e., exponential in the input length).
The question we ask is whether there is a room to reduce the communication complexity of NIMPC. Unfortunately, a few results has been known about limitations on the communication complexity of MPC. Recently, the research to tackle the difficult problem of lower bounds for communication in MPC becomes active like Data et al. in CRYPTO 2014 [9]. They have developed novel information-theoretic tools to prove lower bounds on the communication complexity in the traditional (i.e., interactive) model involving three parties.
In this paper, we study the communication complexity of NIMPC defined in [2, 3]. As a result, we show that the inefficiency of NIMPC is essentially unavoidable except for special classes of functions. The contributions of this paper are as follows.
-
Communication complexity of NIMPC for the set of arbitrary functions: We derive the first lower bound on the communication complexity of NIMPC for any set of functions. The derived lower bound is the logarithm of the size of the function set. In particular, for the set of arbitrary functions \(f:\mathcal{X}\rightarrow \{0,\,1\}^m\) where \(\mathcal{X}\) is the input domain and m is the output length, the lower bound is \(|\mathcal{X}|\cdot m,\) i.e., exponential in the input length.
-
Communication complexity for the set of indicator functions: On the other hand, for the set of indicator functions, where the number of functions is linear in the input and output length, we have a significantly small lower bound. However, the communication complexity of the previous fully robust NIMPC protocol for indicator functions in [2, 3] is exponential in the input length. NIMPC for indicator functions is used as the main building block of NIMPC for arbitrary functions in [2, 3]. Thus, for the previous fully robust NIMPC protocol for arbitrary functions in [2, 3], there is also an exponential gap between the lower and upper bounds.
-
Efficient fully robust NIMPC protocol for indicator functions: We then reduce the exponential gap between the lower and upper bounds on the communication complexity to quadratic by constructing a much more efficient fully robust NIMPC protocol for indicator functions. Specifically, we present a construction of fully robust NIMPC protocols for indicator functions whose communication complexity is quadratic in the input length (Table 1).
-
Some improvements in the offline-online model: In [2] and the above, it is assumed that all communication happens after the inputs are known. It is mentioned in [3] (Remark 2.6) that it is sometimes useful to separate between offline communication, that can take place after the function is known but before the inputs are known, and online communication that takes place once the inputs are known. For this offline-online model for NIMPC, one desirable feature is low online complexity [3]. For the proper set of indicator functions, we show that the exponential amount of offline communication reduces the online communication to the optimum amount in the standard model. This result is useful for any set \(\mathcal{H}\) of functions that have the same output frequency, that is, \(|\{x\in \mathcal{X}\mid h(x)=y\}|=|\{x\in \mathcal{X}\mid h'(x)=y\}|\) holds for any \(h,\,h'\in \mathcal{H}\) and for any \(y\in \{0,\,1\}^m.\)
Our technique for deriving the lower bounds is quite simple and useful for approximating the amount of communication. We use the fact that the NIMPC model considered in [2, 3] requires that the computed function itself is “private” and, in particular, not known in advance while the target class of functions is public. For the target class of functions, we first assume the existence of a correct NIMPC protocol with some communication complexity and show a method for a server to send data to a client by encoding data into a function and evaluating the function with the use of the NIMPC protocol. Thus, the communication complexity is bounded by the size of target class. If the assumed communication complexity is smaller than the logarithm of the size of the target class, the contradiction is implied. Thus, the communication complexity is lower bounded by the logarithm of the size of the target class. A similar technique is used in [1] for proving impossibility of multiplicative secret sharing rather than derivation of lower bounds. We note that we only use the correctness requirement for deriving the lower bound. Thus, the lower bound in this paper is applicable not only to NIMPC against any collusion including constant-size ones considered in [4, 5] but also to other security models including computational and statistical ones. In addition, our lower bound techniques work for such MPC models that the function itself is private rather than for the standard one where the function is assumed to be known (and the protocol may depend on it).
2 Preliminaries
We recall the notations and definitions of NIMPC introduced in [2]. For an integer n, let [n] be the set \(\{1,\,2,\ldots , n\}.\) For a set \(\mathcal{X}=\mathcal{X}_1\times \cdots \times \mathcal{X}_n\) and \(T\subseteq [n],\) we denote \(.\) For \(x\in \mathcal{X},\) we denote by \(x_T\) the restriction of x to \(\mathcal{X}_T,\) and for a function \(h:\mathcal{X}\rightarrow {\varOmega },\) a subset \(T\subseteq [n],\) and \(x_{\overline{T}}\in \mathcal{X}_{\overline{T}},\) we denote by \(h|_{\overline{T},\,x_{\overline{T}}}: \mathcal{X}\rightarrow {\varOmega }\) the function h where the inputs in \(\mathcal{X}_{\overline{T}}\) are fixed to \(x_{\overline{T}}.\) For a set S, let |S| denote its size (i.e., cardinality of S).
An NIMPC protocol for a family of functions \(\mathcal{H}\) is defined by three algorithms: (1) a randomness generation function \(\mathsf{GEN},\) which given a description of a function \(h\in \mathcal{H}\) generates n correlated random inputs \(R_1,\ldots ,R_n,\) (2) a local encoding function \(\mathsf{ENC}_i\) \((1\le i\le n),\) which takes an input \(x_i\) and a random input \(R_i\) and outputs a message, and (3) a decoding algorithm \(\mathsf{DEC}\) that reconstructs \(h(x_1,\ldots ,x_n)\) from the n messages. The formal definition is given as follows:
Definition 1
(NIMPC: syntax and correctness) Let \(\mathcal{X}_1, \ldots , \mathcal{X}_n,\, \mathcal{R}_1,\ldots , \mathcal{R}_n,\, \mathcal{M}_1, \ldots , \mathcal{M}_n\) and \({\varOmega }\) be finite domains. Let  and let \(\mathcal{H}\) be a family of functions \(h:\mathcal{X}\rightarrow {\varOmega }.\) A non-interactive secure MPC (NIMPC) protocol for \(\mathcal{H}\) is a triplet \({\varPi }=(\mathsf{GEN},\,\mathsf{ENC},\,\mathsf{DEC})\) where
and let \(\mathcal{H}\) be a family of functions \(h:\mathcal{X}\rightarrow {\varOmega }.\) A non-interactive secure MPC (NIMPC) protocol for \(\mathcal{H}\) is a triplet \({\varPi }=(\mathsf{GEN},\,\mathsf{ENC},\,\mathsf{DEC})\) where
-
\(\mathsf{GEN}:\mathcal{H}\rightarrow \mathcal{R}_1\times \cdots \times \mathcal{R}_n\) is a randomized function,
-
\(\mathsf{ENC}\) is an n-tuple of deterministic functions \((\mathsf{ENC}_1,\ldots ,\mathsf{ENC}_n),\) where \(\mathsf{ENC}_i:\mathcal{X}_i\times \mathcal{R}_i\rightarrow \mathcal{M}_i,\)
-
\(\mathsf{DEC}:\mathcal{M}_1\times \cdots \times \mathcal{M}_n\rightarrow {\varOmega }\) is a deterministic function satisfying the following correctness requirement: for any \(x=(x_1,\ldots ,x_n)\in \mathcal{X}\) and \(h\in \mathcal{H},\)
$$\begin{aligned} \Pr \left[ R=\left( R_1,\ldots ,R_n\right) \leftarrow \mathsf{GEN}(h): \mathsf{DEC}(\mathsf{ENC}(x,\,R))=h(x)\right] =1, \end{aligned}$$(1)where \(.\)
The individual communication complexity of \({\varPi }\) is the maximum of \(\log |\mathcal{R}_1|,\ldots , \log |\mathcal{R}_n|,\, \log |\mathcal{M}_1|,\ldots ,\log |\mathcal{M}_n|.\) The total communication complexity of \({\varPi }\) is \(\max \{ \sum _{i\in [n]}\log |\mathcal{R}_i|,\, \sum _{i\in [n]}\log |\mathcal{M}_i|\}.\)
We next show the definition of robustness for NIMPC, which states that a coalition can only learn the information they should. In the above setting, a coalition T can repeatedly encode any inputs for T and decode h with the new encoded inputs and the original encoded inputs of \(\overline{T}.\) Thus, the following robustness requires that they learn no other information than the information obtained from oracle access to \(h|_{\overline{T},\,x_{\overline{T}}}.\)
Definition 2
(NIMPC: robustness) For a subset \(T\subseteq [n],\) we say that an NIMPC protocol \({\varPi }\) for \(\mathcal{H}\) is T-robust if there exists a randomized function \(Sim_T\) (a “simulator”) such that, for every \(h\in \mathcal{H}\) and \(x_{\overline{T}}\in \mathcal{X}_{\overline{T}},\) we have \(Sim_T(h|_{\overline{T},\,x_{\overline{T}}})\equiv (M_{\overline{T}},\,R_{T}),\) where R and M are the joint randomness and messages defined by \(R\leftarrow \mathsf{GEN}(h)\) and \(M_i\leftarrow \mathsf{ENC}_i(x_i,\,R_i).\)
For an integer \(0\le t\le n,\) we say that \({\varPi }\) is t-robust if it is T-robust for every \(T\subseteq [n]\) of size \(|T|\le t.\) We say that \({\varPi }\) is fully robust (or simply refer to \({\varPi }\) as an NIMPC for \(\mathcal{H}\)) if \({\varPi }\) is n-robust. Finally, given a concrete function \(h:\mathcal{X}\rightarrow {\varOmega },\) we say that \({\varPi }\) is a (t-robust) NIMPC protocol for h if it is a (t-robust) NIMPC for \(\mathcal{H}=\{h\}.\)
As the same simulator \(Sim_T\) is used for every \(h\in \mathcal{H}\) and the simulator has only access to \(h|_{\overline{T},x_{\overline{T}}},\) NIMPC hides both h and the inputs of \(\overline{T}.\) An NIMPC protocol is 0-robust if it is \(\emptyset \)-robust. In this case, the only requirement is that the messages \((M_1,\ldots ,M_n)\) reveal h(x) and nothing else.
An NIMPC protocol is also described in the language of protocols in [2]. Such a protocol involves n players \(P_1,\ldots ,P_n,\) each holding an input \(x_i\in \mathcal{X}_i,\) and an external “output server,” a player \(P_0\) with no input. The protocol may have an additional input, a function \(h\in \mathcal{H}.\)
Definition 3
(NIMPC: protocol description) For an NIMPC protocol \({\varPi }\) for \(\mathcal{H},\) let \(\hbox {P}({\varPi })\) denote the protocol that may have an additional input, a function \(h\in \mathcal{H},\) and proceeds as follows.
Protocol P\(({\varPi })(h)\)
-
Offline preprocessing: Each player \(P_i,\, 1\le i\le n,\) receives the random input \(.\)
-
Online messages: On input \(R_i,\) each player \(P_i,\, 1\le i\le n,\) sends the message
 to \(P_0.\)
to \(P_0.\) -
Output: \(P_0\) computes and outputs \(\mathsf{DEC}(M_1,\ldots ,M_n).\)
Informally, the relevant properties of protocol P\(({\varPi })\) are given as follows:
-
For any \(h\in \mathcal{H}\) and \(x\in \mathcal{X},\) the output server \(P_0\) outputs, with probability 1, the value \(h(x_1,\ldots ,x_n).\)
-
Fix \(T\subseteq [n].\) Then, \({\varPi }\) is T-robust if in P\(({\varPi })\) the set of players \(\{P_i\}_{i\in T}\cup \{P_0\}\) can simulate their view of the protocol (i.e., the random inputs \(\{R_i\}_{i\in T}\) and the messages \(\{M_i\}_{i\in \overline{T}}\)) given oracle access to the function h restricted by the other inputs (i.e., \(h|_{\overline{T},x_{\overline{T}}}\)).
-
\({\varPi }\) is 0-robust if and only if in P\(({\varPi })\) the output server \(P_0\) learns nothing but \(h(x_1,\ldots ,x_n).\)
We show a claim in [2] stating that for functions outputting more than one bit, we can compute each output bit separately. Based on this fact, in [2], a fully robust NIMPC protocol for the set of indicator functions was first constructed, and then NIMPC protocols for the set of arbitrary functions are constructed based on it.
Proposition 1
(Claim 7 in [2]) Let \(,\) where \(\mathcal{X}_1,\ldots ,\mathcal{X}_n\) are some finite domains. Fix an integer \(m>1.\) Suppose \(\mathcal{H}\) is a family of boolean functions \(h:\mathcal{X}\rightarrow \{0,\,1\}\) admitting an NIMPC protocol with communication complexity \(\delta .\) Then, the family of functions \(\mathcal{H}^m=\{h:\mathcal{X}\rightarrow \{0,\,1\}^m|h=h_1\circ \cdots \circ h_m,\, h_i\in \mathcal{H}\}\) admits an NIMPC protocol with communication complexity \(\delta \cdot m.\)
Definition 4
(Indicator functions) Let \(\mathcal{X}\) be a finite domain. For n-tuple \(a=(a_1,\ldots ,a_n)\in \mathcal{X},\) let \(h_a:\mathcal{X}\rightarrow \{0,\,1\}\) be the function defined by \(h_a(a)=1,\) and \(h_a(x)=0\) for all \(a\not =x\in \mathcal{X}.\) Let \(h_0:\mathcal{X}\rightarrow \{0,\,1\}\) be the function that is identically zero on \(\mathcal{X}.\) Let  be the set of all indicator functions together with \(h_0.\)
be the set of all indicator functions together with \(h_0.\)
Note that every function \(h:\mathcal{X}\rightarrow \{0,\,1\}\) can be expressed as the sum of indicator functions, namely, \(h=\sum _{a\in \mathcal{X}, h(a)=1}h_a.\)
We review the previous results on upper bounds on the individual communication complexity of NIMPC. As described above, the fully robust NIMPC protocols in [2] are constructed from fully robust NIMPC for \(\mathcal{H}_\mathrm{ind}.\) Thus, the previous upper bounds depend on the upper bound for \(\mathcal{H}_\mathrm{ind}.\) This means we have a better upper bound if we obtain a more efficient fully robust NIMPC protocol for \(\mathcal{H}_\mathrm{ind}.\)
Proposition 2
(Arbitrary functions \(\mathcal{H}_\mathrm{all},\) Proof of Theorem 10 in [2]) Fix finite domains \(\mathcal{X}_1, \ldots , \mathcal{X}_n\) such that \(|\mathcal{X}_i|\le d\) for all \(1\le i\le n\) and let \(.\) Let \(\mathcal{H}_\mathrm{all}\) be the set of all functions \(h:\mathcal{X}\rightarrow \{0,\,1\}^m.\) If there exists an NIMPC protocol for \(\mathcal{H}_\mathrm{ind}\) with individual communication complexity \(\delta ,\) then there exists an NIMPC protocol for \(\mathcal{H}\) with individual (resp. total) communication complexity \(|\mathcal{X}|\cdot m\cdot \delta \) (resp. \(|\mathcal{X}|\cdot m\cdot \delta \cdot n).\)
3 Lower bounds on the communication complexity
We derive a lower bound on the total communication complexity for any finite set of functions, and in particular \(\mathcal{H}_\mathrm{all}\) and \(\mathcal{H}_\mathrm{ind}.\)
As described in the Sect. 1, the total communication complexity is bounded by the size of target class. In other words, the total communication complexity cannot be smaller than the logarithm of the size of the target class.
Theorem 1
(Lower bound for any finite set of functions) Fix finite domains \(\mathcal{X}_1, \ldots , \mathcal{X}_n\) and \({\varOmega }.\) Let  and \(\mathcal{H}\) a set of functions \(h:\mathcal{X}\rightarrow {\varOmega }.\) Then, any fully robust NIMPC protocol \({\varPi }\) for \(\mathcal{H}\) satisfies
and \(\mathcal{H}\) a set of functions \(h:\mathcal{X}\rightarrow {\varOmega }.\) Then, any fully robust NIMPC protocol \({\varPi }\) for \(\mathcal{H}\) satisfies
Proof
We first prove Eq. (2). Let \(H=|\mathcal{H}|.\) Let \(\varphi \) be a one-to-one mapping from \(\mathcal{H}\) to \(\{0,\,1,\ldots ,H-1\}.\) (That is, all functions in \(\mathcal{H}\) are numbered according to some rule.) Suppose a server holding a random number \(a\in \{0,\ldots ,H-1\}\) aims to send a to a client. Suppose also that there is an NIMPC protocol \((\mathsf{GEN},\, \mathsf{ENC},\, \mathsf{DEC})\) for \(\mathcal{H}\) that satisfies \(\sum _{i=1}^n\log |\mathcal{R}_i| < \log H.\) For the function \(h=\varphi (a),\) the server executes \(R\leftarrow \mathsf{GEN}(h)\) and sends R to the client. The client obtains a by executing \(\mathsf{ENC}\) and \(\mathsf{DEC}\) for all possible inputs \(x\in \mathcal{X}\) and identifying the function h. We conclude that the server can communicate any \(a\in \{0,\ldots ,H-1\}\) to the client using \(R=(R_1,\ldots ,R_n)\) of which domain size \(\prod _{i=1}^n |\mathcal{R}_i|\) is smaller than H, that is impossible. Thus, we have \(\sum _{i=1}^n\log |\mathcal{R}_i|\ge \log H.\)
In a similar way, we next prove Eq. (3). Suppose a server holding a random element \(b\in {\varOmega }\) and aiming to send b to a client and that there is an NIMPC protocol \((\mathsf{GEN},\, \mathsf{ENC},\, \mathsf{DEC})\) for \(\mathcal{H}\) that satisfies \(\sum _{i=1}^n\log |\mathcal{M}_i| < \log |{\varOmega }|.\) For a function \(h\in \mathcal{H}\) and an element \(a\in \mathcal{X}\) such that \(h(a)=b,\) the server executes \(R\leftarrow \mathsf{GEN}(h)\) and \(M\leftarrow \mathsf{ENC}(a,\,R),\) and sends M to the client. The client obtains b by executing \(\mathsf{DEC}.\) We conclude that the server can communicate any \(b\in {\varOmega }\) to the client using \(M=(M_1,\ldots ,M_n)\) of which domain size \(\prod _{i=1}^n |\mathcal{M}_i|\) is smaller than \(|{\varOmega }|,\) that is impossible. Thus, we have \(\sum _{i=1}^n\log |\mathcal{M}_i|\ge \log |{\varOmega }|.\)
\(\square \)
The following corollary shows a lower bound on the total communication complexity of NIMPC for the set of arbitrary functions. The lower bounds indicate the impossibility of reducing the communication complexity to polynomial in the input length.
Corollary 1
(Lower bound for arbitrary functions) Fix finite domains \(\mathcal{X}_1, \ldots , \mathcal{X}_n\) such that \(|\mathcal{X}_i|\ge d'\) for all \(1\le i\le n.\) Let  and \(\mathcal{H}_\mathrm{all}\) the set of all functions \(h:\mathcal{X}\rightarrow \{0,\,1\}^m.\) Any NIMPC protocol \({\varPi }\) for \(\mathcal{H}_\mathrm{all}\) satisfies
and \(\mathcal{H}_\mathrm{all}\) the set of all functions \(h:\mathcal{X}\rightarrow \{0,\,1\}^m.\) Any NIMPC protocol \({\varPi }\) for \(\mathcal{H}_\mathrm{all}\) satisfies
Proof
The proof is obvious from Theorem 1 by setting \(\mathcal{H}=\mathcal{H}_\mathrm{all}.\) A function maps each input value to some output value. Thus, \(|\mathcal{H}|\) is given by multiplying the number of all possible input values by the number of all possible output values, i.e., \(2^{m\cdot |\mathcal{X}|}.\) Then, \(\sum _{i=1}^n\log |\mathcal{R}_i|\ge \log |\mathcal{H}|=m\cdot |\mathcal{X}|.\) \(\square \)
The following corollary shows a lower bounds on the total communication complexity of NIMPC for \(\mathcal{H}_\mathrm{ind}.\) The gap between this lower bound (linear in the input length) and the previous upper bound (exponential in the input length) is large. In the next section, we will present an efficient NIMPC protocol for \(\mathcal{H}_\mathrm{ind}\) with individual (resp. total) communication complexity at most \(\lceil \log _2 d\rceil ^2\cdot n\) (resp. \(\lceil \log _2 d\rceil ^2\cdot n^2)\).
Corollary 2
(Lower bound for indicator functions) Fix finite domains \(\mathcal{X}_1, \ldots , \mathcal{X}_n\) such that \(|\mathcal{X}_i|\ge d'\) for all \(1\le i\le n\) and let \(.\) Then, any NIMPC protocol \({\varPi }_\mathrm{ind}\) for \(\mathcal{H}_\mathrm{ind}\) satisfies
Proof
The proof is obvious from Theorem 1 by setting \(\mathcal{H}=\mathcal{H}_\mathrm{ind}.\) A function \(h_a\) maps each input value x to zero or one depending on whether \(x=a\) or not. Thus, \(|\mathcal{H}|\) is given by the number of all possible values of a, i.e., \(|\mathcal{X}|.\) Then, \(\sum _{i=1}^n\log |\mathcal{R}_i|\ge \log |\mathcal{H}|=\log |\mathcal{X}|.\) \(\square \)
Remark. We can give a more constructive proof, which need not to assume the existence of a one-to-one mapping \(\phi .\) Suppose a server holding a random vector \(a=(a_1,\ldots ,a_n)\in \mathcal{X}\) and aiming to send a to a client. Suppose that there is an NIMPC protocol \((\mathsf{GEN},\,\mathsf{ENC},\, \mathsf{DEC})\) for \(\mathcal{H}_\mathrm{ind}\) that satisfies \(\sum _{i=1}^n\log |\mathcal{R}_i| < \log |\mathcal{X}|.\) The server executes \(R\leftarrow \mathsf{GEN}(h_a)\) and sends R to the client. The client obtains a by executing \(\mathsf{ENC}\) and \(\mathsf{DEC}\) for all possible inputs \(a'\in \mathcal{X}\) and checking whether the output is 1 or not. The input \(a'\) for which the output is 1 is considered as a. We conclude that the server can communicate any \(a\in \mathcal{X}\) to the client using \(R=(R_1,\ldots ,R_n)\) of which domain size \(\prod _{i=1}^n |\mathcal{R}_i|\) is smaller than \(|\mathcal{X}|,\) that is impossible. Thus, we have \(\sum _{i=1}^n\log |\mathcal{R}_i|\ge \log |\mathcal{X}|.\)
4 Efficient constructions
We now present an efficient construction of fully robust NIMPC for \(\mathcal{H}_\mathrm{ind}.\) In the previous construction in [2], all the possible input values are encoded in a unary way, and thus the communication complexity depends on the size of the input domain. Specifically, each possible input value is represented by a single vector over \(\mathbb F_2\) so that the summation of vectors corresponding to \(a=(a_1,\ldots , a_n)\) is equal to the zero vector while the other combination is linearly independent to satisfy the robustness. Our idea to reduce the communication complexity is to encode all the possible input values in a binary way. Specifically, for each bit in the binary representation, a vector representing “1” is generated so that the summation of all vectors of “1” over the binary representation of a is equal to zero. Since the proposed encoding reduces the required dimension of vectors, the communication complexity of resulting NIMPC is greatly reduced, too.
The detailed description of the protocol is as follows. For \(i\in [n],\) let \(d_i=|\mathcal{X}_i|\) and \(\phi _i\) be a one-to-one mapping from \(\mathcal{X}_i\) to \([d_i].\) Let \(l_i=\lceil \log _2 d_i \rceil \) and \(s=\sum _{i=1}^n l_i.\) Fix a function \(h\in \mathcal{H}_\mathrm{ind}\) that we want to compute.
The proposed fully robust NIMPC \(\text {P}\!({{\varPi }}_{\mathrm{ind}}{)(h)}\)
-
Offline preprocessing: If \(h=h_0,\) then choose s linearly independent random vectors \(\{m_{i,j}\}_{i\in [n],j\in [l_i]}\) in \(\mathbb F_2^s.\) If \(h=h_a\) for some \(a=(a_1,\ldots ,a_n)\in \mathcal{X},\) denote the binary representation of \(\phi _i(a_i)\) by \(b_i=(b_{i,1},\ldots ,b_{i,l_i})\) and define a set of indices \(I_i\) by \(I_i=\{j\in [l_i]\;|\; b_{i,j}=1\}.\) Choose s random vectors \(\{m_{i,j}\}_{i\in [n],j\in [l_i]}\) in \(\mathbb F_2^s\) under the constraint that \(\sum _{i=1}^{n} \sum _{j\in I_j} m_{i,j}=0\) and there are no other linear relations between them (that is, choose all the vectors \(m_{i,j}\) except \(m_{n,\max I_n},\) as random linear independent vectors and set \(m_{n,\max I_n}=-\sum _{i=1}^{n-1}\sum _{j\in I_i} m_{i,j} - \sum _{j\in I_n\setminus \{\max I_n\}} m_{n,j}\)). Define \(\mathsf{GEN}(h)=R=(R_1,\ldots ,R_n),\) where \(R_i=\{m_{i,j}\}_{j\in [l_i]}.\)
-
Online messages: For an input \(x_i,\) let \(\hat{b}_i=(\hat{b}_{i,1},\ldots ,\hat{b}_{i,l_i})\) be the binary representation of \(\phi _i(x_i).\) Let \(\hat{I}_i\) be the set of indices defined by \(\hat{I}_i=\{j\in [l_i]\;|\; \hat{b}_{i,j}=1\}.\) \(\mathsf{ENC}(x,\,R)\triangleq (M_1,\ldots ,M_n)\) where \(M_i=\sum _{j\in \hat{I}_i} m_{i,j}.\)
-
Output \(h(x_1,\ldots ,x_n)\): \(\mathsf{DEC}(M_1,\ldots ,M_n)=1\) if \(\sum _{i=1}^n M_i={{\varvec{0}}}.\)
Mapping from \(\mathcal{X}_i\) to \([d_i],\) which does not contain zero, is an important point of the proposed protocol. If an input \(x_i\) were mapped to the zero vector, \(M_i\) would be always 0. This would disclose extra information (that could not be simulated). That is, whether \(x_i = 0\) leaked. Because every \(\phi _i\) does not map no value of \(x_i\) to the zero vector, no information on the inputs \(x_i\) is disclosed (robustness), and the summation of vectors becomes zero if and only if \(x_i\) are equal to \(a_i\) (correctness).
Theorem 2
Fix finite domains \(\mathcal{X}_1, \ldots , \mathcal{X}_n\) such that \(|\mathcal{X}_i|\le d\) for all \(1\le i\le n\) and let \(.\) Then, there is a fully robust NIMPC protocol \({\varPi }_\mathrm{ind}\) for \(\mathcal{H}_\mathrm{ind}\) with individual (resp. total) communication complexity at most \(\lceil \log _2 d\rceil ^2\cdot n\) (resp. \(\lceil \log _2 d\rceil ^2\cdot n^2).\)
Proof
For the correctness, note that \(\sum _{i=1}^n M_i=\sum _{i=1}^n\sum _{j\in \hat{I}_i} m_{i,j}.\) If \(h=h_a\) for \(a\in \mathcal{X},\) this sum equals 0 if and only if \(I_{i}=\hat{I}_i\) for all \(i\in [n],\) i.e., \(a=x.\) If \(h=h_0,\) this sum is never zero, as all vectors were chosen to be linearly independent in this case.
To prove robustness, fix a subset \(T\subseteq [n]\) and \(x_{\overline{T}}\in \mathcal{X}_{\overline{T}}.\) The encodings \(M_{\overline{T}}\) of \(\overline{T}\) consist of the vectors \(\{M_i\}_{i\in \overline{T}}.\) The randomness \(R_T\) consists of the vectors \(\{m_{i,j}\}_{i\in [n],j\in [l_i]}.\) If \(h|_{\overline{T},x_{\overline{T}}}\equiv 0,\) then these vectors are uniformly distributed in \(\mathbb F_2^s\) under the constraint that they are linearly independent. If \(h|_{\overline{T},x_{\overline{T}}}(x_T)= 1\) for some \(x_T\in \mathcal{X}_T,\) then \(\sum _{i\in \overline{T}}M_i + \sum _{i\in T}\sum _{j\in \hat{I}_i} m_{i,j}=0\) and there are no other linear relations between them. Formally, to prove the robustness, we describe a simulator \(\text {Sim}_T\): the simulator queries \(h|_{\overline{T},x_{\overline{T}}}\) on all possible inputs in \(\mathcal{X}_T.\) If all answers are zero, this simulator generates random independent vectors. Otherwise, there is an \(x_T\in \mathcal{X}_T\) such that \(h|_{\overline{T},x_{\overline{T}}}(x_T)= 1,\) and the simulator outputs random vectors under the constrains described above, that is, all vectors are independent with the exception that \(\sum _{i\in T}M_i+ \sum _{i\in \overline{T}} \sum _{j\in \hat{I}_j} m_{i,j}=0.\)
In the proposed protocol, \(\log _2 |\mathcal{R}_i|\) is larger than \(\log _2 |\mathcal{M}_i|\) for every \(i\in [n].\) Thus, the individual communication complexity is given by the maximum length of correlated randomness. The correlated randomness \(R_i\) is composed of \(l_i\le \lceil \log _2 d \rceil \) binary vectors of length \(s\le \lceil \log _2 d\rceil \cdot n\) and the encoding is the summation of some of them. Hence, the individual communication complexity is at most \(\lceil \log _2 d \rceil ^2 \cdot n.\) \(\square \)
Corollary 3
Fix finite domains \(\mathcal{X}_1, \ldots , \mathcal{X}_n\) such that \(|\mathcal{X}_i|\le d\) for all \(1\le i\le n\) and let \(.\) Then, there is a fully robust NIMPC protocol for \(\mathcal{H}_\mathrm{all}\) with individual (resp. total) communication complexity at most \(|\mathcal{X}|\cdot m\cdot \lceil \log _2 d\rceil ^2\cdot n\) (resp. \(|\mathcal{X}|\cdot m\cdot \lceil \log _2 d\rceil ^2\cdot n^2).\)
Proof
From Proposition 2 and Theorem 1, it is obvious. \(\square \)
5 Some improvements in the offline-online model
The offline-online model is defined by modifying the output of \(\mathsf{GEN}\) to include an additional entry \(R_0,\) which represents the offline communication and is given as an additional input to the decoder \(\mathsf{DEC}\) [3]. The random variable \(R_T\) is redefined to always include \(R_0.\) That is, the value of \(R_0\) should be correctly simulated by Sim. Let \(\mathcal{R}_0\) be a finite domain of \(R_0.\) We refer to NIMPC protocols in the offline-online model as offline-online NIMPC protocols. To distinguish the offline-online protocols, we refer to the NIMPC protocols considered in the previous sections as standard NIMPC protocols.
The formal definition of offline-online NIMPC is given as follows [3]:
Definition 5
(Offline-online NIMPC: syntax and correctness) Let \(\mathcal{X}_1, \ldots , \mathcal{X}_n,\, \mathcal{R}_0,\,\mathcal{R}_1,\ldots , \mathcal{R}_n,\, \mathcal{M}_1, \ldots , \mathcal{M}_n\) and \({\varOmega }\) be finite domains. Let  and let \(\mathcal{H}\) be a family of functions \(h:\mathcal{X}\rightarrow {\varOmega }.\) An offline-online NIMPC protocol for \(\mathcal{H}\) is a triplet \({\varPi }=(\mathsf{GEN},\,\mathsf{ENC},\,\mathsf{DEC})\) where
and let \(\mathcal{H}\) be a family of functions \(h:\mathcal{X}\rightarrow {\varOmega }.\) An offline-online NIMPC protocol for \(\mathcal{H}\) is a triplet \({\varPi }=(\mathsf{GEN},\,\mathsf{ENC},\,\mathsf{DEC})\) where
-
\(\mathsf{GEN}:\mathcal{H}\rightarrow \mathcal{R}_0\times \mathcal{R}_1\times \cdots \times \mathcal{R}_n\) is a randomized function,
-
\(\mathsf{ENC}\) is an n-tuple of deterministic functions \((\mathsf{ENC}_1,\ldots ,\mathsf{ENC}_n),\) where \(\mathsf{ENC}_i:\mathcal{X}_i\times \mathcal{R}_i\rightarrow \mathcal{M}_i,\)
-
\(\mathsf{DEC}:\mathcal{R}_0\times \mathcal{M}_1\times \cdots \times \mathcal{M}_n\rightarrow {\varOmega }\) is a deterministic function satisfying the following correctness requirement: for any \(x=(x_1,\ldots ,x_n)\in \mathcal{X}\) and \(h\in \mathcal{H},\)
$$\begin{aligned} \Pr \left[ R=\left( R_0,\,R_1,\ldots ,R_n\right) \leftarrow \mathsf{GEN}(h): \mathsf{DEC}\left( R_0,\,\mathsf{ENC}(x,\,R)\right) =h(x)\right] =1, \end{aligned}$$(7)where \(.\)
The (online) individual communication complexity of \({\varPi }\) is the maximum of \(\log |\mathcal{R}_1|, \ldots , \log |\mathcal{R}_n|,\, \log |\mathcal{M}_1|,\ldots , \log |\mathcal{M}_n|.\)
Definition 6
(Offline-online NIMPC: robustness) For a subset \(T\subseteq [n],\) we say that an offline-online NIMPC protocol \({\varPi }\) for \(\mathcal{H}\) is T-robust if there exists a randomized function \(Sim_T\) (a “simulator”) such that, for every \(h\in \mathcal{H}\) and \(x_{\overline{T}}\in \mathcal{X}_{\overline{T}},\) we have \(Sim_T(h|_{\overline{T},x_{\overline{T}}})\equiv (M_{\overline{T}},R_{T\cup \{0\}}),\) where R and M are the joint randomness and messages defined by \(R\leftarrow \mathsf{GEN}(h)\) and \(M_i\leftarrow \mathsf{ENC}_i(x_i,\,R_i).\) The t-robustness and fully robustness are defined in a similar way to the standard model.
Definition 7
(Offline-online NIMPC: protocol description) For an offline-online NIMPC protocol \({\varPi }\) for \(\mathcal{H},\) let \({\hbox {P}}({\varPi })\) denote the protocol that may have an additional input, a function \(h\in \mathcal{H},\) and proceeds as follows.
Protocol \(\hbox {P}({\varPi })(h)\)
-
Offline preprocessing: Each player \(P_i,\, 1\le i\le n,\) receives the random input \(.\, P_0\) receives \(.\)
-
Online messages: On input \(R_i,\) each player \(P_i,\, 1\le i\le n,\) sends the message
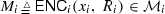 to \(P_0.\)
to \(P_0.\) -
Output: \(P_0\) computes and outputs \(\mathsf{DEC}(R_0,\,M_1,\ldots ,M_n).\)
It is obvious to construct an n-player offline-online protocol for a function h from an n-player standard protocol for h by taking \(R_0\) to be empty (or some constant). However, in this construction, the offline communication \(R_0\) cannot be used for reducing the individual communication complexity of \(P_i\) with \(1\le i\le n.\)
In the following, for any set of functions that have the same output frequency such as \(\mathcal{H}_\mathrm{ind}^*=\mathcal{H}_\mathrm{ind}\setminus \{h_0\},\) we show a fully robust offline-online protocol whose individual communication complexity is smaller than that in Sect. 4.
We first consider the set \(\mathcal{H}_\mathrm{ind}^*,\) i.e., the functions that have just one “1” output. We use a fully robust standard NIMPC protocol \({\varPi }_\mathrm{ind}=(\mathsf{GEN}',\,\mathsf{ENC}',\,\mathsf{DEC}')\) given in Sect. 4 as a subroutine.Footnote 1 Our idea to reduce the individual communication complexity is simple: use \((R_1',\ldots ,R_n')\leftarrow \mathsf{GEN}'(h_a)\) as the offline communication \(R_0\) and specify the inputs \(x_i\) by using the online communication \(M_i\) while keeping a and \(x_i\) secret. To hide a and \(x_i,\) we shift \(a=(a_1,\ldots ,a_n)\) and \(x=(x_i,\ldots ,x_n)\) by random values \(s=(s_1,\ldots ,s_n).\)
The detailed description of the proposed offline-online protocol \({\varPi }_\mathrm{proper}=(\mathsf{GEN},\,\mathsf{ENC},\,\mathsf{DEC})\) is as follows. For \(i\in [n],\) let \(d_i=|\mathcal{X}_i|\) and \(\psi _i\) be a one-to-one mapping from \(\mathcal{X}_i\) to \(\{0,\,1,\ldots , d_i-1\}.\) Fix a function \(h_a\in \mathcal{H}_\mathrm{ind}^*\) that we want to compute.
The proposed offline-online NIMPC \(\text {P}\!({{\varPi }}_\mathrm{proper})(h_a)\)
-
Offline preprocessing: Randomly choose values \(s_i\in \{0,\ldots ,d_i-1\}\) with \(i\in [n].\) Let \(\sigma _i:\mathcal{X}_i\rightarrow \{0,\ldots , d_i-1\}\) be the one-to-one mapping such that \(\sigma _i(x)=\psi _i^{-1}((\psi _i(x)+s_i)\mod d_i),\) i.e., shifting the input x by \(s_i.\) Set \(b=(b_1,\ldots , b_n)=(\sigma _1(a_1),\ldots ,\sigma _n(a_n)).\) Define \(\mathsf{GEN}(h_a)=R=(R_0,\,R_1,\ldots , R_n),\) where \(R_0=(R_1',\ldots ,R_n')=\mathsf{GEN}'(h_b)\) and \(R_i=s_i\) with \(i\in [n].\)
-
Online messages: \(\mathsf{ENC}(x,\,R)=(M_1,\ldots ,M_n)\) where \(M_i=\sigma _i(x_i).\)
-
Output \(h_a(x_1,\ldots ,x_n)\): Let \(M_i'=\mathsf{ENC}'(R_i',\,M_i).\, \mathsf{DEC}(R_0,\, M_1,\ldots ,M_n)=\mathsf{DEC}'(M_1',\ldots ,M_n').\)
Theorem 3
Fix finite domains \(\mathcal{X}_1, \ldots , \mathcal{X}_n\) such that \(|\mathcal{X}_i|\le d\) for all \(1\le i\le n\) and let \(.\) Then, there is a fully robust offline-online NIMPC protocol \({\varPi }_\mathrm{proper}\) for \(\mathcal{H}_\mathrm{ind}\setminus \{h_0\}\) with individual communication complexity at most \(\lceil \log _2 (d-1)\rceil .\)
Proof
For the correctness, note that the output is that of \(h_b\) for inputs \(\sigma _i(x_i).\) Thus, the output is one if and only if \((x_1,\ldots ,x_n)=a,\) as the tuple \((M_1,\ldots , M_n)\) equals b if and only if \((x_1,\ldots ,x_n)=a.\)
To prove the robustness, fix a subset \(T\subseteq [n]\) and \(x_{\overline{T}}\in \mathcal{X}_{\overline{T}}.\) Let \(\sigma _{\overline{T}}(x_{\overline{T}})\) denote \((\sigma _1(x_1),\ldots ,\sigma _n(x_n))_{\overline{T}}.\)
The encodings \(M_{\overline{T}}\) of \(\overline{T}\) consists of \(|\overline{T}|\) integers \(M_i\in \{0,\ldots ,d_i-1\}\) with \(i\in \overline{T}.\) The randomness \(R_T\) consists of the vectors \(\{m_{i,j}\}_{i\in [n], j\in [l_i]}\) and T integers \(s_i\in \{0,\ldots ,d_i-1\}\) with \(i\in T.\) The vectors \(\{m_{i,j}\}_{i\in [n], j\in [l_i]}\) are uniformly distributed under the constraint that for some \(b\in \mathcal{X},\, \sum _{i=1}^{n}\sum _{j\in I_i}m_{i,j}=0\) and there are no other linear relations between them. If \(h|_{\overline{T},x_{\overline{T}}}\equiv 0,\) then \(b_{\overline{T}}\not =M_{\overline{T}}.\) If \(h|_{\overline{T},x_{\overline{T}}}(x_T)=1\) for some \(x_T\in \mathcal{X}_T,\) then \(b_T=\sigma _T(x_T)\) and \(b_{\overline{T}}=M_{\overline{T}}.\)
We construct \(Sim_T\) for the protocol \(P({\varPi }_\mathrm{proper})\) on function \(h_a.\) The simulator first generates random vectors \(\{m_{i,j}\}_{i\in [n], j\in [l_i]}\) under the constraint that for some \(b\in \mathcal{X},\, \sum _{i=1}^{n}\sum _{j\in I_i}m_{i,j}=0\) and there are no other linear relations between them. The simulator then queries \(h|_{\overline{T},x_{\overline{T}}}\) on all possible inputs in \(\mathcal{X}_T.\) If all answers are zero, this simulator generates random \(M_i\in \{0,\ldots ,d_i-1\}\) with \(i\in \overline{T}\) so that \(b_T\not =M_T,\) and generates random \(R_i\in \{0,\ldots ,d_i-1\}\) with \(i\in T.\) Otherwise, there is an \(x_T\in \mathcal{X}_T\) such that \(h|_{\overline{T},x_{\overline{T}}}(x_T)= 1,\) and the simulator sets \(R_i\) and \(M_i\) so that \(b_T=\sigma _T(x_T)\) and \(b_{\overline{T}}=M_{\overline{T}}\) where \(\sigma _i\) is defined as above with \(s_i=R_i.\)
The correlated randomness \(R_i\) with \(i\in [n]\) and encoding \(M_i\) are integers of length \(\lceil \log _2 (d_i-1)\rceil .\) Hence, the (online) individual communication complexity is at most \(\lceil \log _2 (d -1)\rceil .\) \(\square \)
We extend the above result to any set of functions that have the same output frequency. In the fully robust standard NIMPC protocol for \(\mathcal{H}_\mathrm{all}\) in [2], \(h_0\) plays the role of hiding information on how many 1’s the function h has. This is the motivation of including \(h_0\) in \(\mathcal{H}_\mathrm{ind}\) and a standard NIMPC protocol for \(\mathcal{H}_\mathrm{ind}\) is used as a subroutine. Our target set of functions has the same output frequency. Thus, we no longer need to hide this information and thus the offline-online NIMPC protocol \({\varPi }_\mathrm{proper}\) for \(\mathcal{H}_\mathrm{ind}\setminus \{h_0\}\) is enough for our target sets.
Corollary 4
Fix finite domains \(\mathcal{X}_1, \ldots , \mathcal{X}_n\) such that \(|\mathcal{X}_i|\le d\) for all \(1\le i\le n\) and let \(.\) Fix an integer \(m>1.\) Let \(\mathcal{H}\) be a set of functions \(h:\mathcal{X}\rightarrow \{0,\,1\}^m\) that have the same output frequency, that is, \(|\{x\in \mathcal{X}\mid h(x)=y\}|=|\{x\in \mathcal{X}\mid h'(x)=y\}|\) holds for any \(h,\,h'\in \mathcal{H}\) and for any \(y\in \{0,\,1\}^m.\) Then, there is a fully robust offline-online NIMPC protocol for \(\mathcal{H}\) with individual communication complexity at most \( |\mathcal{X}|\cdot m\cdot \lceil \log _2 (d-1)\rceil .\)
Proof
Fix a function \(h\in \mathcal{H}.\) Assume for simplicity that \(m=1.\) The offline-online protocol \({\varPi }_\mathrm{}\) for \(\mathcal{H},\) which uses \({\varPi }_\mathrm{proper}=(\mathsf{GEN},\,\mathsf{ENC},\,\mathsf{DEC}),\) is as follows.
-
Offline preprocessing: Let \(I=h^{-1}(1) \subseteq \mathcal{X},\) i.e., the set of ones of h. Let \(D=|I|,\) i.e., the number of ones of h, and \(I=\{a_1, \ldots ,a_D\}.\) Choose a random permutation \(\phi .\) For each \(k\in [D],\) let \(R^{(k)}=(R^{(k)}_0,\,R^{(k)}_1,\ldots ,R^{(k)}_n)\leftarrow \mathsf{GEN}(h_{a_k}).\) Define a matrix R, where \(R_{i,k}\triangleq R_i^{(\phi (k))}\) for \(0\le i\le n\) and \(k\in [D].\) Send to \(P_i\) the random strings \((R_{i,k})_{k\in [D]},\) i.e., the ith row of R.
-
Online messages: For every \(i\in [n]\) and \(k\in [D],\) let \(M_{i}^{(k)}\triangleq \mathsf{ENC}_i(x_i,\,R_{i,k}).\) Define a matrix M, where \(M_{i,k}\triangleq M_i^{(k)}\) for \(0\le i\le n\) and \(k\in [D].\) Each \(P_i\) sends to \(P_0\) the message \(M_i\triangleq (M_{i,k})_{k\in [D]}.\)
-
Output \(h(x_1,\ldots ,x_n)\): The output is 1 if for some \(k\!\in \! [D],\, \mathsf{DEC}(R_{0,k},\, M_{1,k}, \ldots , M_{n,k})=1.\) Otherwise, the output is zero.
First, we will show the correctness of the above protocol. Fix \(x=(x_1,\ldots ,x_n)\in \mathcal{X}.\) The output is 1 if and only if \(\mathsf{DEC}(R_{0,k},\, M_{1,k}, \ldots , M_{n,k})=1\) for some \(k\in [D],\) that is, \(\mathsf{DEC}(R_{0}^{(\phi (k))},\, \mathsf{ENC}(x_1,\,R_{1}^{(\phi (k))}), \ldots , \mathsf{ENC}(x_n,\,R_{n}^{(\phi (k))}))=1\) for some \(k\in [D].\) Since the underlying \({\varPi }_\mathrm{proper}=(\mathsf{GEN},\,\mathsf{ENC},\,\mathsf{DEC})\) satisfies the correctness, this happens if and only if \(h_{a_k}(x)=1\) holds for some \(a_k\in I.\)
Next, we will show the robustness. The robustness is proven in a similar way to Theorem 3. Fix \(T\subseteq [n]\) and \(x_{\overline{T}}\in \mathcal{X}_{\overline{T}}.\) We construct a simulator for \((M_{\overline{T}},\,R_T)\) given \(h|_{\overline{T},x_{\overline{T}}}.\) Each row k is of the form \((M_{\overline{T}}^{(k)},\, R_{T}^{(k)})\) for \(k\in [D].\) For each \(k\in [D],\) the encodings \(M_{\overline{T}}^{(k)}\) of \(\overline{T}\) consists of \(|\overline{T}|\) integers \(M_i^{(k)}\in \{0,\ldots ,d_i-1\}\) with \(i\in \overline{T}.\) The randomness \(R_T^{(k)}\) consists of the vectors \(\{m_{i,j}^{(k)}\}_{i\in [n], j\in [l_i]}\) and T integers \(s_i^{(k)}\in \{0,\ldots ,d_i-1\}\) with \(i\in T.\) The vectors \(\{m_{i,j}^{(k)}\}_{i\in [n], j\in [l_i]}\) are uniformly distributed under the constraint that for some \(b^{(k)}\in \mathcal{X},\, \sum _{i=1}^{n}\sum _{j\in I_i}m_{i,j}^{(k)}=0\) and there are no other linear relations between them. If \(h|_{\overline{T},x_{\overline{T}}}\equiv 0,\) then \(b_{\overline{T}}^{(k)}\not =M_{\overline{T}}.\) If \(h|_{\overline{T},x_{\overline{T}}}(x_T)=1\) for some \(x_T\in \mathcal{X}_T,\) then \(b_T^{(k)}=\sigma _T(x_T)\) and \(b_{\overline{T}}=M_{\overline{T}}^{(k)}.\)
We construct \(Sim_T\) for the protocol \(P({\varPi })\) on function \(h_a.\) For each \(k\in [D],\) the simulator first generates random vectors \(\{m_{i,j}^{(k)}\}_{i\in [n], j\in [l_i]}\) under the constraint that for some \(b^{(k)}\in \mathcal{X},\, \sum _{i=1}^{n}\sum _{j\in I_i}m_{i,j}^{(k)}=0\) and there are no other linear relations between them. The simulator then queries \(h|_{\overline{T},x_{\overline{T}}}\) on all possible inputs in \(\mathcal{X}_T.\)
Let \(I'\subseteq \mathcal{X}_T\) be the set of ones of \(h|_{\overline{T},x_{\overline{T}}}.\) Let \(D'=|I'|\) and \(I'=\{x_T^{(1)}, \ldots ,x_T^{(D')}\}.\) For \(1\le k\le D',\) this simulator generates random \(M_i^{(k)}\in \{0,\ldots ,d_i-1\}\) with \(i\in \overline{T}\) so that \(b_T^{(k)}\not =M_T^{(k)},\) and generates random \(R_i^{(k)}\in \{0,\ldots ,d_i-1\}\) with \(i\in T.\) For \(D'<k\le D,\) the simulator sets \(R_i^{(k)}\) and \(M_i^{(k)}\) so that \(b_T^{(k)}=\sigma _T^{(k)}(x_T^{(k)})\) and \(b_{\overline{T}}^{(k)}=M_{\overline{T}}^{(k)}\) where \(\sigma _i^{(k)}\) is defined with \(s_i=R_i\) as in Theorem 3.
The correlated randomness \(R_i^{(k)}\) with \(i\in [n]\) and encoding \(M_i^{(k)}\) are integers of length \(\lceil \log _2 (d_i-1)\rceil .\) Hence, the (online) individual communication complexity is at most \(|\mathcal{X}|\cdot m\cdot \lceil \log _2 (d-1)\rceil .\) \(\square \)
6 Conclusion
We have presented the first lower bound on the communication complexity of n-player NIMPC protocols for any set of functions including the set of arbitrary functions and the set of indicator functions. We have constructed novel fully robust NIMPC protocols for the set of arbitrary functions \(\mathcal{H}_\mathrm{all}\) and the set of indicator functions \(\mathcal{H}_\mathrm{ind}.\) The proposed protocols are much more efficient than the previous protocols. For example, for the set of arbitrary functions, while the previous best known protocol in [2] requires \(|\mathcal{X}|\cdot m\cdot d^2 \cdot n\) communication complexity, the communication complexity of the proposed construction is only \(|\mathcal{X}|\cdot m\cdot \lceil \log _2 d\rceil ^2 \cdot n,\) where \(\mathcal{X}\) denote the (total) input domain, d is the maximum domain size of a player, and m is the output length. By this result, the gap between the lower and upper bounds on the communication complexity is significantly reduced from \(d^2 \cdot n\) to \(\lceil \log _2 d\rceil ^2 \cdot n,\) that is, from exponential in the input length to quadratic. In addition, we have shown a possibility of reducing the individual communication complexity much more by employing the offline-online model for some sets of functions (e.g., \(\mathcal{H}_\mathrm{ind}\setminus \{h_0\}\)).
Notes
We note that the communication complexity for \(\mathcal{H}_\mathrm{ind}^*\) is the same as that for \(\mathcal{H}_\mathrm{ind}.\)
References
Barkol O., Ishai Y., Weinreb E.: On $d$-multiplicative secret sharing. J. Cryptol. 23(4), 580–593 (2010).
Beimel A., Gabizon A., Ishai Y., Kushilevitz E., Meldgaard S., Paskin-Cherniavsky A.: Non-interactive secure multiparty computation. In: Advances in Cryptology– -CRYPTO2014. Lecture Notes in Computer Science, vol. 8617, p. 387–404 (2014).
Beimel A., Gabizon A., Ishai Y., Kushilevitz E., Meldgaard S., Paskin-Cherniavsky A.: Non-interactive Secure Multiparty Computation. Cryptology ePrint Archive: Report 2014/960 (2014).
Benhamouda F., Krawczyk H., Rabin T.: Robust non-interactive multiparty computation against constant-size collusion. In: Advances in Cryptology—CRYPTO2017. Lecture Notes in Computer Science, vol. 10401, pp. 391–419.
Benhamouda F., Krawczyk H., Rabin T.: Robust Non-interactive Multiparty Computation Against Constant-Size Collusion. Cryptology ePrint Archive: Report 2017/555.
Ben-Or M., Goldwasser S., Wigderson A.: Completeness theorems for non-cryptographic fault-tolerant distributed computation. In: The 20th Annual ACM Symposium on Theory of Computing (STOC ’88), pp. 1–10 (1988).
Chaum D., Crèpeau C., Damgård I.: Multiparty unconditionally secure protocols. In: The 20th Annual ACM Symposium on Theory of Computing (STOC ’88), pp. 11–19 (1988).
Cramer R., Damagård I., Maurer U.: General secure multi-party computation from any linear secret sharing scheme. In: Advances in Cryptology—EUROCRYPT2000. Lecture Notes in Computer Science, vol. 1807, pp. 316–335 (2000).
Data D., Prabhakaran M., Prabhakaran V.: On the communication complexity of secure computation. In: Advances in Cryptology—CRYPTO2014. Lecture Notes in Computer Science, vol. 861, pp. 199–216 (2014).
Goldwasser S., Micali S., Wigderson A.: How to play any mental game, or a completeness theorem for protocols with an honest majority. In: The 19th Annual ACM Symposium on Theory of Computing (STOC ’87), pp. 218–229 (1987).
Hirt M., Maurer U.: Player simulation and general adversary structures in perfect multiparty computation. J. Cryptol. 13(1), 31–60 (2000).
Hirt M., Tschudi D.: Efficient general-adversary multi-party computation. In: Advances in Cryptology—ASIACRYPT 2013. Part II: Lectures Notes in Computer Science, vol. 8270, pp. 181–200 (2013).
Maurer U.: Secure multi-party computation made simple. In: Security in Communication Networks, Third International Conference, SCN 2002. Lecture Notes in Computer Science, vol. 2576, pp. 14–28 (2003).
Rabin T., Ben-Or M.: Verifiable secret sharing and multiparty protocols with honest majority. In: The 21st Annual ACM Symposium on Theory of Computing (STOC ’89), pp. 73–85 (1989).
Yao A.C.: Protocols for secure computations. In: The 23rd Annual Symposium on Foundations of Computer Science (FOCS ’82), pp. 160–164 (1982).
Yoshida M., Obana S.: On the (in)efficiency of non-interactive secure multiparty computation. In: The 18th Annual International Conference on Information Security and Cryptology, ICISC2015. Lecture Notes in Computer Science, vol. 9558, pp. 185–193 (2016).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by L. Perret.
The preliminary version of this paper is presented in [16]. The difference is an extension to the so-called offline-online model, by which the efficiency of online communication is further improved.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Yoshida, M., Obana, S. On the (in)efficiency of non-interactive secure multiparty computation. Des. Codes Cryptogr. 86, 1793–1805 (2018). https://doi.org/10.1007/s10623-017-0424-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10623-017-0424-7
Keywords
- Secure multi-party computation
- Non-interactive
- Information theoretical security
- Communication complexity
- Lower bound





 to
to 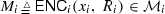 to
to