Decision tree boosted varying coefficient models

Abstract

Varying coefficient models are a flexible extension of generic parametric models whose coefficients are functions of a set of effect-modifying covariates instead of fitted constants. They are capable of achieving higher model complexity while preserving the structure of the underlying parametric models, hence generating interpretable predictions. In this paper we study the use of gradient boosted decision trees as those coefficient-deciding functions in varying coefficient models with linearly structured outputs. In contrast to the traditional choices of splines or kernel smoothers, boosted trees are more flexible since they require no structural assumptions in the effect modifier space. We introduce our proposed method from the perspective of a localized version of gradient descent, prove its theoretical consistency under mild assumptions commonly adapted by decision tree research, and empirically demonstrate that the proposed tree boosted varying coefficient models achieve high performance qualified by their training speed, prediction accuracy and intelligibility as compared to several benchmark algorithms.

1 Introduction

A varying coefficient model (VCM: Hastie and Tibshirani 1993) is, as the name intuitively suggests, a “parametric” model whose coefficients are allowed to vary based on individual model inputs. When presented with a set of covariates and some response of interest, a VCM isolates part of those covariates as effect modifiers based on which model coefficients are determined through a few varying coefficient mappings. These coefficients then join the remaining covariates to assume the form of a parametric model which produces structured predictions.

Consider the data generating distribution $(X, Z, Y)\in {\mathbb {R}}^p \times {\mathbb {A}} \times {\mathbb {R}}$ where $X = (X^1, \dots , X^p)$, X and Z are the covariates and Y the response. A VCM regressing Y on (X, Z) can take the form

$$\begin{aligned} g({\mathbb {E}}\left[ {Y|X, Z}\right] ) = \beta ^{0}(Z) + \sum _{i=1}^p \beta ^i(Z) X^i \end{aligned}$$

(1)

which resembles a generalized linear model (GLM) with the link function g. In this context we refer to X as the predictive covariates and Z the action covariates (effect modifiers) which are drawn from an action space ${\mathbb {A}}$. $\beta ^i(\cdot ): {\mathbb {A}} \rightarrow {\mathbb {R}}, i=0,1,\dots ,p$ are, varying coefficient mappings. This is similar to a fixed effects model with the fixed effects on the slopes. To give an intuitive example, we can imagine a study associating someone’s resting heart rate linearly to their weight, height, and daily caffeine intake, while expecting the linear coefficients would depend on their age Z since younger people might be more responsive to caffeine consumption. In this case, ${\mathbb {A}}$ would be the set of all possible ages. While (1) preserves the linear structure, the dependence of the coefficients $\beta$ on Z grants the model more complexity compared with the underlying GLM. In this paper we assume that each $\beta ^i(Z)$ uses the same action space, but a generalization to allow different coefficients to depend on different features is immediate.

The varying coefficient mappings $\beta (\cdot )$ are conventionally nonparametric to distinguish (1) from any parametric models on a transformed sample space of (X, Z). In this paper we are particularly interested in the use of gradient boosting, especially gradient boosted decision trees (GBDT or GBM: Friedman 2001), as those mappings. Here we propose tree boosted VCM: for each $\beta ^i, i=0,\dots , p$, we represent

$$\begin{aligned} \beta ^i(z) = \sum _{j=1}^b t^i_j(z), \end{aligned}$$

an additive boosted tree ensemble of size b with each $t_j^i$ being a decision tree constructed sequentially through gradient boosting as detailed in Sect. 2. This strategy yields the model

$$\begin{aligned} g({\mathbb {E}}\left[ {Y|X, Z}\right] ) = \sum _{j=1}^b t^0_j(Z) + \sum _{i=1}^p \left( \sum _{j=1}^b t^i_j (Z)\right) X^i. \end{aligned}$$

(2)

Apart from the upgrading of model complexity for parametric models, introducing tree boosted VCM aligns with our attempt to address concerns about model intelligibility and transparency.

There are two mainstream approaches to model interpretation in the literature. The first category suggests we can attach a post hoc explanatory mechanism to a fitted model to inspect its results, hence it is model agnostic. There is a sizable literature on this topic, from the appearance of local methods (LIME: Ribeiro et al. 2016) to recent applications on neural nets (Zhang and Zhu 2018; Sundararajan et al. 2017), random forests (Mentch and Hooker 2016; Basu et al. 2018) and complex model distillation (Lou et al. 2012, 2013; Tan et al. 2018), to name a few. These approaches are especially favored by “black box” models since they do not interfere with model building and training. However, introducing this extra explanatory step also poses questions that involve additional decision making: which form of interpretability is preferred, which method to apply, and if possible, how to relate the external interpretation to the model’s inner workings.

In contrast, we can design inherently-interpretable models. In other words, we simply consider models that consist of concise and intelligible building blocks to spontaneously achieve interpretability. Examples of this approach range from basic models as generalized linear models and decision trees, to complicated ones that guarantee monotonicity (You et al. 2017; Chipman et al. 2016), have identifiable and accountable components (Melis and Jaakkola 2018), or allow more control on the covariate structure though shape constraints (Cotter et al. 2019). Although having the advantage of not requiring the additional inspection, self-explanatory models are more restricted in terms of their flexibility and are often facing the trade-off between generalization accuracy and intelligibility.

Following this discussion, a VCM belongs to the second category as long as the involved parametric form is intelligible. It is an instant generalization of the parametric form to allow the use of local coefficients, which leads to improvements in both model complexity and accuracy. It is worth pointing out again that a VCM is structured: the predictions are produced through parametric (e.g., generalized linear) relations between predictive covariates and coefficients. This combination demonstrates a feasible means to balance the trade-off between flexibility and intelligibility.

There is a substantial literature examining the asymptotic properties of different VCMs when traditional splines or kernel smoothers are implemented as the nonparametric varying coefficient mappings. We refer the readers to Park et al. (2015) for a comprehensive review. In this paper we present similar results regarding the asymptotics of tree boosted VCM.

1.1 Trees and VCMs

While popular choices of varying coefficient mappings are either splines or kernel smoothers, we consider employing decision trees (CART: Breiman et al. 2017) and decision tree ensembles as those nonparametric mappings.

The advantages of applying tree ensembles are two-folded. They form a highly complex and flexible model class, and they are capable of handling any action space ${\mathbb {A}}$ compatible with decision tree splitting rules. The latter is especially convenient when compared to, for instance, cases when ${\mathbb {A}}$ is a high dimensional mixture of continuous and discrete covariates, for which constructing a spline basis or defining a kernel smoother distance measure would require considerably greater attention from the modeler.

There are existing straightforward attempts to utilize a single decision tree as varying coefficient mappings (Buergin and Ritschard 2017; Berger et al. 2017). Although having a simple form, these implementations are subject to the instability rooted in using a single tree. Moreover, the mathematical intractability of single decision trees prevents those varying coefficient mappings from provable optimality. On the other hand, by switching to tree ensembles of either random forests or gradient boosting we would have better variance reduction and asymptotic guarantees. One example applying random forests is based on the linear local forests introduced in Friedberg et al. (2018) that perform local linear regression with an honest random forest kernel, while the predictive covariates X are reused as the effect modifiers Z.

In terms of tree boosting methods, Wang and Hastie (2014) proposed the first tree boosted VCM algorithm. They applied functional trees (Gama 2004) with a linear model in each leaf to fit the negative gradient of the empirical risk. Here, a functional tree is a regression tree whose leaves are linear models instead of constants. Their resulting model updates the coefficients as follows:

$$\begin{aligned} g({\mathbb {E}}\left[ {Y|X, Z}\right] ) = X {\hat{\beta }}(Z)^T= X^T \left( \sum _{j=1}^b t_j(Z)\right) . \end{aligned}$$

Here we assume the first column of X is constant 1 and each decision tree $t_j$ returns a $p+1$ dimensional response. Their algorithm when applied to a regression problem with $L^2$ loss can be summarized as

• 1. Start with an initial guess of ${\hat{\beta }}_0(\cdot )$. A common choice is ${\hat{\beta }}_0(\cdot ) = 0$.

• 2. For each iteration b, calculate the residue for $i=1,\dots , n$:

  $$\begin{aligned} {\hat{\epsilon }}_{b, i} = y_i - x_i^T{\hat{\beta }}_b(z_i). \end{aligned}$$

• 3. Construct a functional tree $t_{b+1}: {\mathbb {A}} \rightarrow {\mathbb {R}}^{p+1}$ on $(z_i, {\hat{\epsilon }}_{b, i})$ each of whose leaves is a linear model i.e. $t_{b+1}(z_i)^T x_i$ with $t_{b+1}(z_i)$ taking the same value for all $x_i$ in the same leaf node.

• 4. Update ${\hat{\beta }}_{b+1} = {\hat{\beta }}_b + t_{b+1}$.

• 5. Keep boosting until the stopping rule is met.

In practice we this approach can result in a number of challenges. Most immediately, constructing optimal functional trees is usually time consuming. Beyond this, correlation between Z and X can produce challenges especially when a deep tree is used and the X covariates in a deep node appear more correlated or even singular due to the result of selection by similar Z’s. As solutions, we can either prevent the tree from making narrow splits or use a penalized leaf model. However, selecting a penalty parameter leaves us without a closed-form expression for the solution, requiring us to optimize numerically, presumably through gradient descent methods.

To address these issues, we propose a new tree boosted VCM framework summarized as follows when applied to regression problems with $L^2$ loss. A general form is presented in Sect. 2.

• 1. Start with an initial guess of ${\hat{\beta }}_0(\cdot )$. A common choice is ${\hat{\beta }}_0(\cdot ) = 0$.

• 2. For each iteration b and for each dimension $j = 0,\dots , p$ of ${\hat{\beta }}_b$,

  • calculate the negative gradient of $L^2$ loss at each $x_i, i = 1,\dots ,n$,

    $$\begin{aligned} \varDelta ^j_i = (y_i - {\hat{\beta }}_b(z_i)^T x_i) x_i^j. \end{aligned}$$

  • construct a decision tree $t_{b+1}^j \in {\mathcal {T}}: {\mathbb {A}} \rightarrow {\mathbb {R}}$ on $(z_i, \varDelta ^j_{i}), i=1,\dots , n$.

• 3. Update ${\hat{\beta }}_b$ with learning rate $\lambda \ll 1$.

  $$\begin{aligned} {\hat{\beta }}_{b+1}(\cdot ) = {\hat{\beta }}_{b}(\cdot ) + \lambda \begin{bmatrix}t_{b+1}^0(\cdot ) \\ \vdots \\ t_{b+1}^p(\cdot )\end{bmatrix}. \end{aligned}$$

In short, instead of functional trees, we directly use tree boosting to perform gradient descent in the functional space of those varying coefficients in the parametric part of the model. We will elaborate later that this framework has several advantages:

• It has provable theoretical performance guarantees.

• This method takes advantage of the standard boosting framework which allows us to use and extend existing gradient descent and gradient boosting techniques and theories.

• Each coefficient can be boosted separately, thereby avoiding singular submodel fitting.

• Any gradient descent or gradient boosting constraints can directly apply in this approach and that can help fit constrained or penalized models.

1.2 Models under VCM

Under the settings of (1), Hastie and Tibshirani (1993) pointed out that VCM is the generalization of generalized linear models, generalized additive models, and various other semi-parametric models with careful choices of the varying coefficient mapping $\beta$. In particular, the partially linear regression model

$$\begin{aligned} Y = X^T\beta + f(Z) + \epsilon _Z, \quad \epsilon _Z \sim N(0, \sigma ^2(Z)), \end{aligned}$$

where $\beta$ is a global linear coefficient (see Härdle et al. 2012) is equivalent to a least square VCM with all varying coefficient mappings except the intercept being constant. We treat the VCM in general throughout this paper, but examine a partially linear regression in Sect. 4.4.

Within this modeling framework, the closest to our approach are functional trees introduced in Gama (2004) and Zeileis et al. (2008). A functional tree segments the action space into disjoint regions, after which a parametric model gets fitted within each region using sample points inside. Zheng and Chen (2019) and Chaudhuri et al. (1994) discussed the cases when these regional models are linear or polynomial. Another example is logistic regression trees, for which there is a sophisticated building algorithm (LOTUS: Chan and Loh 2004). Their prediction on a new point $(x_0, z_0)$ is

$$\begin{aligned} P({\hat{y}}_0=1) = \sum _{i=1}^K \frac{1}{1+e^{-x_0^T\beta _i}}\cdot I\left( z_0 \in A_i\right) = \frac{1}{1+e^{-x_0^T\beta _k}}, \end{aligned}$$

provided ${\mathbb {A}} = \coprod _{i=1}^K A_i$ the tree segmentation, $z_0 \in A_k$ and $\beta _k = \beta (z) ,\forall z \in A_k$.

As mentioned above, constructing functional trees is time consuming. The conventional way of determining the tree structure is to enumerate through candidate splits and choose the one that reduces the empirical risk the most between before and after splitting. Such greedy strategy requires lots of computation and yields mathematically intractable results.

The rest of the paper is structured as follows. In Sect. 2 we present the formal definition of our proposed method and share an alternative perspective of looking at it as local gradient descent: a localized functional version of gradient descent that treats parameters in a parametric model as functions on the action space and optimizes locally. We will prove the consistency of our algorithm in Sect. 3 and present our empirical results in Sect. 4. Further discussions on potential variations of this method follow in Sect. 5. Code to produce results throughout the paper is available at https://github.com/siriuz42/treeboostVCM.

2 Tree boosted varying coefficient models

For the varying coefficient mapping of interests $\beta$, we use superscripts $0, \dots , p$ to indicate individual dimensions, i.e. $\beta = (\beta ^0, \dots , \beta ^p)^T$, and subscripts $1, \dots , n$ to indicate sample points or boosting iterations when there is no ambiguity. For any X, we assume X contains the intercept column, i.e. $X = (1, X^1,\dots , X^p)$, so that $X^T\beta = \beta ^0 + \sum _{i=1}^p X^i \beta ^i$ can be used to specify a linear regression.

2.1 Boosting framework

Here we present the general form of our proposed tree boosted VCM. We first consider fitting a generalized linear model with constant coefficients $\beta \in {\mathbb {R}}^{p+1}$. Given sample $(x_1, z_1, y_1),\dots , (x_n, z_n, y_n)$ and a target loss function l, gradient descent is used to minimize the empirical risk by searching for the optimal ${\hat{\beta }}^*$ - regardless of $z_i$ at this moment - as

$$\begin{aligned} L({\hat{\beta }}) = \frac{1}{n}\sum _{i=1}^n l(y_i, x_i^T{\hat{\beta }}), \quad {\hat{\beta }}^* = \arg \min _{{\hat{\beta }}} L({\hat{\beta }}). \end{aligned}$$

First order gradient descent improves an intermediate ${\hat{\beta }}$ to ${\hat{\beta }}'$ by moving it in the negative gradient direction

$$\begin{aligned} \varDelta _{{\hat{\beta }}} = -\nabla _{\beta } \left( \frac{1}{n}\sum _{i=1}^n l(y_i, x_i^T\beta ) \Big |_{\beta = {\hat{\beta }}}\right) , \quad {\hat{\beta }}' = {\hat{\beta }} + \lambda \varDelta _{{\hat{\beta }}}, \end{aligned}$$

with a learning rate $0 < \lambda \ll 1$. This formula averages the contribution from each of the sample points $-\nabla _{\beta } l(y_i, x_i^T\beta )|_{\beta = {\hat{\beta }}}$ for $i=1,\dots ,n$.

We now consider $\beta$ to be a mapping $\beta = \beta (z): {\mathbb {A}} \rightarrow {\mathbb {R}}^{p+1}$ on the action space so that the effect modifiers now vary the coefficients. The empirical risk remains the same

$$\begin{aligned} L({\hat{\beta }}) = \frac{1}{n}\sum _{i=1}^n l(y_i, x_i^T{\hat{\beta }}(z_i)). \end{aligned}$$

The contributed gradient at each sample point is still

$$\begin{aligned} \varDelta _{{\hat{\beta }}}(z_i) = - \nabla _{\beta } l(y_i, x_i^T\beta ) \Big |_{\beta = {\hat{\beta }} (z_i)}. \end{aligned}$$

(3)

These gradients are the ideal functional improvement of ${\hat{\beta }}$ captured at each of the sample points, i.e. $(z_1, \varDelta _{{\hat{\beta }}}(z_1)), \dots , (z_n, \varDelta _{{\hat{\beta }}}(z_n))$. We can now employ boosting (Friedman 2001) to estimate a functional improvement ${\hat{\varDelta }}_{{\hat{\beta }}}(\cdot )$. For any function family ${\mathcal {T}}$ capable of regressing $\varDelta _{{\hat{\beta }}}(z_1), \dots , \varDelta _{{\hat{\beta }}}(z_n)$ on $z_1,\dots , z_n$, the corresponding boosting framework works as follows.

• (B1) Start with an initial guess of ${\hat{\beta }}_0(\cdot )$.

• (B2) For each iteration b and for each dimension $j = 0,\dots , p$ of ${\hat{\beta }}_b$, we calculate the pseudo gradient at each point as

  $$\begin{aligned} \varDelta ^j_{{\hat{\beta }}}(z_i) = - \frac{\partial {l(y_i, x_i^T\beta )}}{\partial {\beta ^j}}\Big |_{\beta = {\hat{\beta }}_b(z_i)}, \end{aligned}$$

  for $i=1,\dots , n$. Notice that we separate the dimensions of $\beta$ on purpose.

• (B3) For each j, find a good fit $t_{b+1}^j \in {\mathcal {T}}: {\mathbb {A}} \rightarrow {\mathbb {R}}$ on $\left( z_i, \varDelta ^j_{{\hat{\beta }}}(z_i)\right) , i=1,\dots , n$.

• (B4) Update ${\hat{\beta }}_b$ with learning rate $0<\lambda \ll 1$.

  $$\begin{aligned} {\hat{\beta }}_{b+1}(\cdot ) = {\hat{\beta }}_{b}(\cdot ) + \lambda \begin{bmatrix}t_{b+1}^0(\cdot ) \\ \vdots \\ t_{b+1}^p(\cdot )\end{bmatrix}. \end{aligned}$$

When spline methods are implemented in (B3), ${\mathcal {T}}$ is closed under addition and the result of (B4) is a list of coefficients of basis functions for ${\mathcal {T}}$. On the other hand, we propose applying decision trees in (B3):

• (B3’) For each j, build a regression tree $t_{b+1}^j: {\mathbb {A}} \rightarrow {\mathbb {R}}$ on $\left( z_i, \varDelta ^j_{{\hat{\beta }}}(z_i)\right) , i=1,\dots , n$.

the resulting varying coefficient mapping will be an additive tree ensemble, whose model space varies based on the ensemble size. We will refer to this method as tree boosted VCM for the rest of the paper should there be no ambiguity.

2.2 Local gradient descent with tree kernels

Each terminal node of the decision tree fit in (B3’) linearly combines the contributing gradients of the sample points grouped in this node. From a generic viewpoint, for each dimension j we introduce a kernel smoother $K^j = K: {\mathbb {A}}\times {\mathbb {A}} \rightarrow {\mathbb {R}}$ (we drop the j when there is no ambiguity) such that the estimated gradient at any new z is given by

$$\begin{aligned} \varDelta ^j_{{\hat{\beta }}}(z) = \sum _{i=1}^n \left( \varDelta ^j_{{\hat{\beta }}}(z_i) \cdot \frac{K(z, z_i)}{\sum _{j=1}^n K(z, z_j)}\right) . \end{aligned}$$

(4)

In other words, with a fast decaying K, (4) can estimate the gradient at z locally using weights given by

$$\begin{aligned} S(z, z_i) = \frac{K(z, z_i)}{\sum _{j=1}^n K(z, z_j)}. \end{aligned}$$

We refer to such method as local gradient descent.

For the CART strategy, after a decision tree is constructed at each iteration its induced smoother K assigns equal weights to all sample points in the same terminal node. If we write $A(z_i) \subset {\mathbb {A}}$ the region in the action space corresponding to the terminal node containing $z_i$, we have $K(z, z_i) = I(z \in A(z_i))$ and we define the following

$$\begin{aligned} {\mathbf {K}}(z, z_i) \triangleq S(z, z_i)= \frac{I\left( z \in A(z_i)\right) }{\sum _{j=1}^n I(z_j \in A(z_i))} \end{aligned}$$

to be the tree structure function where we also use the convention that $0/0=0$. The denominator is the size of $z_i$’s terminal node and is equal to $\sum _{j=1}^n I(z_j \in A(z))$ when z and $z_i$ fall in the same terminal node. In the cases where subsampling or completely random trees are employed for the purpose of variance reduction, ${\mathbf {K}}$ will be taken to be the expectation such that

$$\begin{aligned} {\mathbf {K}}(z, z_i) \triangleq {\mathbb {E}}\left[ {S(z, z_i)}\right] = {\mathbb {E}}\left[ {\frac{I(z \in A(z_i))I(i \in w)}{\sum _{j=1}^n I(z_j \in A(z_i))I(i \in w)I(j \in w)}}\right] \end{aligned}$$

whose properties have been studied by Zhou and Hooker (2018). This expectation is taken over all possible tree structures and, if subsampling is applied, all possible subsamples w of a fixed size, and the denominator in the expectation is again the size of $z_i$’s terminal node.

In particular, by carefully choosing the rates for tree construction, this tree structure function is related to the random forest kernel introduced in Scornet (2016) that takes the expectation of the numerator and the denominator separately as

$$\begin{aligned} {\mathbf {K}}_{RF}(z, z_i) = \frac{{\mathbb {E}}\left[ {I\left( z \in A(z_i)\right) }\right] }{{\mathbb {E}}\left[ {\sum _{j=1}^n I\left( z_j \in A(z_i)\right) }\right] }, \end{aligned}$$

in the sense that the deviations from these expectations are mutually bounded by constants.

2.3 Regularizing tree boosted VCM

Perfectly “chasing after” $\left( z_i, \varDelta ^j_{{\hat{\beta }}}(z_i)\right)$ can lead to severe overfitting. In general, gradient boosting applied under nonparametric regression setting has to be accompanied by regularization such as using a complexity penalty or early stopping to prevent overfitting (see, for example, Bühlmann et al. 2007; Cortes et al. 2019). Hence we partially rely on the strategy of building a decision tree in (B3’) to safeguard the behavior of the obtained tree boosted VCM. Consider the greedy CART strategy for dimension j:

• (D1) Start at the root node. Given a node, enumerate candidate splits and evaluate their splitting metrics using all $\left( z_i, \varDelta ^j_{{\hat{\beta }}}(z_i)\right)$ such that $z_i$ is contained in the node.

• (D2) Split on the best candidate split. Keep splitting until stopping rules are met to form terminal nodes.

• (D3) Calculate fitted terminal values in each terminal node using the average of all $\varDelta ^j_{{\hat{\beta }}}(z_i)$ such that $z_i$ is contained in the terminal node.

This model has several tuning parameters: the splitting metric, the depth of trees, the minimal number of sample points in a terminal node, and any pruning if needed. All these regularizers are intended to keep the terminal node large enough to avoid isolating a few points with extreme values.

Meanwhile, recent theoretical results on decision trees suggest alternative strategies that produce better theoretical guarantees. We may consider subsampling that generates a subset $w \subset \{1,\dots ,n\}$ and only uses sample points indexed by w in (D1).

• (D1’) ...Given a node, enumerate candidate splits and evaluate their splitting metrics using all $(z_i, \varDelta ^j_{\beta _i})$ such that $i \in w$ and $z_i$ is contained in the node.

We may also consider honesty (Wager and Athey 2018) which avoids using the responses, in our case $\varDelta ^j_{{\hat{\beta }}}(z_i)$, twice during both deciding the tree structure and deciding terminal values. For instance, a version of completely random trees discussed in Zhou and Hooker (2018) chooses the splits using solely $z_i$ without evaluating the splits by the responses $\varDelta ^j_{\beta _i}$ in place of step (D1).

• (D2*) ...Given a node, choose a random split based on $z_i$’s contained in the node.

From the boosting point of view, multiple other methods may also be applied to the additive ensemble to prevent overfitting: early stopping, dropouts (Rashmi and Gilad-Bachrach 2015), or adaptive learning rates.

2.4 Examples

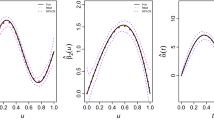
Tree boosted VCM generates a structured model joining the varying coefficient mappings and the predictive covariates. In order to understand these varying coefficient mappings on the actions space, we provide a visual example here by considering the following generative distribution:

$$\begin{aligned}&X \sim \text{ Unif }[0,1]^3, Z = (Z^1, Z^2) \sim \text{ Unif }[0,1]^2, \epsilon \sim N(0, 0.25),\\&Y = X^T \begin{bmatrix} 0\\ 3\\ {}-5 \end{bmatrix}\cdot I(Z^1+Z^2 < 1) + X^T \begin{bmatrix} -5\\ 10\\ 0 \end{bmatrix} \cdot I(Z^1+Z^2 \ge 1) + \epsilon . \end{aligned}$$

We generate a sample of 1000 examples from this distribution, apply the tree boosted VCM with 400 trees, use a learning rate $\lambda = 0.1$, tree maxdepth 3 (excluding root, the same for the rest of the paper) and minsplits 10 (the minimal node size allowed for further splitting), and obtain the following estimation of the varying coefficient mappings $\beta$ on Z in Fig. 1. The fitted values accurately capture the true coefficients.

Fig. 1

Example of varying coefficient mappings on the action space under the OLS settings

Switching to a logistic regression setting and assuming similarly that

$$\begin{aligned} \text{ logit } P(Y=1) = X^T \begin{bmatrix} 0\\ 3\\ {}-5 \end{bmatrix}\cdot I(Z^1+Z^2 < 1) + X^T \begin{bmatrix} -5\\ 10\\ 0 \end{bmatrix} \cdot I(Z^1+Z^2 \ge 1), \end{aligned}$$

with a sample of size 1000, Fig. 2 presents corresponding plots of the tree boosted VCM results, with the same set of parameters as the previous experiment except the learning rate $\lambda = 0.05$. These results are less clear as logistic regression produces noisier gradients.

Fig. 2

Example of varying coefficient mappings on the action space under the logistic regression settings

In both cases our methods correctly identify $\beta (z)$ as segmenting along the diagonal in z, providing clear visual identification of the behavior of $\beta (z)$ without posting any structural assumptions on the action space. Further empirical studies are presented in Sect. 4.

3 Consistency

There is a large literature providing statistical guarantees and asymptotic analyses of different versions of VCM with varying coefficient mappings obtained via splines or local smoothers (Park et al. 2015; Fan et al. 1999, 2005). For decision trees, Bühlmann (2002) established a consistency guarantee for tree-type basis functions for $L^2$ boosting that bounds the gap between the boosting procedure and its population version by the uniform convergence in distribution of the family of hyper-rectangular indicators. We take a similar approach to expand this family of indicators to reflect the tree boosted VCM structure and study its asymptotics. In this section we will sketch the proofs, while the details can be found in the appendix.

Consider $L^2$ boosting setting for regression. Given the relationship

$$\begin{aligned} Y = f(X,Z) + \epsilon _Z, \quad \epsilon _Z \sim N(0, \sigma ^2_Z), \end{aligned}$$

we work with the following assumptions.

• (E1) Unit support of X: $\text{ supp } X = \{1\}\times [-1,1]^{p}$, i.e. $x^0_i=1$.

• (E2) Uniform bounded noise variance: $\sigma _Z \le \sigma ^*$.

• (E3) $L^2$ loss: $l(u,y) = \frac{1}{2} (u-y)^2.$

Under these conditions, evaluating (3) yields

$$\begin{aligned} \varDelta ^j_{{\hat{\beta }}}(z_i) = - \frac{\partial }{\partial \beta ^j}l(y_i, x_i^T\beta ) \Big |_{\beta = {\hat{\beta }} (z_i)} = (y_i -x_i^T{\hat{\beta }}(z_i))\cdot x_i^j. \end{aligned}$$

For a terminal node $R \subseteq {\mathbb {A}}$ for dimension j, as per (4), the decision tree update in R with a possible subsample w is

$$\begin{aligned} \varDelta ^j_{{\hat{\beta }}}(z; z \in R, w) = \frac{\sum _{i=1}^n(y_i -x_i^T{\hat{\beta }}(z_i))\cdot x^j_i\cdot I\left( z_i \in R\right) I\left( i \in w\right) }{\sum _{i=1}^n I\left( z_i \in R\right) I\left( i \in w\right) }. \end{aligned}$$

(5)

3.1 Notations

We assume the action space ${\mathbb {A}}$ can be embedded into a Euclidean space ${\mathbb {R}}^d$ s.t. $d = \text{ dim }({\mathbb {A}})$. Denote ${\mathcal {R}} = \{(a_1, b_1] \times \cdots \times (a_d, b_d] | -\infty \le a_i \le b_i \le \infty \}$ the collection of all hyper rectangles in ${\mathbb {A}}$ which includes all possible terminal nodes of any decision tree built on ${\mathbb {A}}$.

Given the distribution $(Z, 1, X) \sim {\mathbb {P}}$, we define the inner product $\left\langle f_1, f_2 \right\rangle = {\mathbb {E}}_{{\mathbb {P}}}\left[ {f_1f_2}\right] ,$ and the norm $\left\| \cdot \right\| = \left\| \cdot \right\| _{{\mathbb {P}},2}$ on the sample space ${\mathbb {A}} \times \{1\}\times [-1,1]^p$. For a sample of size n, we write the (unscaled) empirical counterpart by $\left\langle f_1, f_2 \right\rangle _n = \sum _{i=1}^n f_1(x_i, z_i) f_2(x_i, z_i),$ such that $n^{-1}\left\langle f_1, f_2 \right\rangle _n \rightarrow \left\langle f_1, f_2 \right\rangle$ by the law of large numbers, with a corresponding norm $\left\| \cdot \right\| _n$.

3.2 Decomposing tree boosted VCM

Our study of decision trees requires their decomposition into the following rectangular indicators:

• ${\mathcal {H}} = \left\{ h_R(x,z) = I\left( z \in R\right) | R \in {\mathcal {R}} \right\}$.

Tree boosted VCM expands ${\mathcal {H}}$ by adding in coordinate mappings within hyper rectangles:

• ${\mathcal {G}} = \left\{ g_{R, j}(x,z) = I\left( z \in R\right) \cdot x^j | R \in {\mathcal {R}}, j=0,\dots , p \right\}$.

In particular we set $1 = x^0$ so that $g_{R, 0} = h_R$. Define the empirical remainder function ${\hat{r}}_b$ (Bühlmann 2002)

$$\begin{aligned} {\hat{r}}_0(x,z) = f(x,z) + \epsilon ,\quad {\hat{r}}_b(x,z) = f(x,z) + \epsilon - {\hat{\beta }}_b(z)^Tx, b>0, \end{aligned}$$

i.e. the remainder term after b-th boosting iteration. Further, consider the b-th iteration utilizing $p+1$ decision trees whose disjoint terminal nodes are $R^j_1,\dots , R^j_m \in {\mathcal {R}}$ for $j=0,\dots ,p$ respectively. (5) is equivalent to the following expression for the boosting update of the remainder ${\hat{r}}_b$

$$\begin{aligned} {\hat{r}}_{b+1} = {\hat{r}}_b - \lambda \sum _{i=1}^m \sum _{j=0}^p \frac{n^{-1}\left\langle {\hat{r}}_b, g_{{R^j_i}, j} \right\rangle _n}{n^{-1}\left\| h_{R^j_i} \right\| _n^2} g_{{R^j_i}, j}. \end{aligned}$$

(6)

Notice in $\left\langle {\hat{r}}_b, g_{{R^j_i}, j} \right\rangle _n$, $g_{{R^j_i}, j}$ is the coordinate mapping of dimension j in its corresponding hyper rectangle $R_i^j$. We flatten the subscripts when there is no ambiguity for simplicity such that

$$\begin{aligned} {\hat{r}}_{b+1} = {\hat{r}}_b - \lambda \sum _{i=1}^{m(p+1)} \frac{n^{-1}\left\langle {\hat{r}}_b, g_{b,i} \right\rangle _n}{n^{-1}\left\| h_{b,i} \right\| _n^2} g_{b,i}, \end{aligned}$$

where as defined above, $g_{b,i} = g_{{R^j_i}, j} = I\left( z \in R^j_i\right) \cdot x^j$. Although the update involves $m(p+1)$ terms, only $p+1$ of them are applicable for a given (x, z) pair as the result of using disjoint terminal nodes.

Mallat and Zhang (1993) and Bühlmann (2002) suggested we consider the population counterparts of these processes defined by the remainder functions that $r_0 = f$ and

$$\begin{aligned} r_{b+1} = r_b - \lambda \sum _{i=1}^{m(p+1)} \frac{\left\langle r_b, g_{b,i} \right\rangle }{\left\| h_{b,i} \right\| ^2} g_{b,i}, \end{aligned}$$

(7)

using the same tree structures. These processes converge to the consistent estimate in the completion of the decision tree family ${\mathcal {T}}$. As a result, we can achieve asymptotic consistency as long as the gap between the sample process and this population process diminishes fast enough along with the increase of sample size. The following lemma provides uniform bounds on the asymptotic variability pertaining to ${\mathcal {G}}$ using Donsker’s theorem (see van der Vaart and Wellner 1996).

Lemma 1

For given $L^2$ function f and random sub-Gaussian noise $\epsilon$, the following empirical gaps

• 1. $\xi _{n,1} = \sup _{R \in {\mathcal {R}}} \left| \left\| h_R \right\| ^2 - \frac{1}{n}\left\| h_R \right\| _n^2 \right| ,$

• 2. $\xi _{n,2} = \sup _{R \in {\mathcal {R}}, j=0, \dots , p} \left| \left\| g_{R, j} \right\| ^2 - \frac{1}{n}\left\| g_{R, j} \right\| _n^2 \right| ,$

• 3. $\xi _{n,3} = \sup _{R \in {\mathcal {R}}, j=0, \dots , p} \left| \left\langle f, g_{R, j} \right\rangle - \frac{1}{n}\left\langle f, g_{R,j} \right\rangle _n \right| ,$

• 4. $\xi _{n,4} = \sup _{R \in {\mathcal {R}}, j=0, \dots , p} \left| \frac{1}{n}\left\langle \epsilon , g_{R, j} \right\rangle _n \right| ,$

• 5. $\xi _{n,5} = \sup _{R_1, R_2 \in {\mathcal {R}}, j, k=0, \dots , p} \left| \left\langle g_{R_1, j}, g_{R_2, k} \right\rangle - \frac{1}{n}\left\langle g_{R_1, j}, g_{R_2, k} \right\rangle _n \right| ,$

• 6. $\xi _{n,6} = \left| \frac{1}{n}\left\| f+\epsilon \right\| _n^2 - \left\| f+\epsilon \right\| ^2\right| ,$

satisfy that $\xi _n = \max _{i=1}^6 \xi _{n,i} = O_{p}\left( n^{-\frac{1}{2}}\right) .$

3.3 Consistency

Lemma 1 quantifies the discrepancy between tree boosted VCM fits and their population versions conditioned on the sequence of trees used during boosting. In addition, we propose several conditions for consistency, as well as practical guidelines for employing tree boosted VCM.

• (C1) The learning rate satisfies $\lambda \le (1+p)^{-1}$. In proofs we use $\lambda = (1+p)^{-1}$.

• (C2) All terminal nodes of the trees in the ensemble should have at least $N_n$ observations such that $N_n \ge O\left( n^{\frac{3}{4}+\eta }\right)$ for some small $\eta > 0$, in which case we will have

  $$\begin{aligned} \frac{1}{n}\left\| h_R \right\| ^2_n = \frac{1}{n} \sum _{i=1}^n I\left( z_i \in R\right) \ge O\left( n^{-\frac{1}{4}+\eta }\right) \end{aligned}$$

  for all $R \in {\mathcal {R}}$ that appear as terminal nodes in the ensemble.

• (C3) We apply early stopping, allowing at most $B = B(n) = o(\log n)$ iterations decided by the sample size n.

• (C4) As commonly assumed by boosting literature, we require that each boosted tree effectively reduces the empirical risk. Consider the best functional rectangular fit during the b-th population iteration

  $$\begin{aligned} g^* = \arg \max _{g \in {\mathcal {G}}} \frac{|\left\langle r_b, g \right\rangle |}{\left\| g \right\| }. \end{aligned}$$

  We expect to empirically select at least one $(R^*, j)$ pair during the iteration to approximate $g^*$ such that

  $$\begin{aligned} \frac{|\left\langle r_b, g_{R^*, j} \right\rangle |}{\left\| g_{R^*,j} \right\| } > \nu \cdot \frac{|\left\langle r_b, g^* \right\rangle |}{\left\| g^* \right\| }, \end{aligned}$$

  for some $0< \nu < 1$. Lemma 1 indicates that by choosing the sample version optimum

  $$\begin{aligned} {\hat{g}}^* = \arg \max _{g \in {\mathcal {G}}} \frac{|\left\langle r_b, g \right\rangle _n|}{\left\| g \right\| _n}, \end{aligned}$$

  we meet the requirement in probability for any fixed number of iterations.

• (C5) $\left\| f \right\| ^2 = M \le \infty$. In addition, due to the linear models in the VCM, to achieve consistency we require that $f \in \text{ span }({\mathcal {G}})$.

• (C6) We also require the identifiability of linear models such that the distribution of X conditioned on any choice of $Z=z$ is not degenerate:

  $$\begin{aligned} \inf _{R \in {\mathcal {R}}, j=0,\dots , p} \frac{\left\| g_{R, j} \right\| }{\left\| h_R \right\| } = \alpha _0 > 0. \end{aligned}$$

• (C7) A stronger version of (C6) is to assume the existence of $s>0, c>0$ s.t. $\forall z$ a.e., there exists an open ball $B_z(x_0, s) \in [-1,1]^p$ centered at $x_0 = x_0(z)$ inside of which $P(X=(1,x)|Z=z)$ is bounded below by c. In other words, conditioned on any choice of $Z=z$ there is enough spread of sample points in an open region of X that assures model identifiability.

Theorem 1

Under conditions (C1)-(C5), consider function $f \in \text{ span }({\mathcal {G}})$,

$$\begin{aligned} {\mathbb {E}}_{(x^*,z^*)}\left[ {|{\hat{\beta }}_B(z^*)^Tx^* - f(x^*,z^*)|^2}\right] = o_p(1), n \rightarrow \infty , \end{aligned}$$

for a random prediction point $(x^*,z^*)$ which are independent from but identically distributed as the training data.

Corollary 1

If we further assume (C6),

Corollary 1 justifies the varying coefficient mappings as valid estimators for the true varying linear relationship. Although we have not explicitly introduced any continuity condition on $\beta$, it is worth noticing that (C5) requires $\beta$ to have relatively invariant local behavior. Hence we hypothesize tree boosted VCM should be the most ideal when ${\mathbb {A}}$ consists of a few flat regions.

When we consider the interpretability of tree boosted VCM, consistency is also the sufficient theoretical guarantee for local fidelity discussed in Ribeiro et al. (2016) that an interpretable local method should also yield accurate local relation between covariates and responses.

4 Empirical study

4.1 Benchmarking tree boosted VCMs

As shown by earlier examples, tree boosted VCMs are capable of adapting to the structure of the action space. An additional example is presented in the Appendix C.2 to demonstrate that it reconstructs the right signal levels.

In this subsection we focus on the training and coefficient estimating aspects to compare our proposed tree boosted VCM (denoted as TBVCM) with Wang and Hastie (2014) (denoted as FVCM, functional-tree boosted VCM). Discussions on prediction accuracy will be presented in the next subsection. We would like to again mention their discrepancy: TBVCM is gradient descent based, while FVCM relies on constructing functional models within trees.

We assume that the effect modifiers $Z = (z_1, z_2)^T \sim \text{ Unif }([0,1]^2)$ and the predictive covariates $X = (x_1, x_2, x_3)^T \sim \text{ Unif }([0,1]^3)$. The coefficients $\beta = (\beta _1, \beta _2, \beta _3)^T$ are given by

$$\begin{aligned} \beta _1&= 10 \cdot z_1,\\ \beta _2&= -10 \cdot z_2,\\ \beta _3&= 5\cdot I((z_1-0.5)^2 + (z_2-0.5)^2 < 0.25), \end{aligned}$$

and the response $y = X^T\beta + \epsilon$ with Gaussian noise $\epsilon \sim N(0, \sigma ^2)$. These formulae are chosen relatively arbitrarily, in order to inspect different relationships between the boundaries and the coordinates.

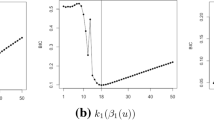
We consider four scenarios: the error is small ($\sigma ^2=1$) or large ($\sigma ^2=4$), the tree is shallow (only split node with more than 50 examples) or deep (only split node with more than 20 examples). We run TBVCM and FVCM 10 times in each scenario using the same setup: 200 trees in the ensemble, 0.1 learning rate for each tree, and the same 10 random samples. For FVCM we use the R code provided by Wang and Hastie (2014) using a custom functional tree logic with LM to extract terminal models. For TBVCM we implement the gradient calculation and utilize rpart to build the regression trees. Table 1 shows different metrics of the two methods:

Table 1 TBVCM and FVCM performance comparison

We focus on three aspects: execution time, convergence speed and vulnerability to overfitting. We draw a couple of conclusions based on Table 1:

• TBVCM runs much faster than FVCM. TBVCM is theoretically more efficient as it avoids building submodels: building linear submodels requires $O(p^2n)$ whereas evaluating impurity (variance reduction) requires O(pn). However the observed performance discrepancy does not scale with this theoretical ratio, which is likely due to implementation details.

• Growing deeper trees does not impact TBVCM too much in contrast to FVCM. Again, this is mostly likely due to the implementation, but it evidently suggests that TBVCM algorithm is simpler.

• Both methods overfit therefore need cross validation or other methods to define early stopping criteria.

• FVCM takes fewer iterations to overfit, while it is also more sensitive to deeper and more flexible trees. We expect FVCM to converge faster: fitting one submodel is equivalent to executing multiple gradient steps were we to replace the explicit solution of linear models by doing gradient descent. However the final MSEs of FVCM and TBVCM are close, suggesting similar convergence of both methods.

Fig. 3

Estimated coefficients: smaller error ($\sigma ^2 =1$) and shallower trees (minimal leaf size being 50)

Fig. 4

Estimated coefficients: larger error ($\sigma ^2=4$) and deeper trees (minimal leaf size being 20)

Figures 3 and 4 plot the distributions of estimated coefficients of two models at the full ensemble size. Both models capture the horizontal transition of $\beta _1$, the vertical transition of $\beta _2$, and the circular boundary of $\beta _3$. However, the overly flexible ensembles in Fig. 4 produces less interpretable plots, indicating again the requirement of proper regularization. FVCM also produces a wider range of coefficient values. TBVCM behaves more conservatively and appears visually similar to applying a small shrinkage.

4.2 Model accuracy

To examine the accuracy of our proposed methods, we have selected 12 real world datasets and run tree boosted VCM (denoted as TBVCM) against other benchmark methods. FVCM is excluded in this experiment due to singularity issues when applying the method on these datasets. Tables 2 and 3 present the results under classification settings with three benchmark algorithms: logistic regression (GLM), a partially saturated logistic regression model (GLM(S)) where each combination of discrete action covariates acts as fixed effect with its own level, and AdaBoost. Table 4 demonstrates the results under regression settings with three benchmark algorithms: linear model (LM), a partially saturated linear model (LM(S)), and gradient boosted trees (GBM). Although with additional constrained model structures, TBVCM performs on a par with both AdaBoost and GBM. It benefits from its capability of modeling the action space without structural conditions to outperform the fixed effect linear model in certain cases.

Table 2 Prediction accuracy of classification: 0–1 loss for six UCI data sets through tenfold cross validation

Table 3 Prediction accuracy of classification: AUC for six UCI data sets through tenfold cross validation

Table 4 Prediction accuracy of regression and mean square error for six UCI data sets through tenfold cross validation

4.3 Regularization and interpretability

One advantage of applying gradient descent based algorithm is the easy adaptation to handling constrained optimization problem.

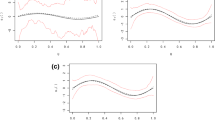
Here we show the results of applying tree boosted VCM on the Beijing housing data (Kaggle 2018). We take the housing unit price as the target regressed on covariates of location, floor, number of living rooms and bathrooms, whether the unit has an elevator and whether the unit has been refurbished. Specially, location has been treated as the action space represented in pairs of longitude and latitude. Location specific linear coefficients of other covariates are displayed in Fig. 5. We allow 200 trees of depth of 5 in the ensemble with a constant learning rate of 0.05.

In particular, from domain knowledge we would expect that the number of bathrooms should not influence the unit price negatively. The same expectations apply to the number of living rooms, the existence of elevator service and the degree of refurbishment. So as to reflect the domain knowledge, we constrain the model to always predict positive coefficients for these covariates by regularizing their local gradient descent to never drop below zero. Results of the regularization-free model are instead presented in Appendix C.2.

Fig. 5

Beijing housing unit price broken down on several factors

Figure 5 provides clear visualization of the fitted tree boosted VCM and can be interpreted in the following way. The urban landscape of Beijing consists of an inner circle with a low skyline and a modern outskirt rim of new buildings. The model intercept provides the baseline of the unit housing prices in each area. Despite their high values, most buildings inside the inner circle are decades old so the refurbishment gets more attention whereas the floor contributes negatively due to the absence of elevators. In contrast, the outskirt housing is new and its unit pricing is unmoved by the refurbishment, but a higher floor with a better city view is more valuable. Based on their coefficient plots, we can also conclude that the contribution of numbers of bathrooms and living rooms provides no additional marginal gain for their added utilities.

4.4 Fitting partially linear models

As noted above, since VCM is the generalization of many specific models, our proposed fitting algorithm and analysis should apply to them as well. We take partially linear models as an example and consider the following data set from Cornell Lab of Ornithology consisting of the recorded observations of four species of vireos along with the location and surrounding terrain types. We apply a tree boosted VCM under logistic regression setting using longitude, latitude and year as the action space and all rest covariates as linear effects without varying coefficients, obtaining the model demonstrated by Table 5. The intercept plot suggests the trend of observed vireos favoring cold climate and inland environment, while the slopes of different territory types indicate a strong preference towards the low elevation between deciduous forests and evergreen needles. It can also be used to compare the baselines across different years in the past decade.

Table 5 Fitting a partially linear model using tree boosted VCM. Plot on the left shows the nonparametric intercept. Table on the right shows the coefficients of predictive covariates

5 Shrinkage, selection and serialization

Tree boosted VCM is compatible with any alternative boosting strategy in place of the boosting steps (B3) and (B4), such as the use of subsampled trees (Friedman 2002; Zhou and Hooker 2018), univariate or bivariate trees (Lou et al. 2012; Hothorn et al. 2013) or adaptive shrinkage (dropout) (Rashmi and Gilad-Bachrach 2015; Rogozhnikov and Likhomanenko 2017; Zhou and Hooker 2018). These alternative approaches have been empirically shown to help avoid overfitting or provide more model interpretability. We also anticipate that the corresponding varying coefficient mappings would inherit certain theoretical properties. For instance, Zhou and Hooker (2018) introduced a regularized boosting framework named Boulevard that guarantees finite sample convergence and asymptotic normality of its predictions. Incorporating Boulevard into our tree boosted VCM framework requires the changes to (B3) and (B4) such that

• (B3*) For each j, find a good fit $t_{b+1}^j \in {\mathcal {T}}: {\mathbb {A}} \rightarrow {\mathbb {R}}$ on $(z_i, \varDelta ^j_{\beta _i})$ for $i \in w \subset \{1,\dots ,n\}$ a random subsample.

• (B4*) Update ${\hat{\beta }}_b$ with learning rate $\lambda < 1$.

  $$\begin{aligned} {\hat{\beta }}_{b+1}(\cdot ) = \frac{b}{b+1}{\hat{\beta }}_{b}(\cdot ) + \frac{\lambda }{b+1} \varGamma _M\left( \begin{bmatrix}t_{b+1}^0(\cdot ) \\ \vdots \\ t_{b+1}^p(\cdot )\end{bmatrix}\right) , \end{aligned}$$

  where $\varGamma _M$ truncates the absolute value at some $M > 0$.

By taking the same approach in the original paper, we can show that boosting VCM with Boulevard will also yield finite sample convergence to a fixed point.

Boulevard modifies the standard boosting strategy to the extent that new theoretical results have to be developed specifically for it. In contrast, there are other boosting variations that fall directly under the theoretical umbrella of tree boosted VCM. Our discussions so far assume we run boosting iterations with a distinct tree built for each coefficient dimension while these trees are simultaneously constructed using the same batch of pseudo-residuals. Despite the possibility of utilizing a single decision tree with multidimensional response to produce outputs of all dimensions, as long as we build separate trees sequentially, the question arises that whether we should update the pseudo-residuals on the fly and in what order if we choose to do so.

One advantage of this approach is that is reduces the boosting iteration from $(1+p)$ trees down to one tree, allowing us to use much larger learning rate $\lambda \le 1/2$ instead of $\lambda \le (1+p)^{-1}$ without changing the arguments we used to establish the consistency. We also anticipate that doing so in practice moderately reduces the cost as the gradients become more accurate for each tree. Here we will consider two approaches to conduct the on-the-fly updates.

The first approach is to introduce a coefficient selection rule to decide which coefficient to update for each boosting iteration. For instance, in Hothorn et al. (2013) the authors proposed the component-wise linear least squares for boosting where they select which $\beta$ to update using the stepwise optimal strategy, i.e., choose $j_b$ and update $\beta ^{j_b}$ if

$$\begin{aligned} j_b = \arg \min _{j=0,\dots ,p} \sum _{i=1}^n l(y_i, x_i^T({\hat{\beta }}_b + \lambda t_b^{j}e_j)(z_i)), \end{aligned}$$

the component tree that reduces the empirical risk the most, where $e_j$ is the $p+1$-vector with j-th element 1 and the rest 0. As a result, (B4) in our algorithm now updates

$$\begin{aligned} {\hat{\beta }}_{b+1} = {\hat{\beta }}_{b} + \lambda t_{b+1}^{j_b} e_{j_b}. \end{aligned}$$

Notice that finding this optimum still requires the comparison among all dimensions and therefore does not save computational cost when there are no better means or prior knowledge to help detect which dimension stands out. That being said, the optimal move is compatible with the key condition (C4) we posed to ensure consistency. Namely, it still guarantees that the population counterpart of boosting is efficient in reducing the gap between the estimate and the truth. However, this greedy strategy also complicates the pattern of the sequence in which $\beta$’s get updated.

We can also consider serialization, which means the $\beta$’s are updated in a predetermined order. An example is given Lou et al. (2012, 2013) where trees were used for univariate functions of each feature in a GAM model; later used in Tan et al. (2018) for model distillation. Their models can either be built through backfitting which eventually produces one additive component for each covariate, or through boosting that generates a sequence of additive terms.

Applying the rotation of coordinates to tree boosted VCM, we can break each of the original boosting iterations into (p+1) micro steps to write

$$\begin{aligned} {\hat{\beta }}_{b, j} = {\hat{\beta }}_{b, j-1} - \lambda \nabla _{\beta ^j} l(y, x^T\beta ) \Big |_{\beta = {\hat{\beta }}_{b, j-1} (z)}, \end{aligned}$$

with j rotating through $0,\dots , p$. This procedure immediately updates the pseudo-residuals after each component tree is built.

However, this procedure is not compatible with our consistency conclusion as the serialized boosting fails to guarantee (C4): each micro boosting step on a single coordinate relies on the current pseudo gradients instead of the gradients before the entire rotation. One solution to this theoretical issue is to consider an alternative to the predetermined updating sequence by randomly and uniformly proposing the coordinate to boost. In this regard,

$$\begin{aligned} {\hat{\beta }}_{b} = {\hat{\beta }}_{b} - \lambda \nabla _{\beta ^j} l(y, x^T\beta ) \Big |_{\beta = \hat{\beta _{b}} (z)}, \end{aligned}$$

where $j \sim \text{ Unif }\{0,\dots , p\}$. This stochastic sequence solves the compatibility issue by satisfying (C4) with a probability bounded from below.

6 Conclusion

In this paper we studied the combination of gradient boosted decision trees and varying coefficient models. We introduced the gradient descent-based algorithm of fitting tree boosted VCM under a generalized linear model setting. We proved the consistency of its coefficient estimators with an early stopping strategy and demonstrated its performance through our empirical study. As a result, we are confident to add gradient boosted decision trees into the collection of apt varying coefficient mappings.

We also discussed the model interpretability of tree boosted VCM, especially its parametric part as a self-explanatory component of reasoning about the covariates through the linear structure. Consistency guarantees the effectiveness of the interpretation.

There are a few future directions of this research. The performance of tree boosted VCM depends on the boosting scheme as well as the component decision trees. It is worth analyzing the discrepancies between different approaches of building the boosting tree ensemble. Finally our discussion has concentrated on the general form of the proposed tree boosted VCM. As mentioned, several regressors and additive models can be considered as its special cases, hence we expect model specific conclusions and training algorithms.

Appendices

Proofs

1.1 Proof of Lemma 1

Proof

$\xi _{n,6}$ is simply CLT. For the rest, we will conclude the corresponding function classes are $P-$Donsker. The collection of indicators for hyper rectangles $(-\infty , a_1] \times \dots , (-\infty , a_p] \subseteq {\mathbb {R}}^p$ is Donsker. By taking difference at most p times we get all elements in ${\mathcal {H}}$, therefore ${\mathcal {G}}$, the indicators of ${\mathcal {R}}$, is Donsker. Thus $\xi _{n,1} = O_{p}\left( n^{-\frac{1}{2}}\right)$.

The basis functions ${\mathcal {E}} = \{1, x^j, j=1,\dots , p\}$ is Donsker since all elements are monotonic and bounded since $x\in [-1,1]^p$. So ${\mathcal {G}} = {\mathcal {H}} \times {\mathcal {E}}$ is Donsker, which gives $\xi _{n,2} = O_{p}\left( n^{-\frac{1}{2}}\right)$ and $\xi _{n,4} = O_{p}\left( n^{-\frac{1}{2}}\right)$.

In addition, for fixed f, $f{\mathcal {G}}$ is therefore Donsker, which gives $\xi _{n,3} = O_{p}\left( n^{-\frac{1}{2}}\right)$. And ${\mathcal {G}} \times {\mathcal {G}}$ is Donsker, which gives $\xi _{n,5} = O_{p}\left( n^{-\frac{1}{2}}\right)$. $\square$

1.2 Proof of Theorem 1

To supplement our discussion of norms, it is immediate that $\left\| g_{R,j} \right\| \le \left\| h_R \right\| \le 1.$ Another key relation is $\left\| g_{R,j} \right\| _{n,1} \le \left\| h_R \right\| _{n,1} = \left\| h_R \right\| _n^2.$ We also assume that all R’s satisfy the terminal node condition.

Lemma 2

$\left\| {\hat{r}}_{b+1} \right\| _n \le \left\| {\hat{r}}_{b} \right\| _n$, $\left\| r_{b+1} \right\| \le \left\| r_{b} \right\|$.

Proof

Consider the $p+1$ trees used for one boosting iteration with the terminal nodes denoted as $R^j_i, 0=1,\dots ,p, i=1,\dots , m$, write $I_{R} = I\left( z \in R\right)$.

$$\begin{aligned} \left\| {\hat{r}}_{b+1} \right\| _n&= \left\| {\hat{r}}_b - \lambda \sum _{j=0}^p\sum _{i=1}^m \frac{n^{-1}\left\langle {\hat{r}}_b, g_{R^j_i, j} \right\rangle _n}{n^{-1}\left\| h_{R^j_i} \right\| _n^2}g_{R^j_i,j} \right\| _n\\&\le \sum _{j=0}^p\left\| \sum _{i=1}^m \left( \lambda {\hat{r}}_{b}I_{R^j_i}- \frac{n^{-1}\left\langle \lambda {\hat{r}}_bI_{R^j_i}, g_{R^j_i, j} \right\rangle _n}{n^{-1}\left\| h_{R^j_i} \right\| _n^2}g_{R^j_i,j}\right) \right\| _n \\&= \sum _{j=0}^p \left( \left\| \sum _{i=1}^m \left( \lambda {\hat{r}}_{b}I_{R^j_i}- \frac{n^{-1}\left\langle \lambda {\hat{r}}_bI_{R^j_i}, g_{R^j_i, j} \right\rangle _n}{n^{-1}\left\| h_{R^j_i} \right\| _n^2}g_{R^j_i,j}\right) \right\| _n^2 \right) ^{\frac{1}{2}} \\&= \sum _{j=0}^p \left( \sum _{i=1}^m \left\| \lambda {\hat{r}}_{b}I_{R^j_i}- \frac{n^{-1}\left\langle \lambda {\hat{r}}_bI_{R^j_i}, g_{R^j_i, j} \right\rangle _n}{n^{-1}\left\| h_{R^j_i} \right\| _n^2}g_{R^j_i,j} \right\| _n^2 \right) ^{\frac{1}{2}} \\&\le \sum _{j=0}^p \left( \sum _{i=1}^m \left\| \lambda {\hat{r}}_{b}I_{R^j_i} \right\| _n^2 \right) ^{\frac{1}{2}} = \sum _{j=0}^p \left\| \lambda {\hat{r}}_{b} \right\| _n = \left\| {\hat{r}}_b \right\| _n, \end{aligned}$$

given $\left\| h_{R^j_i} \right\| _n^2 \ge \left\| g_{R^j_i, j} \right\| _n^2$. Same argument can be applied to the population version hence we get the second part. $\square$

Lemma 3

For any $b\le 0$, as defined in (7),

$$\begin{aligned} \sup _{x, z} |r_{b+1}(x,z)| \le 2 \sup _{x, z} |r_{b}(x,z)|. \end{aligned}$$

Proof

As implied by (6), for (x, z) such that $z \in R$,

$$\begin{aligned} r_{b+1}(x,z) = r_b(x,z) - \lambda \sum _{i=0}^p \frac{\left\langle r_b, g_{R,j} \right\rangle }{\left\| h_{R} \right\| ^2} g_{R, j}(x,z). \end{aligned}$$

The key observation is that

$$\begin{aligned} \left| \frac{\left\langle r_b, g_{R,i} \right\rangle }{\left\| h_{R} \right\| ^2}\right| = \left| \frac{\int r_b I\left( z \in R\right) x^j dP}{\int I\left( z \in R\right) ^2 dP}\right| \le \sup _{x,z}|r_b(x,z)|. \end{aligned}$$

Therefore, provided $|g_{R,i}| \le 1$ and write $z \in R_z$,

$$\begin{aligned} \sup _{x,z} |r_{b+1}|&\le \sup _{x,z} |r_b| + \lambda \sup _{x,z} \sum _{i=0}^{p} \left| \frac{\left\langle r_b, g_{R_z,i} \right\rangle }{\left\| h_{R_z} \right\| ^2}\right| \left| g_{R_z,i}\right| \\&\le \sup |r_b| + \lambda \sum _{i=0}^{p}\sup |r_b| \cdot 1 \\&= 2 \sup _{x, z} |r_b|. \end{aligned}$$

Recursively we can conclude that $\sup _{x,z} |r_b| \le 2^b \sup _{x,z} |r_0|$. $\square$

Lemma 4

Under conditions (C1)-(C6),

$$\begin{aligned} \left\| {\hat{r}}_B \right\| ^2 = \left\| r_B \right\| ^2 + \sigma _{\epsilon }^2 + o_{p}\left( 1\right) , \end{aligned}$$

where $\sigma ^2_{\epsilon } = \left\| \epsilon \right\| ^2$.

Proof

Recall that

$$\begin{aligned} {\hat{r}}_{b+1} = {\hat{r}}_b - \lambda \sum _{j=0}^p\sum _{i=1}^m \frac{n^{-1}\left\langle {\hat{r}}_b, g_{R^j_i, j} \right\rangle _n}{n^{-1}\left\| h_{R^j_i} \right\| _n^2}g_{R^j_i,j} ={\hat{r}}_b - \lambda \sum _{i=1}^{m(p+1)} \frac{n^{-1}\left\langle {\hat{r}}_b, g_{b, i} \right\rangle _n}{n^{-1}\left\| h_{b,i} \right\| _n^2} g_{b,i}, \end{aligned}$$

and

$$\begin{aligned} r_{b+1} =r_b - \lambda \sum _{j=0}^p\sum _{i=1}^m \frac{\left\langle r_b, g_{R^j_i, j} \right\rangle }{\left\| h_{R^j_i} \right\| ^2}g_{R^j_i,j} = r_b - \lambda \sum _{i=1}^{m(p+1)} \frac{\left\langle r_b, g_{b, i} \right\rangle }{\left\| h_{b,i} \right\| ^2} g_{b,i}. \end{aligned}$$

Therefore

$$\begin{aligned} {\hat{r}}_{b+1} - r_{b+1}&= ({\hat{r}}_b - r_b) + \lambda \sum _{j=0}^p\sum _{i=1}^m \left( \frac{\left\langle r_b, g_{R^j_i, j} \right\rangle }{\left\| h_{R^j_i} \right\| ^2} - \frac{n^{-1}\left\langle {\hat{r}}_b, g_{R^j_i, j} \right\rangle _n}{n^{-1}\left\| h_{R^j_i} \right\| _n^2} \right) g_{R^j_i, j} \\&= ({\hat{r}}_b - r_b) + \lambda \sum _{i=1}^{m(p+1)} \left( \frac{\left\langle r_b, g_{b,i} \right\rangle }{\left\| h_{b,i} \right\| ^2} - \frac{n^{-1}\left\langle {\hat{r}}_b, g_{b,i} \right\rangle _n}{n^{-1}\left\| h_{b,i} \right\| _n^2}\right) g_{b,i}\\&\triangleq ({\hat{r}}_b - r_b) + \lambda \delta _{b} \\&= ({\hat{r}}_0 - r_0)+\lambda \sum _{j=0}^b \delta _j = \epsilon + \lambda \sum _{j=0}^b \delta _j. \end{aligned}$$

Since for each fixed j, all $R_i^j$ are disjoint, we therefore define that

$$\begin{aligned} \gamma _b = \sum _{j=0}^{p} \sup _{i=1,\dots , m} \left| \frac{\left\langle r_b, g_{R^j_i, j} \right\rangle }{\left\| h_{R^j_i} \right\| ^2} - \frac{n^{-1}\left\langle {\hat{r}}_b, g_{R^j_i, j} \right\rangle _n}{n^{-1}\left\| h_{R^j_i} \right\| _n^2} \right| , \end{aligned}$$

which guarantees $\sup _{x,z} |\delta _b| \le \gamma _b$. To bound $\gamma _b$, without loss of generality, we consider a single term involved such that

$$\begin{aligned} \frac{\left\langle r_b, g_{b} \right\rangle }{\left\| h_{b} \right\| ^2} - \frac{n^{-1}\left\langle {\hat{r}}_b, g_{b} \right\rangle _n}{n^{-1}\left\| h_{b} \right\| _n^2}&\triangleq \left( \frac{u}{v} - \frac{{\hat{u}}}{{\hat{v}}}\right) \\&= \left( \frac{u-{\hat{u}}}{v} + \left( \frac{1}{v}-\frac{1}{{\hat{v}}}\right) {\hat{u}}\right) . \end{aligned}$$

First consider

$$\begin{aligned} {\hat{u}} - u&= \frac{1}{n} \left\langle {\hat{r}}_b, g_{b} \right\rangle _n - \left\langle r_b, g_{b} \right\rangle \\&= \frac{1}{n} \left\langle \epsilon + r_b + \sum _{j=0}^{b-1}\delta _j, g_b \right\rangle _{n} - \left\langle r_b, g_{b} \right\rangle \\&= \frac{1}{n} \left\langle \epsilon , g_b \right\rangle _n + \left( \frac{1}{n}\left\langle r_b, g_b \right\rangle _n - \left\langle r_b, g_b \right\rangle \right) + \left( \sum _{j=0}^{b-1} \frac{1}{n}\left\langle \delta _j, g_b \right\rangle _n\right) . \end{aligned}$$

Per Lemma 3, we have

$$\begin{aligned} \left| \frac{1}{n} \left\langle \epsilon , g_b \right\rangle _n\right| \le \xi _n \end{aligned}$$

and, by iteratively applying Lemma 3 and setting $C_0 = \max (\sup _{x,z} |f|, 1),$

$$\begin{aligned}&\left| \frac{1}{n}\left\langle r_b, g_b \right\rangle _n - \left\langle r_b, g_b \right\rangle \right| \\&\quad = \left| \frac{1}{n}\left\langle f - \lambda \sum _{j=0}^{b-1}\sum _{i=1}^{m(p+1)}\frac{\left\langle r_j, g_{j, i} \right\rangle }{\left\| h_{j,i} \right\| ^2} g_{j,i}, g_b \right\rangle _n \right. \\&\qquad \left. - \left\langle f - \lambda \sum _{j=0}^{b-1}\sum _{i=1}^{m(p+1)}\frac{\left\langle r_j, g_{j, i} \right\rangle }{\left\| h_{j,i} \right\| ^2} g_{j,i}, g_b \right\rangle \right| \\&\quad \le \left| \frac{1}{n}\left\langle f, g_b \right\rangle _n - \left\langle f, g_b \right\rangle \right| + \lambda \sum _{j=0}^{b-1}\sum _{i=1}^{m(p+1)} \left| \frac{1}{n}\left\langle \frac{\left\langle r_j, g_{j, i} \right\rangle }{\left\| h_{j,i} \right\| ^2} g_{j,i}, g_b \right\rangle _n \right. \\&\qquad \left. - \left\langle \frac{\left\langle r_j, g_{j, i} \right\rangle }{\left\| h_{j,i} \right\| ^2} g_{j,i}, g_b \right\rangle \right| \\&\quad \le \left| \frac{1}{n}\left\langle f, g_b \right\rangle _n - \left\langle f, g_b \right\rangle \right| + \lambda \sum _{j=0}^{b-1}\sum _{i=1}^{m(p+1)} \left| \frac{\left\langle r_j, g_{j, i} \right\rangle }{\left\| h_{j,i} \right\| ^2}\right| \left| \frac{1}{n}\left\langle g_{j,i}, g_b \right\rangle _n - \left\langle g_{j,i}, g_b \right\rangle \right| \\&\quad \le \xi _n + \lambda \sum _{j=0}^{b-1} \sup |r_j| m(p+1) \xi _n \\&\quad \le \xi _n + C_0\sum _{j=0}^{b-1} 2^j m \xi _n \\&\quad \le C_02^bm\xi _n. \end{aligned}$$

The last term could be bounded by

$$\begin{aligned} \left| \sum _{j=0}^{b-1} \frac{1}{n}\left\langle \delta _j, g_b \right\rangle _n\right|&\le \frac{1}{n} \sum _{j=0}^{b-1} \left\| \delta _j \right\| _{n,\infty } \left\| g_b \right\| _{n,1} \le \frac{1}{n}\sum _{j=0}^{b-1} \gamma _j \left\| h_b \right\| _{n}^2, \end{aligned}$$

where

$$\begin{aligned} \left\| g_b \right\| _{n,1} = \sum _{i=1}^n |g_b(x_i)|,\quad \left\| \delta _j \right\| _{n,\infty } = \sup _{i=1,\dots , n} |\delta _j(x_i)|. \end{aligned}$$

Hence

$$\begin{aligned} |{\hat{u}} - u| \le C_02^bm\xi _n + \frac{1}{n}\sum _{j=0}^{b-1} \gamma _j \left\| h_b \right\| _{n}^2. \end{aligned}$$

In order to bound $|{\hat{u}}|$, we notice

$$\begin{aligned} |{\hat{u}}| = \left| \frac{1}{n}\left\langle {\hat{r}}_b, g_{b} \right\rangle _n\right|&\le \left( \frac{1}{n}\left\| {\hat{r}}_n \right\| _n^2\right) ^{\frac{1}{2}}\cdot \left( \frac{1}{n}\left\| g_b \right\| _n^2\right) ^{\frac{1}{2}}\\&\le \left( \frac{1}{n}\left\| {\hat{r}}_0 \right\| _n^2\right) ^{\frac{1}{2}}\cdot \left( \frac{1}{n}\left\| g_b \right\| _n^2\right) ^{\frac{1}{2}}\\&= \left( \frac{1}{n}\left\| f+\epsilon \right\| _n^2\right) ^{\frac{1}{2}}\cdot \left( \frac{1}{n}\left\| g_b \right\| _n^2\right) ^{\frac{1}{2}}\\&\le (M+\sigma ^2_{\epsilon } + \xi _n) \cdot \left\| g_b \right\| \\&\le (M_0 + \xi _n) \cdot \left\| h_b \right\| . \end{aligned}$$

Therefore, we get an upper bound for

$$\begin{aligned}&\left| \frac{\left\langle r_b, g_{b} \right\rangle }{\left\| h_{b} \right\| ^2} - \frac{n^{-1}\left\langle {\hat{r}}_b, g_{b} \right\rangle _n}{n^{-1}\left\| h_{b} \right\| _n^2} \right| \\&\quad \le \frac{|{\hat{u}}-u|}{|v|} + \left| \frac{1}{v} - \frac{1}{{\hat{v}}}\right| |{\hat{u}}| \\&\quad =\frac{C_02^bm\xi _n + n^{-1}\sum _{j=0}^{b-1} \gamma _j \left\| h_b \right\| _{n}^2}{\left\| h_b \right\| ^2} + \frac{\xi _n \cdot (M_0+\xi _n) \cdot \left\| h_b \right\| }{\left\| h_b \right\| ^2 \cdot n^{-1}\left\| h_b \right\| _n^2}\\&\quad \le \frac{C_02^bm\xi _n}{\left\| h_b \right\| ^2} + \sum _{j=0}^{b-1} \gamma _j \left( 1 + \frac{\xi _n}{\left\| h_b \right\| ^2}\right) + \frac{\xi _n(M_0 + \xi _n)}{\left\| h_b \right\| (\left\| h_b \right\| ^2-\xi _n)}. \end{aligned}$$

Denote h be the global minimum of the ensemble that $h = \min _{b,i,j} \left\| h_{R^j_i} \right\|$, since $m \le (h^2-\xi _n)^{-1}$, we obtain

$$\begin{aligned} \gamma _b&\le (p+1) \left( \frac{C_02^b\xi _n}{h^2(h^2-\xi _n)} + \sum _{j=0}^{b-1} \gamma _j \left( 1 + \frac{\xi _n}{h^2}\right) + \frac{\xi _n(M_0 + \xi _n)}{h(h^2-\xi _n)} \right) . \end{aligned}$$

We would like to mention the elementary result that for a series $\{x_n\}$ satisfying

$$\begin{aligned} x_n \le 2^na + \sum _{i=0}^{n-1}bx_i + c, \end{aligned}$$

the partial sums satisfy

$$\begin{aligned} \sum _{i=0}^n x_n \le a\left( \frac{1-\left( \frac{2}{1+b}\right) ^{n+1}}{1-\frac{2}{1+b}} \right) (1+b)^n - \frac{c}{b}. \end{aligned}$$

Hence, we can verify this upper bound that

$$\begin{aligned}&\sum _{j=0}^{B-1} \gamma _j \le (1+p)^B\left( \frac{C_0}{h^2-\xi _n}\left( 2+\frac{\xi _n}{h^2}\right) ^{B}\left( 1-\left( 1-\frac{\frac{\xi _n}{h^2}}{2+\frac{\xi _n}{h^2}}\right) ^{B-1} \right) \right. \\&\quad \left. - \frac{\xi _n(M_0+\xi _n)}{h(h^2-\xi _n)\left( 1+\frac{\xi _n}{h^2}\right) }\right) \end{aligned}$$

Recall the rates that $B = o(\log n), h^2 = O_{p}\left( n^{-\frac{1}{4}+\eta }\right) , \xi _n = O_{p}\left( n^{-\frac{1}{2}}\right)$, thus

$$\begin{aligned}&\left( 2+\frac{\xi _n}{h^2}\right) ^B = 2^B \cdot O_{p}\left( 1\right) , \quad 1-\left( 1-\frac{\frac{\xi _n}{h^2}}{2+\frac{\xi _n}{h^2}}\right) ^{B-1} = \frac{\xi _n}{h^2} \cdot O_{p}\left( 1\right) , \\&\quad \frac{\xi _n(M_0+\xi _n)}{h(h^2-\xi _n)\left( 1+\frac{\xi _n}{h^2}\right) } = \frac{\xi _n}{h^3}\cdot O_{p}\left( 1\right) . \end{aligned}$$

Hence,

$$\begin{aligned} \sum _{j=0}^{B-1} \gamma _j&\le (1+p)^B \left( \frac{ C_0}{h^2} \cdot 2^B \cdot \frac{\xi _n}{h^2} - \frac{\xi _n}{h^3}\right) O_{p}\left( 1\right) = o_p(1), \end{aligned}$$

which is equivalent to

$$\begin{aligned} \left\| \sum _{j=0}^{B-1}\delta _j \right\| \le \sum _{j=0}^{B-1}\left\| \delta _j \right\| \le \sum _{j=0}^{B-1}\gamma _j = o_{p}\left( 1\right) . \end{aligned}$$

Combining all above we have

$$\begin{aligned} \left\| {\hat{r}}_B \right\| ^2&= \left\| r_B + \epsilon + \lambda \sum _{j=0}^{B-1} \delta {j} \right\| ^2 \\&\le \left\| \epsilon \right\| ^2 + \left\| r_B \right\| ^2 + \lambda ^2 \left\| \sum _{j=0}^{B-1}\delta _j \right\| ^2 + 2 \lambda \left\| r_B+\epsilon \right\| \left\| \sum _{j=0}^{B-1}\delta _j \right\| \\&=\sigma _{\epsilon }^2 + \left\| r_B \right\| ^2 + o_{p}\left( 1\right) . \end{aligned}$$

$\square$

Lemma 5

Under condition (C1)-(C6), for any $\rho >0$ there exists $B_0 = B_0(\rho )$ and $n_0 = n_0(\rho )$ such that for all $n > n_0$,

$$\begin{aligned} P(\left\| r_{B_0} \right\| \le \rho ) \ge 1-\rho . \end{aligned}$$

Proof

Lemma 3 in Bühlmann (2002) proves this statement for rectangular indicators. By fixing $\lambda = (1+p)^{-1}$ and introducing conditions (C3) and (C4), formula (11) in Bühlmann (2002) still holds in terms of the single terminal node in each of the trees that corresponds to our defined $R^*$. Therefore cited Lemma 3 holds for our boosted trees. The conclusion is therefore reached by the assumption that $f \in \text{ span }({\mathcal {G}})$. $\square$

Proof of main Theorem

For a given $\rho >0$, since ${\hat{r}}_B(x^*, z^*) - f(x^*,z^*)$ is independent of $\epsilon$,

$$\begin{aligned}&{\mathbb {E}}_{(x^*,z^*)}\left[ {|{\hat{\beta }}_B(z^*)^Tx^* - f(x^*,z^*)|^2}\right] \\&\quad = {\mathbb {E}}_{(x^*,z^*)}\left[ {|{\hat{r}}_B(x^*, z^*) - f(x^*,z^*)- \epsilon |^2}\right] - \left\| \epsilon \right\| ^2\\&\quad = \left\| {\hat{r}}_B \right\| ^2 - \left\| \epsilon \right\| ^2 \\&\quad \le \left\| r_B \right\| ^2 + o_{p}\left( 1\right) \\&\quad \le \left\| r_{B_0} \right\| ^2 + o_{p}\left( 1\right) \\&\quad \le \rho O_{p}\left( 1\right) + o_{p}\left( 1\right) . \end{aligned}$$

We reach the conclusion by sending $\rho \rightarrow 0$. $\square$

1.3 Proof of Corollary 1

Proof

We prove by contradiction. Assume there exists $0< \epsilon _0 < s, c_0 > 0$ s.t.

$$\begin{aligned} P(\left\| \beta _B(z^*) - \beta (z^*) \right\| ^2>\epsilon _0) \ge c_0 \end{aligned}$$

for any sufficiently large n. Fix n and consider any $z_0$ s.t. $\left\| \beta _B(z_0) - \beta (z_0) \right\| >\epsilon _0$. The corresponding open ball $B(x_0, s)$ has volume $v_0 = O(s^p)$. Write $\beta = \begin{bmatrix} \beta ^0\\ \beta ^{-0} \end{bmatrix},$

$$\begin{aligned}&\int _{B(x_0,s)} \left\langle \begin{bmatrix} 1 \\ x \end{bmatrix}, \beta _B(z_0) - \beta (z_0) \right\rangle ^2 dP_{x|z_0} \\&\quad \ge c\int _{B(x_0,s)} \left\langle \begin{bmatrix} 1 \\ x \end{bmatrix}, \beta _B(z_0) - \beta (z_0) \right\rangle ^2 dx \\&\quad \ge cv_0\left\langle \begin{bmatrix} 1 \\ x_0 \end{bmatrix}, \beta _B(z_0) - \beta (z_0) \right\rangle ^2 + c\int _{B(0,s)}\left\langle \begin{bmatrix} 1 \\ x \end{bmatrix}, \beta _B(z_0) - \beta (z_0) \right\rangle ^2 dx\\&\quad \ge cv_0 (\beta _B(z_0)^0 - \beta (z_0)^0)^2 + ct_0 \left\| \beta _B(z_0)^{-0} - \beta (z_0)^{-0} \right\| ^2 \\&\quad \ge c\min (v_0, t_0) \epsilon _0. \end{aligned}$$

where $t_0 = \int _{B(0,s)}x_1^2 dx = O(s^p).$ That is equivalent to

$$\begin{aligned} {\mathbb {E}}_{(x^*,z^*)}\left[ {|{\hat{\beta }}_B(z^*)^Tx^* - f(x^*,z^*)|^2}\right] > c\min (v_0, t_0) \epsilon _0, \end{aligned}$$

contradicting Theorem 1. $\square$

Empirical study details

Table 6 reports the details on the datasets and parameters used for the real world experiments. In particular, all experiments build 100 trees and apply 10-fold cross validation to measure the metrics and their uncertainties.

Table 6 Dataset details and experiment parameters for the 12 real world studies

Fig. 6

Histograms of distributions of fitted coefficient values. Color code: ground truth (grey) and tree boosted VCM (red)

The codebase, along with all empirical study code and data, can be found at

https://github.com/siriuz42/treeboostVCM

Additional empirical study

1.1 Identifying signals

Our theory suggests that tree boosted VCM is capable of identifying local linear structures and their coefficients accurately. To demonstrate this in practice, we apply it to the following regression problem with higher order feature interaction on the action space.

$$\begin{aligned}&z = (z^1, z^2, z^3, z^4), \quad z^1, z^2 \sim \text{ Unif }\{1,\dots , 10\}, \quad z^3, z^4 \sim \text{ Unif }[0,1].\\&x \in {\mathbb {R}}^{7}, \quad x \sim N(0, I_{7}), \quad \epsilon \sim N(0, 0.25). \end{aligned}$$

The data generating process is described by the following pseudo code.

$$\begin{aligned}&\text{ if } z^1< 4:&y = 1 + 3 x^1 + 7 x^2 \\&\text{ else } \text{ if } z^1 > 8:&y = -5 + 2x^1 + 4x^2 + 6x^3\\&\text{ else } \text{ if } z^2 = 1, 3 \text{ or } 5:&y = 5 + 5x^2 + 5x^3\\&\text{ else } \text{ if } z^3< 0.5:&y = 10 + 10x^4 \\&\text{ else } \text{ if } z^4< 0.4:&y = 10+10x^5 \\&\text{ else } \text{ if } z^3 < z^4:&y = 5-5x^2 - 10x^3 \\&\text{ else }:&y = -10 x^1 + 10x^3 \end{aligned}$$

We utilize a sample of size 10,000 and use 100 trees of maximal depth of 6 for boosting with constant learning rate of 0.2. Figure 6 plots the fitted distribution of each coefficient in red against the ground truth in grey, with reported MSE 3.28. We observe that all peaks and their intensities properly reflect the coefficient distributions on the action space. Despite the linear expressions, we have tested interactions among all four action covariates of a tree depth of 6 and have not yet achieved convergence, which we conclude as the reasons for large MSE. It manifests the effectiveness of our straightforward implementation of decision trees segmenting the action space.

1.2 Constrained Beijing housing model

Here we present the plots of the Beijing Housing dataset should we not attach the non-negative regularization on the regressors. Training error in this case is smaller (1.858024 after 200 trees, in contrast to 1.911139 after 200 trees of the regularized model). However, its results are harder to interpret.

Fig. 7

Beijing housing unit price broken down on several factors. No constraints attached

1.3 Beijing housing model by mboost

We present the plots of the Beijing Housing dataset fit through mboost which is a standard fitting method provided along with the dataset. Here the model fit assumes a generalized linear relationship between the covariates and the label, whereas instead of a fixed effect slope, the generalized linear terms are created for each level of the covariates, so the model is indeed more complex then in Fig. 7. Here we are showing the coefficients for bathroom, living room and elevator at levels equal to 1, floor at level 10 and refurbished at level 2.

Fig. 8

Beijing housing dataset fitted by mboost

The shapes of the coefficients here mostly agree with Fig. 7, complying with the overall outline of the city. For floor and elevator, the mboost fit seems to be more smoothed out.