MultiRocket: multiple pooling operators and transformations for fast and effective time series classification

Abstract

We propose MultiRocket, a fast time series classification (TSC) algorithm that achieves state-of-the-art accuracy with a tiny fraction of the time and without the complex ensembling structure of many state-of-the-art methods. MultiRocket improves on MiniRocket, one of the fastest TSC algorithms to date, by adding multiple pooling operators and transformations to improve the diversity of the features generated. In addition to processing the raw input series, MultiRocket also applies first order differences to transform the original series. Convolutions are applied to both representations, and four pooling operators are applied to the convolution outputs. When benchmarked using the University of California Riverside TSC benchmark datasets, MultiRocket is significantly more accurate than MiniRocket, and competitive with the best ranked current method in terms of accuracy, HIVE-COTE 2.0, while being orders of magnitude faster.

1 Introduction

Many of the most accurate methods for time series classification (TSC), such as HIVE-COTE 2.0 (Middlehurst et al. 2021), achieve high classification accuracy at the expense of high computational complexity and limited scalability (Middlehurst et al. 2021). Hence scalable TSC has become an important research topic in recent years (Herrmann and Webb 2021; Tan et al. 2020; Dempster et al. 2021, 2020; Shifaz et al. 2020; Lucas et al. 2019; Schäfer 2016). Rocket and MiniRocket are the fastest and most scalable among all the proposed scalable TSC methods that achieve state-of-the-art (SOTA) accuracy (Dempster et al. 2021, 2020). They achieve SOTA accuracy with a fraction of the computational expense of any other method of similar accuracy (Dempster et al. 2021, 2020). Despite their scalability, Rocket and MiniRocket are somewhat less accurate than the variants of HIVE-COTE (Bagnall et al. 2020), including the most recent HIVE-COTE 2.0 (Middlehurst et al. 2021), which is the current best ranked method with respect to accuracy on 112 datasets in the widely used benchmark UCR archive of time series classification datasets (Dau et al. 2018).

MiniRocket is built on Rocket and is recommended over Rocket due to its scalability (Dempster et al. 2021). We show that it is possible to significantly improve the accuracy of MiniRocket, with some additional computational expense, by transforming the time series prior to the convolution operations, and by expanding the set of pooling operations used to generate features. We call this method MultiRocket – for MiniRocket with multiple pooling operators and transformations.

Rocket and MiniRocket apply convolutional kernels to the raw input series. The resulting outputs are each summarized by the Proportion of Positive Values (PPV) summary statistic. The resulting values are provided as input features to a simple linear model. MiniRocket uses a fixed set of 84 kernels and generates multiple dilations and biases for each kernel, by default producing a total of 10,000 features for the convolution operations.

MultiRocket is based on MiniRocket, using the same set of kernels as MiniRocket. There are two main differences. First, MultiRocket transforms a time series into its first order difference. Then both the original and the first order difference time series are convolved with the 84 MiniRocket kernels. A different set of dilations and biases is used for each representation because both representations have different lengths (first order difference is shorter by 1) and range of values (bias values are sampled from the convolution output). Second, in addition to PPV, MultiRocket adds 3 additional pooling operators to increase the diversity and discriminatory power of the extracted features. By default, MultiRocket produces approximately 50,000 (49,728 to be exact) features per time series (i.e., $6{,}216 \times 2 \times 4$). For simplicity, when discussing the number of features, we round the number to the nearest 10,000 throughout the paper. Finally the transformed features are used to train a linear classifier.

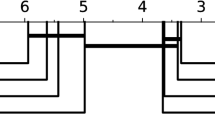
Using first order differencing, expanding the set of pooling operators, and increasing the total number of features to 50,000, increases the diversity of the extracted features. This enhancement makes MultiRocket one of the most accurate TSC methods, on average on the datasets in the UCR time series archive (Dau et al. 2018), as illustrated in a critical difference diagram (Demšar 2006) shown in Fig. 1. Figure 1 shows that MultiRocket is significantly more accurate than MiniRocket (and most top SOTA methods – see Fig. 5 in our experiments section). It is also not significantly less accurate than the most accurate TSC method to-date HIVE-COTE 2.0 (Middlehurst et al. 2021).

Fig. 1

Average rank of MultiRocket with the default configuration, in terms of accuracy over 30 resamples of 109 datasets from the UCR archive (Dau et al. 2018), against the top 4 SOTA methods. Classifiers grouped together by a black line (in the same clique) are not significantly different from each other

The use of first order difference transform and additional pooling operators in MultiRocket substantially increases the computational expense of the transform over MiniRocket. Figure 2a and b compare the total compute time (first order difference transform, convolution transforms, training and testing) for MultiRocket and MiniRocket, both with 10,000 and 50,000 features, over 109 datasets from the UCR archive. Note that the timings are averages over 30 resamples of each dataset, and run on a cluster using AMD EPYC 7702 CPUs with 32 threads. Figure 2a shows that the default MultiRocket with 50,000 features is up to an order of magnitude slower than the default MiniRocket, which has 10,000 features. However, the default MultiRocket takes only 20% longer to process the entire repository than MiniRocket with the same number of features, as illustrated in Fig. 2b.

Although the default MultiRocket (using 50 k features) is approximately 10 times slower than the default MiniRocket (using 10k features), the total compute time for 109 UCR datasets of 5 min, using 32 threads, is still orders of magnitude faster than most SOTA TSC algorithms. The smaller variant of MultiRocket with 10,000 features (the same number as the default MiniRocket) is on average half as fast as MiniRocket while being significantly more accurate. The relative computational disadvantage of MultiRocket relative to MiniRocket with the same number of features decreases as the number of features increases as the relative impact of once off operations such as taking the derivatives of the series decline as a proportion of total time.

Fig. 2

Total compute time of both MultiRocket and MiniRocket with 10,000 and 50,000 features. Compute times are averaged over 30 resamples of 109 UCR datasets, and run on a cluster using AMD EPYC 7702 CPU with 32 threads. Figure best viewed in color

The rest of the paper is organised as follows. In Sect. 2, we review the relevant existing work. In Sect. 3, we describe MultiRocket in detail. In Sect. 4, we present our experimental results and conclude our paper.

2 Related work

2.1 State of the art

The goal of TSC is to learn discriminating patterns that can be used to group time series into predefined categories (classes) (Bagnall et al. 2017). The accuracy of a TSC algorithm is a measure of its discriminating power. The current SOTA TSC algorithms with respect to accuracy include HIVE-COTE and its variants (Middlehurst et al. 2021; Bagnall et al. 2020; Middlehurst et al. 2020a, b), TS-CHIEF (Shifaz et al. 2020), MiniRocket (Dempster et al. 2021), Rocket (Dempster et al. 2020) and InceptionTime (Fawaz et al. 2020). With some exceptions (namely, Rocket and MiniRocket), most SOTA TSC methods are burdened with high computational complexity.

InceptionTime is the most accurate deep learning architecture for TSC (Fawaz et al. 2020). It is an ensemble of 5 Inception-based convolutional neural networks. Ensembling reduces the variance of the model. The resulting method is significantly more accurate compared with other deep learning based TSC methods such as the Fully Convolutional Network (FCN) and Residual Network (ResNet).

TS-CHIEF was first introduced as a scalable TSC algorithm with accuracy competitive with HIVE-COTE (Shifaz et al. 2020). It builds on Proximity Forest (Lucas et al. 2019), an ensemble of decision trees using distance measures at each node as the splitting criterion. TS-CHIEF improves on Proximity Forest by adding interval and spectral based splitting criteria, allowing the ensemble to capture a wider range of representations.

HIVE-COTE is a meta-ensemble that consists of the most accurate ensemble classifiers from different time series representation domains (Bagnall et al. 2020; Lines et al. 2016). The original HIVE-COTE consists of Ensemble of Elastic Distances (EE) (Lines and Bagnall 2015), Shapelet Transform Classifier (STC) (Hills et al. 2014), Bag of SFA Symbols (BOSS) Ensemble (Schäfer 2016), Time Series Forest (TSF) (Deng et al. 2013) and Random Interval Forest (RIF) (Lines et al. 2016), each of them being the most accurate classifier in their respective domains. The authors showed that HIVE-COTE is significantly more accurate than each of its constituent members, and it has stood as a high benchmark for classification accuracy ever since.

Recently HIVE-COTE 2.0 (Middlehurst et al. 2021) was proposed and has been shown to have the best average rank on accuracy against a spread of the SOTA both in the univariate UCR (Dau et al. 2018) and the multivariate UEA (Bagnall et al. 2018) time series archives. HIVE-COTE 2.0 is a meta-ensemble of four main components, STC, Arsenal, Temporal Dictionary Ensemble (TDE) (Middlehurst et al. 2020b), and Diverse Representation Canonical Interval Forest (DrCIF) (Middlehurst et al. 2021). HIVE-COTE 2.0 drops EE from the ensemble as EE is not scalable and does not contribute greatly towards the accuracy of HIVE-COTE (Bagnall et al. 2020). The only module retained from the original HIVE-COTE is STC with some additional modifications to make it scalable. STC in HIVE-COTE 2.0 randomly searches for shapelets within a given contract time and transforms a time series using the distance to each shapelet. It then employs a rotation forest as the classifier. Arsenal is an ensemble of small Rocket classifiers with 4000 features each. This approach allows the ensemble to return a probability distribution over the classes when making predictions, allowing Rocket to be used within the HIVE-COTE framework. The dictionary-based classifier, BOSS was replaced with the more accurate TDE (Middlehurst et al. 2021). TDE combines aspects of various earlier dictionary methods and is significantly more accurate than any existing dictionary method (Middlehurst et al. 2020b).

HIVE-COTE 2.0 updates HIVE-COTE by replacing RISE and TSF with DrCIF. DrCIF is significantly more accurate than RISE, TSF and its predecessor CIF (Middlehurst et al. 2020a). RISE is an ensemble of various classifiers that derives spectral features (periodogram and auto-regressive terms) from intervals of a time series. TSF identifies key intervals within the time series, uses simple summary statistics to extract features from these intervals and then applies Random Forests to those features. DrCIF builds on both RISE and TSF by transforming the time series using the first order difference and periodogram. It expands the original set of features used in TSF, using the catch22 features (Lubba et al. 2019). Diversity is achieved by randomly sampling different intervals and subsets of features for each representation in each tree. The use of diverse representations and additional features from the catch22 feature set within DrCIF results in a considerable improvement in accuracy (Middlehurst et al. 2021). We build on these observations and explore the possibility of extending MiniRocket with expanded feature sets and diverse representations.

While producing high classification accuracy, most of these methods do not scale well. The total compute time (training and testing) on the 109 datasets from the UCR time series archive, using a single CPU thread, is around 2 days for DrCIF, 3 days for TDE, more than a week for Proximity Forest, and more than 2 weeks for HIVE-COTE 2.0 (Middlehurst et al. 2021; Dempster et al. 2021; Middlehurst et al. 2020a, b). On the other hand, MiniRocket was reported to be able to complete training and testing on 109 datasets within 8 min (Dempster et al. 2021). To be comparable to MultiRocket, we ran MiniRocket on the same hardware, single threaded, and completed the whole 109 datasets just under 4 min, while MultiRocket with the default 50,000 features takes 40 min, an order of magnitude slower (see Fig. 7a in Appendix D). However, as shown in Fig. 2a, MultiRocket was able to complete all 109 datasets in around 5 min using 32 threads, while the default MiniRocket with 10,000 features took around 2 min. Regardless, MultiRocket is still significantly faster than all SOTA methods other than MiniRocket and highly competitive on accuracy.

2.2 MiniRocket and Rocket

Rocket is a significantly more scalable TSC algorithm, matching the accuracy of most SOTA TSC methods (Dempster et al. 2020), and taking just 2 h to train and classify the same 109 UCR datasets using a single CPU core (Dempster et al. 2021). Rocket transforms the input time series using 10,000 random convolutional kernels (random in terms of their length, weights, bias, dilation, and padding). It then uses PPV and Max pooling operators to compute two features from each convolution output, producing 20,000 features per time series. The transformed features are used to train a linear classifier. The use of dilation and PPV are the key aspects of Rocket in achieving SOTA accuracy.

MiniRocket is a much faster variant of Rocket. It takes less than 10 min to train and classify the same 109 UCR datasets using a single CPU core, while maintaining the same accuracy as Rocket (Dempster et al. 2021). Unlike Rocket, MiniRocket uses a small, fixed set of kernels (with different bias and dilation combinations) and only computes PPV features. Since MiniRocket has the same accuracy as Rocket and is much faster, MiniRocket is recommended to be the default variant of Rocket (Dempster et al. 2021). In this work, we extend MiniRocket with first order difference and additional pooling operators to achieve a new SOTA TSC algorithm that is also scalable. We describe MultiRocket in Sect. 3.

2.3 Time series representations

Traditionally, time series analysis involves analysing time series data under different transformations, such as the Fourier transform. Different transformations and representations show different information about the time series. Transforming a time series to a useful representation allows us to better capture meaningful and indicative patterns to discriminate different or group similar time series, thus improving the performance of a model. A poor representation may lead to lost performance. For instance, it is easier to analyse time series of different frequencies if they were represented in the frequency domain. This is known as spectral analysis. The Fourier transform transforms a time series into the frequency domain, giving a spectrum of frequencies (Hannan 2009; Bracewell and Bracewell 1986). Then the transformed time series is analysed using the magnitude of each frequency in the spectrum. A limitation of the Fourier transform is that it only gives information on which frequencies are present but has no information about location and time. In consequence, the wavelet transform was proposed to better capture the location of each frequency (Vidakovic 2009).

A recent review (Salles et al. 2019) groups different time series transforms that are often used in time series forecasting tasks into two categories, (1) mapping and (2) splitting transforms. Mapping-based transforms map a time series into another representation through a mathematical process such as logarithm, moving average and differencing. Splitting-based transforms split a time series into a number of component time series, such as Fourier and Wavelet transforms that split a time series into different frequencies. Each component is a simpler time series that can be analysed separately and later be reversed to obtain the original time series representation.

The derivatives can also be used to capture different information about time series. The first order derivative captures the “velocity” (rate of change) of the data points in the time series. The second order derivative then measures the “acceleration” of each data point. Górecki and Łuczak (2013) combines the original raw series and its first order derivative by weighing the distance of the raw series and the first order derivative series. They showed that their approach achieved better classification accuracy than using the two representations separately. Calculating the exact derivatives of a time series is difficult without knowing the underlying function. There are many ways to estimate derivatives. Górecki and Łuczak (2013) explored 3 different methods and they found that they do not statistically differ from one another. Hence, we use the simple differencing approach to estimate the derivatives of a time series.

In Sect. 4, we explore some time series transformation methods to improve the accuracy of MiniRocket and create MultiRocket.

3 MultiRocket

This section describes MultiRocket in detail. MultiRocket shares the overarching architecture of MiniRocket (Dempster et al. 2021) – it transforms time series using convolutional kernels, computes features from the convolution outputs and trains a linear classifier. There are two main differences between MultiRocket and MiniRocket. First is the usage of the first order difference transform and second is the additional 3 pooling operators used per kernel. The combination of these transformations significantly boosts the classification power of MiniRocket. The type of transforms and pooling operators used were tuned on the same 40 “development” datasets as used in (Dempster et al. 2021, 2020) to avoid overfitting the entire UCR archive.

3.1 Time series representations

Diversity is the key to improve a classifier’s accuracy. HIVE-COTE 2.0 is an accurate TSC classifier because it is a meta-ensemble of a diverse set of time series ensembles, each capturing different representations of a time series, e.g., DrCIF.

Drawing inspiration from DrCIF, we first inject diversity into MiniRocket by transforming the original time series into its first order difference. From this point onward, we refer to the original time series that has not been transformed as the base time series. Then convolution is applied to both base and first order difference time series. We explored different transformation combinations in Sect. 4 and found that this combination works best overall on the 40 “development” datasets. Note that different transformations can be considered depending on the dataset and problem, and we consider this exploration as future work.

The first order difference of a time series describes the rate of change of the time series between each unit time step. This gives additional information about the time series , such as identifying the slope of a time series or the presence of certain outliers (or patterns) in a time series that maybe easier to discriminate between two classes. A given time series $X{=}\{x_1,x_2,...,x_l\}$ is transformed into its first order difference, $X'$ using Eq. (1). We will use this notation to refer to a time series throughout the paper.

$$\begin{aligned} X'{=}\{x_t{-}x_{t-1}: \forall t \in \{2,...,l\}\} \end{aligned}$$

(1)

3.2 Convolutional kernels

Now, we describe the convolutional kernels used in MultiRocket. MultiRocket uses the same fixed set of kernels as used in MiniRocket (Dempster et al. 2021), producing high classification accuracy and allowing for a highly optimised transform. Note that the enhancement used in MultiRocket is also applicable to improve the classification accuracy of Rocket. However, MiniRocket is preferable over Rocket due to its scalability (Dempster et al. 2021). We refer interested readers to (Dempster et al. 2020) for details of the kernels used in Rocket. The kernels for MultiRocket are characterised in terms of their length, weights, bias, dilation, and padding:

• Length and weights As per MiniRocket, MultiRocket uses kernels of length 9, with weights restricted to two values and, in particular, the subset of such kernels where six weights have the value $-1$, and three weights have the value 2, e.g., $W {=} [-1, -1, -1, -1, -1, -1, 2, 2, 2]$. This gives a total of 84 fixed kernels.

• Dilation Each kernel uses the same (fixed) set of dilations. Dilations are set in the range $\{\lfloor 2^{0} \rfloor , ..., \lfloor 2^{\text {max}} \rfloor \}$, with the exponents spread uniformly between 0 and $\text {max} {=} \log _2 ( l_{\text {input}} - 1 ) / ( l_{\text {kernel}} - 1 )$, where $l_{\text {input}}$ is the length of the input time series and $l_{\text {kernel}}$ is kernel length.

• Bias Bias values for each kernel/dilation combination are drawn from the convolution output. For each kernel/dilation combination, we compute the convolution output for a randomly-selected training example, and take the quantiles of this output as bias values. (The random selection of training examples is the only random aspect of these kernels.)

• Padding Padding is alternated between kernel/dilation combinations, such that half of the kernel/dilation combinations use padding (standard zero padding), and half do not.

3.3 Convolution operation

The base and first order difference time series use different set of dilations and biases to produce the feature maps. The first order difference time series is shorter by one value than the base time series. Hence, the maximum dilation for the first order difference time series will be shorter than the base time series, resulting in a slightly different set of kernels than the base time series. Additionally, it has a different range of values from the base time series, resulting in a different set of bias values. Apart from these, the length, weights and padding are the same for both base and first order difference time series. The convolution operation then involves a sliding dot product between a kernel and a time series.

3.4 Pooling operators

After the convolution operations, MultiRocket then computes four features per convolution output, Z, with length n. These features summarise the values in Z and are also known as pooling operators. Table 1 shows a summary of the pooling operators used in MultiRocket, Proportion of Positive Values (PPV), Mean of Positive Values (MPV), Mean of Indices of Positive Values (MIPV) and Longest Stretch of Positive Values (LSPV). The features are illustrated in Fig. 3. Algorithm 1 in Appendix A illustrates the procedure to calculate all four features for a given convolution output, Z.

Table 1 Summary of pooling operators (features) used in MultiRocket using a dummy example illustrating different scenarios where PPV will fail to discriminate between different convolution outputs. Each convolution output consists of 6 zeros and 4 positive values giving $PPV {}=0.4$

Fig. 3

Simple visualisation of the features used in MultiRocket, using a convolution output Z of length $n=100$. p1 and p2 are the number of positive values; a1 and a2 are the sum of positive values; i1 and i2 are the sum of the indices of the positive values. Then the features are calculated as shown in the figure and $LSPV {}=p2$ since $p2>p1$

3.4.1 Proportion of positive values

PPV was introduced in Rocket and was found to be an exceptional feature for MiniRocket. It calculates the proportion of positive values from a convolution output Z. PPV is directly related to the bias term which can be seen as a ‘threshold’ for PPV, as described in Eq. (2). A positive bias value means that PPV is able to capture the proportion of the time series reflecting even weak matches between the input and a given pattern, while a negative bias value means that PPV only captures the proportion of the input reflecting strong matches between the input and the given pattern (Dempster et al. 2020). It is important to note that given PPV, computing the proportion of negative values would not add any extra information as they are complementary to each other. Given the exceptional performance and importance of PPV in MiniRocket, we retain PPV in MultiRocket.

$$\begin{aligned} PPV (Z) = \frac{1}{n}\sum _{i=1}^{n}[z_i>0] \end{aligned}$$

(2)

We augment PPV with three further pooling operators that capture forms of information about the convolutional output to which PPV is blind.

3.4.2 Mean of positive values

First, we propose the Mean of Positive Values (MPV) to capture the magnitude of the positive values in a convolution output, Z of length n, for example, distinguishing A from E in Table 1. MPV is calculated using Eq. (3) where $Z^{+}$ represents a vector of positive values of length m and $PPV {}(Z)=|Z^+| / n=m/n$.

$$\begin{aligned} MPV (Z) = \frac{1}{m}\sum _{i=1}^{m}z^{+}_i \end{aligned}$$

(3)

Similar to PPV, MPV is related to the bias term. It captures the intensity of the matches between an input time series and a given pattern – an information that is available when computing PPV but discarded. This means that MPV can be computed with negligible additional computational cost.

3.4.3 Mean of indices of positive values

The Mean of Indices of Positive Values (MIPV) captures information about the relative location of positive values in the convolution outputs, for example, distinguishing A from B in Table 1. Consider the convolution output Z as an array of values, MIPV is computed by first recording the relative location of all positive values in the array, i.e., its indices in the array. Then the mean of the indices is calculated using Eq. (4), where $I^{+}$ indicates the indices of positive values. Note that $PPV {}(Z){=}|I^+|/n{=}m/n$, where m is the number of positive values in Z. In the case where there are no positive values, $m=0$, MIPV returns −1 to differentiate from the first index, considering we start with index 0. For example, the convolution output A in the dummy example in Table 1 has positive values at locations $I^{+}=[6,7,8,9]$ giving $MIPV {}{=}7.5$.

$$\begin{aligned} MIPV (Z) = {\left\{ \begin{array}{ll} \frac{1}{m}\sum \limits _{j=1}^{m}i^{+}_j &{} \text {if } m > 0 \\ -1 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(4)

Since $PPV {}(Z)=|I^+|/n$, the indices of positive values are also available when we are calculating PPV, but currently not used in MiniRocket. Thus, like MPV, MIPV can also be computed with negligible additional cost.

3.4.4 Longest stretch of positive values

MIPV pools all positive values and hence fails to distinguish between many small sequences of successive positive values and a small number of long sequences. This can provide information of the underlying time series as shown in the example in Appendix B. The Longest Stretch of Positive Values (LSPV) returns the maximum length of any subsequence of positive values in a convolution output, calculated using Eq. (5).

$$\begin{aligned} LSPV (Z) = \max \left[ j-i\mid \forall _{i\le k\le j}z_k>0\right] \end{aligned}$$

(5)

This provides a different form of information about the positive values in the convolutional output than is provided by any of the other features, for example, distinguishing C from the remaining series in Table 1. Note that calculating LSPV comes with a slight overhead over both MPV and MIPV.

3.5 Classifier

By default, MultiRocket produces 50,000 features (49,728 to be exact, using 6,216 kernels, 2 representations and 4 pooling operators). Like MiniRocket, the transformed features are used to train a linear classifier. MultiRocket uses a ridge regression classifier by default. As suggested in Dempster et al. (2021, 2020), a logistic regression classifier is preferable for larger datasets as it is faster to train. All of our experiments in Sect. 4 were conducted with the ridge classifier. The software also supports the logistic regression classifier if required.

4 Experiments

In this section, we evaluate MultiRocket on the datasets in the UCR univariate time series archive (Dau et al. 2018). We show that MultiRocket is significantly more accurate than its predecessor, MiniRocket and not significantly less accurate than the current most accurate TSC classifier, HIVE-COTE 2.0. By default, MultiRocket generates 50, 000 features. We show that even with 50, 000 features, MultiRocket is only about 10 times slower than MiniRocket, but orders of magnitude faster than other current state of the art methods. Our experiments also show that the smaller variant of MultiRocket with 10, 000 features (same number of features as MiniRocket) is as fast as MiniRocket while being significantly more accurate. Finally, we explore key design choices, including the choice of transformations, features and the number of features. These design choices are tuned on the 40 “development” datasets as used in (Dempster et al. 2021, 2020) to reduce overfitting of the whole UCR archive.

MultiRocket is implemented in Python, compiled via Numba (Lam et al. 2015) and we use the ridge regression classifier from scikit-learn (Pedregosa et al. 2011). Our code and results are all publicly available in the accompanying website, https://github.com/ChangWeiTan/MultiRocket. All of our experiments were conducted on a cluster with AMD EPYC 7702 CPU, 32 threads and 64 GB memory.

4.1 Comparing with current state of the art

First, we evaluate MultiRocket and compare it with the current most accurate TSC algorithms, namely HIVE-COTE 2.0, TS-CHIEF, InceptionTime, MiniRocket, Arsenal, DrCIF, TDE, STC and ProximityForest. These algorithms¹ are chosen because they are the most accurate in their respective domains. ProximityForest represents the distance-based algorithms; STC represents shapelet-based algorithms; While TDE and DrCIF represent dictionary-based and interval-based algorithms respectively.

For consistency and direct comparability with the SOTA TSC algorithms, we evaluate MultiRocket on the same 30 resamples of 109 datasets from the UCR archive as reported and used in (Middlehurst et al. 2021; Dempster et al. 2021; Bagnall et al. 2020). Note that each resample creates a different distribution for the train and test sets. Resampling of each dataset is achieved by first mixing the train and test sets, then performing a stratified sampling for train and test sets and maintaining the same number of instances for each resample.

Figure 4 shows the average rank of MultiRocket against all SOTA methods mentioned. The black line groups methods that do not have a pairwise statistical difference using a two-sided Wilcoxon signed-rank test ($\alpha =0.05$) with Holm correction as the post-hoc test to the Friedman test (Demšar 2006). MultiRocket is on average significantly more accurate than most SOTA methods. The critical difference diagram with the top 5 algorithms shown in Fig. 1 shows that MultiRocket is significantly more accurate than its predecessor, MiniRocket but not significantly less accurate than HIVE-COTE 2.0, TS-CHIEF and InceptionTime, all of which are ensemble-based algorithms. Note that MultiRocket is one of the few non-ensemble-based algorithms that has achieved SOTA accuracy. Appendix C shows the pairwise comparison of some SOTA algorithms.

Fig. 4

Average rank of MultiRocket with the default configuration, in terms of accuracy over 30 resamples of 109 datasets from the UCR archive (Dau et al. 2018), against 9 other SOTA methods. Classifiers grouped together by a black clique indicate that they are not significantly different from each other.

Figure 5 shows the pairwise statistical significance and comparison of the mentioned top SOTA methods. Every cell in the matrix shows the wins, draws and losses on the first row and the p-value for the two-sided Wilcoxon signed-rank test. The values in bold indicate that the two methods are significantly different after applying Holm correction. Overall, as expected and pointed out in (Middlehurst et al. 2021), HIVE-COTE 2.0 is significantly more accurate than any other method, where the p-values for most of the methods are much less than 0.001, even after applying Holm correction. MultiRocket is the only method with a p-value larger than 0.001 and not significantly different from HIVE-COTE 2.0 after applying Holm correction. The figure also shows that MultiRocket is significantly more accurate than most other methods.

Fig. 5

Pairwise statistical significance and comparison of the top SOTA methods. For every cell in the figure, the first row shows the wins/draws/losses of the horizontal method with the vertical method on 30 resamples of the 109 UCR datasets, calculated on the test set; the second row presents the p-value for the statistical significance test, computed using a two-sided Wilcoxon signed rank test. The values in bold indicate that the two methods are significantly different after applying Holm correction

Although HIVE-COTE 2.0 is significantly more accurate than MultiRocket with 59 wins out of 109 datasets, the difference in accuracy between HIVE-COTE 2.0 and MultiRocket lies within $\pm 5\%$, as shown in Fig. 6a, indicating that there is relatively little difference between the two methods. On the other hand, MultiRocket and InceptionTime are not significantly different from each other, despite MultiRocket having more larger wins, as depicted in Fig. 6b. For instance, MultiRocket is most accurate against InceptionTime on the SemgHandMovementCh2 dataset with accuracy of 0.792 and 0.551. While InceptionTime is the most accurate against MultiRocket on the PigAirwayPressure dataset with accuracy of 0.922 and 0.647. The large variance in the difference in accuracy between MultiRocket and InceptionTime implies that both methods are strong in their own ways and that MultiRocket can potentially be improved on datasets where InceptionTime performed much better.

HIVE-COTE 2.0 , TS-CHIEF and InceptionTime are able to capture the different time series representations that have not been able to be captured by MultiRocket. This shows the importance of diversity in classifiers to achieve high classification accuracy. However, as shown in Fig. 2a, MultiRocket only takes 5 min (using 32 threads) to complete training and classification on all 109 datasets, a time that is at least an order of magnitude faster than HIVE-COTE 2.0, TS-CHIEF and InceptionTime.

As seen on both Fig. 6a and b, MultiRocket performed the worst on the PigAirwayPressure dataset, with the largest difference of 0.308 and 0.275 compared to HIVE-COTE 2.0 and InceptionTime respectively. Rocket achieved poor performance on this dataset as pointed out in (Dempster et al. 2021) due to the way the bias values are sampled. This issue has been mitigated in MiniRocket by sampling the bias values from the convolution output instead of a uniform distribution, $U(-1,1)$ in Rocket (Dempster et al. 2020). MultiRocket samples different sets of bias for the base and first order difference series. It is possible that the first order differences gives rise to the poor performance on this dataset.

Fig. 6

Pairwise accuracy comparison of MultiRocket against a HIVE-COTE 2.0 and b InceptionTime on 109 datasets from the UCR archive. Each point represents the average accuracy value over 30 resamples of each dataset. The dotted lines indicate $\pm 5\%$ intervals on the classification accuracy

4.2 Runtime analysis

The addition of the first order difference transform and additional 3 features increases the total compute time of MiniRocket. Fig. 7a and b show the total compute time (training and testing) of both MultiRocket and MiniRocket with 10,000 and 50,000 features using an AMD EPYC 7702 CPU with a single thread. The default MultiRocket with 50,000 features is about an order of magnitude slower than the default MiniRocket with 10,000 features. Comparing with the same number of 50,000 features, MultiRocket is only 4 times slower than MiniRocket. This makes sense since MultiRocket computes four features per kernel instead of one. Taking approximately 40 min to complete all 109 datasets, MultiRocket is still significantly faster than all other SOTA methods, as shown in Table 2. However, running MultiRocket with 32 threads significantly reduces this time to 5 min as shown in Fig. 2a. Hence it is recommended to use MultiRocket in a multi-threaded setting. Note that MultiRocket with 10,000 features is significantly more accurate than MiniRocket as shown in Appendix D.

Fig. 7

Total compute time (training and testing) of both MiniRocket and MultiRocket, with 10,000 and 50,000 features. Compute times are obtained from 109 UCR datasets, and run on a cluster using AMD EPYC 7702 CPU with a single thread. Figure best viewed in color

All the other SOTA methods have a long run time as reported in (Middlehurst et al. 2021). We took the total train time on 112 UCR datasets from (Middlehurst et al. 2021) and show them in Table 2 together with a few variants of MultiRocket and MiniRocket with 10,000 and 50,000 features as comparison. As expected, MiniRocket is the fastest, taking just under 3 min to train. This is followed by MultiRocket that took around 16 min. Rocket took approximately 3 h to train, while Arsenal, an ensemble of Rocket took 28 h. The fastest non-Rocket algorithm is DrCIF, taking about 2 days to train, followed by TDE with 3 days. Finally, the collective ensembles are the slowest taking at least 14 days to train. Note that the time for InceptionTime is not directly comparable as it was trained on a GPU.

Table 2 Run time to train single resample of 112 UCR problem. MultiRocket and MiniRocket variants are run on a single thread on a cluster using AMD EPYC 7702 CPU with a single thread. The other algorithms are reported in (Middlehurst et al. 2021)

4.3 Ablation study

So far, we have shown that MultiRocket performed well overall. In this section, we explore the effect of key design choices for MultiRocket. The choices include (A) selecting the time series representations (B) selecting the set of pooling operators and (C) increasing the number of features.

4.3.1 Time series representations

We explore the effect of the different representations using MiniRocket as the baseline. We consider the first and second order difference to estimate the derivatives of the time series and periodogram to capture information about the frequencies that are present in the time series. Figure 8 shows the comparison of the different combinations of the all 4 representations (including the base time series) for MiniRocket. The figure shows that using each of the representation alone does not improve the accuracy, as some information is inevitably lost during the transformation process. However, combining the base series with either representation improves MiniRocket, with the first order difference being the most accurate. The result indicates that adding diversity to MiniRocket by combining different time series representations with the base time series improves MiniRocket’s performance.

Fig. 8

Average rank of different transformations applied on MiniRocket with 10,000 features

We then perform the same experiment on MultiRocket and observed similar results, as shown in Fig. 9. We used the smaller variant of MultiRocket to be comparable to MiniRocket. In this case, comparing the base versions (MiniRocket and MultiRocket (10k) base) shows that adding the additional 3 pooling operators also improves the discriminating power of MiniRocket, as indicated in the discussion in Appendix D.

Fig. 9

Average rank of different transformations applied on MultiRocket with 10,000 features

4.3.2 Pooling operators

The previous section shows that applying convolutions to the base and first order difference series improves the discriminating power of MiniRocket and MultiRocket. Hence it is chosen as the default for MultiRocket. Now, we explore the effect of different combinations of pooling operators used by each kernel on classification accuracy. Figure 10 compares the different pooling operator combinations of MultiRocket with 10,000 features with the baseline MiniRocket and MiniRocket with base and first order difference series. The result shows that the variant using all pooling operators performed the best overall. This confirms our justification of using all four pooling operators in Sect. 3. Figure 10 also shows that PPV is a strong feature, where most of the combinations did not perform better than using PPV alone. The use of each pooling operator alone (without the combination) also performed significantly worse than PPV.

Fig. 10

Average rank of different feature combinations applied to base and first order difference with 10,000 features

Fig. 11

Average rank of increasing number of features on the base and first order difference time series

4.3.3 Number of features

The default setting of MultiRocket uses the combination of the base and first order difference and extracts 4 features per convolution kernel. In this section, we explore the effect of increasing the number of features in MultiRocket. Figure 11 shows the comparison of MultiRocket with different numbers of features. We also compare with the default MiniRocket, MiniRocket with 50,000 features and MiniRocket with base and first order difference. Overall, using 50,000 features is the most accurate and there is little benefit in using 100,000 features as more and more features will be similar to one another. A similar phenomenon was shown in Dempster et al. (2021). Figure 12a and b show that MultiRocket with 50,000 features is significantly more accurate than both MiniRocket with 50,000 features and with the first order difference. MultiRocket is more accurate on 76 and 68 datasets respectively. The results show that the increase in accuracy is not just due to the large number of features but also due to the diversity in the extracted features using the four pooling operators and first order difference. Therefore MultiRocket uses 50,000 features by default.

Fig. 12

Pairwise accuracy comparison of MultiRocket against a MiniRocket with 50,000 features and b MiniRocket with 50,000 features, base and first order difference on 109 datasets from the UCR archive. Each point represents the average accuracy value over 30 resamples of the each dataset

5 Conclusion

We introduce MultiRocket, by adding multiple pooling operators and transformations to MiniRocket to improve the diversity of the features generated. MultiRocket is significantly more accurate than MiniRocket but not significantly less accurate than the most accurate univariate TSC algorithm, HIVE-COTE 2.0 on the UCR archive. While being approximately 10 times slower than MiniRocket, MultiRocket is still significantly faster than all other state-of-the-art time series classification algorithms.

MultiRocket applies first order differencing to transform the time series. Then four pooling operators PPV, MPV, MIPV and LSPV are used to extract summary statistics from the convolution outputs of the base and first difference series. As the application of convolutions to time series is designed to highlight useful properties of the series, it seems likely that further development of methods to isolate the relevant signals in these convolutions will be highly productive. Besides, different transformation methods can also be explored to further improve the diversity of MultiRocket. Further promising future directions include exploring the utility of MultiRocket on multivariate time series, regression tasks (Tan et al. 2021) and beyond time series data.

Appendices

Features in MultiRocket

Algorithm 1 illustrates the procedure to calculate all four features for a given convolution output, Z. First, we initialise the variables in lines 1 to 5, such as a counter for positive values, p; $\mu$ to calculate the mean values; i for the mean of indices; and two variables (last_val and max_stretch) to remember the longest stretch of positive values. Lines 6 to 16 iterate through Z and extract the required information to compute the features. After iterating through Z, we do a final check on the longest stretch in lines 17 to 19. Finally the features are computed in lines 20 to 24 and the algorithm terminates on line 25 by returning the feature vector.

Example for Longest Stretch of Positive Values

The Mean of Indices of Positive Values (MIPV) has a limitation in differentiating convolution outputs with positive values at the start and end of convolution outputs with positive values in the middle. MIPV would give the same 4.5 for both convolution outputs C and D in Table 1. However, it is obvious that both C and D come from different time series that could potentially be from two different classes. The underlying time series for C has patterns appearing at the start and end of the time series while D has the same pattern appearing in the middle of the time series. For example, differentiating summer crops from winter crops (based on their satellite image time series), where summer crops could have peaks in the middle of the year for 3 months (Jun–Sep), while winter crops have peaks at the start and end (Dec–Feb), also 3 months. Figure 13 illustrates the example of LSPV, using the satellite image time series of corn and wheat, taken in southern France (Tan et al. 2017). Therefore, we propose the Longest Stretch of Positive Values (LSPV) to mitigate this issue.

Fig. 13

Illustration of convolution outputs C and D from Table 1, with the example of differentiating corn and wheat (in southern France) using the satellite image time series, obtained from (Tan et al. 2017). Corn is a summer crop having peaks in the middle of the year (D); while wheat is a winter crop, having peaks at the start and end of the year (C)

Pairwise comparisons

In this section, we show the pairwise comparison of SOTA methods against MultiRocket. The figures show that MultiRocket is significantly more accurate than all of them, although most of the improvements are within $\pm 5\%$ (see Fig. 14, 15).

Fig. 14

Pairwise accuracy comparison of MultiRocket against SOTA methods on 109 datasets from the UCR archive. Each point represents the average accuracy value over 30 resamples of the each dataset. The dotted lines indicate $\pm 5\%$ interval on the classification accuracy

We also compare HIVE-COTE 2.0 with MultiRocket and the existing top 3 SOTA methods. The figures show that MultiRocket has similar accuracy with HIVE-COTE 2.0 (more datasets within the $\pm 5\%$ range) than any other SOTA methods.

Fig. 15

Pairwise accuracy comparison of HIVE-COTE 2.0 against MultiRocket and existing top 3 other SOTA methods on 109 datasets from the UCR archive. Each point represents the average accuracy value over 30 resamples of the each dataset. The dotted lines indicate $\pm 5\%$ interval on the classification accuracy

MultiRocket versus MiniRocket

This section studies the advantages and limitations of MultiRocket over MiniRocket. Figure 16a shows the pairwise accuracy comparison of MiniRocket and MultiRocket on 109 UCR datasets. MultiRocket by default generates 50,000 features, 5 times more features than MiniRocket. Hence, we created a smaller variant of MultiRocket with 10,000 features to be comparable to the default MiniRocket, as shown in Fig. 16b.

Fig. 16

Pairwise comparison of MiniRocket versus a MultiRocket with the default 50,000 features and b a smaller variant of MultiRocket with 10,000 features on 109 datasets from the UCR archive. Each point represents the average accuracy value over 30 resamples of each dataset. The dotted lines indicate $\pm 5\%$ intervals on the classification accuracy

Overall, MultiRocket is significantly more accurate than MiniRocket, where MultiRocket is consistently more accurate on 76 datasets and less accurate on 29, with 4 ties. However, a closer look at the results indicates that most wins are within the range of $5\%$ accuracy (a phenomenon observed among the top SOTA methods, see C) with the largest difference of 0.119 on the SemgHandMovementCh2 dataset. As expected, MultiRocket performs the worst on the PigAirwayPressure dataset, with a difference of 0.225 in accuracy. Similarly, MultiRocket (10k) is also significantly more accurate than MiniRocket with 70 wins as shown in Fig. 16b.