Matrix sketching for supervised classification with imbalanced classes

Abstract

The presence of imbalanced classes is more and more common in practical applications and it is known to heavily compromise the learning process. In this paper we propose a new method aimed at addressing this issue in binary supervised classification. Re-balancing the class sizes has turned out to be a fruitful strategy to overcome this problem. Our proposal performs re-balancing through matrix sketching. Matrix sketching is a recently developed data compression technique that is characterized by the property of preserving most of the linear information that is present in the data. Such property is guaranteed by the Johnson-Lindenstrauss’ Lemma (1984) and allows to embed an n-dimensional space into a reduced one without distorting, within an $\epsilon$-size interval, the distances between any pair of points. We propose to use matrix sketching as an alternative to the standard re-balancing strategies that are based on random under-sampling the majority class or random over-sampling the minority one. We assess the properties of our method when combined with linear discriminant analysis (LDA), classification trees (C4.5) and Support Vector Machines (SVM) on simulated and real data. Results show that sketching can represent a sound alternative to the most widely used rebalancing methods.

1 Introduction

In many practical contexts, observations have to be classified into two classes of remarkably distinct size. Financial fraud detection, the diagnosis of rare diseases in medicine, cancer gene expressions (Yu et al. 2012), fraudulent credit card transactions (Panigrahi et al. 2009), software defects (Rodriguez et al. 2014), natural disasters and, in general, rare events (Maalouf and Trafalis 2011) are just a few examples. In such cases, many established classifiers often trivially classify instances into the majority class achieving an optimal overall misclassification error rate. This leads to poor performance in classifying the minority class, the correct identification of which is usually of more practical interest.

The presence of imbalanced classes in the big data context also poses relevant computational issues. If the dataset contains thousands or millions of observations from the majority class for each example of the minority one, many of the majority class observations are redundant. Their presence increases the computational cost with no advantage in terms of classification accuracy (Fithian and Hastie 2014). The problem of imbalanced classes is very common in modern classification problems and has received a great attention in the machine learning literature (see, among others, Chawla et al. 2004; Krawczyk 2016; Haixiang et al. 2017).

The error rate (or its complement, the accuracy) is the most widely used measure of a classifier performance. However, it inevitably favors the majority class when the misclassification error has the same importance for the two classes. On the contrary, when the error in the minority class is more important than the one of the majority class, the receiver operating characteristic (ROC) curve and the corresponding area under the curve (AUC), together with the sensitivity, are commonly suggested (Branco et al. 2016).

The ROC curve plots the true positive rate (sensitivity) versus the false positive rate ($1-$specificity) and, hence, a higher AUC generally indicates a better classifier. The ROC is obtained by varying the discriminant threshold, while the error rate is obtained at an optimal discriminant one. Therefore, AUC is independent of the discriminant threshold, while the accuracy is not.

The literature on imbalanced classes in supervised classification is very broad and methodological solutions follow two main streams. One direction is to modify the loss function used in the construction of the classification rule, while the other is to re-balance the data (Maheshwari et al. 2018).

The first solution requires, in most of the cases, the definition of a loss function that is specific for the case at hand and, therefore, not easily generalizable to different empirical problems. Re-balancing strategies are more general and not problem specific. That explains their great success in applied research and the focus on understanding their performances and on improving them.

As far as two-class linear discriminant analysis is concerned, the problem has been addressed, among others, by Xie and Qiu (2007), Xue and Titterington (2008), Xue and Hall (2014).

Through a wide simulation study supported by theoretical considerations, Xue and Titterington (2008) show that AUC generally favors balanced data but the increase in the median AUC for Linear Discriminant Analysis (LDA) after re-balancing is relatively small. On the contrary, error rate favors the original data and re-balancing causes a sharp increase in the median error rate. They also stress that re-balancing affects the performances of LDA in both the equal and unequal covariance case.

Xue and Hall (2014) prove that, in the Gaussian case, using the re-balanced training data can often increase the AUC for the original, imbalanced test data. In particular, they demonstrate that, at least for LDA, there is an intrinsic, positive relationship between the re-balancing of class sizes and the improvement of AUC. The largest improvement in AUC can be achieved, asymptotically, when the two classes are fully re-balanced to be of equal size.

In both the above mentioned papers, and in many others on imbalanced data classification (see, among others Chawla et al. 2002; Branco et al. 2016), re-balancing is obtained either by randomly under-sampling (US) the largest class, by randomly over-sampling (OS) the smallest one or by a combination of both (Bal-USOS). The re-balanced data are then used to train the classifiers.

However, it has been argued that random under-sampling may lose some relevant information, while randomly over-sampling with replacement the smallest class may lead to overfitting (Almogahed and Kakadiaris 2014). More sophisticated sampling techniques may allow to avoid these drawbacks. Hu and Zhang (2013) propose to obtain a new balanced dataset by using clustering-based undersampling, while Jo and Japkowicz (2004) apply a similar approach to oversample the minority class.

Mani and Zhang (2003) proposed selecting majority class examples whose average distance to their three nearest minority class examples is smallest. A similar approach is suggested by Fithian and Hastie (2014) in the context of logistic regression. They propose a method of efficient subsampling by adjusting the class balance locally in the feature space via an acceptance-rejection scheme. The proposal generalizes case-control sampling, using a pilot estimate to preferentially select examples whose responses (i.e. class membership identifiers) are conditionally rare, given their features.

With reference to classification trees and Naïve-Bayes classifiers, Chawla et al. (2002) propose a strategy that combines random under-sampling of the majority class with a special kind of over-sampling for the minority one. According to previous literature results (see, e.g. Domingos 1999; Branco et al. 2016), under-sampling the majority class leads to better classifier performance than over-sampling, and combining the two does not produce much improvement with respect to simple under-sampling. Therefore, they design an over-sampling approach which creates synthetic examples (Synthetic Minority Over-sampling Technique - SMOTE) rather than over-sampling with replacement. The minority class is over-sampled by taking each minority class sample and introducing synthetic examples along the line segments joining any/all of the K minority class nearest neighbors. Depending upon the amount of over-sampling required, neighbors from the K nearest neighbors are randomly chosen. SMOTE over-sampling is combined with majority class under-sampling.

SMOTE has turned out to be really effective in a number of situations. A thorough study of its performances for the analysis of Big Data is reported in Fernández et al. (2017), while Liu and Zhou (2013) apply it in conjunction with ensemble methods.

The synthetic examples allow to create larger and less specific decision regions, thus overcoming the overfitting effect inherent in random over-sampling. However, it should be stressed that little variability is introduced, since the new data are generated in such a way that they lie inside the original minority class convex hull; generalizability issues are therefore not completely addressed. Furthermore Bellinger et al. (2018) show that the performances of SMOTE degrade when dealing with high dimensional data that indeed lie on a lower dimensional manifold. They propose a manifold-based synthetic oversampling method that learns the manifold (using for instance PCA or autoencoders), generates synthetic data from the manifold itself and maps them back to the original high dimensional space.

Another aspect of SMOTE that has attracted broad research interest is that it gives the same weight to all the units in the minority class. However, not all the units are equally difficult to classify. He et al. (2008) proposed to address this issue by Adasyn, which is based on the idea of adaptively generating minority data samples: more synthetic data are generated for minority class units that are harder to classify. Both Bellinger et al. (2018) proposal and Adasyn can be interpreted as “data-aware” methods as they exploit specific data characteristics in order to generate new synthetic samples.

The idea of creating synthetic examples has been followed also by Menardi and Torelli (2014), who proposed a method they called ROSE-Random Over-Sampling Examples (for a description of the corresponding R package see Lunardon et al. 2014). In this solution, units from both classes are generated by resorting to a smoothed bootstrap approach. A unimodal density is centered on randomly selected observations and new artificial data are randomly generated from it. The key parameter of the procedure is the dispersion matrix of the chosen unimodal density, which plays the role of smoothing parameter. The full dataset size is often kept fixed while allowing half of the units to be generated from the minority class and half from the majority one. The method is applied to classification trees and logit models.

In this paper, we propose to address the imbalanced class issue through matrix sketching, a recently developed data transformation technique. It allows to reduce the size of the majority class or to increase the size of the minority one, while preserving the linear information that is present in the original data and performing data perturbation at the same time. In Sect. 2 matrix sketching is described and its properties are clearly highlighted. In Sect. 3 the use of matrix sketching as a re-balancing tool is introduced. Analysis of simulated and real data is reported in Sect. 4, where the performances of matrix sketching are compared with the ones of other common re-balancing methods (over-sampling, under-sampling, SMOTE, Adasyn, ROSE). A final discussion concludes the paper.

2 Matrix sketching

Matrix sketching is a probabilistic data compression technique and it is completely data oblivious (i.e., it compresses data independently from any specific characteristic the data may have). Its goal is to reduce the number of rows in a data set and the task is accomplished by linearly combining the rows of the original data set through randomly generated coefficients. The analysis can then be performed on the reduced matrix, thus saving time and space.

The theoretical justification for this approach to data compression is given by Johnson-Lindenstrauss’ Lemma (Johnson and Lindenstrauss 1984).

Lemma 1

Johnson-Lindenstrauss (1984). Let Q be a subset of p points in ${\mathbb {R}}^{n}$, then for any $\epsilon \in (0,1/2)$ and for $k=\dfrac{20 \, \log {p}}{\epsilon ^{2}}$ there exists a Lipschitz mapping $f:{\mathbb {R}}^{n} \longrightarrow {\mathbb {R}}^{k}$ such that for all ${\mathbf {u}}$, ${\mathbf {v}}$ $\in$ Q:

$$\begin{aligned} (1-\epsilon ) \Vert {\mathbf {u}}-{\mathbf {v}} \Vert ^{2} \le \Vert f({\mathbf {u}})-f({\mathbf {v}}) \Vert ^{2} \le (1+\epsilon ) \Vert {\mathbf {u}}-{\mathbf {v}} \Vert ^{2} \end{aligned}$$

The Lemma says that any $p-$point subset of the Euclidean space can be embedded in k dimensions without distorting the distances between any pair of points by more than a factor of $1\pm \epsilon$, for any $\epsilon$ in (0, 1/2). Moreover, it also gives an explicit bound on the dimensionality required for a projection to ensure that it will approximately preserve distances. This bound depends on the dimension of the data matrix that is not sketched, i.e. p in this case.

The original proof by Johnson and Lindenstrauss is probabilistic, showing that projecting the p-point subset onto a random k-dimensional subspace only changes the inter-point distances by $1\pm \epsilon$ with positive probability.

Practical applications of the Johnson-Lindenstrauss’ Lemma amount to pre-multiply the data matrix ${\mathbf {X}}$ $(n \times p)$ by the so called Sketching Matrix ${\mathbf {S}}$ $(k \times n)$, which reduces the sample size from n to k whilst preserving most of the linear information in the full dataset. As a consequence of Johnson-Lindenstrauss’ Lemma, also the scalar product is preserved after random projections.

The proof by Johnson-Lindenstrauss needed ${\mathbf {S}}$ to have orthogonal rows; subsequent proofs relaxed the orthogonality requirement and assumed the entries of ${\mathbf {S}}$ to be independently randomly generated from a Gaussian distribution, with 0 mean and variance equal to 1/k. This approach to sketching is known as Gaussian sketching and it is largely used in statistical applications as it allows for inferential statistical analysis of the results obtained after sketching.

Gaussian sketching is but one of the possible approaches. For instance, Ailon and Chazelle (2009) have proposed what is known as Hadamard sketch. The sketching matrix is formed as ${\mathbf {S}} = \Phi \mathbf {H D}/\sqrt{k}$, where $\Phi$ is a $k \times n$ matrix and ${\mathbf {H}}$ and ${\mathbf {D}}$ are both $n \times n$ matrices. The matrix ${\mathbf {H}}$ is a Hadamard matrix of order n. A Hadamard matrix is a square matrix with elements that are either $+1$ or $- 1$ and orthogonal rows. As Hadamard matrices do not exist for all integers n, the source dataset can be padded with zeros so that a conformable Hadamard matrix is available. The random matrix ${\mathbf {D}}$ is a diagonal matrix where each nonzero element is an independent Rademacher random variable. The random matrix $\Phi$ subsamples k rows of ${\mathbf {H}}$ with replacement. The structure of the Hadamard sketch allows for fast matrix multiplication, reducing calculation of the sketched dataset from O(npk) of the Gaussian sketch to $O(np \log {k})$ operations.

Another efficient method for generating sketching matrices satisfying the Lemma is the so-called Clarkson-Woodruff one (Clarkson and Woodruff 2017). The sketching matrix is a sparse random matrix $\mathbf {S=} \Gamma \, {\mathbf {D}}$, where $\Gamma$ $(k \times n)$ and ${\mathbf {D}}$ $(n \times n)$ are two independent random matrices. The matrix $\Gamma$ is a random matrix with only one element for each column set to +1. The matrix D is the same as above. This results in a sparse random matrix ${\mathbf {S}}$ with only one nonzero entry per column. The sparsity speeds up matrix multiplication, dropping the complexity of generating the sketched dataset to O(np).

It is worth noticing that the rows of the Gaussian and Clarkson-Woodruff sketching matrices are not orthogonal and this implies that the geometry of the original space is not preserved after sketching. The Gaussian sketching matrix is sometimes orthogonalized according to Gram-Schmidt process (Horn and Johnson 2012), thus leading to what are known as Haar projections (Haar 1933). This operation inevitably increases the computational load. Hadamard sketching matrices, on the contrary, are orthogonal by construction.

Sketching methods have mainly been used as a data compression technique in the context of multiple linear regression, where the computation of the Gram matrix ${\mathbf {X}}^{\top }{\mathbf {X}}$ may become especially demanding for large n (Ahfock et al. 2021; Woodruff 2014; Dobriban and Liu 2018). In Falcone (2019) the use of sketching has been extended to supervised classification.

3 Rebalancing through sketching

As previously said, sketching preserves the scalar product while reducing the data set size. As the sketched data are obtained through random linear combinations of the original ones, most of the linear information is preserved after sketching. This means that, in the imbalanced data case, the size of the majority class can be reduced through sketching without incurring the risk of losing (too much) linear information. Sketching the majority class can therefore be considered as a theoretically sound alternative to majority class under-sampling. We will call this approach “under-sketching”.

Although sketching has been proposed as a data compression technique, as a consequence of Johnson-Lindenstrauss’ lemma, the scalar product preservation also holds when the sketching matrix has a number of rows that is larger than the number of original data points. Therefore, this unconventional way of using sketching can be thought of as an alternative to random over-sampling, that generates synthetic new examples from the minority class (through random non-convex linear combinations of all of them) while preserving the linear structure in the data. This allows to enlarge the decision area and, thus, to avoid overfitting. We will call this approach “over-sketching”. Under-sketching and over-sketching can also be combined, just as under-sampling and over-sampling can. We will denote this approach as “balanced sketching”. Mullick and Datta (2019), in the context of neural networks, also propose a generation scheme that involves linear combinations of all the units of the minority class but, differently from sketching, the linear combinations are required to be convex (while sketching ones are not) and the weights are learnt from the data in a data-aware fashion while sketching is completely data-oblivious.

Fig. 1

Geometric differences between rebalancing methods: plots display the famous Fisher’s iris original dataset (solid points) and the set of data after rebalancing (empty triangles); in the left panel Hadamard balanced sketching has been applied, while SMOTE was performed in the panel on the right

In order to better understand how sketching works, consider as an example Fig. 1 where the famous Fisher’s iris dataset is displayed before (solid points) and after rebalancing (empty triangles) through sketching (left panel) and SMOTE (right panel); while for SMOTE the triangles lie within the point cloud, after sketching the new points may lie outside the original convex hull. This holds for any kind of sketching.

The use of sketching as a re-balancing tool is perfectly coherent when classification is performed by LDA, which is based on the Gram matrix. In that context, (Fisher 1936; Anderson 1962; McLachlan 2004), the optimal discriminant direction (under the homoscedasticity assumption) is defined as:

$$\begin{aligned} {\mathbf {a}}= {\mathbf {W}}^{-1}(\bar{{\mathbf {x}}}_1-\bar{{\mathbf {x}}}_0), \end{aligned}$$

where ${\mathbf {W}}$, the within group covariance matrix, is

$$\begin{aligned} {\mathbf {W}}=({\mathbf {X}}_0^{\top }{\mathbf {X}}_0+{\mathbf {X}}_ 1^{\top }{\mathbf {X}}_1)/(n_0+n_1-2). \end{aligned}$$

(1)

${\mathbf {X}}_0$ and ${\mathbf {X}}_1$ denote the mean centered data matrices of population null and one, respectively, $\bar{\mathbf{x }}_0$ and $\bar{\mathbf{x }}_1$ the corresponding mean vectors, where the subscript 1 identifies the minority class, $n_0$ and $n_1$ represent the majority and the minority class size respectively.

Denoting by $\tilde{{\mathbf {X}}}_0 \ (k_{0} \times p)$ the sketched majority class (with $k_0 \ll n_0$) and by $\tilde{{\mathbf {X}}}_1 \ (k_{1} \times p)$ the over-sketched minority one (with $k_1 \gg n_1$), the linear discriminant direction based on re-balanced data may be obtained after replacing ${\mathbf {X}}_{0}$ in (1) with $\tilde{{\mathbf {X}}}_0$ (under-sketching) or ${\mathbf {X}}_{1}$ with $\tilde{{\mathbf {X}}}_1$ (over-sketching) or both (balanced sketching), based on suitably chosen $k_0$ and $k_1$.

The sketching algorithm is reported in Algorithm 1.

Sketching reduces the dataset size while preserving the scalar product, i.e. the total sum of squares. As a consequence of this, the scale, i.e. the variance of the data, is changed. In particular, it is increased by a factor $n_0/k_0$ in case of under-sketching, and reduced by a factor $n_1/k_1$ in case of over-sketching. While this has no effect on LDA, it prevents sketching from being directly applied to methods that are based on single variable values (e.g. trees, Support Vector Machines, ...) and not on a general scalar product. In fact, the sketched data and the original data now come from distributions having a different variance and this makes classification trees or SVM define classification thresholds which are not coherent with the original variable values. However, the problem can be easily solved by scaling back the data after sketching, i.e., by multiplying the data by $(n_0/k_0)^{-1/2}$ in case of under-sketching and by $(n_1/k_1)^{-1/2}$ in case of over-sketching. The effect of rescaling on over-sketched data is depicted in Fig. 2. The algorithm for non-linear classifiers is outlined in Algorithm 2. The R function MaSk that returns data balanced through matrix sketching is available at https://github.com/landerlucci/MaSk_SuperClass.

Fig. 2

Geometric differences of over-sketching methods, before and after re-scaling: plots display bivariate simulated Gaussian data (solid black points) and the set of over-sketched data (empty red diamonds for Gaussian, empty blue squares for Clarkson-Woodruff and empty green triangles for Hadamard sketching). On the right panel the effect of re-scaling on data dispersion (Color figure online)

In the next section different sketching methods are employed both on simulated and real data and compared with SMOTE, Adasyn, ROSE and the standard re-balancing methods: under-sampling (US), over-sampling (OS) and balanced under-sampling over-sampling (Bal-USOS).

4 Empirical results

The properties of sketching as a re-balancing method have been tested on both synthetic and real datasets, which differ in terms of imbalance degree and group separation. The performance of Linear Discriminant Analysis (LDA), classification trees (C4.5, Quinlan 1993) and Support Vector Machines (SVM, Cortes and Vapnik 1995) has been measured in terms of accuracy (Acc), specificity (Spec), sensitivity (Sens) and area under the ROC curve (AUC).

Gaussian, Hadamard and Clarkson-Woodruff sketching have been applied in order to reduce the size of the majority class to that of the minority one (USGauss, USClark, USHada) and in order to increase the size of the minority class, so that it is as large as the majority class one (OSGauss, OSClark, OSHada). They have also been jointly used so that the size of both classes is twice the minority class size (BalGauss, BalClark, BalHada). For this last case, re-balancing through SMOTE is also performed. For comparison, Adasyn (Adasyn) with unit class size ratio (i.e. $k_1=n_0$) and ROSE with its default option of preserving the total size are considered too. For sake of completeness, performances of the classifiers on the original unbalanced data (Base) are also evaluated and reported in the first line of Tables 1–15.

4.1 Simulated data

The performances of sketching methods for imbalanced data classification have been tested in an extensive simulation study, where the degree of overlapping of the two classes and the imbalance ratio vary. Specifically, the following scenarios have been considered:

• 1. In the first scenario, we generate identically distributed vectors from two homoscedastic p-variate Gaussian distributions (p=10):

  • Population $\Pi _0$ has a zero mean vector.

  • Population $\Pi _1$ has mean vector $\mathbf {\mu }_1=\{\delta , \ldots , \delta \}$, where $\delta$ assumes, in turn, values 0.50, 0.25, 0.10, corresponding to a large, medium and small shift, respectively.

  The dependence structure among the features is introduced by generating a random covariance matrix based on the method proposed by Joe (2006), so that the correlation matrices are uniformly distributed over the space of positive definite correlation matrices, with each correlation marginally distributed as Beta(p/2, p/2) on the interval (-1, 1).

• 2. In the second scenario, we generate identically distributed vectors from two heteroscedastic p-variate Gaussian distributions (p=10):

  • Population $\Pi _0$ has a zero mean vector and identity covariance matrix.

  • Population $\Pi _1$ has the same mean vector and dependence structure as in Scenario 1.

• 3. In the third scenario, we test the behavior of the proposal in highly skewed data by generating identically distributed vectors from a multivariate zero-centered Gaussian distribution, transforming them using the exponential function and shifting the populations according to three different values, $\delta = 0.50, 0.25, 0.10$, respectively. The dependence structure is the same for both populations and equal to that of Scenario 1.

For each scenario an overall sample size n equal to 2000 is considered. Different degrees of imbalance are evaluated, namely $\pi _1=n_1/n=0.25, 0.10, 0.05$. The R function simulation_function that allows to generate data according to these three scenarios is available at https://github.com/landerlucci/MaSk_SuperClass.

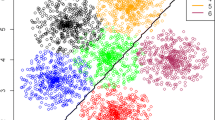
In order to better characterize and to display the simulated data, a graphical representation via the first two Principal Components of the considered scenarios (for $\pi _1=0.05$ only) is reported in Fig. 3; points in red belong the smallest group, class separation decreases from left to right.

Fig. 3

Graphical representation of the simulated data according to the first two principal components for the three scenarios: a Homoscedastic Multivariate Gaussians, b Heteroscedastic Multivariate Gaussians and c Asymmetric Exp-Gaussians. Black points belong to the majority class, while red to the minority one (Color figure online)

Each generated dataset has been randomly split in two parts: $50\%$ of the units for both classes constituted the training set and the remaining $50\%$ formed the test set. The procedure was repeated 100 times. The values in the tables represent the median of the quantity of interest over the 100 replicates.

The code implementing our procedure is available on request; ROSE, SMOTE and Adasyn have been applied using the corresponding R packages ROSE, DMwR and imbalance.

For brevity, results of the simulations for $\pi _1=0.05$ only are shown in Tables 1, 2 and 3. Extensive and complete results are reported in the Supplementary Material.

Table 1 Simulation results of Scenario 1: data generated from 10-variate homoscedastic Gaussian distributions, $n=2000$, Median values (over 100 replications) for LDA classifier. In bold the best performance for each re-balancing strategy

Table 2 Simulation results of Scenario 2: data generated from 10-variate heteroscedastic Gaussian distributions, $n=2000$, Median values (over 100 replications) for LDA classifier. In bold the best performance for each re-balancing strategy

Table 3 Simulation results of Scenario 3: data generated from Asymmetric 10-variate Exp-Gaussian distributions, $n=2000$, Median values (over 100 replications) for LDA classifier. In bold the best performance for each re-balancing strategy

As expected, the overall performances degrade with increasing overlap for all the different scenarios. When $\pi _1$ decreases (see Tables 1-3 on the supplementary material), the performances of LDA in the imbalanced datasets improve in terms of accuracy. Since LDA tends to favor correct allocation of the majority class, the larger the fraction of units belonging to that class, the better the accuracy. On the contrary, sensitivity worsens, as it becomes harder to identify units of the minority class. Confirming recent results by Ramanna et al. (2013), the effect of overlapping seems to be more relevant than the imbalance ratio.

Matrix Sketching proves to be effective in improving the performance of standard LDA in terms of AUC, in almost all of the cases; what is more relevant is the important improvement in the identification of the samples from the smallest class (i.e. the sensitivity), that is the main reason why re-balancing methods are generally employed.

The other considered re-balancing methods show good performances; however, matrix sketching returns better results, both when reducing the size of the biggest class or when increasing the size of the smallest one, but also in re-sizing both classes so as to be twice the smallest one. This holds regardless of the degree of imbalance. The overall best solution is not always achieved by a specific strategy, but it rather depends on the data at hand.

When deviating from the assumptions of the LDA (Tables 2 and 3), classification performances uniformly slightly deteriorate; sketching seems to preserve the robustness of the LDA to assumption violations, and keeps improving the performance via re-balancing.

4.2 Real data

Matrix Sketching for class re-balancing has also been tested on real data. Each dataset has been randomly split in two parts: $75\%$ of the units for both classes constituted the training set and the remaining $25\%$ formed the test set. The procedure has been repeated 100 times. The values in Tables 4 – 12 represent the median of the quantities of interest over the 100 replicates.

The analyzed datasets are the following:

• Abalone (Abalone): the dataset (available at UCI https://archive.ics.uci.edu/ml/datasets/Abalone) has 7 features and 4177 samples. The aim is to predict the age of abalones ($\le 20$ rings or $> 20$ rings) from physical measurements; there are 36 samples with more than 20 rings and 4141 in the other class.

• Abalone 9 vs. 18 (Abalone9vs18): the dataset is a subset of Abalone containing 689 samples of the majority class (9 rings) and 42 samples of the minority class (18 rings).

• Eucalyptus Soil Conservation (Eucalyptus): the dataset (from OpenML https://www.openml.org/d/990) contains 736 seedlots of eucalyptus. The objective is to determine which seedlots in a species are best for soil conservation in seasonally dry hill country. The 13 observed features include measurement of height, diameter by height, survival, and other contributing factors. After missing data removal, the class label divides the seeds into 2 groups (203 ‘good’ and 438 ‘not good’).

• Indian Liver Patient Dataset (Ilpd): the dataset (from UCI https://archive.ics.uci.edu/ml/datasets/ILPD+(Indian+Liver+Patient+Dataset)) contains 416 liver patient records and 167 non liver patient records referred to 9 variables. The data set was collected from north east of Andhra Pradesh, India. (Ramana et al. 2012).

• Mammography (Mammography): the dataset (available at OpenML https://www.openml.org/d/310) has 6 attributes and 11,183 samples that are labeled as noncalcification (10923) and calcifications (260) (Woods et al. 1993).

• Pro Football Scores (Profb): the dataset (from StatLib http://lib.stat.cmu.edu/datasets/profb) contains scores and point spreads for all NFL games in the 1989-91 seasons, specifically 672 cases (all 224 regular season games in each season). The objective is to determine whether there really is a home field advantage from 5 observed features. The class label divides the games into 2 groups (448 ‘at home’ and 224 ‘away’).

• Spotify (Spotify): the dataset (from Kaggle https://www.kaggle.com/mrmorj/dataset-of-songs-in-spotify includes 42305 songs for which a set of 13 audio features are provided by Spotify (e.g., danceability, energy, key, loudness ...). Each track is labelled according to its genre (Trap, Techno, Techhouse, Trance,...); the aim is to distinguish between pop (461) and non-pop (41844).

• Vertebral column (Spine): the dataset (available at UCI http://archive.ics.uci.edu/ml/datasets/vertebral+column) is composed of $p=6$ biomechanical features used to classify $n=310$ orthopedic patients into 2 classes, normal (100) or abnormal (210) (Dua and Graff 2019).

• Yeast (Yeast): the dataset (available at UCI https://archive.ics.uci.edu/ml/datasets/Yeast) contains 1484 proteins and 6 observed features, coming from different signal sequence recognition methods. The aim is to predict the localization site of proteins (1449 ‘negative’ and 35 ‘positive’).

The homoscedasticity and the multivariate normality assumptions of each dataset have been tested: the former by Box’s-M test (Box 1949), the latter by both Mardia (Mardia 1970) and Henze-Zirkler’s (Henze and Zirkler 1990) tests. For all the datasets, LDA assumptions are not satisfied; however, deviations from such hypotheses do not generally affect the classification performances.

Results of real data classification with LDA are displayed in Tables 4, 5 and 6 where it is shown that, coherently with the findings in Xue and Titterington (2008) and Xue and Hall (2014), re-balancing in LDA causes a decrease in the accuracy which is combined with a little increase in the AUC. However a strong increase in sensitivity, i.e. in the ability to correctly identify the minority class, is worth of note. In this context sketching-based methods in most cases outperform the other re-balancing methods. For moderately sized datasets which are moderately imbalanced too, the sketching method that generally returns the best performance is Hadamard, while for large and highly imbalanced ones non-orthogonal sketching methods (i.e. Gaussian and Clarkson-Woodruff) outperform orthogonal ones. There is no evidence of a systematic predominance of over, under or balanced sketching strategies, even with fairly large datasets.

Results employing other non-linear classifiers, namely C4.5 trees and Support Vector Machines (SVM) are displayed in Tables 7, 8, 9 and 10, 11, 12 respectively.

Classification performance of C4.5 is generally the lowest; the quality measures are generally and uniformly smaller, while LDA yields the best results for all the datasets. The rescaled sketching procedure to deal with non-linear classifiers like C4.5 performs fairly well, often resulting among the best methods; however, it is hard to conclude on which is the best procedure. Within the sketching approaches, the one that is usually characterized by the best performances is the Gaussian over-sketching, while Clarkson-Woodruff sketching always gives very low AUC values.

The overall performance quality of SVM is fairly good, coherently with the results in Batista et al. (2012), but sensibly worse than LDA. There is not a single method that always outperforms the others, nor a rebalancing strategy can be recommended for specific data features; as it may often be the case, the optimal classification rule really depends on the data at hand. Also for SVM, OSGauss is the sketching method that most often outperforms other approaches.

Matrix sketching rephrased for non-linear classifiers proved to be an effective method for rebalancing, returning generally good performances. An interesting result is that of Eucalyptus dataset, where sketching does not seem to yield relevant results; a deeper study showed that some of its features are discrete, with very few distinct values. While this aspect proved not to be a problem for LDA, because the classification rule does not depend directly on observed values, it may represent a limit for other classifiers; in fact, the discrete nature of the original values is changed as they are turned into continuous, due to linear combination of points.

Table 4 Real Data: Spine, Ilpd and Eucalyptus. Performance median values (over 100 replications) with LDA classifier. In bold the best performance for each re-balancing strategy.

Table 5 Real Data: Profb, Abalone9VS18 and Yeast. Performance median values (over 100 replications) with LDA classifier. In bold the best performance for each re-balancing strategy.

Table 6 Real Data: Abalone, Mammography and Spotify. Performance median values (over 100 replications) with LDA classifier. In bold the best performance for each re-balancing strategy.

Table 7 Real Data. Performance median values (over 100 replications) with C4.5 classifier. In bold the best performance for each re-balancing strategy

Table 8 Real Data. Real Data: Profb, Abalone9VS18 and Yeast. Performance median values (over 100 replications) with C4.5 classifier. In bold the best performance for each re-balancing strategy.

Table 9 Real Data: Abalone, Mammography and Spotify. Performance median values (over 100 replications) with C4.5 classifier. In bold the best performance for each re-balancing strategy.

Table 10 Real Data: Spine, Ilpd and Eucalyptus. Performance median values (over 100 replications) with SVM classifier. In bold the best performance for each re-balancing strategy.

Table 11 Real Data. Performance median values (over 100 replications) with SVM classifier. In bold the best performance for each re-balancing strategy

Table 12 Real Data: Abalone, Mammography and Spotify. Performance median values (over 100 replications) with SVM classifier. In bold the best performance for each re-balancing strategy.

4.3 Assessment and comparison of the re-balancing methods

The considered real data are very heterogeneous and some rebalancing methods may perform better than others for different datasets; however such information is not always easily inferred from the tables. Therefore, in order to properly rank the performance of the considered methods, for each dataset a one-tailed paired-Wilcoxon test has been performed on the AUCs computed on each of 100 replications, comparing the proposed sketching methods with the existing approaches; in order to assess the potential superiority of a method, both tails were explored. For the reason explained before, Eucalyptus has not been included; the overall number of considered dataset is therefore 8.

Each cell of Table 13 displays two counts: (i) the number of real datasets for which the method in row resulted significantly better than the corresponding method in column (bottom-left, red shade), (ii) the number of datasets for which the latter outperformed the former (top-right, green shade). Results refer to Gaussian sketching and LDA classifier; Tables 14, 15 refer to C4.5 and SVM, respectively. When cell counts do not sum to 8, it means that for the remaining data sets there is no significant difference between the methods.

The Gaussian under-sketching with LDA proved to behave significantly better than ROSE and US, while the superiority is less evident with Adasyn, SMOTE and Bal-USOS; there is no relevant improvement in terms of AUC with respect to the imbalanced case and OS. Gaussian over-sketching largely improves over all the other re-balancing approaches, except for OS and Adasyn, for which the behavior appears to be similar. Balanced sketching does not to seem to be a good alternative for rebalancing, as it always performs worse. Similar considerations can be drawn for C4.5 from Table 14; BalGauss only improves over the imbalanced case and OS. OSGauss is significantly better than any other method, while USGauss always significantly outperforms OS and the imbalanced classifier. The improvement is less marked for Adasyn, ROSE and Bal-USOS. Gaussian sketching with SVM does not seem to improve over the other rebalancing methods: it only largely outperforms the imbalanced classifier. No preference can really be expressed between under-sketching, over-sketching and balanced-sketching. The differences with OS, Adasyn and ROSE are not very marked, while US, SMOTE and BalUSOS outperform sketching.

Table 13 Relative performance of rebalancing methods with LDA. For each cell, the count bottom-left (red shade) refers to the number of real datasets for which method on the left yielded significantly better results in terms of AUC (one-tailed paired-Wilcoxon test, $\alpha =0.05$) than method on the top, while the count top-right (green shade) the opposite

Table 14 Relative performance of rebalancing methods with C4.5. For each cell, the count bottom-left (red shade) refers to the number of real datasets for which method on the left yielded significantly better results in terms of AUC (one-tailed paired-Wilcoxon test, $\alpha =0.05$) than method on the top, while the count top-right (green shade) the opposite

Table 15 Relative performance of rebalancing methods with SVM. For each cell, the count bottom-left (red shade) refers to the number of real datasets for which method on the left yielded significantly better results in terms of AUC (one-tailed paired-Wilcoxon test, $\alpha =0.05$) than method on the top, while the count top-right (green shade) the opposite

Results for Hadamard and Clarkson-Woodruff sketching are displayed in the Supplementary Material. With LDA, Hadamard only slightly improves over ROSE, while comparisons with other methods show mixed patterns. Differently, Clarkson-Woodruff outperforms US, ROSE, SMOTE and BalUSOS; the improvement with respect to the imbalanced case is mild in terms of AUC (Table 4 in the Supplementary). For classification trees both Hadamard and Clarkson-Woodruff sketching largely improve over the imbalanced case and over-sampling; however, OSClark does not generally perform well compared with other methods with neither C4.5 nor SVM. Under-sampling outperforms both sketching methods with trees and SVM. Differences with ROSE are not always very marked (see Tables 5 and 6 in the Supplementary).

A different perspective is provided by barplots in Figs. 4, 5 and 6. For each replication of datasets Spine, Abalone and Spotify (which have been chosen as prototypes for small, medium and large size datasets) the AUC ranking of the considered rebalancing strategies is computed, separately for each classifier; bar height is proportional to the average ranking achieved by each method: the higher the average rank, the higher is the AUC value and, therefore, the more preferable is the method. The use of ranks allows to better highlight the relative performance of the procedures, as the median values reported in the tables are often very close. Barplots for all the remaining datasets can be found in the Supplementary material.

Spine is the smallest considered data and has a mild degree of imbalance ($\pi _1=33.3\%$); for LDA the best re-balancing strategy is over-sketching with Hadamard matrices; notice that Hadamard matrices reach high ranks also for balanced and under-sketching. For classification trees, under- and over-sketching with Gaussian matrices yield the highest rank; SVM seems to better work with Clarkson-Woodruff balanced sketching and over-sketching.

Differently, Abalone is a middle-sized dataset but has a high degree of imbalance ($\pi _1=0.9\%$); Figure 5 shows that, on average, the highest ranks are achieved by Gaussian over-sketching, for both C4.5 and SVM. For LDA, Adasyn outperforms the others methods. Hadamard sketching does not perform remarkably well, coherently with results from Tables 4, 5, 6.

Finally, Spotify is the largest included dataset, with a sample size larger than 40000 units and a high degree of imbalance ($\pi _1=1.1\%$); barplot in Fig. 6 shows that the overall highest average rank is returned by C4.5 classifier combined with Gaussian over-sketching. LDA performs best when combined with Gaussian or Clarkson-Woodruff over-sketching, or with over-sampling. For SVM, the best ranking is that of SMOTE, followed by under-sampling and Bal-USOS.

Fig. 4

Ranking of returned AUC values for each replication of Spine dataset, according to different rebalancing method and separately for classifier

Fig. 5

Ranking of returned AUC values for each replication of Abalone dataset, according to different rebalancing method and separately for classifier

Fig. 6

Ranking of returned AUC values for each replication of Spotify dataset, according to different rebalancing method and separately for classifier

Fig. 7

Computational time for simulated data with increasing size; the minority class is always the 10% of the overall size and $p=10$

Figure 7 shows the computational time (in seconds) required by each rebalancing method to run once with LDA for simulated data with $p=10$ and increasing sample size. Rebalancing strategies aimed at increasing the minority class size to that of the majority one have not been considered for datasets larger than 100.000 units; this would dramatically and uselessly increase the overall size, thus heavily burdening the classifiers. Hadamard matrices could not be computed by the Julia software for datasets with 500 thousands or more units. Computational differences can only be detected for sample sizes larger than 10 thousand units; for such cases, the over-sketching procedure with both Clarkson-Woodruff and Hadamard matrices is more expensive. By exploiting the theoretical properties of the Normal distribution, we were able to considerably reduce the computational burden of Gaussian sketching; in fact, even for samples of 1 million units its cost is negligible and cannot be distinguished from that of other methods. Zooming in the time differences between methods for samples of at most 100 thousand units, balanced and undersketching with Hadamard matrices are the most computationally expensive ones (with a cost of about 2 and 1 minutes, respectively), followed by SMOTE (about 20 seconds) and Adasyn (10 seconds). Clarkson-Woodruff balanced- and under- sketching ranges between 5 and 10 seconds; Gaussian and random sampling rebalancing methods are indistinguishable and need a few seconds to run.

5 Discussion and conclusion

We studied the performances of sketching algorithms when dealing with the issue of imbalanced classes in binary supervised classification, which hampers most of the common classification methods. We propose to use sketching as an alternative to the standard sampling strategy commonly used in that context.

As sketching preserves the scalar product while reducing the data set size, most of the linear information is preserved after sketching. This means that, in the imbalanced data case, the size of the majority class can be reduced through sketching without incurring the risk of losing (too much) linear information. Also the size of the minority class can be increased by sketching, still preserving the linear structure and introducing some variability. Matrix sketching can therefore be considered as a theoretically sound alternative to the other re-balancing methods, generally based on random under-sampling of the majority class or on sampling with replacement from the minority class. Different from other approaches, sketching allows for perturbation and generation of points that may lie outside the convex hull of the distribution, thus reducing the risk of redundancy and of overfitting.

The procedure has been applied to LDA and suitably rephrased in order to be combined with other non-linear classifiers. Specifically, as sketching preserves the scalar product but changes the data scale, sketched data are rescaled, so as to match the variance of the original data.

The properties of sketching have been tested on both synthetic and real data, differing in terms of imbalance degree and overlapping, and compared with other competing alternatives, showing good performances.

When dealing with moderately imbalanced data, sketching based on random matrices with orthogonal columns tends to outperform other sketching methods. Differently, when the degree of imbalance is more pronounced, non-orthogonal sketching matrices return the best results.

When combined with LDA, rebalancing causes a strong decrease in the accuracy with a little increase in the AUC. However a strong increase in sensitivity, i.e. in the ability to correctly identify the minority class, is worth of note. In this context, sketching based methods outperform the other rebalancing methods in most of the cases. As there is no evidence of a systematic predominance of over, under or balanced sketching strategies, the choice should be data-specific.

As already said, sketching preserves the linear structure which is the core element of LDA. The good performances of sketching in this context are therefore coherent with its theoretical properties.

Sketching proves to be an efficient strategy also with other classifiers; in particular Gaussian over-sketching results to be a winning alternative for most of the commonly used rebalancing approaches when classification is performed by C4.5, while Clarkson-Woodruff over-sketching sometimes returns very poor performances. This may be due to the tendency of Clarkson-Woodruff sketching to increase the spread of the points (see Fig. 2). The gain of Gaussian over-sketching is not so marked in conjunction with SVM.

Differently from SMOTE, ROSE and Adasyn, sketching methods do not require the setting of user-driven extra parameters; for instance, SMOTE and Adasyn require to set the number K of units to be interpolated and ROSE requires the definition of the kernel window width. However, one possible limitation of sketching methods lies in the procedure when dealing with non-linear classifiers and discrete or categorical data, as the original observations in the training set are replaced with a linear combination of points. While the classification rule of LDA does not depend directly on the observed values, this may represent a problem with classifiers whose rule is built on the observed values.

We have also analysed additional datasets that are only reported and described in the supplementary material; the performances of the rebalancing methods, in terms of both AUC and sensitivity, are evaluated on the enlarged set of data through a regression tree. The predictors describe data characteristics (class imbalance ratio, sample size, number of features and average absolute correlation between the observed variables), together with classification methods (LDA, trees and SVM) and the considered rebalancing approaches. Clarkson-Woodruff sketching has been excluded; as we have already pointed out, its performance deteriorates when combined with classification trees and its inclusion in the regression tree would mask the influence of other predictors. Focusing on the role of rebalancing methods on AUC, it emerges that almost all the methods tend to give equivalent results, with the exception of Adasyn and OS; their performances are lower when combined with classification trees on datasets involving less than 15 features. A similar behaviour can be observed when dealing with sensitivity; the lowest values correspond to classification trees on data rebalanced by Adasyn, OS, and OSHada. The corresponding trees are reported in the supplementary material.

The paper shows that sketching can represent a sound alternative to the most widely used rebalancing methods and, for moderately sized data sets, its computational cost is comparable to that of SMOTE and Adasyn. However, the paper also confirms the results of the thorough literature review by Branco et al. (2016), which shows that no optimal rebalancing strategy exists and that performances are strictly dependent on specific data characteristics.