Multi-label learning with missing and completely unobserved labels

Abstract

Multi-label learning deals with data examples which are associated with multiple class labels simultaneously. Despite the success of existing approaches to multi-label learning, there is still a problem neglected by researchers, i.e., not only are some of the values of observed labels missing, but also some of the labels are completely unobserved for the training data. We refer to the problem as multi-label learning with missing and completely unobserved labels, and argue that it is necessary to discover these completely unobserved labels in order to mine useful knowledge and make a deeper understanding of what is behind the data. In this paper, we propose a new approach named MCUL to solve multi-label learning with Missing and Completely Unobserved Labels. We try to discover the unobserved labels of a multi-label data set with a clustering based regularization term and describe the semantic meanings of them based on the label-specific features learned by MCUL, and overcome the problem of missing labels by exploiting label correlations. The proposed method MCUL can predict both the observed and newly discovered labels simultaneously for unseen data examples. Experimental results validated over ten benchmark datasets demonstrate that the proposed method can outperform other state-of-the-art approaches on observed labels and obtain an acceptable performance on the new discovered labels as well.

1 Introduction

1.1 Background and motivation

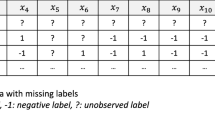
Multi-label learning (Gibaja and Ventura 2015; Herrera et al. 2016; Tsoumakas et al. 2010; Zhang and Zhou 2014) is a learning framework for learning in the presence of label ambiguity, where each instance can be associated with multiple possible class labels simultaneously. Many well-established approaches have been proposed, such as (Chu et al. 2019; Decubber et al. 2019; Liu 2019; Liu and Shen 2019; Masera and Blanzieri 2019; Nguyen and Hüllermeier 2019; Park and Read 2019; Huang et al. 2018; Wydmuch et al. 2018; Zhang and Wu 2019). In multi-label learning, a common assumption is that all the class labels and their values are observed before the training process. However, in some real applications, not only are some of the values of the observed labels missing, but also some of the labels are completely unobserved for the training data. We summarized three possible reasons as follows.

• 1. The labeling process is complex and costly In the labeling process of multi-label learning, a set of possible labels from a target set will be annotated for each data example. This stage is very complex and time-consuming, especially for a large-scale data set with millions of labels (Bhatia et al. 2016). It is inevitable to induce errors and missing values, and even result in some labels totally unlabeled for all the related data examples.

• 2. Some labels are intentionally omitted For example, in image annotation, people may be only interested in the main objects of an image, and the background of image may not be annotated, such as grass and land. However, in (Pham et al. 2015), it has been proved that the performance on observed labels can be improved by discovering these labels.

• 3. Some labels are unknown For example, in disease diagnosis, complicated diseases may exist but are unknown due to the limitation of human’s knowledge or the shortage of examination (Zhang et al. 2018, 2020).

There are several lines of study that are related to the problem proposed in this paper. In Fig. 1, we illustrate the differences between the learning scenario proposed in the paper and other previous related learning problems, i.e., multi-label learning with missing labels, and online or class-incremental learning. The detailed discussions and analyses now follow.

First, in multi-label learning with missing labels, all the class labels are known in advance, whereas some of labelling results are missing or unobserved. A lot of approaches have been proposed for multi-label learning with missing labels, such as (Huang et al. 2019; Sun et al. 2010; Xu et al. 2013; Yu et al. 2014; Zhu et al. 2018). However, to successfully apply these approaches, one essential precondition is that each label has at least one positive data example. The problem setting on this precondition is different from that of multi-label learning with completely unobserved labels.

Fig. 1

Differences between previous related learning problems

Second, class incremental or online learning approaches (Da et al. 2014; Mu et al. 2017; Qu et al. 2009; Zhu et al. 2018) can handle classification with novel labels which are unseen in the training stage but appear in the test stage. The novel labels are unobserved because of the corresponding data examples are unobserved. By contrast, in our problem setting, novel labels are unobserved but the data examples are observed. Moreover, in multi-label learning, novel labels may not be mutually exclusive with existing observed labels, but have correlations with each other. Therefore, these approaches can not be applied to multi-label learning with completely unobserved labels.

The problem of detecting unobserved labels has been studied under single-instance single-label learning (Zhang et al. 2020) and multi-instance multi-label learning (Pham et al. 2015; Zhu et al. 2017). In single-instance single-label learning, unobserved labels are mutually exclusive with each other including the observed ones. In multi-instance multi-label learning, each data example is represented by multiple instances. Different from these two problems, for the proposed problem, each data example is represented by a single instance and associated with multiple class labels (including the unobserved labels) simultaneously which may have correlations with each other. In addition, these approaches can not handle missing values of the observed labels.

We refer to the proposed problem as multi-label learning with missing and completely unobserved labels, and introduce a formal definition of it as follows.

Definition 1

(Multi-label learning with missing and completely unobserved labels.) For a given multi-label learning dataset $\mathcal {D}=\{(\mathbf {x}_i,\mathbf {y}_i)\}_{i=1}^n$, $\mathcal {X}\in \mathbb {R}^d$ indicates the feature space, and $\mathcal {Y}=\{y_1,...,y_q,y_{q+1},...,y_{q+r}\}$ represents the full label space. In the training stage, the first q labels are observed and the rest r labels are completely unobserved. For the q observed labels, some of the annotation results are missing, but each label has at least one positive data example. While for the r completely unobserved labels, the semantic meanings of them and their labelling results for the n data examples are totally unknown.

The task of multi-label learning with missing and completely unobserved labels is to build a robust multi-label classification model which can discover previously unobserved labels and overcome the problem of missing values of the observed labels in the dataset. Meanwhile, the model can predict both the observed and unobserved labels simultaneously for unseen data examples. Besides, it would be better, if the meanings of unobserved labels can be interpreted.

1.2 Significance and contribution

Properly modeling the unobserved labels in multi-label learning can have positive impacts from two aspects. First, it enables effective discovering of unobserved labels and makes a deeper understanding of what is behind the multi-label data. Second, by discovering and making good use of the information of the unobserved labels in the multi-label data, we can better build a robust classification model for the observed labels and improve the accuracy of prediction.

In this paper, we propose a novel approach named MCUL to solve multi-label learning with Missing and Completely Unobserved Labels. MCUL is a robust multi-label classification model which can discover the completely unobserved labels and overcome the problem of partially missing values of the observed labels. In the test stage, it can predict unseen data examples with both the observed and unobserved labels simultaneously. The contributions of this paper are summarized as follows.

• We introduce the problem of multi-label learning with missing and completely unobserved labels. To the best of our knowledge, this topic is firstly addressed in multi-label learning.

• We propose a new approach named MCUL for the proposed problem, where a clustering-based regularization term is utilized to discover the unobserved labels, and label correlations are exploited to overcome the problem of missing values for both the observed and new discovered unobserved labels. We try to describe the semantic meaning of the new discovered labels based on the label-specific features which are learned by MCUL.

• We present three new evaluation metrics for the evaluation on the completely unobserved labels. Since the one-to-one correspondences between the ground-truth and new discovered labels are unknown, the existing evaluation metrics can not be applied directly. We propose to evaluate the results for the labels which are best matched based on some existing evaluation metrics for multi-label learning, such as ranking loss and coverage.

The advantages of the proposed framework are demonstrated by experiments on observed label prediction and novel label discovering over ten real multi-label datasets. The performance on observed labels can be improved by discovering and modeling the completely unobserved labels. The label-specific features with high weights have a strong semantic correlation with the name of the best-matched labels, and can be used to describe the semantic meaning for the new discovered labels.

2 Related work

Multi-label learning (Gibaja and Ventura 2015; Herrera et al. 2016; Tsoumakas et al. 2010; Zhang and Zhou 2014) deals with data examples which are associated with multiple class labels simultaneously. In the past decades, many advanced approaches have been proposed to solve interesting problems in multi-label learning.

According to the popular taxonomy firstly proposed in (Tsoumakas et al. 2010), existing multi-label learning approaches can mainly be divided into two categories: problem transformation (PT) strategy and algorithm adaption (AA) strategy. For the problem transformation strategy, a multi-label classification problem is transformed into one or more single-label classification problems that can be solved with a single-label classification algorithm, such as (Boutell et al. 2004; Dembczyński et al. 2010; Read et al. 2008, 2009; Tsoumakas et al. 2011). For the algorithm adaption strategy, traditional single-label classification algorithms are extended to solve multi-label classification problems directly, such as (Elisseeff and Jason 2001; Fürnkranz et al. 2008; Zhang and Zhou 2006, 2007). Nevertheless, existing approaches mainly assume that all the class labels are observed before the training process and the set of target labels is a closed set. Although the success has been made by existing studies on multi-label learning, there is still a challenging problem that some of the class labels are completely unobserved during the training stage. There are several lines of study that are related to the problem we proposed in this paper, such as multi-label learning with missing labels, class-incremental learning and stream multi-label learning.

Many approaches have been proposed for multi-label learning with missing labels, and can be mainly grouped into two categories. One strategy is to recover a full label matrix based on the matrix completion or factorization techniques by exploiting label or instance correlations, such as (Huang et al. 2019; Xu et al. 2013; Zhu et al. 2018). Another strategy is assuming that we have known which entries are missing, and then to calculate the classification loss without considering them, such as (Sun et al. 2010; Tan et al. 2018; Yu et al. 2014). The essential precondition for these two strategies is that each label has at least one positive data example. Nevertheless, these two strategies both will not work if one label is completely unobserved.

Some approaches have been proposed for class-incremental learning (Da et al. 2014; Shi et al. 2014) and stream multi-label learning (Mu et al. 2017; Qu et al. 2009; Read et al. 2011; Zhu et al. 2018). In these two problems, new labels are unobserved during the training stage, but appear in the test stage. The labels are unobserved because the corresponding data examples are also unobserved during the training stage. While in our problem, the data examples are observed but some labels are completely unobserved during the training stage. In addition, for class-incremental learning and stream classification problems, if one label is unobserved in the training stage and does not appear in the test stage, it will never be discovered.

There are several highly related studies with the purpose of discovering unobserved labels for the training data. ExML (Zhang et al. 2020) assumes that the unobserved labels are wrongly annotated as observed labels, and examines and investigates the training data set by actively augmenting the feature space to discover potentially unobserved labels. However, it can not be applied to multi-label learning, and the problem setting is also different from us. MIMLNC (Pham et al. 2015) is a probabilistic model to identify novel instances for multi-instance multi-label learning, and it assumes that all novel instances belong to a single new label. DMNL (Zhu et al. 2017) assumes that there are k unobserved labels, and tries to discover multiple novel labels for multi-instance multi-label learning with a clustering based regularization term. These two approaches are hardly applied to general single-instance multi-label learning.

By surveying previous studies on multi-label learning, it is found that none of existing approaches can directly address the potential problem of multi-label learning with missing and completely unobserved labels. In this paper, we propose a novel approach named MCUL which can discover the completely unobserved labels and overcome the problem of partially missing values of the observed labels, and predict both the observed and unobserved labels simultaneously to the unseen data examples in the test stage.

3 The proposed approach

3.1 Preliminary

To describe the new problem settings given in definition 1, we provide the following formal notations.

$\mathcal {X}\in \mathbb {R}^d$ indicates the d-dimensional feature space, and $\mathcal {Y}=\{y_1,...,y_q\}$ represents the label set of q observed labels. Assuming there are r different unobserved labels which are indicated by $\bar{\mathcal {Y}}=\{y_{q+1},...,y_{q+r}\}$. As a result, there are l labels totally, and the complete label set will be $\hat{\mathcal {Y}}=\mathcal {Y}\cup \bar{\mathcal {Y}}=\{y_1,...,y_q, y_{q+1},...,y_{l}\}$, where $l=q+r$. $\mathbf {X}=[\mathbf {x}_1,..., \mathbf {x}_n ]^T \in \mathbb {R}^{n\times d}$ is used to indicate the data matrix of a multi-label learning training set, and $\hat{\mathbf {Y}}=[\mathbf {Y},\bar{\mathbf {Y}}]\in \{0,1\}^{n\times l}$ is used to indicate the full label matrix. Here, $\mathbf {Y}\in \{0,1\}^{n\times q}$ indicates the label matrix for the q observed labels and some entries of it are missing. If $y_{ij}=1$, it indicates that the $\mathbf {x}_i$ belongs to $y_j$. If $y_{ij}=0$, it indicates that the $\mathbf {x}_i$ does not belong to $y_j$ or the value is missing. $\bar{\mathbf {Y}} \in \{0, 1\}^{n\times r}$ indicates the label matrix for the unobserved labels, and all the entries of it are missing during the training stage, i.e., $\bar{y}_{ij} = 0$, $\forall ~ 1\le i\le n, 1\le j \le r$.

Fig. 2

The framework of the proposed method MCUL

For the proposed problem, we aim to construct a robust multi-label learning model $h:\mathcal {X}\rightarrow 2^{\hat{\mathcal {Y}}}$ which can predict unseen data examples with both the observed and unobserved labels simultaneously. In this paper, we propose a new method MCUL to solve multi-label learning with Missing and Completely Unobserved Labels. The framework is shown in Fig. 2. The main idea is that we first transform the label matrix from completed missing to partially missing with the help of unsupervised learning techniques, and then we learn a model from the feature space to the augmented label space and try to recover the missing entries by exploiting label correlations. Specifically, MCUL is composed of two parts, i.e., discovering the completely unobserved labels and building a robust multi-label learning classifier for observed and unobserved labels.

3.2 Discovering the completely unobserved labels

To construct a multi-label classification model $h:\mathcal {X}\rightarrow 2^{\hat{\mathcal {Y}}}$, we need the full label matrix $\hat{\mathbf {Y}}=[\mathbf {Y},\bar{\mathbf {Y}}]$ for the training data. However, $\bar{\mathbf {Y}}$ is completely unobserved and unknown during the training stage. Therefore, we need resort to some unsupervised learning techniques, such as clustering. In Ding et al. (2005), it is indicated that the nonnegative matrix factorization (NMF) factorizing a symmetric similarity matrix $\mathbf {S}$ into $\mathbf {H}\mathbf {H}^\top$ is equivalent to the soft k-means clustering. The optimization objective function of it is formulated as

$$\begin{aligned} \min _{\mathbf {H}} ~\Vert \mathbf {S} - \mathbf {H}\mathbf {H}^\top \Vert _F^2,~~ s.t.~ \mathbf {H}\ge 0, \end{aligned}$$

(1)

where $\mathbf {S}\in \mathbb {R}^{n\times n}$ is the similarity matrix containing pairwise similarities or the kernels, and $\mathbf {H}\in \mathbb {R}^{n\times l}$ is the clustering indicator matrix. For a matrix $\mathbf {A}$, $\Vert \mathbf {A}\Vert _F$ indicates the Frobenius norm of it, and $\Vert \mathbf {A}\Vert _F^2=tr(\mathbf {A}^\top \mathbf {A})$.

For the proposed problem, we have already obtained the labeling result for part of the labels, i.e, $\mathbf {Y}\in \mathbb {R}^{n\times q}$ is known in advance. Therefore, part of the results of $\mathbf {H}$ should be consistent with $\mathbf {Y}$. It is noted that $\mathbf {h}_i\mathbf {h}_j^\top =\sum _{m=1}^l h_{im}h_{jm}$, where $\mathbf {h}_i$ indicates the i-th row of $\mathbf {H}$. Changing of the order of the columns of $\mathbf {H}$ will not change the value of $\mathbf {H}\mathbf {H}^\top$. Without loss of generality, we assume that the results of the first q columns of $\mathbf {H}$ should be consistent with that of the q observed labels. Consequently, we extend the problem (1) to the following one

$$\begin{aligned} \min _{\mathbf {H}}~&\Vert \mathbf {S} - \mathbf {H}\mathbf {H}^\top \Vert _F^2,~~s.t.~ \mathbf {HP} = \mathbf {Y},\mathbf {H}\in [0,1]^{n\times l}, \end{aligned}$$

(2)

where $\mathbf {P}\in \{0,1\}^{l\times q}$ is a projection matrix with ones on the main diagonal and zeros elsewhere.

In this paper, the similarity matrix $\mathbf {S}\in \mathbb {R}^{n\times n}$ is calculated by the Gaussian kernel based on the feature and label spaces simultaneously. Each element $s_{ij}$ is defined as

$$\begin{aligned} s_{ij} = \exp \left( \frac{-\Vert \hat{\mathbf {x}}_i - \hat{\mathbf {x}}_j\Vert _2^2}{2\sigma ^2}\right) , \end{aligned}$$

(3)

where $\hat{\mathbf {x}}_i=[\mathbf {x}_i,\mathbf {y}_i]$, and $\sigma$ is set to be 1 in the experiment.

3.3 Building a robust multi-label learning classifier

After obtaining the preliminary labeling results of the r unobserved labels, we can construct a multi-label classifier for both of the q observed and r completely unobserved labels simultaneously. Here, we learn a linear model for $h:\mathcal {X}\rightarrow 2^{\hat{\mathcal {Y}}}$, then the optimization problem becomes

$$\begin{aligned} \min _{\mathbf {W},\mathbf {H}}~&\frac{1}{2}\Vert \mathbf {XW} +\mathbf {1}_n\mathbf {b}^\top - \mathbf {H}\Vert _F^2 + \frac{\lambda _0}{4}\Vert \mathbf {S} - \mathbf {H}\mathbf {H}^\top \Vert _F^2 \nonumber \\&s.t.~ \mathbf {HP} = \mathbf {Y}, \mathbf {H}\in [0,1]^{n\times l}, \end{aligned}$$

(4)

where $\mathbf {W}\in \mathbb {R}^{d\times l}$ is the model coefficient matrix, $\mathbf {b}\in \mathbb {R}^{l}$ is the bias, and $\mathbf {1}_n$ denotes the vector of size n. For simplicity, the bias $\mathbf {b}$ can be absorbed into $\mathbf {W}$ by adding an additional feature with all the values equal to 1 for the data matrix, i.e., $\mathbf {X}=[\mathbf {X},\mathbf {1}_n]$.

As mentioned in the previous section, $\mathbf {Y}$ is observed but with some missing entries. While the problem (1) is not designed for multi-label learning, and thus there will be missing entries in $\mathbf {H}$ as well. In the problem (4), we have tried to recover the full label matrix by exploiting the instance similarity, i.e., if two data instances $\mathbf {x}_i$ and $\mathbf {x}_j$ are similar in the feature space $\mathcal {X}$, their label vectors $\mathbf {h}_i$ and $\mathbf {h}_j$ will similar in the label space $\hat{\mathcal {Y}}$. On the other hand, we can resort to reconstruct the missing entries from the results of other labels by exploiting the label similarity. From the perspective of the similarity of label, the assignment of one certain label to training instances can be reconstructed from other labels, especially from its highly similar labels. The fourth term of (5) is adopted to model label reconstruction, i.e., $h_{ij}\approx \sum _{m=1}^l h_{im}c_{mj}$, where $\mathbf {C}\in \mathbb {R}^{l\times l}$ represents the reconstruction coefficient matrix, and each element $c_{ij}$ indicates the reconstruction coefficient that label $y_j$ is derived from $y_i$.

In addition, we can reconstruct the missing entries in $\mathbf {H}$ by modeling label correlations. In particular, we hope that highly correlated labels have similar outputs. Specifically, if two labels $y_i$ and $y_j$ have a strong correlation, then their model parameters $\mathbf {w}_i$ and $\mathbf {w}_j$ will be similar, and thus the distance (i.e., $\Vert \mathbf {w}_i-\mathbf {w}_j\Vert _2^2$) should be small. Otherwise, the distance should be large. Since all the binary classifiers for each label have the same input data $\mathbf {X}$, if labels $y_i$ and $y_j$ are highly correlated, their corresponding classifiers will have similar outputs by adding the constraint. The fifth term of (5) is adopted to model pairwise label correlation including both observed and unobserved labels, where $\mathbf {L}$ represents the graph Laplacian matrix of the label correlation matrix which is calculated by cosine similarity between label pairs of $\mathbf {H}$. Consequently, the objective function can be rewritten as

$$\begin{aligned} \min _{\mathbf {W},\mathbf {C}, \mathbf {H}}~&\frac{1}{2}\Vert \mathbf {XW} - \mathbf {HC}\Vert _F^2 + \frac{\lambda _0}{4}\Vert \mathbf {S} - \mathbf {H}\mathbf {H}^\top \Vert _F^2 + \frac{\lambda _1}{2}\Vert \mathbf {HP} - \mathbf {Y}\Vert _F^2 + \nonumber \\&\frac{\lambda _2}{2}\Vert \mathbf {HC} - \mathbf {H}\Vert _F^2 + \frac{\lambda _3}{2} tr(\mathbf {WL}\mathbf {W}^\top ) + \lambda _4\Vert \mathbf {W}\Vert _1\nonumber \\&s.t.~ \mathbf {H}\in [0,1]^{n\times l}. \end{aligned}$$

(5)

For the problem (see the definition 1) addressed in this paper, we are also interested in what categories we have discovered and what their semantic concepts are. Motivated by previous studies (Huang et al. 2016, 2019; Wei et al. 2019; Wu et al. 2019; Zhang and Wu 2015) on learning label-specific features which have strong discrimination capabilities to each label, we add the $\ell _1$-norm regularization on the model coefficient matrix $\mathbf {W}$ to learn the sparse label-specific features for each label, and expect to use them to describe the semantic meaning for the new discovered labels, and the results are provided in section 5.3.2.

It is noted that the formulation of the problem (5) is somewhat similar to the work SLEEC (Bhatia et al. 2016) on extreme multi-label classification. SLEEC aims to learn a low dimensional latent label space. While in our approach, we want to learn an augmented label space where the new discovered labels are paralleled with the observed labels, i.e., the new discovered labels have the same semantic level as the existing observed labels.

4 Optimization

For the problem (5), it is convex but non-smooth, and there are three coefficient parameters. We adopt the accelerated proximal gradient method (Beck and Teboulle 2009) to solve it, and update each parameter alternatively. We use $\mathcal {J}(\varvec{\Psi })$ to represent the empirical loss of (5), where $\varvec{\Psi }=\{\mathbf {H},\mathbf {W},\mathbf {C}\}$ indicates the set of the three parameters.

4.1 Solving H

By fixing $\mathbf {W}$ and $\mathbf {C}$, the problem (5) becomes

$$\begin{aligned}&\min _{\mathbf {H}}~ \frac{1}{2}\Vert \mathbf {XW} - \mathbf {HC}\Vert _F^2 + \frac{\lambda _0}{4}\Vert \mathbf {S} - \mathbf {H}\mathbf {H}^\top \Vert _F^2 + \frac{\lambda _1}{2}\Vert \mathbf {HP} - \mathbf {Y}\Vert _F^2 \nonumber \\&\quad +\frac{\lambda _2}{2}\Vert \mathbf {HC} - \mathbf {H}\Vert _F^2,~~~~ s.t.~ \mathbf {H}\in [0,1]^{n\times l}. \end{aligned}$$

(6)

We can obtain the gradient w.r.t $\mathbf {H}$ as

$$\begin{aligned} \nabla _{\mathbf {H}}\mathcal {J} =~&(1+\lambda _2)\mathbf {HC}\mathbf {C}^\top - \mathbf {XW}\mathbf {C}^\top + \lambda _0(\mathbf {H}\mathbf {H}^\top - \mathbf {S})\mathbf {H} + \lambda _1(\mathbf {HP} - \mathbf {Y})\mathbf {P}^\top \nonumber \\&+ \lambda _2( \mathbf {H} - \mathbf {H}(\mathbf {C}+\mathbf {C}^\top )). \end{aligned}$$

(7)

According the proximal gradient descend algorithm (Beck and Teboulle 2009), $\mathbf {H}$ can be updated by

$$\begin{aligned} \mathbf {H}=\mathbf {H}^{(t)}-\frac{1}{L_f} \nabla _{\mathbf {H}} \mathcal {J}(\mathbf {H}^{(t)}, \mathbf {W}, \mathbf {C}), \end{aligned}$$

(8)

where $\mathbf {H}^{(t)}=\mathbf {H}_{t}+\frac{\alpha _{t-1}-1}{\alpha _{t}}(\mathbf {H}_{t}-\mathbf {H}_{t-1})$. For a sequence $\alpha _{t}$, it should satisfy the condition of $\alpha _{t}^{2}-\alpha _{t} \le \alpha _{t-1}^{2}$. Considering the non-negative constraint on $\mathbf {H}\in [0,1]^{n\times m}$, $\mathbf {H}$ should be further post-processed by $\mathbf {H}=\max (\mathbf {H},\mathbf {0})$ and the min-max normalization over each column of it. As a result, for each label, it has at least one positive example.

In Eq. (8), $L_f$ indicates the Lipschitz constant. According to (Beck and Teboulle 2009), an approximate $L_f$ can be obtained with a line-search strategy, where we keep updating $L_f = \eta L_f$, $\eta >1$ until if it satisfies $\mathcal {J}(\varvec{\Psi })<\mathcal {J}(\varvec{\Psi }') +\langle \nabla \mathcal {J}(\varvec{\Psi }'), \varvec{\Psi }-\varvec{\Psi }'\rangle + \frac{L_f}{2}\Vert \varvec{\Psi }-\varvec{\Psi }'\Vert _{F}^{2}$. Here, $\varvec{\Psi }'= \{\mathbf {H}^{(t)},\mathbf {W}^{(t)},\mathbf {C}^{(t)}\}$.

4.2 Solving W

With $\mathbf {H}$ and $\mathbf {C}$ fixed, the problem (5) is simplified as

$$\begin{aligned} \min _{\mathbf {W}}~&\frac{1}{2}\Vert \mathbf {XW} - \mathbf {HC}\Vert _F^2 + \frac{\lambda _3}{2} tr(\mathbf {W}\mathbf {L}\mathbf {W}^\top ). \end{aligned}$$

(9)

Then, we can obtain the gradient w.r.t $\mathbf {W}$ as

$$\begin{aligned} \nabla _{\mathbf {W}}\mathcal {J}= & {} \mathbf {X}^\top (\mathbf {XW}-\mathbf {HC}) + \lambda _3\mathbf {XW}\mathbf {L}. \end{aligned}$$

(10)

Consequently, $\mathbf {W}$ can be updated by

$$\begin{aligned} \mathbf {W}=\mathbf {W}^{(t)}-\frac{1}{L_f} \nabla _{\mathbf {W}} \mathcal {J}(\mathbf {H}, \mathbf {W}^{(t)}, \mathbf {C}), \end{aligned}$$

(11)

where $\mathbf {W}^{(t)}=\mathbf {W}_{t}+\frac{\alpha _{t-1}-1}{\alpha _{t}} (\mathbf {W}_{t}-\mathbf {W}_{t-1})$. Considering the $\ell _1$-norm over parameter $\mathbf {W}$, the result can be further updated by the element-wise soft-threshold operator which is defined as

$$\begin{aligned} \mathbf {W} = \mathbf {prox}_{\frac{\lambda _4}{L_f}}(\mathbf {W}), \end{aligned}$$

(12)

where $\mathbf {prox}_{\epsilon }(a)$ is the element-wise operator which is defined as

$$\begin{aligned} \mathbf {prox}_{\epsilon }(a)=\mathbf {sign}(a) \max (|a|-\epsilon ,0). \end{aligned}$$

(13)

4.3 Solving C

With $\mathbf {H}$ and $\mathbf {W}$ fixed, the problem (5) reduces to

$$\begin{aligned} \min _{\mathbf {C}}~&\frac{1}{2}\Vert \mathbf {XW} - \mathbf {HC}\Vert _F^2 + \frac{\lambda _2}{2}\Vert \mathbf {HC} - \mathbf {H}\Vert _F^2. \end{aligned}$$

(14)

Then, we can obtain the gradient w.r.t $\mathbf {C}$ as

$$\begin{aligned} \nabla _{\mathbf {C}}\mathcal {J} =&\mathbf {H}^\top \mathbf {HC} - \mathbf {H}^\top \mathbf {XW} + \lambda _2(\mathbf {H}^\top \mathbf {HC}-\mathbf {H}^\top \mathbf {H}). \end{aligned}$$

(15)

Therefore, a closed-form solution to $\mathbf {C}$ can be obtained as

$$\begin{aligned} \mathbf {C} =&((\lambda _2+1)\mathbf {H}^\top \mathbf {H})^{-1} (\mathbf {H}^\top \mathbf {XW} +\lambda _2\mathbf {H}^\top \mathbf {H}). \end{aligned}$$

(16)

According to the above optimization procedures, we can summarize all the optimization steps of the proposed method in Algorithm 1.

5 Experiments

5.1 Experimental configuration

5.1.1 Dataset and configuration

Table 1 Description of datasets

The experiment is conducted over ten multi-label benchmark datasets, and the details of which are summarized in Table 1. For each data set, a 5-fold cross validation is adopted three times. To evaluate the performance on completely unobserved labels, we set the first $\lfloor 90\%l\rfloor$ labels as observed and the rest $\lceil 10\%l\rceil$ as unobserved labels, where l indicates the number of all the labels. In addition, to imitate missing labels, we randomly drop some of the labeling results of the $\lfloor 90\%l\rfloor$ observed labels for the training data of each dataset according to a predefined missing rate e.g., $10\%$, $15\%$ and $20\%$.

5.1.2 Comparison approaches

By surveying previous studies on multi-label learning, it was found that there is no previous work on solving multi-label learning with missing and completely unobserved labels. To verify the effectiveness of our approach, we compare it with the following state-of-the-art multi-label classification approaches in terms of their performance on observed labels, and detailed configurations of them are summarized as below. The two approaches LSML (Huang et al. 2019) and Glocal (Zhu et al. 2018) can handle the problem of missing labels for multi-label learning. Parameter tuning for all the comparison approaches is based on a 5-fold cross validation over the training data of each dataset.

• BR (Boutell et al. 2004): Binary relevance. Ridge Regression is utilized as the base learner for each binary classifier of BR approach, and the regularization parameter is tuned in $\{10^i|i=-2,...,2\}$.

• ECC (Read et al. 2009): Ensemble of classifier chains (CC). Ridge Regression is utilized as the base learner for each binary classifier of CC approach, and the regularization parameter is tuned in $\{10^i|i=-2,...,2\}$. The ensemble size is set to be 15, and the chain order for each CC is generated randomly.

• MLkNN (Zhang and Zhou 2007):¹ A lazy learning approach to multi-label learning. The number of nearest neighbors k is tuned in$\{7,...,17\}$.

• LSML (Huang et al. 2019):² It learns label-specific features for multi-label classification with missing labels, classification and label matrix recovery are performed jointly. All the parameters of it are searched in $\{10^i|i=-5,...,3\}$.

• Glocal (Zhu et al. 2018):³ It can simultaneously recover the missing labels, train the linear classifiers, explore and exploit both global and local label correlations. Parameter $\lambda =1$, $\lambda _1$ to $\lambda _5$ are searched in $\{10^i|i=-5,...,1\}$, k is tuned in $\{0.1q,0.2q,...,0.6q\}$, and g is tuned in $\{5, 10, 15, 20\}$.

• MCUL: The proposed approach of this paper. MCUL-O is a simplified version of MCUL without discovering the unobserved labels, i.e., $k=0$. Parameters $\lambda _0$ and $\lambda _4$ are tuned in $\{10^i|i=-1,...,1\}$, $\lambda _1$ is tuned in $\{10^i|i=0,...,3\}$, $\lambda _2$ is tuned in $\{10^i|i=0,...,2\}$, and $\lambda _3$ is tuned in $\{5^i|i=0,...,3\}$.

• LSML-U and Glocal-U: Two different versions of LSML (Huang et al. 2019) and Glocal (Zhu et al. 2018) with a preprocessing step by solving the problem (2) to discover the unobserved labels for the training data. As a result, we can train LSML-U and Glocal-U on the full label matrix $\mathbf {H}$. It is worth noting that the algorithm Glocal-U needs an observation matrix to indicate which entities in the label matrix are observed (i.e., the value is not missing). Therefore, for Glocal-U, the entities of $\mathbf {H}$ for the unknown labels are set as observed if the corresponding values are greater than 0.5.

5.2 Evaluation metrics

5.2.1 Evaluation metrics for observed labels

The performance of the comparison algorithms on observed labels is evaluated in terms of five common metrics (Gibaja and Ventura 2015; Herrera et al. 2016; Tsoumakas et al. 2010; Zhang and Zhou 2014), i.e., One Error, Coverage, Ranking Loss, Average Precision and Macro AUC.

5.2.2 Evaluation metrics for new discovered labels

To evaluate the performance on new discovered labels, we adopt $\text {F}_{\text {U}}$ (Zhu et al. 2017) and propose three new metrics.

Given a test dataset, for the unobserved labels, $\bar{\mathbf {Y}}=[\bar{\mathbf {y}}_1,\bar{\mathbf {y}}_2,... \bar{\mathbf {y}}_r]\in \{0,1\}^{n_t\times r}$ indicates the ground truth of it, $\hat{\mathbf {Y}}=[\hat{\mathbf {y}}_1,\hat{\mathbf {y}}_2,... \hat{\mathbf {y}}_r]\in \{0,1\}^{n_t\times r}$ represents the predicted label matrix, and $\mathbf {A}=[\mathbf {a}_1,\mathbf {a}_2,...,\mathbf {a}_r]\in \mathbb {R}^{n_t\times r}$ indicates the predicted score matrix.

• $\text {F}_{\text {U}}$ was proposed in (Zhu et al. 2017). It measures the average label-based $\hbox {F}_1$-measure on newly discovered and the ground-truth labels that best matches.

  $$\begin{aligned} \text {F}_{\text {U}} = \frac{1}{r} \sum _{i=1}^{r} \max (\{F_1(\hat{\mathbf {y}}_{i},\bar{\mathbf {y}}_{j}), j\in \{1,...,r\}\}) \end{aligned}$$

  (17)

  where $F_1(\cdot )$ is the function to calculate the example-based $F_1$ score.

• $\text {RL}_{\text {U}}$ measures the average label-based Ranking Loss on newly discovered and the ground-truth labels that best matches.

  $$\begin{aligned} \text {RL}_{\text {U}} = \frac{1}{r} \sum _{i=1}^{r} \min (\{\text {RankingLoss}(\mathbf {a}_{i},\bar{\mathbf {y}}_{j}), j\in \{1,...,r\}\}) \end{aligned}$$

  (18)

  where $\text {Ranking Loss}(\cdot )$ evaluates the fraction of reversely ordered label pairs, i.e. an irrelevant label is ranked higher than a relevant label.

• $\text {Cov}_{\text {U}}$ measures the average label-based Coverage on new discovered and the ground-truth labels that best matches.

  $$\begin{aligned} \text {Cov}_{\text {U}} = \frac{1}{r} \sum _{i=1}^{r} \min (\{\text {Coverage}(\mathbf {a}_{i},\bar{\mathbf {y}}_{j}), j\in \{1,...,r\}\}) \end{aligned}$$

  (19)

  For a given output score $\mathbf {a}_{i}$, the function $\text {Coverage}(\cdot )$ evaluates how many steps are needed, on average, to move down the ranked label list so as to cover all the relevant labels of $\bar{\mathbf {y}}_{j}$. Consequently, the smaller the steps are, the better the performance is.

• $\text {LM}_{\text {U}}$ measures the average Label Matching proportion over all the evaluation metrics.

  $$\begin{aligned} \text {LM}_{\text {U}} = \frac{1}{m} \sum _{i=1}^{m}\frac{|\mathcal {S}_i\wedge \bar{\mathcal {Y}}|}{r} \end{aligned}$$

  (20)

  where m is the number of metrics which can return a set of matched labels, and $\mathcal {S}_i$ indicates the set of matched labels returned by the i-th metric. This metric indicates the average proportion of ground-truth labels that we have discovered among the new discovered labels.

For $\text {F}_{\text {U}}$ and $\text {LM}_{\text {U}}$, the bigger the values of them are, the better the performance is. While for $\text {RL}_{\text {U}}$ and $\text {Cov}_{\text {U}}$, the smaller the values of them are, the better the performance is.

5.3 Experiment results

As the compared approaches cannot solve multi-label learning with missing and completely unobserved directly, we evaluate the performance of them on observed and completely unobserved labels respectively.

Fig. 3

Results of each comparison approach over the ten data sets in terms of all the evaluation metrics

5.3.1 Results on observed labels

The experimental results of each comparison algorithm on the observed labels are shown in Fig. 3. Moreover, we calculate the average results of each comparison approach over the ten data sets in terms of different evaluation metrics under different missing rates respectively, and the results are shown in Fig. 5, where the symbol $\uparrow (\downarrow )$ indicates the larger (smaller) the value is, the better the performance is.

Table 2 Summary of the Friedman Statistics $F_F (k=9,N=30)$ and the critical value in terms of each evaluation metric (k: # comparison algorithms; N: # data points)

Fig. 4

Comparison of MCUL against the comparison approaches with the Nemenyi test. Groups of classifiers that are not significantly different from MCUL (at $p = 0.05$) are connected

To analyze the relative performance among the comparison algorithms systematically, Friedman test (Demšar 2006) is employed to conduct performance analysis. The missing rate of observed labels is varied in the range of {10%, 15% 20%}, and as a result, there are 30 ($3 \times 10$) data points totally. Table 2 summarizes the Friedman statistics $F_F$ and the corresponding critical value in terms of each evaluation metric. As shown in Table 2, at significance level $\alpha$ = 0.05, the null hypothesis that all the comparison algorithms perform equivalently is clearly rejected in terms of each evaluation metric. Consequently, we employ the Nemenyi test (Demšar 2006) to test whether our proposed method MCUL achieves a competitive performance against the comparison algorithms, where MCUL is considered as the control algorithm. The performance between two classifiers will be significantly different if their average ranks differ by at least one critical difference $\text {CD}=q_{\alpha }\sqrt{\frac{k(k+1)}{6N}}$. For Nemenyi test, $q_{\alpha }=2.948$ at significance level $\alpha =0.05$, and thus $\text {CD}=2.1934~(k=9, N = 30)$. Fig. 4 shows the CD diagrams on each evaluation metric. In each sub-figure of Fig. 4, any comparison algorithm whose average rank is within one CD is connected. Otherwise, any algorithm not connected is considered to have significantly different performance between them. According to these experimental results, the following observations can be made:

Fig. 5

Average results of each comparison approach over the ten data sets in terms of all the evaluation metrics under different missing rates of observed labels

• As shown in Fig. 5, the performance of each approach decreases with the increasing of missing rate. It verifies the importance of solving the problem of missing labels for multi-label learning.

• The proposed method MCUL significantly outperforms all the comparison approaches in terms of Ranking Loss, Coverage, and Macro AUC, and achieves statistically superior performance to other comparison approaches in terms of Average Precision and One Error. The superiority implies the effectiveness of the proposed method on multi-label learning with missing labels.

• The proposed method MCUL achieves statistically superior or at least comparable performance against its simplified version MCUL-O in terms of all the evaluation metrics. The superior performance of MCUL against MCUL-O definitely verifies that discovering and modeling the unobserved labels can improve the performance of our method on existing observed labels.

• LSML-U and GLocal-U outperform their original versions respectively in terms of Average Precision and Macro AUC, and achieve comparable performance against their original versions in terms of other evaluation metrics. This observation also verifies that discovering and modeling the unobserved labels can improve the performance on existing observed labels.

• MCUL achieves statistically superior performance to LSML and GLocal and their two extended versions in terms of all the evaluation metrics. The superior performance of MCUL demonstrates that our method can handle missing labels better than them.

• MLkNN achieves the worst performance on all the data sets. It is worth noting that MLkNN is constructed based on the information of k nearest neighbors of each instance. When the data set is with missing labels, especially some of the labels are completely unobserved, instances of the k nearest neighbors cannot provide sufficient information for MLkNN to learn reliable prior and posterior probabilities for the prediction. It implies the importance of solving data set with missing and completely unobserved labels.

Fig. 6

Experimental results on the Unobserved labels. BR is trained based on the ground-truth of the unobserved labels

5.3.2 Results on unobserved labels

In this section, we provide both the quantitative and qualitative analysis of the results on unobserved labels.

For the quantitative analysis, we compared MCUL with LSML-U, Glocal-U (For detailed settings, please refer to Sect.5.1.2), and BR. Since BR cannot discover unobserved labels, we trained it based on the ground-truth of the unobserved labels, i.e., $h:\mathcal {X}\rightarrow 2^{\bar{\mathcal {Y}}}$. Although this comparison is unfair, we can still make some observations according to the results. For MCUL, LSML-U, and Glocal-U, $\bar{\mathcal {Y}}$ is unavailable during the training stage, the prediction threshold of them is tuned according to the result of example-based $F_1$ measure on observed labels respectively. Figure 6 shows the results of them on discovered unobserved labels in terms of $\text {F}_{\text {U}}$, $\text {RL}_{\text {U}}$, $\text {Cov}_{\text {U}}$, and $\text {LM}_{\text {U}}$ (Detailed definitions are provided in Sect.5.2.2). According to these results, we have the following observations:

• First, on most of the data sets, MCUL achieves a better performance than LSML-U and Glocal-U in terms of the four evaluation metrics. One possible reason might be that some of the labelling results of the unobserved labels for the training data by a preprocessing step are incorrect, and these incorrect results cannot be well optimized during the training stage of LSML-U and Glocal-U respectively.

• Second, MCUL achieves a better performance than BR in 40% cases in terms of $\text {F}_{\text {U}}$ and $\text {RL}_{\text {U}}$. Besides, MCUL achieves a better performance than BR in 80% cases in terms of $\text {Cov}_{\text {U}}$. These results indicate that MCUL can discover some of the unobserved labels and the results of them are acceptable.

• Last, the results of $\text {LM}_{\text {U}}$ of MCUL are located in the range of [40, 49]. These results clearly indicate that the proposed method can discover at least 40% of the unobserved labels. In addition, according to Fig. 7f, MCUL will achieve a better performance on the unobserved labels if we set a smaller value of r, i.e., the number of unobserved labels. For example, the value of $\text {LM}_{\text {U}}$ can reach 85.6% for stackex-cs dataset when $r=5$.

Table 3 Top 20 features for the five best matched labels of stackex-cooking

Table 4 Top 20 features for the five best matched labels of stackex-cs

Table 5 Top 20 features for the five best matched labels of stackex-philosophy

For the qualitative analysis, we want to show what categories we have discovered and what their semantic concepts are. As discussed in Sect. 3.3, we try to learn the sparse label-specific features for each label, and expect to use them to describe the semantic meaning of new discovered labels. In this section, we provide results of top 20 features and $\text {F}_{\text {U}}$ of the five best matched labels (the criterion $\text {F}_{\text {U}}$ is adopted) for three datasets, e.g., stackex-cooking,stackex-cs, and stackex-philosophy. For each dataset, the first $\lfloor 90\%l\rfloor$ labels are set as the observed labels and the missing rate is 10%, and the rest $\lceil 10\%l\rceil$ labels are set as unobserved labels, where l indicates the total number of labels.

The name of top-five best matched ground-truth labels and their matched results $\text {F}_{\text {U}}$, and top 20 features of each dataset are shown in Tables 3, 4 and 5, where the features are arranged in a descending order according to the values of $\mathbf {W}$. Specifically, if the i-th newly discovered label is best matched with the j-th ground-truth label according to $\text {F}_{\text {U}}(i,j)$, then $y_j$ is the name of best matched ground-truth label, and the top 20 features are arranged in a descending order by sorting the values of $|\mathbf {w}^{(q+i)}|$. As shown in the Tables 3, 4 and 5, for each matched ground truth label, in most cases, the name of it ranks in the first or second place among the corresponding top 20 label-specific features. In addition, most of these features have a strong semantic correlation with it.

In Table 5, it is noted that the labels Theology and Stoicism do not appear in the top 20 features. We also find that the word Stoicism does not exist in the feature space. Besides, we extracted a brief introduction to these two topics Theology⁴ and Stoicism⁵ from Wikipedia respectively. It is found that the top 20 features of these two labels still have strong semantic correlations with the name of labels.

Therefore, we argue that the semantic meaning of the discovered labels can be depicted by these label-specific features. For image data, if the features are extracted based on the sub-area of images or high level features learned by some advanced approaches, such as deep learning approaches, we think that this strategy can also work well. Moreover, if we have the raw data, we can better describe the semantic meaning. The proposed method MCUL can predict both the observed and unobserved labels for data examples. After the prediction, we will know the tentative labelling results of the data examples.

5.3.3 Parameter analysis

Fig. 7

Parameter analysis on MCUL over stackex-cs

The average results (i.e., Average Precision and One Error) of MCUL with different values of $\lambda _0$, $\lambda _1$, $\lambda _2$, $\lambda _3$, and $\lambda _4$ over stackex-cs are shown in Fig. 7a–e. It is noted that the performance of MCUL is insensitive to the parameters, and also the optimal performance is usually achieved at some intermediate values of the parameters.

Figure 7f shows the average results of MCUL over 15 repetitions with different numbers of unobserved labels. The result (i.e., One Error) on observed labels is improved and then dropped down with the increasing of the number of unobserved class labels (i.e., r), and MCUL obtains the best performance when $r=\lceil 10\%l\rceil =28$, where $l=274$ for stackex-cs. As shown in Fig. 7f, the result (i.e., $\text {F}_{\text {U}}$) on unobserved labels decreases with the growing of the number of unobserved class labels. Therefore, it is reasonable that the difficulty of discovering the unobserved labels increases with the growing of the number of unobserved labels, i.e, the larger the number of unobserved class labels is, the more difficult it is to discover them. Therefore, we think that an appropriate value of r could be searched by cross-validation according to the performance of observed labels. This strategy is feasible for data set with a small number of class labels. For a data set with extreme number of class labels, the parameter range for r will be too large, and here we provide a possible way to run our model in real application. Specifically, we can set a small step $r_t$ for the number of unobserved labels, and run the model multiple times until the performance on the observed labels becomes worse or unacceptable.

Fig. 8

Examples of the convergence curve of MCUL

5.3.4 Complexity and convergence

For the proposed objective function (5), the most time-consuming step is to calculate the second term $\Vert \mathbf {S}-\mathbf {H}\mathbf {H}^T\Vert _F^2$ which leads to a time complexity of $\mathcal {O}(n^2(d+l+n))$ and a memory complexity of $\mathcal {O}(n^2)$, where n indicates the number of data instances, d and l represent the number of features and labels respectively.

Figure 8 shows the value $\mathcal {J}(\Psi )$ of the objective function (5) of MCUL w.r.t the number of iterations over bibtex, corel16k001 and medical three datasets, respectively. It is noted that the value of $\mathcal {J}(\Psi )$ drops sharply around 30 iterations and then tends to become stable. For the other experimental data sets, the proposed method MCUL can converge within 100 iterations at most.

6 Conclusion

In this paper, we propose a new approach named MCUL to solve multi-label learning with missing and completely unobserved labels. It can not only discover the unobserved labels for the training data but also predict new data examples with the observed and new discovered labels simultaneously. The experimental results demonstrate the effectiveness of our method, and verify the importance of discovering and modeling unobserved label for multi-label learning.

This work tentatively solves the problem of multi-label learning with missing and completely unobserved labels. We think that this problem may have a long-term benefit to the community of multi-label learning. There are a few issues to this method that will be considered in a future study. First, how to automatically decide the number of the unobserved labels. In real applications, there is no prior knowledge about it. Second, how to describe the semantic meaning of the unobserved labels for various types of data. Third, the proposed problem can be solved together with many other challenging problems in multi-label learning, such as online learning, semi-supervised multi-label learning, feature selection, extreme multi-label learning, etc.