Abstract
Meta-learning, or learning to learn, is a machine learning approach that utilizes prior learning experiences to expedite the learning process on unseen tasks. As a data-driven approach, meta-learning requires meta-features that represent the primary learning tasks or datasets, and are estimated traditonally as engineered dataset statistics that require expert domain knowledge tailored for every meta-task. In this paper, first, we propose a meta-feature extractor called Dataset2Vec that combines the versatility of engineered dataset meta-features with the expressivity of meta-features learned by deep neural networks. Primary learning tasks or datasets are represented as hierarchical sets, i.e., as a set of sets, esp. as a set of predictor/target pairs, and then a DeepSet architecture is employed to regress meta-features on them. Second, we propose a novel auxiliary meta-learning task with abundant data called dataset similarity learning that aims to predict if two batches stem from the same dataset or different ones. In an experiment on a large-scale hyperparameter optimization task for 120 UCI datasets with varying schemas as a meta-learning task, we show that the meta-features of Dataset2Vec outperform the expert engineered meta-features and thus demonstrate the usefulness of learned meta-features for datasets with varying schemas for the first time.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Meta-learning, or learning to learn, refers to any learning approach that systematically makes use of prior learning experiences to accelerate training on unseen tasks or datasets (Vanschoren 2018). For example, after having chosen hyperparameters for dozens of different learning tasks, one would like to learn how to choose them for the next task at hand. Hyperparameter optimization across different datasets is a typical meta-learning task that has shown great success lately (Bardenet et al. 2013; Wistuba et al. 2018; Yogatama and Mann 2014). Domain adaptation and learning to optimize are other such meta-tasks of interest (Finn et al. 2017; Rusu et al. 2018; Finn et al. 2018).
As a data-driven approach, meta-learning requires meta-features that represent the primary learning tasks or datasets to transfer knowledge across them. Traditionally, simple, easy to compute, engineered (Edwards and Storkey 2017a) meta-features, such as the number of instances, the number of predictors, the number of targets (Bardenet et al. 2013), etc., have been employed. More recently, unsupervised methods based on variational autoencoders (Edwards and Storkey 2017b) have been successful in learning such meta-features. However, both approaches suffer from complementary weaknesses. Engineered meta-features often require expert domain knowledge and must be adjusted for each task, hence have limited expressivity. On the other hand, meta-feature extractors modeled as autoencoders can only compute meta-features for datasets having the same schema, i.e. the same number, type, and semantics of predictors and targets.
Thus to be useful, meta-feature extractors should meet the following four desiderata:
D1. Schema Agnosticism The meta-feature extractor should be able to extract meta-features for a population of meta-tasks with varying schema, e.g., datasets containing different predictor and target variables, also having a different number of predictors and targets.
D2. Expressivity The meta-feature extractor should be able to extract meta-features for meta-tasks of varying complexity, i.e., just a handful of meta-features for simple meta-tasks, but hundreds of meta-features for more complex tasks.
D3. Scalability The meta-feature extractor should be able to extract meta-features fast, e.g., it should not require itself some sort of training on new meta-tasks.
D4. Correlation The meta-features extracted by the meta-feature extractor should correlate well with the meta-targets, i.e., improve the performance on meta-tasks such as hyperparameter optimization.
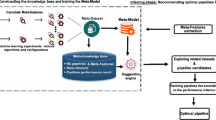
In this paper, we formalize the problem of meta-feature learning as a step that can be shared between all kinds of meta-tasks and asks for meta-feature extractors that combine the versatility of engineered meta-features with the expressivity obtained by learned models such as neural networks, to transfer meta-knowledge across (tabular) datasets with varying schemas (Sect. 3).
First, we design a novel meta-feature extractor called Dataset2Vec, that learns meta-features from (tabular) datasets of a varying number of instances, predictors, or targets. Dataset2Vec makes use of representing primary learning tasks or datasets as hierarchical sets, i.e., as a set of sets, specifically as a set of predictor/target pairs, and then uses a DeepSet architecture (Zaheer et al. 2017) to regress meta-features on them (Sect. 4).
As meta-tasks often have only a limited size of some hundred or thousand observations, it turns out to be difficult to learn an expressive meta-feature extractor solely end-to-end on a single meta-task at hand. We, therefore, second, propose a novel meta-task called dataset similarity learning that has abundant data and can be used as an auxiliary meta-task to learn the meta-feature extractor. The meta-task consists of deciding if two subsets of datasets, where instances, predictors, and targets have been subsampled, so-called multi-fidelity subsets (Falkner et al. 2018), belong to the same dataset or not. Each subset is considered an approximation of the entire dataset that varies in degree of fidelity depending on the size of the subset. In other words, we assume a dataset is similar to a variant of itself with fewer instances, predictors, or targets (Sect. 5).
Finally, we experimentally demonstrate the usefulness of the meta-feature extractor Dataset2Vec by the correlation of the extracted meta-features with meta-targets of interesting meta-tasks (D4). Here, we choose hyperparameter optimization as the meta-task (Sect. 6).
A way more simple, unsupervised plausibility argument for the usefulness of the extracted meta-features is depicted in Fig. 1 showing a 2D embedding of the meta-features of 2000 synthetic classification toy datasets of three different types (circles/moon/blobs) computed by (a) two sets of engineered dataset meta-features: MF1 (Wistuba et al. 2016) and MF2 (Feurer et al. 2015) (see Table 3); (b) a state-of-the-art model based on variational autoencoders, the Neural Statistician (Edwards and Storkey 2017b), and (c) the proposed meta-feature extractor Dataset2Vec. For the 2D embedding, multi-dimensional scaling has been applied (Borg and Groenen 2003) on these meta-features. As can be clearly seen, the meta-features extracted by Dataset2Vec allow us to separate the three different dataset types way better than the other two methods (see Sect. 6.3 for further details).
Meta-features of 2000 toy datasets extracted by (from left to right) engineered dataset meta-features MF1 (Wistuba et al. 2016), MF2 (Feurer et al. 2015), a state-of-the-art model based on variational autoencoders, the Neural Statistician (Edwards and Storkey 2017b), and the proposed meta-feature extractor Dataset2Vec. The methods compute 22, 46, 64, and 64 meta-features respectively. Depicted is their 2D embedding using multi-dimensional scaling. (Best viewed in color)
To sum up, in this paper we make the following key contributions:
-
1.
We formulate a new problem setting, meta-feature learning for datasets with varying schemas.
-
2.
We design and investigate a meta-feature extractor, Dataset2Vec, based on a representation of datasets as hierarchical sets of predictor/target pairs.
-
3.
We design a novel meta-task called dataset similarity learning that has abundant data and is therefore well-suited as an auxiliary meta-task to train the meta-feature extractor Dataset2Vec.
-
4.
We show experimentally that using the meta-features extracted through Dataset2Vec for the hyperparameter optimization meta-task outperforms the use of engineered meta-features specifically designed for this meta-task.
2 Related work
In this section, we attempt to summarize some of the topics that relate to our work and highlight where some of the requirements mentioned earlier are (not) met.
Meta-feature engineering Meta-features represent measurable properties of tasks or datasets and play an essential role in meta-learning. Engineered meta-features can be represented as simple statistics (Reif et al. 2014; Segrera et al. 2008) or even as model-specific parameters with which a dataset is trained (Filchenkov and Pendryak 2015) and are generally applicable to any dataset, schema-agnostic D1. In addition to that, the nature of these meta-features makes them scalable (D3), and thus can be extracted without extra training. For example, the mean of the predictors can be estimated regardless of the number of targets. However, coupling these meta-features with a meta-task is a tedious process of trial-and-error, and must be repeated for every meta-task to find expressive (D2) meta-features with good correlation (D4) to the meta-target.
Meta-feature learning, as a standalone task, i.e. agnostic to a pre-defined meta-task, to the best of our knowledge, is a new concept, with existing solutions bound by a fixed dataset schema. Autoencoder based meta-feature extractors such as the neural statistician (NS) (Edwards and Storkey 2017b) and its variant (Hewitt et al. 2018) propose an extension to the conventional variational autoencoder (Kingma and Welling 2014), such that the item to be encoded is the dataset itself. Nevertheless, these techniques require vast amounts (Edwards and Storkey 2017b) of data and are limited to datasets with similar schema, i.e. not schema-agnostic (D2).
Embedding and metric learning approaches aim at learning semantic distance measures that position similar high-dimensional observations within proximity to each other on a manifold, i.e. the meta-feature space. By transforming the data into embeddings, simple models can be trained to achieve significant performance (Snell et al. 2017; Berlemont et al. 2018). Learning these embeddings involves optimizing a distance metric (Song et al. 2016) and making sure that local feature similarities are observed (Zheng et al. 2018). This leads to more expressive (D2) meta-features that allow for better distinction between observations.
Meta-Learning is the process of learning new tasks by carrying over findings from previous tasks based on defined similarities between existing meta-data. Meta-learning has witnessed great success in domain adaptation, learning scalable internal representations of a model by quickly adapting to new tasks (Finn et al. 2017, 2018; Yoon et al. 2018). Existing approaches learn generic initial model parameters through sampling tasks from a task-distribution with an associated train/validation dataset. Even within this line of research, we notice that learning meta-features helps achieve state-of-the-art performances (Rusu et al. 2018), but do not generalize beyond dataset schema (Achille et al. 2019; Koch et al. 2015). However, potential improvements have been shown with schema-agnostic model initialization (Brinkmeyer et al. 2019). Nevertheless, existing meta-learning approaches result in task-dependent meta-features, and hence the meta-features only correlate (D4) with the respective meta-task.
We notice that none of the existing approaches that involve meta-features fulfills the complete list of desiderata. As a proposed solution, we present a novel meta-feature extractor, Dataset2Vec, that learns to extract expressive (D2) meta-features directly from the dataset. Dataset2Vec, in contrast to the existing work, is schema-agnostic (D1) that does not need to be adjusted for datasets with different schema. We optimize Dataset2Vec by a novel dataset similarity learning approach, that learns expressive (D3) meta-features that maintain inter-dataset and intra-dataset distances depending on the degree of dataset similarities. Finally, we demonstrate the correlation (D4) between the meta-features and unseen meta-tasks, namely hyperparameter optimization, as compared to engineered meta-features.
3 Problem setting: meta-feature learning
A (supervised) learning task is usually understood as a problem to find a function (model) that maps given predictor values to likely target values based on past observations of predictors and associated target values (dataset). Many learning tasks depend on further inputs besides the dataset, e.g., hyperparameters like the depth and width of a neural network model, a regularization weight, a specific way to initialize the parameters of a model, etc. These additional inputs of a learning task often are found heuristically, e.g., hyperparameters can be found by systematic grid or by random search (Bergstra and Bengio 2012), model parameters can be initialized by random normal samples, etc. From a machine learning perspective, finding these additional inputs of a learning task can itself be described as a learning task: its inputs are a whole dataset, its output is a hyperparameter vector or an initial model parameter vector. To differentiate these two learning tasks we call the first task, to learn a model from a dataset, the primary learning task, and the second, to find good hyperparameters or a good model initialization, the meta-learning task. Meta-learning tasks are very special learning tasks as their inputs are not simple vectors like in traditional classification and regression tasks, nor sequences or images like in time-series or image classification, but themselves whole datasets.
To leverage standard vector-based machine learning models for such meta-learning tasks, their inputs, a whole dataset, must be described by a vector. Traditionally, this vector is engineered by experts and contains simple statistics such as the number of instances, the number of predictors, the number of targets, the mean and variance of the mean of the predictors, etc. These vectors that describe whole datasets and that are the inputs of the meta-task are called meta-features. The meta-features together with the meta-targets, i.e. good hyperparameter values or good model parameter initializations for a dataset, form the meta-dataset.
More formally, let \({\mathcal {D}}\) be the space of all possible datasets,
i.e. a data matrix containing a row for each instance and a column for each predictor and target together with the number M of predictors (just to mark which columns are predictors, which targets). For simplicity of notation, for a dataset \(D\in {\mathcal {D}}\) we will denote by \(N^{(D)}, M^{(D)}\) and \(T^{(D)}\) its number of instances, predictors and targets and by \(X^{(D)}, Y^{(D)}\) its predictor and target matrices (see Table 1). Now a meta-task is a learning task that aims to find a meta-model \(\hat{{y}}^{\text {meta}}: {\mathcal {D}} \rightarrow {\mathbb R}^{T^{\text {meta}}}\), e.g., for hyperparameter learning of three hyperparameters depth and width of a neural network and regularization weight, to find good values for each given dataset (hence here \(T^{\text {meta}}=3\)), or for model parameter initialization for a neural network with 1 million parameters, to find good such initial values (here \(T^{\text {meta}}=1,000,000\)).
Most meta-models \(\hat{{y}}^{\text {meta}}\) are the composition of two functions:
-
(i)
the meta-feature extractor \(\hat{\phi }: {\mathcal {D}}\rightarrow \mathbb {R}^K\), that extracts from a dataset a fixed number K of meta-features, and
-
(ii)
a meta-feature based meta-model \(\hat{{Y}}^{\text {meta}}: \mathbb {R}^K \rightarrow \mathbb {R}^{T^{\text {meta}}}\) that predicts the meta-targets based on the meta-features and can be a standard vector-based regression model chosen for the meta-task at hand, e.g., a neural network.
Their composition yields the meta-model \(\hat{{y}}^{\text {meta}}\):
Let \(a^{\text {meta}}\) denote the learning algorithm for the meta-feature based meta-model, i.e. stochastic gradient descent to learn a neural network that predicts good hyperparameter values based on dataset meta-features.
The Meta-feature learning problem then is as follows: given i) a meta-dataset \(({\mathcal {D}}^{\text {meta}}\),\({{\,\mathrm{\mathcal {Y}}\,}}^{\text {meta}})\) of pairs of (primary) datasets D and their meta-targets \(y^{\text {meta}}\), ii) a meta-loss \(\ell ^{\text {meta}}: {{\,\mathrm{\mathcal {Y}}\,}}^{\text {meta}}\times {{\,\mathrm{\mathcal {Y}}\,}}^{\text {meta}}\rightarrow {\mathbb R}\) where \(\ell ^{\text {meta}}(y^{\text {meta}},\hat{{y}}^{\text {meta}})\) measures how bad the predicted meta-target \(\hat{{y}}^{\text {meta}}\) is for the true meta-target \(y^{\text {meta}}\), and iii) a learning algorithm \(a^{\text {meta}}\) for a meta-feature based meta-model (based on \(K\in {\mathbb N}\) meta-features), find a meta-feature extractor \(\hat{\phi }: {\mathcal {D}}\rightarrow {\mathbb R}^K\) s.t. the expected meta-loss of the meta-model learned by \(a^{\text {meta}}\) from the meta-features extracted by \(\hat{\phi }\) over new meta-instances is minimal:
such that:
Different from standard regression problems where the loss is a simple distance between true and predicted targets such as the squared error, the meta-loss is more complex as its computation involves a primary model being learned and evaluated for the primary learning task. For hyperparameter optimization, if the best depth and width of a neural network for a specific task is 10 and 50, it is not very meaningful to measure the squared error distance to a predicted depth and width of say 5 and 20. Instead one is interested in the difference of primary test losses of primary models learned with these hyperparameters. So, more formally again, let \(\ell \) be the primary loss, say squared error for a regression problem, and a be a learning algorithm for the primary model, then
4 The meta-feature extractor Dataset2Vec
To define a learnable meta-feature extractor \(\hat{\phi }: {\mathcal {D}}\rightarrow \mathbb {R}^K\), we will employ the Kolmogorov-Arnold representation theorem (Kuurkova 1991) and use the DeepSet architecture (Zaheer et al. 2017).
4.1 Preliminaries
The Kolmogorov-Arnold representation theorem (Kuurkova 1991) states that any multivariate function \(\phi \) of M-variables \(X_1,\dots ,X_M\) can be represented as an aggregation of univariate functions (Kuurkova 1991), as follows:
The ability to express a multivariate function \(\phi \) as an aggregation h of single variable functions g is a powerful representation in the case where the function \(\phi \) needs to be invariant to the permutation order of the inputs X. In other words, \(\phi \left( X_1,\dots ,X_M\right) = \phi \left( X_{\pi (1)},\dots ,X_{\pi (M)}\right) \) for any index permutation \(\pi (k)\), where \(k \in \{1,\dots , M\}\). To illustrate the point further with \(M=2\), we would like a function \(\phi (X_1, X_2)=\phi \left( X_2,X_1\right) \) to achieve the same output if the order of the inputs \(X_1, X_2\) is swapped. In a multi-layer perceptron, the output changes depending on the order of the input, as long as the values of the input variables are different. The same behavior is observed with recurrent neural networks and convolutional neural networks.
However, permutation invariant representations are crucial if functions are defined on sets, for instance if we would like to train a neural network to output the sum of a set of digit images. Set-wise neural networks have recently gained prominence as the Deep-Set formulation (Zaheer et al. 2017), where the \(2M+1\) functions h of the original Kolmogorov-Arnold representation is simplified with a single large capacity neural network \(h \in {\mathbb R}^K \rightarrow {\mathbb R}\), and the M-many univariate functions g are modeled with a shared cross-variate neural network function \(g \in {\mathbb R}\rightarrow {\mathbb R}^K\):
Permutation-invariant functional representation is highly relevant for deriving meta-features from tabular datasets, especially since we do not want the order in which the predictors of an instance are presented to affect the extracted meta-features.
4.2 Hierarchical set modeling of datasets
In this paper, we design a novel meta-feature extractor called Dataset2Vec for tabular datasets as a hierarchical set model. Tabular datasets are two-dimensional matrices of \((\#\text {rows} \times \#\text {columns})\), where the columns represent the predictors and the target variables and the rows consist of instances. As can be trivially understood, the order/permutation of the columns is not relevant to the semantics of a tabular dataset, while the rows are also permutation invariant due to the identical and independent distribution principle. In that perspective, a tabular dataset is a set of columns (predictors and target variables), where each column is a set of row values (instances):
-
\(\square \) A dataset is a set of \(M^{\left( D\right) }+T^{\left( D\right) }\) predictor and target variables:
-
\(\square D = \left\{ X^{\left( D\right) }_1, \dots , X^{\left( D\right) }_{M^{\left( D\right) }},Y^{\left( D\right) }_1, \dots , Y^{\left( D\right) }_{T^{\left( D\right) }}\right\} \)
-
\(\square \) Where each variable is a set of \(N^{\left( D\right) }\) instances:
-
\(\square X^{\left( D\right) }_m = \left\{ X^{\left( D\right) }_{1,m}, \dots , X^{\left( D\right) }_{N^{\left( D\right) },m}\right\} \), \(m=1,\dots ,M^{\left( D\right) }\)
-
\(\square Y^{\left( D\right) }_t = \left\{ Y^{\left( D\right) }_{1,t}, \dots , Y^{\left( D\right) }_{N^{\left( D\right) },t}\right\} \), \(t=1,\dots ,T^{\left( D\right) }\)
In other words, a dataset is a set of sets. Based on this novel conceptualization we propose to model a dataset as a hierarchical set of two layers. More formally, let us restate that \(\left( X^{\left( D\right) },Y^{\left( D\right) }\right) = D\in {\mathcal {D}}\) is a dataset, where \(X^{\left( D\right) }\in {\mathbb R}^{N^{\left( D\right) }\times M^{\left( D\right) }}\) with \(M^{\left( D\right) }\) represents the number of predictors and \(N^{\left( D\right) }\) the number of instances, and \(Y^{\left( D\right) }\in {\mathbb R}^{N^{\left( D\right) }\times T^{\left( D\right) }}\) with \(T^{\left( D\right) }\) as the number of targets. We model our meta-feature extractor, Dataset2Vec, without loss of generality, as a feed-forward neural network, which accommodates all schemas of datasets. Formally, Dataset2Vec is defined in Equation 4:
with \(f: {\mathbb R}^2\rightarrow {\mathbb R}^{K_f}\), \(g: {\mathbb R}^{K_f}\rightarrow {\mathbb R}^{K_g}\) and \(h: {\mathbb R}^{K_g}\rightarrow {\mathbb R}^{K}\) represented by neural networks with \(K_f\), \(K_g\) and K output units, respectively. Notice that the best way to design a scalable meta-feature extractor is by reducing the input to a single predictor-target pair \(\left( X^{\left( D\right) }_{n,m}, Y^{\left( D\right) }_{n,t}\right) \). This is especially important to capture the underlying correlation between each predictor/target variable. Each function is designed to model a different aspect of the dataset, instances, predictors, and targets. Function f captures the interdependency between an instance feature \(X^{\left( D\right) }_{n,m}\) and the corresponding instance target \(Y^{\left( D\right) }_{n,t}\) followed a pooling layer across all instances \(n\in N^{\left( D\right) }\). Function g extends the model across all targets \(t\in T^{\left( D\right) }\) and predictors \(m\in M^{\left( D\right) }\). Finally, function h applies a transformation to the average of latent representation collapsed over predictors and targets, resulting in the meta-features. Figure 2 depicts the architecture of Dataset2Vec.
Overview of the Dataset2Vec as described in Sect. 4.2
4.3 Network architecture
Our Dataset2Vec architecture is divided into three modules, \(\hat{\phi }{:}{=} f\circ g\circ h\), each implemented as neural network. Let Dense(n) define one fully connected layer with n neurons, and ResidualBlock(n,m) be \(m\times \) Dense(n) with residual connections (Zagoruyko and Komodakis 2016). We present two architectures in Table 2, one for the toy meta-dataset, Sect. 6.1, and a deeper one for the tabular meta-dataset, Sect. 6.2. All layers have Rectified Linear Unit activations (ReLUs). Our reference implementation uses Tensorflow (Abadi et al. 2016).
5 The auxiliary meta-task: dataset similarity learning
Ideally, we can train the composition \(\hat{M}\circ \hat{\phi }\) of meta-feature extractor \(\hat{\phi }\) and meta-feature based meta-model \(\hat{M}\) end-to-end. But most meta-learning datasets are small, rarely containing more than a couple of thousands or 10,000s of meta-instances, as each such meta-instance itself requires an independent primary learning process. Thus training a meta-feature extractor end-to-end directly, is prone to overfitting. Therefore, we propose to employ additionally an auxiliary meta-task with abundant data to extract meaningful meta-features.
5.1 The auxiliary problem
Dataset similarity learning is the following novel, yet simple meta-task: given a pair of datasets and an assigned dataset similarity indicator \((x,x',i)\in {\mathcal {D}^{\text {meta}}}\times {\mathcal{{D}}^{\text {meta}}}\times \{0,1\}\) from a joint distribution p over datasets, learn a dataset similarity learning model \(\hat{i}: {\mathcal {D}^{\text {meta}}}\times {\mathcal {D}^{\text {meta}}}\rightarrow \{0,1\}\) with minimal expected misclassification error
where \(I(\text {true}){:}{=}1\) and \(I(\text {false}){:}{=}0\).
As mentioned previously, learning meta-features from datasets \(D\in {\mathcal {D}^{\text {meta}}}\) directly is impractical and does not scale well to larger datasets, especially due to the lack of an explicit dataset similarity label. To overcome this limitation, we create implicitly similar datasets in the form of multi-fidelity subsets of the datasets, batches, and assign them a dataset similarity label \(i{:}{=}1\), whereas variants of different datasets are assigned a dataset similarity label \(i{:}{=}0\). Hence, we define the multi-fidelity subsets for any specific dataset D as the submatrices pair \((X',Y')\), Equation 6:
with \(N'\subseteq \{1,\ldots ,N^{\left( D\right) }\}\), \(M'\subseteq \{1,\ldots ,M^{\left( D\right) }\}\), and \(T'\subseteq \{1,\ldots ,T^{\left( D\right) }\}\) representing the subset of indices of instances, features, and targets, respectively, sampled from the whole dataset.
The batch sampler, Algorithm 1, returns a batch with random index subsets \(N'\),\(M'\) and \(T'\) drawn uniformly from \(\{2^q | q \in [4,8]\}, [1,M]\) and [1, T], without replacement. Figure 3 is a pictorial representation of two randomly sampled batches from a tabular dataset.

Meta-features of a dataset D can then be computed either directly over the dataset as a whole, \(\hat{\phi }(D)\), or estimated as the average of several random batches, Equation 7:
where B represents the number of random batches.
Let p be any distribution on pairs of dataset batches and i a binary value indicating if both subsets are similar, then given a distribution of data sets \(p_{\mathcal {D}^{\text {meta}}}\), we sample multi-fidelity subset pairs for the dataset similarity learning problem using Algorithm 2.

5.2 The auxiliary meta model and training
To force all information relevant for the dataset similarity learning task to be pooled in the meta-feature space, we use a probabilistic dataset similarity learning model, Equation 8:
with \(\gamma \) as a tuneable hyperparameter. We define pairs of similar batches as \(P=\{(x,x',i) \sim p{}|{}i = 1\}\) and pairs of dissimilar batches \(W=\{(x,x',i) \sim p{}|{}i = 0\}\), and formulate the optimization objective as:
Similar to any meta-learning task, we split the meta-dataset, into \({\mathcal {D}^{\text {meta}}}_{train}\), \({\mathcal {D}^{\text {meta}}}_{valid}\) and \({\mathcal {D}^{\text {meta}}}_{test}\) which include non-overlapping datasets for training, validation and test respectively. While training the dataset similarity learning task, all the latent information are captured in the final layer of Dataset2Vec, our meta-feature extractor, resulting in task-agnostic meta-features. The pairwise loss between batches allows to preserves the intra-dataset similarity, i.e. close proximity of meta-features of similar batches, as well as inter-dataset similarity, i.e. distant meta-features of dissimilar batches.
Dataset2Vec is trained on a large number of batch samples from datasets in a meta-dataset, thus currently does not use any information of the subsequent meta-problem to solve and hence is generic, in this sense unsupervised meta-feature extractor. Any other meta-task could be easily integrated into Dataset2Vec by just learning them jointly in a multi-task setting, especially for dataset reconstruction similar to the dataset reconstruction of the NS (Edwards and Storkey 2017b) could be interesting if one could figure out how to do this across different schemata. We leave this aspect for future work.
6 Experiments
We claim that for a meta-feature extractor to produce useful meta-features it must meet the following requirements: schema-agnostic (D1), expressive (D2), scalable (D3), and correlates to meta-tasks (D4). We train and evaluate Dataset2Vec in support of these claims by designing the following two experiments. Accordingly, we highlight where the criterion is met throughout the section. Implementation can be found here.Footnote 1
6.1 Dataset similarity learning for datasets of similar schema
Dataset similarity learning is designed as an auxiliary meta-task that allows Dataset2Vec to capture all the required information in the meta-feature space to distinguish between datasets. We learn to extract expressive meta-features by minimizing the distance between meta-features of subsets from similar datasets and maximizing the distance between the meta-features of subsets from different datasets. We stratify the sampling during training to avoid class imbalance. The reported results represent the average of a 5-fold cross-validation experiment, i.e. the reported meta-features are extracted from the datasets in the meta-test set to illustrate the scalability (D3) of Dataset2Vec to unseen datasets.
6.1.1 Baselines
We compare with the neural statistician algorithm, NS (Edwards and Storkey 2017b), a meta-feature extractor that learns meta-features as context information by encoding complete datasets with an extended variational autoencoder. We focus on this technique particularly since the algorithm is trained in an unsupervised manner, with no meta-task coupled to the extractor. However, since it is bound by a fixed dataset schema, we generate a 2D labeled synthetic (toy) dataset, to fairly train the spatial model presented by the authors.Footnote 2 We use the same hyperparameters used by the authors. We also compare with two sets of well-established engineered meta-features: MF1 (Wistuba et al. 2016) and MF2 (Feurer et al. 2015). A brief overview of the meta-features provided by these sets is presented in Table 3. For detailed information about meta-features, we refer the readers to (Edwards and Storkey 2017a).
6.1.2 Evaluation metric
We evaluate the similarity between embeddings through pairwise classification accuracy with a cut-off threshold of \(\frac{1}{2}\). We set the hyperparameter \(\gamma \) in Equation 8 to 1,0.1, and 0.1 for MF1, MF2, and NS, respectively, after tuning it on a separate validation set, and keep \(\gamma = 1\) for Dataset2Vec. We evaluate the pairwise classification accuracy over 16,000 pairs of batches containing an equal number of positive and negative pairs. The results are a summary of 5-fold cross validation, during which the test datasets are not observed in the training process.
6.1.3 Toy meta dataset
We generate a collection of 10,000 2D datasets each containing a varying number of samples. The datasets are created using the sklearn library (Pedregosa et al. 2011) and belong to either circles or moons with 2 classes (default), or blobs with varying number of classes drawn uniformly at random within the bounds (2, 8). We also perturb the data by applying random noise. The toy meta-dataset is obtained by Algorithm 3. An example of the resulting datasets is depicted, for clarity, in Fig. 4.

We randomly sample a fixed-size subset of 200 samples from every dataset for both approaches, adhering to the same conditions in NS to ensure a fair comparison, and train both networks until convergence. We also extract the engineered meta-features from these subsets. The pairwise classification accuracy is summarized in Table 4. We conducted a T-test to validate the distinction between the performance of Dataset2Vec and MF1, the second-best performing approach. The test is a standard procedure to compare the statistical difference of methods which are run once over multiple datasets (Demšar 2006). Dataset2Vec has a statistical significance p-value of \(3.25\times 10^{-11}\), hence significantly better than MF1, following a 2-tailed hypothesis with a significance level of 5% (standard test setting). Dataset2Vec, compared to NS, has \(45\times \) fewer parameters in addition to learning more expressive meta-features.
The expressivity (D2) of Dataset2Vec is realized in Fig. 5 which depicts a 2D projection of the learned meta-features, as we observe collections of similar datasets with co-located meta-features in the space, and meta-features of different datasets are distant.
The figure illustrates the 2D projections based on multi-dimensional scaling (Borg and Groenen 2003) of our learned meta-features for three distinct folds. Each point in the figure represents a single dataset that is either a blob, a moon, or a circle, generated synthetically with different parameters selected from the test set of each fold, i.e. never seen by our model during training. The depiction highlights that Dataset2Vec is capable of generating meta-features from unseen datasets while preserving inter-and intra-dataset similarity. This is demonstrated by the co-location of the meta-features of similar datasets, circles near circles, etc. in this 2D space. (Best viewed in color)
Intuitively, it is also easy to understand how the datasets of circles and moons, might be more similar compared to blobs, as seen by the projections in Fig. 5. This might be largely attributed to the large distance between instances of dissimilar classes in the blob datasets, whereas instances of dissimilar classes in the moon and the circle datasets are closer, Fig. 4.
6.2 Dataset similarity learning for datasets of different schema
For a given machine learning problem, say binary classification, it is unimaginable that one can find a large enough collection of similar and dissimilar datasets with the same schema. The schema presents an obstacle that hinders the potential of learning useful meta-tasks. Dataset2Vec is schema-agnostic (D1) by design.
6.2.1 UCI meta dataset
The UCI repository (Dua and Graff 2017) contains a vast collection of datasets. We used 120 preprocessed classification datasetsFootnote 3 with a varying schema to train the meta-feature extractor by randomly sampling pairs of subsets, Algorithm 2, along with the number of instances, predictors, and targets. Other sources of tabular datasets are indeed available (Vanschoren et al. 2014), nevertheless, they suffer from quality issues (missing values, require pre-processing, etc.), which is why we focus on pre-processed and normalized UCI classification datasets.
We achieve a pairwise classification accuracy of 88.20% ± 1.67, where the model has 45424 parameters. In Table 5, we show five randomly selected groups of datasets that have been collected by a 5-Nearest Neighbor method based on the Dataset2Vec meta-features. We rely on the semantic similarity, i.e. similarity of the names, of the UCI datasets to showcase neighboring datasets in the meta-feature space due to the lack of an explicit dataset similarity annotation measure for tabular datasets. For this meta-dataset, NS could not be applied due to the varying dataset schema.
6.3 Hyperparameter optimization
Hyperparameter optimization plays an important role in the machine learning community and can be the main factor in deciding whether a trained model performs at the state-of-the-art or simply moderate. The use of meta-features for this task has led to a significant improvement especially when used for warm-start initialization, the process of selecting initial hyperparameter configurations to fit a surrogate model based on the similarity between the target dataset and other available datasets, of Bayesian optimization techniques based on Gaussian processes (Wistuba et al. 2015; Lindauer and Hutter 2018) or on neural networks (Perrone et al. 2018). Surrogate transfer in sequential model-based optimization (Jones et al. 1998) is also improved with the use of meta-features as seen in the state-of-the-art (Wistuba et al. 2018) and similar approaches (Wistuba et al. 2016; Feurer et al. 2018). Unfortunately, existing meta-features, initially introduced to the hyperparameter optimization problem in (Bardenet et al. 2013), are engineered based on intuition and tuned through trial-and-error. We improve the state-of-the-art in warm-start initialization for hyperparameter optimization by replacing these engineered meta-features with our learned task-agnostic meta-features, proving further the capacity of the learned meta-features to correlate to unseen meta-tasks, (D4).
6.3.1 Baselines
The use of meta-features has led to significant performance improvement in hyperparameter optimization. We follow the warm-start initialization technique presented by Feurer et al. (2015), where we select the top-performing configurations of the most similar datasets to the target dataset to initialize the surrogate model. By simply replacing the engineered meta-features with the meta-features from Dataset2Vec, we can effectively evaluate the capacity of our learned meta-features. Meta-features employed for the initialization of hyperparameter optimization techniques include a battery of summaries calculated as measures from information theory (Castiello et al. 2005), general dataset features and statistical properties (Reif et al. 2014) which require completely labeled data. A brief overview of some of the meta-features used for warm-start initialization is summarized in Table 3. NS is not applicable in this scenario considering that hyperparameter optimization is done across datasets with different schema.
-
1.
Random search (Bergstra and Bengio 2012): As the name suggests, random search simply selects random configurations at every trial, and has proved to outperform conventional grid-search methods.
-
2.
Tree Parzen Estimator (TPE) (Bergstra et al. 2011), A tree-based approach that constructs a density estimate over good and bad instantiations of each hyperparameter.
-
3.
GP (Rasmussen 2003): The surrogate is modeled by a Gaussian process with a Matérn 3/2 kernel
-
4.
SMAC (Hutter et al. 2011): Instead of a Gaussian process, the surrogate is modeled as a random-forest (Breiman 2001) that yields uncertainty estimates.Footnote 4
-
5.
Bohamiann (Springenberg et al. 2016): This approach relies on Bayesian Neural Networks to model the surrogate.
On their own, the proposed baselines do not carry over information across datasets. However, by selecting the best performing configurations of the most similar datasets, we can leverage the meta-knowledge for better initialization.
6.3.2 Evaluation metrics
We follow the evaluation metrics of (Wistuba et al. 2016), particularly, the average distance to the minimum (ADTM). After t trials, ADTM is defined as
with \(\Lambda _t^D\) as the set of hyperparameters that have been selected by a hyperparameter optimization method for data set \(D {:}{=} \in \mathcal {D}\) in the first t trials and \(y(D)^{\min }\), \(y(D)^{\max }\) the range of the loss function on the hyperparameter grid \(\Lambda \) under investigation.
6.3.3 UCI surrogate dataset
To expedite hyperparameter optimization, it is essential to have a surrogate dataset where different hyperparameter configurations are evaluated beforehand. We create the surrogate dataset by training feed-forward neural networks with different configurations on 120 UCI classification datasets. As part of the neural network architecture, we define four layouts: \(\square \) layout, the number of hidden neurons is fixed across all layers; \(\lhd \) layout, the number of neurons in a layer is twice that of the previous layer; \(\rhd \) layout, the number of neurons is half of the previous layer, \(\diamond \) layout, the number of neurons per layer doubles per layer until the middle layer than is halved successively. We also use dropout (Srivastava et al. 2014) and batch normalization (Ioffe and Szegedy 2015) as regularization strategies, and stochastic gradient descent (SGD) (Bottou 2010), ADAM (Kingma and Ba 2015) and RMSProp (Tieleman and Hinton 2012) as optimizers. SeLU (Klambauer et al. 2017) represents the self-normalizing activation unit. We present the complete grid of configurations in Table 6, which results in 3456 configurations per dataset.
6.3.4 Results and discussion
The results depicted in Fig. 6 are estimated using a leave-one-dataset-out cross-validation over the 5 splits of 120 datasets. We notice primarily the importance of meta-features for warm-start initialization, as using meta-knowledge results in outperforming the rest of the randomly initialized algorithms. By investigating the performance of the three initialization variants, we realize that with SMAC and Bohamiann, our learned meta-features consistently outperform the baselines with engineered meta-features. With GP, on the other hand, the use of our meta-features demonstrates an early advantage and better final performance. The reported results demonstrate that our learned meta-features, which are originally uncoupled from the meta-task of hyperparameter optimization prove useful and competitive, i.e. correlate (D4) to the meta-task. It is also worth mentioning that the learned meta-features, do not require access to the whole labeled datasets, making it more generalizable, Eq. 7.
7 Conclusion
We present a novel hierarchical set model for meta-feature learning based on the Kolmogorov-Arnold representation theorem, named Dataset2Vec. We parameterize the model as a feed-forward neural network that accommodates tabular datasets of a varying schema. To learn these meta-features, we design a novel dataset similarity learning task that enforces the proximity of meta-features extracted from similar datasets and increases the distance between meta-features extracted from dissimilar datasets. The learned meta-features can easily be used with unseen meta-tasks, e.g. the same meta-features can be used for hyper-parameter optimization and few-shot learning, which we leave for future work. It seems likely, that meta-features learned jointly with the meta-task at hand will turn out to focus on the characteristics relevant for the particular meta-task and thus provide even better meta-losses, a direction of further research worth investigating.
References
Abadi M, Barham P, Chen J, Chen Z, Davis A, Dean J, Devin M, Ghemawat S, Irving G, Isard M, Kudlur M, Levenberg J, Monga R, Moore S, Murray DG, Steiner B, Tucker PA, Vasudevan V, Warden P, Wicke M, Yu Y, Zheng X (2016) Tensorflow: a system for large-scale machine learning. OSDI, USENIX Association, Berkeley, pp 265–283
Achille A et al. (2019) Task2vec: Task embedding for meta-learning. In: Proceedings of the IEEE/CVF International Conference on Computer Vision, 2019
Bardenet R, Brendel M, Kégl B, Sebag M (2013) Collaborative hyperparameter tuning. In: International conference on machine learning, pp 199–207
Bergstra J, Bengio Y (2012) Random search for hyper-parameter optimization. J Mach Learn Res 13:281–305
Bergstra JS, Bardenet R, Bengio Y, Kégl B (2011) Algorithms for hyper-parameter optimization. In: Advances in neural information processing systems, pp 2546–2554
Berlemont S, Lefebvre G, Duffner S, Garcia C (2018) Class-balanced siamese neural networks. Neurocomputing 273:47–56
Borg I, Groenen P (2003) Modern multidimensional scaling: theory and applications. J Educ Meas 40(3):277–280
Bottou L (2010) Large-scale machine learning with stochastic gradient descent. In: Proceedings of COMPSTAT’2010. Springer, pp 177–186
Breiman L (2001) Random forests. Mach Learn 45(1):5–32
Brinkmeyer L, Drumond RR, Scholz R, Grabocka J, Schmidt-Thieme L (2019) Chameleon: learning model initializations across tasks with different schemas. arXiv preprint arXiv:1909.13576
Castiello C, Castellano G, Fanelli AM (2005) Meta-data: characterization of input features for meta-learning. In: MDAI, Springer, Lecture notes in computer science, vol 3558, pp 457–468
Demšar J (2006) Statistical comparisons of classifiers over multiple data sets. J Mach Learn Res 7:1–30
Dua D, Graff C (2017) UCI machine learning repository. http://archive.ics.uci.edu/ml
Edwards H, Storkey AJ (2017a) Towards a neural statistician https://openreview.net/forum?id=HJDBUF5le
Edwards H, Storkey AJ (2017b) Towards a neural statistician. In: ICLR, OpenReview.net
Falkner S, Klein A, Hutter F (2018) BOHB: robust and efficient hyperparameter optimization at scale 80:1436–1445. http://proceedings.mlr.press/v80/falkner18a.html
Feurer M, Springenberg JT, Hutter F (2015) Initializing bayesian hyperparameter optimization via meta-learning. In: Bonet B, Koenig S (eds) Proceedings of the twenty-ninth AAAI conference on artificial intelligence, January 25–30, 2015, Austin, Texas, USA, AAAI Press, pp 1128–1135, http://www.aaai.org/ocs/index.php/AAAI/AAAI15/paper/view/10029
Feurer M, Letham B, Bakshy E (2018) Scalable meta-learning for bayesian optimization. CoRR arXiv:1802.02219
Filchenkov A, Pendryak A (2015) Datasets meta-feature description for recommending feature selection algorithm. In: 2015 Artificial intelligence and natural language and information extraction, social media and web search FRUCT conference (AINL-ISMW FRUCT), IEEE, pp 11–18
Finn C, Abbeel P, Levine S (2017) Model-agnostic meta-learning for fast adaptation of deep networks. In: Proceedings of the 34th international conference on machine learning-volume 70, JMLR.org, pp 1126–1135
Finn C, Xu K, Levine S (2018) Probabilistic model-agnostic meta-learning. In: NeurIPS, pp 9537–9548
Hewitt LB, Nye MI, Gane A, Jaakkola TS, Tenenbaum JB (2018) The variational homoencoder: learning to learn high capacity generative models from few examples. In: UAI. AUAI Press, pp 988–997
Hutter F, Hoos HH, Leyton-Brown K (2011) Sequential model-based optimization for general algorithm configuration. In: International conference on learning and intelligent optimization. Springer, pp 507–523
Ioffe S, Szegedy C (2015) Batch normalization: accelerating deep network training by reducing internal covariate shift. In: ICML, JMLR.org, JMLR workshop and conference proceedings, vol 37, pp 448–456
Jones DR, Schonlau M, Welch WJ (1998) Efficient global optimization of expensive black-box functions. J Global Optim 13(4):455–492
Kingma DP, Ba J (2015) Adam: A method for stochastic optimization. In: Bengio Y, LeCun Y (eds) 3rd International conference on learning representations, ICLR 2015, San Diego, CA, USA, May 7–9, 2015, conference track proceedings, arXiv:1412.6980
Kingma DP, Welling M (2014) Auto-encoding variational bayes. In: Bengio Y, LeCun Y (eds) 2nd International conference on learning representations, ICLR 2014, Banff, AB, Canada, April 14–16, 2014, conference track proceedings. arXiv:1312.6114
Klambauer G, Unterthiner T, Mayr A, Hochreiter S (2017) Self-normalizing neural networks. In: Advances in neural information processing systems, pp 971–980
Koch G, Zemel R, Salakhutdinov R (2015) Siamese neural networks for one-shot image recognition. In: ICML deep learning workshop, vol 2
Kuurkova V (1991) Kolmogorov’s theorem is relevant. Neural Comput 3(4):617–622
Lindauer M, Hutter F (2018) Warmstarting of model-based algorithm configuration. In: AAAI. AAAI Press, pp 1355–1362
Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, Vanderplas J, Passos A, Cournapeau D, Brucher M, Perrot M, Duchesnay E (2011) Scikit-learn: machine learning in python. J Mach Learn Res 12:2825–2830
Perrone V, Jenatton R, Seeger MW, Archambeau C (2018) Scalable hyperparameter transfer learning. In: NeurIPS, pp 6846–6856
Rasmussen CE (2003) Gaussian processes in machine learning. In: Summer school on machine learning. Springer, pp 63–71
Reif M, Shafait F, Goldstein M, Breuel TM, Dengel A (2014) Automatic classifier selection for non-experts. Pattern Anal Appl 17(1):83–96
Rusu AA, Rao D, Sygnowski J, Vinyals O, Pascanu R, Osindero S, Hadsell R (2018) Meta-learning with latent embedding optimization. CoRR abs/1807.05960
Segrera S, Lucas JP, García MNM (2008) Information-theoretic measures for meta-learning. In: HAIS, Springer, Lecture notes in computer science, vol 5271, pp 458–465
Snell J, Swersky K, Zemel R (2017) Prototypical networks for few-shot learning. In: Advances in neural information processing systems, pp 4077–4087
Song HO, Xiang Y, Jegelka S, Savarese S (2016) Deep metric learning via lifted structured feature embedding. In: CVPR, IEEE computer society, pp 4004–4012
Springenberg JT, Klein A, Falkner S, Hutter F (2016) Bayesian optimization with robust bayesian neural networks. In: Advances in neural information processing systems, pp 4134–4142
Srivastava N, Hinton GE, Krizhevsky A, Sutskever I, Salakhutdinov R (2014) Dropout: a simple way to prevent neural networks from overfitting. J Mach Learn Res 15(1):1929–1958
Tieleman T, Hinton G (2012) Lecture 6.5-rmsprop: divide the gradient by a running average of its recent magnitude. COURSERA Neural Netw Mach Learn 4(2):26–31
Vanschoren J (2018) Meta-learning: a survey. arXiv preprint arXiv:1810.03548
Vanschoren J, Van Rijn JN, Bischl B, Torgo L (2014) Openml: networked science in machine learning. ACM SIGKDD Explor Newslett 15(2):49–60
Wistuba M, Schilling N, Schmidt-Thieme L (2015) Sequential model-free hyperparameter tuning. In: ICDM, IEEE computer society, pp 1033–1038
Wistuba M, Schilling N, Schmidt-Thieme L (2016) Two-stage transfer surrogate model for automatic hyperparameter optimization. In: ECML/PKDD, Springer, Lecture notes in computer science, vol 9851, pp 199–214
Wistuba M, Schilling N, Schmidt-Thieme L (2018) Scalable gaussian process-based transfer surrogates for hyperparameter optimization. Mach Learn 107(1):43–78
Yogatama D, Mann G (2014) Efficient transfer learning method for automatic hyperparameter tuning. In: AISTATS, JMLR.org, JMLR workshop and conference proceedings, vol 33, pp 1077–1085
Yoon J, Kim T, Dia O, Kim S, Bengio Y, Ahn S (2018) Bayesian model-agnostic meta-learning. In: NeurIPS, pp 7343–7353
Zagoruyko S, Komodakis N (2016) Wide residual networks. In: Wilson RC, Hancock ER, Smith WAP (eds) Proceedings of the British machine vision conference 2016, BMVC 2016, York, UK, September 19–22, 2016. BMVA Press. http://www.bmva.org/bmvc/2016/papers/paper087/index.html
Zaheer M, Kottur S, Ravanbakhsh S, Póczos B, Salakhutdinov RR, Smola AJ (2017) Deep sets. In: NIPS, pp 3394–3404
Zheng Z, Zheng L, Yang Y (2018) A discriminatively learned CNN embedding for person reidentification. TOMCCAP 14(1):1–20
Acknowledgements
This work is co-funded by the industry Project “IIP-Ecosphere: Next Level Ecosphere for Intelligent Industrial Production”. Prof. Grabocka is also thankful to the Eva Mayr-Stihl Foundation for their generous research Grant.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible editor: Ira Assent, Carlotta Domeniconi, Aristides Gionis, Eyke Hüllermeier.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jomaa, H.S., Schmidt-Thieme, L. & Grabocka, J. Dataset2Vec: learning dataset meta-features. Data Min Knowl Disc 35, 964–985 (2021). https://doi.org/10.1007/s10618-021-00737-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10618-021-00737-9