Abstract
Early time series classification (eTSC) is the problem of classifying a time series after as few measurements as possible with the highest possible accuracy. The most critical issue of any eTSC method is to decide when enough data of a time series has been seen to take a decision: Waiting for more data points usually makes the classification problem easier but delays the time in which a classification is made; in contrast, earlier classification has to cope with less input data, often leading to inferior accuracy. The state-of-the-art eTSC methods compute a fixed optimal decision time assuming that every times series has the same defined start time (like turning on a machine). However, in many real-life applications measurements start at arbitrary times (like measuring heartbeats of a patient), implying that the best time for taking a decision varies widely between time series. We present TEASER, a novel algorithm that models eTSC as a two-tier classification problem: In the first tier, a classifier periodically assesses the incoming time series to compute class probabilities. However, these class probabilities are only used as output label if a second-tier classifier decides that the predicted label is reliable enough, which can happen after a different number of measurements. In an evaluation using 45 benchmark datasets, TEASER is two to three times earlier at predictions than its competitors while reaching the same or an even higher classification accuracy. We further show TEASER’s superior performance using real-life use cases, namely energy monitoring, and gait detection.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A time series (TS) is a collection of values sequentially ordered in time. One strong force behind their rising importance is the increasing use of sensors for automatic and high resolution monitoring in domains like smart homes (Jerzak and Ziekow 2014), starlight observations (Protopapas et al. 2006), machine surveillance (Mutschler et al. 2013), or smart grids (Hobbs et al. 1999; Lew and Milligan 2016). Time series classification (TSC) is the problem of assigning one of a predefined class to a time series, like recognizing the electronic device producing a certain temporal pattern of energy consumption (Gao et al. 2014; Gisler et al. 2013) or classifying a signal of earth motions as either an earthquake or a passing lorry (Perol et al. 2018).
Conventional TSC works on time series of a given, fixed length and assumes access to the entire input at classification time. In contrast, early time series classification (eTSC), which we study in this work, tries to solve the TSC problem after seeing as few measurements as possible (Xing et al. 2012). This need arises when the classification decision is time-critical, for instance to prevent damage (the earlier a warning system can predict an earthquake from seismic data (Perol et al. 2018), the more time there is for preparation), to speed-up diagnosis (the earlier an abnormal heart-beat is detected, the more time there is for prevention of fatal attacks (Griffin and Moorman 2001)), or to protect markets and systems (the earlier a crisis of a particular stock is detected, the faster it can be banned from trading (Ghalwash et al. 2014)).
eTSC has two goals: Classifying TS early and with high accuracy. However, these two goals are contradictory in nature: The earlier a TS has to be classified, the less data is available for classification, usually leading to lower accuracy. In contrast, the higher the desired classification accuracy, the more data points have to be inspected and the later the eTSC will be able to take a decision. Thus, a critical issue in any eTSC method is the determination of the point in time at which an incoming TS can be classified. Many state-of-the-art methods in eTSC (Xing et al. 2012, 2011; Mori et al. 2017b) assume that all time series being classified have a defined start time. Consequently, these methods assume that characteristic patterns appear roughly at the same offset in all TS, and try to learn the fixed fraction of the TS that is needed to make high accuracy predictions, i.e., when the accuracy of classification is most likely close to the accuracy on the full TS. For instance, the methods based on 1-Nearest Neighbor classification ECTS (Xing et al. 2012) and EDSC (Xing et al. 2011) define/learn a minimal length of a time series prefix based on the train dataset, and predictions can not be made earlier than this prefix length. ECDIRE (Mori et al. 2017b) trains a safe time stamp using the train dataset which states that a prediction can be accepted, i.e., a minimal length of a time series prefix. However, in many real life applications this assumption is wrong. For instance, sensors often start their observations of an essentially indefinite time series at arbitrary points in time. Intuitively, existing methods expect to see a TS from the point in time when the observed system starts working, while in many applications, this system has already been working for an unknown period of time when measurements start. In such settings, it is suboptimal to wait for a fixed number of measurements; instead, the algorithm should wait for the characteristic patterns, which may occur early (in which case an early classification is possible) or later (in which case the eTSC algorithm has to wait longer). As an example, Fig. 1 illustrates traces for the operational state of microwaves (Gisler et al. 2013). Observations started while the microwaves were already under power; the concrete operational state, characterized by high bursts of energy consumption, happened after 5–\(50\%\) of the whole trace (amounting to 1 hour). Current eTSC methods trained on this data would always wait for 30mins, because this was the last time they had seen the important event in the training data. But actually most TS could be classified safely much earlier; instead of assuming a fixed classification time, an algorithm should adapt its decision time to the individual time series.
Traces of microwaves taken from (Gisler et al. 2013). The operational state of the microwave starts between \(5\%\) and \(50\%\) of the whole trace length. To have at least one event (typically a high burst of energy consumption) for each microwave, the threshold has to be set to that of the latest seen operational state (after seeing more than \(46.2\%\))
In this paper we present TEASER, a Two-tier Early and Accurate Series classifiER, that is robust regarding the start time of a TS’s recording. It models eTSC as a two-tier classification problem (see Fig. 3). In the first tier, a slave classifier periodically assesses the input series and computes class probabilities. In the second tier, a master classifier takes the series of class probabilities of the slave as input and computes a binary decision on whether to report these as final result or continue with the observation. As such, TEASER neither presumes a fixed starting time of the recordings nor does it rely on a fixed decision time for predictions, but takes its decisions whenever it is confident of its prediction. On a popular benchmark of 45 datasets (Chen et al. 2015), TEASER is two to three times as early while keeping a competitive level of accuracy, and for some datasets reaching an even higher level of accuracy, when compared to the state of the art (Xing et al. 2012, 2011; Mori et al. 2017b; Parrish et al. 2013). Overall, TEASER achieves the highest average accuracy, lowest average rank, and highest number of wins among all competitors. We furthermore evaluate TEASER’s performance on the basis of real use-cases, namely device-classification of energy load monitoring traces, and classification of walking motions into normal and abnormal.
The rest of the paper is organized as follows: In Sect. 2 we formally describe the background of eTSC. Section 3 discusses related work. Section 4 introduces TEASER and its building blocks. Section 4 presents evaluation results including benchmark data and real use cases. and Sect. 6 presents the conclusion.
2 Background: time series and eTSC
In this section, we formally introduce time series (TS) and early time series classification (eTSC). We also describe the typical learning framework used in eTSC. Table 1 introduces our frequently used notations and symbols.
Definition 1
A time series T is a sequence of \(n \in {\mathbb {N}}\) real values, \(T=(t_{1},\ldots ,t_{n}),t_{i} \in {\mathbb {R}}\). The values are also called data points. A dataset D is a collection of time series.
We assume that all TS of a dataset have the same sampling frequency, i.e., every i-th data point was measured at the same temporal distance from the first point. In accordance to all previous approaches (Xing et al. 2012, 2011; Mori et al. 2017b), we will measure earliness in the number of data points and from now on disregard the actual time of data points. A central assumption of eTSC is that TS data arrives incrementally. If a classifier is to classify a TS after s data points, it has access to these s data points only. This is called a snapshot.
Definition 2
A snapshot \(T(s)=(t_{1},\ldots ,t_{s})\) of a time series T, \(s \le n\), is the prefix of T available for classification after seeing s data points.
In principle, an eTSC system could try to classify a time series after every new data point that was measured. However, it is more practical and efficient to call the eTSC system only after the arrival of a fixed number of new data points (Xing et al. 2012, 2011; Mori et al. 2017b). We call this number the interval length w. Typical values are \(5, 10, 20,\dots \)
eTSC is commonly approached as a supervised learning problem (Xing et al. 2012, 2011; Mori et al. 2017b; Parrish et al. 2013). Thus, we assume the existence of a set \(D_{train}\) of training TS, where each one is assigned to one class of a predefined set of class labels \(Y=\left\{ c_{1},\ldots ,c_{k}\right\} \). The eTSC system learns a model from \(D_{train}\) that can separate the different classes. Its performance is estimated by applying this model to all instances of a test set \(D_{test}\).
The quality of an eTSC system can be measured by different indicators. The accuracy of an eTSC is calculated as the percentage of correct predictions of the instances of a given dataset D (with D being either \(D_{test}\) or \(D_{train}\)), where higher is better:
The earliness of an eTSC is defined as the mean number of data points s after which a label is assigned, where lower is better:
We can now formally define the problem of eTSC.
Definition 3
Early time series classification (eTSC) is the problem of assigning all time series \(T \in D_{test}\) a label from Y as early and as accurately as possible.
eTSC thus has two optimization goals that are contradictory in nature, as later classification typically allows for more accurate predictions and vice versa. Accordingly, eTSC methods can be evaluated in different ways, such as comparing accuracies at a fixed-length snapshot (keeping earliness constant), comparing earliness at which a fixed accuracy is reached (keeping accuracy constant), or by combining these two measures. A popular choice for the latter is the harmonic mean of earliness and accuracy:
An \(\textit{HM}\) of 1 is equal to an earliness of \(0\%\) and an accuracy of \(100\%\). Figure 2 illustrates the problem of eTSC on a load monitoring task differentiating a digital receiver from a microwave. All traces have an underlying oscillating pattern and in total there are three important patterns (a), (b), (c) which are different from appliance to appliances. The characteristic part of a receiver trace is an energy burst with two plateaus (a), which can appear at different offsets. If an eTSC classifies a trace too early (Fig. 2 second from bottom), the signal is easily confused with that of microwaves based on the similarity to the (c) pattern. However, if an eTSC always waits until the offset at which all training traces of microwaves can be correctly classified, the first receiver trace will be classified much later than possible (eventually after seeing the full trace). To achieve optimal earliness at high accuracy, an eTSC system must determine its decision times individually for each TS it analyses.
eTSC on a trace of a digital receiver. The figure shows one traces of a digital receiver, and of microwaves on the top. These have three characteristic patterns a–c. In the bottom part, eTSC is performed on a snapshot of the time series of a digital receiver. In its first snapshot it is easily confused with pattern c of a microwave. However, the trace later contains pattern a which is characteristic for a receiver
3 Related work
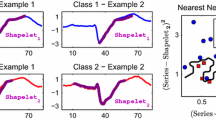
The techniques used for time series classification (TSC) can broadly be categorized into two classes: whole series-based and feature-based methods. Whole series-based methods make use of a point-wise comparison of entire TS like 1-NN Dynamic Time Warping (DTW) (Rakthanmanon et al. 2012), which is commonly used as a baseline in comparisons (Lines and Bagnall 2014; Bagnall et al. 2016). In contrast, feature-based classifiers rely on comparing features generated from substructures of TS. Approaches can be grouped (Bagnall et al. 2016) as either using Shapelets, Random Intervals or Bag-of-Patterns (BOP). Shapelets are defined as TS subsequences that are maximally representative of a class. In (Mueen et al. 2011) a decision tree is built on the distance to a set of Shapelets. The Shapelet Transform (ST) (Lines et al. 2012; Bostrom and Bagnall 2015), which is the most accurate Shapelet approach according to a recent evaluation (Bagnall et al. 2016), uses the distance to the Shapelets as input features for an ensemble of different classification methods. In the Learning Shapelets (LS) approach (Grabocka et al. 2014), optimal Shapelets are synthetically generated. The drawback of Shapelet methods is the high computational complexity of the Shapelet discovery, resulting in rather long training times. In interval-based approaches statistical features over random subsequences at fixed offsets are selected from the TS to then be used as input for classification. For example, the TS bag-of-features framework (TSBF) (Baydogan et al. 2013) first extracts windows at random positions with random lengths and next builds a supervised codebook generated from a random forest classifier. The (BOP) model (Schäfer and Leser 2017; Schäfer 2015; Lin et al. 2012; Schäfer and Högqvist 2012) breaks up a TS into a bag of substructures, represents these substructures as discrete features, and finally builds a histogram of feature counts as basis for classification. The recent Word ExtrAction for time SEries cLassification (WEASEL) (Schäfer and Leser 2017) also conceptually builds on the bag-of-patterns (BOP) approach and is one of the fastest and most accurate classifiers. WEASEL has been applied in the context of eTSC (Lv et al. 2019). Among the most accurate current TSC algorithms are ensembles (Bagnall et al. 2016). These classify a TSC by a set of different core classifiers and then aggregate the results using techniques like bagging or majority voting. The Elastic Ensemble (EE PROP) classifier (Lines and Bagnall 2014) uses 11 whole series classifiers. The COTE ensemble (Bagnall et al. 2015) is based on 35 core-TSC methods including EE PROP, ST and BOSS. Very recently, there has been the extension HIVE-COTE to COTE (Lines et al. 2016) that incorporates classifiers from five domains and claims superior accuracy. In Wang et al. (2017) deep learning networks are applied to TSC. Their best performing Fully Convolutional Neural Networks (FCN) performs not significantly different from state of the art (Bagnall et al. 2016; Lines et al. 2016; Lucas et al. 2019; Schäfer and Leser 2017; Le Nguyen et al. 2019). In (Fawaz et al. 2018) an overview of deep learning approaches applied for TSC is presented, and the best performing Residual Networks (ResNet) significantly outperforms FCN.
Early classification of time series (eTSC) (Santos and Kern 2016) is important when data becomes available over time and decisions need to be taken as early as possible. It addresses two conflicting goals: maximizing accuracy typically reduces earliness and vise-versa. Early Classification on Time Series (ECTS) (Xing et al. 2012) is one of the first papers to introduce the problem. The authors adopt a 1-nearest neighbor (1-NN) approach and introduce the concept of minimum prediction length (MPL) in combination with clustering. Time series with the same 1-NN are clustered. The optimal prefix length for each cluster is obtained by analyzing the stability of the 1-NN decision for increasing time stamps. Only those clusters with stable and accurate offsets are kept. To give a prediction for an unlabeled TS, the 1-NN is searched among clusters. Reliable Early Classification (RelClass) (Parrish et al. 2013) presents a method based on quadratic discriminant analysis (QDA). A reliability score is defined as the probability that the predicted class for the truncated and the whole time series will be the same. At each time stamp, RelClass then checks if the reliability is higher than a user-defined threshold. In Early Classification of Time Series based on Discriminating Classes Over Time (ECDIRE) (Mori et al. 2017b) classifiers are trained at certain time stamps, i.e. at percentages of the full time series length. It learns a safe time stamp (the start time) as the fraction of the time series which states that a prediction is safe. Furthermore, a reliability threshold is learned using the difference between the two highest class probabilities. Only predictions passing this threshold after the safe time stamp are chosen. The idea of EDSC (Xing et al. 2011) is to learn Shapelets that appear early in the time series, and that discriminate between classes as early as possible. In (Mori et al. 2017a) early classification is approached as an optimization problem. The authors combine a set of probabilistic classifiers with a stopping rule that is optimized using a cost function on earliness and accuracy. Their best performing model SR1-CF1 is significantly earlier than ECDIRE and slightly earlier than TEASER but their accuracy falls behind ECTS. Furthermore, this method a-priori z-normalizes values based on the entire time series, which is incompatible with a real-life eTSC scenario, where only a fraction of the series is known at classification time. In contrast, TEASER performs normalization only on the currently known prefix of a times series. We omit SR1-SC1 from our evaluation due to this issue, which gives the method a large but unfair advantage.
In (Mori et al. 2019) eTSC is approached as a multi-objective optimization technique. As most solutions (such as TEASER) are based on combining the accuracy and earliness into a single-objective problem. Their algorithm produces multiple “optimal” solutions with different earliness and accuracy trade-offs using a Gaussian Process classifier and a genetic algorithm. The intention is for the user to choose the most suitable one for her/his specific requirements. Their method dominates the state of the art in eTSC. For a meaningful comparison to TEASER, we would have to compare the multiple solutions of (Mori et al. 2019) to our solution to see if one is better by computing the harmonic mean of the respective accuracy / earliness values. Unfortunately, neither the code nor the raw measurements of this method have been published.
In (Tavenard and Malinowski 2016) a framework is introduced that defines a single objective based on two cost functions: the misclassification cost and the cost of delaying a prediction. Two different methods are introduced that optimize this single objective.
A problem related to eTSC is the classification of streaming time series (Nguyen et al. 2015; Gaber et al. 2005). In these works, the task is to assign class labels to time windows of a potentially infinite data stream, and is similar to event detection in streams (Aggarwal and Subbian 2012). The data enclosed in a time window is considered to be an instance for a classifier. Due to the windowing, multiple class labels can be assigned to a data stream. In contrast, eTSC aims at assigning a label to an entire TS as soon as possible.
TEASER is given a snapshot of an energy consumption time series. After seeing the first s measurements, the first slave classifier \(sc_1\) performs a prediction which the master classifier \( mc_1\) rejects due to low class probabilities. After observing the i-th interval which includes a characteristic energy burst, the slave classifier \(sc_i\) (correctly) predicts RECEIVER, and the master classifier \(mc_i\) eventually accepts this prediction. When the prediction of RECEIVER has been consistently derived v times, it is output as final prediction
4 Early and accurate TS classification: TEASER
TEASER addresses the problem of finding optimal and individual decision times by following a two-tier approach. Intuitively, it trains a pair of classifiers for each snapshot s: A slave classifier computes class probabilities which are passed on to a master classifier that decides whether these probabilities are high enough that a safe classification can be emitted. TEASER monitors these predictions and predicts a class c if it occurred v times in a row; the minimum length v of a series of predictions is an important parameter of TEASER. Intuitively, the slave classifiers give their best prediction based on the data they have seen, whereas the master classifiers decide if these results can be trusted, and the final filter suppresses spurious predictions.
Formally, let w be the user-defined interval length and let \(n_{max}\) be the length of the longest time series in the training set \(D_{train}\). We then extract snapshots \(T(s_i)=T[1 .. i \cdot w]\), i.e., time series snapshots of lengths \(s_i = i \cdot w\). A TEASER model consists of a set of \(S=[n_{max}/w]\) pairs of slave/master classifiers, trained on the snapshots of the TS in \(D_{train}\) (see below for details). When confronted with a new time series, TEASER waits for the next w data points to arrive and then calls the appropriate slave classifier which outputs probabilities for all classes. Next, TEASER passes these probabilities to the slave’s paired master classifier which either returns a class label or NIL, meaning that no decision could be derived. If the answer is a class label c and this answer was also given for the last \(v-1\) snapshots, TEASER returns c as result; otherwise, it keeps waiting. In this context, earliness refers to the time point corresponding to the longest snapshot length seen by the (last) slave classifier before a prediction is accepted by a master classifier.
Before going into the details of TEASER’s components, consider the example shown in Fig. 3. The first slave classifier \(sc_1\) falsely labels this trace of a digital receiver as a microwave (by computing a higher probability of the latter class than for the former class) after seeing the first w data points. However, the master classifier \(mc_{1}\) decides that this prediction is unsafe and TEASER continues to wait. After \(i-1\) further intervals, the i-th pair of slave and master classifiers \(sc_i\) and \(mc_i\) are called. Because the TS contained characteristic patterns in the i-th interval, the slave now computes a high probability for the digital receiver class, and the master decides that this prediction is safe. TEASER counts the number of consecutive predictions for this class and, if a threshold is passed, outputs the predicted class.
Clearly, the interval length w and the threshold v are two important yet opposing parameters of TEASER. A smaller w results in more frequent predictions, due to smaller prediction intervals. However, a classification decision usually only changes after seeing a sufficient number of novel data points; thus, a too small value for w leads to series of very similar class probabilities at the slave classifiers, which may trick the master classifier. This can be compensated by increasing v. In contrast, a large value for w leads to fewer predictions, where each one has seen more new data and thus is probably more reliable. For such settings, v may be reduced without negatively impacting earliness or accuracy. In our experiments, we shall analyze the influence of w on accuracy and earliness in Sect. 5.4. In all experiments v is treated as a hyper-parameter that is learned by performing a grid-search and maximizing HM on the training dataset.
4.1 Slave classifier
Each slave classifier \(sc_i, \textit{ with } i \le S\) is a full-fledged time series classifier of its own, trained to predict classes after seeing a fixed snapshot length. Given a snapshot \(T(s_i)\) of length \(s_i=i \cdot w\), the slave classifier \(sc_i\) computes class probabilities \(P(s_i) = \Bigl [ p\bigl (c_1(s_i)\bigr ), \ldots , p\bigl (c_k(s_i)\bigr ) \Bigr ]\) for this time series for each of the predefined classes and determines the class \(c(s_i)\) with highest probability. Furthermore, it computes the difference \(\triangle d_i\) between the highest
and second highest
class probabilities:
In TEASER, the most probable class label \(c(s_i)\), the vector of class probabilities \(P(s_i)\), and the difference \(\triangle d(s_i)\) are passed as features to the paired i-th master classifier \(mc_i\), which then has to decide if the prediction is reliable (see Fig. 4) or not.
4.2 Master classifier
A master classifier \(mc_i,\) with \(i \le S\) in TEASER learns whether the results of its paired slave classifier should be trusted or not. We model this task as a classification problem of its own, where the i-th master classifier uses the results of the i-th slave classifier as features for learning its model (see Sect. 4.4 for the details on training). However, training this classifier is tricky. To learn accurate decisions, it needs to be trained with a sufficient number of correct and false predictions. However, the more accurate a slave classifier is, the less mis-classifications are produced, and the worse the expected performance of the paired master classifier gets. Figure 5 illustrates this problem by showing a typical slave’s train accuracy with an increasing number of data points. In this example, the slave classifiers start with an accuracy of around \(70\%\) and quickly reach \(100\%\) on the train data. Once the train accuracy reaches \(100\%\), there are no negative samples left for the master classifier to train its decision boundary.
To overcome this issue, we use a so-called one-class classifier as master classifier (Khan and Madden 2009). One-class classification refers to the problem of classifying positive samples in the absence of negative samples. It is closely related to, but non-identical to, outlier/anomaly detection (Cuturi and Doucet 2011). In TEASER, we use a one-class Support Vector Machine (oc-SVM) (Schölkopf et al. 2001) which does not determine a separating hyperplane between positive and negative samples. It instead computes a hyper-sphere around the positively labeled samples with minimal dilation that has the maximal distance to the origin. At classification time, all samples that fall outside this hypersphere are considered as negative samples. In our case, this implies that the master learns a model of positive samples and regards all results not fitting this model as negative. The major challenge is to determine a hyper-sphere that is neither too large nor too small to avoid false positives, leading to lower accuracy, or dismissals, which lead to delayed predictions.
In Fig. 6 a trace is either labeled as microwave or receiver, and the master classifier learns that its paired slave is very precise at predicting receiver traces but produces many false predictions for microwave traces. Thus, only receiver predictions with class probability above \(p('receiver') \,{\ge }\, 0.6\), and microwaves above \(p('microwave')\,{\ge }\, 0.95\) are accepted. As can be seen in this example, using a one-class SVM leads to very flexible decision boundaries.
4.3 Training slave and master classifiers
Consider a labeled set of time series \(D_{train}\) with class labels \(Y=\left\{ c_{1},\ldots , c_{k}\right\} \) and an interval length w. As before, \(n_{max}\) is the length of the longest training instance. Then, the i-th pair of slave / master classifier is trained as follows:
-
1.
First, we truncate the train dataset \(D_{train}\) to the prefix length determined by i (snapshot \(s_i\)):
$$\begin{aligned} D_{train}(s_i)=\{T(s_i) ~|~ T \in D_{train}\} \end{aligned}$$In Fig. 4 (bottom) the four TS are truncated.
-
2.
Next, these truncated snapshots are z-normalized. This is a critical step for training to remove any bias resulting from values that will only be available in the future. I.e., a truncated snapshot must not make use of absolute values resulting from z-normalizing the whole time series, as opposed to (Mori et al. 2017a).
-
3.
The hyper-parameters of the slave classifier are trained on \(D_{train}(s_i)\) using 10-fold-cross validation. Using the derived hyper-parameters we can build the final slave classifier \(sc_i\) producing its 3-tuple output \((c(s_i), P(s_i), \triangle d(s_i))\) for each \(T \in D_{train}\) (Fig. 4 centre).
-
4.
To train the paired master classifier, we first remove all instances which were incorrectly classified by the slave. Let us assume that there were \(N'\le N\) correct predictions. We then train a one-class SVM on the \(N'\)training samples, where each sample is represented by the 3-tuple \((c(s_i), P(s_i), d(s_i)\) produced by the slave classifier.
-
5.
Finally, we perform a grid-search over values \(v\in \{1\dots 5\}\) to find the threshold v which yields the highest harmonic mean HM of earliness and accuracy on \(D_{train}\).

In accordance with prior works (Mori et al. 2017a; Xing et al. 2011; Parrish et al. 2013; Xing et al. 2012), we consider the interval length w to be a user-specified parameter. However, we will also investigate the impact of varying w in Sect. 5.4.
The pseudo-code for training TEASER is given in Algorithm 1. The aim of the training is to obtain S pairs of slave/master classifiers, and the threshold v for consecutive predictions. First, for all z-normalized snapshots (line 4), the slaves are trained and the predicted labels and class probabilities are kept (line 5). Prior to training the master, incorrectly classified instances are removed (line 6). The feature vectors of correctly labeled samples are passed on to train the master (one-class SVM) classifier (line 7). Finally, an optimal value for v is determined using a grid-search (line 9).
4.4 Computational complexity
The runtime of TEASER depends on the used slave classifier. TEASER performs classifications (fitting and prediction) at intervals of \(w=n/S\), e.g., intervals of \(5\%\) for \(S=20\).
For a linear time slave classifier O(n), with time series length n, the increase in the computational complexity accounts to:
For a quadratic time slave classifier \(O(n^2)\), we expect to see an increase of
in terms of the computational complexity.
As such, for a linear (quadratic) time classifier we expect to see a 10.5 (7.175) fold increase in train times for \(S=20\). WEASEL is a quadratic time classifier in terms of n. In Sect. 5.5 we performed an experiment to show the observed increase in the runtime.
5 Experimental evaluation
We first evaluate TEASER using the 45 datasets out of the UCR archive that also have been used in prior works on eTSC (Xing et al. 2012; Parrish et al. 2013; Xing et al. 2011; Mori et al. 2017b). Each UCR dataset provides a train and test split set which we use unchanged. Note that most of these datasets were preprocessed to create approximately aligned patterns of equal length and scale (Schäfer 2014). Such an alignment is advantageous for methods that make use of a fixed decision time but also requires additional effort and introduces new parameters that must be determined, steps that are not required with TEASER. We also evaluated on the basis of additional real-life datasets where no such alignment was performed.
We compared our approach to the state-of-the-art methods, ECTS (Xing et al. 2012), RelClass (Parrish et al. 2013), EDSC (Xing et al. 2011), and ECDIRE (Mori et al. 2017b). On the UCR datasets, we use published numbers on accuracy and earliness of these methods to compare to TEASER’s performance. As in these papers, we used \(w=n_{max}/20\) as default interval length. For ECDIRE, ECTS, and RelCLASS, the respective authors also released their code, which we used to compute their performance on our additional two use-cases. We were not able to obtain runnable code of EDSC, but note that EDSC was the least accurate eTSC on the UCR data. All experiments ran on a server running LINUX with 2xIntel Xeon E5-2630v3 and 64GB RAM, using JAVA JDK x64 1.8.
TEASER is a two-tier model using a slave and a master classifier. As a first tier, TEASER requires a TSC which produces class probabilities as output. Thus, we performed our experiments using three different time series classifiers: WEASEL (Schäfer and Leser 2017), BOSS (Schäfer 2015) and 1-NN Dynamic Time Warping (DTW). As a second tier, we benchmarked three master classifiers, one-class SVM using LIBSVM (Chang and Lin 2011), linear regression using liblinear (Fan et al. 2008), and an SVM using an RBF kernel (Chang and Lin 2011).
For each experiment, we report the evaluation metrics (average) accuracy, (average) earliness, their (average) harmonic mean HM, as introduced in the Background Sect. 2, and Pareto optimality. The Pareto optimality criterion counts a method as better than a competitor whenever it obtains better results in at least one metric without being worse in any other metrics. All performance metrics were computed using only results of the test split. To support reproducibility, we provide the TEASER source code and the raw measurement sheets for all 85 UCR datasets, though the experiments reported were performed using the 45 common UCR datasets used by all eTSC competitors (TEASER Classifier Source Code and Raw Results 2018).
5.1 Choice of slave and master classifiers
In our first experiment we tested the influence of different slave and master classifiers. We compared the three different slave TS classifiers: DTW, BOSS, WEASEL. As WEASEL’s hyper-parameter we learn the best word length between 4 and 6 for WEASEL on each dataset using 10-fold cross-validation on the train data. ocSVM parameters for the remaining experiments were determined as follows: nu-value was fixed to 0.05, i.e. \(5\%\) of the samples may be dismissed, kernel was fixed to RBF and the optimal gamma value was obtained by grid-search within \(\{1 \ldots 100\}\) on the train dataset.
As a master classifier we used one-class SVM (ocSVM), SVM with a RBF kernel (RBF-SVM) and linear regression (Regression). For ocSVM we performed a grid-search over \(gamma \in [100, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1.5, 1]\)kernel was fixed to RBF, nu-value was fixed to 0.05; for RBF-SVM we performed a grid-search over \(C \in [0.1, 1, 10, 100]\). We compare performances in terms of HM to the other competitors ECTS, RelClass, EDSC and ECDIRE.
We make use of critical difference diagrams (as introduced in (Demšar 2006)). The best classifiers with highest HM are shown to the right of the diagram and have the lowest (best) average ranks. The group of classifiers that are not significantly different in their rankings are connected by a bar. The critical difference (CD) length represents statistically significant differences using a Nemenyi two tailed test with alpha=0.05.
We first fix the master classifier to oc-SVM and compare all three different slave classifiers (DTW+ocSVM, BOSS+ocSVM, WEASEL+ocSVM) in Fig. 7. Out of these classifiers, TEASER using WEASEL (WEASEL+ocSVM) has the best (lowest) rank. Next, we fix the slave classifier to WEASEL and compare the three different master classifiers (ocSVM, RBF-SVM, Regression). Again, TEASER using ocSVM performs best. The most significant improvement over the state of the art is archived by TEASER+WEASEL+ocSVM, which justifies our design decision to model early classification as a one-class classification problem.
Based on these results we use WEASEL (Schäfer and Leser 2017) as a slave classifier and ocSVM for all remaining experiments and refer to it as TEASER. A nice aspect of WEASEL is that it is comparably fast, highly accurate, and works with variable length time series.
5.2 Performance on the UCR datasets
eTSC is about predicting accurately and earlier. Figure 8 shows two critical difference diagrams (as introduced in (Demšar 2006)) for earliness and accuracy over the average ranks of the different eTSC methods. The best classifiers are shown to the right of the diagram and have the lowest (best) average ranks. The group of classifiers that are not significantly different in their rankings are connected by a bar. The critical difference (CD) length represents statistically significant differences for either accuracy or earliness using a Nemenyi two tailed test with alpha=0.05. With a rank of 1.44 (earliness) and 2.38 (accuracy) TEASER is significantly earlier than all other methods and overall is among the most accurate approaches. Additionally, on our webpage we have published all raw measurements (TEASER Classifier Source Code and Raw Results 2018) for all 85 UCR datasets. Table 2 presents a summary of the results. TEASER is the most accurate on 22 datasets, followed by ECDIRE and RelClass being best in 9 and 10 sets, respectively. TEASER also has the highest average accuracy of \(75\%\), followed by RelClass (\(74\%\)), ECDIRE (\(72.6\%\)) and ECTS (\(71\%\)). EDSC is clearly inferior to all other methods in terms of accuracy with \(62\%\). TEASER provides the earliest predictions in 32 cases, followed by ECDIRE with 7 cases and the remaining competitors with 2 cases each. On average, TEASER takes its decision after seeing \(23\%\) of the test time series, whereas the second and third earliest methods, i.e., EDCS and ECDIRE, have to wait for \(49\%\) and \(50\%\), respectively. It is also noteworthy that the second most accurate method RelClass provides the overall latest predictions with \(71\%\).
Note that all competitors have been designed for highest possible accuracy, whereas TEASER was optimized for the harmonic mean of earliness and accuracy - recall that TEASER nevertheless also is the most accurate eTSC method on average. It is thus not surprising that TEASER beats all competitors in terms of HM in 36 of the 45 cases. In the following Sect. 5.3 we perform an experiment to show the accuracy and earliness trade-off of TEASER. Figure 9 visualizes the HM value achieved by TEASER (black line) vs. the four other eTSC methods. This graphic sorts the datasets according to a predefined grouping of the benchmark data into four types, namely synthetic, motion sensors, sensor readings and image outlines. TEASER has the best average HM value in all four of these groups; only in the group composed of synthetic datasets EDSC comes close with a difference of just 3 percentage points (pp). In all other groups TEASER improves the HM by at least 20 pp when compared to its best performing competitor.
In some of the UCR datasets classifiers excel in one metric (accuracy or earliness) but are beaten in another. To determine cases were a method is clearly better than a given competitor, we also computed the number of sets where a method is Pareto optimal over this competitor. Results are shown in Table 3. TEASER is dominated in only two cases by another method, whereas it dominates in 19 to 30 out of the 45 cases
In the context of eTSC the most runtime critical aspect is the prediction phase, in which we wish to be able to provide an answer as soon as possible. As all competitors were implemented using different languages, it would not be fair to compare wall-clock-times of implementations. Thus, we count the number of master predictions that are needed on average for TEASER to accept a master’s prediction to take a definite decision. On average, TEASER requires 3.6 predictions (median 3.0) after seeing \(23\%\) of the TS on average. Thus, regardless of the used master classifier, a roughly \(360\%\) faster infrastructure would be needed on average for TEASER, in comparison to a single prediction at a fixed threshold (like the ECTS framework with earliness of \(70\%\)).
5.3 Being early and accurate
Inspired by the previous experiment, we aimed at exploring the earliness/accuracy trade-off in more detail. TEASER and its competitors have different optimization goals: best harmonic mean vs. high accuracy.
Thus, in this experiment we measured how well TEASER performs if one of the two parameters earliness and accuracy was fixed to the value achieved by the best competitor. To this end, we modified TEASER to be able to force it to take a decision after seeing a prefix of a given length of a time series. Thus, even if the master in the original TEASER would decide to wait for additional data at a given time stamp, in the modified version TEASER is forced to take a decision.
Figure 10 shows the average earliness/accuracy results of TEASER, and its competitors on these 45 datasets. By projecting the points of the competitors onto the TEASER line, we can compare earliness and accuracy. The figure shows that TEASER has a competitive average accuracy but is 3 times faster (earlier) than its competitors on average. Also, with a linear increase in TEASER’s earliness, its accuracy increases linearly. E.g. with an average earliness of \(17\%\) TEASER shows an accuracy of \(63.4\%\), which is more accurate and 3 times as early as EDSC with accuracy \(62.43\%\) and earliness \(49\%\).
5.4 Impact of the number of masters and slaves
To make results comparable to that of previous publications, all experiments described so far used a fixed value for the interval length w derived from breaking the time series into \(S=20\) intervals. Figure 11 shows boxplot diagrams for earliness (left) and accuracy (right) when varying the value of \(S=[n_{max}/w]\) so that predictions are made using \(S=10\) up to \(S=30\) masters/slaves. Thus, in the case of \(S=30\) TEASER may output a prediction after seeing \(3\%\), \(6\%\), \(9\%\), etc. of the entire time series. Interestingly, accuracy decreases whereas earliness improves with increasing S (decreasing w), meaning that TEASER tends to make earlier predictions, thus seeing less data, with shorter interval length. Thus, changing S influences the trade-off between earliness and accuracy: If early (accurate) predictions are needed, one should choose a high (low) S value. We further plot the upper bound of TEASER, that is the accuracy at \(S=1\), equal to always using the full TS to do the classification. The difference between \(S=1\) and \(S=10\) is surprisingly small with 5pp difference. Overall, TEASER gets to \(95\%\) of the optimum using on average \(40\%\) of the time series.
5.5 Train/test time and memory consumption
Finally, we measured the average single-core fit and prediction times and the average memory requirements of TEASER compared to a single WEASEL classifier on all 45 datasets. For, TEASER a total of \(S=20\) master/slave classifiers is trained with different prefix lengths, whereas WEASEL is trained on the full time series length. Figure 12 shows the results. From left to right: In terms of median fit times on all 45 datasets, TEASER requires 720s, whereas a single WEASEL classifier performed on the full TS requires 160s. This is equal to a 4.5-fold increase in median train times. This difference becomes smaller for larger datasets due to larger the influence of the number of times series. TEASER takes 1 day on a single core to train the largest datasets NonInvasiveFatalECG_Thorax1 and NonInvasiveFatalECG_Thorax2, whereas WEASEL finishes after 14 hours on a single-core (1.7-fold increase).
When it comes to median prediction times, TEASER shows a time of 41s, and WEASEL has 10s, which is equal to a 3.9-fold increase in median train times. On the two largest datasets NonInvasiveFatalECG_Thorax1 and NonInvasiveFatalECG_Thorax2 TEASER requires 290 seconds and WEASEL takes 144 seconds (2-fold increase).
The TEASER and a single WEASEL classifier require a similar amount of memory to store their models. The memory only slightly increases when moving from \(S=1\) (WEASEL) to \(S=20\) classifiers, as each WEASEL classifier stores just the weight vector obtained from liblinear as a model for each of S slaves. The computed features for the train dataset are discarded after training. We assume that the S slave classifiers are trained sequentially. If trained in parallel there is an additional memory overhead for storing the computed features of multiple slave classifiers.
Overall, the moderate increase in fit and prediction times is a result of the quadratic computational complexity of WEASEL in the time series length n. As such the largest prefix length (full time series) contributes most to the overall runtime, resulting in a moderate (sublinear) increase when adding \(S=20\) smaller prefix lengths for training. The observed runtime difference is close to the theoretical factor of 7.5, as there are also other factors influenced by our implementation such as the dataset size, garbage collection, multi-threading, training of masters, etc.
5.6 Ablation study
In this experiment we study the influence of the features passed to the master classifiers, namely the vector of class probabilities \(P(s_i)\) and the max-difference \(\triangle d(s_i)\) (compare Sect. 4.1). We benchmark three variants of TEASER with different feature sets:
-
1.
TEASER: all features are enabled.
-
2.
No Max-Diff: the max-difference \(\triangle d(s_i)\) is disabled.
-
3.
Only Max-Diff: only the max-difference feature \(\triangle d(s_i)\) and no class probabilities \(P(s_i)\) are used.
Figure 13 shows the results using a critical difference diagram (as introduced in (Demšar 2006)) over the harmonic mean (HM) of earliness and accuracy. The critical difference (CD) length represents statistically significant differences using a Nemenyi two tailed test with alpha=0.05.
Using all features shows the best average rank (TEASER), followed by using only probabilities (No Max-Diff) and using only the maximal difference shows the lowest average rank (Only Max-Diff). There is an improvement in ranks but these results are not statistically significant. Still, we chose to use all features in TEASER.
5.7 Three real-life datasets
The UCR datasets used so far all have been preprocessed to make their analysis easier and, in particular, to achieve roughly the same offsets for the most characteristic patterns. This setting is very favorable for those methods that expect equal offsets, which is true for all eTSC methods discussed here except TEASER; it is even more reassuring that even under such non-favorable settings TEASER generally outperforms its competitors. In the following we describe an experiment performed on three additional datasets, namely ACS-F1 (Gisler et al. 2013), PLAID (Gao et al. 2014), and CMU (CMU 2020). As can be seen from Table 4, these datasets have interesting characteristics which are quite distinct from those of the UCR data, as all UCR datasets have a fixed length and were preprocessed for approximate alignment. The former two use-cases were generated in the context of appliance load monitoring and capture the power consumption of common household appliances over time, whereas the latter records the z-axis accelerometer values of either the right or the left toe of four persons while walking to discriminate normal from abnormal walking styles.
ACS-F1 monitored about 100 home appliances divided into 10 appliance types (mobile phones, coffee machines, personal computers, fridges and freezers, Hi-Fi systems, lamps, laptops, microwave oven, printers, and televisions) over two sessions of one hour each. The time series are very long and have no defined start points. No preprocessing was applied. We expect all eTSC methods to require only a fraction of the overall TS, and we expect TEASER to outperform other methods in terms of earliness.
PLAID monitored 537 home appliances divided into 11 types (air conditioner, compact fluorescent, lamp, fridge, hairdryer, laptop, microwave, washing machine, bulb, vacuum, fan, and heater). For each device, there are two concatenated time series, where the first was taken at the start-up of the device and the second during steady-state operation. The resulting TS were preprocessed to create approximately aligned patterns of equal length and scale. We expect eTSC methods to require a larger fraction of the data and the advantage of TEASER to be less pronounced due to the alignment.
CMU recorded time series taken from four walking persons, with some short walks that last only three seconds and some longer walks that last up to 52 seconds. Each walk is composed of multiple gait cycles. The difficulties in this dataset result from variable length gait cycles, gait styles and paces due to different subjects performing different activities including stops and turns. No preprocessing was applied. Here, we expect TEASER to strongly outperform the other eTSC methods due to the higher heterogeneity of the measurements and the lack of defined start times.
We fixed w to 5% of the maximal time series length of the dataset for each experiment. Table 5 shows results of all methods on these three datasets. TEASER requires \(19\%\) (ACS-F1) and \(64\%\) (PLAID) of the length of the sessions to make reliable predictions with accuracies of \(83\%\) and \(91.6\%\), respectively. As expected, a smaller fraction of the TS is necessary for ACS-F1 than for PLAID. All competitors are considerably less accurate than TEASER with a difference of 10 to 20 percentage points (pp) on ACS-F1 and 29 to 34 pp on PLAID. In terms of earliness TEASER is the earliest method on the ACS-F1 dataset but the slowest on the PLAID dataset; although its accuracy on this dataset is far better than that of the other methods, it is only third best in terms of HM value. As ECDIRE has an earliness of \(21\%\) for the PLAID dataset, we performed an additional experiment where we forced TEASER to always output a prediction after seeing at most \(20\%\) of the data, which is roughly equal to the earliness of ECDIRE. In this case TEASER achieves an accuracy of \(78.2\%\), which is still higher than that of all competitors. Recall that TEASER and its competitors have different optimization goals: HM vs accuracy. Even, if we set the earliness of TEASER to that of its earliest competitor, TEASER obtains a higher accuracy. The advantages of TEASER become even more visible on the difficult CMU dataset. Here, TEASER is 15 to 40 pp more accurate while requiring 35 to 54 pp less data points than its competitors. The reasons become visible when inspecting some examples of this dataset (see Fig. 14). A normal walking motion consists of roughly three repeated similar patterns. TEASER is able to detect normal walking motions after seeing \(34\%\) of the walking patterns on average, which is mostly equal to one out of the three gait cycles. Abnormal walking motions take much longer to classify due to the absence of a gait cycle. Also, one of the normal walking motions (third from top) requires a longer inspection time of two gait cycles, as the first gait cycle seems to start with an abnormal spike.
6 Conclusion
We presented TEASER, a novel method for early classification of time series. TEASER’s decision for the safety (accuracy) of a prediction is treated as a classification problem, in which master classifiers continuously analyze the output of probabilistic slave classifiers to decide if their predictions should be trusted or not. By means of this technique, TEASER adapts to the characteristics of classes irrespective of the moments at which they occur in a TS. In an extensive experimental evaluation using altogether 48 datasets, TEASER outperforms all other methods, often by a large margin and often both in terms of earliness and accuracy.
Future work will include optimizing our early time series classification framework for fast classification in terms of wall-clock-time. This introduces further complications, such as considering the sampling rate of individual time series, and balancing the time required to make predictions with the time it takes to wait for more data, and making the runtime of a classifier a critical issue. Recently, a multi-objective formulation of eTSC has been formulated (Mori et al. 2019), deriving multiple solutions instead of picking a best one based on a single-objective function, combining earliness and accuracy. We will be looking into a multi-objective formulation of early classification for TEASER, too.
References
Aggarwal CC, Subbian K (2012) Event detection in social streams. In: Proceedings of the 2012 SIAM international conference on data mining, SIAM, pp 624–635
Bagnall A, Lines J, Hills J, Bostrom A (2015) Time-series classification with COTE: the collective of transformation-based ensembles. IEEE Trans Knowl Data Eng 27(9):2522–2535
Bagnall A, Lines J, Bostrom A, Large J, Keogh E (2016) The great time series classification bake off: an experimental evaluation of recently proposed algorithms. Extended version. Data mining and knowledge discovery, pp 1–55
Baydogan MG, Runger G, Tuv E (2013) A bag-of-features framework to classify time series. IEEE Trans Pattern Anal Mach Intell 35(11):2796–2802
Bostrom A, Bagnall A (2015) Binary Shapelet transform for multiclass time series classification. In: International conference on big data analytics and knowledge discovery, Springer, Berlin. pp 257–269
Chang CC, Lin CJ (2011) LIBSVM: a library for support vector machines. ACM Trans Intell Syst Technol 2(3):27
CMU (2020) CMU graphics lab motion capture database. http://mocap.cs.cmu.edu/
Cuturi M, Doucet A (2011) Autoregressive kernels for time series. arXiv preprint arXiv:1101.0673
Demšar J (2006) Statistical comparisons of classifiers over multiple data sets. J Mach Learn Res 7:1–30
Fan RE, Chang KW, Hsieh CJ, Wang XR, Lin CJ (2008) LIBLINEAR: a library for large linear classification. J Mach Learn Res 9:1871–1874
Fawaz HI, Forestier G, Weber J, Idoumghar L, Muller PA (2018) Deep learning for time series classification: a review. arXiv preprint arXiv:1809.04356
Gaber MM, Zaslavsky A, Krishnaswamy S (2005) Mining data streams: a review. ACM Sigmod Rec 34(2):18–26
Gao J, Giri S, Kara EC, Bergés M (2014) PLAID: a public dataset of high-resoultion electrical appliance measurements for load identification research: demo abstract. In: Proceedings of the 1st ACM conference on embedded systems for energy-efficient buildings, ACM, pp 198–199
Ghalwash MF, Radosavljevic V, Obradovic Z (2014) Utilizing temporal patterns for estimating uncertainty in interpretable early decision making. In: ACM SIGKDD international conference on knowledge discovery and data mining, ACM, pp 402–411
Gisler C, Ridi A, Zujferey D, Khaled OA, Hennebert J (2013) Appliance consumption signature database and recognition test protocols. In: International workshop on systems, signal processing and their applications (WoSSPA), IEEE, pp 336–341
Grabocka J, Schilling N, Wistuba M, Schmidt-Thieme L (2014) Learning time-series Shapelets. In: ACM SIGKDD international conference on knowledge discovery and data mining, ACM
Griffin MP, Moorman JR (2001) Toward the early diagnosis of neonatal sepsis and sepsis-like illness using novel heart rate analysis. Pediatrics 107(1):97–104
Hobbs BF, Jitprapaikulsarn S, Konda S, Chankong V, Loparo KA, Maratukulam DJ (1999) Analysis of the value for unit commitment of improved load forecasts. IEEE Trans Power Syst 14(4):1342–1348
Jerzak Z, Ziekow H (2014) The DEBS 2014 grand challenge. In: Proceedings of the 2014 ACM international conference on distributed event-based systems, ACM, pp 266–269
Khan SS, Madden MG (2009) A survey of recent trends in one class classification. In: Irish conference on artificial intelligence and cognitive science. pp 188–197. Springer, Berlin
Le Nguyen T, Gsponer S, Ilie I, O’Reilly M, Ifrim G (2019) Interpretable time series classification using linear models and multi-resolution multi-domain symbolic representations. Data mining and knowledge discovery, pp 1–40
Lew D, Milligan M (2016) The value of wind power forecasting. http://www.nrel.gov/docs/fy11osti/50814.pdf
Lin J, Khade R, Li Y (2012) Rotation-invariant similarity in time series using bag-of-patterns representation. J Intell Inf Syst 39(2):287–315
Lines J, Bagnall A (2014) Time series classification with ensembles of elastic distance measures. Data Min Knowl Discov 29(3):565–592
Lines J, Davis LM, Hills J, Bagnall A (2012) A shapelet transform for time series classification. In: ACM SIGKDD international conference on knowledge discovery and data mining, ACM, pp 289–297
Lines J, Taylor S, Bagnall A (2016) HIVE-COTE: the hierarchical vote collective of transformation-based ensembles for time sries classification. In: 2016 IEEE 16th international conference on data mining (ICDM), IEEE, pp 1041–1046
Lucas B, Shifaz A, Pelletier C, O’Neill L, Zaidi N, Goethals B, Petitjean F, Webb GI (2019) Proximity forest: an effective and scalable distance-based classifier for time series. Data Min Knowl Discov 33(3):607–635
Lv J, Hu X, Li L, Li P (2019) An effective confidence-based early classification of time series. IEEE Access 7:96113–96124
Mori U, Mendiburu A, Dasgupta S, Lozano JA (2017a) Early classification of time series by simultaneously optimizing the accuracy and earliness. IEEE transactions on neural networks and learning systems
Mori U, Mendiburu A, Keogh E, Lozano JA (2017b) Reliable early classification of time series based on discriminating the classes over time. Data Min Knowl Discov 31(1):233–263
Mori U, Mendiburu A, Miranda IM, Lozano JA (2019) Early classification of time series using multi-objective optimization techniques. Inf Sci 492:204–218
Mueen A, Keogh EJ, Young N (2011) Logical-shapelets: an expressive primitive for time series classification. In: ACM SIGKDD international conference on knowledge discovery and data mining, ACM, pp 1154–1162
Mutschler C, Ziekow H, Jerzak Z (2013) The DEBS 2013 grand challenge. In: Proceedings of the 2013 ACM international conference on distributed event-based systems, ACM, pp 289–294
Nguyen HL, Woon YK, Ng WK (2015) A survey on data stream clustering and classification. Knowl Inf Syst 45(3):535–569
Parrish N, Anderson HS, Gupta MR, Hsiao DY (2013) Classifying with confidence from incomplete information. J Mach Learn Res 14(1):3561–3589
Perol T, Gharbi M, Denolle M (2018) Convolutional neural network for earthquake detection and location. Sci Adv 4(2):e1700578
Protopapas P, Giammarco J, Faccioli L, Struble M, Dave R, Alcock C (2006) Finding outlier light curves in catalogues of periodic variable stars. Mon Not R Astron Soc 369(2):677–696
Rakthanmanon T, Campana B, Mueen A, Batista G, Westover B, Zhu Q, Zakaria J, Keogh E (2012) Searching and mining trillions of time series subsequences under dynamic time warping. In: ACM SIGKDD international conference on knowledge discovery and data mining, ACM
Santos T, Kern R (2016) A literature survey of early time series classification and deep learning. In: Sami@ iknow
Schäfer P (2014) Towards time series classification without human preprocessing. In: Machine learning and data mining in pattern recognition, pp 228–242. springer, Berlin
Schäfer P (2015) The BOSS is concerned with time series classification in the presence of noise. Data Min Knowl Discov 29(6):1505–1530
Schäfer P, Högqvist M (2012) SFA: A symbolic Fourier approximation and index for similarity search in high dimensional datasets. In: Proceedings of the 2012 international conference on extending database technology, ACM, pp 516–527
Schäfer P, Leser U (2017) Fast and accurate time series classification with WEASEL. In: Proceedings of the 2017 ACM on conference on information and knowledge management, pp 637–646
Schölkopf B, Platt JC, Shawe-Taylor J, Smola AJ, Williamson RC (2001) Estimating the support of a high-dimensional distribution. Neural Comput 13(7):1443–1471
Tavenard R, Malinowski S (2016) Cost-aware early classification of time series. In: Joint European conference on machine learning and knowledge discovery in databases, pp 632–647. Springer, Berlin
TEASER Classifier Source Code and Raw Results (2018). https://www2.informatik.hu-berlin.de/~schaefpa/teaser/
Wang Z, Yan W, Oates T (2017) Time series classification from scratch with deep neural networks: a strong baseline. In: Neural networks (IJCNN), 2017 International joint conference on, IEEE, pp 1578–1585
Xing Z, Pei J, Yu PS, Wang K (2011) Extracting interpretable features for early classification on time series. In: Proceedings of the 2011 SIAM international conference on data mining, SIAM, pp 247–258
Xing Z, Pei J, Philip SY (2012) Early classification on time series. Knowl Inf Syst 31(1):105–127
Chen Y, Keogh E, Hu B, Begum N, Bagnall A, Mueen A and Batista G (2015) The UCR time series classification archive. http://www.cs.ucr.edu/~eamonn/time_series_data
Acknowledgements
Open Access funding provided by Projekt DEAL. The author would like to thank the contributors of the UCR datasets.
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible editors: Ira Assent, Carlotta Domeniconi, Aristides Gionis, Eyke Hüllermeier
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schäfer, P., Leser, U. TEASER: early and accurate time series classification. Data Min Knowl Disc 34, 1336–1362 (2020). https://doi.org/10.1007/s10618-020-00690-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10618-020-00690-z