Abstract
Collective social media provides a vast amount of geo-tagged social posts, which contain various records on spatio-temporal behavior. Modeling spatio-temporal behavior on collective social media is an important task for applications like tourism recommendation, location prediction and urban planning. Properly accomplishing this task requires a model that allows for diverse behavioral patterns on each of the three aspects: spatial location, time, and text. In this paper, we address the following question: how to find representative subgroups of social posts, for which the spatio-temporal behavioral patterns are substantially different from the behavioral patterns in the whole dataset? Selection and evaluation are the two challenging problems for finding the exceptional subgroups. To address these problems, we propose BNPM: a Bayesian non-parametric model, to model spatio-temporal behavior and infer the exceptionality of social posts in subgroups. By training BNPM on a large amount of randomly sampled subgroups, we can get the global distribution of behavioral patterns. For each given subgroup of social posts, its posterior distribution can be inferred by BNPM. By comparing the posterior distribution with the global distribution, we can quantify the exceptionality of each given subgroup. The exceptionality scores are used to guide the search process within the exceptional model mining framework to automatically discover the exceptional subgroups. Various experiments are conducted to evaluate the effectiveness and efficiency of our method. On four real-world datasets our method discovers subgroups coinciding with events, subgroups distinguishing professionals from tourists, and subgroups whose consistent exceptionality can only be truly appreciated by combining exceptional spatio-temporal and exceptional textual behavior.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Popular social media platforms such as Twitter and Instagram have millions of users who share their photos, stories and geo-locations. This allows the collective social media to reflect diverse human behavioral patterns. The behavioral patterns in social posts are represented by distributions of spatial locations, time, and word topics (Hong et al. 2012). Specific deviations across any combination of these three distributions can indicate interesting, exceptional behavior of the population; one can for instance see such deviations surrounding large events, such as sports games and concerts (Zheng et al. 2018). In this paper, instead of social posts for individuals, we are interested in finding social posts for subgroups restricted by descriptions, for which the behavioral patterns are substantially different compared to the behavioral patterns in the whole dataset. Discovering and understanding these behavioral patterns on collective social media is a task of predominant importance, since properly accomplishing this task can benefit applications such as tourism recommendation, location prediction, and urban planning (Kim et al. 2016).
To contribute to this behavioral understanding, instead of finding outlying social posts far from the main activity areas, we are looking for exceptional subgroups: coherent subsets for which we can formulate concise descriptions in terms of conditions on attributes of the data (Herrera et al. 2011; Atzmueller 2015), e.g., ‘Age < 25 \(\wedge \) gender = Female’. The most challenging problems for finding exceptional subgroups are: how to model the spatio-temporal behavior and quantify the exceptionality of the subgroups? Before proposing the solution, we discuss the challenges which need to be overcome at first:
Spatio-temporal modeling Difficulties stem from two aspects. On the one hand, unlike modeling behavior of individuals, where the records are grouped by certain subjects (Yuan et al. 2017), in our problem setting, the candidate subgroups are apriori unknown. We cannot model the spatio-temporal behavior of all the subgroups either, because of the pattern explosion problem (Meeng et al. 2014). This means that we cannot directly model the global distribution of behavioral patterns over the whole dataset. On the other hand, collective social activities typically contain uncertain spatial, temporal, and text information on diverse scales (Jankowiak and Gomez-Rodriguez 2017). To properly overcome these challenges, we need a model that can handle the diverse, uncertain, large scale, and high-dimensional information in collective social posts and induce the global distribution of behavioral patterns in the whole dataset.
Exceptionality evaluation Our aim is to identify exceptional behavioral patterns of social posts in subgroups. The general method would be to learn the distributions of spatial locations, time, and texts empirically by probability mass (Giannotti et al. 2016), followed by comparing the distributions in subgroups with the global distributions in the whole dataset. However, this method is not applicable for the research problem of this paper. The reasons are two-fold. On the one hand, given limited records, we cannot be confident whether a subgroup is exceptional or not in long term behavior only by comparing the empirical distributions. On the other hand, because of the uncertainty and diversity of social posts in collective social media, it is difficult to simply assume a distribution for the behavioral pattern and build a null hypothesis to test (Hooi et al. 2016).
To overcome these challenges, we propose BNPM: a Bayesian non-parametric model for spatio-temporal behavior modeling on the subgroup level. In BNPM, we randomly sample arbitrarily large numbers of subgroups as the training samples in order to estimate the global behavior. We employ a Chinese Restaurant Process (CRP) to gather those randomly sampled subgroups into several components. In this process, the behavioral pattern of each subgroup is assumed to follow a prior distribution. Subgroups in one CRP component are allowed to have variations in distribution, but similar kinds of behavior ought to aggregate within every single component. Hence, the CRP model allows for modeling multiple types of normal behavior to occur simultaneously, which more accurately represents real life than if we assume one monolithic kind of normal behavior. The ‘non-parametric’ in our model means that there are infinitely many parameters indicating the distributions of behavioral patterns. We estimate the global distribution of behavioral patterns in the whole dataset by the mixture of behavioral patterns with mixture coefficients of the components [cf. Eq. (19)]. Specifically, for each given subgroup, we can calculate its posterior distribution with the learned BNPM, according to the information of spatial locations, time, and texts. The exceptionality score of the given subgroup is derived by computing the distance between the posterior distribution and the global distribution. We employ a variant of weighted KL-divergence (van Leeuwen and Knobbe 2012) for multi-variate distribution (Soch and Allefeld 2016), to calculate the distance between the posterior distribution of the subgroup and the global distribution. Finally, we aggregate the exceptionality scores in the aspects of spatial locations, time, and texts as the final exceptionality score of the candidate subgroup.
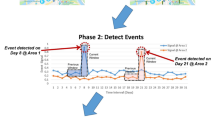
In Fig. 1, we present an artificial example to show the advantage of our method. From the perspective of a point estimate, both the red and the yellow subgroups are exceptional compared with the global population (in blue). However, from the perspective of Bayesian posterior distribution, the yellow one is much more suspicious than the red one. The reason is that the point estimate uses limited data to estimate the behavioral pattern, which might lead to biased results. The Bayesian non-parametric method evaluates the exceptionality of behavioral patterns by comparing the posterior distribution with the global distribution, which can help us effectively find exceptional behavioral patterns and prevent false discoveries.
The training process of our model includes two iteration steps: assigning subgroups into components and updating hyper-parameters for the components. These two processes influence each other iteratively. We integrate these two steps with the collapsed Gibbs sampling (Porteous et al. 2008) algorithm. Having learned the well-trained model over the whole dataset, we can calculate the posterior distribution for any subgroup across the location distribution, time distribution, and text distribution. This allows us to employ Exceptional Model Mining (EMM) to automatically discover subgroups with exceptional spatio-temporal behavior. The whole process of our method is shown in Fig. 2. To demonstrate the effectiveness and scalability of our method, we validate our model by conducting experiments on four real-world datasets from New York, London, Tokyo, and Shenzhen.
The resulting subgroups illustrate the versatility of the method. In London, our method discovers the spatially coherent subgroup of people attending a specific football match. In Tokyo, it discovers a subgroup of people frequenting three locations in a specific ward: two touristic attractions and a station where trains leave for a third touristic attraction (identified by analyzing the texts of the tweets) which is located relatively far away. The combination of spatio-temporal behavior and tweet text behavior can benefit the uncovering of such a subgroup, which is where the added value of our method lies. Finally, in another ward of Tokyo, two subgroups separate the professionals and the tourists by their combined spatio-temporal and tweet text behavior.
1.1 Main contributions
-
We introduce BNPM: a Bayesian non-parametric model for spatio-temporal behavior modeling on the subgroup level. BNPM can handle diverse, uncertain, large scale and multi-modal information in collective spatio-temporal data.
-
We define a new evaluation method for exceptional model mining. The global distribution is generated by the mixture of behavioral patterns in BNPM. By comparing the posterior distribution of a candidate subgroup with the global distribution, we can quantify the exceptionality of subgroups.
-
We conduct various experiments on four real-world datasets. The results show that our method is effective and efficient for finding exceptional social posts on the subgroup level.
2 Related work
Exceptional spatio-temporal behavior mining on the subgroup level is related to three fields: anomaly detection (Chandola et al. 2009), exceptional model mining (Duivesteijn et al. 2016) in the aspect of exceptionality metric; and spatio-temporal modeling (Atluri et al. 2017) in the aspect of behavior modeling.
2.1 Anomaly detection
Anomaly detection is highly explored in online ratings (Hooi et al. 2016), reviews (Xie et al. 2012), and social network analysis (Shin et al. 2017). In order to detect collective anomalies on spatio-temporal datasets with different distributions, densities and scales, researchers have proposed a multi-source topic model for spatio-temporal modeling (Wu et al. 2017; Zheng et al. 2015). Methods such as classification, statistical, and regression models are used for modeling user behavior to discover anomaly patterns (Shipmon et al. 2017).
Unlike anomaly detection, there is no labeled data for identifying anomalies in exceptional model mining. This means that standard supervised learning cannot be used directly for this task. The exceptional subgroups are identified by comparing the performance of the model in subgroups with the performance of the model in the whole dataset, for which the subgroups are restricted by the descriptive variables (Duivesteijn et al. 2016). The whole process of exceptional model mining lies into the fields of knowledge discovery. This formulates the main difference between the research of anomaly detection and exceptional model mining.
2.2 Exceptional model mining
The aim of subgroup discovery (SD) (Atzmueller 2015) is to find subsets described by combinations of attributes, in which the distribution of one predefined target column is significantly different from the distribution in the whole dataset. Exceptional model mining (EMM) (Duivesteijn et al. 2016) can be seen as an extension of SD, focusing on multiple target columns. In EMM, a measure of exceptionality is defined that indicates how different a model fitted on the targets is within the subgroup, as compared to that same model fitted on the targets in the whole dataset. Several model classes (Kaytoue et al. 2017; Jorge et al. 2012) have been defined and explored; for instance, Bayesian networks (Duivesteijn et al. 2010), and regression (Duivesteijn et al. 2012). Though existing model classes can handle all kinds of targets, most cannot model spatio-temporal behavior, which contains geo-spatial coordinates and timestamps. Lemmerich et al. (2016) introduce first-order Markov chains as a model class for sequence data, which can be used for mining exceptional transition behavior. Bendimerad et al. (2016) employ weighted relative accuracy to evaluate characteristics in subgraphs of urban regions. However, they do not consider the text information, especially the word topics. This information integration is the added value of our model.
The exceptionality measure in SD & EMM is called quality measure. Popular examples include WRAcc (van Leeuwen and Knobbe 2011), z-score (Mampaey et al. 2015), and KL-divergence (van Leeuwen and Knobbe 2012). An efficient method to find subgroups optimizing for multiple quality measures at once can be found in Soulet et al. (2011). In order to properly handle the noise inherent to spatial and temporal data and prevent false positives, we introduce a quality measure under the Bayesian framework.
2.3 Spatio-temporal modeling
There is a vast amount of literature about spatio-temporal data mining (Atluri et al. 2017; Lane et al. 2014; Wang et al. 2011; Yuan et al. 2017). Most work focuses on modeling mobility patterns of individuals or groups aiming at location prediction or period discovery. The basic assumption is that individuals or groups might have a regular activity area, which indicates the inner similarity of social and geographic closeness (Cranshaw et al. 2010). Becker et al. (2016) introduce a Bayesian approach for comparing hypotheses about human trails on the web. Piatkowski et al. (2013) present a graphical model designed for efficient probabilistic modeling of spatio-temporal data, which can keep the accuracy as well as efficiency. Knauf et al. (2016) propose a spatio-temporal kernel for multi-object scenarios. A branch of research focuses on visual analytics for spatio-temporal modeling (Zheng et al. 2016). Interactive and human-guided methods are employed to discover the behavioral patterns and understand the heterogeneous information in the urban data (Puolamäki et al. 2016; Chen et al. 2018). The differences between our work and the work before are two-fold. On the one hand, the collective social posts on the subgroup level in our research is constrained by the descriptions, which distinguishes our work from others such as twitter stream clustering or user clustering (Chierichetti et al. 2014). On the other hand, the exceptional subgroups and the components of behavioral distributions are unobserved from the datasets, which means that we have to establish a model for the modeling of global distribution of behavioral pattern as well as discovering the exceptional subgroups comparing with this global distribution.
3 Preliminaries
Assume a dataset \(\varOmega \): a bag of m records \(r\in \varOmega \) of the form:
where s and u are positive integers. We call \(a_1,\ldots ,a_s\) the descriptive attributes or descriptors of r, and \(b_1,\ldots ,b_u\) the target attributes or targets of r. The descriptive attributes are taken from an unrestricted domain \({\mathcal {A}}\). Mathematically, we define descriptions as functions \(D: {\mathcal {A}} \rightarrow \{0,1\}\). A description D covers a record \(r^j\) if and only if \(D(a_1^j, \ldots , a_s^j) = 1\).
Definition 1
(Subgroup) The subgroup corresponding to a description D is the bag of records \(G_D \subseteq \varOmega \) that D covers:
Definition 2
(Quality measure) A quality measure is a function \(\varphi :{\mathcal {D}} \rightarrow {\mathbb {R}}\) that assigns a numeric value to a description D. Occasionally, we use \(\varphi (G)\) to refer to the quality of the induced subgroup: \(\varphi (G_D)=\varphi (D)\).
Typically, a quality measure assesses the subgroup at hand based on some concept in terms of the targets. Hence, a description and a quality measure interact through different partitions of the dataset columns; the former focuses on the descriptors, the latter focuses on the targets, and they are linked through the subgroup.
A Chinese Restaurant process (CRP) (Blei et al. 2010) is a distribution on partitions of integers obtained by imagining a process by which \(n-1\) customers sit down in a Chinese restaurant with an infinite number of tables with infinite capacity. Whenever a new customer arrives, customer n, she can either choose an existing table k with \(n_k\) seated customers or sit at an empty table, following distribution:
In each step a new table is created with non-zero probability, which allows this process to adapt to increasing complexity of the data.
4 Subgroup-level spatio-temporal modeling (BNPM)
We consider the spatio-temporal behavior of geo-tagged social posts on the level of subgroups restricted by descriptive attributes. For notational purposes, we ignore that these subgroups need to be generated somehow; instead, we assume that some process has delivered us a list of subgroups, indexed \(i=1,\ldots ,n\), where subgroup i has \(d_i\) posts, indexed by \(j=1,\ldots ,d_i\). The posts in subgroup i are denoted by the variables \(r_{ij}\in \{1,2,\ldots ,m\}\); posts may belong to multiple subgroups. Each post is a 3-tuple \(r_{ij}\) = (\(l_{ij}\),\(t_{ij}\),\(w_{ij}\)), where \(l_{ij}\) = (x,y), \(t_{ij}\) = t and \(w_{ij}\) = {\(w_1, \dots , w_q\)} represent the spatial location, time, and text in a geo-tagged post. Table 1 lists the notations used in the rest of this paper. We now propose the problem of discovering subgroups with exceptional spatio-temporal behavior as follows:
Problem 1
(Discovering subgroups with exceptional spatio-temporal behavior) Given a dataset of geo-tagged social posts \(\varOmega \), descriptive attributes taken from \({\mathcal {A}}\), descriptions \(D: {\mathcal {A}} \rightarrow \{0,1\}\), and a quality measure \(\varphi \), our aim is to find a bag of subgroups \(\{S_{D_1},\ldots ,S_{D_q}\}\), where \(\forall D' \in {\mathcal {D}}\setminus \{D_1,\ldots ,D_q\}, \forall D \in \{D_1,\ldots ,D_q\}, \varphi (D') \le \varphi (D)\).
The main challenge for this problem is the subgroup selection process with regard to the exceptionality compared with the global population. To accomplish this task, we need a spatio-temporal model on the subgroup level, to model the behavioral patterns in the global population and subgroups.
4.1 The Bayesian non-parametric model
Several intuitions underpin our model:
-
1.
The behavioral patterns of subgroups over the whole dataset can be captured by several components. Each component follows a single triplet of prior distributions: of spatial locations, time, and word topics. We assume that the social posts are generated by the mixtures of components with mixture coefficients, but the number of components and the mixture coefficients are unobserved from the dataset.
-
2.
Despite following the same prior distribution, subgroups within the same component need not have the same distributions of spatial locations, posting time, and texts.
-
3.
Social posts are distributed in spatial regions, with time ranges as well as word topics. These distributions indicate the spatio-temporal behavioral patterns of subgroups. The spatio-temporal behavioral pattern varies according to the center and scale of the region and time, as well as the word topics.
Based on these intuitions, we assume that subgroups and social posts are governed by a generative model. This model for spatio-temporal behavior on the subgroup level is a mixture model in which each subgroup belongs to one of the components, in order to capture different types of behavior. Each component represents a behavioral pattern with specific prior distributions of location, time, and word topics. The spatial location associated to each geo-tagged post is drawn from a multivariate Gaussian distribution, as suggested by Gonzalez et al. (2008):
For each component, we assume that a Normal-Inverse-Wishart (NIW) distribution is the prior distribution that governs the generating of means and covariance matrices (\(\mu ,\varSigma \)) for spatial locations, as suggested by Yuan et al. (2017):
Similarly, we can write down the generative process of time t from a univariate Gaussian distribution, as suggested by Cho et al. (2011), as:
where the mean \(\upsilon \) and variance \(\sigma \) are drawn from a Normal-Gamma prior distribution, as suggested by Yuan et al. (2017):
Each word w in \(\{w_1,\ldots ,w_q\}\) is drawn from a multinomial distribution, as suggested by Jankowiak and Gomez-Rodriguez (2017):
where \(\theta \) is a distribution that represents proportions of words in vocabulary V, which depends on the Dirichlet prior \(\theta _0\) (Jankowiak and Gomez-Rodriguez 2017):
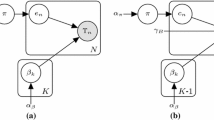
By construction, the proposed generative model gathers the subgroups into several components, which raises the question how many components we should set. If we set the number too high, spatio-temporal behavioral patterns of subgroups may vary too much, which will impede proper evaluation of behavior exceptionality. Conversely, if we set the number too low, exceptional subgroups may be mixed with normal subgroups, which will lead to false positive errors. This is where we employ the Chinese Restaurant Process (cf. Sect. 3). The full generative process (cf. Fig. 3) can be summarized as follows:
-
1.
Set the number of components K \(\leftarrow \) 0
-
2.
For \(i=1,\ldots ,n\):
-
(a)
Assign subgroup i to an existing component \(k \in \{1,\ldots ,K\}\) with probability \(\beta _k\) = \(\frac{n_k}{i-1+\alpha }\), or to a new component \(k = K+1\) with probability \(\frac{\alpha }{i-1+\alpha }\).
-
(b)
Draw \((\mu _{i},\varSigma _{i})|z_i=k \sim \mathcal {NIW}(\mu _{0k},\lambda _k,W_k,\nu _k)\).
-
(c)
Draw \((\upsilon _i,\sigma _i)|z_i=k \sim \mathcal {NG}(\upsilon _{0k},\kappa _k,\rho _k,\psi _k)\).
-
(d)
Draw \(\theta _{i}|z_i=k \sim \text {Dirichlet}(\theta _{0k})\).
-
(e)
For j = 1,...,\(d_i\):
-
(i)
Draw \(l_{ij} \sim {\mathcal {N}}({\mathbf {l}}|\mu _{i},\varSigma _{i})\).
-
(ii)
Draw \(t_{ij} \sim {\mathcal {N}}({\mathbf {t}}|\upsilon _{i},\sigma ^2_{i})\).
-
(iii)
Draw each \(w_{ijq} \in \{w_1,\ldots ,w_q\}\)\(\sim Mult({\mathbf {w}}|\theta _{i})\).
-
(i)
-
(f)
Update hyper-parameters in component k.
-
(a)
4.2 Inference method
As illustrated above, to conduct the whole generating process, we need to estimate the latent variables, which cannot be observed directly from the datasets. We propose to employ collapsed Gibbs sampling to infer the latent variables in the proposed generative model efficiently (Porteous et al. 2008). Given full observation of n subgroups, the total likelihood is:
We exploit the conjugacy between the multinomial and Dirichlet distributions, the Gaussian and Normal-Inverse-Wishart distributions, and the Gaussian and Normal-Gamma distributions. Hence we can analytically integrate out the parameters \({\beta }, {\mu }, {\Sigma }, {\upsilon }, {\sigma }\), and \({\theta }\), and only sample the component assignments \({\mathbf {z}}\), which is done as follows:
The first term of Eq. (6) is governed by the CRP:
The second term is the posterior predictive distribution of \(\mathbf {l}_\mathbf {i}\) in component k, excluding subgroup i. We assume that each post in subgroup i is generated equivalently, hence the second term equals:
Here, \(\mathbf {l_{k \lnot i}}, n_{k \lnot i}\) are locations, and the number thereof in component k after excluding subgroup i,
The posterior predictive distribution of each \(l_{ij}\) follows a bivariate Student’s t-distribution (Murphy 2007). Similarly, we can write down the posterior predictive distribution of \({\mathbf {t_i}}\) in the third term of Eq. (6):
The posterior predictive distribution of each \(t_{ij}\) follows a univariate Student’s t-distribution. For the fourth term of Eq. (6), each posterior predictive distribution of \(\mathbf {w_{ij}}\) for post j in subgroup i follows a Dirichlet-multinomial distribution (Tu 2014):
Here, \(c_{k \lnot i}\) is total number of words in component k so far excluding subgroup i, \(c_{wk \lnot i}\) is how often word w occurs in component k so far excluding subgroup i, \(c_{j}\) is the total number of words in post ij, and \(c_{wj}\) is how often word w occurs in post ij.
Our model assumes that each component has its own specific hyper-parameters. If we fix all the assignments of \({\mathbf {z}}\), we use random search for hyper-parameter optimization (Bergstra and Bengio 2012) to choose \(\mu _{0k},\lambda _k,W_k,\nu _k\), \(\upsilon _{0k},\kappa _k,\rho _k,\psi _k\), and \(\theta _{0k}\). Our goal is maximizing the marginal likelihood of the data in each component (Bergstra et al. 2011):
Now, we can build up the two iteration processes in our inference algorithm. The one is iteratively optimizing hyper-parameters for fitting subgroups in associated components. The other is iteratively sampling component assignments to assign subgroups. These two steps influence each other: better hyper-parameter selection provides more accurate posterior predictive distribution to assign subgroups; better assignments for subgroups can provide more accurate likelihood estimation for hyper-parameter selection. We iteratively run these two steps until a maximum number of iterations is reached. See Algorithm 1 for details.

4.3 Subgroup evaluation method
Having learned the proposed model, we need to evaluate the exceptionality of a subgroup. Behavioral patterns are gauged in terms of the location distribution, time distribution, and text distribution. As an example, we use time distribution to explain our method for exceptionality evaluation. Let \(\mathbf {t_i}\) denote a vector representing the post time of collective social posts in subgroup i. Generally, people will assume a distribution for P(t), e.g., \({\mathcal {N}}(\upsilon ,\sigma )\), and use the point estimate of \(\upsilon \) and \(\sigma \) as the estimated parameters of that distribution. The learned distribution is regarded as an estimation about the temporal behavioral pattern of subgroup i. However, this distribution is not sufficient to represent the real behavioral pattern of subgroup i, because we cannot be confident about the behavior of that subgroup with limited records. Hence, in this paper, instead of a point estimate for a distribution with limited data, we compute the posterior distribution as our belief about the behavioral pattern of a subgroup. For each given candidate subgroup i, we firstly estimate the component assignment \(z_i\) on this subgroup by using Eqs. (6), (7), (8), (10), and (12). Then, with BNPM, we calculate the posterior distribution of subgroup i’s location distribution, time distribution, and text distribution:
Here we calculate the posterior parameters the same way as Eqs. (9), (11), and (12), with the prior hyper-parameters in component \(z_i\). Having obtained the posterior distribution, the next step is to evaluate the exceptionality. In the training process, we learn the mixture proportion of components denoted as \(\beta \). The global distribution of time is governed by both components and the mixture proportion of components. We can calculate the distribution of time in the global population by Eq. (2) as:
This distribution describes the temporal behavioral pattern averaged by the global population. Now we can compare the posterior distribution of time conditioned on a subgroup, with the global distribution of time. The more different they are, the more exceptional the subgroup is. The difference indicates how difficult it is to generate the time distribution in that subgroup under the global population. In order to quantify this difference, we employ KL-divergence as the distance measure between two distributions. For simplicity, we represent Eq. (17) with \(f(\upsilon ,\sigma )\) and Eq. (19) with \(g(\upsilon ,\sigma ) = \sum _{k=1}^{K}\beta _k \cdot g_k(\upsilon ,\sigma )\). The exceptionality score of a given subgroup i in the time aspect is:
where \(\frac{d_i}{m}\) represents the generality of subgroup i, which is a trade-off with exceptionality. Note that \(g(\upsilon ,\sigma )\) is a mixture of several distributions, with which it is difficult to compute the KL-divergence efficiently. In order to overcome this problem, we propose to compute the Goldberger approximation (Goldberger et al. 2003):
According to the properties of conjugate prior, the posterior distribution has the same form as the prior distribution. Thanks to properties of the \(\mathcal {NG}\) function (Soch and Allefeld 2016), we can compute the KL-divergence of two \(\mathcal {NG}\) distributions as follows:
where h(x) is the digamma function. Combining this outcome with Eqs. (20) and (21), we compute the difference between the posterior distribution of time conditioned on one subgroup and the distribution of time in the whole dataset, denoted as \(\varphi _{t_i}\). Similarly, we calculate \(\varphi _{l_i}\) and \(\varphi _{w_i}\). Then we aggregate these three exceptionality indicators after normalizing to get the final exceptionality score:
5 Experiments
We evaluate the performance of our method on four real-world datasets from four cities on three continents: Twitter datasets from London, Tokyo, and New York, and a Weibo dataset from Shenzhen. The details of datasets are shown in Table 2. The attributes of tweets contain: country, current living place, followers, following, listed, language, favourites, retweets, bio, date, source, gender, hour, latitude, longitude, and tweet text. We preprocess the tweets as follows:
-
1.
Converting the date into weekdays from 1 to 7;
-
2.
Extracting occupation from bio, such as student, driver, writer, editor, and so on;
-
3.
Removing stop words;
-
4.
Converting hours to float, from 1 to 24.
We use hour, latitude and longitude, and tweet text as the input values for temporal, spatial, and text information, respectively. All other attributes are used as the descriptors to generate subgroups. All the experiments are carried out on an Intel Core i7 2.60 GHz laptop, 24GB RAM, Windows 10.Footnote 1
To train BNPM by Algorithm 1, we must generate a set of input subgroups. To do so, we randomly sample 100,000 subgroups for which the coverages are ranging from 10 to 50% of the posts in the original dataset. For the spatial part, we calculate the mean coordinate and covariance from the data itself as the prior mean \(\mu _0\) and prior covariance W. The other hyper-parameters are initialized as follows: \(\lambda = 1, \nu = 30\). For the temporal part, we calculate the prior mean of post time \(v_0\) and initialize other hyper-parameters as follows: \(\alpha =0.1, \kappa = 0.1, \rho = 0.5, \psi = 0.1\). Through these settings and parametrizations, we train the BNPM model to capture the behavioral patterns in the global dataset; for instance the time distribution can now be estimated with Eq. (19).
Having captured the global behavior, we can now mine for subgroups exhibiting exceptional behavior, by contrasting their behavior against the norm. We employ the beam search algorithm given in Duivesteijn et al. (2016), Algorithm 1 for the subgroup search process. In the quality measure step, we calculate the exceptionality score of a subgroup by the method in Sect. 4.3. We set the beam width to 50 and the search depth to 2. This last parameter setting is relatively narrow; it ensures that we find subgroups expressed as a conjunction of at most two conditions on descriptive attributes. The reason to not mine to a greater search depth is philosophical rather than technical: computational complexity would allow us to mine deeper without prohibitive time cost, but when we allow our resulting subgroups to be defined in terms of a conjunction of more conditions on attributes, it becomes more and more opaque which of these conditions are actually relevant, and it becomes less clear what to do with the resulting information: mining deeper leads to subgroups which are no longer actionable.
5.1 London and Shenzhen
In Tables 3 and 4, we present the top 5 most exceptional subgroups found in Shenzhen and London, respectively. High frequency words in those subgroups are presented to show the main topics in the text of the tweets. We can see that the discovered subgroups restricted by specific descriptions show specific topical behavior, which can help us to further discover special events reflected by the group of social posts.
The top subgroup found in London encompasses the collective social posts described by “weekday: 6–7 \(\wedge \) Place == Hammersmith London”. The spatio-temporal behavior focuses on Saturday and Sunday in the borough of Hammersmith & Fulham in west London, a map of which is shown in Fig. 4 with in red a heatmap of the spatial locations of the tweets. We visualize the texts of the posts by generating a word cloud shown in Fig. 5, which shows that the main keywords of the tweets frequently contain Chelsea, Stamford, Football, VS, etcetera. It just so happens that on April 16, 2016, a Premier League football match between Chelsea and Manchester City was played at Stamford Bridge, which is the football stadium surrounding the green cross in Fig. 4. Our model accurately captured this subgroup that has specific spatio-temporal behavior with specific word topics. This shows that our method can discover and identify meaningful exceptional collective behavior.
5.2 New York
Figure 6 displays subgroups found in New York. Our method discovers a subgroup of people who live in Manhattan but do not speak English (D:Language != ‘en’ \(\wedge \) Place == Manhattan). From the word topics in those social posts, we can see that they are talking about the attractions and entertainments in Manhattan. In addition, we discover a subgroup of people discussing protest rallies in a suburb (D:Place == Yonkers), and a group of French speakers (Language == ‘fr’) sending tweets about a famous French restaurant, Aux Merveilleux de Fred. These findings show that characterizing groups of the dataset by the defined descriptive variables such as ‘Language’ and ‘Place’ contains sufficient information to discover subgroups with exceptional behavior in terms of spatial location, time, and texts.
Word cloud generated from the texts of tweets covered by the subgroup plotted in Figure 4
5.3 Tokyo
The full versatility of results that one could find with BNPM is on display in Fig. 7, featuring the top subgroups found in Tokyo.
The top subgroup (D:Place == Chiyoda-ku) concentrates on the centrally-located ward of Chiyoda. The heatmap shows that the people in this specific subgroup are mainly concentrated in three locations. The bottom-left location is the top attraction in Chiyoda ward: the imperial palace. The top-right location is Akihabara, nicknamed Akihabara Electric Town, which is a shopping district for video games, anime, manga, and computer goods; its function as a cultural center for all things electronic makes Akihabara a major touristic attraction in its own right. The bottom-right location is Tokyo station, which is far from a touristic attraction. Its relevance becomes clear when looking at the tweet texts, which include references to DisneySea. This is yet another major touristic attraction of Tokyo, but it is located 15 kilometers away from Chiyoda ward. However, the easiest way for tourists to reach this destination is by taking a train on the Keiyo line, whose trains depart from Tokyo station. Hence, tourists that visit the imperial palace and Akihabara also express interest through tweets in visiting DisneySea, which is to be reached by a train departing from the ward in which the other two attractions lie. This finding shows that the combination of spatio-temporal behavior and word topics can benefit the discovery of such exceptional subgroups.
The second subgroup found in Tokyo (D:Language != ‘es’ \(\wedge \) Place == Shinjuku-ku) contrasts with subgroups discussed so far: these clearly are not tourists. Shinjuku is the major commercial and administrative center. Filtering out the people who tweet in Spanish (we will discuss this group later, in the fourth subgroup), we are left with a group of people discussing topics like job hiring and career. Spatial locations of these people are strongly concentrated around Shinjuku train station (where big department stores, electronic stores, banks, and city hall are located), which makes sense for professionals.
The third subgroup (D:Place == Shibuya-ku) focuses on Shibuya ward, which is a major destination for fashion and nightlife. Arguably its most famous attraction is the Shibuya scramble crossing, a crosswalk at a busy intersection just outside of Shibuya station, where pedestrians in all directions (including diagonal) get the green light at the same time. The main spatial focus in this subgroup is located at that crossing. In the tweet texts we find references to Tsutaya, which is a book store located on a corner of that crossing. On the second floor of Tsutaya is a Starbucks coffee shop, whose numerous window seats overlook the scramble crossing.
In contrast with the second subgroup, the fourth subgroup found in Tokyo (D:Language == ‘es’ \(\wedge \) Place == Shinjuku-ku) concentrates on the same ward (Shinjuku), but this time only on those people who tweet in Spanish. These are more likely to be tourists. The spatial location of these people is concentrated a few blocks to the west of Shinjuku station, where Tokyo Metropolitan Government Building is located. This building is famous for its observation deck, which provides a view over all of Tokyo and, if the weather is good, of Mount Fuji. This is the one place in Shinjuku which is of specific interest to tourists, and our BNPM model manages to separate out these from the professionals in the second subgroup. Notice also the interest expressed in the tweet texts of the fourth subgroup for Disney, which is absent from the tweets of the second subgroups.
5.4 Scalability
In this paper, we consider the scalability of our BNPM method in the aspect of model learning. According to Algorithm 1, the runtime is \({\mathcal {O}}(MAX \times n \times {\bar{K}})\). MAX represents the maximum number of loops we run random search for hyper-parameter optimization (\({\bar{K}}\) time) and collapsed Gibbs sampling (\(n\times {{\bar{K}}}\) time). \({\bar{K}}\) represents the average number of latent components. n represents the number of input subgroups. Figure 8 shows the relation between runtime behavior and n.
6 Conclusions
We propose a novel method for mining exceptional spatio-temporal behavior on collective social media. Behavior in this setting can be exceptional in three distinct ways: in terms of spatial locations, time, and texts. We develop a Bayesian non-parametric model (BNPM) to automatically identify spatio-temporal behavioral patterns on the subgroup level, explicitly modeling the three exceptional behavior types. Using a Chinese Restaurant Process, our model can cater for several distinct forms of global behavioral patterns, while also allowing for subgroup behavior that is exceptional w.r.t. all the kinds of global behavior. This behavioral dissimilarity can manifest itself in any subset of the three behavior types. The global distribution of the whole dataset can be summarized by the mixture of behavioral patterns with mixture coefficients in the components gathered by our model. We can also induce the distribution of a candidate subgroup by calculating its posterior distribution with BNPM, according to the behavioral data in that subgroup. The distance between the posterior distribution of the candidate subgroup and the global distribution indicates the exceptionality of that subgroup. This allows us to provide an effective evaluation method to measure the exceptionality of a behavioral pattern and to employ it in finding exceptional subgroups with collective social behavior. We develop an efficient learning algorithm based on collapsed Gibbs sampling to train the model.
We report results on datasets from various countries, continents, and cultures: BNPM finds exceptional subgroups in Shenzhen (cf. Table 3), London (cf. Table 4 and Figs. 4 and 5 ), New York (cf. Fig. 6), and Tokyo (cf. Fig. 7). The results in London illustrate how BNPM can discovery unusual spatio-temporal tweeting behavior that coincides with a specific event: a Premier League football match of Chelsea F.C. (cf. Figs. 4 and 5 ). But the capabilities of BNPM range far beyond event detection, as illustrated by the top subgroup found in Tokyo (cf. Fig. 7, leftmost figure). Here, we discover a subgroup whose spatial behavior mostly revolves around three locations: two touristic attractions and a train station. The relevance of the train station becomes apparent when analyzing the tweet text behavior of the subgroup: the involved people frequently talk about a third touristic attraction 15 kilometers away, which is easiest reached by a train that departs from the discovered station. Hence, the exceptionality of this subgroup can only be properly appreciated by jointly analyzing the exceptionality of spatio-temporal and tweet text behavior, which is precisely what BNPM is designed to do. Similarly, contrasting the second and fourth most exceptional subgroups found in Tokyo, we can distinguish the professionals from the tourists in Shinjuku ward by their exceptional joint spatial and tweet text behavior.
The four datasets analyzed in this paper stem from four countries on three continents. Hence, we illustrate that BNPM is effective across various languages, religions, and cultures. In future work, it would be interesting to further investigate exactly how the vastly varying language patterns affect the proposed model.
Notes
The code and datasets of our work are available for reviewing purposes: https://www.dropbox.com/sh/m8fb6iz29gq3r0l/AAABS7vMYFx-kS6S3t-9o0ZQa?dl=0.
References
Atluri G, Karpatne A, Kumar V (2017) Spatio-temporal data mining: a survey of problems and methods. arXiv preprint arXiv:1711.04710
Atzmueller M (2015) Subgroup discovery. Wiley Interdiscip Rev Data Min Knowl Discov 5(1):35–49
Becker M, Mewes H, Hotho A, Dimitrov D, Lemmerich F, Strohmaier M (2016) SparkTrails: a MapReduce implementation of HypTrails for comparing hypotheses about human trails, WWW Companion, pp 17–18
Bendimerad AA, Plantevit M, Robardet C (2016) Unsupervised exceptional attributed sub-graph mining in urban data. In: 2016 IEEE 16th international conference on data mining (ICDM), IEEE, pp 21–30
Bergstra J, Bengio Y (2012) Random search for hyper-parameter optimization. J Mach Learn Res 13(Feb):281–305
Bergstra JS, Bardenet R, Bengio Y, Kégl B (2011) Algorithms for hyper-parameter optimization. In: Advances in neural information processing systems, pp 2546–2554
Blei DM, Griffiths TL, Jordan MI (2010) The nested Chinese restaurant process and Bayesian nonparametric inference of topic hierarchies. J ACM 57(2):7:1–7:30
Chandola V, Banerjee A, Kumar V (2009) Anomaly detection: a survey. ACM Comput Surv 41(3):151–1558
Chen W, Huang Z, Wu F, Zhu M, Guan H, Maciejewski R (2018) Vaud: a visual analysis approach for exploring spatio-temporal urban data. IEEE Trans Visual Comput Gr 24(9):2636–2648
Chierichetti F, Kleinberg JM, Kumar R, Mahdian M, Pandey S (2014) Event detection via communication pattern analysis. In: Proc ICWSM, pp 51–60
Cho E, Myers SA, Leskovec J (2011) Friendship and mobility: user movement in location-based social networks. In: Proceedings of the 17th ACM SIGKDD international conference on knowledge discovery and data mining, ACM, pp 1082–1090
Cranshaw J, Toch E, Hong J, Kittur A, Sadeh N (2010) Bridging the gap between physical location and online social networks. In: Proceedings of the 12th ACM international conference on Ubiquitous computing, ACM, pp 119–128
Duivesteijn W, Knobbe A, Feelders A, van Leeuwen M (2010) Subgroup discovery meets Bayesian networks—an exceptional model mining approach. In: 10th international conference on data mining (ICDM), IEEE, pp 158–167
Duivesteijn W, Feelders A, Knobbe A (2012) Different slopes for different folks: mining for exceptional regression models with cook’s distance. In: Proceedings of the 18th ACM SIGKDD international conference on Knowledge discovery and data mining, ACM, pp 868–876
Duivesteijn W, Feelders AJ, Knobbe A (2016) Exceptional model mining. Data Min Knowl Disc 30(1):47–98
Giannotti F, Gabrielli L, Pedreschi D, Rinzivillo S (2016) Understanding human mobility with big data. Solving large scale learning tasks. Springer, Challenges and Algorithms, pp 208–220
Goldberger J, Gordon S, Greenspan H (2003) An efficient image similarity measure based on approximations of kl-divergence between two gaussian mixtures. In: Proceedings of the ninth IEEE international conference on computer vision–volume 1, IEEE Computer Society, Washington, DC, USA, ICCV ’03, pp 487–493
Gonzalez MC, Hidalgo CA, Barabasi AL (2008) Understanding individual human mobility patterns. Nature 453(7196):779–782
Herrera F, Carmona CJ, González P, Del Jesus MJ (2011) An overview on subgroup discovery: foundations and applications. Knowl Inf Syst 29(3):495–525
Hong L, Ahmed A, Gurumurthy S, Smola AJ, Tsioutsiouliklis K (2012) Discovering geographical topics in the twitter stream. In: Proceedings of the 21st international conference on World Wide Web, ACM, pp 769–778
Hooi B, Shah N, Beutel A, Günnemann S, Akoglu L, Kumar M, Makhija D, Faloutsos C (2016) Birdnest: Bayesian inference for ratings-fraud detection. In: Proceedings of the SIAM international conference on data mining, SIAM, pp 495–503
Jankowiak M, Gomez-Rodriguez M (2017) Uncovering the spatiotemporal patterns of collective social activity. In: Proceedings of the SIAM international conference on data mining, SIAM, pp 822–830
Jorge AM, Mendes-Moreira J, de Sousa JF, Soares C, Azevedo PJ (2012) Finding interesting contexts for explaining deviations in bus trip duration using distribution rules. In: International symposium on intelligent data analysis, Springer, pp 139–149
Kaytoue M, Plantevit M, Zimmermann A, Bendimerad A, Robardet C (2017) Exceptional contextual subgraph mining. Mach Learn 106(8):1171–1211
Kim KS, Kojima I, Ogawa H (2016) Discovery of local topics by using latent spatio-temporal relationships in geo-social mediaa. Int J Geogr Inf Sci 30(9):1899–1922
Knauf K, Memmert D, Brefeld U (2016) Spatio-temporal convolution kernels. Mach Learn 102(2):247–273
Lane ND, Pengyu L, Zhou L, Zhao F (2014) Connecting personal-scale sensing and networked community behavior to infer human activities. In: Proceedings of the 2014 ACM international joint conference on pervasive and ubiquitous computing, ACM, pp 595–606
Lemmerich F, Becker M, Singer P, Helic D, Hotho A, Strohmaier M (2016) Mining subgroups with exceptional transition behavior. In: Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining, ACM, pp 965–974
Mampaey M, Nijssen S, Feelders A, Konijn R, Knobbe A (2015) Efficient algorithms for finding optimal binary features in numeric and nominal labeled data. Knowl Inf Syst 42(2):465–492
Meeng M, Duivesteijn W, Knobbe A (2014) ROCsearch — an ROC guided search strategy for subgroup discovery. In: Proceedings of the 2014 SIAM international conference on data mining, society for industrial and applied mathematics, pp 704–712
Murphy KP (2007) Conjugate bayesian analysis of the gaussian distribution. University of British Columbia, Tech. rep
Piatkowski N, Lee S, Morik K (2013) Spatio-temporal random fields: compressible representation and distributed estimation. Mach Learn 93(1):115–139
Porteous I, Newman D, Ihler A, Asuncion A, Smyth P, Welling M (2008) Fast collapsed Gibbs sampling for latent Dirichlet allocation. In: Proceedings of the 14th ACM SIGKDD international conference on Knowledge discovery and data mining, ACM, pp 569–577
Puolamäki K, Kang B, Lijffijt J, De Bie T (2016) Interactive visual data exploration with subjective feedback. In: Joint European conference on machine learning and knowledge discovery in databases, Springer, Berlin, pp 214–229
Shin K, Eliassi-Rad T, Faloutsos C (2017) Patterns and anomalies in k-cores of real-world graphs with applications. Knowl Inf Syst 54:677–710
Shipmon DT, Gurevitch JM, Piselli PM, Edwards ST (2017) Time series anomaly detection; detection of anomalous drops with limited features and sparse examples in noisy highly periodic data. arXiv preprint arXiv:1708.03665
Soch J, Allefeld C (2016) Kullback-Leibler divergence for the normal-gamma distribution. arXiv preprint arXiv:1611.01437
Soulet A, Raïssi C, Plantevit M, Cremilleux B (2011) Mining dominant patterns in the sky. In: 11th International conference on data mining, IEEE, pp 655–664
Tu S (2014) The Dirichlet-multinomial and Dirichlet-categorical models for Bayesian inference. Tech. rep., Computer Science Division, UC Berkeley
van Leeuwen M, Knobbe AJ (2011) Non-redundant subgroup discovery in large and complex data. In: Gunopulos D, Hofmann T, Malerba D, Vazirgiannis M (eds) Proceedings of the European conference on machine learning and principles and practice of knowledge discovery in databases, ECML PKDD 2011, Springer, vol 6913, pp 459–474
van Leeuwen M, Knobbe AJ (2012) Diverse subgroup set discovery. Data Min Knowl Discov 25(2):208–242
Wu X, Dong Y, Huang C, Xu J, Wang D, Chawla NV (2017) Uapd: Predicting urban anomalies from spatial-temporal data. In: Joint European conference on machine learning and knowledge discovery in databases, Springer, pp 622–638
Wang D, Pedreschi D, Song C, Giannotti F, Barabasi AL (2011) Human mobility, social ties, and link prediction. In: Proceedings of the 17th ACM SIGKDD international conference on knowledge discovery and data mining, ACM, pp 1100–1108
Xie S, Wang G, Lin S, Yu PS (2012) Review spam detection via temporal pattern discovery. In: Proceedings of the 18th ACM SIGKDD international conference on knowledge discovery and data mining, ACM, pp 823–831
Yuan Q, Zhang W, Zhang C, Geng X, Cong G, Han J (2017) Pred: Periodic region detection for mobility modeling of social media users. In: Proceedings of the 10th international conference on web search and data mining, ACM, pp 263–272
Zheng X, Han J, Sun A (2018) A survey of location prediction on twitter. IEEE Trans Knowl Data Eng 30(9):1652–1671
Zheng Y, Zhang H, Yu Y (2015) Detecting collective anomalies from multiple spatio-temporal datasets across different domains. In: Proceedings of the 23rd SIGSPATIAL international conference on advances in geographic information systems, ACM
Zheng Y, Wu W, Chen Y, Qu H, Ni LM (2016) Visual analytics in urban computing: an overview. IEEE Transactions on Big Data 2(3):276–296
Funding
The funding was provided by Technische Universiteit Eindhoven.
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible editor: Karsten Borgwardt, Po-Ling Loh, Evimaria Terzi, Antti Ukkonen.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Du, X., Pei, Y., Duivesteijn, W. et al. Exceptional spatio-temporal behavior mining through Bayesian non-parametric modeling. Data Min Knowl Disc 34, 1267–1290 (2020). https://doi.org/10.1007/s10618-020-00674-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10618-020-00674-z