Abstract
We consider the class of linear predictors over all logical conjunctions of binary attributes, which we refer to as the class of combinatorial binary models (CBMs) in this paper. CBMs are of high knowledge interpretability but naïve learning of them from labeled data requires exponentially high computational cost with respect to the length of the conjunctions. On the other hand, in the case of large-scale datasets, long conjunctions are effective for learning predictors. To overcome this computational difficulty, we propose an algorithm, GRAfting for Binary datasets (GRAB), which efficiently learns CBMs within the \(L_1\)-regularized loss minimization framework. The key idea of GRAB is to adopt weighted frequent itemset mining for the most time-consuming step in the grafting algorithm, which is designed to solve large-scale \(L_1\)-RERM problems by an iterative approach. Furthermore, we experimentally showed that linear predictors of CBMs are effective in terms of prediction accuracy and knowledge discovery.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Learning of linear predictors is a widely used method for discovering data attributes that characterize the given data. Linear predictors are suitable for knowledge discovery in the sense that the attributes whose weights are large can be interpreted as more important features for classification or regression. The power of knowledge representation for linear predictor models is, however, quite limited in the sense that an important feature is represented by a single attribute only.
We are rather interested in a wider class of linear prediction models such that features may be represented by combinations of attributes. In particular, we are concerned with learning a linear model from labeled data, the features of which are based on all conjunctions of binary attributes. Let \(\mathscr {X}=\left\{ x_1,\ldots ,x_d\right\} \) be the set of all the binary attributes. We define the combinatorial feature set \(\varPhi ^{(d,k)}\) as a set of conjunctions of at most k distinct attributes chosen from \(\mathscr {X}\). For example, in the case of \(d=4\) and \(k=2\), \(\varPhi ^{(d,k)}\) is given as follows:
where \(\top \) returns 1 for any data \(\varvec{x}\in \{0,1\}^d\). Note that \(|\varPhi ^{(d,k)}|=\sum _{k'=0}^k \left( {\begin{array}{c}d\\ k'\end{array}}\right) \). Specifically, \(|\varPhi ^{(d,d)}|=2^d.\) When d is fixed, we denote \(\varPhi ^{(d,k)}\) as \(\varPhi ^{(k)}\) in the following discussion. We define a linear predictor associated with \(\varPhi ^{(k)}\) by
where \(\varvec{w}=(w_{\phi })_{\phi \in \varPhi ^{(k)}}\) is a real-valued \(|\varPhi ^{(k)}|\)-dimensional parameter vector. We refer to the class of all functions of the form (1) as the class of combinatorial binary models, which we abbreviate as CBMs. Further, we refer to \(\phi \in \varPhi ^{(k)}\) as a feature and k as the degree. The weight \(w_{\phi }\) in \(\varvec{w}\) for \(\phi \) represents the importance of the feature \(\phi \).
It is expected that CBMs can capture effective predictors involving long logical conjunctions, especially when a large-scale dataset is available. In cases attributes of given data are interpretable, the function obtained from CBMs is suitable for knowledge discovery in the sense that attributes with large weights can be interpreted as more important features for classification or regression. For example, let us consider a task to predict incomes of individuals from various attributes such as native country, education level and occupation. In this case, combinatorial features can represent, e.g., an individual is from the U.S., has a master degree and is a software engineer. It can be useful knowledge that such combinatorial features contribute to the better prediction, because it means that possessing a set of attributes all together has a special effect on prediction. Although non-linear models, such as the kernel method or multi-layer neural networks, may achieve higher classification accuracy, they do so at the cost of interpretability. There are several work that aim for recovering the interpretation of attributes from any black-box predictors (Ribeiro et al. 2016; Lundberg and Lee 2017).
Let us consider the problem of learning CBMs, i.e., estimation of the parameter vector \(\varvec{w}\), from given labeled examples \((\varvec{x}_{1},y_{1}),\dots , (\varvec{x}_{m},y_{m})\), where \(y_{i}\) is the label corresponding to \(\varvec{x}_{i}\) and m is the sample size. We employ the framework of regularized loss minimization as the learning framework. CBMs can represent highly complex prediction functions. In fact, CBMs with the degree d can represent any function from binary vectors to real values. It implies that any optimal predictor can be learned in the limit of large samples if empirical risk minimizer can be computed and that appropriate regularization is necessary in practical application to data samples of limited size.
Learning of such a class may entail high computational complexity because the total number of combinations of attributes is exponential in the dimension d and the degree k. Therefore, learning such a class of rich knowledge representations at low computational cost is an important issue. From the standpoint of both interpretation of learned predictors and computational efficiency, large weights should be assigned to a relatively small number of features \(\phi \in \varPhi ^{(k)}\) after learning. Toward this end, we focus on the framework of sparse learning (Rish and Grabarnik 2014) by the \(L_1\)-regularizer, which we refer to as \(L_1\)-regularized empirical risk minimization or \(L_1\)-RERM. Then, the objective function to be minimized can be expressed as
where \(\ell \) is a loss function and C is a real positive constant and \(\Vert \varvec{w}\Vert _1 \triangleq \ \sum _{\phi \in \varPhi ^{(k)}} |w_\phi |\). Hence, learning CBMs can be boiled down to a large-scale \(L_1\)-RERM using feature maps with a special structure.
It is still computationally difficult to solve the optimization problem (2) using existing standard techniques for loss minimization owing to the following two factors. First, in applying such techniques, all the values \(\phi \left( \varvec{x}_i\right) \) should be stored for all \(\phi \) and i beforehand. This requires an exponentially large memory size with respect to the data dimension. Second, it is computationally expensive to solve a large-scale optimization problem associated with loss minimization because the total number of parameters is \(\sum _{k'=0}^k \left( {\begin{array}{c}d\\ k'\end{array}}\right) \), which is at most \(2^d\).
1.1 Significance and novelty
The purpose of this paper is twofold. The first and main purpose is to propose an efficient algorithm that learns a class of linear predictors over all possible combination of binary attributes by solving large-scale \(L_1\)-regularized problems. The second is to empirically demonstrate that the proposed algorithm efficiently produces predictors having higher accuracy as well as better interpretability than competitive methods. The significance of this paper is summarized as follows:
(1) Proposal of an efficient algorithm that learns a class of linear predictors over all conjunctions of attributes We consider the problem of learning CBMs from labeled examples within the regularized loss minimization framework. Because the size of CBM is exponential in the data dimension, it is challenging to learn CBMs efficiently. We propose a novel algorithm, namely the GRAfting for Binary datasets algorithm (GRAB), to learn CBMs efficiently. The key idea of GRAB is to adopt the technique of frequent itemset mining (FIM) for the most time-consuming step in the grafting algorithm (Perkins et al. 2003), which is designed for large-scale \(L_1\)-regularized loss minimization. We observe that the grafting algorithm includes FIM as a sub-procedure. We successfully unify the efficient FIM algorithm and the grafting algorithm to achieve efficient execution of GRAB.
(2) Empirical demonstration of the validity of GRAB in terms of computational efficiency, prediction accuracy and knowledge interpretability We employ benchmark datasets to demonstrate that GRAB is effective in terms of computational efficiency, prediction accuracy and knowledge interpretability. First, we show that GRAB can learn CBMs with high degree more efficiently than other algorithms and that CBMs of higher degrees exhibit higher prediction accuracy in the \(L_1\)-RERM framework as the amount of data increases. Then, we empirically show that GRAB achieves higher or comparable prediction accuracy in comparison to existing methods, such as random forests (Ho 1995, 1998) and extreme gradient boosting (Chen and Guestrin 2016). We also examine the behavior of the solution of GRAB by changing stopping condition. Furthermore, we show that GRAB can acquire important knowledge in a comprehensive form by demonstration on several datasets.
1.2 Related work
Numerous studies have investigated learning of interpretable knowledge representations from binary datasets, such as decision trees (Breiman et al. 1984), random forest (Ho 1995, 1998), and extreme gradient boosting (Chen and Guestrin 2016). Our concern here is that their learning algorithms have little guarantees from the perspective of optimization due to the nature of combinatorial optimization. Therefore, statistical analysis under the principle of the empirical loss minimization are not applied, although their performance largely depend on experimental heuristics such as early stopping. Our aim in this paper is to develop a learning method that works under the framework of empirical loss minimization and achieves the global solution, which immediately provides basic theoretical guarantees on the predictor.
In the case of classification tasks, learning of CBMs is related to learning Boolean functions, especially disjunctive normal forms (DNFs), which have been investigated extensively in the area of computational learning theory, e.g., Aizenstein and Pitt (1995) and Bshouty (1995). However, CBMs differ from DNFs in two aspects: 1. CBMs take a weighted sum of conjunctions of attributes rather than disjunctive operations. 2. CBMs include all real-valued functions: \(\{0,1\}^{d}\rightarrow \mathbb {R}\). Hence, CBMs can be regarded as a wider class of functions than DNFs. Learning CBMs is significant in this sense.
There are several approaches that learn CBMs by selecting combinatorial features first and then learning models only with those features (Deshpande et al. 2005; Cheng et al. 2007). Instead, we focus on solving large-scale \(L_1\)-regularized problems to learn CBMs directly. In this context, our learning setting is closely related to loss minimization using polynomial kernels. In the case where \(\varvec{x}\) is a binary vector, the loss minimization for CBMs is analogous with that using polynomial kernels (Shawe-Taylor and Cristianini 2004):
However, the weights for \(\phi \in \varPhi ^{(k)}\)s depend on their degrees or their numbers of conjunctions. Thus, features for CBMs are uniformly weighted, whereas those for polynomial kernels are non-uniformly weighted.
Our learning algorithm follows the framework of the grafting algorithm (Perkins et al. 2003), which is designed for \(L_1\)-regularized loss minimization when the number of available features are large. Some variants of boosting algorithms can be seen as optimization algorithms for \(L_1\)-regularized loss minimization although it covers only convex losses (Schapire and Freund 2012). The column generation procedure is a terminology in general optimization problems with a large number of constraints, especially when the optimization problem is reduced to mathematical programming such as linear programming and quadratic programming (Dantzig and Wolfe 1960; Desaulniers et al. 2006). When the grafting algorithm is reduced to such a mathematical programming, it coincides with a column generation procedure.
FIM has been successfully adopted in several emerging machine learning tasks, such as clustering and boosting (Saigo et al. 2007; Tsuda and Kudo 2006; Kudo et al. 2004). One of the most closely related studies is Saigo et al. (2007), in which FIM was adopted for boosting; a model similar (but not identical) to CBMs was also considered, and regression tasks were examined in a biological context.
The remainder of this paper is organized as follows. Section 2 introduces the grafting algorithm for loss minimization. Section 3 introduces the frequent itemset mining methodology. Section 4 describes GRAB, which combines the grafting algorithm with frequent itemset mining. Section 5 presents the experimental results. Finally, Sect. 6 concludes the paper.
2 Grafting algorithm
In this section, we introduce the grafting algorithm (Perkins et al. 2003), which is designed to solve large-scale \(L_1\)-RERM problems efficiently. We define the objective function as \(G(\varvec{w})= L(\varvec{w}) + \Vert \varvec{w}\Vert _1\), where we assume \(L(\varvec{w})\) is differentiable. The key idea of the grafting algorithm is to construct a set of active features by adding features incrementally.
In each iteration of the grafting algorithm, a (sub)gradient-based heuristic is employed to first find the feature that seemingly improves the model most effectively and then add it to the set of active features. In the t-th iteration, the grafting algorithm divides the set of all attributes of parameter vector \(\varvec{w}\) into two disjoint sets: \(F^t\) and \(Z^t\triangleq \lnot F^t\). We refer to \(w_j^t \in F^t\) as a free weight. Further, \(Z^t\) is constructed implicitly so that it always satisfies \(w_j^t =0\) if \(w_j^t \in Z^t\).
The procedure of the grafting algorithm is as follows: First, it minimizes (2) with respect to free weights, resulting in
for \(\forall j\in F^t\), where \(\partial _{w_j^t}G \) is the subdifferential of G with respect to \(w_j^t\). Then, for \(\forall j\in Z^t\),
is a necessary and sufficient condition for the value of the objective function to decrease by changing \(w_j^t\) (globally when G is convex and locally in general). Second, the grafting algorithm selects a parameter from \(Z^t\) that is seemingly the most effective in decreasing the objective function and adds it into \(F^{t+1}\). Then, \(Z^{t+1}\) is also implicitly updated by removing the selected parameter, and the grafting algorithm iterates the procedure mentioned above.
The subdifferential of the objective function with respect to \(w_j^t\in Z^t\) is calculated as
Hence, the condition (5) is equivalent to
This implies that changing the value of \(w_j^t\) from 0 will not decrease the objective function if (7) is not satisfied. This is the main reason why \(L_1\)-regularization gives a sparse solution. It also leads to a stopping condition of the grafting algorithm as described below.
We consider the problem of selecting a parameter to be moved from \(Z^t\) to \(F^t\). From the above argument, we see that \(w_j^t\in Z^t\) satisfying (7) makes the value of the objective function decrease by changing its value from 0. There may be more than one candidate satisfying (7). In such a case, the grafting algorithm selects a parameter \(w_{\mathrm {best}}^t\) that makes the value of the objective function decrease the most by using the following gradient-based heuristic:
If the condition (7) is not satisfied for \(w_{\mathrm {best}}^t\), a local optimum (or the global optimum in case of convex G) is achieved. The overall procedure is given in Algorithm 1.
Note that the derivatives of the objective function with respect to all parameters must be calculated to obtain the maximum in (7) in general. However, this naïve method is computationally intractable when the data dimension and sample size are large as in our case.

3 Frequent itemset mining
It is computationally difficult to find the best parameter according to (8). This is because it requires computation of the gradient of loss over all the components of the parameter. To overcome this difficulty, we adopt the frequent itemset mining (FIM) technique. In this section, we briefly review FIM.
3.1 Terminology
A set of items \(\mathscr {I}=\{1,\ldots ,d\}\) is called the item base. The set \(\mathscr {T}=\{t_1,\ldots ,t_m\}\) is called the transaction database, where each \(t_i\) is a subset of \(\mathscr {I}\). Each element of the transaction database is called a transaction. Given a transaction database, an occurrence set of p, denoted by \(\mathscr {T}(p)\), is a set of all transactions that include p, i.e.,
We refer to p as an itemset. The cardinality of \(\mathscr {T}(p)\) is referred to as the frequency, which is denoted as \(\mathrm {frq}(p;\mathscr {T})\), i.e., \(\mathrm {frq}(p;\mathscr {T}) \triangleq \sum _{ t \in \mathscr {T}(p)} 1\). When \(\mathscr {T}\) is fixed, \(\mathrm {frq}(p;\mathscr {T})\) is written as \(\mathrm {frq}(p)\) in the following discussion. The simplest example of the FIM problem is given as follows: For a given transaction database \(\mathscr {T}\) and threshold \(\theta \), find \(\mathscr {P}\), which is the set of all itemsets with a larger frequency than \(\theta \), i.e.,
3.2 Efficient algorithms using monotonicity
It is obvious that any subset of an itemset p is included by a transaction t when p is included by t. In other words, a type of monotonicity holds in the following sense:
By exploiting this property, we can search all frequent itemsets by adding items one by one from \(\varnothing \). The apriori algorithm performs this search in the breadth-first manner, whereas the backtracking algorithm performs this search in the depth-first manner. The apriori algorithm was originally proposed by Agrawal and Srikant (1994). An FIM algorithm based on the backtracking algorithm was proposed in, e.g., Zaki et al. (1997) and Bayardo Jr (1998).
The size of the transaction database, denoted as \(\left\| \mathscr {T}\right\| \), is defined by \(\Vert \mathscr {T}\Vert \triangleq \sum _{i=1}^m|t_i|\). The time complexities of the apriori and backtracking algorithms are the same, i.e., \(\mathscr {O}(d\Vert \mathscr {T}\Vert |\mathscr {P}|)\), which is called the output-polynomial time. Note that it is necessary to incur \(|\mathscr {P}|\) time to identify \(\mathscr {P}\), although \(|\mathscr {P}|\) can be exponentially large in the worst case. In other words, the smaller \(|\mathscr {P}|\) is, the more the computational cost decreases. Hence, the algorithms are expected to run in practical time as long as \(|\mathscr {P}|\) is of reasonable size.
3.3 Extension to weighted FIM
Standard FIM methods handle transactions as if there were no difference in importance among the transactions. However, there often appear cases in which the transactions may differ from one another in importance depending on the nature of the transactions. Furthermore, the values of importance may be positive or negative. If each transaction is allocated to a positive or negative label, then we may be interested in discovering itemsets that appear frequently in positive transactions but not frequently in negative ones. Letting \((\alpha _t)_{t\in \mathscr {T}} \in \mathbb {R}^\mathscr {T}\) represent the importance, we define weighted frequency as follows:
which is denoted as \(\mathrm {wfrq}(p; \alpha )\) when \(\mathscr {T}\) is fixed in the following discussion. We then introduce weighted frequent itemset mining (WFIM), which aims to find all itemsets whose weighted frequency is larger than a given threshold. We call such itemsets weighted frequent itemsets in the rest of the paper.
In the setting where the values of importance are non-negative, the same monotonicity as that given by (11) still holds for the weighted frequency. We call this special case of WFIM non-negatively weighted frequent itemset mining (NWFIM), for which we can employ the backtracking algorithm or the apriori algorithm.
In the setting where both positive and negative importance has to be dealt with, the monotonicity does not hold any longer. Then, any algorithm of output-polynomial time do not exist to the best of our knowledge. Instead, we may employ the following two-stage strategy: Let the sets of positive and negative transactions in \(\mathscr {T} \) be \(\mathscr {T}_+ \) and \(\mathscr {T}_- \), respectively. In the first stage, by ignoring transactions with negative importance, we obtain weighted frequent itemsets such that
In the second stage, for each itemset in \(\mathscr {P}_+\), we check if the weighted frequency \(\mathrm {wfrq}(p;\mathscr {T}, \alpha )\) is still larger than \(\theta \). The first stage is executed using the aforementioned algorithms in time \(\mathscr {O}(d\Vert \mathscr {T}_+\Vert |\mathscr {P_+}|)\), while the second stage is executed in time \(\mathscr {O}(d\Vert \mathscr {T_-}\Vert |\mathscr {P_+}|)\) by accessing all negative transactions for each itemset obtained in the first stage. Then, the total computation time is \(\mathscr {O}(d\Vert \mathscr {T}\Vert |\mathscr {P}_+|)\).
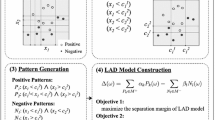
Demonstration of frequent itemset mining (FIM) and its variants: Those three diagrams above show the results of the problems of FIM, NWFIM and WFIM, in which the transaction database \({\mathscr {T}}= \left\{ t_1,t_2,t_3,t_4\right\} \) is defined as in the left table and \(\theta =1\). A node in the diagrams represents each itemset and an arrow represents the inclusion relation. The green-shaded area in each diagram represents \(\mathscr {P}=\left\{ p \subseteq \mathscr {I}| \mathrm{wfrq}(p;\alpha ) >1\right\} \) for each \(\alpha \) described in the table next to the diagram. We can see the monotonicity holds in the case of FIM and NWFIM, whereas it does not in the case of WFIM (Color figure online)
The three types of FIM, namely FIM, non-negatively weighted FIM (NWFIM), and weighted FIM (WFIM), are shown in Fig. 1.
A variant of WFIM can be designed by restricting the itemsets such that their sizes are at most k. Then, it will output \(\mathscr {P}=\{p\subseteq \mathscr {I}\ |\ \mathrm {wfrq}(p;\mathscr {T},\alpha ), |p|\le k\}\). This is realized by stopping the breadth-/depth-first search of weighted frequent itemsets at depth k.
4 Proposed algorithm (GRAB)
In this section, we introduce the proposed algorithm for learning CBMs, which we refer to as GRAfting for Binary datasets (GRAB). In our case, the grafting algorithm itself is not efficient because selecting the best parameter expressed in (8) involves an exponentially large number of candidate features in its maximization. The key to overcoming this issue is to adopt WFIM techniques to compute this maximization efficiently. In fact, we see from (7) that the value of the objective function is decreased by changing the value of \(w_\phi \) if and only if
Thus, the problem of finding the best feature can be solved after finding \(\phi \in \varPhi ^{(k)}\) satisfying (14). It turns out that this problem is reduced to two WFIM problems. To explain this, we prove the following statement.
Theorem 1
Define
for each feature vector \(\varvec{x}_i\ (i=1,\ldots ,m)\) and \(\phi \in \varPhi ^{(k)}\), respectively. Then, (14) is equivalent to
where

Proof
\(\phi \) can be expressed as
Therefore, the left-hand side of (14) is rewritten as
where \(\mathscr {T}(p_\phi )\) is an occurrence set of \(p_\phi \) with respect to the transaction database \(\mathscr {T}\triangleq \{t_i\}_{i=1}^m\). Hence, the proposition is true. \(\square \)
We can obtain a set of all \(p_\phi \)s that satisfy each inequality in (15) by employing WFIM. Therefore, finding \(\phi \in \varPhi ^{(k)}\) satisfying (14) is reduced to two WFIM problems.
According to the original form of grafting algorithm, only one parameter is newly added to the set of free weights by (8) in each iteration. Knowing that (14) is a necessary and sufficient condition for the objective function to decrease, we may select more than one parameter, such as the top-K most weighted frequent parameters \(\{w_{\phi _{k}}\}_{k=1}^{K}\), where \(\phi _{k}\) has the k-th largest value in the left-hand side of (14). This method is more efficient in the case where the parameter selection procedure of WFIM requires a longer computation time than the parameter estimation step of the grafting algorithm. The overall flow of GRAB is given in Algorithm 2.
We describe the implementation techniques for acceleration of GRAB.
Dynamic threshold control for the acceleration of WFIM WFIM terminates faster if the threshold \(\theta \) is larger and \(|\mathscr {P}_+|\) is smaller, because the time complexity of WFIM is \(\mathscr {O}(d\Vert \mathscr {T}\Vert |\mathscr {P}_+|)\), as noted previously. It is desirable to find the top-K most weighted frequent itemsets without extracting all the features that satisfy (14). Toward this end, first, we execute WFIM by setting the threshold \(\theta = 2^M\) with \(M=10\), and we decrement M by 1 until we obtain K itemsets or \(\theta =2^0=1\). When WFIM is called next, we use the same value of M as that used previously.
Incomplete Termination of WFIM When the total number of outputs of WFIM is too large, we terminate WFIM after extracting 100K weighted frequent itemsets and select the top-K most weighted frequent itemsets among them. In such cases, selection of the top-K most weighted frequent itemsets may not be guaranteed. However, as the selection of a new feature based on (8) is already a heuristic, we do not expect that it significantly deteriorates the performance of the optimization step.
Lastly, we note that GRAB converges to the optimal solution as long as \(\ell \) is convex, because it follows the procedure of the framework of the grafting algorithms. Even with the implementation techniques, the convergence still holds as GRAB with these techniques finds features that satisfies (14) for each iteration.
5 Experiments
We implemented GRAB in C/C++.Footnote 1 To select new features to be added, we used Linear time Closed itemset Miner (LCM, Uno et al. 2003, 2004, 2005), which is a backtracking-based FIM algorithm. All the experiments described below were executed on Linux (CentOS 6.4) machines with 96 GB memory and Intel(R) Xeon(R) X5690 CPU (3.47 GHz). We restricted the computation time to within one day, and experiments with overtime were regarded as time-outs. We employ the following stopping condition: First, we define the suboptimality of a solution as follows:
where
We terminate the algorithm when \(V^t < \varepsilon V^0\) is satisfied for a given tolerance \(\varepsilon >0\). In our experiments, we set \(\varepsilon =10^{-2}\). The first term of \(V^t\) is computed using the parameter obtained by the optimization step. The second term is computed by summing over the features obtained by WFIM. Note that it may not be possible to compute \(V^0\) exactly when we employ the heuristic for acceleration noted above. In this case, we underestimate \(V^0\) by computing the summand in the second term of (17) among the obtained features. This makes the stopping condition stricter and the proposed algorithm run longer.
We examined the following five aspects. First, we demonstrated the efficiency of GRAB algorithm in solving the optimization problem (2). Second, we demonstrated the benefit of high-order CBMs in predictive performance. Third, we demonstrated the predictive performance compared to that of other state-of-the-art supervised learning methods. Fourth, we evaluated the effect of tolerance on learned models. Finally, we demonstrated interpretability of learned models using various kinds of datasets.
5.1 Evaluation of computation time
In this section, we examined the efficiency of GRAB. Toward this end, we adopted the following two methods as baselines of comparison:
- 1.
Grafting + Naïve feature selection
We employed the grafting algorithm without combining it with WFIM. We calculated (8) by searching exhaustively over the set of all features \(\phi \in \varPhi ^{(k)}\).
- 2.
Expansion + LIBLINEAR
First, we expanded a dataset so that all possible features in \(\phi \in \varPhi ^{(k)}\) are explicitly developed (expansion). Then, we trained linear models on the expanded dataset within the \(L_1\)-RERM framework. We used LIBLINEAR as a solver (Fan et al. 2008).
Note that GRAB and the compared methods share the objective function (2).
In our experiment, we used the logistic loss function \(\ell (x, y)= \log \left( 1+\exp \left( -xy\right) \right) \) as a loss function for learning CBM. Further, we used a1a (Platt 1999; Lichman 2013) as a benchmark dataset. It has 32,561 datapoints and 123 binary attributes. We conducted training of CBM with \(C=0.1, 1\), and \(1\le k\le 6\). The computation time results are summarized in Fig. 2.
First, we observed that the computation time for GRAB is significantly shorter than that for Grafting + Naïve feature selection. This implies that WFIM is sufficiently efficient to select the features even when exhaustive search is impractical. Next, we focus on the comparison between GRAB and Expansion + LIBLINEAR. GRAB selects only promising features to decrease the objective function, whereas Expansion + LIBLINEAR considers all possible features. This difference was clearly reflected in the results. When the degree of CBM is small (\(k=1, 2\)), which means that the feature space is not large, Expansion + LIBLINEAR can be executed faster than GRAB. However, as k increases, the number of unnecessary features increases considerably and GRAB becomes more efficient. Therefore, we conclude that GRAB is efficient not only because it employs WFIM but also because it can extract features selectively as a characteristic of grafting algorithms.
5.2 Evaluation of combinatorial models
CBMs of high degree have an extraordinary high-dimensional feature space consisting of complex combinatorial features. In this section, we demonstrate how such complex combinatorial features contribute to prediction accuracy. In the experiment, we employed the logistic loss function \(\ell \left( x, y\right) =\log \left( 1+\exp \left( -xy\right) \right) \) as a loss function for learning CBMs. As benchmark datasets, we employed the covtype.binary dataset and the SUSY dataset, both of which have quantitative attributes. As GRAB can be applied only to binary datasets, we transformed each quantitative attribute into a binary one as follows: We divided the interval from the minimum value to the maximum value into 50 cells of equal length. We expressed each attribute in a binary form by indicating which section its value fell into. Thus, we obtained the binarized covtype.binary dataset and the binarized SUSY dataset. We used 500,000 data for training and 81,012 for testing on covtype.binary, while 1,000,000 data points are used for training and 100,000 are used for testing on SUSY.
We examined the prediction accuracy of CBMs of degree \(k=1, 2, 3, 4\) with various sizes of the training data for each dataset. For each k, we selected the best hyperparameter C from \(C=10^{-3},\ldots ,10^3\) by 5-fold cross-validation. We created the subsets of the training dataset of sizes \(m = 300, 1\times 10^l, 3\times 10^l (3 \le l \le 5)\) and \(5 \times 10^5\) for covtype.binary and \(m = 1\times 10^l, 3\times 10^l (3\le l \le 5)\) and \(1\times 10^6\) for SUSY, respectively. Figure 3 shows the prediction accuracy of each CBM trained with each subset of each dataset.
From the Fig. 3a, we can see that the model with \(k=1\) performed the best when the number of training data was small, e.g., \(m=1\times 10^3, 3\times 10^3\), but it showed the worst performance when the number of training data was large, as in the case of \(m=3\times 10^5, 5\times 10^5\), which is potentially due to the poor representation ability of the model known as underfitting. By contrast, the model with \(k=4\) achieved the highest prediction accuracy when the number of training data was large, as in the case of \(m=3\times 10^5, 5\times 10^5\). These observations imply that complex combinatorial features are more useful for improving the prediction accuracy as the size of available datasets increases on covtype.binary dataset. On the other hand, from the Fig. 3b, we can see that the prediction accuracy of the models with the various k is not much different from each other on SUSY. The CBM with \(k=2\) achieved the best prediction accuracy when the number of training data was large, e.g., \(m=3\times 10^5, 1\times 10^6\), which implies that the learning SUSY does not require complex learning models.
5.3 Evaluation of prediction accuracy
To evaluate the prediction performance of GRAB, we compared it with that of state-of-the-art methods using 10 benchmark datasets.Footnote 2 In addtion, we employed a FIM-based method in order to compare our method with FIM. We performed the same preprocessing as that described in the previous section for each dataset. We employed the following classification methods for comparison:
- 1.
Support vector classification (SVC, Bishop 2006)
We used a polynomial kernel function for its kernel. The polynomial kernel is defined as \(k(\varvec{x},\varvec{x}')=\left( \gamma \varvec{x}^\top \varvec{x}'+\left( 1-\gamma \right) \right) ^d\), where \(d\in \mathbb {N}\) and \(\gamma \in (0,1]\) are hyperparameters. We selected the hyperparameters from the grid of \(d=1, 3\), \(\gamma =0.1, 0.4, 0.7, 1.0\), and \(C=10^{-3}, 10^{-2},\ldots , 10^3\).
- 2.
Decision tree (DT, Breiman et al. 1984; Quinlan 1993)
One of its hyperparameters is max depth d, which controls the growth complexity of the decision tree. We chose max depths from \(d=2^3, 2^4, \ldots , 2^9\).
- 3.
Random forest (RF, Ho 1995, 1998)
It has the max depth d and the number of trees n in its hyperparameters. We chose them from the grid of \(d=2^3, 2^4, \ldots , 2^9\) and \(n=2^4, 2^5, \ldots , 2^8\).
- 4.
Extreme gradient boosting (XGB, Chen and Guestrin 2016)
Although it has numerous hyperparameters, we only tuned max depth d and the hyperparameter \(\lambda \) for the \(L_2\) regularizer. We searched for the best hyperparameter combination within the grid of \(d=2^3, 2^4, \ldots , 2^9\) and \(\lambda =\frac{10^{-3}}{m}, \frac{10^{-2}}{m}, \ldots , \frac{10^3}{m}\), where m is the number of training datapoints.
- 5.
\(L_1\)-regularized logistic regression on the preprocessed datasets with frequent itemset mining (LRFIM)
First, we extracted the frequent itemsets from the training data with (non-weighted) frequent itemset mining by setting minimum frequency \(\theta \) to 1% of the number of training datapoints and maximum itemset length k to 5. Then, we trained \(L_1\)-regularized logistic regression based on the features corresponding to the extracted frequent itemsets. We selected the hyperparameter in \(L_1\)-regularized logistic regression from \(C=10^{-3}, 10^{-2},\ldots , 10^3\).
For each of the algorithms, we selected the hyperparameters using 5-fold cross-validation from all the possible combination of hyperparameters. We limited the computation time for each combination within 100 hours and excluded all the combinations of time-out from the cross-validation candidates. After the hyperparameter selection, we retrained the model using all the training data and calculated prediction accuracy on the test data. We used scikit-learn (Pedregosa et al. 2011) for SVC, DT, and RF, the XGBoost package (Chen and Guestrin 2016) for XGB and LCM (Uno et al. 2003, 2004, 2005) and scikit-learn for LRFIM. We note that from the perspective of hyperparameter selection, GRAB is preferable to the other methods because it has fewer hyperparameters.
We employed logistic loss and \(L_2\)-hinge loss as loss functions for learning CBMs. The \(L_2\)-hinge loss function is defined as
Note that the WFIM procedure in GRAB can be accelerated using \(L_2\)-hinge loss. This is because \(\partial \ell (f(\varvec{x}_i),y_i)/\partial f^{(k)}(\varvec{x}_i)\), i.e., the i-th transaction weight of WFIM, is 0 for all i satisfying \(1-y_if(\varvec{x}_i)\le 0\), and we can remove the corresponding data from the transaction database. We trained each GRAB model with \(k=1,2,3,4,5,\infty \) and \(C=10^{-3},10^{-2},\ldots ,10^3\).
Table 1 lists the accuracy of each algorithm on various benchmark datasets. In our experiments, GRAB with the logistic loss function achieved the best predictive performance on diabetes (Lichman 2013), whereas GRAB with the \(L_2\)-hinge loss function achieved the best predictive performance on madelon (Guyon et al. 2005), phishing (Lichman 2013), a1a (Lichman 2013) and SUSY (Baldi et al. 2014; Lichman 2013).
SVC achieved the best accuracy on fourclass (Ho and Kleinberg 1996), ijcnn1 (Prokhorov 2001) and cod-rna (Andrew et al. 2006); RF, on german.numer (Lichman 2013); and XGB, on covtype.binary (Collobert et al. 2002; Lichman 2013).
Next, let us compare the results of GRAB (logistic) and LRFIM. GRAB (logistic) achieved the higher prediction performance on 7 out of 10 datasets. Among them, our method performed significantly better on ijcnn1, cod-rna and covtype.binary. Our method extracts features based on whether they contribute to decreasing the objective function, while LRFIM does based on their frequency. It is considered that this difference leads to the better performance on these datasets. This implies that our method makes use of features that are less frequent but effective for prediction.
We note that our method achieves better performance than decision tree and random forest nearly consistently. In addition, the overall results are very competitive compared to SVC and XGBoost. Specifically, GRAB with \(L_2\)-hinge performs the best on 4 out of 10 datasets among all the competitors. Therefore, we conclude that GRAB generally achieves state-of-the-art prediction accuracy, which means that the regularized empirical risk minimization framework works well for high-degree CBMs, even though the formal number of features is significantly large.
5.4 Evaluation of the effect of tolerance on learned models
In general, there can be completely different sets of features that achieve similarly high predictive performance. We evaluate how much the learned models differ from each other when the tolerance \(\varepsilon \) is set differently in our algorithm. In this section, we conducted the experiment in order to evaluate the effect of tolerance.
In this experiment, we trained CBMs by GRAB algorithm with various tolerance values \(\varepsilon =10^{-7},10^{-6},\ldots ,10^{-2}\) on the benchmark datasets ijcnn1 and phishing. We regarded the model trained with \(\varepsilon =10^{-7}\) as the global solution. We used the hyperparameters of CBMs \((C, k) = (1, 4)\) and (1, 5) for ijcnn1 and phishing, respectively, both of which were chosen as the best for predictive performance in the experiment in 5.3. We note that the numbers of the combinatorial features that appeared at least once in the dataset are 15,203,016 and 8,222,207 in case of in ijcnn1 with \(k=4\) and phishing with \(k=5\), respectively.
We define a learned model by setting the tolerance to \(\varepsilon \) as \(\varvec{w}^\varepsilon \) and a representative feature set \(\hat{\varPhi }_\varepsilon \) of the learned model as \(\hat{\varPhi }_\varepsilon \triangleq \{\phi | |w^\varepsilon _\phi \ | \ \ge \max _{\phi '} |w^\varepsilon _{\phi '}| / 10\}\). By setting \(\hat{\varPhi }= \hat{\varPhi }_{10^{-7}}\), we evaluated the difference as sets between \(\hat{\varPhi }\) and \(\hat{\varPhi }_\varepsilon \). We show the results of the experiment in Table 2. This table shows the values of \(|\hat{\varPhi }_\varepsilon |\), \(|\hat{\varPhi } \setminus \hat{\varPhi }_\varepsilon |\) and \(|\hat{\varPhi }_\varepsilon \setminus \hat{\varPhi }|\) for each \(\varepsilon \) on ijcnn1 2a and phishing 2b. It also shows the prediction accuracy on the test data for each tolerance and dataset.
First, we explain the result on ijcnn1. The representative feature set of size 688 is obtained in \(\varepsilon =10^{-7}\) and we can observe that the differences from it are very small in \(\varepsilon =10^{-6}\) and \(\varepsilon =10^{-5}\). As \(\varepsilon \) increases, the difference increases eventually. In the case of \(\varepsilon =10^{-2}\), the learned model contains about 75% of representative features in the global solution and around 40% of representative features in the learned model are not contained in \(\hat{\varPhi }\). These sets of representative features are very close to each other, considering that the total number of possibly useful features is 15,203,016.
Next, we discuss the result on phishing. The global solution consists of as small as 74 representative features. In this case, The difference between sets of representative features by different values of \(\varepsilon \) are large. One possible reason is that there are completely different combinatorial features that result in similar features in this dataset and such a kind of multicollinearity makes the solution of (2) unstable. We note that the predictive performance of all models are similarly good and sometimes better than the global solution. From the perspective of knowledge discovery, there is no such a concept of a unique ground truth of representative features and a set of features can be useful for knowledge discovery whenever the predictive performance is sufficiently high. Therefore, this experiment concludes that various sets of representative features can be obtained with various values of the tolerance while the predictive performance is quite stable.
5.5 Evaluation of interpretability
We can conduct knowledge acquisition by observing the predictor learned by GRAB and then interpreting such features that corresponding weights have large absolute values as important ones. This is because such features greatly affect the prediction results. Hence, by simply extracting large-valued features, we can acquire knowledge about what features are important for prediction. Specifically, features used in GRAB are easy to comprehend since they are represented as conjunctions of attributes. This implies that GRAB is of high interpretability of the acquired knowledge.
Below we show the results on knowledge discovery for a1a dataset (Lichman 2013; Platt 1999). This dataset was obtained by binarizing the Adult dataset (Lichman 2013), which was extracted from the census bureau database. The a1a dataset has been used as a benchmark for classification of people with more than $50,000 annual income or the others, on the basis of their attributes.
We trained GRAB with \(L_2\)-hinge loss on a1a dataset with the hyperparameters \(k=2\) and \(C=0.1\), which achieved the highest prediction performance in 5.3. Note that the numbers of the possible attribute combinations are 5,439 in a1a with \(k=2\) and we obtained the trained CBM with 682 non-zero coefficients of the combinations. Table 3a shows weights with large absolute values listed in a descending order. For each row, we have two columns Weight and Combination of Attributes, which describe a learned weight for each combinatorial feature and the interpretation of the feature, respectively. Each single feature is described in a form of \(A=B\), where A is a type of the feature in the original dataset and B is its value, respectively. For each discretized feature, we assigned a fraction m / n, where n means the original feature was discretized into n segments and m describes which segment the feature fell into. The bigger m is assigned to the segment with the greater value in the original dataset. This list itself is of high interpretability and represents knowledge acquired from the dataset.
The feature with the largest absolute value of weight is (marital-status \(=\) Married-AF-spouse) & (native-country \(=\) United-States), which has a positive gain for classification. We also observe two results related to education-num, which corresponds to the time period of education: 1. (education-num \(=\) 1 / 5) has a negative weight and 2. (education-num \(=\) 5 / 5) & (marital-status \(=\) Married-civ-spouse) has a positive weight, both of which are consistent with our prior knowledge.
Next, we show the knowledge discovery results from covtype.binary dataset (Collobert et al. 2002; Lichman 2013), which was gained by converting Covertype dataset from multi-labeled data into binary-labeled data. Each record in the dataset describes a region of 30 meter square in Roosevelt National Forest. The original Covertype dataset has geographical attributes such as elevation and soil type as feature values and forest cover type classified into seven types as a label value. Covtype.binary dataset is gained by converting the second forest type to the positive label and the other types to the negative label.
We trained GRAB with \(L_2\)-hinge loss on covertype.binary dataset with the hyperparameters \(k=\infty \) and \(C=0.1\), which achieved the highest prediction performance in 5.3. Note that the numbers of the possible attribute combinations are 1,384,529,117 in covtype.binary with \(k=\infty \) and we obtained the trained CBM with 91,110 non-zero coefficients of the combinations. Table 3b shows weights with large absolute values listed in a descending order. We can easily find that the weights related to elevation feature have relatively large absolute values. Figure 4 describes the relationship between elevation and weight of features, which has positive values from 2450 to 3050 and negative values from 3300 to 3600. As we explained above, we binarized all the quantitative features into 50 cells of equal length, which means GRAB never tells binarized elevation features are obtained from the same quantitative feature at the time of training; nevertheless two neighbor elevation features have the weights close to each other as shown in the Fig. 4. Therefore, it can be considered that GRAB selected important features for prediction properly on covtype.binary dataset from this result.
6 Conclusion
In this paper, we proposed GRAB for learning combinatorial binary models. The key idea of GRAB is to combine frequent itemset mining with the grafting algorithm in the \(L_1\)-RERM framework. We experimentally showed that GRAB can learn CBMs much more efficiently than naïve algorithms and that CBMs of the high degree contribute to good predictive performance. We also conducted additional experiments, in which we empirically proved that the prediction accuracy achieved by GRAB is generally comparable to that achieved by state-of-the-art classification methods. We also demonstrated that GRAB enabled us to discover knowledge in a form of conjunctions of attributes of given data. This knowledge representation turned out to be very comprehensive.
The main reason for the efficiency of GRAB is that the monotonicity of itemsets, or binary inputs, makes it easy to search over all possible features. Therefore, any other data structures having monotonicity, e.g., sequences and graphs, can also be incorporated with our methodology.
In this paper, we considered only convex loss functions in order to prevent the algorithm from being trapped in local minima of the objective function. However, it is also possible for GRAB to work in the case of non-convex loss functions. It is noteworthy that GRAB works whenever the loss function is differentiable. Hence, a challenging direction for future work is to adopt our GRAB methodology for efficient computation of multi-layer neural networks or other types of highly predictive machine learning models.
Notes
Our experimental code is available at https://gitlab.com/taitor/GRAB-experiments.
All datasets are available on the LIBSVM Data website at https://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/binary.html.
References
Agrawal R, Srikant R (1994) Fast algorithms for mining association rules. In: Proceedings of the 20th international conference on very large databases, pp 487–499
Aizenstein H, Pitt L (1995) On the learnability of disjunctive normal form formulas. Mach Learn 19(3):183–208
Andrew V, Uzilov JMK, Mathews DH (2006) Detection of non-coding RNAs on the basis of predicted secondary structure formation free energy change. BMC Bioinform 7(1):173
Baldi P, Sadowski P, Whiteson D (2014) Searching for exotic particles in high-energy physics with deep learning. Nat Commun 5:4308
Bayardo RJ Jr (1998) Efficiently mining long patterns from databases. In: Proceedings of the 1998 ACM SIGMOD international conference on management of data, pp 85–93
Bishop CM (2006) Pattern recognition and machine learning (information science and statistics). Springer-Verlag New York Inc., Secaucus
Breiman L, Friedman J, Stone CJ, Olshen RA (1984) Classification and regression trees. CRC Press, Boca Raton
Bshouty NH (1995) Exact learning boolean functions via the monotone theory. Inf Comput 123(1):146–153
Chen T, Guestrin C (2016) XGBoost: a scalable tree boosting system. In: Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining, ACM, New York, NY, USA, KDD ’16, pp 785–794. https://doi.org/10.1145/2939672.2939785
Cheng H, Yan X, Han J, Hsu CW (2007) Discriminative frequent pattern analysis for effective classification. In: Proceedings of 2007 IEEE 23rd international conference on data engineering. IEEE, pp 716–725
Collobert R, Bengio S, Bengio Y (2002) A parallel mixture of SVMs for very large scale problems. Neural Comput 14(5):1105–1114
Dantzig GB, Wolfe P (1960) Decomposition principle for linear programs. Oper Res 8(1):101–111
Desaulniers G, Desrosiers J, Solomon MM (2006) Column generation, vol 5. Springer, Berlin
Deshpande M, Kuramochi M, Wale N, Karypis G (2005) Frequent substructure-based approaches for classifying chemical compounds. IEEE Trans Knowl Data Eng 17(8):1036–1050
Fan RE, Chang KW, Hsieh CJ, Wang XR, Lin CJ (2008) LIBLINEAR: a library for large linear classification. J Mach Learn Res 9(Aug):1871–1874
Guyon I, Gunn S, Ben-Hur A, Dror G (2005) Result analysis of the NIPS 2003 feature selection challenge. Adv Neural Inf Process Syst 17:545–552
Ho TK (1995) Random decision forests. In: Proceedings of the third international conference on document analysis and recognition, vol 1. IEEE, pp 278–282
Ho TK (1998) The random subspace method for constructing decision forests. IEEE Trans Pattern Anal Mach Intell 20(8):832–844
Ho TK, Kleinberg EM (1996) Building projectable classifiers of arbitrary complexity. In: Proceedings of the 13th international conference on pattern recognition, vol 2. IEEE, pp 880–885
Kudo T, Maeda E, Matsumoto Y (2004) An application of boosting to graph classification. Adv Neural Inf Process Syst 17:729–736
Lichman M (2013) UCI machine learning repository. http://archive.ics.uci.edu/ml. Accessed 30 Aug 2019
Lundberg SM, Lee SI (2017) A unified approach to interpreting model predictions. Adv Neural Inf Process Syst 30:4765–4774
Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, Vanderplas J, Passos A, Cournapeau D, Brucher M, Perrot M, Duchesnay E (2011) Scikit-learn: machine learning in Python. J Mach Learn Res 12:2825–2830
Perkins S, Lacker K, Theiler J (2003) Grafting: fast, incremental feature selection by gradient descent in function space. J Mach Learn Res 3:1333–1356
Platt JC (1999) Advances in kernel methods. MIT Press, Cambridge, MA, USA. Chapter fast training of support vector machines using sequential minimal optimization, pp 185–208
Prokhorov D (2001) IJCNN 2001 neural network competition. In: Slide presentation in international joint conference on neural networks 2001. http://www.geocities.ws/ijcnn/nnc_ijcnn01.pdf. Accessed 30 Aug 2019
Quinlan JR (1993) C4.5: programs for machine learning. Morgan Kaufmann Publishers, Burlington
Ribeiro MT, Singh S, Guestrin C (2016) Why should I trust you? Explaining the predictions of any classifier. In: Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining, pp 1135–1144
Rish I, Grabarnik G (2014) Sparse modeling: theory, algorithms, and applications, 1st edn. CRC Press Inc., Boca Raton
Saigo H, Uno T, Tsuda K (2007) Mining complex genotypic features for predicting HIV-1 drug resistance. Bioinformatics 23(18):2455–2462
Schapire RE, Freund Y (2012) Boosting: foundations and algorithms. The MIT Press, Cambridge
Shawe-Taylor J, Cristianini N (2004) Kernel methods for pattern analysis. Cambridge University Press, New York
Tsuda K, Kudo T (2006) Clustering graphs by weighted substructure mining. In: Proceedings of the 23rd international conference on Machine learning, pp 953–960
Uno T, Asai T, Uchida Y, Arimura H (2003) LCM: an efficient algorithm for enumerating frequent closed item sets. In: Proceedings of the third IEEE international conference on data mining workshop on frequent itemset mining implementations, available as CEUR workshop proceedings, vol 90. http://ceur-ws.org/Vol-90/. Accessed 30 Aug 2019
Uno T, Kiyomi M, Arimura H (2004) LCM ver. 2: efficient mining algorithms for frequent/closed/maximal itemsets. In: Proceedings of the fourth IEEE international conference on data mining workshop on frequent itemset mining implementations, available as CEUR workshop proceedings, vol 126. http://ceur-ws.org/Vol-126/. Accessed 30 Aug 2019
Uno T, Kiyomi M, Arimura H (2005) LCM ver. 3: collaboration of array, bitmap and prefix tree for frequent itemset mining. In: Proceedings of the first international workshop on open source data mining: frequent pattern mining implementations, pp 77–86
Zaki MJ, Parthasarathy S, Ogihara M, Li W (1997) New algorithms for fast discovery of association rules. In: Proceedings of the third international conference on knowledge discovery and data mining, pp 283–286
Acknowledgements
This work was partially supported by JST KAKENHI 19H01114 and JST-AIP JPMJCR19U4.
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible editor: Toon Calders.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lee, T., Matsushima, S. & Yamanishi, K. Grafting for combinatorial binary model using frequent itemset mining. Data Min Knowl Disc 34, 101–123 (2020). https://doi.org/10.1007/s10618-019-00657-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10618-019-00657-9