An adaptive algorithm for anomaly and novelty detection in evolving data streams

Abstract

In the era of big data, considerable research focus is being put on designing efficient algorithms capable of learning and extracting high-level knowledge from ubiquitous data streams in an online fashion. While, most existing algorithms assume that data samples are drawn from a stationary distribution, several complex environments deal with data streams that are subject to change over time. Taking this aspect into consideration is an important step towards building truly aware and intelligent systems. In this paper, we propose GNG-A, an adaptive method for incremental unsupervised learning from evolving data streams experiencing various types of change. The proposed method maintains a continuously updated network (graph) of neurons by extending the Growing Neural Gas algorithm with three complementary mechanisms, allowing it to closely track both gradual and sudden changes in the data distribution. First, an adaptation mechanism handles local changes where the distribution is only non-stationary in some regions of the feature space. Second, an adaptive forgetting mechanism identifies and removes neurons that become irrelevant due to the evolving nature of the stream. Finally, a probabilistic evolution mechanism creates new neurons when there is a need to represent data in new regions of the feature space. The proposed method is demonstrated for anomaly and novelty detection in non-stationary environments. Results show that the method handles different data distributions and efficiently reacts to various types of change.

1 Introduction

Usual machine learning and data mining methods learn a model by performing several passes over a static dataset. Such methods are not suitable when the data is massive and continuously arriving as a stream. With the big data phenomenon, designing efficient algorithms for incremental learning from data streams is attracting more and more research attention. Several domains require an online processing where each data point is visited only once and processed as soon as it is available, e.g., due to real-time or limited memory constraints. Applications in dynamic environments experience the so-called concept drift (Gama et al. 2014) where the target concepts or the data characteristics change over time. Such change in streaming data can happen at different speed, being sudden (Nishida et al. 2008; Gama et al. 2004) or progressive (Ditzler and Polikar 2013; GonçAlves and Barros 2013). Change in streaming data also includes the so called concept evolution (Masud et al. 2010) where new concepts (e.g., classes or clusters) can emerge and disappear at any point in time. Most existing methods, such as those reviewed in Gama et al. (2014) and Žliobaitė et al. (2016), address the problem of concept drift and evolution with a focus on supervised learning tasks. In this paper, we focus on online unsupervised learning from an evolving data stream. Specifically, we address the question of how to incrementally adapt to changes in a non-stationary distribution without requiring sensitive hyper-parameters to be manually tuned.

The problem is both interesting and important as evolving data streams are present in a large number of dynamic processes (Žliobaitė et al. 2016). For example, on-board vehicle signals (e.g., air pressure or engine temperature), often used to detect anomalies and deviations (Byttner et al. 2011; Fan et al. 2015b, a), are subject to changes due to external factors such as seasons. Other examples include decision support systems in the healthcare domain (Middleton et al. 2016) where advances in medicine lead to gradual changes in diagnoses and treatments, modeling of the human behavior which naturally change over time (Webb et al. 2001; Pentland and Liu 1999), or the tracking of moving objects on a video (Santosh et al. 2013; Patel and Thakore 2013), to mention but a few.

A naive approach to address the problem of evolving data streams would be to periodically retrain the machine learning model of interest. However, such retraining being triggered without detecting whether it is currently needed or not, often leads to wasted computations. The most widely used approach to deal with changes in data steams consists of training the model based on a sliding window (Zhang et al. 2017; Hong and Vatsavai 2016; Ahmed et al. 2008; Bifet and Gavalda 2007; Jiang et al. 2011). However, choosing a correct window size is not straightforward, since it depends on the speed and type of changes, which are usually unknown. Moreover, existing approaches are specialized for a particular type of change (e.g., sudden, progressive, cyclic). There exist few methods which can handle different types of concept drift, such as (Losing et al. 2016; Dongre and Malik 2014; Webb et al. 2016; Brzezinski and Stefanowski 2014), however, most of those methods are dedicated for supervised learning problems, where the change is primarily detected by estimating a degradation in the classification performance. Other approaches such as (Kifer et al. 2004; Bifet 2010) are designed to explicitly detect, in an unsupervised way, when a change happens. Unfortunately, such approaches require hyper-parameters which are hard to set manually when no prior knowledge is available.

Unsupervised neural learning methods such as Fritzke (1995), Prudent and Ennaji (2005) and Shen et al. (2013) are good candidates for modeling dynamic environments as they are trained incrementally and take into account relations of neighborhood between neurons (data representatives). Specifically, the Growing Neural Gas (GNG) algorithm (Fritzke 1995) creates neurons and edges between them during learning by continuously updating a graph of neurons using a competitive Hebbian learning strategy (Martinetz et al. 1993), allowing it to represent any data topology. This provides an important feature in the context of unsupervised learning from data streams where no prior knowledge about the data is available. However, GNG does not explicitly handle changes in the data distribution.

Some adaptations of GNG such as Frezza-Buet (2014), Shen et al. (2013), Marsland et al. (2002) and Fritzke (1997) try to address some of the problems related to either concept evolution (Shen et al. 2013; Marsland et al. 2002) or drift (Frezza-Buet 2014; Fritzke 1997). However, these methods require an expert to specify some sensitive parameters that directly affect the evolution or the forgetting rate of the neural network. Setting such global parameters prior to the learning does not address the more general case where the speed of changes can vary over time, or when the distribution becomes non-stationary only in some specific regions of the feature space.

We propose in this paper an extension of the GNG algorithm named GNG-A (for Adaptive) and we show how it is used for novelty and anomaly detection in evolving data streams. The contributions of this paper are summarized as follows. First, an adaptive learning rate which depends on local characteristics of each neuron is proposed. Such learning rate allows for a better adaptation of the neurons in stationary and non-stationary distributions. Second, a criterion characterizing the relevance of neurons is proposed and used to remove neurons that become irrelevant due to a change in the data distribution. An adaptive threshold for removing irrelevant neurons while ensuring consistency when no change occurs is also proposed. Third, a probabilistic criterion is defined to create new neurons in the network when there is a need to represent new regions of the feature space. The probabilistic criterion depends on the competitiveness between neurons and ensures stabilization of the network’s size if the distribution is stationary. The proposed method is adaptive, highly dynamic, and does not depend on critical parameters. It is fully online as it visits each data point only once, and can adapt to various types of change in the data distribution.

This paper is organized as follows. In Sect. 2 we give a background related to the growing neural gas based methods. In Sect. 3 we propose a mechanism that allows to continuously adapt neurons in order to closely follow a shift in the data distribution. In Sect. 4 we present an adaptive forgetting mechanism that allows to detect and remove neurons that become irrelevant as a consequence of a change in the data distribution. In Sect. 5 we present an evolution mechanism that allows to create new neurons when necessary. In Sect. 6 we summarize the proposed algorithm and we show how it is used for novelty and anomaly detection. In Sect. 7 we justify the contribution using experimental evaluation. Finally, we conclude and present future work in Sect. 8.

2 Preliminaries and related work

In this section, we describe the self-organizing unsupervised learning methods that are at the origin of the algorithm proposed in this paper.

The neural gas (NG) (Martinetz et al. 1993) is a simple algorithm based on the self-organizing maps (Kohonen 1998), which seeks an optimal representation of an input data by a set of representatives called neurons, where each neuron is represented as a feature vector. In this algorithm, the number of neurons is finite and set manually. This constitutes a major drawback, because the number of representatives needed to approximate any given distribution, is usually unknown.

The growing neural gas algorithm (GNG) (Fritzke 1995) solves the previous problem by allowing the number of neurons to increase. It maintains a graph G which takes into account the neighborhood relations between neurons (vertices of the graph). As shown in Algorithm 1, a minimum number of neurons is initially created (line 3), then, new neurons and new neighborhood connections (edges) are added between them during learning, according to the input instances. For each new instance x from the stream (line 4), the two nearest neurons $n_x^*$ and $n_x^{**}$ are found (line 6) as follows

$$\begin{aligned} n_x^* = {\mathop {{\mathrm{argmin}}}\limits _{n \in G}} ||x - n || ; \quad \quad n_x^{**} = {\mathop {{\mathrm{argmin}}}\limits _{n \in G, n \ne n_x^*}} ||x - n ||. , \end{aligned}$$

where $||a - b ||$ is the Euclidean distance between vectors a and b. A local representation error $err_{n_x^*}$ is increased for the wining neuron $n_x^*$ (line 7) and the age of the edges connected to this neuron is updated (line 8). The wining neuron (i.e., $n_x^*$) is adapted to get closer to x, according to a learning rate $\epsilon _1 \in [0, 1]$. The neighboring neurons (linked to $n_x^*$ by an edge) are also adapted according to a learning rate $\epsilon _2 < \epsilon _1$ (line 9). Furthermore, the two neurons $n_x^*$ and $n_x^{**}$ are linked by a new edge (of age 0). The edges that reached a maximum age $a_{max}$ without being reset, are deleted. If, as a consequence, any neuron becomes isolated, it is also deleted (lines 10–13). The creation of a new neuron is done periodically (i.e., after each $\lambda$ iterations) between the two neighboring neurons that have accumulated the largest representation error (lines 14–20). Finally, the representation error of all neurons is subject to an exponential decay (line 21) in order to emphasize the importance of the most recently measured errors.

Fig. 1

GNG is able to learn the topology of data in a stationary environment

The preservation of neighborhood relations in GNG allows it to represent data of any shape (as shown on Fig. 1), which makes it particularly interesting for a wide range of applications. However, in a non-stationary environment, the GNG algorithm suffers from several drawbacks.

First, it organizes neurons to represent the input distribution by continuously adapting the feature vectors of neurons based on two learning rates $\epsilon _1$, $\epsilon _2$ (see Algorithm 1, line 9), whose values are set manually. If those values are not chosen appropriately, the neural network will not be able to closely follow changes in the data distribution.

Fig. 2

In GNG, with a non-stationary distribution, some irrelevant neurons are not updated anymore and are never removed

Second, when the distribution changes fast, many neurons will not be updated anymore, and will consequently not be able to follow the change. As such neurons do not become isolated, they will never be removed by GNG. Figure 2 shows a data distribution which initially forms one cluster and then splits into two clusters. The first cluster, in the bottom left region of Fig. 2(1), is stationary. The other cluster is moving and getting farther from the first cluster, as shown by the sequence of Fig. 2a–d. Neurons that are not able to follow the moving cluster are kept as part of the graph even if they not relevant anymore.

Third, the GNG algorithm suffers from the need to choose the parameter $\lambda$ (see Algorithm 1, line 14), used to periodically create a new neuron. The periodic evolution of the neural network is clearly not convenient for handling sudden changes where new neurons need to be created immediately. Some adaptations of GNG, like those proposed in Prudent and Ennaji (2005), Shen et al. (2013) and Marsland et al. (2002), try to overcome the problem of periodic evolution by replacing the parameter $\lambda$ by a distance threshold which can be defined globally or according to local characteristics of each neuron. For each new instance x, if $||x - n_x^* ||$ is higher than some threshold, then a new neuron is created at the position of x. However, although this overcomes the problem of periodic evolution, setting an appropriate value for the threshold is not straightforward as it highly depends on the unknown distribution of the input data. Moreover, such methods are more prone to representing noise because they create a new neuron directly at the position of x instead of regions where the accumulated representation error is highest (as in the original GNG).

There exist several variants of GNG for non-stationary environments such as Frezza-Buet (2014), Fritzke (1997) and Frezza-Buet (2008). Perhaps the most known variant is GNG-U (Fritzke 1997) which is proposed by the original authors of GNG. It defines a utility measure that removes neurons located in low density regions and inserts them in regions of high density. The utility measure is defined as follows. Let $n_r$ be the neuron with the lowest estimated density $u_{n_r}$. Let $n_q$ be the neuron which accumulated the highest representation error $err_{n_q}$ (as in line 15 of Algorithm 1). If the ratio $\frac{err_{n_q}}{u_{n_r}}$ is higher than some threshold $\theta$, then the neuron $n_r$ is removed from its current location and inserted close to $n_q$. However, the threshold $\theta$ is yet another user defined parameter which is hard to set because the ratio $\frac{err_{n_q}}{u_{n_r}}$ is unbounded and highly depend on the input data. Moreover, removing $n_r$ and immediately inserting it close to $n_q$ assumes that the distribution is shifting (i.e., the removal and insertion operations are synchronized). Yet, in many cases, we may need to create new neurons without necessarily removing others (e.g., the appearance of a new cluster). Moreover, the evolution of the neural network is still periodic, as in GNG. The only way to limit the network’s size is to set a user-specified limit on the number of neurons, which otherwise leads to a permanent increase in the size of the network.

A state of the art method called GNG-T (Frezza-Buet 2014), which is an improved version of the method proposed in Frezza-Buet (2008), allows to follow non-stationary distributions by controlling the representation error of the neural network. During an epoch of N successive iterations (i.e., successive inputs to the algorithm), let $\{x_j^i\}_{1 \le j \le l_i}$ denote the set of $l_i$ input data for which $n_i$ is the winning neuron. Then the representation error of the neuron $n_i$ is defined as $E_{n_i} = \frac{1}{N} \sum \limits _{j = 1}^{l_i} ||x_j^i - n_i ||$. The method determines the $\sigma$-shortest confidence interval (Guenther 1969) $(E_{min}, E_{max})$ based on the errors of all neurons $\{E_{n_i}\}_{n_i \in G}$. Let T be a target representation error specified by the user. GNG-T seeks to keep the representation error of the neural network close to T by maintaining $T \in [E_{min}, E_{max}]$. More specifically, after each period, if $E_{max}$ becomes less than T, then a neuron is removed. Similarly, if $E_{min}$ becomes higher than T, then a new neuron is inserted. After each epoch, the neurons that have not won are simply considered as irrelevant, and are removed. GNG-T is the closest work to what we propose in this paper. Unfortunately, it depends on critical parameters (mainly, the epoch N, the target error T and the confidence $\sigma$) which directly guide the insertion and removal of neurons. Moreover, splitting the stream into epochs of N successive input data means that GNG-T is only partially online.

In order to relax the constraints related to GNG and its derivatives in non-stationary environments we propose, in the following sections, new mechanisms for: (1) a better adaptation of the neurons in stationary and non-stationary distributions (Sect. 3); (2) an adaptive removal of irrelevant neurons, while ensuring consistency when no change occurs (Sect. 4); (3) creating new neurons when necessary, while ensuring stabilization of the network’s size if the distribution is stationary (Sect. 5).

3 Adaptation of existing neurons

GNG, and the self-organizing neural gas based methods in general, can intrinsically adapt to the slowly changing distributions by continuously updating the feature vector of neurons. As shown in Algorithm 1 (line 9), this adaptation depends on two constant learning rates $\epsilon _1$ (for adapting the closest neuron $n_x^*$ to the input) and $\epsilon _2$ (for adapting the topological neighbors of $n_x^*$) such that $0< \epsilon _2 < \epsilon _1 \ll 1$. If the learning rates $\epsilon _1$ and $\epsilon _2$ are too small, then neurons learn very little from their assigned data points. This causes the neural network to adapt very slowly to the data distribution. In contrast, too high learning rates can cause the neural network to oscillate too much.

Many existing methods try to address this problem by decreasing the learning rate over time (also referred to as “annealing” the learning rate), so that the network converges, the same way as it is done for the stochastic gradient descent (Zeiler 2012). However, in a streaming setting, as time goes, this may cause neurons to adapt very slowly to changes in data distribution that happen far in the future (as the learning rate will be very small). Moreover, such a global learning rate is not convenient for handling local changes where the distribution is only stationary in some regions of feature space. Some methods like (Shen et al. 2013) define the learning rate for the winning neuron $n_x^*$ as being inversely proportional to the number of instances associated with that neuron (i.e., the more it learns, the more it becomes stable). However, such learning rate is constantly decreasing over time, thus still causes neurons to adapt slowly to changes in data distribution as time goes.

In order to closely follow the changing distribution and properly handle local changes, we propose to use an adaptive local learning rate $\epsilon _n$ for each neuron n. Intuitively, a local change is likely to increase the local error of nearby neurons without affecting the ones far away. Therefore, we define the learning rate of a neuron n as being related to its local error $err_n$. By doing so, at each point in time, the learning rate of each neuron can increase or decrease, depending on the locally accumulated error.

Let E be the set of local errors for all neurons in the graph G, sorted in the descending order (i.e., from high error to low error). The learning rate for each neuron $n \in G$ is then defined as follows

$$\begin{aligned} \epsilon _n = \frac{1}{ 2 + {\text {Index}}(err_n, E) }, \end{aligned}$$

(1)

where ${\text {Index}}(err_n, E)$ is the index (or rank) of $err_n$ in E. Therefore, we define the learning rate used for adapting the winning neuron as $\epsilon _1 = \epsilon _{n_x^*}$, and the learning rate for adapting each neighboring neuron $n_v \in {\text {Neighbors}}(n_x^*)$ as $\epsilon _2 = {\text {min}}(\epsilon _1, \epsilon _{n_v})$.

By adapting the wining neurons with a learning rate which depends on the ordering of their local errors, the algorithm manages to better adapt to local changes. However, it should be noted that when the number of neurons is static and the concepts are stationary, the learning rates will still be different for different neurons in the network. An alternative solution consists in adapting the learning rates by magnitude instead of ordering. However, this solution is prone to outliers and the local errors are constantly subject to an exponential decay, making their values significantly different from each other. Therefore, we prefer to use the solution which is based on ordering.

4 Forgetting by removing irrelevant neurons

Dealing with concept drifting data implies not only adapting to the new data but also forgetting the information that is no longer relevant. GNG is able to remove neurons that become isolated after removing old edges (lines 12–13 of Algorithm 1). However, as shown previously on Fig. 2, when the data distribution changes sufficiently fast, some neurons will not be adapted anymore and they will still be kept, representing old data points that are no longer relevant. The forgetting mechanism proposed in this section allows us to eliminate such irrelevant neurons in an adaptive way.

4.1 Estimating the relevance of a neuron

In order to estimate the “relevance” of neurons, we introduce a local variable $C_n$ for each neuron n. This local variable allows to ensure that removing neurons will not negatively affect the currently represented data when no change occurs. For this purpose, $C_n$ captures the cost of removing the neuron n. This cost represents how much the total error of the neighboring neurons of n would increase, if n is removed. In order to define $C_n$, let us consider $X_n = \{ x_i \mid n = n_{x_i}^* \}$ as the set of instances (data points) associated with a given neuron n (instances closest to n, i.e., for which n was winner). If n is removed, instances in $X_n$ would be associated to their nearest neurons in the neighborhood of n. Associating an instance $x_i \in X_n$ to its (newly) nearest neuron $n_{x_i}^{**}$ would increase the local error of that neuron by $||x - n_{x_i}^{**} ||$. Therefore, we define $C_n$ for a neuron n according to the distance from its associated instances to their second nearest neurons, as follows

$$\begin{aligned} C_n = \sum \limits _{i = 0}^{t} {\mathbb {1}}(n = n_{x_i}^*) \times ||x_i - n_{x_i}^{**} ||, \end{aligned}$$

where t is the current time step (i.e., t’th instance from the stream), and ${\mathbb {1}}(Cond)$ is the 0-1 indicator function of condition Cond, defined as

$$\begin{aligned} {\mathbb {1}}(Cond) = {\left\{ \begin{array}{ll} 1 &{} \quad \text {if }Cond\text { is true} \\ 0 &{} \quad \text {otherwise.} \end{array}\right. } \end{aligned}$$

In order to compute an approximation of $C_n$ for each neuron n in an online fashion, each time a new instance x is received from the stream, the local variable $C_{n_x^*}$ of its closest neuron $n_x^*$ (i.e., the winning neuron) is increased by $||x - n_x^{**} ||$ (i.e., by the distance to the second closest neuron)

$$\begin{aligned} C_{n_x^*} \leftarrow C_{n_x^*} + ||x - n_x^{**} ||. \end{aligned}$$

(2)

The local variable $C_n$ is then an estimation for the cost of removing the neuron n. At each iteration, this local variable is exponentially decreased for all the existing neurons (the same way as it is done for the local representation error in line 21 of Algorithm 1):

$$\begin{aligned} \forall n \in G, \quad C_n \leftarrow 0.9 \times C_n. \end{aligned}$$

(3)

It follows that a very small value $C_n$ for a neuron n, may indicate two things. First, when the distribution is stationary, it indicates that n is competing with other neurons in its neighborhood (i.e., the cost of removing n is low), which suggests that the data points associated with n can be safely represented by its neighboring neurons instead. Second, when the distribution is not stationary, a low value of $C_n$ indicates that n is no longer often selected as the closest neuron to the input data point, which suggests that it is no longer relevant. In both of those cases, n can be safely removed for a sufficiently small value of $C_n$.

Note that if n is the closest neuron to some input data points but is far away from these points (i.e. all the neurons are far from these data points, since n is the closest), then $C_n$ is high because n needs to be adapted to represent these data points instead of being removed.

Let us denote by $\hat{n}$ the neuron which is most likely to be removed (i.e. with the smallest $C_n$):

$$\begin{aligned} \hat{n} = {\mathop {{\mathrm{argmin}}}\limits _{n \in G}} C_n. \end{aligned}$$

Naturally, the forgetting can be triggered by removing $\hat{n}$ if the value of its local variable $C_{\hat{n}}$ falls below a given threshold. However, such value may quickly become small (approaching 0) as it is constantly subject to an exponential decay, which makes it hard to directly set a threshold on this value. Instead of removing $\hat{n}$ when $C_{\hat{n}}$ is sufficiently small, a more convenient strategy is to remove it when $-\log C_{\hat{n}}$ is sufficiently high, that is, when

$$\begin{aligned} -\log C_{\hat{n}} > \tau , \end{aligned}$$

where $\tau$ is an upper survival threshold. The smaller $\tau$, the faster the forgetting. Larger values of $\tau$ would imply a longer term memory (i.e. forgetting less quickly). The exact value of the threshold $\tau$ depends, among other factors, on the data distribution and how fast it is changing. This is clearly an unknown information. Therefore, a problem that still remains is: when do we trigger the forgetting mechanism? In other words, how do we decide that $C_n$ is sufficiently small, without requiring the user to directly specify such a sensitive threshold? To define a convenient value for $\tau$, we propose in the following subsection an adaptive threshold.

In order to analyze the proposed removal process for a given neuron n, remember that $C_n$ is exponentially decreased at each iteration according to Eq. 3 and only increased when n is a winning neuron according to Eq. 2. Since $||x - n_x^{**} ||$ can be assumed to be bounded and to simplify the analysis, let us assume that when n wins, $C_n$ is simply increased by a constant value, e.g. 1. If the input data follow a stationary uniform distribution and the number of neurons at some iteration is g, then n is expected to win once after g iterations. Therefore, $C_n$ decreases g times according Eq. 3 before it is increased by 1. In this case, $C_n$ at time t can be expressed as:

$$\begin{aligned} C^{(t)}_n = (((1 \times 0.9^{g_1} + 1) \times 0.9^{g_2} + 1) \times 0.9^{g_3} + \cdots + 1) * 0.9^{g_v}, \end{aligned}$$

(4)

where v is the winning count¹ of n, and $g_i$ is the number of neurons at the i’th time where n was winner. If the number of neurons is fixed, i.e., $g_1 = g_2 = \dots = g$, then $v = \left\lfloor \frac{t}{g} \right\rfloor$ and $C_n$ becomes the sum of a geometric series:

$$\begin{aligned} C^{(t)}_n = 0.9^{g} + 0.9^{2g} + 0.9^{3g} + \dots + 0.9^{vg} = \frac{0.9^g}{1 - 0.9^g} (1 - 0.9^t). \end{aligned}$$

In this case, $C_n$ represents a stationary process because $\lim \limits _{t\rightarrow \infty } C^{(t)}_n = \frac{0.9^g}{1 - 0.9^g}$ and neurons will not be removed (i.e. the network stays stable). However, if the distribution changes and n is not winning anymore, then it is obvious that $C_n$ will keep decreasing and n get’s removed as soon as $C_n$ falls below $\tau$. In this case, if $c_0$ is the last value of $C_n$ when n was winner, then n is removed when $c_0 \times 0.9^\alpha \le \tau$. In order words, n is removed after $\alpha = \frac{1}{\log 0.9} \log \frac{\tau }{c_0}$ iterations.

Fig. 3

The value $-\log C_{\hat{n}}$ for the neuron $\hat{n}$ (which is most likely to be removed at each iteration) in two cases: a stationary distribution (blue) and a non-stationary distribution (red) (Color figure online)

4.2 Adaptive removal of neurons

In order to motivate the adaptive threshold we propose, let us consider Fig. 3, which shows the value of $-\log C_{\hat{n}}$ for a stationary (blue curve) and a non-stationary (red curve) distributions. On the one hand, if the neuron $\hat{n}$ has not been selected as winner during some short period of time, then $-\log C_{\hat{n}}$ may temporarily be high, but would decrease again as soon as $\hat{n}$ is updated (see the blue curve on Fig. 3). In this case, if the threshold $\tau$ is chosen too low, then it wrongly causes $\hat{n}$ to be immediately removed. On the other hand, if $\hat{n}$ is not anymore selected as winner (in the case of a non-stationary distribution), then $-\log C_{\hat{n}}$ keeps increasing (see the red curve on Fig. 3). In this case, if the threshold $\tau$ is chosen too high, then it causes long delay in removing neurons that are not relevant anymore (leading to results similar to those previously shown on Fig. 2), which is not in favor of a real-time tracking of the non-stationary distribution. In order to automatically adapt the threshold $\tau$, we consider the two following cases:

• 1. Increasing $\tau$:

  If $-\log C_{\hat{n}} > \tau$ (i.e., $\hat{n}$ should be removed) but $\hat{n}$ would still be winning in the future, then the threshold $\tau$ should be increased (to remove less neurons in the future). The reason for increasing $\tau$ in this case is that a neuron which should be removed is expected to not be winner anymore (or very rarely) in the future.

• 2. Decreasing $\tau$:

  If $-\log C_{\hat{n}} \le \tau$ (i.e., $\hat{n}$ is not removed) but $\hat{n}$ is not winning anymore, then the threshold $\tau$ should be decreased (to remove more neurons in the future). The reason for decreasing $\tau$ in this case is that a neuron which is not removed is expected to be a winner sufficiently frequently.

To address the first case, when a neuron $\hat{n}$ is removed from G because $-\log C_{\hat{n}} > \tau$, we do not discard it completely; instead, we keep it temporarily, in order to use it for a possible adaptation of the threshold $\tau$. Let R be a buffer (a Queue with FIFO order) where the removed neurons are temporarily kept². Let x be a new instance from the stream, and $n_x^{*}$ be the nearest neuron to x in G. Let $r_x^{*} \in R$ be the nearest neuron to x in R. If x is closer to $r_x^{*}$ than to $n_x^{*}$ (i.e., $||x - r_x^{*} || < ||x - n_x^{*} ||$), then $r_x^{*}$ would have been the winner instead of $n_x^{*}$. In this case, we increase $\tau$ as follows:

$$\begin{aligned} \tau \leftarrow \tau + \epsilon \times [ (-\log C_{r_x^{*}}) - \tau ], \end{aligned}$$

(5)

where $\epsilon \in [0, 1]$ is a small learning rate (discussed thereafter in this section).

Finally, we need to design a strategy to maintain the R buffer. Let $W_n$ be the number of times where a neuron n has been winner during the W last time steps (iterations). Let $R' = \{ r \in R | W_r = 0 \}$ be the subset of neurons from R that has never been a winner during the W last time steps. If $|R'| > k$ (i.e., a sufficient number of neurons are not updated anymore), then we definitively remove the oldest neuron from R.

For the second case, let $|\{ n \in G | W_n = 0 \}|$ be the number of neurons from G that has never been a winner during the W last time steps. If this number is higher than k and $-\log C_{\hat{n}} \le \tau$, then we decrease $\tau$ as follows:

$$\begin{aligned} \tau \leftarrow \tau - \epsilon \times [ \tau - (-\log C_{\hat{n}})] \end{aligned}$$

(6)

The learning rate $\epsilon \in [0,1]$ used in Eqs. 5 and 6 for updating $\tau$ can be decreased over time, as shown in Eq. 7, so that $\tau$ converges more quickly.

$$\begin{aligned} \epsilon = \frac{1}{1 + N_{\tau }}, \end{aligned}$$

(7)

where $N_{\tau }$ is the number of times where $\tau$ has been updated (increased or decreased). Alternatively, $\epsilon$ can be kept constant if the speed of the changing distribution is expected to change over time (i.e., acceleration is not constant), depending on the application domain.

In order to give a chance for each neuron in G to be selected as winner at least once, W needs to be at least equal to the number of neurons. Therefore, instead of having a manually fixed value for W, this latter is simply increased if the number of neurons reaches W (i.e. if $|G| \ge W$). Note that in all our experiments W is simply increased by 10 each time $|G| \ge W$.

Besides, the parameter k plays a role in the adaptation of the threshold $\tau$ used to remove neurons. If more than k neurons are not updated anymore (i.e. their $W_n = 0$), then $\tau$ is adapted to increase the chance of removing such neurons in future. Consequently, higher values of k lead to a less frequent adaptation of $\tau$ (i.e. promoting more stability). Note that setting k to a too high value can introduce some delay in removing irrelevant neurons. On the opposite side, by setting k too low (e.g. $k = 1$), it is possible (even when the distribution is stationary) that any neuron n would occasionally have $W_n = 0$ and causes the adaptation of $\tau$.

5 Dynamic creation of new neurons

As explained in Sect. 2, GNG creates a new neuron periodically. If there is a sudden change in the distribution and data points starts to come in new regions of the feature space, the algorithm cannot immediately adapt to represent those regions. This is mainly due to the fact that a new neuron is created only every $\lambda$ iterations. In many real-time applications, new neurons need to be created immediately without affecting the existing ones (i.e., concept evolution). In order to handle such changes faster, we propose a dynamic strategy that allows creation of new neurons when necessary. The proposed strategy ensures that less neurons are created when the distribution is stationary, while being able to create more neurons if necessary, i.e. when there is a change in the data distribution.

Remember that $W_n$ is the number of times where a neuron n has been winner during the W last time steps (iterations). Let us define the ratio $\frac{W_n}{W} \in [0,1]$ as the winning frequency of a neuron n. When the number of neurons in G is low, their winning frequency is high. This is essentially due to a low competition between neurons, which gives a higher chance for each neuron to be selected as winner. An extreme case example is when G contains only one neuron which is always winning (i.e. its winning frequency is 1). In contrast, as the number of neurons in G increases, their winning frequency decreases due to a higher competitiveness between neurons. We propose a strategy for creating new neurons in a probabilistic way, based on the current winning frequency of neurons in G.

Let ${\mathrm{f}}_\mathrm{q} \in [0, 1]$ be the overall winning frequency in the graph G defined as

$$\begin{aligned} \mathrm{f}_\mathrm{q} = \frac{1}{k} \times \sum \limits _{n \in S} \frac{W_n}{W}, \end{aligned}$$

(8)

where S is a set of k neurons with the highest winning frequencies³ among all neurons in G. The higher the overall winning frequency $\mathrm{f}_\mathrm{q}$, the higher the probability of creating a new neuron, and vice-versa.

Let $S'$ be a set of $k'$ neurons with the highest winning frequencies. It is easy to prove that for any $k' > k$ (i.e. $S \subset S'$), we have $\mathrm{f}_\mathrm{q}' = \frac{1}{k'} \times \sum _{n \in S'} \frac{W_n}{W} \le \mathrm{f}_\mathrm{q}$. Therefore, higher values of k lead to creating neurons less frequently (i.e. promoting more stability).

If the data distribution is stationary, then creating new neurons is likely to decrease $\mathrm{f}_\mathrm{q}$, which implies a smaller probability to create more neurons in the future. However, if there is a change in the data distribution so that new neurons actually need to be created, then $\mathrm{f}_\mathrm{q}$ will automatically increase (which leads to a higher probability of creating more neurons). Indeed, let us assume that data points from a new cluster start to appear. Some existing neurons that are the closest to those points will be selected as winner, making their winning frequencies high, which consequently increases ${rm f}_\mathrm{q}$. As $\mathrm{f}_\mathrm{q}$ increases, there is more chance for creating new neurons to represent the new cluster. This is illustrated in Fig. 4 which shows $\mathrm{f}_\mathrm{q}$ for a stationary distribution (blue curve) and for a non-stationary distribution (red curve) where a new cluster is suddenly introduced after time step 1000 .

Fig. 4

The value of $\mathrm{f}_\mathrm{q}$ with synthetic data, in two cases: a stationary distribution (blue) and a non-stationary distribution (red) (Color figure online)

The insertion of a new neuron is done with a probability proportional to $\mathrm{f}_\mathrm{q}$. However, in order to lower the chance of performing insertions too close in time and give time for the newly inserted neuron to adapt, we introduce a retarder term $\mathrm{r}_\mathrm{t}$ defined as follows:

$$\begin{aligned} \mathrm{r}_\mathrm{t} = \frac{1}{t - t'}, \end{aligned}$$

where t is the current time step and $t' < t$ is the previous time when the last insertion of a neuron occurred. Hence, a new neuron is created with a probability ${\text {max}}(0, \mathrm{f}_\mathrm{q} - \mathrm{r}_\mathrm{t})$. In other words, a new neuron is created if ${\text {rand}} < \mathrm{f}_\mathrm{q} - \mathrm{r}_\mathrm{t}$, where ${\text {rand}} \in [0, 1]$ is randomly generated according to a uniform distribution.

For the purpose of analysis, let us assume that the input data follow a stationary uniform distribution. If $|G| = g$ is the number of neurons at some iteration t, then all neurons are equally likely to win and the winning frequency of each neuron is $\frac{W_n}{W} = \mathrm{f}_\mathrm{q} = \frac{1}{g}$. Since the insertion of a new neuron happens with a probability which is essentially $\mathrm{f}_\mathrm{q}$, then when $|G| = 2$, $\mathrm{f}_\mathrm{q} = \frac{1}{2}$ and a new neuron is added after 2 iterations; when $|G| = 3$, $\mathrm{f}_\mathrm{q} = \frac{1}{3}$ and one more neuron is added after 3 more iterations, etc. Thus, the expected number of neurons at time t (when no removal occurs) can be expressed as:

$$\begin{aligned} \underbrace{ \frac{1}{1} + \frac{1}{2} + \frac{1}{2} + \frac{1}{3} + \frac{1}{3} + \frac{1}{3} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} }_\text {e.g. at t = 10 iterations, g = 4 neurons} + \dots \simeq \left\lfloor \sqrt{\frac{1}{4}+2t} - \frac{1}{2} \right\rfloor \end{aligned}$$

Therefore, if no removal occurs, the number of neurons increases continuously (but slowly) over time. However, as the number of neurons increases, each neuron will win less frequently. It follows that some neurons would have their $C_n$ decreasing and would eventually be removed, keeping the number of neurons stable. In order to show that $C_n$ decreases, let us consider again Eq. 4. If the initial number of neurons is $g_1 = 1$, then as explained previously, after two more iterations $g_2 = 2$, and after three more iterations $g_3 = 3$, etc. Therefore Eq. 4 becomes:

$$\begin{aligned} C^{(t)}_n = (((1 \times 0.9^1 + 1) \times 0.9^2 + 1) \times 0.9^3 + \cdots + 1) * 0.9^{v} = \sum _{i=1}^v 0.9^{\frac{1}{2}(v-i+1)(i+v)} \end{aligned}$$

The sum above has no closed-form expression. However, it can be re-written recursively as $C^{(t)}_n = 0.9^t(C^{(t-1)}_n + 1)$, and it is easy to show that $\forall t'> t > 5$, we have $C^{(t')}_n \le C^{(t)}_n$. Therefore, n would eventually be removed as $C_n$ is monotonically decreasing.

6 Algorithm

GNG-A is summarized in Algorithm 2, which makes a call to Algorithm 3 to check for the removal of neurons (see Sect. 4) and Algorithm 4 to check for the creation of neurons (see Sect. 5).

First, Algorithm 2 initializes the graph G with two neurons (line 3). For each new data point x, the two nearest neurons $n_x^*$ and $n_x^{**}$ are found (line 7). The local error $err_{n_x^*}$ is updated for the wining neuron $n_x^*$ and the age of the edges emanating from this neuron is incremented (lines 8–9). The local relevance variable $C_{n_x^*}$ is increased in order to record the cost of removing this neuron (line 10), as described in Sect. 4.1. The neuron $n_x^*$ and its neighbors (linked to $n_x^*$ by an edge) are adapted to get closer to x (lines 11–12), using the local learning rates that are computed according to Eq. 1 as described in Sect. 3. As in GNG, $n_x^*$ and $n_x^{**}$ are linked by an edge, old edges are deleted, and neurons that becomes isolated are also deleted. Algorithm 3 is called (line 17) to adapt the forgetting threshold $\tau$ and to check if there is any irrelevant neuron that needs to be removed, as described in Sect. 4. Then, Algorithm 4 is called (line 18) in order to insert a new neuron according to a probabilistic criterion described in Sect. 5. Finally, the local errors and relevance variables of all neurons are subject to an exponential decay (line 19).

Note that the parameter k used in Algorithms 3 and 4 serves different but related purposes. Indeed, as higher values of k promote stability in both the removal and the creation cases, it is reasonable and more practical to collapse the value of the parameter k for both cases into one.

Let f be the size of x (i.e. the number of features), g be the number of neurons (i.e. the size of the graph |G|), and r be the number of neurons in R, with $r \ll g$. The most time consuming operation in Algorithm 2 is finding the neurons in G that are closest from the input x (line 7 of Algorithm 2). For each input x, this operation takes ${\mathcal {O}}(f \times g)$. Additionally, the adaptation of the local variables of neurons (e.g. lines 19–22 of Algorithm 2) has ${\mathcal {O}}(g)$ time complexity. Algorithm 3 has a time complexity of ${\mathcal {O}}(f \times r)$ as it needs to find $r_x^{*}$, and Algorithm 4 has a time complexity of ${\mathcal {O}}(g)$. Therefore, the overall complexity of the proposed method (GNG-A) for learning from each instance x is ${\mathcal {O}}(f \times (g + r))$, which is very similar to the original GNG algorithm.

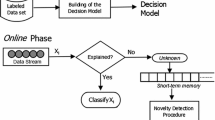
Anomaly and novelty detection methods (Liu et al. 2008; Krawczyk and Woźniak 2015; Li et al. 2003; Schölkopf et al. 2000) learn a model from a reference set of regular (or normal) data, and classify a new test data point as irregular (or abnormal) if it deviates from that model. If the reference data comes as a stream and its distribution is subject to change over time, such methods are typically trained over a sliding window as described in Ding and Fei (2013) and Krawczyk and Woźniak (2015).

The method we proposed is able to adapt to various types of change without keeping data points in a sliding window, and therefore it is straightforward to use it for the task of anomaly and novelty detection where the distribution of the reference data is non-stationary. More specifically, each neuron in G can be considered as the center of a hyper-sphere of a given radius d (a distance threshold). Therefore, at any time t, the graph G (i.e., all hyper-spheres) covers the area of space that represents regular data. It follows that a test data point x whose distance to the nearest neuron is larger than d, is not part of the area covered by G. More formally, x is considered as abnormal (or novel) if

$$\begin{aligned} {\text {min}}_{n \in G} ||x - n || > d \end{aligned}$$

Manually choosing a convenient value for the decision parameter d is hard because it not only depends on the dataset but also on the number of neurons in G, which varies over time. Indeed, a higher number of neurons requires a smaller d. However, it is also natural to expect that a higher number of neurons in G would cause the distance between neighboring neurons to be smaller (and vise versa). Therefore, we heuristically set d equal to the expected distance between neighboring neurons in G. In order words, d at any time is defined as the average length of edges at that time:

$$\begin{aligned} d = \frac{1}{|E|} \sum _{(n_i, n_j) \in E} ||n_i - n_j ||, \end{aligned}$$

where E is the current set of edges in the graph, and $(n_i, n_j)$ is an edge linking two neurons $n_i$ and $n_j$.

7 Experiments

In this section, we evaluate the proposed method. First, we present the datasets used for evaluation in Sect. 7.1. Then, we evaluate the general properties of the proposed method in terms of the ability to follow a non-stationary distribution, in Sect. 7.2. Finally, we present and discuss the results of the anomaly and novelty detection using the proposed method, in comparison to other benchmarking methods in Sect. 7.3.

7.1 Datasets

We consider in our experimental evaluation several real-world and artificial datasets covering a wide range of non-stationary distributions. Table 1 gives a brief summary of all the considered datasets. The column Classes indicates the number of classes or clusters in each dataset. The column Change indicates the interval, in number of examples, between consecutive changes in the data distribution. For example, if Change is 400, then there is a change in the data distribution after each (approximately) 400 examples from the stream. Note that NA refers to “no change”, and “unknown” refers to an unknown rate of change (where changes can happen at any moment) with variable or significantly different intervals between consecutive changes. The column Regular reports the percentage of regular instances in each dataset.

Table 1 Summary of the datasets characteristics

The first group consists in various real world datasets: Covtype, Elec2, Outdoor, Rialto, Weather, Spamdata, Keystroke and Opendigits; in addition to two commonly used artificial datasets: Usenet and Sea-Concepts. All the datasets are publicly available for download.⁴ Details of each dataset are given in “Appendix A”.

Fig. 5

Snapshots from the artificial non-stationary datasets

The other datasets are provided in Souza et al. (2015) and publicity available for download.⁵ These datasets experience various levels of change over time, thus, are ideal to showcase the performance of algorithms in non-stationary environments. All these artificial non-stationary datasets are illustrated in Fig. 5. The last four artificial datasets in Table 1 are stationary datasets with distributions corresponding to various shapes, as illustrated in Fig. 5.

7.2 General properties of GNG-A

The first set of experiments shows the general properties of the proposed method in terms of the adaptability, the ability to represent stationary distributions, and to follow non-stationary distributions.

Fig. 6

The location of neurons for a one-dimensional non-stationary distribution over time. $|G| \le 10$, $k=10$

As an initial step, Fig. 6 illustrates a simple proof of concept of the proposed method for a simulated one-dimensional non-stationary data distribution, which is initially shown by the grey box on the left. The location, over time, of the created neurons is shown with red points. The size of the graph G is limited to 10 neurons for better visualization purposes. At time 1000, the distribution is moderately shifted, which makes half of the neurons to be reused, and others to be created. At time 3000 the distribution suddenly changes, which makes only few neurons change their location, and leads to the creation of many new neurons and the removal of existing ones. After time 5000, the distribution splits into two parts (clusters), and the proposed method follows the change.

Fig. 7

a, b The value of the adaptive threshold $\tau$ according to different initial values. c The effect of $\epsilon$ on the adaptation of the threshold $\tau$. Parameter $k=10$

Figure 7 shows an experiment performed on the 1CDT dataset (non-stationary) with the goal to showcase the adaptive removal of neurons described in Sect. 4.2. Remember that, for a given dataset, the forgetting rate depends on the value to which the threshold $\tau$ is set. As $\tau$ is adaptive, we show in this experiment that it is not very sensitive to the initial value to which it is set. Figure 7a shows the final values of $\tau$ (i.e., after adaptation) according to the initial values of $\tau$. Figure 7b shows the current value of $\tau$ over time, based on different initial values. Despite the fact that there is some influence from the initial value of $\tau$, we can see from Fig. 7a, b that any initial value of $\tau$, leads to values of $\tau$ that are close to each other.

Moreover, a learning rate $\epsilon$ is used during the adaptation of $\tau$ (see Eqs. 6, 5). In the experiment of Fig. 7a, b, this learning rate was set according to Eq. 7 as described in Sect. 4.2. In order to illustrate the effect of $\epsilon$ on $\tau$, Fig. 7c shows the value of $\tau$ over time, based on different values of $\epsilon$. It is natural that when $\epsilon$ is low (e.g. 0.005), $\tau$ changes slowly at each adaptation step. For $\tau$ to eventually stabilize, $\epsilon$ needs only to be sufficiently small. Nonetheless, for the reminder of this paper, $\epsilon$ is adapted according to Eq. 7.

Fig. 8

The evolution of the overall winning frequency $\mathrm{f}_\mathrm{q}$ and the number of neurons over time, for a fixed $\tau = 30$, according to different values of the parameter k. a The winning frequency and b the number of neurons. The non stationary dataset 1CDT is used. a The larger k, the smaller the winning frequency

Fig. 9

The evolution of the adaptive threshold $\tau$ and the number of neurons over time, according to different values of the parameter k. a The values of $\tau$ and b the number of neurons. The non stationary dataset 1CDT is used

In order to illustrate the influence of the parameter k on the creation of neurons and how fast the network grows, Fig. 8 shows (for the non stationary dataset 1CDT) the evolution of the overall winning frequency $\mathrm{f}_\mathrm{q}$ (A) and the number of neurons (B) over time, for a fixed threshold $\tau$, according to different values of the parameter k. We can see from Fig. 8 that higher values of k lead to a smaller overall winning frequency $\mathrm{f}_\mathrm{q}$, which consequently lead to a less frequent creation of neurons. Figure 9 shows the same experiment with the adaptive threshold $\tau$, in order to illustrate the influence of the parameter k on both the adaptive creation and removal of neurons. We can see from Fig. 9 that smaller values of k lead to a more frequent adaptation of $\tau$. If more than k neurons are not updated anymore, then $\tau$ is decreased in order to remove more neurons in future. Specifically, by setting k to the lowest value $k=1$, $\tau$ is decreased frequently causing the removal of many neurons and the insertion of others, which leads to an unstable network. Besides the fact that higher values of k lead to less frequent removals and insertions (and vice versa), Figs. 8 and 9 also show that for a reasonable choice of k (e.g. $k=10$), the number of neurons stabilizes over time.

Fig. 10

The winning frequency $\mathrm{f}_\mathrm{q}$ over time for data generated by one cluster (a Gaussian). At time $t = 3000$ an additional number of clusters are introduced

The overall winning frequency $\mathrm{f}_\mathrm{q}$ defines the probability of creating new neurons. This probability is especially important in the case of a sudden appearance of new concepts. Figure 10 shows the values of $\mathrm{f}_\mathrm{q}$ over time where a variable number of new clusters are introduced at time $t = 3000$. We can see that $\mathrm{f}_\mathrm{q}$ increases at time $t = 3000$ allowing for the creation of new neurons to represent the new clusters. Moreover, Fig. 10 shows that the probability of inserting new neurons is higher and lasts longer when the number of newly introduced clusters is higher, which is a desired behavior.

Fig. 11

The period $\lambda = 100$ in GNG, GNG-U and GNG-T. The removal threshold $\theta = 10^9$, $10^5$ and $10^7$ for the three respective datasets in GNG-U. The epoch $N = 500$, the confidence $\sigma = 0.8$, and target error $T = 0.3$, 0.01 and 0.4, for the three respective datasets in GNG-T. $k=10$ for the proposed method. Note that in the first column the plot of GNG-T (blue) is thicker (appears to be black) because points in the graph are very close. Also, the plot of GNG (thin black) in the first line is hidden behind the plot of GNG-U (green) (Color figure online)

Figure 11 illustrates the behavior of proposed method in comparison to GNG (Fritzke 1995) and two other variants for non-stationary distributions described in Sect. 2, namely GNG-U (Fritzke 1997) and GNG-T (Frezza-Buet 2014). For each method, we show the evolution of the number of neurons over time in first column of figures, the overall representation error (i.e., average over all neurons) in the second column of figures, and the percentage of irrelevant neurons (i.e., that have never been updated during the last 100 steps) in the third column of figures. We show the results in three situations: a stationary distribution using dataset 2D-1 (the three top figures), a non-stationary distribution with a progressive change using dataset 1CDT (the three middle figures), and a stationary distribution with a sudden change happening after time 2500, using dataset 2D-4 (the three bottom figures). We can observe from Fig. 11 that the proposed method manages to create more neurons at early stages, which leads to a lower representation error. The number of neurons automatically stabilizes over time for the proposed method (unlike GNG and GNG-U). It also stabilizes for GNG-T depending on the user specified target parameter T. Moreover, all three methods (unlike GNG) efficiently remove irrelevant neurons. Nonetheless, it should be noted that the proposed method is adaptive, and unlike GNG-U and GNG-T, there is no need to adapt any parameter across the three datasets.⁶

7.3 Anomaly and novelty detection

In the following, the proposed method (GNG-A) is compared against: One Class SVM (OCSVM) (Schölkopf et al. 2000), Isolation Forest (Liu et al. 2008), and KNNPaw (Bifet et al. 2013), in addition to GNG, GNG-U and GNG-T. The KNNPaw method consists in a kNN with dynamic sliding window size able to handle drift. The anomaly detection with the KNNPaw method is done by checking whether the mean sample distance to the k Neighbors is higher than the mean distance between samples in the sliding window. The two anomaly detection methods OCSVM and Isolation Forest are trained over a sliding window, allowing them to handle non-stationary distributions. The Python implementations available on the scikit-learn machine learning library (Pedregosa et al. 2011) have been used. A sliding window of 500 instances is chosen for OCSVM and Isolation Forest, as it provides the best overall results across all datasets.

For each dataset, instances from a subset of classes (roughly half of the number of classes) are considered as normal (or regular) instances, and the instances from the other half are considered as abnormal (or novel). The considered methods are trained based on the stream of regular instances. As advocated by Gama et al. (2009), a prequential accuracy is used for evaluating the performance of the methods in correctly distinguishing the regular vs. novel instances. This measure corresponds to the average accuracy computed online, by predicting for every instance whether it is regular or novel, prior to its learning. The average accuracy is estimated using a sliding window of 500 instances.

Note that during predication, the anomaly detector classifies unlabeled examples as normal or abnormal without having access to true labels. However, to asses and evaluate its performance, true labels are needed. Labels information is not used during prediction, it is only used to “evaluate” the performance of the system(s). Moreover, the prequential evaluation is preconized for streaming algorithms. Our novelty detection algorithm is a streaming algorithm in non-stationary environments, therefore, it makes sense to use a prequential evaluation (over a sliding window) to report a performance which reflect the current time (i.e. forget about previous predictions that happened long in the past).

A search of some parameters of each algorithm is performed and the best results are reported. Details about the parameters for each algorithm are provided in “Appendix B”.

Table 2 Average accuracy for distinguishing normal and abnormal (or novel) data

Table 3 Average accuracy for distinguishing normal and abnormal (or novel) data

Tables 2 and 3 show the overall results by presenting the average accuracy over time, as well as the p-value obtained based on the Student’s t-test. This p-value indicates how much significantly the results of the proposed method differ from the results of the best performing method. For each dataset, the result of the best performing method is highlighted with bold text in Tables 2 and 3. If the result of the best performing method is not significantly different from the other methods (i.e. ${p}\hbox { value} > 0.05$) then the result of those methods is also highlighted with bold text.

It can be seen from Tables 2 and 3 that the proposed method achieves a better overall performance than the other methods. Moreover, as indicated by the p-values, in the vast majority of cases, the results achieved by the proposed method are significantly different from the results achieved by the other methods. This is especially true for real datasets with a variable or unknown rate of drift. These results confirm that the adaptive proposed method is generally more convenient for various types of non-stationary environments, due to its dynamic adaptation over time.

8 Conclusion and future work

In this paper we have introduced a new method (GNG-A) for online learning from evolving data streams for the task of anomaly and novelty detection. The method extends GNG for a better adaptation, removal and creation of neurons. The usefulness of the proposed method was demonstrated on various real-world and artificial datasets covering a wide range of non-stationary distributions. The empirical and statistical evaluation that we performed show that the proposed method achieved the best overall performance compared to three other methods (two methods designed for stationary data and one state of the art method in non-stationary data), while being much less sensitive to initialization parameters. Results show that the proposed adaptive forgetting and evolution mechanisms allow the method to deal with various stationary and non-stationary distributions without the need to manually fine-tune different sensitive hyper-parameters. Hence, the proposed method is suitable for a wide range of application domains varying from static environments to highly dynamic ones.

For future work, we plan to design a parallel version of the proposed method and take advantage of data intensive computing platforms, such as Apache Spark, for the implementation. In order to do this, one way is to parallelize independent parts of the data and process them in parallel while sharing the same graph of neurons. Another alternative is to design algorithms to adequately split and distribute the graph of neurons on multiple machines running in parallel.

Appendices

Appendix

A Details about datasets

The Weather dataset is originally proposed and described in Elwell and Polikar (2011) in order to predict whether it is going to rain on a certain day or not. The dataset contains 18159 instances with an imbalance towards no rain (69%). Each sample is described with eight weather-related features such as temperature, pressure, wind speed etc.

The Elec2 dataset, described in Harries and Wales (1999), holds information of the Australian New South Wales Electricity Market, whose prices are affected by supply and demand. Each sample is described by attributes such as day of week, time-stamp, market demand etc., and the relative change of the price (higher or lower) is identified based on a moving average of the last 24 h.

The Covtype dataset is introduced in Blackard and Dean (1999) and often used as a benchmark for drift algorithms. It assigns cartographic variables such as elevation, slope, soil type, etc. to different forest cover types. Only forests with minimal human-caused disturbances were used, so that resulting forest cover types are more a result of ecological processes.

The Outdoor dataset (Losing et al. 2015) is obtained from images recorded by a mobile in a garden environment. Images contain 40 different objects, each approached ten times under varying lighting conditions affecting the color based representation. Each approach consists of 10 images and is represented in temporal order within the dataset.

The Rialto dataset (Losing et al. 2016) consists of images of colorful buildings next to the famous Rialto bridge in Venice, encoded in a normalized 27-dimensional RGB histogram. Images are obtained from time-lapse videos captured by a webcam with fixed position. The recordings cover 20 consecutive days. Continuously changing weather and lighting conditions affect the representation.

The Spamdata dataset is introduced in Katakis et al. (2010) and consists of email messages from the Apache Spam Assassin Collection http://spamassassin.apache.org. A bag-of-words approach was used for representing emails, resulting in 9324 instances and 500 attributes. There are two classes, legitimate and spam. As observed in Katakis et al. (2010), the characteristics of spam messages in this dataset gradually change as time passes.

The Sea Concepts dataset is an artificial adapted for novelty detection and originally proposed by Street and Kim (2001). It consists of 60,000 instances with three attributes of which only two are relevant. The two class decision boundary is given by $f_1 + f_2 = b$, where $f_1$, $f_2$ are the two relevant features and b is a predefined threshold. Abrupt drift is simulated with four different concepts by changing the value of b. The dataset contains $~10\%$ of noise.

Table 4 Parameters used for the considered methods

The Keystroke dataset (described in Souza et al. (2015)) is from a real-world application related to keystroke dynamics for recognizing users by their typing rhythm, where user profiles evolve incrementally over time.

The Usenet dataset is a text dataset inspired by Katakis et al. (2010) and processed for novelty detection. It consists of a simulation of news filtering with concept drift related to the change of interest of a user over time. A user can decide to unsubscribe from news groups that he is not interested in and subscribe for new ones that he becomes interested in, and the previously interesting topics become out of his main interest.

The Optdigits dataset is a real-word stationary dataset of handwritten digits, described in the UCI machine learning repository (Frank and Asuncion 2010). It is introduced to test the performance of the proposed method in a stationary environment, where the data is split across multiple clusters.

B Details about parameters

Table 4 lists, for each dataset, the parameters selected for each method, which lead to the best results. The parameter values which are not variable across the different datasets are reported here (not in the table). For Isolation Forest, the ensemble size is fixed to $e = 50$. The training set size used to train each isolation tree is fixed to a default value of $s=256$ provided by the scikit-learn library. The parameter ø of Isolation Forest refers to the amount of contamination of the dataset (i.e., the proportion of outliers in the dataset). The respective parameters $\gamma$ and $\nu$ of OCSVM refer to the kernel coefficient for the radial basis function (RBF) and to the upper bound on the fraction of training errors. The parameter w of KNNPaw represents the expected window size as described in Bifet et al. (2013) (not the exact size, as it is probabilistic), and k is the usual parameter of kNN. The parameters of GNG, GNG-U and GNG-T in Table 4 are explained in Sect. 2. The parameters $\epsilon _1$ and $\epsilon _2$ for GNG, GNG-U and GNG-T are set to 0.1 and 0.005 respectively. The parameter $a_{max}$ is set to 10 for all the GNG-based algorithms (including the proposed one) on all datasets. Finally, the parameter k of the proposed method is set to 10.