Inhibiting diffusion of complex contagions in social networks: theoretical and experimental results

Abstract

We consider the problem of inhibiting undesirable contagions (e.g. rumors, spread of mob behavior) in social networks. Much of the work in this context has been carried out under the 1-threshold model, where diffusion occurs when a node has just one neighbor with the contagion. We study the problem of inhibiting more complex contagions in social networks where nodes may have thresholds larger than 1. The goal is to minimize the propagation of the contagion by removing a small number of nodes (called critical nodes) from the network. We study several versions of this problem and prove that, in general, they cannot even be efficiently approximated to within any factor $\rho \ge 1$, unless P = NP. We develop efficient and practical heuristics for these problems and carry out an experimental study of their performance on three well known social networks, namely epinions, wikipedia and slashdot. Our results show that these heuristics perform significantly better than five other known methods. We also establish an efficiently computable upper bound on the number of nodes to which a contagion can spread and evaluate this bound on many real and synthetic networks.

1 Introduction and motivation

Analyzing social networks has become an important topic in the data mining community (Richardson and Domingos 2002; Domingos and Richardson 2001; Kempe et al. 2003, 2005; Chakrabarti et al. 2008; Tantipathananandh et al. 2007; Anderson et al. 2012). Many researchers have studied diffusion processes in social networks. Some examples are the propagation of favorite photographs in a Flickr network (Cha et al. 2008), the spread of information (Gruhl et al. 2004; Kossinets et al. 2008) via Internet communication, the effects of online purchase recommendations (Leskovec et al. 2007), formation of online communities (Shi et al. 2009), hashtag propagation in Twitter (Romero et al. 2011), and virus propagation between computers (Pastor-Satorras and Vespignani 2001). In some instances, models of diffusion are combined with data mining to predict social phenomena; e.g., product marketing (Domingos and Richardson 2001; Richardson and Domingos 2002), trust propagation (Guha et al. 2004), and epidemics through social contacts (Martin et al. 2011). Furthermore, coupled processes of network and dynamics evolutions are studied with comparisons against experimental data (Centola et al. 2007; Centola 2010); see Vespignani (2012) for an overview.

Here, we are interested in a particular class of diffusion, that of complex contagions. As stated in Centola and Macy (2007), “Complex contagions require social affirmation from multiple sources.” That is, a person acquires a complex social contagion through interaction with $t>1$ other individuals, as opposed to only a single individual (i.e., $t=1$). The latter is called a simple contagion, perhaps the most notable of which are disease propagation (Pastor-Satorras and Vespignani 2001; Longini et al. 2005) and computer virus transmission (Jin et al. 2009).

The idea of complex contagions dates back to at least the 1960s as described in (Granovetter 1978; Schelling 1978), and more current studies are referenced in (Centola and Macy 2007; Barash et al. 2012; Barash 2011). Such phenomena, according to these researchers, include diffusion of innovations, spread of rumors and worker strikes, educational attainment, fashion trends, and growth of social movements. For example, in strikes, mob violence, and political upheavals, individuals can be reluctant to participate for fear of reprisals to themselves and their families. It is safer for one to wait for a critical mass of one’s acquaintances to commit before committing oneself. These models are concerned with the onset of a behavior and thus focus on the transition from non-participating to participating. Like many epidemic models, they use only one active or contagious state. A notable exception is the threshold model of Melnik et al. (2013) which uses two such states, with different strengths of contagion associated with them. Here, we use a contagion model with one active state.

Crucially, recent data mining analyses and experiments have provided evidence for complex contagion dynamics on appropriate social networks. Examples include online DVD purchases (Leskovec et al. 2007), teenage smoking initiation (Harris 2008; Kuhlman et al. 2011), spread of health-related information (Centola 2010), joining LiveJournal (Kleinberg 2007), and recruitment of people to join Facebook (Ugander et al. 2012).

The threshold model that we employ in this work has been used by many social scientists (e.g., Granovetter 1978; Watts 2002; Centola and Macy 2007) to understand social behaviors. It is argued in (Watts 2002) that threshold dynamics may be used in several situations where more detailed human reasoning is precluded. In a recent study (Gonzalez-Bailon et al. 2011), joining a protest in Spain in 2011 was analyzed through Twitter messages. In that study, deterministic thresholds¹ were used to explain the onset of user involvement in the protest.

Another motivation for our work is from recent quantitative work (Centola and Macy 2007; Centola 2009) showing that simple contagions and complex contagions can differ significantly in behavior. It is well known (Granovetter 1973) that weak edges play a dominant role in spreading a simple contagion between clusters within a population, thereby dictating whether a contagion will reach a large segment of a population. However, for complex contagions, this effect is greatly diminished (Centola and Macy 2007). Another difference between simple and complex contagions, discussed in (Centola 2009), is the following: scale-free (SF) communication graphs (i.e., those with power-law degree distributions) show high tolerance for random node failures (i.e., diffusion can still reach the majority of nodes when nodes are removed randomly from the network) for simple contagions, but have low tolerance to random failures for complex contagions.

Additional differences between simple and complex contagions are presented in this paper, where the focus is on the problem of finding agents (called critical nodes) in a population that will thwart the spread of complex contagions. In particular, our theoretical results (presented in Sect. 4) show that one variant of this problem can be solved efficiently for simple contagions, while it is computationally intractable for complex contagions. Furthermore, we show experimentally that several effective heuristics (Habiba et al. 2008; Bonacich 1972; Kleinberg 1999; Tong et al. 2010) for determining critical nodes for simple contagions perform poorly in stopping complex contagions. Thus, our results point out some fundamental differences between simple and complex contagions with respect to diffusion.

Computing effective sets of critical nodes is important because it has wide applicability in several domains of network dynamics. Examples include thwarting the spread of sensitive information that has been leaked (Chakrabarti et al. 2008), disrupting communication of adversaries (Arulselvan et al. 2009), marketing to counteract the advertising of a competing product (Richardson and Domingos 2002; Domingos and Richardson 2001), calming a mob (Granovetter 1978), or changing people’s opinions (Dreyer and Roberts 2009). Indeed, contagion dynamics with critical nodes have been used in several domains, including peer influence in youth behavior, repression of social movements, opinion dynamics, and social isolation in epidemiology (Albert et al. 2000; Mobilia 2003; Mobilia et al. 2007; Kawachi 2008; Centola 2009; Siegel 2010; Salathe and Jones 2010; Acemoglu and Ozdaglar 2011; Yildiz et al. 2011). But these studies overwhelmingly use simple contagion dynamics and/or simple heuristics for determining critical nodes (e.g. using high degree nodes). For complex contagions, we provide diffusion blocking methods that are far better than such methods. More generally, inhibiting diffusion is one aspect of a broader goal of controlling diffusion in complex networks as advocated in (Liu et al. 2011).

Another aspect of our work complements previous studies of contagion blocking. Many previous works (Albert et al. 2000; Barash 2011; Habiba et al. 2008; Centola 2009; Tong et al. 2010) assume that the seed set—the set of nodes initially possessing a contagion—is unknown and a single set of critical nodes is selected to halt diffusion from any seed set. Here, we study the contagion blocking problem assuming that the seed set is known. We compare our methods’ results with those from several others, and demonstrate the improved performance that can be realized with this extra information.

Following (Granovetter 1978; Schelling 1978; Watts 2002; Centola and Macy 2007), we utilize a two-state system where nodes in state 0 (1) do not (do) possess the contagion. A node transitions from state 0 to state 1 if the number of its neighbors in state 1 is at least a specified threshold $t$. Nodes may not transition back to state 0 from state 1 (Macy 1991; Kempe et al. 2003; Siegel 2009; Gonzalez-Bailon et al. 2011; Ugander et al. 2012). Critical nodes are initially in state 0, and remain in state 0 throughout the diffusion process, regardless of the states of their neighbors, and thereby retard contagion propagation.

Overview of contributions We formulate several variants of the problem of finding a smallest critical set and prove that, in general, they cannot even be efficiently approximated to within any factor $\rho \ge 1$, unless P = NP. These results motivate the development and evaluation of two practical heuristics for finding critical sets. We compare our methods against five state-of-the-art methods and demonstrate that our methods are much more effective in blocking diffusion of complex contagions. We also provide a detailed set of blocking results to understand the range of applicability and the limitations of our methods. Finally, using thousands of networks, we critically evaluate a method to bound the maximum possible (MP) spread size (i.e., the maximum number of nodes to which a contagion can spread) in a network, which is useful in quantifying the effectiveness of blocking schemes. (A detailed summary of results is provided in Sect. 3.1.)

Paper organization  Section 2 describes the model employed in this work and develops problem formulations. Section 3 contains a summary of our main results and related work. Theoretical results are provided in Sect. 4. Our two heuristics are described in Sect. 5. Section 6 contains experimental results on blocking, including the experimental setup, comparisons against five state-of-the-art blocking methods, and further results over a larger parameter space. We present in Sect. 7 theoretical and experimental results for maximum spread sizes of complex contagions in social networks. Conclusions and future work constitute Sect. 8.

This paper combines and extends the results in a conference paper (Kuhlman et al. 2010b) and a workshop paper (Kuhlman et al. 2010a). The former contains preliminary versions of the results in Sect. 4 through 6, while the latter contains a preliminary version of the results in Sect. 7.

2 Dynamical system model and problem formulation

2.1 System model and associated definitions

We model the propagation of complex contagions over a social network using discrete dynamical systems (Barrett et al. 2006, 2007). We begin with the necessary definitions.

Let $\mathbb {B}$ denote the Boolean domain {0,1}. A Synchronous Dynamical System (SyDS) $\mathcal {S}$ over $\mathbb {B}$ is specified as a pair $\mathcal{S} = (G, \mathcal{F})$, where

• (a) $G(V,E)$, an undirected graph with a set $V$ of $n$ nodes and a set $E$ of $m$ edges, represents the underlying social network over which the contagion propagates, and

• (b) $\mathcal{F} = \{f_1, f_2, \ldots , f_n \}$ is a collection of functions, with $f_i$ denoting the local transition function associated with node $v_i$, $1 \le i \le n$.

Each function $f_i$ specifies the local interaction between node $v_i$ and its neighbors in $G$. To provide additional details regarding these functions, we note that each node of $G$ has a state value from $\mathbb {B}$. To encompass various types of social contagions described in Sect. 1, nodes in state 0 (1) are said to be unaffected (affected). Thus, in the case of information flow, for example, an affected node has received the information and will pass it on. It is assumed that once a node reaches the state 1, it cannot return to state 0. We refer to a discrete dynamical system with this property as a ratcheted dynamical system. (Other names such as “progressive systems” (Kleinberg 2007) and “irreversible systems” (Dreyer and Roberts 2009) have also been used.)

We can now formally describe the local transition functions. The inputs to function $f_i$ are the state of $v_i$ and those of the neighbors of $v_i$ in $G$; function $f_i$ maps each combination of inputs to a value in $\mathbb {B}$. For the propagation of contagions in social networks, it is natural to model each function $f_i\, (1 \le i \le n)$ as a $t_i$-threshold function (Eubank et al. 2006; Chakrabarti et al. 2008; Dreyer and Roberts 2009; Centola et al. 2006; Centola and Macy 2007; Kempe et al. 2003; Kleinberg 2007) for an appropriate nonnegative integer $t_i$. Such a threshold function (taking into account the ratcheted nature of the dynamical system) is defined as follows.

• (a) If the state of $v_i$ is 1, then the value of $f_i$ is 1, regardless of the values of the other inputs to $f_i$.

• (b) If the state of $v_i$ is 0, then the value of $f_i$ is 1 if at least $t_i$ of the inputs are 1; otherwise, the value of $f_i$ is 0.

A configuration $\mathcal {C}$ of a SyDS at any time is an $n$-vector $(s_1, s_2, \ldots , s_n)$, where $s_i \in \mathbb {B}$ is the value of the state of node $v_i\, (1 \le i \le n)$. A single SyDS transition from one configuration to another can be expressed by the following pseudocode.

for  each node $v_i$  do in parallel

• (i) Compute the value of $f_i$. Let $s_i'$ denote this value.

• (ii) Update the state of $v_i$ to $s_i'$.

end for

Thus, in a SyDS, nodes update their state synchronously. Other update disciplines (e.g. sequential updates) for discrete dynamical systems have also been considered in the literature (Barrett et al. 2006, 2007).

If a SyDS has a transition from configuration $\mathcal {C}$ to configuration $\mathcal {C'}$, we say that $\mathcal {C'}$ is the successor of $\mathcal {C}$ and that $\mathcal {C}$ is a predecessor of  $\mathcal {C'}$. A configuration $\mathcal {C}$ is called a fixed point if the successor of $\mathcal {C}$ is $\mathcal {C}$ itself.

Example

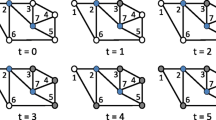
Consider the graph shown in Fig. 1. Suppose the local interaction function at each node is the 2-threshold function. Initially, $v_1$ and $v_2$ are in state 1 and all other nodes are in state 0. During the first time step, the state of node $v_3$ changes to 1 since two of its neighbors (namely $v_1$ and $v_2$) are in state 1; the states of other nodes remain the same. In the second time step, the state of node $v_4$ changes to 1 since two of its neighbors (namely $v_2$ and $v_3$) are in state 1; again the states of the other nodes remain the same. The resulting configuration $(1, 1, 1, 1, 0, 0)$ is a fixed point for this system.

Fig. 1

An example of a synchronous dynamical system. Each configuration has the form ($s_1, s_2, s_3, s_4, s_5, s_6$) where $s_i$ is the state of node ${\nu _i}$, ($1 \le i \le 6$). The configuration at time 2 is a fixed point

The SyDS in the above example reached a fixed point. This is not a coincidence. The following simple result shows that every ratcheted dynamical system over $\mathbb {B}$ reaches a fixed point.

Proposition 1

Every ratcheted discrete dynamical system over $\mathbb {B}$ reaches a fixed point in at most $n$ transitions, where $n$ is the number of nodes in the underlying graph.

Proof

Consider any ratcheted dynamical system $\mathcal {S}$ over $\mathbb {B}$. In any transition of $\mathcal {S}$ from one configuration to another, nodes can only change from 0 to 1 (but not from 1 to 0). Thus, after at most $n$ transitions where nodes change from 0 to 1, there can be no more state changes, i.e., $\mathcal {S}$ reaches a fixed point.$\square$

In the context of opinion propagation, reaching a fixed point means that everyone has formed an unalterable opinion, and hence will not change their mind.

2.2 Problem formulation

For simplicity, statements of problems and results in this paper use terminology from the context of information propagation in social networks, such as that for social unrest. It is straightforward to interpret the results for other contagions.

Suppose we have a social network in which some nodes are initially affected. In the absence of any action to contain the unrest, it may spread to a large part of the population. Decision-makers must decide on suitable actions (interventions) to inhibit information spread, such as quarantining a subset of people. Usually, there are resource constraints or societal pressures to keep the number of isolated people to a minimum (e.g., quarantining too many people may fuel unrest or it may be difficult to apprehend particular individuals). Thus, the problem formulation must take into account both information containment and appropriate resource constraints.

We assume that only people who are as yet unaffected can be quarantined. Under the dynamical system model, quarantining a person is represented by removing the corresponding node (and all the edges incident on that node) from the graph. Equivalently, removing a node $v$ corresponds to changing the local transition function at $v$ so that $v$’s state remains 0 for all combinations of input values. The goal of isolation is to minimize the number of new affected nodes that occur over time until the system reaches a fixed point (when no additional nodes can be affected). We use the term critical set to refer to the set of nodes removed from the graph to reduce the number of newly affected nodes. Resource constraints can be modeled as a budget constraint on the size of the critical set. We can now provide a precise statement of the problem of finding critical sets. (This problem was first formulated in (Eubank et al. 2006) for the case where each node computes a 1-threshold function.)

2.2.1 Smallest critical set to minimize the number of new affected nodes (SCS-MNA)

Given  A social network represented by the SyDS $\mathcal {S}$ = $(G(V,E), \mathcal {F})$ over $\mathbb {B}$, with each function $f \in \mathcal {F}$ being a threshold function; the set $I$ of nodes which are initially in state 1 (the elements of $I$ are called seed nodes); an upper bound $\beta$ on the size of the critical set.

Requirement  A critical set $C \subseteq V-I$ such that $|C| \le \beta$ and among all subsets of $V-I$ of size at most $\beta$, the removal of $C$ from $G$ leads to the smallest number of new affected nodes.

An alternative formulation, where the objective is to maximize the number of nodes who are not affected, can also be considered. We use the name “Smallest Critical Set to Maximize Unaffected Nodes” for this problem and abbreviate it as SCS-MUN. To maintain the complementary relationship between the minimization (SCS-MNA) and maximization (SCS-MUN) versions, we assume that critical nodes are not included in the set of unaffected nodes in the formulation of SCS-MUN. With that assumption, any optimal solution for SCS-MUN is also an optimal solution for SCS-MNA. Our results in Sect. 4 provide an indication of the difficulties in obtaining provably good approximation algorithms for either version of the problem. So, our focus is on obtaining heuristics that work well in practice.

We also consider the problem of finding critical sets in a related context. Let $\mathcal {S}{} = (G(V,E), \mathcal {F})$ be a SyDS and let $I \subseteq V$ denote the set of seed nodes. We say that a node $v \in V-I$ is salvageable if there is a critical set $C \subseteq V - (I \cup \{v\})$ whose removal ensures that $v$ remains in state 0 when the modified SyDS (i.e., the SyDS obtained by removing $C$) reaches a fixed point. Otherwise, $v$ is called an unsalvageable node. Thus, in any SyDS, only salvageable nodes can possibly be saved from becoming affected.

Example

Consider the 2-threshold SyDS shown in Fig. 1. Node $v_4$ in that figure is salvageable since removal of $v_3$ ensures that $v_4$ won’t be affected. Nodes $v_5$ and $v_6$ are salvageable since they are not affected even when no nodes are removed from the system. However, node $v_3$ is not salvageable since it has two neighbors ($v_1$ and $v_2$) who are initially affected.

We now formulate a problem whose goal is to find a smallest critical set that saves all salvageable nodes.

2.2.2 Smallest critical set to save all salvageable nodes (SCS-SASN)

Given A social network represented by the SyDS $\mathcal {S}$ = $(G(V,E), \mathcal {F})$ over $\mathbb {B}$, with each function $f \in \mathcal {F}$ being a threshold function; the set $I$ of seed nodes which are initially in state 1.

Requirement A critical set $C \subseteq V-I$ of minimum cardinality whose removal ensures that all salvageable nodes are saved from being affected.

As will be shown in Sect. 4, the complexity of the SCS-SASN problem for simple contagions is significantly different from that for complex contagions.

2.3 Types of thresholds

In the above discussion, the threshold (also called the absolute threshold) of each node was specified as a non-negative integer. A homogeneous threshold SyDS is one where all the nodes of a SyDS have the same threshold $t$, for some integer $t \ge 0$. A heterogeneous threshold SyDS is one where nodes may have different thresholds. Researchers (e.g. Centola and Macy 2007) have also considered relative thresholds, where the threshold value of a node is a non-negative fraction of the number of neighbors of the node. (Here, each node is considered a neighbor of itself.) Similar to absolute thresholds, one can also consider homogeneous and heterogeneous relative thresholds. We refer to these variants as the “$t$-threshold variants.” Most of our theoretical results (Sect. 4) are presented in terms of absolute thresholds. Extensions of these results to the other $t$-threshold variants are straightforward, as outlined in the Appendix.

2.4 Additional terminology

Here, we present some terminology used in the later sections of this paper. The term “$t$-threshold system” is used to denote a SyDS with a homogeneous absolute threshold $t \ge 0$ (thus, the value of $t$ is the same for all nodes of the system).

We also need some terminology with respect to approximation algorithms for optimization problems (Garey and Johnson 1979). For any $\rho \ge 1$, a $\rho$-approximation for an optimization problem is an efficient algorithm that produces a solution which is within a factor of $\rho$ of the optimal value for all instances of the problem. Such an approximation algorithm is also said to provide a performance guarantee of $\rho$. Clearly, the smaller the value of $\rho$, the better is the performance of the approximation algorithm.

The following terms are used in describing simulation results and the behavior of the heuristics that produce critical sets. The spread size is the number (or fraction) of nodes in the affected state; the final spread size is the value at the end of a diffusion instance. A cascade occurs when diffusion starts from a set of seed nodes and the final fractional or absolute spread size is large relative to the number of nodes that can possibly be affected. Halt means that the chosen set of critical nodes will stop the diffusion process, thus preventing a cascade. A delay means that the chosen set of critical nodes will increase the time at which the peak number of newly affected nodes occurs, but will not necessarily halt diffusion. Finally, Table 1 provides acronyms and Table 2 lists variables used throughout this document.

Table 1 Acronyms used in this paper

Table 2 Variables used in this paper

3 Summary of results and related work

3.1 Summary of results

Section 2 presented the formulations of the problems studied in this paper. The following is a summary of our main results.

• (a) We show that for any $t \ge 2$ and any $\rho \ge 1$, it is NP-hard to obtain a $\rho$-approximation for either the SCS-MNA problem or the SCS-MUN problem for $t$-threshold systems. (The result holds even when $\rho$ is a function of the form $n^{\delta }$, where $\delta < 1$ is a constant and $n$ is the number of nodes in the underlying network).

• (b) We show that the problem of saving all salvageable nodes (SCS-SASN) can be solved in linear time for 1-threshold systems and that the required critical set is unique. In contrast, we show that the problem is NP-hard for $t$-threshold systems for any $t \ge 2$. We present an approximation algorithm for this problem with a performance guarantee of $\rho < 1 + \ln {(s)}$, where $s$ is the number of salvageable nodes in the system. We also show that the performance guarantee cannot be improved significantly, unless P = NP.

• (c) We develop two intuitively appealing heuristics, designated covering-based heuristic (CBH) and potential-based heuristic (PBH), for the SCS-MNA problem, and carry out an experimental study of their performance on three social networks, namely epinions, wikipedia and slashdot. We compare our schemes against five known methods for determining critical nodes (representing a range of blocking methods): random assignment, high-degree nodes, nodes of high betweenness centrality (Freeman 1976), nodes of high eigenvector centrality (Bonacich 1972), which can also be computed for undirected graphs using the hyperlink-induced topic search (HITS) algorithm (Kleinberg 1999), and maximum eigenvalue drop (also called NetShield) (Tong et al. 2010). We show that our methods are far more effective in blocking complex contagions.

• (d) We establish an upper bound on the spread size for diffusion in $t$-threshold systems, for $t \ge 1$. Interestingly, this upper bound estimates a dynamic quantity (maximum spread size) using an easily computable static parameter of the network. We show experimentally that this upper bound is achievable for several values of $t$ for real social networks. We also evaluate the effectiveness of the bound for a large number of synthetic networks.

Our heuristics can be used with heterogeneous thresholds. They can also be extended for use under more general transition criteria for nodes (e.g. generalized contagion models of Dodds and Watts 2005) and with probabilistic diffusion (where a node transitions from 0 to 1 with probability $p$ when its threshold is met). Finally, our methods can also be extended for use in time-varying networks where the edges of the network and transition criteria change in a repeatable pattern (e.g., to reflect daytime and night-time interactions as in Prakash et al. 2010).

3.2 Related work

Work on finding critical sets has been almost exclusively confined to simple contagions (i.e., 1-threshold systems). Critical nodes are called “blockers” in (Habiba et al. 2008); they examine dynamic networks and use a probabilistic diffusion model with threshold = 1. They utilize graph metrics such as degree, diameter, and betweenness centrality (adapted to time-varying networks) to identify critical nodes. Anshelevich et al. (2009) also study dynamic networks and threshold-1 behavior. They use newly affected nodes to specify a predefined number of new blocking nodes per time step as deterministic diffusion emanates from a single seed node.

Many sophisticated methods for blocking simple contagions involve eigenvalue (and eigenvector) computations. Eigenvector centrality (Bonacich 1972) is used to rank nodes from best blocker to worst blocker in decreasing order of the magnitude of their eigenvector components for the dominant eigenvalue (e.g., Habiba et al. 2008; Tong et al. 2010). HITS (Kleinberg 1999) is another eigenvector-based approach for identifying blocking nodes when applied to undirected graphs. PageRank (Page et al. 1999) of a node $v$ is closely aligned with eigenvector centrality, and was also studied in (Habiba et al. 2008; Tong et al. 2010). Initially in (Wang et al. 2003), and later in (Ganesh et al. 2005; Chakrabarti et al. 2008), a blocking scheme based on eigenvalues of the adjacency matrix of the underlying graph is discussed. A drawback of this method is that it is not practical for large networks, since it requires a large number of eigenvalue computations. To overcome this drawback, an efficient eigenvector-based heuristic has recently been proposed and evaluated on three social networks in (Tong et al. 2010).

A variety of network-based candidate measures for identifying critical nodes for simple contagions are described in (Borgatti 2006); however, the applications are confined to small networks. The effectiveness of removing nodes at random and removing high degree nodes has been studied in (Holme 2004; Albert et al. 2000; Crucitti et al. 2004; Cohen et al. 2003; Madar et al. 2004; Dezso and Barabasi 2002; Briesemeister et al. 2003). An approximation algorithm for the problem of minimizing the number of new affected nodes for simple contagions is presented in (Eubank et al. 2006).

Moving now to complex contagions, we are aware of only one work on inhibiting diffusion, and that is for 2-threshold systems. Centola (2009) examined how removal of nodes from 10,000-node synthetic exponential and power law (i.e., SF) graphs affects the diffusion of complex contagions. His motivation was to determine how resilient a network is to random and targeted node removal schemes; the former scheme removes nodes uniformly randomly while the latter removes high degree nodes. His work differs from ours in that it is focused on observing the spread size under the two node removal schemes rather than on stopping diffusion. While the results in (Centola 2009) show that the targeted method works well in inhibiting diffusion in some synthetic networks, we show herein that this method does not work well for realistic social networks, for $t=2, 3$, and 5.

Although we limit ourselves to static networks, our methods can be applied to time-varying networks if the network modifications are deterministic in time. As motivated in (Prakash et al. 2010), this is a reasonable first approximation of people’s regular, repeatable behavior and is used extensively in epidemiological modeling (e.g., Barrett et al. 2008; Perumalla and Seal 2010). Our methods can also be used without modification for probabilistic diffusion where below the threshold $t$, the probability of node transition is zero, and at or above the threshold, a node $v$ transitions with probability $p_v$.

4 Theoretical results for the critical set problems

4.1 Overview and a preliminary lemma

In this section, we first establish complexity results for finding critical sets. We also present results that show a significant difference between 1-threshold systems and $t$-threshold systems where $t \ge 2$. Most of the results in this section are for homogeneous thresholds; extensions of the results to heterogeneous and relative thresholds are outlined in the Appendix.

Lemma 1

Given a SyDS $\mathcal {S}$ = $(G(V,E), \mathcal {F})$, the set $I \subseteq V$ of initially affected (i.e., seed) nodes and a critical set $C \subseteq V-I$, the number of new affected nodes in the system that results when $C$ is removed from $V$ can be computed in $O(|V|+|E|)$ time.

Proof

Recall that the removal of $C$ is equivalent to changing the local transition function $f_v$ of each node $v \in C$ to the function that remains 0 for all inputs. Since the resulting SyDS $\mathcal {S}_1$ is also a ratcheted SyDS, by Proposition 1, it reaches a fixed point in at most $n = |V|$ steps. The fact that each local transition function is a threshold function can be exploited to find all the nodes that are affected over the time steps in $O(|V|+|E|)$ time.

The idea is to have for each node $v \in V$, a counter $c_v$ that stores the number of neighbors of $v$ that are currently affected. To begin with, for each unaffected node, the counter is initialized to 0. In time step 1, for each node $w \in I$, the counter for each unaffected neighbor $x$ of $w$ is incremented. If the count for $x$ reaches its threshold, then $x$ is added to a list $L$ of nodes which will contain all the nodes that are affected at time step 1. At the next time step, the above procedure is repeated using the nodes in $L$ (instead of the nodes in $I$). This method can be carried out for each subsequent time step until the system reaches a fixed point (i.e., until the list of newly affected nodes becomes empty). It can be seen that for each node $v$ of $G$, this method explores the adjacency list of $v$ just once through all the time steps. So, the total time spent in the computation is $O(\sum _{v \in V} \mathrm{degree}(v)) = O(|E|)$. The initialization of the counters and the final step to output the newly affected nodes take $O(|V|)$ time. Therefore, the total time is $O(|V|+|E|)$. $\square$

4.2 Complexity results

As mentioned earlier, the SCS-MNA problem was shown to be NP-complete in (Eubank et al. 2006) for the case when each node has a 1-threshold function. We now extend that result to show that even obtaining a $\rho$-approximate solution is NP-hard for systems in which each node computes the $t$-threshold function for any $t \ge 2$.

Theorem 1

Assuming that the bound $\beta$ on the size of the critical set cannot be violated, for any $\rho \ge 1$ and any $t \ge 2$, there is no polynomial time $\rho$-approximation algorithm for the SCS-MNA problem for $t$-threshold systems, unless P = NP.

Proof

Suppose $\mathcal {A}$ is a $\rho$-approximation algorithm for the SCS-MNA problem for $t$-threshold systems for some $\rho \ge 1$ and $t \ge 2$. We will show that $\mathcal {A}$ can be used to efficiently solve the Minimum Vertex Cover (MVC) decision problem (Garey and Johnson 1979): Given an undirected graph $G(V,E)$ and an integer $k$, is there a subset $V'$ of $V$ such that $|V'| \le k$ and for each edge $\{u,v\} \in E$, at least one of $u$ and $v$ is in $V'$?

Let $G = (V, E)$ be the given graph for the vertex cover problem, with $n = |V|$ and $m = |E|$. We construct a SyDS $\mathcal {S}$ = $(H(V_H, E_H), \mathcal {F})$ as follows. The vertex set $V_H$ consists of three pairwise disjoint groups of nodes denoted by $X$, $Y$ and $Z$. The set $X =\{x_1, x_2, \ldots , x_t\}$ consists of $t$ nodes all of which are initially 1. The set $Y = \{y_1, y_2, \ldots , y_n\}$ contains a node for each member of $V$. Let $\alpha = \lceil \rho (n-k) \rceil + k+1$. The set $Z = \{z_1, z_2, \ldots , z_{\alpha m}\}$ contains a total of $\alpha m$ nodes, with $\alpha$ nodes corresponding to each edge of $G$. All the nodes in $Y \cup Z$ are initially 0. The edges in $E_H$ are as follows.

• (a) Each node in $Y$ is adjacent to each node in $X$.

• (b) Each node in $Z$ is adjacent to the first $t-2$ nodes (i.e., nodes $x_1,\, \ldots ,\, x_{t-2}$) of $X$.

• (c) Let $g_j$ denote the group of $\alpha$ nodes corresponding to edge $e_j \in E$; each node of $g_j$ is adjacent to the two nodes in $Y$ which correspond to the end points of the edge $e_j \in E$, $1 \le j \le m$.

The local transition function at each node of $\mathcal {S}$ is the $t$-threshold function. The value of $\beta$ (the upper bound on the critical set size) is set to $k$. This completes the construction of the SCS-MNA instance. Obviously, the construction can be done in polynomial time.

Suppose $G$ has a vertex cover $V' = \{v_{i_1}, v_{i_2}, \ldots , v_{i_k}\}$ of size $k$. It can be verified that when the critical set $C = \{y_{i_1}, y_{i_2}, \ldots , y_{i_k}\}$ is removed, only the $n-k$ nodes in $Y-C$ are affected; that is, the number of new affected nodes is $n-k$. Since Algorithm $\mathcal {A}$ provides a performance guarantee of $\rho$, the critical set output by $\mathcal {A}$ in this case leads to at most $\rho (n-k)$ new affected nodes.

Now suppose that a minimum vertex cover for $G$ has $k+1$ or more nodes. We claim that no matter which subset of $k$ (or fewer) nodes from $Y \cup Z$ is chosen as the critical set, the number of newly affected nodes is at least $\rho (n-k) +1$. To see this, note that any critical set can use at most $k$ nodes of $Y$. Since any minimum vertex cover for $G$ has $k+1$ or more nodes, no matter which subset of $k$ nodes from $V$ is chosen, at least one edge $e_j = \{v_p, v_q\}$ remains uncovered (i.e., neither $v_p$ nor $v_q$ is in the chosen set). As a consequence, no matter which subset of $k$ nodes from $Y$ is chosen, there is at least one group $g_j$ of $\alpha$ nodes in $Z$ such that for each node $z \in g_j$, the two nodes in $Y$, say $y_p$ and $y_q$, that are adjacent to $z$ are not in the critical set. Thus, $y_p$ and $y_q$ will become affected and consequently all nodes in group $g_j$ become affected. Since $g_j$ contains $\alpha = \lceil \rho (n-k) \rceil + k+1$ nodes, even if $C$ includes $k$ nodes from $g_j$, at least $\lceil \rho (n-k) \rceil + 1$ nodes of $g_j$ will become affected. Thus, when the minimum vertex cover for $G$ is of size $k+1$ or more, the number of newly affected nodes is strictly greater than $\rho (n-k)$.

Now, suppose we execute $\mathcal {A}$ on the resulting SCS-MNA instance and obtain a critical set $C$. From the above argument, $G$ has a vertex cover of size at most $k$ if and only if the number of new affected nodes that result from the removal of $C$ is at most $\rho (n-k)$. From Lemma 1, the number of new affected nodes after the removal of a critical set can be found in polynomial time. Thus, using $\mathcal {A}$, we have a polynomial time algorithm for the MVC problem, contradicting the assumption that P $\ne$ NP. $\square$

We note that, in the above proof, the factor $\rho$ need not be a constant; it may be a function of the form $n^{\delta }$, where $\delta < 1$ is a constant and $n$ is the number of nodes of the graph in the MVC instance.

We now present a result similar to that of Theorem 1 for the maximization version of the problem (SCS-MUN).

Theorem 2

Assuming that the bound $\beta$ on the size of the critical set cannot be violated, for any $\rho \ge 1$ and any $t \ge 2$, there is no polynomial time $\rho$-approximation algorithm for the SCS-MUN problem for $t$-threshold systems, unless P = NP.

Proof

Assume that $\mathcal {A}$ is a $\rho$-approximation algorithm for the SCS-MUN problem. We prove the result by a reduction from the Minimum Vertex Cover problem, similar to the one used to prove Theorem 1. The modifications are as follows.

• (a) In addition to the sets of nodes $X$, $Y$ and $Z$, we have another set of nodes $W = \{w_1, w_2, \ldots , w_h\}$, where $h = \lceil (\rho -1) |Z| \rceil$.

• (b) Each node in $W$ is adjacent to the first $t-1$ nodes in $X$ and all nodes in $Z$.

Now, if $G$ has a vertex cover of size $k$, then by choosing the corresponding nodes of $Y$, all the nodes in $Z \cup W$ can be saved from becoming affected. Recall from Sect. 2.2 that the chosen critical nodes are not included in the set of unaffected nodes. Thus, in this case, the number of unaffected nodes is $|Z| + \lceil (\rho -1) |Z|\rceil \,\ge \,\rho |Z|$. Since $\mathcal {A}$ is a $\rho$-approximation algorithm, it must produce a critical set of size $k$ such that the number of nodes which are not affected is at least $|Z|$.

If every vertex cover for $G$ has $k+1$ or more nodes, then no matter which subset of $k$ (or fewer) nodes is chosen from $Y$, at least one node of $Z$ will become affected. Consequently, all the nodes in $W$ (which are not in the critical set) will also become affected. Therefore, no matter which critical set of size $k$ is chosen, the number of unaffected nodes is at most $|Z|-1$.

Thus, using $\mathcal {A}$, we can obtain a polynomial time algorithm for the MVC problem, contradicting the assumption that P $\ne$ NP. $\square$

4.3 Critical sets for saving all salvageable nodes

Recall from Sect. 2.2 that a node $v$ of a SyDS is salvageable if there is a critical set whose removal ensures that $v$ will not be affected. The problem of finding optimal critical sets to save all salvageable nodes, denoted by SCS-SASN, was also formulated in that section. We now present results for SCS-SASN that show a significant difference between 1-threshold systems and $t$-threshold systems where $t \ge 2$.

Theorem 3

Let $\mathcal {S}{} = (G(V,E), \mathcal {F})$ be a 1-threshold SyDS. The SCS-SASN problem for $\mathcal {S}$ can be solved in $O(|V|+|E|)$ time. Moreover, the solution is unique.

Proof

Call a given unsalvageable node of $G$ a fringe node if it has at least one neighbor that is salvageable. We now argue that the set of all fringe nodes in $G$ is the smallest critical set whose removal ensures that all salvageable nodes are saved from being affected.

First, observe that for a 1-threshold system, a given node is salvageable iff its initial state is 0 and the initial states of all its neighbors are also 0 (thus, determining whether a node $v$ is salvageable can be done in time $O(\mathrm{degree}(v))$ time, where the degree is the number of edges incident on $v$). It can be seen that removing all the fringe nodes saves all salvageable nodes. Further, this is the smallest critical set since if any fringe node is not removed, all of its salvageable neighbors would become affected. Thus, there is a unique smallest critical set for the system.

As mentioned above, determining whether a node $v$ is salvageable can be done in $O(\mathrm{degree}(v))$ time. Therefore, the time to identify all salvageable nodes is $O(\sum _{v\in V} \mathrm{degree}(v)) = O(|E|)$. The set of fringe nodes consists of those nodes that are initially 0, have at least one neighbor that is initially 1, and have at least one neighbor that is salvageable. Thus, once all salvageable nodes have been identified, determining all the fringe nodes can also be done in $O(|E|)$ time. Outputting the fringe nodes takes $O(|V|)$ time. Thus, the set of all fringe nodes can be found and output in $O(|V|+|E|)$ time. $\square$

The next set of results concerns the SCS-SASN problem for $t$-threshold systems, where $t \ge 2$.

Theorem 4

• (a) For any integer $t \ge 2$, the SCS-SASN problem is NP-hard for $t$-threshold systems.

• (b) There is an integer $t$ such that for $t$-threshold systems, there is no polynomial time approximation algorithm for the SCS-SASN problem with a performance guarantee of $(1-\epsilon )\ln (|Z|)$ for any $\epsilon > 0$, where $Z$ is the set of salvageable nodes in the system, unless $\mathbf{P} = \mathbf{NP}$.

Proof of Part (a)

This result can be shown by a simple modification to the reduction from Minimum Vertex Cover to the SCS-MNA problem given in the proof of Theorem 1. The modification is that the set $Z$ contains only $m = |E|$ nodes, one corresponding to each edge of $G$. In the resulting SyDS, the salvageable nodes are those in the set $Z$. Nodes in the set $Y$ are unsalvageable (each of them has $t$ neighbors who are initially affected). It can be verified that $G$ has a vertex cover of size at most $k$ iff there is a subset $C$ of $Y$, with $|C| \le k$, whose removal saves all the nodes of $Z$ from becoming affected.$\square$

Proof of Part (b)

We use a reduction from the Minimum Set Cover (MSC) problem (Garey and Johnson 1979): Given a universal set $U = \{u_1, u_2,\, \ldots ,\, u_n\}$ and a collection $C = \{C_1, C_2, \ldots , C_m\}$ of subsets of $U$, find a minimum cardinality subcollection $C'$ of $C$ such that the union of the sets in $C'$ is equal to $U$. We will use the fact that the MSC problem cannot be approximated to within the factor $(1-\epsilon )\ln (|U|)$ for any $\epsilon > 0$, unless $\mathbf{P} = \mathbf{NP}$ (Raz and Safra 1997).

Given an instance of the MSC problem, let $q$ denote the maximum number of occurrences of an element of $U$ in the sets in $C$. We construct an instance of the SCS-SASN problem as follows. The node set of the underlying graph of the SyDS consists of three pairwise disjoint sets $X,\, Y$ and $Z$, where $X = \{x_1, x_2, \ldots , x_q\}$ is the set of initially affected nodes, $Y = \{y_1, y_2, \ldots , y_m\}$ is in one-to-one correspondence with the collection $C$ and $Z = \{z_1, z_2, \ldots , z_n\}$ is in one-to-one correspondence with the set $U$. Thus, the initial states of the nodes in $X$ are 1 while those of the nodes in $Y \cup Z$ are 0. The edges of the underlying graph are as follows.

• (a ) Each node in $X$ is adjacent to every node in $Y$.

• (b) Consider each element $u_i \in U$ and suppose $u_i$ appears in sets $C_{i_1},\, C_{i_2},\, \ldots ,\,C_{i_r}$, for some $r \le q$; then, node $z_i$ is joined to the first $q-r$ nodes of $X$ and the $r$ nodes $y_{i_1},\, y_{i_2},\, \ldots ,\, y_{i_r}$ of $Y$.

The threshold for each node is set to $q$. Thus, the constructed SyDS is a $q$-threshold system.

It can be seen that none of the nodes in $Y$ is salvageable while all the nodes in $Z$ are salvageable. Thus, every critical set must be a subset of $Y$. It can also be verified that any critical set of size $\alpha$ corresponds to a solution to the MSC problem with $\alpha$ subsets from $C$ and vice versa. It follows that if there is an approximation algorithm for the SCS-SASN problem with a performance guarantee of $(1-\epsilon )\ln (|Z|)$ for the SCS-SASN problem, where $\epsilon > 0$, then, since $|Z| = |U|$, there is an approximation algorithm with a performance guarantee of $(1-\epsilon )\ln (|U|)$ for the MSC problem. The result of Part (b) follows with $t = q$.$\square$

We now discuss an approximation algorithm for the SCS-SASN problem with a performance guarantee of $H_s$, where $s$ is the number of salvageable nodes in the system and $H_s = \sum _{i=1}^{s} (1/i)$ is the $s^{\mathrm{th}}$ Harmonic Number. Since $H_s < 1\,+\,\ln {(s)}$, this algorithm shows that the lower bound result of Part (b) of Theorem 4 is nearly tight. Moreover, our approximation algorithm is valid even when nodes have different thresholds (i.e., for systems with heterogeneous thresholds).

The idea is to reduce the SCS-SASN problem to a more general form of the MSC problem, called the set multicover (SMC) problem (Vazirani 2001). Like the MSC problem, the input to the SMC problem consists of the set $U$ and the collection $C$ of subsets of $U$. In addition, for each element $u \in U$, a coverage requirement $\sigma _u \in \mathbb {Z}^+$ is also given, and the goal of the SMC problem is to pick a minimum cardinality subcollection $C'$ of $C$ such that for each element $u \in U$, there are at least $\sigma _u$ subsets in $C'$ that contain $u$. An approximation algorithm with a performance guarantee of $H_p$, where $p = |U|$, is known for the SMC problem (Vazirani 2001). This fact is used in our approximation algorithm for the SCS-SASN problem shown in Fig. 2. It can be seen that the approximation algorithm runs in polynomial time. We now prove its correctness and its performance guarantee.

Fig. 2

An approximation algorithm for the SCS-SASN problem

Theorem 5

The critical set $Q$ produced by the algorithm in Fig. 2 ensures that none of the salvageable nodes is affected. Also, $|Q| \le |Q^*| H_s$, where $Q^*$ is an optimal critical set and $s$ is the number of salvageable nodes in the system.

Proof

We first observe that the set $Z$ constructed in Step 2 of the algorithm contains all the salvageable nodes. The reason is that no node in $Y$ is salvageable since for each node $v \in Y$, the number of initially affected neighbors is at least the threshold of $v$. Moreover, by removing all the nodes in $Y$, we can ensure that none of the nodes in $Z$ is affected.

We now argue that the set $Q$ produced by the algorithm is indeed a critical set; that is, the removal of $Q$ ensures that none of the nodes in $Z$ is affected. To see this, consider any node $v_i \in Z$ and let $p_i$ and $q_i$ denote the number of neighbors of $v_i$ in $I$ and $Y$ respectively. The coverage requirement for $v_i$ was chosen as $\sigma _i = \max \{0,~ p_i + q_i - t_i + 1\}$. If $\sigma _i = 0$, then $p_i + q_i \le t_i -1$, and therefore, $v_i$ cannot be affected. If $\sigma _i \ge 1$, then the number of neighbors of $v_i$ after removing all the nodes in $Q$ is at most $p_i + q_i - \sigma _i$ which is at most $t_i -1$ by the definition of $\sigma _i$. Hence, $v_i$ will not get affected.$\square$

To prove the performance guarantee, we have the following claim.

Claim 1

Any critical set of size $\alpha$ corresponds to a solution to the SMC problem with $\alpha$ sets and vice versa.

Proof of Claim 1

Consider any critical set $Q' = \{v_{j_1}, v_{j_2}, \ldots , v_{j_{\alpha }}\}$ of size $\alpha$. We argue that the corresponding collection $C' = \{C_{j_1}, C_{j_2}, \ldots , C_{j_{\alpha }}\}$ of sets is a solution to the SMC problem. Since $Q'$ is a critical set, for any node $v_i \in Z$, after the removal of $Q'$, the number of neighbors of $v_i$ in $I \cup (Y-Q)$ is at most $t_i - 1$. Using this fact, it can be verified that each node $v_i \in Z$ is covered at least $\sigma _i$ times by $C'$. In other words, $C'$ is a solution to the SMC problem. The proof that any solution to SMC problem with $\alpha$ sets corresponds to a critical set of size $\alpha$ is similar, and this establishes Claim 1.

To establish the performance guarantee, let $Q^*$ be an optimal critical set. Thus, by the above claim, there is a solution to the SMC problem with at most $|Q^*|$ sets. Since the approximation algorithm for the SMC problem provides a performance guarantee of $H_s$, where $s = |U| = |Z|$, the size of the solution to the SMC problem obtained in Step 4 of the algorithm is at most $|Q^*| H_s$. Since the approximation algorithm produces a critical set whose size is exactly the number of sets in the approximate solution to the SMC problem, we have $|Q| \,\le \, |Q^*| H_s$. $\square$

5 Heuristics for finding small critical sets

5.1 Overview

The complexity results presented in Sect. 4 point out the difficulty of developing heuristics with provably good performance guarantees for the SCS-MNA and SCS-MUN problems. So, we focus on the development of heuristics that work well in practice for one of these problems, namely SCS-MNA. In this section, we present two such heuristics. The first heuristic uses a greedy set cover computation. The second heuristic relies on a potential function, which provides an indication of a node’s ability to affect other nodes. Experimental evaluation of these heuristics on several social networks is discussed in Sect. 6.

5.2 Covering-based heuristic (CBH)

Given a SyDS $\mathcal {S}{} = (G(V,E), \mathcal {F})$ and the set $I \subseteq V$ of nodes whose initial state is 1, one can compute the set $S_i \subseteq V$ of nodes that change to state 1 at the $i^{\mathrm{th}}$ time step, $1 \le i \le T$, for some suitable $T \le |V|$, which can be taken as the time to reach a fixed point (this can be done efficiently as explained in the proof of Lemma 1). The CBH, whose details appear in Fig. 3, chooses a critical set $C$ as a subset of $S_i$ for some suitable $i$. The intuitive reason for doing this is that each node $v$ in $S_{i+1}$ has at least one neighbor $w$ in $S_i$ (otherwise, $v$ would have changed to 1 in an earlier time step). Therefore, if a suitable subset of $S_i$ can be chosen as critical so that none of the nodes in $S_{i+1}$ changes to 1 during the $(i+1)^{\mathrm{st}}$ time step, the contagion cannot spread beyond $S_i$. Consistent with the goal of the SCS-MNA problem, we seek to halt the diffusion process as early as possible in Step 2 of Fig. 3. There are two means by which this can be accomplished at each time $i$: Step 2(i)(a) which checks whether $S_i$ can itself serve as a critical set (i.e., $|S_i| \le \beta$) and Step 2(i)(e) which checks whether the covering procedure discussed below produces a suitable critical set from $S_i$.

Fig. 3

Details of the CBH

In general, when nodes have thresholds $\ge 2$, the problem of choosing at most $\beta$ nodes from $S_i$ to prevent a maximum number of nodes in $S_{i+1}$ from changing to 1 corresponds to the SMC problem mentioned in Sect. 4. Step 2(i)(b) constructs an instance of SMC, where each set $\Gamma _j$ in the collection $\Gamma$ corresponds to a node $v_j$ of $S_i$. The elements to be covered are the nodes in $S_{i+1}$. The coverage requirement for each node $v_k \in S_{i+1}$ is determined as follows. Suppose $v_k$ has threshold $t_k$ and has $n_k$ affected neighbors in $S_1 \cup S_2 \cup \ldots \cup S_i$. Since $v_k \in S_{i+1}$ is affected in time step $i+1$ in the absence of any critical nodes, we have $n_k \ge t_k$. Thus, to prevent $v_k$ from getting affected, at least $n_k - (t_k -1)$ = $n_k - t_k +1$ nodes from $S_i$ must be chosen as critical nodes. In the SMC formulation, this number corresponds to the coverage requirement for node $v_k$.

Since SMC is NP-hard, a greedy approach is used (Step 2(i)(c)) for this covering problem (Vazirani 2001). This approach iterates over the sets of $\Gamma$; in each iteration, the chosen set from $\Gamma$ corresponds to a node $v_j$ from $S_i$ that contributes to saving the largest number of nodes in $S_{i+1}$ from becoming affected. That is, $v_j$ is the node that has the greatest number of edges in $G(V,E)$ to nodes in $S_{i+1}$ that are still affected (ties are broken arbitrarily). Thus, the subcollection $\Gamma '$ produced by Step 2(i)(c) corresponds to a subset of $S_i$.

If the conditions in Steps 2(i)(a) and 2(i)(e) are not satisfied for any $T,\,1 \le i \le T-1$, then a solution that has the smallest number of nodes whose coverage requirement is not met is chosen as the output. We now establish the running time of CBH.

Proposition 2

Let $G(V,E)$ denote the underlying graph of the given SyDS $\mathcal {S}$. The running time of CBH is $O(|V||E|)$.

Proof

Consider the description of CBH in Fig. 3. Using Lemma 1, Step 1 can be implemented to run in $O(|V|+|E|)$ time. In each iteration of Step 2(i), it can be seen that the dominant part of the running time is due to the greedy heuristic for SMC. This heuristic can be implemented to run in $O(\sigma )$ time, where $\sigma$ is the sum of the sizes of the given sets (Vazirani 2001). In CBH, since the set constructed for any node $v$ is of size at most $\mathrm{degree}(v)$, the sum of the sizes of all the sets is at most $\sum _{v \in V} \mathrm{degree}(v) = |E|$. Thus, each execution of the greedy heuristic runs in $O(|E|)$ time. Since Step 2(i) runs the greedy set cover heuristic $T - 1$ times, the running time of that step is $O(T |E|)$. Since $T \le |V|$, the worst-case running time of CBH is $O(|V| |E|)$. $\square$

5.3 Potential-based heuristic

Here, we provide the details of the PBH. The idea is to assign a potential to each node $v$ depending on how early $v$ is affected and how many nodes it can affect later. Nodes with larger potential values are more desirable for inclusion in the critical set. While the CBH chooses a critical set from one of the $S_i$ sets, the potential based approach may select nodes in a more global fashion from the whole graph.

We assume that set $S_i$ of newly affected nodes at time $i$ has been computed for each $i,\, 1 \le i \le T$, where $T$ is the time at which the system reaches a fixed point. For any node $x \in S_i$, let $N_{i+1}[x]$ denote the set of nodes in $S_{i+1}$ which are adjacent to $x$ in $G$. The potential $P[x]$ of a node $x$ is computed as follows.

• For each node $x$ in $S_T,\, P[x] = 0$. (Justification  Since there is no diffusion beyond level $T$, it is useless to have nodes from $S_T$ in the critical set).

• For each node $x$ in level $S_i,\, 1 \le i \le T-1$,

  $$\begin{aligned} P[x] = (T-i)^2 \left[ |N_{i+1}[x]| + \sum _{y \in N_{i+1}[x]} P[y] \right] \end{aligned}$$

  (1)

  (Justification  The term $(T-i)^2$ decreases as $i$ increases. Thus, the term enables us to assign higher potentials to nodes that are affected earlier. The term $|N_{i+1}[x]|$ is included in the expression for potential so that nodes which have a large number of neighbors in the next level become desirable candidates for inclusion in the critical set.)

The steps of the PBH are shown in Fig. 4. Steps 1, 2 and 3 compute the potentials for all the nodes in $S_1 \cup S_2 \cup \ldots \cup S_T$ in a bottom-up fashion. Step 4 indicates how the critical set is chosen. We now establish the running time of PBH.

Fig. 4

Details of the PBH

Proposition 3

Let $G(V,E)$ denote the underlying graph of the given SyDS $\mathcal {S}$. The running time of PBH is $O(|V|+|E|)$.

Proof

Consider the description of PBH in Fig. 4. From Lemma 1, Step 1 can be implemented to run in $O(|V|+|E|)$ time. Step 2 runs in $O(|V|)$ time. In Step 3, the potential for each node $v$ is computed by examining the neighbors of $v$. Thus, for any node $v$, the time used to compute $v$’s potential is $O(\mathrm{degree}(v))$. Hence, the time used to compute the potentials of all the nodes is $O(\sum _{v \in V} \mathrm{degree}(v))$ = $O(|E|)$. Step 4 can be carried out in $O(|V|)$ time since the $\beta ^{\mathrm{th}}$ largest potential value can be computed in $O(|V|)$ time using the well known linear time selection algorithm (Cormen et al. 2001). Hence, the overall running time of PBH is $O(|V|+|E|)$. $\square$

The next section presents a simple example to illustrate similarities and differences between the behaviors of PBH and CBH.

5.4 Comparison of critical node heuristics

We compare behaviors of the two critical node heuristics PBH and CBH with respect to how they block $t=2$ diffusion on the graph of Fig. 5 when the two nodes $A$ and $B$ are the seed nodes. We note that this graph could be embedded in a larger graph. Also, we have chosen the edges among the nodes to be somewhat regular for expository reasons. However, there are many edge sets among this set of nodes that will give the same behavior as that discussed below. Furthermore, many additional edges can be introduced without affecting the spread size.

Fig. 5

Example graph where threshold-2 diffusion starts from the two seed nodes $A$ and $B$. Without critical nodes, the four brown nodes ($C,\, D,\, E$ and $F$) are affected at time $i=1$ and the four green nodes ($G,\, H,\, J$ and $K$) are affected at $i=2$ (Color figure online)

In the absence of critical nodes, the contagion will propagate throughout the network. In particular, nodes $G$ and $H$ are affected by nodes $C$ and $D$, and hence nodes $L,\, M,\, N$, and $P$ are all affected through the nodes $C$ and $D$. We consider two cases of critical nodes: one in which CBH performs much better than PBH and a second case where the two methods perform comparably. We now consider the case where the number of blocking nodes is $\beta =2$ and demonstrate that CBH performs far better than PBH.

For CBH, we start with the nodes (in green) that are affected at time $i=2$. The candidate nodes that may be specified as critical are the four brown nodes, namely $C,\, D,\, E$ and $F$. If either of $C$ or $D$ is not affected at $i=1$, then neither $G$ nor $H$ can be affected at $i=2$ (because their thresholds are 2). Similarly, if either $E$ or $F$ is not affected at $i=1$, then neither $J$ nor $K$ can be affected at $i=2$, and the contagion is halted in that direction. Thus, CBH will select one of $\{C,D\}$ and one of $\{E,F\}$ as critical nodes (ties are broken arbitrarily) and the final spread size is four nodes: the two seeds and whichever two of the four brown nodes are not set critical.

For PBH, we note that potentials are computed first for the nodes that are affected last, and the computations proceed backwards to the seed nodes. Starting from nodes $N$ and $P$, whose potentials are zero, the potentials of nodes will increase as one moves up toward the seed nodes. Thus, the nodes with the largest potential, and hence the nodes that will form the set critical, are $C$ and $D$. The resulting spread size is 12 since all nodes except $C$ and $D$ will be affected.

Now, for the second case, suppose instead that $\beta$ is increased from 2 to 4. The critical sets for CBH and PBH are, respectively, $\{C, D, E, F\}$ and $\{C, D, G, H\}$ and the final spread sizes are 2 and 6. Thus, with four critical nodes, the difference in spread sizes between the two heuristics is cut in half (from a difference of 8 when $\beta =2$, to a difference of 4 when $\beta =4$).

In Sect. 6.4 (Fig. 12) we discuss parameter settings which show significant differences between the blocking performances of PBH and CBH for realistic social networks.

6 Blocking experiments and results

6.1 Overview

We first describe the social networks used for testing. Next, we compare the blocking performance of our heuristics with those of five known heuristics. When then provide further results from an experimental evaluation of our methods to illustrate additional aspects of blocking. Our results provide answers for the SCS-MNA problem. We also provide timing data for our heuristics to emphasize the tradeoff between execution speed and quality of critical sets.

6.2 Networks and generation of seed nodes

Table 3 provides selected features of the three social networks used in this study (we refer to these as “realistic social networks,” since they were produced by mining real social datasets). We assume that all edges are undirected to accentuate diffusion and thereby test the heuristics more stringently. Average degree and average clustering coefficient vary by more than a factor of 2 across the networks. Power law degree distributions for the three networks are shown in Fig. 6a. While we use mined networks to investigate realistic structures, other works (e.g., Barash 2011) look at the effects of stylized structures on contagion processes without blocking nodes.

Table 3 Selected characteristics of three realistic social networks (Richardson et al. 2003; Leskovec et al. 2008, 2010)

A $\mathbf{k}$-core of a graph is a subgraph in which each node has a degree of at least $k$ (Seidman 1983). A $k$-core is maximal if there is no larger subgraph (in terms of number of nodes) which is also a $k$-core.² Figure 6b provides maximal $k$-core sizes for the three networks. The number of nodes in each maximal $k$-core must be non-increasing as $k$ increases. We will be particularly interested in $k=2$, 3, 5, and 20 in this paper, and for each of these values, the maximal $k$-core forms one connected component (although in general, a $k$-core need not consist of only one component).

Fig. 6

a Degree distributions and b k-core sizes for the three networks of this study

All our diffusion experiments use the following method of generating seed sets. For a given value of number $n_s$ of seeds, 100 sets of seed nodes are determined from each network to provide a range of cases for testing the heuristics. Each set of seed nodes is taken from a 20-core; thus, each seed node has a degree of at least 20. Choosing seed nodes from the 20-core provides a good compromise between selecting high-degree nodes, and having a sufficiently large pool of nodes to choose from so that there is no duplication of seed node sets. Moreover, each set of seed nodes forms a connected subgraph, which fosters diffusion. Thus, the test cases utilize two means (namely, seeding of high-degree nodes and ensuring that they form a connected subgraph) to foster diffusion and hence tax the heuristics.

Barash et al. (2012) demonstrate that there are conditions under which complex contagions will not spread in stylized graphs; as mentioned earlier, they do not consider critical nodes. Since our goal is to study the effectiveness of critical nodes in blocking diffusion, we seek to generate widespread diffusion in the absence of critical nodes, even for small seed sets. Then, the number of affected nodes when including critical nodes indicates the effectiveness of a blocking method in inhibiting contagion spread.

6.3 Comparisons of CBH and PBH with other blocking methods

We now turn to evaluating the heuristics in halting and delaying diffusion by first comparing our heuristics with five other heuristics: (1) randomly setting nodes critical (RCH), (2) setting high-degree nodes critical (HCH), (3) setting critical the nodes with greatest betweenness centrality (BCH), (4) setting critical nodes with greatest eigenvector centrality (ECH), which for undirected graphs is the same as the HITS method (Kleinberg 1999), and (5) the maximum eigenvalue drop method called NetShield (Tong et al. 2010). As mentioned earlier, methods referred to in items (2) through (5) above were proposed in the literature for blocking simple contagions. The random choice method (RCH) serves as a baseline. In the remainder of this section, the above five approaches are referred to collectively as other blocking methods.

Our experimental procedure is as follows. We consider the three networks (epinions, slashdot and wikipedia) discussed in Sect. 6.2 and set the threshold value $t = 2$. We use two values (namely, 2 and 3) for the number $n_s$ of seed nodes. For each value of $n_s$, 100 sets of seed nodes are generated from the 20-core of the corresponding social network. The budget $\beta$ on the number of blocking nodes is set to 500. We chose the values of $n_s$ and $\beta$ to give the blocking methods a good opportunity to succeed since the value of $\beta /n_s$ is reasonably large (250 and 166.7 respectively for $n_s$ = 2 and 3). For each combination of social network, value of $n_s$ and blocking method with $\beta =500$, we ran 100 diffusion instances (one corresponding to each seed set) and recorded the number of nodes in the affected state (state 1). The seed sets are the same for each blocking method. For each set of 100 diffusion instances, we provide the average number of affected nodes.

We also provide, in the last column of the following tables, the ratio of average number of affected nodes to the maximum possible (MP) number of nodes that can be affected. This ratio is crucial because for complex contagions, graph structure itself can retard contagion propagation, and a blocking method should not be given credit for a seemingly smaller spread size when the effect is due to the graph structure. For example, 47 % of epinions nodes (i.e., 35755 nodes) have degree 1. With $t=2$ diffusion, it is impossible for these nodes to become affected (unless they are seed nodes) because they cannot have two neighbors in state 1. Thus, one upper bound on the maximum spread size for $t=2$ contagion in epinions is 40124 $(=75879-35755)$ nodes. In fact, a tighter upper bound is the size of the largest connected component of the 2-core, which for epinions is 37300 nodes (a general result, from which this bound for epinions follows, will be established in Sect. 7). Thus, with no blocking nodes, the MP spread size in epinions for $t = 2$ diffusion is 37300. To illustrate why this MP spread size is important, suppose a method that uses blocking nodes allows a spread size of 30000 on the epinions network. Here, one might conclude (erroneously) that the blocking method is effective because only a fraction $30000/75879 ~\approx ~ 0.4$ of all the nodes are affected. In actuality, the method is not effective because a fraction $30000/37300 ~\approx ~ 0.8$ of all the nodes that the contagion can reach in the absence of blocking nodes are affected, even though blocking nodes are used. Therefore, the values in the final column of the following tables normalize the average spread size (computed over 100 diffusion instances via simulation) by the theoretical MP spread size. This ratio assists in the interpretation of the reported spread size.

Our experimental results for epinions, slashdot, and wikipedia, are given in Tables 4 through 9, where each table contains data for one network and one seed set size. Our findings can be summarized as follows.

• 1. For all three networks, CBH and PBH perform well in blocking diffusion, allowing almost no spreading for any diffusion instance. Over the conditions of all tables, PBH permits widespread contagion propagation for only one diffusion instance; CBH permits no widespread diffusion. The random choice method RCH allows the greatest fractions of affected nodes for all three networks (the reason for the poor performance by RCH is that nodes of degree 1 account for between 35 and 50 % of nodes in these networks. RCH has a good chance of choosing such nodes as critical nodes even though other nodes which are better suited to block the complex contagion are available).

• 2. For the epinions network (Tables 4, 5), HCH, BCH, ECH/HITS and NetShield permit average spread sizes between 18809 and 27119 nodes. For slashdot (Tables 6, 7), the range in numbers of affected nodes is 12440 to 31882 nodes, while for wikipedia (Tables 8, 9), the range in numbers of affected nodes across other methods is 1877 to 3185 nodes. For all three networks, when the number of seed nodes increases to $n_s=3$, contagion spreading significantly increases. These results suggest that in the three networks, complex contagions are often able to circumvent the nodes of high degree or high centrality and find alternate paths to reach many nodes.

• 3. Average numbers of affected nodes for PBH and CBH are two orders of magnitude less, and in most cases are three to four orders of magnitude less, than those for the five other methods. These results highlight the improved blocking performance that can be realized by using the additional information provided by the seed node sets.

• 4. It is also useful to compare the performance of the other blocking methods. The high degree heuristic performs just as well as—in some cases better than—the more sophisticated methods in blocking complex contagions. This result provides an interesting contrast with the findings in Tong et al. (2010) for simple contagions, where NetShield was shown to have the best performance.

• 5. The results also show that all five of the other methods are more effective in blocking complex contagions in slashdot than in epinions and wikipedia. We believe that this is related to the average clustering coefficients $(C_{ave})$ of the networks. As can be seen from Table 3 (Sect. 6.2), the slashdot network has the smallest $C_{ave}$ among the three networks. For complex contagions, where multiple affected neighbors are required to propagate a contagion, the clustering coefficient is potentially an important factor in determining a network’s ability to spread contagions. The $C_{ave}$ values for epinions and wikipedia are somewhat more typical of social networks, while that for slashdot is smaller (Newman and Park 2003). These results suggest that networks with smaller $C_{ave}$ can still spread complex contagions, but blocking their progression is easier.

Table 4 Performance of blocking methods for epinions ($t=2$ and $\beta =500$) with two seed nodes

Table 5 Performance of blocking methods for epinions ($t=2$ and $\beta =500$) with three seed nodes

We end this section by noting that the other blocking methods are sensitive to the number of seed nodes: an increase in numbers $n_s$ of seed nodes from 2 to 3 significantly decreases the effectiveness of these methods. We will see this sensitivity to $n_s$ in CBH and PBH as well in Sect. 6.4; however, in our methods, this sensitivity is pushed further out to larger values of $n_s$.

Table 6 Performance of blocking methods for slashdot ($t=2$ and $\beta =500$) and two seed nodes

Table 7 Performance of blocking methods for slashdot ($t=2$ and $\beta =500$) and three seed nodes

Table 8 Performance of blocking methods for wikipedia ($t=2$ and $\beta =500$) and two seed nodes

6.4 Experimental evaluation of CBH and PBH

We carried out a parametric study to experimentally evaluate the performance of PBH and CBH. Table 10 lists the parameters and values used in the parametric study.

The test plan consists of running 100 simulations of diffusion instances (one instance per seed node set) on each of the three networks for all combinations of $t,\, n_s$, and $\beta$ values shown in Table 10. Our simulator outputs for each node $v$ the time at which $v$ is affected. The heuristics use this as input data and calculate one set of $\beta$ critical nodes for each iteration (i.e., diffusion instance). The simulations are then repeated, but now they include the critical nodes, so that the decrease in the total number of affected nodes caused by a critical set can be quantified. The main results from this full-factorial parametric study are outlined below. For brevity, when results for different networks and combinations of parameter values are similar, only results for one representative network and some specific combinations of parameter values are presented.

Table 9 Performance of blocking methods for wikipedia ($t=2$ and $\beta =500$) and three seed nodes

Table 10 Parameters and values of the full-factorial parametric study

For reasons discussed in Sect. 6.3, all results are given as the average number of affected nodes over 100 diffusion instances, divided by the MP number of affected nodes, designated “(Ave. Affected)/(MP Affected).” We also refer to this ratio as the spread fraction. The denominator is the theoretical upper bound on spread size, derived from Theorem 6 (which is established in Sect. 7).

Effect of critical set budget and number of seed nodes on spread fraction  Figure 7 compares the spread fraction for CBH and PBH across all three networks for $n_s=5$ (solid curves) and $10$ (dashed curves). As one would expect, for both the methods, given a value for $n_s$, the spread fraction decreases as the budget $\beta$ on critical nodes increases. The two plots show how a doubling of the number of seed nodes can produce a six-fold increase in the spread fraction; compare the slashdot data for $\beta =100$, where increasing the number of seed nodes from 5 to 10 increases the spread fraction from about 0.1 to 0.6. The blocking performance of CBH and PBH are similar for slashdot; however, CBH significantly outperforms PBH for epinions and wikipedia when the number of seed nodes is increased to 10. As mentioned in Sect. 6.3, this behavior can be attributed to the significantly smaller average clustering coefficient of slashdot compared to the other networks.

Fig. 7

Comparisons of the a CBH and b PBH for inhibiting diffusion in all networks, for two seed set sizes and $t=2$. The ordinate is the average number of affected nodes (counting seed nodes) over 100 diffusion instances divided by the MP number of affected nodes

Effect of threshold and critical set budget on spread fraction The effect of increasing threshold values on the spread fraction is shown in Fig. 8 for the epinions network using CBH for four values of $\beta$; the two plots correspond to $n_s=20$ and 50, respectively. In Fig. 8a, if we use $t=2$ and $\beta =1000$ as a baseline case, we see that increasing the threshold from 2 to 3 enables the number of blocking nodes to be reduced by 500 while achieving a slightly lower spread fraction (0.27 vs. 0.22). If the threshold is increased to 5, the number of blocking nodes can be decreased by an order of magnitude, from 1000 to 100, with only a 50 % increase in the spread fraction (0.27 vs. 0.38). Thus, increasing the threshold can significantly decrease the critical node budget needed to achieve the same spread fraction. However, by comparing Fig. 8a, b, it is seen that increasing the number of seed nodes from 20 to 50 significantly increases the spread fraction.

Fig. 8

Effect of threshold on spread fraction in the epinions network, with $\beta$ = 50, 100, 500 and 1000. CBH is used in both plots, with a $n_s=20$ and b $n_s=50$

Figure 8b also illustrates the benefit of normalizing the average spread size by the size of the seeded component of the $t$-core. For $\beta =50$ and 100, as $t$ increases from two to five, the average number of affected nodes decreases from about 32000 for $t=2$, to 22000 for $t=3$, to 14000 for $t=5$. Yet, these decreases are essentially attributable to graph structure, rather than the effectiveness of critical nodes, as indicated by the relatively constant spread fraction for varying threshold.

Effect of critical nodes on the spread size per diffusion instance  To this point, parametric study results have focused on the spread fraction, an average quantity over all 100 diffusion instances for a given $n_s$. Here, we instead examine the character of slashdot data for each diffusion instance for $n_s=10$ in Fig. 9. For each value of $\beta$, the (normalized) spread size for each of the 100 diffusion instances is arranged in increasing numerical order and plotted in Fig. 9a for $t = 3$. To explain this figure, consider the plot for $\beta =10$. The curve makes a steep transition from essentially 0 (i.e., essentially zero diffusion) to 0.95 at 30 % of iterations, indicating that 70 % of iterations produce significant diffusion. Increasing the value of $\beta$ shifts the curves to the right, that is, reduces the fraction of iterations that produces large spread sizes. The value $\beta =500$ halts all diffusion. Note that the maximum normalized spread size across all values of $\beta$ is relatively constant. Because the ordinate value is near 1.0—for instances where the contagion spreads significantly—these data indicate that the number of affected nodes is a very large fraction of the $t$-core size.

Figure 9b provides similar data, but for $t=5$. As a result, these curves are shifted to the right compared to those in Fig. 9a. Nonetheless, the transitions from small to large numbers of affected nodes are sharp, and for diffusion instances with large numbers of affected nodes, the numbers are very close to the numbers of nodes in the $t$-core since the ordinate values are near 1.0. We also observe that the large ordinate values are essentially independent of $\beta$. All data generated in this study possess these features.

Fig. 9

Final fractions of affected nodes arranged in increasing order for each of the 100 iterations (to generate each curve) for the slashdot network and CBH heuristic for $n_s=10$ and a $t=3$ and b $t=5$. The legend is the same in both plots

Effect of critical set budget in delaying peak spread fraction  In Fig. 10, the spread fraction, in terms of newly affected nodes at each time step, over the 100 diffusion instances is plotted for different $\beta$ values. These results are for epinions with $t = 2$ and $n_s = 10$ when PBH is used. From the figure, it can be seen that while a budget of $\beta =500$ does not halt the diffusion, it slows down the diffusion compared to the other budget sizes, moving the time of the peak in the number of newly affected nodes from 3 to 6. In applications such as disease propagation over a population or worm propagation in computer networks, this delay provides additional time for decision-makers to devise appropriate intervention strategies (Cohen et al. 2003; Porras et al. 2004) and could be used analogously for social contagions.

Fig. 10

Average curves of newly affected nodes for PBH for the case $t=2$, $n_s=10$, and different values of $\beta$ with the epinions network

Blocking performance of CBH and PBH with a small number of seed nodes  Figure 11 examines the regime of small numbers of seed nodes, and depicts the spread fraction as a function of $\beta$ for wikipedia. A $(1/\beta )$ behavior is observed, so that the spread fraction drops off sharply with increasing budget. However, to completely eliminate all cascades, $\beta =500$ is required for both heuristics when $n_s=5$. In most of our experiments, $\beta /n_s \ge 100$ was required to halt all diffusion. However, the $n_s=3$ curves demonstrate that for very small seed sets and when $n_s=t$, $< 100$ critical nodes can halt all diffusion, which corresponds to $\beta /n_s < 33$. Further, all of these curves depict more precipitous drops than those in Fig. 7.

Fig. 11

Comparisons of the CBH and PBH in inhibiting diffusion in the wikipedia network for $t=3$

Parameter settings that show significant differences between the blocking performances of CBH and PBH  Figure 12 provides results showing the greatest differences in performance between the two heuristics in thwarting diffusion. This is done by comparing spread fractions. From Fig. 12, it is seen that for the epinions network with $n_s = 10$, the spread fraction under CBH and PBH are respectively 0.14 and 0.52 when $\beta$ is fixed at 500. A similar difference is seen for the wikipedia network with $n_s = 20$.

Fig. 12

Comparisons of the CBH and PBH in inhibiting diffusion in the epinions with $t=2$ and wikipedia (wiki) with $t=3$. The number $\beta$ of critical nodes is 500

It can be seen from Fig. 12 that, critically, once a value of $n_s$ produces even a small $(\sim 0.10)$ spread fraction for a fixed $\beta$, further increases in $n_s$ will result in large increases in spread fraction. For both networks, we observe that $\beta /n_s=500/3=167$ will halt all diffusion. However, the epinions data illustrate that for $n_s=5$ and $\beta =500$, the ratio of $\beta /n_s=100$ does not halt all diffusion for either CBH or PBH. Hence, as $n_s$ increases, the ratio $\beta /n_s$ required to stop all diffusion can be quite large.

Timing profiles for CBH and PBH We now compare the execution times of CBH and PBH. To carry out this study, serial implementations of CBH and PBH were run on a single core (with 2GB of memory) of a system with a 3 GHz Intel Xeon processor. Figure 13 depicts the execution times for each heuristic for $\beta =5$ as $n_s$ is varied. The two plots are for epinions and wikipedia respectively, with different curves in the same plot corresponding to the two heuristics and three different threshold values (2, 3 and 5). For the epinions network, Fig. 13a, these times translate into a maximum of roughly 1.5 hours for CBH to determine 100 sets of critical nodes, versus less than 5 minutes for PBH. The execution times for wikipedia are significantly smaller than those for epinions since the former network is smaller in size (by a factor of 10) than the latter. In general, PBH is clearly faster than CBH, and this experimental result is in agreement with the worst-case running time estimates for the two methods obtained in Sect. 5. Since CBH is better than PBH in blocking complex contagions, we see a tradeoff between blocking performance and speed of algorithm execution.

Fig. 13

Times for CBH and PBH to compute one set of critical nodes for $\beta =5$ as a function of number of seed nodes for three threshold values. Part a is for the epinions network and Part b is for the wikipedia network. Times are averages over 100 iterations. The legend is the same for both plots

7 Comparisons of spread sizes against theoretical upper bound

As demonstrated in Sect. 6.4, it is useful to reason about the effectiveness of a blocking scheme in terms of how many nodes still get affected when using critical nodes, relative to the total number of nodes that could possibly be affected without critical nodes. We now address that issue in a quantitative manner by presenting an upper bound on the spread size of a complex contagion. Our approach uses a static network property that is easily computed to provide a bound on system dynamics. Furthermore, we provide an extensive experimental evaluation of our bound on many networks and different threshold values.

7.1 Theoretical bounds on spread size

Recall that the maximum spread size in a social network is the total number of nodes whose state is 1 at the end of the diffusion process. We assume that the given SyDS is a $t$-threshold system for some $t \ge 1$; that is, each local transition function is the $t$-threshold function. We start with a graph theoretic definition, extending (Seidman 1983).

Definition 1

Let $G(V,E)$ be an undirected graph and let $t \ge 0$ be an integer. A $\mathbf{t}$-core of $G$ is an induced subgraph $G'(V',E')$ of $G$ such that each node in $G'$ has a degree of at least $t$. A $t$-core $G'(V',E')$ of $G$ is maximal if there is no strict superset $V^{\prime \prime } \supset V'$ of nodes such that the subgraph of $G$ induced on $V^{\prime \prime }$ is also a $t$-core.

Example

Consider the graph $G(V,E)$ shown in Fig. 14. The induced subgraph formed on the node set $\{v_4, v_5, v_6\}$ is a 2-core of $G$. Likewise, the induced subgraph formed on the node set $\{v_2, v_3, v_5\}$ is also 2-core of $G$. The induced subgraph formed on the node set $\{v_2, v_3, v_4, v_5, v_6\}$ is the maximal 2-core of $G$.

Fig. 14

An example to illustrate the definitions of $t$-core and maximal $t$-core

For any graph $G$ and integer $t \ge 0$, it is easy to see that the maximal $t$-core is unique. In fact, the maximal $t$-core of $G$ can be constructed efficiently by repeatedly removing nodes whose degree is less than $t$. The removal process ends when all remaining nodes have degree $\ge t$ (Seidman 1983).

Even if $G$ is connected, the maximal $t$-core may not be connected. For a graph $G$ and integer $t \ge 0$, we use $L_{G}(t)$ to denote the number of nodes in a largest connected component of the maximal $t$-core of $G$. As will be seen from the results of this section, the parameter $L_{G}(t)$ can be used to bound the maximum spread size in $t$-threshold systems. We begin with a simple lemma.

Lemma 2

Let $G(V,E)$ be an undirected graph. For any $t \ge 0$, a node $v \in V$ is in the maximal $t$-core of $G$ if and only if node $v$ has at least $t$ neighbors that are also in the maximal $t$-core.

Proof

Let $G'(V',E')$ denote the maximal $t$-core of $G$. If $v$ is in $V'$, then by definition, its degree in $G'$ is $\ge t$; that is, $v$ has at least $t$ neighbors in $G'$. For the other direction, assume that $t$ of the neighbors of $v$ are in $G'$. Consider the node removal process that produced $G'$. This process did not remove any of the $t$ neighbors of $v$ which are in $G'$. Thus, throughout the removal process, the degree of $v$ was at least $t$. In other words, $v$ remains in $G'$.$\square$

We present a result that bounds the maximum spread size in a $t$-threshold system in terms of the size of the largest connected component of its maximal $t$-core. In stating this result, we assume that the seed set is of size $t$. If the seed set has less than $t$ nodes, obviously, there will be no further diffusion in a $t$-threshold system.

Theorem 6

Let $G$ be the underlying graph of a $t$-threshold SyDS, where $t \ge 1$. Let $G'(V',E')$ denote the maximal $t$-core of $G$. For any seed set $I \subseteq V'$ with $|I| = t$, the maximum spread size is bounded by $L_G(t)$, the size of a largest connected component of $G'$. Moreover, for each $t \ge 1$, this bound is achievable.

Proof

We first prove the upper bound. For $t = 1$, the set $I$ contains only one node, say $v$, and diffusion can lead to new affected nodes only in the connected component that contains $v$. Thus, the upper bound is trivial for $t = 1$.

So, assume that $t \ge 2$. First, consider the case where the nodes in $I$ are distributed over two or more connected components of the maximal $t$-core $G'$. Thus, no node of $G'$ is adjacent to all the nodes in $I$. In this case, we can prove by contradiction no further diffusion can occur. To see this, consider a node $v \in V$ whose state changes from 0 to 1 in the first time step. Since the threshold is $t$, node $v$ must be adjacent to all the $t$ nodes of $I$. Then, by Lemma 2, $v$ will also be in $G'$. However, this contradicts the previous conclusion that no node in $G'$ is adjacent to all the nodes of $I$.

Thus, we may assume that all nodes of $I$ are in the same connected component of $G'$. In such a case, all the newly affected nodes will also be part of that component. Therefore, the spread size is bounded by $L_{G}(t)$ when $t \ge 2$.

We now argue that this bound is achievable through a simple example. For each $t \ge 1$, let the graph $G(V,E)$ consist of a clique on $t+1$ nodes. Since the degree of each node of $G$ is $t$, $L_G(t)$ = $|V|$. Further, choosing any $t$ nodes of the $t+1$ clique as the seed nodes ensures that all the nodes in $V$ are affected; that is, the maximum spread size is $t+1$ = $L_G(t)$. $\square$

The bound given by Theorem 6 enables us to determine that maximum spread sizes such as those in Fig. 9 (Sect. 6.4) are indeed the largest possible spread sizes for a given network and threshold. Also, our approach of computing the size of a largest connected component of a $t$-core is closely aligned with determining the largest possible spread size for $t=1$ diffusion by computing the largest connected component of a graph (Albert et al. 2000; Holme 2004).

There are classes of graphs for which the bound given by Theorem 6 is pessimistic. For example, consider an $r \times r$-node lattice graph $G(V,E)$, with $r \gg 2$, where each node is connected to its four neighbors (if they exist) along the four geographic directions (thus, nodes along the boundary have degrees less than 4). Since all nodes have degree $\ge 2$, $L_G(2)=|V|$. Yet, it can be seen that for any seed set with $|I|=t=2$, the MP spread size is $4 \ll L_G(2)$. Thus, it is of interest to experimentally evaluate the effectiveness of the bound for different classes of graphs and values of $t$. This evaluation is carried out in the next section.

7.2 Experimental evaluation of the spread size upper bound

In this section, we use two sets of experiments to carry out an evaluation of the upper bound of Theorem 6 for various synthetic and real social networks. The first set chooses seed nodes from appropriate core subgraphs as used in the proof of Theorem 6. The second set considers a different seeding method and evaluates whether the theoretical bound remains robust. We now discuss the two sets of experiments and results.

Experimental evaluation using core construction  Our experimental procedure is as follows. We consider the three real social networks of this study (slashdot, epinions and wikipedia) along with three synthetic networks: two SF networks (sf-01 and sf-02) constructed using two well-known methods (preferential attachment (Barabasi and Albert 1999) and configuration model (Newman 2003), respectively), and an Erdős–Renyi (ER) random graph. The purpose of using synthetic networks in this study is to evaluate whether particular construction methods yield graph structures that affect the upper bound on spread size. Data for the three synthetic graphs are given in Table 11. The average clustering coefficients for the two sf graphs differ by an order of magnitude and these values are also far different from those in Table 3; recall the strong effect of clustering on the results in Sect. 6.3. Although not shown, the degree distributions for the two SF networks are different, even though the average degree is about the same.

Table 11 Selected characteristics of three synthetic networks

We consider three different values of $t$, namely 2, 3 and 5. We construct the corresponding maximal cores and use Theorem 6 to determine the upper bound on the spread sizes for various graphs. We compare these values against the maximum measured spread sizes from simulations. In these simulations, seed nodes for the three real networks were chosen from their maximal 20-core subgraphs (which are themselves subgraphs of the corresponding 2-cores, 3-cores and 5-cores). Since the average degree of the nodes in the three synthetic graphs is around 10, simulations for the three synthetic networks were done using seed sets from the maximal 10-cores.

Figure 15 provides results for the six networks and three threshold values. There are three data points in the plot for each network, corresponding to $t=2$, 3, and 5, respectively. For all networks except the ER network, the agreement between the experimentally measured spread size (ordinate) and the theoretical bound (abscissa) is excellent, illustrating that in real and synthetic networks, the maximum spread size can be achieved. As just one representative example, consider wikipedia. When $n_s=t=2$, 97 % of simulated diffusion instances achieve the upper bound spread size. When $n_s=t=3$ and $n_s=t=5$, the corresponding percentages are 77 and 35 %, respectively.

The ER random graph data, however, show that the spread size is much smaller than the theoretical maximum. We can explain this behavior as follows. For the 99998-node ER random graph, with an average degree of 10, the probability of having an edge between any pair of nodes is $10/(99998-1) \approx 10^{-4}$. It follows that the probability of having two seed nodes each forming an edge with a third node $v$ (so that $v$ will be affected for $t=2$ diffusion) is roughly $10^{-8}$. A simple repetition of this argument shows that ER random graphs with tens of thousands of nodes (or more) and small to moderate degrees will propagate complex contagions with very low probability. Accordingly, the measured spread sizes are nearly zero in Fig. 15, while the theoretical bound is large. These extremes of tight and pessimistic upper bounds motivate our next experiments.

Fig. 15

Comparisons of maximum measured spread sizes from simulations (ordinate values) and upper bound spread sizes from Theorem 6 (abscissa values). The $45^{\circ }$ line of perfect agreement is also provided. The data are for the networks of Tables 3 and 11, with thresholds $t=2,3,$ and 5. Note the data for sf-01 in the upper right hand corner at $(x,y)=(1,1)$

Experimental evaluation using a random seeding and a node removal scheme To understand whether the theoretical upper bound on spread size is robust when the assumptions used in deriving the bound are relaxed, we now consider a second method of seeding. We utilize the random seeding method of (Centola and Macy 2007; Centola 2009) where a node $v$ is chosen uniformly at random and the seed set consists of $v$ and all of its neighbors. Since these experiments involve a large number of graphs (as described momentarily), only one threshold value, namely $t = 2$, was used. Thus, the seed node sets are not from the maximal 2-core, as used in Theorem 6.

For this study, we also explored graph structure effects by considering two types of synthetic graphs, namely growth model SF networks and growth model exponential-decay networks, whose degree distributions are often found in real social networks (Centola 2009). These graphs are generated using a combined approach from (Barabasi and Albert 1999) and (Schank and Wagner 2005), producing graphs with $d_{ave}=4$ and $C_{ave}=0.24$; using the cited construction procedures enabled us to control both of these properties.

Thirty graph instances of each type are generated, each with 10000 nodes, and these constitute the original graphs. For each of the 30 original instances, six values (namely, $0,\, 10^{-4},\, 10^{-3},\, 10^{-2},\, 10^{-1}$ and $2 \times 10^{-1}$) of the fraction $f$ of removed nodes are considered. These removed node fractions alter the graph structure and hence provide another means of evaluating graph structure effects on the theoretical upper bound spread size. For each value of $f$, 20 sets of nodes are removed from each original graph, in turn, resulting in 3600 ($=30 \cdot 6 \cdot 20$) graph instances. For each graph, the size of the largest connected component of the 2-core is computed. Then, $t=2$ diffusion is simulated, with 20 seed sets for each graph, to experimentally determine the largest spread size.

Figure 16a contains data for the 3600 growth model exponential-decay (gm-ed) networks, and Fig. 16b contains comparable data for 3600 growth model SF (gm-sf) networks. With respect to the data in Fig. 16a, over 20 % of the 3600 graph instances produce spread sizes near the line of agreement and 80 % of the graphs produce virtually no diffusion. For the graphs without any removed nodes, 27 % of diffusion instances achieve close to the maximum spread size. However, even a few graphs with 20 % of nodes removed generate spread sizes close to the theoretical limit. With respect to the data in Fig. 16b, over 98 % of the 3600 graph instances produce spread sizes near the line of agreement. For the conditions of this study, the maximum spread size is more readily achieved in gm-sf networks. More generally, these results suggest that the bound given by Theorem 6 provides a reasonable indication of the maximum spread size even when the conditions of the theorem are relaxed.

Fig. 16

Comparisons of maximum measured spread sizes from simulations (ordinate values) and upper bound spread sizes from Theorem 6 (abscissa values). The $45^{\circ }$ line of perfect agreement is also provided. a Data for 3600 graph instances of gm-ed networks with different fractions $f$ of nodes removed at random from the 30 original graph instances. b Data for 3600 graph instances of gm-sf networks with different fractions $f$ of nodes removed at random from the 30 original graph instances

8 Conclusions and future work

We considered the problem of inhibiting the propagation of complex contagions in social networks. We developed analytical formulations for several versions of the problem. We showed that obtaining provably good heuristics for these problems is computationally intractable. We developed two intuitively appealing heuristics for the problem and showed that they perform well on several social networks. Both theoretical and experimental results also demonstrated ways in which simple contagions differ from complex contagions.

There are several directions for future work. First, it is of interest to develop practical heuristics for the critical set problem for complex contagions when there are weights on edges (to model the degree to which a node is influenced by a neighbor). A second research direction is to study the critical set problem for complex contagions when the diffusion process is probabilistic; that is, for each combination of input values, the local transition function at a node gives the probability that the node’s state changes to 1. Both analytical and experimental results in that context are of interest. A related avenue is investigation of contagion propagation and inhibition under incomplete information. Experimental studies of contagion blocking are also important to undertake. Although edge deletion, rather than node removal, has been studied (Zhang et al. 2009), we feel there is much more work to be done. Another direction to explore is theoretical models that explain differences in results between the CBH and PBH heuristics. Finally, a challenging research direction is to formulate and study the problem for time-varying networks in which nodes and edges may appear and disappear over time.

Appendix: Results beyond homogeneous thresholds

Many of the results presented in Sect. 4 were for the case of homogeneous absolute thresholds. We now briefly indicate how the results can also be extended to other forms of thresholds defined in Sect. 2.3.

We note that heterogeneous thresholds (absolute and relative) are a special case of the corresponding form of homogeneous thresholds. Therefore, any hardness result that holds for homogeneous thresholds also holds for heterogeneous thresholds. We use this fact several times in the following description. The statements and proofs of all the lemmas and theorems referenced below appear in Sect. 4.

• 1. Lemma 1 holds for both homogeneous and heterogeneous absolute thresholds. With a minor modification to the proof, the result can be shown to hold for homogeneous and heterogeneous relative thresholds as well. The modification is that when the counter value for a node indicates that the node has reached its relative threshold, the node is added to the list of affected nodes.

• 2. Theorem 1 holds for homogeneous absolute thresholds and hence for heterogeneous absolute thresholds. To see that it holds for relative thresholds as well, we note that the absolute threshold value $t$ for a node $v$ can be thought of as the relative threshold value of $t/\mathrm{deg}(v)$, where $\mathrm{deg}(v)$ is the number of neighbors of $v$ (including $v$ itself). The same approach can be used to show that Theorems 2, 3 and 4 hold for heterogeneous absolute thresholds and both forms of relative thresholds.

• 3. It was pointed out in Sect. 4 that the approximation algorithm for the SCS-SASN problem actually works for heterogeneous absolute thresholds. Hence, it works for homogeneous absolute thresholds as well. To see that it also works for relative thresholds, we first convert a relative threshold value of $\tau$ for a node $v$ to the absolute threshold value $\lceil \tau * \mathrm{deg}(v) \rceil$ and then use the given approximation algorithm.