1 Introduction

The utility of Artificial Intelligence (AI) models in the financial industry, particularly in identifying hidden patterns within extensive datasets and enhancing market predictions, signifies substantial progress in financial modeling (Ko et al., 2024a). Recent developments in generative AI (Ho et al., 2020), such as DALL·E 2Footnote 1 for image generation and ChatGPTFootnote 2 for natural language processing, highlights the usefulness of deep generative models in the real-world. As the goal of deep generative models is to synthesize new samples by learning training data, the models can be simulated under the condition of unseen data or diverse hypotheses.

The application of deep generative models in financial modeling has been less explored in financial research compared to its importance (Assefa et al., 2020; Ko & Lee, 2024). Most previous studies have primarily focused on applying deep learning for predicting stock or option prices (Lai et al., 2023; Gan & Liu, 2023; Tripathi & Sharma, 2022), and designing hedging strategies (Mikkilä & Kanniainen, 2023). The generation of synthetic financial data is a recent application of deep generative models, with studies specifically generating data that mirrors actual market conditions (Wiese et al., 2020; Li et al., 2020; Xia et al., 2024). Diqi et al. (2022) utilized a Generative Adversarial Network (GAN) (Goodfellow et al., 2020) to generate stock prices for forecasting, whereas Koshiyama et al., (2021) applied a deep generative model to optimize financial trading strategies. Nonetheless, the comprehensive study of deep generative models for financial simulation and option pricing, particularly using generative diffusion models (Ho et al., 2020), remains unexplored. This paper aims to fill this research gap by exploring how generative networks can model the unpredictable nature of asset price processes in financial simulations.

Traditional asset price dynamics rely on stochastic processes such as the Itô process (Taylor, 2011; Rostek & Schöbel, 2013). However, real-world pricing may not follow these diffusion price processes (Hendershott et al., 2022). To address this limitation, we propose training deep learning models to learn the underlying process of stock price movements, allowing us to generate new data samples that capture the underlying patterns. We then leverage these synthetic paths in financial simulations with Monte Carlo methods to provide a flexible solution where analytical formulas are not feasible (Clewlow & Strickland, 1998; Marks, 2007; Wang et al., 2023).

Furthermore, we focus on generating opening, high, low, and closing (OHLC) stock chart images. As deep learning models are well-performing in image processing, previous studies have revealed the benefits of treating stock price charts as images of OHLC (Jiang et al., 2023) and candle charts (Kim & Kim, 2019; Chen & Tsai, 2020). The fundamental idea is that AI can estimate human decision-making based on visual representations rather than numerical time series data. Furthermore, deep learning models can identify trends and fluctuations within 2D images, capturing information such as momentum, reversal, or volatility (Jiang et al., 2023).

For empirical settings, we train generative diffusion models (Ho et al., 2020) to synthesize OHLC chart images without relying on any prior assumptions about the asset price process. It might be considered a branch of approaches to using deep learning models to mimic market patterns (Koshiyama et al., 2021; Wiese et al., 2020; Yilmaz, 2023). Empirical findings demonstrate that the synthetic images can mimic the well-known asset price processes and accurate estimation of option pricing for the real-world market S &P 500.

Our study contributes to understanding asset price processes by examining the potential of deep generative models to learn unknown processes. Our approach offers financial profit as a viable alternative for financial simulation, eliminating the need for any preexisting knowledge regarding underlying processes.

The rest of this study is structured as follows: Sect. 2 introduces important preliminaries concerning financial simulation and diffusion models; Sect. 3 details our methodology for imaging and synthesizing; Sect. 4 discusses our data and experimental design; Sect. 5 provides the empirical results of generating stochastic processes and applying our model to the real-world S &P 500 option pricing; and Sect. 6 provides our concluding remarks.

2 Preliminaries

2.1 Financial Simulation and Asset Price Dynamics

Financial simulation is traditionally based on the mathematical or statistical model to mimic the asset price dynamics, which can be used in various fields such as option pricing (Black & Scholes, 1973), portfolio analysis (Byun et al., 2023; Guastaroba et al., 2009; Ko et al., 2023), risk management (Chan & Wong, 2015; Ko et al., 2024b), forecasting (Bou-Hamad & Jamali, 2020) and stress testing (Brechmann et al., 2013). As the stock prices are random and unpredictable, finding the true dynamics of asset prices is infeasible. Thus, various studies assume the chaotic stock price follows a stochastic process with a specific formula. By assuming the underlying dynamics with known differential equations, we can calculate the infeasible dynamics of real-world asset prices and estimate future prices, such as stock prices, option prices, and optimal portfolios. The general form of the Itô process for variable S is as follows:

$$\begin{aligned} dS = \mu (S,t)dt + \sigma (S,t)dW, \end{aligned}$$
(1)

where \(\mu (S,t)\) and \(\sigma (S,t)\) are general functions for the drift and volatility (Clewlow & Strickland, 1998). To simplify the dynamics, some stochastic processes, such as Geometric Brownian Motion (GBM) or Merton jump processes, are widely used as an underlying dynamics of stock prices (Taylor, 2011). Specifically, we assume the asset behaviors with GBM for non-dividend paying asset \(S_t\) (Clewlow & Strickland, 1998; Hull, 2003):

$$\begin{aligned} \frac{dS_t}{S_t} = \mu dt + \sigma dW_t, \end{aligned}$$
(2)

where \(dS_t\) represents the changes of asset price over a small interval of time dt and \(dW_t\) is normally distributed with mean zero and variance dt. Moreover, the jump model is formulated as follows (Matsuda, 2004):

$$\begin{aligned} \frac{dS_t}{S_t} =\mu dt + \sigma dW_t + (y_t-1)dN_t,\end{aligned}$$
(3)

where \(N_t\) is a Poisson process with rate \(\lambda \) and \(y_t\) is a log-normally distributed random variable with mean k and variance \(v^2\). However, Gan and Liu (2023) pointed out that this assumption might not always hold in real markets, such as specific asset price dynamics and no-arbitrage assumptions.

2.2 Option Pricing

By assuming the underlying price processes such as GBM, we can derive the prices of derivative products in the Black-Scholes world (Black & Scholes, 1973). Consider a European call option that pays \(C_T=\max (0,S_T-K)\) at maturity date T, where \(S_T\) is the stock price at time T and the strike price K with a risk-free interest rate r. Following (Clewlow & Strickland, 1998), consider a European call option that gives

$$\begin{aligned} C = e^{-r(T-t)} \int _{0}^{\infty } \max (0, S_T - K)g(S_T) dS_T, \end{aligned}$$
(4)

where \(g(S_T)\) is the probability density function of the terminal asset process. Then, Itô lemma gives the process for \(x=\ln (S)\) as follows:

$$\begin{aligned} dx = (r - \delta - \frac{1}{2}\sigma ^2)dt + \sigma dW, \end{aligned}$$
(5)

As the drift and volatility are constant, \(\ln (S_T)\) at step T are normally distributed with

$$\begin{aligned} \ln S_T \sim \mathcal {N}(\ln S + (r - \delta - \frac{1}{2}\sigma ^2)(T-t), \sigma \sqrt{T-t}). \end{aligned}$$
(6)

Analytically, Black and Scholes (1973) estimated the option prices in a risk-neutral world, where the Black-Scholes differential equation for GBM processes is formulated as:

$$\begin{aligned} \frac{\partial C}{\partial t} +rS \frac{\partial C}{\partial S}+ \frac{1}{2}\sigma ^2 S^2 \frac{\partial ^2 C}{\partial S^2} - rC = 0. \end{aligned}$$
(7)

The solution to the Eq. (7) for the estimated price of a European call option c can be calculated as follows (Hull, 2003):

$$\begin{aligned} c=Se^{-\delta (T-t)}N(d_1)-Ke^{-r(T-t)}N(d_2), \end{aligned}$$
(8)

where \(d_1= \frac{\ln (\frac{S}{K})+(r-\delta +\frac{1}{2}\sigma ^2)(T-t)}{\sigma \sqrt{T-t}}\) and \(d_2=d_1-\sigma \sqrt{T-t}\). Thus, Eq. (8) enables the management of the risk of an option position (Ko et al., 2024c; Leland & Rubinstein, 1988; Zieling et al., 2014).

Nevertheless, accurately identifying the intrinsic stochastic process governing real-world market data in Eq. (1) presents a significant challenge. Note that the Monte Carlo simulation method can offer a versatile solution, which will be discussed in Sect. 3.3.

2.3 Generative Diffusion Model for Image Synthesis

Fig. 1
figure 1

Illustration of generation process by denoising diffusion models. Starting from the normal distribution, diffusion models can generate diversified multiple synthetic data, which can be utilized as stochastic simulation

Full size image

To approximate the distribution of the underlying process and generate the multiple paths, we now explore the generative deep learning models (Goodfellow et al., 2020; McClelland et al., 1987; Song et al., 2021) as probabilistic simulation models. Rather than suppose specific process dynamics, we aim to learn the dynamics using deep learning models. Contrasting with previous research on prediction or classification deep learning models (Gan & Liu, 2023; Ozbayoglu et al., 2020; Jiang et al., 2023) that generate deterministic outcomes without stochastic variations, generative models can produce varied simulation results within a trained probabilistic distribution. Given conditions such as past stock prices or market states, these models present a viable alternative for overcoming the pricing bias inherent in existing simulation models.

Recently, generative (denoising) diffusion models (Song et al., 2021; Ho et al., 2020) have emerged as the new state-of-the-art generative models in terms of quality and diversity. Among various generative networks such as autoencoders (AE) (McClelland et al., 1987) and generative adversarial networks (GAN) (Goodfellow et al., 2020), diffusion models are widely known to generate better outputs than other existing models (Song et al., 2021). The basic idea of diffusion models is to find patterns by noising and denoising a stochastic differential equation (SDE). Specifically, diffusion models first add random normal noise to the original image \(X_0\) into normal distribution \(X_N\):

$$\begin{aligned} X_n | X_{n-1}&\sim \mathcal {N}(\sqrt{1-\beta _n }X_{n-1},\beta _n I), \end{aligned}$$
(9)
$$\begin{aligned} X_N | X_0&\sim \mathcal {N}(\sqrt{\bar{\alpha }} X_0, (1-\bar{\alpha }_N)I), \end{aligned}$$
(10)

where \(\bar{\alpha }_N=\prod _{s=1}^N(1-\beta _s)\) where \(\beta _1,\ldots ,\beta _N \ge 0\) is chosen such that \(\bar{\alpha }_N \approx 0\), then \(p(X_N)\approx \mathcal {N}(0,I)\). As the mathematical reverse process of It\(\hat{\text {o}}\) SDE is known (Anderson, 1982), The networks \(\theta \) of diffusion model learn how to denoise the image \(X_0\) from random noise \(X_N\), which solves the reverse of Eq. (9) as follows:

$$\begin{aligned} p_\theta (X_{n-1}|X_n)&=\mathcal {N}(\mu _\theta (X_n,n),\beta _n I), \end{aligned}$$
(11)
$$\begin{aligned} \mu _\theta (X_n,n)&=\frac{1}{\sqrt{(1-\beta _n)}}(X_n+\beta _ns_\theta (X_n,n)), \end{aligned}$$
(12)

where \(\nabla _X\log p_n(X)\) is called score with unknown marginal probability densities \(p_n(X)\) and \(s_\theta \) is the score function to estimate the score with the model \(\theta \). Therefore, as shown in Fig. 1, we can generate synthetic data \(X_0\) using diffusion models from random noise \(X_N\) by denoising, which have a similar distribution to the training data.

Generally, diffusion models leverage the U-Net (Ronneberger et al., 2015), a Convolutional Neural Network (CNN) with a U-shaped architecture, to effectively capture spatial patterns. Note that convolutional filters allow for the detection and quantification of changes in stock prices (Jiang et al., 2023). For example, we demonstrate the examples of 3 × 2 convolutional 2D filters to detect price change, e.g., no change with \(\begin{bmatrix} 0 &{} 0 \\ 0 &{} 0 \\ {\textbf {1}} &{} {\textbf {1}} \end{bmatrix}\), small increase with \(\begin{bmatrix} 0 &{} 0 \\ 0 &{} {\textbf {1}} \\ {\textbf {1}} &{} 0 \end{bmatrix}\), and large increase with \(\begin{bmatrix} 0 &{} {\textbf {1}} \\ 0 &{} 0 \\ {\textbf {1}} &{} 0 \end{bmatrix}\).

3 Proposed Methodology

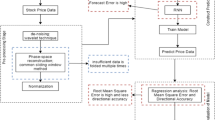
Our framework is designed to train deep generative models to capture the dynamics of asset price processes within the training data. The first step is to pre-process the data by converting stock price charts into image representations. Afterward, we train deep generative models on these chart images to learn patterns. Lastly, the trained models can be used to produce synthetic price chart images, where each image corresponds to one simulation. The primary advantages of our methodology are twofold: (i) the deep generative model is designed to learn the actual market dynamics without relying on strong dynamics assumptions, enabling the generation of multiple probabilistic samples appropriate for Monte Carlo simulations; and (ii) by modeling with OHLC images, we leverage the visual patterns that often influence human trading decisions (Jiang et al., 2023). If the trained generative model can mimic the underlying dynamics, we can verify its effectiveness by estimating the option price with the generated simulation paths. The whole procedure is illustrated in Fig. 2, and detailed descriptions of each step are provided in the following subsections.

Fig. 2
figure 2

Illustration of the stock image generation framework. The framework includes pre-processing the OHLC stock charts and training a diffusion model to capture patterns in the charts. After training, we can generate synthetic OHLC chart images

Full size image

3.1 Data Pre-processing: Imaging Price Charts

To represent stock price charts as images, we adopt the OHLC chart representation inspired by Jiang et al. (2023). This representation converts the chart into pixel images, where the chart pixels are white and the background is black. This pre-processing is suitable for image generation since it eliminates the need to generate all RGB colors. Figure 3a illustrates an example of an OHLC image of stock prices. Each time period is depicted as three pixels wide: the open price on the left, the high and low prices at the top and bottom of the middle bar, and the closing price on the right.

In pre-processing, the stock prices \([\mathcal {S}_0,\ldots ,\mathcal {S}_P]\) are transformed into images with corresponding heights \([\mathcal {H}_0,\ldots ,\mathcal {H}_P]\), covering a total period of P. To represent the OHLC chart, we denote the stock prices at period p as \(\mathcal {S}_p=\{S_p^{open}, S_p^{low}, S_p^{high}, S_p^{close}\}\), where \(S_p^{(\cdot )}\in \mathcal {S}_p\), and the image heights as \(\mathcal {H}_p=\{h_p^{open}, h_p^{low}, h_p^{high}, h_p^{close}\}\), where \(h_p^{(\cdot )}\in \mathcal {H}_p\). The key concept here is to ensure reversibility in the pre-processing step, enabling the recovery of \(\mathcal {S}_p\) from \(\mathcal {H}_p\) within synthetic images. This is crucial for calculating returns or derivatives by estimating the proportion of price \(\mathcal {S}_p\) at period p relative to the initial price \(\mathcal {S}_0\), or correspondingly any price \(\mathcal {S}_t\) at time t. To achieve this, we fix the minimum value of the image to a fraction \(\rho \) of the initial open price \({S}_0^{open}\). With the image height \(h_p^{(\cdot )}\), we can determine the synthetic stock price ratio of \(S_p^{(\cdot )}\) to the initial price \(S_0^{open}\) as follows:

$$\begin{aligned} \frac{S_p^{(\cdot )}}{S_0^{open}} = \frac{h_p^{(\cdot )}+\rho h_0^{open}}{h_0^{open}+\rho h_0^{open}}. \end{aligned}$$
(13)

Note that the ratio \({h_p^{(\cdot )}}/{h_0^{open}}\) differs from \({S_p^{(\cdot )}}/{S_0^{open}}\). For the upper bound, we define it as the maximum value within the total periods in the image.Footnote 3 We visualized an image of pre-processed OHLC values for 21 consecutive days into a single image and its conversion to stock prices in Fig. 3b. This pre-processing mechanism can facilitate further analysis of synthetic images.

Fig. 3
figure 3

Conversion of stock charts and OHLC images

Full size image

3.2 Model Training and Image Generation

With the pre-processed OHLC chart images, we now train diffusion models to synthesize image simulations that mimic the intrinsic stock patterns in training data. As the synthetic data are probabilistically sampled from the learned model’s probability distribution, this method serves as an effective stochastic financial simulation. By noising images with Eq. (10) and updating model parameters to denoise the images similar to the original one with Eq. (11), we can obtain the trained diffusion model for generating OHLC chart images. The trained model can efficiently capture the intrinsic patterns in the training dataset and generate synthetic images mimicking the asset price dynamics.

However, some generated images do not meet the conditions of OHLC stock chart images. To address this issue, we employ the Accept-Reject method (Chib & Greenberg, 1995) with a threshold to filter out awkward simulation paths for improved decision-making in finance (Goutte et al., 2023). Specifically, we drop the images by the following conditions: (i) any column containing more than two values or empty values, (ii) open or close values falling outside the range of high and low values, and (iii) the low value exceeding the high value. We demonstrate the generated images before post-processing in Fig. 4 and after post-processing in Fig. 5. After post-processing, the images show near-perfect charts without any prior knowledge of chart patterns during training.

Fig. 4
figure 4

Generated images before post-processing of 21-day chart images

Full size image
Fig. 5
figure 5

Generated images after post-processing of 21-day OHLC chart

Full size image

3.3 Monte Carlo Simulation

Based on the law of large numbers, Monte Carlo simulation presents a simple and flexible way to value complex derivatives where analytical formulas are not feasible (Clewlow & Strickland, 1998). Instead of using specific dynamics such as GBM (Eq. (2)), we can numerically estimate the price of a call option with the multiple generated paths using a large number of Monte Carlo simulations. When combined with our diffusion models that generate synthetic simulations, we can estimate the option price without predetermined processes, where the closed-form solution, such as the analytic solution of Eq. (8) for GBM process, does not exist. Thus, we calculate the estimation of the option price \(\hat{c}\) as follows:

$$\begin{aligned} \hat{c} = \exp (-rT)\frac{1}{M} \sum _{j=1}^{M}\max (0,S_{T,j}-K), \end{aligned}$$
(14)

where \(j\in \{1,\ldots ,M\}\) with M generated paths and \(S_{T,j}\) is the price at T for simulation j. It is well known that the estimated option \(\hat{c}\) converges to the optimal option price when the simulations are sampled from the true distribution (Hull, 2003). Thus, if the trained model appropriately captures the true distribution of the underlying process, our simulation results will converge to the optimal. We highlight our strength that simulation-based option pricing does not require any underlying dynamics to calculate the option price, in contrast to Eq. (8).

4 Data and Experimental design

4.1 Data

For experiments, we generated various price dynamics with constants \(t=1\), \(\mu =0.1\), and \(\sigma \in \{0.1, 0.2\}\)Footnote 4 for GBM and \(t=1\), \(\mu =0.1\), \(\sigma =0.2\), \(v=0.3\), and \(\lambda \in \{0.1,0.2\}\) for jump processes. For OHLC modeling, we divided each GBM time step into 5 smaller steps to determine the highest and lowest prices of a period.

For our real-world application, we tested S &P 500 index European call options during two distinct periods: pre-Covid19 (July 2016 to July 2019) and post-Covid19 (January 2020 to January 2023)Footnote 5. During the training phase, we utilized three years of data, while the option pricing was tested on the final month of each period: July 2019 and January 2023. The corresponding risk-free interest rates r were set at 0.025 and 0.045, respectively. The data contained all daily call option data within these periods, and we extracted the last traded call option price with a minimum trading volume of one. As pre-Covid19 and post-Covid19 show distinct market conditions and stock price movements (Sakurai & Kurosaki, 2022), analyzing both periods can prove the robustness of the proposed methods. Table 1 provides the descriptive statistics of S &P 500 index call options for both periods, categorized by moneynessFootnote 6 and maturity.

Table 1 Summary statistics of S & P 500 index European call options by moneyness and maturity
Full size table

4.2 Experimental Design

Our evaluation comprises two phases: (i) initially, we assess whether the generative diffusion model can accurately replicate the dynamics of known price processes, such as GBM and jump processes, by estimating their mean, variance, and the corresponding option prices using Monte Carlo simulations in the Black-Scholes world. Subsequently, (ii) we leverage the generative model’s ability to discover unknown underlying dynamics on the real-world dataset of the S &P 500.

Specifically, we evaluated the ability of the generated images to capture the underlying asset dynamics present in the training OHLC chart images. We assessed the homogeneity between the distributions of the generated images and those of both GBM and jump processes. Additionally, we compared the true expectation and variance of the asset dynamics with those obtained from the generated images, varying the number of simulations and time steps for estimation. As determining the true asset dynamics is unattainable for the real-world market, we tested the effectiveness of synthetic images through option pricing. Specifically, we examined whether the model trained with the S &P 500 price data could effectively replicate the unknown asset dynamics observed in the market. Our focus was on European options, characterized by the payoff function \(C_T=\max (0, S_T-K)\) using Monte Carlo simulations in Eq. (14).

For measuring the error of S &P 500 option pricing, we used various widely used error metrics (Jang & Lee, 2019). Let the market price \(c_i^{market}\), predicted call option price \(\hat{c}_i\), and corresponding errors \(e_i=\hat{c}_i-c_i^{market}\) for i-th option.

  1. 1.

    Mean Absolute Percentage Error (MAPE), \(\frac{1}{L}\sum _{i=1}^L (|e_i|/c_i^{market})\), indicates the percentage error regardless of the option price scale.

  2. 2.

    Root Mean Squared Percentage Error (RMSPE), \(\sqrt{\frac{1}{L}\sum _{i=1}^L (|e_i|/c_i^{market})^2}\), describes the error direction while giving more penalty to larger errors of options.

  3. 3.

    Mean Absolute Error (MAE), \(\frac{1}{L}\sum _{i=1}^L |e_i|\), estimates the absolute distance of the predicted option prices to the real values.

  4. 4.

    Root Mean Squared Error (RMSE), \(\sqrt{\frac{1}{L}\sum _{i=1}^L e_i^2}\), measures the standard error of underlying option prices.

During training, we used 10,000 samples of OHLC images for each GBM and jump process and all the historical S &P index data in the training period without any historical option pricing data. For the fraction value \(\rho \) in Eq. (13), we set \(\rho =0.5\) for GBMs, \(\rho =0\) for jump processes, and \(\rho =0.66\) for S &P 500. We implemented the U-Net architecture, employing convolutional filters and residual connections as delineated in Ho et al. (2020), and minimized the score-based loss function \(s_\theta \) for 500 epochs. After a grid search, we found the best hyperparameters with a batch size of 32 and a learning rate of \(10^{-4}\) using the AdamW optimizer. Our grid search space and the best hyperparameters are presented in Table 2. We conducted all experiments using PyTorch and Python on four NVIDIA GeForce RTX 3090 GPUs.

Table 2 Hyperparameters for training diffusion models
Full size table

5 Empirical Findings

5.1 Testing the Homogeneity

Fig. 6
figure 6

Cumulative distribution and results of Kolmogorov-Smirnov test between generated images and stochastic processes

Full size image

To validate the hypothesis that the synthetic images mimic the financial movement of the training data, we first conducted a two-sample Kolmogorov-Smirnov (K-S) test. The null hypothesis of this test is that the two testing distributions are identical. We compared 1000 randomly selected examples of \(S_t\) when \(t=1\) with the simulations of stochastic processes and synthetic images generated from GBM and Jump processes. The results are shown in Fig. 6 by varying volatility \(\sigma \) and jump intensity \(\lambda \). In all settings, we find that the cumulative distributions of the real and synthetic data are almost identical. The p-values from the K-S test are 0.610, 0.314, 0.610, and 0.501, respectively. As all the p-values exceeded the threshold of 0.05 by large margins, the null hypothesis of both samples being drawn from the same distribution cannot be rejected.

Table 3 Expectation of generated OHLC simulations by varying the number of image samples
Full size table

We additionally explored the predictive capabilities of these simulations in estimating the expectation \(E[S_t]\) and variance \(Var[S_t]\) at \(t=1\) across different sample sizes \(M=100, 1000\), and 5000 of generated images, as shown in Table 3. If the trained generative models accurately replicate the distribution of the training dataset, then, by the law of large numbers, the expected values and variances in the Monte Carlo simulations will converge to their true statistics. One significant advantage of deep generative models is their capacity to generate multiple simulation paths, which effectively act as a form of compression and reconstruct multiple paths in probabilistic manners. Note that a substantial number of samples, over \(10^3\), are required for a thorough distributional estimation (Gao, 2019).

When \(M=100\), the expected mean is dislocated from the true mean and the standard deviation is large. As the sample size increased, such as \(M=5000\), we observed a convergence of the expectation \(E[S_{t=1}]\) and variance \(Var[S_{t=1}]\) toward the true statistics of the stochastic processes. This convergence suggests that the generated images possess a similar distribution to the training set. Thus, we concluded that a sample size of \(M=5000\) provides sufficiently low variance for generating OHLC chart images. This indicates that given a large number of generated image samples, the trained model can mimic the distribution of stock prices by memorizing the dynamics of underlying processes.

Table 4 Imaged-based estimation of the expectation \(E[S_t]\) and variance \(Var[S_t]\) for different time steps
Full size table

To push further, we explored the predictive capabilities of these simulations in estimating the expectation \(E[S_t]\) and variance \(Var[S_t]\) across different internal time steps \(t\in \{0.2, 0.4, 0.6, 0.8,1\}\) with generated sample size of \(M=5000\).Footnote 7 Table 4 showed that the estimated expectation and variance at these internal steps are closely aligned with the true values.Footnote 8 This implies that synthetic images can be used to estimate the price movement in any steps within images, which can be used for financial applications such as pricing options of different maturities.

5.2 Option Pricing

We now present a clear application for using generated images, which is the option pricing for the Black-Scholes world and S &P 500. As the Black-Scholes formula holds fundamental importance in option pricing, Table 5 illustrated the results of calculating call option prices in the Black-Scholes world. We trained diffusion models with OHLC images of GBM with \(\mu =0.1\) and \(\sigma \in \{0.1, 0.2\}.\) We reported the results of different simulation sizes M, as in Table 3. We calculated option prices for various interest rates r and strike prices K given an initial stock price of \(S_0=100\). We first calculated call option prices based on Eq. (14) and then multiplied \(e^{r+\sigma ^2/2-\mu }\) to convert the simulations generated from \(\sigma \) to the risk-free rate r. The results demonstrated that synthetic images accurately approximate true call option prices in all experimental settings.

Table 5 Call option pricing with GBM in black-scholes world
Full size table

We conduct a comparison of errors between the Black-Scholes formula and the image-based method for two dissimilar periods: pre-Covid19 and post-Covid19. It is known that the post-Covid19 period exhibits higher volatility compared to the post-Covid19 period (Baek et al., 2020). The experimental results are shown in Table 6. In both panels, the proposed approach exhibits superior prediction performance regardless of moneyness and maturity. Panel A demonstrates that the proposed method yields superior results across various maturity conditions in terms of MAPE, RMSPE, and MAE. The Monte Carlo simulation results, utilizing synthetic images, suggest robustness against option price scale variations, minimal percentage error, and adherence to true values. The larger RMSE may occur when synthetic images present a significant discrepancy between the initial and the corresponding stock prices, often attributable to a diminutive initial price. In Panel B, the efficacy of the proposed method is evident in high-volatility markets, where it surpasses expectations in all 12 average values. The proposed method proves to be more robust than the Black-Scholes model in various market scenarios, where the significance is amplified in volatile market conditions. Particularly, it significantly reduces the prediction error rates for scenarios involving longer maturities and greater moneyness values across both panels. Thus, experimental results of both pre-Covid19 and post-Covid19 periods confirmed that image-based option pricing predicts adequately regardless of the underlying market condition. Therefore, trained diffusion models can be used to mimic unidentifiable underlying processes in real markets.

Table 6 Prediction error for S &P 500 index call option
Full size table

Table 7 presents a comparative analysis of various deep learning models for predicting call options with a 20-day maturity. Gan and Liu (2023) identified the Residual neural network (ResNet) (He et al., 2016) as the most effective deep learning model for option pricing. We slightly modify their methods to conduct a fair comparison within our experimental context. We predict the stock prices rather than estimate option prices directly, employing multiple forecast values in a Monte Carlo simulation as described in Eq. (14). Both panels confirm the superiority of our diffusion methods over existing deep learning techniques for option pricing. As notated in Gan and Liu (2023), ResNet shows better results than Multi-Layer Perceptron (MLP), Recurrent Neural Networks (RNN), Long short-term memory (LSTM) (Graves & Graves, 2012), or Black-Scholes formula. Still, our approach exceeds baseline model performances in 11 out of 12 evaluative metrics on average. The performance gap is prominent in Panel B, highlighting the method’s robustness in high-volatility markets.

Table 7 Comparison with different deep learning forecasting models for S &P 500 index call option with a 20-day maturity
Full size table

5.3 Sensitivity Analysis

5.3.1 Effects of Training Length

Table 8 Prediction error for S &P 500 index call option using 63-day (3 month) charts
Full size table

From a methodological standpoint, we explore different settings of different lengths of days consisting of chart images. To match the size of the images, we calculate the OHLC price over three days and estimate the option price using generated images with 63-day (3 months) OHLC charts. Table 8 validates the robustness of our method trained on 63-day chart images. When trained with a larger length, Panel A demonstrates better results on MAE and RMSE, which demonstrates the difference in value rather than percentage is reduced than 21-day chart images. In panel B, 21-day chart images perform better since the market is highly volatile after Covid19, short-term images have more benefit to forecast option prices with maturity lower than 20 days. Still, the proposed method using 63-day charts outperforms the Black-Scholes formula on average.

5.3.2 Robustness on Different Measures

Table 9 Prediction error for S &P 500 index call option
Full size table

To evaluate the robustness of our proposed method across various metrics, we calculate the different measures on the option pricing for S &P 500 on two dissimilar periods: pre-Covid19 and post-Covid19 as in Table 6. Additional employed measures are as follows:

  1. (a)

    Mean Bias Error (MBE): The average values of the predicted relative errors.

  2. (b)

    Median Bias Error (MedBE): The median values of the predicted relative errors.

  3. (c)

    Mean Bias 99 (MBE\(_{99}\)): The average values of the predicted relative errors that are less than the 99% quantile.

  4. (d)

    Pearson Correlation Coefficient (PCC): The linear correlation between the known prices and the predicted prices.

For MBE, MedBE, and MBE\(_{99}\), we consider the absolute values, represented as |MBE|, |MedBE|, |MBE\(_{99}\) \(|\), which effectively indicate their distance from zero. Table 9 presents these results, with Panel B illustrating our method’s superior performance across all metrics in the post-Covid19 market condition. In Panel A, the proposed method outperforms on |MBE|, |MedBE|, |MBE\(_{99}\) \(|\). Similar to the RMSE observations in Table 6, which noted some values with extreme prices, PCC demonstrates a lower linear correlation compared to the Black-Scholes model. These experiments affirm the robustness of our method over various metrics.

6 Concluding Remarks

In conclusion, our empirical analysis confirms that the use of generative diffusion models with OHLC images successfully imitates the dynamics of asset price processes, including distribution homogeneity and statistical variables. Moreover, we demonstrate the ability to predict option prices for S &P 500 call options through simulations, by capturing the underlying market price process.

From an academic perspective, our study demonstrates the usage of generative diffusion models in mimicking price trends for unknown market trends. This will help the researchers to find better modeling of the asset price processes. From an investment perspective, our framework enables us to leverage generative networks for forecasting stock prices and predicting options, futures, and other derivatives.

As the primary focus is to investigate the dynamics of asset price processes, we have a limitation of lacking generation depending on time stamps or other market conditions. When combined with text-conditioned foundational models such as DALL·E 2 and ChatGPT, our method can be extended to condition stock generation according to texts depicting market conditions.