1 Introduction

As widely known, the term structure of interest rates depicts the relationship between different times to maturity and the interest rate. Its graphical companion is the yield curve, that plots the interest rates of bonds with equal credit quality at different maturities: its shape and time changes are conventionally considered a key indicator for the economic outlook of a country (Chadha et al., 2014).

The yield curve can be used to represent either spot rates, that is the yield associated to a zero-coupon bond from now to maturity, or forward rates, that is the yield of a zero–coupon bond between two future dates. Indeed, the yield curve plays a valuable role as alerting tool for inflation, possible recession or upturn of the economy (Gürkaynak & Wright, 2012); additionally it can be employed to target and manage monetary policy operations. Furthermore, the knowledge of the yield curve dynamics is essential also in the actuarial practice and it represents an important component for the implementation of International Accounting (IAS) and Financial Reporting (IFRS) Standards. Due to this pivotal role, the development of proper modeling techniques suitable for both stable and turbulent periods is of great importance for different market players.

Over the past decades various methods have been suggested to analyze, fit and predict the yield curve. Actually the most popular models are those in the so–called Nelson–Siegel (NS) family, pioneered by Nelson and Siegel (1987) and since then by Bliss (1996) who discussed an extension with an additional decay parameter, Svensson (1994) with a four–factor model including a further curvature term and De Rezende and Ferreira (2008) introducing a five–factor model with two slope terms instead of only one. A dynamic version of the NS model was then suggested by Diebold and Li (2006) who considered parameters as time–varying latent factors to achieve a more effective forecasting of the yield curve. Further attempts to increase the flexibility of NS models are described in Koopman et al. (2007), who examined time–varying factors loading and volatility, Christensen et al. (2007, 2009) who introduced the new class of Affine Arbitrage–free Dynamic Nelson–Siegel models and in Ullah (2017) who discussed time–varying asymmetric volatility. The fitting and forecasting abilities of NS models have been also studied in De Pooter et al. (2010) and Fernandes and Vieira (2019) whose models also include the interaction between the yield curve and the economic system.

For what it concerns empirical studies, there are plenty of works dealing with the use of the above parametric models both for in–sample fitting and out–of–sample forecasting of the yield curve: Linton et al. (2001) analyzed the U.S. bond market, Chou et al. (2009) compared the modeling performances of different parametric models for Taiwan Government Bonds, Hoffmaister et al. (2010) examined a dynamic parametric representation of the Central and Eastern European Countries yield curves, Kang (2012) forecasted the term structure of Korean Government bond yields with various types of dynamic parametric models, Gogas et al. (2015) investigated the abilities of parametric and machine learning methods to predict the U.S. GDP and Treasury Bills, Lorenčič (2016) and Nagy (2020) analyzed the estimation abilities of parametric models on the Austrian and the Hungarian term structures with missing data, respectively. Finally, Luo et al. (2021) fitted and predicted U.S. Treasury yield curves using the Dynamic Nelson–Siegel Model with random level shift parameters, Idilbi-Bayaa and Qadan (2021, 2022) analyzed and predicted the dynamic linkage amidst the U.S. term structure and commodity prices, while Umar et al. (2022) applied NS models to the countries in the Group of Seven to investigate the risk transmission mechanism.

The overwhelming majority of the above studies focused on economies with enhanced resilience to economic downturns and relatively stable term structure dynamics, i.e. absence of spikes or drops in the level of interest rates. Additionally, such a "favourable" modeling context encouraged the development of methodological frameworks characterized by constant decay–terms, (i.e. sub–optimal parameters), for yield curve estimation and prediction. In fact this popular choice simplifies the models optimization process and the forecasting procedure as well. Nevertheless, it is a good compromise to ensure satisfying fitting performances with relatively low computational efforts.

However, such an approach may lead to inconsistent results when applied to markets that show a volatile behavior, as the models would result in a lack of flexibility and ability to approximate complex shapes thus causing, as a consequence, poor predictions. This is especially true in the case of emerging markets since their yield curves are characterized by frequent trend inversions, jumps and/or falls, especially during market turmoil. Therefore, parametric models that exploits the benefits of optimal estimated parameters could ensure stable results and improve the overall models performance.

Our work nests in the above debate and tries to contribute to the literature by introducing a methodology that makes use of optimal time–varying decay factors and parameters for parametric factor models that can be employed for an effective in–sample fitting and out–of–sample forecasting of yield curves. The proposed framework was evaluated in the context of different emerging markets. The rationale arises because various studies highlighted that those markets are more sensitive to both endogenous and exogenous shocks (Chiţu & Quint, 2018; Bhattarai et al., 2021), thus representing the ideal context to assess and validate the modeling power of the proposed framework. In our opinion, the use of optimal decay terms and parameters endows these models with necessary flexibility to manage the challenging dynamics characterizing these markets.

Existing contributions related to emerging economies so far were oriented either to model (e.g. Zoricic and Orsag, 2013; Petousis and Barr, 2016; Chouikh et al., 2017; Lartey and Li, 2018; Lartey et al., 2019; Ertan et al., 2020) or to predict (e.g. Caldeira et al., 2016; Poghosyan and Poghosyan, 2019) the term structure of single countries. This approach has an evident drawback since it is not necessary true that the same methodology is still good for more than a country.

The scope of our research is therefore twofold: on the one hand we discuss the use of optimal factors and parameters for models in the Nelson–Siegel Family and test their capabilities outside the comfort zone of developed and stable markets; on the other hand we provide a comprehensive study focused on in–sample modeling at first, and then on out–of–sample predictions in order to asses the overall effectiveness of the proposed methodology.

In this respect, our paper contributes in several ways. First, within the dynamic framework discussed in Diebold and Li (2006), we use both the Three Factor Dynamic Nelson–Siegel (3F–DNS) and the Five Factor Dynamic De Rezende–Ferreira (5F–DRF) models and we discuss an estimation technique based on time–varying decay factors that leads to significant enhancements of both models fitting abilities. Furthermore we focus on the forecasting issue and suggest an approach overcoming the well–known trade–off between the stability of factor models’ parameters and the optimal decay terms. In general, it has been noted that in the forecasting task optimal dynamic decay terms cause high fluctuations in parameters values. To avoid this issue, we use various either auto–regressive or machine learning techniques as local data generating processes based on the optimal parameters time series derived in the in–line fitting step; the so–obtained values are then employed for day–ahead predictions. In this way we give greater emphasis to the information content of the period close to that of forecast. This approach allows also to considerably reduce the volatility of predictions which may result from the use of considerable amounts of data given the characteristics of emerging markets. In detail, we focused on: the Univariate Autoregressive process AR(1), the Trigonometric Seasonal Box–Cox Transformation with ARMA residuals Trend and Seasonal Components (TBATS) and the Autoregressive Integrated Moving Average (ARIMA) that we combined to a Nonlinear Autoregressive Neural Network (NAR–NN). To the best of our knowledge, this study is the first to test the potentials of combining factor models to TBATS and ARIMA–NARNN models with the purpose of forecasting the term structure of interest rates.

Finally, we run our analysis on a pool of 5 countries, that is Brazil, Russia, India, China and South Africa, considering a wide time span of at least 10 years of daily observations thus including global shocks and the most recent financial crises. This offers a breeding ground for the stress-testing of the proposed framework.

The remainder of the paper is organized as follows. Section 2 describes materials and models and it is divided into three parts: a part presenting the data employed in the simulation; a part introducing the 3F–DNS and 5F–DRF models and after that the approach followed to estimate each models parameters. In Sect. 3 we discuss the fitting results, while Sect. 4 discusses the forecasting of the BRICS yield curves. Section 5 closes the paper with final remarks and outlooks to address further research.

2 Materials and Models

2.1 Data

The data set in use consists of daily spot rates for the government zero–coupon bonds (ZCB) of Brazil, Russia, India, China and South Africa, i.e. the so–called BRICS. We examined maturities in the range from 3 months (i.e. 0.25 of the year) to 30 years. The data were collected from Thomson Reuters Datastream (TRD) and the Central Bank of the Russian Federation (CBR). The observation period is not homogeneous for the examined countries; starting points are 09/2011 for Brazil, 01/2003 for Russia, 02/2012 for India, 01/2005 for China and 02/2011 for South Africa; on the contrary, the ending period, 09/2022, is common to all markets. As a consequence, the sample period ranges between a minimum of 10 and a maximum of 19 years, depending on the examined market, for an overall amount of 2557 observations for Brazil, 4995 for Russia, 2631 for India, 4234 for China and 2908 for South Africa. We examined daily data to ensure richer market information, which can be beneficial for predicting short/medium–term bonds and provide market players with valuable insights for bond trading strategies or portfolio risk management. Moreover, focusing on daily rates provides a more detailed idea of the term structure trends and dynamics, which could be helpful for an extensive market analysis from a historical–economic perspective.

In Tables 7, 8, 9, 10 and 11 in Appendix A, we present the main descriptive statistics of each markets dataset. For each maturity the tables report the Mean, the Standard Deviation (SD), the Minimum (Min), the Maximum (Max) the Skewness, the Kurtosis and Autocorrelation coefficients values. The results indicate the presence of some common stylized facts in all the considered markets: the average yield curves have an upward sloping trend, long rates are less volatile than shorter ones, and strong persistence is observed across short, medium and long–term rates. Additionally, the data show that kurtosis of long–term rates is higher than that of short rates indicating a higher probability of outliers.

The time span was chosen to include critical situations such as global shocks and events like the Subprime Mortgage crisis of 2007–2009 and the consequent Great Recession, the 2015–2016 Chinese stock market crisis as well as the oil and pandemic turmoil of 2020 and the more recent geopolitical crisis of 2022 induced by the conflict in Ukraine. Those events had a significant impact on BRICS securities market and caused extreme dynamics in the yield curve behavior as it is evident from Fig. 1 where we plot the term structures 3D surface for each market obtained varying both the time (on x–axis) and the maturity (on the y–axis). The Euro Zone (EU) term structure surface is also shown for benchmarking purposes. Given the same historical time frame and market events, it can be noted that the EU surface is overall flatter and less volatile.

Furthermore, the 3D surface plot makes possible to highlight all the yield curve shapes occurring in the period, that is almost all typical patterns: the normal trend, upward sloping and concave, indicating a quite stable economic outlook; the flat behavior, with short–term rates similar to medium and long–term ones, indicating a possible slowdown of the economic system; the inverted curve, with short–term rates higher than long–term ones, usually interpreted as a signal for recession; and the S–shaped curve characterized by sudden and marked multiple changes in the level, slope and curvature, indicating markets’ uncertainty about economic conditions, inflation, or monetary policy.

Fig. 1
figure 1

From top to bottom in clockwise sense, the yield curve surface for Brazil, Russia, India, China, South Africa and Euro Zone. Time is represented on the x–axis, while the tenor (expressed in fractions or multiples of the year) is on the y–axis and the yield on the z–axis

Full size image

Examining, for instance, the Russian bond market shown in Fig. 1, it is possible to observe the absence of structural changes and shocks from mid–2003 up to early 2008, as well as from 2010 to 2014 and, more recently, from 2016 till 2020, with average yield values at different maturities in the range 4.88–8.44% and curve shapes mostly upward or flat. However, these conditions are broken by unstable periods characterized by greater volatility and the presence of relevant jumps for all maturities, as it can be also seen in Fig. 2a.

Fig. 2
figure 2

Plot of the daily rates setting the maturity to 1, 3, and 10 years (a) and yield curve shapes (b) extracted from the Russian term structure 3D surface. Time is represented on the x–axis, while the tenor (expressed in fractions or multiples of the year) is on the y–axis and the yield on the z–axis

Full size image

The plot shows three slices of the Russian yield surface of Fig. 1, i.e. three time series extracted at the maturities 1, 3 and 10 years. In all the three cases it is possible to highlight instability patterns that can be indicative of the presence of structural breaks. To statistically validate the presence of these breaks and determine their number as well as the most probable time the break points occurred, we run the sequential Bai and Perron (2003) Test for multiple structural breaks summarizing the obtained results in Table 1. In Panel A of Table 1 we reported the supremum F Statistic (supF) results of the performed sequential testing of \(H_{0}:b\) breaks versus \(H_{1}:b+1\) breaks applying the approach outlined by Bai (1997) and Bai and Perron (1998, 2003). In Panel B we provided the number of break points, dates and the associated confidence intervals.

Table 1 Panel A shows the results of the Hypothesis Test for a different number of break points (b).
Full size table

The test identified four break dates at the 95% significance level. For the purpose of our analysis we considered the three most relevant dates, i.e. the 1st, the 3rd and the 4th, as the ones associated to the most volatile periods. The first break point is estimated to the end of July 2008 and it roughly coincides to the events of the period August 2008–May 2010 which are a kind of follow–up of the recession due to the Subprime crisis, where a growth of approximately 11% on short–term rates and 7–9% for longer maturities took place.

The other two breaks we examined relate to two unstable situations occurred in the period April 2014–July 2015 and, more recently, from May 2021 to June 2022, with rates increments in the range 7–12% and 4–8% respectively across all maturities. This spiky behavior sinks its roots in both the 2014 and 2022 crisis which opposed the Russian Federation and the Western countries and brought to economic and trade sanctions, combined to the weakening of the Russian National currency. In both the occasions, the Central Bank of the Russian Federation increased interest rates and adopted policies like inflation targeting and the floating exchange rate regime to support the banking sector and the national currency against external shocks. Such periods of political and economic tension led, as a consequence, to extreme yield curves behaviour. This is evident from Fig. 2b. Here we illustrate yield curves at various times highlighting in red the flat and the inverted behavior that occurred in correspondence of the above described events.

Considering, ceteris paribus, the Euro Zone case illustrated in Figs. 1 and 3, it is possible to pinpoint that spot rates across the maturity spectrum are less volatile and that the level of spot rates is 3 to 10 times lower: peaks do not exceed the 5% threshold or in some occasion are even negative. These facts indicate an overall higher resistance to exogenous shocks due to higher confidence of the markets and its participants in the macro–economic and financial structure and stability of the EU.

Fig. 3
figure 3

Euro Zone daily rates setting the maturity to 1, 3, and 10 years

Full size image

In the light of all the above, it clearly emerges that economic and geopolitical crises exert significant pressure on bond markets of emerging countries which seem to be less "immune" to shocks than more developed economies. This, in turn, supports the rationale that it could be not appropriate to extend modeling methods with constant terms, usually employed in stable markets, to more turbulent ones.

As financial turmoils are frequent events in emerging markets, we can reasonally extend to other markets in the sample the remarks discussed in the case of Russia.

2.2 Models

The Nelson–Siegel model (3F–NS) is a parsimonious three–factor parametric model which has proved to capture a wide range of monotonic, humped and S–type yield curve shapes.

Let us consider a Zero–Coupon Bond (ZCB) and denote by y(t, m) the observable rate at time \(t = 1, 2, \ldots , T\), where T is the number of available observations, and maturity \(m \in M=(m_1, m_2, \ldots , m_N)'\) representing either a fraction or a multiple of the year, with N being the maximum number of examined maturities. Following Nelson and Siegel (1987), the interpolated spot value at time t can be represented via the parametric function:

$$\begin{aligned} NS(t,m,\varvec{\beta },\lambda )=\beta _0+\beta _1\left( \frac{1-e^{-\lambda \,m}}{\lambda \, m}\right) +\beta _2\left( \frac{1-e^{-\lambda \, m}}{\lambda \, m}-e^{-\lambda \,m}\right) + \eta _m \end{aligned}$$
(1)

where \(\varvec{\beta } = (\beta _0,\beta _1,\beta _2)'\) is the parameters vector whose components represent, respectively, the impact of the constant long–term component (\(\beta _0\)) that moves the curve up or down; the contribution of the short–term component (\(\beta _1\)) controlling the curve slope, and the effect of the medium–term component (\(\beta _2\)), ruling out the magnitude and direction of the yield curve curvature. The model includes also a decay term \(\lambda \) which controls the convergence speed of the exponential components and determines the position of the peak of the medium–term element, while \(\eta _m \sim \mathcal {N}(0,\,\sigma ^{2}_{m}\)) is the normally distributed error term with \(cov(\eta _r,\eta _s)=0\), for all \(r,s=m_1,\ldots ,m_N,\,r\ne s\).

A proper calibration of \(\varvec{\beta }\) and \(\lambda \) makes possible an effective replication of a wide variety of yield curve shapes. Parameters estimation is the result of a two–step procedure, where grid search methods (Nelson & Siegel, 1987; Muthoni et al., 2015) identify the value of \(\lambda \) that maximizes the medium–term component, varying the maturity. For each \(\lambda \) the vector of parameters \(\varvec{\hat{\beta }}\) is then estimated through an OLS regression choosing in the end the values \(\lambda ^*\) and \(\varvec{\hat{\beta }^*}\) associated to the highest coefficient of determination.

Later, De Rezende and Ferreira (2008) introduced a five–factor variant (5F–RF) aimed at increasing the flexibility of previous models with additional parameters and decay factors to capture a wider variety of trends. The 5F–RF model, in fact, extends (1) including additional short and medium–term components characterized by different decaying factors, to ensure a faster decaying rate and to increase the fitting ability of yield curve shapes in presence of multiple short–term maxima/minima:

$$\begin{aligned} \begin{aligned} RF(t,m,\varvec{\beta },\varvec{\tau })&= \beta _0 + \beta _1\left( \frac{1-e^{-m/\tau _1}}{m/\tau _1}\right) +\beta _2\left( \frac{1-e^{-m/\tau _2}}{m/\tau _2}\right) +\\&+\beta _3\left( \frac{1-e^{-m/\tau _1}}{m/\tau _1}-e^{-m/\tau _1}\right) +\beta _4\left( \frac{1-e^{-m/\tau _2}}{m/\tau _2}-e^{-m/\tau _2}\right) + \eta _m \end{aligned} \end{aligned}$$
(2)

where \(\varvec{\beta }=(\beta _0,\beta _1,\beta _2,\beta _3,\beta _4)'\) and \(\varvec{\tau }=(\tau _1,\tau _2)'\) are the 5–dimension parameters vector and the decay terms vector, respectively. The estimation of both \(\varvec{\tau }\) and \(\varvec{\beta }\) is based on a two–step procedure that at first identifies the optimal decay parameters \({\hat{\tau }_1}\), and \({\hat{\tau }_2}\) in the space \(\Omega \) of admissible values, by minimizing the Root Mean Square Error (RMSE):

$$\begin{aligned} \varvec{{\hat{\tau }}}=\left( {\hat{\tau }}_1\ ,{\hat{\tau }}_2\right) '= \underset{({{\tau }}_{1},\ {{\tau }}_{2})~\in ~{{\Omega }}}{arg\ min} \left\{ \dfrac{1}{N}\sum _{n=1}^{N}\sqrt{\dfrac{1}{T}\sum _{t=1}^{T}[y(t,m_n) - {\widehat{RF}}(t,m_n, \varvec{\tau }, \hat{{\varvec{\beta }}_t} ) ]^2} \right\} \end{aligned}$$
(3)

where N is the overall number of examined maturities, and T is the number of available observations. Once obtained the optimal vector \(\varvec{\hat{\tau }}\), the estimation of the parameters vector \(\varvec{\hat{\beta }}\) takes place by applying the OLS regression for each time t.

2.3 Optimal Parameters Estimation

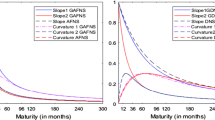
As seen in the previous section, the parameters \(\lambda \) and \(\varvec{\tau }=(\tau _1,\tau _2)'\) play a fundamental role in the 3F–NS and 5F–RF models respectively, because they drive the decay rate of the exponential components controlling the trend dynamics of the fitted yield curves. The choice of \(\lambda \) and \(\varvec{\tau }\) generates a trade–off in the fitting accuracy at both the left and right–handed tails of the yield curve. In fact, small values of \(\lambda \) (big values of \(\tau _1,\tau _2\)) lead to a slow decay of the curve, and hence assure a better fit at longer maturities, but the same is not true at short maturities, especially in presence of sudden and marked curvatures. Conversely, higher values of \(\lambda \) (small values of \(\tau _1,\tau _2\)) result in a quick decay and hence a better fit at short maturities, with an accuracy loss in the long run.

Managing the decay parameters is therefore of paramount importance, as testified by the solutions suggested in the literature. A common approach consists in setting them to the value that maximises the curvature factor at the maturity m where humps or basins are empirically observed. For example, working on U.S. Treasury data, Diebold and Li (2006) and De Pooter (2007) set \(\hat{\lambda }= 0.0609\) (\(m=30\) months), while Diebold et al. (2006) assumed \(\hat{\lambda }=0.077\) (\(m= 23.3\) months). Moreover, Muvingi and Kwinjo (2014) assumed \(\hat{\lambda }=0.25\) (\(m= 7\) months) for the Bank of Zimbabwe certificates, while De Rezende and Ferreira (2008), based on ID–PRE Swap data of the Brazilian market, set \(\hat{\tau }_1\) and \(\hat{\tau }_2\) at the best of the estimated values according to (3). This latter approach simplifies the numerical optimization process as it linearizes the estimation process of the model with the use of the least–squares regression; in addition, it seems to reach a good compromise between the long and short–run accuracy issues. However assuming constant decay terms is in conflict with the evidence that the term structure of interest rates may show time changes of different intensity in terms of both slope and curvature as observed for all the BRICS (see Fig. 1): an a priori selection of either \(\lambda \) or \(\varvec{\tau }\) can therefore lead to non–optimal estimations, weakening the models fitting ability.

For the above reasons, we adopted a different approach, and we considered the decay components as time–varying parameters as well. We applied a two–step estimation procedure to determine the proper values \({\lambda ^*}(t)\), \({\tau _1^*}(t)\), \({\tau _2^*}(t)\) and \(\varvec{\hat{\beta }}^*(t)\) such that the complete sets of parameters in both the three and five factor cases (herein after named 3F–DNS and 5F–DRF respectively) are at the best for each time t.

For the 3F–DNS model, the algorithm is organized into three steps:

  1. Step 1:

    For each market define the set \(\varvec{M}\) = \(\{m_{k}\}_{k = 1,\ldots ,N}\) of maturities \(m_{k}\) with N equal to the sets cardinality. In particular, \(m_{1} = m_{L}\) is the lower bound of \(\varvec{M}\) and corresponds to the first available maturity in the market, while the upper bound \(m_{U}\) is the longest observed maturity. Values in \(\varvec{M}\) ranges between corresponding lower/upper values by proper step size \(\Delta \).

  2. Step 2:

    For each \(m_k\in \varvec{M}\) with \(k = 1, \ldots , N\), estimate at time t the value \(\lambda ^*_{k}(t)\) that maximizes the curvature term component:

    $$\begin{aligned} \dfrac{1-\ e^{-\lambda (t) m_k}}{\lambda (t) m_k} - e^{-\lambda (t) m_k}, ~~~~~ k = 1, \ldots , N \end{aligned}$$

    In this way, at each time t it is possible to associate the array \(\varvec{\hat{\lambda }}(t)\) = \(\{\lambda ^*_{k}(t)\}_{k = 1,\ldots ,N}\).

  3. Step 3:

    For each time \(t=1,\ldots ,T\):

    1. i)

      use each component of the array \(\varvec{\hat{\lambda }}(t)\) found in Step 2 to estimate the parameters vector \(\varvec{\hat{\beta }}(t)\) via the OLS regression. Clearly there are as many vectors of parameters as the number of \(\varvec{\hat{\lambda }}(t)\) components;

    2. ii)

      choose the vector \(\varvec{\hat{\beta }}^*(t)\) associated to the lowest Sum of Squared Residuals (SSR):

      $$\begin{aligned} SSR(t) = \displaystyle {\sum _{k=1}^{N}}[y(t,m_k) - \widehat{DNS} (t,m_k,\varvec{\hat{\beta }}(t),{\lambda ^*_k}(t)]^2 \end{aligned}$$
    3. iii)

      repeat steps (i) – (ii) for each time t to get the time series of the parameter \({\lambda }^*(t)\).

For what it concerns the 5F–DRF model the estimation procedure is similar to that discussed for the 3F–DNS, although a bit more tricky, due to the presence of two decay factors (\(\tau _1\) and \(\tau _2\)) at each time instead that only one. In this case, the procedure works as follows:

  1. Step 1:

    For each market define the set \(\varvec{M}_j\) = \(\{m_{j,k}\}_{k = 1,\ldots ,N_j}\) of maturities \(m_{j,k}\) with \(j=1,2\) and \(N_j\) equal to the sets cardinality; \(m_{1,1} = m_{1,L}\) represents the lower bound of \(\varvec{M}_1\) and corresponds to the first available maturity of the market, while the upper bound \(m_{1,U}\) is, at the same time, the lower bound of \(\varvec{M}_2\) (\(m_{1,U} = m_{2,L}\)) and it is equal to the straddling maturity between the short and medium–term period. Finally, the upper bound of \(\varvec{M}_2\) (\(m_{2,U}\)) is the longest observed maturity. As above, values in \(\varvec{M}_1\) and \(\varvec{M}_2\) range between corresponding lower/upper values by proper step sizes \(\Delta _1\) and \(\Delta _2\).

  2. Step 2:

    For each \(m_{j,k}\in \varvec{M}_j\) with \(k = 1, \ldots , N_j\) and \(j = 1,2\) estimate the vectors \(\varvec{\hat{\tau }_{1}}(t)\) and \(\varvec{\hat{\tau }_{2}}(t)\) that maximize the curvature term components:

    $$\begin{aligned} \dfrac{1-e^{-m_{j,k}/\tau _j(t)}}{m_{j,k}/\tau _j(t)}-e^{-m_{j,k}/\tau _j(t)}, ~~~~~ k = 1, \ldots , N \end{aligned}$$
  3. Step 3:

    For every \(t=1,\ldots , T\):

    1. i)

      for each component of \(\varvec{\hat{\tau }_{1}}\), vary the components of \(\varvec{\hat{\tau }_{2}}\) to estimate by OLS regression different array sets \(\varvec{\hat{\beta }}(t)\) choosing the one with the lowest Sum of Squared Residuals (SSR) computed as the squared difference between the observed and estimated rates:

      $$\begin{aligned} SSR(t) = \displaystyle {\sum _{n=1}^{N}}[y(t,m_k) - \widehat{DRF} (t,m_k,\varvec{\hat{\beta }}(t),\varvec{\tau }(t)) ]^2 \end{aligned}$$

      Clearly there are as many sets of optimal parameters as the number of \(\varvec{\hat{\tau }_{1}}\) components;

    2. ii)

      choose the optimal set of parameters \(\varvec{\hat{\beta }}^*(t)\) associated to the lowest SSR.

    3. iii)

      repeat steps (i) – (ii) for each time t to get the time series parameters of both \({\tau }^*_{1}(t)\) and \({\tau }^*_{2}(t)\).

3 Discussion of the Fitting Results

The study was carried on using the routines of the R package DeRezende.Ferreira (Castello & Resta, 2019), developed by the authors and freely available at the Comprehensive R Archive Network (CRAN) repository.Footnote 1

3.1 Optimal vs. Constant Decay Factors

In this subsection we provide empirical evidence of the advantages deriving from the use of optimal time–varying decay parameters. In detail, we are going to corroborate the assertion made in the introduction that is inserting constant terms in the models of the Nelson–Siegel family can lead to weaker performances on turbulent markets essentially due to lack of flexibility.

Table 2 for the 3F–DNS and Table 3 for the 5F–DRF compare for each country the Average Coefficient of Determination (\(R^2\)) obtained according to three distinct approaches: (i) employing the optimal values computed through our estimation procedure; (ii) using constant decay terms as suggested in Diebold and Li and in De Rezende and Ferreira for the three and five factor models, respectively; (iii) using constant parameters equal to the optimal decay parameters average values.

Table 2 Comparison of the average \(R^2\) in the 3F–DNS model associated to the estimation of the optimal \({\lambda }^*(t)\) values (second column), constant \(\lambda \) value (third column) and average value (fourth column)
Full size table

Analyzing the results it sticks out to eyes that the choice of optimal decay terms (second column in Tables 2 and 3) returns an increase in the degree of the fitting accuracy of both models for every BRICS country. In fact, if we consider the results for the 3F–DNS model in Table 2 the \(R^2\) values are on average 3.90% better than those obtained with constant \(\lambda \) (the lowest increase is 1.22% for Brazil and the highest is 8.03% for China). Furthermore the results with our technique are also higher than those obtained using \(\lambda \) average values: the appreciation of the \(R^2\) ranges from 1.13% for China to 4.62% for South Africa.

Table 3 Comparison of the average \(R^2\) for the 5F–DRF model using optimal \(\varvec{\tau ^*_1}(t)\), \(\varvec{\tau ^*_2}(t)\) values (second column), constant values (third column) and average values (fourth column)
Full size table

Similar remarks hold also when we turn on Table 3 and we analyze the 5F–DRF model. In this case the average improvement with respect to keep \(\tau _{1}\) and \(\tau _{2}\) constant is 1.55%, with the minimum (+0.1%) for South Africa and the maximum (+4.50%) for Russia. In addition, when comparing the results in columns 2 and 4 we observe that time–varying parameters \(\tau _{1}(t)\) and \(\tau _{2}(t)\) make it possible to get higher \(R^2\) values with an average increase of +1.51%; the minimum increase (+0.1%) is associated to South Africa and the highest (+4.50%) is recorded for Russia.

To gain a better intuition of these results, Fig. 4a for the 3F–DNS and Fig. 5a for the 5F–DRF models respectively plot the most complex curve shapes observed for each countries bond market; the aim is to highlight the fitting abilities of the three and five factor models under different choices of the decay parameters. Furthermore, Figs. 4b and 5b compare the average MSE generated by each model according to the approaches (i) to (iii).

Fig. 4
figure 4

Observable and fitted yield curves a with the 3F-DNS model using different \(\lambda \) values in some sample days indicated within round brackets. Black line is associated to the observed yield curve (YC) while red, blue and green are associated to the fitting with optimal time–variant, constant and averaged \(\lambda \) respectively. In b we provide the MSE curve generated by the three estimation approaches

Full size image
Fig. 5
figure 5

Observable and fitted yield curves a with different \(\tau _{1}\) and \(\tau _{2}\) values in the 5F–DRF case in some sample days indicated within round brackets. Black line is associated to the observed yield curve (YC) while red, blue and green are associated to the fitting with optimal time–variant, constant and averaged parameters respectively. In b we plot the MSE curve generated by the three estimation approaches

Full size image

From the analysis of the plots it clearly turns out that time–variant \(\lambda \) and \(\varvec{\tau }\) bring additional flexibility to the examined models. The fitting improves moving from constant (blue) to average (green) and time–variant (red) parameters: the red–colored line in fact, is almost always overlapping to the black one representing the observed yield curve. On the contrary, constant \(\lambda \) and \(\varvec{\tau }\) values make harder the fitting especially with much cumbersome curves like those of the BRICS markets. Similar conclusions can be drawn by looking at the plots reporting the behavior associated to the MSE curves generated by the three estimation approaches: lower values are always associated to the estimations obtained with time–variant \(\lambda \) and \(\varvec{\tau }\).

We can therefore preliminary assert that our framework assures a better in–sample fit as it endows the parametric models with the necessary modeling power to cope with the challenging dynamics of emerging countries yield curves.

3.2 In–Sample Fitting Performance Analysis

The results of the comparison between the three and five factor models are firstly presented in terms of average fitted spot rates per maturity, plotted in Fig. 6 for each country and model.

Overall, the 3F–DNS (blue) and 5F–DRF (red) estimated curves are almost perfectly matching to the observed (black) ones. The 3F–DNS model, however, exhibits some overestimation issues in correspondence of the medium–term maturities as can be seen in the Russian and Chinese cases with the estimated curve lying slightly above the observed one, and underestimation in the long term which are particularly evident in the Indian, Chinese and South African markets with the blue curve going under the observed one; on the contrary when using the 5F–DRF model a slight over (under)–estimation is present in the middle (final) section of the curve only in the case of the Indian market.

Fig. 6
figure 6

Comparison of average observable yield curves (black) with average yield estimates obtained with the 3F-DNS (blue) and 5F-DRF (red) models

Full size image

We have also calculated the Average Squared Error, given as the difference between the observed and fitted average yield curve values. Both models performed very well: error values span from a minimum of \(7.01\times 10^{-5}\) (Brazil) to a maximum of \(1.02\times 10^{-3}\) (South Africa) for the 3F–DNS model, and from a minimum of \(2.15\times 10^{-7}\) (Russia) to a maximum of \(6.80\times 10^{-5}\) (India) for the 5F–DRF model.

Furthermore, we analyzed the models fitting ability using some well–known goodness of fit indicators: the Coefficient of Determination (\(R^2\)), the Mean Square Error (MSE) and the Root Mean Square Error (RMSE). The \(R^2\) was obtained as the result of the parameters estimation process via the Ordinary Least–Squares (OLS) method and was computed for each period t. Using the residuals generated by the OLS we then computed the MSE and RMSE metrics for each yield curve as well, hence obtaining the related time series which are plotted in Appendix 8. The main statistics of the three metrics are shown in Table 4. Here we reported the Mean, the Standard Deviation, the Minimum and the Maximum values for each indicator, model and country. Additionally, in order to give a more granular view of the models performances, we determined the average MSE and RMSE generated by the 3F–DNS and 5F–DRF models at each maturity for every country and we summarized the results in Table 5.

A first look at Table 4 reveals that (I) both the competing models performed well: they generated, on average, low error values, thus ensuring over the 97.4% and 99.7% of modeling accuracy for the 3F–DNS and 5F–DRF, respectively; and (II) the 5F–DRF achieved, on average, the best approximation results.

Nevertheless, Table 5 and Fig. 8 provide a more detailed insight into the models’ fitting ability and highlight the differences in approximation accuracy among the models. In this context, looking at Fig. 8, it can be noted that both the 3F–DNS and 5F–DRF provided MSE (RMSE) values of very small magnitude with highest spikes in the range [0.04, 1.18] ([0.02, 1.08]); furthermore, with regard to the MSE (RMSE) metrics summarized in Table 5 it can be highlighted that the range of variation of the worst outcomes lies between [\(10^{-3}\),\(10^{-2}\)] ([\(10^{-2}\),\(10^{-1}\)]). These results lead to the conclusion that both models were able to preserve the yield curve shapes, avoiding unreasonable under/over estimation issues, hence confirming the capability to fit the wide variety of shapes exhibited by the BRICS yield curves under various market statuses.

However, deepening the analysis it can be pointed out that the 3F–DNS model presents larger error values with respect to the 5F–DRF in all the examined countries. Consider for instance the MSE and RMSE metrics time series of Fig. 8: it is possible to notice that the 3F–DNS produced higher error peaks along the whole data sample, especially during turbulent periods. This is probably due to the well–known difficulties of the 3F–DNS model (Wahlstrøm et al., 2021) to fit more dynamic yield curve behavior, i.e. twisted and/or humped shapes, induced by the models lower flexibility.

With regard to the five–factor model, results strongly indicate that the enhanced models flexibility improves the curve adjustment in all the considered markets as well as also during higher market volatility. As depicted in Tables 4 and 5, in fact, the 5F–DRF model has superior performances not only in the time domain, but also in the maturity domain. In detail, the data show that the model generated the lowest MSE and RMSE values, achieving a significant improvement over the 3F–DNS model as well: in fact, based on Table 4, for each country we can observe a reduction of the MSE ranging between a minimum of 84.34% and a maximum of 98.99% for China and Brazil, respectively; if we consider the average results for each country and maturity (see Table 5) we detect a reduction of the MSE by a factor of 10 to 1000.

In the light of the above outcomes it is possible to state that both models with time–varying parameters are adequate tools for yield curve modeling when applied to developing countries whose bond market has more complex dynamics, especially during market turmoil. However, the 5F–DRF performs better since it benefits of improved flexibility due to both time–variant decay parameters and additional slope and curvature terms.

Table 4 Comparison of \({R^2}\), MSE and RMSE for the 3F-DNS and 5F-DRF models
Full size table
Table 5 Comparison of the average MSE and RMSE generated by the 3F-DNS and 5F-DRF models for each countries maturity
Full size table

4 Forecasting the BRICS Term Structure

4.1 The Models

In addition to in–sample fitting, a term structure model should be also able to ensure effective out–of–sample predictions of the yield curve. The latter is made possible by the existing equivalence between forecasting the yield curve and forecasting the models parameters as stated in Diebold and Li.

With this in mind, instead of directly predicting spot rates, we forecasted the building blocks of the yield curve, that is the parameters (\(\varvec{\hat{\beta }}\)) and the decay terms (\(\hat{\lambda }\), \(\varvec{\hat{\tau }}\)) time series. In this case the novelty of our approach relies on the techniques used to carry out the task, that is: the Univariate Autoregressive AR(1) model, the Trigonometric seasonal Box–Cox Transformation with ARMA residuals Trend and Seasonal components (TBATS), and a combination of Autoregressive Integrated Moving Average and Nonlinear Autoregressive Neural Network (ARIMA–NARNN). We then used the predicted outcomes to calculate spot rates at the time \(t+h\) and maturity \(m \in M=(m_1, m_2, \ldots , m_N)'\):

$$\begin{aligned} \begin{aligned} \hat{y}_{{DNS}}(t+h|t)&= \hat{\beta }_{0,t+h|t}+\hat{\beta }_{1,t+h|t}\left( \frac{1-e^{-\hat{\lambda }_{t+h|t} \,m}}{\hat{\lambda }_{t+h|t} \,m}\right) \\&+\hat{\beta }_{2,t+h|t}\left( \frac{1-e^{-\hat{\lambda }_{t+h|t} \,m}}{\hat{\lambda }_{t+h|t} \,m}-e^{-\hat{\lambda }_{t+h|t} \,m}\right) , \end{aligned} \end{aligned}$$
(4)

for the three factor model, and

$$\begin{aligned} \begin{aligned} \hat{y}_{{DRF}} (t+h|t)&= \hat{\beta }_{0,t+h|t} +\hat{\beta }_{1,t+h|t}\left( \frac{1-e^{-m/\hat{\tau }_{1,t+h|t}}}{m/\hat{\tau }_{1,t+h|t}}\right) +\hat{\beta }_{2,t+h|t}\left( \frac{1-e^{-m/\hat{\tau }_{2,t+h|t}}}{m/\hat{\tau }_{2,t+h|t}}\right) \\&+\hat{\beta }_{3,t+h|t}\left( \frac{1-e^{-m/\hat{\tau }_{1,t+h|t}}}{m/\hat{\tau }_{1,t+h|t}}-e^{-m/\hat{\tau }_{1,t+h|t}}\right) \\&+\hat{\beta }_{4,t+h|t}\left( \frac{1-e^{-m/\hat{\tau }_{2,t+h|t}}}{m/\hat{\tau }_{1,t+h|t}}-e^{-m/\hat{\tau }_{2,t+h|t}}\right) , \end{aligned} \end{aligned}$$
(5)

for the five factor model.

When using the AR(1) process to predict the parameters in (4) and (5) we have:

$$\begin{aligned} {x}_{k,t+h} = \alpha _{0} + \alpha _{1} x_{k, t} + \varepsilon _{k,t} \end{aligned}$$
(6)

where \({x}_{k,t+h}(x_{k,t})\) is the variable to model, i.e. either \(\beta \), \(\lambda \) or \(\tau _{1}\), \(\tau _{2}\), while \(\alpha _{0}\) is the coefficient of the zero degree term; \(\alpha _{1}\) is the coefficient of the autoregressive term and \(\varepsilon _t\) is a white noise error term with \(E(\varepsilon _{k,t}) = 0\) and \(Var (\varepsilon _{k,t}) = \sigma ^2_{k}\).

In a similar fashion, when using the TBATS, we have:

$$\begin{aligned} {x}^{(\omega )}_{k,t+h} = l_{t} + \phi b_{t} + \sum _{j=1}^{T}s^{(i)}_{t+h-\eta _{j}} + d_{t+h} \end{aligned}$$
(7)

where \({x}^{(\omega )}_{k,t+h}\) is the Box–Cox transformation of the observations \({x}_{k,t+h}\) with the Box–Cox parameter \(\omega \); \(l_t\) and \(b_t\) represent, respectively, the local level and the short–run trend at time t; \(\phi \) is the dampening parameter for the trend; \(s^{(i)}_{t+h}\) is the ith seasonal component while \(\eta _j\) is the seasonal period; and \(d_{t+h}\) is the prediction error modeled as an ARMA(p,q) process.

Finally, the combination of the ARIMA(p,d,q) process and NAR–NN is aimed to provide more flexibility in forecasting the parameters. In fact, the ARIMA(p,d,q) is used to predict each models coefficient \(\varvec{\beta }_k\) which is expressed as a linear function of both its past observations and past residual error terms (or random shocks):

$$\begin{aligned} {x}_{k,t+h} = \alpha _{0} + \sum _{j=1}^{p} \alpha _{j} {x}_{k,t+h-j} + \sum _{i=1}^{q} \gamma _{i} \varepsilon _{k,t+h-i} + \varepsilon _{k,t+h} \end{aligned}$$
(8)

with \({x}_{k,t+h}(x_{k,t})\) as above, \(\alpha _{0}\) being the intercept, \(\alpha _{j}\) and \(\gamma _{i}\) the autoregressive and moving average coefficients respectively, p and q the lag order of the Autoregressive (AR) and Moving Average (MA) terms respectively, and \(\varepsilon _{k,t+h}\) a white noise process.

On the other hand, the NAR-NN is used to forecast the future values of the decay terms \(\lambda \) and \(\varvec{\tau }\) according to the:

$$\begin{aligned} {x}_{k,t+h} = \omega _{k,0} + \sum _{i=1}^{n} \omega _{k,i} ~\Lambda \left( \alpha _{i,0} + \sum _{j=1}^{m} \alpha _{i,j} {x}_{k,t+h-j} \right) + \varepsilon _{k,t} \end{aligned}$$
(9)

where m is the number of lagged input values \({x}_{k,t+h-j}\); \(\alpha _{i,j}\) is the connection weight between the input unit j and the closest hidden unit i; \(\Lambda \) represents the activation function; \(\omega _{k,i}\) is the connection weight between the hidden unit i and the output unit k; while \(\alpha _{i,0}\) and \(\omega _{k,0}\) are the bias used to optimize the working point of the neurons in the hidden and output units respectively; finally \(\varepsilon _{k,t}\) represents the error term.

Relatively to the ARIMA model, we followed the Box–Jenkins and Hyndman–Khandakar method to determine the most appropriate (p,d,q) specification. For what concerns the development of the NAR–NNs architecture (i.e. the time delays, number of nodes, hidden layers, activation functions etc.) we followed a trial and error approach due to the absence of specific rules.

4.2 Methodology and Performance Evaluation

From a practical viewpoint, we adopted the static approach to implement forecasting. Parameters and hence yield curves prediction was performed on a daily basis in the period June 2022 – September 2022 using the sliding window method. The out–of–sample prediction period covers the last three months of our dataset, for an overall number of 50 predicted days for each BRICS country. We collected the observed spot rates for the same period and used them to evaluate the forecasting performance of our approach. We selected a three month time–span as it includes different stable and spiky periods with yield curves exhibiting frequent temporary reversals. This enables us to validate the effectiveness and robustness of the proposed methods under different market statuses.

We chose a quite limited range of values close to the forecasting period on which the models are firstly calibrated and then used for one–step–ahead predictions. After each forecast the window is shifted and updated with a new observed value in order to predict the next one. The advantage of this approach consists in giving priority to the information content of the period close to that of forecasts since it is intended to deeply influence the events of the near future, thus incorporating the autocorrelation features of the series into the model. Moreover, this procedure allows to avoid the impact of noisy data which may result from the use of large data–sets, and thus considerably reduce the volatility of predictions.

To investigate the predictive performance of the candidate models, we evaluated the statistical accuracy of the forecasts with the Mean Square Forecasting Error (MSFE) and the Mean Absolute Percentage Error (MAPE) performance metrics:

$$\begin{aligned} MSFE&= \frac{1}{n}\sum _{j=1}^{n} ({y}_{t+h} - \hat{y}_{t+h})^2 \end{aligned}$$
(10)
$$\begin{aligned} MAPE&= \frac{100}{n}\sum _{j=1}^{n} \bigg |\frac{{y}_{t+h} - \hat{y}_{t+h}}{{y}_{t+h}} \bigg | \end{aligned}$$
(11)

where \({y}_{t+h}\) is the observed value in \(t+h\) and \(\hat{y}_{t+h}\) the related forecast.

Main results are summarized in Table 6 for each country and method. Furthermore, in Fig. 7 we compare the average observed yield curves to the average forecasted ones for each country, model and method.

Table 6 Comparison of the average MSFE and MAPE (%) metrics obtained with different competing methods
Full size table

Data in Table 6 can be interpreted in at least two ways. On the one hand, it is possible to detect the most effective forecasting method within each parametric model and market; on the other hand, for each market it is possible to determine which combination of parametric model/forecasting method delivered the overall best results.

Looking at the results of the MAPE indicator over the whole forecasting window we can clearly see the dominance of the 3F–DNS model, which produced overall the best performance delivering accurate predictions over the entire maturity spectrum and across all the countries, with an average accuracy of over 98%.

For what is concerning the 5F–DRF model, the presence of further slope and curvature terms, so important to ensure higher in–sample fitting performances, didn’t assure any advantage to the models predictive power with respect to the 3F–DNS. Nevertheless, the 5F–DRF model can effectively replicate the average trends of the BRICS curves; moreover, the small error measures jointly with 95% level of predictive precision makes the 5F–DRF an ideal alternative to the three factor model in every considered market despite the high variability of the parameters.

Fig. 7
figure 7

For each BRICS country (in column) the graph compares average observed yield curves to average forecasted ones with different techniques for the 3F-DNS and 5F-DRF models. For both models, the blue line is associated to the average forecasted curve obtained with the ARIMA–NARNN method, the red line with the AR(1) process, while the green one with the TBATS model. The black line represents the average observed curve

Full size image

Going into details and considering the 3F–DNS model, the AR(1) process ensured the best result within all the countries achieving 98.65% of average forecasting accuracy; then comes TBATS with 98.28% and ARIMA–NARNN with 96.47%. Moving to the 5F–DRF model, AR(1) and TBATS achieved the 94.71% and 90.16% predictive accuracy, respectively, while the best result was obtained with the ARIMA–NARNN combination with 95.10% precision. The latter result was attained due to the ability of the neural network to better handle the nonlinear behavior of the decay terms.

Turning our attention to the forecasting combinations and cross–checking the tabulated results, it is possible to highlight that the best predictions were systematically provided by the 3F–DNS–AR(1) combination in every considered country, with an overall average MAPE improvement of 24.52 % with respect to its direct competitors (3F–DNS–TBATS and 3F–DNS–ARIMA–NARNN), and of 68.26 % with respect to the methods used within the 5F–DRF model.

Summarizing the results, it is possible to state that the proposed framework makes it possible to predict with high precision and reliability the challenging dynamics characterizing BRICS yield curves avoiding the need to resort to constant decay terms unlike most of similar research. Moreover, the comparison between the two models revealed the existence of a fitting–forecast trade–off: depending on the need, it is possible to opt for the 3F–DNS which ensures more accurate yield curves predictions, but slightly less precise in–sample–fitting; or rely on the 5F–DRF which ensures better fitting abilities but less accurate spot rates predictions.

5 Conclusion

In this paper we analyzed a methodology aimed at identifying optimal time–varying parameters for the Three Factor Dynamic Nelson–Siegel (3F–DNS) and the Five Factor Dynamic De Rezende–Ferreira (5F–DRF) models. We tested the modeling and predictive abilities of the proposed framework outside the comfort zone of western economies, that is we focused our attention on BRICS countries. Within the estimation phase we highlighted the advantages of using optimal time–varying decay terms over the constant alternatives. With regard to the predictive process, we moved within the Diebold–Li dynamic framework and employed AR(1), TBATS and a combination of ARIMA–NARNN as Local Data Generating Processes to predict models parameters, and hence yield curves, as an alternative approach to direct interest rates forecasting.

According to the in–sample fitting results, we first found that the use of time–varying decay terms allowed to outperform the results obtained keeping \(\lambda \) and \(\varvec{\tau }\) constant or averaging them and ensure the desired flexibility to manage anomalies and extreme dynamics characterizing BRICS markets. Additionally, we showed that both models performed well in–sample as they can describe and replicate the main trends and shapes of BRICS yield curves. However, the 5F–DRF model with multiple decay parameters and additional slope and curvature factors assures improved fitting results. On the contrary the 3F–DNS model generates significantly larger errors due to its well known limitations in approximating the short and long term maturities as well as curves with more inflexion points.

Relatively to the models out–of sample performances, we obtained satisfying results with an average predictive accuracy of over 95%. Overall, the out–of–sample predictions of the 3F–DNS–AR(1) model turned out to be more accurate with lower errors in every market, so that we concluded that not necessarily a richer parametrization ensures also better predictive abilities. The results obtained herein confirm the relevant predictive power of our approach also within emerging economies without the need to resort to constant decay terms.

Overall, our research introduced an innovative approach to model yield curve dynamics that could potentially bring several benefits to market players and policy–makers. The yield curve offers important insights on the future macroeconomic environment as well as on investors expectations about future inflation, interest rates and economic dynamics and plays a central role in the transmission of monetary policy and it is a determinant of the profitability of different market participants. Our findings can therefore help central banks to more accurately analyze interest rates dynamics, trends and their response to changes in the macroeconomic policy, and plan more efficient monetary policy interventions (e.g. lower short–term interest rates in an attempt to stimulate economic activity). On the other hand, governments can take advantage of an accurate modeling framework to manage interest rate risk, design and implement the necessary adjustments in the fiscal policy and public debt structure (e.g. conduct tax cuts or increase public spending, to stimulate the economy and counteract the effects of a potential recession).

Furthermore our study could be extended in different ways. First of all alternative estimation approaches (e.g. the Maximum Likelihood, Kalman Filter or Machine Learning methods) can be tested, thus avoiding the a priori selection of the decay terms. Eventually, a refined version of the models which integrates financial and macroeconomic factors (e.g. monetary policy, inflation, economic growth) can be considered for the BRICS bond market. Finally it would be interesting to test the proposed framework in different markets (e.g. commodity, derivatives, forex) or for different financial instruments (e.g. corporate bonds, credit default swaps). Actually all these topics represent a part of our ongoing research.