Insights on the Theory of Robust Games

Abstract

A robust game is a distribution-free model to handle ambiguity generated by a bounded set of possible realizations of the values of players’ payoff functions. The players are worst-case optimizers and a solution, called robust-optimization equilibrium, is guaranteed by standard regularity conditions. The paper investigates the sensitivity to the level of uncertainty of this equilibrium focusing on robust games with no private information. Specifically, we prove that a robust-optimization equilibrium is an $\epsilon$-Nash equilibrium of the nominal counterpart game, where $\epsilon$ measures the extra profit that a player would obtain by reducing his level of uncertainty. Moreover, given an $\epsilon$-Nash equilibrium of a nominal game, we prove that it is always possible to introduce uncertainty such that the $\epsilon$-Nash equilibrium is a robust-optimization equilibrium. These theoretical insights increase our understanding on how uncertainty impacts on the solutions of a robust game. Solutions that can be extremely sensitive to the level of uncertainty as the worst-case approach introduces non-linearity in the payoff functions. An example shows that a robust Cournot duopoly model can admit multiple and asymmetric robust-optimization equilibria despite only a symmetric Nash equilibrium exists for the nominal counterpart game.

1 Introduction

Ambiguity affects the choice of economic agents, as demonstrated in his seminal contribution by Ellsberg (1961). As opposed to risk, where an objective probability distribution describes some possible occurrence, ambiguity (also known as uncertainty or Knightian uncertainty, see (Knight, 1921)) is characterized by the inability of the decision maker to formulate a unique probability distribution or by his lack of trust in any single probability estimate. The experimentally documented attitude to prefer situations with known probabilities to unknown ones is defined uncertainty aversion or ambiguity aversion, see (Epstein, 1999).

In game theory, uncertainty emerges due to incomplete information about player’s own payoff. It can be originated by individually known private information, that is incomplete information about the types of the opponents, or it can be independent from private information. Regarding incomplete information about opponents’ types, a cornerstone model is the Bayesian-game framework proposed by Harsanyi, see, e.g., Harsanyi (1967, 1968a, 1968b). In a Bayesian game a type space indicates all the possible types of each player, who has only a probabilistic knowledge of the types of the opponents. Different types can use different strategies. In this case, incomplete information about the opponents’ types leads to incomplete information about player’s own payoff. This modeling framework has been generalized by introducing uncertainty about opponents’ type following two main different approaches. The first one is given by the ambiguous games, see Marinacci (2000), a generalization of the normal form games that allows the presence of vagueness in players’ beliefs over the opponents’ choice of strategies. In ambiguous games, players’ behavior is expressed through the Choquet expected utility model axiomatized in Schmeidler (1989), where non-additive probability measures reflect the ambiguity aversion of agents. The second approach is represented by the incomplete information games with multiple priors, see, e.g., Kajii and Ui (2005) and references therein. In this setup, uncertainty about the opponents is represented by a set of probability distributions and the maxmin expected utility model axiomatized in Gilboa and Schmeidler (1989) is adopted by players for decision making.

The uncertainty about player’s own payoff not originated by private information requires a different modeling and is complementary to the uncertainty about the opponents’ types. Consider a first-price sealed bid auction. To obtain a positive payoff, a player needs to make a bid higher than opponents’ bids and lower than his own valuation for the good being auctioned. A player may be uncertain about the types of the opponents, therefore of their bids. In an auction for a vintage car, the opponent’ bid is different if the opponent is a car enthusiast instead of a speculator. This uncertainty is originated by private information. Only the player knows his own type. At the same time, a player may be uncertain about his own valuation for the good sold at auction. In an auction for a vintage car, for example, it is difficult to foresee the future quotations of the car being auctioned. This uncertainty persists after the game is played and regards all players. Therefore, it is not due to private information and it does not require to introduce a type space as uncertainty about opponents’ types requires. Similarly, in an oligopoly game the lack of knowledge about competitors’ cost functions is an example of uncertainty due to private information, while the lack of knowledge of the demand function is an example of uncertainty not originated by private information.

Despite considered even in Bayesian games, when we come to uncertainty in game theory, the unique attempt to accommodate Ellsberg paradox type problem not originated by private information is made in Aghassi and Bertsimas (2006). In a context of bounded-uncertainty about the possible values of the parameters of the payoff functions, Aghassi and Bertsimas (2006) employ a robust-optimization approach to ambiguity where agents rely on deterministic-set representations of uncertainty. A game where agents have an ambiguity aversion expressed by the robust-optimization approach to uncertainty, is denoted robust game. A robust game is a distribution-free model that offers an equilibrium concept, known as robust-optimization equilibrium. It belongs to the set of distribution-free equilibrium concepts for strategic-form games together with the ex-post equilibrium, which is a Nash equilibrium under all possible realizations of the uncertain parameters, see, e.g., Kalai (2004). Despite the worst-case approach, the robust-optimization equilibrium is less conservative than the ex-post equilibrium, in fact the first one implies the second one but not the vice versa, see (Aghassi & Bertsimas, 2006). Additional advantages are an existence theorem, computational methods offered by the robust-optimization techniques, see, e.g., Ben-Tal and Nemirovski (1998); Ben-Tal et al. (2009) and Suzuki et al. (2013), and theoretical results showing the relations with other equilibrium concepts in game theory.

Regarding this last aspect and focusing on robust games without private information, Crespi et al. (2017) propose a parametric representation of the level of uncertainty. According to this representation, the level of uncertainty is the parameter of the convex combination between a singleton, representing the nominal realization, and a bounded uncertainty set representing the maximum level of uncertainty. In the spirit of Knight, see Knight (1921), the level of uncertainty can be interpreted as the amount of confidence that a player has on his knowledge of the nominal realization. Setting to zero the level of uncertainty, the so-called nominal counterpart game is indeed obtained, which is the complete information version of a robust game. Employing this parametric representation of uncertainty, and introducing an opportunity cost of uncertainty that is the analogous for a strategic-form game of the loss (or regret) function proposed in Savage (1951), we provide insights on the impact of uncertainty on the solutions of games. In particular, after providing some generic results on the existence of a robust-optimization equilibrium, we prove that it is an $\epsilon$-Nash equilibrium of the nominal counterpart game, where $\epsilon$ is not smaller than the players’ opportunity costs of uncertainty.¹ Moreover, we provide an uncertainty-averse motivation for $\epsilon$-Nash equilibria by showing that it is always possible to introduce uncertainty in a complete information game, obtaining in this way a robust game, such that an $\epsilon$-Nash equilibrium of the first game is a robust-optimization equilibrium of the second one. Finally, we investigate the sensitivity of the solution of a game to the level of uncertainty. To this aim, we first introduce the definition of Nash equilibrium counterpart as the equilibrium towards which a robust-optimization equilibrium converges by following a continuous trajectory as the level of uncertainty of a robust game decreases. Then, we provide sufficient conditions for the existence of such a Nash equilibrium counterpart and, furthermore, for its uniqueness. Assuming that a game satisfies these conditions, its equilibrium solutions react smoothly to the level of uncertainty, in the sense that the equilibrium values are a continuous functions of the level of uncertainty.

An application completes the investigation. It is given by a robust version of the Cournot duopoly model as in Singh and Vives (1984) where players are uncertain about the parameters of the inverse demand function. This application shows the potentiality of our theoretical insights and helps to their interpretation. In addition, it shows that robust-optimization equilibria are not only sensitive to the level of uncertainty but also to the shape of the uncertainty set, which is the second ingredient that defines the uncertainty of a player in a robust game. This last aspect could be the object of a future research.

The road map of the paper is as follows. Section 2 introduces the basic concepts of robust game theory. Section 3 generalizes the existence result for robust-optimization equilibria in Crespi et al. (2017) to robust games with quasi-concave functions. Section 4 introduces the concept of opportunity cost of uncertainty and contains the main theoretical insights on robust games. An example underlines the importance of the theoretical insights. Section 5 introduces a robust version of a duopoly model similar to the one in Singh and Vives (1984) and provides results about the existence of robust-optimization equilibria. It is shown that only one of the three possible equilibria of the robust duopoly game has a Nash equilibrium counterpart. Section 6 concludes and provides suggestions for future research directions in robust-game theory. Appendix A discusses an upper-bound approximation of the opportunity cost of uncertainty that is a linear function with respect to the level of uncertainty. Appendix B identifies a class of robust games with unique robust-optimization equilibrium. Appendix C contains the proofs of the theoretical results in Sects. 3 and 4 and in Appendix B. Appendix D contains an algorithm to compute the worst-case best reply functions when the uncertainty sets are of polyhedral shape. Appendix E contains the proofs of the conditions for the existence of the robust-optimization equilibria of the robust duopoly model in Sect. 5.

2 Robust Games and Equilibria

Considering finite-person, non-cooperative, simultaneous-move, one-shot games only, we focus on payoff uncertainty assuming the absence of private information. Specifically, we consider incomplete-information games where payoff functions depend on some parameters, the values of which are not known in advance. Players are aware of this uncertainty and they have perfect knowledge of the set of all possible realizations of the uncertain parameters, the so called uncertainty set. Employing the information about the uncertainty set, each player chooses the action that maximizes his own maximum guaranteed payoff. Such a player is denoted robust player, and a game populated by robust players is called a robust game, see (Aghassi & Bertsimas, 2006).

More formally, ${\mathcal {N}}=\left\{ 1,2,\ldots ,n\right\}$ is the finite set of players and $A_{i}$ is the action space of player i. Set $A = \times _{i=1}^{n}A_{i}$, we define by $f_{i}: W^{\delta _{i}}_{i} \times A \rightarrow {\mathbb {R}}$ the payoff function of player i which is known except for the value of a parameter vector $\varvec{\alpha }_{i}\in W^{\delta _{i}}_{i}$. Denoted by $f_{i}\left( \varvec{\alpha }_{i};x_{i},{\textbf{x}}_{-i}\right)$, the payoff function of a robust player i depends on the realization of the uncertain parameter vector $\varvec{\alpha }_{i}\in W^{\delta _{i}}_{i}$, on the player i’s action $x_{i}\in A_{i}$ and on the action of his opponents ${\textbf{x}}_{-i}\in A_{-i}=\times _{j\in {\mathcal {N}};j\ne i}A_{j}$. Here, $W^{\delta _{i}}_{i}$ is a deterministic uncertainty set depending on a parameter $\delta _{i}\in \left[ 0,1\right]$ and defined as $W^{\delta _{i}}_{i}=\delta _{i} U_{i}+\left( 1-\delta _{i}\right) \varvec{\alpha }^{0}_{i}$, where $U_{i}$ is a closed and bounded deterministic set representing all possible realizations of the vector parameter $\varvec{\alpha }_{i}$, while $\varvec{\alpha }^{0}_{i}\in U_{i}$ is a singleton.² According to this setting and given an action profile $\left( x_{i},{\textbf{x}}_{-i}\right)$, player i’s vagueness about payoff is represented by the set $\left\{ \left. f_{i}\left( \varvec{\alpha }_{i};x_{i},{\textbf{x}}_{-i}\right) \right| \varvec{\alpha }_{i} \in W^{\delta _{i}}_{i}\right\}$ and $\delta _{i}$ measures the level of uncertainty, which vanishes when $\delta _{i}=0$ and it is maximum when $\delta _{i} = 1$.³ Inspired by Knight, see (Knight, 1921), the level of uncertainty $\delta _{i}$ can be interpreted as the inverse of the level of confidence that player i has on his knowledge of the true values of the parameters of the payoff function. Therefore, player i knows that $\varvec{\alpha }^{0}_{i}$ should be the array of the real values of the unknown parameters. Although, he is only sure of the fact that the real values of the unknown parameters are included in $W^{\delta _{i}}_{i}$.⁴ Introduced in Crespi et al. (2017), this parametric representation of the player’s uncertainty set allows to define a unique complete-information counterpart of a robust game, obtained when $\max _{i\in {\mathcal {N}}}\delta _{i}=0$. This latter game is called the nominal counterpart of the robust game.⁵

In a robust game with no private information (simply robust game hereafter), each player knows the level of uncertainty of all players. Moreover, each player i is ambiguity averse (or uncertainty averse), knows that all players adopt a worst-case approach to uncertainty, and determines his action $x_{i}$ by maximizing his worst-case payoff function:

$$\begin{aligned} \rho ^{\delta _{i}}_{i}\left( x_{i},{\textbf{x}}_{-i}\right) \triangleq \min _{\varvec{\alpha }_{i}\in W^{\delta _{i}}_{i}}f_{i}\left( \varvec{\alpha }_{i};x_{i},{\textbf{x}}_{-i}\right) \end{aligned}$$

(1)

The actions that players undertake by maximizing their worst-case payoff functions are denoted robust-optimization strategies. In case uncertainty vanishes, the robust-optimization strategies become the well-known Nash strategies. Assuming, instead, that player i’s uncertainty is represented by all probability distributions with support set given by $W^{\delta _{i}}_{i}$, player i’s robust-optimization strategy is consistent with the approach à la Gilboa and Schmeidler (1989).

A robust-optimization strategy derives therefore from an extreme form of ambiguity aversion, in the sense that any possible probability knowledge assigned to a player would not make an action profile less appealing to him than the worst-case approach to uncertainty. This extreme uncertainty attitude may appear paranoid in the sense that it is equivalent to assuming that nature will choose a realization of the unknown values of the parameters as if to spite the player. This extreme feeling can be however relaxed by reducing player’s level of uncertainty. In this way, we increase the confidence that the player has on his knowledge of the true values of the parameters of the payoff function. In a robust game, therefore, the ambiguity aversion of a player can be measured by his level of uncertainty.

To underline this aspect, note that a worst-case payoff function depends on the level of uncertainty and has the following property.

Property 1

The worst-case payoff functions are such that $\rho ^{\delta _{i}^{1}}_{i}\left( x_{i},{\textbf{x}}_{-i}\right) \ge \rho ^{\delta _{i}^{2}}_{i}\left( x_{i},{\textbf{x}}_{-i}\right)$, for all $\delta _{i}^{2}>\delta _{i}^{1}$, $\delta _{i}^{1},\delta _{i}^{2}\in \left[ 0,1\right]$, $\forall \left( x_{i},{\textbf{x}}_{-i}\right) \in A$ and $\forall i\in {\mathcal {N}}$.

Assuming that the worst-case payoff functions are well defined, i.e. the minimum of functions $f_{i}$ with respect to $\varvec{\alpha }_{i}\in W^{\delta _{i}}_{i}$ exists and is finite for all $\left( x_{i},{\textbf{x}}_{-i}\right) \in A$, a robust game is defined as follows.

Definition 1

Denoted by $\left\{ A_{i},f_{i},W_{i}^{\delta _{i}}: i \in {\mathcal {N}} \right\}$, a robust game is a normal form game $\left\{ A_{i},f_{i}: i \in {\mathcal {N}} \right\}$ and an n-tuple $\left\{ W_{i}^{\delta _{i}}\right\} _{i=1}^{n}$ of uncertainty sets, such that player i possible payoffs related to action $\left( x_{i},{\textbf{x}}_{-i}\right)$ belong to $\left\{ \left. f_{i}\left( \varvec{\alpha }_{i};x_{i},{\textbf{x}}_{-i}\right) \right| \varvec{\alpha }_{i} \in W_{i}^{\delta _{i}}\right\}$ and he maximizes his own worst-case payoff function $\rho ^{\delta _{i}}_{i}\left( x_{i},{\textbf{x}}_{-i}\right)$.

According to this definition and by defining equivalent two games that have the same players, the same action spaces and players’ behavior is independent of which of the two games is considered, we have that a robust game is equivalent to a complete information game that we denote nominal-game representation of the robust game. For each player, the worst-case payoff function of the robust game coincides with the payoff function of its nominal-game representation.⁶ In order to avoid confusion with the nominal counterpart game, we specify the differences.

Definition 2

Given the robust game $\left\{ A_{i},f_{i},W_{i}^{\delta _{i}}: i \in {\mathcal {N}}\right\}$:

• The nominal counterpart game is the unique complete information game obtained setting to zero the level of uncertainty of each player, that is $\left\{ A_{i},f_{i},W_{i}^{0}: i \in {\mathcal {N}}\right\}$;

• The nominal-game representation is the unique complete information game $\left\{ A_{i},\rho ^{\delta _{i}}_{i}: i \in {\mathcal {N}} \right\}$ equivalent to it.

By exploiting the equivalence between a robust game and its nominal-game representation, Aghassi and Bertsimas (2006) and Crespi et al. (2017) introduce the following equilibrium notion for robust games.⁷

Definition 3

A robust-optimization equilibrium (ROE in short) of a robust game is a Nash equilibrium of its nominal-game representation.

Introduced the robust-game framework and the related solution concept, we underline that we have restricted our attention to robust games without private information despite, as underlined in Aghassi and Bertsimas (2006), robust games can also accommodate private information. This choice is motivated by the desire to focus on a source of uncertainty that, despite being so far almost neglected by the game-theory literature, can have a relevant impact on the outcome of a game. Moreover, it allows us to mark the differences between the current framework and the other game-theory models proposed to deal with uncertainty. In fact, the robust approach to uncertainty is a limit case of the maxmin expected utility with a non-unique prior, see, e.g. Gilboa and Schmeidler (1989), and a robust game with private information can be considered a limit case of an incomplete information game with multiple priors, see e.g. Kajii and Ui (2005). Instead, the absence of a type space makes a robust game with no private information a simpler and different modeling framework. Its simplicity allows us to study the sensitivity of a robust-optimization equilibrium with respect to changes in the uncertainty sets. To the best of our knowledge, similar results have never been obtained for incomplete information games with multiple priors. For the sake of simplicity and by an abuse of terminology, in this paper we always write robust games to refer to robust games with no private information.

3 The existence of a robust-optimization equilibrium

The definition of robust-optimization equilibrium emphasizes the similarities with the Nash equilibria in many respects. Indeed, once the worst-case payoff functions are derived, searching for a robust-optimization equilibrium of a robust game is equivalent to searching for a Nash equilibrium. Therefore, the same techniques and algorithms can be used. Moreover, the problem of existence for a robust-optimization equilibrium is equivalent to the problem of existence for a Nash equilibrium. Specifically, when the usual properties (see, e.g., Arrow and Debreu (1954)) imposed on the payoff functions for the existence of a Nash equilibrium are satisfied by the worst-case payoff functions of a robust game, a robust-optimization equilibrium exists.

Theorem 1

Consider a finite-person, non-cooperative, simultaneous-move, one-shot robust game $\left\{ A_{i},f_{i},W_{i}^{\delta _{i}}: i \in {\mathcal {N}} \right\}$. Assume that $A_{i}$ is a non-empty, closed, bounded and convex subset of an Euclidean space for all $i\in {\mathcal {N}}$. Moreover, assume that the game is equivalent to the nominal game $\left\{ A_{i},\rho _{i}^{\delta _{i}}: i \in {\mathcal {N}} \right\}$ with the worst-case payoff functions that are continuous in $A_{i}\times A_{-i}$, and quasi-concave in $A_{i}$ for every ${\textbf{x}}_{-i}\in A_{-i}$. Then, a robust-optimization equilibrium of the robust game $\left\{ A_{i},f_{i},W_{i}^{\delta _{i}}: i \in {\mathcal {N}} \right\}$ exists.

The existence result in Theorem 1 is based on the assumption that the worst-case payoff functions satisfy the usual properties, that means continuity and quasi-concavity. Instead of considering the worst-case payoff functions, the conditions for the existence of a robust-optimization equilibrium can be imposed directly on the payoff functions that define a robust game.

Assumption 1

Let $A_{i}$, with $i\in {\mathcal {N}}$, be subsets of Euclidean spaces. We assume that:

• $A_{i}$ is a non-empty, closed, bounded, and convex set, for all $i\in {\mathcal {N}}$;

• $U_{i}\subset {\mathbb {R}}^{\nu _{i}}$ is a non-empty, closed, bounded, and convex set, for all $i\in {\mathcal {N}}$, where $\nu _{i}$ is the number of entries in vector $\varvec{\alpha }_{i}$;

• $f_{i}\left( \varvec{\alpha }_{i};x_{i},{\textbf{x}}_{-i}\right)$, $i=1,\ldots ,n$, are continuous on $W^{\delta _{i}}_{i}\times A$;

• $f_{i}\left( \varvec{\alpha }_{i};x_{i},{\textbf{x}}_{-i}\right)$, $i=1,\ldots ,n$, are quasi-concave in $x_{i}$, for every $\left( \varvec{\alpha }_{i},{\textbf{x}}_{-i}\right) \in W^{\delta _{i}}_{i}\times A_{-i}$.

These restrictions are imposed hereafter and they ensure that the worst-case payoff functions satisfy the conditions imposed in Theorem 1 for the existence of a robust-optimization equilibrium.

Lemma 1

Under the conditions imposed in Assumption 1, for all $i\in {\mathcal {N}}$ the following properties hold true:

• $\rho ^{\delta _{i}}_{i}:A\rightarrow {\mathbb {R}}$ is a continuous function;

• $\rho ^{\delta _{i}}_{i}\left( x_{i},{\textbf{x}}_{-i}\right)$ is quasi-concave in $x_{i}$ for every ${\textbf{x}}_{-i}\in A_{-i}$.

The results in Lemma 1 indicate that the conditions imposed in Assumption 1 are a particular case of the more general sufficient conditions imposed in Theorem 1 for the existence of a robust-optimization equilibrium. However, the conditions imposed in Assumption 1 regard directly the elements that define a robust game. Therefore, they allow a direct comparison with the sufficient conditions imposed by the Nash’s Theorem in the generalized version proposed in Arrow and Debreu (1954)[Lemma 2.5, p. 274], see also Dutang (2013) for a recent survey. The comparison underlines that the sufficient conditions to impose on the payoff function for the existence of a robust-optimization equilibrium are stronger than the ones required for the existence of a Nash equilibrium. In fact, the continuity of the payoff function is also required with respect to the uncertainty set, and the quasi-concavity is required for all possible realizations of the unknown values of the parameters.

The results in Lemma 1, also discussed in Crespi et al. (2017) but without a formal proof and limited to concavity, indicate therefore that the restrictions in Assumption 1 are sufficient (but not necessary) to ensure the existence of a robust-optimization equilibrium as stated in the following theorem, the proof of which is in Appendix C.

Theorem 2

Consider a finite-person, non-cooperative, simultaneous-move, one-shot robust game $\left\{ A_{i},f_{i},W_{i}^{\delta _{i}}: i \in {\mathcal {N}} \right\}$. Under Assumption 1, we have that:

• The robust game has at least a robust-optimization equilibrium;

• All robust games $\left\{ A_{i},f_{i},W_{i}^{\delta ^{+}_{i}}: i \in {\mathcal {N}} \right\}$, with $\delta ^{+}_{i}\in \left[ 0,\delta _{i}\right)$, have a robust-optimization equilibrium.

The first point of Theorem 2 generalizes the existence result in Crespi et al. (2017) to robust games with quasi-concave payoff functions. Moreover, the existence result for the solution of a robust game in matrix form derived in Aghassi and Bertsimas (2006) is a particular case of the existence result in Theorem 2. At the same time, the second point of Theorem 2 indicates the existence of a robust-optimization equilibrium even reducing the level of uncertainty. Therefore, the existence of a Nash equilibrium for the nominal counterpart game is guaranteed and Theorem 2 implies Nash’s Theorem, see, e.g., Arrow and Debreu (1954)[Lemma 2.5, p. 274]. Note that in general, when the conditions in Assumption 1 are not satisfied, the presence of a robust-optimization equilibrium does not guarantee the presence of a Nash equilibrium of the nominal counterpart game.

4 Foundations and Theoretical Insights

Uncertainty implies a loss of profit for player i which determines the so-called opportunity cost of uncertainty for player i.⁸ Given the actions of player i’s opponents, the opportunity cost of uncertainty for players i measures the extra profit that player i gains if the uncertainty about his payoff function vanishes. Therefore, given the vector of actions of player i’s opponents ${\textbf{x}}_{-i}$ and let $\delta _{i}$ be the level of uncertainty for player i, the opportunity cost of uncertainty for player i is

$$\begin{aligned} C^{\delta _{i}}_{i}\left( {\textbf{x}}_{-i}\right) {:}{=}\max _{x_{i}\in A_{i}}\rho ^{0}_{i}\left( x_{i},{\textbf{x}}_{-i}\right) -\rho ^{0}_{i}\left( x^{+}_{i}\left( \delta _{i}\right) ,{\textbf{x}}_{-i}\right) \text {; }\quad \text {where} \quad x^{+}_{i}\left( \delta _{i}\right) \in \arg \max _{x_{i}}\rho ^{\delta _{i}}_{i}\left( x_{i},{\textbf{x}}_{-i}\right) \end{aligned}$$

(2)

According to the definition, for each given set of actions of the opponents, player i’s opportunity cost of uncertainty is the difference between the payoff player i would obtain by maximizing his nominal payoff function and the value of the nominal payoff function in correspondence of his robust strategy. Therefore, the opportunity cost of uncertainty is not the extra payoff player i obtains in the nominal counterpart game, but it is the extra profit he obtains when the actions of the opponents are fixed and his uncertainty vanishes.⁹

Summarizing, the opportunity cost of uncertainty measures the regret when the nominal realization takes place. In this respect, the opportunity cost of uncertainty is the analogous for game theory of the loss function proposed in Savage (1951). It is worth observing that Nash equilibria of the nominal counterpart game are those strategic profiles that minimize to zero the opportunity cost of uncertainty of all players.

4.1 Uncertainty Aversion Leads to Play an $\epsilon$-Nash Equilibrium

The opportunity cost of uncertainty does not represent, therefore, the players’ loss of profit when a robust-optimization equilibrium is played instead of a Nash equilibrium of the nominal counterpart game. This notwithstanding, it links a robust-optimization equilibrium of a robust game to an $\epsilon$-Nash equilibrium of the nominal counterpart game.

Definition 4

The action profile $\left( x_{1}^{*},\ldots ,x_{n}^{*}\right) \in A$ is an $\epsilon$-Nash equilibrium of game $\left\{ A_{i},f_{i}: i \in {\mathcal {N}} \right\}$, when for each $i\in {\mathcal {N}}$

$$\begin{aligned} f_{i}\left( \varvec{\alpha }^{0}_{i};x^{*}_{i},{\textbf{x}}^{*}_{-i}\right) \ge f_{i}\left( \varvec{\alpha }^{0}_{i};x_{i},{\textbf{x}}^{*}_{-i}\right) -\epsilon \quad \forall x_{i}\in A_{i} \end{aligned}$$

(3)

The basic idea behind the notion of $\epsilon$-Nash equilibrium is that a player accepts to play a strategy that is not optimal with respect to Nash definition, yet he will not deviate unless the payoff improvement is greater than $\epsilon$. The following theorem (see proof in Appendix C) underlines that a robust-optimization equilibrium is an $\epsilon$-Nash equilibrium of the nominal counterpart game, where $\epsilon$ is the maximum of players’ opportunity costs of uncertainty.

Theorem 3

If $\left( x_{1}^{*},\ldots ,x_{n}^{*}\right) \in A$ is a robust-optimization equilibrium of the robust game $\left\{ A_{i},f_{i},W_{i}^{\delta _{i}}: i \in {\mathcal {N}} \right\}$, then $\left( x_{1}^{*},\ldots ,x_{n}^{*}\right)$ is an $\epsilon$-Nash equilibrium of its nominal counterpart, with $\epsilon =\max \left\{ C^{\delta _{1}}_{1}\left( {\textbf{x}}_{-1}^{*}\right) ,\ldots ,C^{\delta _{n}}_{n}\left( {\textbf{x}}_{-n}^{*}\right) \right\}$. Moreover, for ${\hat{\epsilon }}<\epsilon$, $\left( x_{1}^{*},\ldots ,x_{n}^{*}\right)$ is not an ${\hat{\epsilon }}$-Nash equilibrium of the nominal counterpart game.

Thus, in case of payoff uncertainty, uncertainty-averse players play an $\epsilon$-Nash equilibrium instead of a Nash equilibrium, where the level of approximation $\epsilon$ is the largest of players’ opportunity costs of uncertainty. Moreover, reaching a better approximation is not possible in the sense that $\epsilon$ cannot be smaller than the greatest of the players’ opportunity costs of uncertainty.

Measuring the level of approximation that can be obtained in a robust game, the opportunity costs of uncertainty vanish when uncertainty vanishes. Nevertheless, the opportunity cost of uncertainty of a generic player i does not necessary reduce when his level of uncertainty reduces and it is not necessarily continuous in $\delta _{i}=0$. This because, given the actions of the opponents ${\textbf{x}}_{-i}$, the opportunity cost of uncertainty of player i depends on his robust best-response to ${\textbf{x}}_{-i}$. This robust best-response is a function of $\delta _{i}$, can be nonlinear and its properties change game by game. Further assuming concavity of the payoff functions with respect to the uncertain parameters, it is possible to construct a linear function of $\delta _{i}$ that provides an upper bound of the opportunity costs of uncertainty, see Appendix A.

4.2 An Alternative Foundation for $\epsilon$-Nash Equilibria

The concept of $\epsilon$-Nash equilibrium is more general than the one of Nash equilibrium. Therefore, a game can admit an $\epsilon$-Nash equilibrium but not having a Nash equilibrium. The same holds true for robust-optimization equilibria. In fact, Theorem 3 underlines that the concept of $\epsilon$-Nash equilibrium is more general than the one of robust-optimization equilibrium, i.e. the existence of a robust-optimization equilibrium of a robust game implies the existence of an $\epsilon$-Nash equilibrium of the nominal counterpart game. However, the vice versa is not true in general. Nevertheless, as specified in the following Theorem (see proof in Appendix C), for each $\epsilon$-Nash equilibrium of a nominal game, it is possible to construct a robust game by introducing payoff uncertainty in such a way that the $\epsilon$-Nash equilibrium of the nominal game is also a robust-optimization equilibrium of the robust game.

Theorem 4

Consider a nominal game $\left\{ A_{i},f_{i}: i \in {\mathcal {N}} \right\}$. Then, for each $\epsilon$-Nash equilibrium $\left( x_{1}^{*},\ldots ,x^{*}_{n}\right)$ of this game there exists at least a robust game such that $\left( x_{1}^{*},\ldots ,x^{*}_{n}\right)$ is a robust-optimization equilibrium of the robust game and $\left\{ A_{i},f_{i}: i \in {\mathcal {N}} \right\}$ is its nominal counterpart.

The game-theory literature motivates players’ waiver of an extra $\epsilon$ profit required to have that an $\epsilon$-Nash configuration is an equilibrium, as an extra cost for searching a better solution or for changing strategy, see, e.g., Radner (1980) and Dixon (1987). The result in Theorem 4 provides a further motivation. Specifically, the $\epsilon$ profit that players give up when they play an $\epsilon$-Nash equilibrium can be interpreted as the opportunity cost of uncertainty. The opportunity cost of uncertainty depends on players’ worst-case approach to uncertainty. Therefore, interpreting uncertainty as the lack of trust on the nominal realization, see Knight (1921), the $\epsilon$ profit that players waive when they play an $\epsilon$-Nash equilibrium can also be considered the cost of ambiguity aversion (or cost of aversion to uncertainty). A sort of regret which vanishes only at a Nash equilibrium.

Therefore, the current work shows for the first time that there is a rational motivation for $\epsilon$-Nash equilibria in terms of ambiguity aversion. This is particularly relevant from an application point of view. Indeed, in most of the real-world applications to discriminate the $\epsilon$-Nash equilibrium that will be considered is the numerical algorithm employed to solve a nominal game and its setting. Theorem 4 indicates that for the $\epsilon$-approximation chosen and for the $\epsilon$-Nash equilibrium computed, there exists an uncertainty set, a level of uncertainty and a robust game such that the $\epsilon$-Nash equilibrium can be interpreted as a robust-optimization equilibrium and $\epsilon$ is the maximum of the opportunity costs of uncertainty (or costs of aversion to uncertainty) of the players of the robust game. Moreover, Theorem 4 indicates that we can introduce a robust game to provide a selection criterion to discriminate among $\epsilon$-Nash equilibria. Beyond that, and in light of the theoretical insights derived in this work, from an $\epsilon$-Nash equilibrium is possible to estimate players’ opportunity cost of uncertainty, without knowing players’ uncertainty sets. An information that could possibly be used either by a policy maker to craft suitable incentives that lead players to invest in reducing uncertainty or by an information provider to set the price of an extra piece of information.

4.3 An Example of Robust Game and Remarks on Computing Equilibria

Summarizing, a robust-optimization equilibrium of a robust game is an $\epsilon$-Nash equilibrium of the nominal counterpart game, where $\epsilon$ measures the opportunity cost of uncertainty. At the same time, each $\epsilon$-Nash equilibrium of a nominal game can be interpreted as a robust-optimization equilibrium of a robust game that has the first one as its nominal counterpart. Despite these analogies, there are differences in terms of complexity and methods to adopt when computing an $\epsilon$-Nash equilibrium of a nominal game instead of a robust-optimization equilibrium of a robust game. In very large games, the $\epsilon$-Nash equilibria can be computed using polynomial-time algorithms, while to find a Nash solution requires non-polynomial-time algorithms in general, see, e.g., Daskalakis and Papadimitriou (2015). Since searching for a robust-optimization equilibrium is equivalent to finding a Nash equilibrium once the worst-case payoff functions are derived (see again the definition of robust-optimization equilibrium above), the same computational complexity involves robust-optimization equilibria. In stylized games, on the contrary, the $\epsilon$-Nash equilibria cannot be computed with general analytical methods, while the robust-optimization equilibria can be computed employing standard techniques used for searching Nash equilibria in nominal games. For example, it is possible to construct the worst-case (or robust) best-reply functions, which are the robust counterpart of the best-reply functions and are defined as follows, see Crespi et al. (2017):

$$\begin{aligned} R_{i}^{\delta _{i}}\left( {\textbf{x}}_{-i}\right) =\arg \max _{x_{i}\in A_{i}}\left[ \min _{\varvec{\alpha }_{i}\in W_{i}^{\delta _{i}}} f_{i}\left( \varvec{\alpha }_{i};x_{i},{\textbf{x}}_{-i}\right) \right] \end{aligned}$$

(4)

These functions can be used to identify the robust-optimization equilibria. In fact, the action profile $\left( x^{*}_{1},\ldots ,x^{*}_{n}\right) \in A$ is a robust-optimization equilibrium if and only if

$$\begin{aligned} x^{*}_{i}\in R_{i}^{\delta _{i}}\left( {\textbf{x}}^{*}_{-i}\right) \quad \forall i \in {\mathcal {N}} \end{aligned}$$

(5)

If the worst-case best-reply functions can be used to compute robust-optimization equilibria of a robust game, their derivation may not be so straightforward as it is for the best-reply functions of a nominal game. To overcome the issue, a simple procedure is proposed in Appendix D. It can be employed when the uncertainty sets are polyhedra, which is a common assumption in robust optimization. This algorithm is used to obtain the worst-case best-reply functions in the example that follows. The example regards a simple robust game where players’ payoff functions are linear-quadratic and depend on a single unknown parameter.

Example 1

Consider the finite-person, non-cooperative, simultaneous-move, one-shot robust game $\left\{ A_{i},f_{i},W_{i}^{\delta _{i}}: i \in \left\{ 1,2\right\} \right\}$, where

• The action spaces are $A_{i}{:}{=}\left[ 0,1.8\right] \subset {\mathbb {R}}$, for $i=1,2$;

• The uncertainty sets are $W_{i}^{\delta _{i}}{:}{=}\delta _{i} U_{i}+ \left( 1-\delta _{i}\right) \varvec{\alpha }_{i}^{0}=\delta _{i} \left[ 0.1,0.8\right] + \left( 1-\delta _{i}\right) 0.6\subset {\mathbb {R}}$, for $i=1,2$.

• The level of uncertainty is the same for both players, i.e. $\delta _{1}=\delta _{2}=\delta$.

• The payoff functions are $f_{i}\left( \varvec{\alpha }_{i};x_{i},{\textbf{x}}_{-i}\right) {:}{=}\left( 1+\varvec{\alpha }_{i}\left( 1-x_{i}\right) -{\textbf{x}}_{-i} \right) x_{i}$, for $i=1,2$;

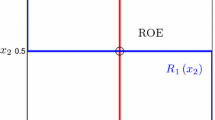
This is a two-player game. The action spaces, the uncertainty sets and the payoff functions are the same for both players. Hence, the game is symmetric. For analogy with the notation in the rest of the section, variables $\varvec{\alpha }_{i}$ and ${\textbf{x}}_{-i}$ are in bold despite being single-entry vectors. All conditions in Assumption 1 are satisfied when $\delta =1$, therefore at least a robust-optimization equilibrium exists for the robust game of the example, whatever level of uncertainty $\delta$. See Theorem 2. Specifically, the nominal counterpart of the game, obtained for $\delta =0$, has a unique Nash equilibrium, which is the intersection point of the best-reply functions, as observable in Fig. 1, picture in the middle. Therefore, the nominal counterpart game is a symmetric game with a unique symmetric Nash equilibrium. This feature is not preserved in the robust version of the game when the levels of uncertainty are large. Consider for example the case $\delta = 1$ and build the worst-case best-reply functions using the algorithm suggested in Appendix D. As observable in Fig. 1, first picture from the left, the robust game has multiple robust-optimization equilibria, which correspond to the intersection points of the worst-case best reply functions. Moreover, only one of the seven robust-optimization equilibria is symmetric. Figure 1, last picture from the left, reports the projections of the equilibrium outputs of the robust game on the action space of the first player. The graphic shows that when the level of uncertainty converges to zero only one of the robust-optimization equilibria of the robust game survives and converges smoothly to the Nash equilibrium of the nominal game. The other robust-optimization equilibria disappear. The unique robust-optimization equilibrium that survives to small level of uncertainty is the only equilibrium output of the robust game that in the next section will be classified as the robust-optimization equilibrium with a Nash equilibrium counterpart.

The example marks the large differences that could occur between a simple robust game and its nominal counterpart. These differences are inherited from the robust optimization employed by the players of the game to handle uncertainty. Indeed, a robust-optimization problem can be more complicated, and can generate a different output, than its nominal correspondence. In robust optimization, the complexity of the optimization problem to solve depends on the shapes of the uncertainty sets. There are conservative formulations of the uncertainty set, where the worst-case realization of the uncertain parameters does not depend on the decision variables. In this case, the robust problem is equivalent to the nominal optimization problem by setting the values of the uncertain parameters equal to their worst-case realizations, see Soyster (1973). As the shape of the uncertainty sets becomes more complex, the complexity of the robust-optimization problem increases and the optimal solution can be substantially different from the one of the nominal optimization problem, see, e.g., Ben-Tal et al. (2009). This aspect of the robust optimization is reflected and magnified in robust game theory. To magnify the difference between a robust game and its nominal counterpart is the strategic interaction among players. In fact, in game theory a worst-case realization of the value of an uncertain parameter does not change as a function of the decision variables of a player only but it depends on the actions of the opponents as well. This is witnessed by the current example, where the uncertainty sets considered are the simplest possible,¹⁰ the uncertainty regards a single parameter of the payoff functions, and despite those features the solution of the robust game for $\delta =1$ is very different from the one of the nominal counterpart game.

Fig. 1

Graphical representation of worst-case best-reply functions for the robust game in Example 1, left panel. Graphical representation of the best-response functions of the nominal counterpart of the robust game in Example 1, panel in the middle. Projections in the action space of player 1 of the robust-optimization equilibria of the robust game as a function of the level of uncertainty, right panel

4.4 Measuring the Effect of Uncertainty

The example above underlines that not all robust-optimization equilibria converge to a Nash equilibrium. Some disappear as uncertainty reduces. Some change and become Nash equilibria when uncertainty vanishes. Considering for simplicity of notation $\delta _{i}=\delta$, for all $i\in {\mathcal {N}}$, in this section we discriminate between robust-optimization equilibria with a Nash equilibrium counterpart and robust-optimization equilibria without it. Specifically, a Nash equilibrium is the counterpart of a robust-optimization equilibrium when the latter belongs to a continuous trajectory of robust-optimization equilibria that converges to the first one when uncertainty vanishes. A formal definition of Nash equilibrium counterpart is provided in the following and it allows us to discuss similarities and differences between a robust game and its nominal counterpart.

Definition 5

The action profile ${\textbf{x}}^{*}\left( 0\right)$ is a Nash equilibrium counterpart of a robust-optimization equilibrium ${\textbf{x}}^{*}\left( \bar{\delta }\right)$ when there exists a continuous function $\chi :\left[ 0,\bar{\delta }\right] \rightarrow A$, such that $\chi \left( \delta \right)$ is a robust-optimization equilibrium of $\left\{ A_{i},f_{i},W_{i}^{\delta }: i \in {\mathcal {N}} \right\}$, $\chi \left( 0\right) ={\textbf{x}}^{*}\left( 0\right)$ and $\chi \left( \bar{\delta }\right) ={\textbf{x}}^{*}\left( \bar{\delta }\right)$.

According to the definition, the counterparty relationship occurs only between a robust-optimization equilibrium and a Nash equilibrium of the nominal counterpart game. Specifically, given a robust game with a robust-optimization equilibrium, if a Nash equilibrium counterpart of a robust-optimization equilibrium exists, then it is a Nash equilibrium of the nominal counterpart game.

The existence of a robust-optimization equilibrium without a Nash equilibrium counterpart indicates that the equilibrium strategies of the players of a robust game can have an abrupt change when uncertainty vanishes. This has several implications. Small changes on the level of uncertainty may imply big changes on the equilibrium output of the game. Moreover, small errors in measuring the level of uncertainty affecting players may cause big errors on the estimated output of the game. On the other hand, the non-uniqueness of the Nash equilibrium counterpart is a further element of complexity in predicting the effects of an uncertainty reduction. This form of complexity is avoided when dealing with a robust game that admits a unique robust-optimization equilibrium, which has a Nash equilibrium counterpart, and the uniqueness of the equilibrium output is preserved varying the level of uncertainty. This is a robust game such that small changes in the level of uncertainty will cause small changes in the equilibrium output. In this respect, the definition of Nash-equilibrium counterpart of a robust-optimization equilibrium allows us to identify a class of robust games with solutions that react smoothly to uncertainty. More generally, for this class of games small levels of uncertainty ensure that a robust-optimization equilibrium is confined in the neighborhood of the Nash equilibrium of the nominal counterpart game.

A set of sufficient conditions to impose on the payoff functions to have a game with a unique equilibrium output may be very restrictive and technical. The interested reader is referred to Appendix B, where the conditions derived in Rosen (1965) for the uniqueness of Nash equilibrium are generalized to robust games. These conditions identify a class of robust games that have a unique robust-optimization equilibrium for each level of uncertainty. Here, we avoid these technical results and we start assuming robust games that have a unique robust-optimization equilibrium, with uniqueness preserved reducing the level of uncertainty. Then, we investigate the conditions to impose on the payoff functions for the existence of a unique Nash-equilibrium counterpart. In particular, the following theorem, the proof of which is in Appendix C, provides sufficient conditions to identify such robust games.

Theorem 5

(Existence of Nash-equilibrium counterpart) Consider $\bar{\delta }\in \left( 0,1\right]$ and a robust game $\left\{ A_{i},f_{i},W_{i}^{\bar{\delta }} {:} i \in {\mathcal {N}} \right\}$ that satisfies the conditions in Assumption 1. Assume that whatever $\delta \in \left[ 0,\bar{\delta }\right)$ robust game $\left\{ A_{i},f_{i},W_{i}^{\delta } {:} i \in {\mathcal {N}} \right\}$ has a unique robust-optimization equilibrium. This robust-optimization equilibrium has a Nash equilibrium counterpart when, for each $i\in {\mathcal {N}}$, one of the following conditions is satisfied:

• A1) $f_{i}\left( \varvec{\alpha }_{i};x_{i},{\textbf{x}}_{-i}\right)$ is strictly concave in $x_{i}\in A_{i}$, for all ${\textbf{x}}_{-i}\in A_{-i}$ and $\varvec{\alpha }_{i}\in W^{\bar{\delta }}_{i}$;

• A2) $\rho ^{\delta }_{i}\left( x_{i},{\textbf{x}}_{-i}\right)$ is strictly concave in $x_{i}\in A_{i}$, for all $\delta \in \left[ 0,\bar{\delta }\right]$ and ${\textbf{x}}_{-i}\in A_{-i}$.

Imposing some further restrictions on the payoff functions (in some cases of the nominal game only), the existence of a robust-optimization equilibrium with Nash equilibrium counterpart allows us to characterize the behavior of the opportunity cost of uncertainty as uncertainty vanishes. Moreover, under these further assumptions, the existence of a Nash equilibrium counterpart is sufficient to confine a robust-optimization equilibrium of a robust game into the set of $\epsilon$-Nash equilibria of the nominal counterpart game, with $\epsilon$ arbitrary, as long as the level of uncertainty is sufficiently low as stated in the following theorem, the proof of which is in Appendix C.

Theorem 6

Consider a robust game with a positive level of uncertainty, i.e. $\delta >0$, which admits a robust-optimization equilibrium $\left( x^{*}_{i}\left( \delta \right) ,{\textbf{x}}^{*}_{-i}\left( \delta \right) \right)$ which has a Nash equilibrium counterpart $\left( x^{*}_{i}\left( 0\right) ,{\textbf{x}}^{*}_{-i}\left( 0\right) \right)$. Then,

• The opportunity cost of uncertainty evaluated in ${\textbf{x}}^{*}_{-i}\left( \delta \right)$ is a continuous function in $\delta =0$;

• For each $\epsilon >0$, there exists $\delta \left( \epsilon \right) \in \left( 0,1\right)$ and there exists an $\epsilon$-Nash equilibrium of the nominal counterpart game that is also a robust-optimization equilibrium of the same robust game but with $\delta \left( \epsilon \right)$-level of uncertainty;

when one of the following conditions is satisfied:

• H1) for each $i\in {\mathcal {N}}$, $f_{i}\left( \varvec{\alpha }^{0}_{i};\cdot ,\cdot \right)$ is a continuous function;

• H2) for each $i\in {\mathcal {N}}$, $f_{i}\left( \varvec{\alpha }_{i};x_{i},{\textbf{x}}_{-i}\right)$ is concave in $\varvec{\alpha }_{i}\in U_{i}$, for every $\left( x_{i},{\textbf{x}}_{-i}\right) \in A$.

The results in Theorem 6 underline further similarities that exist between a robust-optimization equilibrium of a robust game and an $\epsilon$-Nash equilibrium of the nominal counterpart game. Indeed, Theorem 3 states that a robust-optimization equilibrium is a $\epsilon$-Nash equilibrium of the nominal counterpart game and Theorem 4 ensures that each $\epsilon$-Nash equilibrium can be interpreted as a robust-optimization equilibrium by introducing uncertainty on the payoff functions in a suitable way. Moreover, Theorem 6 identifies a robust game such that, for each $\epsilon$, the set of $\epsilon$-Nash equilibria of the nominal counterpart game contains at least a robust-optimization equilibrium. The requirement is to set the level of uncertainty sufficiently small. Therefore, Theorem 6 provides conditions such that a robust game represents a criterion of choice to select a subgroup of $\epsilon$-Nash equilibria.

This last theoretical result has at least an operational implication. The effects of a small level of uncertainty on the solution of a robust game can be approximated by studying the $\epsilon$-Nash equilibria of the nominal counterpart game. Since computing $\epsilon$-Nash equilibria is an easier task than computing robust-optimization equilibria (polynomial-time algorithms are available), the impact on the application side of this result maybe relevant.

Concerning the generality of the results stated in Theorem 6, we remark that condition H1 regards the nominal payoff functions only and the theorem assumes the existence of a robust-optimization equilibrium and of a Nash equilibrium counterpart. We refer to Theorems 2 and 5, respectively, for sufficient conditions ensuring these two requirements. All in all, the assumptions imposed by Theorems 2, 5 and 6 regard the strictly concavity of the payoff function for all parameter realizations, concavity with respect to the possible parameter realizations and uniqueness of the equilibrium solution. At least for suitable sets of uncertainty, these conditions are often satisfied by typical textbook configurations of classical games of industrial organizations such as Cournot, Bertrand and Stackelberg models, see, e.g., Singh and Vives (1984); Puu (1998); Fanti et al. (2013); Gori and Sodini (2017) and Yu and Yu (2019).

Coming back to a possible rational motivation for playing $\epsilon$-Nash equilibria, we underline that justifying $\epsilon$ waiver of an extra profit as the cost for searching for a better solution, does not allow to discriminate among the set of $\epsilon$-Nash equilibria. On the contrary, by interpreting $\epsilon$-Nash equilibria as robust-optimization equilibria of a robust game, we select a subgroup of $\epsilon$-Nash equilibria. The subgroup is not empty when, for example, the conditions in Theorem 6 are satisfied and the level of uncertainty is sufficiently small. In addition to this, by employing the opportunity cost of uncertainty we can classify in two groups those $\epsilon$-Nash equilibria that are not robust-optimization equilibria. One group is made of $\epsilon$-Nash equilibria that admit at least a unilateral deviation that is desirable for the robust game but it is not for the nominal counterpart game. A second group consists of $\epsilon$-Nash equilibria that are dominated in terms of robust game and in terms of nominal counterpart game, as a unilateral deviation that is desirable in both sense is possible.

Theorem 7

Consider an $\epsilon$-Nash equilibrium of the nominal counterpart game which is not an $\epsilon ^{1}$-Nash equilibrium, with $\epsilon ^{1}<\epsilon$.

• (1) If the opportunity cost of uncertainty is lower than $\epsilon$ for all players, for at least one player the unilateral deviation obtained by playing a robust strategy is desirable respect to both the robust game and the nominal counterpart game;

• (2) If the opportunity cost of uncertainty of one player is higher than $\epsilon$, for at least one player the unilateral deviation obtained by playing a robust strategy is desirable respect to the robust game but it is not respect to the nominal counterpart game;

• (3) If the opportunity cost of uncertainty is higher than $\epsilon$ for all players, for all players the unilateral deviation obtained by playing a robust strategy is desirable respect to the robust game but it is not respect to the nominal counterpart game.

4.5 Further Remarks

The study of the similarities between an equilibrium output of a robust game and the one of the nominal counterpart game leads us to introduce the concept of counterpart Nash equilibrium. A counterpart Nash equilibrium exists when a robust-optimization equilibrium moves smoothly towards a Nash equilibrium of the nominal counterpart game as uncertainty vanishes. The presence of such an equilibrium indicates a form of regularity in the way in which the game reacts to uncertainty. The existence of a robust-optimization equilibrium that converges smoothly towards a Nash equilibrium of the nominal counterpart game does not exclude, however, the existence of other equilibria that have a less regular behavior as uncertainty vanishes. In addition, the existence of a counterpart Nash equilibrium is guaranteed under stringent conditions on the payoff functions of a game. More general theoretical insights indicate that a robust-optimization equilibrium of a robust game can be confined in the set of $\epsilon$-Nash equilibria of the nominal counterpart game, where the $\epsilon$ measures the opportunity cost of uncertainty. These theoretical results are based on a parametrization of the uncertainty set and allow to measure the sensitivity of a game with respect to the level of uncertainty. This is only one feature of the uncertainty that influences the behavior of a robust player. The second element is the shape of the uncertainty set. The representation of the uncertainty proposed in this work is indeed characterized by these two elements. In forecasting or policy analysis, it is also relevant to measure the sensitivity of the equilibrium outputs of a robust game with respect to the shape of the uncertainty set. In fact, a large sensitivity to the configuration of the uncertainty set by the equilibrium output of a robust game can lead to wrong forecasts when the uncertainty is misspecified. Hence, the study of robust game theory here proposed is far from being complete.

These remarks underline that the validity of the results of this paper are confined to the assumption of a correct specification of the shape of the uncertainty set. In fact, only under this hypothesis, the theoretical insights on the analogies between robust games and their nominal counterparts allow us to measure the effect of uncertainty. However, independently of the correct specification of the shape of uncertainty set, the results in this paper do not allow us to neglect uncertainty. Indeed, its impact on the solutions of a game is relevant even though the uncertainty that we consider is not originated by private information.

Summarizing, the narrative in this section goes in the direction to underline analogies, similarities and differences between a robust game and its nominal counterpart. In the following we consider an economic application. Specifically, a robust version of a Cournot duopoly model is considered. This duopoly model has a setup similar to the one proposed in Singh and Vives (1984). The investigation of the model aims to underline and discuss the complexity that emerges in robust games even considering very simple settings. Consistently with the scope of the example, only a simple configuration of the robust version of the Cournot duopoly model is considered.

5 An Application: A Cournot Duopoly Game with Payoff Uncertainty and Robust Firms

In this section we consider a Cournot duopoly game with linear inverse demand functions, non constant marginal costs of production and differentiated products. The production is totally sold in the market which is characterized by a representative consumer that expresses a certain degree of substitutability between the two products. The two firms (robust players) that populate the duopoly produce differentiated goods, with each firm that produces one type of output only as in Singh and Vives (1984). Denote by $q_{1}$ the production of firm 1 and by $q_{2}$ the production of firm 2. The feasible levels of production for firm i are represented by A, which is a subset of ${\mathbb {R}}$.

The price at which firm i sells its output (or commodity) $q_{i}$, with $i=1,2$, is given by $P\left( q_{i},q_{-i}\right) =\max \left\{ \beta _{i}-s_{i}q_{i}-\gamma q_{-i};0\right\}$, where $q_{-i}$ is the production of the competitor, $\beta _{i}\in {\mathbb {R}}_{+}$ is the choke price of the commodity produced by firm i, $s_{i}\in {\mathbb {R}}_{+}$ is the price sensitivity of output of firm i with respect to its own production, and $\gamma \in \left[ 0,s_{i}\right]$ is the degree of substitutability between the two products. The cost of production of output $q_{i}$ is given by $C_{i}\left( q_{i}\right) =c_{i}q_{i}+d_{i}q^2_{i}$, where $c_{i}\in {\mathbb {R}}_{+}$ and $d_{i}\in {\mathbb {R}}$.¹¹ Confining the firms’ action spaces to levels of production for which the price functions are positive, assuming equal price functions and cost functions, and setting $b=s_{i}+d_{i}$ and $a=\beta _{i}-c_{i}$, firm i’s profit (or payoff) function is then given by:

$$\begin{aligned} f_{i}\left( \varvec{\alpha };q_{i},q_{-i}\right) = \left( a - \gamma q_{-i} - bq_{i}\right) q_{i} \end{aligned}$$

(6)

where $\varvec{\alpha }=\left( b,\gamma \right)$ is the vector of the uncertain parameters that affects the profit (payoff) function of each firm (player) i.

Firms (or players) know that the inverse demand functions are linear and downward sloping. However, the slopes of the inverse demand functions, as well as the degree of substitutability of the products, are uncertain.¹² In particular, adopting the parametric representation of uncertainty proposed above, the uncertainty set of player i is given by $W^{\delta }=\delta U+\left( 1-\delta \right) \varvec{\alpha }^{0}$, where $\delta \in \left[ 0,1\right]$ measures the level of uncertainty, U is a non-empty compact set that includes all the possible values of $\varvec{\alpha }=\left( b,\gamma \right)$, i.e. it represents the maximum level of uncertainty, while $\varvec{\alpha }^{0}\subset U$ is the singleton $\left( {\widehat{b}},\widehat{\gamma }\right)$. The uncertainty set is the same for the two firms.

The shape of the uncertainty set U should reflect the economic relationship among the variables of the game, for example some variables are positively related, others negatively related. However, the uncertainty set does not need to be known by a robust player, who, being a worst-case maximizer, needs to know only the subset made by the worst-case parameter realizations, see Sect. 3. This subset does not need to reflect the shape of the uncertainty set, hence the choice of a specific worst-case frontier is only apparently an arbitrary assumption. For example, assuming a worst-case frontier represented by a downward sloping segment in the $b-\gamma$ plane, it does not imply that lower values of b are associated to higher values of $\gamma$ and vice versa. See Fig. 2 for an example of three different uncertainty sets that, despite having the same worst-case frontier, indicate different economic relationships between the parameters b and $\gamma$.

Fig. 2

Examples of uncertainty sets with the same worst-case frontier. First picture from the left, example of uncertainty set equal to the worst-case frontier. Second picture from the left, uncertainty set of octagonal shape. Third picture from the left, uncertainty set of rectangular shape. In the pictures, the uncertainty set is denoted by U and its worst-case frontier by $U^{*}$

In the light of these considerations, in the following only the worst-case realizations will be defined and the economic interpretation of the worst-case frontier is neglected as it is not relevant. In particular, $U\subset {\mathbb {R}}^{2}$ is assumed to be made of the segment joining the two worst-case realizations $\left( {\bar{b}},{\underline{\gamma }}\right)$ and $\left( {\underline{b}},\bar{\gamma }\right)$, with ${\bar{b}}>{\underline{b}}$ and $\bar{\gamma }>{\underline{\gamma }}$. This is one of the simplest representations of a worst-case frontier that makes the outputs of the robust game different from the output of the nominal game.¹³

Underlying the differences that can occur between a robust game and its nominal counterpart is one of the aims of this example. Consistently with this aim, the duopoly model described is a symmetric game and the following restrictions are imposed.

Assumption 2

These restrictions hold true in the following:

• 1. All the parameters are non-negative: $a,{\bar{b}},{\underline{b}},\bar{\gamma },{\underline{\gamma }}\ge 0$;

• 2. The action space A is a non-empty, closed, bounded and convex subset of ${\mathbb {R}}_{\ge 0}$;

• 3. $2{\widehat{b}}>\widehat{\gamma }$ (technical condition that implies a unique Nash equilibrium for the nominal game);

• 4. The set U is defined as follows:

  $$\begin{aligned} U=\left\{ \varvec{\alpha }=\left( b,\gamma \right) \ | \ {\bar{b}} \ge b \ge {\underline{b}} \ \wedge \ \gamma =\frac{\bar{\gamma }{\bar{b}}-{\underline{b}}{\underline{\gamma }}}{{\bar{b}}-{\underline{b}}} - \frac{\bar{\gamma }-{\underline{\gamma }}}{{\bar{b}} - {\underline{b}}}b\right\} \end{aligned}$$

  (7)

According to Assumption 2, the uncertainty set $W^{\delta }$ is given by:

$$\begin{aligned} W^{\delta }=\left\{ \left( b,\gamma \right) \ | \ {\bar{b}}\left( \delta \right) \ge b\ge {\underline{b}} \left( \delta \right) \ \wedge \ \gamma =\frac{\bar{\gamma }\left( \delta \right) {\bar{b}}\left( \delta \right) -{\underline{b}}\left( \delta \right) {\underline{\gamma }}\left( \delta \right) }{{\bar{b}}\left( \delta \right) -{\underline{b}}\left( \delta \right) } -\frac{\bar{\gamma }\left( \delta \right) -{\underline{\gamma }}\left( \delta \right) }{{\bar{b}}\left( \delta \right) -{\underline{b}}\left( \delta \right) }b\left( \delta \right) \right\} \end{aligned}$$

(8)

where

$$\begin{aligned} {\overline{b}}\left( \delta \right)= & {} \left( 1-\delta \right) {\widehat{b}}+ \delta {\overline{b}} \end{aligned}$$

(9)

$$\begin{aligned} {\underline{b}}\left( \delta \right)= & {} \left( 1-\delta \right) {\widehat{b}}+\delta {\underline{b}} \end{aligned}$$

(10)

$$\begin{aligned} {\overline{\gamma }}\left( \delta \right)= & {} \left( 1-\delta \right) \widehat{\gamma } +\delta {\overline{\gamma }} \end{aligned}$$

(11)

$$\begin{aligned} {\underline{\gamma }}\left( \delta \right)= & {} \left( 1-\delta \right) \widehat{\gamma } +\delta {\underline{\gamma }} \end{aligned}$$

(12)

Hence $W^{\delta }$ is a non-empty, closed, bounded and convex subset of ${\mathbb {R}}^{2}$.

Consistently with the definition of robust game proposed in Sect. 2, the robust Cournot duopoly game is defined as follows:

$$\begin{aligned} \left\{ A_{i},f_{i},W_{i}^{\delta _{i}}:i\in \left\{ 1,2\right\} \right\} \end{aligned}$$

(13)

where the dependence of $W^{\delta }$, f and A on i can be dropped because the game is symmetric. By Definition 1, the worst-case payoff function of firm (player) i is given by

$$\begin{aligned} \rho ^{\delta }\left( q_{i},q_{-i}\right) =\min _{\varvec{\alpha }\in W ^{\delta }}f \left( \varvec{\alpha };q_{i},q_{-i}\right) \end{aligned}$$

(14)

The restrictions imposed in Assumption 2 ensure that action spaces of firms, as well as the uncertainty sets, respect the conditions imposed in Assumption 1. In addition, under the parameter value restrictions imposed in Assumption 2, it is straightforward to verify that the payoff function of firm i defined in (6) is continuous and it is concave with respect to $q_{i}$ for all $\left( \varvec{\alpha },q_{-i}\right) \in U\times A$. Therefore, independently of the level of uncertainty, the worst-case payoff function of player i is well-defined, continuous and concave with respect to the action space of the player himself, and by Theorem 2 a robust-optimization equilibrium of the robust duopoly game exists as well as a Nash equilibrium of the nominal counterpart game.

To verify the number of robust-optimization equilibria that exist and to compute them, we derive the worst-case best reply functions. For $\delta >0$, the worst-case best reply (or reaction) function for robust firm i is defined as follows¹⁴:

$$\begin{aligned} R^{\delta }\left( q_{-i}\right) : =\arg \max _{q_{i}\in A }\rho ^{\delta }\left( q_{i},q_{-i}\right) = \left\{ \begin{array}{lcr} \frac{a}{2{\overline{b}}\left( \delta \right) }-\frac{{\underline{\gamma }}\left( \delta \right) }{2{\overline{b}}\left( \delta \right) }q_{-i} &{}\quad \text {if} \quad \quad &{} {\underline{q}}\left( \delta \right)> \text { }q_{-i}\ge 0 \\ \\ \frac{{\overline{\gamma }} -{\underline{\gamma }} }{{\overline{b}} -{\underline{b}} }q_{-i} &{} \quad \text {if} \quad \quad &{} {\overline{q}}\left( \delta \right) \ge q_{-i}\ge {\underline{q}}\left( \delta \right) \\ \\ \frac{a}{2{\underline{b}}\left( \delta \right) }-\frac{{\overline{\gamma }}\left( \delta \right) }{2{\underline{b}}\left( \delta \right) }q_{-i}\text { } &{} \quad \text {if} \quad \quad &{} q^{M}\left( \delta \right)> q_{-i}>{\overline{q}}\left( \delta \right) \\ \\ 0 &{} \quad \text {if} \quad \quad &{} q_{-i}\ge q^{M}\left( \delta \right) \end{array} \right. \end{aligned}$$

(15)

where

$$\begin{aligned} {\underline{q}}\left( \delta \right)= & {} \frac{a\left( {\overline{b}} -{\underline{b}} \right) }{2{\overline{b}}\left( \delta \right) \left( {\overline{\gamma }} -{\underline{\gamma }} \right) +{\underline{\gamma }}\left( \delta \right) \left( {\overline{b}} -{\underline{b}} \right) } \end{aligned}$$

(16)

$$\begin{aligned} {\overline{q}}\left( \delta \right)= & {} \frac{a \left( {\overline{b}} -{\underline{b}} \right) }{2{\underline{b}}\left( \delta \right) \left( {\overline{\gamma }} -{\underline{\gamma }} \right) +{\overline{\gamma }}\left( \delta \right) \left( {\overline{b}} -{\underline{b}} \right) } \end{aligned}$$

(17)

$$\begin{aligned} q^{M}\left( \delta \right)= & {} \frac{a}{\bar{\gamma }\left( \delta \right) } \end{aligned}$$

(18)

In accordance to the definition of robust-optimization equilibrium in (5), see also Aghassi and Bertsimas (2006) and Crespi et al. (2017), given an uncertainty level $\delta \in \left[ 0,1\right]$ and the robust best-reply function in (15), the output set $\left( q^{*}_{i},q^{*}_{-i}\right) \in A$ is a robust-optimization equilibrium of the robust game (13) if and only if

$$\begin{aligned} q_{i}^{*}= R^{\delta }\left( q^{*}_{-i}\right) \quad \forall i \in \left\{ 1,2\right\} \end{aligned}$$

(19)

where “$=$” substitutes “$\in$” in (5), as for robust game here considered the robust best replies are functions instead of correspondences. Hereafter, a robust-optimization equilibrium of the robust duopoly model (15) will be called Cournot robust-optimization equilibrium (Cournot ROE in short), which becomes a Cournot-Nash equilibrium when uncertainty vanishes.

Setting $\delta =0$, uncertainty vanishes and the robust duopoly game with Cournot competition becomes a nominal Cournot duopoly game where players’ behavior is characterized by a classical best-reply function:

$$\begin{aligned} R^{0}\left( q_{-i}\right) =\left\{ \begin{array}{lcr} \frac{a}{2{\widehat{b}} }-\frac{\widehat{ \gamma }}{2{\widehat{b}} }q_{-i} &{} \quad \text {if} \quad \quad &{} q^{M}\left( 0\right)> q_{-i}>0 \\ \\ 0 &{} \quad \text {if} \quad \quad &{} q_{-i}\ge q^{M}\left( 0\right) \end{array} \right. \end{aligned}$$

(20)

Solving system (19) when $\delta =0$, it results that the unique Cournot-Nash equilibrium of the nominal counterpart of the duopoly game is the one provided in the following proposition (see proof in Appendix E).

Proposition 1

Consider Assumption 2. The nominal version of the Cournot duopoly game, i.e. game (13) with $\delta =0$, admits one and only one Cournot-Nash equilibrium which is given by

$$\begin{aligned} \left( q^{NE},q^{NE}\right) =\left( \frac{a}{2{\widehat{b}}+\widehat{\gamma }},\frac{a}{2{\widehat{b}}+\widehat{\gamma }}\right) \end{aligned}$$

(21)

The strategic profile in (21) represents a symmetric Nash equilibrium; all the players involved play the same Nash strategy, which is unique. Symmetry and uniqueness of the equilibrium solution are not guaranteed in the robust duopoly game. A striking feature of the robust duopoly model arises comparing the robust reaction function (15) with its nominal counterpart (20). The latter one is monotonically decreasing while the robust counterpart is in general a non-monotone function. This difference reflects in the number of the robust-optimization equilibria of the robust game, which can be multiple and even asymmetric as stated in the following proposition (see proof in Appendix E).

Proposition 2

Consider the robust Cournot duopoly in (13), with $\delta >0$. If the shape of the uncertainty set U is such that:

• 1. ${\overline{b}}-{\underline{b}}>\overline{\gamma }-{\underline{\gamma }}$, then

  $$\begin{aligned} \left( q^{ROE_{1}},q^{ROE_{1}}\right) =\left( \frac{a}{2{\overline{b}}\left( \delta \right) +{\underline{\gamma }}\left( \delta \right) }, \frac{a}{2 {\overline{b}}\left( \delta \right) + {\underline{\gamma }}\left( \delta \right) }\right) \end{aligned}$$

  (22)

  is the unique robust-optimization equilibrium of the robust Cournot duopoly in (13) and it converges to Cournot-Nash equilibrium of its nominal counterpart game when $\delta \rightarrow 0$.

• 2. ${\overline{b}}-{\underline{b}}={\overline{\gamma }}-{\underline{\gamma }}$, then robust-optimization equilibria fill the interval $E_{1}=\left\{ \left( q,q\right) |{\overline{q}}\left( \delta \right) \ge q\ge {\underline{q}}\left( \delta \right) \right\}$, where ${\underline{q}}\left( \delta \right)$ and ${\overline{q}}\left( \delta \right)$ are defined in (16) and in (17), respectively. For $\delta \rightarrow 0$, the segment E shrinks into the Cournot-Nash equilibrium $\left( q^{NE},q^{NE}\right)$ in (21).

• 3. ${\overline{b}}-{\underline{b}}<{\overline{\gamma }}-{\underline{\gamma }}$ and the level of uncertainty is such that

• i) $\delta <\delta ^{*}$, where

  $$\begin{aligned} \delta ^{*} = \frac{{\overline{\gamma }}-2{\underline{b}}}{{\overline{\gamma }}-2{\underline{b}}+2{\widehat{b}}-\widehat{\gamma }}\left( <1\right) , \end{aligned}$$

  (23)

  then

  $$\begin{aligned} \left( q^{ROE_{2}},q^{ROE_{2}}\right) =\left( \frac{a}{2 {\underline{b}}\left( \delta \right) +{\overline{\gamma }}\left( \delta \right) }, \frac{a}{2 {\underline{b}}\left( \delta \right) + {\overline{\gamma }} \left( \delta \right) } \right) \end{aligned}$$

  (24)

  is the unique robust-optimization equilibrium of the Cournot duopoly in (13) and it converges to Cournot-Nash equilibrium of its nominal counterpart when $\delta \rightarrow 0$.

• ii) $\delta =\delta ^{*}$, then robust-optimization equilibria fill the segment $E_{2}=\left\{ \left( q,\frac{a}{2{\underline{b}}\left( \delta \right) }-q\right) | q^{M}\left( \delta ^{*}\right)>\frac{a}{2{\underline{b}}\left( \delta \right) }-q,q>{\overline{q}}\left( \delta ^{*}\right) \right\}$, where ${\overline{q}}\left( \delta \right)$ and $q^{M}\left( \delta \right)$ are defined in (17) and in (18), respectively.

• iii) $\delta ^{*}<\delta <1$ ($\delta ^{*}>0$ is equivalent to $2{\underline{b}} < {\overline{\gamma }}$), then $\left( q^{ROE_{2}},q^{ROE_{2}}\right)$,

  $$\begin{aligned} \left( q^{ROE_{3}},q^{ROE_{4}}\right) = \left( \frac{a \left( {\overline{b}} -{\underline{b}} \right) }{2{\underline{b}}\left( \delta \right) \left( {\overline{b}} -{\underline{b}} \right) +{\overline{\gamma }}\left( \delta \right) \left( {\overline{\gamma }} -{\underline{\gamma }} \right) }, \frac{a \left( {\overline{\gamma }} -{\underline{\gamma }} \right) }{2 {\underline{b}}\left( \delta \right) \left( {\overline{b}} -{\underline{b}} \right) + {\overline{\gamma }}\left( \delta \right) \left( {\overline{\gamma }} -{\underline{\gamma }} \right) } \right) \end{aligned}$$

  (25)

  and $\left( q^{ROE_{4}},q^{ROE_{3}}\right)$ are robust-optimization equilibrium of the Cournot duopoly in (13).

Proposition 2 underlines that a robust Cournot duopoly can have multiple robust-optimization equilibria.¹⁵ An example of coexisting robust-optimization equilibria is shown in Fig. 3, where the constellation of the values of the parameters used falls under case 3.iii) in Proposition 2. Therefore, in a robust Cournot duopoly game there may even be uncertainty about the Cournot-robust-optimization equilibrium the firms play. The multiplicity of equilibria vanishes as uncertainty vanishes: The nominal counterpart of the game admits a unique Cournot-Nash equilibrium, as indicated in Proposition 1.

The existence of multiple robust-optimization equilibria is only one peculiarity of the robust duopoly model (13). The second peculiarity is the presence of asymmetric robust-optimization equilibria (where a robust firm produces more/less than the other one) despite the assumption of identical robust players.¹⁶ Proposition 2 underlines that the coexistence of asymmetric Cournot-robust-optimization equilibria requires a certain level of uncertainty, that is $\delta >\delta ^{*}$, as well as a certain shape of the uncertainty set, that is ${\overline{b}}-{\underline{b}}<{\overline{\gamma }}-{\underline{\gamma }}$.

The existence of asymmetric equilibria in a symmetric game is not prerogative of robust games. It occurs in nominal games as well.¹⁷ After all, a robust game admits a nominal-game representation as shown in Sect. 2. The interesting point to underline here is indeed another one, that is the difference between a robust game that admits asymmetric equilibria and its nominal counterpart game that does not. This aspect has relevant economic implications. In fact, predictions made according to a nominal game can be misleading and uncertainty can have a strong impact on the final outcome of a game. It is also worth underlining that the worst-case frontier considered in this robust duopoly game is among the simplest ones. Thus, the differences between the robust duopoly model and its nominal counterpart is not the result of an ad-hoc worst-case frontier of the uncertainty set. A more complicated shape of the worst-case frontier (or simply asymmetric uncertainty sets) could imply an even more marked contrast between the output of robust game and the one of its nominal counterpart, see, e.g., Gardini and Radi (2023), suggesting that using a nominal game to infer the output of a robust game can lead to wrong forecasts.

The presence of multiple and asymmetric robust-optimization equilibria in a symmetric robust duopoly game implies heterogeneous levels of production for the two identical firms. This implies that a firm experiences a maximum guaranteed payoff (profit) at the equilibrium output which is higher than the one of the competitor, as specified in the following proposition (see proof in Appendix E).

Proposition 3

Assume that $\left( q^{ROE_{3}},q^{ROE_{4}}\right)$ is a robust-optimization equilibrium for game (13). Playing this robust-optimization equilibrium, robust firm (or player) 1 produces less then the competitor and it records a lower maximum-guaranteed profit. The opposite holds true in $\left( q^{ROE_{4}},q^{ROE_{3}}\right)$.

It comes out that in a robust Cournot duopoly game, which is symmetric and whose nominal counterpart has a unique symmetric Cournot-Nash equilibrium, an increase of uncertainty may generate asymmetry in the final outcome of the game and the earnings are not equally distributed. In other words, the aversion to uncertainty can cause two identical firms to coordinate to play an asymmetric robust-optimization equilibrium where one firm produces more and records a higher maximum guaranteed payoff. Moreover, the asymmetric robust-optimization equilibrium does not have a nominal counterpart, consistently with Definition 5. This confirms that uncertainty and ambiguity aversion can favor forms of coordination between firms non consistent with the ones predicted by a nominal game. On the contrary, the symmetric Cournot-robust-optimization equilibrium has a Cournot-Nash equilibrium counterpart. As indicated in Proposition 2, the Cournot-robust-optimization equilibrium $\left( q^{ROE_{1}},q^{ROE_{1}}\right)$ converges smoothly towards the Cournot-Nash equilibrium $\left( q^{NE},q^{NE}\right)$ when the level of uncertainty goes to zero. Specifically, the existence of a Cournot-robust-optimization equilibrium with a Cournot-Nash equilibrium counterpart is ensured when $\delta <\delta ^{*}$ and ${\overline{b}}-{\underline{b}}\ne {\overline{\gamma }}-{\underline{\gamma }}$. In fact the robust-duopoly model here considered satisfies all the conditions imposed in Theorem 5.

Concerning the payoffs of the players at the robust-optimization equilibria, an asymmetric robust-optimization equilibrium ensures to a firm a higher profit than the one the same firm would experience by playing the symmetric robust-optimization equilibrium. The same asymmetric robust-optimization equilibrium is not convenient for the competitor. In particular, we have the following result (see proof Appendix E).

Proposition 4

Assume that $\left( q^{ROE_{3}},q^{ROE_{4}}\right)$, $\left( q ^{ROE_{2}},q^{ROE_{2}}\right)$ and $\left( q^{ROE_{4}},q^{ROE_{3}}\right)$ are robust-optimization equilibria, then

$$\begin{aligned} \rho ^{\delta }\left( q^{ROE_{4}},q^{ROE_{3}}\right) \ge \rho ^{\delta }\left( q^{ROE_{2}},q ^{ROE_{2}}\right) \ge \rho ^{\delta }\left( q^{ROE_{3}},q^{ROE_{4}}\right) \end{aligned}$$

(26)

Therefore, for firm 2 it is convenient (in terms of maximum guaranteed payoff) to play the asymmetric robust-optimization equilibrium $\left( q^{ROE_{3}},q^{ROE_{4}}\right)$ rather than the symmetric robust-optimization equilibrium $\left( q^{ROE_{2}},q^{ROE_{2}}\right)$. On the contrary, for firm 1 it is convenient to play the symmetric robust-optimization equilibrium $\left( q^{ROE_{2}},q^{ROE_{2}}\right)$, rather than the asymmetric robust-optimization equilibrium $\left( q^{ROE_{3}},q^{ROE_{4}}\right)$. Symmetric arguments suggest that the vice versa is true when the asymmetric robust-optimization equilibrium $\left( q^{ROE_{4}},q^{ROE_{3}}\right)$ is considered in place of $\left( q^{ROE_{3}},q^{ROE_{4}}\right)$.

As a further remark on this point, for the example in Fig. 3 we can observe that the nominal profit of a firm at a robust-optimization equilibrium is larger than the one at the Nash equilibrium, see third picture from the left. Despite the profit of a firm at the Nash equilibrium being lower than the one at a robust-optimization equilibrium, it is always convenient to reduce one’s own level of uncertainty. This benefit can also be quantified. As underlined in the previous section, each firm (robust player) associates an opportunity cost of uncertainty to each possible action profile of this robust duopoly game. This opportunity cost of uncertainty measures the maximum amount that a single firm would pay to eliminate uncertainty when the competitor does not modify its own level of production. According to definition (2), the opportunity cost of uncertainty for firm i is given by

$$\begin{aligned} C^{\delta }\left( q_{-i}\right) =\rho ^{0}\left( R^{0}\left( q_{-i}\right) ,q_{-i}\right) -\rho ^{0}\left( R^{\delta }\left( q_{-i}\right) ,q_{-i}\right) \end{aligned}$$

(27)

where the best-reply function $R^{\delta }$ is as in (15).

An example of the behavior of firm i’s opportunity cost of uncertainty at a robust-optimization equilibrium is drawn in Fig. 3, picture in the middle. Considering the symmetric Cournot-robust-optimization equilibrium, we observe that the opportunity cost of uncertainty converges to zero when the level of uncertainty of the game vanishes. Considering the asymmetric Cournot-robust-optimization equilibria, we observe that the opportunity cost of uncertainty reduces reducing the level of uncertainty, but it is available only for $\delta \ge \delta ^{*}$, as these equilibria do not exist for $\delta \le \delta ^{*}$, see Proposition 2. Noting that the payoff functions of the robust Cournot duopoly game are concave with respect to the uncertain parameters, Theorem 8 applies and confirms that the opportunity cost of uncertainty goes to zero when uncertainty vanishes.

As a final remark, the theoretical results developed in the previous section, specifically Theorem 3, indicate that in equilibrium robust players play an $\epsilon$-Nash equilibrium, where $\epsilon$ measures the maximum of players’ opportunity cost of uncertainty. To underline this aspect, consider the example of Fig. 3, which is based on a constellation of parameter values such that three Cournot-robust-optimization equilibria exist. Figure 3, first picture from the left, shows that the Cournot-robust-optimization equilibria of the duopoly game belong to the set of $\epsilon$-Cournot-Nash equilibria. Specifically, the symmetric robust-optimization equilibrium belongs to the light gray region, which is the set of $\epsilon$-Nash equilibria, where $\epsilon$ is the maximum of players’ opportunity costs of information computed at this equilibrium. Moreover, the asymmetric robust-optimization equilibria belong to the dark gray region which is the set of $\epsilon$-Cournot-Nash equilibria, where $\epsilon$ is the maximum of players’ opportunity costs of information computed at these equilibria.

Fig. 3

First picture form the left, we observe in light-gray the set of all $\epsilon$-Nash equilibria of the nominal duopoly game, with $\epsilon = \max \left\{ C_{1}^{\delta }\left( q^{ROE_{4}}\right) ,C_{2}^{\delta }\left( q^{ROE_{3}}\right) \right\}$, which contains the robust-optimization equilibrium $\left( q^{ROE_{3}},q^{ROE_{4}}\right)$, see Theorem 3, and $\left( q^{ROE_{4}},q^{ROE_{3}}\right)$ by symmetry. In dark gray the set of all $\epsilon$-Nash equilibria of the nominal duopoly game, with $\epsilon = \max \left\{ C_{1}^{\delta }\left( q^{ROE_{2}}\right) ,C_{2}^{\delta }\left( q^{ROE_{2}}\right) \right\}$, which contains the robust-optimization equilibrium $\left( q^{ROE_{2}},q^{ROE_{2}}\right)$, see Theorem 3. Second picture from the left, the opportunity cost of uncertainty for firm i as a function of the level of uncertainty $\delta$. The third picture form the left, the different of profit that a firm obtain at a robust-optimization equilibrium with respect to the Nash equilibrium of the game. Parameters: $a=2$, ${\widehat{b}}=0.6$, ${\bar{b}}=0.8$, ${\underline{b}}=0.34$,, ${\widehat{b}}=0.4$, $\bar{\gamma }=0.79$, ${\underline{\gamma }}=0.0$, $\delta =1$

At the end of this section, it is worth noting the modeling flexibility offered by the robust game theory. As already pointed out, the worst-case best-reply functions are not monotonically decreasing despite the assumptions of a linear inverse demand function and of linear marginal costs. This is a relevant point. In fact non-monotone reaction functions are assumed by many, see for example (Rand, 1978), to show the inherent chaotic nature of a Cournot system. However, microeconomic foundations of Cournot duopoly games characterized by non-monotonic reaction curves usually require ad-hoc assumptions, such as marginal costs represented by cubic functions see, e.g. Furth (1986), or cost functions with an inter-firm externalities, see, e.g., Poston and Stewart (1978). This opens the puzzle on which market structures are capable of generating non-descending best reply functions. Robust game theory shows that non-monotonic reaction curves are possible even assuming simple market structures as long as there is some uncertainty about payoffs and firms are worst-case maximizers. As a final remark, by introducing uncertainty and worst-case players, we expect that non-monotonic reaction curves emerge even in other simple market models, such as Bertrand or Stackelberg ones. This conjecture is motivated by similar structures of these type games and their similarity with the Cournot duopoly game here analyzed, see, e.g., Fanti et al. (2013) and Gori and Sodini (2017).

6 Summary and Conclusions

A robust game is a generalization of a complete-information game where the worst-case approach is employed by players to handle uncertainty about their own payoffs and this uncertainty is represented by a bounded set of possible realizations. The solution concept of a robust game is known as robust-optimization equilibrium. The theoretical insights in this work underline the analogies, similarities and differences between a robust game and the so-called nominal counterpart game. The latter is the complete information game that is obtained when the level of uncertainty of a robust game is set to zero, while the former includes uncertainty on the payoffs. Specifically, this paper adds to the literature on robust games by showing, for the first time, that a robust-optimization equilibrium is an $\epsilon$-Nash equilibrium of the nominal counterpart game. A lower bound for $\epsilon$ is also obtained and coincides with the so-called opportunity cost of uncertainty, which measures the player’s advantage in knowing his own payoffs when the competitors do not change their strategies. Moreover, an ambiguity-aversion motivation for $\epsilon$-Nash equilibrium is provided by showing that it is always possible to add uncertainty to a complete information game, obtaining a robust game, such that the $\epsilon$-Nash equilibrium of the complete information game is a robust-optimization equilibrium of the robust game. Further theoretical insights show that it is possible to use $\epsilon$-Nash equilibria of the nominal counterpart game to study the effect of uncertainty on the solutions of a robust game.

The robust-game framework considered accommodates uncertainty generated by non private information only. A natural extension of the current work is to develop a general game-theoretical framework that accounts for both ambiguity on the opponents’ actions and uncertainty generated by non private information. An intermediate research project could be limited to introducing soft-robust games where players’ uncertain payoff environment is described by a distribution that belongs to some set of probability measures and players adopt the maxmin expected utility model axiomatized in Gilboa and Schmeidler (1989) as in soft-robust optimization, see, e.g., Ben-Tal et al. (2010). Moreover, the robust-game framework can be generalized to account for different degrees of uncertainty aversion. As a player may be pessimistic and looks for the maximum guaranteed payoff, another player may be optimistic and looks for the maximum profit possible. Furthermore, employing robust multiobjective optimization, see, e.g, Kuroiwa and Lee (2012), the extension of these results to vector-valued robust games, see Crespi et al. (2020), is interesting to investigate.

Appendices

Appendix A - Upper-Bound Approximation of the Opportunity Cost of Uncertainty

There is a class of robust games for which the behavior of the opportunity cost of uncertainty (which we assume to exist and being finite) can be approximated by a linear function of $\delta _{i}$. In fact, under the further assumption of $f_{i}\left( \varvec{\alpha }_{i};x_{i},{\textbf{x}}_{-i}\right)$ concave in $\varvec{\alpha }_{i}\in U_{i}$, for every $\left( x_{i},{\textbf{x}}_{-i}\right) \in A$ and $i\in {\mathcal {N}}$, as suggested in Crespi et al. (2017) it is possible to construct a function that is linear with respect to the parametrized level of uncertainty and that approximates by excess player i’s opportunity costs of uncertainty. To this aim, define

$$\begin{aligned} E_{i}\left( x_{i},{\textbf{x}}_{-i}\right) {:}{=} \rho ^{0}_{i}\left( x_{i},{\textbf{x}}_{-i}\right) -\rho ^{1}_{i}\left( x_{i},{\textbf{x}}_{-i}\right) \quad \forall i \in {\mathcal {N}} \end{aligned}$$

(28)

and the function

$$\begin{aligned} {\bar{E}}_{i}\left( {\textbf{x}}_{-i}\right) {:}{=} \max _{x_{i}\in A_{i}}E_{i}\left( x_{i},{\textbf{x}}_{-i}\right) \quad \forall i \in {\mathcal {N}} \end{aligned}$$

(29)

which can be used to construct an approximation by excess of the opportunity cost of uncertainty of player i as indicated in the following Lemma (see proof in Appendix C).

Lemma 2

Let $f_{i}\left( \varvec{\alpha }_{i};x_{i},{\textbf{x}}_{-i}\right)$ be concave in $\varvec{\alpha }_{i}\in U_{i}$, $\forall \left( x_{i},{\textbf{x}}_{-i}\right) \in A$ and $\forall i\in {\mathcal {N}}$. Then, $\delta _{i}{\bar{E}}_{i}\left( {\textbf{x}}_{-i}\right) \ge C^{\delta _{i}}_{i}\left( {\textbf{x}}_{-i}\right)$ $\forall {\textbf{x}}_{-i}\in A_{-i}$ and $\forall i \in {\mathcal {N}}$.

By definition, an $\epsilon ^{1}$-Nash equilibrium is also an $\epsilon ^{2}$-Nash equilibrium as long as $\epsilon ^{2}\ge \epsilon ^{1}$. Hence, Lemma 2 implies the following result.¹⁸

Theorem 8

Let $f_{i}\left( \varvec{\alpha }_{i};x_{i},{\textbf{x}}_{-i}\right)$ be concave in $\varvec{\alpha }_{i}\in U_{i}$, $\forall \left( x_{i},{\textbf{x}}_{-i}\right) \in A$ and $\forall i\in {\mathcal {N}}$. If $\left( x_{1}^{*},\ldots ,x_{n}^{*}\right) \in A$ is a robust-optimization equilibrium of the robust game $\left\{ A_{i},f_{i},W_{i}^{\delta _{i}}: i \in {\mathcal {N}} \right\}$, then $\left( x_{1}^{*},\ldots ,x_{n}^{*}\right)$ is an $\epsilon$-Nash equilibrium of its nominal counterpart, with $\epsilon =\max \left\{ \delta _{1}{\bar{E}}_{1}\left( {\textbf{x}}_{-1}^{*}\right) ,\ldots ,\delta _{n}{\bar{E}}_{n}\left( {\textbf{x}}_{-n}^{*}\right) \right\}$.

Theorem 8 underlines the relationship between a robust-optimization equilibrium of a robust game and an $\epsilon$-Nash equilibrium of the nominal counterpart game, where $\epsilon$ represents an upper bound of players’ opportunity costs of uncertainty. Differently from the opportunity cost of uncertainty defined in (2), this upper bound is a function that is both linear and strictly increasing in the level of uncertainty. In fact, by definition of $E_{i}$ in (28), the function ${\bar{E}}_{i}$ in (29) does not depend on $\delta _{i}$. Therefore, despite its being based on an upper-bound approximation of the opportunity cost of uncertainty, the result in Theorem 8 can be useful whenever a closed form expression for the opportunity cost of uncertainty is difficult do obtain. Note that the result in Theorem 8 can be used instead of the one in Theorem 3 to study the loss of profit derived by uncertainty only when the payoff functions are concave with respect to the uncertain parameters. In this respect, the scope of Theorem 8 is very large as players’ payoff functions are linear with respect to the uncertain parameters, therefore concave, in the majority of the games proposed in the literature.

Despite the broad applicability of Theorem 8, the current contribution represents a strong generalization of the results in Crespi et al. (2017). Indeed, Theorem 3 proves for the first time that a robust-optimization equilibrium is always an $\epsilon$-Nash equilibrium of the nominal counterpart game and, as a further addition to Crespi et al. (2017), a lower bound for $\epsilon$ is provided.

Appendix B - Uniqueness of Robust-Optimization Equilibrium

Considering the case $\delta _{i}=\delta$, in Theorem 5 uniqueness of the robust-optimization equilibrium is assumed. Conditions ensuring uniqueness of a Nash equilibrium date back to Rosen (1965). They apply to the case in which for every i the payoff function of player i has continuous partial derivatives with respect to the decision variables of the player, that is $x_i$. Hence, in order to apply Rosen’s result to a robust game, we need to exploit conditions ensuring that function $\rho _i^{\delta }\left( x_i, {\textbf{x}}_{-i}\right)$ has continuous partial derivatives with respect to $x_i$. These conditions are provided in the following theorem (see proof in Appendix C).

Theorem 9

Consider $M_{i}^{\delta }\left( x_{i},{\textbf{x}}_{-i}\right) = \arg \min _{\varvec{\alpha }_{i} \in W_{i}^{\delta }} f_{i}\left( \varvec{\alpha }_{i};x_{i},{\textbf{x}}_{-i}\right)$. Then, the following results hold true:

• (i) The set $M_{i}^{\delta }\left( x_{i},{\textbf{x}}_{-i}\right)$ is a singleton for every $\delta \in (0, 1]$ and for every $\left( x_{i},{\textbf{x}}_{-i}\right) \in A$, when one of the following conditions is satisfied¹⁹:

• (1) $f_{i}\left( \varvec{\alpha }_{i};x_{i}, {\textbf{x}}_{-i}\right)$ is linear in $\varvec{\alpha }_{i}$ for every $\left( x_{i},{\textbf{x}}_{-i}\right) \in A$ and the set $U_{i}$ is strictly convex;

• (2) $f_{i}\left( \varvec{\alpha }_{i}; x_{i},{\textbf{x}}_{-i}\right)$ is strictly quasi-convex in $\varvec{\alpha }_{i}$ for every $\left( x_{i},{\textbf{x}}_{-i}\right) \in A$.

• (ii) Assume that the first three points in Assumption 1 hold and, for every $\left( \varvec{\alpha }_{i},{\textbf{x}}_{-i}\right) \in W_{i}^{\delta _{i}}\times A_{-i}$, function $f_{i}\left( \varvec{\alpha }_{i};x_{i}, {\textbf{x}}_{-i}\right)$ is concave in $x_{i}$ and has partial derivatives with respect to $x_{i}\in D_{i}$, with $D_{i}$ open set containing $A_i$. If $M_{i}^{\delta }\left( x_{i},{\textbf{x}}_{-i}\right)$ is a singleton for every $\left( x_{i},{\textbf{x}}_{-i}\right) \in A$, then for every ${\textbf{x}}_{-i}\in A_{-i}$ function $\rho _i^{\delta }\left( x_{i},{\textbf{x}}_{-i}\right)$ has continuous partial derivatives with respect to $x_i$.

Having stated Theorem 9, we can now state Rosen’s conditions for the uniqueness of the robust-optimization equilibrium. Following (Rosen, 1965), in the next theorem we assume that each set $A_i$ can be represented as

$$\begin{aligned} A_i=\left\{ x_i: h_{ij}\left( x_i\right) \ge 0, j=1, \ldots , m_i\right\} \end{aligned}$$

(30)

where $h_{i j}$ are functions which admit continuous partial derivatives. Consider a positive vector ${\textbf{r}}=\left( r_{1},\ldots ,r_{n}\right)$, the vector of players’ actions ${\textbf{x}}\in A$, and set

$$\begin{aligned} g_{\rho ^{\delta }}\left( {\textbf{x}},{\textbf{r}}\right) =\left[ r_1 \nabla _{x_1}\rho _1^{\delta }\left( x_1,{\textbf{x}}_{-1}\right) , \ldots , r_n \nabla _{x_n}\rho _n^{\delta }\left( x_n,{\textbf{x}}_{-n}\right) \right] \end{aligned}$$

(31)

The following theorem (see proof in Appendix C) indicates under which conditions a robust game has a unique robust-optimization equilibrium.

Theorem 10

Consider a robust game with players’ action space as in (30). For all $i \in {\mathcal {N}}$, assume that $M_i^{\delta }\left( x_{i},{\textbf{x}}_{-i}\right)$ is a singleton $\forall \left( x_{i},{\textbf{x}}_{-i}\right) \in D_{i}\times D_{-i}$ and, $\forall \left( \varvec{\alpha }_{i},{\textbf{x}}_{-i}\right) \in W_{i}^{\delta _{i}}\times A_{-i}$, $f_i\left( \varvec{\alpha }_{i};x_{i},{\textbf{x}}_{-i}\right)$ is concave function with respect to $x_i$ and has partial derivatives with respect to $x_i\in D_i$. Assume furthermore that for some positive vector ${\textbf{r}}$ the following condition holds:

$$\begin{aligned} \left( {\textbf{x}}^1-{\textbf{x}}^0\right) '\left[ g_{\rho ^{\delta }}\left( {\textbf{x}}^1,{\textbf{r}}\right) -g_{\rho ^{\delta }}\left( {\textbf{x}}^0,{\textbf{r}}\right) \right] <0 \quad \forall {\textbf{x}}^1, {\textbf{x}}^0 \in A\ \text { with } \ {\textbf{x}}^1\ne {\textbf{x}}^0 \end{aligned}$$

(32)

where $g_{\rho ^{\delta }}$ is defined as in (31). Then, the robust game $\left\{ A_{i},f_{i},W_i^{\delta }: i \in {\mathcal {N}}\right\}$ has a unique robust-optimization equilibrium.

Condition (32) amounts to say that the map $g_{\rho ^{\delta }}(\cdot ,{\textbf{r}})$ is a strictly monotone map, see, e.g., Nagurney (1999). If condition (32) holds with $r_i=1$ for all $i\in {\mathcal {N}}$, then it can be shown that the previous theorem holds for general closed convex sets $A_i$, i.e. without requiring (30), see again (Nagurney, 1999). Condition (32) can be hard to check in practice. For this reason, we investigate now the particular case in which functions $f_{i}\left( \varvec{\alpha }_{i};x_{i},{\textbf{x}}_{-i}\right)$, $i=1,\ldots ,n$, are linear with respect to $\varvec{\alpha }_{i}$, for every $\left( x_{i},{\textbf{x}}_{-i}\right) \in A$. For the sake of simplicity, we assume that $U_i$ is a subset of ${\mathbb {R}}^{v_{i}}$, with $v_{i}=k$, for all $i \in \mathcal{N}$. In this case, the payoff function of each player $i \in {\mathcal {N}}$ con be expressed as:

$$\begin{aligned} f_{i}\left( \varvec{\alpha }_{i};x_{i},{\textbf{x}}_{-i}\right) = \sum _{j=1}^k\alpha _{ij}\gamma _{ij}\left( x_{i},{\textbf{x}}_{-i}\right) \end{aligned}$$

(33)

for some functions $\gamma _{ij}\left( x_i,{\textbf{x}}_{-i}\right)$, $j=1,\ldots ,k$. Set

$$\begin{aligned} z\left( \varvec{\alpha }_{1},\ldots ,\varvec{\alpha }_{n},{\textbf{x}}\right) =\left[ \nabla _{x_1} f_{1}\left( \varvec{\alpha }_{1};x_{1},{\textbf{x}}_{-1}\right) ,\ldots ,\nabla _{x_n} f_{n}\left( \varvec{\alpha }_{n};x_n,{\textbf{x}}_{-n}\right) \right] \end{aligned}$$

(34)

The following theorem (see proof in Appendix C) provides conditions for the uniqueness of a robust-optimization equilibrium in the particular case of payoff functions defined as in (33).

Theorem 11

Consider a robust game with payoff functions as in (33) and recall that $W_i^{\delta }=\delta U_{i}+\left( 1-\delta \right) \varvec{\alpha }_{i}^{0}$. For all $i \in {\mathcal {N}}$ and for each ${\textbf{x}}_{-i}\in A_{-i}$, assume that functions $\gamma _{ij}\left( x_i,{\textbf{x}}_{-i}\right)$, $j=1,\ldots ,k$, are concave with respect to $x_{i}$ and have partial derivatives with respect to $x_{i} \in D_{i}$, which are continuous with respect to $\left( x_i,{\textbf{x}}_{-i}\right) \in A$. Assume furthermore that $U_{i}\subseteq {\mathbb {R}}^k$, $i=1,\ldots ,n$, are strictly convex. The following applies:

• (i) If map $z\left( \varvec{\alpha }_{1}^{0},\ldots ,\varvec{\alpha }_{n}^{0},{\textbf{x}}\right)$ defined in (34) is strictly monotone, that is

  $$\begin{aligned} &\left( {\textbf{x}}^{1}-{\textbf{x}}^{0}\right) '\left[ z\left( \varvec{\alpha }_{1}^{0},\ldots ,\varvec{\alpha }_{n}^{0},{\textbf{x}}^{1}\right) -z\left( \varvec{\alpha }_{1}^{0},\ldots ,\varvec{\alpha }_{n}^{0},{\textbf{x}}^{0}\right) \right] <0\\ &\quad \forall {\textbf{x}}^1, {\textbf{x}}^0 \in A \ { with } \ {\textbf{x}}^1\ne {\textbf{x}}^0 \end{aligned}$$

  (35)

  then, there exists ${{\overline{\delta }}} >0$ such that the robust game $\left\{ A_{i}, f_{i},W_i^{\delta }: i \in {\mathcal {N}}\right\}$ has a unique robust-optimization equilibrium for every $\delta \in (0,{{\overline{\delta }}}]$;

• (ii) Set

  $$\begin{aligned} {\tilde{z}}_{j}\left( {\textbf{x}}\right) {:}{=}z_{j}\left( \varvec{\alpha }^{0}_{1},\ldots ,\varvec{\alpha }^{0}_{n},{\textbf{x}}\right) =\left( \varvec{\alpha }_{1j}^0\nabla _{x_1}\gamma _{1j}\left( x_{1},{\textbf{x}}_{-1}\right) , \ldots , \varvec{\alpha }_{nj}^0\nabla _{x_n}\gamma _{nj}\left( x_n,{\textbf{x}}_{-n}\right) \right) \end{aligned}$$

  (36)

  and further assume that functions ${\tilde{z}}_j$ are differentiable (which holds if functions $\gamma _{ij}$ are twice differentiable). Denote by $G_{j}\left( {\textbf{x}}\right)$ the Jacobian of ${\tilde{z}}_j$. If $G_{j}\left( {\textbf{x}}\right)$ is negative definite for all $j\in \left\{ 1,\ldots ,k\right\}$ and ${\textbf{x}}\in A$, then there exists ${{\overline{\delta }}} >0$ such that the robust game $\left\{ A_{i}, f_{i},W_i^{\delta }: i \in {\mathcal {N}}\right\}$ has a unique robust-optimization equilibrium for every $\delta \in \left( 0,{{\overline{\delta }}}\right]$.

Appendix C - Proofs of Results on Robust Games

Proof of Theorem 1

The complete information game $\left\{ A_{i},\rho _{i}^{\delta _{i}}: i \in {\mathcal {N}} \right\}$ has a Nash equilibrium by Lemma 2.5 in Arrow and Debreu (1954)[p. 274]. Since by hypothesis $\left\{ A_{i},\rho _{i}^{\delta _{i}}: i \in {\mathcal {N}} \right\}$ is equivalent to $\left\{ A_{i},f_{i},W_{i}^{\delta _{i}}: i \in {\mathcal {N}} \right\}$. Then, a Nash equilibrium of the first game is a robust-optimization equilibrium of the second one. This completes the proof. $\square$

Proof of Lemma 1

Since $f_{i}$ are continuous on $W^{\delta _{i}}_{i}\times A$ by hypothesis, $W^{\delta _{i}}_{i}\times A$ is bounded by hypothesis, and the worst-case payoff function is defined as

$$\begin{aligned} \rho ^{\delta _{i}}_{i}\left( x_{i},{\textbf{x}}_{-i}\right) = \min _{\varvec{\alpha }_{i}\in W^{\delta _{i}}_{i}}f_{i}\left( \varvec{\alpha }_{i};x_{i},{\textbf{x}}_{-i}\right) \end{aligned}$$

(37)

the continuity of $\rho ^{\delta _{i}}_{i}$ follows from Berge’s Maximum Theorem, see (Berge, 1963, pp. 115-117). Consider $x_{i}\in A_{i}$ and $y_{i} \in A_{i}$. By the hypothesis of the convexity of $A_{i}$ and the quasi-concavity of $f_{i}$ on $A_{i}$, for each $\lambda \in \left[ 0,1\right]$ and for each ${\textbf{x}}_{-i}\in A_{-i}$ we have:

$$\begin{aligned} \begin{array}{lll} \rho ^{\delta _{i}}_{i}\left( \lambda x_{i}+\left( 1-\lambda \right) y_{i},{\textbf{x}}_{-i}\right) &{} = &{} \min _{\varvec{\alpha }_{i}\in W^{\delta _{i}}_{i}}f\left( \varvec{\alpha }_{i};\lambda x_{i}+\left( 1-\lambda \right) y_{i},{\textbf{x}}_{-i}\right) \\ \\ &{} = &{} f\left( \varvec{\alpha }^{*}_{i};\lambda x_{i}+\left( 1-\lambda \right) y_{i},{\textbf{x}}_{-i}\right) \\ \\ &{} \ge &{} \min \left\{ f\left( \varvec{\alpha }^{*}_{i}; x_{i},{\textbf{x}}_{-i}\right) ; f\left( \varvec{\alpha }^{*}_{i}; y_{i},{\textbf{x}}_{-i}\right) \right\} \\ \\ &{} \ge &{} \min \left\{ \min _{\varvec{\alpha }_{i}\in W^{\delta _{i}}_{i}}f\left( \varvec{\alpha }_{i}; x_{i},{\textbf{x}}_{-i}\right) ; \min _{\varvec{\alpha }_{i}\in W^{\delta _{i}}_{i}}f\left( \varvec{\alpha }_{i}; y_{i},{\textbf{x}}_{-i}\right) \right\} \\ \\ &{} \ge &{} \min \left\{ \rho ^{\delta _{i}}_{i}\left( x_{i},{\textbf{x}}_{-i}\right) ;\rho ^{\delta _{i}}_{i}\left( y_{i},{\textbf{x}}_{-i}\right) \right\} \end{array} \end{aligned}$$

(38)

which proves the quasi-concavity of $\rho ^{\delta _{i}}_{i}\left( \cdot ,{\textbf{x}}_{-i}\right)$ for every ${\textbf{x}}_{-i}\in A_{-i}$. $\square$

Proof of Theorem 2

The conditions in Assumption 1 imply that the worst-case payoff functions satisfy the conditions imposed in Theorem 1, see Lemma 1. Then, the first point of the theorem follows (the first point is also considered in Crespi et al. (2017), the proof is reported here for the sake of completeness). Consider the second point. If $\left\{ A_{i},f_{i},W_{i}^{\delta _{i}}: i \in {\mathcal {N}} \right\}$ satisfies the conditions in Assumption 1, then $\left\{ A_{i},f_{i},W_{i}^{\bar{\delta }_{i}}: i \in {\mathcal {N}} \right\}$, with $\bar{\delta }_{i}\in \left[ 0,\delta _{i}\right]$, satisfies the conditions in Assumption 1 since $W^{\bar{\delta }_{i}}\subseteq W^{\delta _{i}}$. Hence, the proof of the second point of theorem follows from the first one. $\square$

Proof of Theorem 3

Given a generic strategic profile $\left( x_{1}^{+},\ldots ,x_{n}^{+}\right) \in A$, we have that

$$\begin{aligned} \rho ^{0}_{i}\left( x^{+}_{i},{\textbf{x}}^{+}_{-i}\right) \ge \rho ^{0}_{i}\left( x_{i},{\textbf{x}}^{+}_{-i}\right) - \max _{x_{i}\in A_{i}}\rho ^{0}_{i}\left( x_{i},{\textbf{x}}^{+}_{-i}\right) +\rho ^{0}_{i}\left( x^{+}_{i},{\textbf{x}}^{+}_{-i}\right) \text {, } \quad \forall x_{i} \in A_{i} \ \text { and } \ \forall i\in {\mathcal {N}} \end{aligned}$$

(39)

Then, let $\left( x_{1}^{*},\ldots ,x_{n}^{*}\right) \in A$ be a robust-optimization equilibrium of $\left\{ A_{i},f_{i},W_{i}^{\delta _{i}}: i \in {\mathcal {N}} \right\}$, it follows that

$$\begin{aligned} \rho ^{0}_{i}\left( x^{*}_{i},{\textbf{x}}^{*}_{-i}\right) \ge \rho ^{0}_{i}\left( x_{i},{\textbf{x}}^{*}_{-i}\right) - \max _{x_{i}\in A_{i}}\rho ^{0}_{i}\left( x_{i},{\textbf{x}}^{*}_{-i}\right) +\rho ^{0}_{i}\left( x^{*}_{i},{\textbf{x}}^{*}_{-i}\right) = \rho ^{0}_{i}\left( x_{i},{\textbf{x}}^{*}_{-i}\right) -C^{\delta _{i}}_{i}\left( {\textbf{x}}^{*}_{-i}\right) \text {, } \quad \forall i\in {\mathcal {N}} \end{aligned}$$

(40)

where $C_{i}^{\delta _{i}}\left( {\textbf{x}}_{-i}\right)$ is defined in (2). Set $\epsilon =\max \left\{ C^{\delta _{1}}_{1}\left( {\textbf{x}}_{-1}^{*}\right) ,\ldots , C^{\delta _{n}}_{n}\left( {\textbf{x}}_{-n}^{*}\right) \right\}$, we get

$$\begin{aligned} \rho ^{0}_{i}\left( x_{i}^{*},{\textbf{x}}_{-i}^{*}\right) \ge \rho ^{0}_{i}\left( x_{i},{\textbf{x}}_{-i}^{*}\right) -\epsilon \text {, } \quad \forall x_{i} \in A_{i} \ \text { and } \ \forall i\in {\mathcal {N}} \end{aligned}$$

(41)

Since $\rho ^{0}_{i}$ corresponds to the payoff function of agent i in the nominal counterpart game, for every $i \in {\mathcal {N}}$, (41) proves the first result of the theorem. To prove that $\left( x_{1}^{*},\ldots ,x_{n}^{*}\right) \in A$ is not an ${\hat{\epsilon }}$-Nash equilibrium, with ${\hat{\epsilon }}\in \left( 0,\epsilon \right)$, note that by definition $C_{i}^{\delta _{i}}\left( {\textbf{x}}^{*}_{-i}\right) \ge 0$. If $C_{i}^{\delta _{i}}\left( {\textbf{x}}^{*}_{-i}\right) =0$ for all $i\in {\mathcal {N}}$, then $\epsilon =0$ by definition and ${\hat{\epsilon }}\in \left( 0,\epsilon \right)$ cannot exist. If $\exists$ $i\in {\mathcal {N}}$ such that $C_{i}^{\delta _{i}}\left( {\textbf{x}}^{*}_{-i}\right) >0$, then $\exists$ $\left( x^{o}_{i},{\textbf{x}}^{*}_{-i}\right) \in A$, and $\left( x^{o}_{i},{\textbf{x}}^{*}_{-i}\right) \ne \left( x^{*}_{i},{\textbf{x}}^{*}_{-i}\right)$, such that $\rho _{i}^{0}\left( x^{o}_{i},{\textbf{x}}^{*}_{-i}\right) - \rho _{i}^{0}\left( x^{*}_{i},{\textbf{x}}^{*}_{-i}\right) =\epsilon >0$. It follows that $\left( x^{*}_{i},{\textbf{x}}^{*}_{-i}\right)$ cannot be an ${\hat{\epsilon }}$-Nash equilibrium, with ${\hat{\epsilon }}\in \left( 0,\epsilon \right)$. This proves the second result of the theorem. $\square$

Proof of Lemma 2

From the assumption of concavity of $f_{i}\left( \varvec{\alpha }_{i};x_{i},{\textbf{x}}_{-i}\right)$ with respect to $\varvec{\alpha }_{i}$, $\forall i\in {\mathcal {N}}$, we have that

$$\begin{aligned} \rho _{i}^{0}\left( x_{i},{\textbf{x}}_{-i}\right) -\rho _{i}^{\delta _{i}}\left( x_{i},{\textbf{x}}_{-i}\right) -\delta _{i}\left( \rho _{i}^{0}\left( x_{i},{\textbf{x}}_{-i}\right) -\rho _{i}^{1}\left( x_{i},{\textbf{x}}_{-i}\right) \right) \le 0 \end{aligned}$$

(42)

Then, by the sub-additivity property of the maximum operator, it follows that

$$\begin{aligned} \begin{array}{lll} \max _{x_{i}\in A_{i}}\rho _{i}^{0}\left( x_{i},{\textbf{x}}_{-i}\right) &{} \le &{} \max _{x_{i}\in A_{i}}\rho _{i}^{\delta _{i}}\left( x_{i},{\textbf{x}}_{-i}\right) +\max _{x_{i}\in A_{i}} \delta _{i} \left( \rho _{i}^{0}\left( x_{i},{\textbf{x}}_{-i}\right) -\rho _{i}^{1}\left( x_{i},{\textbf{x}}_{-i}\right) \right) \\ \\ &{}\le &{}\rho _{i}^{0}\left( x^{+}_{i}\left( \delta _{i}\right) ,{\textbf{x}}_{-i}\right) +\max _{x_{i}\in A_{i}}\delta _{i}\left( \rho _{i}^{0}\left( x_{i},{\textbf{x}}_{-i} \right) -\rho _{i}^{1}\left( x_{i},{\textbf{x}}_{-i}\right) \right) \end{array} \end{aligned}$$

(43)

where $x^{+}_{i}\left( \delta _{i}\right)$ is as in (2) and the last inequality follows from the property of the worst-case payoff function (see Property 1). This proves the lemma. $\square$

Proof of Theorem 4

By assumption $\left( x_{1}^{*},\ldots ,x^{*}_{n}\right)$ is an $\epsilon$-Nash equilibrium of the nominal game $\left\{ A_{i},f_{i}: i \in {\mathcal {N}} \right\}$. Define $\left\{ A_{i},{\bar{f}}_{i},W_{i}^{\delta _{i}}: i \in {\mathcal {N}} \right\}$ such that:

$$\begin{aligned} {\bar{f}}_{i}\left( \varvec{\alpha }_{i};x_{i},{\textbf{x}}_{-i}\right) =f_{i}\left( x_{i},{\textbf{x}}_{-i}\right) -\varvec{\alpha }_{i}{\textbf{1}}_{\left\{ x_{i}\ne x^{*}_{i}\right\} }\text {,}\quad \forall i \in {\mathcal {N}} \end{aligned}$$

(44)

where ${\textbf{1}}_{\left\{ \cdot \right\} }$ is the indicator function and $W_{i}^{\delta _{i}}=\delta _{i} \left[ 0,H\right]$, with $H>\epsilon$. Set $\delta _{i} =\frac{\epsilon }{H}$. Then, the worst-case payoff functions $\rho ^{\delta _{i}}_{i}$ of the robust game $\left\{ A_{i},{\bar{f}}_{i},W_{i}^{\delta _{i}}: i \in {\mathcal {N}} \right\}$ are such that $\rho ^{\delta _{i}}_{i}\left( x^{*}_{i},{\textbf{x}}^{*}_{-i}\right) =f_{i}\left( x^{*}_{i},{\textbf{x}}^{*}_{-i}\right)$ and $\rho ^{\delta _{i}}_{i}\left( x_{i},{\textbf{x}}_{-i}\right) =f_{i}\left( x_{i},{\textbf{x}}_{-i}\right) -\epsilon$ if $\left( x_{i},{\textbf{x}}_{-i}\right) \ne \left( x^{*}_{i},{\textbf{x}}^{*}_{-i}\right)$. It follows that $\left( x^{*}_{i},{\textbf{x}}^{*}_{-i}\right)$ is a robust-optimization equilibrium of the robust game $\left\{ A_{i},{\bar{f}}_{i},W_{i}^{\delta _{i}}: i \in {\mathcal {N}} \right\}$, which reduces to the nominal game $\left\{ A_{i},f_{i}: i \in {\mathcal {N}} \right\}$ when $\delta _{i} =0$. This completes the proof. $\square$

Proof of Theorem 5

Note that condition A1) implies condition A2), see Lemma 1. Therefore, it is sufficient to prove that the statement of the theorem holds true under condition A2). Moreover, considering the case $\bar{\delta }=1$, the generalization to the case $\bar{\delta }\in \left( 0,1\right]$ is straightforward. Choose $\delta \in \left[ 0,1\right]$ arbitrarily. By the conditions imposed in Assumption 1 and since by hypothesis $\rho ^{\delta }_{i}\left( x_{i},{\textbf{x}}_{-i}\right)$ are strictly concave in $x_{i}$ for all ${\textbf{x}}_{-i}\in A_{-i}$, the (robust) best reply $R^{\delta }_{i}$ defined in (4), with $i=1,\ldots ,n$, are single valued, i.e. they are real valued functions instead of more general correspondences: $R^{\delta }_{i}:A_{-i}\rightarrow A_{i}$. In fact, it is well-known that the maximum set of a strictly concave function is either empty or single-valued. Since the conditions imposed in Assumption 1 ensure that it is not empty, then it is single valued. Moreover, due to the assumption of continuity of $\rho _{i}^{\delta }$ with respect to $\left( x_{i},{\textbf{x}}_{-i}\right)$, by the Berge’s Maximum Theorem we known that $R^{\delta }_{i}\left( {\textbf{x}}_{-i}\right)$, for all $i=1,\ldots ,n$, are upper hemicontinuous in ${\textbf{x}}_{-i}\in A_{-i}$. Since it is well-known that a single-valued correspondence (a function) is upper hemicontinuous if and only if it is continuous, we have that $R^{\delta }_{i}\left( {\textbf{x}}_{-i}\right)$, for all $i=1,\ldots ,n$, are continuous functions in ${\textbf{x}}_{-i}\in A_{-i}$. Consider now $R^{\delta }_{i}\left( {\textbf{x}}_{-i}\right)$ as a function of $\left( {\textbf{x}}_{-i},\delta \right)$, i.e. $R^{\delta }_{i}:A_{-i}\times \left[ 0,1\right] \rightarrow A_{i}$. By the same argument and noting that $\delta$ defines a linear and convex combination of $\varvec{\alpha }_{i}\in W_{i}^{\bar{\delta }}$, the further hypothesis of $f_{i}\left( \varvec{\alpha }_{i};x_{i},{\textbf{x}}_{-i}\right)$ continuous on $W_{i}^{\bar{\delta }}\times A$ ensures $R^{\delta }_{i}\left( {\textbf{x}}_{-i}\right)$, for all $i=1,\ldots ,n$, continuous in $\left( {\textbf{x}}_{-i},\delta \right)$. Define $T\left( {\textbf{x}},\delta \right) =\left( R^{\delta }_{1}\left( {\textbf{x}}_{-1}\right) ,\ldots ,R^{\delta }_{n}\left( {\textbf{x}}_{-n}\right) \right)$. By construction $T\left( {\textbf{x}},\delta \right) : A\times \left[ 0,1\right] \rightarrow A$ is a single-valued correspondence (a function), it is continuous, and the robust-optimization equilibria of the robust game $\left\{ A_{i},f_{i},W_{i}^{\delta }: i \in N \right\}$ are the solution of $T\left( {\textbf{x}},\delta \right) ={\textbf{x}}$. Hence, by Theorem 2 it follows that for each $\delta \in \left[ 0,1\right]$ there is a solution (not necessarily unique), labeled by ${\textbf{x}}^{*}\left( \delta \right)$, of $T\left( {\textbf{x}},\delta \right) ={\textbf{x}}$. Moreover, by hypothesis that the robust game has a unique robust-optimization equilibrium, there exists a unique solution of $T\left( {\textbf{x}},\delta \right) ={\textbf{x}}$, labeled by ${\textbf{x}}^{*}\left( \delta \right)$. Consider a $\delta ^{*}\in \left[ 0,1\right]$. Suppose $\left\{ \delta ^{k}\right\}$ is an arbitrary sequence converging to $\delta ^{*}$, as $k\rightarrow +\infty$, and consider the set $B{:}{=}\left\{ {\textbf{x}}^{*}\left( \delta ^{k}\right) :k=1,2,\ldots \right\} \subset A$, where ${\textbf{x}}^{*}\left( \delta ^{k}\right)$ is solution of $T\left( {\textbf{x}},\delta ^{k}\right) ={\textbf{x}}$ in A (i.e. it is a robust-optimization equilibrium of $\left\{ A_{i},f_{i},W_{i}^{\delta ^{k}}: i \in {\mathcal {N}} \right\}$). Since A is complete, there exists a subsequence $\left\{ v^{k}\right\}$ of $\left\{ \delta ^{k}\right\}$ such that $\left\{ {\textbf{x}}^{*}\left( v^{k}\right) \right\}$ is convergent to some ${\textbf{z}}\in A$. By the assumption of continuity of T in $\left( {\textbf{x}},\delta \right)$ for each ${\textbf{x}}\in A$, it follows that ${\textbf{z}} =T\left( {\textbf{z}},\delta \right)$. Since ${\textbf{x}} =T\left( {\textbf{x}},\delta \right)$ has a unique solution by the hypothesis of a unique robust-optimization equilibrium for the robust game, we have ${\textbf{z}}={\textbf{x}}^{*}\left( \delta ^{*}\right)$. This implies that ${\textbf{x}}^{*}\left( \delta ^{k}\right)$ converges to ${\textbf{x}}^{*}\left( \delta ^{*}\right)$. Since $\left\{ \delta ^{k}\right\}$ is an arbitrary sequence converging to $\delta ^{*}$, we have that for each $\delta \in \left[ 0,1\right]$, equation $T\left( {\textbf{x}},\delta \right) ={\textbf{x}}$ has a solution (at least a solution) ${\textbf{x}}^{*}\left( \delta \right) \in A$ and ${\textbf{x}}^{*}\left( \delta \right) \rightarrow {\textbf{x}}^{*}\left( \delta ^{*}\right)$ as $\delta \rightarrow \delta ^{*}$. By the arbitrariness of $\delta ^{*}\in \left[ 0,1\right]$ and since ${\textbf{x}}^{*}\left( \delta \right)$ is a robust-optimization equilibrium for the robust game with $\delta$-level of uncertainty and ${\textbf{x}}^{*}\left( 0\right)$ is the Nash equilibrium of the nominal counterpart game by definition of T, the proof of the theorem is complete. $\square$

Proof of Theorem 6

Assume H1) holds. By hypothesis, a robust-optimization equilibrium exists, let us denote it by ${\textbf{x}}^{*}\left( \delta \right)$ which has a Nash-equilibrium counterpart ${\textbf{x}}^{*}\left( 0\right)$, which implies ${\textbf{x}}^{*}\left( \delta \right) \rightarrow {\textbf{x}}^{*}\left( 0\right)$, as $\delta \rightarrow 0^{+}$. By definition, see (2), the opportunity cost of uncertainty of player i is given by

$$\begin{aligned} C_{i}^{\delta }\left( {\textbf{x}}^{*}_{-i}\left( \delta \right) \right) =\max _{x_{i}\in A_{i}}\rho _{i}^{0}\left( x_{i},{\textbf{x}}_{-i}^{*}\left( \delta \right) \right) - \rho _{i}^{0}\left( x_{i}^{*}\left( \delta \right) ,{\textbf{x}}_{-i}^{*}\left( \delta \right) \right) \end{aligned}$$

(45)

It holds:

$$\begin{aligned} \begin{array}{lll} \lim _{\delta \rightarrow 0^{+}}C_{i}^{\delta }\left( {\textbf{x}}^{*}_{-i}\left( \delta \right) \right) &{} =&{} \lim _{\delta \rightarrow 0^{+}}\max _{x_{i}\in A_{i}}\rho _{i}^{0}\left( x_{i},{\textbf{x}}_{-i}^{*}\left( \delta \right) \right) -\lim _{\delta \rightarrow 0^{+}}\rho _{i}^{0}\left( x^{*}_{i}\left( \delta \right) ,{\textbf{x}}_{-i}^{*}\left( \delta \right) \right) \\ \\ &{} = &{} \lim _{\delta \rightarrow 0^{+}}\max _{x_{i}\in A_{i}}\rho _{i}^{0}\left( x_{i},{\textbf{x}}_{-i}^{*}\left( \delta \right) \right) -\rho _{i}^{0}\left( x^{*}_{i}\left( 0\right) ,{\textbf{x}}_{-i}^{*}\left( 0\right) \right) \end{array} \end{aligned}$$

(46)

The last inequality follows from the continuity assumption on $f_{i}\left( \varvec{\alpha }_{i}^{0};\cdot ,\cdot \right) {:}{=}\rho _{i}^{0}\left( \cdot ,\cdot \right)$, while the existence of the maximum follows from the continuity assumption on $\rho _{i}^{0}\left( \cdot ,\cdot \right)$ and compactness of $A_{i}$. Take a sequence $\delta _{n}\rightarrow 0^{+}$ as $n\rightarrow +\infty$ and consider

$$\begin{aligned} x_{i}\left( \delta _{n}\right) \in \arg \max _{x_{i}\in A_{i}}\rho _{i}^{0}\left( x_{i},{\textbf{x}}^{*}_{-i}\left( \delta _{n}\right) \right) \end{aligned}$$

(47)

Since $A_{i}$ is compact, without loss of generality we can assume $x_{i}\left( \delta _{n}\right) \rightarrow {\bar{x}}_{i}\in A_{i}$. The continuity assumption on $\rho ^{0}_{i}$ gives

$$\begin{aligned} \lim _{n\rightarrow +\infty }\rho _{i}^{0}\left( x_{i}\left( \delta _{n}\right) ,{\textbf{x}}^{*}_{-i}\left( \delta _{n}\right) \right) \rightarrow \rho _{i}^{0}\left( {\bar{x}}_{i},{\textbf{x}}^{*}_{-i}\left( 0\right) \right) \end{aligned}$$

(48)

Then, from

$$\begin{aligned} \rho _{i}^{0}\left( x_{i}\left( \delta _{n}\right) ,{\textbf{x}}^{*}_{-i}\left( \delta _{n}\right) \right) \ge \rho _{i}^{0}\left( x_{i},{\textbf{x}}^{*}_{-i}\left( \delta _{n}\right) \right) \text {, } \quad \forall x_{i}\in A_{i} \end{aligned}$$

(49)

it follows

$$\begin{aligned} \rho _{i}^{0}\left( {\bar{x}}_{i},{\textbf{x}}^{*}_{-i}\left( 0\right) \right) \ge \rho _{i}^{0}\left( x_{i},{\textbf{x}}^{*}_{-i}\left( 0\right) \right) \text {, }\quad \forall x_{i}\in A_{i} \end{aligned}$$

(50)

which gives

$$\begin{aligned} {\bar{x}}_{i} \in \arg \max _{x_{i}\in A_{i}}\rho ^{0}_{i}\left( x_{i},{\textbf{x}}^{*}_{-i}\left( 0\right) \right) \end{aligned}$$

(51)

Hence

$$\begin{aligned} \rho ^{0}_{i}\left( {\bar{x}}_{i},{\textbf{x}}^{*}_{-i}\left( 0\right) \right) =\rho ^{0}_{i}\left( x^{*}_{i}\left( 0\right) ,{\textbf{x}}^{*}_{-i}\left( 0\right) \right) \end{aligned}$$

(52)

and the proof of the first point of the theorem under assumption H1) is completed. Assume H2) holds. The continuity of opportunity cost of uncertainty (i.e. the first point of the theorem) follows from Lemma 2. If the first point holds true, the second point of the theorem is a consequence of Theorem 3 and of the definition of $\epsilon$-Nash equilibrium. $\square$

Proof of Theorem 7

Assume that $\left( {\bar{x}}_{i},\bar{{\textbf{x}}}_{-i}\right)$ is an $\epsilon$-Nash equilibrium and it is not an $\epsilon ^{1}$-Nash equilibrium, with $\epsilon ^{1}<\epsilon$. Then,

$$\begin{aligned} \epsilon = \max _{x_{i}\in A_{i}}\rho _{i}^{0}\left( x_{i},\bar{{\textbf{x}}}_{-i}\right) -\rho _{i}^{0}\left( {\bar{x}}_{i},\bar{{\textbf{x}}}_{-i}\right) \end{aligned}$$

(53)

for at least one $i\in {\mathcal {N}}$ and

$$\begin{aligned} \epsilon \ge \max _{x_{i}\in A_{i}}\rho _{i}^{0}\left( x_{i},\bar{{\textbf{x}}}_{-i}\right) -\rho _{i}^{0}\left( {\bar{x}}_{i},\bar{{\textbf{x}}}_{-i}\right) \end{aligned}$$

(54)

for all the other $i\in {\mathcal {N}}$. Further assuming $C^{\delta _{i}}_{i}\left( \bar{{\textbf{x}}}_{-i}\right) <\epsilon$ $\forall i \in {\mathcal {N}}$ implies that $\exists i \in {\mathcal {N}}$ such that:

$$\begin{aligned} \rho ^{0}_{i}\left( x^{+}_{i}\left( \delta _{i}\right) ,\bar{{\textbf{x}}}_{-i}\right) >\rho ^{0}_{i}\left( {\bar{x}}_{i},\bar{{\textbf{x}}}_{-i}\right) \quad \text {where} \quad x^{+}_{i}\left( \delta _{i}\right) \in \arg \max _{x_{i}\in A_{i}}\rho ^{\delta _{i}}_{i}\left( x_{i},\bar{{\textbf{x}}}_{-i}\right) \end{aligned}$$

(55)

Therefore ${\bar{x}}_{i}\left( \ne x^{+}_{i}\left( \delta _{i}\right) \right) \notin \arg \max _{x_{i}\in A_{i}}\rho ^{\delta _{i}}_{i}\left( x_{i},\bar{{\textbf{x}}}_{-i}\right)$ and $\left( {\bar{x}}_{i},\bar{{\textbf{x}}}_{-i}\right)$ is not a robust-optimization equilibrium. It follows that $\left( {\bar{x}}_{i},\bar{{\textbf{x}}}_{-i}\right)$ is strictly dominated by $\left( x_{i}^{+}\left( \delta _{i}\right) ,\bar{{\textbf{x}}}_{-i}\right)$ in the sense that the latter provides to player i a strictly-higher maximum-guaranteed payoff and a strictly-higher payoff in the nominal counterpart game. This proves point 1). Assume, instead, that $\exists i \in {\mathcal {N}}$ such that $C^{\delta _{i}}_{i}\left( \bar{{\textbf{x}}}_{-i}\right) >\epsilon$. Then, the hypothesis that $\left( {\bar{x}}_{i},\bar{{\textbf{x}}}_{-i}\right)$ is an $\epsilon$-Nash equilibrium and it is not an $\epsilon ^{1}$-Nash equilibrium, with $\epsilon ^{1}<\epsilon$, implies

$$\begin{aligned} \rho ^{0}_{i}\left( {\bar{x}}_{i},\bar{{\textbf{x}}}_{-i}\right) > \rho ^{0}_{i}\left( x^{+}_{i}\left( \delta _{i}\right) ,\bar{{\textbf{x}}}_{-i}\right) \end{aligned}$$

(56)

Therefore ${\bar{x}}_{i}\left( \ne x^{+}_{i}\left( \delta _{i}\right) \right) \notin \arg \max _{x_{i}\in A_{i}}\rho ^{\delta _{i}}_{i}\left( x_{i},\bar{{\textbf{x}}}_{-i}\right)$ and $\left( {\bar{x}}_{i},\bar{{\textbf{x}}}_{-i}\right)$ is not a robust-optimization equilibrium. It follows that $\left( {\bar{x}}_{i},\bar{{\textbf{x}}}_{-i}\right)$ is not strictly dominated by $\left( x_{i}^{+}\left( \delta _{i}\right) ,\bar{{\textbf{x}}}_{-i}\right)$ in the sense that the latter provides to player i a strictly-lower maximum-guaranteed payoff but the first one provides to the same player a strictly-higher payoff in the nominal counterpart game. This proves point 2). Given the arbitrary choice of $i\in {\mathcal {N}}$, the same hold true for all players when $C^{\delta _{i}}_{i}\left( \bar{{\textbf{x}}}_{-i}\right) >\epsilon$ $\forall i \in {\mathcal {N}}$. This proves point 3). $\square$

Proof of Theorem 9

Consider point i), case 1). By assumption the sets $W_i^{\delta }$, $i=1,\ldots ,n$, are strictly convex for every $\delta \in \left( 0,1\right]$. Hence function $f_i\left( \cdot ;x_i, {\textbf{x}}_{-i}\right)$ has a unique minimizer over the set $W_i^{\delta }$ or equivalently $M_i^{\delta }\left( x_i,{\textbf{x}}_{-i}\right)$ is a singleton for every $\left( x_{i},{\textbf{x}}_{-i}\right) \in A$, see, e.g., Berger and Svindland (2019). Results in the same reference ensure $M_i^{\delta }\left( x_i,{\textbf{x}}_{-i}\right)$ is a singleton in case 2). This proves point i). Consider point ii). Denote by ${{\overline{\partial }}}_{x_i} \rho _i^{\delta }\left( x_i,{\textbf{x}}_{-i}\right)$ the superdifferential of $\rho _i^{\delta }\left( x_i,{\textbf{x}}_{-i}\right)$ with respect to $x_i$. It is known that

$$\begin{aligned} {{\overline{\partial }}}_{x_i} \rho _i^{\delta }\left( x_i, {\textbf{x}}_{-i}\right) = \overline{\textrm{conv}}\{\nabla _{x_i}f_{i}\left( \varvec{\alpha }_{i};x_{i},{\textbf{x}}_{-i}\right) , \varvec{\alpha }_{i} \in M_i^{\delta }\left( x_i, {\textbf{x}}_{-i}\right) \} \end{aligned}$$

(57)

where $\overline{\textrm{conv}}\left\{ C\right\}$ denotes the closed convex hull of the set C and $\nabla _{x_i}f_i$ is the gradient of $f_i$ with respect to $x_i$, see, e.g., Ioffe and Tihomirov (1979). Since $M_i^{\delta }\left( x_i,{\textbf{x}}_{-i}\right)$ is a singleton, we get

$$\begin{aligned} {{\overline{\partial }}}_{x_i} \rho _i^{\delta }\left( x_i, {\textbf{x}}_{-i}\right) = \nabla _{x_i}f_i\left( \overline{\varvec{\alpha }}_i; x_i, {\textbf{x}}_{-i}\right) \end{aligned}$$

(58)

where $\overline{\varvec{\alpha }}_{i}= \overline{\varvec{\alpha }}_{i}\left( x_i, {\textbf{x}}_{-i}\right)$ is the unique element in $M_i^{\delta }\left( x_i, {\textbf{x}}_{-i}\right)$. Hence, ${{\overline{\partial }}}_{x_i} \rho _i^{\delta }\left( x_i, {\textbf{x}}_{-i}\right)$ is a singleton for every $\left( x_i,{\textbf{x}}_{-i}\right) \in D_i\times D_{-i}$. By assumption $f_{i}\left( \varvec{\alpha }_{i};x_{i}, {\textbf{x}}_{-i}\right)$ is concave in $x_{i}$ for every $\left( \varvec{\alpha }_{i},{\textbf{x}}_{-i}\right) \in W_{i}^{\delta _{i}}\times A_{-i}$. Therefore, $\rho _i^{\delta }\left( x_i, {\textbf{x}}_{-i}\right)$ is a concave function in $x_i$ for every ${\textbf{x}}_{-i}\in A_{-i}$. This implies that it has continuous partial derivatives with respect to $x_{i}$, see, e.g., Roberts and Varberg (1973). This proves point ii) and completes the proof. $\square$

Proof of Theorem 10

According to Theorem 9, functions $\rho _i^{\delta }$, $i=\left\{ 1,\ldots ,n\right\}$, have continuous partial derivatives with respect to $x_{i}$. Then, according to Rosen (1965), condition (32) is sufficient to ensure uniqueness of equilibrium for $\left\{ A_{i},\rho ^{\delta }_{i}: i \in {\mathcal {N}}\right\}$, which is the nominal-game representation of the robust game $\left\{ A_{i},f_{i},W_i^{\delta }: i \in {\mathcal {N}}\right\}$. Therefore, the two games have the same equilibria, see Theorem 1. This completes the proof. $\square$

Proof of Theorem 11

Consider point i). Let

$$\begin{aligned} \nabla _{x_{i}}f_{i}\left( \varvec{\alpha }_{i};x_{i},{\textbf{x}}_{-i}\right) =\sum _{j=1}^k\alpha _{ij}\nabla _{x_i}\gamma _{ij}\left( x_{i},{\textbf{x}}_{-i}\right) \end{aligned}$$

(59)

and for each $x_{i},y_{i}\in A_{i}$ set

$$\begin{aligned} w_{i}\left( \varvec{\alpha }_1, \ldots ,\varvec{\alpha }_n,x_{i},y_{i},{\textbf{x}}_{-i}\right) =\left( x_{i}-y_{i}\right) '\nabla _{x_i} f_i\left( \varvec{\alpha }_{i};x_i,{\textbf{x}}_{-i}\right) =\sum _{j=1}^k\alpha _{ij}\left( x_{i}-y_{i}\right) '\nabla _{x_i}\gamma _{ij}\left( x_i,{\textbf{x}}_{-i}\right) \end{aligned}$$

(60)

It is easy to see that functions $w_{i}\left( \varvec{\alpha }_1, \ldots ,\varvec{\alpha }_n,x_{i},y_{i},{\textbf{x}}_{-i}\right)$, $i=1,\ldots ,n$, are continuous in $\varvec{\alpha }_{i}\in U_i$, for all $i \in \mathcal{N}$, uniformly with respect to $x_i, y_i\in A_i$ and ${\textbf{x}}_{-i}\in A_{-i}$ (this is a consequence of the continuity of $\nabla _{x_i}\gamma _{ij}\left( x_i, {\textbf{x}}_{-i}\right)$ and the compactness of $A_i$). Since condition (35) can be written as

$$\begin{aligned} \sum _{i=1}^n \left( w_i\left( \varvec{\alpha }^{0}_1, \ldots ,\varvec{\alpha }^{0}_n,x_i^1, x_i^0,{\textbf{x}}_{-i}\right) +w_i\left( \varvec{\alpha }^{0}_1, \ldots ,\varvec{\alpha }^{0}_n,x_i^0, x_i^1,{\textbf{x}}_{-i}\right) \right) <0 \end{aligned}$$

(61)

uniform continuity of $w_i$ implies the existence of neighborhoods $V_{i}$ of $\varvec{\alpha }_i^0$, $i \in {\mathcal {N}}$, such that condition (35) holds for $\varvec{\alpha }_i \in V_i$, and $x_{i}^0, x_{i}^1 \in A_{i}$ with $x_{i}^1\ne x_{i}^0$. Choose now ${{\overline{\delta }}}$ such that $W_i^{{{\overline{\delta }}}}\subseteq V_i$, $\forall i \in \mathcal{N}$. $W_i^{\delta }$ is strictly convex for all $\delta \in \left[ 0,1\right]$ because by assumption $U_{i}$ is strictly convex. Then, from Theorem 9 we obtain that $\rho _i^{\delta }\left( x_i,{\textbf{x}}_{-i}\right)$, with $\delta \in (0, {{\overline{\delta }}}]$, has continuous partial derivatives with respect to $x_{i}$ and

$$\begin{aligned} \nabla _{x_i}\rho _i^{\delta }\left( x_i,{\textbf{x}}_{-i}\right) =\nabla _{x_i}f_{i}\left( \overline{\varvec{\alpha }}_{i}; x_i,{\textbf{x}}_{-i}\right) \end{aligned}$$

(62)

where $\overline{\varvec{\alpha }}_{i}$ is the unique element in $M_i^{\delta }\left( x_{i},{\textbf{x}}_{-i}\right) \subseteq W_i^{\delta }$. Hence, condition (32) with $r_i=1$ for all $i\in {\mathcal {N}}$ holds. This proves point i). Consider point ii). Observe that the Jacobian of $z\left( \varvec{\alpha }^{0}_{1},\ldots ,\varvec{\alpha }^{0}_{n},{\textbf{x}}\right)$ is given by

$$\begin{aligned} G\left( \varvec{\alpha }^{0}_{1},\ldots ,\varvec{\alpha }^{0}_{n},{\textbf{x}}\right) = \sum _{j=1}^k G_j\left( {\textbf{x}}\right) \end{aligned}$$

(63)

Hence $G\left( \varvec{\alpha }^{0}_{1},\ldots ,\varvec{\alpha }^{0}_{n},{\textbf{x}}\right)$ is negative definite for ${\textbf{x}}$ in A. This implies that condition (35) holds, see, e.g., Nagurney (1999), and proves point ii). $\square$

Appendix D - Algorithm for Worst-Case Best-Reply Functions

Consider a robust game, where the uncertainty sets are polyhedral, then the following algorithm can used to obtain the worst-case best-reply functions.

Appendix E - Proofs of the Results on the Robust Duopoly Model in Sect. 5

Proof of Proposition 1

The action space of the nominal Cournot duopoly model can be partitioned in 4 regions

$$\begin{aligned} \begin{array}{lllcclll} \Omega _{1} &{}=&{}\left\{ \left( q_{1},q_{2}\right) |\frac{a}{\widehat{ \gamma }}>\text { }q_{2}\ge 0\wedge \frac{a}{\widehat{\gamma }}>\text { }q_{1}\ge 0\right\} &{} \quad \quad &{} \Omega _{3} &{}=&{}\left\{ \left( q_{1},q_{2}\right) |\text { }q_{2}\ge \frac{a}{\widehat{\gamma }}\wedge \frac{a}{\widehat{\gamma }}>\text { } q_{1}\ge 0\right\} \\ \Omega _{2} &{}=&{}\left\{ \left( q_{1},q_{2}\right) |\frac{a}{\widehat{ \gamma }}>\text { }q_{2}\ge 0\wedge \text { }q_{1}\ge \frac{a}{\widehat{\gamma }}\right\} &{} \quad \quad &{} \Omega _{4} &{}=&{}\left\{ \left( q_{1},q_{2}\right) |q_{2}\ge \frac{a}{\widehat{\gamma }}0\wedge q_{1}\ge \frac{a}{\widehat{\gamma }} \right\} \\ \end{array} \end{aligned}$$

Moreover, by definition a Nash equilibrium $\left( q_{1}^{*},q_{2}^{*}\right)$ of the game solves

$$\begin{aligned} \left( q_{1}^{*},q_{2}^{*}\right) =\left( R^{0}\left( q_{2}^{*}\right) ,R^{0}\left( q_{1}^{*}\right) \right) \end{aligned}$$

(67)

Hence, a sufficient condition for $\left( q_{1}^{*},q_{2}^{*}\right) \in \Omega _{i}$, with $i\in \left\{ 1,2,3,4\right\}$, to be a Nash equilibrium is $\left( R^{0}\left( q_{2}^{*}\right) ,R^{0}\left( q_{1}^{*}\right) \right) \in \Omega _{i}$. Then, since $\forall \left( q_{1}^{*},q_{2}^{*}\right) \in$ $\Omega _{4}$ holds that $\left( R^{0}\left( q_{2}^{*}\right) ,R^{0}\left( q_{1}^{*}\right) \right) =\left( 0,0\right) \notin \Omega _{4}$, Nash equilibria do not exist in $\Omega _{4}$. At the same time, $\forall \left( q_{1}^{*},q_{2}^{*}\right) \in$ $\Omega _{3}$ the condition $\left( R^{0}\left( q_{2}^{*}\right) ,R^{0}\left( q_{1}^{*}\right) \right) =\left( 0,R^{0}\left( 0\right) \right) \in \Omega _{3}$ implies $R^{0}\left( 0\right) \ge \frac{a}{\widehat{\gamma }}$, or equivalently $\widehat{\gamma }>2{\widehat{b}}$, which violates Assumption 2. Thus, there are no Nash equilibria in $\Omega _{3}$. By symmetry, there are no Nash equilibria in $\Omega _{2}$. Finally, straightforward algebra shows that the Nash equilibrium in (21) is the unique solution of the system $\left( q_{1},q_{2}\right) =\left( R^{0}\left( q_{2}\right) ,R^{0}\left( q_{1}\right) \right)$ in $\Omega _{1}$ and it always exists under Assumption 2. $\square$

Proof of Proposition 2

By hypothesis $\delta >0$. Then, the action space of the robust Cournot duopoly model in (13) can be partitioned in 16 regions.

$$\begin{aligned} \begin{array}{*{20}l} {\Omega _{1} = \left\{ {\left( {q_{1} ,q_{2} } \right)|\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q} \left( \delta \right) > q_{1} \ge 0 \wedge \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q} \left( \delta \right) > q_{2} \ge 0} \right\}} \hfill & {\Omega _{9} = \left\{ {\left( {q_{1} ,q_{2} } \right)|q^{M} \left( \delta \right) > q_{1} \ge \bar{q}\left( \delta \right) \wedge \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q} \left( \delta \right) > q_{2} \ge 0} \right\}} \hfill \\ {\Omega _{2} = \left\{ {\left( {q_{1} ,q_{2} } \right)|\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q} \left( \delta \right) > q_{1} \ge 0 \wedge \bar{q}\left( \delta \right) > q_{2} \ge \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q} \left( \delta \right)} \right\}} \hfill & {\Omega _{{10}} = \left\{ {\left( {q_{1} ,q_{2} } \right)|q^{M} \left( \delta \right) > q_{1} \ge \bar{q}\left( \delta \right) \wedge \bar{q}\left( \delta \right) > q_{2} \ge \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q} \left( \delta \right)} \right\}} \hfill \\ {\Omega _{3} = \left\{ {\left( {q_{1} ,q_{2} } \right)|\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q} \left( \delta \right) > q_{1} \ge 0 \wedge q^{M} \left( \delta \right) > q_{2} \ge \bar{q}\left( \delta \right)} \right\}} \hfill & {\Omega _{{11}} = \left\{ {\left( {q_{1} ,q_{2} } \right)|q^{M} \left( \delta \right) > q_{1} \ge \bar{q}\left( \delta \right) \wedge q^{M} \left( \delta \right) > q_{2} \ge \bar{q}\left( \delta \right)} \right\}} \hfill \\ {\Omega _{4} = \left\{ {\left( {q_{1} ,q_{2} } \right)|\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q} \left( \delta \right) > q_{1} \ge 0 \wedge q_{2} \ge q^{M} \left( \delta \right)} \right\}} \hfill & {\Omega _{{12}} = \left\{ {\left( {q_{1} ,q_{2} } \right)|q^{M} \left( \delta \right) > q_{1} \ge \bar{q}\left( \delta \right) \wedge q_{2} \ge q^{M} \left( \delta \right)} \right\}} \hfill \\ {\Omega _{5} = \left\{ {\left( {q_{1} ,q_{2} } \right)|\bar{q}\left( \delta \right) > q_{1} \ge \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q} \left( \delta \right) \wedge \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q} \left( \delta \right) > q_{2} \ge 0} \right\}} \hfill & {\Omega _{{13}} = \left\{ {\left( {q_{1} ,q_{2} } \right)|q_{1} \ge q^{M} \left( \delta \right) \wedge \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q} \left( \delta \right) > q_{2} \ge 0} \right\}} \hfill \\ {\Omega _{6} = \left\{ {\left( {q_{1} ,q_{2} } \right)|\bar{q}\left( \delta \right) > q_{1} \ge \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q} \left( \delta \right) \wedge \bar{q}\left( \delta \right) > q_{2} \ge \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q} \left( \delta \right)} \right\}} \hfill & {\Omega _{{14}} = \left\{ {\left( {q_{1} ,q_{2} } \right)|q_{1} \ge q^{M} \left( \delta \right) \wedge \bar{q}\left( \delta \right) > q_{2} \ge \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q} \left( \delta \right)} \right\}} \hfill \\ {\Omega _{7} = \left\{ {\left( {q_{1} ,q_{2} } \right)|\bar{q}\left( \delta \right) > q_{1} \ge \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q} \left( \delta \right) \wedge q^{M} \left( \delta \right) > q_{2} \ge \bar{q}\left( \delta \right)} \right\}} \hfill & {\Omega _{{15}} = \left\{ {\left( {q_{1} ,q_{2} } \right)|q_{1} \ge q^{M} \left( \delta \right) \wedge q^{M} \left( \delta \right) > q_{2} \ge \bar{q}\left( \delta \right)} \right\}} \hfill \\ {\Omega _{8} = \left\{ {\left( {q_{1} ,q_{2} } \right)|\bar{q}\left( \delta \right) > q_{1} \ge \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q} \left( \delta \right) \wedge q_{2} \ge q^{M} \left( \delta \right)} \right\}} \hfill & {\Omega _{{16}} = \left\{ {\left( {q_{1} ,q_{2} } \right)|q_{1} \ge q^{M} \left( \delta \right) \wedge q_{2} \ge q^{M} \left( \delta \right)} \right\}} \hfill \\ \end{array} \end{aligned}$$

According to definition (19), $\left( q_{1}^{*},q_{2}^{*}\right)$ is a robust-optimization equilibrium of our Cournot duopoly model if and only if

$$\begin{aligned} \left( q_{1}^{*},q_{2}^{*}\right) =\left( R^{\delta }\left( q_{2}^{*}\right) ,R^{\delta }\left( q_{1}^{*}\right) \right) \end{aligned}$$

(68)

Then, a necessary condition for $\left( q_{1}^{*},q_{2}^{*}\right) \in \Omega _{i}$, with $i\in \left\{ 1,2,...,16\right\}$, is $\left( R^{\delta }\left( q_{2}^{*}\right) ,R^{\delta }\left( q_{1}^{*}\right) \right) \in \Omega _{i}$. It follows that:

• There are no robust-optimization equilibria in $\Omega _{16}$. Indeed $\forall \left( q_{1},q_{2}\right) \in$ $\Omega _{16}$, we have that $\left( R^{\delta }\left( q_{2}\right) ,R^{\delta }\left( q_{1}\right) \right) =\left( 0,0\right) \notin \Omega _{16}$;

• There are no robust-optimization equilibria in $\Omega _{15}\cup \Omega _{14}$. Indeed $\forall \left( q_{1},q_{2}\right) \in \Omega _{15}\cup \Omega _{14}$ we have $\left( R^{\delta }\left( q_{2}\right) ,R^{\delta }\left( q_{1}\right) \right) =\left( R^{\delta }\left( q_{2}\right) ,0\right) \notin$ $\Omega _{15}\cup \Omega _{14}$. By symmetric arguments, the same holds true in $\Omega _{8}\cup \Omega _{12}$;

• There are no robust-optimization equilibria in $\Omega _{4}$. Indeed $\forall \left( q_{1}^{*},q_{2}^{*}\right) \in \Omega _{4}$ the condition $\left( R^{\delta }\left( q_{2}^{*}\right) ,R^{\delta }\left( q_{1}^{*}\right) \right) =\left( 0,R^{\delta }\left( 0\right) \right) \in \Omega _{4}$ implies $R^{\delta }\left( 0\right) \ge q^{M}\left( \delta \right)$, or equivalently ${\underline{\gamma }}\left( \delta \right) >2{\overline{b}}\left( \delta \right)$ which contradicts Assumption 2. By symmetric arguments, the same holds true in $\Omega _{13}$;

• There are no robust-optimization equilibria in $\Omega _{9}$. Indeed, solving (68) in $\Omega _{9}$ we obtain

  $$\begin{aligned} q_{1}^{*}=\frac{ \left( 2 {\underline{b}}\left( \delta \right) -{\underline{\gamma }}\left( \delta \right) \right) a}{ 4{\overline{b}}\left( \delta \right) {\underline{b}}\left( \delta \right) -{\overline{\gamma }}\left( \delta \right) {\underline{\gamma }} \left( \delta \right) } \quad \text {and} \quad q_{2}^{*}=\frac{\left( 2{\overline{b}}\left( \delta \right) -{\overline{\gamma }}\left( \delta \right) \right) a }{4{\overline{b}}\left( \delta \right) {\underline{b}}\left( \delta \right) -{\overline{\gamma }}\left( \delta \right) {\underline{\gamma }}\left( \delta \right) } \end{aligned}$$

  (69)

  imposing $\left( q_{1}^{*},q_{2}^{*}\right) \in \Omega _{9}$ is equivalent to $q ^{M}\left( \delta \right) > q_{1}^{*}\ge {\overline{q}}\left( \delta \right)$ and ${\underline{q}}\left( \delta \right)>q_{2}^{*}>0$, which implies

  $$\begin{aligned}{} & {} \left( 2{\underline{b}}\left( \delta \right) -{\underline{\gamma }}\left( \delta \right) \right) \left( {\overline{\gamma }} -{\underline{\gamma }} \right)>\left( 2{\overline{b}}\left( \delta \right) -{\overline{\gamma }}\left( \delta \right) \right) \left( {\overline{b}} -{\underline{b}} \right) \quad \nonumber \\{} & {} \text {and}\quad \left( 2{\underline{b}}\left( \delta \right) -{\underline{\gamma }}\left( \delta \right) \right) \left( {\overline{b}} -{\underline{b}}\right) > \left( 2{\overline{b}}\left( \delta \right) -{\overline{\gamma }}\left( \delta \right) \right) \left( {\overline{\gamma }} -{\underline{\gamma }} \right) \end{aligned}$$

  (70)

  where one condition contradicts the other one. By symmetric arguments, there are not robust-optimization equilibria in $\Omega _{3}$.

• There are no robust-optimization equilibria in $\Omega _{2}$. Indeed, solving (68) in $\Omega _{2}$ we obtain

  $$\begin{aligned} q_{1}^{*}=\frac{\left( {\overline{\gamma }} - {\underline{\gamma }} \right) a }{2 {\overline{b}}\left( \delta \right) \left( {\overline{b}} -{\underline{b}} \right) + {\underline{\gamma }}\left( \delta \right) \left( {\overline{\gamma }} -{\underline{\gamma }} \right) } \quad \text {and}\quad q_{2}^{*}=\frac{\left( {\overline{b}} - {\underline{b}} \right) a }{2{\overline{b}}\left( \delta \right) \left( {\overline{b}}-{\underline{b}} \right) + {\underline{\gamma }}\left( \delta \right) \left( {\overline{\gamma }} -{\underline{\gamma }} \right) } \end{aligned}$$

  (71)

  imposing $\left( q_{1}^{*},q_{2}^{*}\right) \in \Omega _{2}$ is equivalent to have ${\underline{q}}\left( \delta \right)>q_{1}^{*}>0$ and ${\overline{q}}\left( \delta \right) >q_{2}^{*}\ge {\underline{q}}\left( \delta \right)$, which implies ${\overline{b}} -{\underline{b}} >{\overline{\gamma }} -{\underline{\gamma }}$ to have $q_{2}^{*}>q_{1}^{*}$ and $2{\overline{b}}\left( \delta \right) <{\underline{\gamma }}\left( \delta \right)$ to have $q_{2}^{*}\ge {\underline{q}}\left( \delta \right)$. However, the latter condition violates Assumption 2, in fact $2{\widehat{b}}\left( \delta \right) >\widehat{\gamma }\left( \delta \right)$ implies $2{\overline{b}}\left( \delta \right) \left(>2{\widehat{b}}\left( \delta \right)>\widehat{\gamma }\left( \delta \right) \right) >{\underline{\gamma }}\left( \delta \right)$. By symmetric arguments, there are no robust-optimization equilibria in $\Omega _{5}$.

In the reminder partitions of the state space of the game, robust-optimization equilibria exist under certain conditions:

• Solving (68) in $\Omega _{1}$, we obtain $q_{1}^{*}=q_{2}^{*}=q^{ROE_{1}}$. Imposing $\left( q^{ROE_{1}},q^{ROE_{1}}\right) \in \Omega _{1}$ is equivalent to ${\underline{q}}\left( \delta \right)>q^{ROE_{1}}>0$ and it is satisfied if and only if ${\overline{b}} -{\underline{b}} >{\overline{\gamma }} -{\underline{\gamma }}$. Then $\left( q^{ROE_{1}},q^{ROE_{1}}\right)$ is a robust-optimization equilibrium if and only if the latter condition is satisfied.

• According to (68), a robust-optimization equilibrium in $\Omega _{6}$ implies

  $$\begin{aligned} q^{*}_{1}=\frac{{\overline{\gamma }} -{\underline{\gamma }} }{{\overline{b}} -{\underline{b}} }q^{*}_{2} \quad \text {and} \quad q^{*}_{2}=\frac{{\overline{\gamma }} -{\underline{\gamma }} }{{\overline{b}} - {\underline{b}} }q^{*}_{1} \end{aligned}$$

  (72)

  Then, ${\overline{b}} -{\underline{b}} ={\overline{\gamma }} -{\underline{\gamma }}$ and $q^{*}_{1}=q^{*}_{2}=q^{*}$. Hence, a continuum of robust-optimization equilibria exists and is given by

  $$\begin{aligned} \left\{ \left( q^{*},q^{*}\right) \ | \ {\overline{q}}\left( \delta \right) >\text { }q^{*}\ge {\underline{q}}\left( \delta \right) \right\} \end{aligned}$$

  (73)

  where (73) is obtained imposing the feasibility condition $\left( q_{1}^{*},q_{2}^{*}\right) \in \Omega _{6}$, or there are no robust-optimization equilibria.

• Solving (68) in $\Omega _{11}$ under condition ${\overline{\gamma }}\left( \delta \right) \ne 2{\underline{b}}\left( \delta \right)$, we obtain $q_{1}^{*}= q_{2}^{*}=q^{ROE_{2}}$. Imposing $\left( q^{ROE_{2}},q^{ROE_{2}}\right) \in \Omega _{11}$, we have that it is a robust-optimization equilibrium if and only if ${\overline{b}} -{\underline{b}} <{\overline{\gamma }} -{\underline{\gamma }}$. For ${\overline{\gamma }}\left( \delta \right) = 2{\underline{b}}\left( \delta \right)$, solving (68) in $\Omega _{11}$ we obtain $q^{*}_{1}=\frac{a }{2{\underline{b}}\left( \delta \right) }-q^{*}_{2}$. Therefore, $\left( q,\frac{a-c}{2{\underline{b}}\left( \delta \right) }-q\right) \in \Omega _{11}$ are robust-optimization equilibria.

• Solving (19) in $\Omega _{7}$, we obtain $q_{1}^{*}=q^{ROE_{3}}$ and $q_{2}^{*}=q^{ROE_{4}}$. Imposing $\left( q^{ROE_{3}},q^{ROE_{4}}\right) \in \Omega _{7}$, we have $q^{M}\left( \delta \right) >q^{ROE_{4}}\ge {\overline{q}}\left( \delta \right)$ and ${\overline{q}}\left( \delta \right) >q^{ROE_{3}}\ge {\underline{q}}\left( \delta \right)$. The first condition is equivalent to ${\overline{\gamma }} -{\underline{\gamma }} >{\overline{b}} -{\underline{b}}$, which implies that the second reduces to ${\overline{\gamma }}\left( \delta \right) >2{\underline{b}}\left( \delta \right)$. Then $\left( q^{ROE_{3}},q^{ROE_{4}}\right)$ is a robust-optimization equilibrium if and only if the latter two conditions are both satisfied. By symmetric arguments, $\left( q^{ROE_{4}},q^{ROE_{3}}\right) \in \Omega _{10}$ is a robust-optimization equilibrium if and only if the latter two conditions hold.

This completes the proof. $\square$

Proof of Proposition 3

By assumption $\left( q^{ROE_{3}},q^{ROE_{4}}\right)$ is a robust-optimization equilibrium of the game, then ${\overline{\gamma }}-{\underline{\gamma }}>{\overline{b}}-{\underline{b}}$ and $\delta >\delta ^{*}$ by Theorem 2. The first condition implies $q^{ROE_{4}}>q^{ROE_{3}}$, while the second condition is equivalent to ${\overline{\gamma }}\left( \delta \right) >2{\underline{b}}\left( \delta \right)$ and implies

$$\begin{aligned}{} & {} \rho ^{\delta }\left( q^{ROE_{3}},q^{ROE_{4}}\right) -\rho ^{\delta }\left( q^{ROE_{4}},q^{ROE_{3}}\right) =\nonumber \\{} & {} a\left( 1- \frac{{\underline{b}}\left( \delta \right) \left( {\overline{b}}\left( \delta \right) -{\underline{b}}\left( \delta \right) \right) +{\underline{b}}\left( \delta \right) \left( \overline{\gamma }\left( \delta \right) -{\underline{\gamma }}\left( \delta \right) \right) }{2{\underline{b}}\left( \delta \right) \left( {\overline{b}}\left( \delta \right) -{\underline{b}}\left( \delta \right) \right) +{\overline{\gamma }}\left( \delta \right) \left( {\overline{\gamma }}\left( \delta \right) -{\underline{\gamma }}\left( \delta \right) \right) }\right) \left( q^{ROE_{3}}-q^{ROE_{4}}\right) <0 \end{aligned}$$

(74)

The symmetry of the game completes the proof. $\square$

Proof of Proposition 4

The existence of the three robust-optimization equilibria implies ${\overline{\gamma }}-{\underline{\gamma }}>{\overline{b}}-{\underline{b}}$ and $\delta \in \left( \delta ^*,1\right]$ (or equivalently ${\overline{\gamma }}\left( \delta \right) >2{\underline{b}}\left( \delta \right)$), from which it follows that $q^{ROE_{4}}>q^{ROE_{2}}>q^{ROE_{3}}$. Moreover, we have

$$\begin{aligned} \rho ^{\delta }\left( q^{ROE_{2}},q^{ROE_{2}}\right) = {\underline{b}} \left( q^{ROE_{2}}\right) ^2\quad \quad \quad \quad \rho ^{\delta }\left( q^{ROE_{3}},q^{ROE_{4}}\right) ={\underline{b}} \left( q^{ROE_{3}}\right) ^2 \end{aligned}$$

(75)

and

$$\begin{aligned} \rho ^{\delta }\left( q^{ROE_{4}},q^{ROE_{3}}\right) =\frac{ \left( 2{\underline{b}}-{\overline{\gamma }}\right) \left( {\overline{b}}-{\underline{b}}\right) +\left( {\overline{\gamma }}-{\underline{b}}\right) \left( {\overline{\gamma }}-{\underline{\gamma }}\right) }{{\overline{\gamma }}-{\underline{\gamma }}} \left( q^{ROE_{4}}\right) ^2 \end{aligned}$$

(76)

for all $\delta \in \left[ \delta ^{*},1\right]$. Therefore,

$$ \rho ^{\delta } \left( {q^{{ROE_{2} }} ,q^{{ROE_{2} }} } \right) - \rho ^{\delta } \left( {q^{{ROE_{3} }} ,q^{{ROE_{4} }} } \right) = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} \left( {q^{{ROE_{2} }} - q^{{ROE_{3} }} } \right)\left( {q^{{ROE_{2} }} + q^{{ROE_{3} }} } \right) > 0 $$

(77)

and

$$ \rho ^{\delta }\left( q^{ROE_{4}},q^{ROE_{3}}\right) -\rho ^{\delta }\left( q^{ROE_{2}},q^{ROE_{2}}\right)> {\underline{b}}\left( q^{ROE_{4}}- q^{ROE_{2}} \right) \left( q^{ROE_{4}} + q^{ROE_{2}} \right) >0 $$

(78)

which proves the Proposition. $\square$