Portfolio Selection with a Rank-Deficient Covariance Matrix

Abstract

In this paper, we consider optimal portfolio selection when the covariance matrix of the asset returns is rank-deficient. For this case, the original Markowitz’ problem does not have a unique solution. The possible solutions belong to either two subspaces namely the range- or nullspace of the covariance matrix. The former case has been treated elsewhere but not the latter. We derive an analytical unique solution, assuming the solution is in the null space, that is risk-free and has minimum norm. Furthermore, we analyse the iterative method which is called the discrete functional particle method in the rank-deficient case. It is shown that the method is convergent giving a risk-free solution and we derive the initial condition that gives the smallest possible weights in the norm. Finally, simulation results on artificial problems as well as real-world applications verify that the method is both efficient and stable.

1 Introduction

Modern portfolio theory plays an important role in finance for both researchers and practitioners. Its fundamental goal is to provide efficient ways for the allocation of investments among different assets in the portfolio. The basic concepts of modern portfolio theory were developed in Markowitz (1952), who introduced a mean-variance portfolio optimization procedure in which investors incorporate their preferences towards variance and their expectation of the return on different assets. The original Markowitz problem is formulated as follows

$$\begin{aligned} \begin{aligned} \min _{\textbf{w}} \textbf{w}^\top \varvec{\Sigma }\textbf{w}\ \ \ \text {s.t.}\ \ \ \textbf{w}^\top \textbf{1} = 1, \ \textbf{w}^\top \varvec{\mu } = q, \end{aligned} \end{aligned}$$

(1)

where $\textbf{w}$ is a vector of portfolio weights, $\varvec{\mu }$ and $\varvec{\Sigma }$ are mean vector and covariance matrix of the asset returns, $\textbf{1}$ denotes the vector of ones, and q stands for the expected rate of return on the portfolio. In practice, both parameters $\varvec{\mu }$ and $\varvec{\Sigma }$ are unobservable and, therefore, need to be estimated from historical data. The most common estimators are sample mean vector and sample covariance matrix (see, for example, Bodnar and Schmid, 2011; Bodnar et al., 2017; Bauder et al., 2018; Javed et al., 2021a, b; Okhrin and Schmid, 2006 among many others). The sample covariance matrix is positive definite when the number of observations is greater than the portfolio size, otherwise, it is positive semi-definite and rank-deficient.¹ Let us note that there is also a strand of the literature on robust optimization this is aiming at reducing the impact of parameter uncertainty (see, for example, Dai and Wang, 2019; Dai and Wen, 2018; Goldfarb and Iyengar, 2003; Lobo and Boyd, 2000 among many others).

If $\varvec{\Sigma }$ is a positive definite matrix, then the optimization problem in (1) has a unique (global) minimum given by

$$\begin{aligned} \begin{aligned} \textbf{w} = \dfrac{c - b q}{ac - b^2} \varvec{\Sigma }^{-1}\textbf{1} + \dfrac{a q - b}{ac - b^2}\varvec{\Sigma }^{-1}\varvec{\mu }, \end{aligned} \end{aligned}$$

(2)

where $a = \textbf{1}^\top \varvec{\Sigma }^{-1}\textbf{1},\; b = \textbf{1}^\top \varvec{\Sigma }^{-1}\varvec{\mu }$, and $c = \varvec{\mu }^\top \varvec{\Sigma }^{-1}\varvec{\mu }$. It is worth mentioning that considering the constraint $\textbf{w}^\top \varvec{\mu }\ge q$ instead of $\textbf{w}^\top \varvec{\mu }= q$ in (1) leads us back to the solution (2) unless the expected return q is such that $q< \varvec{\mu }^\top {\varvec{\Sigma }^{-1} \textbf{1}}/({\textbf{1}^\top \varvec{\Sigma }^{-1} \textbf{1}}).$ In this case the solution is given as

$$\begin{aligned} \textbf{w}= \frac{\varvec{\Sigma }^{-1} \textbf{1}}{\textbf{1}^\top \varvec{\Sigma }^{-1} \textbf{1}}. \end{aligned}$$

(3)

The optimal portfolio weights obtained as in (3) are known in the literature as global minimum variance portfolio weights (see, for example, Bodnar et al. 2017). Meanwhile, if $\varvec{\Sigma }$ is rank-deficient, the minimum is not necessarily unique and the solution given in (2) is not valid since the regular inverse of $\varvec{\Sigma }$ does not exist. In Pappas et al. (2010), it has been shown that if, in addition to the constraints in (1), one would assume that $\textbf{w}$ does not belong to the null space of $\varvec{\Sigma }$, $\mathcal {N}(\varvec{\Sigma })$, the minimum would be achieved at

$$\begin{aligned} \begin{aligned} \textbf{w} = \dfrac{c - b q}{ac - b^2} \varvec{\Sigma }^{+}\textbf{1} + \dfrac{a q - b}{ac - b^2}\varvec{\Sigma }^{+}\varvec{\mu } \end{aligned} \end{aligned}$$

(4)

where $a = \textbf{1}^\top \varvec{\Sigma }^{+}\textbf{1},\; b = \textbf{1}^\top \varvec{\Sigma }^{+}\varvec{\mu }$, $c = \varvec{\mu }^\top \varvec{\Sigma }^{+}\varvec{\mu },$ and $\varvec{\Sigma }^{+}$ denotes the Moore–Penrose inverse of $\varvec{\Sigma }.$ Note that the expression in (4) is used in several papers with a focus on statistical analysis (Alfelt and Mazur 2022; Bodnar et al. 2016, 2017, 2019, 2022). However, there is no obvious motivation for the additional constraint $\textbf{w}\not \in \mathcal {N}(\varvec{\Sigma })$, except the apparent similarity between solutions given in (4) and (2). Moreover, the expression in (4) is not a solution to the classical Markowitz’ problem formulated in (1) unless this constraint is imposed. Further on, we refer to this solution as a Range Space (RS) solution.

The focus of this paper is on the rank-deficient case. We contribute to the existing literature by deriving an analytical solution to (1) that can be obtained via the singular value decomposition (SVD). This solution lies in the null space of $\varvec{\Sigma }$ and, therefore, is a global (non-unique) minimum of (1). In addition, this global minimum corresponds to the smallest portfolio weight norm among all the other minima. For these reasons, we call the solution as a risk-free minimum norm solution or, when comparing to the RS soltuion (4), as a null space minimum norm (NSMN) solution to (1). There are disadvantages of using the SVD approach. Firstly, the SVD may be computationally costly. Secondly, if there is a need to find many portfolios even smaller size SVDs might increase the computational cost too much. Consequently, it might be of value to use an iterative method. Here, our second contribution to the existing literature comes in. We further develop the iterative method presented in Gulliksson and Mazur (2020), called the Discrete Functional Particle Method (DFPM), and analyze its convergence properties for rank-deficient $\varvec{\Sigma }$. We show that DFPM always converges to a risk-free solution and, for a specific choice of the initial value, the same minimum norm solution to (1) as mentioned above.

The structure of the paper is as follows. In Sect. 2, we present the analytical form of the risk-free minimum norm solution. Section 3 discuss the solution obtained via the DFPM. Sections 4 and 5 consist of a simulation and empirical studies, respectively.

2 Risk-Free Minimum Norm Solution

We begin by stating the conditions for a unique solution of (1). It is then convenient to use a more compact form of our problem

$$\begin{aligned} \begin{aligned} \min _{\textbf{w}} \textbf{w}^\top \varvec{\Sigma }\textbf{w}\ \ \ \text {s.t.}\ \ \ \mathbf {Bw = c},\\ \end{aligned} \end{aligned}$$

(5)

where

$$\begin{aligned} \textbf{B} = \begin{bmatrix} \textbf{1}^\top \\ \varvec{\mu }^\top \end{bmatrix} \in \mathbb {R}^{2\times p}, \quad \textbf{c} = \begin{bmatrix} 1 \\ q \\ \end{bmatrix}\in \mathbb {R}^{2}. \end{aligned}$$

(6)

From now on, we assume that $\textbf{B}$ has full rank, i.e., $\varvec{\mu }$ is not parallel to $\textbf{1}$. It is straight forward to treat the case of $\textbf{B}$ rank-deficient. For the analysis to come, we use the singular value decomposition of $\varvec{\Sigma }$,

$$\begin{aligned} {\varvec{\Sigma }} = \textbf{V}_{\varvec{\Sigma }} \textbf{D}_{\varvec{\Sigma }} \textbf{V}_{\varvec{\Sigma }}^\top , \end{aligned}$$

(7)

where $\mathbf {V_{\varvec{\Sigma }}}\in \mathbb {R}^{p\times p}$ is orthonormal and $\mathbf {D_{\varvec{\Sigma }}} = \text {diag}(\sigma _1, \ldots , \sigma _r, 0, \ldots , 0)$, $\sigma _j>0,$ $j=1, \ldots , r$ with r the rank of $\varvec{\Sigma }$. We will also need the following partition

$$\begin{aligned} \begin{aligned} \mathbf {V_{\varvec{\Sigma }}} = \begin{bmatrix} \textbf{V}_{{\varvec{\Sigma }}_{1}} &{} \textbf{V}_{{\varvec{\Sigma }}_{2}}\\ \end{bmatrix}, \quad \mathbf {D_{\varvec{\Sigma }}} = \begin{bmatrix} \textbf{D}_{{\varvec{\Sigma }}_{1}} &{} \textbf{0 }\\ \textbf{0 }&{} \textbf{0 }\end{bmatrix}, \end{aligned} \end{aligned}$$

(8)

where $\textbf{V}_{{\varvec{\Sigma }}_{1}}\in \mathbb {R}^{p\times r}$, $\textbf{V}_{{\varvec{\Sigma }}_{2}}\in \mathbb {R}^{p\times (p-r)}$, $\textbf{D}_{{\varvec{\Sigma }}_{1}} = \text {diag}(\sigma _1, \ldots , \sigma _r)$, and $\textbf{0}$ stands for the matrix of zeros. Due to this partition, the decomposition (7) can be written in reduced form

$$\begin{aligned} {\varvec{\Sigma }} = \textbf{V}_{{\varvec{\Sigma }}_{1}}\textbf{D}_{{\varvec{\Sigma }}_{1}}\textbf{V}_{{\varvec{\Sigma }}_{1}}^\top . \end{aligned}$$

(9)

In the next lemma, we show that if the rank of $\varvec{\Sigma }$ is less than $p-2$, a solution to (1) is non-unique.

Lemma 2.1

The solution to the optimization problem given in (1) is not unique if $r<p-2.$

Proof

Using the KKT-conditions with the Lagrange function $L = \textbf{w}^\top \varvec{\Sigma }\textbf{w} + \varvec{\lambda }^\top (\mathbf {Bw - c})$, the solution is given by the linear system

$$\begin{aligned} \begin{bmatrix} \varvec{\Sigma }&{} \textbf{B}^\top \\ \textbf{B} &{} \textbf{0} \end{bmatrix} \begin{bmatrix} \textbf{w} \\ \varvec{\lambda } \end{bmatrix} = \begin{bmatrix} \textbf{0} \\ \textbf{c} \end{bmatrix}, \end{aligned}$$

(10)

where the elements in $\varvec{\lambda }$ contains the two Lagrange parameters. Substituting the SVD given in (7) into (10), we get

$$\begin{aligned} \begin{bmatrix} \mathbf {D_{\varvec{\Sigma }}} &{} \textbf{V}^\top \textbf{B}^\top \\ \textbf{B}\textbf{V}&{} \textbf{0} \end{bmatrix} \begin{bmatrix} \textbf{V}^\top \textbf{w}\\ \varvec{\lambda } \end{bmatrix} = \begin{bmatrix} \textbf{0} \\ \textbf{c} \end{bmatrix}. \end{aligned}$$

(11)

Next, using the partition (8), we can write

$$\begin{aligned} \begin{bmatrix} \textbf{D}_{{\varvec{\Sigma }}_{1}} &{} \textbf{0} &{} \left( \textbf{B}\textbf{V}_{\varvec{\Sigma }_1}\right) ^\top \, \\ \textbf{0} &{} \textbf{0} &{} \left( \textbf{B}\textbf{V}_{\varvec{\Sigma }_2}\right) ^\top \, \\ \textbf{B}\textbf{V}_{\varvec{\Sigma }_1} &{} \textbf{B}\textbf{V}_{\varvec{\Sigma }_2} &{} \textbf{0} \end{bmatrix} \begin{bmatrix} \textbf{V}_{\varvec{\Sigma }_1}^\top \textbf{w}\\ \textbf{V}_{\varvec{\Sigma }_2}^\top \textbf{w}\\ \varvec{\lambda } \end{bmatrix} = \begin{bmatrix} \textbf{0} \\ \textbf{0} \\ \textbf{c} \end{bmatrix}. \end{aligned}$$

(12)

The matrix $\textbf{B}\textbf{V}_{\varvec{\Sigma }_2}$ is of size $2 \times (n-r)$. Therefore, if $r<p-2$, i.e. $p-r>2$, the matrix in (10) will be rank-deficient and, consequently, the solution will not be unique. The lemma is proved. $\square$

Since we are only interested in the case of a non-unique solution, we from now on assume that $r<p-2$.

The next lemma gives us a condition for a solution to be risk-free, i.e., $\textbf{w}^\top \varvec{\Sigma }\textbf{w}=0.$

Lemma 2.2

Let $r<p-2$. Then $\textbf{w}^\top \varvec{\Sigma }\textbf{w}=0$ if and only if $\textbf{w}= \textbf{V}_{{\varvec{\Sigma }}_{2}}\textbf{y},$ where $\textbf{V}_{{\varvec{\Sigma }}_{2}}$ is defined in the partition (8) and $\textbf{y}\in \mathbb {R}^{p-r}$.

Proof

Using the SVD of $\varvec{\Sigma }$ in (7) and (8), we have

$$\begin{aligned} \textbf{w}^\top \varvec{\Sigma }\textbf{w} = \textbf{w}^\top \textbf{V}_{{\varvec{\Sigma }}_{1}}\textbf{D}_{{\varvec{\Sigma }}_{1}}\textbf{V}_{{\varvec{\Sigma }}_{1}}^\top \textbf{w} = \varvec{\xi }^\top \textbf{D}_{{\varvec{\Sigma }}_{1}} \varvec{\xi } = \sum _{j=1}^r {\xi }_j^2\sigma _j, \end{aligned}$$

where $\varvec{\xi } = \textbf{V}_{{\varvec{\Sigma }}_{1}}^\top \textbf{w}$. Therefore, $\textbf{w}^\top \varvec{\Sigma }\textbf{w}=0$ implies $\varvec{\xi }= \textbf{0}$ and $\textbf{V}_{{\varvec{\Sigma }}_{1}}^\top \textbf{w}= \textbf{0}$. Since $\textbf{V}_{{\varvec{\Sigma }}_{1}}^\top \textbf{V}_{{\varvec{\Sigma }}_{2}}=0$, we get $\textbf{w} = \textbf{V}_{{\varvec{\Sigma }}_{2}}\textbf{y}$. The other implication in the lemma is obvious. The proof of the lemma is complete. $\square$

Next, we show how to choose a risk-free solution with a minimal $\ell _2$ norm. For this, we need yet another SVD decomposition. We introduce $\textbf{Y}= \textbf{B} \textbf{V}_{{\varvec{\Sigma }}_{2}} \in \mathbb R^{2\times (p-r)}$ and define its decomposition as

$$\begin{aligned} \textbf{Y}= \textbf{U}_{\textbf{Y}}\textbf{D}_{\textbf{Y}} \textbf{V}_{\textbf{Y}}^\top , \end{aligned}$$

(13)

or in the reduced form,

$$\begin{aligned} \textbf{Y}=\textbf{U}_{\textbf{Y}_1} \textbf{D}_{\textbf{Y}_1} \textbf{V}_{\textbf{Y}_1}^\top , \end{aligned}$$

(14)

where

$$\begin{aligned} \begin{aligned} \textbf{V}_{\textbf{Y}} = \begin{bmatrix} \textbf{V}_{\textbf{Y}_1}&\textbf{V}_{\textbf{Y}_2} \end{bmatrix}, \quad \textbf{D}_{\textbf{Y}_1} = \begin{bmatrix} \gamma _1&{} 0\\ 0&{}\gamma _2\\ \end{bmatrix} , \quad \gamma _j>0,\ j \in \{1,2\}, \end{aligned} \end{aligned}$$

(15)

and ${\textbf{V}_{\textbf{Y}}}_1\in \mathbb {R}^{(p-r)\times 2}$, ${\textbf{V}_{\textbf{Y}}}_2\in \mathbb {R}^{(p-r)\times (p-r-2)}$. Let $\mathcal N (\textbf{A})$ stands for the null space of the matrix $\textbf{A}.$ We can now formulate our main theorem.

Theorem 2.1

Let $r<p-2$ and $\textbf{V}_{\varvec{\Sigma }_2}$ is defined as in (8), $\textbf{Y}= \textbf{B}\textbf{V}_{\varvec{\Sigma }_{2}}$ and $\textbf{V}_{\textbf{Y}_2}$ is given as in (15). Then

$$\begin{aligned} \textbf{w}= \textbf{V}_{\varvec{\Sigma }_2} \textbf{Y}^{+} \textbf{c}+ \textbf{V}_{\varvec{\Sigma }_2} \textbf{x}, \quad \textbf{x}\in \mathcal {N}(\textbf{Y}), \end{aligned}$$

(16)

is a solution to (1) and it gives zero risk. The minimum norm solution among (16), or specifically, the solution to

$$\begin{aligned} \begin{aligned}&\underset{\textbf{w}\in \mathbb {R}^p}{\textrm{min}} \; \frac{1}{2} \Vert \textbf{w}\Vert _2^2 \\&\text {s.t.} \; \textbf{w}^\top \varvec{\Sigma }\textbf{w}= 0\\&\quad \quad \mathbf {Bw = c},\\ \end{aligned} \end{aligned}$$

(17)

is given as

$$\begin{aligned} \textbf{w}_{\textrm{min}} = \big (\textbf{I}- (\textbf{V}_{\varvec{\Sigma }_2} \textbf{V}_{\textbf{Y}_2})(\textbf{V}_{\varvec{\Sigma }_2} \textbf{V}_{\textbf{Y}_2})^+\big ) \textbf{Y}^+\textbf{c}. \end{aligned}$$

(18)

Proof

From Lemma 2.2 the problem (1) simplifies to finding $\textbf{y}\in \mathbb R^{p-r}$ that satisfies the equation

$$\begin{aligned} \textbf{B}\textbf{V}_{\varvec{\Sigma }_2} \textbf{y}= \textbf{c}, \text{ or } \text{ equivalently, } \textbf{Y}\textbf{y}= \textbf{c}, \end{aligned}$$

(19)

which is a system of two equations with $p-r$ unknowns. It is straightforward to see that any solution to (19) can be written in the following form

$$\begin{aligned} \textbf{y}= \textbf{Y}^{+} \textbf{c}+ \textbf{x}, \quad \textbf{x}\in \mathcal {N}(\textbf{Y}). \end{aligned}$$

Then, as $\textbf{w}= \textbf{V}_{\varvec{\Sigma }_2} \textbf{y}$, we arrive at the expression in (16).

Next, we observe that $\textbf{x}\in \mathcal {N}(\textbf{Y})$ is equivalent to $\textbf{x}= \textbf{V}_{\textbf{Y}_2} \textbf{v},$ $\textbf{v}\in \mathbb R^{p-r-2},$ and therefore

$$\begin{aligned} \textbf{w}= \textbf{V}_{\varvec{\Sigma }_2} \textbf{Y}^{+} \textbf{c}+ \textbf{V}_{\varvec{\Sigma }_2} \textbf{V}_{\textbf{Y}_2}\textbf{v}. \end{aligned}$$

(20)

Thus, the constrained optimization in (17) simply could be written as the unconstrained problem

$$\begin{aligned} \underset{\textbf{v}\in \mathbb {R}^{p-r-2}}{\text {min}} \; \frac{1}{2} \Vert \textbf{V}_{\varvec{\Sigma }_2} (\textbf{B}\textbf{V}_{\varvec{\Sigma }_2})^{+} \textbf{c}+ \textbf{V}_{\varvec{\Sigma }_2} \textbf{V}_{\textbf{Y}_2}\textbf{v}\Vert _2^2. \end{aligned}$$

(21)

The linear least squares problem in (21) is overdetermined and has the unique solution expressed as

$$\begin{aligned} \textbf{v}= - (\textbf{V}_{\Sigma _2} \textbf{V}_{\textbf{Y}_2})^+ \, \textbf{V}_{\varvec{\Sigma }_2} \, \textbf{Y}^+ \, \textbf{c}. \end{aligned}$$

(22)

Finally, we insert (22) into (20) to obtain (18). The theorem is proved.

$\square$

The computational complexity to calculate $\textbf{w}_{\text {min}}$ in (18) is mainly due to the SVDs of $\varvec{\Sigma }$, $\textbf{Y}$, and $\textbf{V}_{\varvec{\Sigma }_2} \textbf{V}_{\textbf{Y}_2}$. Since the SVD of an $r_1 \times r_2$ matrix is approximately $2r_1 r_2^2 + 11r_2^3$ (see Trefethen and Bau III, 1997), we get a total cost of

$$\begin{aligned} N_{TOT}=13p^3 + 4(p-r)^2 + 11(p-r)^3 + 2p(p-r-2)^2 + (p-r-2)^3. \end{aligned}$$

An interesting special case is when $r\ll p$. Expanding factors we get

$$\begin{aligned} N_{TOT}=27p^3 - 40p^2r - 10p^2 + 38pr^2 + 12pr + 20p - 12r^3 - 2r^2 - 12r - 8 \end{aligned}$$

with leading term, the main computational cost, $27p^3$. Thus, we have a complexity of order $\mathcal {O}(p^3)$, and for large p it is of interest to use an iterative method of lower complexity. In the next section, we will present such an iterative method that generally has $\mathcal {O}(p^2)$ in complexity.

Another aspect is that an iterative method can be used to get an approximate solution just stopping the iterations early as well as producing a set of possibly interesting portfolios.

3 The Discrete Functional Particle Method

Our approach for solving optimization problem stated in (1) iteratively is the Discrete Functional Particle method (DFPM), see Gulliksson and Mazur (2020) and Gulliksson et al. (2018) for details. DFPM is based on formulating a damped dynamical system and we will show that the stationary solution is the solution to (1) or with a specific initial value the solution given in (17).

This method can either be formulated by first eliminating the constraints in (1) or formulating an additional dynamical system for the constraints. We choose the former here and leave the latter for future research.

The null space of $\textbf{B}$ can be formulated using the SVD decomposition

$$\begin{aligned} \textbf{B}= \textbf{U}_{\textbf{B}} \, \begin{bmatrix} \textbf{D}_{\textbf{B}_1}&{} \textbf{0}\\ \textbf{0}&{} \textbf{0}\\ \end{bmatrix} \, \begin{bmatrix} \textbf{V}_{\textbf{B}_1}^\top \\ \textbf{V}_{\textbf{B}_2}^\top \\ \end{bmatrix}, \end{aligned}$$

where $\textbf{V}_{\textbf{B}_2} \in \mathbb R^{p\times (p-2) }$ spans $\mathcal {N}(\textbf{B}).$ Thus, any solution to (1) can be written in the form

$$\begin{aligned} \textbf{w}= \textbf{V}_{\textbf{B}_2} \textbf{u}+ \textbf{g}, \end{aligned}$$

(23)

where $\textbf{g}$ is any solution to $\textbf{B}\textbf{w}=\textbf{c}$. Since $\textbf{B}$ has only two rows, the matrix $\textbf{V}_{\textbf{B}_2}$ can be found by doing a reduced (or thin) SVD of $\textbf{B}$ or a reduced QR-decomposition of $\textbf{B}^\top$ together with Gram-Schmidt orthogonalization at a cost of order $\mathcal {O}(p^2)$.

Let, e.g., $\textbf{g} = \textbf{B}^{+}\textbf{c}$, then (1) can be written as

$$\begin{aligned} \begin{aligned} \min _{\textbf{u}} \dfrac{1}{2} (\textbf{V}_{\textbf{B}_2} \textbf{u}+\textbf{g})^\top \,\varvec{\Sigma }\,(\textbf{V}_{\textbf{B}_2} \textbf{u}+\textbf{g}), \end{aligned} \end{aligned}$$

(24)

or

$$\begin{aligned} \begin{aligned} \min _{\textbf{u}} \left( \dfrac{1}{2}\textbf{u}^\top \textbf{V}_{\textbf{B}_2} ^\top \,\varvec{\Sigma }\, \textbf{V}_{\textbf{B}_2} \textbf{u}+ \textbf{g}^\top \,\varvec{\Sigma }\,\textbf{V}_{\textbf{B}_2} \textbf{u}+ \dfrac{1}{2}\textbf{g}^\top \mathbf {\Sigma g} \right) . \end{aligned} \end{aligned}$$

(25)

Calculating $\textbf{g}$ can be done efficiently by a QR-decomposition of $\textbf{B}^\top$ with a cost of $\mathcal {O}(p^2)$. We can exclude the last term in (25) as it is constant and introduce

$$\begin{aligned} \textbf{M}= \textbf{V}_{\textbf{B}_2} ^\top \,\varvec{\Sigma }\, \textbf{V}_{\textbf{B}_2} \text{ and } \textbf{d} = \textbf{V}_{\textbf{B}_2} ^\top \,\varvec{\Sigma }\, \textbf{g}, \end{aligned}$$

(26)

to simplify the notation. Finally, we get the unconstrained problem

$$\begin{aligned} \begin{aligned} \underset{\textbf{u}\in \mathbb {R}^{p-2}}{\text {min}} \; \dfrac{1}{2}\textbf{u}^\top \textbf{Mu} + \textbf{u}^\top \textbf{d}. \end{aligned} \end{aligned}$$

(27)

Here, $\textbf{M}\in \mathbb {R}^{(p-2)\times (p-2)}$ and $\textbf{d}\in \mathbb {R}^{p-2}$.

The idea is to solve (27) by finding the stationary solution, say $\textbf{u}^*$, to the second order damped dynamical system

$$\begin{aligned} \begin{array}{l} \dfrac{\textrm{d}^2 \textbf{u}}{\textrm{d} t^2} + \eta \dfrac{\textrm{d} \textbf{u}}{\textrm{d} t} = \mathbf {-d - Mu}, \quad \eta > 0, \\ \textbf{u}(0) = \textbf{u}_0, \quad \dfrac{\textrm{d} \textbf{u}}{\textrm{d} t}(0) =\textbf{ v}_0. \end{array} \end{aligned}$$

(28)

We remind the reader about our assumption on the rank of $\varvec{\Sigma },$ i.e., $r<p-2.$ This implies that $\textbf{M}$ is rank-deficient as well with the rank $s \le r$ and a solution to (27) is not unique. We show here that as $t\rightarrow \infty ,$ the solution to (28) converges to $\textbf{u}^*$ which corresponds to a zero risk solution $\textbf{w}$ via (23). Moreover, we show that there is a choice of the initial condition $\textbf{u}_0$, that ensures that $\textbf{u}^*$ converges to the risk-free minimum norm solution. Let us note that if $\varvec{\Sigma }$ is positive definite, then so is $\textbf{M},$ giving $\textbf{u}^* = -\textbf{M}^{-1} \textbf{d}$. We refer to Gulliksson and Mazur (2020) for this special case.

3.1 Stationary Solutions

Let the SVD of $\textbf{M}\in \mathbb R^{(p-2)\times (p-2)}$ of rank s be defined as

$$\begin{aligned} \begin{aligned}&\textbf{M} = \textbf{V}_{\textbf{M}} \textbf{D}_{\textbf{M}}\textbf{V}_{\textbf{M}}^\top = {\textbf{V}_{\textbf{M}}}_1{\textbf{D}_{\textbf{M}}}_1{\textbf{V}_{\textbf{M}}}_1^\top \end{aligned} \end{aligned}$$

(29)

where

$$\begin{aligned} \textbf{V}_{\textbf{M}} = \begin{bmatrix} {\textbf{V}_{\textbf{M}}}_1 &{} {\textbf{V}_{\textbf{M}}}_2\\ \end{bmatrix} \, , \; \textbf{D}_{\textbf{M}} = \begin{bmatrix} {\textbf{D}_{\textbf{M}}}_1 &{} \textbf{0 }\\ \textbf{0 }&{} \textbf{0 }\end{bmatrix}, \end{aligned}$$

(30)

$\textbf{V}_{\textbf{M}}\in \mathbb {R}^{(p-2)\times (p-2)}$, ${\textbf{V}_{\textbf{M}}}_1\in \mathbb {R}^{(p-2)\times s}$, ${\textbf{V}_{\textbf{M}}}_2\in \mathbb {R}^{(p-2)\times (p-2-s)}$, $\textbf{D}\in \mathbb {R}^{(p-2)\times (p-2)}$, and ${\textbf{D}_{\textbf{M}}}_1\in \mathbb {R}^{s\times s}$. Here, the diagonal matrix ${\textbf{D}_{\textbf{M}}}_1$ contains the non-zero singular values of $\textbf{M}$, i.e., ${\textbf{D}_{\textbf{M}}}_1= \text {diag}(\gamma _1, \ldots , \gamma _s)$. Substituting (29) into (28) and introducing the change of variables $\textbf{z} = \textbf{V}_{\textbf{M}}^\top \textbf{u}$, we transform (28) into

$$\begin{aligned} \begin{aligned} \frac{\textrm{d}^2 \textbf{z}}{\textrm{d} t^2} + \eta \frac{\textrm{d} \textbf{z}}{\textrm{d} t} = -\textbf{V}_{\textbf{M}}^\top \textbf{d}- \textbf{D}_{\textbf{M}}\textbf{z}. \end{aligned} \end{aligned}$$

(31)

From (26), $\textbf{d}\in \mathcal {R}(\textbf{V}_{\varvec{\Sigma }_2}^\top )$ and as $\mathcal {R}(\textbf{V}_{\varvec{\Sigma }_2}^\top )=\mathcal {R}(\textbf{M}) = \mathcal {R}({\textbf{V}_{\textbf{M}}}_1)$, we have $\textbf{d} = {\textbf{V}_{\textbf{M}}}_1\textbf{h}$ for some $\textbf{h} \in \mathbb R^s$. As $\textbf{V}_{\textbf{M}}^\top \textbf{V}_{\textbf{M}_1} = [\textbf{I}\quad \textbf{0}]^\top ,$ (31) can be partitioned as

$$\begin{aligned}&\frac{\textrm{d}^2 \textbf{z}_1}{\textrm{d} t^2} + \eta \frac{\textrm{d} \textbf{z}_1}{\textrm{d} t} = -\textbf{h}_1 - {\textbf{D}_{\textbf{M}}}_1\textbf{z}_1, \end{aligned}$$

(32a)

$$\begin{aligned}&\frac{\textrm{d}^2 \textbf{z}_2}{\textrm{d} t^2} + \eta \frac{\textrm{d} \textbf{z}_2}{\textrm{d} t} = 0, \end{aligned}$$

(32b)

where the sizes of the partitions should be evident. System (32) was already considered in Gulliksson and Mazur (2020) but the following results are new.

Lemma 3.1

Let $\textbf{u}_0$ and $\textbf{v}_0$ be fixed initial conditions. Then a solution of (28) approaches to

$$\begin{aligned} \textbf{u}^* = \textbf{V}_{\textbf{M}1} \textbf{D}_{\textbf{M}1}^{-1}\textbf{V}_{\textbf{M}1}^\top \textbf{d}+ \textbf{V}_{\textbf{M}2} \textbf{V}_{\textbf{M}2}^\top \left( \textbf{u}_0 + \frac{1}{\eta } \textbf{v}_0\right) . \end{aligned}$$

(33)

Proof

A solution of (32a)–(32b) is given as

$$\begin{aligned} \begin{array}{l} \textbf{z}_1(t)= e^{-\mathbf {\Lambda }_1 t}\textbf{a}_1 + e^{-\mathbf {\Lambda }_2 t}\textbf{a}_2 - {\textbf{D}^{-1}_{\textbf{M}1}}\textbf{h}_1, \\ \textbf{z}_2(t)= \textbf{a}_3 + \textbf{a}_4e^{-\eta t}, \end{array} \end{aligned}$$

(34)

with $\textbf{a}_i, i=1, \ldots , 4$, that are given by the initial conditions,

$$\begin{aligned} \mathbf {\Lambda }_j = \begin{bmatrix} -\eta /2\pm \sqrt{\eta ^2/4 - \gamma _1}&{}\quad \ldots &{}\quad 0\\ \vdots &{}\quad \ddots &{}\quad \vdots \\ 0&{}\quad \ldots &{}\quad -\eta /2\pm \sqrt{\eta ^2/4 - \gamma _s}) \end{bmatrix} \end{aligned}$$

where index j refers to the two different roots. Further, we have

$$\begin{aligned} \begin{aligned} \textbf{u}(t) = {\textbf{V}_{\textbf{M}}}\textbf{z}(t) = \textbf{V}_{\textbf{M}}\begin{bmatrix} \textbf{z}_1(t) \\ \textbf{z}_2(t) \end{bmatrix} = {\textbf{V}_{\textbf{M}}}_1 \textbf{z}_1(t) + {\textbf{V}_{\textbf{M}}}_2\textbf{z}_2(t). \end{aligned} \end{aligned}$$

(35)

Since $\textbf{V}_{\textbf{M}_2}^\top \textbf{V}_{\textbf{M}_1} = \textbf{0}$ and ${\textbf{V}_{\textbf{M}}}_2^\top {\textbf{V}_{\textbf{M}}}_2 = \textbf{I}$, we have

$$\begin{aligned} \textbf{V}_{\textbf{M}_2}^\top \textbf{u}(t) = \textbf{V}_{\textbf{M}_2}^\top {\textbf{V}_{\textbf{M}}}_1 \textbf{z}_1(t) + \textbf{V}_{\textbf{M}_2}^\top {\textbf{V}_{\textbf{M}}}_2\textbf{z}_2(t) = \textbf{z}_2(t). \end{aligned}$$

(36)

Inserting the initial condition we conclude that

$$\begin{aligned} \textbf{z}_2(t) = \textbf{V}_{\textbf{M}2}^\top \left( \textbf{u}_0 + \frac{1}{\eta } \textbf{v}_0\right) -\frac{1}{\eta }\textbf{V}_{\textbf{M}_2}^\top \textbf{v}_0 e^{-\eta t}, \end{aligned}$$

and, therefore,

$$\begin{aligned} \begin{aligned} \textbf{u}^* = \lim _{t\rightarrow \infty } \textbf{V}_{\textbf{M}}\textbf{z}(t) = \textbf{V}_{\textbf{M}}\begin{bmatrix} -\textbf{D}_{\textbf{M}1}^{-1}\textbf{h}_1 \\ \textbf{V}_{\textbf{M}2}^\top \left( \textbf{u}_0 + \frac{1}{\eta } \textbf{v}_0\right) \end{bmatrix}. \end{aligned} \end{aligned}$$

(37)

After completing the matrix multiplication, we obtain the result. $\square$

Note that $\textbf{u}^*$ in (33) consists of two terms lying in perpendicular subspaces. Therefore, a simple way of decreasing the norm of $\textbf{u}^*$ is to choose $\textbf{u}_0+ \textbf{v}_0/\eta =\textbf{0}$ but that does not necessarily give the smallest $\textbf{w}$. Next, we establish which initial conditions would lead to the minimal norm $\textbf{w}$.

Given $\textbf{u}^*$, we can easily calculate

$$\begin{aligned} \textbf{w}^* = \textbf{V}_{\textbf{B}_2}\textbf{u}^* + \textbf{g}. \end{aligned}$$

(38)

We see from Lemma 3.1 that the stationary solution is dependent on the initial condition $\textbf{u}_0$. Therefore, we are able to choose $\textbf{u}_0$ such that the norm of $\textbf{w}^*$ is as small as possible.

Theorem 3.1

Let $\textbf{M}$ be of rank $s \le r,$ $\textbf{w}^*$ given by (38) and (33), $\textbf{F}= \textbf{V}_{\textbf{B}_2}{\textbf{V}_{\textbf{M}}}_2{\textbf{V}_{\textbf{M}}}_2^\top$, and $\textbf{f}= \textbf{V}_{\textbf{B}_2} \left( \textbf{V}_{\textbf{M}_1} \textbf{D}_{\textbf{M}_1}^{-1} \textbf{V}_{\textbf{M}_1}^\top \right) \textbf{d}+ \textbf{g}.$ Then

$$\begin{aligned} \min _{(\textbf{u}_0,\textbf{v}_0)} ||\textbf{w}^*||_2, \end{aligned}$$

(39)

is attained at

$$\begin{aligned} \textbf{u}_0 +\frac{1}{\eta } \textbf{v}_0 = - \textbf{F}^+ \textbf{f}\end{aligned}$$

(40)

and it is equal to

$$\begin{aligned} \textbf{w}^*_+ = (\textbf{I}-\textbf{F}\textbf{F}^+ )\textbf{f}. \end{aligned}$$

In addition, $\textbf{w}^*_+=\textbf{w}_{\textrm{min}}$, where $\textbf{w}_{\textrm{min}}$ is given by (18), i.e., $\textbf{w}^*_+$ solves (17).

Proof

For $\textbf{F}$ and $\textbf{f}$ chosen as above and (33), we have

$$\begin{aligned} \begin{aligned} \textbf{w}^*&= \textbf{V}_{\textbf{B}_2}\left( \textbf{V}_{\textbf{M}_1} \textbf{D}_{\textbf{M}_1}^{-1} \textbf{h}+ \textbf{V}_{\textbf{M}_2}\textbf{V}_{\textbf{M}_2}^\top (\textbf{u}_0 + \frac{1}{\eta }\textbf{v}_0)\right) + \textbf{g}\\&=\textbf{F}\left( \textbf{u}_0 +\frac{1}{\eta }\textbf{v}_0\right) + \textbf{f}. \end{aligned} \end{aligned}$$

(41)

The norm is then

$$\begin{aligned} \begin{aligned} ||\textbf{w}^*||_2 = \left\| \textbf{F}\left( \textbf{u}_0 +\frac{1}{\eta }\textbf{v}_0\right) + \textbf{f} \right\| _2. \end{aligned} \end{aligned}$$

(42)

Consequently, we get (40) and calculate

$$\begin{aligned} \textbf{w}^*_+ =-\textbf{F}\left( \textbf{u}_0 + \frac{1}{\eta }\textbf{v}_0\right) + \textbf{f}= \textbf{FF}^+\textbf{f}- \textbf{f}=(\textbf{I} -\textbf{FF}^+)\textbf{f}. \end{aligned}$$

To prove the last claim, we notice that $\textbf{w}^*$ lies in the null space of $\varvec{\Sigma }$. Furthermore, it satisfies $\textbf{B}\textbf{w}=\textbf{c}$ by construction. Since, $\textbf{w}^*_+$ is minimal, it solves (17). It completes the proof of the theorem. $\square$

Remark 3.1

From Theorem 3.1 one choice of the initial condition is

$$\begin{aligned} \textbf{u}_0 = -\textbf{F}^+ \textbf{f} \text{ and } \textbf{v}_0 = \textbf{0}, \end{aligned}$$

which we will assume for simplicity further on.

While Theorem 3.1 gives a way to find an optimally small $\textbf{w}^*$ it also requires the SVD of $\varvec{\Sigma }$ and $\textbf{M}$ which increase the computational complexity considerably. However, we would like to emphasise that any choice of $\textbf{u}_0$ and $\textbf{v}_0$ results in a risk-free solution. Indeed, numerical tests in Sect. 4 show that DFPM is a competitive method in many cases.

3.2 Symplectic Euler with Optimal Parameters

In order to solve (28) through an numerical iterative method, we start by writing (28) as the first order system

$$\begin{aligned} \begin{aligned}&\frac{\textrm{d} \textbf{u}}{\textrm{d} t} = \textbf{v}, \\&\frac{\textrm{d} \textbf{v}}{\textrm{d} t} = -\eta \textbf{v} -\mathbf {d - Mu} . \end{aligned} \end{aligned}$$

(43)

with $\textbf{u}(0) = \textbf{u}_0$ and $\textbf{v}(0) = 0.$ The latter is assumed for simplicity and does not affect further analysis, see also Remark 3.1.

We first note that (43) may be numerically solved with a small error using any stable and consistent numerical method if the time step $\Delta t$ is small enough. However, we are only interested in reaching the stationary solution as efficiently as possible. As shown in Gulliksson et al. (2018), an excellent choice for this purpose is the symplectic Euler method. Thus, for some initial conditions $\textbf{u}(0) = \mathbf {u_0}$ and $\dot{\textbf{u}}(0) = \mathbf {v_0}$ we use the symplectic Euler method on (43) defined as

$$\begin{aligned} \begin{aligned}&\textbf{v}_{k+1} = (I - \Delta t\eta )\textbf{v}_k - \Delta t (\mathbf {d + Mu}_k), \\&\textbf{u}_{k+1} = \textbf{u}_k + \Delta t \textbf{v}_{k+1} ,\quad k = 0,1,\ldots , \end{aligned} \end{aligned}$$

(44)

or more concisely $\varvec{\xi }_{k+1} = \textbf{G}\varvec{\xi }_k + \textbf{b},$ where

$$\begin{aligned} \textbf{G} = \begin{bmatrix} \textbf{I} - \Delta t^2\textbf{M} &{}\quad \Delta t(1 - \Delta t \eta )\textbf{I} \\ \Delta t\textbf{I} &{}\quad (1 - \Delta t \eta )\textbf{I} \end{bmatrix}, \quad \varvec{\xi }_k = \begin{bmatrix} \textbf{v}_k \\ \textbf{u}_k \end{bmatrix}, \quad \textbf{b} = \begin{bmatrix} -\Delta t^2\textbf{d} \\ -\Delta t\textbf{d} \end{bmatrix}. \end{aligned}$$

(45)

We emphasize that symplectic methods are very well suited for the case when $\textbf{M}$ has non-negative eigenvalues, see Gulliksson et al. (2018). In order to ensure fast convergence of the method one must choose a time step $\Delta t$ and damping factor $\eta$ such that $\Vert \textbf{G} \Vert$ is as small as possible.

Theorem 3.2

Assume that $\textbf{M}$ has rank s and let $\gamma _{i}, i=1, \ldots , s$, denote its non-zero singular values with $\gamma _{1}\ge \cdots \ge \gamma _s$. Then symplectic Euler (45) with parameters

$$\begin{aligned} \begin{aligned} \Delta t = \frac{2}{\sqrt{\gamma _{s}}+\sqrt{\gamma _1}}, \, \eta = \frac{2\gamma _{s}\gamma _{1}}{\sqrt{\gamma _{s}}+\sqrt{\gamma _{1}}} \end{aligned} \end{aligned}$$

(46)

is convergent, i.e.,

$$\begin{aligned} \begin{aligned} \lim _{k\rightarrow \infty } \textbf{u}_k = -{\textbf{V}_{\textbf{M}}}_1{\textbf{D}_{\textbf{M}}}_1^{-1}{\textbf{V}_{\textbf{M}}}_1^\top \textbf{d} + {\textbf{V}_{\textbf{M}}}_2\textbf{V}_{\textbf{M}_2}^\top \textbf{u}_0. \end{aligned} \end{aligned}$$

(47)

Moreover, $\Delta t$ and $\eta$ are optimal in the sense that they are the solution to the problem

$$\begin{aligned} \min _{\Delta t, \eta } \max _{1\le i \le 2p} |\mu _i (\textbf{G}) |, \end{aligned}$$

where $\mu _i (\textbf{G})$ are the eigenvalues of $\textbf{G}$.

Proof

By using (29), we define the transformations $\widetilde{\textbf{u}}_k = \textbf{V}_{\textbf{M}}\textbf{u}_k$ and $\widetilde{\textbf{v}}_k = \textbf{V}_{\textbf{M}}\textbf{v}_k$ resulting into $\widetilde{\varvec{\xi }}_{k+1} = \widetilde{\textbf{G}} \widetilde{\varvec{\xi }}_k + \widetilde{\textbf{b}}$, where

$$\begin{aligned} \widetilde{\textbf{G}} = \left[ \begin{array}{cc} \textbf{V}_{\textbf{M}}^\top &{}\quad \textbf{0}\\ \textbf{0 }&{} \quad \textbf{V}_{\textbf{M}}^\top \end{array} \right] \textbf{G}\left[ \begin{array}{cc} \textbf{V}_{\textbf{M}} &{}\quad \textbf{0}\\ \textbf{0 }&{}\quad \textbf{V}_{\textbf{M}} \end{array} \right] = \left[ \begin{array}{cc} \textbf{I}- \Delta t^2\, {\textbf{D}_{\textbf{M}}} &{} \quad \Delta t (1 - \Delta t \, \eta )\, \textbf{I}\\ \Delta t \, {\textbf{D}_{\textbf{M}}} &{}\quad (1 - \Delta t \, \eta )\, \textbf{I}\end{array} \right] , \end{aligned}$$

and obvious similar definitions of $\widetilde{\varvec{\xi }}_{k+1}, \widetilde{\textbf{b}}$. Since, $\gamma _{s+1} = \cdots = \gamma _{p-2}=0$ we can partition $\widetilde{\textbf{G}}$ further using the reduced SVD of ${\textbf{M}}$ so that

$$\begin{aligned} \widetilde{\textbf{G}} = \left[ \begin{array}{cccc} \textbf{I}- \Delta t^2\, {\textbf{D}_{\textbf{M}1}} &{}\quad \textbf{0 }&{}\quad \Delta t (1 - \Delta t \, \eta )\, \textbf{I}&{}\quad \textbf{0}\\ \textbf{0 }&{} \quad \textbf{I}&{}\quad \textbf{0 }&{}\quad \Delta t (1 - \Delta t \, \eta )\, \textbf{I}\\ \Delta t \, {\textbf{D}_{\textbf{M}1}} &{}\quad 0 &{}\quad (1 - \Delta t \, \eta )\, \textbf{I}&{}\quad \textbf{0}\\ \textbf{0 }&{} \quad \textbf{0 }&{}\quad \textbf{0 }&{}\quad (1 - \Delta t \, \eta )\, \textbf{I}\end{array} \right] . \end{aligned}$$

Due to the structure of $\widetilde{\textbf{G}},$ we can solve for the last $p-2-s$ components of $\widetilde{\textbf{u}}_k$, denoted by $\widetilde{\textbf{u}}^{(k)}_2$, and eliminate the corresponding elements in $\widetilde{\textbf{v}}_k$ (that will play no further role). In other words the iterations $\widetilde{\varvec{\xi }}_{k+1} = \widetilde{\textbf{G}} \widetilde{\varvec{\xi }}_k + \widetilde{\textbf{b}}$ will separate into one part with the iteration matrix

$$\begin{aligned} \widetilde{\textbf{G}}_1 = \left[ \begin{array}{cc} \textbf{I}- \Delta t^2\, {\textbf{D}_{\textbf{M}1}} &{} \quad \Delta t (1 - \Delta t \, \eta )\, \textbf{I}\\ \Delta t \, {\textbf{D}_{\textbf{M}1}} &{}\quad (1 - \Delta t \, \eta )\, \textbf{I}\end{array} \right] \end{aligned}$$

and the constant part $\widetilde{\textbf{u}}^{(k)}_2$ now to be determined. We have

$$\begin{aligned} \begin{aligned} \textbf{u}_k = {\textbf{V}_{\textbf{M}}}\widetilde{\textbf{u}}^{(k)} = \textbf{V}_{\textbf{M}} \begin{bmatrix} \widetilde{\textbf{u}}^{(k)}_1 \\ \widetilde{\textbf{u}}^{(k)}_2 \end{bmatrix} = {\textbf{V}_{\textbf{M}}}_1 \widetilde{\textbf{u}}^{(k)}_1+ {\textbf{V}_{\textbf{M}}}_2\widetilde{\textbf{u}}^{(k)}_2 \end{aligned} \end{aligned}$$

(48)

that gives

$$\begin{aligned} \textbf{V}_{\textbf{M}_2}^\top \widetilde{\textbf{u}}^{(k)} = \textbf{V}_{\textbf{M}_2}^\top {\textbf{V}_{\textbf{M}}}_1 \widetilde{\textbf{u}}^{(k)}_1 + \textbf{V}_{\textbf{M}_2}^\top {\textbf{V}_{\textbf{M}}}_2\widetilde{\textbf{u}}^{(k)}_2= \widetilde{\textbf{u}}^{(k)}_2 \end{aligned}$$

(49)

since $\textbf{V}_{\textbf{M}_2}^\top \textbf{V}_{\textbf{M}_1} = \textbf{0}$ and ${\textbf{V}_{\textbf{M}}}_2^\top {\textbf{V}_{\textbf{M}}}_2 = \textbf{I}$. Inserting the initial condition we conclude that $\widetilde{\textbf{u}}^{(k)}_2 = \textbf{V}_{\textbf{M}_2}^\top \textbf{u}_0$ and, therefore,

$$\begin{aligned} \begin{aligned} \textbf{u}^* = \lim _{k\rightarrow \infty } {\textbf{V}_{\textbf{M}}}\widetilde{\textbf{u}}^{(k)}&= \lim _{k\rightarrow \infty } \left( {\textbf{V}_{\textbf{M}}}_1 \widetilde{\textbf{u}}^{(k)}_1+ {\textbf{V}_{\textbf{M}}}_2\widetilde{\textbf{u}}^{(k)}_2 \right) \\&= {\textbf{V}_{\textbf{M}}}_2\textbf{V}_{\textbf{M}_2}^\top \textbf{u}_0+ \lim _{k\rightarrow \infty } {\textbf{V}_{\textbf{M}}}_1 \widetilde{\textbf{u}}^{(k)}_1. \end{aligned} \end{aligned}$$

(50)

Following already known results in Gulliksson et al. (2018), we get

$$\begin{aligned} \lim _{k\rightarrow \infty } {\textbf{V}_{\textbf{M}}}_1 \widetilde{\textbf{u}}^{(k)}_1 = -{\textbf{V}_{\textbf{M}}}_1{\textbf{D}_{\textbf{M}}}_1^{-1}{\textbf{V}_{\textbf{M}}}_1^\top \textbf{d} \end{aligned}$$

which concludes the proof. $\square$

Attaining estimates of $\gamma _{1}/\gamma _{s}$ and the rank for the optimal parameters can be done by standard condition and rank estimators at a cost of $\mathcal {O}(p^2)$, Hager (1984).

4 Simulation Study

There are several aspects that we illustrate in this simulation study. In Sect. 4.1 we compare the outcomes of three different approaches of finding a portfolio, namely, the analytic Range Space (RS), see (4), and Null Space Minimum Norm (NSMN), see (18), approaches, and the iterative DFPM with zero initial value $\textbf{u}_0 = 0$, see Sect. 3. In particular, we investigate how the portfolio risk and portfolio weights’ norm vary for each method depending on the problem size, rank of $\varvec{\Sigma }$, and its condition number. In Sect. 4.2 we touch upon robustness of these different approaches in relation to rank underestimation due to the sampling of $\varvec{\Sigma }$.

The setup for the simulation study is as follows. Each element of the mean vector $\varvec{\mu }$ is drawn from the uniform distribution on the interval $[-0.01, 0.01]$. The expected rate of return on the portfolio q is equal to the return on a naive equal-weighted (EW) portfolio, i.e., $q=\textbf{1}^\top \varvec{\mu }/p$. The population covariance matrix $\varvec{\Sigma }$ of rank r was obtained as $\varvec{\Sigma }= \sum _{i=1}^r \textbf{x}_i \textbf{x}_i^\top ,$ where $\textbf{x}_i \in N(\textbf{0},\textbf{I}), i=1, \ldots , r$, i.e., $\textbf{x}_i \in \mathbb {R}^p$ are normally distributed vectors with mean vector $\textbf{0}$ and covariance matrix $\textbf{I}$. In Sect. 4.1, the condition number of $\varvec{\Sigma }$, defined by $\kappa = \sigma _1/\sigma _r$, was then set through a similarity transformation.

In order to define the convergence criterium we set $V(\textbf{u}) = \textbf{u}^\top \textbf{Mu}/2 + \textbf{u}^\top \textbf{d}$ and $\nabla V(\textbf{u}) = \textbf{Mu} +\textbf{d}.$ Then, given a tolerance $\varepsilon$ we end the iterations at iteration k if $\Vert \nabla V(\textbf{u}_k) \Vert _2/V(\textbf{u}_k) < \varepsilon$. Here, we set the tolerance $\varepsilon = 10^{-6}.$ In accordance with Gulliksson et al. (2018), the number of iterations is proportional to the square root of the condition number, which is observed in all the numerical tests.

In order to estimate method performances, we solve 1000 problems with random matrices $\varvec{\Sigma }$ for a specific set of p, r and $\kappa$, and random $\varvec{\mu }.$ The results presented as scatter- and box-plots. In addition we provide the tables with mean estimates for the norm and the risk.

4.1 Comparison of the RS, NSMN, and DFPM Solutions

Here, we solve 1000 problems (1) with random matrices $\varvec{\Sigma }$ and $\varvec{\mu }$ for a specific set of p, r and $\kappa$ with three different approaches: The RS and NSMN methods, and DFPM. For the DFPM we set the initial value $\textbf{u}_0 = 0.$ Thus, the method provides an approximation of a null space solution (and, therefore, risk-free solution), but is not expected to converge to the NSMN solution.

We consider four different cases of the condition number $\kappa = \sigma _1/\sigma _r \in \{1.01, 10^2, 10^3, 10^5\}.$ The dimension of the portfolio, p,  was set to 70 and 140, while the rank r of the covariance matrix $\varvec{\Sigma }$ is 60. More tests were performed with other choices of p and r. However, as the results were very similar to the ones presented here, we do not include them.

Fig. 1

Scatter plot of portfolio weights’ norm vs portfolio risk for three different approaches, with $p=70,$ $r=60,$ and four different condition numbers

Fig. 2

Scatter plot of portfolio weights’ norm vs portfolio risk for three different approaches, with $p=140,$ $r=60,$ and four different condition numbers

Fig. 3

Boxplot of the portfolio weights’ norm and related portfolio risk, for the test case I. On each box, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the most extreme data points not considered outliers, and the outliers are plotted individually using the ‘+’ symbol

Fig. 4

Boxplot of the portfolio weights’ norm and related portfolio risk, for the test case II. On each box, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the most extreme data points not considered outliers, and the outliers are plotted individually using the ‘+’ symbol

In Figs. 1 and 2 we plot the portfolio weights’ norm vs the portfolio risk for different solutions types and different condition numbers. In Figs. 3 and 4 the norm and the corresponding risk as box plots are displayed. The red boxes correspond to the NSMN solution, yellow to the DFPM solutions, and blue to the RS solutions.

Our first observation is that the risk-norm distributions corresponding to the NSMN and DFPM solutions are not sensitive to the condition number $\kappa ,$ which is not the case for the RS approach. For the RS solution, the larger condition number gives a lower risk and higher norm variance. Secondly, the norm distribution for the NSMN approach and DFPM is flatter for a lower p to r ratio ($p=70,$ $r=60$), see Fig. 1.

Figure 3 illustrates well the trade off between getting a smaller norm and smaller risk. While the the RS solution norm is the smallest, among the approaches, for the lower p to r ratio $(p=70, r=60)$, the risk is the highest. This is rather expected, as the NSMN solution minimizes the norm among zero-risk solutions and the DFPM solution is only approximating a risk-free solution without minimizing the norm. Interestingly, for the high p to r ratio ($p=140$, $r=60$), see Fig. 4, the NSMN solution gives both the smallest norm and zero risk. The DFPM solution norm is typically larger than the norm of the NSMN solution, which is expected.

Table 1 Mean estimation (out of 1000 random simulations) of the portfolio weights’ norm and the corresponding portfolio risk, for different condition numbers

Table 2 Mean estimation (out of 1000 random simulations) of the portfolio weights’ norm and the corresponding portfolio risk, for different condition numbers

In Table 1, the portfolio weights’ norm and portfolio risk are shown as the mean of the 1000 randomly generated problems with $p=70$ and $r=60$ for four different cases of $\kappa$. Similarly, in Table 2 we list the mean estimation of the norm and risk for $p=140$ and $r=60,$ for the four different $\kappa .$ We would like to point out here, that the risk for both DFPM and NSMN is close to zero and of the order of computational accuracy (floating double precision). For that reason, the computed risk can be negative, see Tables 1 and 2. In order to use logarithmic scale in the plots, we plot absolute values of the computed risk in Figs. 3 and 2.

Fig. 5

Iterates from DFPM with three different choices of the initial conditions for $p=70,$ $r=60$ and $\kappa = 10^3.$

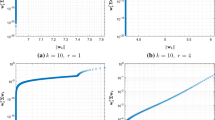
In Fig. 5 we give an example of the portfolio weights’ norm and portfolio risk for the DFPM iterations. Here, the smallest norm is not attained at the stationary point, but at an intermediate iteration where the risk is rather high. Further note that there is a consistent relation between the norm of weights and risks for the different initial values; blue is right of black is right of red. From other numerical experiments, this seems to be generally the case but we have not been able to prove that.

4.2 How Rank Deficiency of $\varvec{\Sigma }$ Effects Different Solutions

Let $\varvec{\Sigma }$ have the rank $r<p-2$. The reason for the rank deficiency could be (i) low sampling number $N=r+1$ compared to the portfolio size, or (ii) collinearity of data samples.

Thus, assume that $\varvec{\Sigma }_r$ is a covariance matrix obtained from the limited data, and $\varvec{\Sigma }_R$ is the true covariance matrix, then $\varvec{\Sigma }_r \rightarrow \varvec{\Sigma }_R$ if the number of samples $N \rightarrow \infty .$ Here $r\le R \le p,$ and $r<p-2.$ In another words, the matrix $\varvec{\Sigma }= \varvec{\Sigma }_r$ in (1) is an (under-sampled) approximation of $\varvec{\Sigma }_R,$ and neither $\textbf{w}$ in (4) nor (18) are true solutions of the problem when $\varvec{\Sigma }= \varvec{\Sigma }_R.$

Let $\textbf{w}_r$ denote a solution to (1) with $\varvec{\Sigma }= \varvec{\Sigma }_r.$ We computed the risk associated with $\textbf{w}_r$, $\textbf{w}_r^\top \varvec{\Sigma }_R \textbf{w}_r$ to see if any of the RS, NSMN or DFPM solutions consistently give higher risk.

Fig. 6

Risk $\textbf{w}_r^\top \varvec{\Sigma }_R \textbf{w}_r$ calculated with $\textbf{w}_r$ obtained using different methods: RS, NSMN, and DFPM. Here $r=60$, $p=140,$ and R varies between 61 and 80. Number of random simulations is 1000

Here, the matrices $\varvec{\Sigma }_r$ and $\varvec{\Sigma }_R$ obtained as follows. Assume $\textbf{x}_i \in N(\textbf{0},\textbf{I}), i=1, \ldots , R$, i.e., $\textbf{x}_i \in \mathbb {R}^p$ are normally distributed vectors with mean vector $\textbf{0}$ and covariance matrix $\textbf{I}$. Here we perform a simulation study where $\varvec{\Sigma }_r = \sum _{i=1}^r \textbf{x}_i \textbf{x}_i^\top$ and $\varvec{\Sigma }_R = \varvec{\Sigma }_r + \sum _{i=r+1}^{R} \textbf{x}_i \textbf{x}_i^\top$. We do not monitor the condition numbers for $\varvec{\Sigma }_r$ and $\varvec{\Sigma }_R$ since we do not consider it important enough to perform the theoretical derivation for that, which can be quite elaborate. In Fig. 6, we plot the risk associated with different solutions for $r=60$, $p=140,$ and varying R. We chose $R \in [61,80]$ to illustrated what seems to be a generic case for this construction of $\varvec{\Sigma }_r$ and $\varvec{\Sigma }_R.$ That is, solution obtained using the NSMN theoretical approach gives the smallest risk that other methods as for any R. When $R-r$ is small, DFPM method with zero initial guess gives better results, but as R increases, the method becomes less reliable. Finally, as R grows, the risk is increasing for all considered methods.

Fig. 7

Relative risk $\textbf{w}_r^\top \varvec{\Sigma }_R \textbf{w}_r / \Vert \textbf{w}_r\Vert ^2$ calculated with $\textbf{w}_r$ obtained using different methods: RS, NSMN, and DFPM. Here $r=60$, $p=140,$ and R varies between 61 and 80. Number of random simulations is 1000

In Fig. 7, we plot the relative risk, that is, $\textbf{w}_r^\top \varvec{\Sigma }_R \textbf{w}_r / \Vert \textbf{w}_r\Vert ^2$. This plot illustrates that the higher risk obtained using the DFPM seems to be due to the larger magnitude of the weights $\textbf{w}$.

We conclude that all methods do have a predictive capacity, i.e., the original weight vector does not give a much larger risk when adding non-correlated data.

5 Empirical Study

To get a better understanding of the results obtained in Sects. 2 and 3, we consider examples with real datasets. In this study, we compare the performance of NSMN, DFPM, RS and EW portfolios. We make use of the log return weekly data from S &P 500 of 250 stocks for the period from 2016W34 to 2021W11. The analysis is performed for different sample sizes such as $N \in \{30,60,120,240\}$. The expected rate of return on the portfolio q is set to the return on the equal-weighted portfolio. For the DFPM, we set the same convergence criterion, the tolerance and the maximum number of iterations as in Sect. 4.

Since the mean vector $\varvec{\mu }$ and covariance matrix $\varvec{\Sigma }$ of the logarithmic stock returns are unknown, we should estimate them using historical data. For that, we use the corresponding sample estimators. In this case, the sample estimator of the covariance matrix $\varvec{\Sigma }$ is singular with rank $N-1$ because the number of stocks $p=250$ is greater than the number of observations in the sample $N \in \{30,60,120,240\}$. Having estimated $\varvec{\mu }$ and $\varvec{\Sigma }$, we can build optimal portfolio strategies using NSMN, DFPM and RS methods. These methods are compared with a naive EW portfolio strategy.

Table 3 Norm and risk of $p=250$ stocks and different sample sizes $N\in \{30,60,120,240\}$ obtained using NSMN, DFPM, RS and EW approaches

In Table 3, we present the values of the portfolio weights’ norm and portfolio risk for four approaches. Economically speaking, the portfolio weights’ norm considered in this paper can be associated with a concentration ratio of the portfolio. High values of the portfolio weights’ norm might coincide with high exposures to one specific asset. Hence, one should be careful in investing in only a few assets with high quantities. In our empirical study, the portfolio weights’ norm of RS and EW approaches is lower than for NSMN and DFPM for all considered sample sizes. The highest portfolio weights’ norm is observed for DFPM except for the case $N=240$ where the NSMN approach has a slightly higher norm. Therefore, NSMN and DFPM approaches lead us to the higher concentration ratios of the portfolios compared to the ones obtained via RS and EW approaches. At the same time, the difference between portfolio weights’ norms is not too large meaning that issues with risk exposure are similar across the considered approaches. For the portfolio risk, solutions obtained via NSMN and DFPM approaches deliver much lower portfolio risk in comparison with RS and EW methods. Moreover, NSMN and DFPM attain risks close to zero for all considered cases. It can be observed that some values of the portfolio risk obtained via the NSMN approach are negative. This happens due to numerical errors. Overall, NSMN and DFPM strategies have much lower portfolio risk and higher portfolio weight’s norm in comparison with RS and EW strategies.

6 Conclusions

We have analyzed the classical Markowitz’problem for a rank-deficient covariance matrix assuming the solutions lie in the nullspace. Thus, the solutions will be risk-free but not unique. We derive a unique risk-free solution that has minimum norm through the use of several SVD decompositions which is our main theoretical result. Our analysis then fills a gap so that all possible relevant solutions to the classical Markowitz problem are derived and analysed. We also show the dependence on the size of the risk and the norm of the weights depending on the condition number of the covariance matrix (quotient between largest and smallest non-zero singular value). Finally, we illustrate the fairly strong predictive capacity of our methods, i.e., in most cases they still give solutions with a smaller risk than the range space solution when adding more (non-correlated) data to the model.

The other part of our results is a thorough analysis of the iterative method DFPM for the rank-deficient case. This was partly covered in Gulliksson and Mazur (2020) but without a strict convergence analysis. Here, we show that DFPM always converges to a risk-free solution. Further, we derive an initial condition such that DFPM converges to the unique minimum norm solution. Numerical results verify the theoretical findings through simulations on random generated problems as well as real-world data. Moreover, the numerical results show several advantages of using DFPM such as being more efficient for fairly well-conditioned problems and the possibility to pick any one of the iterates that for some reason has preferable properties.

Economically speaking, suggested approaches to the original Markowitz’s problem give an investor tools on how to get a guaranteed portfolio return with no possibility of loss in the case when the covariance matrix of the asset returns is rank-deficient. Those approaches can be quite useful when an investor is constructing a portfolio with a large investment universe compared to the available data observations.