1 Introduction

The general concept of exchange rate may be explained as the value of a currency in terms of another currency (Hinkle & Montiel, 1999). For instance, if the nominal exchange rate of a United Sates (US) Dollar in terms of the Ethiopian Birr is 50, then this implies that one US Dollar is equivalent to 50 Ethiopian Birr. In this case, the Ethiopian Birr will be regarded as the base currency whereas the US Dollar is the target currency. In other words, the currency whose value is being determined is known as the base currency while the currency against which the value would be determined is the target currency (Teall, 2013).

Issues pertaining to foreign exchange rate and its volatility have always been of great interest to researchers and policy makers (including financial managers) because of their multiple implications in modern day economic scenario. For example, a potential investor may assess the stability of a given economy using the exchange rate of the country where he intends to invest. Of course, it is well known that whenever the currency exchange rate of a country drops too far below the desired level, that is an indication of the weakening of the economy. In this case, governments are expected to take reasonable steps to counteract or change the situation. As noted by Suranovic (2015), under excessively volatile exchange rates, international trade and investment decisions become more demanding as businesses are exposed to higher risk from both accounting and operational perspectives. Given this, characterization and quantification of risks associated with exchange rate volatility become crucial so as to minimize and avert the dramatic negative developments that emanate from the excessive fluctuation of currencies.

Exchange rate risk quantification is concerned with modeling price and/or return uncertainty due to market volatility. In finance and general portfolio optimization, value at risk and expected shortfall are the two most commonly used techniques for risk assessment. Value at risk is a quantile of the loss distribution which is generally defined as the maximum or worst expected loss oa given time horizon at a given or pre-defined confidence level under normal market conditions. Expected shortfall is defined as the mean of all losses that are beyond the value at risk (Pfaff, 2016). For these risk measures to perform optimally, the right distributional model must be assumed. For example, if we assume that the conditional asset return distribution is Gaussian that will be precarious as the Gaussian distribution will not be able to account for the leptokurtic properties of financial asset returns.

Given that exchange rate volatility has several economic implications, it is important to correctly quantify the risk associated with asset volatility via the two most commonly used techniques for financial risk assessment (value at risk and expected shortfall). Hence, it is fundamental to consider flexible models that can fully account for the salient features of financial series such as leptokurtosis, heteroskedasticity, etc. Most popular models for financial volatility are based on the Generalized Autoregressive Conditional Heteroskedasticity (GARCH) class of models. GARCH and related class of models have a long history and have received wide range of applications in economics and similar areas [See Engle (1982), Bollerslev (1986), Hentschel (1995), Lanne and Saikkonen (2005), Platanios and Chatzis (2014) and Otto et al. (2018)]. In particular, foreign exchange rates data have received attention based on the GARCH class of models. For example, McCurdy and Morgan (1987) estimated the time varying volatility of five major currencies (the British Pound, the Canadian Dollar, the Deutschmark, the Japanese Yen, and the Swiss Franc) via GARCH models. McCurdy and Morgan (1987) also tested the martingale hypothesis. They concluded that there is evidence of time-varying premium risk in weekly series. Hsieh (1988) adopted a version of the ARCH model due to Engle (1982) to describe daily rates of changes of five foreign currencies to the US Dollar from 1974 to 1983. Special attention was paid to discrimination between two competing explanations regarding heavy-tailedness of financial data. Baillie and Bollerslev (1989) employed the GARCH model to characterize 1245 observations based on the currencies of France, Italy, Japan, Switzerland, the United Kingdom and West Germany. They illustrated that there is a unit root in the autoregressive polynomial of the respective series and concluded that the degree of leptokurtosis and time-dependent heteroscedasticity decreases as the length of observations increases. Bollerslev (1990) analysed five nominal European-US Dollar exchange rates using a multivariate GARCH model with time varying conditional covariances and constant conditional correlations. Dunis et al. (2003) examined the medium-term forecasting ability of several alternative GARCH models using foreign exchange data of DEM/JPY, GBP/DEM, GBP/USD, USD/CHF, USD/DEM and USD/JPY. Using a short memory ARMA model, a long memory ARFIMA model, and a GARCH model, Pong et al. (2004) found significant incremental information in the historical forecast of the realized volatility of the Pound, Mark and Yen exchange rates against the Dollar. Corlu and Corlu (2015) employed distributional models to explore 1565 observations from nine different exchange rates (the Australian Dollar-AUD, the Brazilian Real-BRL, the Canadian Dollar-CAD, the Swiss Franc-CHF, the Euro-EUR, the Sterling-GBP, the Mexican Peso-MXN, the Turkish Lira-TRY and the Japanese Yen-JPY) in terms of the US Dollar. Pilbeam and Langeland (2015) forecasted the exchange rate volatility of four currencies (the Euro, Pound, Swiss Franc and Yen against the US Dollar) based on GARCH models. They compared their results with implied volatility forecasts. Adi (2019) examined exchange rate return volatility of Chinese Yuan (against the US Dollar) using a GARCH family of models. For more recent applications on exchange rate volatility, including Bayesian-MCMC GARCH type models and their estimation procedures, see Adıgüzel Mercangöz (2021) and the references therein. See also Gospodinov et al. (2006) and Plíhal and Lyócsa (2021).

Remarkably, research on the exchange rate volatility and dynamic conditional correlation analysis of financial market interdependence has focused on the financial markets in developed countries. Little attention has been paid to the exchange rate volatility of emerging economies, especially African countries, for example, see Karanasos et al. (2022), Niyitegeka and Tewari (2020), Carsamer (2015), Jordaan (2015), Raputsoane (2008), Yonis (2011), Emenike (2018) and Mohammed et al. (2021). Even the few papers appear to be limited in their scope. It is true that African markets/economies (including their currencies) are generally small when compared to other markets and many African countries have not taken reasonable steps towards financial liberalization due to poor economic conditions, political unrest as well as regulated and restrictive practices (Tolikas, 2011). However, no matter how small the economy is, there is a growing body of evidence that crisis (financial/economic/health) in one country (or one part of the world) can spread economic pain to other countries (other parts of the world). Some typical examples include: 2008 financial crisis; Covid 19 pandemic; 2015-16 Zika virus outbreaks; migration crisis as a result of displacement due to conflicts/wars. We believe that characterizing the exchange rate volatility of major African countries will help the policy makers to make informed evidence-based decisions at the most appropriate times even as many countries within the region are trying to recover from recessions and economic hardship due to Covid 19. In addition, this can be of interest to investors (both local and international) who are concerned with the chances of losing a big part of the value of their portfolios in a short time period given the economic and security outlook of most of the countries in the region. For example, in the nearest possible future, a country like Nigeria may not have the ability to attract external private financial flows due to macroeconomic imbalances and policy uncertainty (African Economic Outlook, 2021). The same can be said about many other African countries. In particular, Africa’s public debts are growing at an alarming rate. Majority of the countries in this region are witnessing a slowdown in economic growth due to debt and repayment crises. As a consequence, many are re-negotiating terms of their loans with the global lending agencies/bodies and countries as their economies are being hurt by excessive debt, making their currency more volatile (Chaudhury, 2021). To cite an instance, at the beginning of January 2015, United States Dollar-US$1 was exchanged for Nigerian-Naira187.91, however by the end of June 2021, the Naira/Dollar exchange rate was 409.50 to $1, indicating roughly 117.9235% drop in value. For Ghana, at the beginning of January 2014, US$1 was exchanged for Cedi2.3975, then by the end of June 2021, the Cedi/Dollar exchange rate stood at 5.75 to $1, representing about 139.8332% decrease in value. Also, for Angola, at the beginning of December 2016, US$1 was exchanged for Angolan-Kwanza 65.08, then by the end of June 2021, the Kwanza/Dollar exchange rate stood at 643.0 to $1, representing about \(289.5081\%\) decrease in value. Hence, it is pertinent to study the exchange rate volatility of African countries. This is part of our motivation for this paper.

The primary aim of this paper is to perform GARCH-type modelling of the exchange rate volatility of eight major African currencies with emphasis on the distribution for innovations. The currencies considered include the Nigerian Naira (NGN), Ghanaian Cedi (GHS), South African Rand (ZAR), Algerian Dinar (DZD), Moroccan Dirham (MAD), Kenyan Shilling (KES), Ethiopian Birr (ETB) and Angolan Kwanza (AOA). We used the method of maximum likelihood to fit the models and assessed the performance of the models using five different criteria. The predictive ability of the best performing model was assessed in term of the two most commonly used financial risk measures: value at risk and expected shortfall.

The contents of this paper are organized as follows. The data used and associated summary statistics are described in Sect. 2. The GARCH model, its multivariate extension as well as fifteen distributions for innovations are described in Sect. 3. The results and their discussion are given in Sect. 4. Finally, conclusions are given in Sect. 5. All of the computations for this paper were performed using R (R Development Core Team, 2022).

2 Data

Our data consists of eight different African currency exchange rates in terms of the US Dollar. The currencies include the Nigerian Naira (NGN), Ghanaian Cedi (GHS), South African Rand (ZAR), Algerian Dinar (DZD), Moroccan Dirham (MAD), Kenyan Shilling (KES), Ethiopian Birr (ETB) and Angolan Kwanza (AOA). The daily closing rates were obtained from the database DataStream for the period from 18 April 2013 to 15 May 2020, which corresponds to a total of 1846 data points. The choice of these countries is not just because they provide a good geographical representation of the continent, but they also represent the top eight African currencies according to the gross domestic product (GDP), see Fig. 1. Following common practice, we computed the daily log returns as first order differences of logarithms of daily exchange rates. That is, logarithmic returns were calculated as

$$\begin{aligned} \displaystyle Y_{i,t} = \log \left( \frac{X_{i,t}}{X_{i,t-1}} \right) \end{aligned}$$
(1)

for \(i = 1, 2, \ldots , n\), where \(Y_{i,t}\) is the return on the index i for period t, \(X_{i,t}\) is the daily closing rate of the index at the end of the period t and \(X_{i,t-1}\) is the exchange rate of the index at the end of the period \(t-1\).

Fig. 1
figure 1

The map of Africa showing the eight countries: Nigeria, Ghana, South Africa, Algeria, Morocco, Kenya, Ethiopia, and Angola

Full size image
Table 1 Summary statistics of the log returns of the US Dollar exchange rates of major African currencies: Nigeria-Naira, Ghana-Cedi, South Africa-Rand, Algeria-Dinar, Morocco-Dirham, Kenya-Shilling, Ethiopia-Birr, and Angola-Kwanza
Full size table

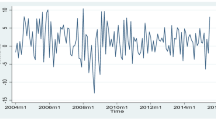
Figure 2 shows time series plots with two dashed lines representing pointwise 95% predictive intervals based on the fitted GARCH model with GH innovations, see Sect. 3. The plots look reasonable and suggest that the fitted model is good. Similar observations emerged for GARCH(1,1) with AST innovations. However, due to space concerns, we do not present the plots from the AST innovations. Also, we can observe that log returns of each market are in general more volatile than the market index (again not shown here due to space concerns). Periods of low and high volatility which fluctuate around zero with no visible trend are depicted. This confirms that there is a strong first order persistence in returns.

Fig. 2
figure 2

Time series plots with 95% predictive intervals of the daily log returns of the US Dollar exchange rates of eight major African currencies from the 18th April of 2013 to 15th of May 2020. Predictions are based on the GARCH(1,1) model with GH innovations

Full size image

The descriptive statistics based on the transformed data are given in Table 1. The computed statistics include the following: minimum, maximum, median, mean, skewness, kurtosis, standard deviation (SD), variance, coefficient of variation (CV), range, and interquartile range (IQR). Predictably, the minimum values for the daily log returns for each of the eight currencies are negative. The smallest of the minimum is for Ghana and the largest of the minimum is for Kenya. The maximum is the largest for Nigeria log returns and smallest for Kenya log returns. The values of mean and median are all positive and close to zero for the eight countries. The Ghana log returns give the largest mean. Except for Morocco and Kenya, the skewness is positive for the African countries. The values of the kurtosis indicate deviations from normality for all the countries as they are significantly larger than three with the exception of South Africa. This is in tandem with the early empirical evidence about the non-normality behaviour associated with financial returns (Mandelbrot, 1963; Fama, 1965). The values of the coefficient of variation are generally positive for all the countries. The coefficient of variation is smallest for Angola and largest for Morocco. In terms of variability, Nigeria log returns have the largest standard deviation while Kenya log returns have the smallest standard deviation. Furthermore, we tested normality of each data set using the Anderson–Darling test (Anderson & Darling, 1954), the Jarque–Bera test (Jarque & Bera, 1980), the Shapiro–Wilk test (Shapiro & Wilk, 1965), the Shapiro–Francia test (Shapiro & Francia, 1972) and the Lilliefors test (Lilliefors, 1967). The test statistics and associated p values are given in Table 2. The results indicate that all of the eight exchange rates are not Gaussian.

Table 2 Tests for normality of the data on the eight African currencies
Full size table

3 Methodology

3.1 GARCH Model

In this section, we describe the GARCH model as well as the distributions for the innovation process used. GARCH class of models consists of two parts: the volatility and innovation components. The volatility part of the GARCH describes the volatility process of an asset/exchange rate return. The innovation part characterizes the innovation process which is generally assumed to follow the standardized version of any of the distributional models listed in the later part of this section. Let X denote a continuous random variable representing the log returns of the exchange rate of Nigeria-Naira, Ghana-Cedi, South Africa-Rand, Algeria-Dinar, Morocco-Dirham, Kenya-Shilling, Ethiopia-Birr, and Angola-Kwanza. The functional form of the general GARCH model for \(X_t\) is specified as

$$\begin{aligned}&\displaystyle X_t = \mu _t+\varepsilon _t, \nonumber \\&\displaystyle \varepsilon _t = \sigma _t\eta _t, \nonumber \\&\displaystyle \eta _t \sim \psi _{\theta }(0, 1), \end{aligned}$$
(2)
$$\begin{aligned}&\displaystyle \sigma _t^2 = \omega +\sum _{i=1}^q\alpha _i \varepsilon _{t-i}^2+\sum _{j=1}^p\beta _j\sigma _{t-j}^2, \end{aligned}$$
(3)

where \(X_t\) represents the observed log returns of the exchange rate for the countries under consideration, \(\mu _t\) and \(\sigma _t>0\) signify measurable functions with respect to a \(\sigma \)-field \({\mathcal {F}}_{t-1}\) generated by \(X_{t-j} \) at time \(t-1\) for \(j\ge 1\), \(\left\{ \eta _t\right\} \) are unobservable independent and identical random variables with zero mean and unit variance, that is E\(\left( \eta _t \right) =0\), Var\( \left( \eta _t\right) =1\). Additionally, we assume that \(\left\{ \eta _t\right\} \) is independent of the past of the process \(\varepsilon _{t}\). For simplicity, we shall adopt the most widely used formulation of the GARCH model:

$$\begin{aligned} \displaystyle \sigma _t^2 = \omega +\alpha _1 \varepsilon _{t-1}^2+\beta _1\sigma _{t-1}^2, \quad \displaystyle 0\le \alpha _1, \ \displaystyle \beta _1\le 1, \ \displaystyle \alpha _1 +\beta _1 <1. \end{aligned}$$
(4)

We assume that \(\left\{ \eta _t\right\} \), the innovation process, is distributed according to \(\psi _{\theta }(0,1)\), which could be any of the listed distributions:

  • the normal distribution with

    $$\begin{aligned} \displaystyle f (x) = \frac{1}{\sqrt{2 \pi } \sigma } \exp \left\{ -\frac{\displaystyle (x - \mu )^2}{\displaystyle 2 \sigma ^2} \right\} \end{aligned}$$
    (5)

    for \(-\infty< x < \infty \), \(-\infty< \mu < \infty \) and \(\sigma > 0\);

  • the skew normal distribution (Azzalini, 1985) with

    $$\begin{aligned} f (x) = \displaystyle \frac{2}{\sigma } \phi \left( \frac{\displaystyle x - \mu }{\displaystyle \sigma } \right) \Phi \left( \lambda \frac{\displaystyle x - \mu }{\displaystyle \sigma } \right) \end{aligned}$$
    (6)

    for \(-\infty< x < \infty \), \(-\infty< \mu < \infty \), \(-\infty< \lambda < \infty \) and \(\sigma > 0\), where \(\phi (\cdot )\) and \(\Phi (\cdot )\) denote, respectively, the probability density and cumulative distribution functions of the standard normal distribution;

  • the logistic distribution with

    $$\begin{aligned} f (x) = \displaystyle \frac{1}{\sigma } \exp \left( -\frac{\displaystyle x - \mu }{\displaystyle \sigma } \right) \left\{ 1 + \exp \left( -\frac{\displaystyle x - \mu }{\displaystyle \sigma } \right) \right\} ^{-2} \end{aligned}$$
    (7)

    for \(-\infty< x < \infty \), \(-\infty< \mu < \infty \) and \(\sigma > 0\);

  • Student’s t distribution (Gosset, 1908) with

    $$\begin{aligned} f (x) = \displaystyle \frac{\displaystyle K (\nu )}{\displaystyle \sigma } \left[ 1 + \frac{\displaystyle (x - \mu )^2}{\displaystyle \sigma ^2 \nu } \right] ^{-\frac{1 + \nu }{2}} \end{aligned}$$
    (8)

    for \(-\infty< x < \infty \), \(-\infty< \mu < \infty \), \(\sigma > 0\) and \(\nu > 0\), where \(K (\nu ) = \sqrt{\nu } B \left( \frac{\nu }{2}, \frac{1}{2} \right) \) and \(B (\cdot , \cdot )\) denotes the beta function defined by

    $$\begin{aligned} B (a, b) = \displaystyle \int _0^1 t^{a - 1} (1 - t)^{b - 1} dt; \end{aligned}$$
    (9)

  • the skew t distribution (Azzalini & Capitanio, 2003) with

    $$\begin{aligned} f (x)= & {} \displaystyle \frac{\displaystyle K (\nu )}{\displaystyle \sigma } \left[ 1 + \frac{\displaystyle (x - \mu )^2}{\displaystyle \sigma ^2 \nu } \right] ^{-\frac{1 + \nu }{2}} \end{aligned}$$
    (10)
    $$\begin{aligned}&\displaystyle +\frac{\displaystyle 2 K^2 (\nu ) \lambda (x - \mu )}{\displaystyle \sigma ^2} \ {}_2F_1 \left( \frac{\displaystyle 1}{\displaystyle 2}, \frac{\displaystyle 1 + \nu }{\displaystyle 2}; \frac{\displaystyle 3}{\displaystyle 2}; -\frac{\displaystyle \lambda ^2 (x - \mu )^2}{\displaystyle \sigma ^2 \nu } \right) \end{aligned}$$
    (11)

    for \(-\infty< x < \infty \), \(-\infty< \mu < \infty \), \(-\infty< \lambda < \infty \), \(\sigma > 0\) and \(\nu > 0\), where \({}_2F_1 (a, b; c; x)\) denotes the Gauss hypergeometric function defined by

    $$\begin{aligned} \displaystyle {}_2F_1 \left( a, b; c; x \right) = \displaystyle \sum _{k = 0}^{\infty } \frac{\displaystyle \left( a \right) _k \left( b \right) _k}{\displaystyle \left( c \right) _k} \frac{\displaystyle x^k}{\displaystyle k!}, \end{aligned}$$
    (12)

    where \((e)_k = e (e + 1) \cdots (e + k - 1)\) denotes the ascending factorial;

  • Laplace distribution (Laplace, 1774) with

    $$\begin{aligned} f (x) = \displaystyle \frac{1}{2 \sigma } \exp \left( -\frac{\displaystyle \mid x - \mu \mid }{\displaystyle \sigma } \right) \end{aligned}$$
    (13)

    for \(-\infty< x < \infty \), \(-\infty< \mu < \infty \) and \(\sigma > 0\);

  • the exponential power distribution (Subbotin, 1923) with

    $$\begin{aligned} \displaystyle f(x) = \frac{\displaystyle \beta }{\displaystyle 2\sigma \Gamma \left( \frac{1}{\beta } \right) } \exp \left\{ -\left( \frac{\displaystyle |x - \mu |}{\displaystyle \sigma }\right) ^\beta \right\} \end{aligned}$$
    (14)

    for \(-\infty< x < \infty \), \(-\infty< \mu < \infty \), \(\sigma > 0\) and \(\beta > 0\), where \(\Gamma (\cdot )\) denotes the gamma function defined by

    $$\begin{aligned} \Gamma (a) = \displaystyle \int _0^\infty t^{a - 1} \exp (-t) dt; \end{aligned}$$
    (15)

  • the generalized t distribution (McDonald & Newey, 1988) with

    $$\begin{aligned} f (x) = \displaystyle \frac{\displaystyle \tau }{\displaystyle 2 \sigma \nu ^{\frac{1}{\nu }} B \left( \nu , \frac{1}{\tau } \right) } \left[ 1 + \frac{\displaystyle 1}{\displaystyle \nu } \left| \frac{\displaystyle x - \mu }{\displaystyle \sigma } \right| ^\tau \right] ^{-\left( \nu + \frac{1}{\tau } \right) } \end{aligned}$$
    (16)

    for \(-\infty< x < \infty \), \(-\infty< \mu < \infty \), \(\sigma > 0\), \(\nu > 0\) and \(\tau > 0\);

  • the skewed exponential power distribution (Zhu & Zinde-Walsh, 2009) with

    $$\begin{aligned} \displaystyle f (x) = C \left\{ \begin{array}{ll} \displaystyle \exp \left\{ -\frac{1}{p} \left[ \frac{\displaystyle \mu - x}{\displaystyle 2 \sigma \alpha } \right] ^p \right\} , &{} \text{ if } x \le \mu , \\ \displaystyle \exp \left\{ -\frac{1}{p} \left[ \frac{\displaystyle x - \mu }{\displaystyle 2 \sigma (1 - \alpha )} \right] ^p \right\} , &{} \text{ if } x > \mu \end{array} \right. \end{aligned}$$
    (17)

    for \(-\infty< x < \infty \), \(-\infty< \mu < \infty \), \(\alpha > 0\), \(\sigma > 0\) and \(p > 0\), where \(C = \frac{1}{2 \sigma A_0 \left( p \right) }\) and and \(A_0 (x) = x^{\frac{1}{x} - 1} \Gamma \left( \frac{1}{x} \right) \);

  • the asymmetric exponential power distribution (Zhu & Zinde-Walsh, 2009) with

    $$\begin{aligned} \displaystyle f (x) = C \left\{ \begin{array}{ll} \displaystyle \exp \left\{ -\frac{1}{p_1} \left[ \frac{\displaystyle \mu - x}{\displaystyle 2 \sigma \alpha } \right] ^{p_1} \right\} , &{} \text{ if } x \le \mu , \\ \displaystyle \exp \left\{ -\frac{1}{p_2} \left[ \frac{\displaystyle x - \mu }{\displaystyle 2 \sigma (1 - \alpha )} \right] ^{p_2} \right\} , &{} \text{ if } x > \mu \end{array} \right. \end{aligned}$$
    (18)

    for \(-\infty< x < \infty \), \(-\infty< \mu < \infty \), \(\sigma > 0\), \(\alpha > 0\), \(p_1 > 0\) and \(p_2 > 0\), where C is given by

    $$\begin{aligned} C = \frac{\displaystyle 1}{\displaystyle 2 \sigma \alpha A_0 \left( p_1 \right) + 2 \sigma (1 - \alpha ) A_0 \left( p_2 \right) }; \end{aligned}$$
    (19)

  • the skewed Student’s t distribution (Zhu & Galbraith, 2010) with

    $$\begin{aligned} \displaystyle f (x) = \frac{\displaystyle K \left( \nu \right) }{\displaystyle \sigma } \left\{ \begin{array}{ll} \displaystyle \left\{ 1 + \frac{1}{\nu } \left[ \frac{\displaystyle x - \mu }{\displaystyle 2 \sigma \alpha } \right] ^2 \right\} ^{-\frac{\nu + 1}{2}}, &{} \text{ if } x \le \mu \text{, } \\ \displaystyle \left\{ 1 + \frac{1}{\nu } \left[ \frac{\displaystyle x - \mu }{\displaystyle 2 \sigma \left( 1 - \alpha \right) } \right] ^2 \right\} ^{-\frac{\nu + 1}{2}}, &{} \hbox { if}\ x > \mu \end{array} \right. \end{aligned}$$
    (20)

    for \(-\infty< x < \infty \), \(-\infty< \mu < \infty \), \(0< \alpha < 1\) and \(\nu > 0\);

  • the asymmetric Student’s t distribution (Zhu & Galbraith, 2010) with

    $$\begin{aligned} \displaystyle f (x) = \frac{1}{\sigma } \left\{ \begin{array}{ll} \displaystyle \frac{\alpha }{\alpha ^{*}} K \left( \nu _1 \right) \left\{ 1 + \frac{\displaystyle 1}{\displaystyle \nu _1} \left[ \frac{\displaystyle x - \mu }{\displaystyle 2 \sigma \alpha ^{*}} \right] ^2 \right\} ^{-\frac{\nu _1 + 1}{2}}, &{} \text{ if } x \le \mu \text{, } \\ \displaystyle \frac{\displaystyle 1 - \alpha }{\displaystyle 1 - \alpha ^{*}} K \left( \nu _2 \right) \left\{ 1 + \frac{\displaystyle 1}{\displaystyle \nu _2} \left[ \frac{\displaystyle x - \mu }{\displaystyle 2 \sigma \left( 1 - \alpha ^{*} \right) } \right] ^2 \right\} ^{-\frac{\nu _2 + 1}{2}}, &{} \hbox { if}\ x > \mu \end{array} \right. \end{aligned}$$
    (21)

    for \(-\infty< x < \infty \), \(-\infty< \mu < \infty \), \(0< \alpha < 1\), \(\nu _1 > 0\) and \(\nu _2 > 0\), where

    $$\begin{aligned} \displaystyle \alpha ^{*} = \frac{\displaystyle \alpha K \left( \nu _1 \right) }{\displaystyle \alpha K \left( \nu _1 \right) + (1 - \alpha ) K \left( \nu _2 \right) }; \end{aligned}$$
    (22)

  • the normal inverse gamma distribution (Barndorff-Nielsen, 1977) with

    $$\begin{aligned} f (x) = \displaystyle \frac{\displaystyle \left( \frac{\gamma }{\delta } \right) ^\lambda \alpha }{\displaystyle \sqrt{2 \pi } K_{-\frac{1}{2}} \left( \delta \gamma \right) } \left[ \delta ^2 + (x - \mu )^2 \right] ^{-1} K_{-1} \left( \alpha \sqrt{\delta ^2 + (x - \mu )^2} \right) \end{aligned}$$
    (23)

    for \(-\infty< x < \infty \), \(-\infty< \mu < \infty \), \(\delta > 0\), \(\alpha > 0\) and \(\beta > 0\), where \(\gamma = \sqrt{\alpha ^2 - \beta ^2}\) and \(K_\nu (\cdot )\) denotes the modified Bessel function of the second kind of order \(\nu \) defined by

    $$\begin{aligned} \displaystyle K_\nu (x) = \displaystyle \left\{ \begin{array}{ll} \displaystyle \frac{\displaystyle \pi \mathrm{csc} (\pi \nu )}{\displaystyle 2} \left[ I_{-\nu } (x) - I_{\nu } (x) \right] , &{} \text{ if } \nu \not \in {\mathbb {Z}}\text{, } \\ \displaystyle \lim _{\mu \rightarrow \nu } K_\mu (x), &{} \text{ if } \nu \in {\mathbb {Z}}\text{, } \end{array} \right. \end{aligned}$$
    (24)

    where \(I_\nu (\cdot )\) denotes the modified Bessel function of the first kind of order \(\nu \) defined by

    $$\begin{aligned} \displaystyle I_\nu (x) = \sum _{k = 0}^\infty \frac{\displaystyle 1}{\displaystyle \Gamma (k + \nu + 1) k!} \left( \frac{\displaystyle x}{\displaystyle 2} \right) ^{2k + \nu }; \end{aligned}$$
    (25)

  • the hyperbolic distribution (Barndorff-Nielsen, 1977) with

    $$\begin{aligned} f (x) = \displaystyle \frac{\displaystyle \left( \frac{\gamma }{\delta } \right) ^\lambda \alpha ^{-\frac{1}{2}}}{\displaystyle \sqrt{2 \pi } K_1 \left( \delta \gamma \right) } \left[ \delta ^2 + (x - \mu )^2 \right] ^{\frac{1}{2}} K_{\frac{1}{2}} \left( \alpha \sqrt{\delta ^2 + (x - \mu )^2} \right) \end{aligned}$$
    (26)

    for \(-\infty< x < \infty \), \(-\infty< \mu < \infty \), \(\delta > 0\), \(\alpha > 0\) and \(\beta > 0\), where \(\gamma = \sqrt{\alpha ^2 - \beta ^2}\);

  • the generalized hyperbolic distribution (Barndorff-Nielsen, 1977) with

    $$\begin{aligned} f (x) = \displaystyle \frac{\displaystyle \left( \frac{\gamma }{\delta } \right) ^\lambda \alpha ^{\frac{1}{2} - \lambda }}{\displaystyle \sqrt{2 \pi } K_\lambda \left( \delta \gamma \right) } \left[ \delta ^2 + (x - \mu )^2 \right] ^{\lambda - \frac{1}{2}} K_{\lambda - \frac{1}{2}} \left( \alpha \sqrt{\delta ^2 + (x - \mu )^2} \right) \end{aligned}$$
    (27)

    for \(-\infty< x < \infty \), \(-\infty< \mu < \infty \), \(-\infty< \lambda < \infty \), \(\delta > 0\), \(\alpha > 0\) and \(\beta > 0\), where \(\gamma = \sqrt{\alpha ^2 - \beta ^2}\).

Of these, one of the most suitable leptokurtic distributions is the generalized hyperbolic distribution as it contains the normal, Student’s t, hyperbolic, normal inverse gamma and Laplace distributions as particular cases.

The performance of GARCH models in terms of capturing volatility clustering and leptokurtosis depends on the probability distributions assumed for the innovation process. It is not difficult to see that if either large (small) \(\varepsilon _{t-1}^2\) or \(\sigma _{t-1}^2\) results in a large (small) \(\sigma _t^2\), then the implication is that a pocket of large \(\varepsilon _{t-1}^2\) will be followed by a pocket of large \(\sigma _{t-1}^2\), a pocket of small \(\varepsilon _{t-1}^2\) will be followed by a pocket of small \(\sigma _{t-1}^2\) and so on. This process is called volatility clustering (Tsay, 2014). Additionally, if \(1-2\alpha _1^2 - \left( \alpha _1+\beta _1 \right) ^2 > 0\) then

$$\begin{aligned} \displaystyle \frac{E\varepsilon _t^4}{\left[ E\varepsilon _t^2 \right] ^2} = \frac{3\left[ 1 - \left( \alpha _1+\beta _1\right) ^2 \right] }{1 - \left( \alpha _1+\beta _1\right) ^2-2a\alpha _1^2}>3, \end{aligned}$$
(28)

suggesting that the tail distribution of a GARCH process of order 1 is heavier than that of the normal. For this purpose, we have included as many flexible probability distributions as possible. We perform our analysis in a slightly different way and use a “2-steps selection” process. First, we fitted the innovation process distributions on their own to the data sets, then selected the best five distributions and employed them as distributions for the GARCH (1,1) innovations. Then, the GARCH(1,1) models with the associated best performing distributions for the innovation were fitted and compared. The two step fitting was done to ensure that our model performance as well as selection are consistent and to also gain a better understanding of the exchange rate returns. In each case, we used the following selection criteria to discriminate among the fitted models:

  • the Akaike information criterion due to Akaike (1974) defined by

    $$\begin{aligned} \displaystyle \mathrm{AIC} = 2 k - 2 \log L \left( \widehat{\varvec{\Theta }} \right) , \end{aligned}$$
    (29)

    where \({\varvec{\Theta }}\) are the parameters of the fitted model, \(\widehat{\varvec{\Theta }}\) their maximum likelihood estimates, \(L \left( \widehat{\varvec{\Theta }} \right) \) their likelihood function and k the length of \({\varvec{\Theta }}\);

  • the Bayesian information criterion due to Schwarz (1978) defined by

    $$\begin{aligned} \displaystyle \mathrm{BIC} = k \log n - 2 \log L \left( \widehat{\varvec{\Theta }} \right) ; \end{aligned}$$
    (30)

  • the consistent Akaike information criterion (CAIC) due to Bozdogan (1987) defined by

    $$\begin{aligned} \displaystyle \mathrm{CAIC} = -2 \log L \left( \widehat{\varvec{\Theta }} \right) + k \left( \log n + 1 \right) ; \end{aligned}$$
    (31)

  • the corrected Akaike information criterion (AICc) due to Hurvich and Tsai (1989) defined by

    $$\begin{aligned} \displaystyle \mathrm{AICc} = \mathrm{AIC} + \frac{2 k (k + 1)}{n - k - 1}; \end{aligned}$$
    (32)

  • the Hannan-Quinn criterion due to Hannan and Quinn (1979) defined by

    $$\begin{aligned} \displaystyle \mathrm{HQC} = -2 \log L \left( \widehat{\varvec{\Theta }} \right) + 2 k \log \log n. \end{aligned}$$
    (33)

The smaller the values of these criteria the better the fit. For more discussion on these criteria, see Burnham and Anderson (2004) and Fang (2011).

We used likelihood ratio tests to discriminate between nested distributions: Student’s t distribution contains the normal distribution as the limiting case for \(\nu \rightarrow \infty \); for \(\lambda =0\) the skew normal distribution reduces to the normal distribution; for \(\beta =2\) the exponential power distribution reduces to the normal distribution; for \(\beta =1\) the exponential power distribution reduces to Laplace distribution; the skew Student’s t reduces to Student’s t distribution when \(\lambda =0\); for \(\alpha =\frac{1}{2}\) the skewed exponential power distribution reduces to the exponential power distribution; for \(\tau =2\) the generalized t distribution reduces to Student’s t distribution; the asymmetric exponential power distribution reduces to the skewed exponential power distribution if \(p_1=p_2\); for \(\alpha =\frac{1}{2}\) the skewed Student’s t distribution reduces to Student’s t distribution; the asymmetric Student’s t distribution reduces to the skewed Student’s t distribution if \(\nu _1=\nu _2\); for \(\lambda =1 \) and \(\lambda =-\frac{1}{2}\) the generalized hyperbolic distribution reduces to the hyperbolic and normal inverse gamma distributions, respectively; for \(\lambda =-\frac{\nu }{2}\) and \(\alpha \rightarrow |\beta |\) the generalized hyperbolic distribution reduces to the skewed Student’s t distribution.

3.2 Multivariate GARCH: DCC Model

Due to the growing number of emerging technologies giving rise to rapid advancements in communication, trade and businesses, exchange rate volatility and dynamic correlation of market interdependence have increased as well. To investigate this, we utilize a dynamic conditional correlation (DCC) model, one of the notable multivariate volatility models within the class of multi-variable generalizations of GARCH. Other models within this class include the BEKK model of Engle and Kroner (1995) as well as the exponentially weighted moving average (EWMA) model. However, we are sticking to DCC because the model guarantees that the time dependent conditional correlation matrix is positive definite at every point in time (Kuper & Lestano,, 2007). Also, as noted by Engle and Kroner (1995), the model is relatively parsimonious compared to others like the constant conditional correlations model due to Bollerslev (1990) and the BEKK model.

Suppose \(\mathbf{X}_t\) represents the returns from \(k-\)assets (in our case, log returns of the exchange rates of eight major African currencies) with a \(k-\)dimensional innovation say \(\mathbf{a}_t\). Let \({\varvec{\Sigma }}_t =\left\{ \sigma _{ij,t}\right\} \) denote the volatility matrix of the innovations \(\mathbf{a}_t\) such that all the available information up to \(t-1\) is accommodated in \({\mathcal {F}}_{t-1} = {\varvec{\Phi }}_{t-1}\). The dynamic conditional correlation matrix is given by

$$\begin{aligned} \displaystyle {\varvec{\rho }}_t = {\varvec{\Psi }}_t^{-1} {\varvec{\Sigma }}_t {\varvec{\Psi }}_t^{-1}, \end{aligned}$$
(34)

where \({\varvec{\Psi }}_t=\)diag\(\left\{ \sqrt{\sigma _{11,t}}, \ldots , \sqrt{\sigma _{kk,t}}\right\} \) represents the diagonal matrix of the k volatilities. The total number of elements in the correlation matrix \({\varvec{\rho }}_t\) is \(\frac{k (k - 1)}{2}\). Then, the DCC model due to Engle (2002) is defined by

$$\begin{aligned}&\displaystyle {\mathbf {Q}}_t = \left( 1-\theta _1-\theta _2\right) \overline{\mathbf{Q}}+\theta _1 \mathbf{Q}_{t-1}+\theta _2{\varvec{\eta }}_{t-1} {\varvec{\eta }}_{t-1}^{\prime }, \end{aligned}$$
(35)
$$\begin{aligned}&\displaystyle {\varvec{\rho }}_t = \mathbf{J}_t \mathbf{Q}_t \mathbf{J}_t, \end{aligned}$$
(36)

where \({\varvec{\eta }}_t =\left( \eta _{1t},\ldots ,\eta _{kt} \right) ^{\prime }\) is the vector of the marginals of the standardized distributions of the innovations with \(\eta _{it} = \frac{a_{it}}{\sqrt{\sigma _{ii,t}}}\), \(\overline{\mathbf{Q}}\) is the unconditional covariance matrix of the marginally standardized innovation vector, \({\varvec{\rho }}_t\) denotes the volatility matrix of \({\varvec{\eta }}_t\), \(\theta _i\) are the model parameters which are non-negative real numbers satisfying \(1-\theta _1 -\theta _2>0\), and \(\mathbf{J}_t =\) diag\(\left\{ q_{11,t}^{-\frac{1}{2}}, \ldots , q_{kk,t}^{-\frac{1}{2}}\right\} \), where \(q_{ii,t}\) are the elements of the positive-definite matrix \(\mathbf{Q}_t\). For details on the DCC model, the readers are referred to Tsay (2014) and references therein.

4 Results and Discussion

All of the models described in Sect. 3 were fitted to the data sets on the exchange rates returns explained in Sect. 2. The method of maximum likelihood was used to estimate the parameters of these models. Our analysis was carried out in a sequential fashion as we have fifteen distributions for innovations. This was done to single out the most suitable leptokurtic distributions required in financial data analysis within the GARCH modeling context. First, for a given dataset, we fitted the fifteen distributions. The function optimize in R was used to perform maximization. The log likelihood values and the values of the five model selection criteria are shown in Table 3 for the six best performing distributions.

Table 3 Log likelihood and the five information criteria values based on the best performing distributions for the log returns of the exchange rates of eight major African currencies
Full size table

The six best performing distributions (Student’s t, skew t, AEP, SEP, AST and GH) were employed as the innovation distributions in the GARCH(1,1) model. We chose the first order of GARCH because of its simplicity. In addition, it has been the most popular and commonly used GARCH type of model for characterizing volatility and is readily available in R packages such as rugarch and fGarch due to Ghalanos (2020) and Wuertz and Chalabi (2020), respectively. For fitting the GARCH model with Student’s t, skew t and GH innovations, we used the rugarch package. For fitting the GARCH model with SEP, AEP and AST innovations, we employed the VaRES package due to Nadarajah et al. (2013). The log likelihood values, the values of AIC, BIC, HQC and parameter estimates are given in Table 4.

Table 4 Log likelihood and the information criteria values based on the best and second best performing distributions for the GARCH(1,1) model and their parameter estimates
Full size table

Table 4 reveals that there is no jointly best fitting model for the daily log returns of the exchange rate between the US Dollar and the eight major African currencies. However, the GARCH(1,1) model with Student’s t, AST and GH innovations has consistently performed better than others in all the countries with the exception for Algerian Dinar. According to AIC, BIC and HQC, the best fitting model for Nigerian-Naira is GARCH(1,1) with AST innovations. According to AIC, BIC and HQC, the best fitting model for Ghanaian-Cedi is GARCH(1,1) with GH innovations. According to AIC and BIC, the best fitting models for South African-Rand are GARCH(1,1) with AST and t innovations. According to AIC and BIC, the best fitting models for Algerian-Dinar are GARCH(1,1) with AST and t innovations. According to AIC and HQC, the best fitting model for Moroccan-Dirham is GARCH(1,1) with GH innovations. According to HQC, the best fitting model for Kenyan-Shilling is GARCH(1,1) with GH innovations. According to AIC, BIC and HQC, the best fitting model for Ethiopian-Birr is GARCH(1,1) with AST innovations. According to AIC, BIC and HQC, the best fitting model for Angolan-Kwanza is GARCH(1,1) with AST innovations. However, it is important to note that the differences between the information criteria values across these distributions are marginal. For example, if the information criteria values are rounded to one or two decimal places, then similar results will be obtained for virtually all the participating log returns with few exceptions. Thus, it is safe to assume that the best fitting model for each of the eight data sets is GARCH(1,1) model with either Student’t, AST or GH innovations.

As noted earlier, Student’s t distribution is nested within the AST and GH distributions. Table 5 performs the likelihood ratio tests that the AST and GH distributions do not provide significant improvements over Student’s t distribution.

Table 5 p values of likelihood ratio tests of Student’s t distribution versus the AST and GH distributions
Full size table

Table 5 shows that the null hypothesis is rejected overwhelmingly in favour of the two more general models (i.e. GARCH(1,1) with AST and GH innovations) for each data. The likelihood ratio test supports our earlier results based on AIC, BIC and HQC. Hence, we can conclude that the GARCH(1,1) model with AST innovations provides the best fit for all the data sets except for Algerian-Dinar, Moroccan-Dirham and Kenyan-Shilling. The GARCH(1,1) model with GH innovations provides the best fit for all the data sets except for Algerian-Dinar, Ethiopian-Birr and Angolan-Kwanza.

Figure 3 shows the time series plots of volatility of the fitted GARCH (1,1) model with GH innovations. We can observe that the estimated volatility for Algerian-Dinar, Moroccan-Dirham and Kenyan-Shilling are essentially the same; they are indistinguishable and represent the least volatile currencies. Nigerian-Naira and Ghanian-Cedi are the most volatile among the currencies. The estimated volatility for Ethiopian-Birr and Angolan-Kwanza are also identical. Figure 4 shows boxplots of the estimated volatility and the correlation coefficients between the estimated volatility series. We can observe that the correlations between the volatilities of African currencies are generally low, suggesting that these currencies are not greatly aligned. This is not surprising as emerging markets tend to be affected by local factors such as diverging monetary policies and unique economic and political factors. The largest correlation is between Moroccan-Dirham and Algerian-Dinar, followed by (Algerian-Dinar, South African-Rand) and (Moroccan-Dirham, South African-Rand).

Fig. 3
figure 3

Time series plots of volatility of GARCH(1,1) model with GH innovations for daily log returns of the exchange rates between the US Dollar and eight major African currencies from the 18th April of 2013 to 15th of May 2020

Full size image
Fig. 4
figure 4

Boxplots of volatility (top) and their correlations (bottom) based on GARCH(1,1) with GH innovations for daily log returns of the exchange rates between the US Dollar and eight major African currencies from the 18th April of 2013 to 15th of May 2020

Full size image

Now, based on GARCH(1,1) model with AST innovations, we compute the VaR and ES. If \({\widehat{F}}(\cdot )\) denotes the cumulative distribution function of the best fitting distribution, then VaR and ES corresponding to probability q are defined by

$$\begin{aligned} \displaystyle \text{ VaR}_{(q)}= {\widehat{F}}^{-1}(q) \end{aligned}$$
(37)

and

$$\begin{aligned} \displaystyle \text{ ES}_{(q)}= \frac{1}{q}\int _0^q\text{ VaR }(u)du, \end{aligned}$$
(38)

respectively, where \(0<q<1\). The VaR, ES as well as expected volatility based on GARCH(1,1) with AST innovations are given in Figs. 5 and 6.

Fig. 5
figure 5

Value at risk and expected shortfall based on the GARCH(1,1) model with AST innovations for daily log returns of the exchange rates of Nigerian-Naira (NGN), Ghanaian-Cedi (GHS), South African-Rand (ZAR), Algerian-Dinar (DZD), Moroccan-Dirham (MAD), Kenyan Shilling (KES), Ethiopian-Birr (ETB) and Angolan-Kwanza (AOA) from the 18th April of 2013 to 15th of May 2020

Full size image
Fig. 6
figure 6

Expected volatility based on the GARCH(1,1) model with AST innovations for daily log returns of the exchange rates between the US Dollar and eight major Africa currencies from the 18th April of 2013 to 15th of May 2020

Full size image

For VaR, we can observe that Nigerian-Naira is the riskiest, followed by South African-Rand and Ghanaian-Cedi. Algerian-Dinar, Moroccan-Dirham and Kenyan-Shilling are the least riskiest. The median of VaR is largest for South African-Rand and smallest for Kenyan-Shilling, Algerian-Dinar and Moroccan-Dirham. In term of variability, VaR is the largest for Ghanaian-Cedi, followed by Angolan-Kwanza and Ethiopian-Birr. The variability of VaR is the smallest for Nigerian-Naira, followed by Algerian-Dinar, Kenyan-Shilling and Moroccan-Dirham. For ES, the median is the largest for South African-Rand and the smallest for Nigerian-Naira. The variability is the largest for Ghanaian-Cedi and the smallest for Nigerian-Naira.

The expected volatility varies through time and we can observe that the expected volatility for all t is maximum for Nigerian-Naira; the expected volatility for all t is second maximum for South African-Rand; the expected volatility for all t is minimum for Algerian-Dinar; the expected volatility for all t is second minimum for Moroccan-Dirham. The expected volatilities for Angolan-Kwanza and Ghanaian-Cedi appear to be in tandem for all t except for all sufficiently large t; the expected volatilities for Kenyan-Shilling and Moroccan-Dirham are almost in tandem for small t but for all sufficiently large t the expected volatility for Kenyan-Shilling is larger.

Figure 7 forecasts of the best fitting model in terms of VaR for each of the eight exchange rates by fifty additional days for \(p = 0.9, 0.95, 0.975, 0.99\), by one hundred additional days for \(p=0.9\) and by two hundred additional days for \(p=0.9\). We can observe that the forecast for each daily log returns is strictly increasing with respect to time. For every p and t, the forecast is largest for Nigeria, the forecast is second largest for South Africa, and the forecast is third largest for Ghana. The smallest of the forecast is for Algeria and Morocco for every p and t.

Fig. 7
figure 7

Forecasting of the daily log returns of the exchange rates between the US Dollar and eight major Africa currencies in terms of value at risk based on the GARCH(1,1) model with AST innovations for \(p = 0.9, 0.95, 0.975, 0.99\)

Full size image

In addition to fitting of the univariate GARCH models, we fitted the DCC-GARCH model due to Engle (2002) discussed in Sect. 3.2 to account for the dynamics of correlation structures between exchange rates. This is essential because not only returns and volatilities are vital in the portfolio selection process and investment destination choices, but also correlations between assets (Kuper & Lestano,, 2007). Again, parameter estimation was done using R via the rugarch and rmgarch packages. The method of maximum likelihood was used. To ensure that there is a dynamic structure in the correlations that will justify using the DCC-GARCH model, a test of constant correlation was performed. The test gave a p value of 0 which amounted to rejection of the null hypothesis of constant correlation. The log likelihood values and the values of the selection criteria for the fitted DCC-GARCH(1,1) model with multivariate Student’s t innovations are in Table 6. Other higher classes of DCC-GARCH type models were fitted, however none of them provided significantly better fits. We used the multivariate Student’s t distribution for the innovation processes because it was among the three best fitting distributions in the univariate case. Also it is readily available in the R packages for GARCH and MGARCH.

Table 6 Parameter estimates for some of the fitted DCC-GARCH type models, their standard errors, t-values, p values, log likelihood values and three information criteria values for the major African currencies
Full size table

We have provided only the DCC-GARCH parameter estimates in Table 6 due to space concerns. Also, the GARCH(1,1) parameter estimates for each of the currencies are similar to those obtained in the univariate case, especially for the DCC-GARCH(1,1) model.

From Table 6, we can observe that all the DCC conditional correlation parameters of DCC-GARCH(1,1) are significant at 10%, 5% and 1% levels. According to the selection criteria, the DCC-GARCH(1,1) with multivariate Student’s t distribution provides the best fit. Furthermore, the conditional correlation parameters of the best fitting model show adherence to the restriction imposed on them; that is they are all greater than zero with their sum less than one \(\left( \texttt {dcca1}=\theta _1=0.007272+\texttt {dccb1}=\theta _2=0.978871<1 \right) \). Hence, we can conclude that the correlation across the major African currencies is significantly time varying. The dynamic conditional correlations between the exchange rates of the major African countries are shown in Figs. 8 and 9. We observe that there is a significant variation through time across the countries with the correlation values generally ranging between \(-\) 0.10 and 0.5. In other words, there are periods of low and high correlations, no visible trends and there are no simultaneous drops or jumps across the currencies. The structural breaks in the patterns are unique and peculiar to each country except for the few like (Algerian-Dinar, Kenyan-Shilling), (Moroccan-Dirham, Kenyan-Shilling), (Ghanian-Cedi, Algerian-Dinar) and (Ghanian-Cedi, Moroccan-Dirham). One possible explanation for this uniqueness could be the differences in inflation rates, lack of close ties between the countries (this is common with emerging economies), retreat in stock values due to liquidity drops, socio-political factors and state of the economies. For example, the dynamic correlations between the exchange rates of Algeria and Morocco are largest for all days and appear to be the only increasing interdependent economies. This could be attributed to the fact that these two countries are members of Arab League; whose main goal is to draw closer the association between member states and at the same time coordinate collaboration between them to promote their welfare and interest (Katramiz et al., 2019). Pairs involving Angolan Kwanza (for example, NGN/AOA, ETB/AOA, MAD/AOA, DZD/AOA and KES/AOA with the exception ZAR/AOA) yield the smallest dynamic conditional correlations. This could be attributed to the fall in oil prices in recent years which reduced the country’s growth momentum and generated huge macroeconomic imbalance. Of course Angola is very rich in natural resources. The country is the second largest oil producer in Sub-Saharan Africa, after Nigeria (Carey et al., 2018). However, Angola has the worst diversification attitude; as such, the government has not been able to convert the country’s considerable natural endowment into various forms of capital (Angola Systematic Country Diagnostic, 2018). Pairs involving Nigerian Naira (for example, ZAR/NGN, GHS/NGN and AOA/NGN) give the second smallest dynamic conditional correlations. For the pairs in Fig. 8, the estimated conditional correlations are generally low, drifting around 0, and falling to levels as low as \(-\,0.06\). This could be due to fall in crude oil prices on account of falling global demand. Nigeria is a mono economy and more than 80% of its export earning comes from oil. So this contraction in the export earning from oil has given rise to debase in real GDP; causing the economy to shrink by 3% in 2019 and 2020. As a consequence, inflation set in and rose from 11.4% in 2019 to 12.8% in 2020 (African Economic Outlook, 2021).

Fig. 8
figure 8

Time varying correlations based on the DCC-GARCH(1,1) model with multivariate Student’s t innovations for daily log returns of the exchange rates between the US Dollar and eight major Africa currencies from the 18th April of 2013 to 15th of May 2020

Full size image
Fig. 9
figure 9

Time varying correlations based on the DCC-GARCH(1,1) model with multivariate Student’s t innovations for daily log returns of the exchange rates between the US Dollar and eight major African currencies from the 18th April of 2013 to 15th of May 2020

Full size image

In general, we note that the low to moderate dynamic correlations between the exchange rates of the eight African currencies are due to the fact that emerging economies are vastly regulated and in many instances governed by certain economic factors like political regimes and social events. This is in line with Tolikas (2011)’s observations, who noted that emerging economies offer better diversification opportunities and larger returns but with higher volatility due to minimal correlation with other markets/economies.

5 Conclusions

In this paper, we have described the log returns of the exchange rate volatilities of eight major African currencies using the GARCH(1,1) model with fifteen distributions for innovations (the normal distribution, the skew normal distribution, the logistic distribution, Student’s t distribution, the skew Student’s t distribution, Laplace distribution, the exponential power distribution, the generalized t distribution, the skewed exponential power distribution, the asymmetric exponential power distribution, the skewed Student’s t distribution, the asymmetric Student’s t distribution, the normal inverse gamma distribution, the hyperbolic distribution and the generalized hyperbolic distribution). The fit of these distributions for characterizing the innovation processes of GARCH(1,1) was assessed using the following criteria: log likelihood, the Akaike information criterion, the Bayesian information criterion, the consistent Akaike information criterion, the corrected Akaike information criterion, the Hannan-Quinn criterion and the likelihood ratio test. Our results suggest that the GARCH(1,1) with the asymmetric Student’s t, the generalized hyperbolic and Student’s t distributions provided the most number of best, second best, and third best fits. Based on the GARCH(1,1) with the asymmetric Student’s t innovations, estimates and forecasts of value at risk and expected shortfall for each country were obtained.

In addition, we employed the multivariate GARCH model with a dynamic conditional correlation specification to investigate the cross-border relationship in terms of the currencies. Our results suggest that there is a wide range of fluctuations in the conditional correlation of the exchange rates of major African currencies. That is, the sign of the correlation switches over time for most of the pairs with few exceptions. This shows that the relationship among the exchange rates of African countries is time varying and is mainly dominated by small to moderate correlations in absolute values. The pattern of the relationship between these currencies is highlighted in countries with strong expanding economic ties. For example, (Algeria, Morocco) and South Africa are members of Arab league and BRICS, respectively. In general, the linkages between major African currencies are significantly affected by local politics, economic and social events as well as restrictive regulations. This is not surprising as it is a typical nature of emerging economies and has been noted by several authors (Bekaert et al., 1998; Bekaert & Harvey, 1997; De Santis & Improhoroglu, 1997).

Some future work are to: consider longer periods of the data; consider a semi-parametric or a non-parametric approach such as that considered in Hou and Suardi (2012) for univariate data or Scheffer and Weib (2016) for multivariate data.