Market Clearing and Krusell-Smith Algorithm in an Economy with Multiple Assets

Abstract

This paper proposes a novel method to compute the Krusell and Smith (1997, 1998) algorithm, used for solving heterogeneous-agents models with aggregate risk and incomplete markets when households can save in more than one asset. When used to solve a model with more than one asset, the standard algorithm has to impose equilibria for each additional asset (find the market-clearing price) in each period simulated. This procedure entails root-finding in each period, which is computationally expensive. I show that it is possible to avoid root-finding at this level by not imposing equilibria each period, but instead temporarily suspending market clearing. The proposed method then updates the law of motion for asset prices by using the information on the excess demand for assets via a Newton-like method. Since the method avoids the root-finding for each time period simulated, it leads to a significant reduction in computation time. In the example model with two assets, the proposed version of the algorithm leads to an 80% decrease in computational time, even when measured conservatively. This method is potentially useful in computing general equilibrium asset-pricing models with risky and safe assets, featuring both aggregate and uninsurable idiosyncratic risk, since methods that use linearisation in the neighborhood of the aggregate steady state are considered to be less accurate than global solution methods for such models.

1 Introduction

I present a relatively simple way of modifying a widely-used¹ Krusell and Smith (1997, 1998) algorithm, which can significantly reduce its computational time when solving models with multiple assets. The method is particularly useful in computing general equilibrium asset pricing models with risky and safe assets, since alternative computationally efficient algorithms are considered not sufficiently accurate when it comes to these particular types of models. Such models are used when studying asset prices in models with heterogeneous agents. As it is becoming increasingly recognized that asset prices play an important role in changing the wealth distribution and macroeconomic aggregates in developed economies, one can expect that these types of models will continue to be used to study these relationships. At the same time, when additional features are added to the basic model to capture important empirical insights, the above-mentioned models can quickly become very complex and computationally expensive. This paper reduces the run-time of the solution algorithm used to solve these models.

This paper proposes a novel method to compute the simulation part of the Krusell-Smith algorithm when market-clearing has to be imposed explicitly. The classic example is the general equilibrium macroeconomic model with both idiosyncratic and aggregate risk, with a borrowing constraint, where agents can choose to save in two assets: risky capital and safe bonds. In a model where the households can only trade claims to capital, the rental rate of capital changes in such a way to make supply and demand for the assets equalize. However, when there is an additional asset, a risk-free bond, there is no similar force to impose market clearing, and it has to be imposed externally. This usually results in a root-finding process. The Krusell-Smith algorithm (1997) updates the law of motion for the bond price based on the difference between the predicted bond price and the actual market-clearing bond price. This makes the Krusell and Smith (1997) algorithm very slow in obtaining a model solution.

The idea of this paper is to avoid the above-mentioned root-finding in the simulation part of the algorithm, where it is necessary to obtain a market-clearing bond price. Instead, the proposed algorithm lets the economy proceed to the next period with the markets uncleared and updates the perceived law of motions for the bond price based on the simulated excess demand for bonds. The paper shows how to employ a Newton-like method to use the information on excess demand for bonds directly, instead of using the market-clearing bond prices, which are not known when market clearing is temporarily suspended for computational gains. The idea of finding a market-clearing price by using the information on excess demand can be traced far back in the history of economics, not necessarily as a solution method but as an actual process by which general equilibrium emerges in markets. The process was called tâtonnement (French for “trial and error” or “groping”) by Walras (1874) (translated to English: Walras (1954)). However, the proposed algorithm does not imply anything about the process of reaching equilibrium but uses the idea purely as a part of the solution algorithm.

The computational gain of using the proposed algorithm is a shorter run-time due to the avoidance of bond-market clearing. Market clearing involves a root-finding process, which is computationally very expensive. The root-finding consists of finding a bond interest rate (or equity premium), which will clear the bond market in each period simulated. However, in equilibrium, all the markets are supposed to clear. Nevertheless, during the process of finding the general equilibrium laws of motion, it can be computationally beneficial to relax market clearing in the interim stages and use the information on excess demand to make subsequent updates.

The proposed method could be especially useful in computing general equilibrium asset pricing models (for example, models with risky and safe assets) with both aggregate and uninsurable idiosyncratic risk. This is because the methods that use linearisation in the neighborhood of the aggregate steady state are considered less accurate than global solution methods for these particular types of models. For example, Reiter (2009) proposes a solution using projection and perturbation instead of attempting to represent the cross-sectional distribution of wealth by a small number of statistics in order to reduce the dimensions in state space as in Krusell and Smith (1997), Den Haan (1997) and Reiter (2002). However, a solution method based on projection and perturbation is most likely not accurate enough for solving the models with asset pricing, as it assumes linearity in the aggregate variables, which is not sufficient for the problems of portfolio choice and asset pricing (Reiter 2009). For similar reasons, explicit aggregation, as in (Den Haan and Rendahl 2010), who develop a global solution method using projection on policy functions, is not very suitable for asset pricing problems as well. The authors note that the inclusion of occasionally binding constraints (which is a predominant feature of the portfolio choice problem in this context) introduces bias, which is computationally expensive to correct. In addition to this specific application, further use of the method proposed in the current paper could be useful to accelerate the Krusell-Smith algorithm where any market-clearing has to be imposed during the simulation of the model.

The rest of the paper is organized as follows: Sect. 2 describes the example model, Sect. 3 illustrates the classical Krusell-Smith algorithm (Krusell and Smith 1997) used to solve the models with both aggregate and idiosyncratic risk and a portfolio choice and describes the proposed algorithm, Sect. 4 shows the computational performance comparisons between the classic and the proposed algorithm. Section 5 discusses the results and potential applications of the proposed algorithm, and Sect. 6 concludes.

2 Example Model

The presented model is based on Algan et al. (2009), and in the tradition of Krusell and Smith (1997). The model consists of a continuum of heterogeneous agents facing aggregate risk, uninsurable idiosyncratic labor risk, borrowing constraint, and portfolio choice constraints and who save in two assets: risky equity and safe bonds. Unlike Algan et al. (2009), the model parsimoniously captures the life-cycle dynamics of the households in the fashion of Krueger et al. (2016), where working-age agents face the retirement shock and retired households face the risk of dying.

The considered model is a modified version of the original Krusell and Smith (1997) model.² Rather than the original model, a modified model is chosen for studying the novel solution techniques to address several drawbacks of the original model, on which a lot of research was done since the publishing of their seminal paper. The first is that the original model generates an unrealistically low equity risk premium, which is an important issue when studying portfolio choice problems. This model studied here allows for Epstein and Zin (1989) preferences and shocks to capital depreciation rates and idiosyncratic labor productivity shocks, which together generate a more realistic equity risk premium (although still not as high as observed in the historical US data for the parameter values chosen). Second, in Krusell and Smith (1997) most of the households are constrained in their portfolio choice. Depending on the version of the model, only $10\%$ or $4\%$ of the households have internal portfolio choice in Krusell and Smith (1997).³ This is driven by the comparatively low risk aversion on the one hand and the relatively low idiosyncratic risk that the households face. This makes the households’ portfolio choice very sensitive to the change in their wealth. This can potentially have implications when comparing different solution algorithms for the portfolio choice problem. The example model in this section addresses the issue of corner-solution to portfolio choice, by having a higher risk premium and by introducing additional labor income shocks as in Algan et al. (2009), to generate a higher share of households who invest both in risky and safe assets. This can be seen in policy functions in Appendix 3. Thirdly, the model in Krusell and Smith (1997) generates a low share of households who are close to the absolute borrowing constraint. Parsimonious life-cycle structure and pension scheme, taken from Krueger et al. (2016), helps in generating a more realistic share of agents who are wealth-poor and therefore close to the borrowing constraint. This is important in matching the data. However, it can additionally create accuracy issues in the Krusell-Smith algorithm, as there is a significant mass of agents close to the borrowing constraint, where the policy functions are potentially very non-linear. This makes the approximate aggregation result from Krusell and Smith (1998) weaker.⁴ To sum up, the modifications of the original Krusell and Smith (1997) model bring some key model-generated moments closer to the ones observed in the data. Therefore, the purpose of modifying the original Krusell and Smith (1997) model is to compare the different versions of the solution algorithm in a setting that is as realistic as possible. This is especially important because the introduction of these realistic patterns into the model (higher share of households with internal portfolio choice and higher share of wealth-poor households) creates the above-mentioned technical difficulties, which the algorithm should handle well if it is to be used for solving the models with empirically relevant features.

2.1 Production Technology

In each period t, the representative firm uses aggregate capital $K_t$, and aggregate labor $L_t$, to produce y units of final good with the aggregate technology $y_t=f(z_t,K_t,L_t)$, where $z_t$ is an aggregate total factor productivity (TFP) shock. I assume that $z_t$ follows a stationary Markov process with transition function $\Pi _t(z,z')=Pr(z_{t+1}=z'|z_t=z)$. The production function is continuously differentiable, strictly increasing, strictly concave and homogeneous of degree one in K and L. Aggregate labor supply varies, is perfectly correlated with the TFP shock and given exogenously, same as in the Krusell and Smith (1998). Capital depreciates at the rate $\delta _t \in (0,1)$ which is stochastic⁵ (and perfectly correlated with the TFP shock) and it accumulates according to the standard law of motion:

$$\begin{aligned} K_{t+1}=I_t + (1-\delta _t) K_t \end{aligned}$$

(1)

where $I_t$ is aggregate investment. The particular aggregate production technology is:

$$\begin{aligned} Y_t=z_tAK_t^{\Delta }L_t^{1-\Delta } \end{aligned}$$

(2)

2.2 Parsimonious Life-Cycle Structure

In each period, working-age households have a chance of retiring $1-\theta$, and retired households have a chance of dying $1-v$, similarly as in Castaneda et al. (2003) and Krueger et al. (2016). Therefore the share of working age households in the total population is:

$$\begin{aligned} \Pi _W=\frac{1-v}{(1-\theta )+(1-v)} \end{aligned}$$

and the share of the retired households in the total population is:

$$\begin{aligned} \Pi _R=\frac{1-\theta }{(1-\theta )+(1-v)} \end{aligned}$$

The retired households who die in period t are replaced by new-born agents who start at a working age without any assets. For simplicity, the retired households have perfect annuity markets, which make their returns larger by a fraction of $\frac{1}{v}$, as in Krueger et al. (2016). This life-cycle structure with stochastic aging and death helps capture important life-cycle aspects of the economy and risks that households face without adding an excessive computational burden.

2.3 Preferences

Households are indexed by i, and they have Epstein-Zin preferences (Epstein and Zin 1989). These preferences are often used in asset-pricing models since they allow one to separate the intertemporal elasticity of substitution and risk aversion.

Households’ preferences are expressed recursively. For the retired agents:

$$\begin{aligned} V_{R,i,t}=\{ c_t^{1-\rho } + v \beta [ E_t V_{R,i,t+1}^{(1-\alpha )}]^{\frac{1-\rho }{1-\alpha }} \}^{\frac{1}{1-\rho }} \end{aligned}$$

(3)

where $V_{R,i,t}$ is the recursively defined value function of a retired household i, at time period t.

Working-age agents maximize:

$$\begin{aligned} V_{W,i,t}=\{ c_t^{1-\rho } + \beta \big [\theta E_t V_{W,i,t+1}^{1-\alpha } + (1-\theta ) E_t V_{R,i,t+1}^{1-\alpha } \big ]^{\frac{1-\rho }{1-\alpha }} \}^{\frac{1}{1-\rho }} \end{aligned}$$

(4)

where $V_{i,t}$ is recursively defined value function of household i, at time period t. Furthermore, c denotes consumption, $\beta$ denotes the subjective discount factor, $E_t$ denotes expectations conditional on information at time t, $\alpha$ is the risk aversion, $\frac{1}{\rho }$ is the intertemporal elasticity of substitution and $c_t$ is the consumption in period t.

2.4 Idiosyncratic Uncertainty

In each period, working-age households are subject to idiosyncratic labor income risk that can be decomposed into two parts. The first part is the employment probability that depends on aggregate risk and is denoted by $e_t \in (0,1)$. $e=1$ denotes that the agent is employed, and $e=0$ that the agent is unemployed. Conditional on $z_t$ and $z_{t+1}$, I assume that the period $t+1$ realization of the employment shock follows the Markov process.

$$\begin{aligned} \Pi _e (z,z',e,e')= Pr(e_{t+1}=e'| e_t=e, z_t=z, z_{t+1}=z') \end{aligned}$$

This labor risk structure allows idiosyncratic shocks to be correlated with the aggregate productivity shocks, which is consistent with the data and generates the portfolio choice profile such that the share of wealth invested in risky assets is increasing in wealth. The condition imposed on the transition matrix and the law of large numbers implies that aggregate employment is only a function of the aggregate productivity shock.

If $e=1$ and the agent is employed, one can assume that the agent is endowed with $l_t \in L \equiv \{ l_1, l_2, l_3, ... l_m \}$ efficiency labor units, which she can supply to the firm. Labor efficiency is independent of the aggregate productivity shock, and is governed by a stationary Markov process with transition function $\Pi _l (l,l')= Pr(l_{t+1}=l'|l_t=l)$. If the agent is unemployed, (s)he receives unemployment benefits $g_{u,t}$ , which are financed by the government.

2.5 Financial Markets

As stated earlier, households can save in two assets: risky equity and safe bonds (firm debt). There are borrowing constraints for both assets, the lowest amounts of equity and debt that households can hold in period t are: $\kappa ^s$ and $\kappa ^b$, respectively. Markets are assumed to be incomplete in the sense that there are no markets for the assets contingent on the realization of individual idiosyncratic shocks.

2.6 Government

The government runs an unemployment insurance program, which is modeled similar as in Krueger et al. (2016) and is financed by special labor income taxes $\tau ^{ss}_t$ which varies depending on the current TFP shock. The social security benefits are then:

$$\begin{aligned} T_t^{ss}=\frac{\Pi _W}{\Pi _R} w_t \tau ^{ss} \end{aligned}$$

(5)

Unemployment benefits are financed with a labor tax rate $\tau ^l_t$. The amount of the unemployment benefits $g_{u,t}$ is determined by a constant $\eta$, which represents the fraction of the average wage in each period.

To finance the unemployment benefits, government has to tax labor at the tax rate:

$$\begin{aligned} \tau ^u_t=\frac{1}{1+\frac{1-\Pi _u(z)}{\Pi _u(z) \eta }} \end{aligned}$$

(6)

where $\Pi _u$ is the share of unemployed people in the total working-age population. Additionally, government finances its wasteful consumption $G_t=L_t w_t x_t$ by levying a additional tax with the rate $\tau _t^g=x_t$, which can also vary with the TFP shock.

The overall labor tax rate is denoted by $\tau _t^l$ which is a sum of all the tax rates $\tau _t^l=\tau _t^u+\tau _t^g+\tau _t^{ss}$.

2.7 Household Problem

Household i maximizes its expected lifetime utility defined by Eqs. (3) and (4), subject to the constraints below:

$$\begin{aligned} c_{i,t}+s_{i,t+1}+b_{i,t+1} \le \omega _{i,t} \\ \omega _{i,t+1}={\left\{ \begin{array}{ll} w_{t+1} l_{i,t+1} (1-\tau _{t+1}^l)+(1+r^s_{t+1}) s_{i,t+1} +(1+r^b_{t+1}) b_{i,t+1} &{} \text {if } e=1\\ w_{t+1} \eta (1-\tau _{t+1}^l) +(1+r^s_{t+1}) s_{i,t+1} +(1+r^b_{t+1}) b_{i,t+1} &{} \text {if } e=0\\ T^{ss}_{t+1} + \frac{1}{v} \left[ (1+r^s_{t+1}) s_{i,t+1} +(1+r^b_{t+1}) b_{i,t+1} \right] &{} \text {if retired} \\ \end{array}\right. } \\ \left( c_{i,t}, b_{i,t+1} ,s_{i,t+1} \right) \ge \left( 0, \kappa ^b, \kappa ^s \right) \end{aligned}$$

Household i has the following aggregate state variables: TFP shock $z_t$ (which is perfectly correlated with the capital depreciation shock) and distribution of wealth in the economy, which is measured by $\mu _t$. Furthermore, it has individual state variables: wealth $\omega$ and if they are working-age households: employment $e_t$ and labor productivity $l_t$. The households optimize over three choice (control) variables: consumption $c_t$, savings in stocks $s_t$ and savings in bonds $b_t$. Furthermore, w denotes wages, $T^{ss}$ denotes social security payments for households in retirement, $\eta$ is the replacement rate for the unemployed households, $r^s$ denotes returns to stocks, and $r^b$ denotes returns to bonds.

Individual stochastic marginal rate of substitution (stochastic discount factor) between periods t and $t+1$, for the retired agent is:

$$\begin{aligned} m_{t,t+1}^{R,i}=\beta \left( \frac{V_{R,i,t+1}}{E_t (V_{R,i,t+1}^{1-\alpha })^{\frac{1}{1-\alpha }}} \right) ^{\rho -\alpha } \left( \frac{c_{t+1}^{i}}{c_{t}^{i}} \right) ^{-\rho } \end{aligned}$$

(7)

and for the working-age agent:

$$\begin{aligned} m_{t,t+1}^{W,i}=\beta \left( \frac{V_{W,i,t+1}}{ \left( (1-\theta ) E_t (V_{W,i,t+1}^{1-\alpha }) + \theta E_t (V_{R,i,t+1}^{1-\alpha }) \right) ^{\frac{1}{1-\alpha }}} \right) ^{\rho -\alpha } \left( \frac{c_{t+1}^{i}}{c_{t}^{i}} \right) ^{-\rho } \end{aligned}$$

(8)

if the agent does not retire in the period $t+1$, and

$$\begin{aligned} m_{t,t+1}^{W,i}=\beta \left( \frac{V_{R,i,t+1}}{ \left( (1-\theta ) E_t (V_{W,i,t+1}^{1-\alpha }) + \theta E_t (V_{R,i,t+1}^{1-\alpha }) \right) ^{\frac{1}{1-\alpha }}} \right) ^{\rho -\alpha } \left( \frac{c_{t+1}^{i}}{c_{t}^{i}} \right) ^{-\rho } \end{aligned}$$

(9)

if the agent retires in the period $t+1$. Consequently, from the first order conditions, it follows:

$$\begin{aligned} 1 \ge E_t \left( m_{t,t+1}^{i} (1+r_{t+1}^s) \right) \\ 1 \ge E_t \left( m_{t,t+1}^{i} (1+r_{t+1}^b) \right) \end{aligned}$$

where the equations hold with equality if $s_{i,t+1}>\kappa ^s$ and $s_{i,t+1}>\kappa ^b$, respectively. Furthermore, it is possible to define the stochastic marginal rate of substitution for the households who are unconstrained in stocks $q_{t,t+1}^s$:

$$\begin{aligned} 1 = E_t \left( q_{t,t+1}^{s} (1+r_{t+1}^s) \right) \end{aligned}$$

(10)

and bonds $q_{t,t+1}^b$:

$$\begin{aligned} 1 = E_t \left( q_{t,t+1}^{b} (1+r_{t+1}^b) \right) \end{aligned}$$

(11)

2.8 The Representative Firm

As in Algan et al. (2009), firm leverage in this model is given exogenously. The leverage of the firm is determined exogenously by the parameter $\lambda$. The Modigliani and Miller (1958, 1963) theorem does not hold, as some of the agents are borrowing constrained, and some are portfolio constrained. Therefore, theoretically, the leverage of the firm has some macroeconomic relevance. Additionally, debt is taxed differently than equity returns, and this additionally weakens the adjustment from the Modigliani-Miller theorem.

The representative firm can finance its investment with two types of contracts. The first is a one-period risk-free bond that promises to pay a fixed return to the owner. The second is risky equity that entitles the owner to claim the residual profits of the firm after the firm pays out wages and debt from the previous period. Both of these assets are freely traded in competitive financial markets. By construction, there is no default in the equilibrium.

The return on the bond $r_{t+1}^b$ is determined by the clearing of the bond market, where the net supply of the bonds is generated by the firm $\lambda K_{t+1}$, and the net demand is given by the sum of all the bond holdings of all households in period t.

In each period t, the return on the stock is residual, i.e., the value after the production and depreciation have taken place, and wages and debt has been paid. Therefore, the return on the risky equity depends on the realizations of the aggregate shocks and is given by the following equation:

$$\begin{aligned}&1+r_{t+1}^s= \frac{ f(z_{t+1},K_{t+1},L_{t+1}) - f_L(z_{t+1},K_{t+1},L_{t+1})L_{t+1} -\lambda K_{t+1} (1+ r_{t+1}^b) + (1-\delta _{t+1}) K_{t+1} }{ (1-\lambda ) K_{t+1} } \end{aligned}$$

If there is no leverage: $\lambda =0$, the expression simplifies to $r_{t+1}^s=z_t \Delta \left( \frac{L_t}{K_t} \right) ^{1-\Delta } - \delta _t$. The outcomes in the studied economy are consistent with two interpretations of the representative firm. The first interpretation is that the households own the capital and make investment decisions, and the firm rents it and hires labor to maximize the profits in period t, and it is a standard interpretation also made in Krusell and Smith (1997). The other interpretation is the one made in (Algan et al. 2009), that the firm is the owner of the capital and makes investment decisions to maximize the current value of its future cash flows according to a stochastic discount factor defined below (equivalent to the discount factor of a household which is never constrained).⁶ The equivalence result of the two approaches is derived in Carceles-Poveda and Pirani (2010).

With the interpretation that the firm is the owner of the capital, it maximizes its ex dividend value: $V_t^f=p_t^s S_r+B_{t+1}$, and its budget constraint is $d_t^s S_t=N_t+p_t^s(S_{t+1}-S_t)+B_{t+1}-(1-r_t^b)B_t$, where $N_t=f(z_t,K_t,L_t)-w_tL_t-I_t$ is the firm’s cash flow in the period t. With this interpretation the representative firm maximizes:

$$\begin{aligned} E_t \sum _{j=0}^{\infty } m_{t+j}^f N_{t+j} \end{aligned}$$

(12)

where $m^f_{t,t}=1, m^f_{t,t+j}=m^f_{t,t+j-1} m^f_{t+j-1,t+j}$ for $j \ge 1$ and $E_t m^f_{t,t+1}= \frac{E_t q_{t,t+1}^s}{1-\lambda +\lambda \frac{q_{t,t+1}^s}{q_{t,t+1}^b}}$

The optimality conditions of the firm imply the wage rate and aggregate capital:

$$\begin{aligned}&w_t=z_t A (1-\Delta ) \left( \frac{K_t}{L_t} \right) ^{\Delta } \end{aligned}$$

(13)

$$\begin{aligned}&1=E_t \left\{ m^f_{t,t+1} \left( z_{t+1} \Delta \left( \frac{L_{t+1}}{K_{t+1}} \right) ^{1-\Delta } +1- \delta _{t+1} \right) \right\} \end{aligned}$$

(14)

As in Algan et al. (2009), it is possible to use the fact that for a given stochastic discount factor $V_t=K_{t+1}$, which enables the elimination of the capital Euler equation from the equilibrium conditions.

2.9 Recursive Household Problem

The idiosyncratic state variables of the household problem are: current wealth $\omega$, current employment e, and productivity state, l. $\Theta$ denotes the vector of all discrete individual states (all except the current wealth).⁷

The aggregate state variables of the household problem are: state of the TFP shock: z, and distribution which is captured by the probability measure $\mu$. $\mu$ is a probability measure on $(S,\beta _s)$, where $S=[\underline{\omega }, \overline{\omega } ] \times \Theta$, and $\beta _s$ is the Borel $\sigma$-algebra. $\underline{\omega }$ and $\overline{\omega }$ denote the minimal and maximal allowed amount of wealth the household can hold.⁸ Therefore, for $B \in \beta _s$, $\mu (B)$ indicates the mass of households whose individual states fall in B. Intuitively, one can think of $\mu$ as a distribution variable that measures the mass of agents in a certain interval of wealth for each possible combination of other idiosyncratic variables. The individual state variables of the households are its wealth $\omega$, employment state e, and if employed, its labor productivity l. The households control variables are consumption in the current period c and investments made in stocks s and bonds b.

The recursive household problem for the retired households is:

$$\begin{aligned} \upsilon _R(\omega ;z , \mu , \delta ) = \max _{c,b',s'} \left\{ c^{1-\rho }+v \beta E_{z',\mu ',\delta '|z,\mu ,\delta } [\upsilon _R(\omega ';z', \mu ',\delta ')^{1-\alpha } ]^{\frac{1-\rho }{1-\alpha }} \right\} ^{\frac{1}{1-\rho }} \end{aligned}$$

(15)

subject to:

$$\begin{aligned} c+s'+b'=\omega \\ \omega '= T_{ss}'+ \left[ s' (1+r'^s) + b' (1+r'^b) \right] \frac{1}{v} \\ \mu '=\Gamma (\mu ,z,z',d,d') \\ \left( c, b' ,s' \right) \ge \left( 0, \kappa ^b, \kappa ^s \right) \end{aligned}$$

The recursive household problem for the working-age households is:

$$\begin{aligned}&\upsilon _W(\omega , e , l ;z , \mu , \delta ) =\nonumber \\&\quad \max _{c,b',s'} \left\{ c^{1-\rho }+\beta E_{e',l',z',\mu ',\delta '|e,l,z,\mu ,\delta } [(1-\theta ) \upsilon _W(\omega ',e',l';z', \mu ',\delta ')^{1-\alpha } + \theta \upsilon _R(\omega ',e',l';z', \mu ',\delta ')^{1-\alpha } ]^{\frac{1-\rho }{1-\alpha }} \right\} ^{\frac{1}{1-\rho }} \end{aligned}$$

(16)

subject to:

$$\begin{aligned}&c+s'+b'=\omega \\&\omega '={\left\{ \begin{array}{ll} w' l' (1-\tau '^l)+ s' (1+r'^s) + b' (1+r'^b) &{} \text {if } e=1\\ \eta w' (1-\tau '^l)+ s' (1+r'^s) + b' (1+r'^b) &{} \text {if } e=0\\ \end{array}\right. } \\&\mu '=\Gamma (\mu ,z,z',d,d') \\&\left( c, b' ,s' \right) \ge \left( 0, \kappa ^b, \kappa ^s \right) \end{aligned}$$

where $\omega$ is the vector of individual wealth of all agents, $\mu$ is the probability measure generated by the set $\Omega x E x L$, $\mu '=\Gamma (\mu ,z,z')$ is a transition function and $'$ denotes the next period.

In the tradition of Krusell and Smith (1998), in order to reduce the state-space to a tractable level, the distribution of wealth $\mu$ is replaced with a set of first moments of the distribution. In particular, only the first moment (mean) is used, which is equivalent of tracking only the amount of aggregate capital $K_t$.

2.10 General Equilibrium

The economy-wide state is described by $(\omega ,e,l;z,\mu )$. Therefore the individual household policy functions are: $c^{j}=g^{c,j} \left( \omega ,e,l;z,\mu \right)$, $b'^{j}=g^{b,j} \left( \omega ,e,l;z,\mu \right)$ and $s'^{j}=g^{s,j} \left( \omega ,e,l;z,\mu \right)$, and law of motion for the aggregate capital is $K'=g^K \left( \omega ,e,l;z,\mu \right)$.

A recursive competitive equilibrium is defined by the set of individual policy and value functions $\left\{ \upsilon _R,g^{c,R},g^{s,R},g^{b,R},\upsilon _W,g^{c,W},g^{s,W},g^{b,W} \right\}$, the laws of motion for the aggregate capital $g^K$, a set of pricing functions $\left\{ w,R^b,R^s \right\}$, government policies in period t: $\left\{ \tau ^{u},\tau _ss \right\}$, and forecasting equations $g^L$, such that:

• (1) The law of motion for the aggregate capital $g^K$ and the aggregate “wage function” w, given the taxes satisfy the optimality conditions of the firm: $w_t=z A (1-\Delta ) \left( \frac{K}{L} \right) ^{\Delta }$.

• (2) Given $\left\{ w,R^b,R^s \right\}$, the law of motion $\Gamma$, the exogenous transition matrices $\left\{ \Pi _z, Pi_e, Pi_l \right\}$, the forecasting equation $g^L$, the law of motion for the aggregate capital $g^K$, and the tax rates, the policy functions $\left\{ g^{c,j},g^{b,j},g^{s,j} \right\}$ solve the household problem.

• (3) Labor, shares and the bond markets clear (goods market clears by Walras’ law):

  • $$\begin{aligned} L=\int _S el d \mu \end{aligned}$$
  • $$\begin{aligned} \int _S g^{s,j} \left( \omega ,e,l;z,\mu \right) d \mu = (1-\lambda )K' \end{aligned}$$
  • $$\begin{aligned} \int _S g^{b,j} \left( \omega ,e,l;z,\mu \right) d \mu = \lambda K' \end{aligned}$$

• (4) The law of motion $\Gamma (\mu ,z,z')$ for $\mu$ is generated by the optimal policy functions $\left\{ g^c,g^b,g^s \right\}$, which are endogenous, and by the transition matrices for the aggregate shocks z .⁹ Additionally, the forecasting equation for aggregate labor is consistent with the labor market clearing: $g^L(z')=\int _S e l d \mu$.

• (5) Government budget constraints are satisfied:

  $$\begin{aligned}&T_t^{ss}=\frac{\Pi _W}{\Pi _R} w_t \tau ^{ss}\\&\tau ^g_t L_t w_t = G_t\\&\tau ^u_t=\frac{1}{1+\frac{1-\Pi _u(z)}{\Pi _u(z) \eta }} \end{aligned}$$

3 Classical and Proposed Solution Algorithms

Unlike in Bewley (1977, 1983), Huggett (1993) and Aiyagari (1994) type of models, where aggregate prices are constant, in a Krusell-Smith type economy (featuring both idiosyncratic and aggregate shocks), we need to compute the whole aggregate dynamics. This means that we need to find not only the equilibrium levels of capital and bond prices but also their laws of motion. The proper state variable of the economy is the whole distribution of assets among the household, which is an infinite-dimensional object. To make this tractable, wealth distribution is replaced with the set of the distribution’s moments, as in Krusell and Smith (1997). Following Storesletten et al. (2007), instead of using a law of motion for a bond price, I use a law of motion on equity premium, as it has better technical properties.¹⁰

3.1 Classical Solution Algorithm

• (1) Guess the law of motion for aggregate capital $K_{t+1}$ and equity premium $P^e_{t}$. This means guessing the starting 8 coefficients following the equations (since there are two possible realizations of z):

  $$\begin{aligned}&ln K'=a_0(z)+a_1(z) ln K \end{aligned}$$

  (17)
  $$\begin{aligned}&ln P^{e}=b_0(z)+b_1(z) ln K' \end{aligned}$$

  (18)

• (2) Given the perceived laws of motion, solve the individual problem described earlier. In this step, the endogenous grid method (Carroll 2006) is used. Instead of constructing the grid on the state variable $\omega$, and searching for the optimal decision for savings $\tilde{\omega }$, this method creates a grid on the optimal savings amounts $\tilde{\omega }$, and evaluates the individual optimality conditions to obtain the level of wealth $\omega$ at which it is optimal to save $\tilde{\omega }$. This way, the root-finding process is avoided since finding optimal $\omega$ given $\tilde{\omega }$, involves only the evaluation of a function (households optimality condition). However, the root-finding process is necessary to find the optimal portfolio choice of the household, which is carried out after finding the optimal pairs $\omega$ and $\tilde{\omega }$.

• (3) Simulate the economy, given the perceived aggregate laws of motion. To keep track of wealth distribution, instead of a Monte Carlo simulation, the method proposed by Young (2010) is used. For each realized value of $\omega$, the method distributes the mass of agents between two grid points: $\omega _i$ and $\omega _{i+1}$, where $\omega _i<\omega <\omega _{i+1}$, based on the distance of $\omega$, based on Euclidean distance between $\omega _i$, $\omega$ and $\omega _{i+1}$. Do this in the following steps:

  • (a) Set up an initial distribution in period 1: $\mu$ over a simulation grid $i=1,2,...N_{sgrid}$, for each pair of efficiency and employment status, where $N_{sgrid}$ is the number of wealth grid points. Set up an initial value for aggregate states z.

  • (b) Find the bond interest rate (pinned down by the expected equity premium $P^e$) in the given period, which clears the market for bonds. This is performed by iterating on $P^e$ (or on a bond return), until the following equation is satisfied (bond market clears)¹¹

    $$\begin{aligned} \sum g^{b}(\omega ,e,l;z,K,P^e)d \mu = \lambda \sum \left\{ g^{b}(\omega ,e,l;z,K,P^e)d \mu + g^{s}(\omega ,e,l;z,K,P^e)d \mu \right\} \end{aligned}$$

    where $g^{b}(\omega ,e,l;z,K,P^e)$ and $g^{s}(\omega ,e,l;z,K,P^e)$ are the policy functions for bonds and shares that solve the following recursive household maximization problems: Retired households:

    $$\begin{aligned} \upsilon (\omega ;z , \mu , P^e) = \max _{c,b',s'} \left\{ c^{1-\rho }+ \beta E_{z',\mu ',P^{e'}|z,\mu ,P^e} [\upsilon (\omega ';z', \mu ')^{1-\alpha } ]^{\frac{1-\rho }{1-\alpha }} \right\} ^{\frac{1}{1-\rho }} \end{aligned}$$

    (19)

    subject to:

    $$\begin{aligned}&c+s'+b'=\omega \\&\omega '= T_{ss}'+ \left[ s' \left( 1+r'^s(P^e)\right) + b' \left( 1+r'^b(P^e)\right) \right] \frac{1}{v} \\&\mu '=\Gamma (\mu ,z,z',d,d') \\&\left( c, b' ,s' \right) \ge \left( 0, \kappa ^b, \kappa ^s \right) \end{aligned}$$

    Working age households

    $$\begin{aligned}&\upsilon _W(\omega , e , l ;z , \mu , P^e) =\nonumber \\&\quad \max _{c,b',s'} \left\{ c^{1-\rho }+\beta E_{e',l',z',\mu ',\delta '|e,l,z,\mu ,\delta } [(1-\theta ) \upsilon _W(\omega ',e',l';z', \mu ',\delta ')^{1-\alpha } + \theta \upsilon _R(\omega ',e',l';z', \mu ',\delta ')^{1-\alpha } ]^{\frac{1-\rho }{1-\alpha }} \right\} ^{\frac{1}{1-\rho }} \end{aligned}$$

    (20)

    subject to:

    $$\begin{aligned}&c+s'+b'=\omega \\&\omega '={\left\{ \begin{array}{ll} w' l' (1-\tau '^l)+ s' \left( 1+r'^s(P^e)\right) + b' \left( 1+r'^b(P^e)\right) &{} \text {if } e=1\\ \eta w' (1-\tau '^l)+ s' \left( 1+r'^s(P^e)\right) + b' \left( 1+r'^b(P^e)\right) &{} \text {if } e=0\\ \end{array}\right. } \\&\mu '=\Gamma (\mu ,z,z',d,d') \\&\left( c, b' ,s' \right) \ge \left( 0, \kappa ^b, \kappa ^s \right) \end{aligned}$$

    Compared to the problems in Eqs. 15 and 16, there is an additional state variable $P^e$ (expected equity premium).

  • (c) Depending on the realization for $z'$, compute the joint distribution of wealth, labor efficiency, and employment status.

  • (d) To generate a long time series of the movement of the economy, repeat substeps b) and c).

• (4) Use the time series from step 2 and perform a regression of $ln K'$ and $P^e$ on constants and lnK, for all possible values of z and d. This way, the new aggregate laws of motion are obtained.

• (5) Make a comparison of the laws of motion from step 4 and step 1. If they are almost identical and their predictive power is sufficiently good, the solution algorithm is completed. If not, make a new guess for the laws of motion based on a linear combination of laws from steps 1 and 4. Then, proceed to step 2.

3.2 Proposed Solution Algorithm

• (1) Same as in the classical version. (Guess the laws of motion )

• (2) Same as in the classical version. (Solve the household problem given the guessed law of motion to obtain value and policy functions.)

• (3) Simulate the economy. Do this in the following steps:

  • (a) Set up an initial distribution in period 1: $\mu$ over a simulation grid $i=1,2,...N_{sgrid}$,for each pair of efficiency and employment status, where $N_{sgrid}$ is the number of wealth grid points. Set up an initial value for aggregate states z.

  • (b) Simulate the economy given the perceived laws of motion.

    This means obtaining $g^{b}(\omega ,e,l;z,K)$ and $g^{s}(\omega ,e,l;z,K)$, which are the policy functions for bonds and shares. The policy functions are obtained after solving problems from the Eqs. 15 and 16. Unlike in the previous algorithm, the expected equity premium in the current period is not included as an additional state variable.

    The market for bonds will not necessarily clear. Instead, in each period there will be an excess demand, which will be denoted by $\xi _t$.

  • (c) Depending on the realization for $z'$, compute the joint distribution of wealth, labor efficiency and employment status in the period $t+1$. Set the return on stocks to be equal to

    $$\begin{aligned} 1+r'^s=\frac{f(z',K',L')-f_L(z',K',L')-\sum g^b(\omega ,e,l;z,K) d \mu +(1-\delta ')K_t}{\sum g^s(\omega ,e,l;z,K) d \mu } \end{aligned}$$

    (21)

    This helps the algorithm to avoid over(under)accumulation of capital in the economy resulting from the uncleared bonds market.

  • (d) To generate a long time series of the movement of the economy, repeat substeps b) and c).

• (4) Use the time series from step 3 and perform a regression of $ln K'$ on constants and lnK, for all possible values of z. This way, the new aggregate laws of motion for capital are obtained ($a_0(z)$ and $a_1(z)$). However, now for the law of motion for the equity premium, we cannot run a regression, since we do not have “true” market-clearing bond prices (equity premium). Instead, we have excess demand in each time period, given the perceived equity premium. We can use this information to update the perceived law of motion for equity premium directly. To do this, the Broyden method (Broyden 1965) is used:

  Consider a system of equations

  $$\begin{aligned} f(x^*)=0 \end{aligned},$$

  where x are the “true” coefficients of the perceived law of motion for equity premium

  $$\begin{aligned} x^*=(b^*_0(z),b^*_1(z)) \end{aligned}$$

  and

  $$\begin{aligned} f(x)=\left( f_1(b^*_0(z),b^*_1(z)), f_2(b^*_0(z),b^*_1(z)) \right) \end{aligned}$$

  (22)

  $f_1$ and $f_2$ denote the error measures that are chosen.¹² For this algorithm, I propose these two measures to be coefficients of a linear regression of excess demand on a constant and capital. The true solution to the model would have the coefficients of this regression equal to 0. This would mean that the mean value of excess demand is 0 and also that the excess demand does not depend on the amount of capital K. Therefore, to obtain $f_1$ and $f_2$, one has to run the following regressions:¹³

  $$\begin{aligned} \xi _t (z)=\varrho _1(z)+\varrho _2(z) K_t + \epsilon _t \end{aligned}$$

  (23)

  One can also use a linear coefficient and, instead of a coefficient on a constant, use an average excess demand for a given aggregate state. In this particular example this provides a faster convergence. After this, step error measures are obtained:

  $$\begin{aligned} f_1(b^*_0(z),b^*_1(z))= \varphi \sum \xi _t (z) \end{aligned}$$

  where $\varphi$ is arbitrary constant.¹⁴

  $$\begin{aligned} f_2(b^*_0(z),b^*_1(z))= \varrho _2(z) \end{aligned}$$

  Now, the goal is to find the true $x^*$. This is conducted in the following steps:

  • (a) First, define $\chi ^{n}=f(x^n)$. Where $\chi ^n$ and $x^n$ denote the excess demand measure and the coefficients in the iteration n.

    $$\begin{aligned} \chi ^{n}=\left( f_1(b_0(z),b_1(z)), f_2(b_0(z),b_1(z)) \right) \end{aligned}$$

    (24)

    Furthermore: $\Delta x_n= x_n-x_{n-1}$, $\Delta \chi _n= \chi _n-\chi _{n-1}$

  • (b) For the initial iteration, we guess the Jacobian matrix. For each additional iteration, we update the Jacobian matrix by:

    $$\begin{aligned} J_n=J_{n-1} + \frac{\Delta \chi -J_{n-1} \Delta x_n}{||x||^2} \Delta x_n^T \end{aligned}$$

    (25)

    after updating the matrix, we update the guess of the perceived law of motion for equity premium:

    $$\begin{aligned} x_{n+1}=x_n-J_n^{-1} f(x_n) \end{aligned}$$

    (26)

  We do these steps two times, for $z=good$ and $z=bad$. This will give us the updated candidates for the law of motion parameters $\begin{bmatrix} b_0(good) \\ b_1(good) \end{bmatrix}=x_{n+1}^{good}$ and $\begin{bmatrix} b_0(bad) \\ b_1(bad) \end{bmatrix}=x_{n+1}^{bad}$.

• (5) Same as in the classical version, compare the laws of motion from step 4 and step 1. If they are almost identical and their predictive power is sufficiently good, the solution algorithm is completed. If not, make a new guess for the laws of motion based on a linear combination of laws of motion from steps 1 and 4. Then, proceed to step 2.

The idea of the proposed algorithm is to avoid the root-finding that is necessary to clear the bond markets in each period simulated t. This root-finding in the step 3 of the classical version of the algorithm, shown in red in the diagram in Appendix 4.2, is causing a significant slow-down of the algorithm. Eliminating it, however, means that the market-clearing prices, used to update the perceived laws of motion, are not available. Instead, the proposed algorithm uses the information on excess bond demand directly and updates the perceived laws of motion by a Newton-like method.

To clarify the differences between clearing the bond market and other markets, it is helpful to see how the solution method clears other markets. First, to get the quantity of labor employed in period t, one simply uses the exogenously specified aggregate labor supply contingent on the TFP shock. This is simply a parameter since the households do not have disutility of labor and supply labor inelastically. Then, to obtain a wage in period t, we compute the first derivative of the production function (equation 2) with respect to labor. If bonds were not traded and there was no firm leverage, consumption and capital markets would also clear in a similarly simple manner. The sum of all agents’ savings would sum up to the capital in the period $t+1$. Therefore, misperceptions about the return on capital (implied by the level of capital next period) would not cause a non-cleared capital market, but only a deviation from the expected and realized return to the capital next period. Therefore, the market would be cleared since the firm would invest all the savings of the agents (since the equilibrium condition in this economy imply that all the savings in period t have to be equal to $K_{t+1}$). Consumption good market would clear by Warlas law (since all of the other goods in the economy clear). However, if bonds are also traded in the economy, a need for explicit market clearing (finding the bond price/equity premium which clears the bond market) would arise. This is because now, not only do the savings have to equal investments, but we have an additional requirement that those savings have to be comprised of a fixed share between stocks and bonds. If they are not, there is no economic mechanism that can adjust to clear the bond market (as there is with the other markets). Krusell and Smith (1997) deal with this issue by iterating on the bond price in the current period until the bond market clears. The version of the algorithm proposed in my paper is not doing this but instead leaves the bond market uncleared and adjusts the return on stocks in period $t+1$ accordingly to prevent artificial over/under accumulation of wealth in the economy. Another way to interpret the proposed algorithm is to say that leverage in period t unexpectedly adjusts in such a way that allows the perceived bond price (implied by the perceived laws of motion) to clear the bond market.¹⁵

Fig. 1

Step 4 in the two algorithms. The graphs show the updating for the good TFP state, when $b_0(z=good)=-8.3470$ and $b_1(z=good)=-0.4498$

The idea of the new algorithm is demonstrated in Fig. 1, which visualizes step 4 of the classical and proposed version of the algorithm. The left graph shows the situation in step 4 in the classical algorithm. Since the blue line (gained by regressing market-clearing equity premium on capital) is not close to the red line (determined by the equity premium law of motion), we need to adjust the perceived laws of motion (red line). In other words, we need to shift the red line in the direction indicated by the arrows. This is done by using a linear combination of the parameters in the perceived laws of motion (red line) and the regression on the realized equity premium (or bond prices), indicated by the blue line. If the right and blue lines coincide, the perceived laws of motion are accurate enough, and the stopping criteria are satisfied. However, obtaining the market-clearing bond prices (or equivalently, equity premium) is computationally expensive, and the aim of the proposed algorithm is to suspend it during the computation of the laws of motion. However, by doing so, we can not update the laws of motion in a way that the classical algorithm does since we never computed the market-clearing prices. Consequently, the proposed algorithm uses the information on excess bond demands directly, as shown on the right graph of Fig. 1. Now, instead of regressing capital market-clearing prices, we regress excess bond demand on capital (blue line). If the blue line on the right graph approximately coincides with the zero-line, the laws of motion are sufficiently accurate since there is no systematic error in predicting equity premium (bond prices).

The way to update the perceived laws of motion for equity premium in the proposed version of the algorithm is given by a Newton-like method, in this case, Broyden (1965) method. The method tells us how we should adjust the laws of motion to get the blue line in the right graph of Fig. 1 to coincide with the zero line approximately. The size and direction of the adjustments of the laws of motion are based on the approximated Jacobian matrix, which contains the first derivatives of measures of error $\chi ^n$ with respect to the parameters of the laws of motion. In the used example, measures of error are the average excess demand¹⁶ and the slope of the blue line in the right graph. We need two measures of error since the laws of motion contain two parameters (for each realization of the aggregate shock): the constant $b_0 (z)$ and the slope $b_1 (z)$. If we were to increase the number of parameters in the laws of motion, we would need to increase the number of parameters measuring the errors accordingly.

4 Performance Comparison on an Example Model

To demonstrate the potential reduction in the computation speed of the discussed model, I solve the model described in Sect. 2, both with the classical solution method (Krusell and Smith 1997) and the proposed method from Sect. 3. The particular implementation of the proposed algorithm is described in the Appendix. To compare the two algorithms, the parametrized model will be solved 50 times by the two algorithms, each time starting from the different initial perceived law of motions. The initially perceived law of motion is obtained as follows: Each parameter of the true laws of motion is randomly perturbed by a normally distributed shock with the standard deviation $\sigma =0.01$. The size of the perturbation is large enough so that the initial guess is not too close to the solution and not too large to cause all of the households to have a corner portfolio solution.¹⁷ The stopping criterion for the perceived laws of motion is twofold. The first condition is that the excess demand of the bonds has to be on average smaller than $0.2\%$ of the aggregate capital, without imposing the market-clearing.¹⁸ The other criterion is that all of the parameters have converged approximately, i.e.,, none of the parameters don’t differ from the ones in the previous guess by more than $0.01\%$.¹⁹ For each iteration, simulated time-series has $T=3500$ time periods. When updating the laws of motion parameters, the weight of the new guess is always 1. This is only because, for this specific model, this happens to minimize the time necessary for convergence.²⁰ In the value function iteration, 135 grid points are used in the individual wealth dimension, and 12 grid points are used in the aggregate capital dimension. Cubic splines are used to interpolate the values in between the grid points. The code is written in a FORTRAN 90 programming language and compiled using Intel Fortran Compiler. All the simulations are executed on a personal computer using Windows 7 (64-bit) operating system, with Intel i7-8700 Central Processing Unit (6 cores and 12 threads), clocked at 3.19 GHz. I report both the number of iterations necessary to obtain a solution (a convergence) and an overall run-time.

4.1 Parametrization

The model is parametrized to a quarterly frequency. The choices of the main parameters are reported in Table 1.

Table 1 Parameters

The TFP shocks and capital depreciation shocks are assumed to be perfectly correlated, and thus there are only two aggregate states good, where TFP is high and depreciation is low, and bad, where TFP is low and depreciation is high.

4.1.1 Idiosyncratic Shocks

There are 5 possible idiosyncratic states in which the household can find itself (5 for each aggregate state). Following Pijoan-Mas (2007), labor productivity among the working-age employed households is governed by the transitional Markov matrix:

$$\begin{aligned} \Pi _l= \begin{bmatrix} 0.9850 &{} 0.0100 &{} 0.0050 \\ 0.0025 &{} 0.9850 &{} 0.0125 \\ 0.0050 &{} 0.0100 &{} 0.9850 \end{bmatrix} \end{aligned}$$

and for the individual labor productivity levels, the following values are used: $l \in \left\{ 30,8,1\right\}$. In addition to this risk, the households face a risk of becoming unemployed, which is the same regardless of the labor productivity level. Finally, working-age households also face a risk of becoming retired $1-\theta$. The average unemployment spell is set to 1.5 quarters in the good state (boom) and 2.5 quarters in the bad state (recession). The replacement rate for the unemployed is set to $4.2 \%$ of the average wage in the given period. The probabilities of becoming/remaining unemployed when the economy moves from a good to bad state and vice-versa are adjusted to match the movement of the overall employment, which is set to $95.9 \%$ in the good state and $92.8 \%$ in the bad state.

4.1.2 Generated Moments

The selection of the moments in the model is presented in Table 2.

Table 2 Moments in the model

On average, $57.81\%$ of the households are portfolio constrained in a given time period, meaning that $42.19\%$ of households have an internal portfolio choice in a given period. This is much higher than in the original paper from Krusell and Smith (1997), in which only $10\%$ or $4\%$ of households have an internal portfolio choice (depending on the calibration). Having an unrealistically high share of agents with a corner solution with portfolio choice can clearly influence the accuracy and speed of a certain algorithm (corner solutions are more quickly computed, for example). Therefore, having a benchmark model which allows for a higher share of agents with internal portfolio choice allows for more relevant comparison. Additionally, on average, $15.61\%$ households are absolutely constrained in a given time period, meaning that they can not decrease their savings in either capital or bonds. This share is insignificantly small in the Krusell and Smith (1997). Generating a significant amount of households at (or close) to the absolute borrowing constraint is useful, as it makes sure that we are measuring the accuracy of the proposed algorithm when the approximate aggregation result is weakened.

4.2 Solution for Perceived Laws of Motions

$$\begin{aligned}&ln K'=a_0(z,\delta )+a_1(z,\delta ) ln K \end{aligned}$$

(27)

$$\begin{aligned}&ln P^e=b_0(z,\delta )+b_1(z,\delta ) ln K' \end{aligned}$$

(28)

The initial solution is obtained by the original version of the algorithm, using “gradual updating” where the new guesses have the weight of 0.45. For the example model, in the initial solution, the perceived aggregate laws of motions are:

In a good TFP and $\delta$ state:

$$\begin{aligned}&ln K'=0.0949+0.9476 ln K \\&ln P^e=-8.3391-0.4214 ln K' \end{aligned}$$

In a bad TFP and $\delta$ state:

$$\begin{aligned}&ln K'=0.0895+0.9469 ln K \\&ln P^e=-7.5870-0.3793 ln K' \end{aligned}$$

The perceived laws of motion predict the actual movements of capital and equity premium with $R^2=0.999987$ for capital and $R^2=0.999977$ for equity premium.

The average error for the aggregate capital law of motion is $0.0059 \%$ percent of the average capital stock, while the maximum error is $0.0413 \%$ of average capital stock.

4.3 Comparison

Table 3 Algorithm execution comparisons (including the obtaining of derivatives)

The use of the proposed algorithm leads to a reduction in the run-time of $80 \%$. The execution performance of the proposed model is measured conservatively, since taking the numerical derivatives to construct the initial Jacobian matrix is considered. Alternatively, if one has a reasonably good guess for the Jabocian matrix (perhaps from the previous simulations of the model with similar parameters), it can be guessed directly, without taking the numeric derivative. If the initial Jacobian was guessed, instead of computed, then the proposed algorithm would take 2 iterations less, and lead to an $83 \%$ reduction in run-time.

Table 4 Bond market errors: average absolute excess demand (in terms of percentage of aggregate capital)

Looking at the errors in the next period aggregate capital prediction ($K'$), both the the classical version of the algorithm (Krusell and Smith 1997) and the proposed algorithm made an average error of $0.00613\%$ of average aggregate capital.

After obtaining final laws of motion, the simulation of the model is ran with clearing of the bond market in each time period (like in the classical version of the algorithm). This is to show that the obtained laws of motion are of approximately the same accuracy (they are basically approximately identical). In terms of $R^2$, both versions of the algorithm generate on average $R^2$ of 0.999987 for capital and 0.999977 for equity premium. Both by looking at the $R^2$ and Tables 4–6, one can see that the laws of motion produce arguably almost identical results.

Table 5 Difference in the simulated aggregate variables by the two version of the algorithm

The differences in aggregate capital are expressed in terms of percentage of aggregate capital, while differences in equity premium are expressed in percentage points. Maximal values are taken from the single time-period from all simulated periods, from all 50 simulations.

In Table 5., the simulated time-series of aggregate capital and equity premium by both algorithms are compared. To put the differences in perspective, they are smaller than the differences between the values predicted by the laws of motion and actual simulated values.

Table 6 Average parameters for the perceived laws of motion obtained by the two algorithms

Two algorithms seem to converge to approximately same values. Even when there are slight discrepancies, for example $b_0$ and $b_1$ in Table 6, they balance each other out, resulting in a very similar predictions of the equity premium, and very small deviations in the outcomes of the economy (as can be seen in Table 5). To make sure that the parameters converge to approximately the same value, regardless of the initial guesses, further simulations are performed. The results are presented in the Appendix 2. Despite varying initial guesses and doubling T, the proposed version of the algorithm still produces approximately the same values as the classical version of the algorithm described in Krusell and Smith (1997).

5 Discussion

In a model where the households can trade both claims to capital and risk-free bonds, the standard Krusell-Smith algorithm needs to explicitly impose bond market-clearing during the simulations stage of the algorithm,²¹ which results in a root-finding process. The main reason for the computational speed-up in the proposed algorithm is avoiding root-finding (finding the bond market-clearing price) for each simulated period t. However, the proposed algorithm takes more iterations to converge to the true solution. Therefore, the proposed algorithm is able to perform each iteration much faster but takes more iterations to converge. Overall, the gain from a faster simulation of the economy significantly outweighs the effect of an increase in the number of iterations.

The reported speed-up due to the proposed algorithm is conservative. The reason is twofold. First, the reported time and number of iterations include numerically taking derivatives used to construct the initial guess for the Jacobian matrix J. If one would have a reasonably good guess for the Jacobian (which is often the case if the changes in parameters are small compared to the previously computed model), then it is possible to avoid the first two iterations of the proposed algorithm. For example, if the values of the initial Jacobian were guessed instead of computed, the proposed algorithm would take two iterations less and would lead to an $83\%$ reduction in run-time. The second reason is that the initial guess for the value function computation stage is always the same, and it is the value of consuming the entire wealth in one period. An alternative option would be to use the value function from the previous iteration as the initial guess for the value function for the current iteration. The choice is also biased towards the classical algorithm from Krusell and Smith (1997), since the proposed algorithm needs more iterations to converge. Using better (circumstantial) initial value function guesses would decrease the run-time of the proposed algorithm even more (for example, final guesses from previous iterations).

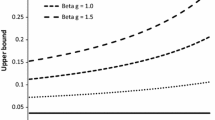
The run-time of the algorithms is relatively long²² for several reasons. First, the household’s problem features portfolio choice, which contributes to the well-known curse of dimensionality. This means the value function iteration step is slowed down significantly. Even when using the endogenous-grid method (Carroll 2006), only one dimension can be sped-up (consumption-savings problem), but not the portfolio choice problem. Second, there are five types of households in the economy: one for each of three productivity levels, unemployed, and retired. Lastly, the portfolio choice problem is a highly non-linear problem with multiple kinks. This means that during the value function iteration step, a relatively fine grid has to be used, since it is impossible to a priori know where the kinks will appear. This can be seen in Fig. 2. Furthermore, simple policy function interpolation is not used during the simulation step. The households still solve the recursive problem in a period t, which increases accuracy. Finally, in the classical algorithm, the simulation of the economy given the perceived laws of motion is slow due to the imposition of market clearing. This issue is tackled by the algorithm proposed in this paper.

An important parameter choice that influences the relative performance of the two versions of the algorithm is the number of time periods simulated in each iteration. The number of time periods simulated is $T=3500$ in the comparison section and $T=7000$ in the robustness check appendix, where the time-performance is not measured. Increasing this number would favor the proposed version of the algorithm, as it is able to simulate each time period much faster than the classical version.

As mentioned in Sect. 5, all the initial guesses for the laws of motion are such that at least some households have an internal portfolio choice. This is to ensure that the derivative of excess demand with respect to perceived equity premium would not be zero. This condition is important when constructing the initial Jacobian matrix in the proposed algorithm. If the condition is not satisfied, this does not mean that the proposed algorithm cannot be used. One can simply use the classical version of the algorithm until the condition is satisfied and then continue updating using the proposed version of the algorithm.²³

Furthermore, the threshold for the excess demand caused by using the predicted equity premium is $0.2 \%$ (on average) of mean aggregate capital.²⁴ This is true for both the classical and the proposed versions of the algorithm. However, excess demand is orders of magnitude smaller after market clearing (which the classical algorithm computes in the process) since the equity premium is then not restricted by the (linear) shape of the perceived laws of motion. Nevertheless, this should not necessarily be perceived as a disadvantage of the proposed algorithm. The algorithm’s outputs are the true laws of motion, and the proposed algorithm suggests a novel method to compute them. Once the correct perceived laws of motion are obtained (by using either algorithm), market-clearing can be imposed in the last, arbitrarily long simulation/iteration. An alternative to imposing the market-clearing after the laws of motion are obtained would be to adjust the bond holdings ex-post, similar to Den Haan and Rendahl (2010).

The reader might also be concerned that, despite imposing exact market clearing in the final iteration, by not imposing the exact market clearing in the interim stages, the algorithm produces a bias by accumulating small deviations over the course of the simulations. However, this turns out not to be a problem for this specific application. The reason is that during the interim stages of the algorithm, we are interested in improving the guesses for the law of motion and not necessarily in computing the exact equilibrium allocations. For example, if under the current perceived laws of motion, the bond return in the previous period was overestimated, the aggregate capital this period will be overestimated by an amount that we can call $\epsilon ^b$. Therefore, in the current period t, instead of generating the guessed variables of interest (capital next period $K_{t+1}$ and equity premium $P^e_t$), given the current aggregate state variables (in a case when only the first moment of the wealth distribution is used: TFP shock and $K_t$), we will generate the variables of interest given the TFP shock and $K_{t}+\epsilon ^b$. Therefore, despite this bias in the simulated equilibrium outcomes, the generated sequence still contains enough information to improve our guess of the perceived law of motion. With the improved guesses in the subsequent iterations, the bias $\epsilon ^b$ decreases. This is why the guesses for the laws of motion converged to approximately the same ones that were generated by the classical version of the algorithm. The adjustment of the stock returns in the Eq. 21 prevents the excessive over(under) accumulation of capital created by the misperception of bond returns (similar to the adjustment proposed by Den Haan and Rendahl (2010)). This stock return adjustment slightly reduces the number of iterations necessary for the proposed algorithm to converge. Consequently, the main innovation of the paper is proposing the described process of updating the laws of motion, as when one simply avoids root-finding (market clearing), the usual way of updating the laws of motion for the bond price is not possible since the market-clearing bond prices are not computed. The clearing adjustments simply increase the efficiency of the method.

The basic intuition of why the proposed algorithm converges to approximately the values generated by its classical counterpart is that the change in allocations due to misperception of equity premium (bond prices) will be captured by the change of the tracked moments in the law of motion. As shown by Cozzi (2015), the multiple self-sustaining equilibria do not seem to appear when using the classical version of the algorithm and standard calibration practices. Consequently, it would be extremely unlikely that they appear when using the proposed algorithm, for the reasons described above. Furthermore, if the changes in allocations caused by the misperception of equity premium matter for the dynamics of the aggregates in the economybeyond what is captured by the tracked moments of wealth distribution (in this case, only the mean), this means that the basic intuition on which classical algorithm is built is not valid. This would therefore be a contradiction, and more moments of wealth distribution should be tracked to obtain an accurate solution (by both classical and proposed versions of the algorithm). The intuition is furthermore backed by the results shown in Appendix 2, which introduces the biases in the initial guesses, and despite this, the results still converge to approximately the same values.

The proposed version of the algorithm is particularly useful in solving asset pricing models with uninsurable idiosyncratic and aggregate risks. This is because the perturbation methods in the style of Reiter (2009) are not precise when applied to these types of models, as they assume linearity in the aggregate states (Reiter 2009).²⁵ Similarly, the explicit aggregation method developed by Den Haan and Rendahl (2010)²⁶ is not suitable for solving models with both risky and safe assets, because of the bias that is introduced by the binding portfolio constraints, which is computationally expensive to correct. Because of this, to the best of my knowledge, it has not been implemented in a model with a risky and safe asset portfolio choice (it has only been implemented in an endowment economy model featuring only risk-free bonds with different maturities). To this date, the usual method for solving models with a portfolio choice between risky and safe financial assets are variations of the algorithm described in Krusell and Smith (1997). The method developed in this paper can be used to improve on the classical algorithm in Krusell and Smith (1997) whenever market-clearing has to be imposed explicitly,²⁷ such as models with endogenous labor supply.

It is worth mentioning that avoiding the root-finding in each period simulated might speed up the computation of the simulation step on the graphical processing units (GPUs). Hatcher and Scheffel (2016) show how Krusell and Smith (1998) algorithm can be accelerated by having the panel simulation performed on GPUs.²⁸ Since GPUs are not designed to perform heavy computation but are good at handling relatively simple transformations of multiple data elements in parallel; they are not ideal for solving root-finding problems. Therefore, eliminating the root-finding from the simulation step can potentially facilitate the use of GPUs in solving the models with multiple tradable assets.

6 Conclusion

This paper shows how to reduce the run-time of the Krusell-Smith algorithm (Krusell and Smith 1997) by proposing an alternative version of the algorithm. The reduction in computation time is achieved by avoiding the computationally expensive root-finding procedure to clear the bond markets in every simulated period while finding the correct perceived laws of motion. Instead, the proposed algorithm lets the economy proceed with the uncleared bond markets, and uses the information on the excess demand to update the perceived laws of motion. The guesses on the perceived laws of motion are updated using the Newton-like method described in Broyden (1965).

Measured conservatively, the proposed algorithm leads to a decrease in computation time of $80\%$ in the example model. The computational improvement would be even higher by using better circumstantial initial guesses on the value function and initial Jacobian matrix.

The described algorithm is useful in reducing the computational time of asset pricing models with uninsurable idiosyncratic and aggregate risk, although it can be used in other models that require market-clearing to be explicitly imposed.

Appendices

Appendix 1 Implementation of the Proposed Algorithm

• 1. Guess the law of motion for aggregate capital $K_{t+1}$ and equity premium $P^e_{t}$. This means guessing all initial coefficients. In this particular case, this would mean we have 8 coefficients overall, since both relationships are assumed to be linear, and there are two possible realizations of aggregate state z (2 equations $\times$ 2 coefficients $\times$ 2 aggregate states).

  $$\begin{aligned}&ln K'=a_0(z)+a_1(z) ln K \\&ln P^e=b_0(z)+b_1(z) ln K' \end{aligned}$$

• 2. Given the perceived laws of motion, solve the individual problem described earlier. This is done by value function iteration. First, construct a grid in two dimensions: individual wealth and aggregate capital, generating 135x12 grid-points in those two continuous-support state variables. Furthermore, at each grid-point, there will be 2 possible realization states for the aggregate shock and 5 possible idiosyncratic discrete states. Altogether, this means that there are 16200 grid points. At each of those grid points, optimal consumption and bond and stock investments are chosen, and corresponding updated value functions are obtained.²⁹ Choice of the values in between grid points is allowed, and the value function is in this case interpolated by cubic splines in the individual wealth dimension, and linearly in the aggregate capital dimension. This process is repeated until the Value function obtained in the previous iteration is approximately equal to the one computer in the current iteration.

• 3. Simulate the economy, given the perceived aggregate laws of motion. Do this in the following steps:

  • (a) Set up an initial distribution in period 1: $\mu$ over a simulation grid $i=1,2,...N_{sgrid}$,for each pair of efficiency and employment status, where $N_{sgrid}$ is the number of wealth grid points. Set up an initial value for aggregate states z.

  • (b) Simulate the economy given the perceived laws of motion. This means obtaining $g^{b}(\omega ,e,l;z,K)$ and $g^{s}(\omega ,e,l;z,K)$, which are the policy functions for bonds and shares. The policy functions are obtained after solving problems from the Eqs. 15 and 16. The market for bonds will not necessarily clear. Instead, in each period, there will be an excess demand. Policy functions are obtained each period given the current level of aggregate capital (instead of simply interpolating the policy functions obtained in step 2). Unlike in the classical version of the algorithm, the expected equity premium is not included as the additional state variable.

  • (c) Depending on the realization for $z'$, compute the joint distribution of wealth, labor efficiency, and employment status.

  • (d) To generate a long time series of the movement of the economy, repeat substeps b) and c).

• 4. Use the time series from step 3 and perform a regression of $ln K'$ on constants and lnK, for all possible values of z. This way, the new aggregate laws of motion for capital are obtained.

  In case there is still no initial guess for the Jacobian matrix:

  • If the $R^2$ for capital prediction is less than $99\%$, update only the perceived aggregate laws of motion for capital. This is done because the obtained Jacobian will not be very accurate. Then go to the step 2.

  • If the $R^2$ for capital prediction is higher than $99\%$, perturb the constant coefficients in the aggregate laws of motion for equity premium: $b_0(z)$, and simulate the economy using the step 3. Next, perturb the linear coefficients in the aggregate laws of motion for equity premium: $b_1(z)$, and perform the step 3 again. Using the excess demands from these simulations, construct the initial guess for the Jacobian matrix.

  In case Jacobian matrix exists:

  Run the regression:

  $$\begin{aligned} \xi _t (z)=\varrho _1(z)+\varrho _2(z) K_t + \epsilon _t \end{aligned}$$

  After this, step error measures are obtained:

  $$\begin{aligned} f_1(b^*_0(z),b^*_1(z))= \varphi \sum \xi _t (z) \end{aligned}$$

  where $\varphi =1$.

  $$\begin{aligned} f_2(b^*_0(z),b^*_1(z))= \varrho _2(z) \end{aligned}$$

  Update the Jacobian matrix with the following equation:

  $$\begin{aligned} J_n=J_{n-1} + \frac{\Delta \chi -J_{n-1} \Delta x_n}{||x||^2} \Delta x_n^T \end{aligned}$$

  and, update the guess for the perceived law of motion for equity premium:

  $$\begin{aligned} x_{n+1}=x_n-J_n^{-1} f(x_n) \end{aligned}$$

  for both possible realization of aggregate shock aggregate states for $z=good$ and $z=bad$. This will give us the updated candidates for the law of motion parameters $\begin{bmatrix} b_0(good) \\ b_1(good) \end{bmatrix}=x_{n+1}^{good}$ and $\begin{bmatrix} b_0(bad) \\ b_1(bad) \end{bmatrix}=x_{n+1}^{bad}$.

• 5. Compare the laws of motion from step 4 and step 1. If

  $$\begin{aligned} max(max (|\frac{a_n -a_{n-1}}{a_{n-1}}|),max (|\frac{b_n -b_{n-1}}{b_{n-1}}|))<0.0001 and avg (|\sum g^b - \lambda K_{t+1}|) < 0.00185 avg(K_t) \end{aligned}$$

  , the parameters converged and the accuracy is sufficiently good. Therefore, the solution algorithm is completed. If not, take the obtained parameters in step for as a new guess in the laws of motion. Then, proceed to step 2.

Appendix 2 Additional Simulations and Robustness Checks

1.1 2.1. Increasing the Number of Periods Simulated T

In the following simulations, the number of periods simulated is doubled from $T=3500$ to $T=7000$. The perturbations are made around the “true” model-solving parameters. This means that, same as before, additive, normally distributed shocks with mean 0 and $\sigma =0.01$ are drawn for each of the 8 parameters and then added to them. Since the realizations of the TFP shocks are different, there are differences in the coefficients when compared to the $T=3500$ case. Therefore, the obtained coefficients are again compared to the ones produced by the original version of the algorithm. The hardware used for the computation in this appendix is a computer cluster consisting of Intel(R) Xeon(R) Platinum predecessor nodes either at 2.20 or 2.30 GHz, and running Linux operating system. Intel compiler for FORTRAN is used Tables 7, 8, 9, 10 and 11. Because it is not straightforward to consistently measure and compare the run-time of the algorithm on a computer cluster, the run-times are not reported.³⁰ Classical version of the algorithm takes on average 5.53 iterations, while the proposed version of the algorithm takes on average 12.65 iterations to converge. As these are similar values to the ones in Table 3, one could expect a similar improvement in run-time.

Table 7 Average parameters for the perceived laws of motion obtained by the two algorithms, $T=7000$, $N=20$

Table 8 Bond market errors: average absolute excess demand (in terms of percentage of aggregate capital), $T=7000$

Both versions of the algorithm predict the capital next period with the average mistake of $0.0063 \%$.

Table 9 Difference in the simulated aggregate variables by the two version of the algorithm, $T=7000$

The differences in aggregate capital are expressed in terms of percentage of aggregate capital, while differences in equity premium are expressed in percentage points. Maximal values are taken from the single time period from all simulated periods, from all 20 simulations.

1.2 2.2. Initial Conditions with Non-symmetric Perturbations

In this exercise, I perform additional simulations, but the initial starting conditions make systemic mistakes in estimating both equity premium and future capital. In the first set of simulations, the equity premium is overestimated by $10\%$ (the “mistake” is equally “spread” among the constant and the linear parameter), and future capital is underestimated by $1\%$. Since equity premium is inversely correlated with capital, this causes an even larger overestimation of the equity premium.

The perturbation is then made around $b_0=b_0^*+0.5*ln(1.10)$, $b_1=b_1^*+0.5*\frac{ln(1.10)}{mean(K_t)}$, $a_0=a_0^*+0.5*ln(0.99)$, $a_1=a_1^*+0.5*\frac{ln(0.99)}{mean(K_t)}$.³¹

The second set of simulations underestimates equity premium by $10 \%$ and overestimates capital by $1\%$.

Table 10 Biased perturbations, $T=7000$,

1.3 2.3. Multiplicative Shocks and Non-symmetric Perturbations

In this exercise, perturbative shocks are multiplicative rather than additive. This means that the shocks have a mean 1 and $\sigma =0.01$. Results are shown in Table 11.

Table 11 Biased perturbations, $T=7000$

Appendix 3 Policy Functions

See Fig. 2.

φ. 2

Policy functions of the households, $z_t=good,K_t=5.92$

Appendix 4 Algorithm Diagrams

1.1 Krusell-Smith (1998) Algorithm with Only One Asset

1.2 Classical Version of Krusell-Smith (1997) Algorithm with Two Assets

The red section is causing a significant slow-down in run-time.

1.3 Proposed Version of the Algorithm (two assets)

Note that the red section from E.2 is eliminated.