Abstract
Investors usually resort to financial advisors to improve their investment process until the point of complete delegation on investment decisions. Surely, financial advice is potentially a correcting factor in investment decisions but, in the past, the media and regulators blamed biased advisors for manipulating the expectations of naive investors. In order to give an analytic formulation of the problem, we present an Agent-Based Model formed by individual investors and a financial advisor. We parametrize the games by considering a compromise for the financial advisor (between a sufficient reward by bank and to keep her reputation), and a compromise for the customers (between the desired return and the proposed return by advisor), and incorporating the social psychological concepts of truthfulness and cognitive dissonance. Then we obtain the Nash equilibria and the best response functions of the resulting game. We also describe the parameter regions in which these points result acceptable equilibria. In this way, the greediness/naivety of the customers emerge naturally from the model. Finally, we focus on the efficiency of the best Nash equilibrium.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Individuals take decisions concerning personal finance based on a variety of factors. For example, the investment decision process appears to incorporate a broad range of variables that may influence the individual investor’s behaviour, such as the perceived ethics of a firm, and recommendations from individual stockbrokers or friends/coworkers (Nagy and Obenberger 1994). Investors may resort to financial advisors to improve their investment process even to the point of complete delegation on investment decisions (or even follow self-proclaimed experts on social forums (Naldi 2019)). In that case, financial advice is potentially a driving/correcting factor in investment decisions (Fischer and Gerhardt 2007).
Nevertheless, in the aftermath of the global financial crisis, the media and the regulators have also placed much of the blame on biased advisors for manipulating the expectations of naive investors (Hong et al. 2008; Ferguson 2012). According to this view, an analyst may receive incentives to generate biased, optimistic forecasts while naive individual investors are unable to recognise that these biased recommendations are motivated by incentives to sell financial products. When asked for professional advice (i.e. an opinion), advisors may not straightforwardly state what they truly think, but rather be tempted to misrepresent their opinion to conform to the bank they are paid by. In any case, the role of financial advisors, as well as that of other influencers, is to be properly accounted for in the analysis of personal finance decisions.
However, though the decisions taken in personal finance have been a subject of interest in several papers (Bruhn and Steffensen 2011; ChiangLin and Lin 2008; Jensen and Steffensen 2015; Konicz et al. 2015; Kraft and Steffensen 2008), so far the adopted framework has considered an individual, acting without interaction with influencers of any kind.
In this paper, we wish instead to consider such interactions, to understand how the opinions of an individual investor may change under the influence of her advisors, considering the aims of the stakeholders involved. For this purpose, we formulate an Agent-Based Model (ABM) that includes three classes of agents: a bank, a financial advisor, a set of investors or customers. In this model, the advisor and the customers are decision-makers, and the bank is an exogenous agent that sets some conditions for the advisor. This model mimics the environment an individual investor finds when she manages her investment through the local branch of a bank, where a financial advisor oversees a group of bank’s customers. The major advantage that we expect from the adoption of an analytic framework like ABM is that analytic derivations of the properties of the model can be equally used as descriptive and as prescriptive tools, as widely noticed in the literature (Monica and Bergenti 2017; Glass and Glass 2020; Mastroeni et al. 2017, 2019b, a; Vellucci and Zanella 2018; Sharifi Kolarijani et al. 2020; Proskurnikov et al. 2016; Wang et al. 2011; Leitner and Behrens 2014; Leitner et al. 2017; Pan 2012; Fatas-Villafranca et al. 2011; Hegselmann and Krause 2005; Krause 2020; Xu and Cao 2020; Dacrema and Benati 2020; Steinbacher and Steinbacher 2019).
The influence we model through the ABM incorporates the effect of two social psychological concepts: truthfulness and cognitive dissonance.
As to truthfulness, the psychological literature claims that the probability of people showing dishonest behaviour is proportional to the number of benefits gained from being dishonest (Mazar and Ariely 2006). In our case, we can imagine financial advisors to see attractive incentives to act dishonestly: since they are typically rewarded based on the volume of transactions and the sales figures of bank products, they could be tempted to put their earnings ahead of the interests of their customers by suggesting them to buy more bank products (McDonald 2002; Davis 2004; Kliger and Qadan 2019).
The latter concept, cognitive dissonance, can be defined as the discomfort experienced when holding two different cognitions, e.g. two different opinions. It has been observed in several contexts (Mogiliansky et al. 2009; Martínez-Martínez 2014; Busemeyer et al. 2009; Khrennikov and Basieva 2014; McDonald et al. 2013; Spiekermann and Weiss 2016; Houser et al. 2008). The theory behind it (Festinger 1962; Akerlof and Dickens 1982) can be adequately represented in economic terms if we give its definition in terms of a person’s expectations. As soon as we were born, we immediately began accumulating a large number of expectations on what our life should be like. When one of these expectations is not met, dissonance occurs. In our case, the dissonance may take place between the customer’s expectations about its investments, as related to its opinions about a financial product, and the advice given by the financial advisor. It may also take place between the customer’s expectations and its actual investment results, which may lead it to rely more on the financial advisor’s suggestions. The investor’s general attitude may also influence dissonance (Rieger 2017; Cenci et al. 2015): a very confident investor could expect to succeed in any task she carries out, while an investor with a low opinion of herself might instead expect failures. Indeed, the advisor’s ability to manipulate or induce optimism or pessimism in this context can be explained by the theory of cognitive dissonance (Aronson 1992; Dickinson and Oxoby 2011), since the generation of an optimistic or pessimistic belief can reduce an intrinsic conflict between cognitions. Since dissonance can be reduced by changing one’s own opinion (Festinger 1962; Groeber et al. 2014), the dissonance of an investor can be assumed to depend on the dissonance caused by the difference between its opinion and the opinions of all the other agents with whom she interacts. Following Bindel et al. (2015) and Groeber et al. (2014), we will assume that the magnitude of dissonance is a function of the distance between opinions.
Hence, the different aims of the stakeholders convey the effect of truthfulness and cognitive dissonance. We consider those aims by resorting to a game-theoretic model, where each personal investment decision consists in selecting a strategy, and the agents’ payoff depends on the strategies chosen by herself and other players. We wish to see how the stakeholders’ strategies may find an equilibrium, and how incentives and payoffs may tilt it towards some players’ interests. We refer to this game as the personal finance game and provide the following contributions:
-
we fully formulate a game where the possible untruthfulness of financial advisors, the bank’s interest, and the customers’ sensitivity to cognitive dissonance are all factored in (Section 3.1);
-
we provide a closed-form equilibrium solution of that game, providing the advise output by the financial advisor and the customers’ decisions as the result of the game (Section 3);
-
we analyse the impact of cognitive dissonance, advisor’s truthfulness, and her influence on customers (Sections 4.1.1, 4.1.2, and 4.1.3);
-
we analyse the efficiency of the game through the Price of Stability (Section 5).
The results of our analysis show that
2 Related literature
Our paper is related to the literature framework of opinion formation games that relax the assumption of truthfulness (a.k.a as honesty) in the process of opinion formation, allowing game players to express some opinions which need not coincide with their true opinions.
The players whose opinions we wish to model are represented as nodes of a social network (i.e., vertices on a graph), where the links between the nodes represent the direct influence between players in forming their opinions.
We therefore introduce a connected undirected graph \(G =({\mathcal {V}}, {\mathcal {E}})\) be with \(|{\mathcal {V}}| =n\) and for each edge \(e =(i, j) \in {\mathcal {E}}\) let \(w_{ij}\ge 0\) be its weight. Let \(W=[w_{ij}]_{ij}\) be the matrix of weights. Every vertex of the graph (i.e., each player or agent) is characterized by an internal opinion \(s_i\) and a stated opinion \(z_i\). The set of neighbors of agent i in the social network represented by the graph G is denoted by N(i).
This game can be expressed as an instance \(\left( G,W, \mathbf{s }, \mathbf{z } \right) \) that combines a weighted graph (G, W) and the vectors of opinions \(\mathbf{s }=(s_1,\dots ,s_n)\) and \(\mathbf{z }=(z_1,\dots ,z_n)\), which are attributes of the nodes. The internal opinion \(s_i\) is unchanged and not affected by opinion updates, while each player’s strategy is represented by her stated opinion \(z_i\), which may be different from her \(s_i\) and gets updated (Bindel et al. 2015; Gionis et al. 2013; Bhawalkar et al. 2013; Ferraioli et al. 2016; Chierichetti et al. 2018; Auletta et al. 2016, 2017; Bilò et al. 2016; Chen et al. 2016). The approach followed by Buechel et al. (2015) differs from all these papers mainly as it considers true and stated opinions evolving over time according to different laws.
Buechel et al. (2015) adopt for agent i a utility function that depends on the distance of true opinion \(s_i\) to stated opinion \(z_i\) as well as on the distance of stated opinion \(z_i\) to group opinion \(q_i\). Bindel et al. (2015) study the price of anarchy — the ratio between the cost of the Nash equilibrium and the cost of the optimal solution — in a game of opinion formation. They assume that person i has an internal opinion \(s_i\), which remains unchanged from external influences, and a stated opinion \(z_i\) which is updated as a weighted sum of her neighbours’ stated opinions
where \(w_{i,j}\ge 0\). Both opinions are assumed to be real numbers. Updating \(z_i\) as in (1) allows to minimize the cost function
Both papers, are inspired by classical models due to Degroot (1974) and Friedkin and Johnsen (1999). Also Buechel et al. (2015) consider both opinions \(z_i\) and \(s_i\) are assumed to be real numbers.
Gionis et al. (2013) follow the framework of Bindel et al. (2015), by considering equations (1) and (2) as update rule and personal cost function. The internal and external opinions have been modeled as real values in the interval [0, 1]. Gionis et al. (2013) study the CAMPAIGN problem, whose goal is to identify a set of target nodes T, whose positive opinion about an information item will maximize the overall positive opinion for the item in the social network. The objective function to maximize is therefore \(g(\mathbf{z })=\sum _{i=1}^n z_i\).
Bhawalkar et al. (2013) analyze the equilibrium outcomes of symmetric co-evolutionary game and the K-nearest neighbor (K-NN) game, distinguishing between internal and stated opinions with the usual symbols \(s_i\) and \(z_i\) (which are real numbers). In the K-NN game, each agent has exactly K friends, so the interaction is of the nearest neighbors type and the size of N(i) is exactly K for each agent i.
Ferraioli et al. (2016) continue the study of Bindel et al. (2015) by simplifying their model to the case of binary opinion \(z_i\), which can be found in the individual’s voting intention in a referendum, while \(s_i\in [0,1]\). They study best-response dynamics and show upper and lower bounds on the convergence to Nash equilibria.
The cost function considered by Chierichetti et al. (2018) (where update rules for \(z_i\) and \(s_i\) are not present) replaces the quadratic terms in Bindel et al. (2015) by distances in a discrete metric space while \(s_i\) belongs to a discrete set (binary in some special cases)Footnote 1 and \(z_i\in {\mathbb {R}}\). The authors adopt a strategy \(\mathbf{z }\) minimizing the social cost function as an optimal solution and establish bounds on the price of stabilityFootnote 2
Auletta et al. (2016) consider a personal cost that is defined through a monotone non-decreasing function of \(\mathbf{z }\), assuming binary \(z_i\) and \(s_i\) (without update rules for them). The authors called that class generalized discrete preference games. In particular, they show that every game with two strategies per agent that admits a generalized ordinal potential is structurally equivalent (in particular, better-response equivalent) to a generalized discrete preference game. Another work by Auletta et al. (2017) considers the game in which agents are utility maximizers, \(z_i\), \(s_i\in \{0,1\}\) and address the questions of price of stability/price of anarchy of a game in terms of the social welfare: \(SW(\mathbf{z }):=\sum _i u_i(\mathbf{z })\).
Bilò et al. (2016) focus on the case in which, for each player i, the innate opinion \(s_i\in [0,1]\), while the expressed opinion \(z_i\in \{0,1\}\). They define a cost-minimization n-player game. Bilò et al. (2016) show that any game in this class always admits an ordinal potential that implies the existence of pure Nash equilibria and convergence of better-response dynamics starting from any arbitrary strategy profile. The social optimum is obtained with respect to the problem of minimizing the sum of the players’ costs. They also focus on the efficiency losses due to selfish behavior and give upper and lower bounds on the price of anarchy and lower bounds on the price of stability.
Chen et al. (2016), bound the price of anarchy for a game in which both \(s_i\) and \(z_i\) are real numbers.
3 Personal finance game and Nash equilibria
In order to understand the strategic interactions that lead to personal finance decision, we develop a model where the major stakeholders act as agents. In this section, we first describe that model and then adopt a game-theoretic approach to study their interactions and their equilibrium decisions.
3.1 The agent-based model
In this section, we introduce an ABM to study the personal finance game. In our ABM there are three classes of agents:
-
a bank (B);
-
a financial advisor (A);
-
a set of n customers (\(CL_i\), \(i=1,\dots ,n\)).
The bank acts as an external stakeholder, since it sets some conditions that influence the game between the advisor and the customers but does not interact otherwise with the other stakeholders.
Our model falls in the literature framework of opinion formation games where game players can express some opinions and may change them according to the interactions with the other agents. For some of them, the opinions they express need not coincide with their true opinions. The opinions concern investment decisions.
The aim of bank B is to steer the customers towards a particular investment decision, represented by an opinion \(w\in {\mathbb {R}}^+\). For example, w could concern the decision to buy a security \(S_1\) rather than a different one \(S_2\) or other financial instruments.
The financial advisor A expresses an opinion \(s\in {\mathbb {R}}^+\) which need not coincide with her true opinion \(x\in {\mathbb {R}}^+\), respectively referred to in the following as the stated opinion and the internal opinion. If the two opinions do not coincide, the financial advisor is untruthful. A is paid by B, and she gives advice (by way of s) to customers when invited to do so, but the stated opinion s might not perfectly correspond to the one recommended by the bank, w (to preserve her good reputation, for instance).
Customers have their opinions \(c_i\), \(i=1,\dots , n\) , which fall within the range \([d_i,s]\) where \(d_i\le s\) is a positive lower bound, which represents the opinion that the customer i would assume if there weren’t any interaction with A. The opinions of all customers are collected in \(\mathbf{c }:=(c_1,\dots ,c_n)\in {\mathbb {R}}^n\).
Opinions \(c_i\), \(i=1,\dots , n\) and s change over time, i.e. \(c_i=c_i\left( t\right) \) \(i=1,\dots , n\) and \(s=s(t)\), while w, x and d are fixed over time. However, we assume that all the opinions lie within the range [0, 1].
Following the models introduced by Bernheim (1994) and Buechel et al. (2015), we consider a utility function for A that depends on the incentive to be truthful (the intrinsic part) and the incentive to steer the customers towards w (the remunerative part). The incentive to be truthful could be related to the advisor’s conscience or to the desire of the advisor to keep her reputation. Additionally, we assume that the utility function for A also depends on the desire to influence the customers. The resulting utility function is supposed to be a quadratic form in the opinions and to be additive.
Thus, the utility of the financial advisor depends on the distance between her true opinion x and her stated opinion s as well as on the distance between the bank’s desired investment decision w and customers’ opinions \(\mathbf{c }\) as well as the distance between s and \(\mathbf{c }\):
where \(\alpha ,\beta ,\gamma >0\). The coefficient \(\beta \) is the remuneration coefficient for A and is paid by bank B: the more customers eventually buy the security pushed forward by the bank B, the more the advisor A is remunerated. The coefficient \(\alpha \) measures the importance of truthfulness, while the coefficient \(\gamma \), measures the importance of the advisor’s influence on customers. The last term in Equation (3) is exactly the same as that appearing in the next Equation (5), where it represents the cognitive dissonance, i.e., the strain put on the customer by its opinion being different from the of the advisor, who is an expert in the field. Here, it represents the same effect from a different perspective: it models the strain put on the advisor by the customer not following its advice or, in other terms, but its incapability of having the customer follow its advice.
The advisor’s strategic leverage is the stated opinion s, and her aim is to maximize her utility:
In order to define the utility of customers \(CL_i\), \(i=1,\dots ,n\), we introduce the following returns on their investments:
-
\(r_s\), which is the return proposed by A to all the customers;
-
\(r_{d_i}\), which is the return that each customer considers as achievable through a “good” investment decision.
The customer i would like to get \(r_{d_i}\). Still, she does not completely trust herself (the customer is not assumed to be a financial expert) and moves towards \(r_s\). In general, two possible situations may occur: \(r_s\le r_{d_i}\) and \(r_s > r_{d_i}\). In the first case, we assume that customers have unrealistic expectations due to their poor knowledge of financial markets. The consequence is that A proposes the customer i a return lower (or equal) than the expectations of \(CL_i\). In the second case, the advisor proposes an investment whose expected return is higher than what the customer hopes for, so that \(r_s > r_{d_i}\). The rationale for the second case is that the financial advisor can find a better investment than the customers due to her superior financial expertise.
Due to the stochastic nature of financial markets, by return we mean an average return, implicitly assuming a risk-return tradeoff.
We assume that the utility of each customer i depends on her lack of agreement with the advisor A. This cognitive dissonance (Bindel et al. 2015) provides customers with an incentive to modify their behavior to reduce the cost of this lack of consensus. If we assume that \(s > d_i\), customers’ opinions \(c_i\) fall within the range \([d_i,s]\), where the advisor’s stated opinion s is a positive upper bound for them, and that parameter \(d_i\) represents the opinion that the customer i would assume if there weren’t any interaction with A. Thus, the utility of \(\hbox {CL}_i\) takes the value \(r_s\) if \(c_i=s\) but depends on the distance between her opinion \(c_i\) and the advisor’s stated opinion s in all the other cases:
where \(\zeta >0\) (\(\forall i=1,\dots ,n\)) represents the customer’s sensitivity to cognitive dissonance. We do not consider the reverse case here, where \(s < d_i\), i.e. the case where the customer’s opinion would be dragged down by the advisor since it appears less frequent. At any rate, Equation (5) would hold even in the reverse case, with \(c_i\) now falling within the range \([s, d_i]\). since both terms in the fraction would switch sign. It is to be noted that the returns included in the first two terms of Equation (5) are not real economic benefits but represent the returns envisaged by the two parties. The real return will show once the investment is actually carried out and its results are observed. Equation (5) considers two contributions to the customer’s utility as measured through its satisfaction. The first contribution is related to the envisaged returns and will be higher the higher those returns are. As the customer’s opinion moves towards the advisor’s, so does the envisaged returns. If the return put forward by the advisor is lower than that initially expected by the customer (\(r_s < r_{d_i}\)), that contribution to utility will decrease. At the same time, the second contribution to Equation (5) is related to the strain put on the customer by its opinion being different from that of the advisor. Suppose the customer does not follow the advisor’s recommendation. In that case, it will receive a negative utility contribution (since its opinion differs from that of an expert), regardless of the return envisaged by the advisor (which is kept into account in the first contribution).
Acting as a decision-maker, the customer (investor) wishes to gain money from the purchase of financial instruments by resorting to a financial advisor. However, she is affected by dissonance when there is a difference between her opinion and the advisor’s one, i.e. when the investor expects an average return that is different from that proposed by the advisor. If \(\zeta \) is close to zero, the investor pays little attention to the dissonance because, for example, she tends to overestimate the desirability of the chosen alternative and to underestimate the desirability of the rejected alternative. In other words, she thinks she has made the right choice since the idea of making a mistake conflicts with the cognition that she is a smart person (Akerlof and Dickens 1982). The factor \(\zeta \) sets the sensitivity to the magnitude of dissonance.
Let us observe that the following consequences hold:
-
(a)
\(0\le \frac{c_i-d_i}{s-d_i}\le 1\) since \(d_{i}\le c_{i} \le s\);
-
(b)
\(r_{d_i}+\frac{c_i-d_i}{s-d_i}(r_s-r_{d_i})\ge 0\) for \(c_i\in [d_i,s]\) because of consequence (a) and \(r_{s},r_{d_{i}}>0\);
-
(c)
\(\left[ r_{d_i}+\frac{c_i-d_i}{s-d_i}(r_s-r_{d_i})\right] _{c_i=d_i}=r_{d_i}\) and \(\left[ r_{d_i}+\frac{c_i-d_i}{s-d_i}(r_s-r_{d_i})\right] _{c_i=s}=r_{s} \rightarrow u_{CL_i}(s,d_i,s)=r_s\) and \(u_{CL_i}(d_i,d_i,s)= r_{d_i}-\zeta (d_i-c_i)^2\) (in the latter case the cost of lack of consensus is maximum).
3.2 Nash equilibria
The model described in Section 3.1 describes the opinion dynamics of a financial advisor and her customers when the opinions are influenced by each other’s choice. This interaction can be considered as a strategic game, where the players are the financial advisor and her customers (the bank’s role is just to set the fixed aim w and the incentive \(\beta \)) and their strategic leverages are respectively the stated opinion s and the opinions \(c_{i}'s\). In this section, we solve the personal finance game by deriving the Nash equilibria.
We now find the Nash equilibrium of the \(n+1\)-player game (n customers plus one financial advisor) using their best response functions. The best response functions aim at maximizing the players’ utilities:
For any \(c_i\), we obtain the optimal s by zeroing the derivative of the utility
Turning to customers utility and fixing s, we obtain
Then the system (6) that expresses best response functions becomes:
The solution of the system of linear equations is the advisor’s best response function
which is a linear function of the customers’ opinions. Similarly, the customers’ best response function is given by
For the sake of simplicity, consider the special case where all the customers have the same initial opinion and expectations, i.e., \(r_{d_i}=r_{d}\) and \(d_i=d\) \(\forall i=1,\dots ,n\), so that all the customers take the same investment decision, i.e., \(c_i=c\). Sometimes we will denote this case as the case of homogeneous investors.
Then, the best response functions become simply
and
Now, we can examine the impact of the parameter \(\alpha \) on the advisor’s utility as embodied by the first term of Equation (3). From that equation we derive that \(\alpha =0\) means that the advisor’s untruthfulness does not impact on its utility. However, when \(\alpha \) increases, the impact is not linear. By replacing the advisor’s stated opinion s defined by (10) into the truthfulness part of \(u_A\) in Equation (3), we obtain:
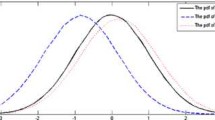
In Fig. 1 (plotted for \(d=0.05469973\), \(x=0.7287941\), \(\gamma =0.3957729\)), we see that the impact of \(\alpha \) first grows very quickly but reaches its peak around \(\alpha =4\)
We plot the best response functions of both players in Fig. 2 for a sample case. We see that the best response function of the financial advisor in Equation (12) is a linear function of the customers’ opinion, with a slope \(\frac{\gamma n}{\alpha +\gamma n}<1\), while the best response function of the customers in Equation (13) is the sum of an angle bisector and a homographic function with a vertical asymptote at \(s=d\). The Nash equilibria are represented by the intersection of the two curves. Note the presence of two Nash equilibria.
In order to compute the the equilibria, we solve the system (9) for \(d_i=d\). Here, by substitution we obtain
from which
for \(s\ne d\). Accordingly, the two Nash equilibria are:
where
are the roots of quadratic equation (16).
We can finally consider the impact of stochastic changes in the returns that both parties expect. Expectations can sometimes be detached from reality or being overly influenced by interactions with other people’s beliefs, giving rise to collective investment frenzies, as in the model developed in Bénabou (2013). In Section A.3, we have computed the variance of the customers’ utility when both those returns are random. We have obtained that
The variance of the utility grows with the ratio between the average difference in the returns expected by the two parties and the squared difference of their opinions. This is partly in line with the model developed in Cho and Jang (2019), where volatility in asset markets increases the variability of output dynamics (which may call for a macro-prudential regulation advocated in Freixas et al. (2015)). Here we see that it is actually the detachment between opinions and return expectations (namely an overestimation of returns) that can increase the volatility in the utility of customers.
4 Nash equilibria movements
We can now examine the dependence of the Nash equilibria on the model parameters, recalling that \(\gamma \) measures the importance of the advisor’s influence on customers, \(\alpha \) measures the importance of truthfulness, \(\beta \) measures the importance of remuneration for the advisor’s choice, and \(\zeta \) measures the importance of belief in the advisor’s stated opinion (i.e., the cognitive dissonance). The parametric curves are shown in Figs. 3, 4, 5, where the parameters are held fixed excepting that of interest, as reported in Table 1. In all the three figures, we have assumed \(r_d = r_s + 0.1\), i.e., the customer has expectations superior to the financial advisors (probably overestimating her own financial expertise).
The curves shows how the two equilibria move, with an arrow indicating the direction of growth of the parameter of interest. A triangular region is shown as bounded by the two straight lines: equilibria falling outside that region are not acceptable since they violate the constraint on customers’ opinion (\(d\le c \le s\)). We see that in all cases the upper equilibrium point (\(P^*\)), where both players exhibit a high opinion, indicate a progressive reduction of cognitive dissonance, with the customer converging towards the financial advisor’s opinion. The opposite case takes place for the lower equilibrium point (\(P^\dagger \)), where, in the presence of a low opinion by the financial advisor, the customer is led to take an even lower opinion, increasing the cognitive dissonance. This latter behaviour could be summed up in the words "If the financial advisors doesn’t believe in that security, why should I?" In addition, we note that the lower equilibrium point stops being valid (i.e., it escapes the triangular validity region) when the parameter of interest grows.
4.1 The impact of parameters on Nash equilibria
In this subsection we analyse the impact of cognitive dissonance, advisor’s influence on customers, and her truthfulness on Nash equilibria.
4.1.1 Impact of cognitive dissonance
In response to changes in \(\zeta \), Nash equilibria are placed along the dash-dotted line in Fig. 3. When \(\zeta \) increases, both equilibria tend to pull away and to accumulate in different areas. This is because, if we fix \(n=1\) and assume e.g. \(d<x\), as \(\zeta \) tends to \(\infty \) the equilibria \(P^*\) and \(P^\dagger \) in (17) become
As \(\zeta \) tends to \(\infty \), the second of (20) represents an unreachable limit because there exists a number \({{\bar{\zeta }}}>0\) such that, for each \(\zeta >{\bar{\zeta }}\), the support of the curve
goes out the triangular acceptance region (see Fig. 3, the squared branch). If we assume that, for \(\zeta ={\bar{\zeta }}\), the curve \( \left( \frac{1}{2\zeta }\frac{r_s-r_{d}}{b -d}+ b,b\right) \) falls right onto the horizontal side of the triangle, we define Equation (21) as the last useful equilibrium. The critical value \({\bar{\zeta }}\) can be found by imposing
because \(c=d\) represents the horizontal side of the triangular acceptance region (let us remember that \(d\le c \le s\)). Then, from (22) it is easily to prove that
The value in (23) is positive if \(r_s<r_d\). Calculated in (23), the last useful equilibrium is
Remark 1
For the sake of simplicity, Eq. (20) have been obtained for the particular case \(d<x\). Anyway, it is possible to prove that
In order to investigate the behaviour of the equilibrium solutions as the importance of cognitive dissonance varies, we can consider the case of homogeneous customers for which \(c_1^*=\dots =c_n^*=c^*\) and \(c_1^\dagger =\dots =c_n^\dagger =c^\dagger \). Then, from Eqs. (17) and (18) we have
and
From these equations it is clear that, when the cognitive dissonance parameter \(\zeta \) is large enough and \(r_d-r_s>0\), a branch of the curve increases with \(\zeta \) whereas another decreases (the derivatives with respect \(\zeta \) of \(c^*-d\) and \(c^\dagger -d\) are opposed to each other). This explains the result depicted in Fig. 3. The curve with solid dot markers, describing the higher advisor’s stated opinion, moves by decreasing the cognitive dissonance. Instead, if the advisor’s stated opinion is low (curve with square markers), the cognitive dissonance grows, with the customers moving towards an even lower opinion (ending up with non-valid solutions).
4.1.2 Impact of advisor’s truthfulness
A similar result also applies to the case \(\alpha \rightarrow +\infty \). Actually, if we assume \(d<x\), as \(\alpha \) tends to \(\infty \) the equilibria \(P^*\) in (17) is
while \(P^\dagger \) is excluded because this time
This case corresponds to an advisor that is very sensitive to the difference between her stated and true opinion, i.e. to the difference between what she says and what she really thinks. See Fig. 4.
4.1.3 Impact of advisor’s influence on customers
Figure 5 shows that, as \(\gamma \) approaches to zero, only one equilibrium survives. Actually, for \(n=1\) and \(d<x\), as \(\gamma \rightarrow 0\) the equilibrium \(P^*\) in (17) is
while \(P^\dagger \) is excluded because
Since \(\gamma \) tells us how wide is the advisor’s desire to influence the customers, when \(\gamma =0\) (and all the other parameters are fixed and \(\ne 0\)) her equilibrium is represented by her internal opinion. (There is no desire to influence the customers, then there is no reason to tell a lie.) Observe also that \(\frac{r_s-r_d}{2\zeta (x-d)}+ x<x\) if \(r_s<r_d\); in this situation the Nash equilibrium is acceptable and the equilibrium solution for customer is different from the advisor’s internal opinion.
Let us conclude this section by considering the dependence of Nash equilibria on the increasing measure of advisor’s influence on customers, \(\gamma \). Observe that, if \(\gamma \) gets too big, both equilibria become not real because of the sign of \(r_s-r_d\) in the square root of Eq. (18). In fact, as we have assumed to plot Fig. 3, 4, 5 and as we will see in more details in Section 4.2, we have that \(r_s<r_d\) is a condition to have Nash equilibria and that solution would contradict the hypothesis.
4.1.4 Non-asymptotic analysis of Nash equilibria
In the above subsections we have considered \(\alpha \), \(\zeta \rightarrow + \infty \) and \(\gamma \rightarrow 0\). The same considerations remain true, in approximation(i.e. considering the presence of a deviation from the asymptotic result), if we replace \(\alpha \), \(\zeta \rightarrow + \infty \) and \(\gamma \rightarrow 0\) with finite values such that \(\frac{2\gamma n}{\alpha \zeta } \, \frac{r_s-r_{d}}{\left( d- x \right) ^2}\ll 1\). For example, in Equation (18) we have
whenever \(\frac{2\gamma n}{\alpha \zeta } \, \frac{|r_s-r_{d}|}{\left( d- x \right) ^2}<1\). If we set \(\chi =\frac{2\gamma n}{\alpha \zeta } \, \frac{r_s-r_{d}}{\left( d- x \right) ^2}\), from (32), the equilibrium \(P^*\) defined in (17) assumes the following form:
where \(o(\cdot )\) denotes higher-order infinitesimal and we fixed \(n=1\), \(d<x\). A similar expression can be found also for \(P^\dagger \).
4.2 Admissibility of the Nash equilibria
In this Section we derive the parameter region in which Nash equilibria, obtained in Section 3.2, stay coherent with opinion variable definition. For example, since \(c_1\), \(\dots \), \(c_n\), s shall fall within the range [0, 1], the coordinates of Nash equilibria are constrained between 0 and 1, and hence we obtain the conditions on parameters to ensure that. We will focus on the special case, i.e. \(r_{d_i}=r_{d}\) and \(d_i=d\) \(\forall i=1,\dots ,n\).
In our model we distinguish between strategic variables and parameters. The first of these are \(c_i\), \(i=1,2,\dots ,n\), and s, while the latter are d, x, w, n, \(\alpha \), \(\beta \), \(\gamma \), \(\zeta \), \(r_d\), \(r_s\). The set of all numeric values that they can assume are called, respectively, the domain \({\mathcal {D}}\) and the admissible parameter region \({\mathcal {R}}\).
From the assumptions on opinion variables and parameters, we have that
Let us denote with
the n-ary Cartesian power of a set Y. Hence, the domain can be rewritten as
Let us derive conditions on the parameters (in other words, subsets of \({\mathcal {R}}\)) which ensure the existence of \(P^*\) and \(P^\dagger \), by distinguishing between two cases, (A) \(r_s=r_d\) and (B) \(r_s\ne r_d\).
Case (A), \(r_s=r_d\). In view of this, Nash equilibria becomes:
We have the following result:
Proposition 1
Let \(r_s=r_d\). The Personal Finance Game admits the following Nash equilibria:
Proof
By virtue of constraints (34), the admissible parameter regions in which \(P^*\) and \(P^\dagger \) are acceptable Nash equilibria are described by:
and
where we denoted by \({\mathcal {R}}_1^*\), \({\mathcal {R}}_1^\dagger \subseteq {\mathcal {R}}\) these regions (\({\mathcal {R}}_1^*\) for \(P^*\) and \({\mathcal {R}}_1^\dagger \) for \(P^\dagger \)). \(\square \)
Case (B), \(r_s\ne r_d\). Let us denoted by \({\mathcal {R}}_1^*\), \({\mathcal {R}}_1^\dagger \subseteq {\mathcal {R}}\) the admissible parameter regions in which, respectively, \(P^*\) and \(P^\dagger \) are acceptable Nash equilibria. Then
Proposition 2
Let \(r_s\ne r_d\), then
and
where with \(r_d^{(1)},r_d^{(2)}\) we denoted, respectively, \(\frac{\alpha \zeta }{2\gamma n}(x-d)^2\) and \(2\zeta \alpha ^2 \left( \frac{x-d}{\alpha +\gamma n}\right) ^2\).
Proof
The completed proof is given in Appendix. \(\square \)
Remark 2
The intersection \({\mathcal {R}}_1^\dagger \cap {\mathcal {R}}_1^*\) is not empty. Then, for parameters values in \({\mathcal {R}}_1^\dagger \cap {\mathcal {R}}_1^*\), the two Nash equilibria \(P^*\) and \(P^\dagger \) are both acceptable (see e.g. Fig. 2).
Remark 3
Focusing on \(r_s\) range in the equation of admissible parameter region \({\mathcal {R}}_1^*\cup {\mathcal {R}}_1^\dagger \), the equations (41) and (42), we notice that \(r_s< r_{d_i}\). The customer i, that in our paper is a small investor, could be naive about incentives and expects a return bigger than the one advisor A proposes instead to her.
4.3 Best response dynamics
In the above subsections, we have recalled a well-known property of Nash equilibrium. Actually, it can be defined as a fixed point of the best-response mapping: a strategy \(\mathbf{z }\) is said to be a Nash equilibrium if
where \(\mathbf{z }=(c,s)\) and BR denotes the (set-valued) best-response mapping. A formal definition of BR has been employed in the previous subsections in order to obtain the best response functions. For the case of two players (one advisor and one customer), it is:
The fixed solution provides the equilibrium solution. Of course, in the reality, players would continuously revise their strategy, choosing best choices BR(z) to the current mean population strategy z, till reaching equilibrium. This is equivalent to postulating that players, who are intelligent enough to gauge the current population state and to respond optimally, adaptively learn to play a Nash equilibrium strategy over time. If we follow the adaptive best response evolution over time, we obtain the best response dynamics, the dynamical system induced by the best response mapping itself (Swenson et al. 2018; Hofbauer and Sigmund 2003; Gilboa and Matsui 1991; Matsui 1992):
The map BR is in general set-valued, so that the dynamical system expressed by Eq. (45) will be a differential inclusion rather than a differential equation. But this is not the case of our model, so that it is relatively safe to think of (45) as a differential equation. Hence:
From Equations (12) and (13) we know that the best response functions are \(s=\frac{\alpha x +\gamma c}{\alpha +\gamma }\) and \(c=\frac{r_s-r_{d}}{2\zeta (s-d)}+s\). Hence, the dynamical system (46) becomes
Once we find any solution of (47) it is natural to try to determine if the solution is stable. The answer to this question can be obtained from the following theorem.
Theorem 1
The equilibrium solution of the nonlinear vector field (47) is asymptotically stable.
Proof
As we can see, by definition, the set of Nash equilibrium of our model coincides with the equilibrium points of dynamical system in (47). From (17) and (18) there are then two fixed points given by
where
The matrix associated with the linearized vector field is given by
(Note that J depends only on advisor’s strategic leverage s.) The characteristic polynomial of J(s) is given by
It is a polynomial with respect to \(\lambda \) and dependent on s. Looking for the zeros of \(q(\lambda ,s)\), we obtain the equation:
By parameters definition and since, as we have seen in Section 4.2, \(r_s<r_d\), we have obviously two real roots. Now, lets write the roots precisely
Note that both eigenvalues depend on s, so they will assume different values if we estimate the Jacobian in \(\mathbf{z }^*\) or \(\mathbf{z }^\dagger \) but, clearly, \(\lambda _2(s)\) is negative for both equilibria.
For \(\lambda _1(s)\) let us now proceed by reductio ad absurdum. Let us assume that \(\lambda _1(s)>0\) and start with \(s=s^*=a\). Then, after some algebra, we obtain
But this inequality has no solution. Similar considerations can be done also for \(\mathbf{z }^\dagger \). \(\square \)
In other words, Theorem 1 states that solutions starting “close” to \(\mathbf{z }^*(t)\) (or \(\mathbf{z }^\dagger (t)\)) not only stay close, but also converge to \(\mathbf{z }^*(t)\) (or \(\mathbf{z }^\dagger (t)\)) as \(t\rightarrow \infty \).
In order to examine the transient behaviour of the advisor and its customers while reaching the game steady-state, we discretize equation (47) and obtain
If we follow this discrete-time version of the evolution of the stakeholders’ opinions, we obtain Fig. 6 where the time evolution of c(t) and s(t) is plotted for \(t\in [0,20]\) and time step \(\varDelta t= 0.1005025\) (the parameter settings are: \(d=0.05469973\), \(x=0.7287941\), \(w=0.4678351\), \(n=1\), \(\gamma =0.3957729\), \(\beta =3.206756\), \(\alpha =0.3881699\), \(r_d=0.5759116\), \(r_s=0.1377676\), \(\zeta =1.96627\). Initial conditions: \(s(0)=0.7548916\), \(c(0)=0.4565133\)). We see that the advisor’s opinion seems to adjust downwards to the customer’s one since the beginning. Instead the customer exhibits an early move upwards towards the advisor but soon inverts the trend. Overall, the interaction leads both to lower their opinions.
However, the same similarity between the trends of their opinions is not found when we consider their utilities. In Fig. 7, we see that the advisor achieved a sudden growth and then keeps increasing its utility, while the customer, after the initial move sees its utility lowering. Since the respective goals are to maximize their utility, the advisor is much smarter in driving the game.
4.4 The boundary of \({\mathcal {D}}\)
The following result characterizes mathematically the boundary of the set \({\mathcal {D}}\) described in (34) and denoted by \(\partial {\mathcal {D}}\). A graphical representation of \(\partial {\mathcal {D}}\) for two and three dimensional spaces is depicted in Fig. 8, where the boundaries are highlighted in different colors. Mathematically, since
and
they are described respectively by
for \(n=1\), and
for \(n=2\). Another example (four dimensional space) has equation
for \(n=3\) and then
Proposition 3
The boundary of domain \({\mathcal {D}}\), described by (34), is
Proof
Let us consider the set (34), where \(d \le c_i\le s\le 1\) \(\forall i=1,\dots ,n\). Fix \(j\in \{1,2,\dots ,n\}\) and assume \(\max _{i=1,\dots ,n} c_i=c_j\).
Fix, for example, \(c_1=d\) then we still have \(d \le c_i\le s\le 1\), i.e. \(d \le c_i\le s\) \(\wedge \) \(d \le s\le 1\), \(\forall i=2,\dots ,n\). Relation \(d \le s\le 1\) and \(d \le c_i\le 1\) are verified by definition while the truthfulness of \(c_i\le s\) is ensured by \(c_j \le s\), because \(c_i\le c_j\) \(\forall i=1,\dots ,n\) by definition. The same can be concluded for every \(c_i=d\).
Finally, we note that if \(s=1\) then \(\max _{i=1,\dots ,n} c_i\le 1\) which corresponds to require \((c_1,\dots ,c_n)\in [d,1]^{n}\). \(\square \)
5 Price of stability
In Section 3, we have seen that our game may have at most two Nash equilibria. Those equilibria represent the outcome of the strategic interaction of the players, i.e. the advisor and the customers (the individual investors), to maximize their own utilities. However, their decisions may differ from what could be achieved if the overall maximum utility would be sought. Therefore, the utility achieved under a Nash equilibrium could be not efficient on the overall. When we have a single Nash equilibrium, this loss of efficiency can be computed through the Price of Anarchy. Since we have more Nash equilibria here, that concept can be generalized into the Price of Stability (PoS) (Anshelevich et al. 2008). In this section, we compute the Price of Stability for our game.
For the price of stability, we adopt the definition introduced by Anshelevich et al. (2008):
Let us denote \(u_A(\mathbf{c },s,w,x):=u_A(\mathbf{c },s)\) and \(u_{CL_i}(c_i,d_i,s):=u_{CL_i}(c_i,s)\). We now calculate the utility functions outcomes in Nash equilibria \(P^*\) and \(P^\dagger \). Then:
and
The social welfare, i.e. the total utility of the agents, is:
Because of the mixed terms in \(c_i\) and s, the optimal solution of i-th customer depends on the choices made by the financial advisor.
Whether the maxima of SW belong to \({\mathcal {D}}\) or \(\partial {\mathcal {D}}\), is a question that is addressed and fully solved by Proposition 4 below.
In the following, for any complex number \(z=x+iy\) where x and y are real numbers, the absolute value or modulus of z is denoted |z| and is defined by \(|z|=\sqrt{x^{2}+y^{2}}\).
The following preliminary result concerns the roots of a quartic equation. A general method for solving quartic equations is found in Cardano’s Ars Magna, but it is attributed to Cardano’s assistant Ludovico Ferrari (1522-1565) (Leung et al. 1992).
Proposition 4
Let us consider
where \(\omega _0,\omega _4>0\), \(\omega _1,\omega _3\in {\mathbb {R}}\) (\(\omega _1,\omega _3\) both negative or both positive). Let also
The following are proved:
-
(i)
All the roots of (67) are non-real if and only if \(\varDelta >0\) and \(D> 0\).
-
(ii)
There exists at least one root of (67) which has positive real part.
-
(iii)
Let
$$\begin{aligned} \varOmega =\Bigl \{\omega _0,\omega _1,&\omega _3,\omega _4\, :\, \omega _4-|\omega _1|-|\omega _3|+\omega _0>0\, , \nonumber \\&4\omega _4-|\omega _1|-3|\omega _3|<0\, , \, (\varDelta \le 0\ \text {or}\ D\le 0)\Bigr \} \end{aligned}$$(69)be a subset of the admissible parameter region \({\mathcal {R}}\). Then, \(\forall \omega _i\in \varOmega \) all the roots of (67) have modulus \(> 1\).
Proof
The completed proof is given in Appendix. \(\square \)
We now turn our attention to finding the maximum of the function \((\mathbf{c },s)\rightarrow SW(\mathbf{c },s)\) in the set \({\mathcal {D}}\) described in (34).
Theorem 2
Let \(\varDelta \), D, P, R and \(\varOmega \) as in Proposition 4. Let also SW be the social welfare function as in (66) and let
Then the following claims hold.
-
i)
If \(\varDelta >0\) and \(D> 0\), or \(\omega _i\in \varOmega \) \(\forall i=0,\dots ,4\), the function SW attains its maximum in a point belonging to \(\partial {\mathcal {D}}\).
-
ii)
Let \(y=s-d\in [0,1]\). In all the other cases in which SW results concave, the function attains its maximum in a point \((c_1,\dots ,c_n,s)\in {\mathcal {D}}\) such that
$$\begin{aligned} \omega _4 y^4+\omega _3 y^3+\omega _2 y^2+\omega _1 y+\omega _0=0 \end{aligned}$$(71)and
$$\begin{aligned} c_1=\dots =c_n=\frac{2\beta w+2(\gamma +\zeta ) s +\frac{r_s-r_{d}}{s-d}}{2\beta +2(\gamma +\zeta )}\, . \end{aligned}$$(72)
Proof
Let us first consider the maximum points of SW that are internal to \({\mathcal {D}}\), namely in
Being SW of class \(C^\infty \), the maximum points in \({\text {int}}\left( {\mathcal {D}}\right) \) can be found amongst the stationary points, in other words amongst the points \((c_1,\dots ,c_n,s)\in {\text {int}}\left( {\mathcal {D}}\right) \) such that \(\nabla SW(c_1,\dots ,c_n,s) = (0,\dots ,0)\). We have that
thus
and
After rearranging the terms of the latter equation, we get:
which, replacing the new variable \(y=s-d\in [0,1]\), yields the polynomial equation (71), where \(\omega _0\), ..., \(\omega _4\) are described in (70). This proves claim ii).
However, as we can see, \(\omega _0\) and \(\omega _4\) are \(\ge 0\). Accordingly, by assumption of claim i) and from Proposition 4 the social welfare function does not assume (admissible) maxima in \({\mathcal {D}}\) and so we have to focus on \(\partial {\mathcal {D}}\). And this proves claim i). \(\square \)
According to Theorem 2, let us denote the maximum values assumed by function SW with \(\text {SW}_M\) and assume that it is global. Then, from the definition of PoS described by Eq. (63), we have
where the utility functions estimated in \(P^*\) and \(P^\dagger \) are shown in (64) and (65). By striving for the maximum social welfare, the central authority could achieve a more balanced solution where both the players (advisor and customers) get a reasonable amount of utility.
The computation of the social welfare allows us to consider the overall effect of the model’s parameter on the joint utilities of the advisor and the customer. In particular, we can measure the impact of the third stakeholder we have not considered explicitly so far, i.e., the bank. The bank’s role is represented by the coefficient \(\beta \) in Equation (3). The higher \(\beta \), the more the advisor’s utility is bent downwards if the customer drifts away from the bank’s goals. We expect then \(\beta \) to have a negative role on the social welfare. This is confirmed in Fig. 9, where we see that increasing \(\beta \) leads to reducing the social welfare, though at a lowering rate as \(\beta \) grows. Actually, we can spot a knee-like point at roughly \(\beta =1.5\): the impact of \(\beta \) seems to be relatively small beyond that knee point. Figure 9 has been plot for the following parameter settings: \(d=0.05469973\), \(x=0.7287941\), \(w=0.4678351\), \(n=10\), \(\gamma =0.3957729\), \(\alpha =3.881699\), \(r_d=0.5759116\), \(r_s=0.1377676\), \(\zeta =1.96627\). The Nelder-Mead method (a.k.a. the multidimensional simplex method) has been employed to look for the maximum social welfare with 10, 000 vertices Singer and Nelder (2009). The termination criterion was based on the standard error of function values of the current simplex with tolerance fixed to 0.05. In the same picture we have plotted a superimposed best-fit curve, which is a fifth-order polynomial.
6 Discussion and conclusion
Investors usually resort to financial advisors (paid by a bank) to improve their investment process until the point of complete delegation on investment decisions. Surely, financial advice is potentially an improving factor in investment decisions but, in the past, the media and regulators have often blamed biased advisors for manipulating the expectations of naive investors. Our ABM model allows us to investigate the effects of the bank’s actions and the potentially untruthful behaviour of financial advisors on customers’ investing decisions.
In our personal finance game, acceptable Nash equilibria arise if and only if \(r_s< r_{d_i}\), i.e., when the investor is naive about potential returns and expects a return bigger than what its advisor proposes.
Though we solved for the game and found two Nash equilibria (respectively corresponding to convergence on low and high opinions), one of these equilibria is not always acceptable. Actually, when the advisor is truthful, the only Nash equilibrium leads customers towards the advisor’s internal opinion. Again, if the advisor has a low incentive to influence the customers, a single Nash equilibrium is reached consisting in the advisor’s internal opinion. The same equilibria associated to advisor’s internal opinion survive when the sensitivity of customers to cognitive dissonance becomes strong. Cognitive dissonance provides customers with an incentive to modify their behavior to reduce the psychological cost of the lack of agreement between advisor and customers. Then this case corresponds to customers that are very sensitive to the difference between their opinion and the advisor’s stated opinion.
These results seem to describe an optimistic framework where the advisor follows her true opinion, but they are just asymptotic results and, in fact, describe extreme cases where, e.g., the advisor is fully truthful or customers are fully sensitive to the dissonance. Mathematically speaking, this means that \(\zeta ,\alpha \rightarrow +\infty \) and \(\gamma \rightarrow 0\). Instead, Eq. (33) tells another story: when we are not in extreme cases, the advisor’s stated opinion (s) can also be very far from her true opinion x and, at the same time, the opinion of the customer (c) could still be close to s. It represents the worst case because the advisor is untruthful and customers follow her recommendations.
Then, our game shows that customers may be led into decisions contrary to their interests, which could be avoided if a central authority would regulate such activities. That is illustrated by the use of the Price of Stability, which can allow us to investigate to which extent the efficiency of the game efficiency can be reduced when decisions are influenced by undue factors and cognitive dissonance plays a role. Though a closed-form expression of the Price of Stability seems to be unmanageable, we report a number of analytic results that can help towards that goal.
As a long-reaching perspective, these results show that legislation may be needed to protect naive individual investors from losing money as a result of overoptimistic recommendations or their unrealistic expectations. This would make it possible to act on the advisor side, improving her incentive to be truthful. A step forward could also be taken on the customer side by reducing the proportion of naive investors through an education program. This approach may also compel the investment bankers and stockbrokers to behave honestly, considering the cost to them of committing fraud through lost reputation or legal penalties (Huang et al. 2019; Karpoff 2012).
Our results, inspired by the social-psychological concepts of cognitive dissonance (on the customers’ side) and truthfulness (on the advisor’s side), confirm the insights carried out by Hong et al. (2008) (where, however, advisors are assumed to act truthfully), i.e., that naive investors may take advisors’ suggestions at face value and be driven into wrong investment decisions. Actually, after the latest financial bubbles, the public opinion has accused financial advisors of manipulating the expectations of naive investors (Ferguson 2012). While our model shows that advisors’ suggestions may unduly influence investors, we also observe that there is something deeper in the influence exerted by advisors on investors’ decisions. Actually, customers’ expectations may get very high (\(r_{d_i} \gg r_s \)), even without any explicit incentives on the part of analysts. Even if advisors are well-intentioned (i.e. they care about the welfare of their customers and want to disclose their true opinions), naive or greedy investors may trigger their inappropriate behaviour. For instance, Hong et al. (2008) have shown that well-intentioned advisors during the Internet bubble had an incentive to issue optimistic forecasts, based on their desire to be listened to by future advisees.
Our results somewhat complement the findings of Malmendier and Shanthikumar (2007), where advisors’ strong recommendations are literally followed by investors, showing an abnormally large reaction. Here, we show that biased information by advisors (typically providing an overestimation of some financial products’ value) may drive naive investors into a follower mode because of their desire to gain a higher return.
The results of the paper concern the special case of homogeneous investors. It would be interesting to extend the results of the paper to the more general case of non-homogeneous investors. We feel that a widespread use of simulation tools may help the investigation of this case for future papers.
It would also be interesting to study the case in which the client got (noisy) feedback from the returns of her investment that she made using the advisor’s input. In real life it’s never totally clear whether an advisor was good or lucky (and whether it was bad or unlucky). To model that, we also would have to give advise on more than one single scalar variable.
Besides, according to our model we can’t answer question like this: what parameters should we aim to change in order to increase the utility for the investor? Because we should look at investor expected return, given that her (behavioral) utility might make her do the wrong thing. But in our model the returns are fixed parameters, and could also be the results of erroneous considerations by, e.g., the customer (because of her dissonance). In other words, we chose not to introduce a mapping from opinions to returns. Our paper provides instead an example of how psychological theory can be incorporated into an ABM for personal finance decisions. In particular, a decision-making model, motivated by the social psychological concepts of cognitive dissonance and truthfulness, has been built.
Lastly, in this paper the financial advisor and the consumers move at the same time. As future extensions of our model, we might consider a delay between them; for example, given the story that the financial advisor moves first, the consumers observe her decisions and move second.
Additional works are surely required to address these cases.
Change history
22 July 2022
Missing Open Access funding information has been added in the Funding Note.
Notes
The authors refer to this class of games as discrete preference games.
The price of stability is a measure of the game efficiency that is commonly adopted instead of the price of anarchy when multiple Nash equilibria are present, and is defined as on the ratio between the social cost of the best Nash equilibrium and the optimal solution. We return to the subject in Section 5.
References
Akerlof, G. A., & Dickens, W. T. (1982). The economic consequences of cognitive dissonance. The American Economic Review, 72(3), 307–319.
Anshelevich, E., Dasgupta, A., Kleinberg, J., Tardos, E., Wexler, T., & Roughgarden, T. (2008). The price of stability for network design with fair cost allocation. SIAM Journal on Computing, 38(4), 1602–1623.
Aronson, E. (1992). The return of the repressed: Dissonance theory makes a comeback. Psychological Inquiry, 3(4), 303–311.
Auletta, V., Caragiannis, I., Ferraioli, D., Galdi, C., & Persiano, G. (2016). Generalized discrete preference games. IJCAI, 16, 53–59.
Auletta, V., Caragiannis, I., Ferraioli, D., Galdi, C., & Persiano, G. (2017). Robustness in discrete preference games. In Proceedings of the 16th Conference on Autonomous Agents and MultiAgent Systems, AAMAS ’17, pp 1314–1322
Bénabou, R. (2013). Groupthink: Collective delusions in organizations and markets. Review of Economic Studies, 80(2), 429–462.
Bernheim, B. D. (1994). A theory of conformity. Journal of Political Economy, 102(5), 841–877.
Bhawalkar, K., Gollapudi, S., & Munagala, K. (2013). Coevolutionary opinion formation games. In Proceedings of the Forty-fifth Annual ACM Symposium on Theory of Computing, STOC ’13, pp 41–50
Bilò, V., Fanelli, A., & Moscardelli, L. (2016). Opinion formation games with dynamic social influences. In Y. Cai & A. Vetta (Eds.), Web and internet economics (pp. 444–458). Berlin Heidelberg: Springer.
Bindel, D., Kleinberg, J., & Oren, S. (2015). How bad is forming your own opinion? Games and Economic Behavior, 92, 248–265.
Borwein, P., & Erdélyi, T. (2012). Polynomials and polynomial inequalities (Vol. 161). New York: Springer Science & Business Media.
Bruhn, K., & Steffensen, M. (2011). Household consumption, investment and life insurance. Insurance: Mathematics and Economics, 48(3), 315–325.
Buechel, B., Hellmann, T., & Klößner, S. (2015). Opinion dynamics and wisdom under conformity. Journal of Economic Dynamics and Control, 52(Supplement C), 240–257.
Busemeyer, J. R., Wang, Z., & Lambert-Mogiliansky, A. (2009). Empirical comparison of markov and quantum models of decision making. Journal of Mathematical Psychology, 53(5), 423–433.
Cenci, M., Corradini, M., Feduzi, A., & Gheno, A. (2015). Half-full or half-empty? a model of decision making under risk. Journal of Mathematical Psychology, 68–69, 1–6.
Chen, P. A., Chen, Y. L., & Lu, C. J. (2016). Bounds on the price of anarchy for a more general class of directed graphs in opinion formation games. Operations Research Letters, 44(6), 808–811.
ChiangLin, C. Y., & Lin, C. C. (2008). Personal financial planning based on fuzzy multiple objective programming. Expert Systems with Applications, 35(1), 373–378.
Chierichetti, F., Kleinberg, J., & Oren, S. (2018). On discrete preferences and coordination. Journal of Computer and System Sciences, 93, 11–29.
Cho, N., & Jang, T. S. (2019). Asset market volatility and new keynesian macroeconomics: A game-theoretic approach. Computational Economics, 54(1), 245–266.
Dacrema, E., & Benati, S. (2020). The mechanics of contentious politics: an agent-based modeling approach. The Journal of Mathematical Sociology, 44(3), 163–198.
Davis, A. (2004). Open secrets; head of the line: Client comes first? on wall street, it isn’t always so; investing own money, firms can misuse knowledge of a big impending order; mischief in the “back books.” The Wall Street Journal, 5, 71.
Degroot, M. H. (1974). Reaching a consensus. Journal of the American Statistical Association, 69(345), 118–121.
Dickinson, D. L., & Oxoby, R. J. (2011). Cognitive dissonance, pessimism, and behavioral spillover effects. Journal of Economic Psychology, 32(3), 295–306.
Fatas-Villafranca, F., Saura, D., & Vázquez, F. J. (2011). A dynamic model of public opinion formation. Journal of Public Economic Theory, 13(3), 417–441.
Ferguson, C. (2012). Inside job: The financiers who pulled off the heist of the century. New York: Simon and Schuster.
Ferraioli, D., Goldberg, P. W., & Ventre, C. (2016). Decentralized dynamics for finite opinion games. Theoretical Computer Science, 648, 96–115.
Festinger, L. (1962). Cognitive dissonance. Scientific American, 207(4), 93–106.
Fischer, R., & Gerhardt, R. (2007). Investment mistakes of individual investors and the impact of financial advice. In 20th Australasian Finance & Banking Conference, pp 1–33
Freixas, X., Laeven, L., & Peydró, J. L. (2015). Systemic risk, crises, and macroprudential regulation. Cambridge: Mit Press.
Friedkin, N. E., & Johnsen, E. C. (1999). Social influence networks and opinion change. Advances in Group Processes, 16, 1–29.
Gilboa, I., & Matsui, A. (1991). Social stability and equilibrium. Econometrica, 59(3), 859–867.
Gionis, A., Terzi, E., & Tsaparas, P. (2013). Opinion maximization in social networks, pp 387–395
Glass, C. A., & Glass, D. H. (2020). Social influence of competing groups and leaders in opinion dynamics. Computational Economics, 28, 1–25.
Groeber, P., Lorenz, J., & Schweitzer, F. (2014). Dissonance minimization as a microfoundation of social influence in models of opinion formation. The Journal of Mathematical Sociology, 38(3), 147–174.
Hegselmann, R., & Krause, U. (2005). Opinion dynamics driven by various ways of averaging. Computational Economics, 25(4), 381–405.
Hofbauer, J., & Sigmund, K. (2003). Evolutionary game dynamics. Bulletin of the American mathematical society, 40(4), 479–519.
Hong, H., Scheinkman, J., & Xiong, W. (2008). Advisors and asset prices: A model of the origins of bubbles. Journal of Financial Economics, 89(2), 268–287.
Houser, D., Xiao, E., McCabe, K., & Smith, V. (2008). When punishment fails: Research on sanctions, intentions and non-cooperation. Games and Economic Behavior, 62(2), 509–532.
Huang, Y. S., et al. (2019). Financial fraud and investor awareness. HKUST Institute for Emerging Market Studies, Tech rep
Jensen, N., & Steffensen, M. (2015). Personal finance and life insurance under separation of risk aversion and elasticity of substitution. Insurance: Mathematics and Economics, 62, 28–41.
Karpoff, J. M. (2012). The Oxford handbook of corporate reputation. Oxford: Oxford University Press.
Khrennikov, A., & Basieva, I. (2014). Possibility to agree on disagree from quantum information and decision making. Journal of Mathematical Psychology, 62–63, 1–15.
Kliger, D., & Qadan, M. (2019). The high holidays: Psychological mechanisms of honesty in real-life financial decisions. Journal of Behavioral and Experimental Economics, 78, 121–137.
Konicz, A. K., Pisinger, D., Rasmussen, K. M., & Steffensen, M. (2015). A combined stochastic programming and optimal control approach to personal finance and pensions. OR Spectrum, 3, 583–616.
Kraft, H., & Steffensen, M. (2008). Optimal consumption and insurance: A continuous-time markov chain approach. ASTIN Bulletin, 38(1), 231–257.
Krause, U. (2020). Reply on comments on “opinion dynamics driven by various ways of averaging’’ by youzong xu and yunfei cao. Computational Economics, 55(1), 327–334.
Leitner, S., & Behrens, D. A. (2014). On the robustness of coordination mechanisms for investment decisions involving ‘incompetent’agents. in artificial economics and self organization. New York: Springer.
Leitner, S., Rausch, A., & Behrens, D. A. (2017). Distributed investment decisions and forecasting errors: An analysis based on a multi-agent simulation model. European Journal of Operational Research, 258(1), 279–294.
Leung, K., Suen, S., & Mok, I. A. (1992). Polynomials and equations. Hong Kong: Hong Kong University Press.
Malmendier, U., & Shanthikumar, D. (2007). Are small investors naive about incentives? Journal of Financial Economics, 85(2), 457–489.
Martínez-Martínez, I. (2014). A connection between quantum decision theory and quantum games: The hamiltonian of strategic interaction. Journal of Mathematical Psychology, 58, 33–44.
Mastroeni, L., Vellucci, P., & Naldi, M. (2017). Individual competence evolution under equality bias. In 2017 European Modelling Symposium (EMS), pp 123–128
Mastroeni, L., Naldi, M., & Vellucci, P. (2019). Opinion dynamics in multi-agent systems under proportional updating and any-to-any influence (pp. 279–290). Cham: Springer International Publishing.
Mastroeni, L., Vellucci, P., & Naldi, M. (2019). Agent-based models for opinion formation: A bibliographic survey. IEEE Access, 7, 58,836-58,848.
Matsui, A. (1992). Best response dynamics and socially stable strategies. Journal of Economic Theory, 57(2), 343–362.
Mazar, N., & Ariely, D. (2006). Dishonesty in everyday life and its policy implications. Journal of Public Policy & Marketing, 25(1), 117–126.
McDonald, I. (2002). Brokers get extra incentive to push funds. The Wall Street Journal C, 17, 326.
McDonald, I. M., Nikiforakis, N., Olekalns, N., & Sibly, H. (2013). Social comparisons and reference group formation: Some experimental evidence. Games and Economic Behavior, 79, 75–89.
Mogiliansky, A. L., Zamir, S., & Zwirn, H. (2009). Type indeterminacy: A model of the KT(Kahneman-Tversky)-man. Journal of Mathematical Psychology, 53(5), 349–361.
Monica, S., & Bergenti, F. (2017). An analytic study of opinion dynamics in multi-agent systems. Computers & Mathematics with Applications, 73(10), 2272–2284.
Nagy, R. A., & Obenberger, R. W. (1994). Factors influencing individual investor behavior. Financial Analysts Journal, 50(4), 63–68.
Naldi, M. (2019). Interactions and sentiment in personal finance forums: An exploratory analysis. Information, 10(7), 237.
Pan, Z. (2012). Opinions and networks: how do they effect each other. Computational Economics, 39(2), 157–171.
Proskurnikov, A. V., Matveev, A. S., & Cao, M. (2016). Opinion dynamics in social networks with hostile camps: Consensus vs. polarization. IEEE Transactions on Automatic Control, 61(6), 1524–1536.
Rieger, M. O. (2017). Comment on cenci et al. (2015): “half-full or half-empty? a model of decision making under risk”. Journal of Mathematical Psychology, 81, 110–113.
Sharifi Kolarijani, M. A., Proskurnikov, A. V., & Mohajerin Esfahani, P. (2020). Macroscopic noisy bounded confidence models with distributed radical opinions. IEEE Transactions on Automatic Control, 65, 1.
Singer, S., & Nelder, J. (2009). Nelder-mead algorithm. Scholarpedia, 4(7), 2928.
Spiekermann, K., & Weiss, A. (2016). Objective and subjective compliance: A norm-based explanation of ‘moral wiggle room’. Games and Economic Behavior, 96, 170–183.
Steinbacher, M., & Steinbacher, M. (2019). Opinion formation with imperfect agents as an evolutionary process. Computational Economics, 53(2), 479–505.
Swenson, B., Murray, R., & Kar, S. (2018). On best-response dynamics in potential games. SIAM Journal on Control and Optimization, 56(4), 2734–2767.
Tignol, J. P. (2015). Galois’ theory of algebraic equations. Singapore: World Scientific Publishing Company.
Vellucci, P., & Zanella, M. (2018). Microscopic modeling and analysis of collective decision making: equality bias leads suboptimal solutions. Annali Dell’Universita’ Di Ferrara, 64(1), 185–207.
Wang, L., Markdahl, J., & Hu, X. (2011). Distributed attitude control of multi-agent formations. IFAC Proceedings Volumes, 44(1), 4513–4518.
Wolter, K. (2007). Introduction to variance estimation. Berlin/Heidelberg: Springer Science & Business Media.
Xu, Y., & Cao, Y. (2020). Comments on “opinion dynamics driven by various ways of averaging’’. Computational Economics, 55(1), 303–326.
Funding
Open access funding provided by Università degli Studi Roma Tre within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Contributions
All the authors provided an equal contribution to designing and carrying out the research, analysing the results, and writing the paper.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Informed consent
Informed consent was obtained from all individual participants included in the study.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Proof of Proposition 2
Let’s start to prove (41) and focus on (34). Then the admissible parameter region in which \(P^*\) is an acceptable Nash equilibrium derives from the following inequalities:
from which
By third equation of (P2.b) — \(d\le a\) — from \(a\ge 0\) and, from a’s definition in (18), the system (P2.b) becomes
Let us consider the first inequality of (P2.c):
It has solution:
which can be simplified in
Let us consider the second inequality of (P2.c),
whose solution is
i.e.
But the third inequality of the first system of (P2.cbb) is at odds with third inequality of (P2.c) and, hence, the (P2.cbb) comes down to
Let us consider the third inequality of (P2.c), which can be rewritten as follows
and, since \(d<x\) — by (P2.cbc) —, it follows that
from which
It should be noted that \(d\ne x\). Actually, if we substituted \(d=x\) in Eq. (P2.cc), we would get \(r_d-r_s+\frac{\gamma n}{\alpha } (r_d-r_{s}) \le 0\) which does not have solutions for \(r_s<r_d\).
We can rewrite system (P2.ccb) in the following way
The solutions of the first two inequalities intersect if \(\alpha > \gamma n\) while for the last one we have
which becomes
whose solution is
Then system (P2.ccb) has an empty solution if \(\alpha < \gamma n\) and becomes
for \(\alpha > \gamma n\). The solution of (P2.ccb) is empty for \(\alpha < \gamma n\) but, for \(\alpha > \gamma n\) it is
since we have that \(r_{d} -\frac{\alpha \zeta }{2\gamma n}(x-d)^2\le r_d-2\zeta \alpha ^2 \left( \frac{x-d}{\alpha +\gamma n}\right) ^2\) for each parameters’ values. We now focus on system (P2.ccc):
whose solution is
Accordingly, by merging (P2.ccbf) — for \(\alpha >\gamma n\) — and (P2.cccb) we obtain the solution of third inequality of (P2.c):
Hence, the solution of the third inequality of (P2.c) is
Let us observe that, by this, the system (P2.c) admits solution only if \(-\frac{1}{2}(x-d)^2\le 2 (1-d-x+dx)\), which is actually equivalent to \((x+d-2)^2\ge 0\). Moreover, \(r_d\ge r_{d} -\frac{\alpha \zeta }{2\gamma n}(x-d)^2\). By substituting (P2.cab), (P2.cbc) and (P2.cccd) in the system (P2.c) we obtain
and
Since \(d,x\in [0,1]\) we have that, for both systems, \(r_{d}+ \frac{2\alpha \zeta }{\gamma n} (1-d)(1-x)\ge r_d\). Moreover, to (P2.d) and (P2.e) should be added the conditions \(r_d\), \(r_s\in [0,1]\). Hence we obtained thesis (41).
We now come to prove (42), by focusing on (34). Then the admissible parameter region in which \(P^\dagger \) is an acceptable Nash equilibrium derives from the following inequalities:
from which
By third formula of system (P2.fa) — \(d\le b\) — we can rearrange its fourth and fifth equations as, respectively, \(-(b-d)^2 \le \frac{1}{2\zeta }(r_s-r_{d})\) and \(r_s< r_{d}\). Moreover, \(b\ge 0\) if
but since \(d,x\ge 0\) and \(r_s< r_{d}\), the latter becomes \(r_{d} -\frac{\alpha \zeta }{2\gamma n}(x-d)^2 \le r_s\). Then the system (P2.fa) can be rewritten as
or, from b’s definition in (18)
Let us consider first inequality of (P2.h):
We have
System (P2.haa) does not admit solution because \(d,x\in [0,1]\) while the solution of (P2.hab) comes down to
which hence is the solution of first inequality of system (P2.h).
Let us consider the second inequality of system (P2.h),
Its solution is
Let us consider the third inequality of system (P2.h):
It can be rewritten as follows
and, since \(d< x\) — by (P2.hba) —, we obtain
from which
It should be noted that \(d\ne x\) because, if we substituted \(d=x\) in Eq. (P2.hca), we would get \((r_s-r_d)\left[ 1+\frac{\gamma n}{\alpha }\right] \ge 0\) which does not have solutions for \(r_s<r_d\).
We can rewrite system (P2.hcc) in the following way
For the last inequality we have
which becomes
whose (acceptable) solution is
Hence we rewrite system (P2.hcd) as
Since
for \(\alpha <\gamma n\), and
for \(\alpha >\gamma n\), the solution of system (P2.hch) and then of the third inequality of system (P2.h), is empty if \(\alpha >\gamma n\) but it equals
Accordingly, by substituting (P2.hac), (P2.hba) and (P2.hck) into the system (P2.h) we obtain
which turns into
Hence we obtained thesis (42).
1.2 Proof of Proposition 4
According to the theory of quartic equations (Tignol 2015), all the roots of (67) are non-real only in the following cases
-
\(\varDelta > 0\) and \(D> 0\)
-
\(\varDelta > 0\) and \(P> 0\)
-
\(\varDelta =0\) and \(D=0\) and \(P> 0\) and \(R=0\).
Since \(P=-3\omega _3^2< 0\), we see that all the roots of (67) are non-real if and only if \(\varDelta >0\) and \(D> 0\).
For the proof of (ii) let f(z) be LHS of (67). Then, \(f'(z)=4\omega _4z^3+3\omega _3z^2+\omega _1\). We have that \(f'(z)=0\) has only one real root because the discriminant of the cubic equation \(f'(z)=0\), \(\varDelta _3\) (Tignol 2015), is negative
It follows that the number of the real roots of the quartic equation (67) is at most two.
Our proof proceeds by reductio ad absurdum. Let us assume that all the roots of (67) have negative real part. The roots may be a, b, \(c+di\), \(c-di\) where a, b, c, \(d\in {\mathbb {R}}^+\) with \(a< 0\), \(b< 0\), \(c< 0\), \(d> 0\) or \(a+bi\), \(a-bi\), \(c+di\), \(c-di\) where a, b, c, \(d\in {\mathbb {R}}^+\) with \(a< 0\), \(b> 0\), \(c< 0\), \(d> 0\).
Since the coefficient of \(z^2\) is 0, we get, by Vieta’s formulas (Borwein and Erdélyi 2012, Newton’s Identities),
for the first case and
for the second. In both cases, the LHS equals 0 while the RHS is positive. This is impossible.
For the proof of (iii) we already know, from (ii), that \(f'(z)=0\) has only one real root. Besides, we have \(f''(z)=0\) \(\iff \) \(z=-\frac{\omega _3}{2\omega _4}\) and \(z=0\).
Now, depending on the sign of \(\omega _1\) and \(\omega _3\) we have two different cases.
Case 1. Let \(\omega _1> 0\) and \(\omega _3> 0\). Since \(f'(0)=\omega _1> 0\), we see that \(f'(z)=0\) has only one real root \(z=\alpha \) where \(\alpha < 0\). It is necessary that \(f(-1)=\omega _4-\omega _3-\omega _1+\omega _0> 0\) and that \(f(z)=0\) has at least one real root, i.e. \(\varDelta \le 0\) or \(D\le 0\) from (i). Since we have \(-\frac{\omega _3}{2\omega _4}< 0\) and \(f'(0)=\omega _1> 0\) considering graphs in Fig. 10, we see that it is necessary that \(f'(-1)=-4\omega _4+3\omega _3+\omega _1> 0\).
On the other hand, if \(f(-1)> 0\), \(f'(-1)> 0\) and \((\varDelta \le 0\) or \(D\le 0)\) then, we see that all the real roots of (67) have modulus greater than 1.
Case 2. Let \(\omega _1< 0\) and \(\omega _3< 0\). Since \(f'(0)=\omega _1< 0\), we see that \(f'(z)=0\) has only one real root \(z=\beta \) where \(\beta > 0\). It is necessary that \(f(1)=\omega _4+\omega _3+\omega _1+\omega _0> 0\) and that \(f(z)=0\) has at least one real root, i.e. \(\varDelta \le 0\) or \(D\le 0\) from (i). Since we have \(0< -\frac{\omega _3}{2\omega _4}\) and \(f'(0)=\omega _1< 0\) considering graphs in Fig. 11, we see that it is necessary that \(f'(1)=4\omega _4+3\omega _3+\omega _1< 0\).
On the other hand, if \(f(1)> 0\), \(f'(1)< 0\) and (\(\varDelta \le 0\) or \(D\le 0\)) then, we see that all the real roots of (67) have modulus greater than 1.
From the two cases, all the real roots of (67) have modulus \(> 1\) whenever \(\omega _0\), \(\dots \), \(\omega _4\) belong to the subset \(\varOmega \).
1.3 Derivation of the volatility expression
Let us substitute (13) in (5):
Let us also consider \(r_s\) and \(r_{d}\) as two independent random variables. Then the expected value of \(u_{CL}\) is:
Moreover,
Then, the expected value of \(u_{CL}^2\), i.e. \({\text {E}}[u_{CL}^2]\), is:
Since the standard deviation \(\sigma _X\) of a random variable X is defined as \(\sqrt{{\text {E}} \left[ X^{2}\right] -({\text {E}} [X])^{2}}\) and from \({\text {cov}}(X^2,X)={\text {E}}[X^3]-{\text {E}}[X^2]{\text {E}}[X]\), we obtain:
Lastly, since \(r_s\) and \(r_{d}\) as two independent random variables, \({\text {E}}[r_d^2] {\text {E}}[r_s^2]={\text {E}}[r_d^2 r_s^2]\) and \({\text {E}}[r_{s}]{\text {E}}[r_{d}]={\text {E}}[r_{s} r_{d}]\), then
Eq. (A3.f) assumes both returns as random variables. Let us now consider only one of them as a random variable and keep the other deterministic. Then:
We can obtain a simpler, though approximate, expression by applying a method based on Taylor’s series expansion Wolter (2007). Since we assume that the two expected returns \(r_s\) and \(r_d\) are independent, the variance of the utility of customers is
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mastroeni, L., Naldi, M. & Vellucci, P. Personal Finance Decisions with Untruthful Advisors: An Agent-Based Model. Comput Econ 61, 1477–1522 (2023). https://doi.org/10.1007/s10614-022-10256-4
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10614-022-10256-4