Bayesian Estimation of Agent-Based Models via Adaptive Particle Markov Chain Monte Carlo

Abstract

Over the last decade, agent-based models in economics have reached a state of maturity that brought the tasks of statistical inference and goodness-of-fit of such models on the agenda of the research community. While most available papers have pursued a frequentist approach adopting either likelihood-based algorithms or simulated moment estimators, here we explore Bayesian estimation using a Markov chain Monte Carlo approach (MCMC). One major problem in the design of MCMC estimators is finding a parametrization that leads to a reasonable acceptance probability for new draws from the proposal density. With agent-based models the appropriate choice of the proposal density and its parameters becomes even more complex since such models often require a numerical approximation of the likelihood. This brings in additional factors affecting the acceptance rate as it will also depend on the approximation error of the likelihood. In this paper, we take advantage of a number of recent innovations in MCMC: We combine Particle Filter Markov Chain Monte Carlo as proposed by Andrieu et al. (J R Stat Soc B 72(Part 3):269–342, 2010) with adaptive choice of the proposal distribution and delayed rejection in order to identify an appropriate design of the MCMC estimator. We illustrate the methodology using two well-known behavioral asset pricing models.

1 Introduction

Over the last decade, agent-based models in economics have reached a state of maturity that brought the tasks of statistical inference and goodness-of-fit of such models on the agenda of the research community. Using mostly relatively simple models of financial markets, a variety of statistical tools have meanwhile been developed to this end (cf. Lux and Zwinkels, 2018, for a review of this literature). Most available papers have used a frequentist approach adopting either likelihood-based algorithms or simulated moment estimators. In contrast, Bayesian estimation approaches can be found in very few papers only. This is surprising insofar as Bayesian methods have become the dominating paradigm in estimation of contemporaneous dynamic general equilibrium models in macroeconomics (cf., Herbst and Schorfheide, 2015).

At the time of writing, to my knowledge only three contributions exist applying a Bayesian methodology to agent-based models: Grazzini et al. (2017), Lux (2018) and Bertschinger and Mozzhorin (2021). Grazzini et al. (2017) use both Markov Chain Monte Carlo (MCMC) and Approximate Bayesian Computation (ABC) to estimate the posterior of the parameters of a medium-scale macroeconomic model with heterogeneous expectations. In contrast to traditional MCMC, the ABC algorithm uses auxiliary measures of fit rather than the likelihood to sample from the posterior distribution (cf. Sisson et al., 2007). Since the likelihood is often not available in analytical form in agent-based models, the authors adopt a kernel density estimator to approximate this component of the MCMC algorithm.

Lux (2018) applies both frequentist and Bayesian methods for estimation of two basic financial ABMs. All his implementations of various estimators are based on an approximation of the likelihood using the concept of a particle filter as introduced in the statistical literature by Gordon et al. (1993) and Kitagawa (1996). This approach presumes a state-space representation of the underlying model (which is natural for many ABMs). A particle filter approximation is initiated by sampling the initial values of the particles for the hidden states of the model from their unconditional distribution. The collection of particles is, then, updated via sampling-importance-resampling over the length of the available time series of the observable variables. Andrieu et al. (2010) show that when using the particle filter within MCMC the resulting Markov chain converges to the posterior under very general conditions on the structure of the likelihood and the proposal density. More generally, they demonstrate that using an unbiased estimate of the likelihood (which is, for instance, the case with the particle filter), leaves the equilibrium distribution of the posterior of the MCMC chain unchanged.¹ One advantage of using a particle filter approximation of the likelihood within an MCMC algorithm is that together with estimation of the posterior distribution it also allows for filtering of the time variation of the unobservable variables which are often at the center of interest in ABMs (e.g. agents’ expectations, opinions or strategies).

One problem of traditional MCMC and PMCMC alike is finding a parametrization that leads to a reasonable acceptance probability for new draws from the proposal density. While with an analytical likelihood this requires an appropriate choice of the proposal density and its parameters, in PMCMC the number of particles enters as another factor that influences the acceptance rate as it determines the extent of approximation error of the likelihood. Most empirical applications first run a number of trials to determine an appropriate specification for the proposal density before turning to estimation proper. Doing so, Lux (2018) identifies scenarios with conventional acceptance rates for the three-parameter model of Alfarano et al. (2008), but admits that he had been unable to find a satisfactory combination of proposal density and number of particles for a second model with four parameters based upon Franke and Westerhoff (2012).

He states that in all trial runs, the acceptance rate remained extremely low. While this would not impede the statistical validity of the approach as established by Andrieu et al. (2010), it makes its implementation impractical as very long simulation runs would be required to compensate for a low acceptance rate.

The very problem of low acceptance rates is addressed by the third entry on this topic in the recent literature by Bertschinger and Mozzhorin (2021). These authors use so-called Hamiltonian MCMC for Bayesian estimation of two agent-based models. Hamiltonian MCMC attempts to find regions with high probabilities of acceptance by introducing an auxiliary momentum variable (cf., Neal, 2011). Adopting the principle of joint preservation of volume in conservative dynamic systems, the dynamics of the parameters and their associated momentum variables is modeled as a Hamiltonian system which when used to draw new proposals of the parameters, should select these approximately along an iso-line of equal probability and, thus, should guarantee high acceptance rates. Unfortunately, this approach requires numerical derivatives of the log probability density to implement the Hamiltonian dynamics as a conservative system of differential equations.

This is particularly problematic in the present setting: First, in most agent-based models with a finite number of agents, the probabilistic elements in the individuals’ behavior will make any statistics derived from the underlying process non-smooth. For instance, if agents’ behavior is described by probabilities to switch from one behavioral alternative to another, even with a fixed sequence of random numbers, a discrete change will happen at a certain value of any one of the parameters of the model. Second, the same type of discrete changes happens in the particle filter in the resampling step when the acceptance of any particle to the new population is decided via multinomial draws based on their relative likelihood (implying that the Hamiltonian approach is generally not computable with a particle filter approximation). The first type of complication is not relevant for the models explored in Bertschinger and Mozzhorin (2021) since these are either based on a limiting case with an infite number of agents or on a dynamic process with two uniform groups of agents without consideration of individual agents per se. The examples in Lux (2018), however, do consider a finite number of autonomous agents and, thus, the elegant approach of Hamiltonian MCMC appears unfeasible because of the lack of smoothness of the numerical approximation of the likelihood. To make MCMC work, we, therefore, have to choose an alternative route: adaptive adjustment of the parameters of the proposal density.

The rest of the paper proceeds as follows: The next section introduces the principles of PMCMC together with algorithms for the adaptive choice of the proposal density and delayed rejection. Delayed rejection generates a second proposal from a different transition kernel if the first one is rejected, and, thus, helps to increase the acceptance rate of the Markov Chain. Section 3 provides a short outline of the theoretical asset-pricing models we use as test cases for adaptive PMCMC. Section 4 provides Monte Carlo results on the performance of the algorithms, and Sect. 5 presents empirical results obtained for data of three major stock markets. Section 6 provides conclusions.

2 Adaptive Markov Chain Monte Carlo for Agent-Based-Models

We set the stage by introducing the seminal framework of MCMC. Markov Chain Monte Carlo consists in generating a Markov chain that converges to a certain invariant distribution. In this context, the distribution we are after is the posterior distribution of the parameters of an agent-based model. To this end, one needs to introduce a prior distribution, denoted by $p(\cdot )$ in Eq. (1) below, from which an initial set of parameters, say $\theta _0$, is drawn. One then determines the marginal likelihood of the observed data under this initial choice of parameters, which we denote by $P_{\theta _0}(y)$. For typical agent-based-models, no closed-form likelihood function is available for this evaluation so that we resort to an unbiased estimation of the likelihood using the particle filter.

The Markov chain develops with draws from a proposal density $g(\theta _{\xi } | \theta _{\xi -1})$ with $\xi$ the sequential order of the chain. New draws from this proposal density, say $\theta ^*$, are accepted with a probability:

$$\begin{aligned} \alpha (\theta ^*|\theta _{\xi -1}) = min \left\{ \frac{P_{\theta ^*}(y) p(\theta ^*) g(\theta _{\xi -1}|\theta ^*)}{P_{\theta _{\xi -1}}(y) p(\theta _{\xi -1}) g(\theta ^*|\theta _{\xi -1})} ,1 \right\} \end{aligned}$$

(1)

If the new draw is not accepted, the chain will continue with a replication of the previous values, $\theta _{\xi }=\theta _{\xi -1}$. The strength of MCMC lies in the fact, that the chain generated in this way will converge to the limiting invariant distribution under very mild regularity conditions on the marginal likelihood of the proposal density.

Difficulties often appear in the practical implementation. Namely, any particular choice of starting value will lead to a more or less extended transient prior to convergence to the invariant distribution. Second, the overall acceptance rate should be high enough to provide for sufficient exploration of the invariant distribution. If, in contrast, the acceptance rate is too low, the overwhelming majority of computations will be wasted as their draws will not be accepted and, for a finite run time of the Markov process, the few accepted proposals will only provide an incomplete representation of the posterior density. To achieve the goal of a sufficiently high acceptance rate, fine-tuning of the parameters of the proposal density is required. One simple approach consists in conducting some preliminary experiments to identify a set of parameters of the proposal density that lead to an acceptable dynamics of the Markov chain. However, the higher the number of parameters of the invariant distribution, the more time-consuming this step becomes. It might, therefore, be desirable to choose the parameters adaptively in response to the observed rate of acceptances. Luckily, the convergence properties of MCMC can even be maintained under adaptation provided some minimal conditions are fulfilled. The basic requirement is that the degree of adaptation goes to zero as $\xi \rightarrow \infty$ (cf. Andrieu and Thomas, 2008). Rules with decreasing intensity of adaptation are easy to construct. In most applications of MCMC, the proposals are following a random walk, i.e. $\theta ^*$ is drawn from a multivariate Normal distribution, $\theta ^* \sim N(\theta _{\xi _-1} , \Sigma )$. The focus of adaptation would then be the covariance matrix $\Sigma$. In fine-tuning the acceptance probability, it would be important to adjust $\Sigma$ in a way to reflect the unknown covariance structure of the invariant posterior distribution. To see this, consider as an example a bivariate Normal with high degree of correlation. It is obvious that a proposal distribution with off-diagonal elements equal to zero would be accepted the less often the higher the correlation between parameters and the higher the dimension of the parameter space.

Andrieu and Thomas (2008) and Rosenthal (2011) provide details of various algorithms for adaptive choice of the proposal density. Typically, these algorithms use iterative estimates of the covariance of the target invariant distribution. Let $\mu$ denote the mean and ${\hat{\Sigma }}$ the covariance of the sampled realizations of the vector of parameters, $\theta$, over the Markov chain. One would, then, obtain an update of the covariance matrix over the course of the simulation using:

$$\begin{aligned} \mu _{\xi +1}= & {} \mu _{\xi } + \gamma _{\xi +1} (\theta _{\xi +1} - \mu _{\xi }) \\ {\hat{\Sigma }}_{\xi +1}= & {} {\hat{\Sigma }}_{\xi } + \gamma _{\xi +1} \left( (\theta _{\xi +1} - \mu _{\xi })(\theta _{\xi +1} - \mu _{\xi })^T - {\hat{\Sigma }}_{\xi }\right) .\nonumber \end{aligned}$$

(2)

In order to ensure convergence of the Markov chain, the degree of adaptation as incorporated in $\gamma _{\xi }$ should vanish asymptotically. Hence, $\gamma _{\xi }$ should be chosen so that $\gamma _{\xi }\rightarrow 0$ for $\xi \rightarrow \infty$. With this adaptive estimation of the covariance of the posterior distribution, new proposals would be drawn according to $\theta ^* \sim N(\theta _{\xi }, \frac{2.38^2}{d}{{\hat{\Sigma }}}_{\xi })$ with d the dimension of the parameter space. The scaling by $\frac{2.38^2}{d}$ is motivated by theoretical results showing that under certain conditions this scaling leads to an optimal proposal distribution in terms of convergence speed and asymptotic variance (cf. Rosenthal, 2011).

Since this optimal scaling has been obtained for relatively simple cases, it needs, however, not necessarily apply to the posterior distribution of the parameters of a complex agent-based model. Alternatively, one might then introduce an arbitrary scaling parameter $\lambda _{\xi }$ and draw proposals according to $\theta ^* \sim N(\theta _{\xi }, \lambda _{\xi }{\hat{\Sigma }}_{\xi })$. The scaling could then vary according to the observed acceptance rate $\alpha$ and a predetermined target $\alpha ^*$:

$$\begin{aligned} \ln (\lambda _{\xi +1}) = ln(\lambda _{\xi }) + \gamma _{\xi +1} (\alpha _{\xi } - \alpha ^*) \end{aligned}$$

(3)

where $\alpha _{\xi }$ is the acceptance rate of new proposals until iteration $\xi$ and $\alpha ^*$ is often chosen as 0.234 reflecting what has been found to be optimal in certain analytically accessible cases (again, this number need not be optimal for our more complex applications). Equation (3) indicates that the covariance matrix of the proposals should be linearly increased if the acceptance rate is deemed too high (as larger changes would make acceptance less likely) and vice versa. Note that the task of guiding the proposal distribution towards a satisfactory acceptance level could not be fulfilled by the adjustment of the covariance matrix as per Eq. (2) alone as this part of the adaption would rather have a tendency to preserve the current rate of acceptances.

Besides adaptation of the scale of the proposal distribution, we will also implement another variation of the baseline MCMC adjustment that has been introduced in recent literature, the so-called delayed rejection. First proposed by Tierney (1994), this generalization allows for subsequent moves after rejection of a proposal in the first round. Here we will confine ourselves to adding a second stage of another new proposal. The distribution of the second proposal need not be identical to that of the first stage, and indeed, it will typically be useful to choose a different distribution. Denoting the stage two proposal distributions by $g^{(2)} (\theta _{\xi }|\theta _{\xi -1})$ and the resulting proposal by $\theta ^{**}$, the delayed rejection adjustment works in the following way: (i) draw $\theta ^{*}$ from g() and accept $\theta ^{*}$ with probability $\alpha$ as given in Eq. (1). If $\theta ^{*}$ in rejected, draw another proposal $\theta ^{**}$ from $g^{(2)} ()$ and accept it with probability $\beta$ given by:

$$\begin{aligned} \beta (\theta ^{**}|\theta ^{*},\theta _{\xi -1}) = min\left\{ \frac{P_{\theta ^{**}}(y) g(\theta ^{*}|\theta ^{**})(1-\alpha (\theta ^{*}|\theta ^{**})) g^{(2)}(\theta _{\xi -1}|\theta ^{**})}{P_{\theta _{\xi -1}}(y) g(\theta ^{*}|\theta _{\xi -1})(1-\alpha (\theta ^{*}|\theta _{\xi -1})) g^{(2)} (\theta ^{**}|\theta _{\xi -1})} ,1 \right\} \end{aligned}$$

(4)

Haario et al. (2006) propose to combine adaptation and delayed rejection to enhance the efficiency of MCMC estimation (denoting the combination by DRAM: Delayed Acceptance Adaptive Metropolis).

3 Models

Our basic test case in this paper are two alternative models of asset-price dynamics including non-fundamental factors based on Franke and Westerhoff (2012) and Alfarano et al. (2008).

The present version of the model of Franke and Westerhoff² is a slightly modified one that has also been used already by Lux (2018). It uses the distinction between the notorious fundamentalists and chartists that are characterized by their excess demand functions:

$$\begin{aligned} ED_{f,t}&= N_{f,t} a(p_{f,t} - p_t), \end{aligned}$$

(5)

$$\begin{aligned} ED_{c,t}&= N_{c,t} b(p_{t-1} - p_{t-2}) \end{aligned}$$

(6)

with $N_{f,t}$ and $N_{c,t}$ their respective numbers at time t and a, b the elasticities of their demand functions. $p_{f,t}$ and $p_t$ denote the log fundamental value and the log price, respectivity.

Defining $c = \dfrac{b}{a}$ and $z_t = \dfrac{N_{c,t}}{N}$ $(N = N_{f,t} + N_{c,t})$, the log price is determined in market equilibrium with zero excess demand by:

$$\begin{aligned} p_t = p_{f,t} + \frac{z_t}{1-z_t} c(p_{t-1} - p_{t-2}). \end{aligned}$$

(7)

If the log fundamental value is assumed to follow a Brownian motion with increments $\varepsilon _{f,t} \sim N(0,\sigma _f)$, we obtain returns $r_t = p_t - p_{t-1}$ obeying:

$$\begin{aligned} r_t = \varepsilon _{f,t} + \frac{z_t}{1-z_{t}} c(p_{t-1} - p_{t-2}) - \frac{z_{t-1}}{1-z_{t-1}} c(p_{t-2} - p_{t-3}). \end{aligned}$$

(8)

The observable variable $r_t$ is, thus, a noisy signal for the realization of the latent variable $z_t$ with the similarity unobservable fundamental innovations constituting the noise that distorts the signal.

In one version of their battery of models, Franke and Westerhoff (2012) assume that the fractions of fundamentalists and chartists follow a herding process with simple transition rates between both groups. Denoting $\pi _{c,t}(\pi _{f,t})$ the transition rate for a change of a fundamentalist to a chartist strategy (and vice versa), a baseline herding dynamics can be expressed as:

$$\begin{aligned} \pi _{c,t} = \nu {\mathrm {e}}^{\alpha x_t}, \ \pi _{f,t} = \nu {\mathrm {e}}^{-\alpha x_t} \end{aligned}$$

(9)

with

$$\begin{aligned} x_{t} = \frac{N_{c,t} - N_{f,t}}{N} = 2z_t - 1 \, . \end{aligned}$$

(10)

This model comes with four parameters that one would like to estimate when confronting the model with data: the ratio of demand elasticities of both groups of traders, c, the standard deviation of the distribution of the fundamental shocks, $\sigma _f$, the constant $\nu$ that expresses the overall tendency of agents to change their strategies, and $\alpha$, the herding coefficient. In contrast to Franke and Westerhoff (2012), we apply the transition rates (9) to a true ensemble of agents (using $N = 100$) while the original paper has assumed an infinite population. This implies that the latent state variable $z_t$ is driven not by a single noise factor, but by the joint distribution characterizing N Poisson processes with time-varying intensities as defined in Eq. (9). Lux (2018) found this prototype model combining chartists/fundamentalists and herding dynamics to be inferior to a simple framework proposed by Alfarano et al. (2008). The basic aim here is to revisit this comparison on the base of Bayesian estimation instead of the frequentist model comparison of the earlier paper.

The Alfarano et al. (2008) framework includes the same demand of fundamentalists, but assumes that the second group are pure noise traders and that agents do not switch between the groups of noise traders and fundamentalists. The former are either optimistic or pessimistic and their attitude is determined by a similar contagion dynamics as has been assumed for the choice of trading strategy in the modified Franke/Westerhoff approach.

Noise traders’ and fundamentalists’ excess demand are given by:

$$\begin{aligned} ED_c&= T_c y_t , \end{aligned}$$

(11)

$$\begin{aligned} ED_f&= T_f(p_{f,t}-p_t) \end{aligned}$$

(12)

with $T_c,T_f$ denoting trading volumes of both groups, respectively, and the sentiment index $y_t$ being defined as

$$\begin{aligned} y_t = \frac{n_{+,t} - n_{-,t}}{N_c} \end{aligned}$$

(13)

with $n_{+,t}(n_{-,t})$ the currently optimistic (pessimistic) individuals among the constant overall number of noise tenders, $N_c$. The equilibrium price in this model is obtained as:

$$\begin{aligned} p_t = p_{f,t} + \frac{T_c}{T_f} y_t. \end{aligned}$$

(14)

Hence, returns are given by:

$$\begin{aligned} r_t = \varepsilon _{f,t} + \frac{T_c}{T_f}(y_t - y_{t-1}) \end{aligned}$$

(15)

Again, asset returns are a noisy signal for the realization of the latent variable, now denoted by $y_t$.

The within-group dynamics are determined by the following transition rates:

$$\begin{aligned} \pi _{+,t}&= a + bn_{+,t} \;, \end{aligned}$$

(16)

$$\begin{aligned} \pi _{-,t}&= a + bn_{-,t} \end{aligned}$$

(17)

for the switch from pessimistic to optimistic opinion $(\pi _{+,t})$ and vice versa. It includes a autonomous propensity to change opinion, a, and one that is driven by the current majority, b.

Normalizing $\frac{T_c}{T_f} = 1$, the model leaves the parameters, $\sigma _f$, a and b to be estimated. Again, to preserve the spirit of a ‘true’ ABM, a finite number of agents $(N_c = 100)$ is used to simulate the time-variation of the latent variable $y_t$.

The present models have been chosen for our study because their dynamics is genuinely driven by the interactions of the agents and their characteristic features would not be preserved by a reduction to their deterministic counterparts. Indeed, while there exists a rich literature of heterogeneous agent models in finance with highly complex dynamics of their deterministic ‘skeleton’ (surveyed, for instance by Dieci and He 2018), the present models have relatively simple deterministic counterparts, and their main attraction comes from the interplay of the stochastic factors governing the interaction of agents. Many of the models surveyed by Dieci and He are based on the deterministic trajectories of occupation numbers of different groups within an infinite population, leading to cyclical or chaotic asset price dynamics. In contrast, in the above models, the finiteness of the pool of agents and their autonomous behaviour is crucial to the dynamic outcome (and therefore the stochastic elements cannot be reduced to an additive factor superimposed on the deterministic skeleton).

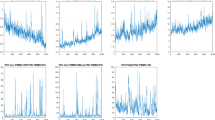
Figure 1 serves to illustrate this feature. In this figure, we exhibit a typical simulation of both the models by Alfarano et al. (2008) and Franke and Westerhoff (2012). Both realisations show the proximity of the model-generated returns to typical such time series from financial markets. In particular, both synthetic time series show clear signs of volatility clustering or ARCH-type effects, and, therefore, could count as possible behavioural explanations of these ubiquitous stylized facts. The clustered volatility is intrinsic to the stochastic nature of these models and would not be present in a reduction to a deterministic skeleton plus additive noise. Lux (1997) shows how ARCH-type behaviour of second moments emerges generically from the interaction of the agents in models with a stochastic formalisation of a finite ensemble of agents.

As shown in Alfarano et al. (2008), a deterministic approximation of their model (its mean-valued dynamics) would simply lead to a mean-reverting autoregressive process. Similarly, the model of Franke and Westerhoff (2012) would give rise to either a unique fundamental equilibrium or two speculative market equilibria (one with overvaluation, the other with undervaluation) depending on whether the parameter $\alpha$ is below or above unity.

Fig. 1

Simulated returns from the models of Franke and Westerhoff and Alfarano et al. Parameters are the same as used in the computational experiments with the PMCMC estimator in Sect. 4

In all these cases, the deterministic ‘skeleton’ would just consist in a monotonic convergence from any initial condition to one of these equilibria (the nearest one in the case of two equilibria).³ Adding a noise factor, the returns would just reflect the realisations of this noise factors as fluctuations around a constant equilibrium value for the price. It is this irreducibility of the agent-based component of the above models that motivates our focus on these particular examples from the wide spectrum of heterogeneous agent models in finance.⁴

Another welcome property of the present models is that despite the complex interactions of an ensemble of agents, they constitute well-behaved stochastic processes. Both models introduced above are actually Markov processes, quite in contrast to models that are reduced to a deterministic dynamics of the fractions of agents in different groups that often generate chaotic trajectories (cf. Dieci and He, 2018). The underlying agent-based processes characterized by the transition rates of Eqs. (9), and (16) and (17), respectively, are easily seen to be aperiodic and recurrent, and all their states are irreducible which guarantees ergodicity of the Markov chain. This ergodicity should carry over to the processes governing returns (Eqs. 8 and 15, respectively) that consist of normally distributed changes of the fundamentals and a sentiment factor generated by the agent-based dynamics. Ghonghadze and Lux (2016) compute various moments of the returns process of the model of Alfarano et al. (Eq. 15). From their results it can be inferred that the parameters a, b and $\sigma _f$ of this model are all identified, for instance, by a moment estimator using the variance, kurtosis, and the autocovariance of squared returns. Since in MCMC we are using information about the complete shape of the distribution of returns, identification necessarily carries over to the present framework as well.⁵

4 Simulation Results

In the following we provide details on explorative simulations of Adaptive Markov Chain Monte Carlo estimation using both adaptation of the proposals and delayed rejection. For the adaptive component, we set $\gamma _{\xi }$ in Eqs. (2) and (3) as follows:

$$\begin{aligned} \gamma _{\xi } = \dfrac{1}{(\xi -\xi _{Trans})^{\eta }} \end{aligned}$$

(18)

with $\xi _{Trans}$ the number of iterations during the burn-in phase of the MCMC run. Since with $\eta >0$ adaptation vanishes asymptotically, this extension of PMCMC preserves the convergence of the Markov chain. Experimentation showed that the results were not very sensitive to $\eta$ if this parameter were not chosen too large. In the results reported below, $\eta = 0.1$ has been used.

In the following, we first report the results of two sets of computational experiments for the modified model of Franke and Westerhoff (2012). All simulations have the purpose of estimating the posterior distribution of the parameters on the base of returns generated for a typical length of financial time series with $T=2000$ observations. The underlying parameters were: $\nu =1$, $\alpha =0.85$, $c=0.5$, $\sigma _{f}=0.03$ and $N=100$. In the first series of experiments we run 10 Markov chains with a length of 7500 iterations and the number of particles $B=1000$. We consider the first 1500 data points as transient observations. Since with little experience on the estimation of this model, we have hardly any guidance for the prior, we choose a uniform prior over the interval [0,5] for parameters $\nu , \alpha$ and c, and a uniform prior over [0,$\sigma _{r}$] for the parameter $\sigma _{f}$. In the latter case, $\sigma _{r}$ is the pseudo-empirical standard deviation of the underlying time series of returns. This constitutes a natural upper bound for this parameter as the fundamental innovations could at most generate fluctuations of the size of the entire return volatility if the parameters for the behavioral components all converge towards zero. For the parameters $\nu$ and $\alpha$, upper restrictions are also needed in order to limit the computational demands of the repeated simulations of the model in the development of the Markov chains. In particular, high $\nu$ leads to increasing frequency of agents’ revision of their strategy per unit time. Since we simulate the Poisson processes governing the agents’ change of behavior as discrete events, more frequent switches increase the computational demands.

During the burn-in phase, proposals have been drawn from a relatively wide multivariate Normal distribution with variances of the parameters $\nu$, $\alpha$ and c set all to 0.5, and the variance of $\sigma _f$ to 0.1 times the standard deviation of the synthetic returns, and all covariance terms set equal to zero. The burn-in, thus, serves to learn about correlations between the parameters of the model. Once the burn-in phase is completed, Eqs. (2) and (3) are applied in order to adapt the proposals to the correlation structure of the parameters and to adjust the scale of the proposal distribution in a way to get close to an optimal acceptance rate. In order to avoid degenerate outcomes of the adaptation process, the proposal density is modified slightly by adding a small constant term:

$\theta ^{*} \sim N(\theta _{\xi }, \lambda _{\xi } {\hat{\Sigma }}_{\xi }) + 0.01 \, N \, (\theta _{\xi }, \Sigma _{0})$ with $\Sigma _{0}$ the proposal density used in the burn-in phase. In cases with delayed rejection, a second round has been added after the rejection of the initial proposal with the new proposal distribution $g^{(2)}( {\theta ^{**}|\theta _{\xi -1}})$ set equal to $0.01 g( \theta ^*|\theta _{\xi -1})$. Choosing a more concentrated distribution in the second round leads to a proposal close to the last accepted set of parameters and, therefore, makes acceptance of this second draw more likely. The following plots and tables illustrate the results of ten shorter runs with adaptation only (denoted AM runs) and one longer run using the full DRAM (delayed rejection plus adaptive Metropolis algorithm) as proposed by Haario et al. (2006).

As can be seen in Fig. 2 the burn-in phase of the first 1500 iterations generates very few accepted proposals. As displayed in Table 1, the average acceptance rate is just 0.039 with as few as 10 in one particular run. After this burn-in phase we start adaptation: We compute the covariance matrix of the proposals in a data-driven way and adapt its scale $\lambda$ as prescribed in Eqs. (2), (3) and (18). As we can see, adaptation leads immediately to a much higher acceptance rate of about 0.147 with indeed relatively little variation between runs.

Fig. 2

Evolution of parameters during 10 adaptive MCMC runs for the modified Franke and Westerhoff model. The ‘true’ parameter values are demarcated by the dotted lines

Figure 3 exhibits in the first ten boxplots in each panel the resulting posterior distributions. Overall, they appear relatively uniform particularly with respect to their interquartile range (the boxes) while the extremes show somewhat more variation. It transpires from the posterior distributions that $\sigma _{f}$ is estimated very precisely from the mean of the posterior distribution while the other parameters are all somewhat biased upward or downward. Note that this graph just shows multiple estimations via MCMC for the same underlying time series. Since we would not expect a perfect parameter estimate with the limited information of one single series, the bias per se is not surprising. What is, however, reassuring is that the various runs of the MCMC algorithm all generate a posterior distribution that is apparently very similar with almost the same mean parameter estimates and dispersion. Note that we know from Andrieu et al. (2010) that Particle MCMC converges to the posterior density under very general conditions on the likelihood and prior density. While MCMC is too computation intense to check the behavior of our estimator for longer time series, we know that the particle approximation of the likelihood is consistent and obeys a central limit law as the number of particles goes to infinity. For an increasing number of observations and appropriately increasing number of particles for longer time series, we thus would expect any bias to vanish asymptotically also in the posterior distribution (see Lux, 2018, for a summary of available results on the asymptotics of particle filters).

Fig. 3

Boxplots of parameters for ten AM runs (numbers 1 through 10) and one DRAM run (number 11). To guarantee roughly similar magnitudes of the estimated parameters, $\sigma _f$ has been multiplied by 100 in our experiments

Figure 4 shows the adjustment of the scale parameter for the ten different runs. From its value of one upon initialization $\lambda$ drops relatively fast initially and eventually converges to a constant level between 0.2 and 0.6. The numbers appear specific to each run, but they interact, of course, with the estimated covariance matrix. Since the resulting distributions are very similar, the ‘degree of freedom’ implied by the adjustment of both ${\widehat{\Sigma }}$ and $\lambda$ can lead to different specific trajectories of adaptation. Note that despite this apparent flexibility in combining $\lambda$ and ${\widehat{\Sigma }}$, we cannot dispense with either of both: Without an adjustment of the scale (via $\lambda$) we would get stuck at the covariance matrix of previously explored sets of parameter values and would have no chance for increasing or decreasing the acceptance rate: Without ${\widehat{\Sigma }}$ we would not be able to learn about the correlation of the parameters.

Fig. 4

Development of adaptive scale parameter $\lambda$ after the burn-in phase for 10 AM runs (main plot) and one DRAM run (inlet)

Table 1 presents diagnostic statistics that are typically reported to assess the convergence of an MCMC chain. Indeed, we have run 10 separate chains to be able to compute the celebrated Gelman–Rubin diagnostic, denoted by R in Table 1. It compares the within-chain variance to the between-chain variance and computes a potential scale reduction factor, i.e., the factor by which the variance of the pertinent parameters in the Markov chain can be reduced by doubling the running time of the chain. Our computation of this statistics follows Flegal et al. (2008) and we also report the upper 0.95% bound of the point estimates of R using a Student t approximation to its distribution (cf. Flegal et al., 2008). A rule of thumb for an acceptable range of R is to choose the length of the chain so that R falls below 1.1. Since the scale reduction rate can be computed for any parameter or function of parameters, we report it both for the four parameters of the model and for the resulting likelihood. We find that in all cases the point estimate and the upper 95% bound are much smaller than 1.1 indicating good convergence properties.

Table 1 The table shows the results of computational experiments with different specifications of PMCMC to estimate the posterior distribution of the parameters of the modified Franke and Westerhoff (2012) model and the Alfarano et al. (2008) model

Our second experiment uses the DRAM algorithm, i.e. it combines the adaptive adjustment of the proposal distribution with a second round of proposals in the case of a rejection of the first proposal. We use the same covariance matrix like in the first round but multiply it by a factor 0.01 to obtain proposals closer to the last accepted value. In this way, we have a much higher chance of acceptance for the second round, i.e. conditional on rejection in the first round which on balance should provide for a much higher overall acceptance rate. In contrast to the previous experiment, we have also reduced the number of particles to $B=500$ while the AM runs had used $B=1000$ in the particle filter. As can be seen, the delayed adjustment algorithm increases the acceptance rate to 0.265, slightly above the target, while indeed the AM runs had never been able to achieve the target rate of 0.234 recommended by Rosenthal (2011). As the last boxplots in Fig. 3 show there is no obvious difference between the resulting quantiles of this run and the previous shorter runs with a different design.

Figure 5 compares the overall distributions for one of the parameters, $\nu$, and the likelihood function. On the upper panel, the pooled results from the 10 AM runs after burn-in are displayed. On the lower panel, we show those from the single DRAM run, for the last 30,000 iterations. Both histograms are virtually indistinguishable. The same holds for the estimated means listed in Table 1. The last column of the table also shows the half-width of the 95% confidence interval of the mean parameter estimates based upon batch means (splitting the last 30,000 data points into subsamples of 5.000). Following, for example, Flegal et al. (2008) this half-width can be interpreted as another convergence criterion applicable to cases where one prefers to perform one single run. With all parameters having confidence intervals for their mean of at most 0.02 and the likelihood a confidence interval smaller than 0.5, the precision appears within conventional bounds. It is interesting to compare the trajectory for $\lambda$ for the DRAM experiment to those of the previous runs. As shown in Fig. 4 this case shows an initial increase, but with a hump-shaped continuation actually converges back to some limiting value close to 1. With the more frequent acceptances, this run started out close to the target rate after the burn-in and even exceeded it during the adaption phase so that the adaptation widened the covariance matrix in order to reduce the acceptance rate back towards the desired level of 0.234.

Fig. 5

Histograms of parameter $\nu$ and the likelihood for both the ten AM runs and the single DRAM run

Table 1 also shows results of a similar set of experiments for the model of Alfarano et al. (2008). The underlying parameter values are $a=0.0003$, $b=0.0014$, and $\sigma _{f} = 0.03$ as in the other model. As it can be seen, the results are broadly similar in terms of the precision as measured by the scale reduction factor and the half-width of the estimates of the posterior mean. In this model, the parameter b exhibits the smallest bias while a shows a larger deviation between the assumed value and the posterior mean. Acceptance rates remain somewhat below target for both the AM and DRAM experiments. In the case of this model the adjustment leads to ever decreasing $\lambda$ indicating that a distribution for the proposals with zero values in its off-diagonal entries is sufficient to arrive at the indicated acceptance rates. However, for the model of Alfarano et al., neither the AM nor the DRAM algorithm are able to meet the target rate of acceptance.

Given the adaptive nature of our choice of the proposal densities, it appears mysterious how the adjustment could underachieve relative to its set target rate. The difference is likely due to the influence of another crucial parameter, the number of particles used in the approximation of the likelihood function. Efficient choice of this parameter has been studied by Pitt et al. (2012), Sherlock et al. (2015) and Doucet et al. (2015). These contributions derive various results on the efficient choice of the number of particles, B, by assuming that the approximation of the likelihood function leads to a distortion against the exact likelihood that can itself be approximated by a Gaussian noise governing the behavior of the log-likelihood. Their general recommendation is choosing B so that the standard deviation of the log-likelihood is in the range of 1.0 to 1.7 in order to minimize overall computing time (balancing the computational effort due to a longer Markov chain needed to compensate for a higher rejection rate against the effort needed to reduce the rejection rate through a higher number of particles). A larger standard deviation of the particle approximation to log-likelihood implies more sampling variability in the likelihood ratio $P_{\theta ^*}(y) / P_{\theta _{\xi -1}}(y)$ in Eq. (1). This leads to occasional large deviations of the particle approximation from the ’true’ likelihood for a draw $\theta _{\xi }$ that would not be exceeded by new draws for new parameters for a long time, and, thus, would reduce the acceptance rate. However, how exactly the standard deviation of the log-likelihood scales with the number of particles depends on the structure of the model and the (true) parameters.

Table 2 Standard deviation of log-likelihood for different data

Table 2 shows in its second and third column estimates of the standard deviation of the log-likelihood at the chosen parameter values, using 100 replications of its computations with different random number seeds for the particle filter. We find that for $B=1000$ the Franke /Westerhoff model gets very close to the target of unity, and also for $\textit{B} =500$ the increase of the standard deviation appears moderate and acceptable. In contrast, the Alfarano et al. model has a much higher standard deviation at $\textit{B} =500$ which explains the low acceptance rate of 0.160 in the DRAM experiments reported in Table 1.

5 Empirical Application

Equipped with the insights of the previous section on how to design an adaptive PMCMC algorithm efficiently, we apply this approach to a selection of time series of major stock markets. The series we consider consist of the S&P500 for the U.S. economy, the German DAX and the Japanese Nikkei index. To obtain a series with a length comparable to that of our previous simulations initially the time period January 2008 through February 2015 had been chosen, with a total of 1886 observations of daily returns. If the PMCMC algorithm would attain an acceptance rate close to its target, the empirical estimation should allow for an efficiency of parameter estimation that should be comparable to the results obtained by the synthetic data in Table 2. The chosen sample is also part of the larger sample used in Lux (2018) for the same series so that results of the present exercise could be compared with his previous parameter estimates on the base of a frequentist use of the particle filter.

The empirical exercise was initiated with a complete replication of the design of the simulations reported in the previous section using the DRAM algorithm with the same initial distribution of the proposals and the same length of the burn-in phase before initiating the adaptation. Unfortunately, what had been working well in the simulations, did not work so well in the practical applications: For both models, we obtained Monte Carlo chains with an acceptance rate way below the usual target of 0.234, even in the adaptation phase. In many cases, the chains showed rejection rates close to hundred percent and only two digit numbers of accepted values over runs of 60,000 iterations. As can be inferred from Table 2, the reason for this dismal performance of the algorithm lies in the high variability of the log-likelihood for these two models with the chosen number of particles in the approximation of the likelihood. In order to assess this variability, a preliminary set of parameter estimates, obtained as posterior means of the last 30,000 observations of our initial APMCMC runs with a burn-in period of length 1500 and adaptation period of length 60,000, have been used to simulate the model and compute the standard deviation of its log likelihood for the given data.

As can bee seen in Table 2, the log likelihood for the S&P 500 data has a standard deviation of about 50 for the Alfarano et al. model with number of particles set as $B=500$. Increasing the number of particles leads to a monotonic decrease of the variability, but even with $B=8000$ the standard deviation is still as high as 2.011. While for the Franke/Westerhoff model, the variability is somewhat lower than for the first model, increasing the number of particles has only a small effect, and even with $B=8000$ the standard deviation remained above 9. While one could in principle still increase the number of particles further, the computational demands of an efficient PMCMC estimation, unfortunately, appear out of reach for this time series, period of investigation and hypothesized models. The same actually was found for the DAX and the Nikkei. Closer inspection shows that the log-likelihood is so volatile over the chosen period because of the large fluctuations at the start of this period which coincides with the time of the worldwide financial crises after the collapse of Lehman brothers. When removing this part, the log-likelihood shows distinctly less variations. To see whether a shorter series would be amenable to PMCMC estimation, the last 1000 observations have been used stretching from 04/26/2011 to 02/28/2015. In terms of the standard deviation of the log likelihood this time window appears better-behaved: For the Alfarano et al. model one obtains a standard deviation of 1.226 with $B=1000$ while for the Franke/Westerhoff model it is 0.873, obtained again from simulations with parameters estimated from our first implementation of the DRAM algorithm. For the two other series, the same restriction of the time window yielded the following results: With the Alfarano et al. model, the DAX showed similar behavior like the S&P 500 while the Nikkei index showed still too high variability of the likelihood which only receded to acceptable levels with $B=8000$. In contrast, the same series showed a standard deviation of the log likelihood under the Franke/Westerhoff model that was almost two orders of magnitude lower with entries all below 0.05 over the entire range from $B=500$ to $B=8000$ displayed in Table 2. Since a value below the optimal one of a about unity indicates a high acceptance rate this somewhat unexpected behavior is not really an obstacle for PMCMC estimation. Indeed, it would rather indicate that we would need a relatively short chain only to achieve a given target of efficiency. In the following we repeat the results using the DRAM algorithm for these three series with $T=1000$ observations, using as the default setting $B=1000$ for the model of Alfarano et al. and $B=500$ for the Franke/Westerhoff model and a chain of length 61,500 with adaptation starting after the first 1500 iterations.

Table 3 displays the results for the Alfarano et al. model. For the S&P500 and the DAX, the acceptance rates for this setting are very close to target, while for the Nikkei it remains distinctly lower (as expected). For the later, another run with $B=6000$ has been conducted which shows more satisfying behavior (somewhat surprisingly so since the standard deviation of the log-likelihood reported it Table 2 is still relatively high with 3.672 for this setting). Together with the mean of the posterior distribution of the parameters and the likelihood, the table also shows the 95% confidence interval for the mean and the 95% credible interval for the pertinent parameter inferred from the full posterior distribution (i.e., the 2.5 and 97.5 simulated quantiles). The interesting aspects are the following: First, in all three cases, we conclude that $b > a$ with at least a confidence level of 95% as the 95% credible intervals of both parameters are non-overlapping. In the context of this model, this implies that the equilibrium distribution of the latent variable $y_t$ from Eq. (12) is bimodal. Hence, the fluctuations between volatile and tranquil market phases are caused by changes between a dominance of optimistic and pessimistic sentiment. Second, the estimates for the parameters $\sigma _f$ are all distinctly smaller than the standard deviations of the underlying time series of returns (numbers are given in Table 4): this is again significant at least at the 95% level as the credible intervals do not include the empirical standard deviation of the data. The conclusion within the model is that fundamental shocks explain only parts of the variation of returns, and the impact of sentiment dynamics (represented by the parameters a and b) is non-negligible.

Figure 6 displays the Markov chains for the parameter a for the three time series (all with $B=1000$). As can be seen, convergence to the limiting distribution is almost immediate, and the fluctuations appear very regular. The lower acceptance rate in the case of the Nikkei Index is also well visible in the simulation. Parameters b and $\sigma _f$ behave very similarly. Also shown in Fig. 6 is the dynamics of the adaptation parameter $\lambda$ for the S&P500 and the DAX series. In both cases, the adaptation proceeds in cycles that at least up to the range of 60,000 iterations performed here show no tendency of dying out. Since Eqs. (2) and (3) define the dynamics of a dynamic system such a behavior is a possible outcome of the adaptive choice of the proposal distribution. Since all the conditions for convergence of the Markov chain are fulfilled, this should not have any impact on the posterior, and indeed the chains of the parameters’ posteriors appear to be unaffected by the fluctuations of $\lambda$ (which likely goes hand-in-hand with compensating fluctuations of ${\hat{\sum }}$))

For the Nikkei, the adaptation parameter $\lambda$ converges monotonically to zero, so that the proposal density tends to $N(\theta _{\xi },0.01 \Sigma _0)$. This is probably a consequence of the inability of the algorithm to find acceptable proposals because of the large variation of the log-likelihood. In an attempt at increasing the acceptance rate, the adaption parameter reduces the variance of the proposal distribution further and further, albeit without sufficient success, so that this tendency drives $\lambda$ to zero. Interestingly, an alternative MCMC run with $B=6.000$ particles (Nikkei II in Table 3) shows again the oscillatory dynamics that were found for the two other stock market series.

Table 4 and Fig. 7 provide the results for the Franke/Westerhoff model. This time, we find the acceptance rate to be close to the target of 0.234 (cf. Sect. 2 above) in the cases of the DAX and the Nikkei, while the adaption underperforms in the case of the S&P500. Again the ‘satisfactory’ cases came along with cyclical adjustments of $\lambda$, while in the ‘unsatisfactory’ case of the S&P500 we find $\lambda$ converging to zero again. The estimate of the parameter c is negative in the case of the S&P500 and the NIKKEI and would have to be explained by strong contrarian behavior of chartists or ‘anti-fundamentalist’ behavior of the group of fundamentalists (i.e., expectations of a movement of the price away from the fundamental value).

For all three time series, we find a very large credible 95% interval of the posterior of the parameter $\nu$. The same applies to parameters c while $\alpha$ and $\sigma _f$ have more narrow 95% credible intervals.

However, for $\sigma _f$ the pertinent numbers are all very close to the standard deviations of returns $\sigma _r$ themselves meaning that - according to the estimates of the Franke and Westerhoff model- most if not all of the dynamics of returns would have to be explained by fundamental news. The remaining behavioral parameters would, then, loose their economic relevance. Indeed, the credible 95% confidence intervals for $\sigma _f$ include $\sigma _r$ for the DAX and Nikkei, and only for the S&P is $\sigma _r$ marginally located outside this interval. Comparing the posterior distribution of $\sigma _f$ (which has the same role in both models) for both models, we find that their 95% credible intervals are non-overlapping for all three series. The same applies to the 95% credible intervals of the estimated likelihoods. In all cases, the Alfarano et al. model has higher values and can, thus, be said to outperform its competitor at least at a confidence level of 95%. The results indicate that at least this version of the Franke/Westerhoff model is not an appropriate data generating process for the time series under consideration. With the estimate of $\sigma _f$ being almost the same as the standard deviation of the data, the results of the estimation suggest that this model is consistently (at least for these three series) unable to explain the deviations of financial returns from a Normal distribution: Since $\sigma _f$ is about the same as the standard deviation, the sentiment part of Eq. (8) would become negligible. With a very weak influence of sentiment on returns the parameters driving the sentiment dynamics ($\nu$, $\alpha$ and c) can only be estimated with a high degree of uncertainty. This is exactly what we see in Table 4 and Fig. 7. Note in particular, that the high confidence intervals only affect $\nu$ and c, while they are much smaller for $\sigma _f$. This result is remarkable as the estimates of the Alfarano et al. model speak in favor of a significant influence of sentiment which in this model explains a sizable fraction of the variability of returns (the estimated $\sigma _f$ in the Alfarano et al. model is always much smaller than the standard deviation of the data and, thus, leaves room for the sentiment factor). Reducing the model almost to the Gaussian process for the fundamental factors only, the estimates for the Franke and Westerhoff model are, in contrast, unable to explain the typical feature of volatility clustering in financial data. It is not surprising then that the average liklihood of its posterior distribution is always smaller then that of the alternative model.

The illustrations of the Markov chains of the parameters of the Franke and Westerhoff model in Fig. 7 clearly indicate that $\nu$, $\alpha$ and c are at best weakly identified, whereas $\sigma _f$ exhibits very small variations in the neighboorhood of the standard deviation of the data. Even much longer simulations still convey the same impression as those depicted in the figure. Note, however, that at least for the DAX and NIKKEI, the acceptance rates are close to what is considered optimal for MCMC. Hence, the meandering paths of the chains for parameters $\nu$, $\alpha$ and c and their occasional jumps speak for a high uncertainty in the estimation of these parameters, not for a lack of exploration of the parameter space. One may also note that one restriction that can be inferred for all three time series is that the parameter $\alpha$ of the Franke/Westerhoff model has a 95% credible interval above unity. In this case, the collective state of the agents converges to a constant majority of either chartists or fundamentalists. With $z_t$ in Eq. (8) remaining practically constant, the sentiment part turns into a small autoregressive component, and, thus, given the negligible value of the autocorrelation of financial returns, its contribution to the likelihood also becomes marginal.

The interesting insight from this exercise is that the Franke/Westerhoff model does not seem to have the potential to explain the particular statistical features of financial returns. It can generate sentiment dynamics with clustering of volatility (cf. Fig. 1) that appears visually appealing. However, as indicated by the estimates, it is unable to match the particular form of heteroscedasticity prevailing in the data, and the best it can do with the data is to fit it by parameters that are not too different from a pure Gaussian process. In this sense the present Bayesian estimation serves to identify a lack of fit of this particular model. This insight exemplifies the observation by Siekmann et al. (2012) that MCMC can be used to check for problems of identification of competing models. Since a Bayesian approach provides information on the full posterior distribution, it appears more suitable than frequentist point estimates for this purpose. In the present case, we might not have found a complete lack of identification, but a close proximity of the posterior of the parameters to a case in which the observed and hidden parts of the state-space model are nearly decoupled and, hence, the parameters of the hidden component would trivially be unidentified. This leaves us with the conclusion that this particular model is not a suitable representation of the asset price dynamics of our selection of stock indices although from a purely phenomenological perspective it appeared an attractive candidate. This confirms results reported by Lux (2018) on the base of a frequentist comparison of both models (albeit for longer time series). However, while the frequentist estimation just documents the significant difference in the likelihood of both models, the Bayesian approach provides deeper diagnostic insights.

Table 3 Estimates of ALW model

Fig. 6

Evolution of model parameter a and adaptation parameter $\lambda$ during the MCMC run with 1.000 particles using the DRAM algorithm for the model of Alfarano et al. Not shown is the scale parameter $\lambda$ for the Nikkei as it converges to zero very quickly

Table 4 Estimates of FW model

Fig. 7

Evolution of model parameters during the MCMC run with 500 particles using the DRAM algorithm for the model of Franke and Westerhoff. For parameters $\nu$ and $\alpha$, only the cases of the S&P500 and DAX are shown as the NIKKEI shows a very wide distribution which would conceal the other series. In the upper-right hand panel the broken lines show the empirical standard deviations of the return series to illustrate how close the estimates of $\sigma _f$ are to the empirical volatility (the standard deviations for the DAX and NIKKEI are so close that they cannot be distinguished from each other)

6 Conclusions

This paper has explored the potential use of refined Markov Chain Monte Carlo approaches for estimation of the parameters of agent-based models. Using an adaptive choice of the distribution of proposals, we indeed found a convenient convergence of the acceptance rates towards their target in our exploratory runs of two behavioral stock market models with a finite number of interacting agents. Unfortunately, the application to empirical data turned out to still be cumbersome in certain cases. In particular, we found this approach to be still infeasible for our initially chosen time series of three major stock indices covering daily data from 2008 though 2015. As it turned out the variation of the log-likelihood values for this sample appeared so large in all three cases that a reasonably high acceptance rate would have required an enormous number of particles in the simulations. This particular behavior of our initial time series obviously stems from a number of extreme realisations during the financial crisis that lead to large fluctuations of the likelihood values across observations. In order to be able to apply Particle MCMC at all, we have reduced the sample to a better-behaved subsample skipping the years 2008 to 2010. This method-driven reduction of the time series under scrutiny is obviously unsatisfactory. As a general insight of our analyses, we find that the flexibility of APMCMC still depends on the combination of data at hand, hypothesized model and best-fitting parameter values of this model that taken together is, of course, outside the control of the researcher.

Despite these limitations, the present exercise brought some interesting results to the fore: parameter estimates for the Alfarano et al. model where in line with the results of Lux (2018) using frequentist methods and a much larger sample, and also the dominance of this model over the competitor of Franke and Westerhoff (2012) has been confirmed. As in the previous paper, the parameter estimates of the latter model basically indicated very little relevance of speculative activity and a dominant influence of fundamental news on asset price movements, while the Alfarano et al. model, in contrast, diagnoses a strong influence of sentiment.

While it has been demonstrated in the literature, that the use of an unbiased estimator of the likelihood leaves the equilibrium distribution of the posterior unchanged in MCMC estimation (Andrieu et al. 2010), the present paper shows the practical limitations of this approach. If the computational demands of PMCMC become infeasible, one would likely have to resort to Approximate Bayesian Computing (ABC) using auxiliary measures of fit rather than the likelihood. A few recent attempts at the application of ABC, for agent-based models can be found in ecology (Parry et al. 2013; Zhang et al. 2017). The adaptation of these methods should be on the research agenda as one of the possible avenues to proceed in the validation of agent-based models in economics.