Abstract
This study assesses macroeconomic and sectoral impacts of demographic changes in the Czech Republic as a result of population ageing and international migration. To do so, it develops a unique dynamic Overlapping Generations Computable General Equilibrium (OLG–CGE) model with detailed representation of individuals of different ages, educational attainment and occupations, as well as interrelations among industrial sectors in producing intermediate and final outputs. The numerical simulations show that the Czech economy will face a substantial reduction in its effective labour supply and changes in aggregate as well as sectoral demand patterns, leading to lower economic growth (4.4% lower GDP by 2050 in absence of technological progress), increase in unit labour costs (5.2% higher wages in absence of inflation) and lower competitiveness of the economy as a whole. Replacement migration may alleviate the pressure, yet the current gross immigration would need to increase by at least 8-17 thousand individuals per year compared to the UN projections (a 15–34% increase) without changing emigration patterns in order to offset the adverse long-term effects.
Similar content being viewed by others
Notes
The classification of educational attainment follows the International Standard Classification of Education (ISCE; UNESCO Institute for Statistics , 2012), industrial sectors are categorised following the Statistical Classification of Economic Activities in the European Community (NACE; European Commission , 2007), and occupations using the International Standard Classification of Occupations (ISCO; International Labour Organization , 2016).
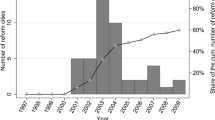
The migration patterns depicted in Fig. 2 vary over time, with the initial high migration being caused primarily by the Czech Republic joining the Schengen Area of free movement within Europe. The UN estimate that there should be approx. zero net migration to the Czech Republic in the next decades (United Nations, 2017).
Since the model does not assume any technological progress over time, the GDP impact shows as an absolute decrease. In reality, this would rather be manifested as a decrease in economic growth rate.
References
Aguiar, A., Narayanan, B., & McDougall, R. (2016). An overview of the GTAP 9 data base. Journal of Global Economic Analysis, 1(1), 181–208.
Aldén, L., & Hammarstedt, M. (2016). Refugee immigration and public sector finances: Longitudinal evidence from Sweden. Sweden: Linnaeus University Centre for Labour Market and Discrimination Studies.
Ashby, S., & Beech, R. (2016). Addressing the healthcare needs of an ageing population: The need for an integrated solution. International Journal of Collaborative Research on Internal Medicine & Public Health, 8(4), 284.
Auerbach, A. J., & Kotlikoff, L. J. (1987). Dynamic fiscal policy (Vol. 11). Cambridge, United Kingdom: Cambridge University Press.
Barrell, R., FitzGerald, J., & Riley, R. (2010). EU enlargement and migration: Assessing the macroeconomic impacts. JCMS Journal of Common Market Studies, 48(2), 373–395.
Barsbai, T., Rapoport, H., Steinmayr, A., & Trebesch, C. (2017). The effect of labor migration on the diffusion of democracy: Evidence from a former Soviet Republic. American Economic Journal: Applied Economics, 9(3), 36–69.
Beine, M., Docquier, F., & Rapoport, H. (2008). Brain drain and human capital formation in developing countries: Winners and losers. The Economic Journal, 118(528), 631–652.
Bloom, D. E., Canning, D., & Fink, G. (2010). Implications of population ageing for economic growth. Oxford Review of Economic Policy, 26(4), 583–612.
Bosetti, V., Cattaneo, C., & Verdolini, E. (2015). Migration of skilled workers and innovation: A European perspective. Journal of International Economics, 96(2), 311–322.
Bou-Habib, P. (2018). The case for replacement migration. The Journal of Political Philosophy, 27(1), 67–86.
Burfisher, M. E. (2017). Introduction to computable general equilibrium models. Cambridge, United Kingdom: Cambridge University Press.
Capello, R., & Lenzi, C. (2019). Structural dynamics of regional innovation patterns in Europe: The role of inventors’ mobility. Regional Studies, 53(1), 30–42.
Catalano, M., & Pezzolla, E. (2016). The effects of education and aging in an OLG model: Long-run growth in France. Germany and Italy. Empirica, 43(4), 757–800.
Corong, E. L., Hertel, T. W., McDougall, R., Tsigas, M. E., & van der Mensbrugghe, D. (2017). The standard gtap model, version 7. Journal of Global Economic Analysis, 2(1), 1–119.
Craveiro, D., de Oliveira, I. T., Gomes, M. S., Malheiros, J., Moreira, M. J. G., & Peixoto, J. (2019). Back to replacement migration. Demographic Research, 40, 1323–1344.
CSO (2018). Czech Statistical Office, Household and Labour Force statistics for 2017. Available at https://www.czso.cz. Accessed 2018-11-12.
Culling, J., & Skilling, H. (2018). How does New Zealand stack up? A comparison of labour supply across the OECD. The Reserve Bank of New Zealand Bulletin, 81(2).
Czaika, M. (2018). High-skilled migration: Drivers and policies. Oxford, UK: Oxford University Press.
Dervis, K., de Melo, J., & Robinson, S. (1982). General equilibrium models for development policy. New York: Cambridge University Press.
Diamond, P. A. (1965). National debt in a neoclassical growth model. The American Economic Review, 55(5), 1126–1150.
Dimaranan, B. V., McDougall, R., and Hertel, T. (2006). GTAP 6, Chapter 14: Behavioral parameters. Available at https://www.gtap.agecon.purdue.edu/resources/download/4184.pdf. Accessed 2018-12-02.
Dinkelman, T., & Mariotti, M. (2016). The long-run effects of labor migration on human capital formation in communities of origin. American Economic Journal: Applied Economics, 8(4), 1–35.
Dixon, P. B., & Jorgenson, D. (2012). Handbook of computable general equilibrium modeling. London, United Kingdom: Newnes.
European Commission (2007). Statistical Classification of Economic Activities in the European Community (NACE), Rev. 2. Available at https://ec.europa.eu/eurostat/statistics-explained/index.php/Glossary:Statistical_classification_of_economic_activities_in_the_European_Community_(NACE), accessed 2019-02-26.
European Commission (2019). Eurostat, statistics on Immigration (migration\_immi) and Emigration (migration\_emi). Available at https://ec.europa.eu/eurostat/data/database?node_code=migr_immi. Accessed 2019-03-05.
Feenstra, R. C., Inklaar, R., & Timmer, M. P. (2015). The next generation of the Penn World Tables. American Economic Review, 105(10), 3150–3182.
Fehr, H. (2009). Computable stochastic equilibrium models and their use in pension-and ageing research. De Economist, 157(4), 359–416.
Foster, L. (2018). Active ageing, pensions and retirement in the UK. Journal of population ageing, 11(2), 117–132.
Fougére, M., & Mérette, M. (1999). Population ageing and economic growth in seven oecd countries. Economic Modelling, 16(3), 411–427.
Garau, G., Lecca, P., & Mandras, G. (2013). The impact of population ageing on energy use: Evidence from Italy. Economic Modelling, 35, 970–980.
Geue, C., Briggs, A., Lewsey, J., & Lorgelly, P. (2014). Population ageing and healthcare expenditure projections: New evidence from a time to death approach. The European Journal of Health Economics, 15(8), 885–896.
Harper, S. (2016). The important role of migration for an ageing nation. Journal of Population Ageing, 9(3), 183–189.
Havranek, T., Horvath, R., Irsova, Z., & Rusnak, M. (2015). Cross-country heterogeneity in intertemporal substitution. Journal of International Economics, 96(1), 100–118.
Heer, B., & Maussner, A. (2009). Dynamic general equilibrium modeling: Computational methods and applications. New York: Springer.
Hess, M., Nauman, E., & Steinkopf, L. (2017). Population ageing, the intergenerational conflict, and active ageing policies-A multilevel study of 27 European countries. Journal of Population Ageing, 10(1), 11–23.
Hobijn, B., & Nechio, F. (2018). Sticker shocks: Using vat changes to estimate upper-level elasticities of substitution. Journal of the European Economic Association, 17(3), 799–833.
Hoff, A. (2016). Introduction: The drivers of population ageing in Central and Eastern Europe–fertility, mortality and migration. In Population Ageing in Central and Eastern Europe, pages 31–38. Routledge.
Horvat, V. (2004). Brain drain. Threat to successful transition in South East Europe. Southeast European Politics, 5(1), 76–93.
Ihori, T. (1996). Public finance in an overlapping generations economy. London, United Kingdom: Palgrave Macmillan UK.
International Labour Organization (2016). International Standard Classification of Occupations (ISCO), version ISCO-08. Available at https://www.ilo.org/public/english/bureau/stat/isco/isco08/index.htm. Accessed 2019-02-26.
IOM (2019). International organisation for migration: Migration data portal. Available at https://migration.iom.int/europe?type=arrivals. Accessed 2019-11-15.
Issac, J. (2013). Economics of migration. Abindgon, UK: Routledge.
Karl, U., & Torres, S. (2015). Ageing in contexts of migration. Abindgon, UK: Routledge.
Kim, E., Hewings, G. J., & Lee, C. (2016). Impact of educational investments on economic losses from population ageing using an interregional cge-population model. Economic Modelling, 54, 126–138.
Kiuila, O. (2015). Interactions between trade and environmental policies in the Czech Republic. The Journal of International Trade & Economic Development, 24(7), 1014–1035.
Křístková, Z., et al. (2012). Impact of R&D investment on economic growth of the Czech Republic-a recursively dynamic CGE Approach. Prague economic papers, 4, 412–433.
Křístková, Z., & Habrychova, A. (2011). Modelling direct payments to agriculture in a CGE Framework-analysis of the Czech Republic. Agricultural Economics, 57(11), 517–528.
Lecca, P., McGregor, P. G., & Swales, J. K. (2013). Forward-looking and myopic regional Computable General Equilibrium models: How significant is the distinction? Economic Modelling, 31, 160–176.
Lim, W., Wong, S., Leong, I., Choo, P., & Pang, W. (2017). Forging a frailty-ready healthcare system to meet population ageing. International journal of environmental research and public health, 14(12), 1448.
Lisenkova, K., Mérette, M., & Wright, R. (2013). Population ageing and the labour market: Modelling size and age-specific effects. Economic modelling, 35, 981–989.
Lofgren, H., Harris, R. L., & Robinson, S. (2002). A standard computable general equilibrium (CGE) model in GAMS (Vol. 5). Washington, DC: International Food Policy Research Institute.
Marek, D. (2008). Pension reform in the Czech republic: A switch to mixed system with regard for limits of fiscal policy. Politická ekonomie, 2008(1), 80–101.
Martin, W. E., & Skinner, R. K. (1998). Resource taxation and sustainability: A CGE model of the Czech Republic. Nonrenewable resources, 7(4), 287–300.
Martinsen, D. S., & Pons Rotger, G. (2017). The fiscal impact of EU immigration on the tax-financed welfare state: Testing the ‘welfare burden’thesis. European Union Politics, 18(4), 620–639.
MICZ (2019). Ministry of the Interior of the Czech Republic, information on asylum, migration and integration. Available at https://www.mvcr.cz/mvcren/article/migration.aspx. Accessed 2019-03-22.
Miles, D., & Černý, A. (2006). Risk, return and portfolio allocation under alternative pension systems with incomplete and imperfect financial markets. Economic Journal, 116(511), 529–557.
Nagarajan, N. R., Teixeira, A. A., & Silva, S. T. (2016). The impact of an ageing population on economic growth: An exploratory review of the main mechanisms. Análise Social, 4–35.
Nishiyama, S., & Smetters, K. (2007). Does social security privatization produce efficiency gains? The Quarterly Journal of Economics, 122(4), 1677–1719.
Nordhaus, W. D., & Yang, Z. (1996). A regional dynamic general-equilibrium model of alternative climate-change strategies. The American Economic Review, 741–765.
Preston, I. (2014). The effect of immigration on public finances. The Economic Journal, 124(580), F569–F592.
Pullen, J. (2009). The marginal productivity theory of distribution: A critical history. Abingdon, UK: Routledge.
Ratha, D., Mohapatra, S., and Scheja, E. (2011). Impact of migration on economic and social development : A review of evidence and emerging issues. The World Bank Policy Research Working Paper WPS 5558, World Bank, Washington, DC.
Saczuk, K. (2013). Development and critique of the concept of replacement migration. In International Migration and the Future of Populations and Labour in Europe, pages 233–242. Springer.
Samuelson, P. A. (1958). An exact consumption-loan model of interest with or without the social contrivance of money. Journal of Political Economy, 66, 467.
Snudden, S. and Klyuev, M. V. (2011). Effects of fiscal consolidation in the Czech Republic. Imf working paper no. 11/65, International Monetary Fund, Washington, DC.
Stepanek, M. (2019). Pension reforms and adverse demographics: Options for the Czech Republic. Czech Journal of Economics and Finance, 69(2), 174–210.
UNESCO Institute for Statistics (2012). International Standard Classification of Education (ISCED), version 2011. Available at http://uis.unesco.org/en/topic/international-standard-classification-education-isced. Accessed 2019-02-26.
United Nations (2017). World Population Prospects: The 2017 revision, key findings and advance tables. Working Paper No. ESA/P/WP.248, United Nations, New York.
Vargas-Silva, C. (2015). The fiscal impact of immigration in the UK. Migration observatory briefing: COMPAS, University of Oxford, UK.
Veugelers, R. (2017). Countering European brain drain. Science, 356(6339), 695–696.
World Bank (2018). World bank open data. Available at https://data.worldbank.org/. Accessed 2018-02-28.
Zhang, Q. A., & Lucey, B. M. (2017). Globalisation, the mobility of skilled workers, and economic growth: constructing a novel brain drain/gain index for European countries. Journal of the Knowledge Economy, 1–23.
Zodrow, G. R., Diamond, J. W., et al. (2013). Dynamic overlapping generations computable general equilibrium models and the analysis of tax policy: The Diamond-Zodrow Model. Handbook of Computable General Equilibrium Modeling (pp. 743–813). London, United Kingdom: Elsevier.
Funding
This study received support from the Charles University, project GA UK No. 824218, in 2018 and 2019.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declared that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
The following text expands on the model description from Section 3 and provides additional details on the computation methodology.
Model equilibrium
The economy is assumed to be in an equilibrium in each period. The concept of equilibrium uses a recursive representation of the consumer’s problem following Heer & Maussner (2009) and is characterised by the following properties:
-
1.
Individual and aggregate behaviour are consistent:
$$\begin{aligned} N_t&= \sum \limits _{s=1}^{T} \sum \limits _{z \in Z} e_{s,z} w_{z,t} \end{aligned}$$(16)$$\begin{aligned} K_t&= \sum \limits _{s=1}^{T+T^R} \sum \limits _{z \in Z} A_{s,z,t} \end{aligned}$$(17)$$\begin{aligned} C_t&= \sum \limits _{s=1}^{T+T^R} \sum \limits _{z \in Z} C_{s,z,t} \end{aligned}$$(18) -
2.
Agents’ dynamic programs and firms’ optimisation problems are solved by satisfying Eqs. (2)–(13) using the relative prices \({w_t,r_t}\), pensions, and the individual policy rules \(C_s(.) \) and \(A_{s+1}(.)\).
-
3.
The goods market clears:
$$\begin{aligned} X_{t} = C_t + K_{t+1} - (1-\delta )K_t, \end{aligned}$$(19) -
4.
Intermediate goods \( V_{i,p,t} \) and value added \( Y_{p,t} \) are sufficient to generate production in each sector:
$$\begin{aligned} X_{t}&\le \alpha _p^y \cdot Y_{p,t} \end{aligned}$$(20)$$\begin{aligned} X_{t}&\le \alpha _p^v \cdot V_{i,p,t} \end{aligned}$$(21) -
5.
Prices of goods and services \( P_{p,t}^c \) are set so that the sectoral goods market clears given Eqs. 7, 8:
$$\begin{aligned} X_{p,t} = Q_{p,t}^d \end{aligned}$$(22)
1.1 Solution Method
The simulation algorithm used in this study is based on Stepanek (2019), which follows earlier works of Heer & Maussner (2009) and Nishiyama & Smetters (2007), and further developed to work in a multi-sectoral environment following principally the works of Garau et al. (2013) and Fehr (2009). It utilises value function iteration to compute agents’ policy functions governing their optimal consumption and savings patterns conditional on the economic situation in each period. With a set of police functions for each group of agents z, firms set prices \( P_{p,t}^c \) to put the sectoral demand and supply in equilibrium.
Specifically, the agent’s decision functions are calculated using backward induction, i.e. by analysing the optimal behaviour in the last period of agent’s live and, conditional on that, in all preceding periods. Let \(V_s(A_{s,z},z_{s})\) be the value of the objective function of an s-year old agent from group z with wealth \(A_{s,z}\). \(V_s(A_{s,z},z)\) is defined as the solution to the dynamic program:
That is, subject to the budget constraints, optimal decision rules for consumption and next-period capital stock are functions of wealth and the idiosyncratic productivity shock, and associated with every optimal next period capital stock \(A_{s+1}(A_{s,z},z)\) is an optimal consumption policy C(s, z) . Consequently, in each period, all agents can calculate the optimal aggregate consumption and saving behaviour in that period given their age, income group, probability of death, and other variables in the model.
Given the total consumption policy C(s, z) , agents then determine their sectoral consumption given the set of prices \( P_{p,t}^q \) according to Eq. 8. At the same time, firms use the available capital and effective labour to produce goods and services for consumption. If there is a mismatch between demand and supply at the sectoral and/or aggregate level, prices \( P_{p,t}^q \), \( w_t \) and \( r_t \) adjust accordingly.
The main simulation process can thus be characterised as follows:
-
1.
Parametrise the model using behavioural parameters, calculate the optimal consumption and savings profile and set the scaling constants so that the outputs correspond to the empirical data in period \( t = 1 \).
-
2.
In each subsequent period, use the outputs from the previous period \( t - 1 \) as a starting point and demographic changes as a source of variation to compute changes in \( w_t \) and \( r_t \) and, consequently, the set of endogenous parameters, such as pensions.
-
3.
Compute the household’s decision functions by backward induction as for \( t = 1 \), resulting in the optimal aggregate consumption and saving behaviour for each cohort alive in period t.
-
4.
Calculate the optimal sectoral demand and supply of goods and services.
-
5.
Update prices \( P_{p,t}^q \), \( w_t \) and \( r_t \) to increase/decrease the amount of consumption, savings and production to minimise the demand/supply differences.
-
6.
Repeat steps 2-5 until the sectoral and aggregate demand and supply are in balance and proceed to the next period.

Source CSO (2018)
Total number of employees and median wage by sector, occupation group and educational attainment.

Source CSO (2018)
Selected income profiles used in the model.
Rights and permissions
About this article
Cite this article
Stepanek, M. Sectoral Impacts of International Labour Migration and Population Ageing in the Czech Republic. Comput Econ 60, 375–400 (2022). https://doi.org/10.1007/s10614-021-10152-3
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10614-021-10152-3