Is Deep-Learning and Natural Language Processing Transcending the Financial Forecasting? Investigation Through Lens of News Analytic Process

Abstract

This study tries to unravel the stock market prediction puzzle using the textual analytic with the help of natural language processing (NLP) techniques and Deep-learning recurrent model called long short term memory (LSTM). Instead of using count-based traditional sentiment index methods, the study uses its own sum and relevance based sentiment index mechanism. Hourly price data has been used in this research as daily data is too late and minutes data is too early for getting the exclusive effect of sentiments. Normally, hourly data is extremely costly and difficult to manage and analyze. Hourly data has been rarely used in similar kinds of researches. To built sentiment index, text analytic information has been parsed and analyzed, textual information that is relevant to selected stocks has been collected, aggregated, categorized, and refined with NLP and eventually converted scientifically into hourly sentiment index. News analytic sources include mainstream media, print media, social media, news feeds, blogs, investors’ advisory portals, experts’ opinions, brokers updates, web-based information, company’ internal news and public announcements regarding policies and reforms. The results of the study indicate that sentiments significantly influence the direction of stocks, on average after 3–4 h. Top ten companies from High-tech, financial, medical, automobile sectors are selected, and six LSTM models, three for using text-analytic and other without analytic are used. Every model includes 1, 3, and 6 h steps back. For all sectors, a 6-hour steps based model outperforms the other models due to LSTM specialty of keeping long term memory. Collective accuracy of textual analytic models is way higher relative to non-textual analytic models.

Introduction

Accurate forecasting of returns is crucial for individual investors, investment banks and corporate investment managers. It is also equally important for investors to foresee the returns accurately and design the investment or trading strategies keeping in view all relevant aspects of forecasting. For many years stock market forecasting studies have been emphasizing the volatility models. Few studies inculcate the role of technological forecasting i.e. artificial intelligence. The efficient market hypothesis (EMH) is proposed by Fama (1998) is under criticism, because the proposed model is in contrast to the behavioral finance concept (Kahneman & Tversky, 1979; Kahneman, 2003; Shefrin, 2008). It has been much debated and considered as a limitation of EMH that this model is not considering the role of investor’s sentiments and their behavioral aspect. Technological advancements and inventions of the new artificial intelligence-based model are reshaping the method of forecasting (Wang et al., 2018; Kuo & Huang, 2018; Makridakis et al., 2018). Normally, the artificial intelligence-based model takes previous stock prices and other variables into account but news analytic consideration is less researched. In this specific context news analytic is in the early stages and needs advancements for better forecasting and efficiency of intelligent trading systems. In the last decade, soft computing methods and techniques have grown rapidly that entice researchers to explore more sophisticated techniques for the stock market and time-series predictions. Time series financial modeling has a long history and time-series data is characterized by hidden relationships, high uncertainty, and unstructured in nature. To estimate the behavior of financial time series there are two types of models are available; linear model and non-linear models. Whereas, linear models are affected by techniques like Box Jenkins and Kalman filters, piece-wise regression, and Brown’s exponential smoothing. All these theories are turning data into the linear functions. However, recent evidence shows that financial markets behave in a non-linear fashion. In addition to these problems, there are other factors that intact with financial markets like, general economic conditions, political events, news, and investor’s psychology that makes a stock market prediction so difficult (Cheng & Chan, 2018; Huang et al., 2007). To address these issues, artificial intelligence has been evolved as a very good technique due to its learning, generalization, and non-linear behavior to overcome these problems and to give better forecasting (Makridakis et al., 2018; Li & Ma, 2010). In this connection, the most relevant techniques are; Recurrent Neural networks, Neural Networks, fuzzy logic, and genetic algorithm (Hiransha et al., 2018; Ergen et al., 2017; Nelson et al., 2017; AlFalahi et al., 2014). Artificial Neural Networks model are pretty good with flexibility and adaptability to learn from changes and previous trend in a given set of input and predicts the trends based on network training. There is a fair deal of evidence that exists in the literature that models that based on artificial neural networks outperform the traditional time series model, for example, see Adebiyi (2012), AlFalahi et al. (2014), Trippi and DeSieno (1992), Correa et al. (2009) and Hansson (2017). There are many soft-computing techniques available under the umbrella of artificial intelligence but finding appropriate techniques is very important to get accurate forecasting results. Study of Li et al. (2018) and Atsalakis and Valavanis (2009) can be referred here each has surveyed more than 100 articles by researchers who have used fuzzy logic, genetic algorithms, and neural networks and recurrent neural network as modeling techniques in their studies. It is evident from these articles that mostly researcher have used feed-forward neural networks (FFNN), currently, some studies use Recurrent Neural Networks(RNN) multilayer perceptron (MLP) to forecast the stock markets (Arora et al., 2019; Pawar et al., 2019). This survey study also testifies the magnitude of the importance of non-conventional tools for stock market prediction. For the stock market prediction process we cannot rely upon past stock prices and some other variable but we need to embed the impact of market news to achieve maximum accuracy. In the prediction process, it can be very tedious for managers to focus on every news that just pops up and align their investment strategies. A human being can miss much information and even information can be out of his reach as well. So, here natural language processing (NLP) techniques come into play. So, there is an urgent need to automate the news analysis process based on NLP technique so that the investment manager and the corporations can be benefited as well as AI-based predictive models can be supplied with more relevant information instead of just past prices. Natural language processing is a subfield of AI where Algos and deep learning model tries to make computers understand language intuitively near to the human level (Nadkarni et al., 2011). A human being has evolved from thousands of year training to understanding the emotion and feeling of language elicits but computers are struggling with the help of deep learning and AI-based models. In this study, we have used the NLP model (see Fig. 1) with the help naive Bayes classifier to process the raw information that is parsed out of many sources. These sources include mainstream media, print media, social media news feeds, blogs, investors’ advisory portals, expert’s opinions, brokers updates, web-based information, company’ internal news and public announcements regarding policies and reforms. Detail of the news analytic and sentiment analysis can be seen in Sect. 3.1.2. Many studies propose soft computing techniques for better and most of the researches have focused on the comparison of traditional time series stock prediction models and artificial neural embedded network models. This study contributes to the existing body of knowledge in the following ways: Normally, studies use news information and stock price data for indices. Apart from other motivations to choose indices for the prediction process, one benefit is that data collection and aggregation is relatively easier because of its ready availability. However, collecting news information for each company individually and make meaningful sentiments for that stock is challenging. However, this study focuses on individual-level stock and news information that makes this study bit challenging because not only news from all possible sources need to accumulate but also company internal news is also taken care. For example, the company changes the top echelon due to any reason or decides to change the level of dividends, any commentary on ‘hashtags’ is not covered by prominent media sources but still, they impact upon the prediction. Secondly, this study is emphasizing NLP techniques and the way how to raw news text can be used for sentiments building processes. So, NLP based models are simply efficient in extracting emotion, feelings, and sentiments out of a raw text. Thirdly, this study not using simple neural networks for predictions process but Long Short Term Memory (LSTM) model based upon the newly developed and highly proven performance in different fields. LSTM models are specifically designed to remember the long-term dependencies. A point that makes it different is mostly, LSTM model is supplied with past stock prices as an input to predict the future price of the stock, however, this study has used sentiments, extracted with help of NLP techniques, to predict the stock price and it is evident from results that model with sentiments has significantly increased the accuracy of the model. This study will be generically beneficial to all institutional and individual investors, all kinds of traders, portfolio managers, and specifically for short-term and long-term investors who invest in the equity market, future marks, derivative and foreign exchange market.

Fig. 1

Natural language processing model

The rest of the paper is divided into the following sections; Literature review, Methodology section that discusses data collection processes, sentiment index development process, NLP techniques, and implementation of the study model. Then comes results and their interpretations and finally the conclusion of the study.

Literature Review

By exploring existing literature on the application of neural networks and machine learning in the area of business and finance we found that neural network literature is rooted back to 1988. Research articles have started publishing in 1990 exclusively in the area of finance (Zhang et al., 1998). The neural network are gaining popularity in organizations that are investing money in neural network and data mining solutions for the resolution of their problems (Smith & Gupta, 2000). In the year 1988 researchers were more focused on the application of artificial intelligence in the area of production and operational management. In the area of finance more articles are published in the field of financial firm’s bankruptcy prediction. Whereas the focus of stock market prediction was restrained to comparison of traditional time series models with ANNS. Despite the fact that a substantial effort has been made for time series prediction via kernel methods (Chang & Liu, 2008), ensemble methods (Qin et al., 2017), and Gaussian processes (Frigola & Rasmussen, 2013), the drawback is that most of these approaches employ a predefined linear form and may not be able to capture the true underlying non-linear relationship appropriately. Recurrent neural networks (RNNs) (Rumelhart et al., 1986; Werbos, 1990; Elman, 1991), a type of deep neural network specially designed for sequence modeling, have received a great amount of attention due to their flexibility in capturing non-linear relationships. In particular, RNNs have shown their success in NARX time series forecasting in recent years (Diaconescu, 2008; Gao & Er, 2005). Traditional RNNs, however, suffer from the problem of vanishing gradients (Bahdanau et al., 2017) and thus have difficulty capturing long-term dependencies. Recently, long short term memory units (LSTM) (Hochreiter & Schmidhuber, 1997) and the gated recurrent unit (GRU) (Cho et al., 2014) have overcome this limitation and achieved great success in various applications, e.g., The reason suggested by researchers is that the neural network has the capability to outperform the time series models because these models can efficiently predict without the requirement of data being following any distribution and linearity. In addition to the comparison of ANNs and traditional model, in literature evidence exists where models based upon artificial intelligence are compared with each other e.g. Tan et al. (2011) have compared three models; ANN, decision tree and hybrid model with the conclusion that ANN has the highest accuracy in stock price prediction.

In early stages of development for financial forecasting using ANNS, researcher and professionals emphasizes on a comparison of traditional time series models and ANNs to measure the better accuracy in forecasting process for an instant see Swanson and White (1997), Yoon et al. (1993), Kaastra and Boyd (1996), Lawrence (1997) and Kryzanowski et al. (1993). ANNs gives 72 percent accuracy of predicting stock market returns and also able to accurately predict the positive and negative returns by training and validating the neural networks (Kryzanowski et al., 1993).

As for as methods of artificial neural networks are concerned researches have used different ways to mimic the neural networks of the human brain.

Many efforts have been made to solve the issue of linearity, for example, Kernam method has been used by Chang and Liu (2008), Bouchachia and Bouchachia (2008) and Frigola and Rasmussen (2013), with the help of traditional non-machine learning-based model that are unable to capture underlying non-linear relationships. Stock market data is always stochastic and noisy in nature so, LSTM is more suitable. Normally, statistical and metamathematical models are used for financial prediction and these model are handcrafted and aligned with respect to observation and thus compromise accuracy (Tsantekidis et al., 2017). Fischer and Krauss (2018) suggested that LSTM performs well as compared to Random forecast, Deep neural network, and logistic classifier. Recurrent Neural Network(RNN) model gained popularity due to the flexibility of use and coping up the problem of linearity in time series (Rumelhart et al., 1986; Werbos, 1990; Elman, 1991).

Artificial intelligence based expert system is also catering to the needs of auditing, banking sector, credit risk management but along with it matchless benefits there is the dark side of these expert systems of being costly. Omoteso (2012) have studied the cost and benefit analysis of an intelligent system that can predict the future direction and softwares development in this area. It is concluded that in small and medium organization it may be not suitable to apply such system to achieve the marginal benefit by incurring heavy cost. Oreski et al. (2012) apply neural networks to reduce the data dimensionality by coping redundant data and removing irrelevant factors to enhance the predictive ability of genetic algorithm. Similarly, López Iturriaga and Sanz (2015) designed the artificial neural network-based model that have predicted the financial distress of US bank 3 years before the bankruptcy occurs.

NLP

Recently, natural language processing (NLP) has grown up as powerful techniques for many fields due to its capability to capture sentiments and feeling into the text in more nuanced way. Many applications have started adopting the NLP techniques to give their users better experience (Xing et al., 2018). Though it relatively easy to get the external news with help of many sources but it difficult to access and parse the data through financial statement of company. So, developing information content from companies financial statements is tedious and difficult. Here information means voluntary information disclosed by firm that is not obligatory by law to disclose to stakeholders (Xing et al., 2018). With help of databases this paper includes all sort of internal information whether it reaches to external media or not as well as external news and information.

Textual information extraction and news articles processing rooted back to 1934 (Bühler, 1934; Chomsky, 1956). Previous two decade people have been giving much focus upon bag of word approach to seek sentiments of text with help of stop words and frequencies. Serous drawback of these model is that they are unable to capture the context of sentence. For example, company A is gaining advantage over company B or company B is gaining advantage over A are two completed opposite sentiments but belongs to same bag- of-word. Recent advances like, word to vector representation , word embedding and LSTM have addressed these problems very well. Sentiment analysis is very important phenomena for stock market and financial forecasting (Poria et al., 2016). With increasing use of web.2.0 Standards (Cooke & Buckley, 2008) users have easy access and ways to sharing the information across platform like Facebook, twitter, etc thus market sentiments become importance for financial market. Businesses dealing in financial products and services reshaping their approach to make their application more informed and sophisticated to gain competitive edge over rivals. New NLP techniques are promising them for their required edge. Existing sentiment technique can be broadly categorized into three domains; namely, hybrid , knowledge-based and statistical approach (Poria et al., 2017). Knowledge-based sentiment analysis is based upon list of words and its frequencies- a relatively old approach that categorizes text into different categories and then further compares the frequencies with the lexicon. Second is statistical method, this approach is not only focusing on list of word but also use statistical model to classify the text with help of probabilities. Third category is mixture of these two Lenat (Lenat et al., 1990; Liu & Singh, 2004; Fellbaum, 1998). This study has used hybrid approach with help of modern available NLP techniques that supports programming languages environments as well.

Methodology

Data Pre-processing

This section describes a summary of approaches and methods that have been used to process the data from raw text to machine-readable data. Data preprocessing has been divided into four major sections, namely; hourly stock returns, News Analytics preprocessing, Naive Bayes Classifier and sentiment index development. All three sections give the snapshot of preprocessing of data. Let’s briefly describe one by one.

Hourly Stock Data

Hourly stock returns are calculated with help of opening and closing price of all 10 companies. Hourly stock data is obtained from Thoumson Retures data portal. Simple formula for calculating the stock return is as follows:

$$\begin{aligned} R_{ij}= \frac{closing_{ij}-opening_{ij}}{opening{ij}} \end{aligned}$$

(1)

whereas $R_{ij}$ is $j_{th}$ stock at $i_{th}$ hours, $closing_{ij}$ is closing price of $j_{th}$ stock at $i_{th}$ hours, opening ij is opening price of $j_{th}$ stock at $i_{th}$ hours.

News Analytic Processing

There are many sources through which information flows into the stock exchanges related to a specific stock. News and information sources that have been used in this paper are: mainstream media, print media, social media news feeds, blogs, investors’ advisory portals, experts opinions, brokers updates, web-based information, company’ internal news and public announcements regarding policies and reforms. We have collected the news stories from a very well known and reliable database, named; Thomson Returns. Using Thomson Reuters’s API we were able to collect new stories if these stories would be related to any of ten stocks which, we have chosen for analysis. The reason for choosing individual stock instead of the stock exchange is; stock exchanges absorb and react to collective level information and thus, specifically event-level information is hard to be separated. Every news story has its timestamp according to GMT and precise at the millisecond level. The time frame for news collection is 10 years, so, collecting every news resulted to have very large text corpus. The timestamp for news is strictly matched with the stock exchange’s opening and closing time. Although, we have thrown a lot of use full collected news information that lies outside of the stock exchange opening and closing time window. However, it was necessary to gauge the impact of news analytics on the stock price movement.

Naive Bayes Classifier

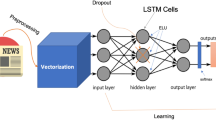
After the raw text regarding news is extracted from sources, the text is refined in the way that it can be used in the Navie Bayes Classification model. Originally text was in ‘HTML’ form with a lot of unnecessary information, but with help of parser and some lines of coding, ‘HTML’ based- text is refined and filtered into ‘lxml’ form. ‘XML’ form of text is accurately and quickly readable by machines. Naive Bayes Classification model has been used to calculate the sentiments out of news text. The Fig. 1 shows how information filters though raw sources to sentiment score. The left column of the diagram shows that Raw text, which includes ‘HTML’ meta-information in it. The first step is to split the complete sentences into a list of unique words, the process is called tokenizing. Next comes, creating a filter of stop words, these stop words are mostly related to pronouns. At the next stage, the text is filtered from hyperlinks and unnecessary information. In the next step, lemmatization is applied to address spelling mistakes. The list of all words is labeled with a part of speech. Then, data is a little bit more refined to see any redundancies. As a next step, with the help of the already available NLTK database, each word has been assigned with negative or positive labels. In the next two steps data is prepared for test and train dataset - ready to feed to the ’Naive Bayes’ Model for training. After the training process is completed each sentence is tested to get sentiments scores out of it. The outcome of the NLP model is utilized in building the sentiment index and LSTM data at the later stages.

Sentiment Index

Following variables are taken into account while building the sentiments index: ‘sentiment time window’, ‘score value’, ‘class of sentiment score ’, ‘relevance’ of score towards the underpinning stock; time window means how many times news/information, related to the selected stock appeared during 1 h time period. The logic behind keeping the time window to 1 h is that stock exchanges need a bit of time to absorb the information related to an individual stock. secondly, Minute level analysis is too early and day level analysis is too late. Next factor is ‘score value’. Sore value is the outcome of a trained NLP model, the process is given in the Fig. 1. Sentiment score values are classified into three categories based on their scores; positive, negative, and neutral. All the negative score are carrying the negative signs and neural sentiment are equal to zero. The scores for all three type of classes are ranges from 0 to 1. Thus ’score value’ are summed up during the 1 h time window, if the sum of the score is negative and greater than − 0.10, it is labeled as negative score, if the sum is between − 0.10 and 0.10 it is considered as neural score and, from 0.10 to 0.90, the ’score value’ is positive. In the Next step, the sentiment score outcome is finally multiplied by variable ‘relevance’ to weight the sentiment with respect to its relevance score. ‘Relevance score’ is percentage number, calculated; the number of times news story mentioned the name of a stock divided by the total count of words in the news story. The mathematical expression of the sentiment index is as under:

$$\begin{aligned} S_{ij} = \sum _{i\in I}\bigg (e_{i}\times R_{i}\times C_{i}\bigg ) \end{aligned}$$

(2)

whereas I = time windows for every$i_{th}$ and $j_{th}$ stock. $e = \max \big (pos_{i},neg_{i},neut_{i}\big ) \ \exists$, $C_{i} = \left\{ \begin{array}{ll} +1&{} argmax \big (pos_{i},neg_{i},neut_{i}\big ) =1\\ 0&{} argmax \big (pos_{i},neg_{i},neut_{i}\big ) =3\\ -1&{} argmax \big (pos_{i},neg_{i},neut_{i}\big ) =2\\ \end{array}\right.$. $R_{i} = Relevance$.

$$\begin{aligned} P ( w_{j} | x_{i} ) = \frac{ P ( x_{i} | w_{j} ). P ( w_{j} ) }{ P ( x_{i} ) } \end{aligned}$$

(3)

whereas $w_{i}$ is a particular class (e.g. Negative or positive) and $x_{i}$ is an given features, $P ( x_{i} | w_{j} )$ is called the posterior or in other word probability of feature $x_{i}$ belongs to class $w_{j}$, $P (w_{j})$ probability of class itself with respect to total sample also called the prior and finally, $P(x_{i})$ is called the marginal probability or evidence. based upon above-stated Bayes theorem, conditional class probabilities of the equation can be calculated as follows:

$$\begin{aligned} P ( \mathbf { x_{i} } | \omega _ { j } ) = P \left( x _ { 1 } | \omega _ { j } \right) \cdot P \left( x _ { 2 } | \omega _ { j } \right) \cdot \cdots \cdot P \left( x _ { d } | \omega _ { j } \right) \end{aligned}$$

Posterior probabilities can be calculated with following expression:

$$\begin{aligned} P ( \mathbf { x_{i} } | \omega _ { j } )= \prod _ { k = 1 } ^ { d } P ( \mathbf { x_{k} } | \omega _ { j } ) \end{aligned}$$

So,probability of class can be calculated with this expression:

$$\begin{aligned}P(\omega _ { j })= \frac{N_{\omega _ { j }}}{N_c}\end{aligned}$$

Model Equation

Artificial intelligence-based models have proved their importance and efficiency in almost all spheres of life and the field of economics and finance can not be excluded. Our model can be used practically in a variety of ways. For example, online trading expert systems are forced to integrate advanced ways for the prediction process. The current model could be specifically very relevant for the trading system to reshape the prediction process and reduces the effort of organizing and search the relevant market info through millions of text records with either human-based effort or the traditional text filtering approaches. The model already uses sophisticated NLP techniques to include the sentimental-based market information into the model. For example, building the information-related index is very crucial. Keep this point in view we have built a customized sentiment index that collects the market information at one minute level and sums it up for a 1-h window. On one hand, it enables LSMT model to capture high-level precision and on other hand, its overcome the limitation to rely upon daily-based market information. There are many traditional models which try to achieve precise forecasting using economic data i.e. simple regression, Moving Averages, and autoregressive-based models (see.ARMA, ARIMA, ARCH GARCH), simple regression, and a bunch of other time series forecasting models. The universal problem for all these models is the limitation to handle the assumption of linear distribution, handling long past lags, and very strict criteria of data structure. These limitations come with a lot of compromises in terms of efficiency and accuracy. Artificial neural network-based model and most specifically, LSTM is very good at handling long-term dependencies i.e. you can keep tracing the past data without losing the information it carries. Moreover, With help of different activation functions and specific approaches model works flexibly without setting many assumptions Let’s elaborate how this model works.

The current model is based upon original scientific publications made by Hochreiter and Schmidhuber (1997). The research is regarded highly by the research community because of its ability to work on long-term dependencies and the ability to remember important information in previous steps. The cases where the dependency of information does not matter much, simple neural network models work fine, but this is not an ideal situation in the practical business world. Stock market prediction, natural language processing, sentimental analysis, and language translation are the example where information of model is highly dependent and context is very important thus recurrent neural network model are good alternatives of simple neural networks. Here is a short description of how the model of this study is fitted.

Hidden state function can be written in the following way:

$$\begin{aligned} h_{t}=f(h_{t-n},X_{t}) \end{aligned}$$

(4)

So, the hidden state of LSTM model has been written with the help of the following equation.

$$\begin{aligned} h_{t}=tanh(W_{h}h_{t-n}+W_{x}X_{t}) \end{aligned}$$

(5)

Weight matrix is first multiplied with current input.Previous time steps hidden states are one by one multiplied with weight matrix for hidden state. Finally, tanh has been applied on result after adding both, current input and previous time steps hidden states. Now output layer of LSTM model is as under:

$$\begin{aligned} O_{t}=\sigma (W_{o}.[h_{t-1},X]_{t}+b_{o}) \end{aligned}$$

(6)

whereas W is weight matrix for output layer and $h_{t}$ we have calculated in Eq. 5.

Equations 5 and 6 simply shows how hidden and output layers of the LSTM model are formulated but this formulation is not much different from simple neural network models. The true secret of LSTM model lies in its unique way of developing cell and memory state with help of gating mechanism.

Signalling and Gates

Gates are basically fully connected feed-forward networks that receive information, applies functions, usually sigmoid activation functions, and do point-wise operations and then return outputs. Thus, we have applied here sigmoid activation function that spits outputs between the range of 0 and 1. So, all the outputs values closer to 0 are considered unimportant and cell deletes them, on the other hand, all information that is close to 1 is important for the prediction process and therefore updated in cell state. In this section, we will describe how signals and gates for LSTM work. Not all information in cell state is important to know for the prediction process and overflow of unnecessary information means disinformation. Primarily there are three gates of LSTM, namely: forget gate, input gates, and the output gate.

Forget Gates

Forget gate receives information from current input and earlier hidden layer input, it applies the sigmoid function on this number and multiplies it with previous cell state. This decides that whether we want information in previous cell state with respect to new information and $t-1$ information in state $C_{t-1}$ . The mathematical equation of forget gate is as under:

$$\begin{aligned} f_{t}=\sigma (W_{f}.[h_{t-1},X]_{t}+b_{f}) \end{aligned}$$

(7)

Input Gate

This is the second part of the signalling process. In the first part, we have decided that the previous cell state is importation to keep or not. Now it is time to store new essential information on cell state, that will be later judged again by forgetting gate with respect to its importance for the model learning process. Input gate is a multiplication of t − 1 hidden state and t input by input weight matrix, that will be later merged into the new candidate. The activation function of the input gate is sigmoid. Mathematical equation of $i_{t}$ is as under:

$$\begin{aligned} i_{t}=\sigma (W_{i}.[h_{t-1},X]_{t}+b_{i}) \end{aligned}$$

(8)

New Candidate

Similar to input gate new candidate is multiplication of hidden state’s current input with weighted matrix of new candidate denoted with symbol $\tilde{C_{t}}$ with combination of $i_{t}$ new candidate will decide with how much information model wants to write on new cell state. Mathematical equation of $\tilde{C_{t}}$ is as under:

$$\begin{aligned} \tilde{C_{t}}=\tanh (W_{c}.[h_{t-1},X]_{t}+b_{c}) \end{aligned}$$

(9)

Now cell sate is updated with help of input gate and new candidate the equation is as follows:

$$\begin{aligned} C_{t}=f_{t}\times C_{t-1}+i_{t}\times \tilde{C_{t}} \end{aligned}$$

(10)

Output layer is the multiplication of the weight matrix of the output layer by previously hidden state and current input.

$$\begin{aligned} O_{t}=\sigma (W_{o}.[h_{t-1},X]_{t}+b_{o}) \end{aligned}$$

(11)

Finally output $h_{t}$ is product of output layer and hidden state and mathematical expression of $h_{t}$ is as under:

$$\begin{aligned} h_{t}=o_{t}\times tanh(C_{t}) \end{aligned}$$

(12)

Model Optimization

As a model optimization function Stochastic Gradient Descent (SGD) has been used in this study. As our model is not supposed to be linear so slop of non-liner error between two point can be calculated with help of derivative as under:

$$\begin{aligned} \frac{{f(x)}=\varDelta f(x)}{\varDelta x}=\underset{\varDelta \rightarrow 0}{lim}\frac{f(x+\varDelta x)-f(x)}{\varDelta x} \end{aligned}$$

(13)

Cost of the model is always an outcome of the specific function. In our model cost is the difference between the actual price of the entity—predicted price of the entity and based on Mean Square Errors. There are two major parameters that need to be tuned to reach the global minimum level of error.

$$\begin{aligned} \frac{\delta f}{\delta _{\beta }} \end{aligned}$$

(14)

As there in our function of cost two parameters are involved namely, $\alpha$ and $\beta$. Because there are two parameters we need partial derivation $\delta$.

$$\begin{aligned} \frac{\delta f}{\delta _{\alpha }} \end{aligned}$$

(15)

In the direction of the slop we can calculate all possible partial derivatives and map them on a vector and can be called gradient vector. Mathematical expression is as under:

$$\begin{aligned} {{f:R}^{n}}\rightarrow R:\nabla f=\left[ \begin{array}{c} \frac{\delta f}{{\delta \theta _{1}}}\\ \\ \frac{\delta f}{\delta \theta _{2}}\\ \vdots \\ \frac{\delta f}{\delta \theta _{n}} \end{array}\right] \end{aligned}$$

(16)

$\theta$ is the point toward slop to achieve the global minima and $\delta f$ changes in function due to change in slop. So, in this way, we can make a vector of all possible partial derivatives to go down to hill.

So, gradient descent update rule is as under:

$$\begin{aligned} \theta _ { \text{ new } } = \theta _ { \text{ old } } - \eta \nabla _ { \theta } f\end{aligned}$$

(17)

whereas $\theta _ { \text{ new } }$ is updated parameter $\theta _ { \text{ old } }$ is old parameter ’-’ sign means we want to go downhill $\eta$ is step size that model should take on slop line to go down hill,$\nabla _ { \theta }$ is gradient with respect to parameters.

RMS Prop

To really speed up the model learning and error reduction, RSMprop algorithm has been used in the model. The idea behind this algo is to divide the gradient decent into two parts, a gradient that moves in vertical and gradients that moves in a horizontal direction. Vertical movement is called oscillation that is not much beneficial of error reduction. Thus, this algorithm focus on horizontal movement to achieve the global minima.

$$\begin{aligned} s_{dW} = \beta s_{dW} + (1 - \beta ) (s_{dw})^2 \end{aligned}$$

(18)

$$\begin{aligned}W = W - \alpha \frac{s_{dw}}{\sqrt{s_{dW}} + \varepsilon }\\s_{db} = \beta s_{db} + (1 - \beta ) (s_{db})^2 \\ b = b - \alpha \frac{s_{db}}{\sqrt{s_{db}} + \varepsilon }\end{aligned}$$

whereas $s_{dW}$ is gradient in horizontal direction and $s_{db}$ is gradient in vertical direction. $\alpha$ is learning rate and $\beta$ is simply parameter for moving average that separate for $s_{dW}$ and $s_{db}$. Whereas, $(s_{dw})^2$ square of past gradient. $\varepsilon$ is very small value to avoid dividing by zero.Moving average is effective in this algo because it gives higher weight to current value of gradient and less weight to square of past gradient.

Overall schematic of the study model is as follows.

Now, we will start next section where we have described our results of model (Fig. 2).

Fig. 2

Study model

Results and Interpretations

This section shows the result of model and gives short detail and analysis of the results. Volume wise top ten companies from four major sectors has been selected for analysis purpose. Prediction accuracy results are given in the Table 1. Some figures and tables are omitted from the result section on account of brevity.

Table 1 Training loss for all models

The Fig. 3 shows the top ten companies with the highest trade volume during the period of 2008–2016. These top ten companies are the sample that is under the study in this paper. These ten companies roughly are big names in the financial, IT, medical, electronics and auto-mobile sectors. The reason for selecting diversified companies is to show the reflection of big sectors onto study model. Due to data collection issue, the latest year of study is 2016 but year of the study does not matter in study because purpose of the study to investigate prediction accuracies with machine learning based models and importance of textual analytic (Figs. 4, 5, 6, 7, 8, 9, 10).

Fig. 3

Top ten companies from different sectors

Fig. 4

Microsoft price predictions with sentiments

Fig. 5

Intel price predictions with sentiments

Fig. 6

GE price predictions with sentiments

Fig. 7

Ford stock predictions with sentiments

Fig. 8

Bank of America price prediction without sentiments

Fig. 9

JP Morgan price prediction with sentiments

Fig. 10

pfe price prediction with sentiments

There are some interesting results to show regarding the above-shown figures. Six types of different models have been applied to each of the ten companies. The first three models are related to the stock market prediction with embedding the company related sentiments and the other three are related to the forecasting without sentiments. There are six types of models for each group i.e with sentiment and without sentiments. The legends in the figures for both types of groups i.e with sentiments and without sentiments is the same. Let’s describe the six types of models. The actual price is a simple plot of Actual price for a given period. ‘t − 3’ is a model that is based upon 3 h time windows. That essentially means that the model knows the actual price of 1 h in the future as a label for t − 3 time price. ‘t − 3’. The curve shift is a simple 1-h curve shift without sliding windows. For the sliding window, we mean that model gets a price and certain t and gets the output as a window of 1, 3, and 6 h future prices as the label. So in the curve shift is just the next day as and as the label for current t price. Similarly, t − 1 and t − 6 are sliding windows of 1 and six-time steps respectively. sentiment curve legend only appears in the graphs where the sentiment index has been used as an input in all input models.

The model (t − 1) is looking back to 1 h past data along with sentiments and try to predict the price of the next hour and so on. The second model is looking 3 h back and the third model is looking 6 h back. The purpose behind selecting these different models is to get the idea to what extent the model needs past information to be able to render better results. It can be observed from figures that model is consistently giving very good results when we have given it 6 h of information of the company, as compared to three and one time steps respectively. In most of the cases, the one-time step is relatively the least accurate model and the reason is obvious that the model is getting less information. The sentiment line is plotted on the secondary axis of the figures, as scales of both axes are very different, so to avoid convolution and getting a better overview, we have used the secondary axis. All sentiment scores are exponential with $x_i^{3}$. Referred to method section for detailed formulation and algorithm for sentiment scores building. Selected companies are quite large and famous around the world thus the frequency of the company’s information is high. So there are many cases of small sentiments that don’t influence the market much. So, in the exponentiation process most strong sentiments get prominent and gives better visualization for analysis purpose. The sentiment line is giving a very insightful and meaningful indication for the next market direction. Sentiments on average are getting 2–3 h advance the company-specific information and that information reflects stock direction very effectively.

The results of all six models of study are given in the Table 1. For comparison purposes, three different criteria of model accuracies are given. This is a very comprehensive table that shows a complete training process and achieved the prediction accuracy of the study model. To get a generic overview, the sum for two panels, namely, with sentiments and without sentiment is given at the end of the table. It is obvious from the results that the error sum using all criteria is greater in a case where models don’t use company-specific textual analytic.

Conclusion

In the recent past, the basic way of operating businesses and corporations, penetrating the new market and reaching to the customers and providing the financial services is exponentially influenced by the new wave of data sciences and artificial intelligence. The research study is motivated by the same phenomenon and empirically investigates the forecasting the stock prices with out-of-box cutting edge soft-computing techniques. The forecasting process is inherited with three unique parts: text analytic, hourly Sentiment index building process, and LSTM AI-based model. First, company-specific text information has been collected, aggregated, classified, and cleansed from thousands of different Thomson Reuters’s based information channels that include, mainstream media, print media, social media, blogs, investors advisory services, discussion forums, brokers commentaries. Useful information was lurking in a pile of unwanted information, using natural language processing techniques information is cleaned and useful features have been extracted to be fed to Naive Bayes Classifier to get its sentiments. The second part is building an hourly sentiment index. Though much information from raw text has been collected at the end only three important features related to the sentiment have been preserved for the index building process, namely class of sentiment, the direction of sentiment, and relevance of the sentiments to a specific company. Sentiment information can come anytime round the clock but stock exchange only works for a specific time range. So first, the time of sentiment is matched with the operational time of stock exchange, then based on the self-discovered equation sentiment index has been built. Most of the research studies in similar direction use daily bases stock market values along with other variables but uniquely this study uses an hourly based model for the forecasting process. The reason for the hourly-based model is that getting the accurate influence of the information because 1 day is too late and minute-interval is too early, thus, the direction of stock may not be aligned with sentiments. Third, and final part of the study is the usage of the LSTM neural network model that works in a very special way when it comes to time series or long term dependency of the information.

The results of the study show that sentiments are playing a very important role in the prediction process. Exponentiated sentiments are concisely followed by the big companies traded at US major stock exchanges. That makes our new way of measuring the sentiments robust. Top ten companies from High-tech, financial, medical, automobile sectors are selected, and six LSTM models are applied, three for using text-analytic and other three without analytic being used. Every model includes 1, 3, and 6 h steps back. For all sectors, a 6-h steps based model outperforms the others due to LSTM specialty of keeping long term memory. collective accuracy of having textual analytic models is way higher relative to non-textual analytic models.

Limitation of study Limitation of the study includes a waste of a lot of useful information due to matching the time of news and information strictly with an opening and closing time of stock exchange. However, top companies are operating worldwide and universal time varies across the globe. Almost every hour round the clock information regarding these companies is coming in. but during time matching processing very useful information of almost 18 h has been thrown out. The next challenge in this connection is to come up with a sophisticated mechanism to cope with the issue.