A Comparative Analysis of Parsimonious Yield Curve Models with Focus on the Nelson-Siegel, Svensson and Bliss Versions

Abstract

We shed light on computational challenges when fitting the Nelson-Siegel, Bliss and Svensson parsimonious yield curve models to observed US Treasury securities with maturities up to 30 years. As model parameters have a specific financial meaning, the stability of their estimated values over time becomes relevant when their dynamic behavior is interpreted in risk-return models. Our study is the first in the literature that compares the stability of estimated model parameters among different parsimonious models and for different approaches for predefining initial parameter values. We find that the Nelson-Siegel parameter estimates are more stable and conserve their intrinsic economical interpretation. Results reveal in addition the patterns of confounding effects in the Svensson model. To obtain the most stable and intuitive parameter estimates over time, we recommend the use of the Nelson-Siegel model by taking initial parameter values derived from the observed yields. The implications of excluding Treasury bills, constraining parameters and reducing clusters across time to maturity are also investigated.

1 Introduction

The term structure of interest rates describes the relationship between yields and time to maturity of fixed-income instruments. Another name, which is often connected with the graphical representation of this relation, is yield curve. The discount function, which is considered the most basic building block of finance, can be inferred directly from it (Gürkaynak et al., 2007). Both financial market participants, policymakers and academics are concerned with modeling the yield curve (Duffee, 2013). From the perspective of a central bank, the yield curve can be used for drawing correct inferences regarding the appropriateness of its monetary policy stance (BIS, 2005; Cœuré, 2017). Many central banks use parsimonious data-driven models for this purpose.

In this paper, we empirically investigate implications of relevant modelling choices for central banks when using such models. We investigate the implications on both the goodness of fit and the stability of estimated model parameter values over time. The latter becomes relevant as parameters of parsimonious models used by (central) banks have a specific financial meaning, e.g., when their dynamic behavior is interpreted in bond risk-return models (Gimeno & Nave, 2009). We perform our analysis using data of US Treasury bills, notes and bonds for all 4996 trading days between 2000 and 2019.

Some previous studies estimate model parameters in monthly steps using synthetic zero bond yields for constant maturities up to 10 years. These must be derived in a preliminary step from prices of coupon-bearing bonds by other approaches. In this case, after fixing certain parameters the model under consideration can be estimated simply by ordinary least squares (OLS) regression. By further assuming stochastic processes for the non-fixed parameters, some authors then derive dynamic versions of parsimonious models. We instead follow the common practice of central banks of estimating all parameters of the original static models directly to the daily observed market prices of the above mentioned Treasury instruments with maturities up to 30 years. As no parameters are fixed, the full set of model parameters must be obtained by solving a non-convex optimization problem by means of a non-linear least squares method, which requires the specification of a set of initial values. As Gimeno & Nave (2009) point out, the latter is crucial for the stability of estimated parameters. Using daily data gives us more observations to fit the models, lowers the influence of any month-end effects and is consistent with the practice of central banks (BIS, 2005; Gürkaynak et al., 2007; Nymand-Andersen, 2018). Our study complements the existing literature on the following points: We offer a comprehensive picture of the robustness of parsimonious models with respect to different approaches for selecting initial values for the fitting procedure, constraints on certain parameters in relation to confounding effects, as well as filter criteria for the selection of instruments considered in the estimation.

Our results support previous evidence suggesting that the magnitudes of the first two factors of the parsimonious models represent the level of the yield curve. However, we show that one of the two curvature factors of the parsimonious Svensson model is superfluous due to confounding effects. Furthermore, our tests of yield curve models as well as different approaches for the selection of initial parameter values for the non-linear fitting procedure imply that central banks, when using the yield curve for monetary policy decisions, should prefer the less flexible Nelson-Siegel model, as well as initial values that are derived from observed yields. These suggestions lead to the most stable and intuitive parameter estimates over time, which makes it easier to give them a financial interpretation, without compromising the goodness of fit. Finally, we test the implications on our findings when preimposing restrictions on the distance between the locations of humps or troughs in the yield curve (like in De Pooter, 2007; Ferstl & Hayden, 2010), excluding Treasury bills (like in Gürkaynak et al., 2007) and controlling for clustering of instruments across time to maturity. Overall, we observe persisting confounding effects in the curvature factors of the Svensson model and an insignificant effect on the goodness of fit. In the cases of controlling for clustering of instruments across time to maturity or preimposing restrictions on the distance between the locations of the humps or troughs in the yield curve, we observe a significant increase in the variation in parameter values. In particular, we observe more variation in the level factor of the yield curve when instruments with more than 10 years are excluded, meaning that the inclusion of longer maturities leads to a better approximation for the long end of the yield curve.

The rest of this paper is organized as follows. Section 2 introduces formally the relevant parsimonious yield curve models that are investigated in this study, and reviews earlier related empirical work. Section 3 explains the data and the fitting procedure applied here, including the different approaches for selecting initial values. Results are presented and interpreted in Sect. 4. Finally, conclusions are given in Sect. 5.

2 Theoretical Background

Let us first introduce important definitions related to the construction of discount factors, spot rates and yields to maturity. Suppose that $\mathbf {C}=\{c_{(i,j)}\}_{i=1,\dots ,N,j=1,\dots ,L}$ is a matrix of cash flows from all coupon payments and the repayment of the face value from government securities i at times j, and that $\mathbf {p}=\{p_{i}\}_{i=1,\dots ,N}$ is the corresponding price vector. Then it is possible to find a vector ${\delta }=\{\delta _{j}\}_{j=1,\dots ,L}$ of discount factors from the following equation (James and Webber 2000):

$$\begin{aligned} \mathbf {p}=\mathbf {C}{\delta }+{\epsilon } \end{aligned}$$

(1)

where ${\epsilon }=\{\epsilon _{i}\}_{i=1,\dots ,N}$ is a vector of errors. Finding ${\delta }$ directly by solving (1) using OLS regression does not work very well, because $\mathbf {C}$ has too many columns compared to the length of $\mathbf {p}$, and too many zeros since the cash flows of government instruments rarely occur on the same date (James & Webber 2000). A better way is to define the discount factor as a function $\delta (m)$ of time to maturity $m\in [0,\infty )$, and then let ${\delta }=(\delta (m_{1}),\dots ,\delta (m_{L}))'$ be the vector of discount factors for all cash flow dates $\{m_{j}\}_{j=1,\dots ,L}$. $\delta (m)$ is an example of a term structure, which links time to maturity and discount factors.

The term structure may also be represented by the spot rate s(m) (Müller, 2002; BIS, 2005), which is the annualized percentage return for an instrument which pays no coupons.¹ It relates to the discount factor by

$$\begin{aligned} s(m)=-\frac{1}{m}\log (\delta (m)). \end{aligned}$$

(2)

The yield to maturity $y_i$ is the internal rate of return that sets the present value of a instrument’s cash flows (coupon payments and repayment of face value) equal to its market price $p_i$:

$$\begin{aligned} p_i = \sum _{j=1}^L c_{ij}\, e^{-y_i\cdot m_j} \end{aligned}$$

(3)

2.1 Models for Estimating the Term Structure

There exist many types of models for estimating the term structure. Some models are concerned with using the spread between long- and short-term interest rates to forecast inflation and real activity of a country or region (Fama & Bliss, 1987; Mishkin, 1990b, a; Shiller & Campbell, 1991; Estrella et al., 2003; Bernanke et al., 2005; Ang et al., 2006; Estrella & Trubin, 2006; Rudebusch & Williams, 2009). Such models require as input yields of specific maturities. However, since usually we do not observe the yields of arbitrary maturities directly, other models are needed that derive them from the prices of traded instruments. Often these models describe the term structure by a continuous function, whose parameters are found by fitting the resulting yield curve to observed market data. Furthermore, there are dynamic models which focus mainly on pricing fixed-income derivatives, and less on forecasting or interpolating the yield curve. Such models include equilibrium models (Vasicek, 1977; Cox et al., 1985; Duffie & Kan, 1996; Bianchi & Cleur, 1996; De Rossi, 2010), no-arbitrage models (Ho & Lee, 1986; Hull & White, 1990; Heath et al., 1992; Eydeland, 1996) and models stating that the interest rates depend on macroeconomic variables (Ang & Piazzesi, 2003; Moench, 2008; Rudebusch & Wu, 2008; Audrino, 2012). Other models rely on machine learning techniques that are capable of incorporating non-linear relationships between economic variables to predict interest rates. These techniques include support vector machines (Gogas et al., 2015), fuzzy logic and genetic algorithms (Ju et al., 1997), neural networks (Kim & Noh, 1997; Oh & Han, 2000; Hong & Han, 2002; Bianchi et al. 2020b, a) and case-based reasoning (Kim & Noh 1997). However, the financial literature has been slow to adapt such methods (Bianchi et al. 2020b), possibly because it is not necessary straightforward to understand their abundant non-linear patterns (Diaz et al., 2016) and it is claimed that they are not suitable for parameter inference (see Mullainathan & Spiess, 2017). Finally, data-driven yield curve models fit mathematical functions, including spline-based and parsimonious functions, to discount factors, spot rates, forward rates or par yields (Müller, 2002; BIS, 2005).

Many central banks use parsimonious data-driven models for the interpolation of yield curves and the assessment of monetary policy measures (BIS, 2005). Indeed, such models have an economic interpretation and provide a good fit of the resulting term structures to observed yields or prices, respectively, of fixed income instruments. This also makes them ideal as basis for measuring risk in fixed income portfolios (Caldeira et al., 2015). The parsimonious Nelson-Siegel model of Nelson & Siegel (1987) and its extensions by Svensson (1994, 1995) and Bliss (1997) use a single exponential function over the entire maturity range. The popularity of these models stems from the fact that – unlike for example spline models – they provide a parsimonious approximation of the yield curve and use only a small number of parameters, yet are flexible enough to capture a range of monotonic, humped and S-type shapes observed in yield data (De Pooter, 2007).

2.2 Specification of Parsimonious Yield Curve Models

The Nelson-Siegel model was proposed by Nelson & Siegel (1987) to interpolate the yield curve (in terms of spot rates) by the following function:

$$\begin{aligned} s(m)=\beta _{0}+\beta _{1}\frac{1-e^{\frac{-m}{\tau _{1}}}}{\frac{m}{\tau _{1}}}+\beta _{2}\left( \frac{1-e^{\frac{-m}{\tau _{1}}}}{\frac{m}{\tau _{1}}}-e^{\frac{-m}{\tau _{1}}}\right) \end{aligned}$$

(4)

where s(m) is the spot rate at any given time to maturity m, and $\beta _{0}$, $\beta _{1}$, $\beta _{2}$ and $\tau _{1}$ are parameters whose specific values result from the fitting procedure. The first, second and third factors of Equation (4) may be interpreted as the level, slope and curvature factors, respectively, as they control the long, short and medium segments of the yield curve (Nelson & Siegel, 1987; Diebold & Li, 2006). This is due to the characteristics of the factor loadings for different times to maturity, which we illustrate in Fig. 1.

Fig. 1

Illustration of the factor loadings over time to maturity in months of the Nelson-Siegel model as given in Eq. (4)

The level factor $\beta _{0}$ represents the limit value of the spot rate when the maturity m goes to infinity and must be strictly positive. The assumption that its loading is constantly one reflects a market where participants have no information to distinguish expectations for different times to maturity far into the future (Dahlquist & Svensson, 1996). The loading of the slope factor $\beta _1$ starts at one when $m=0$ and monotonically decreases towards zero as time to maturity increases. The loading of the curvature factor $\beta _{2}$ starts at zero, its absolute value attains a certain maximum as time to maturity increases, and then decays to zero with further increasing time to maturity. Its sign controls if a hump-shape ($\beta _{2}>0$) or a trough-shape ($\beta _{2}<0$) is generated. The decay parameter $\tau _{1} > 0$ determines the exponential decay rate (in years to maturity) of the slope and curvature factors. In addition, its value controls the location of the hump or trough, respectively, associated with the curvature factor. The sum $\beta _{0}+\beta _{1}$ determines the level of the short end, i.e., the starting value of the yield curve for $m = 0$.

Diebold et al., (2005) propsed a reduced Nelson–Siegel model without the curvature factor. They argued the level and slope factors explain almost all variation, but acknowledged that for shaping the entire yield curve two factors are most likely not enough. This was confirmed by De Pooter (2007), who found that this reduced two-factor Nelson-Siegel model performed poorly in yield curve fitting because of the lack of the curvature factor.

As the slope and curvature factors of the Nelson–Siegel model rapidly approach zero (see Diebold & Li, 2006), only the level factor is left to fit the yield curve at longer maturities (Diebold & Rudebusch, 2013). To address this, Svensson (1994, 1995) extended the Nelson-Siegel model to a four-factor model by adding a second curvature factor, which allows to reflect a second hump or trough in the yield curve and increases the flexibility to fit it to observed market data:

$$\begin{aligned} s(m)=\beta _{0}+\beta _{1}\frac{1-e^{\frac{-m}{\tau _{1}}}}{\frac{m}{\tau _{1}}}+\beta _{2}\left( \frac{1-e^{\frac{-m}{\tau _{1}}}}{\frac{m}{\tau _{1}}}-e^{\frac{-m}{\tau _{1}}}\right) +\beta _{3}\left( \frac{1-e^{\frac{-m}{\tau _{2}}}}{\frac{m}{\tau _{2}}}-e^{\frac{-m}{\tau _{2}}}\right) \end{aligned}$$

(5)

where $\beta _{3}$ determines the magnitude of the second curvature factor, while $\tau _{2}$ determines the location of the second hump (if $\beta _{3} > 0$) or trough (if $\beta _{3} < 0$). Gürkaynak et al. (2007) argue that the Svensson model should be preferred to the Nelson-Siegel model since the yield curve slopes down at the very long end, and thus the second curvature factor of the Svensson model is needed to model a second hump at longer maturities. Using government bonds from the Euro zone, Nymand-Andersen (2018) also found that the Svensson model performs slightly better than the Nelson-Siegel model with respect to flexibility and goodness of fit. He also compared both models with spline-based approaches and concluded that the latter are sensitive to the applied optimization algorithm, the fixing of smoothing parameters, the selection of penalty functions and the location of knot points.

Björk & Christensen (1999) extended the original Nelson–Siegel model to a four-factor model by adding a second slope factor, as opposed to the Svensson model which adds a second curvature factor. Furthermore, they constructed a five factor model by extending the latter by a fifth factor, which increases linearly with time to maturity. Diebold et al. (2006) found that these two extensions provide only negligible improvement in the model fit, suggesting that fewer factors are sufficient. De Pooter (2007) argued that the fifth factor is problematic since it implies a linear increase in yields with maturity.

While in (4) the loadings of the slope and the curvature factor are governed by the same decay parameter $\tau _1$, Nelson & Siegel (1987) discussed already in their original paper a generalization where this restriction is relaxed by introduction of an individual decay parameter $\tau _2 > 0$ in the last term:

$$\begin{aligned} s(m)=\beta _{0}+\beta _{1}\frac{1-e^{\frac{-m}{\tau _{1}}}}{\frac{m}{\tau _{1}}}+\beta _{2}\left( \frac{1-e^{\frac{-m}{\tau _{2}}}}{\frac{m}{\tau _{2}}}-e^{\frac{-m}{\tau _{2}}}\right) . \end{aligned}$$

(6)

Here, $\tau _{1}$ determines again the exponential decay rate of the slope factor, while $\tau _{2}$ controls the decay rate of the curvature factor as well as the location of the hump or trough. Nelson & Siegel (1987) found in tests that the model variant in equation (6) with individual decay parameters was overparameterized. Therefore they proposed the more parsimonious formulation in equation (4). However, Bliss (1997) remarked that their finding of overparameterization resulted from using a sample of instruments with maturity of up to one year only, and that overparameterization should not pose any problem when also longer maturities were considered. Thus, we will also consider the generalized version in equation (6) in the sequel and refer to it as Bliss model. By comparison of (5) and (6), it is obvious that the Bliss model may also be seen as a special case of the Svensson model with its $\beta _{2}=0$.

Any model that is an extension of the Nelson-Siegel model can be used to obtain a fit that is at least as good as the one obtained with the Nelson–Siegel model, since it includes the latter as a special case. However, a lower number of factors in the yield curve model is typically adequate (Diebold & Rudebusch, 2013). Dahlquist & Svensson (1996) compared the Nelson-Siegel model with the dynamic Longstaff & Schwartz (1992) term structure model and found that the former is well above what is needed for monetary policy analysis. Söderlind & Svensson (1997) stated that the original Nelson-Siegel model gives a satisfactory fit in many cases, but in some cases, when the term structure is very complex, the Svensson model improves the fit considerably. Both studies used data for Swedish government bonds denoted in Swedish Krona. Similarly, De Pooter (2007) found that the parsimonious Nelson-Siegel model offers a satisfactory fit, while the more elaborate models with multiple decay parameters (the Bliss model) or additional factors (the Svensson model) lead to an improvement for specific time points when the yield curve exhibits more complex shapes.

2.3 Challenges with the Estimation of Parsimonious Yield Curve Models

Since the parameters $\beta _0, \beta _1$ and $\beta _2$ of the Nelson–Siegel model can be associated with the level, slope and curvature of the yield curve, Diebold & Li (2006) recognized that they must vary over time along with the curve’s changing shape. However, the authors assumed that the fourth parameter $\tau _1$ can be fixed at a specific value such that the loading of the curvature factor in (4) achieves its maximum for a maturity of 2.5 years, which is commonly seen as “medium-term”. By fixing the value of $\tau _1$ and fitting the model in (4) directly to spot rates, the remaining parameters on each observation date can be estimated simply by OLS regression as then the factor loadings only depend on the maturity. In a subsequent step, Diebold & Li (2006) fit autoregressive models to the obtained series of $\beta _0, \beta _1$ and $\beta _2$, which leads to a dynamic version of the Nelson-Siegel model. This approach has been extended by Koopman et al. (2010), who treated also $\tau _1$ in (4) as a fourth latent factor and modeled its dynamics jointly with the other parameters by a vector autoregressive process. The corresponding non-linear model was estimated with an extended Kalman filter.

Not fixing the value of $\tau _1$ (and $\tau _2$) leads generally to a better fit of the yield curve since it allows the location of humps or troughs in the curve to vary over time (Koopman et al., 2010; Diebold & Rudebusch, 2013). If the non-dynamic yield curve models in (4), (5) and (6) were fitted to spot rates, one could also perform a grid search over different values of $\tau _1$ (and $\tau _2$), estimate for each grid point the remaining parameters by OLS and select the solution with the best goodness of fit. However, as spot rates are usually not directly observable, this requires to derive them first from prices of traded instruments with another term structure estimation method like, e.g., unsmoothed Fama-Bliss rates (Fama & Bliss, 1987) or bootstrapping (Hagan & West, 2006). Yet, such approaches suffer from a lack of available instruments with very long maturities. Therefore, the above-mentioned papers consider only spot rates up to 10 years.

As central banks usually estimate the yield curve up to maturities of 30 years, their common practice is to fit parsimonious models directly to observed market prices of the relevant instruments (BIS, 2005; Gürkaynak et al., 2007; Nymand-Andersen, 2018). Estimating the full parameter set $\beta _0, \beta _1, \beta _2, \tau _1$ (and $\beta _3, \tau _2$) then leads to a non-linear optimization problem due to the specific form of equations (4), (5) and (6), where the non-linearity is introduced by $\tau _1$ (and $\tau _2$, respectively). In practice, the estimation task is further complicated by the fact that the corresponding non-linear problem is also non-convex and has many local minima, and small changes in instrument prices as well as different initial values for the optimization algorithm may lead to different solutions (Gimeno & Nave, 2009; Manousopoulos & Michalopoulos, 2009; Gilli et al., 2010). As a result, the empirically observed model parameter values become instable and occasionally jump discretely from one day to the next. Gürkaynak et al. (2007) pointed out that although the jumps in parameters can be large, the changes in fitted yields over most of the considered maturity range are quite muted. Indeed, the estimation may arrive at similar yield curve shapes for very different combinations of parameters.

However, parameter instability poses difficulties when giving them an economic interpretation. Lengwiler & Lenz (2010) highlighted that the three factors in the Nelson-Siegel model are not mutually orthogonal, which means that each of them has innovations that are dependent on the other two factors. The authors argued that this results in difficulties in forming expectations about each factor. To address this issue, the authors demonstrated how to construct mutually orthogonal factors. Furthermore, they constructed their own three factors, which can be identified as the long, short and curvature factors. To our knowledge, this approach has not become widely accepted among academics and practitioners, and therefore we do not consider it in this paper.

Due to the similar factor loading structure for the third and fourth factors of the Svensson model, a specific potential problem arises when the decay parameters $\tau _1$ and $\tau _2$ assume similar values. In this case, the Svensson model reduces to the three-factor Nelson-Siegel model with a magnitude of the curvature factor equal to the sum of $\beta _2$ and $\beta _3$, and the parameters cannot be identified individually but only by their sum (De Pooter, 2007). This effect can be observed in Gürkaynak et al. (2007), where the estimates of $\beta _2$ and $\beta _3$ take large absolute values up to $10^5$, but with opposite signs when the values of $\tau _1$ and $\tau _2$ coincide.² To make sure that the second curvature factor of the Svensson model increases the flexibility at other times to maturity than the first curvature factor, i.e., in order to prevent confounding effects, previous studies have suggested to preimpose restrictions on the distance between the values of $\tau _1$ and $\tau _2$. De Pooter (2007), who used instruments with maturities up to 10 years, preimposed the restriction of $\tau _1 \ge \tau _2 + 6.69$ to ensure that the maximum loading of the second curvature factor is at least twelve months shorter than the maximum loading of the first curvature factor. This effectively adds the extra flexibility gained from the fourth factor of the Svensson model at maturities shorter than that of the third factor, which is counterintuitive if the motivation for the second curvature factor is a better fit for the long end of the yield curve. On the other hand, Sasongko et al. (2019) preimposed the restriction $\tau _2 > \tau _1$, which implies that the maximum loading of the second curvature factor is at longer maturities than the maximum loading of the first curvature factor. This is in accordance with Ferstl & Hayden (2010) who introduced the R package termstrc for fitting yield curves. The authors proposed the restriction of $\tau _2 > \tau _1 + \Delta \tau$, where $\Delta \tau$ is predefined and has the default value of 0.5 in their package.³ Furthermore, the authors also use $\Delta \tau = 0.5$ in one of their examples of using the package.

2.4 Data Choices when Estimating Parsimonious Yield Curve Models

Bolder & Stréliski (1999) emphasized that besides the optimization problem, a second key issue in the application of yield curve models is the data problem, i.e., the selection of instruments to be considered. This aspect is particularly important for parsimonious models where a single instrument can have a large impact on the shape of the whole curve and not only near its maturity (Manousopoulos & Michalopoulos, 2009).

The earlier cited papers by Diebold et al. (2006), De Pooter (2007) and Koopman et al. (2010) use Kalman filter-based estimation methods to identify the evolution of the latent factors in the context of a dynamic Nelson-Siegel model or one of its extensions. This requires the use of spot rates with constant maturities to model the measurement equation, which links observations with latent factors over time. With the exception of Treasury bills, which are essentially zero bonds with maturities up to one year at the time of issue, spot rates are not directly observable. Therefore, the authors use monthly updated unsmoothed Fama-Bliss (Fama & Bliss, 1987) rates of synthetic instruments with constant maturities that are derived from prices of coupon-bearing Treasury notes and bonds by an iterative procedure. Due to the unavailability of long-term bonds, the above-mentioned papers restrict themselves to set of constant maturities up to 10 years. Only Christensen et al. (2007, 2009) considered maturities up to 30 years, taking into account a specific sample period in which Treasury bonds with the corresponding maturities were actually issued, and found clear evidence that models with more than three factors provide a better fit to the long end of the yield curve. Details on the derivation of unsmoothed Fama-Bliss rates are described in Bliss (1997), where the method is tested against other approaches, among them the Nelson-Siegel curve. However, the practice of central banks is to fit the models directly to observed prices of government securities instead of spot rates of synthetic instruments (BIS, 2005; Gürkaynak et al., 2007; Nymand-Andersen, 2018).

When selecting instruments for fitting the models, securities with special features such as being callable, variable coupon or perpetual bonds should be excluded (Nymand-Andersen, 2018). There are also reasons for excluding standard “plain-vanilla” instruments. For example, the trading volume of bonds often decreases considerably close to the maturity date, and thus the quoted prices may not accurately reflect the theoretically correct ones (BIS, 2005). Gürkaynak et al., (2007) excluded all Treasury bills and consider only notes and bonds for the purpose of yield curve fitting. This was motivated by the observation that bills are priced differently from notes and bonds with less than one year to maturity due to liquidity, taxes, and other effects. The authors also referred to Duffee (1996), who found that movements in bill yields are often disconnected from yields of notes and bonds. They also excluded the two most recently issued securities of each original term to maturity because these instruments often trade at a premium due to demand from the repurchase agreement (Repo) market and higher liquidity.

The overview in BIS (2005) showed that most central banks, which either use the Nelson-Siegel or the Svensson models to derive yield curves, follow different approaches in excluding securities, often because of country-specific reasons. The Bank of Canada excludes instruments that trade at a premium or discount of more than 500 basis points from their coupon because the price of these instruments may be distorted by tax effects (BIS, 2005). Several central banks exclude securities close to their maturity, among them the Federal Reserve (maturities below 30 days), the European Central Bank (ECB, maturities below three months), the Bank of Japan (below six months with the exception of some short-term instruments), the Bank of France (depending on the type of instrument) as well as the Swiss National Bank (below one year).

The Bundesbank found for their data set that excluding treasuries with maturities between three and twelve months implies imprecise estimates for the one-year rate, which is of particular interest for policy makers. Therefore, they exclude only instruments with less than three months time to maturity. Other central banks reflect the short end of the term structure by replacing bonds with other, more liquid instruments such as repo rates (England, Spain) or money market rates (Norway, Switzerland). In order to consider only instruments with sufficient liquidity, the European Central Bank requires a minimum daily trading volume of EUR 1 million and a maximum bid-ask spread of 3 basis points, while Canada applies a minimum outstanding amount as filter. For an extended overview of the various approaches applied by different central banks, we refer to the report by the BIS (2005).

2.5 Parsimonious Models for Forecasting

Some authors investigate also the use of parsimonious models for forecasting future interest rates. Diebold & Li (2006) reported a good forecasting performance of their dynamic extension of the Nelson-Siegel model for US Treasury yields between January 1985 and December 2000. Carriero (2011) found that the out-of-sample performance deteriorates if the sample period is extended to 2009. Duffee (2011) reported that the model is inferior to random walk forecasts when the data sample is expanded with more recent observations. Moench (2008) concluded on the basis of a subsample analysis that the strong forecasting performance documented by Diebold & Li (2006) might be due to their specific choice of the forecasting period. De Pooter (2007) found that only the four-factor model by Björk & Christensen (1999) could compete with Moench’s favorite model, which uses several macroeconomic variables and parameter restrictions implied by no-arbitrage constraints. Doshi et al. (2020) proposed to use horizon-specific forecasting loss functions when estimating term structure models, instead of traditional loss functions like mean-squared error, and found that this improves out-of-sample forecasting performance. However, a further assessment of forecasting capabilities of yield curve models is beyond the scope of this paper. We refer to Duffee (2013) for a profound examination of yield curve models used for forecasting and to Carriero et al. (2012) for an extensive comparison of different modelling approaches that are estimated with Bayesian vector autoregression. It should be emphasized that parsimonious yield curve models were originally not intended for forecasting since they do not contain information on the dynamics of the yield curve (Lengwiler & Lenz, 2010; Diaz et al., 2016), unless further assumptions are made on the evolution of the factors as, e.g., in the extension by Diebold & Li (2006).

3 Data and Methodology

We fit the Nelson–Siegel, the Svensson and the Bliss models to mid prices of US Treasury securities for each of the 4996 trading days between 1st January 2000 and 31st December 2019, calculated as average of the closing bid and ask price for non-callable US bills, notes and bonds retrieved from the database of the Center for Research in Security Prices (CRSP). Following the procedures applied by several central banks, we exclude instruments with a remaining time to maturity of less than three months, as suggested by Gürkaynak et al. (2007). As mentioned earlier, they also proposed to exclude Treasury bills motivated by the findings in Duffee (1996). We test the effect of excluding vs. including the T-bills in Section 4.4.

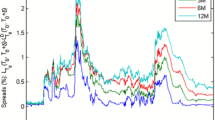
Figure 2 shows the evolution of daily spot rates for fixed maturities of 3, 6, 9, 12, 15, 18, 21, 24, 30, 36, 48, 60, 72, 84, 96, 108, 120, 180, 240, 300 and 360 months. Based on the distances between the spot rates of shorter and longer maturities, we observe that the period of investigation covers times with normal, flat and inverted yield curves. Further, the investigation period covers the shocks on the global markets after the 9/11 terror attacks in 2001, the Financial Crisis of 2007–2008, as well as rising and falling interest rates. Note that the spot rates shown are yields of synthetic instruments derived from the market prices of Treasury bills, notes and bonds by bootstrapping. They are displayed here to illustrate the different yield curve regimes during the investigation period, while the parsimonious yield curve models considered in this paper are directly fitted to prices of traded instruments.

Fig. 2

Evolution of daily spot rates for fixed maturities from 3 to 360 months (30 years). The lines have unique colors from blue shades for the shortest maturities to red shades for the longest maturities. The spot rates shown are yields of synthetic instruments and are derived from market prices of Treasury instruments by bootstrapping

3.1 Optimization Problem

As outlined previously, fitting a yield curve model to market data requires the minimization of an error measure $\chi$, which is based on the differences between observed and fitted (i.e., obtained from the model) yields or prices. The choice between yield or price error minimization is not definite and depends on the intended use of the yield curve. When the purpose is deriving interest rates for monetary policy decisions, it suggests itself to minimize yield errors. By contrast, if the purpose is pricing of bonds, minimizing price errors appears more suitable. In both cases, a discount function is calculated from the yield curve obtained for the current choice of parameters and used to calculate the bond prices implied by the model. In the case of price error minimization, observed prices can be compared directly with estimated prices. A beneficial feature from a computational point of view is that analytical gradients for the error measure $\chi$ can be derived (Ferstl & Hayden, 2010), which facilitates the numerical solution of the fitting procedure. In the case of yield error minimization, in addition Eq. (3) must be solved for each instrument i to obtain its estimated yield to maturity from the corresponding model-implied price. Since this requires an iterative procedure for all coupon-bearing bonds in each step of the optimization algorithm, minimizing yield errors is computationally more demanding than price error minimization. Furthermore, gradients of the error measure must be estimated numerically.

Svensson (1994) pointed out that bond prices are rather insensitive to changes in yields for short maturities and, thus, a minimization of price errors may lead to large yield errors for short-term securities. Since a change in the yield results in a small (large) change in the price of a bond with a short (long) maturity, minimizing price errors would lead to an over-fitting of the long end of the term structure at the expense of the short end (BIS, 2005). This may be corrected by weighting the price errors of each individual bond by the inverse of its (modified) duration. In this way, yields for short maturities may be captured more accurately with less computational effort. Among the nine central banks in the overview of the BIS (2005) that adopted the Nelson-Siegel or the Svensson model, five apply a minimization of duration-weighted prices, while four use yield error minimization.

Formally, let $y_i$ be the yield to maturity and $p_i$ the price of security i observed on a specific trading day. For ease of notation, the time indices will be dropped in the sequel. The corresponding values derived from one of the parsimonious yield curve models (4), (5) or (6) are denoted by $\hat{y}_i({\gamma })$ and $\hat{p}_i({\gamma })$, respectively, where ${\gamma }$ is the vector of parameters. The error for instrument i is the difference between observed and fitted value, i.e., $\epsilon _i({\gamma }) = y_i - \hat{y}_i({\gamma })$ if yield errors are minimized or $\epsilon _i({\gamma }) = ( p_i - \hat{p}_i({\gamma }) ) / dur _i$ for minimization of duration-weighted price errors, where $dur _i$ is the modified duration of security i. Thus, with N securities (after filtering) considered in the estimation, the error measure to be minimized is

$$\begin{aligned} \chi ({\gamma }) = \sum _{i=1}^N \left[ \epsilon _i({\gamma })\right] ^2. \end{aligned}$$

(7)

The resulting optimization problem

$$\begin{aligned} \min \limits _{\mathbf {l}\le {\gamma }\le \mathbf {u}} \chi ({\gamma }) \end{aligned}$$

(8)

is a (bound-constrained) non-linear least squares problem with lower and upper bounds $\mathbf {l}$ and $\mathbf {u}$ on the values of the parameters. If additional restrictions on the distance between the parameters $\tau _1$ and $\tau _2$ for the Svensson model are taken into account, problem (8) becomes a constrained non-linear optimization problem. Depending on the setting, we apply different solution algorithms. Details are described in Appendix A.

3.2 Bounds, Restrictions and Initial Values

The lower and upper bounds $\mathbf {l}$ and $\mathbf {u}$ defined above help to avoid that the fitting procedure results in a local minimum where the yield curve model parameters have (too) extreme values without any intuitive financial interpretation. As mentioned earlier, such extreme values can be observed, for example, from the data of Gürkaynak et al. (2007), where no bounds were defined and the estimated parameters assume extreme magnitudes up to absolute values above $10^5$. We apply the same values for the bounds as in section 2 of Gilli et al. (2010), which are listed in Table 1. $\tau _1$ and $\tau _2$ must be strictly positive since they control the location of the first and, in case of the Svensson model, second hump (trough). We allow for values up to 30 which permits the model to take into account potential humps (troughs) at the very long end of the yield curve.

Table 1 Initial values derived from observed yields in accordance with the financial interpretation of parameters (Manousopoulos & Michalopoulos, 2009) as well as lower and upper bounds (Gilli et al., 2010) used when fitting model parameters

For the time being, we choose not to preimpose any restrictions on the distance between $\tau _1$ and $\tau _2$, but rather aim at understanding the behavior of the original model specification. However, in Sect. 4.3 we present the implications of our findings when preimposing constraints on the distance between $\tau _1$ and $\tau _2$, and conclude that such restrictions are disadvantageous when using the yield curve for monetary policy decisions.

Any non-linear fitting procedure requires the specification of an initial choice of the parameters and then tries to improve the fit by updating ${\gamma }$ iteratively until it converges to a (local) minimum. Due to the existence of many local minima, the resulting goodness of fit depends largely on the choice of the starting values (Gimeno & Nave, 2009; Manousopoulos & Michalopoulos, 2009). For fitting the Svensson model, we consider six different approaches to determine these initial values.⁴

Approach #1 uses the initial values listed in Table 1, which are directly derived from observed yields and consistent with the financial interpretation of the parameters as in Manousopoulos & Michalopoulos (2009). The initial values of the magnitudes of the long-term (level) factor $\beta _{0}$ and the short-term (slope) factor $\beta _{1}$ are approximated for each trading day by

$$\begin{aligned} initial\,\beta _{0}= & {} \frac{y_{1} + y_{2} + y_{3}}{3} \end{aligned}$$

(9)

$$\begin{aligned} initial\,\beta _{1}= & {} y_{s}-initial\,\beta _{0} \end{aligned}$$

(10)

where $y_{1}$, $y_{2}$ and $y_{3}$ are the observed yield to maturity in percent of the three instruments with the longest time to maturity and $y_{s}$ is the observed yield to maturity in percent of the instrument with the shortest time to maturity observed on that day.⁵

In approach #2 we fit first the less flexible Nelson-Siegel model to the data, where the initial values for the corresponding parameters are set as in the first approach. In a second step, the obtained values of $\beta _0$, $\beta _1$, $\beta _2$ and $\tau _1$ for the Nelson-Siegel model are used as initial values for fitting the Svensson model, together with the values for $\beta _3$ and $\tau _2$ from Table 1. According to BIS (2005), a similar approach is applied by the Bank of France. Approach #3 works analogously to approach #2, but uses the Bliss model to find values for $\beta _0$, $\beta _1$, $\beta _2$, $\tau _1$ and $\tau _2$, which are then used as initial values for fitting the Svensson model.

Approach #4 is inspired by the Swiss National Bank (Müller, 2002). It uses the Nelder-Mead or downhill simplex algorithm (Nelder & Mead, 1965; Box, 1965) with initial values from Table 1 to obtain a full set of all six parameters of the Svensson model by solving problem (8). In order to further improve the goodness of fit, the obtained six parameters are used again as initial values for the non-linear optimization described before.

The assumption that the yield curve should usually not change much from one day to the next is the motivation for approach #5, which uses as initial values for any trading day the parameters found from the non-linear optimization on the previous trading day.⁶ However, we observed in preliminary tests that using only this approach might lead to extreme parameter values that tend to persist over longer time periods as the optimization algorithm gets trapped in a far from optimal local minimum. A remedy for this problem is to choose randomly alternative initial values that are uniformly distributed between the specified bounds (Gilli & Schumann, 2010).

This leads to the last approach #6, in which we compare for each trading day the goodness of fit obtained from solving the non-convex optimization problem for 105 different sets of initial values for the six parameters. These include 100 randomly selected sets drawn from intervals defined by the bounds in Table 1, the four sets of starting values used also by approaches #1 to #4, as well as the set of parameter estimates identified by approach #6 for the previous trading day. By selecting the parameter set with the best goodness of fit among all alternatives, approach #6 always results in the best fit according to the chosen error measure. The consideration of many sets of randomly chosen starting values in addition to those of the other approaches reduces significantly the risk that the algorithm gets trapped in a “bad” local minimum.

4 Results

In this section, we present and discuss the results obtained through the methodology described in the previous section. Section 4.1 shows comparatively the implications of approaches for selecting initial parameter values. Section 4.2 presents a comparative examination of parsimonious yield curve models and sheds light on confounding effects in the Svensson model. Section 4.3 shows the implications when preimposing restrictions on the distance between $\tau _1$ and $\tau _2$, while Section 4.4 presents robustness checks performed by considering different subsets of the data.

4.1 Implications of Approaches for Selecting Initial Parameter Values

Tables 2a and 2b show the proportion of all trading days (between 2000 and 2019) on which the various approaches for initial values lead to the best goodness of fit in terms of the lowest sum of squared errors when the Svensson model is fitted. The tables have two columns for the proportions when minimizing yield errors vs. duration-weighted price errors, i.e., price errors are divided by the modified duration of the corresponding bonds to avoid an overweighting of instruments with high duration. Table 2a shows how often approach #6 selects a solution in which one of the 100 combinations of random numbers was chosen to initialize the fitting procedure, compared to a parameter set obtained from one of the other approaches. We observe that in most cases one of the randomly selected sets of initial values leads to the best goodness of fit, followed by using the parameter values found with approach #6 on the previous day. Table 2b shows how often approaches #1 to #5 lead to the best goodness of fit. In this case, the proportions of the different approaches among the best solutions are more balanced as none of them are based on the comparison of several sets of initial values. Overall, without consideration of approach #6, using the initial values from the fitted Nelson-Siegel model (approach #2) or always using the values identified on the previous day (approach #5) result in the best goodness of fit.

Table 2 Proportion of all trading days between 2000 and 2019 when different approaches for initial values lead to the best goodness of fit

Figure 3 summarizes the goodness of fit when the yield curve is fitted with the Svensson model by minimizing yield errors using the different approaches for initial values. To assess the magnitude of the mispricing of individual instruments in terms of yield to maturity, we report here the average absolute yield error $\frac{1}{N} \sum _{i=1}^N |y_i - \hat{y}_i({\gamma })|$ in basis points (bps) of the N instruments taken into account on each trading day between 2000 and 2019. We observe a maximum and minimum value of 23.72 bps and 0.90 bps, respectively, as well as a mean of 3.67 bps regardless of which approach for initial values is chosen. Further, we observe a worse goodness of fit from late 2007 to mid 2009, which corresponds to the Financial Crisis of 2007–2008. However, this is the same for all approaches for initial values. No significant deterioration in the goodness of fit can be found during the shocks on the global markets after the 9/11 terror attacks in 2001. Further, we observe that the times of normal, flat and inverted yield curves, as well as rising and falling interest rates, are not indicators for the choice of a specific approach for initial values. Overall, we observe rather small differences (of a few basis points) in the goodness of fit between the various approaches for the selection of initial values.⁷

Fig. 3

Evolution of average absolute yield errors $\frac{1}{N} \sum _{i=1}^N |y_i - \hat{y}_i({\gamma }))|$ in basis points (bps) of the N instruments taken into account on each trading day between 2000 and 2019, when the yield curve is fitted with the Svensson model by minimizing yield errors and using different approaches for initial values. The approaches #1 to #6 are defined in Sect. 3.2

Yet, the choice of the initial values has significant implications on the stability of the resulting Svensson model parameter estimates and their interpretability. Figures 4 and 5 display the evolution of $\beta _0$ and $\beta _1$ across all trading days between 2000 and 2019 when yield errors are minimized. Obviously, the estimated parameters exhibit a more stable and intuitive pattern when initial values are derived from observed yields, as illustrated in the top and middle panels of Fig. 4 for approach #1 and #2, respectively. Also, for approach #5 we observe in the middle panels of Figure 5 a more stable pattern, but there is tendency of getting trapped in local minima with extreme parameter values. The top and bottom panels of Fig. 5 imply that the variation increases significantly when approaches #4 and #6 for initial values are applied. In particular, parameters can take very different values over consecutive trading days. This is counterintuitive, since market conditions under normal circumstances persist. Thus, the financial interpretation of parameters drops for both approaches. The optimization with the downhill simplex algorithm in approach #4 and the random sampling in approach #6 lead to larger deviations compared to the use of initial values derived directly from data. Based on these insights, approaches #4 and #6 are not recommended if the goal is to interpret parameter values for monetary policy decisions.

Fig. 4

Values of $\beta _{0}$ and $\beta _{1}$ across trading days derived from the Svensson model fitted by minimizing yield errors and using different approaches for initial values. Top panels show values when using approach #1 for initial values. Middle panels display values when using approach #2 for initial values. Bottom panels present values when using approach #3 for initial values. The approaches are defined in Sect. 3.2

Fig. 5

Values of $\beta _{0}$ and $\beta _{1}$ across trading days derived from the Svensson model fitted by minimizing yield errors and using different approaches for initial values. Top panels show values when using approach #4 for initial values. Middle panels display values when using approach #5 for initial values. Bottom panels present values when using approach #6 for initial values. The approaches are defined in Sect. 3.2

For reasons of space we have limited ourselves to the presentation of evolution of the first two parameters $\beta _0$ and $\beta _1$ since we focus on these in subsequent discussions. However, our findings concerning the stability of parameter values applies also to $\beta _2$, $\beta _3$, $\tau _1$ and $\tau _2$. This becomes evident in Table 3, which exhibits the standard deviations of all estimated parameters of the Svensson model over the entire sample period.

Table 3 Standard deviation across all trading days between 2000 and 2019 of estimated parameter values derived from the Svensson model fitted by minimizing yield errors and using different approaches for initial values, which are defined in Section 3.2

In conclusion, we suggest using initial values derived from observed yields (approaches #1 and #2) since this leads to the most stable and intuitive parameter estimates. However, we achieve a slightly better goodness of fit by using many combinations of initial values (approach #6), but at the expense of large variations in the estimated values of model parameters. Thus, this approach should rather be avoided when the interpretability of the estimated parameter values is important. In addition, simultaneously testing many initial values is computationally expensive. Using the parameter values obtained from fitting the model on the previous trading day as initial values (approach #5) provides a compromise between parameter stability and goodness of fit. However, this approach gets too often trapped in a local minimum with extreme parameter values and, thus, alternative initial values should be considered as well.

4.2 Comparative Examination of Parsimonious Yield Curve Models and Confounding Effects in the Svensson Model

This section presents a comparative examination of the Nelson-Siegel, Bliss and Svensson models. First, we compare the evolution of the level and the slope factors with a short- and a long-term spot rate. Second, we investigate the curvature factors, and find confounding effects in the two curvature factors of the Svensson model, which suggests that one of them is superfluous. Finally, we compare the models with respect to their goodness of fit and the behavior of the estimated parameter values.

The two top panels of Fig. 6 show the values of the magnitudes of the level and slope factors over time, derived from the Nelson–Siegel model fitted by minimizing yield errors and using approach #1 for initial values. The left panel shows the evolution of $\beta _0$ together with the 30 year spot rate, while the right panel illustrates the evolution of the sum $\beta _0+\beta _1$ together with the 3 month spot rate. Both market rates are given in percent and were derived from the bond price data set by bootstrapping. We observe that $\beta _{0}$ matches the spot rates for longer times to maturity (360 months), with a correlation of 0.95 during 2000–2019. Further, we observe that $\beta _{0}+\beta _{1}$ matches the spot rates for shorter times to maturity (3 months), with a correlation of 1.00 during 2000–2019. This is an empirical evidence that the magnitudes of the first two factors of the Nelson–Siegel model represent the level of the yield curve, as discussed in Sect. 2.2. We find the same evidence when using the Bliss and Svensson models and other approaches for initial values.⁸ Further, we observe an almost perfect negative correlation between $\beta _{0}$ and $\beta _{1}$ over consecutive trading days. This is illustrated in the bottom panel of Fig. 6, which shows the joint evolution of $\beta _{0}$ and $\beta _{1}$ for all trading days derived from the Nelson–Siegel model fitted by minimizing yield errors and using approach #1 for initial values. To illustrate different patterns across different trading day intervals, each plot in the panel has a unique color representing the trading day, which goes from blue for $1^{\mathrm{st}}$ of January 2000 to red for $31^{\mathrm{st}}$ of December 2019, as shown in the color bar on the right. The same colors are also used in subsequent figures. The observed high negative correlation means that the starting value of the yield curve at zero maturity $\left( \beta _{0}+\beta _{1}\right)$ remains almost constant in the corresponding trading day intervals. That is, investors’ expectations for the near future remain practically constant over consecutive trading days, even if their expectations far into the future (represented by $\beta _0$) vary. We find the same evidence when using the Bliss and Svensson models and other approaches for initial values.⁹ To sum up, the level and slope factors have a high degree of financial interpretation, which make them well suited for monetary policy decisions.

Fig. 6

Top left panel shows daily values of $\beta _{0}$ and spot rates for 360 months in percent derived from bootstrapping. The correlation between $\beta _{0}$ and the spot rates is 0.95 for the whole period of 2000–2019. Top right panel displays daily values of $\beta _{0} + \beta _{1}$ and spot rates for 3 months in percent derived from bootstrapping. The correlation between $\beta _{0} + \beta _{1}$ and the spot rates is 1.00 for the complete investigation period. Bottom panel presents joint evolution of $\beta _{0}$ and $\beta _{1}$ values for all trading days between 2000 and 2019. Each plot in the bottom panel has an unique color representing the trading day, which goes from blue for $1^{\mathrm{st}}$ of January 2000 to red for $31^{\mathrm{st}}$ of December 2019. All values of $\beta _{0}$ and $\beta _{1}$ in the three panels are derived from the Nelson-Siegel model fitted by minimizing yield errors and using approach #1 for initial values

For the curvature factors, however, we observe confounding effects. Figure 7 shows exemplary the joint evolution of daily parameter values derived from the Svensson model fitted by minimizing yield errors and using approach #2 (fit first the Nelson–Siegel model). We observe positive correlations between $\tau _{1}$ and $\tau _{2}$, as well as negative correlations between $\beta _{2}$ and $\beta _{3}$. These observations are regardless of which approach for initial values is applied, however most obvious when using approach #1, #2, #3 and #4.¹⁰ This is in line with De Pooter (2007) who reported a correlation of -0.47 between the values of $\beta _2$ and $\beta _3$ derived from the fitted Svensson model over the period 1984-2003.¹¹ The correlations observed here are even stronger. For example, for all trading days from February 2012 to May 2013 there is a correlation of 0.99 between $\tau _{1}$ and $\tau _{2}$. Furthermore, the correlation between $\beta _{2}$ and $\beta _{3}$ is -1.00 for all trading days between 2012 and 2013, as well as − 0.96 throughout all trading days between 2000 and 2019. In summary, these findings indicate difficulties in forming expectations about each curvature factor of the Svensson model, since they have innovations that are dependent on the other, as suggested by Lengwiler & Lenz (2010). Furthermore, this interconnection indicates confounding effects between the two curvature factors, implying that one of them is superfluous.

Fig. 7

Joint evolution of parameter values for all trading days between 2000 and 2019, derived from the Svensson model fitted by minimizing yield errors and using approach #2 for initial values. Each plot in the figure has an unique color representing the trading day, which goes from blue for $1^{\mathrm{st}}$ of January 2000 to red for $31^{\mathrm{st}}$ of December 2019

Figures 8a and b show parameter values for all trading days between 2000 and 2019 in ascending order derived from different models. Figure 8a shows that the values of $\tau _1$ and $\tau _2$, derived from the fitted Svensson model, are very similar and often the difference is zero. This means that the locations of the hump or trough of the curvature factors coincide, and the loadings of the third and fourth term in equation (5) become equal. As a consequence, the parameters $\beta _2$ and $\beta _3$ cannot be identified separately, and only their sum can be interpreted. Thus, the extra flexibility by introducing the additional curvature term in the Svensson model is most of the time not exploited. This is confirmed by Figure 8b, which shows the difference between the magnitude of the single curvature factor of the Nelson-Siegel model ($\beta _2$) and the sum of the two magnitudes of the curvature factors of the Svensson model ($\beta _2$ and $\beta _3$). Most of the time, differences are close to zero, and the Svensson model does not provide a better fit than the less flexible Nelson-Siegel model. In summary, these findings are another evidence of the confounding effects in the curvature factors of the Svensson model.

Fig. 8

Parameter values for all trading days between 2000 and 2019 in ascending order, when yield curve models are fitted by minimizing yield errors. Each plot in the figure has an unique color representing the trading day, which goes from blue for $1^{\mathrm{st}}$ of January 2000 to red for $31^{\mathrm{st}}$ of December 2019

To assess if and when the additional curvature factor of the Svensson model is beneficial compared to the Nelson-Siegel and Bliss models, we evaluate the goodness of fit for each individual yield curve over the whole sample period. Let $\Lambda _j^{mod}$ be the average of the absolute values of all the yield errors $\epsilon _i^{mod}({\gamma }) = y_i - \hat{y}^{mod}_i({\gamma })$ of all the instruments $i=\{1,\dots ,N\}$ given in bps for trading day j, defined as

$$\begin{aligned} \Lambda _j^{mod} = \frac{1}{N} \sum _{i=1}^N |\epsilon _i^{mod}({\gamma }) | \end{aligned}$$

where mod has the value NS, B or S indicating if the yield curve is fitted with the Nelson-Siegel, Bliss or Svensson model, respectively. Figure 9a shows $\Lambda _j^{NS}$, $\Lambda _j^{B}$ and $\Lambda _j^{S}$ obtained when the yield curve models are fitted by minimizing yield errors and using approach #1 for initial values. As before, we observe a worse goodness of fit from late 2007 to mid 2009 for all models, which corresponds to the Financial Crisis of 2007–2008. Again, no significant change in goodness of fit can be found during the shocks on the global markets after the 9/11 terror attacks in 2001. Furthermore, from the comparison with Fig. 2 we observe that times of normal, flat and inverted yield curves, as well as rising and falling interest rates, are not indicators for the choice of a specific model. We observe a better goodness of fit when using the Svensson model compared to the Nelson-Siegel model, as illustrated by the difference $\Lambda _j^{NS} - \Lambda _j^{S}$ in Fig. 9b. In addition, we observe a better goodness of fit when using the Bliss model compared to the Nelson-Siegel model, as illustrated by the difference $\Lambda _j^{NS} - \Lambda _j^{B}$ in Fig. 9c. This better goodness of fit when using the Svensson and Bliss models, compared to the Nelson–Siegel model, can be attributed to their extra flexibility. We also observe a better goodness of fit when using the Bliss model compared to using the Svensson model, even if the latter is more flexible, as illustrated by the difference $\Lambda _j^{B} - \Lambda _j^{S}$ in Fig. 9d. This stems from the fact that the optimization algorithm gets often trapped in a sub-optimal local minimum. Due to the higher dimensionality of the parameter space, the Svensson model is more sensitive to the choice of initial values when the non-convex data fitting problem is solved. Nevertheless, these differences in goodness of fit in Fig. 9b, c and d are so small that we do not consider them relevant when using the yield curve for monetary policy analysis. The difference is often close to zero, and the averages of the data shown in Fig. 9b,c and d are 0.57 bps, 0.76 bps and − 0.19 bps, respectively. In summary, we find that the extra flexibility of the Svensson model does not bring a significant contribution to the goodness of fit. It may even lead to a poorer goodness of fit compared to the less flexible Bliss model due to the challenge of identifying a “good” local optimum for the non-convex data fitting problem.¹²

Fig. 9

Evolution of the averages of absolute yield errors in basis points (bps) on each trading day j between 2000 and 2019, when yield curves are fitted with the Nelson-Siegel ($\Lambda _j^{NS}$), Bliss ($\Lambda _j^{B}$) and Svensson ($\Lambda _j^{S}$) models by minimizing yield errors and using approach #1 for initial values

To sum up, our findings confirm the statement of Söderlind & Svensson (1997) that the less flexible Nelson-Siegel model gives a satisfactory fit in many cases, as well as the conclusion of Dahlquist & Svensson (1996) that it is well above what is needed for monetary policy analysis. In particular, our findings are consistent with those of Diebold et al. (2006) and De Pooter (2007) that the Nelson-Siegel model gives a satisfactory fit compared to more flexible models, and illustrate that a lower number of factors in the yield curve model is typically adequate (Diebold & Rudebusch, 2013).

Furthermore, we observe that the model choice has an impact on the variation of parameter values, as also found by De Pooter (2007). This becomes evident in Fig. 10, which displays the evolution of the estimated values of $\beta _0$ and $\beta _1$ when yield curves are fitted by minimizing yield errors with approach #1 for initial values. In particular, we observe most variation in parameter values for the Svensson model, as shown in the top panels of Fig. 10. However, this variation is reduced with the Bliss model (middle panels of Fig. 10). The parameter values variate least when fitting the Nelson–Siegel model (bottom panels). Moreover, we observe that the variation of parameter values is not dependent on financial crises, times of different yield curve shapes or regimes of rising or falling interest rates. A similar pattern of variation in parameter values does also apply for the other parameters, but we have omitted their presentation for reasons of space.¹³ Table 4 summarizes for all three models the standard deviations of the complete set of estimated parameters.¹⁴

Fig. 10

Estimated values of $\beta _{0}$ and $\beta _{1}$ across trading days when yield curves are fitted by minimizing yield errors and using approach #1 for initial values. Top panels show values when using the Svensson model. Middle panels display values when using the Bliss model. Bottom panels present values when using the Nelson-Siegel model

Table 4 Standard deviation across all trading days between 2000 and 2019 of estimated parameter values derived from the Svensson, Bliss and Nelson–Siegel models, respectively, fitted by minimizing yield errors and using approach #1 for initial values

Overall, if the focus is on employing the estimated parameters for monetary policy decisions, we conclude that the Nelson-Siegel model is a better choice than the Bliss and Svensson models.

4.3 Preimposing Restrictions on the Distance Between $\tau _1$ and $\tau _2$

If the motivation for the second curvature factor in the Svensson model is a better fit for the long end of the yield curve, we would expect $\tau _2 > \tau _1$. However, in our results above, where we preimpose no restrictions on the distance between $\tau _1$ and $\tau _2$ like in Gürkaynak et al. (2007), this is most often not the case, as illustrated in Fig. 8a. Furthermore, using approach #5 for initial values results in solutions with $\tau _2 < \tau _1$ for all trading days. In addition, regardless of the approach for initial values, we observe less outliers and more stability in all estimated parameter values for trading days when $\tau _2 < \tau _1$, compared to trading days when $\tau _2 > \tau _1$.¹⁵

These counter-intuitive insights, and the observation that confounding effects are partly due to correlations between $\tau _1$ and $\tau _2$, are the motivation for testing the implications on our findings when preimposing restrictions on the distance between $\tau _1$ and $\tau _2$. First, we regenerate results when making sure that $\tau _2$ is larger than $\tau _1$, like in Ferstl & Hayden (2010) and Sasongko et al. (2019). Second, we regenerate results when making sure that $\tau _1$ is larger than $\tau _2$, like in De Pooter (2007). In particular, we investigate the implications on our findings by refitting the yield curve with the Svensson model by minimizing yield errors, using approach #1 for initial values and adding the constraints $\tau _2 \ge \tau _1 + 0.5$ and $\tau _1 \ge \tau _2 + 0.5$, respectively.¹⁶

Figure 11 shows yield errors when preimposing no restriction, when preimposing $\tau _2 \ge \tau _1 + 0.5$ and preimposing $\tau _1 \ge \tau _2 + 0.5$, respectively. We observe that in most cases the restrictions have an insignificant effect on the goodness of fit. Furthermore, we still observe positive correlations between $\tau _{1}$ and $\tau _{2}$ and negative correlations between $\beta _{2}$ and $\beta _{3}$, which indicates that confounding effects in the curvature factors of the Svensson model persist.¹⁷ However, we observe that preimposing restrictions on the distance between $\tau _1$ and $\tau _2$ has a significant effect on the variation in parameter values across trading days. Indeed, the variation of estimated values increases for all parameters. This is displayed in Fig. 12, in which we again restrict ourselves to the presentation of $\beta _0$ and $\beta _1$. The increasing variation can also be seen in Table 5, which exhibits the standard deviations of the complete parameter set for the entire sample period. Based on these results, we recommend not to preimpose restrictions on the distance between $\tau _1$ and $\tau _2$ when using the yield curve for monetary policy decisions.

Fig. 11

Evolution of average absolute yield errors $\frac{1}{N} \sum _{i=1}^N |y_i - \hat{y}_i({\gamma }))|$ in basis points (bps) of the N instruments taken into account on each trading day between 2000 and 2019, when the yield curve is fitted with the Svensson model by minimizing yield errors, using approach #1 for initial values and preimposing different restrictions on the distance between $\tau _1$ and $\tau _2$

Fig. 12

Estimated values of $\beta _{0}$ and $\beta _{1}$ across trading days when yield curves are fitted to the Svensson model by minimizing yield errors and using approach #1 for initial values. Top panels show values when preimposing no restrictions on the distance between $\tau _1$ and $\tau _2$. Middle panels display values when preimposing $\tau _2 \ge \tau _1 + 0.5$. Bottom panels present values when preimposing $\tau _1 \ge \tau _2 + 0.5$

Table 5 Standard deviation across all trading days between 2000 and 2019 of estimated parameter values derived from the Svensson model fitted by minimizing yield errors, using approach #1 for initial values and preimposing different restrictions on the distance between $\tau _1$ and $\tau _2$

4.4 Robustness Checks

In this section, we present case studies where we use subsets of the total data set to regenerate results for checking the robustness of our findings. Our focus is on confounding effects in the curvature factors of the Svensson model, parameter stability and goodness of fit. Initial values for the fitting procedure are derived from approaches #1 and #2, respectively. For reasons of space we show only results for the former.¹⁸ The various case studies are (i) excluding certain instruments that behave differently than others, namely Treasury bills, and (ii) controlling for the observed clustering of instruments across time to maturity by restricting the maturity segments with different concentration of available instruments. The effects on goodness of fit in both cases are presented in Figure 13, which compares yield errors when using the different subsets of data.

Fig. 13

Evolution of average absolute yield errors $\frac{1}{N} \sum _{i=1}^N |y_i - \hat{y}_i({\gamma }))|$ in basis points (bps) of the N instruments taken into account on each trading day between 2000 and 2019, when the yield curve is fitted with the Svensson model by minimizing yield errors, using approach # 1 for initial values and for different subsets of data

In the first case study, we investigate the effects of excluding Treasury bills from the data. This was suggested by Gürkaynak et al. (2007), who motivated it with the observation that bills are priced measurably differently from notes and bonds with less than one year to maturity due to liquidity, taxes and other effects. They referred here to Duffee (1996), who found that movements in bill yields are often disconnected from yields of notes and bonds. However, we find that excluding Treasury bills from the data has an insignificant effect on the goodness of fit, as shown in Fig. 13. In addition, the effect on the evolution of parameters is marginal, which can be seen in the middle panels of Fig. 14 for the example of $\beta _0$ and $\beta _1$, but the findings prevail for the other parameters as well. This can be seen also in Table 6, which shows again the standard deviations of estimated parameters across all trading days between 2000 and 2019 when different subsets of data are used. Insignificant effects on the goodness of fit and parameter stability are also observed when fitting the Nelson–Siegel model. We still observe positive correlations between $\tau _{1}$ and $\tau _{2}$ and negative correlations between $\beta _{2}$ and $\beta _{3}$, which indicate confounding effects in the curvature factors of the Svensson model.¹⁹

Fig. 14

Estimated values of $\beta _{0}$ and $\beta _{1}$ across trading days when yield curves are fitted to the Svensson model by minimizing yield errors and using approach #1 for initial values. Top panels show values when including all instruments in the data. Middle panels display values when excluding Treasury bills. Bottom panels present values when including only instruments up to 10 years to maturity

Table 6 Standard deviation across all trading days between 2000 and 2019 of estimated parameter values derived from the Svensson model fitted by minimizing yield errors, using approach #1 for initial values and using different subsets of data

As a consequence of the Treasury’s issuing policy, certain maturity segments contain a larger number of instruments than others. This clustering is illustrated in Fig. 15a, which shows the number of instruments in the original data set per trading day within different intervals of years to maturity. Since parts of the yield curve with higher concentration of data points have a higher contribution to the error measure, the goodness of fit in maturity segments with less observations may degrade. Therefore, we investigate in a second case study whether a clustering of instruments has any impact on our findings. First, we exclude instruments separated by less than 45 days to maturity. In particular, if any two instruments at any specific trading day are separated by less than 45 days to maturity, the instrument with the smallest outstanding amount is excluded. The number of instruments per trading day within different intervals of years to maturity after this exclusion is shown in Fig. 15b. Second, since various authors restrict their data sets to instruments with maturities up to 10 years only, we investigate if excluding the very long end of the yield curve affects our findings. We observe that confounding effects in the curvature factors of the Svensson model persist. The smaller number of instruments in the data leads to a higher variation in parameter values for both procedures. This is evident in the standard deviations across all trading days between 2000 and 2019 shown in Table 6, as well as in the bottom panels of Fig. 14 that show the evolution of $\beta _0$ and $\beta _1$ when including only instruments up to 10 years to maturity. Findings prevail when considering the evolution of parameters after excluding instruments separated by less than 45 days to maturity, also with respect to $\beta _{2}$, $\beta _{3}$, $\tau _{1}$ and $\tau _{2}$.²⁰ In particular, the higher variation in the values of $\beta _{0}$ in the case of including only instruments up to 10 years to maturity means that including instruments with maturities up to 30 years leads to a better approximation of the long end of the yield curve.

Fig. 15

Number of instruments in the data per trading day within different intervals of years to maturity

In conclusion, we observe that goodness of fit and confounding effects in the curvature factors hold for all cases. However, for the sake of the parameter stability, we recommend not to reduce the clustering of instruments across time to maturity.²¹

5 Conclusions

We assess and make recommendations concerning modelling and estimation choices relevant for central banks when using parsimonious yield curve models for monetary policy decisions. In this context, we illustrate that winning the objective function race is not a relevant criterion since different choices result in negligible differences in the goodness of fit, rather the stability of model parameters becomes relevant as they have a specific financial interpretation. For every trading day between 2000 and 2019, we fit the Nelson–Siegel, Svensson and Bliss models to observed US Treasury securities with maturities up to 30 years. Following the practice of central banks, we do not fix any model parameters. Consequently, parameters are estimated by solving a non-linear optimization problem, which requires a predefinition of initial parameter values. Our study is the first in the literature that compares the stability of estimated model parameters (i) among different parsimonious models and (ii) for different approaches for predefining initial parameter values. Furthermore, it investigates the impact of (iii) constraints on the parameters that define the location of humps and troughs as well as (iv) filter criteria for the selection of instruments considered in the estimation on parameter stability, confounding effects and goodness of fit.

To obtain the most stable and intuitive parameter estimates over time, we recommend that central banks employ the Nelson-Siegel model by taking initial parameter values derived from the observed yields. Our findings are consistent with previous studies (Diebold & Rudebusch, 2013) and confirm that the Nelson–Siegel model gives a satisfactory fit compared to more flexible models (Diebold et al., 2006; De Pooter, 2007) and is also well above what is needed for monetary policy analysis (Söderlind & Svensson, 1997; Dahlquist & Svensson, 1996). The recommendation of using the Nelson-Siegel model is further supported by the concluding result that the Svensson model is often superfluous due to confounding effects between the curvature factors. In general, our findings hold regardless of whether parameters are estimated by minimizing yield errors or duration-weighted price errors. We observe that neither regimes of normal, flat or inverted yield curve shapes, financial crises, rising/falling interest rates are indicators for the choice of a specific model.

The observed confounding effects in the Svensson model are partly due to correlations between the parameters controlling the location of the humps or troughs of the yield curve. Consequently, we study the implications of constraining them as suggested by De Pooter (2007), Ferstl & Hayden (2010) and Sasongko et al. (2019). Indeed, to our knowledge, we are the first to investigate the implications of such constraints on the stability of estimated parameters and the goodness of fit. Our findings suggest not to use such constraints as they result in reduced parameter stability, while the impacts on confounding effects and goodness of fit are insignificant.

Since there is evidence that yields of Treasury bills are often disconnected from yields of notes and bonds (Duffee, 1996; Gürkaynak et al., 2007), we investigate the impact of excluding them from the data. Our finding is that an exclusion of bills has insignificant impact on the goodness of fit, parameter stability and confounding effects in the Svensson model. Furthermore, as the maturity dates of observed bonds are not uniformly distributed along the curve, we assess the impact of a concentration of instruments in certain maturity segments on our results. An elimination of instruments in segments with higher concentration neither improves the goodness of fit nor eliminates confounding effects. In particular, we observe that the exclusion of instruments with maturities above ten years, which is often done in empirical studies, leads to higher parameter instability. Therefore, including also the available long-term instruments provides a better approximation for the long end of the yield curve.

Appendix A. Numerical Solution

The fitting procedures of all parsimonious models are implemented in Matlab. The spot rates shown in Fig. 2 were derived from prices of Treasury instruments with the function “bootstrap” from the Financial Instrument Toolbox. While the latter contains also standard functions to fit the Nelson–Siegel and the Svensson model, we have implemented our own estimation routines for all three models that allow also to take into account constraints like on the distance between parameters. We use the interior point solver “fmincon” from the Optimization Toolbox to solve the non-linear optimization problem (8) with optional constraints and analytical gradients when appropriate. For the minimization of yield errors without additional constraints, we used the solver “lsqnonlin”, which implements a trust-region reflective least-squares algorithm (Moré & Sorensen, 1983; Sorensen, 1997), with numerical gradients. The parameter for the termination tolerance on the first-order optimality was set to $10^{-12}$. The implementation of the Nelder-Mead method used for approach #4 is taken from the NLopt library (Johnson, 2017).

For the computationally more demanding yield curve error minimization, the solution of the most complex approach #6 that solves the non-linear optimization problem 105 times with different starting values takes about 45 minutes on a PC with Intel i7 processor at 1.9 GHz. This is numerically feasible in the daily practice of a financial institution. However, we used the NTNU IDUN computing cluster (Själander et al., 2019) to carry out the various case studies for each of the 4996 trading days. Each study was performed twice: For the minimization of errors in yields and errors in duration-weighted prices. The cluster has more than 70 nodes and 90 GPGPUs. Each node contains two Intel Xeon cores, at least 128 GB of main memory, and is connected to an Infiniband network. Half of the nodes are equipped with two or more Nvidia Tesla P100 or V100 GPGPUs. Idun’s storage is provided by two storage arrays and a Lustre parallel distributed file system.