Estimating the Unrestricted and Restricted Liu Estimators for the Poisson Regression Model: Method and Application

Abstract

This paper considers both unrestricted and restricted Liu estimators in the presence of multicollinearity for the Poisson regression model. It also considers some new estimators of the shrinkage parameter for both unrestricted and restricted Liu estimators. Based on a simulation study and its empirical application, we found that the restricted estimator outperforms the unrestricted one. Further, the restricted Liu estimator also outperforms both the unrestricted Liu and restricted Liu estimators. Hence, this new method is a preferred option when the coefficient vector β may belong to a linear sub-space defined by Rβ = r.

1 Introduction

In empirical applications in economics when modeling the gene expression data, the dependent variables are often in the form of non-negative integers of counts, for example, in analyzing the determinants of the number of patents by a firm or in biostatistics. In such a situation, a common distributional assumption for the dependent variable $y_{i}$ is that it follows a Poisson distribution. More specifically, it is distributed as $Po\left( {\mu_{i} } \right)$, where $\mu_{i} = \exp \left( {{\mathbf{x}}_{{\mathbf{i}}} '{\varvec{\upbeta}}} \right)$, ${\mathbf{x}}_{{\mathbf{i}}}$ is the ith row of ${\mathbf{X}}$ which is a $n \times \left( {p + 1} \right)$ data matrix with p explanatory variables and ${\varvec{\upbeta}}$ is a $\left( {p + 1} \right) \times 1$ vector of coefficients. The parameter for the unrestricted Poisson regression model is usually estimated using the iterative weighted least squares (IWLS) algorithm as:

$$ {\varvec{\upbeta}}_{ML} {\mathbf{ = }}\left( {{\mathbf{X}}'{\hat{\mathbf{W}}\mathbf{X}}} \right)^{ - 1} \left( {{\mathbf{X}}'{\mathbf{\hat{W}\hat{z}}}} \right) , $$

(1)

where ${\hat{\mathbf{W}}} = diag\left[ {\hat{\mu }_{i} } \right]$ and ${\hat{\mathbf{z}}}$ is a vector where the ith element equals $\hat{z}_{i} = \log \left( {\hat{\mu }_{i} } \right) + \frac{{y_{i} - \hat{\mu }_{i} }}{{\hat{\mu }_{i} }}$. Hence, it is an iterative maximum likelihood (ML) procedure. As has been shown by Kaçiranlar and Dawoud (2018), Månsson et al. (2012) and Türkan and Özel (2016) among others this estimator is sensitive to multicollinearity. A common solution to this problem is applying the ridge regression method (Hoerl and Kennard 1970). Another widely used method is applying the Liu type estimator introduced by Liu (1993) and introduced in the context of the Poisson regression model by Månsson et al. (2012). This method has certain advantages over the ridge regression method since it is a linear function of the biasing parameter d. Therefore, this method has become more popular during recent years (see, for example, Akdeniz and Kaciranlar 1995; Kaciranlar 2003). The unrestricted Liu type estimator for the Poisson regression model is defined by Månsson et al. (2012) as:

$$ {\hat{\mathbf{\beta }}}_{{\mathbf{d}}} {\mathbf{ = }}\left( {{\mathbf{X'\hat{W}X + I}}} \right)^{{{\mathbf{ - 1}}}} \left( {{\mathbf{X'\hat{W}X + }}d{\mathbf{I}}} \right){\hat{\mathbf{\beta }}}_{{{\mathbf{ML}}}} $$

(2)

where $0 \le d \le 1$. Different versions of this estimator for count data models have been considered by Asar and Genç (2017), where a two parameter estimator is considered, Asar (2018), where the author discussed different perspectives on this estimator and Türkan and Özel (2018) in which the authors considered a jack-knifed estimator. A review article with detailed literature review is written by Algamal (2018). In some situations, the coefficient vector ${\varvec{\upbeta}}$ is suspected to belong to a linear sub-space:

$$ {\mathbf{R\beta = r}} , $$

(3)

where R is an qxp matrix of full rank with q < p and r is an qx1 vector. Under this restriction, the restricted estimator is more efficient than the OLS estimator. This method has been considered by several authors for the linear regression model (Alheety and Kibria 2009; Ehsanes Saleh and Golam Kibria 1993). The restricted maximum likelihood estimator (RMLE) of β suggested by Kibria and Saleh (2012) is given by:

$$ {\hat{\mathbf{\beta }}}_{{\mathbf{R}}} {\mathbf{ = \hat{\beta }}}_{{{\mathbf{ML}}}} {\mathbf{ - \hat{C}}}^{{{\mathbf{ - 1}}}} {\mathbf{R'}}\left[ {{\mathbf{R\hat{C}}}^{{{\mathbf{ - 1}}}} {\mathbf{R'}}} \right]^{{{\mathbf{ - 1}}}} \left( {{\mathbf{R\hat{\beta }}}_{{{\mathbf{ML}}}} {\mathbf{ - r}}} \right) , $$

(4)

where ${\mathbf{\hat{C} = X'\hat{W}X}}$. However, the issue of multicollinearity still exists since the inverse of ${\hat{\mathbf{C}}}$ is instable as it is near singular. Therefore, the estimated coefficient vector has a high variance. As a solution one can use a combination of the Liu type estimator in Eq. (2) and the restricted estimator in Eq. (4). Kaçiranlar et al. (1999) have already done this and it has also been used by many others (Kibria and Saleh 2012; Li and Yang 2010; Yang and Xu 2009). Also for the logit model, Şiray et al. (2015) suggested the following estimator:

$$ {\hat{\mathbf{\beta }}}_{{{\mathbf{R,Liu}}}} {\mathbf{ = \hat{F}}}_{{\mathbf{d}}} {\hat{\mathbf{\beta }}}_{{{\mathbf{ML}}}} {\mathbf{ - \hat{F}}}_{{\mathbf{d}}} {\hat{\mathbf{C}}}^{{{\mathbf{ - 1}}}} {\mathbf{R'}}\left[ {{\mathbf{R\hat{C}}}^{{{\mathbf{ - 1}}}} {\mathbf{R'}}} \right]^{{{\mathbf{ - 1}}}} \left( {{\mathbf{R\hat{\beta }}}_{{{\mathbf{ML}}}} {\mathbf{ - r}}} \right) . $$

(5)

where ${\hat{\mathbf{F}}}_{{\mathbf{d}}} {\mathbf{ = }}\left( {{\mathbf{X'\hat{W}X + I}}} \right)^{{{\mathbf{ - 1}}}} \left( {{\mathbf{X'\hat{W}X + }}d{\mathbf{I}}} \right)$. This estimator has later been considered in Månsson et al. (2016), Wu and Asar (2017) and Varathan and Wijekoon (2018). The purpose of our paper is to introduce the restricted estimator and the restricted Liu type estimator in the context of the Poisson regression model. We also introduce some new estimators for the shrinkage parameter d. The new methods are mainly evaluated using a simulation study where one can clearly see the benefits of applying a restricted estimator.

The rest of the paper is organized as follows: Sect. 2 gives the statistical methodology and estimation technique. A simulation study has been conducted in Sect. 3 and Sect. 4 analyzes real life data to illustrate our findings. Some concluding remarks are given in Sect. 5.

2 Statistical Methodology

This section starts with the MSE properties of different estimators and then suggests some estimators for the shrinkage parameter d.

2.1 MSE Properties of Different Estimators

This section first considers the MSE functions of the estimators (a detailed discussion on the derivations of the MSE functions for the Liu model are found in Månsson et al. 2012) and the expressions are presented as:

$$ MSE\left( {{\hat{\mathbf{\beta }}}_{{{\mathbf{ML}}}} } \right) = \sum {\frac{1}{{\lambda_{j} }}} $$

(6)

$$ MSE\left( {{\hat{\mathbf{\beta }}}_{d} } \right) = \sum\limits_{{}}^{{}} {\frac{{\left( {\lambda_{j} + d} \right)^{2} }}{{\lambda_{j} \left( {\lambda_{j} + 1} \right)^{2} }}} + \left( {d - 1} \right)^{2} \sum\limits_{{}}^{{}} {\frac{{\alpha_{j}^{2} }}{{\left( {\lambda_{j} + 1} \right)^{2} }}} $$

(7)

where $\alpha_{j}^{2}$ corresponds to the jth element of ${\varvec{\upgamma \upbeta }}$ and ${\varvec{\upgamma}}$ is the eigenvector defined so that ${\mathbf{X'WX = \gamma '\varLambda \gamma }}$, where ${\varvec{\Lambda}}$ equals $diag\left( {\lambda_{j} } \right)$ and λ_i are eigenvalues of the matrix X’WX. Here it is clear that the Liu estimator can be superior to the ML estimator if one can find a value of d such that an increase in MSE due to the bias in the second term in Eq. (7) is smaller than the decrease in the variance in the first term (for details see Månsson 2013). The MSE functions for the restricted estimator and the restricted Liu type of estimator are discussed in detail in Månsson et al. (2016) and shown as:

$$ MSE\left( {{\hat{\mathbf{\beta }}}_{{\mathbf{R}}} } \right) = tr\left( {\mathbf{A}} \right) = \sum\limits_{{}}^{{}} {b_{jj} } $$

(8)

$$ MSE\left( {{\hat{\mathbf{\beta }}}_{{{\mathbf{R,Liu}}}} } \right) = \sum\limits_{{}}^{{}} {\frac{{\left( {\lambda_{j} + d} \right)^{2} }}{{\left( {\lambda_{j} + 1} \right)^{2} }}} b_{jj} + \left( {d - 1} \right)^{2} \sum\limits_{{}}^{{}} {\frac{{\alpha_{j}^{2} }}{{\left( {\lambda_{j} + 1} \right)^{2} }}} $$

(9)

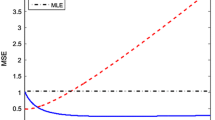
where ${\mathbf{A = C}}^{{{\mathbf{ - 1}}}} {\mathbf{ - C}}^{{{\mathbf{ - 1}}}} {\mathbf{R'}}\left( {{\mathbf{RC}}^{{{\mathbf{ - 1}}}} {\mathbf{R'}}} \right)^{{{\mathbf{ - 1}}}} {\mathbf{RC}}^{{{\mathbf{ - 1}}}}$ and $b_{jj}$ are the inverse of the eigenvalues of A matrix. The effect of multicollinearity is that some of the eigenvalues of the X’WX matrix are small which inflates the MSE of the restricted Poisson estimator. However, it is possible to find a value of the shrinkage parameter d such that the restricted Liu estimator outperforms the restricted estimator (see Månsson et al. 2016).

2.2 Estimation of the Shrinkage Parameter

Following Månsson (2013) we suggest the following estimators of the shrinkage parameter d for the unrestricted Liu estimator:

$$ D1 = \hbox{max} \left( {0,\frac{{\hat{\alpha }_{\hbox{max} }^{2} - 1}}{{\frac{1}{{\hat{\lambda }_{\hbox{max} } }} + \hat{\alpha }_{\hbox{max} }^{2} }}} \right),\quad D2 = \hbox{max} \left( {0,median\left( {\frac{{\hat{\alpha }_{j}^{2} - 1}}{{\frac{1}{{\hat{\lambda }_{j} }} + \hat{\alpha }_{j}^{2} }}} \right)} \right)D3 = \hbox{max} \left( {0,\frac{1}{p}\sum\limits_{j}^{J} {\frac{{\hat{\alpha }_{j}^{2} - 1}}{{\frac{1}{{\hat{\lambda }_{j} }} + \hat{\alpha }_{j}^{2} }}} } \right) $$

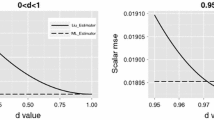
The first one is a version of the Hoerl and Kennard (1970 ) estimator and the other two are based on Kibria (2003). For the restricted Poisson estimator, we follow Månsson et al. (2016) and suggest the following estimators:

$$ \begin{aligned} D1 & = \hbox{max} \left( {0,\frac{{\hat{\alpha }_{\hbox{max} }^{2} - 1}}{{\frac{1}{{\hat{\lambda }_{\hbox{max} } }} + \hat{\alpha }_{\hbox{max} }^{2} }}b_{jj,\hbox{max} } } \right),\quad D2 = \hbox{max} \left( {0, \, median\left( {\frac{{\alpha_{j}^{2} - \lambda_{j} }}{{b_{jj} + \alpha_{j}^{2} }}b_{jj} } \right)} \right) \\ {\text{and}}\;D3 & = \hbox{max} \left( {0, \, \frac{1}{p}\sum\limits_{j = 1}^{p} {\frac{{\alpha_{j}^{2} - \lambda_{j} }}{{b_{jj} + \alpha_{j}^{2} }}b_{jj} } } \right). \\ \end{aligned} $$

We propose the following new estimators: D4 = min (D1, D2, D3), D5 = median (D1, D2, D3) and D6 = max (D1, D2, D3). This is done for both the unrestricted and restricted estimators.

3 Simulation Study

Since a theoretical comparison of the estimators is not possible, in this section we do a simulation study to compare the performance of the shrinkage estimators.

3.1 Simulation Techniques

Since the dependent variable is count, it is generated using pseudo-random numbers from the Poisson distribution with mean, μ_i, i.e. $Po\left( {\mu_{i} } \right)$ where:

$$ \mu_{i} = \exp \left( {\beta_{0} + \beta_{1} x_{i1} + \cdots + \beta_{p} x_{ip} } \right),\quad i = 1,2, \ldots ,n,\quad j = 1,2, \ldots ,p $$

(10)

The parameter values in Eq. (10) are chosen so that sum of squared parameters equals one. The main factor we chose to vary is the degree of correlation between the explanatory variables which is defined as ρ. We consider the following three values of ρ: 0.80, 0.90, and 0.95. Following Kibria (2003), we generate explanatory variables with different degrees of correlation as:

$$ x_{ij} = \left( {1 - \rho^{2} } \right)^{{\left( {1/2} \right)}} z_{ij} + \rho z_{ip} ,\quad i = 1,2, \ldots ,n,\quad j = 1,2, \ldots ,p $$

(11)

where $z_{ij}$ are pseudo-random numbers generated using the standard normal distribution. To reduce eventual start-up value effects, we discard the first 200 observations. We change the number of independent variables and set p = 4, 8 and 12. We also change the number of observations and generate models with 20, 30, 50 and 100 degrees of freedom (denoted by df). The restrictions when p = 4 are set as:

$$ R = \left[ 1\quad 0\quad - 2 \quad 1 \right]{\text{ and r}} = \left[ 0\right] $$

(12)

while the restrictions when p = 8 are:

$$ R = \left[ 1\quad 0 \quad - 2\quad 1\quad - 3\quad 1\quad 1\quad 1 \right]{\text{ and r}} = \left[ 0\right] $$

(13)

Finally, the restrictions when p = 12 are:

$$ R = \left[ {\begin{array}{*{20}c} 1 & 0 & { - 2} & 1 & { - 3} & 1 & 1 & 1 & 1 & 0 & { - 2} & 1 \\ \end{array} } \right]{\text{ and r}} = \left[ 0\right] $$

(14)

We repeated this experiment 2000 times by generating new pseudo-random numbers and then estimated MSE using the formula:

$$ MSE = \frac{{\sum\nolimits_{i = 1}^{2000} {\left( {\hat{\beta } - \beta } \right)^{2} } }}{2000} , $$

(15)

where $\hat{\beta }$ is the estimated parameter for the restricted estimator or the restricted Liu estimator and $\beta$ is the true value of the parameter.

3.2 Results

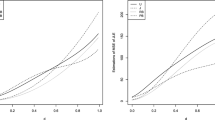
The simulated MSE values for the unrestricted and restricted estimators are presented in Tables 1 and 2 for p = 4; in Tables 3 and 4 for p = 8; and in Tables 5 and 6 for p = 8. To save space, we only give the MSE values graphically for p = 4 in Figs. 1 and 2 for unrestricted and restricted estimators respectively. In the appendix the result for the proportion of nonzero values of d are shown in Tables 11, 12, 13. The proportions are the same for the unrestricted and the restricted estimators. One can see that the degree of correlation increases the proportion of nonzero values decreases since the instability increases. The reverse effect may also be noticed for the sample size. The estimator with the least non-zero values is the optimal ones since they tend to induce more bias which is necessary to combat the multicollinearity problem. The pattern is the same for all p, df and ρ. One can see that the MSE values for all the estimators increase with the number of explanatory variables and the degree of multicollinearity and decrease with an increase in the number of observations. As can be observed from the tables and figures the MSE for the unrestricted ML estimator is always higher than the restricted estimator. There is always (for all sample sizes and different number of explanatory variables) a benefit in using the restricted estimator when the restriction holds. Further, we also observe that the unrestricted Liu estimator outperforms both the restricted and unrestricted ML estimators in the presence of multicollinearity. One can also see that the performance of the estimators of the shrinkage parameter is fairly similar. However, the new estimator D4 consistently performs better than the other estimators. The potential explanation for this is that by using information from three different estimators we can find one that is usually closer to the optimal value.

Table 1 Estimated MSE for unrestricted Poisson regression model for p = 4

Table 2 Estimated MSE for restricted Poisson regression model for p = 4

Table 3 Estimated MSE for unrestricted Poisson regression model for p = 8

Table 4 Estimated MSE for restricted Poisson regression model for p = 8

Table 5 Estimated MSE for unrestricted Poisson regression model for p = 12

Table 6 Estimated MSE for restricted Poisson regression model for p = 12

Fig. 1

Estimated MSE when p = 4 for the unrestricted estimator

Fig. 2

Estimated MSE when p = 4 for the restricted estimator

4 Empirical Application

In this empirical application, we use a dataset from Cameron and Trivedi (2013) to estimate a recreation demand function. This is survey data on the number of recreational boating trips to Lake Somerville, East Texas in 1980. We use some explanatory variables where we focus on the cost of taking a trip to that particular lake and also to competing or substitute boating attractions at Lake Conroe and Lake Houston. When considering competitors’ prices in this demand system, it is expected that we will find multicollinearity since the costs are not independent. The correlation matrix is given in Table 7 in which one can see that all prices are correlated with at least a value of 0.87 as the correlation coefficient. This indicates a multicollinearity problem.

Table 7 Correlation matrix

When looking at the coefficients of the unrestricted ML estimator in Table 8 one can see that the value is negative for lakes Conroe and Sommerville and positive for Lake Houston. The negative coefficient for Lake Conroe is not as per theory since an increase in a competitor’s cost should increase demand for the others. This may be due to multicollinearity as it may produce a wrong sign (Hoerl and Kennard 1970). Excluding this variable has only a very marginal effect on the Akaike Information Criteria (it increases from 3978 to 3993). When Lake Houston’s price is excluded AIC increases to over 5000. The counter intuitive value of the coefficient and the marginal effect that this variable actually has leads us to the following restriction:

$$ R = \left[ { 0 { 1}\;\;\;\; \, 1} \right]{\text{ and r}} = \left[ 0\right] $$

(16)

Table 8 The estimated coefficients

Hence, we assume that a substitution effect exists only between Lake Somerville and Lake Houston. The coefficients for the full sample for both the restricted and unrestricted estimators is provided in Table 8. The largest effect is for Lake Conroe where the coefficient remains negative but is pushed towards zero indicating no substitution effect. The estimated coefficients are fairly similar for both ML and shrinkage estimators. This in all probability is due to the large sample size (660 observations). To illustrate the differences in the methods we chose to bootstrap the different observations. This is also done to link the results of our simulation study to empirical applications by changing the sample size. We chose to bootstrap 50, 100 and the full sample which corresponds to 660 observations. The full sample’s standard errors are standard ones reported and associated with the coefficients in Table 8. The bootstrapped standard errors for the shrinkage estimators are given in Tables 9 and 10 for the unrestricted and restricted estimators respectively. By bootstrapping different observation (50, 100 and the full sample of 660 observations) one can clearly see that the standard error decreases for all estimators as the sample size increases; this is as expected from theory and the simulation study. We also see that the benefits of using a shrinkage estimator are higher for a small number of observations since a decrease (compared to ML) in standard errors is more significant in such a situation. Further, the standard errors are smaller for all sample sizes for the restricted estimator. The unrestricted Liu estimator is also better than the corresponding unrestricted ML estimator. But when we observe the results of the simulation study, it is the restricted Liu estimator that has the lowest standard errors. It is always the estimator D4 that minimizes the bootstrapped standard errors.

Table 9 Standard errors for the unrestricted estimator

Table 10 Standard errors for the restricted estimator

5 Summary and Concluding Remarks

This paper introduces the unrestricted and restricted Liu estimators for the Poisson regression model. We also introduced some new estimators of d based on different percentiles of existing estimators. Using simulation techniques, we showed that the restricted estimator outperformed the unrestricted one. We also found that the restricted Liu type estimator was superior to the restricted Poisson estimator in the presence of multicollinearity. Our study also shows that the new estimator D4 always has the lowest MSE. Finally, we illustrated the benefit of the new method using an empirical application where the demand for recreational boat trips was studied and once again we found that the proposed D4 estimator performed the best and may be recommended for practitioners.

Appendix

See Tables 11, 12 and 13.

Table 11 Proportion of nonzero d for both restricted and unrestricted Poisson regression model for p = 4

Table 12 Proportion of nonzero d for both restricted and unrestricted Poisson regression model for p = 8

Table 13 Proportion of nonzero d for both restricted and unrestricted Poisson regression model for p = 12