Abstract
The imperfect decision-making of human buyers participating in retail markets varies from fundamental models that assume rational economic choices: even in markets with identical items human buyers are not rational, i.e., buyers do not always choose the cheapest option. Recent developments in artificial intelligence and e-commerce enable market participation by software agents that are (almost) perfectly rational due to their computational capacity. However, the increasing degree of buyers’ rationality might have unfavorable effects on retail markets with regards to the competition between sellers and the resulting prices. In this paper, we study the effects of varying degrees of buyers’ rationality on the competition and the prices buyers face in retail markets with identical items. We use the multinomial logit function to model different degrees of buyers’ rationality. We further model the competition between sellers using k-level reasoning: each seller computes the price to offer (best response strategy) with regards to its belief for the competition. First, we derive an analytical best response strategy (price) of a seller given the competing prices and the degree of buyers’ rationality, and show that there exists an optimal degree of buyers’ rationality that minimizes the price. Last, we use evolutionary game theory to show that perfect rationality leads to unstable competition dynamics increasing the overall cost for buyers. In contrast, bounded rationality leads to smoother dynamics and lower cost for buyers. Our insights raise the need to revisit design objectives for software agents in retail markets in light of their wider systematic impact.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Classical game theoretical models that study strategic interactions between self-interested decision-makers (agents) assume the presence of intelligent and rational agents (Nisan et al. 2007; Nash 1950; Sutton and Barto 1998). However, the application of these models in specific domains mitigates the rationality assumption since agents do not usually have perfect knowledge of the environment (Russell and Thaler 1985). Economic markets and consequently economic decisions of human buyers that participate in these markets is one instance where agents do not exhibit rational behavior (Conlisk 1996; Rubinstein 1998). Bounded rationality is a fundamental model that studies the imperfect decision-making of otherwise rational agents due to, e.g., imperfect information, limited computational resources or decision time (Simon 1982). Without perfect information, a bounded rational decision-maker may act rationally over a limited set of choices. For the remainder of this paper, we describe rational agents as perfectly rational, while bounded rational agents are agents of lower (unspecified) degree of rationality.
Automated agents already operate in agent-mediated e-commerce (He et al. 2003; Guttman et al. 1999; Maes et al. 1999), and it is inevitable that in future economies human will be replaced by software as a principal agent of economic decision making (Marwala and Hurwitz 2017). In addition, recent advancements in e-commerce and fields of Artificial Intelligence such as Deep Learning (Goodfellow et al. 2016) and Automated Negotiation (Baarslag et al. 2017) illustrate the potential to further enhance the abilities of agents in the complex settings of economic markets. It is therefore of great interest to study the effects that perfectly rational decision makers have on fundamental economic paradigms such as retail markets, and try gain further insights in order to answer the following question: should the behavior of self-interested agents be made perfectly rational?
In this paper, we consider retail markets where sellers compete by offering prices for identical items to buyers, e.g., electricity markets. Each seller has a private cost for the items, e.g., procurement or production cost, and an infinite inventory of items. Sellers offer items to buyers at specific prices simultaneously in order to control a high market share and increase their profits. Assuming that buyers are perfectly rational (i.e., they choose the lowest price with probability one), this is known as the Bertrand competition, of which the Nash equilibrium is the competitive price in the case that sellers have the same private costs (Bertrand 1988). At the competitive price equilibrium, each seller sets a price equal to its private cost and market is shared equally among the sellers; no seller has an incentive to deviate from the competitive price since a higher price results in zero market share, and a lower price in negative utility for the seller.
The resulting competitive price equilibrium is formed under the following assumptions: (i) sellers have no model of opponent sellers, and thus no information regarding the competing prices, and (ii) buyers are perfectly rational, i.e., they select the lowest price with probability one. However, assumption (i) is not trivial in repeated markets where sellers can observe opponent prices and therefore model their competition (i.e., opponent modeling) (Albrecht and Stone 2017). Also, assumption (ii) does not hold in practice, unless we consider small-scale markets with limited options for buyers and thus perfect knowledge.
Motivated by assumptions (i) and (ii), we study the effects of different degrees of buyers’ rationality in retail markets on the competition and consequently the resulting prices for the buyers. To study the influence of varying degrees of buyers’ rationality we use the multinomial logit function (McFadden 1975; Anas 1983), which is widely used in the economics literature to model buyers’ stochastic decision-making when facing different prices. Furthermore, to model the competition between sellers we use k-level reasoning (Stahl and Wilson 1995; Camerer et al. 2004). In k-level reasoning, k denotes the depth of strategic reasoning of an agent. A 0-level agent has no model of the opponents and therefore is not strategic, 0-level agent uses a fixed or a random strategy. A k-level agent reasons with regards to its belief for the reasoning levels of its opponents. According to the standard assumption of k-level reasoning, a k-level agent believes to be facing \((k-1)\)-level agents. In the studied setting, we analyze the best response strategy of a strategic seller (i.e., the price to offers to buyers) with regards to the prices posted by the competition. We further use evolutionary game theory to study the evolution of the competition in repeated interactions between sellers for a given degree of buyers’ rationality.
The main contributions of this work can be summarized as follows:
-
First, we derive an analytical best response strategy of a strategic seller given a set of opponent prices and the degree of buyers’ rationality.
-
Interestingly, we show that buyers maximize their utility by not being perfectly rational in their choices.
-
We use evolutionary dynamics to study the evolution of competition between sellers and show an evolutionary advantage of higher-level reasoning sellers when using the standard assumption of k-level reasoning.
-
We extend the standard assumption of k-level reasoning towards a more realistic belief model for the competition (true distribution over lower reasoning levels), and we observe that perfect rationality contributes to monopolistic behavior of higher-level reasoning sellers and unstable competition dynamics.
-
In contrast to perfect rationality, we show that bounded rationality leads to smoother competition dynamics and higher benefits for buyers.
To the best of our knowledge, we present the first study that combines bounded rationality in the price selection of buyers and opponent modeling for the sellers (k-level reasoning) within the Bertrand competition model to study the effects of different degrees of buyers’ rationality on the competition and prices.
Overall, the main objective of this work is not limited to study the consequences of varying degrees of buyers’ rationality in retail markets with identical items on the competition between sellers and the resulting evolutionary dynamics of the competition; it also adds fundamental knowledge that can be used for the design of future agent-based automated markets with commodities (e.g., future electricity markets), and general competitive multi-agent settings with heterogeneous agents.
The remainder of this paper is organized as follows: Sect. 2 provides an overview of the literature that is relevant to our work. Next, in Sect. 3 we introduce the market model. In Sect. 4 we derive analytical best response strategies for strategic sellers with regards to prices offered by the competition and the degree of buyers’ rationality, we also present experiments to verify our theoretical findings. In Sect. 5 we introduce concepts from evolutionary game theory and use them to show the effects of the degree of buyers’ rationality in repeated interactions in retail markets. In Sect. 6 we provide a discussion on the insights of our results. Last, in Sect. 7 we conclude this paper.
2 Related Work
Bertrand competition and many of its variants is a well-studied market model in the literature (Spulber 1995; Dufwenberg and Gneezy 2000; Caragiannis et al. 2017). For instance, Spulber (1995) studies the Nash equilibrium in the Bertrand competition and shows that when rivals’ costs are unknown, each seller offers a price above its marginal cost and has positive expected utility. In other work, Caragiannis et al. (2017) study markets with multiple sellers that offer identical items to buyers with different valuations on each seller. The authors model this setting as a two-stage full-information game and show the price of anarchy and the efficiency of computing equilibria in this game. In this work we study settings within the Bertrand market model without assuming a full-information setting for sellers: sellers have only a belief about the competition they face.
A similar model to Bertrand in which sellers decide on the quantity of items to sell without any knowledge of the competition is the Cournot (Allaz and Vila 1993). Singh and Vives (1984) study the connection between the Bertrand and the Cournot competition models by analyzing the duality of prices and quantities in differentiated duopolies. For retail markets we study in this paper, the Bertrand model is better suited than the Cournot, in which sellers can only alter the price for items but not the quantity to sell (Weber 2006).
As described in the introduction of this paper, the classical price competition model named after Bertrand (1988) prescribes that in equilibrium sellers set prices equal to their private costs. However, this equilibrium outcome is not in line with real-life observations in which buyers are not rational in their choices over prices, and in which sellers model their competition. In addition, Dufwenberg and Gneezy (2000) show that the resulting prices that sellers offer to buyers further depend on the number of sellers that compete in the market. This is known as the Bertrand Paradox (Bruttel 2009; Dufwenberg and Gneezy 2000). Aligned with the Bertrand Paradox, we consider buyers that are bounded rational and use a stochastic model of choosing over prices. More specifically, we use the multinomial logit function to model the stochastic price selection of buyers (Anas 1983). Other works make use of the Luce choice axiom (Luce 1959), or the Softmax function (Sutton and Barto 1998) to model bounded rationality of buyers in markets (Basov and Danilkina 2015; Ait Omar et al. 2017).
Previous work has also studied the effects of bounded rationality on Bertrand markets (Basov and Danilkina 2015; Ait Omar et al. 2017; Zhang et al. 2009). For instance, Zhang et al. (2009) consider a Bertrand model with bounded rational sellers and study convergence properties of the competition. In the closest to ours work, Basov and Danilkina (2015) study price equilibria with regards to the degree of buyers’ rationality. They propose a model where sellers can choose to educate or confuse buyers, i.e., increase or decrease their degree of rationality respectively, and present the effects of these choices. Extending previous results (Basov and Danilkina 2015), Ait Omar et al. (2017) show that within a Bertrand oligopoly, sellers can benefit if buyers have lower degree of rationality. Our model substantially differentiates from the aforementioned work in the following ways. First, we consider automated (software) agents in place of human buyers. In this setting, agents of high computational capacity can reach levels of (almost) perfect rationality, and thus the degree of buyers’ rationality can not be manipulated by sellers.
The effects of bounded rational agents have also been studied with regards to learning agents, as the concept of bounded rationality is associated to the exploration Vs. exploitation problem in reinforcement learning (Sutton and Barto 1998). For instance, Wunder et al. (2010b) study the effects of the exploration rate of players on the resulting players’ payoffs in two-player prisoners’ dilemma games. The authors show that increasing exploration rate (i.e., lowering the frequency of using a greedy policy) results in higher than in Nash equilibrium payoffs for players.
Last, in this work we consider sellers of heterogeneous reasoning levels using hierarchical reasoning to model competition. Hierarchical (k-level) reasoning has also been used in other fundamental game-theoretical domains to model opponents (Hu and Wellman 2001; Hennes et al. 2012; Wunder et al. 2010a; Lindner and Sutter 2013). Hu and Wellman (2001) use k-level reasoning to learn the strategies of opponent agents (opponent modeling) in double-auctions. The authors conclude that more sophisticated modeling (high hierarchical reasoning level) does not guarantee an improvement in the performance of agents. In contrast to work by Hu and Wellman (2001), we use k-level reasoning to compute the best response strategy of a reasoning seller with regards to lower levels of reasoning. Consequently, higher levels of reasoning result in higher performance, since lower levels of reasoning function under limited information with regards to the competition. Our work is more related to literature that uses hierarchical reasoning to model varying information levels. More specifically, Hennes et al. (2012) use k-level reasoning to analyze the competitive advantage of high information access in markets. They conclude that random traders achieve in expectation higher gains than traders under partial information, who are in turn exploited by higher information level traders.
3 Market Model
In this section, we present our basic market setting, we also show how we model different degrees of buyers’ rationality and the competition between sellers.
We use the Bertrand model (Bertrand 1988) to study retail markets where sellers offer identical items to a finite population of buyers, assuming that sellers have an infinite inventory of items, and equal private costs. In practice, e.g., in electricity retail markets private costs for electricity do not vary significantly. We define \(c_i > 0\) as the private cost of seller i, and \(p_i\) as the price that seller i offers to buyers (\(p_i\) is the decision of seller i), p is the vector of prices set by all sellers. Furthermore, \(p_{-i}\) denotes the vector of prices set by sellers other that i. Both the price \(p_i\) and the prices of sellers other than i, determine the utility of seller i,
where \(s_i(p)\) is the function that maps the vector of prices p to the market share of seller i, i.e., \(s_i: p \rightarrow [0,1] \in {\mathbb {R}}\), such that \(\sum _i s_i(p) = 1\). We assume that the price of seller i can not be lower than its private cost \(c_i\), \(p_i \ge c\), since for any positive market share, \(s_i(p)>0\), \(p_i < c_i\) results in negative utility for seller i.
3.1 Degree of Buyers’ Rationality
In the retail market setting we consider, sellers offer identical items at specific prices to buyers. Buyers choose the price and consequently the seller to buy the items from. Assuming that buyers are perfectly rational, they choose the lowest price with probability one. In practice, however, buyers use a stochastic model for choosing over the offered prices (i.e., buyers are bounded rational) (Rubinstein 1998).
We use the multinomial logit function alongside the Bertrand market model, to study the effects of different degrees of buyers’ rationality as is standard in economic literature (McFadden 1975; Berry and Pakes 2007). The fraction of buyers that choose price \(p_i\) (market share of seller i) is given by:
where \(\tau \) is the coefficient that exaggerates or diminishes the contrast between different prices for the buyers.
Remark 1
We model the collective degree of buyers’ rationality and not the individual degrees of rationality within the population of buyers.
The quantity \(s_i(p)\) can be interpreted as the probability that an individual buyer out of the buyers’ population chooses price \(p_i\). For \(\tau \) close to zero (\(\tau \rightarrow 0\)), buyers are approximately perfectly rational choosing the lowest price with probability one, while for high values of \(\tau \) (\(\tau \rightarrow \infty \)), buyers choose over prices with equal probability (uniformly random). The parameter \(\tau \) can be adjusted to model different degrees of buyers’ rationality, between (almost) perfect rational buyers and buyers that choose over prices randomly. Equation (2) is identical to the Quantal response function (Mattsson and Weibull 2002), and the Softmax function (Sutton and Barto 1998) that is used in reinforcement learning to map a learning agent’s actions into probabilities.
Last, we compute the cost for the buyers as follows:
where the cost is equal to the sum of sellers’ prices weighted by the market share of each seller (average price for the buyers).
3.2 k-level Reasoning and Competition
In the previous section, we described the basic market model and outlined the decision of buyers over different prices with regards to their collective degree of rationality \(\tau \) (see Eq. 2).
The present and following sections discuss how sellers decide the prices to offer to buyers. Since sellers can not influence the degree of buyers’ rationality, the decision of a seller with regards to the price (i.e., strategy) to offer to buyers is only influenced by prices posted by its competition (other sellers). We consider that sellers model their competition using k-level reasoning, where k denotes the reasoning level of a seller (Stahl and Wilson 1995). This resembles sellers that can have varying information levels or computational resources. For the remainder of the paper, Lk stands for the k-th level of reasoning.
First, we consider L0 sellers. A L0 seller does not model opponent sellers, and therefore its strategy (price) does not consider opponent prices. For higher levels of reasoning (\(k>0\)), standard models of k-level reasoning assume the following: A Lk agent believes to be facing \(L(k-1)\) agents (Arad and Rubinstein 2012; Hu and Wellman 2001). Other models of k-level reasoning modify the aforementioned assumption as follows: A Lk agent has a belief with regards to the probability of meeting each of the lower levels (Camerer et al. 2004). In this paper, we use both models. Last, in k-level reasoning no Lk agent believes that it competes against agents of equal or higher reasoning levels.
For generality, we assume that Lk seller has a belief distribution over lower reasoning levels. Let x denote the vector of the true distribution over levels of reasoning, where each entry \(x_k\) denotes the probability (frequency) that Lk appears in the population of sellers. We define \(\lambda _k\) as the belief distribution of Lk seller with regards to the true distribution x, \(\lambda _k\) consists of k entries (the first entry is the frequency of L0 in the population), \(\lambda _k = \langle \lambda _0, \lambda _1, \ldots , \lambda _{k-1} \rangle \). Each entry \(\lambda _k^z\) is the probability of competing against Lz seller, \(\sum _{z=0}^{k-1} \lambda _k^z = 1\). Note that, L0 does not have a belief for the competition and for \(k>0\), sellers of the same reasoning level have identical beliefs with regards to the competition. Given the belief \(\lambda _k\), we proceed to derive the best response strategy of Lk seller, i.e., the price to offer to buyers that maximizes its utility.
4 k-Level Best Response Strategies
In this section, we illustrate the best response strategy (price) of Lk seller i given \(\lambda _k\) and the private cost \(c_i\). For brevity, we omit i from the notation since Lk is independent of seller i.
We define \(\pi _k^*\) as the best response strategy of Lk; \(\pi _k^*\) is the function that maps: (i) the private cost c, (ii) the belief \(\lambda _k\), and (iii) the degree of buyers’ rationality \(\tau \), to the price \(p_k^*\), i.e., \(\pi _k^*: (c, \lambda _k, \tau ) \rightarrow p_k^*\). To simplify notation, we also use \(p_k^*\) as the function \(\pi _k^*\) in the remainder of the paper. Considering a known L0 strategy, \(p_0\), the strategy of Lk agent is computed by iteratively best respond to lower levels of reasoning. To illustrate this, consider that Lk seller competes against one \(L(k-1)\) opponent seller. Then, the best response of Lk is given by:
where \(p_{k-1}^*\) is the best response to \(p_{k-2}^*\). Next, by taking into account the belief \(\lambda _k\),
is the best response of Lk seller with regards to the probability of meeting each of the lower levels z. The Lk best response strategy presented here serves as an illustration of the iterated best response model. In what follows, we derive an analytical solution for the best response strategy of Lk for any number of opponents with regards to the opponent prices.
4.1 Analytical Best Response and Rationality
Recall that \(p_{-i}\) denotes the vector of prices set by sellers other than i. Here, we assume a known \(p_{-i}\) since prices of opponent sellers result out of iterated best response strategies in k-level reasoning. We make no further assumptions for the private costs of opponent sellers, note that \(c_i\) is the private cost of seller i.
Theorem 1
The price \(p_i^*\) maximizes the utility of seller i given the vector of opponent prices \(p_{-i}\), the private cost \(c_i\), and the degree of buyers’ rationality \(\tau \):
where W is the Lambert function, i.e., \(x = f^{-1}(x e^x) = W(x e^x)\) (Corless et al. 1996).
Proof
Given seller i, and the vector of opponent prices \(p_{-i}\), the utility of seller i is equal to:
To derive the price \(p_i^*\), we first use the quotient rule to compute the derivative of the utility of seller i in Eq. (6) with respect to the price \(p_i\):
Equation (7) is the derivative of the utility of seller i with respect to the price \(p_i\). By solving Eq. (7) to be equal to zero, we get Eq. (5). It can be shown that \(({\partial u_i} / {\partial p_i }) > 0\) for any \(p_i < p_i^*\) and \(({\partial u_i} / {\partial p_i }) < 0\) for any \(p_i > p_i^*\). Hence, \(p_i^*\) is the price that maximizes the function \(u_i\).\(\square \)
Theorem 1 shows the best response strategy of seller i with regards to the opponent prices \(p_{-i}\), the private cost \(c_i\), and the degree of buyers’ rationality \(\tau \). The above theorem is relevant for markets where prices are public knowledge, while the degree of buyers’ rationality \(\tau \) can be approximated.
We proceed to show some interesting theoretical results that follow from Theorem 1 under the following assumption:
Assumption 1
We consider a Bertrand duopoly with a reasoning seller i with private cost \(c_i\) that observes: (i) the price of the opponent \(p_{-i}\), which we assume is fixed for all \(\tau \), and (ii) the degree of buyers’ rationality \(\tau \).
Intuitively, the above assumption considers a duopoly market in which the opponent seller can not observe or estimate the degree of buyers’ rationality \(\tau \) and uses a fixed price \(p_{-i}\). The competitive price \(p_{-i}\) can also resemble the price of an outside option for buyers, e.g., their private cost for producing the items on their own, that does not depend on the degree of their rationality \(\tau \). In contrast, the reasoning seller can observe the degree of buyers’ rationality, motivated by the example of a company with resources for market research.
In the remainder of this section we abbreviate the notation of the best response function in Eq. (5), \(p_i^*(p_{-i}, c_i, \tau )\), where possible. First, by using Eq. (5) we get the following lemma:
Lemma 1
Given Assumption 1,
Proof
We use the property of the Lambert function, \(W(f(x)) = g(x) \Leftrightarrow f(x) = g(x) e^{g(x)}\), to solve the following inequality,
which results in the inequality in Eq. (8).\(\square \)
The above lemma shows the upper bound for the private cost \(c_i\), such that the best response strategy \(p_i^*\) is lower than the opponent price \(p_{-i}\), and thus buyers can benefit. A less intuitive bound for the cost \(c_i\) than in Eq. (8) can be computed for more than one opponent prices.
We proceed to show that buyers benefit if they are not perfectly rational, i.e., \(\tau > 0\), under the same setting.
Lemma 2
Given Assumption 1 and \(c_i < p_{-i}\), there exists \(\tau ^* \in (0, (p_{-i} - c_{i}) / 2)\), such that \(p_i^*(\tau ^*) \le p_i^*(\tau ), \forall \tau \in (0, \infty )\).
Proof
Given that the quantity \((p_{-i} - c_i)\) is fixed for all \(\tau \), and \(\tau ' = (p_{-i} - c_{i}) / 2\), Eq. (8) implies that \(p_i^* < p_{-i}\) for \(\tau < \tau '\).
Given that Eq. (5) is not defined for \(\tau =0\), we compute the limit as \(\tau \) tends to 0,
By the L’Hospital’s rule we get that \(\lim _{\tau \rightarrow 0} p_i^* = c_i + (p_{-i} - c_i) = p_{-i}\). As \(\tau \rightarrow 0\), \(p_i^*\) tends to \(p_{-i}\).
Thus, for every \(\varepsilon > 0\) sufficiently small, the continuous function \(p_i^*\) lies below \(p_{-i}\) for every \(\tau \) that belongs to \([\varepsilon , \tau '-\varepsilon ]\).
Given the extreme value theorem for continuous functions in compact intervals, there is a \(\tau ^* \in [\varepsilon , \tau '-\varepsilon ]\) for which \(p_i^*(\tau ^*) \le p_i^*(\tau ) ,~\forall \tau \in [\varepsilon , \tau '-\varepsilon ]\). In addition, we know from Eq. (8) that \(\lim _{\varepsilon \rightarrow 0} p_i^*(\tau ' - \varepsilon ) = p_i^*(\tau ') \ge p_{-i}\), and \(\lim _{\varepsilon \rightarrow 0} p_i^*(\varepsilon ) = p_{-i}\). By taking \(\varepsilon \) sufficiently small, and by \(\inf _{\tau \in [\varepsilon ,\tau ']} p_i^*(\tau ) \le \inf _{\tau \in [\tau ', \infty ]} p_i^*(\tau )\), we get that \(p_i^*(\tau ^*) \le p_i^*(\tau ), \forall \tau \in (0, \infty )\).\(\square \)
Theorem 2
Given Assumption 1 and \(c_i < p_{-i}\), the optimal price of the reasoning seller i, \(p_i^*\), is minimum for a degree of buyers’ rationality \(\tau ^*\), with \(\tau ^* > 0\), and thus not for perfect rational buyers.
Proof
It follows from Lemmas 1 and 2 .\(\square \)
Theorem 2 shows that the minimum price of the reasoning seller is obtained for a degree of rationality \(\tau > 0\) (not perfect rationality).
In this section, we derived analytical results with regards to the best response price of a reasoning seller, and the degree of buyers’ rationality that minimize the price of the reasoning seller. We illustrate these results experimentally in the next section.
4.2 Duopoly Markets
In line with our assumptions in the previous section, we consider a duopoly market where both sellers have identical private costs. We further use the standard assumption of k-level reasoning, namely, a Lk seller believes to be competing against a \(L(k-1)\) opponent seller, and thus \(\lambda _{k}^{z} = 1\) for \(z=(k-1)\) and \(\lambda _k^{z} = 0\) for \(z<(k-1)\). To derive the price of each Lk seller we use the iterated best response strategy of Lk similarly to Eq. (4) and the analytical best response price as this was derived in Eq. (5). More specifically, the price of Lk is given by: \(p_k^*(p_{k-1}, c_i, \tau )\), where we replace \(p_{-i}\) in Eq. (5) with \(p_{k-1}\), i.e., the price of the \((k-1)\) reasoning level. For the remainder of this section, we use 3 levels of reasoning; while our results generalize to any number of levels of reasoning, levels 0, 1 and 2 exemplify the cases of no, partial and (almost) full information respectively. Note that, the number of possible strategies (levels of reasoning) is distinct from the number of sellers. Furthermore, L0 is a naive strategy that sells at an arbitrary fixed profitable price \(p_0\), i.e. for L0 seller i, \(p_0\) is larger than the private cost \(c_i\).
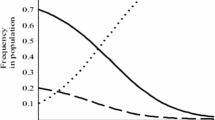
Figure 1 (left) presents the best response strategy (price) of the 3 levels of reasoning with regards to the logarithm of the degree of buyers’ rationality \(\tau \). All sellers have identical private costs, \(c = 0.2\), for L0 we use \(p_0 = 0.6\). Values on the horizontal axis approximate different degrees of rationality from \(\log (\tau ) = -3\) (almost perfect rationality) to \(\log (\tau ) = 0\) (almost random price selection). For \(\log (\tau ) = -3\), the best response strategy of Lk is marginally lower than the price of \(L(k-1)\). Given that for \(\log (\tau ) = -3\), buyers are almost perfectly rational, a marginal decrease in the price of Lk with regards to \(L(k-1)\) results in Lk to attain almost the full market share. As \(\tau \) increases, the difference between prices becomes larger to counterbalance the stochastic selection of buyers over different prices. Intuitively, sellers choose a lower profit margin in order to achieve a higher market share.
For each reasoning level k for \(k>0\), there exists \(\tau _k^*\) for which the price \(p^{*}_k\) becomes minimum. For instance, for \(k = 1\) and \(k = 2\), the degree of buyers’ rationality that minimizes the price \(p^{*}_k\) is when \(\log (\tau _k^*) \approx -1.3\). For higher values of \(\tau \), buyers assign more equal probabilities for selecting among different prices. Hence, sellers of varying levels of reasoning achieve almost equal divisions of the market share that are only slightly influenced by the prices, and thus prices inflate in face of maximizing profits.
4.2.1 Utility of Sellers and Buyers
We proceed to show the influence of the degree of buyers’ rationality \(\tau \) on the cost for buyers which we compute as in Eq. (3). Here, we use a uniform distribution for x, i.e., \(x_0 = x_1 = x_2\) (recall that x is the true distribution over levels of reasoning). Figure 1 (right) presents the cost for buyers with regards to logarithm of their collective degree of rationality \(\log (\tau )\). For \(\log (\tau ) = -3\), the cost is marginally lower than the price \(p_0\), however, it decreases further as \(\tau \) becomes larger. For \(\log (\tau ) \approx -1.3\), the cost for the buyers is minimum. As \(\tau \) increases further, buyers choose randomly over prices and thus the cost is increasing, since prices inflate.
The results presented throughout this section verify our theoretical findings for the existence of a degree of rationality (not perfect rationality) for which prices of reasoning sellers become minimum (see Theorem 2). To compute the cost for buyers we have considered a uniform distribution over levels of reasoning x. In the following section, we show that the distribution x can be influenced by the success rate of each reasoning level Lk in repeated settings.
5 Evolutionary Dynamics
Considering repeated interactions that take place in markets, the frequency with which each strategy (i.e., reasoning level) appears in the population is influenced by its success rate (i.e., fitness). In this section, we use evolutionary game theory (Smith and Price 1973; Weibull 1997), to study the evolutionary dynamics of reasoning levels in the population of sellers.
Given the distribution over levels of reasoning x, the frequency change \({\dot{x}}\) is given by the replicator equation (Hofbauer 1985):
Recall that \(x_k\) is the frequency that strategy Lk appears in the population, \(f_k\) is the fitness of Lk, and \(\varphi (x)\) is the average fitness of the population.
We revisit the duopoly scenario of the previous section (see Sect. 4.2) to apply the replicator equation. We compute the fitness \(f_k\) for every possible duopoly as follows:
where K is the highest reasoning level (here, \(K = 2\)). Figure 2 presents the replicator dynamics for the duopoly model of Sect. 4.2. Arrows at each point of the simplex show the derivative \({\dot{x}}\) (direction and magnitude). We observe that evolution favors the highest reasoning level L2, i.e., L2 has a competitive advantage.
We used the replicator equation to study the evolution over reasoning levels in the duopoly scenario of Sect. 4.2, assuming that a Lk seller believes to be facing a \(L(k-1)\) opponent seller (standard assumption of k-level reasoning). We showed that in such settings the highest reasoning level has always an evolutionary advantage since the belief is not influenced by changes in the distribution x. In addition, this result generalizes to any number of reasoning levels.
5.1 Dynamic Belief of Competition
In this section, we alter the standard assumption of k-level reasoning to a dynamic belief model that is influenced by the distribution x.
We generalize our setting to consider an oligopoly market with n sellers, and identical private costs for sellers. We consider that the belief of a Lk seller with regards to opponent levels of reasoning sellers is the real distribution x for all levels lower than k, such that \(\lambda _k = \left\langle x_0, x_1, \ldots , x_{k-1} \right\rangle \). Note that, \(\sum _{z=0}^{k-1} \lambda _k^z < 1\), since \(x_k > 0\), i.e., only lower than k levels of reasoning are included in the belief distribution of Lk. In addition, for \(x_k\) close to one (i.e., Lk dominates the population), \(\sum _{z=0}^{k-1} \lambda _k^z\) is close to zero. We define \(x_{out} = 1 - \sum _{z=0}^{k-1} \lambda _k^z\) as the probability of facing equal or higher levels of reasoning opponents. The probability \(x_{out}\) can only be computed for \(k > 0\), since L0 does not have a belief distribution. Hence, the belief of Lk becomes \(\lambda _k = \left\langle x_0, x_1, \ldots , x_{k-1}, x_{out} \right\rangle \). We interpret the probability \(x_{out}\) as the probability of competing with an unknown opponent, e.g., outside option for buyers. The opponent price associated with the probability \(x_{out}\) is denoted with \(p_{out}\). The price \(p_{out}\) can be set equal to the maximum price buyers are willing to pay to alleviate the risk of extreme prices set by dominant strategies.
5.2 Optimal Pricing and Generalized Replicator Equation
We use Eq. (5) to approximate the price of each reasoning level \(p_k^*\). Lk seller draws samples (opponent price vectors \(p_{-i}\) of length \(n-1\)) with regards to its belief \(\lambda _k\). In our experiments, the Lk best response (optimal price for k-level of reasoning) is averaged over 100 sampled opponent price vectors. More samples do not change the behavior of the simulation in experiments presented later in this paper.
Evolution of levels of reasoning and price for almost perfect rationality (top, \(\log (\tau ) = -2.7\)), bounded rationality (middle, \(\log (\tau ) = -0.7\)), and random behavior (bottom, \(\log (\tau ) = 0\)). Stack plots at the top show the evolution of distribution x, and plots at the bottom illustrate the prices set by different levels of reasoning, the dashed line shows the development of the cost for the buyers
Furthermore, to model innovation of strategies in the population, i.e., new sellers that enter competition or sellers that increase/decrease their level of reasoning, we use the generalized replicator equation (Hofbauer and Sigmund 1998):
where \(Q_{z \rightarrow k}\) is the transition probability of an individual (from the population) from Lz to Lk (i.e., mutation probability). The fitness of Lk, \(f_k (x)\), is computed by:
where each \(z^{(j)}_\mu \sim x\) are independent samples (i.e., \(n-1\) opponent prices) from the true distribution over reasoning levels x, and the fitness is averaged out of M sampled opponent price vectors. Considering that the population of sellers is finite, \({\dot{x}}\) is not deterministic for a given x, therefore computing the average fitness improves the approximation (Kemenade et al. 1998). We use \(M = 100\) for experiments presented in the remainder of this paper.
5.2.1 Evolution of Reasoning Levels
Figure 3 illustrates the evolution over levels of reasoning and price with regards to time t for \(c = 0.2\), \(p_0=0.9\), \(p_{out}=1\), and 10 levels of reasoning (from the lowest L0 to the highest L9, here \(K=9\)). The initial distribution \(x_0\) is set to \(\left\langle 1, 0, \ldots , 0 \right\rangle \), only L0 is present at time \(t=0\). The mutation probability is set to 0.01, where transition probabilities are uniformly distributed over all different levels, i.e., \(\sum _{z \ne k} Q_{k \rightarrow z} = 0.01 / (\text {number of levels}-1)\), and \(Q_{k \rightarrow k} = 0.99\). Stack plots placed at the top show the evolution of the distribution x over levels of reasoning, and plots at the bottom show the price evolution for \(\log (\tau ) \in \lbrace -2.7, -0.7, 0 \rbrace \). The bold dashed line shows the average cost for the buyers.
First, we discuss the case of almost perfect rationality, \(\log (\tau ) = -2.7\) (see Fig. 3, top). Given the positive mutation probability in Eq. (13), higher levels (\(L1 - K\)) of reasoning “invade” the population of L0. LK best responds to all lower levels of reasoning, thus it increases its share in x. For \(t > 50\), LK becomes dominant in the population, at the same time the frequency of reasoning levels between L0 and LK diminish in the distribution x. In addition, prices as well as the distribution x are not stable, resulting in price spikes that lead prices higher than the price \(p_0\) (\(p_0 = 0.9\)). Both price spikes and the instability in the evolution of the distribution x are caused due to: (i) the low probability for LK to compete with lower level of reasoning opponents (\(\sum _{j=0}^{K-1} x_j \approx 0.2\)), and (ii) the high probability \(x_{out}\) to face the outside option price \(p_{out}\). The level of price spikes is subject to the outside price \(p_{out}\), higher values for \(p_{out}\) result in higher spikes further away from the price \(p_0\). During price spikes, L0 benefits due to the high prices of (\(L1 - K\)) and increases its share in x. Thereafter, higher levels of reasoning (\(L1 -K\)) decrease their price in face of the increasing share of L0 in x until L0 share decreases again. This results in chaotic evolutionary dynamics while similar behavior is observed for \(\log (\tau ) < -1.7\).
We observe smoother evolutionary dynamics and lower average price for buyers for lower degrees of buyers’ rationality, more specifically, for \(\log (\tau ) > -1.7\). For instance, for \(\log (\tau ) = -0.7\) (see Fig. 3, middle), evolution reaches an equilibrium state at \(t>3\)k, where the distribution x and the prices become stable. On the contrary to the case of almost perfect rationality (see Fig. 3, top), the prices set by higher levels of reasoning (\(L1 - K\)) are lower than \(p_0\) (\(p_0 = 0.9\)), and thus the average cost for the buyers decrease. Note that, the frequency of reasoning levels between L0 and LK is not diminished as in the case of almost perfect rationality. The lower average price for buyers is a result of sustaining competition between different levels of reasoning sellers and the smoother dynamics of the evolution.
Last, we show the evolution of the distribution x and the prices when the buyers’ price selection is almost random (see Fig. 3, bottom). For \(\log (\tau ) = 0\), reasoning levels (\(L1 - K\)) share the distribution x equally, where all reasoning sellers offer prices that exceed the price of L0, \(p_0\), and the price \(p_{out}\), and therefore increase the cost for buyers.
Overall, higher degrees of buyers’ rationality yield higher average cost for buyers than lower degrees of rationality, e.g., \(\log (\tau ) = -0.7\). Furthermore, unstable evolutionary dynamics under almost perfect rationality increase prices further due to price spikes. In our experiments, we additionally used gradual updates to the prices in order to study the possibility more stable states can be reached in the evolution even in the case of perfect rationality. When gradual updates were used, results were consistent to the results presented here, however, the evolution of the distribution x was slower.
5.2.2 Competitive Advantage and Price
We proceed to show how the degree of buyers’ rationality affects the competition in terms of the evolutionary advantage of higher reasoning levels, the resulting prices for buyers, and the stability of the competition.
Figure 4 (left) illustrates the distribution x over levels of reasoning after 10k steps (mean of the last 100 steps) of the evolution averaged over 20 independent runs. LK is the dominant in x for almost all values of \(\tau \), i.e., \(\log (\tau ) < -\,0.25\). For \(\log (\tau ) \approx -\,0.25\), all levels L0 to LK have approximately equal shares in x. This is due to the almost equal prices reasoning levels set (similarly to the duopoly setting examined in earlier sections, see Fig. 1, left). For \(\log (\tau ) > -\,0.25\), the market is shared among levels L1 and LK, since all levels of reasoning but L0 offer very high prices to (almost) random buyers.
We further show the effect of varying degrees of rationality \(\tau \) on buyers’ cost (see Fig. 4, right). The cost is averaged over the last 100 out of 10k steps of evolution and over 20 independent evolution runs. For low \(\tau \), the average cost for buyers is marginally higher than the cost without the presence of higher than L0 reasoning levels, \(p_0 = 0.9\). This is the result of unstable competition dynamics that cause price spikes, during which prices become higher than the price of L0 strategy, \(p_0\). Recall, that \(p_{out} = 1\) alleviates the possibility of extreme prices, and thus the cost for buyers would increase further for higher \(p_{out}\) due to the increasing level of price spikes. In contrast, from \(\log (\tau ) = -\,1.7\) to \(\log (\tau ) = -\,0.2\) buyers’ cost drops below the price \(p_0 = 0.9\), this is mainly caused by the smoother behavior of evolution that converges to stable distributions and alleviate price spikes. In line with our theoretical findings in Sect. 4, we observe that there is a degree of rationality \(\log (\tau ^*) \approx -\,0.7\) that minimizes the average cost for buyers (shown in the figure by the dashed vertical line).
In the presented experiments, we demonstrated that lower degrees than almost perfect buyers’ rationality decrease the prices sellers offer to buyers during the evolution of the competition. For almost perfect buyers’ rationality, the highest reasoning level sellers exploit instances of monopoly situations and increase their prices, while under bounded buyers’ rationality competition is sustained decreasing prices for buyers. In the section that follows, we evaluate the stability of the competition with regards to the degree of buyers’ rationality.
5.2.3 Asymptotic Behavior of the Competition
If the dynamics were known in explicit closed form, one could apply analytical notions of stability (e.g., evolutionary stable strategies, asymptotically stable) to analyze equilibrium strategies (Smith 1972). However, given our implicit dynamics arising from system simulation (see Sect. 5.2), we need to draw on empirical means for characterizing the asymptotic behavior of the evolution. In the remainder of this section we analyze both the first-order derivative and the distribution trajectory x, and examine how the degree of buyers’ rationality influences the stability of the evolution.
First, we use the average magnitude (Euclidean norm) of the derivative of x, \(\overline{|{\dot{x}}|}\), that is shown by the solid line in Fig. 5 (left vertical axis). We compute \(\overline{|{\dot{x}}|}\) over the last 100 out of 10k steps of the evolution while results are averaged over 20 independent runs. The quantity \(\overline{|{\dot{x}}|}\) is maximum for almost perfect buyers’ rationality, specifically, \(\overline{|{\dot{x}}|} > 10^{-3},~\forall \log (\tau ) < -2\). This is in line with our observations in Fig. 3 (top), where we showed chaotic behavior in the evolution of x for a low \(\tau \) value. As \(\tau \) increases, steps in the evolution become smaller and consequently \(\overline{|{\dot{x}}|}\) decreases. For \(\log (\tau ^*) \approx -0.7\), which minimizes the average cost for buyers in Fig. 4 (right), \(\overline{|{\dot{x}}|}\) is very low (\(10^{-5}\)).
Next, we use the Euclidean distance between x and the average distribution \({\bar{x}}\), \(\overline{|x - {\bar{x}}|}\), which is shown by the dashed line in Fig. 5 (right vertical axis). The quantities \({\bar{x}}\) and \(\overline{|x - {\bar{x}}|}\) are computed over the last 100 out of 10k steps of evolution, and averaged over 20 independent runs. Similarly to \(\overline{|{\dot{x}}|}\), \(\overline{|x - {\bar{x}}|}\) decreases as \(\tau \) increases, and hence the distribution x stays closer to the average distribution \({\bar{x}}\) for bounded rational buyers.
Our results suggest that imperfect rationality contributes to smoother competition dynamics, corroborating our observations in Sect. 5.2.1.
5.2.4 Strategy of Zero Reasoning Level
So far we have shown the effects of different degrees of buyers’ rationality on the behavior of retail markets with regards to: the evolution of competition, the resulting prices for buyers, and the stability of evolutionary dynamics. Here, we show that the properties shown in previous sections generalize for different prices of L0 strategy, \(p_0\). Figure 6 illustrates both the degree of rationality \(\log (\tau ^*)\) that minimizes the cost for buyers (left), and the corresponding cost for the values of \(\log (\tau ^*)\) (right). The cost for buyers is minimum if buyers are not perfectly rational for all values of \(p_0\), however as the difference \((p_0 - c)\) becomes larger, \(\log (\tau ^*)\) increases (lower degree of rationality). At the same time, buyers’ cost is relatively lower than \(p_0\) as \(p_0\) increases. Intuitively, the margin between the resulting average cost for buyers (computed for the optimal degree of buyers’ rationality) and the price \(p_0\) increase as the difference (\(p_0 - c\)) increase.
6 Discussion and Future Work
In this work, we illustrated the effects of varying the degree of buyers’ rationality in retail markets. In the presented experiments, we showed that almost perfect rationality caused spikes in price due to the unstable evolutionary dynamics, and thus increased the cost for buyers. On the contrary, lower degrees of rationality resulted in lower cost for buyers, by both sustaining competition between sellers of varying levels of reasoning and by increasing the stability of evolutionary dynamics. In line with related work (Wunder et al. 2010b), we can also conclude that using a stochastic choice model for decision-making in our setting leads in higher payoffs for the buyers.
Arriving at this non-trivial conclusion, we have made some simplifying assumptions with regards to the market setting and the model of competition between sellers. On the contrary, real-world retail markets involve highly perplexing dynamics and demonstrate extremely complex behavior, which can not be fully delineated in fundamental market models. Our results are thus not conclusive but instead seek to provide insights and add fundamental knowledge that can be used for the design of future retail markets with commodities that enable market participation by software agents, and general competitive multi-agent settings with heterogeneous agents.
This work further serves as a basis for a number of extensions. First, we have considered the collective behavior of buyers and showed some favourable properties of the competition for lower than perfect degrees of buyers’ collective rationality. However, if we consider an individual buyer, it is always optimal to be perfectly rational given a set of prices. It is of interest to study the connection between individual and collective buyers’ rationality. Second, throughout this paper we have assumed that there is no cost associated with the reasoning level of sellers. In the same settings we can consider arbitrary cost models for each reasoning level, or compute bounds up to which it is beneficial for sellers of higher levels of reasoning to enter the competition. Last, more elaborate market models and finite population replicator dynamics (Taylor et al. 2004) can be considered by future work.
7 Conclusion
In this work, we studied the effects of varying degrees of buyers’ rationality and sellers’ opponent modeling (using k-level reasoning), in the Bertrand competition. In Theorem 1, we mathematically derived the best response strategy (price) given a set of opponent prices and the degree of buyers’ rationality. We used evolutionary dynamics to show the evolution of competition and prices in both duopoly and oligopoly scenarios. By replacing the standard assumption of k-level reasoning with a dynamic belief that depends on the distribution over reasoning levels, we showed that perfect rationality results in monopolistic behavior of higher reasoning level sellers, spikes in price, and unstable competition dynamics. The existence of an optimal degree of rationality stated in Theorem 2 and the improved evolutionary dynamics illustrated in our experiments thus provide a rationale for agents’ bounded rationality in retail markets, raising the need to revisit design objectives for software agents in retail markets in light of their wider systematic impact.
References
Ait Omar, D., Outanoute, M., Baslam, M., Fakir, M., & Bouikhalne, B. (2017). Joint price and QoS competition with bounded rational customers (pp. 457–471). Cham: Springer International Publishing.
Albrecht, S. V., & Stone, P. (2017). Autonomous agents modelling other agents: A comprehensive survey and open problems. CoRR arXiv:1709.08071.
Allaz, B., & Vila, J. L. (1993). Cournot competition, forward markets and efficiency. Journal of Economic Theory, 59(1), 1–16.
Anas, A. (1983). Discrete choice theory, information theory and the multinomial logit and gravity models. Transportation Research Part B: Methodological, 17(1), 13–23.
Arad, A., & Rubinstein, A. (2012). The 11–20 money request game: A level-k reasoning study. The American Economic Review, 102(7), 3561–3573.
Baarslag, T., Kaisers, M., Gerding, E.H., Jonker, C.M., & Gratch, J. (2017). When will negotiation agents be able to represent us? the challenges and opportunities for autonomous negotiators. In: Proceedings of the Twenty-sixth International Joint Conference on Artificial Intelligence, Melbourne, Australia, IJCAI’17, pp 4684–4690.
Basov, S., & Danilkina, S. (2015). Bertrand oligopoly with boundedly rational consumers. The BE Journal of Theoretical Economics, 15(1), 107–123.
Berry, S., & Pakes, A. (2007). The pure characteristics demand model. International Economic Review, 48(4), 1193–1225.
Bertrand, J. (1988). Review of Walrass théorie mathématique de la richesse sociale and Cournots recherches sur les principes mathematiques de la theorie des richesses in Cournot oligopoly: Characterization and applications. edited by AF Daughety. Cambridge University Press.
Bruttel, L. V. (2009). Group dynamics in experimental studies–the bertrand paradox revisited. Journal of Economic Behavior & Organization, 69(1), 51–63.
Camerer, C. F., Ho, T. H., & Chong, J. K. (2004). A cognitive hierarchy model of games. The Quarterly Journal of Economics, 119(3), 861.
Caragiannis, I., Chatzigeorgiou, X., Kanellopoulos, P., Krimpas, G. A., Protopapas, N., & Voudouris, A. A. (2017). Efficiency and complexity of price competition among single-product vendors. Artificial Intelligence, 248, 9–25.
Conlisk, J. (1996). Why bounded rationality? Journal of Economic Literature, 34(2), 669–700.
Corless, R. M., Gonnet, G. H., Hare, D. E. G., Jeffrey, D. J., & Knuth, D. E. (1996). On the lambertw function. Advances in Computational Mathematics, 5(1), 329–359.
Dufwenberg, M., & Gneezy, U. (2000). Price competition and market concentration: an experimental study. International Journal of Industrial Organization, 18(1), 7–22.
Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. Cambridge: MIT Press.
Guttman, R., Moukas, A., & Maes, P. (1999). Agents as mediators in electronic commerce (pp. 131–152). Berlin: Springer.
He, M., Jennings, N. R., & Leung, H. F. (2003). On agent-mediated electronic commerce. IEEE Transactions on Knowledge and Data Engineering, 15(4), 985–1003.
Hennes, D., Bloembergen, D., Kaisers, M., Tuyls, K., & Parsons, S. (2012). Evolutionary advantage of foresight in markets. In: Proceedings of the 14th annual conference on genetic and evolutionary computation. New York: ACM, GECCO ’12, pp 943–950.
Hofbauer, J. (1985). The selection mutation equation. Journal of Mathematical Biology, 23(1), 41–53.
Hofbauer, J., & Sigmund, K. (1998). Evolutionary games and population dynamics. Cambridge: Cambridge University Press.
Hu, J., & Wellman, M. P. (2001). Learning about other agents in a dynamic multiagent system. Cognitive Systems Research, 2(1), 67–79.
Kemenade, C. H., Kok, J. N., Poutre, J. A. L., & Thierens, D. (1998). Transmission function models of finite population genetic algorithms. Tech. rep., Amsterdam, The Netherlands.
Lindner, F., & Sutter, M. (2013). Level-k reasoning and time pressure in the 11–20 money request game. Economics Letters, 120(3), 542–545.
Luce, R. D. (1959). Individual choice behavior a theoretical analysis. New York: Wiley.
Maes, P., Guttman, R. H., & Moukas, A. G. (1999). Agents that buy and sell. Commun ACM, 42(3), 81–87.
Marwala, T., & Hurwitz, E. (2017). Artificial intelligence and economic theory: Skynet in the market. New York: Springer.
Mattsson, L. G., & Weibull, J. W. (2002). Probabilistic choice and procedurally bounded rationality. Games and Economic Behavior, 41(1), 61–78.
McFadden, D. (1975). The revealed preferences of a government bureaucracy: Theory. The Bell Journal of Economics, 6(2), 401–416.
Nash, J. F. (1950). The bargaining problem. Econometrica, 18(2), 155–162.
Nisan, N., Roughgarden, T., Tardos, E., & Vazirani, V. V. (2007). Algorithmic game theory. New York: Cambridge University Press.
Rubinstein, A. (1998). Modeling bounded rationality. New York: MIT Press.
Russell, T., & Thaler, R. (1985). The relevance of quasi rationality in competitive markets. The American Economic Review, 75(5), 1071–1082.
Simon, H. A. (1982). Models of bounded rationality: Empirically grounded economic reason (Vol. 3). New York: MIT Press.
Singh, N., & Vives, X. (1984). Price and quantity competition in a differentiated duopoly. The RAND Journal of Economics, 15(4), 546–554.
Smith, J. M. (1972). Game theory and the evolution of fighting. On evolution pp 8–28.
Smith, J. M., & Price, G. R. (1973). The logic of animal conflict. Nature, 246(5427), 15–18.
Spulber, D. F. (1995). Bertrand competition when rivals’ costs are unknown. The Journal of Industrial Economics, 43(1), 1–11.
Stahl, D. O., & Wilson, P. W. (1995). On players’ models of other players: Theory and experimental evidence. Games and Economic Behavior, 10(1), 218–254.
Sutton, R. S., & Barto, A. G. (1998). Reinforcement learning: An introduction (Vol. 1). Cambridge: MIT Press.
Taylor, C., Fudenberg, D., Sasaki, A., & Nowak, M. A. (2004). Evolutionary game dynamics in finite populations. Bulletin of Mathematical Biology, 66(6), 1621–1644.
Weber, C. (2006). Uncertainty in the electric power industry: Methods and models for decision support (Vol. 77). New York: Springer.
Weibull, J. W. (1997). Evolutionary game theory. Cambridge: MIT Press.
Wunder, M., Kaisers, M., Littman, M., & Yaros, J. R. (2010a). A cognitive hierarchy model applied to the lemonade game. In: Proceedings of the 3rd AAAI conference on interactive decision theory and game theory, AAAIWS’10-03 (pp 66–73). AAAI Press.
Wunder, M., Littman, M., & Babes, M. (2010b). Classes of multiagent q-learning dynamics with e-greedy exploration. In: Proceedings of the 27th international conference on international conference on machine learning, Omnipress, USA, ICML’10 (pp 1167–1174).
Zhang, J., Da, Q., & Wang, Y. (2009). The dynamics of bertrand model with bounded rationality. Chaos, Solitons and Fractals, 39(5), 2048–2055.
Acknowledgements
This work is part of the research programme Uncertainty Reduction in Smart Energy Systems (URSES) with Project Number 408-13-012, which is partly financed by the Netherlands Organisation for Scientific Research (NWO).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which~permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Methenitis, G., Kaisers, M. & La Poutré, H. Degrees of Rationality in Agent-Based Retail Markets. Comput Econ 56, 953–973 (2020). https://doi.org/10.1007/s10614-019-09955-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10614-019-09955-2