Are Central Bankers Inflation Nutters? An MCMC Estimator of the Long-Memory Parameter in a State Space Model

Abstract

Inflation targeting is a common monetary policy regime. Inflation targets are often flexible in the sense that the central bank allows inflation to temporarily deviate from the target to avoid causing unnecessary volatility in the real economy. In this paper, we propose modeling the degree of flexibility using an autoregressive fractionally integrated moving average (ARFIMA) model. Assuming that the central bank controls the long-run inflation rate, the fractional integration order becomes a measure of how flexible the inflation target is. A higher integration order implies that inflation deviates from the target for longer periods of time and consequently, that the target is flexible. Several estimators of the fractional integration order have been proposed in the literature. Grassi and Magistris (2014) show that a state-based maximum likelihood estimator is superior to other estimators, but our simulations show that their finding is over-biased for a nearly non-stationary time series. To resolve this issue, we first proposed a Bayesian Monte Carlo Markov Chain (MCMC) estimator for fractional integration parameters. This estimator resolves the problem of over-bias. We estimate the fractional integration order for 6 countries for the period 1993M1 to 2017M9. We found that inflation was integrated to an order of 0.8 to 0.9 indicating that the inflation targets are implemented with a high degree of flexibility.

1 Introduction

Inflation targeting has become an increasingly popular monetary policy regime since the early 1990s (Hammond 2012). Bank of Canada was the first central bank, in the modern era, to shift to inflation targeting in 1991, and the Federal Reserve was one of the last to do so in 2012. Although the Federal Reserve was late in adopting an official inflation target, it had targeted the rate of inflation since at least the late 1970s, but without having announced an official target rate. Its inflation target was in other words implicit rather than explicit until 2012.

All inflation targeting central banks are faced with a dilemma. A strict focus on inflation targeting may increase volatility elsewhere in the economy (Svensson 1997). On the other had a too flexible approach to inflation targeting may undermine credibility in the target. Most central banks have opted for policy strategy somewhere in the middle between strict and flexible inflation targeting. In the long-run, the bank focuses narrowly on inflation, while it takes other non-inflation considerations into account over the short- to medium-rum. Or in the words of the former Governor of the Bank of England, Mervyn King, central bankers are not ‘inflation nutters’. How the rest of the economy develops also has an impact on the decisions of the central bank. In fact, one reasons the Federal Reserve had an implicit rather than explicit inflation target was to ensure that the bank had the flexibility to respond to non-inflationary events in the economy (Lindsey et al. 2005).

Although there are benefits from having a flexible inflation target (for a discussion see e.g. Woodford 2003; Kuttner and Posen 2012; Andersson and Jonung 2017) it also raises a few questions. First, it becomes more difficult to hold the central bank accountable when the target is flexible. Because inflation is allowed to deviate from the target under a flexible regime, comparing the inflation outcome with the inflation target is not necessarily a good indicator of the success of the central bank. Second, for consumers, firms, and investors, it becomes more difficult to forecast the future behavior of the central bank. A simple measure of how flexible the inflation target policy is would help to solve some of the issues around a flexible policy. So far, no such simple measure has been found.

In this paper, we propose that the fractional integration order from an autoregressive fractionally integrated moving average (ARFIMA) model can serve as an estimate of the degree of flexibility. Several studies have found that inflation is a highly persistent series. In fact, several studies have failed to reject that inflation contains a unit root, even in those cases in which the central bank has an inflation target and inflation clearly fluctuates around a stationary long-run mean (Hassler and Wolters 1995; Caggiano and Castelnuovo 2011). The results from those studies suggest that inflation is mean-reverting, but a covariance non-stationary series, i.e., fractional integration with an integration order between 0.5 and 1. Under the assumption that in the long-run inflation is entirely caused by monetary policy, as is commonly assumed (see e.g. ECB 2004), the fractional integration order represents the central bankers preferences. The higher (lower) the fractional integration order is, the longer (shorter) are the deviations from the mean (i.e., the target), and the more flexible (strict) is the inflation target policy. Hence, by estimating the fractional integration order, we obtain a simple estimate of the degree of flexibility.

Several estimators of ARFIMA models have been proposed in the econometric literature. These include the parametric method, which is based on the maximum likelihood function (Fox and Taqqu 1986; Sowell 1992; Giraitis and Taqqu 1999) and the regression-based approach in spectral domain (Geweke and Porter-Hudak 1983). Additional estimators include the semi-parametric (Robinson 1995a, b; Shimotsu and Phillips 2005) and the wavelet-based semi-parametric (McCoy and Walden 1996; Jensen 2004) methods.

Chan and Palma (1998) established a theoretical foundation to estimate the ARFIMA model with an approximate maximum likelihood estimation (MLE)-based state space model. The authors truncated the infinite autoregressive (AR) or moving average (MA) representations of the ARFIMA model into finite lags and calculated the approximate maximum likelihood using the Kalman filter. Chan and Palma (1998) show that the approximate MLE-based state space model has desirable asymptotic properties and a rapid convergence rate. Recently, Grassi and Magistris (2014) conducted a simulation study to compare the state space model-based long-memory estimation with several widely applied parametric and semi-parametric methods. Grassi and Magistris (2014) show that compared with the other estimations, the state space model method is robust to the t distribution and missing value, measurement error and level shift.

Chan and Palma (1998) and Grassi and Magistris (2014) consider the stationary case with $0 < d < 0.4$. While inflation likely has an integration order above 0.5, we first propose a Metropolis–Hastings algorithm in Markov chain Monte Carlo (MCMC) to extend the possible range of integration orders to also include the non-stationary case with $d > 0.5$. Simulation studies provided in the paper shows that the approach works well even when the integration order is close to 1.

We then applied the algorithm to estimate the fractional integration order for seven economies (Canada, Euro area, Germany, Norway, Sweden, the United Kingdom, and the United States) between 1993 and 2017 using monthly data. All countries have central banks with inflation targets, although both Germany (1993–1997) and the United States (1993–2012) had implicit rather than explicit inflation targets during parts of the sample period. Our estimation results show that all central banks have flexible targets and are no “inflation nutters”. The fractional integration order is high and close to 0.9. The integration order tends to be higher for larger economies and lower for smaller economies. There is no evidence of having an implicit rather than explicit inflation target makes the target more flexible. The fractional integration order appears to be unrelated to whether the target is explicit or implicit. Out results also indicate that the inflation targets have become more flexible since the financial crisis of 2008/09. Financial stability and the economic crisis that followed have likely changed the focus of central banks away from inflation targeting to other important variables.

The remainder of the paper is organized as follows: Sect. 2 discusses inflation and inflation targets. Section 3 introduces the state space model-based MLE for long-memory series, Sect. 4 combines the state space model with the MCMC algorithm to estimate the fractional difference parameters, Sect. 5 applies empirical examples, and the conclusion can be found in Sect. 6.

2 Inflation and Inflation Targets

2.1 Monetary Policy and Inflation Targets

There is a general consensus in the literature that in the long-run, inflation is caused by the central bank’s monetary policy (ECB 2004), or as Milton Friedman put it, “inflation is always and everywhere a monetary phenomenon” (Friedman 1963). In the short-run, however, there are other factors, such as energy prices, business cycles, shocks, and crises that also affect inflation. Because inflation has no positive long-run effects on the economy, limiting the rate of inflation has always been one of the key tasks for the central bank (Goodhart 2011). How central banks work to achieve price stability has changed over time. Implicit inflation targeting became popular in the late 1970s and early 1980s with both the Federal Reserve and the German Bundesbank setting implicit inflation targets (Svensson 1998; Gerberding et al. 2004; Lindsey et al. 2005). These targets were never publically announced, but central banks acted to stabilize the inflation rate around its unofficial target. In the early 1990s a shift towards explicit and publically announced inflation targets began with Canada in 1991, followed by Sweden and the United Kingdom in 1993 (Hammond 2012).

The difference between an explicit and an implicit inflation target is whether the central bank has publically committed to a specific inflation target. Either in terms of a publically announced target rate or target range (Bernanke et al. 1999). There are advantages and disadvantages with both the explicit and the implicit target. A public commitment to a specific target may enhance the central banks credibility and contribute to anchoring inflation expectations, which in turn helps the central bank to reach its target (Blinder et al. 2008). On the other hand, commitment to a specific target reduces the central banks flexibility to respond to non-inflation events in the economy (Lindsey et al. 2005).

In the long-run, a narrow focus on inflation stability has positive welfare effects. In the short-run, a strict inflation focus can reduce welfare for 2 main reasons: First, to stabilize inflation, the central bank has to neutralize the effects of the economic shocks that affect the rate of inflation. The central bank can only do so by increasing or decreasing the interest rate. These changes in the interest rate affect not only inflation, but also unemployment, economic growth, exchange rates, and financial markets. To keep inflation stable, the central bank must constantly adjust the interest rate, which makes the rest of the economy less stable. In other words, short-run inflation stability comes at the expense of volatility elsewhere in the economy. Consequently, at times, the central bank deliberately allows inflation to deviate from the inflation target to ensure that it does not introduce unnecessary volatility in the real economy or on financial markets (Svensson 1997; Woodford. 2003). Second, inflation stability is the central bank’s main target. However, the bank also has an important role to play in stabilizing the business cycle and acting as a lender of last resort during major financial crises (Goodhart 2011). At times, the central bank has to limit its focus on inflation to address other important problems in the economy.

All inflation targeting central banks have what is called flexible inflation targets. In the long-run they focus entirely on inflation, but in the short-run, they may allow inflation to temporarily deviate from the target for various reasons as long as it does not jeopardize the inflation target in the long run. How flexible the target should be is an important policy question. In theory, the behavior of the central bank should reflect the preferences of the public. In practice, it is often left to the central bank to decide how to implement the inflation target.

Sometimes the law offers some guidance to the central bank on how flexible their policy is allowed to be. For example, article 127 in the Lisbon treaty setting out the aims of the European Central Bank (ECB) states: ‘The primary objective of the European System of Central Banks (hereinafter referred to as “the ESCB”) shall be to maintain price stability. Without prejudice to the objective of price stability, the ESCB shall support the general economic policies in the Union with a view to contributing to the achievement of the objectives of the Union as laid down in Article 3 of the Treaty on European Union” (Lisbon Treaty, article 127). The ECB may consider other variables, but only if the bank satisfies the price stability target, i.e., the inflation target. In the Euro area, the scope for inflation to deviate from the target is limited, and inflation should return to the target relatively quickly.

In contrast, in the United States, the goal is to ‘maintain long-run growth of the monetary and credit aggregates commensurate with the economy’s long-run potential to increase production, so as to promote effectively the goals of maximum employment, stable prices, and moderate long-term interest rates; (Federal Reserve 2018)¹’. Although inflation should be mean-reverting to the target, deviations could be longer given the wider mandate. The wider mandate is potentially once reason the Federal Reserve was one of the last major central banks to publically announce an official inflation target.

Allowing the central bank to have a flexible policy raises the questions of how flexible should the policy be and how flexible is the present policy? In such a discussion, a measure of the degree of flexibility of the policy is needed. Currently, there is no simple measure of how flexible the inflation target is.

2.2 Estimating the Degree of Flexibility

There is no generally agreed-upon method to estimate the flexibility of an inflation target. One common approach is to do so indirectly, by modeling the central bank’s interest-setting policy. According to the Taylor rule, an inflation-targeting central bank with a strict inflation target sets the interest rate solely as a function of the degree to which inflation deviates from the target. Central banks with flexible targets also take other variables into account, such as growth, unemployment, asset prices, and credit growth. An estimate of flexibility is thus obtained by regressing the central bank’s policy rate on a set of variables and determining whether any variable beyond inflation systematically affects the central bank’s interest rate policy (see, e.g., Clarida et al. 1998; Cobion and Goldstein 2012). This indirect approach is sensitive to which variables are included in the analysis. Omitting an important variable may bias the results and produce misleading conclusions.

An alternative, direct approach to measuring the flexibility is to study the persistence of the inflation process. Strict inflation targeting implies that deviations from the target are small and brief. Flexible inflation targeting, on the other hand, implies that inflation may deviate from the target for long periods of time. An estimate of the inflation target’s flexibility is obtained by estimating the persistence of the inflation process. This approach does not require determining which variables to include in the analysis. Rather, it is based solely on studying the inflation process itself.

One method of measuring the degree of flexibility is to study the persistence of inflation using an ARFIMA model. Assume in accordance with theory that (i) long-run inflation is caused by the central bank’s monetary policy, and (ii) over the short- to medium-run, inflation is affected by external factors, such as the business cycle and energy prices, that the central bank may or may not wish to neutralize to stabilize inflation. Under these assumptions, the long-run persistence in inflation is determined by the central bank’s monetary policy. The higher the long run persistence, the more flexible is the inflation target.

In the ARFIMA model, there are 3 sets of parameters: the MA parameters capture the persistence of the external shocks affecting inflation. The AR parameters capture the short- to medium-run persistence in inflation. The fractional integration order captures the long-run persistence in inflation. In accordance with theory, we assume that long run inflation is determined by monetary policy. The fractional integration order is thus an estimate of how flexible the central bank has chosen the inflation target to be. A higher integration order implies that the central bank allows inflation to deviate from the inflation target for a longer period of time, and the inflation target is thus flexible. A lower integration order implies that inflation returns to the inflation target relatively quickly, and the inflation target is thus flexible.

The AR-parameters measures the short- to medium-run persistence of inflation. These parameters are both a measure of the central banks willingness to neutralize external shocks affecting inflation and how successful they are in neutralizing them. The AR parameters are not an estimate of how flexible the inflation target is since the central bank does not perfectly control inflation over the short- to medium-term.

By estimating an ARFRIMA model, we can obtain an estimate of the long-run persistence in inflation and thus the central bank’s willingness to allow inflation to deviate from the inflation target. This approach is a simple technique to complement already existing methods to estimate how flexible the inflation targets are.

3 State Space Maximum Likelihood Estimator of the Fractional Difference Parameter

Consider the ARFIMA (p,d,q) process ${\text{y}} = \left\{ {y_{t} , \, t = 1, \ldots ,n \, } \right\}$, which is defined by:

$$ \varPhi (B)(1 - B)^{d} y_{t} = \varTheta (B)\varepsilon_{t} , $$

(2.1)

where $0 < d < 1$, $\varepsilon_{t} \sim i.i.d.N(0,\sigma_{\varepsilon }^{2} )$; $B$ is the backward difference operator $By_{t} = y_{t - 1}$; while $\varPhi (B) = 1 - \phi_{1} B - \ldots - \phi_{p} B^{p}$ and $\varTheta (B) = 1 - \theta_{1} B - \ldots - \theta_{q} B^{q}$. When p and q are less than or equal to 1, we can obtain a truncated AR or MA representation of the ARFIMA (p,d,q) model, and estimate the parameters by approximate MLE. It is difficult to write out closed-form AR or MA representations and carry out the estimation when p and q exceed 1. However, we can use Hosking’s (1981) method and estimate the parameters in the ARFIMA model recursively:

Step 1 Estimate $d^{0}$ by viewing $y_{t}$ as a pure fractional difference series and then applying the ARIMA (p,0,q) process $u_{t}^{0} = (1 - B)^{{d^{0} }} y_{t}$;

Step 2 Use the Box-Jenkins method to identify and estimate $\varPhi^{0}$ and $\varTheta^{0}$ parameters in the ARIMA (p,0,q) model $\varPhi (B)u_{t}^{0} = \varTheta (B)\varepsilon_{t}$;

Step 3 Apply the ARIMA (0, d, 0) process $x_{t}^{0} = \{ \varTheta^{0} (B)\}^{ - 1} \varPhi^{0} (B)y_{t}$, and estimate $d^{ \, 1}$ in the fractional difference process $(1 - B)^{{d^{1} }} x_{t} = \varepsilon_{t}$;

Step 4 Check for convergence with the convergence rule $d^{ \, i} - d^{ \, i - 1} < 0.005$, and obtain the estimation results $d^{ \, i}$, $\varPhi^{i}$ and $\varTheta^{i}$.

The most essential step in this procedure is to estimate parameter $d$ in the fractional difference process. The literature of the estimator for $d$ is comprehensive, and several methods have been proposed. Chan and Palma (1998) established a theoretical foundation for estimating the ARFIMA model in the framework of a state space model based on the approximate MLE. The authors mention that although the ARFIMA model has infinite AR or MA state-space-model representation, the exact likelihood function can be computed recursively in finite steps by applying the Kalman filter. To estimate the fractional difference parameters, the authors truncate the infinite AR or MA representations into finite lags and calculate the approximate maximum likelihood. Chan and Palma (1998) show that the state space model estimator based on approximate maximum likelihood has desirable asymptotic properties as well as a rapid converging rate.

Recently, Grassi and Magistris (2014) carried out a simulation study to compare the state space model-based long memory estimation with some of the widely applied parametric and semi-parametric methods. They show that, compared to the other estimations, the method proposed by Chan and Palma (1998) is robust to the t distribution, missing value, measurement error, and level shift. However, both Chan and Palma (1998) and Grassi and Magistris (2014) concentrate mainly on estimating d in a stationary time series when $0 < d < 0.4$, or no estimation of greater magnitude of $\sigma_{\varepsilon }^{2}$ rather than unit variance is provided. We have thus extended the estimation to a wider range of combinations, where d$\in$ (0.2, 0.3, 0.4, 0.45, 0.48, 0.7, 0.8, 0.9, 0.95, 0.98) and $\sigma_{\varepsilon }^{{}} \in (1,3,5)$ in the framework of the state space model. Two different estimation methods were applied: the first was based on MLE, and the second was our Bayesian MCMC method. We compared how the estimation methodologies perform when the series are divided into 4 categories: pure stationary with d$\in$ (0.2, 0.3, 0.4); nearly non-stationary with d$\in$ (0.45, 0.48); pure non-stationary with d$\in$ (0.7, 0.8, 0.9); nearly unit root with d$\in$ (0.95, 0.98). Due to its overall superior performance, the Bayesian MCMC method will be used in later empirical analysis.

To obtain the state space form representation for the long memory series $(1 - B)^{d} y_{t} = \varepsilon_{t}$ with $\varepsilon_{t} \sim i.i.d.N(0,\sigma_{\varepsilon }^{2} )$, Chan and Palma (1998) suggest writing the model in the form of truncated AR or MA expansions: $y_{t} = \sum\nolimits_{j = 1}^{m} {\pi_{j} } y_{t - j} + \varepsilon_{t} \;{\text{or}}\;y_{t} = \sum\nolimits_{j = 0}^{m} {\psi_{j} } \varepsilon_{t - j} ,$ where $m$ is truncated lag length. The AR coefficients are given by $\pi_{j} = \frac{\varGamma (j - d)}{\varGamma (j + 1)\varGamma ( - d)}$ and MA coefficients are given by $\psi_{j} = \frac{\varGamma (j + d)}{\varGamma (j + 1)\varGamma (d)}$, where $\varGamma$ denoting the Gamma function. This paper use AR expansion where $\pi_{j} = \frac{ - (j - d - 1)!}{j!( - d - 1)!}$, and the state space form representation can be expressed as:

$$ \left\{ {\begin{array}{ll} {y_{t} = Z\alpha_{t} } & { ( {\text{Measurement equation)}}} \\ {\alpha_{t + 1} = T\alpha_{t} + H\varepsilon_{t} } & { ( {\text{State equation)}}} \\ \end{array} } \right. $$

(2.2)

With the truncation parameter setting as $m$, we have $\alpha_{t} = \left( \begin{aligned} y_{t} \hfill \\ y_{t - 1} \hfill \\ \ldots \hfill \\ y_{t - (m - 1)} \hfill \\ \end{aligned} \right)_{m*1}$, $Z = [1,0, \ldots ,0]_{1*m} \,$, $H = \left( \begin{aligned} 1 \hfill \\ 0 \hfill \\ \ldots \hfill \\ 0 \hfill \\ \end{aligned} \right)_{m*1}$, $T{ = }\left( \begin{aligned} \pi_{ 1} \, \ldots \, \pi_{m} \hfill \\ {\text{ I}}_{m - 1} \ldots { 0} \hfill \\ \end{aligned} \right)_{m*m}$ where ${\text{I}}_{m - 1}$ is identity matrix. Based on the truncated state space form representation, we can obtain the approximate likelihood function with the corresponding estimation algorithm order $O(n)$. Compared with order $O(n^{3} )$ in exact MLE, the reduced computation order achieves a more efficient estimation and faster computation time (Chan and Palma 1998).

The Kalman filter is thereafter utilized to calculate the approximate likelihood function and we give a very brief presentation of the estimation process here. Let $I_{t - 1} = \left\{ {y_{1} ,y_{2} , \ldots ,y_{t - 1} } \right\}$ denote the information set at $t - 1$. $m*1$ vector $\tilde{\alpha }_{t - 1}$ and $m*m$ matrix are defined as follows:

$$ \tilde{\alpha }_{t - 1} = E[\alpha_{t - 1} \left| {I_{t - 1} } \right.] , $$

(2.3)

$$ P_{t - 1} = Var[\alpha_{t - 1} \left| {I_{t - 1} } \right.] , $$

(2.4)

Based on the state equation in (2), the optimal predictor for $\alpha_{t}$, based on information at $t - 1$, is $\alpha_{{t\left| {t - 1} \right.}} = T\tilde{\alpha }_{t - 1}$, while the optimal predictor for $P_{t}$ is $P_{{t\left| {t - 1} \right.}} = TP_{t - 1} T^{{\prime }} + Q$, where $Q = {\text{Var}}(H\varepsilon_{t} ) = H{\text{Var}}(\varepsilon_{t} )H^{{\prime }} = \left( \begin{aligned} \sigma_{\varepsilon }^{2} \ldots \, 0 \hfill \\ { 0 } \ldots { 0} \hfill \\ \end{aligned} \right)_{m*m}$ Based on the measurement equation in (2.2), the corresponding optimal predictor for $y_{t}$ is $y_{{t\left| {t - 1} \right.}} = Z\alpha_{{t\left| {t - 1} \right.}}$. Once the new observation $y_{t}$ is available, we can get prediction error $\nu_{t}^{{}} = y_{t} - y_{{t\left| {t - 1} \right.}} = y_{t} - Z\alpha_{{t\left| {t - 1} \right.}}$. The expectation vector in (2.3) and variance matrix in (2.4) can also be updated as:

$$ \tilde{\alpha }_{t} = \alpha_{{t\left| {t - 1} \right.}} + P_{{t\left| {t - 1} \right.}} Z^{{\prime }} F_{t}^{ - 1} \nu_{t} , $$

(2.5)

$$ P_{t} = P_{{t\left| {t - 1} \right.}} - P_{{t\left| {t - 1} \right.}} Z^{{\prime }} F_{t}^{ - 1} ZP_{{t\left| {t - 1} \right.}} , $$

(2.6)

where $F_{t}$ is the variance of $\nu_{t}^{{}}$ with $F_{t} = E(\nu_{t} \nu_{t}^{{\prime }} ) = ZP_{{t\left| {t - 1} \right.}} Z^{{\prime }}$, and we can further update $\alpha_{t + 1\left| t \right.} = T\tilde{\alpha }_{t}$, $P_{t + 1\left| t \right.} = TP_{t} T^{{\prime }} + Q$. Thus, when the initial values $\tilde{\alpha }_{0}$ and $P_{0}$ are specified, the Kalman filter will return a sequence of prediction errors $\nu_{t}^{{}}$, and the variance $F_{t}$, $t = 1, \, \ldots ,n$. Finally, by maximizing the log likelihood function

$$ \ln L(\left. y \right|\theta ) = - \frac{n}{2}\ln (2\pi ) - \frac{1}{2}\left\{ {\sum\limits_{t = 1}^{n} {\ln F_{t} + \sum\limits_{t = 1}^{n} {v_{t}^{{\prime }} F_{t}^{ - 1} v_{t} } } } \right\} . $$

(2.7)

the parameters $\theta = (d,\sigma_{\varepsilon }^{2} )$ can be estimated. More detailed procedure of estimation can refer to Chan and Palma (1998), Grassi and Magistris (2014), and Tusell (2011).

However, Chan and Palma (1998) as well as Grassi and Magistris (2014) considered only stationary series with $0 < d < 0.4$ where $\sigma_{\varepsilon }^{2} = 1$ and is assumed to be known. The range of integration orders considered in their simulations is relatively narrow from an economic point of view. Several economic time series, such as exchange rates (Andersson 2014), inflation (Hassler and Wolters 1995; Caggiano and Castelnuovo 2011), and interest rates (Tkacz 2001); Coelman and Sirichand 2012) have been found to be covariance non-stationary yet mean-reverting. We have thus expanded the simulations (see Tables 1, 2 and 3) to also include nearly non-stationary where d$\in$ (0.45, 0.48), non-stationary though mean-reverting where d$\in$ (0.7, 0.8, 0.9), and nearly unit root where d$\in$ (0.95, 0.98) time series. Unlike Chan and Palma (1998) and Grassi and Magistris (2014) we also consider both situations where $\sigma_{\varepsilon }^{2}$ is known (Table 1), and when $\sigma_{\varepsilon }^{2}$ is unknown and estimated jointly with $d$ (Table 2). In the simulation, the initial value of $\tilde{\alpha }_{0}$ is set to 0, and $P_{0}$ is the empirical auto-covariance matrix up to lag $m$, which is set to 10. We concentrated on the case where $n = 170$, which corresponds to the sample size in our empirical analysis. The standard deviation of the shocks is set to $\sigma_{\varepsilon }^{{}} \in (1,3,5)$. The simulation is based on 500 repetitions.

Table 1 Estimation of $d$ based on the state space model when $\sigma_{\varepsilon }^{{}}$ is known

Table 2 Estimation of $d$ based on the state space model when $\sigma_{\varepsilon }^{{}}$ is unknown

Table 3 Estimation of $\sigma_{\varepsilon }^{{}}$ based on the state space model

The estimates of the integration order are unbiased for all cases except where $d$ is close to 0.5 and the estimates contain a positive bias. The bias is relatively large (between 0.10 and 0.12). In an empirical analysis, this bias increases the risk of concluding that a series is non-stationary when it is actually stationary.

As shown in Tables 1 and 2, the bias is independent of whether $\sigma_{\varepsilon }^{2}$ is known or unknown and of the value of $\sigma_{\varepsilon }^{2}$. Estimates of $\sigma_{\varepsilon }^{2}$ are unbiased irrespective of d (see Table 3), and only the estimates of $d$ are biased for the series with an integration order close to 0.5.

Generally speaking, the state space model-based estimation yields satisfactory results in most cases. The only exception occurs in the nearly non-stationary situation, when d$\in$ (0.7, 0.8, 0.9), and the serious over-bias causes the estimated series to become non-stationary. The over-bias will continue to be a problem if we have no prior information about the series. However, in certain situations, we have some prior knowledge as to whether the series is stationary or not. In that case, it is worthwhile to guarantee that the estimation of $d$ lies in the correct ranges. It is natural to apply the Bayesian approach to incorporate the prior information into the estimation. In the next section, we combine the state-space representation with the Bayesian approach to make further comparisons.

4 Bayesian MCMC Estimator

The estimation in Sect. 2 is based on the maximization of the log-likelihood function $\ln L\left( {\left. y \right|\theta } \right) = - \frac{n}{2}\ln (2\pi ) - \frac{1}{2}\left\{ {\sum\nolimits_{t = 1}^{n} {\ln F_{t} } + \sum\nolimits_{t = 1}^{n} {v_{t}^{{\prime }} F_{t}^{ - 1} v_{t} } } \right\}$, where $\theta$ is assumed to be fixed but unknown. When prior information indicates whether or not the series is stationary, we can use this knowledge by setting $d$ as a random variable with its domain defined separately as 0 < d < 0.5 or0.5 < d <1. This paper combines the Bayesian inference with the state-space model to estimate $\theta$. Instead of estimating the parameters by maximizing the log-likelihood function $\ln L(\left. {\text{y}} \right|\theta )$, we first construct the posterior distribution $L(\left. \theta \right|{\text{y}})$ based on the prior distribution $\pi (\theta )$ and the approximate likelihood function $L(\left. {\text{y}} \right|\theta )$ by $L(\left. \theta \right|{\text{y}})\infty L(\left. {\text{y}} \right|\theta )\pi (\theta )$. The MCMC algorithm is implemented to generate values directly from the $L(\left. \theta \right|{\text{y}})$, and the estimator for the parameters is the expected value from the posterior distribution.

The prior information $\pi (\theta )$ is chosen as the independent prior information for d and $\sigma_{\varepsilon }$ with $\pi (\theta ) = \pi (d)\pi (\sigma )$. In cases where we already know that the series is stationary with 0 < d < 0.5 and non-stationary with 0.5 < d <1, we chose the uniform distributions Unif (0,0.5) and Unif (0.5,1), respectively, for d. The prior distribution $\sigma_{\varepsilon }$ does not depend on $d$, and this paper uses Unif (0,10). Then, the posterior distributions for d and $\sigma_{\varepsilon }$ are:

$$ p(d\left| {\sigma ,y} \right.)\infty \exp \left\{ { - \frac{1}{2}\sum\limits_{t = 1}^{n} {\ln F_{t} - \frac{1}{2}\sum\limits_{t = 1}^{T} {v_{t}^{\prime } F_{t}^{ - 1} v_{t} } } } \right\} \times I_{(0,0.5)} (d) $$

$$ p(\sigma \left| {d,y} \right.)\infty \exp \left\{ { - \frac{1}{2}\sum\limits_{t = 1}^{T} {\ln F_{t} - \frac{1}{2}\sum\limits_{t = 1}^{T} {v_{t}^{\prime } F_{t}^{ - 1} v_{t} } } } \right\} \times I_{(0,10)} (\sigma ) $$

The estimators for $d$ and $\sigma_{\varepsilon }$ are simply the posterior mean, and $\hat{\sigma } = \int {\sigma {\text{ d}}} P(\sigma \left| {{\text{y}})} \right.$. As the marginal posterior $P(d\left| {{\text{y}})} \right.$ and $P(\sigma \left| {{\text{y}})} \right.$ cause the integration to be analytically intractable, we utilized the Metropolis-Hastings algorithm to generate samples from the posterior distribution and then took the mean value of the samples as the posterior mean. Furthermore, since the posterior distributions for d and $\sigma_{\varepsilon }$ depend conditionally on one another, a 2-step iterative Metropolis-Hastings method was applied as follows:

• Step 1 Set initial values for d and $\sigma_{\varepsilon }$ with $d^{0}$ and $\sigma_{\varepsilon }^{0}$.

• Step 2 Generate $d^{ \, * }$ from Unif (0, 0.5) for stationary series and Unif (0.5,1) for non-stationary series.

  ${\text{For}}i = 1, \, 2 \ldots$

• Step 3 Set $\alpha_{d} = \hbox{min} \left\{ {1, \, \frac{{p(d^{*} \left| {\sigma^{i - 1} ,y} \right.)}}{{p(d^{i - 1} \left| {\sigma^{i - 1} ,y} \right.)}}} \right\}$, take $u$ from Unif (0,1), if $u < \alpha_{d}$ set $d^{ \, i} = d^{ \, *}$; otherwise set $d^{ \, i} = d^{ \, i - 1}$.

• Step 4 Generate $\sigma_{\varepsilon }^{*}$ from Unif (0,10).

• Step 5 Set $\alpha_{\sigma } = \hbox{min} \left\{ {1, \, \frac{{p(\sigma^{*} \left| {d^{i} ,y} \right.)}}{{p(\sigma^{i - 1} \left| {d^{i} ,y} \right.)}}} \right\}$, take $u$ from Unif (0,1), if $u < \alpha_{\sigma }$ set $\sigma_{\varepsilon }^{i} = \sigma_{\varepsilon }^{*}$; otherwise set $\sigma_{\varepsilon }^{i} = \sigma_{\varepsilon }^{i - 1}$.

• Step 6 Repeat Step 2–5 $N$ times, burn in the first $N_{0}$ samples. The estimators are

  $$ \hat{d} = \frac{{\sum\nolimits_{{i = N_{0} }}^{N} {d^{ \, i} } }}{{N - N_{0} }}\;{\text{and}}\;\hat{\sigma }_{\varepsilon } = \frac{{\sum\nolimits_{{i = N_{0} }}^{N} {\sigma_{\varepsilon }^{i} } }}{{N - N_{0} }} $$

In this algorithm, Steps 3 and 5 guarantee that the new proposed values $d^{ \, * }$ and $\sigma_{\varepsilon }^{*}$ are accepted with acceptance probabilities $\alpha_{d}$ and $\alpha_{\sigma }$. This procedure is the necessary condition in order for $d^{ \, i}$ and $\sigma_{\varepsilon }^{i}$ to converge to the posterior distribution. For a theoretical discussion of MCMC and Metropolis-Hastings algorithm, see Scollnik (1996), Brooks (1998), and Besag (2004).

We set $d^{0} = 0.25$ for stationary series, $d^{0} = 0.75$ for non-stationary series, and $\sigma_{\varepsilon }^{0} = sd(y)$. $N$ is set at 300, and $N_{0}$ is set at 50, because the simulation result shows both $d^{i}$ and $\sigma_{\varepsilon }^{i}$ converging to stability at a very fast rate. If the other initial values are chosen, the estimation results are similar. The new estimation is shown in Tables 4, 5, and 6:

Table 4 Estimation of $d$ based on the MCMC when $\sigma_{\varepsilon }^{{}}$ is known

Table 5 Estimation of $d$ based on the MCMC when $\sigma_{\varepsilon }^{{}}$ is unknown

Table 6 Estimation of $\sigma_{\varepsilon }^{{}}$ based on the MCMC

Tables 4 and 5 show that the MCMC-based method produces almost exactly the same result when d$\in$$( 0. 2 , 0. 3 , 0. 4 , 0. 7 , 0. 8 , 0. 9 , 0. 9 5 , 0. 9 8 )$, but makes much better estimations when d$\in$$( 0. 4 , 0. 4 5 , 0. 4 8 )$, meaning that when prior information is available, the Bayesian-based method can greatly improve the estimation. Table 6 shows that the estimation of $\sigma_{\varepsilon }$ is more over-biased than Table 3 when d = 0.48; this is because we chose the prior distribution for $\sigma_{\varepsilon }$ with a much larger range of Unif (0,10). This is consistent with the extreme importance of choosing the correct prior distribution in Bayesian inference. However, compared with the improved estimation when d$\in$$( 0. 4 , 0. 4 5 , 0. 4 8 )$, the bias of $\hat{\sigma }_{\varepsilon }$ is acceptable.

Clearly, the Bayesian MCMC estimator attains superior performance compared to the MLE in Sect. 2; thus, the 6-step estimation process described in Sect. 3 was adopted to estimate the fractional difference parameter in the following empirical analysis.

5 Empirical Analysis

5.1 Countries and Data

We tested the flexibility of inflation targets in 7 developed and inflation-targeting economies: Canada, the Euro area, Germany, Norway, Sweden, the United Kingdom and the United States. The sample period begins in January 1993 and ends in October 2017. Germany is included as a compliment to the euro area data since the euro was first introduced in 1999. The European Central Bank is to a large extent modelled on the German Bundesbank whereby we expect the results for Germany prior to 1999 to closely follow the behavior of ECB post 1999.

Each economy’s inflation target is presented in Table 7. Canada was the first country to introduce an explicit target in 1991, followed by Sweden and the United Kingdom in 1993.² The Euro area began to explicitly target inflation when the euro was introduced in 1999. Norway followed in 2001, and the United States announced a formal target in 2012. Although Norway, the Germany/Euro area and the United States formally began to target inflation after our sample begins in 1993, at least Germany and the United states had implicit inflation targets prior to this time (Svensson 1998; Gerberding et al. 2004; Lindsey et al. 2005). Whether having an implicit or explicit inflation target affects the results is one issue we will consider in our analysis.

Table 7 Descriptive statistics

We estimate the fractional integration order for three periods (i) the full sample 1993–2017, (ii) the period before the international financial crisis 1993–2006; (iii) the period after the introduction of the euro (1999–2017). By splitting the sample into sub-samples allows us to consider two important questions. First, whether having an implicit or explicit inflation target affects the results.³ And second, whether the financial crisis and its aftermath has affected the behavior of central banks. The crisis and its real economic consequences may have shifted central banks attention from inflation targeting to stabilizing the financial system and the real economy whereby we expect the inflation targets to have become more flexible after 2007/09.

Almost all countries have chosen inflation targets of 2%; Norway is an outlier, with a target rate of 2.5%. Some economies’ inflation targets include a tolerance band showing the range within which inflation is allowed to or likely to deviate from the target due to factors outside the central bank’s control (for a discussion see Hammond 2012; Andersson and Jonung 2017). Tolerance bands are often announced to allow the central bank to consider other non-inflation events in the economy while maintaining credibility for its inflation target. Consequently, we may expect the integration order to be higher for countries with tolerance bands.

Inflation is always measured using an estimate of consumer price inflation. The exact construction of the index varies across countries. Some countries use their domestic Consumer Price Index (CPI); Sweden uses the CPI but with a fixed mortgage rate (CPIF), the United States relies on the price index for Personal Consumption Expenditures (PCE), and the Euro area uses the Harmonized Index of Consumer Prices (HICP). Average inflation for the full sample was between 1.7% (Sweden) and 2.1% (Norway). In other words, average inflation was close to the numerical targets. For the shorter 1999–2017 sample, average inflation was between 1.5% (Sweden) and 2.1% (Norway). On average, inflation is close to the targets’ respective central values. For most economies, inflation is slightly below the target, between − 0.4 (Norway) and − 0.2 percentage points (United States) for the full sample, and between − 0.4 (Norway) and − 0.1 percentage points (Canada) for the shorter sample. The exception is the United Kingdom, where average inflation is exactly equal to the central value. All deviations from the central value are small and within the tolerance band for those countries with explicit bands. Moreover, inflation estimates are subject to measurement error, whereby we cannot rule out that inflation is actually equal to the target.

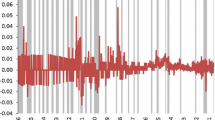
While average inflation is close to the targets, there have been relatively large fluctuations in inflation. Inflation for the 3 largest economies (Euro area, United Kingdom and the United States) is shown in Fig. 1. Figure 2 illustrates inflation for the 3 minor economies (Canada, Norway, and Sweden). Inflation fluctuates within the range of − 2% to 6%. It appears to be more volatile in the smaller economies; however, judging from the figures, the deviations from the mean are more persistent in the larger economies. The long persistence in the inflation process is particularly noticeable for the United Kingdom, where inflation trended downward from 1993 and 1999 before it began to trend upward for the next 8 years, rising above 5% in 2008. Following the financial crisis, inflation in the United Kingdom has fluctuated in shorter cycles of 3 to 4 years. In contrast, the persistence of inflation in Sweden is much shorter compared to the larger economies. Inflation in Canada and Norway also displays less persistence. The figures indicate that inflation among the smaller economies is likely to have a smaller integration order compared to the larger economies.

Fig. 1

Inflation in the Euro area, Germany, the United Kingdom, and the United States, January 1993 to September 2017

Fig. 2

Inflation in Canada, Norway, and Sweden, January 1993 to September 2017

The larger economies were all directly affected by the financial crisis of 2007–09, which is visible in the figure by large drops in inflation in 2008–09. The smaller economies were not directly affected by the crisis by having a banking crisis themselves, but were indirectly affected as the crisis spread across the world. In these countries, inflation was more stable than in the larger economies through the end of the 2000s. Inflation in the 2010s has shown relatively large fluctuations, indicating that central banks have potentially focused less on inflation targets and more on financial stability and economic recovery after the crisis.

5.2 Estimation Results

To estimate the ARFIMA model, we followed the 4-step process outlined in Sect. 2, which was proposed by Hoskings (1981). When we estimated the fractional difference parameters in the process, we applied our 6-step MCMC method in Sect. 3. Estimation results of the ARFIMA model for the large economies are shown in Table 8, and for the small economies in Table 9. The results confirm that inflation is a persistent process characterized by relatively long swings away from the mean. The fractional integration order is significantly larger than 0 for all economies. In addition, the fractional integration order is larger than 0.5, indicating that inflation is a variance–covariance non-stationary, yet still mean-reverting process. In other words, inflation exhibits long swings around its mean.

Table 8 Estimation results: Euro area, Germany, the United Kingdom, and the United States

Table 9 Estimation results: Canada, Norway, and Sweden

Reviewing the full sample period from 1993–2017, Sweden and the United Kingdom stand out compared to the other countries. For most economies, the fractional integration order was within the interval 0.74 (Germany) and 0.83 (Canada). Sweden had a lower integration order of 0.59, and the United Kingdom’s was 1.09. In other words, Sweden has a strict inflation target compared to the other countries and the United Kingdom a very flexible target. For most economies, the persistence in inflation was captured by the fractional integration order, but for Sweden the AR parameter was also significant and relatively high at 0.56. This result is clear evidence that Sweden has a stricter inflation target compared to the other countries.

We can draw two main conclusions from the Swedish and the United Kingdom results. First, having a tolerance band does not automatically make the inflation target more flexible. The Swedish inflation target included a tolerance band for most of the sample period but the Swedish monetary policy is still the strictest. Second, both Sweden and the United Kingdom have had explicit inflation targets throughout the sample period. Still, they represent the countries with the smallest and highest integration orders. In other words, there is no systematic evidence of the results being affected by whether the central bank has an explicit or implicit inflation target.

The United Kingdom’s integration order of more than 1 suggests that British inflation is a non-stationary process, i.e., the Bank of England has not stabilized inflation around a stationary mean. This result is possibly explained by 1 of 3 factors: (i) the swings away from the mean are very long, and the sample period too short to capture the mean-reversion of the inflation series; (ii) the financial crisis in 2008–09 caused the bank to deviate from its inflation target to focusing on stabilizing the economy; or (iii) there is a break in the mean, which may bias the estimate of the fractional integration order. Figure 1 lends some support to factors 1 and 3. United Kingdom inflation is characterized by persistent trends from 1993 to 2008. First, inflation was on a downward trajectory—from 3 to 0.5%—from 1993 to 1999. Thereafter, it trended upward, reaching 5% in 2008. Following the crisis, inflation fluctuated substantially, falling to 1% in 2009 before again reaching 5% in 2012, then falling to 0% in 2016 before increasing to 3% in 2017. The financial crisis has clearly affected inflation, indicating a change of focus from central banks. A break in the mean may bias any estimate of the integration order (see, e.g., Narayan and Narayan 2010). However, average United Kingdom inflation is stable over time (see Table 7), which makes the third explanation less likely.

All 3 major economies were clearly affected by the financial crisis, which may affect how central banks conduct monetary policy. To test this hypothesis, we re-estimated the model from 1993 to 2006, the year before the financial crisis began. Excluding the years after the crisis reduced the fractional integration order for the United Kingdom from 1.09 to 0.95. The fractional integration order was relatively high, but remained below 1, indicating mean-reversion. The fractional integration order for the United States was similar at 0.93, which is higher compared to the full sample period. Interestingly, the United Kingdom and the United States have almost the same integration order despite the Federal Reserve having an implicit inflation target and the Bank of England an explicit inflation target throughout this time period. Again, the results point to having explicit or implicit inflation targets does not affect the results. The fractional integration order of the German inflation rate remains stable over time (between 0.71 and 0.74).

For the three smaller economies that were only indirectly affected by the financial crisis, the results were similar to those for the full sample period. The fractional integration order for Sweden was smaller compared to the other countries, while the AR parameter was larger, indicating a relatively strict implementation of the inflation target. For Canada and Norway, the inflation targets were more flexible, and the integration order was higher; however, the results still clearly point toward a mean-reverting processes. The estimated fractional integration order was 0.88 for Canada and 0.78 for Norway. Similar to Germany, the estimated integration order for Norway is similar irrespective of sample period despite the Bank of Norway having shifted from an implicit to an explicit inflation target in 2001.

Next, we re-estimated the model for the period 1999–2017, which allowed us to include the Euro area in the analysis. We only considered the full-time period in this case, as restricting the sample to the 1999–2006 period would leave us with too few time observations to capture inflation’s long-run properties. The pattern of the results remained similar to the previous results: (i) inflation is a mean-reverting process, yet with long swings; (ii) larger economies tend to have a higher integration order compared to smaller countries, and (iii) having an explicit or implicit inflation target does not appear to impact the results. In this sample the estimated integration orders were 0.97 for the Euro, area 1.00 for the United Kingdom, and the United States it was 0.94. For the smaller countries, the corresponding estimates were Canada 0.93, Norway 0.82, and Sweden 0.89.

One change in the results when excluding the early parts of the 1990 s is that the estimated fractional integration order increased for all small countries. The increase was particularly large for Sweden, where the integration order increased from 0.59 to close to 0.89. Judging from Fig. 2, the swings in inflation became longer after the financial crisis, especially in comparison to the 1990s. The increased integration order indicates a change in policy focus from a stricter inflation-targeting perspective in the 1990s to a more flexible approach, especially after the financial crisis. Smaller countries adopted inflation targets in the 1990s following 2 decades of relatively high inflation. It is possible that a strict focus on inflation targeting in the early years was necessary to build confidence for the target, while over time, central banks have gained sufficient public confidence for the target to consider more than inflation when making interest rate decisions. It is also possible that the shift in focus was forced upon the central banks by the financial crisis, after which they needed to take action to stabilize both the real economy and the financial system at the expense of the inflation target.

6 Conclusions

This paper answers the question ‘Are central bankers inflation nutters?’ by testing the flexibility of inflation targets. We define flexibility based on the persistence of inflation. A higher degree of persistence implies that inflation deviates from the mean for a longer period of time, and the inflation target is thus flexible. A lower degree of persistence implies that the deviations from the mean do not last very long and that the inflation target is flexible. Persistence is modeled using an ARFIMA model. To estimate the fractional difference parameter in the ARFIMA model, we applied the Metropolis–Hastings algorithm in MCMC, as this method can achieve the same precise estimation as the approximate maximum likelihood method while resolving the problem of over-bias when $0.4 < d < 0.5$.

The empirical results show that inflation is a mean-reverting process, but that deviations from the mean are persistent. This persistence, judged by the fractional integration order, is higher among larger economies than among smaller ones. The financial crisis of 2008–09 likely caused central banks to shift focus from relatively strict inflation targeting to a more flexible approach. We find no evidence of central banks having implicit inflation targets being more flexible compared to countries with an explicit target.