Possibilistic Moment Models for Multi-period Portfolio Selection with Fuzzy Returns

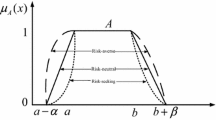
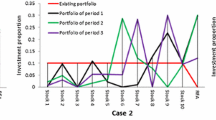
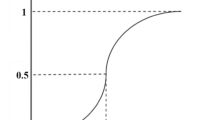
Abstract

The aim of this paper is to investigate the effects of higher moments on multi-period portfolio selection with fuzzy returns. This paper gives the definitions of possibilistic mean and variance about the product of multiple fuzzy numbers. Based on these definitions, three multi-period fuzzy portfolio optimization models are proposed. The proposed models aim to maximize terminal wealth and minimize terminal risk by taking into account some realistic constraints including higher moments, budget constraint, round-lot constraint, cardinality constraint and bound constraint. To ensure the selection of the best solutions, a novel fuzzy programming approach-based self-adaptive differential evolution algorithm is designed to solve the proposed models. A numerical example is given to demonstrate the application of the proposed models. Computational results show that the designed algorithm is effective for solving complex portfolio selection model with realistic constraints.

Appendix

Proof

(i) By Definition 1, we have $M^{-}(A_{i})={\int }_{0}^{1}\gamma \underline{a}_{i}(\gamma )\text {d}\gamma$, $M^{+}(A_{i})={\int }_{0}^{1}\gamma \overline{a}_{i}(\gamma )\text {d}\gamma$ and $E(A_{i})=\tfrac{1}{2}(M^{-}(A_{i})+M^{+}(A_{i}))$. Then, by Eq. (7), we have

$$\begin{aligned} E\left[ \prod \limits _{i = 1}^n A_{i}\right]&=\int _{0}^{1}\ldots \int _{0}^{1}\gamma _{1}\ldots \gamma _{n}\left[ \prod \limits _{i = 1}^n\underline{a}_{i}(\gamma _{i})+\sum \limits _{k=1}^{n}\overline{a}_{k}(\gamma _{k})\mathop {\mathop {\mathop {\prod }\limits _{i= 1}} \limits _{i \ne k}}^n\underline{a}_{i}(\gamma _{i})\right. \nonumber \\&\quad \left. +\,\mathop {\mathop {\mathop {\sum }\limits _{k=1}}\limits _{k<j}}^{n}\overline{a}_{k}(\gamma _{k})\overline{a}_{j}(\gamma _{j}) \mathop {\mathop {\mathop {\mathop {\prod }\limits _{i = 1}}\limits _{ i \ne j}}\limits _{i \ne k}}^n\underline{a}_{i}(\gamma _{i})+\sum \limits _{k=1}^{n}\underline{a}_{k}(\gamma _{k}) \mathop {\mathop {\mathop {\prod }\limits _{i = 1}} \limits _{i \ne k}}^n\overline{a}_{i}(\gamma _{i})+\prod \limits _{i = 1}^n\overline{a}_{i}(\gamma _{i})\right] \text {d}\gamma _{1}\ldots \text {d}\gamma _{n}\\&= \prod \limits _{i = 1}^n\int _{0}^{1}\gamma _{i}\underline{a}_{i}(\gamma _{i})\text {d}\gamma _{i}+\sum \limits _{k=1}^{n}\int _{0}^{1}\gamma _{k}\overline{a}_{k}(\gamma _{k})\text {d}\gamma _{k}\mathop {\mathop {\mathop {\prod }\limits _{i = 1}}\limits _{i \ne k}}^n\int _{0}^{1}\gamma _{i}\underline{a}_{i}(\gamma _{i})\text {d}\gamma _{i}\nonumber \\&\quad +\,\mathop {\mathop {\mathop {\sum }\limits _{k=1}}\limits _{k<j}}^{n}\int _{0}^{1}\gamma _{k}\overline{a}_{k}(\gamma _{k})\text {d}\gamma _{k}\int _{0}^{1}\gamma _{j}\overline{a}_{j}(\gamma _{j})\text {d}\gamma _{j} \mathop {\mathop {\mathop {\mathop {\prod }\limits _{i = 1}} \limits _{ i \ne j}}\limits _{i \ne k }}^n\int _{0}^{1}\gamma _{i}\underline{a}_{i}(\gamma _{i})\text {d}\gamma _{i}+\cdots \nonumber \\&\quad \left. +\,\sum \limits _{k=1}^{n}\int _{0}^{1}\gamma _{k}\underline{a}_{k}(\gamma _{k})\text {d}\gamma _{k} \mathop {\mathop {\mathop {\prod }\limits _{i = 1}} \limits _{i \ne k}}^n\int _{0}^{1}\gamma _{i}\overline{a}_{i}(\gamma _{i})\text {d}\gamma _{i}+\prod \limits _{i = 1}^n\int _{0}^{1}\gamma _{i}\overline{a}_{i}(\gamma _{i})\text {d}\gamma _{i}\right] \\&= \frac{1}{2^{n}}M^{-}(A_{i})\left[ \prod \limits _{i = 1}^n M^{-}(A_{i})+\sum \limits _{k=1}^{n}M^{+}(A_{k}) \mathop {\mathop {\mathop {\prod }\limits _{i = 1}} \limits _{i \ne k}}^n M^{-}(A_{i})+ \mathop {\mathop {\mathop {\sum }\limits _{k=1}} \limits _{k<j}}^{n}M^{+}(A_{k})M^{+}(A_{j})\right. \nonumber \\&\quad \left. \times \mathop {\mathop {\mathop {\mathop {\prod }\limits _{ i = 1}}\limits _{ i \ne j}}\limits _{i \ne k }}^n M^{-}(A_{i})+\cdots +\sum \limits _{k=1}^{n}M^{-}(A_{k}) \mathop {\mathop {\mathop {\prod }\limits _{i = 1}} \limits _{i \ne k}}^n M^{+}(A_{i})+\prod \limits _{i = 1}^n M^{+}(A_{i})\right] \\&= \frac{1}{2^{n-1}}E(A_{1})\left[ \prod \limits _{i =2}^n M^{-}(A_{i})+\sum \limits _{k=2}^{n}M^{+}(A_{k}) \mathop {\mathop {\mathop {\prod }\limits _{i =2}} \limits _{i \ne k}}^n M^{-}(A_{i})+ \mathop {\mathop {\mathop {\sum }\limits _{k=2}} \limits _{k<j}}^{n}M^{+}(A_{k})M^{+}(A_{j})\right. \nonumber \\&\quad \left. \times \mathop {\mathop {\mathop {\mathop {\prod }\limits _{ i =2}}\limits _{ i \ne j}}\limits _{i \ne k }}^n M^{-}(A_{i})+\cdots +\sum \limits _{k=2}^{n}M^{-}(A_{k}) \mathop {\mathop {\mathop {\prod }\limits _{i =2}} \limits _{i \ne k}}^n M^{+}(A_{i})+\prod \limits _{i =2}^n M^{+}(A_{i})\right] \\&\qquad \vdots \\&= \frac{1}{2^{n-l}}\prod \limits _{i =1}^l E(A_{i})\left[ \prod \limits _{i =l}^n M^{-}(A_{i})+\sum \limits _{k=l}^{n}M^{+}(A_{k}) \mathop {\mathop {\mathop {\prod }\limits _{i =l}} \limits _{i \ne k}}^n M^{-}(A_{i}) \mathop {+\mathop {\mathop {\sum }\limits _{k=l}} \limits _{k<j}}^{n}M^{+}(A_{k})M^{+}(A_{j})\right. \nonumber \\&\quad \left. \times \mathop {\mathop {\mathop {\mathop {\prod }\limits _{ i =l}} \limits _{ i \ne j }}\limits _{i \ne k }}^n M^{-}(A_{i})+\cdots +\sum \limits _{k=l}^{n}M^{-}(A_{k}) \mathop {\mathop {\mathop {\prod }\limits _{i =l}} \limits _{i \ne k}}^n M^{+}(A_{i})+\prod \limits _{i =l}^n M^{+}(A_{i})\right] \\&\qquad \vdots \\&=\prod \limits _{i = 1}^n E(A_{i}). \end{aligned}$$

(ii) According to Eq. (8), we have

$$\begin{aligned}&Var\left( \prod \limits _{i = 1}^n A_{i}\right) =\int _{0}^{1}\ldots \int _{0}^{1} \gamma _{1}\ldots \gamma _{n}\left[ \left( \prod \limits _{i = 1}^n E(A_{i})- \prod \limits _{i = 1}^n\underline{a}_{i}(\gamma _{i})\right) ^{2} \right. \nonumber \\&\quad +\sum \limits _{k=1}^{n}\left( \prod \limits _{i = 1}^n E(A_{i})-\overline{a}_{k} (\gamma _{k}) \mathop {\mathop {\mathop {\prod }\limits _{i = 1}} \limits _{i \ne k}}^T \underline{a}_{i}(\gamma _{i})\right) ^{2}\nonumber \\&\quad +\,\mathop {\mathop {\mathop {\sum }\limits _{k=1}}\limits _{k<j}}^{T} \left( \prod \limits _{i = 1}^n E(A_{i})-\overline{a}_{k}(\gamma _{k})\overline{a}_{j}(\gamma _{j}) \mathop {\mathop {\mathop {\mathop {\prod }\limits _{i = 1}} \limits _{ i \ne j }}\limits _{i \ne k }}^T\underline{a}_{i} (\gamma _{i})\right) ^{2}+\cdots +\sum \limits _{k=1}^{n}\left( \prod \limits _{i = 1}^n E(A_{i})-\underline{a}_{k}(\gamma _{k})\prod \limits _{i = 1}^n \overline{a}_{i}(\gamma _{i})^{2}\right. \nonumber \\&\quad +\,\left. \left( \prod \limits _{i = 1}^n E(A_{i})-\prod \limits _{i = 1}^n\overline{a}_{i}(\gamma _{i})\right) ^{2}\right] \text {d}\gamma _{1} \ldots \text {d}\gamma _{n}. \end{aligned}$$

(36)

Notice that the rth item in Eq. (36) can be represented by

$$\begin{aligned}&\int _{0}^{1}\ldots \int _{0}^{1}\gamma _{1}\ldots \gamma _{n} \mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}}\limits _{j\in \{1,2, \ldots ,r\}}}^{n}\left( \prod \limits _{i = 1}^n E(A_{i})-\prod \limits _{j = 1}^r\overline{a}_{k_{j}}(\gamma _{k_{j}}) \mathop {\mathop {\mathop {\prod }\limits _{ i = 1}}\limits _{ i \ne k_{j}}}^n \underline{a}_{i}(\gamma _{i})\right) ^{2}\text {d}\gamma _{1}\ldots \text {d} \gamma _{n}\nonumber \\&=\int _{0}^{1}\ldots \int _{0}^{1}\gamma _{1}\ldots \gamma _{n} \mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}}\limits _{\;j\in \{1,2, \ldots ,r\}}}^{n}\left[ \left( \prod \limits _{i = 1}^n E(A_{i})\right) ^{2}-2\prod \limits _{i = 1}^n E(A_{i})\prod \limits _{j = 1}^r\overline{a}_{k_{j}}(\gamma _{k_{j}}) \mathop {\mathop {\mathop {\prod }\limits _{ i = 1}}\limits _{ i \ne k_{j}}}^n\underline{a}_{i}(\gamma _{i})\right. \nonumber \\&\quad +\,\left. \left( \prod \limits _{j =1}^r\overline{a}_{k_{j}}(\gamma _{k_{j}}) \mathop {\mathop {\mathop {\prod }\limits _{ i = 1}}\limits _{ i \ne k_{j}}}^T\underline{a}_{i}(\gamma _{i})\right) ^{2}\right] \text {d}\gamma _{1}\ldots \text {d}\gamma _{n}\nonumber \\&= \frac{1}{2^{n}} \left( \prod \limits _{i = 1}^n E(A_{i})\right) ^{2}-2\prod \limits _{i = 1}^n \mathop {\mathop {E(A_{i})\mathop {\sum }\limits _{k_{j}=1}} \mathop {\;j\in \{1,2,\ldots ,r\}}}^{n}\prod \limits _{j = 1}^r\int _{0}^{1}\gamma _{k_{j}}\overline{a}_{k_{j}}(\gamma _{k_{j}}) \text {d}\gamma _{k_{j}}\nonumber \\&\quad \times \mathop {\mathop {\mathop {\prod }\limits _{i = 1}}\limits _{ i \ne k_{j}}}^n\int _{0}^{1}\gamma _{i}\underline{a}_{i}(\gamma _{i}) \text {d}\gamma _{i}+\mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}} \limits _{\;j\in \{1,2,\ldots ,r\}}}^{n}\prod \limits _{j = 1}^r\int _{0}^{1}\gamma _{k_{j}}(\overline{a}_{k_{j}}(\gamma _{k_{j}}))^2 \text {d}\gamma _{k_{j}} \mathop {\mathop {\mathop {\prod }\limits _{i = 1}}\limits _{ i \ne k_{j}}}^T \int _{0}^{1}\gamma _{i}(\underline{a}_{i}(\gamma _{i})\text {d} \gamma _{i})^{2}\nonumber \\&= \frac{1}{2^{n}} \left( \prod \limits _{i = 1}^n E(A_{i})\right) ^{2}-\tfrac{1}{2^{n-1}}\prod \limits _{i = 1}^n E(A_{i}) \mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}}\limits _{\;j\in \{1,2, \ldots ,r\}}}^{n}\prod \limits _{j = 1}^r M^{+}(A_{k_{j}}) \mathop {\mathop {\mathop {\prod }\limits _{ i = 1}} \limits _{ i \ne k_{j}}}^n M^{-}(A_{i})\nonumber \\&\quad +\,\mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}} \limits _{\;j\in \{1,2,\ldots ,r\}}}^{n}\prod \limits _{j = 1}^r\int _{0}^{1}\gamma _{k_{j}}(\overline{a}_{k_{j}} (\gamma _{k_{j}}))^2\text {d}\gamma _{k_{j}} \mathop {\mathop {\mathop {\prod }\limits _{i = 1}} \limits _{ i \ne k_{j}}}^T\int _{0}^{1}\gamma _{i}(\underline{a}_{i} (\gamma _{i}))^{2}\text {d}\gamma _{i} \end{aligned}$$

(37)

It follows that Eq. (37) can be rewritten as the following form

$$\begin{aligned}&Var\left( \prod \limits _{i = 1}^n A_{i}\right) =\frac{1}{2^{n}} \left( \prod \limits _{i = 1}^n E(A_{i})\right) ^{2}-\frac{1}{2^{n-1}}\prod \limits _{i = 1}^n E(A_{i})\prod \limits _{i = 1}^n M^{-}(A_{i})+\prod \limits _{ i = 1}^n\int _{0}^{1}\gamma _{i}(\underline{a}_{i}(\gamma _{i}))^{2}\text {d}\gamma _{i}\nonumber \\&\quad +\,2^{n-2}\times \frac{1}{2^{n}} \left( \prod \limits _{i = 1}^n E(A_{i})\right) ^{2}-\frac{1}{2^{n-1}}\prod \limits _{i = 1}^n E(A_{i})\sum \limits _{r = 1}^{n-2} \mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}} \limits _{\;j\in \{1,2,\ldots ,r\}}}^{n}\prod \limits _{j = 1}^r M^{+}(A_{k_{j}}) \mathop {\mathop {\mathop {\prod }\limits _{ i = 1}} \limits _{ i \ne k_{j}}}^n M^{-}(A_{i})\nonumber \\&\quad +\,\sum \limits _{r = 1}^{n-2} \mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}} \limits _{\;j\in \{1,2,\ldots ,r\}}}^{n}\prod \limits _{j = 1}^r\int _{0}^{1}\gamma _{k_{j}}(\overline{a}_{k_{j}} (\gamma _{k_{j}}))^2\text {d}\gamma _{k_{j}} \mathop {\mathop {\mathop {\prod }\limits _{i = 1}} \limits _{ i \ne k_{j}}}^n\int _{0}^{1}\gamma _{i}(\underline{a}_{i} (\gamma _{i}))^{2}\text {d}\gamma _{i}+\tfrac{1}{2^{n}}(\prod \limits _{i = 1}^n E(A_{i}))^{2}\nonumber \\&\quad -\,\frac{1}{2^{n-1}}\prod \limits _{i = 1}^n E(A_{i}) \prod \limits _{i = 1}^n M^{+}(A_{i})+\prod \limits _{ i = 1}^n \int _{0}^{1}\gamma _{i}(\overline{a}_{i}(\gamma _{i}))^{2}\text {d} \gamma _{i}\nonumber \\&=\left( \prod \limits _{i = 1}^n E(A_{i})\right) ^{2}-\frac{1}{2^{n-1}}\prod \limits _{i = 1}^n E(A_{i})\left[ \prod \limits _{i = 1}^n M^{-}(A_{i})+\sum \limits _{r = 1}^{n-2} \mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}} \limits _{\;j\in \{1,2,\ldots ,r\}}}^{n}\prod \limits _{j = 1}^r M^{+}(A_{k_{j}}) \mathop {\mathop {\mathop {\prod }\limits _{ i = 1}} \limits _{ i \ne k_{j}}}^n M^{-}(A_{i})\right. \nonumber \\&\quad +\,\left. \prod \limits _{i = 1}^n M^{+}(A_{i})\right] +\prod \limits _{ i = 1}^n\int _{0}^{1}\gamma _{i}(\underline{a}_{i} (\gamma _{i}))^{2}\text {d}\gamma _{i}+\sum \limits _{r = 1}^{n-2} \mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}} \limits _{\;j\in \{1,2,\ldots ,r\}}}^{n}\prod \limits _{j = 1}^r \int _{0}^{1}\gamma _{k_{j}}(\overline{a}_{k_{j}}(\gamma _{k_{j}}))^2 \text {d}\gamma _{k_{j}}\nonumber \\&\quad \times \,\mathop {\mathop {\mathop {\prod }\limits _{ i = 1}} \limits _{ i \ne k_{j}}}^n\int _{0}^{1}\gamma _{i}(\underline{a}_{i}(\gamma _{i}))^{2} \text {d}\gamma _{i}+\prod \limits _{ i = 1}^n\int _{0}^{1}\gamma _{i}(\overline{a}_{i}(\gamma _{i}))^{2} \text {d}\gamma _{i}. \end{aligned}$$

Notice that $\tfrac{1}{2^{n-1}}\prod \limits _{i = 1}^n E(A_{i})[\prod \limits _{i = 1}^n M^{-}(A_{i})+\sum \limits _{r = 1}^{n-2}\mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}}\limits _{\;j\in \{1,2,\ldots ,r\}}}^{n}\prod \limits _{j = 1}^r M^{+}(A_{k_{j}}) \mathop {\mathop {\mathop {\prod }\limits _{ i = 1}} \limits _{ i \ne k_{j}}}^n M^{-}(A_{i})+\prod \limits _{i = 1}^n M^{+}(A_{i})]=2(\prod \limits _{i = 1}^n E(A_{i}))^{2}$. Then, we have

$$\begin{aligned} Var\left( \prod \limits _{i = 1}^n A_{i}\right)&=\prod \limits _{ i = 1}^n\int _{0}^{1}\gamma _{i}(\underline{a}_{i}(\gamma _{i}))^{2}\text {d}\gamma _{i}+\sum \limits _{r = 1}^{n-2} \mathop {\mathop {\mathop {\sum }\limits _{k_{j}=1}}\limits _{\;j\in \{1,2,\ldots ,r\}}}^{n}\prod \limits _{j = 1}^r\int _{0}^{1}\gamma _{k_{j}}(\overline{a}_{k_{j}}(\gamma _{k_{j}}))^2\text {d}\gamma _{k_{j}}\nonumber \\&\quad \times \mathop {\mathop {\mathop {\prod }\limits _{ i = 1}}\limits _{ i \ne k_{j}}}^n\int _{0}^{1}\gamma _{i}(\underline{a}_{i}(\gamma _{i}))^{2}\text {d}\gamma _{i}+\prod \limits _{ i = 1}^n\int _{0}^{1}\gamma _{i}(\overline{a}_{i}(\gamma _{i}))^{2}\text {d}\gamma _{i}-\left( \prod \limits _{i = 1}^n E(A_{i})\right) ^{2}. \end{aligned}$$

The theorem is proved. $\square$