Abstract
This paper suggests that Herbert Simon’s concept of proof and predictions, in the solution of problems by human’s, considered as Information Processing Agents subject to boundedly rational behaviour and satisficing objectives, is to be interpreted in terms of constructive mathematics.
Similar content being viewed by others
Notes
Not in the least ‘provocative’, as far as I am concerned.
Simon’s early joint work, together with Allen Newell & Cliff Shaw, on the construction of the Logic Theorist to ‘discover’ the Propositional Logic theorems in the first part of the 1st volume of the 2nd edition of Principia Mathematica (see below, pp. 3/4, f.n. 8 & §4), was almost simultaneous with Martin Davis’s mechanized decision models on Presburger arithmetic. Both of them were years ahead of the fundamental studies of Dag Prawitz on mechanizing formal, logical, deduction.
In that, either White or Black has a winning strategy, but an algorithm—in computability theoretic senses—for implementing this is not derivable—unless some variant of constructive mathematics is used, as in Euwe (1929).
For Simon, who spent almost the last 50 years of his life in trying to understand chess (and lived through Deep Blue’s victory over Gary Kasparov).
This entails a constructive—whether of Brouwerian, Bishop’s, Martin-Löf’s or any of the ‘modern’ variants of these—interpretation of proof, which is why I consider Simon a ‘closet constructivist’! The Halting Problem for Turing Machines, or the (recursive) Undecidability of Gödel’s 2nd Incompleteness Theorem, comes into ‘play’, when the game reaches a ‘Dead Position’ (Turing 1953, p. 166; De Groot, p. 24, f.n., 19).
Pro tempore, remembering that Simon had a more nuanced interpretation of the process, I shall ‘work’ with Polya’s elegant and apposite definition of heuristic:
I wish to call heuristics … the study of means and methods of problem solving
Polya (1981, p. x; italics in the original).
As Simon (1996, p. 202; italics in the original) wrote: ‘.. in evaluating chess moves.. [We—i.e., Newell & Simon] … discussed the necessity for “rules of thumb” (later called heuristics) to reduce to manageable size the enormous search space … of possible chess moves and replies.’ King (2016, p. 134; italics added) is only one example of those who are un-nuanced about such things: ‘[R]ules of thumb—[are] technically known as heuristics—…. A heuristic is a decision rule that deliberately ignores information.’ Simon must be ‘turning in his grave’!
‘Art’ & ‘theory’ [=SCIENCE] in Knuth’s senses (above), as I – not Simon - interpret them.
MacKenzie (2001, p. 307) is ambiguous, at best, in attributing the work on the Logic Theory Machine to be based on the 1st edition of Principia Mathematica. Moreover, I am less than enthusiastic about the Topological exposition of the work that led to the Appel and Haken (partly) machine-based proof of the 4-Colour Theorem when, in fact, it is better studied as a graph-theoretic problem (cf., in particular, Fritsch and Fritsch 1998, p. 105). Incidentally, I am even less convinced that MacKenzie should quote Weyl (p. 259 & note 5, p. 398) and Gödel (p. 90 & note 115, p. 360) in German when easily accessible English translations of the classic works by both these distinguished authors are available! Neither Weyl, nor van Heijenoort, are indexed in MacKenzie (ibid)! Although Turing (1948, p. 126), refers to ‘Russell’s Principia Mathematica’, the authors were Whitehead & Russell—and that, contrary to the normal practice of alphabetical ordering of the names of authors, is how it appears in the cover page of the book!.
In my own Mother tongue, Tamil, the word for the concept of proof, both in mathematics and law, is atharam (
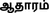 ). In the Japanese and Italian languages, in both of which I am reasonably fluent, the words for mathematical proof is close to demonstration (being shomei—
). In the Japanese and Italian languages, in both of which I am reasonably fluent, the words for mathematical proof is close to demonstration (being shomei—
 —and dimostrazione, respectively).
—and dimostrazione, respectively).The ‘dead position’ and the Newell–Simon Alpha–Beta procedure was directly from Turing (1953), but that, itself, was already in Alan Turing’s early work on the paper-machine ‘programmed’ to play chess, resulting in the Turochamp—named in honour of his joint author and friend, David Champernowne—with intuitive ‘pruning’ of alternatives. The proof of the ‘correctness’ of the (slightly modified) Alpha–Beta procedure of Newell et al. (1958a), with a statement of their pioneering contribution, is provided in the illuminating work of Knuth and Moore (1975, cf., especially p. 11).
Not in the tiresome sense of the dichotomy in terms of syntax and semantics.
This is not unlike the Bolzano–Weierstrass Theorem (which has no intuitionistic constructive equivalence) on the existence of convergent sub-sequences in bounded sequences, in finite-dimensional (Euclidean) spaces.
In the sense that the tapes in a Turing Machine are indefinitely extensible, although at any one point in time it is of given, definite, length. It is not fanciful, by any means, to say that Brouwer’s creative mathematician is a Turing Machine (and vice versa).
Kreisel’s ‘understandability’ of proofs (cf. Feferman 1998, pp. 185–186) seems no different from the joint validity of principles B & C, above, together.
Tymoczko (op.cit) relies on Thom’s (1971) restricted argument against Bourbakism as an ‘aide’ in his weak, if not also irrelevant, case for local versus global stability; moreover, his citation of Thom (ibid) on p. 61, fn., 3, is in error. Incidentally, I feel that Tymoczko’s Simon says as ‘a new method of proof’ Martian story (ibid, p. 71, ff.), as referring to Herbert Simon and disapprove of it.
‘Aided’ in the sense of proof by man–machine interaction.
Originally, by Karl Kristian Steincke, in the 4th volume of Farvel Og Tak, 1948.
The digital computer, as a machine, was barred from ‘winning money in tournaments’ (Hsu et al. 1990, p. 44).
The imitation game refers, of course, to what has become ‘notorious’ as the ‘Turing Test’ for intelligent machines, playing a game with a ‘naturally’ intelligent human being, with an ‘interrogator’ (who could be a machine or a human). In this connection, it may well be apposite to quote from the Introduction to Turing (1992, p. XIV; italics in the original) by the Editor (E. L. Ince):
Turing’s paper [Turing 1950] is, almost certainly, the fundamental paper on artificial intelligence and provides a theoretical base point from which subsequent discussion about the nature of thinking and its relationship to computation has been based.
Especially because I endorse the essential message of Hales (2013)—mathematics in the age of the Turing Machine will, surely, lead to an appreciative evaluation of that part of the proof of Appel and Haken which owes its undoubted success to computations by a machine.
See the remark in footnote 15, above.
It must be remembered that every constructive function—especially in Brouwerian constructive mathematics—is continuous. This is added so that Simon (1954) can also be brought into the constructive fold.
In: From Cardinals to Chaos: Reflections on the Life and Legacy of Stanislaw Ulam, edited by Necia Grant Cooper, p. 312, Cambridge University Press, Cambridge.
This is my way of saying that the ‘proof’ was not (even) partly machine-based (i.e., analogue or digital computer underpinned), but entirely human (I may have been influenced, in the choice of this phrase, by an analogous—not identical—use by Hales 2013, §1.1).
GO rules, as distinct from those of Chess, allow an unlimited—effectively indefinite—endowment of stones to both players, at the start of a game. This is similar to the nature of the tape in a Turing Machine, which is indefinitely long, and effectively extensible (see also footnote 14, above).
The first author, to the best of my knowledge, ‘discovered’ (first) the errors in Dulac’s ‘chalk & blackboard’ alleged proof.
Russian constructivism is more akin to formal computability theory than any of the constructivist principles of Brouwer, Bishop or Martin-Löf, depending more on the acceptance of (the equivalents of) the so-called Church-Turing thesis. This is the main reason for me to enunciate my thesis on Simon’s notion of proof being constructive in the sense of Bishop (but I could have said (almost) the same things in terms of Brouwer or Martin-Löf.
It should be observed that Berg et al. (op.cit) was published before the final proof of Appel-Haken on 4-CT, in 1976. The authors, moreover do acknowledge Brouwer’s priority, but opt for a modernised Bishop-style constructive proof, with a crystal clear constructive version of proof by contradiction (using the tertium non datur). Hales (2007) is squarely computable, with the intricacies of presenting an algorithm for constructing a Jordan Curve given explicitly. This is made clear from Hales, ibid, p. 883; italics added:
A formal proof typically begins with a careful conventional proof. Each lemma is then expanded in meticulous detail and then transcribed to computer for exhaustive checking.
iff ≡ if and only if.
The construction in terms of separation theorems must be carefully distinguished from propositions based on theorems of the separating hyperplanes (the mistake of not differentiating is made by Bosch and Smith 1998).
References
Appel, K., & Haken, W. (1978). The four-color problem. In L. A. Steen (Ed.), Mathematics today: Twelve informal essays (pp. 153–180). New York: Springer.
Berg, G., Julian, W., Mines, R., & Richman, F. (1975). The constructive Jordan curve theorem. Rocky Mountain Journal of Mathematics, 5(2), 225–236.
Bishop, E. (1985). Schizophrenia in contemporary mathematics. In M. Rosenblatt (Ed.), Errett Bishop: Reflections on him and his research (Vol. 39)., Contemporary mathematics Rhode Island: American Mathematical Society, Providence.
Bosch, R. A., & Smith, J. A. (1998). Separating hyperplanes and the authorship of the disputed federalist papers. The American Mathematical Monthly, 105(7), 601–608.
Bourbaki, N. (2004). Theory of sets. Berlin: Springer (This is the edition I have access to).
De Groot, A. D. (1946). Het Denken van den Schaker. Amsterdam: North-Holland.
De Groot, A. D. (1978). Thought and choice in chess (2nd English ed.). The Hague: Mouton Publishers.
Dowek, G. (2015). Computation, proof, machine—Mathematics enters a new age. Cambridge: Cambridge University Press.
Euwe, M. (1929). Mengentheoretische Betrachtungen über das Schachspiel. Koninklijke Nederlandske Akademie van Wetenschappen, 32, 633–642.
Feferman, S. (1998). What does logic have to tell us about mathematical proofs? In S. Feferman (Ed.), In the light of logic, chapter 9 (pp. 177–186). Oxford: Oxford University Press.
Fritsch, R., & Fritsch, G. (1998). The four-color theorem—History, topological foundations and idea of proof. New York: Springer.
Gonzáles-Velasco, E. A. (1980). On limit cycles of two-dimensional analytic flows. Funkcialaj Ekvacioj, 23, 351–355.
Hacking, I. (1973). Leibniz and descartes: Proof and eternal truths. In Dawes Hicks lecture on philosophy, Proceedings of the British Academy (Vol. LIX, 16 pages). London: Oxford University Press.
Hales, T. C. (2007). The Jordan curve theorem, formally and informally. The American Mathematical Monthly, 114(10), 882–894.
Hales, T. C. (2013). Mathematics in the age of the Turing machine. In R. G. Downey (Ed.), Turing’s legacy. ASL lecture notes in logic (pp. 253–298). Cambridge: Cambridge University Press.
Hardy, G. H. (1929). Mathematical proof. Mind, 38(149), 1–25.
Hassabis, D. (2017). Artificial intelligence: Chess match of the century. Review of Deep thinking: Where machine intelligence ends and human creativity begins by Gary Kasparov. Nature, 544(7651), 413–414.
Hsu, F. H., Anantharaman, T., Campbell, M., & Nowatzyk, A. (1990). A grandmaster chess machine. Scientific American, 263(4), 44–50.
Ilyashenko, Y., & Yakovenko, S. (1995). Concerning the Hilbert sixteenth problem, chapter 1. In Y. Ilyashenko & S. Yakovenko (Eds.), Concerning the Hilbert 16th problem (Vol. 165, pp. 1–19)., American Mathematical Society Translations, Series 2 Providence: American Mathematical Society.
Jones, J. P. (1981). Classification of quantifier prefixes over diophantine equations. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, 27, 403–410.
Kasparov, G. (2010). The chess master and the computer. The New York Review of Books, 57(2), 16–19.
King, M. (2016). The end of alchemy: Money, banking and the future of the global economy. London: Little, Brown Book Group.
Knuth, D. E. (1996). Foreward to: A = B, by Petkovšek, Marko, Herbert S. Wilf & Doron Zeilberger, A K Peters, Wellesley, MA.
Knuth, D. E., & Moore, R. W. (1975). An analysis of alpha-beta pruning. Artificial Intelligence, 6(4), 293–326.
Lakatos, I. (1976). Proofs and refutations: The logic of mathematical discovery, edited by John Worrall and Elie Zahar, Cambridge University Press, Cambridge.
Littlewood, J. E. (1957). A mathematician’s miscellany (reprint edition, with ‘minor corrections’). London: Methuen & Co., Ltd.
MacKenzie, D. (2001). Mechanizing proof. Cambridge, MA: The MIT Press.
Newell, A., Shaw, J. C., & Simon, H. A. (1958a). Chess-playing programs and the problem of complexity. IBM Journal of Research and Development, 2, 320–335.
Newell, A., Shaw, J. C., & Simon, H. A. (1958b). Elements of a theory of human problem solving. Psychological Review, 65(3), 41–56.
Newell, A., & Simon, H. A. (1958). Heuristic problem solving: The next advance in operations research. Operations Research, 6(1), 1–10.
Newell, A., & Simon, H. (1972). Human problem solving. Englewood Cliffs, NJ: Prentice-Hall, Inc.
Newman, M. H. A. (1951). Elements of the topology of plane sets of points (2nd ed.). Cambridge: Cambridge University Press.
Polya, G. (1981). Mathematical discovery—On understanding, learning, and teaching problem solving (Combined ed.). New York: Wiley.
Post, E. L. (1936). Finite combinatory processes-formulation 1. Journal of Symbolic Logic, 1(3), 103–105.
Ramsey, F. P. (1978 (1928)). Universals of law and of fact, chapter 6. A, pp. 128–132. In: D. H. Mellor (Ed.), Foundations—Essays in philosophy, logic mathematics and economics by F. P. Ramsey. London: Routledge & Kegan Paul.
Sieg, W. (2001). Remembrances of Herbert Simon. www.cs.cmu.edu/simon/all.html. Accessed 27 December, 2015.
Silver, D., et al. (2017). Mastering the game of go without human knowledge. Nature, 550(7676), 354–359.
Simon, H. A. (1954). Bandwagon and underdog effects and the possibility of election predictions. The Public Opinion Quarterly, 18(3), 245–253.
Simon, H. A. (1977). Models of discovery—And other topics in the methods of science. Dordrecht: D. Reidel Publishing Company.
Simon, H. A. (1989). The scientist as problem solver, chapter 14. In D. Klahr & K. Kotovsky (Eds.), Complex information processing: The impact of Herbert Simon (21st Carnegie-Mellon symposium on cognition) (pp. 375–398). Hillsdale, NJ: Lawrence Earlbaum Associates Inc.
Simon, H. A. (1996). Models of my life. Cambridge, MA: MIT Press.
Stone, R., & Brown, A. (Eds.). (1962). A computable model of economic growth, vol. 1, A programme for growth. London: Chapman and Hall.
Strichartz, R. S. (2000). The way of analysis (Revised ed.). Sudbury, MA: Jones and Bartlett Publishers.
Sundholm, G. (1993). Questions of proof. Manuscrito – Revista Internacional de Filosofia, Campinas, XVI(2), 47–70.
Thom, R. (1971). ”Modern” mathematics: An educational and philosophic error? American Scientist, 59(6), 695–699.
Turing, A. M. (1947). Lecture to the London Mathematical Society on 20 February 1947 (pp. 87–105). In Turing (1992).
Turing, A. M. (1948). Intelligent machinery (pp. 107–127). In Turing (1992).
Turing, A. M. (1950). Computing machinery and intelligence. Mind, 59(236), 433–460.
Turing A. M. (1953). Digital computers applied to games (pp. 161–185). In Turing (1992).
Turing, A. M. (1992). Collected works of A. M. Turing—Mechanical intelligence, D. C. Ince (Ed.). North-Holland, Amsterdam.
Tymoczco, T. (1979). The four-color problem and its philosophical significance. The Journal of Philosophy, 76(2), 57–83.
Whitehead, A. N., & Russell, B. (1927). Principia Mathematica (2nd ed., Vol. 1). Cambridge: Cambridge University Press.
Author information
Authors and Affiliations
Additional information
Human Problem Solving: This is, in particular, a reference to Newell and Simon (1972), the magnum opus which codified Information Processing Systems (IPS) as boundedly rational agents, via heuristic search over (numerically) vast spaces of alternatives, seeking satisficing solutions, to problems. However, it is also meant to emphasise the way Simon systematised Human, as against Machine, Problem Solving. Simon’s notion of information was algorithmic; it had nothing to do with the notions of information in Marschak, Muth, Phelps, Lucas and others, with ad hoc probability foundations to buttress their classical mathematical formulations.
Proofs: The notion of PROOF, even if only mathematically conceived, is many-faceted. My fascination with this concept was consolidated in Ian Hacking’s lectures in the Philosophy Faculty at Cambridge University, during the Michaelmas Term of 1973—having been formed in high-school teaching by Mr. Arasaratnam and kind undergraduate instruction at Kyoto University by Professor Kawai, both in physics and mathematics. Dr. Hacking gave me a reprint of his Dawes Hicks Lecture of 1973, which referred to Hardy’s Rouse Ball Lecture of 1928 (Hacking 1973, p. 7), which has been a guiding light in my struggles to come to terms with Simon’s rich and varied notions of proof.
Rights and permissions
About this article
Cite this article
Velupillai, K.V. Proofs and Predictions in Human Problem Solving. Comput Econ 57, 935–947 (2021). https://doi.org/10.1007/s10614-018-9810-0
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10614-018-9810-0





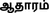 ). In the Japanese and Italian languages, in both of which I am reasonably fluent, the words for mathematical proof is close to demonstration (being shomei—
). In the Japanese and Italian languages, in both of which I am reasonably fluent, the words for mathematical proof is close to demonstration (being shomei—
 —and dimostrazione, respectively).
—and dimostrazione, respectively).