Abstract
The recent increase in the breath of computational methodologies has been matched with a corresponding increase in the difficulty of comparing the relative explanatory power of models from different methodological lineages. In order to help address this problem a Markovian information criterion (MIC) is developed that is analogous to the Akaike information criterion (AIC) in its theoretical derivation and yet can be applied to any model able to generate simulated or predicted data, regardless of its methodology. Both the AIC and proposed MIC rely on the Kullback–Leibler (KL) distance between model predictions and real data as a measure of prediction accuracy. Instead of using the maximum likelihood approach like the AIC, the proposed MIC relies instead on the literal interpretation of the KL distance as the inefficiency of compressing real data using modelled probabilities, and therefore uses the output of a universal compression algorithm to obtain an estimate of the KL distance. Several Monte Carlo tests are carried out in order to (a) confirm the performance of the algorithm and (b) evaluate the ability of the MIC to identify the true data-generating process from a set of alternative models.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The rapid growth in computing power over the last couple of decades, combined with the development of user-friendly programming languages and an improvement of fundamental statistical and algorithmic knowledge have lead to a widening of the range of the computational methods available to researchers, from formal modelling to estimation, calibration or simulation methodologies. While this multiplication of available methods has offered a greater modelling flexibility, allowing for the investigation of richer dynamics, complex systems, model switching, time varying parameters, etc., it has come at the cost of complicating the problem of comparing the predictions or performance of models from radically different methodological classes. Two recent examples of this, which are by no means exclusive, are the development of the dynamic stochastic general equilibrium (DSGE) approach in economics, and the increase in the popularity of what is generally referred to as agent-based modelling (ABM), which uses agent-level simulations as a method of modelling complex systems, and for which even the issue of bringing models to the empirical data can prove to be a problem.
Within the DSGE literature on model validation and comparison, one of the first to identify and address this problem in a direct and systematic manner is Schorfheide (2000), who introduces a loss function-based method for evaluating DSGE models. This is then complemented by the DSGE-VAR procedure of Del Negro and Schorfheide (2006) and Negro et al. (2007), which explicitly sets out to answer the question ‘How good is my DSGE model?’ (p. 28). The procedures gradually developed over time in this literature are summarised in the section on DSGE model evaluation of Negro and Schorfheide (2011), which outlines several methods for evaluating DSGE performance, such as posterior odds ratios, predictive checks and the use of VAR benchmarking.
Similar concerns relating to model evaluation and comparison also exist in the ABM literature, to the extent that two special journal issues have been published in order to identify and address them. Fagiolo et al. (2007), as part of the special issue on empirical validation in ABM of Computational Economics, provide a very good review of the existing practices and provide advice as to how to approach the problem of validating an agent-based simulation model. The most obvious example of the need for validation methodologies is the recent development of several large-scale agent-based frameworks that allow the investigation of key macroeconomic questions, such as Keynes/Schumpeter model developed in Dosi et al. (2010, (2013, (2015), which allows for analysis of fiscal and monetary policies, or the European-wide EURACE collaboration of Deissenberg et al. (2008), Van Der Hoog et al. (2008) and Holcombe et al. (2013), which aims to allow large-scale modelling of economic systems. As pointed out by Fagiolo and Roventini (2012), these would greatly benefit from being compared to the standard DSGE macroeconomic workhorse models. Nevertheless, as outlined by Dawid and Fagiolo (2008) in the introduction of the special issue of the Journal of Economic Behavior and Organization on adapting ABM for policy design, finding effective procedures for empirical testing, validation and comparison of such models is still very much an active field of research. Some of the recent developments in this regard are related to the approach suggested here, for example the state similarity measure of Marks (2010, (2013), which aims to measure the distance between two time-series vectors, as is the case here. Similarly, ongoing work by Lamperti (2015) also explores the possibility of comparing models on the basis of simulated data alone with an information based measure, using however a very different measurement approach. Finally, another approach of note is Fabretti (2014), which treats the simulated data from an implementation of the Kirman (1993) model as a Markov chain in order to estimate its parameters. While again the objective and methodology used are different from what is proposed here, the idea of mapping the simulated data to a Markov process is very similar in spirit.
The paper aims to contribute to this general issue of comparing different lineages of models by providing a proof-of-concept for a Markovian information criterion (MIC) that generalises the Akaike (1974) information criterion (AIC) to any class of model able to generate simulated data. Like the AIC, the proposed criterion is fundamentally an estimate of the Kullback and Leibler (1951) (KL) distance between two sets of probability densities. The AIC uses the maximised value of the likelihood function as an indirect estimate of the KL distance, however, this obviously requires the model to have a parametric likelihood function, which is no longer straightforward for many classes of modelling methodologies. The proposed criterion overcomes this problem by relying instead on the original data compression interpretation of the KL distance as the inefficiency resulting from compressing a data series using conditional probabilities that are an estimate or approximation of the true data generating process. This fundamental equivalence between data compression and information criteria has led to the emergence of what is known as the minimum description length (MDL) principle, which relies on the efficiency of data compression as a measure of the accuracy of a model’s prediction. Grünewald (2007) provides a good introduction to the MDL principle and its general relation to more traditional information criteria, while Hansen and Yu (2001) explore the use of MDL within a model selection framework, concluding that “MDL provides an objective umbrella under which rather disparate approaches to statistical modelling can coexist and be compared” (Hansen and Yu 2001, p. 772).
The proposed methodology provides three key contributions compared to existing methods. The first is to provide a standardised measurement, as the procedure places all models on an equal footing, regardless of their numerical methodology or structure, by treating the simulated data they produce as the result of a Nth order Markov process, where the number of lags is chosen to capture the time dependency of the data. As pointed out by Rissanen (1986), Markov processes of arbitrary order form a large subclass (denoted FSMX) of finite-state machines (FSMs), i.e., systems where transitions are governed by a fixed, finite transition table. By mapping every model to be compared to its FSM representation and scoring these transition probabilities on the empirical data, the MIC is able to overcome differences in modelling methodologies and produce a standardised criterion for any model reducible to a Markov process. This is designed to take advantage of the fact, pointed out by Tauchen (1986a, (1986b) and Kopecky and Suen (2010), that many economic variables and modelling approaches can in fact be approximated by a Markov process.Footnote 1 A second contribution is that the algorithm used to obtain the transition table possess a guaranteed optimal performance over Markov processes of arbitrary order, which as will be shown below, allows an accurate measurement for the MIC. Finally, the algorithm measures cross-entropy at the observation level, producing a vector which sums up to the MIC which enables the reliability of a measurement to be tested statistically.
Because purpose of the approach is to use the MIC to compare a set of models \(\{M_{1},\,M_{2},\ldots ,M_{m} \}\) against a fixed-size data set, it is important to also highlight the data snooping problem identified by White (2000) and the reality check procedures that must be carried out to avoid it. Essentially, because statistical tests always have a probability of type I error, repeated testing of a large (and possibly increasing) set of models on a fixed amount of data creates the risk of incorrectly selecting a model that is not truly the best model in the set. White (2000) therefore proposes a procedure that takes into account the size of the model comparison set \(\{M_{1},\,M_{2},\ldots ,M_{m} \}\) when testing for performance against a benchmark model \(M_0.\) A recent development in this literature is the model confidence set (MCS) methodology of Hansen et al. (2011), which differs from White’s reality check in that it does not test against a benchmark model, but instead identifies the subset \(\hat{\mathcal {M}}_{1-\alpha }\) of models in the set which cannot be distinguished from each other at significance level \(\alpha .\) This is well suited to the model-specific vectors of scores produced by the MIC, therefore the MCS is included in the Monte Carlo analyses presented below.
The remainder of the paper is organised as follows. Section 2 first discusses the use of universal data compression as an empirical tool for evaluating prediction accuracy and details the theoretical properties of the MIC. A Monte Carlo analysis is then performed in Sect. 3 in order to compare the MIC against the AIC benchmark in an ARMA-ARCH setting and evaluate the criterion’s performance. Section 4 discusses the use of the methodology in practical settings and Sect. 5 concludes.
2 The MIC: Motivation and Theoretical Properties
Before examining the information-theoretical motivation for the MIC methodology and the core properties that justify the choice of algorithms, it is important to first briefly clarify the terminology and notation that will be used throughout the paper.
First of all, we define a prediction as a conditional probability mass function over the discrete states a system can occupy, given knowledge of the system’s history. A model is very loosely defined as any device that can produce a complete set of predictions, i.e., a prediction for every acceptable history. This is very similar to the loose definition adopted by Hansen et al. (2011) for their MCS procedure. Furthermore, no assumption is made on the quality of the predictions: a uniform distribution over the system’s states is acceptable. Conceptually, this set of predictions corresponds to the state transition table of a FSMX or, equivalently, as the transition matrix of a Markov process. This loose definition of a model is intended to be very general: anything from personal belief systems to formal analytical models, as well as calibrated simulations or estimated econometric specifications are reducible to this class of processes, as all can provide a predictive density for future observations given the history of the system.
Regarding notation, the binary logarithm will be clearly identified as ‘\(\log _2\)’, while the natural logarithm will be ‘\(\ln \)’. \(X_t\) is an unobserved, real-valued random variable describing the state of a system at time t and \(x_t\) its observed realisation. Data series are denoted as \(x_{1}^{t} = \{ x_1,\,x_2,\ldots , x_{t} \}.\, \) and  are the discretised versions of the same variables, with r being the number of bits of resolution used for the discretisation and \(\varOmega = 2^r\) the resulting number of discrete states the system can occupy. Because of the binary discretisation used,
are the discretised versions of the same variables, with r being the number of bits of resolution used for the discretisation and \(\varOmega = 2^r\) the resulting number of discrete states the system can occupy. Because of the binary discretisation used,  will refer to both the numerical value of the observation and the corresponding r-length binary string encoding it. When necessary, the kth bit of a given observation
will refer to both the numerical value of the observation and the corresponding r-length binary string encoding it. When necessary, the kth bit of a given observation  will be identified as \(.\, \) is the true probability distribution over the \(\varOmega \) states at time t conditional on the past realisations of the variable.
will be identified as \(.\, \) is the true probability distribution over the \(\varOmega \) states at time t conditional on the past realisations of the variable.  is a corresponding conditional probability distribution predicted by a model \(M_i\) at the same time and over the same state space, using a limited number of lags L. Using the chain rule for conditional probabilities,
is a corresponding conditional probability distribution predicted by a model \(M_i\) at the same time and over the same state space, using a limited number of lags L. Using the chain rule for conditional probabilities,  , the model predictions and true conditional probabilities can be used recursively to build the overall probabilities for the series
, the model predictions and true conditional probabilities can be used recursively to build the overall probabilities for the series  and
and  .
.
2.1 Information Criteria and Minimum Description Length
Given a model \(M_i,\) a reasonable metric for evaluating the accuracy of the overall prediction \(P_{M_i} ( {x_1^t} )\) with respect to \(P_{dgp} ( {x_1^t})\) is the Kullback and Leibler (1951) (KL) distance measure between the two distributions, which was developed as an extension of the fundamental concept of information entropy introduced in Shannon (1948).
In terms of notation, the \(E_{dgp} [ \ldots ]\) operator indicates that the expectation is taken with respect to the true distribution \(P_{dgp} ( {x_1^t } ).\) The first obvious consequence of (1) is that the KL divergence \(D_{KL}\) is zero whenever \(P_{M_i} ( {x_1^t } ) = P_{dgp}( {x_1^t }).\) As shown by Cover and Thomas (1991), by taking into account the strict concavity of the logarithm and applying Jensen’s inequality to the expectation term in (1) one can show that the KL distance is strictly positive for \(P_{M_i} ( {x_1^t } ) \ne P_{dgp} ( {x_1^t } ),\) making it a strictly proper scoring rule in the sense of Gneiting and Raftery (2007). This property underpins the use of the KL distance as a conceptual criterion for determining the accuracy of a model, as minimising the KL distance with respect to the choice of prediction model should theoretically lead to the identification of the true model.
While the KL distance is a desirable measure of accuracy in theory, it suffers from not being directly computable in practice, as this would require knowledge of \(P_{dgp}\). The key insight of Akaike (1974) was to identify that it is possible to use the maximum likelihood estimation of the model \(M_i,\) to obtain an estimate of the following cross entropy, without requiring knowledge of the true distribution \(P_{dgp}{\text {:}}\)
Assuming that the model \(M_i\) uses a vector of \(\kappa _i\) parameters \(\theta _i,\) and that \(\hat{\theta }_i\) are the parameter values that maximise the likelihood \(\mathcal {L}( {{ \theta _i } |x_1^t} ),\) Akaike (1974) showed the cross entropy between the data and the model can be estimated asymptotically by the following relation, directly leading to the classical definition of the AIC for a set of models:
The fact that (3) is not directly an estimate of the KL distance (1) but instead of the cross entropy (2) explains why Akaike (1974) recommends looking at the AIC differences between models, \(\varDelta \mathrm{AIC}_{i,j} = \mathrm{AIC}_i - \mathrm{AIC}_j,\) as this removes the model-independent Shannon entropy terms and keep only the relative KL distance \(\varDelta D_{KL} ( \phantom {\frac{x}{x}} { {P_{M_i } ( {x_1^t } )} \Vert P_{dgp} ( {x_1^t } )} )_{i,j}\).
As emphasised by the MDL literature, the original interpretation of the KL distance (1) relates to the fundamental theoretical limits to compressibility of data. Given a discretised data series  , the binary Shannon entropy
, the binary Shannon entropy  gives the number of bits below which the data series cannot be compressed without loss. Because the true probability over states of nature \(P_{dgp}\) is unknown, practical data compression has to rely on a predetermined model of how the data is distributed, \(P_{M_i}\). Intuitively, this should introduce some inefficiency, thus increasing the theoretical limit below which the data cannot be compressed. This higher limit, measured by the cross entropy (2), is the sum of the Shannon entropy and the KL distance between M and the true data generating process. In other words, on top of the number of bits required to encode the true information content of the data, one has to add extra bits to account for the fact that the model distribution \(P_{M_i}\) does not exactly match the true distribution \(P_{dgp}\).
gives the number of bits below which the data series cannot be compressed without loss. Because the true probability over states of nature \(P_{dgp}\) is unknown, practical data compression has to rely on a predetermined model of how the data is distributed, \(P_{M_i}\). Intuitively, this should introduce some inefficiency, thus increasing the theoretical limit below which the data cannot be compressed. This higher limit, measured by the cross entropy (2), is the sum of the Shannon entropy and the KL distance between M and the true data generating process. In other words, on top of the number of bits required to encode the true information content of the data, one has to add extra bits to account for the fact that the model distribution \(P_{M_i}\) does not exactly match the true distribution \(P_{dgp}\).
The MDL principle is at the core of the proposed MIC precisely because of the flexibility it offers, enabling practical model comparison on the basis of simulated data alone. However, as pointed out by Grünewald (2007), MDL only provides a guiding principle for analysis and does not prescribe a specific methodology. It is therefore important to choose any implementation carefully and verify its efficiency. The context tree weighting (CTW) algorithm proposed by Willems et al. (1995), which forms the basis of the proposed MIC, is chosen specifically because of its desirable theoretical properties, discussed below.
2.2 Theoretical Properties of the MIC Procedure
Discounting a preliminary data preparation step required to convert the real-valued vector of data \(x_1^t\) to a discretised vector  , the methodology uses a two stage procedure to obtain the MIC. In the first stage, the CTW algorithm processes the simulated data generated by each candidate model \(M_i\) and produces a set of tree structures from which model-specific conditional probabilities
, the methodology uses a two stage procedure to obtain the MIC. In the first stage, the CTW algorithm processes the simulated data generated by each candidate model \(M_i\) and produces a set of tree structures from which model-specific conditional probabilities  can be recovered. In the second stage, each observation
can be recovered. In the second stage, each observation  of the real data is scored using the corresponding CTW probability, providing a binary log score
of the real data is scored using the corresponding CTW probability, providing a binary log score  which sums to the following cross entropy measure (2), which will form the basis of the MIC:Footnote 2
which sums to the following cross entropy measure (2), which will form the basis of the MIC:Footnote 2

The justification for using the CTW algorithm in a two-stage procedure is that it endows the resulting criterion with the following properties. First of all, the measurement of cross-entropy (2) is optimal, as the inefficiency resulting from having to learn a model’s conditional probability structure from simulated data attains the theoretical minimum and can therefore be controlled for. Importantly, the CTW is universal over FSMs, i.e., this optimal performance is guaranteed for all Markov processes of arbitrary order. This key guaranteed performance for all Markov processes underpins the name of the criterion. Finally, because the methodology processes observations sequentially in the second stage, it measures entropy at the level of each individual observation. This key property, which is not present in alternative methods which measure aggregate entropy by relying on empirical frequencies over the entire set of observations, allows for both analysis of model fit at the local level and confidence testing of the aggregate MIC value.
The actual measurement of cross entropy using the CTW probabilities is carried out using arithmetic encoding, a simple, elegant and efficient approach to data compression initially outlined by Elias (1975), and further developed by Rissanen (1976) and Rissanen and Langdon (1979) into a practical algorithm. In practice, the cross entropy of an r-bit observation  is simply the sum of the binary log scores for each bit, where
is simply the sum of the binary log scores for each bit, where  is the probability of the kth bit being a ‘1’ conditional on L lags of history and the previous \(k-1\) bits of the observation:
is the probability of the kth bit being a ‘1’ conditional on L lags of history and the previous \(k-1\) bits of the observation:

One of the key contributions of Elias (1975) is a proof that the difference between the binary log scores summed over the entire length of the data (4) and the theoretical cross entropy (2) is guaranteed to be less than two bits:

The inefficiency incurred in the first stage by having to learn model probabilities using the CTW algorithm can similarly be bounded. The general intuition behind CTW is that each \(\{0,\,1\}\) bit in a binary string is treated as the result of a Bernoulli trial. More precisely, all the bits in the series that have the same past historical context  , identified by the binary string s, and the same initial observation bits
, identified by the binary string s, and the same initial observation bits  , identified by string o, are governed by the same Bernoulli process with unknown parameter \(\theta _{s,o}\). As the training series is processed, each node in the tree maintains a set of internal counters \(\{a_{s,o},\,b_{s,o}\}\) for the number of times it has respectively observed a ‘0’ or a ‘1’ after having seen both context s and the first o bits of the current observation. Given these \(\{a_{s,o},\,b_{s,o}\}\) counters, the estimator for Bernoulli processes developed by Krichevsky and Trofimov (1981) (henceforth referred to as the KT estimator) can be used to update the underlying probability of the binary sequence, by using the following recursion:
, identified by string o, are governed by the same Bernoulli process with unknown parameter \(\theta _{s,o}\). As the training series is processed, each node in the tree maintains a set of internal counters \(\{a_{s,o},\,b_{s,o}\}\) for the number of times it has respectively observed a ‘0’ or a ‘1’ after having seen both context s and the first o bits of the current observation. Given these \(\{a_{s,o},\,b_{s,o}\}\) counters, the estimator for Bernoulli processes developed by Krichevsky and Trofimov (1981) (henceforth referred to as the KT estimator) can be used to update the underlying probability of the binary sequence, by using the following recursion:
The ratios in the second and third equations of this recursion can be interpreted as frequency-based estimators of \(\theta _{s,o}\) and \(1-\theta _{s,o}\), respectively. Clearly such a learning process has an efficiency cost, as one can see that the KT estimator (7) is initialised with an uninformative prior, where \(P_e ( {1,\, 0}) = P_e ( {0,\, 1}) = 0.5,\) regardless of the true value of \(\theta _{s,o}\). While the frequencies will converge to \(\theta _{s,o}\) and \(1-\theta _{s,o}\) as more training data is observed, the cost of compressing the observations sequentially using (7) rather than the true Bernoulli process with parameter \(\theta _{s,o}\) can be expressed as:Footnote 3
The key contribution of Willems et al. (1995) is to prove that \(\chi \) is bounded above by the following term:
In order to show that this bound on \(\chi \) is optimal, Willems et al. (1995) refer to the key contributions of Rissanen (1978, (1984, (1986), which show that if the probabilities \(P_{M_i}\) used to encode data come from a Markov process \(M_i\) parametrised by a vector \(\theta _i\) that has to be estimated from the observations, then the effective lower bound on compression is higher than the Shannon entropy alone. This bound, known as the Rissanen bound, is the denominator of the following expression and depends on the number of parameters \(\kappa _i\) used in model \(M_i\) and the number of observations N available from which to estimate the parameters:
This result, which resembles the Bayesian information criterion (BIC) developed during the same time period by Schwarz (1978), can be used to show that the bound on the inefficiency of the (9) estimator is optimal.Footnote 4 Because the KT estimator (7) estimates the parameter of a Bernoulli source, the number of ones and zeros observed must give the total number of observations, so \(N_{s,o} = a_{s,o} + b_{s,o}\), and there is only a single parameter \(\theta _{s,o}\), so \(\kappa _{s,o}=1,\) and the Rissanen bound (10) for the KT estimator can be expressed as:
As pointed out by Willems et al. (1995), this makes the bound (9) optimal: the inefficiency of the KT estimator has to be greater in expectation than its Rissanen bound \(1/2 \times \log _2 (a+b),\) yet its realisation is proven to be less than the Rissanen bound plus the smallest possible information increment, i.e., one bit. This optimality argument lead Willems et al. (1995) to use the bound (9) as the measure of the learning cost of each KT estimator (7) in the tree. Because all the nodes in a context tree use the KT estimator (7), the aggregate inefficiency of learning the full set of transition probabilities in a context tree is bounded above by the following term, which simply sums the KT bound (9) over all contexts s and observations o, using a continuation term \(\gamma (x)\) that ensures that nodes that have never been observed do not contribute to the expression:
Crucially, Willems et al. (1995) prove that because all FSMX sources can be mapped to a context tree, and all nodes in the tree use the KT estimator (7), the aggregate learning cost for the full tree (12) is itself optimal for all FSMX sources, in particular all Markov process of arbitrary order L. This proven optimal performance over the very general class of Markov processes corresponds to the second important property mentioned above, universality, and justifies the choice of this algorithm for the proposed information criterion, rather than other existing Markov approximation methods such as the ones proposed by Tauchen (1986a, (1986b) or reviewed in Kopecky and Suen (2010). Furthermore, in line with the MDL literature, this aggregate cost (12) can be used as a measure of the complexity of a model for the purpose of penalisation, which will be discussed further in Sect. 4.
The final property of interest is the fact that the empirical observations are scored sequentially in the second stage, generating an observation-specific score  , which sums up to the total length of the code string (4). This has three important implications, the first of which is the ability to assess the relative accuracy of models both at the global and local level, which will be illustrated in Sec. 3.3. Secondly, the availability of an observation-by-observation score provides the basis for statistical analysis and confidence testing of the MIC measurements obtained. In fact, as will be shown in Sect. 3.2, this makes the MIC methodology naturally suited to the MCS approach. Finally, the node counters \(a_{s,o},\,b_{s,o}\) which are used to calculate the transition probabilities (7) can also be used to produce a correction term for the measurement bias incurred by using these probabilities to calculate the entropy of the observation in the log score (5).
, which sums up to the total length of the code string (4). This has three important implications, the first of which is the ability to assess the relative accuracy of models both at the global and local level, which will be illustrated in Sec. 3.3. Secondly, the availability of an observation-by-observation score provides the basis for statistical analysis and confidence testing of the MIC measurements obtained. In fact, as will be shown in Sect. 3.2, this makes the MIC methodology naturally suited to the MCS approach. Finally, the node counters \(a_{s,o},\,b_{s,o}\) which are used to calculate the transition probabilities (7) can also be used to produce a correction term for the measurement bias incurred by using these probabilities to calculate the entropy of the observation in the log score (5).
This bias occurs due to the fact that the KT estimator (7) uses the \(a_{s,o}\) and \(b_{s,o}\) counts to approximate the true parameters \(\theta _{s,o}\), and this approximation may be poor, especially for transitions that are infrequently observed or for low lengths of training data. As pointed out in the literature initiated by Miller (1955) and Basharin (1959) on biased measurement of entropy, such a use of empirical frequencies instead of true probabilities will create a systematic bias.Footnote 5 In the case of the KT estimator, it is possible to take advantage of the optimal bound (9) to correct this bias.
It is important to point out, however, that one cannot directly use expressions (9) or (12) to correct this bias. These measure the learning cost incurred should one try to compress the training data in a single pass, i.e., when sequentially compressing each binary training observation after having used it to update the KT estimator (7). This is not what is done here: only the empirical data is compressed, and this is processed separately from the training data. What is required instead is the size of the learning cost at the margin, for the specific empirical observation being compressed, after having already observed a sequence of training observations. This can be obtained from (9) by calculating how much the overall learning cost of the KT estimator increases when an empirical observation is added to the existing tree built with the training data. Treating (9) as an equality and calculating the increase in the expression after adding a single extra zero or one observation provides the following approximation for the learning cost at the margin:
Because the KT estimator only predicts the value of a single bit, the overall bias for a given data observation, identified by its specific context string \(s*\) is calculated by summing (13) over the r set of counters \(\{a_{s*,o},\,b_{s*,o}\}\) within node \(s*\) that correspond to the bits of the observation string \(o{\text {:}}\)

Subtracting the observation-level bias vector (14) from the raw score vector (4) results in a bias-corrected score  which sums to the overall MIC:
which sums to the overall MIC:

One might legitimately worry about the accuracy of the bias correction term (14) given that (13) is calculated by treating the bound (9) as an equality, rather than an inequality. However, given the tightness of this bound compared to the theoretical expectation (11), the approximation is expected to be accurate. Furthermore, it is shown in Appendix 1 that (14) corresponds to the bias one obtains by generalising Roulston (1999) to cross entropy. The benchmarking exercise carried out in the next section also establishes that (14) closely tracks the bias observed in practice.
2.3 Benchmarking the MIC’s Theoretical Efficiency
The MIC (15) aims provide a reliable and statistically testable measurement of the cross entropy (2) between data and a model, for all models that are reducible to a Markov process. What makes this proposition feasible are the desirable theoretical properties of the two algorithms used to generate the MIC, i.e., the fact that difference between the log score provided by the Elias (1975) algorithm  and the true cross entropy over an entire sequence of data is tightly bounded by (6) and that bias term (14) provides an effective correction for having imperfectly learnt the probabilities in the first stage. Because these theoretical properties form the central justification for the procedure, it is important to check, as a first step, that they are achieved in practice when the procedure is implemented.
and the true cross entropy over an entire sequence of data is tightly bounded by (6) and that bias term (14) provides an effective correction for having imperfectly learnt the probabilities in the first stage. Because these theoretical properties form the central justification for the procedure, it is important to check, as a first step, that they are achieved in practice when the procedure is implemented.
The benchmarking strategy chosen is to run the MIC procedure on a stream of data with known distribution, and therefore known entropy, and to compare the performance achieved in practice to the one expected in theory. In order to provide a reliable test of performance, 1000 random data series of length \(N = 2^{19}\) are generated from the following beta distribution.Footnote 6
The beta distribution is chosen for its [0, 1] support, which simplifies the process of discretising the observations, and for its asymmetry under the chosen parameters, in order to test the CTW’s ability to identify asymmetric distribution shapes. Furthermore, the iid assumption means that each data series is memoryless, ensuring that the best possible compression performance per observation is simply the Shannon entropy of the overall distribution. For the purpose of the analysis, the 1000 series are quantised to an eight-bit level, i.e., \(r=8.\)
For each of the 1000 data series, the eight-bit theoretical entropy is calculated by collecting the N observations into a 256 bin histogram on the [0, 1] support, which when normalised by N provides an empirical frequency vector f from which the Shannon entropy \(S = {-} \sum \nolimits _{i = 1}^{256} {f_i \log _2 f_i }\) can be calculated. This provides the theoretical lower bound for compression and serves as the performance benchmark, the descriptive statistics of which are presented in the first column of Table 1.
The bound on the Elias algorithm (6) is tested by scoring each data series with the algorithm using its corresponding frequency vector f, and comparing the result against the theoretical benchmark. The result, displayed the second column of Table 1, confirms that the difference in performance between arithmetic encoding using the fixed probabilities f and the theoretical benchmark is vanishingly small (on the order of 1 / N) and remains below the Elias bound (6) of 2 / N. One can conclude from this result that as expected the implementation of the Elias algorithm provides an extremely reliable measure of cross-entropy (2).
A second test evaluates the learning cost of the CTW algorithm by training it with an additional, independent, stream of beta distributed data (16) and using the resulting CTW probabilities to compress the 1000 Monte Carlo data series. In order to provide an illustration of the literal learning curve of the CTW algorithm, the Monte Carlo analysis is run for increasing amounts of training data, from \(T=1\) to \(T = 2^{19} = N,\) the result being illustrated in Fig. 1.
Along with the third column of Table 1, Fig. 1a provides two key conclusions. The first is that, as expected, there is a learning curve: the performance of the algorithm is poor at very low levels of training but converges to the benchmark as the amount of training data is increased. The second important element is that the bias correction term (14) closely tracks the mean value of the relative log scores (5) for the fixed and CTW probabilities, and is noticeable up until \(2^{17}\)–\(2^{18}\) observations. Using the bias correction term, as shown in Fig. 1b, c, therefore ensures that even at low levels of training (around \(2^{15} \approx 32,000\) observations) the expected difference between the MIC score with CTW probabilities and the score for fixed probability f is near zero. Beyond that point, additional training data is only useful in reducing the variance of the measurement, albeit with strongly diminishing returns. Figure 1c shows that most of the noise reduction is achieved around \(2^{18} \approx 250,000\) observations, and doubling the amount of training data to \(2^{19}\) observations brings little further improvement. A final confirmation of the CTW algorithm’s good learning properties is seen in Fig. 1d, which shows that probability distribution learnt by the algorithm closely follows the beta distributed probability mass function (16).
3 Monte Carlo Validation on ARMA–ARCH Models
The practical usefulness of the MIC as an information criterion is tested on a series of ARMA–ARCH models by evaluating its ability to identify the true model as well as correctly rank the alternative models. This will also illustrate the MIC’s performance on subsets of data, by attempting to identify portions of the data where the relative explanatory power of two models switches over.
3.1 The ARMA–ARCH Model Specification and Monte Carlo Analysis
Because the MIC aims to generalise the AIC to all FSMX models, the analysis uses a set of ARMA models with ARCH errors, as it is possible to obtain the AIC for each of the models and use this as a basis for comparing the rankings produced by the MIC. The general structure for the set of models, presented in Eq. (17), allows for two autoregressive lags, two moving average lags and two ARCH lags.
The various specifications used in the analysis only differ in their parameters, shown in Table 2. Only the parameters for the true model \(M_0\) are chosen ex-ante with an aim to generate persistence in the auto-regressive components. The parameters for the alternate models \(M_1\)–\(M_6\) are estimated using the following procedure. Firstly, a training data series with \(T = 2^{19}\) observations is generated using the parameters for the true model and random draws \(\varepsilon _t \mathop \sim \limits _{iid} \mathrm{N} ({0,\,1}).\) The parameters for the alternate models are then obtained by using this data series to estimate the ARMA–ARCH equation (17) with the corresponding lag(s) omitted.Footnote 7
Once the parameters are obtained, the various data series required for the Monte Carlo analysis of the MIC can be generated using Eq. (17) parameterised with the relevant column from Table 2 and further random draws \(\varepsilon _t \mathop \sim \limits _{iid} \mathrm{N} ({0,\,1}).\,T\)-length training series are generated for each of the six alternate specifications, and used in stage 1 to train the CTW algorithm. Similarly, 1000 ‘real’ data series of \(N = 2^{13} = 8192\) observations are generated using the parameters for \(M_0.\) These are used in a Monte Carlo analysis of the MIC’s ability to correctly rank the set of models.
The test benchmark is obtained by estimating the set of models using the 1000 N-length data series and calculating the respective AIC for each model and estimation. The descriptive AIC statistics are shown at the bottom of Table 2 and, as expected, the true model is consistently ranked first. An important point to keep in mind for the following section is that because the two AR parameters for \(M_0\) are chosen so as to approach a unit-root behaviour, the AR(1) model \(M_2\) is ranked an extremely close second. In fact, given the average \(\varDelta \mathrm{AIC}_{2,0} = 38.32,\) normalising by the number of observations N gives a mean AIC gap per observation of \(4.7\times 10^{-3}\), making those models difficult to distinguish in practice.
Finally, for the purpose of illustrating the local version of the MIC explored in Sect. 3.3, two additional sets of 1000 N-length data series are generated using model switching. In the first case, the data generating process uses \(M_0\) for the first half of the observations before switching to \(M_2.\) In the second case, the data generating process starts with \(M_5\) for half the observations before switching to \(M_0\) for N / 4 observations and then switching back to \(M_5\) for the remainder of the series.
3.2 MIC Performance on ARMA–ARCH Models
The Monte Carlo analysis carried out on the ARMA–ARCH models follows the protocol outlined in Appendix 2. As a preliminary step, the data and training series are all discretised to a \(r = 7\) bit resolution over the \([-30,\,30]\) range. In the training stage (stage 1), the CTW algorithm was run on varying lengths of training series with a chosen tree depth of \(d= 21\) bits, which corresponds to 3 observation lags L if one accounts for the seven-bit resolution. Finally, in stage 2, the trees are used to compress the 1000 data series, providing a MIC value for each of the models on each of the series.
Table 3 summarises the three main tests that were carried out to evaluate the MIC performance.Footnote 8 The first section examines whether the ranking assigned by the MIC to each model, \(\rho _i,\) matches the AIC ranking \(\rho _i^*\) in Table 2. This is a relatively strict test because the ranking for a given model i is affected by the performance of the MIC on all the other models, making this a global test of performance on the full model comparison set. Nevertheless, at training lengths \(T = 2^{22}\) the probability P(\(\rho _i=\rho _i^*\)) of correctly replicating the AIC relative ranking is high for most models, except for \(M_0\) and \(M_2,\) where the MIC does little better than random chance. The second test is less strict, as it instead looks at the probability of correctly selecting the best model in a simple head-to-head competition against the true model \(M_0\). The P(\(\varDelta \mathrm{MIC}_{i,0} > 0\)) values reveal that the MIC performs as expected, with a high probability of identifying the true model \(M_0,\) in all cases except \(M_2,\) where again the MIC does little better than a coin flip.
In addition to using Monte Carlo frequencies to evaluate the MIC’s ability to rank models, one can take advantage of the availability of an N-length observation-level score  which sums to the MIC to directly test the statistical reliability of the overall measurement at the level of each individual series. As stated previously, availability of this score means that the most natural and rigourous testing approach for the MIC is the reality check proposed White (2000) or the MCS of Hansen et al. (2011). The last part of Table 3 reveals the percentage of series for which the ith model is included in the MCS \(\hat{\mathcal {M}}_{1-\alpha }\) at the 5 and 10 % confidence levels. The MCS procedure relies on 1000 iterations of the Politis and Romano (1994) stationary bootstrap for each of the Monte Carlo series, the block length for the bootstrap being determined using the optimal block length procedure of Politis and White (2004). Even accounting for the conservative nature of the MCS test, the procedure is able to effectively narrow down the confidence set to the subset of models that have the lowest MIC ranking. The MCS procedure also confirms the MIC’s inability to distinguish \(M_0\) and \(M_2,\) as they are almost always included in the confidence set \(\hat{\mathcal {M}}_{1-\alpha }\).
which sums to the MIC to directly test the statistical reliability of the overall measurement at the level of each individual series. As stated previously, availability of this score means that the most natural and rigourous testing approach for the MIC is the reality check proposed White (2000) or the MCS of Hansen et al. (2011). The last part of Table 3 reveals the percentage of series for which the ith model is included in the MCS \(\hat{\mathcal {M}}_{1-\alpha }\) at the 5 and 10 % confidence levels. The MCS procedure relies on 1000 iterations of the Politis and Romano (1994) stationary bootstrap for each of the Monte Carlo series, the block length for the bootstrap being determined using the optimal block length procedure of Politis and White (2004). Even accounting for the conservative nature of the MCS test, the procedure is able to effectively narrow down the confidence set to the subset of models that have the lowest MIC ranking. The MCS procedure also confirms the MIC’s inability to distinguish \(M_0\) and \(M_2,\) as they are almost always included in the confidence set \(\hat{\mathcal {M}}_{1-\alpha }\).
Localised MIC performance. a Single data series, \(M_0\) and \(M_2\) switching. b Single data series, \(M_0\) and \(M_5\) switching. c Corresponding \(\varDelta \hbox {MIC}_{2,0}\). d Corresponding \(\varDelta \hbox {MIC}_{5,0}\). e \(\varDelta \hbox {MIC}_{2,0}\), Monte Carlo average. f \(\varDelta \hbox {MIC}_{5,0}\), Monte Carlo average
3.3 Localised MIC Performance on ARMA–ARCH Models
The availability of the observation-level score  also enables the calculation of a local version of the MIC, allowing models to be compared over subsets of the data. This is illustrated by running the procedure on the two sets of 1000 model-switching series mentioned in Sect. 3.1 using the CTW trees obtained for \(T = 2^{22}\) training observations in the previous section. The results, which are presented in Fig. 2, have been smoothed using a 200 observation-wide moving average window. In order to also illustrate the small-sample properties of the MIC, the MCS procedure is run on the resulting 200-observation averages. These are shown in Fig. 2c, d, where the dark gray areas indicate observations for which the confidence set \(\hat{\mathcal {M}}_{0.95}\) only includes \(M_0,\) and the lighter gray cases where the procedure is unable to separate \(M_0\) from the alternate model (\(M_2\) or \(M_5\) depending on the case) and both remain in the confidence set \(\hat{\mathcal {M}}_{0.95}\). The areas in white implicitly identify those data points where the confidence set \(\hat{\mathcal {M}}_{0.95}\) is reduced to the alternate model.
also enables the calculation of a local version of the MIC, allowing models to be compared over subsets of the data. This is illustrated by running the procedure on the two sets of 1000 model-switching series mentioned in Sect. 3.1 using the CTW trees obtained for \(T = 2^{22}\) training observations in the previous section. The results, which are presented in Fig. 2, have been smoothed using a 200 observation-wide moving average window. In order to also illustrate the small-sample properties of the MIC, the MCS procedure is run on the resulting 200-observation averages. These are shown in Fig. 2c, d, where the dark gray areas indicate observations for which the confidence set \(\hat{\mathcal {M}}_{0.95}\) only includes \(M_0,\) and the lighter gray cases where the procedure is unable to separate \(M_0\) from the alternate model (\(M_2\) or \(M_5\) depending on the case) and both remain in the confidence set \(\hat{\mathcal {M}}_{0.95}\). The areas in white implicitly identify those data points where the confidence set \(\hat{\mathcal {M}}_{0.95}\) is reduced to the alternate model.
In the first case, the localised version of the algorithm is unable to detect the transition from \(M_0\) to \(M_2,\) for both the individual data series and the Monte Carlo average. This is not surprising given that the MIC is unable to reliably distinguish between \(M_0\) and \(M_2\) at the aggregate level in Table 3. In the second case, however, the temporary switch from \(M_5\) to \(M_0\) is clearly visible in the Monte Carlo average and is detected by the MCS procedure on the individual data series. This localised version of the MIC may prove to be as useful for comparing model performance as the aggregate version presented above. It is indeed reasonable to expect that in practical situations one model may outperform others on aggregate yet may be beaten on some specific features of the data, as is the case in Fig. 2.
4 Robustness and Practical Applicability
The Monte Carlo analysis of Sect. 3 is designed in order to establish that the MIC can replicate the rankings of a known experimental setting under ideal conditions, as there is little purpose to a methodology that cannot achieve even this most basic task. It is therefore important to also clarify some of the practical issues related to using the methodology in a more realistic and restricted setting, as well as present some supplementary Monte Carlo analyses corresponding to those more realistic settings. An outline of the overall protocol and the more technical aspects of the algorithms are detailed in Appendix 2, while the extended tables of the Monte Carlo analyses are presented in Appendix 3.
4.1 Transforming and Discretising the Data
Because the MIC protocol operates on a binary description of the data, the first task to be carried out is to discretise the data to a binary resolution. This is done by choosing a set of bounds \(\{b_l,\,b_u\}\) representing the range of variation of the data, and a resolution parameter r which both determines the number of bits used to describe an observation and the number of distinct discrete values the variable can take, i.e., \(2^r.\) The bounds \(\{b_l,\,b_u\}\) on the range of variation can be set in such a way that a small fraction of the observations are allowed to be out of bounds, in which case they are assigned the value of the corresponding bound, in what is essentially a winsorization of the data.
The first issue that discretisation procedure raises is one of stationarity. Clearly, the fact that the data have to be bounded within a range of variation imposes a requirement that the empirical and training data series used be weakly stationary, as is the case for example of the ARMA–ARCH processes used in Sect. 3. This is not the case of many economic variables in their original form, which are typically integrated of degree one. This imposes a prior transformation of data in order to ensure they can be bounded. As is the case for many econometric applications, the recommendation is to take first differences or growth rates (first log-differences) of variables before discretising them, in order to ensure that the number of observations falling out of bounds does not exceed a small fraction of the sample (5 %, for example).
A second, related, issue is the ergodicity and time-homogeneity of the training data. Both are standard assumptions in the data compression literature, starting with Shannon (1948), as they underpin the ability to learn the stable transition probabilities of a data source by taking the time average of its output. While time-homogeneity is not a strict requirement for the CTW algorithm, if a model possesses a tipping point which irreversibly changes the transition probabilities, CTW will learn a mixture of the two regimes. In practice, it might then be preferable to learn two separate sub-models corresponding to each regime. Similarly, if a model possesses absorbing states, it is preferable to run multiple simulations, each cut at the point of absorbtion, in order to improve the learning of the transition probabilities before absorbtion. It is important to point out that neither time homogeneity or ergodicity are required for the empirical data. As shown in Sect. 3.3, any tipping point in the empirical probabilities will be detected by a sharp degradation (or improvement) in the performance of the MIC for a given fixed model.
Finally, one must choose a resolution parameter r for the discretisation, which is also relatively straightforward. As explained in Appendix 2, discretising the data creates a quantisation error, and the resolution parameter should be chosen such that this error is distributed as an iid uniform variable over the discretisation interval. This can be tested statistically, and the recommended procedure is to run the quantisation tests from Appendix 2 on the empirical data and to choose the smallest value of r which satisfies the tests.
4.2 Choosing the Lags and Training Length
Once the resolution parameter has been set the next parameter to choose is the order of the Markov process L, or equivalently, the depth \(d = rL\) of the tree. Two conflicting factors have to be considered in this decision. The first is that the worst-case memory requirement of the binary tree is \(\mathcal {O}(2^d).\) Even though the implementation detailed in Appendix 2 uses the integer arithmetic of Willems and Tjalkens (1997) to reduce memory costs, this implies that setting \(d > 32\) can potentially require an infeasible amount of memory to store the nodes. A related consideration is that the higher the order of the Markov process, the more training data will be required to adequately explore the larger transition space.
Conversely, there is the risk that setting the order of the Markov process too low compared to the true order of the underlying process will distort the measurement. Given the memory constraint previously mentioned, the immediate implication is that situations where the empirical data exhibits long memory will pose a problem for the methodology, and this should be tested for beforehand by looking, for instance, at the number of significant lags of the partial autocorrelation function.Footnote 9 The MIC methodology does seem to be robust to L, however, and in situations of non-persistent time dependence it should perform well. As an example, the order is set to \(L=3\) in the Monte Carlo analysis of Sect. 3, which is already less than the correct length \(L=4\) given (17).Footnote 10 This is tested further in Tables 8 and 9, which show the results of the ARMA–ARCH Monte Carlo analysis for \(L = 2,\) which is even more misspecified. As one would expect, this reduces the ability of the MIC to identify the true model, as is visible from the fact the number of models included in the MCS increases and the frequency at which models are correctly ranked falls. Nevertheless, when comparing the specifications head-to-head with the true model, the MIC is still able to correctly pick the true model in the great majority of cases. In practice, given resolutions of around 6–8 and having tested for long-range dependence, it is therefore reasonable to set the Markov order L to 3–4.
The final choice for any practical application is the amount of training and empirical data to be used for the analysis. Because the purpose of Sect. 3 is to establish that the MIC rankings can match the AIC rankings in the limit, long training sequences of between \(2^{19}\) and \(2^{22}\) are used, as well as a relatively large ‘empirical’ sample size \(N = 2^{13} = 8192.\) This is unrealistic for a practical setting, therefore further Monte Carlo robustness checks are carried out Tables 6, 8 and 10, for shorter training lengths of \(2^{15} \approx 32{,}000\) to \(2^{18} \approx 250{,}000\) and Tables 10 and 11 for shorter empirical series of \(N=500,\) in order to clarify these choices.
The findings for the shorter empirical setting of \(N = 500,\) first of all, confirm that sample size is important for a correct identification of the model rankings, which is what one would expect intuitively. The MIC is able to correctly rank and reject the two worst models for even relatively low levels of training, but it has trouble distinguishing the remaining models, as seen both by the size of the MCS and the frequency of correct rankings. As was the case for the misspecified \(L=2\) example, however, head-to-head comparisons with the true model do frequently lead to the true model being correctly picked. This is also in line with the analysis in Fig. 2, which used a moving average window of \(N = 200\) for its head-to-head analysis.
Finally, the Monte Carlo analyses for \(T=2^{15}\) to \(2^{22}\) help to confirm the learning curve of the MIC for a more complex setting than the Beta benchmarking exercise in Sect. 2.3. Crucially, the main finding is consistent with the benchmarking in that for the three settings examined, the mean MIC measurement converges relatively quickly (stabilising after about \(T=2^{17}\)), while the variance (as measured by the MCS size) takes longer to settle down. In most cases, the results seem reliable at some point between \(T = 2^{18}\) and \(2^{19}\), suggesting that 250,000–500,000 training observations provide a good learning performance. An important clarification in this regard is that the training observations need not be generated in a single simulation run, as is the case for the simple ARMA–ARCH example used here. As an example, one could also use a set of 1000 Monte Carlo runs of 250 or 500 observations each. Given that ABM simulations or DSGE stochastic simulations often generate such Monte Carlo sets as part of their internal validation, these can directly be re-used in the MIC procedure.
4.3 Penalising Complexity
At this stage, it is important to mention how the penalisation of model complexity can be handled within the methodology. This has not been done in the main analysis, as its main focus is to test the accuracy of the cross entropy measurement based on the CTW algorithm, and the benchmark for comparison is therefore the AIC, which does not strongly penalise the complexity of the models involved. Furthermore, given the similar parameter dimensions of the ARMA models in Table 2, simply adding a BIC-like penalisation term \(\kappa _i/2 \times \log _2 N\) to the MIC (15), where \(\kappa _i\) is the number of parameters in the ith model, will not generate meaningful differences in complexity.
A more interesting penalisation strategy, following Grünewald (2007) and consistent with the MDL underpinning of the methodology, is to use a two-part code based on the complexity cost of the context tree corresponding to each mode \(M_i.\) This accounts not only for the parameter dimension of the models, but also for their stochastic complexity, by taking advantage of the fact this complexity is directly measured by the cost term (12) of the context tree corresponding to each model. As was the case for the calculation of the bias correction term (14), however, one must account for the fact that the length of the training data T and empirical data N are not the same: naively using (12) would make the relative weight of the penalisation and the cross entropy directly dependent on T.Footnote 11 This implies that the calculation of the complexity (12) must be modified in order to produce a stable measurement. This can be done by normalising the \((a_{s,o},\,b_{s,o})\) to their expectation values had only N training observations been observed:
Normalised penalisations (18) for various training lengths T in the main Monte Carlo exercise with \(L=3\) and \(N = 2^{13}\) are presented in Table 4.Footnote 12 Although these values do seem to decrease with increasing T, the sensitivity is very limited, and the relative complexity of the models is stable. Interestingly, the results suggest that from a complexity viewpoint, the simplest models from the set in Table 2 are the ones with little or no moving average component, while dropping either the autoregressive or ARCH components significantly increases the complexity of the resulting model.
5 Conclusion
This paper develops a methodology which follows the MDL principle and aims provide an information criterion with practically no formal requirement on model structure, other that it be able to generate a simulated data series. While the MDL-inspired algorithms might be unfamiliar, it is important to emphasise that this methodology nevertheless follows the same logic as the AIC, which is that one can measure the cross entropy between some data and a model without knowing the true conditional probability distributions for the events observed. Because these measurements contain an unobservable constant (the true information entropy of the data generating process), one then has to take differences across models to obtain the difference in KL distance, which is the desired indicator of relative model accuracy. The difference between the AIC and the methodology suggested here rests simply in the choice of method used to measure the cross entropy.
The main benefit of the proposed methodology is that it compares models on the basis of the predictive data they produce, by using the CTW algorithm to estimate the transition tables of the underlying FSMs corresponding to the candidate models. This mapping of models to a general class of FSMs explains why there is no requirement that the candidate models have a specific functional form or estimation methodology, only that they be able to generate a predicted data series. It is this specific aspect which, while unfamiliar, enables the information criterion to compare across classes of models, from regression to simulation.
The Monte Carlo analyses in Sects. 2.3 and 3 provide several validations of the methodology by demonstrating that, given enough training data, the MIC procedure provides model ranking information that is comparable to the AIC, and also illustrates a bias correction procedure that can be used to increase the accuracy of the MIC measurement and a penalisation term based on the complexity of the context tree corresponding to each model. The main drawback of the procedure is that some inefficiency is incurred by the CTW algorithm having to learn the transition table of a model from the training data. A large part of this can be corrected using the known theoretical bounds of the CTW algorithm, however the residual variation creates a “blind spot” which limits the MIC’s ability to distinguish similar Markov models. The Monte Carlo analysis shows that this blind spot is reduced by increasing both training and empirical data, and crucially because cross entropy is measured at the observation level, the reliability of any comparison between models can be tested statistically using the MCS approach. This feature also allows comparison of models on subsets of the data, thus detecting data locations where the relative performance of models switches over.
This paper only provides a proof-of-concept, however, and it is important to point how one might extend this methodology to more common settings. Indeed, the work presented here focuses on a univariate time-series specification, where the candidate models attempt to predict the value of a single random outcome conditional on its past realisations, i.e., \(P ( {{X_t} |x_{t-L}^{t - 1} }).\) While this is reasonable as a starting point for establishing that the methodology works on small-scale problems, it is important to outline how it can be scaled up to larger settings.
First of all, extending the approach to multivariate models poses no conceptual problem, as the current state of a FSM does not have to be restricted to a single variable. Supposing that \(X_t\) represents instead a state vector made up of several variables \(\{A_t,\,B_t,\,C_t,\ldots \}\), one could use the preliminary step of the protocol in Appendix 2 to discretise each variable at its required resolution \(r({a} ),\,r({b}),\,r({c} ),\ldots \) The binary string for an observation  is then simply the concatenation of the individual observations
is then simply the concatenation of the individual observations  and its resolution r is the sum of the individual variable resolutions, i.e., \(\Sigma _i r({i} ).\)
and its resolution r is the sum of the individual variable resolutions, i.e., \(\Sigma _i r({i} ).\)
Secondly, in the time-series setting presented here, the observations in \(x_1^t\) are used both as the outcome to be predicted (in the case of the current observation) and the conditioning information for the prediction (for past observations). However, there no reason why the outcome and conditioning data could not be separated. Keeping \(x_1^t\) as the conditioning data, the methodology can also generate predictions about the state of a separate outcome variable or vector \(Y_t,\) i.e., probability distributions of the type \(P( { {Y_t} |x_{t-L}^{t} }),\) which can be used to extend the MIC approach beyond time-series analysis.
While both these extensions are conceptually feasible, they create implementation challenges. As stated previously, the larger resolution \(\Sigma _i r({i})\) of a multivariate setting implies a correspondingly larger depth d of the binary context tree for any given number of time lags L, increasing the memory requirement for storing the tree nodes. Ongoing work on the implementation of the CTW algorithm is specifically directed at improving the memory efficiency of the algorithm in order to address this last point and turn the proposed methodology into a practical tool.
Notes
This is because, as was pointed out by Shannon (1948) at the very start of the data compression literature, “any stochastic process which produces a discrete sequence of symbols chosen from a finite set may be considered a discrete source” and modelled by a Markov process. As shown by Shannon using the example of the English language, even systems that are not strictly generated through a Markov process can be successfully approximated by one.
Because the aim of the paper is to present the desirable theoretical properties of the proposed criterion and assess their usefulness in practice, the more technical aspects relating to the algorithmic implementation are detailed in Appendix 2.
One should note that the numerator of (8) differs from a standard binomial probability in that it does not contain the binomial coefficient \(\Big ( \begin{array}{c} a + b \\ b \\ \end{array} \Big ),\) which counts the number of ways one can distribute b successes within \(a+b\) trials. This is because we are interested in the probability of a specific sequence of zeros and ones, therefore the multiplicity is omitted.
This similarity becomes even clearer when one considers that, as shown by Akaike (1974), the maximised likelihood function is a good estimator of the cross entropy (2). Rissanen (1984) is very aware of the similarity of the bound (10) with the BIC, and refers several time to the lineage of his work with Akaike (1974).
This literature mainly focuses on biases that occur when measuring Shannon entropy. This is discussed further in Appendix 1, which derives the expected bias for the case of a cross entropy measurement, which is what the MIC measures.
Because of the binary nature of the data and algorithm, the data lengths used throughout the paper are powers of two as this simplifies calculations requiring the binary logarithm \(\log _2.\)
This was done in STATA using the ‘arch’ routine. As a robustness check, the true data series was also re-estimated, and the chosen parameters for the true model all fall within the 95 % confidence interval for the estimates.
It is important to note, however, that long memory processes are typically problematic regardless of the statistical method used to analyse them.
One can see from (17) that \(X_t\) depends on \(\sigma _{t-2}\), which itself depends on \(\varepsilon _{t-4}\).
As an example, note the similarity of MIC scores in Table 7 for \(T=2^{21}\) and \(2^{22}\). One would expect a penalised version of the MIC scores to also be similar in both cases, given the large training lengths involved. However, the naive complexity (12) of the trees for \(T=2^{22}\) will be much higher than for \(T=2^{21}\) even thought the number of empirical observations is unchanged at \(N = 8192,\) as twice as many \((a_{s,o},\,b_{s,o})\) observations will have been processed.
In the interest of simplification, the tree in Fig. 5 is truncated at a depth \(d=3.\)
In particular, the root node \(\varnothing \) is visited every time the tree is updated, however it corresponds to an unconditional probability as no historical conditioning information is used.
For the parent of the leaf node, it is the case of course that \(P_{0s,o}^e = P_{0s,o}^w,\) however for nodes deeper in the tree this will no longer be the case.
References
Akaike, H. (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control, AC–19, 716–723.
Basharin, G. P. (1959). On a statistical estimate for the entropy of a sequence of independent random variables. Theory of Probability and Its Applications, 4(3), 333–336.
Carlton, A. (1969). On the bias of information estimates. Psychological Bulletin, 71(2), 108–109.
Cover, T. M., & Thomas, J. A. (1991). Elements of information theory. New York: Wiley.
Dawid, H., & Fagiolo, G. (2008). Agent-based models for economic policy design: Introduction to the special issue. Journal of Economic Behavior and Organization, 67, 351–354.
Deissenberg, C., Van Der Hoog, S., & Dawid, H. (2008). EURACE: A massively parallel agent-based model of the European economy. Applied Mathematics and Computation, 204(2), 541–552.
Del Negro, M., & Schorfheide, F. (2006). How good is what you’ve got? DGSE-VAR as a toolkit for evaluating DGSE models. Economic Review: Federal Reserve Bank of Atlanta, 91, 21–337.
Del Negro, M., & Schorfheide, F. (2011). Chapter: Bayesian Macroeconometrics. In The Oxford handbook of Bayesian econometrics. Oxford: Oxford University Press.
Del Negro, M., Schorfheide, F., Smets, F., & Wouters, R. (2007). On the fit of new Keynesian models. Journal of Business and Economic Statistics, 25, 123–143.
Dosi, G., Fagiolo, G., & Roventini, A. (2010). Schumpeter meeting Keynes: A policy-friendly model of endogenous growth and business cycles. Journal of Economic Dynamics and Control, 34(9), 1748–1767.
Dosi, G., Fagiolo, G., Napoletano, M., & Roventini, A. (2013). Income distribution, credit and fiscal policies in an agent-based Keynesian model. Journal of Economic Dynamics and Control, 37(8), 1598–1625.
Dosi, G., Fagiolo, G., Napoletano, M., Roventini, A., & Treibich, T. (2015). Fiscal and monetary policies in complex evolving economies. Journal of Economic Dynamics and Control, 52, 166–189.
Elias, P. (1975). Universal codeword sets and representations of the integers. IEEE Transactions on Information Theory, IT–21, 194–203.
Fabretti, A. (2014). A Markov chain approach to ABM calibration. In F. J. Miguel Quesada, F. Amblard, J. A. Barcel, & M. Madella (Eds.), Advances in computational social science and social simulation. Barcelona: Autonomous University of Barcelona.
Fagiolo, G., & Roventini, A. (2012). Macroeconomic policy in DSGE and agent-based models. Revue de l’OFCE, 5, 67–116.
Fagiolo, G., Moneta, A., & Windrum, P. (2007). A critical guide to empirical validation of agent-based models in economics: Methodologies, procedures, and open problems. Computational Economics, 30, 195–226.
Gneiting, T., & Raftery, A. E. (2007). Strictly proper scoring rules, prediction, and estimation. Journal of the American Statistical Association, 102, 359–378.
Grünewald, P. D. (2007). The minimum description length principle. Cambridge: MIT Press.
Hansen, M. M., & Yu, B. (2001). Model selection and the principle of minimum description length. Journal of the American Statistical Association, 96, 746–774.
Hansen, P. R., Lunde, A., & Nason, J. M. (2011). The model confidence set. Econometrica, 79, 453–497.
Holcombe, M., Chin, S., Cincotti, S., Raberto, M., Teglio, A., Coakley, S., et al. (2013). Large-scale modelling of economic systems. Complex Systems, 22(2), 175–191.
Kirman, A. (1993). Ants, rationality and recruitment. Quarterly Journal of Economics, 108, 137–156.
Kopecky, K. A., & Suen, R. M. (2010). Finite state Markov-chain approximations to highly persistent processes. Review of Economic Dynamics, 13(3), 701–714.
Krichevsky, R. E., & Trofimov, V. K. (1981). The performance of universal encoding. IEEE Transactions on Information Theory, IT–27, 629–636.
Kullback, S., & Leibler, R. A. (1951). On information and sufficiency. Annals of Mathematical Statistics, 22, 79–86.
Lamperti, F. (2015). An information theoretic criterion for empirical validation of time series models. LEM working paper series 2015/02.
Marks, R. (2010). Comparing two sets of time-series: The state similarity measure. In 2010 Joint statistical meetings proceedings—Statistics: A key to innovation in a data-centric world (pp. 539–551). Alexandria, VA: Statistical Computing Section, American Statistical Association.
Marks, R. E. (2013). Validation and model selection: Three similarity measures compared. Complexity Economics, 2(1), 41–61.
Miller, G. A. (1955). Note on the bias of information estimates. Information Theory in Psychology: Problems and Methods, 2, 95–100.
Panzeri, S., & Treves, A. (1996). Analytical estimates of limited sampling biases in different information measures. Network: Computation in Neural Systems, 7, 87–107.
Politis, D. N., & Romano, J. P. (1994). The stationary bootstrap. Journal of the American Statistical Association, 89, 1303–1313.
Politis, D. N., & White, H. (2004). Automatic block-length selection for the dependent bootstrap. Econometric Reviews, 23, 53–70.
Rissanen, J. (1976). Generalized Kraft inequality and arithmetic coding. IBM Journal of Research and Development, 20, 198–203.
Rissanen, J. (1978). Modeling by shortest data description. Automatica, 14, 465–471.
Rissanen, J. (1984). Universal coding, information, prediction and estimation. IEEE Transactions on Information Theory, IT–30, 629–636.
Rissanen, J. (1986). Complexity of strings in the class of Markov sources. IEEE Transactions on Information Theory, IT–32, 526–532.
Rissanen, J., & Langdon, G. G. J. (1979). Modeling by shortest data description. IBM Journal of Research and Development, 28, 149–162.
Roulston, M. S. (1999). Estimating the errors on measured entropy and mutual information. Physica D, 125, 285–294.
Schorfheide, F. (2000). Loss function-based evaluation of DSGE models. Journal of Applied Econometrics, 15, 645–670.
Schwarz, G. (1978). Estimating the dimension of a model. The Annals of Statistics, 6, 461–464.
Shannon, C. E. (1948). A mathematical theory of communication. The Bell System Technical Journal, 27, 379–423.
Tauchen, G. (1986a). Finite state Markov-chain approximations to univariate and vector autoregressions. Economics Letters, 20(2), 177–181.
Tauchen, G. (1986b). Statistical properties of generalized method-of-moments estimators of structural parameters obtained from financial market data. Journal of Business and Economic Statistics, 4(4), 397–416.
Van Der Hoog, S., Deissenberg, C., & Dawid, H. (2008). Production and finance in EURACE. In Complexity and artificial markets (pp. 147–158). Berlin: Springer.
White, H. (2000). A reality check for data snooping. Econometrica, 68, 1097–1126.
Willems, F. M. J., & Tjalkens, T. J. (1997). Complexity reduction of the context-tree weighting algorithm: A study for KPN research. EIDMA Report RS.97.01.
Willems, F. M. J., Shtarkov, Y. M., & Tjalkens, T. J. (1995). The context-tree weighting method: Basic properties. IEEE Transactions on Information Theory, IT–41, 653–664.
Willems, F. M. J., Tjalkens, T. J., & Ignatenko, T. (2006) Context-tree weighting and maximizing: Processing betas. In Proceedings of the inaugural workshop of the ITA (information theory and its applications).
Acknowledgments
The author is grateful to WEHIA 2013, CFE 2013 and CEF 2014 participants for their comments and suggestions on earlier versions of this paper. The author would like to thank particularly Jagjit Chadha, Stefano Grassi, Philipp Harting, Sander van der Hoog, Sandrine Jacob-Léal, Miguel León-Ledesma, Thomas Lux, Mauro Napoletano, Lionel Nesta, John Peirson and the two anonymous referees whose suggestions greatly helped to improve the manuscript. Finally, a special thanks to James Holdsworth, Steve Sanders and Mark Wallis for their invaluable help in setting up and maintaining the SAL and PHOENIX Computer Clusters on which the Monte Carlo analysis was run. Any errors in the manuscript remain of course the author’s.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Bias Correction in Measured Cross-Entropy
It has been known since Miller (1955) and Basharin (1959) that measuring Shannon entropy using observed frequencies rather than the true underlying probabilities generates a negative bias due to the interaction of Jensen’s inequality with the inherent measurement error of the frequencies. A large literature exists calculating analytical expressions for this bias, good examples of which are Carlton (1969), Panzeri and Treves (1996) or Roulston (1999). These expressions can be generalised to the case of measuring the cross entropy between empirical and simulated data, in order to provide a clarification of the bias correction term derived in Sect. 2.2. As will be shown in the derivation below, which generalises the approach of Roulston (1999), in the case of cross entropy the resulting bias is in fact positive.
Letting B be the number of states a system can occupy, \(q_i\) the probability of observing the ith state in the empirical data and \(p_i\) the corresponding model probability, the theoretical cross entropy is given by:
In practice, this is measured using frequencies \(f_i\) and \(g_i,\) where \(n_i,\,t_i\) are the observed realisations for the ith state in the empirical and simulated data, respectively, with N and T as the overall number of observations.
The count variables \(n_i\) and \(t_i\) can be considered as binomial distributed variables with parameters \(q_i\) and \(p_i,\) with the following expectations and variances:
Following Roulston (1999), the frequencies \(f_i\) and \(g_i\) can be redefined in terms of a measurement error relative to the true underlying probabilities \(q_i\) and \(p_i.\)
Given the mean and variance of the binomial counts (21), one can see that the measurement errors have mean \(E [\eta _i] = E [\varepsilon _i] = 0\) and variances:
Replacing (22) into the measured cross entropy term (20) allows the bias to be expressed in terms of \(\eta _i\) and \(\varepsilon _i{\text {:}}\)
Because it is expected that \(|\varepsilon _i| < 1,\)Roulston (1999) uses a second order Taylor expansion for the logarithmic term, \(\ln (1+\varepsilon _i) \approx \varepsilon _i - \varepsilon _i^2/2.\) Replacing in the previous expression and rearranging provides the following expression.
The critical component of the bias is the product of errors, labeled b. Suppose for the moment that the empirical and simulated data are identical, so that \(q_i = p_i,\,f_i = g_i,\,\eta _i = \varepsilon _i\) and \(N=T.\) In that case the cross entropy term (19) measures the Shannon entropy, b offsets the negative \(\varepsilon _i^2/2\) term in equation (25), and one recovers the derivation in Roulston (1999):
Given \(E[\varepsilon _i]=0\) and the variance \(E[\varepsilon _i^2]\) in (23) the second order approximation for the bias is given by the following expression, where \(B^*\) corresponds to the number of states for which \(p_i \ne 0.\)
This is the finding reported by Roulston (1999), which is that measured Shannon entropy systematically underestimates the true Shannon entropy, and to a second order the bias does not depend on the distribution \(p_i.\)
This is not the case for the more general situation where \(q_i \ne p_i\) and \(f_i \ne g_i.\) Because it is reasonable to assume that the measurement errors on the real and simulated probabilities are independent, their covariance \(E[\eta _i \varepsilon _i]\) will be zero and the bias term b in (25) no longer counteracts the negative \(\varepsilon _i^2/2\) term. Furthermore, the weighting of the bias terms by \(q_i\) rather than \(p_i\) means that the \(p_i\) denominator in the variance of \(\varepsilon _i\) will not cancel out. The expectation of the second order approximation is now:
This produces a situation which is the opposite of the one observed for Shannon entropy in (27): measured cross entropy systematically overestimates the true cross entropy and the bias (28) now depend on the unknown \(q_i\) and \(p_i\) distributions. We now show that the bias correction term (14) approximates this bias in expectation. Recall that given an observation  , identified by the binary string o and a context
, identified by the binary string o and a context  , identified by the binary string s, the correction is given by:
, identified by the binary string s, the correction is given by:

Letting \(\tau _{s,o} = a_{s*,o} + b_{s*,o}\) be the number of times the Markov transition identified by the \(s,\,o\) binary strings has been seen in the training data, and taking a first order approximation of the binary logarithm, the correction for that specific observation  is approximated by
is approximated by

Summing this term over all the observations in the empirical data on the left hand side is equivalent to summing over all the contexts and observation strings \(s,\,o\) on the right hand side:

Dividing both sides by the number of transitions observed \(N-L\) provides the expected correction term for the empirical data set. Note that the total number of observations T is added to both the numerator and denominator of the right hand side:

The two ratios in the right hand side terms correspond to the observed frequencies of the Markov transition identified by binary strings \(s,\,o\) in the empirical and training data, respectively, therefore \(E[{n_{s*,o}/(N-L)}] = q_{s*,o}\) and \(E [{\tau _{s*,o}/T}] = p_{s8,o}\). One can therefore see that allowing for the change in logarithmic base, the expectation of (32) is essentially equivalent to (28). The main advantage of using the error correction term (14) is that the bias is corrected at the level of each observation rather than over the entire empirical data, which facilitates the evaluation of model performance at the local level.
Appendix 2: Technical Appendix—The MIC Protocol
Only two inputs are required in order to run the protocol. The first is a \(N \times 1\) data series that provides the empirical benchmark for model comparison. The second input is a set of training series produced from the various fitted, calibrated or simulated models in the comparison set \(\{M_{1},\,M_{2},\ldots ,M_{m} \}\), etc., which should be \(T \gg N\) observations in length. An overview of the stages of the methodologies is provided in Table 5, and each stage is discussed in the subsequent subsections
1.1 Stage 0: Discretising the State Space and Testing for Quantisation Error
The Krichevsky and Trofimov (1981) estimator, at the core of the CTW and context tree maximising (CTM) algorithms, can only be used to predict the probability distribution of a binary event, and can only therefore deal with binary data. As a result, a preliminary step is to digitise the data and model training series and convert them into binary strings. It is important, ensure that the no essential information about the variation in the data is lost through the quantisation error.
1.1.1 Data Discretisation and Observation Structure
The discretisation of the data is controlled by two sets of parameters, first a set of bounds \(\{b_l,\,b_u\}\) representing the range of variation of the data, and secondly a resolution parameter r, which determines the number of bits used to describe an observation and the number of distinct discrete values the variable can take, i.e., \(2^r.\) It needs to large enough to capture the significant variation in the data and training series, but not so large that it increases the complexity and memory requirements of the CTW algorithm unnecessarily. Figure 3 provides an illustration of the process for \(r=3.\)
The digitisation itself is carried out in a straightforward manner: Given a choice of bounds \(\{b_l,\,b_u\}\) and a resolution r, the data vector x is first normalised to the \([0,\,2^{r-1}]\) interval as follows:
The normalised data values \(x^{\prime }\) are then rounded to the nearest integer, with any values outside the bounds being rounded to the bounds themselves.

The resulting vector of integers  is mapped to its binary values, using the scheme illustrated in Fig. 3. The most significant bit (MSB), which indicates whether the observation is in the top or bottom half of the range is on the right, with the least significant bit (LSB) on the left. It is this structure which allows the Krichevsky and Trofimov (1981) estimator, which can only deal with Bernoulli processes, to be extended to any arbitrary categorical distribution.
is mapped to its binary values, using the scheme illustrated in Fig. 3. The most significant bit (MSB), which indicates whether the observation is in the top or bottom half of the range is on the right, with the least significant bit (LSB) on the left. It is this structure which allows the Krichevsky and Trofimov (1981) estimator, which can only deal with Bernoulli processes, to be extended to any arbitrary categorical distribution.
Once each observation is discretised, the binary strings are concatenated, as shown in Fig. 4. The specific configuration illustrated in the figure corresponds to the one used for the ARMA–ARCH analysis presented in the paper: the range of variation was bounded within \([-30,\,30],\) 7 bits were chosen to represent each observation and the tree depth was set at 21 bits, or 3 lags.
1.1.2 The Choice of \(r{\text {:}}\) Testing for Quantisation Error
It should be apparent that the rounding operation (34) creates a quantisation error  which given the normalisation (33) is distributed over the unit length interval \([-0.5,\,0.5[.\) Some of the information content of the data x is therefore inevitably discarded by the quantisation (34), and it is important to check that this does not affect the measurements. If the quantisation error \(\varepsilon \) satisfies the following two assumptions, then the information loss will not affect the MIC:
which given the normalisation (33) is distributed over the unit length interval \([-0.5,\,0.5[.\) Some of the information content of the data x is therefore inevitably discarded by the quantisation (34), and it is important to check that this does not affect the measurements. If the quantisation error \(\varepsilon \) satisfies the following two assumptions, then the information loss will not affect the MIC:

Proposition
If the quantisation error  satisfies iid uniformity and uncorrelatedness at a resolution \(r^*,\) then choosing a larger \(r=r^*+\phi \) increases the log score
satisfies iid uniformity and uncorrelatedness at a resolution \(r^*,\) then choosing a larger \(r=r^*+\phi \) increases the log score  by an additive constant for all models \(M_i.\)
by an additive constant for all models \(M_i.\)
Proof
Given a data vector x, let \(r^*\) be the lowest resolution such that the quantisation error \(\varepsilon ^*\) resulting from the corresponding digitisation  satisfies the iid uniformity and uncorrelatedness assumptions. Let
satisfies the iid uniformity and uncorrelatedness assumptions. Let  be an alternative digitisation of x with the same bounds \(\{b_l,\,b_u\}\) but a higher resolution \(r = r^* + \phi .\) Let us calculate the number of bits required to encode the tth observation at resolution \(r{\text {:}}\)
be an alternative digitisation of x with the same bounds \(\{b_l,\,b_u\}\) but a higher resolution \(r = r^* + \phi .\) Let us calculate the number of bits required to encode the tth observation at resolution \(r{\text {:}}\)

First, because the conditional probability of each of the r observation bits is conditioned on the values of previous observation bits, the chain rule for conditional probabilities ensures that (35) is simply the sum of the cross entropies for each bit.

Additivity of the expectations operator \(E_{dgp} [ \ldots ]\) then implies:

Second, the normalisation (33) and rounding (34) operations ensure that by construction the binary string formed by  contains the shorter
contains the shorter  as a substring:
as a substring:

Regarding the first \(r^*\) bits in the sum (37), the nesting of  in
in  implies that the only difference between predicting
implies that the only difference between predicting  and
and  is that each of the lagged observations in
is that each of the lagged observations in  contains more information than in
contains more information than in  , specifically, \(\phi \) bits of information drawn from the quantisation error \(\varepsilon ^*.\) However, \(\varepsilon ^*\) is iid and uncorrelated with
, specifically, \(\phi \) bits of information drawn from the quantisation error \(\varepsilon ^*.\) However, \(\varepsilon ^*\) is iid and uncorrelated with  , therefore this extra information cannot improve the conditioning compared to what is achieved using only the \(r^*\)-length substring \({\text {:}}\)
, therefore this extra information cannot improve the conditioning compared to what is achieved using only the \(r^*\)-length substring \({\text {:}}\)

Predicting the values of the last \(\phi \) bits of  in (37) is equivalent to predicting the value of \(\varepsilon ^*_t\) at a resolution \(\phi .\) However, \(\varepsilon ^*\) is iid uniformly distributed over \([-0.5,\,0.5]\) and uncorrelated with
in (37) is equivalent to predicting the value of \(\varepsilon ^*_t\) at a resolution \(\phi .\) However, \(\varepsilon ^*\) is iid uniformly distributed over \([-0.5,\,0.5]\) and uncorrelated with  therefore:
therefore:

Replacing (39) and (40) in the sum of conditional entropies (37) provides the following result:

One therefore has  . \(\square \)
. \(\square \)
In essence, if the iid uniformity and uncorrelatedness assumptions on \(\varepsilon \) are satisfied at resolution \(r^*,\) then choosing a higher resolution \(r^* + \phi \) for the N data observations will simply result in a log score \(\lambda \) equal to the one obtained at resolution \(r^*,\) plus an additional \(\phi \times N\) extra bits, for all models in the comparison set \(\{M_{1},\,M_{2},\ldots ,M_{m} \}\). This additive term will drop out when taking differences between models.
We therefore suggest an incremental testing procedure, starting at \(r=1,\) where the following three tests are carried out to ensure that the quantisation error satisfies the uniformity, independence and uncorrelatedness assumptions above. The correct value of r is the lowest value that satisfies the three following tests:
-
A Kolmogorov–Smirnov (KS) test on the quantisation error \(\eta ,\) where \(H_0\) is that \(\eta \) is uniformly distributed over the range \([-0.5,\,0.5[.\)
-
A Ljung–Box (LB) test on the autocorrelation coefficients of \(\eta ,\) where \(H_0\) is that \(\eta \) is independently distributed.
-
A second LB test on the cross correlation coefficients of \(\eta \) and the quantised values
 , where \(H_0\) is that \(\eta \) and
, where \(H_0\) is that \(\eta \) and  are independent.
are independent.
1.2 Stage 1: The Context Tree Weighting (CTW) and Maximising (CTM) Algorithms
The general implementation of the CTW and CTM algorithms in the MIC toolbox broadly follows the technical report of Willems and Tjalkens (1997), however, some aspects have been modified. It is recommended that the reader download this report from http://www.ele.tue.nl/ctw for more general background information.
1.2.1 Tree Structure
The information used to reconstruct the \(2^d \times 2^r\) Markov transition table of model \(M_i\) is stored in a set of \(2^r - 1\) binary trees, one of which is illustrated in Fig. 5. Following from the discussion in 2.1 each tree is indexed by a \(k \le r\) length string o corresponding to possible substrings of the observation string  , and each node within a tree is indexed by a substring s of the full context
, and each node within a tree is indexed by a substring s of the full context  . As is illustrated in Fig. 6, each node contains two internal counters \(a_{s,o}\) and \(b_{s,o}\) which count the number of times a 0 or a 1 have been observed after context s and observation bits o, as well as two internal ratios \(\beta _{s,o}\) and \(Q_{s,o}\) which are used respectively to weight the probabilities of the node with respect to its children nodes and to select between the node and its children when drawing probabilities. As a result each node in a tree can be used to generate the probability that
. As is illustrated in Fig. 6, each node contains two internal counters \(a_{s,o}\) and \(b_{s,o}\) which count the number of times a 0 or a 1 have been observed after context s and observation bits o, as well as two internal ratios \(\beta _{s,o}\) and \(Q_{s,o}\) which are used respectively to weight the probabilities of the node with respect to its children nodes and to select between the node and its children when drawing probabilities. As a result each node in a tree can be used to generate the probability that  conditional on the history of the system, given by the context string s and on the previous \(k-1\) bits of the observation string o.
conditional on the history of the system, given by the context string s and on the previous \(k-1\) bits of the observation string o.
Given a full context of length \(d = rL,\) one can identify a path in each tree (in bold in Fig. 5) linking the corresponding leaf node to the root node \(\varnothing .\) Footnote 13 Selecting which node on the path to draw the probability from involves a tradeoff between precision and conditioning. Nodes close to the leaf benefit from more conditioning information, as the context string s is longer, but suffer from not being observed very often. Nodes closer to the root will be visited more often and produce more precise probabilities, but suffer from weaker conditioning.Footnote 14 The intuition behind the effectiveness of the CTW and CTM algorithms is that they provide a method of optimally resolving this tradeoff and selecting the point on the leaf-to-root path which minimises prediction error.
1.2.2 Updating the Tree During Training
During the training stage, the simulated data from model \(M_i\) is used sequentially to update the trees. Starting at the beginning of the training data string, the first L observations  specify the d-length context string with the following r bits making up the observation string
specify the d-length context string with the following r bits making up the observation string  , as shown in Fig. 4. The bits in o are used to identify the r trees corresponding to the observation and the bits in s identify the nodes making up the leaf to root path.
, as shown in Fig. 4. The bits in o are used to identify the r trees corresponding to the observation and the bits in s identify the nodes making up the leaf to root path.
For each of the r trees, the node on the path is updated in sequence, as illustrated in Fig. 6. Because leaf nodes do not have any children, there is no weighting to be performed, and the probabilities in the node are directly given by the Krichevsky and Trofimov (1981) estimates using counts \(a_{s,o}\) and \(b_{s,o}{\text {:}}\)
The probabilities from the leaf node are used to calculate the initial value of the odds ratio \(\eta ,\) which is send to the parent of the leaf node.
The incoming odds ratio are used to calculate the weighted probability given by the child node:Footnote 15
These allow the \(\eta \) odds ratio to be updated, using the internal mixing ratio \(\beta _{s,o}\), which weight the probabilities that  as measured in the current node (42) and as measured in the child node (44):
as measured in the current node (42) and as measured in the child node (44):
The outgoing odds ratio \(\eta _{out}\) will become the incoming odds ratio \(\eta _{in}\) for the next node on the leaf to root path. Before proceeding to the next node, the algorithm updates the internal \(\beta _{s,o},\,Q_{s,o}\) ratios and \(a_{s,o},\,b{s,o}\) counters. First of all, the internal \(\beta _{s,o}\) ratio is updated as follows, in order to reflect the new observation, and the internal counter corresponding to the observation is incremented by one.
Secondly, the Q-ratio is updated using \(\beta _{s,o}\) and the Q-ratios of the two children of node \((s,\,o),\) following the CTM procedure of Willems et al. (2006):
Once the node has been updated, the algorithm passes the updated value of \(\eta \) (45) to the next node on the path and updates it using (44)–(47). This process continues until the root node is reached for all r trees, at which point the algorithm moves on to the next context/observation pair  , the procedure continuing until all the training data has been processed.
, the procedure continuing until all the training data has been processed.
1.3 Stage 2: Scoring the Empirical Data
The \(N-L\) empirical observations are processed sequentially, starting with the first context/ observation pair  , and finishing with the last one,
, and finishing with the last one,  . The conditional probabilities
. The conditional probabilities  required to score each observation are drawn from the context trees corresponding to model \(M_i.\)
required to score each observation are drawn from the context trees corresponding to model \(M_i.\)
1.3.1 Drawing Probabilities from the Tree
As was the case for the training data in stage 1, each context/observation pair is used to identify the r trees corresponding to the observation string and the leaf-to-root path corresponding to the context. Because each node on this path can potentially be used to generate a conditional probability, the context tree maximisation approach of Willems et al. (2006) is used to select the correct node on the path. Starting at the root of the tree, the \(\beta _{s,o}\) ratio of the node is compared to product of the Q ratio of the children nodes as follows:
Once the best node on the path \(s^*\) is identified, its \(a_{s^*,o},\,b_{s^*,o}\) counters are used to calculate the probability of the kth bit being a ‘1’, 
 , using the Krichevsky and Trofimov (1981) estimator. This is carried out for all r bits in the observation string, providing a r length vector of probabilities \(p{\text {:}}\)
, using the Krichevsky and Trofimov (1981) estimator. This is carried out for all r bits in the observation string, providing a r length vector of probabilities \(p{\text {:}}\)

1.3.2 Scoring the Observations
The nested binary structure of the r-bits in an observation, explained in Sect. 1, means that the log score for the observation is simply sum of the individual binary log scores obtained using the vector of model probabilities p and observation bits \({\text {:}}\)

In addition to this, the \(a_{s^*,o},\,b_{s^*,o}\) counters used to generate the vector of probabilities (49) are used to generate the marginal bound of the KT estimator (13) which is used in the MIC procedure to correct for the measurement bias induced by the stage 1 learning process:

Finally, an MDL complexity penalisation can be obtained by summing the log of the normalised counter observations for all the nodes in the tree:
Appendix 3: Extended Monte Carlo Results
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Barde, S. A Practical, Accurate, Information Criterion for Nth Order Markov Processes. Comput Econ 50, 281–324 (2017). https://doi.org/10.1007/s10614-016-9617-9
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10614-016-9617-9


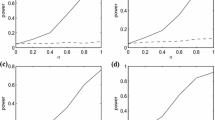






 , where
, where  are independent.
are independent.
