Abstract
In this paper, an analytic approach is applied to approximate stochastic differential utility for both endowment and production economies. This utility function satisfies a second order nonlinear differential equation and is analytic near the stationary mean of the state variable. The radius of convergence of its power series representation is at lease two standard deviations of the stationary distribution of the state variable around its mean. The main contribution of this paper is to use a higher order Taylor polynomial to accurately approximate the utility function, which confirms the empirical properties of the pricing kernel and equity premium on wealth.








Similar content being viewed by others
Notes
Epstein and Zin (1989, 1990, 1991) and Weil (1989) are the first to use recursive preferences to explain the equity premium in discrete time. Duffie and Epstein (1992b) explain how SDU can be used to price financial assets in continuous time. Also see Duffie et al. (1997), and Duffie and Skiadas (1994). See Skiadas (2009, Chap. 6) for a recent exposition of recursive utility and its relation to asset pricing.
Throughout the text we refer only to the elasticity of wealth to consumption ratio with respect to the state variable. This state variable is the long run risk variable in the Bansal and Yaron model and the long run economic growth in the production economy of Ai. Also, the elasticity of the lifetime utility with respect to these variables is the elasticity of the wealth to consumption ratio multiplied by \(\frac{(1-\gamma )\psi }{\psi -1}\) where \(\gamma \) is the coefficient of risk aversion and \(\psi \) is the investor’s intertemporal rate of substitution.
Ai also uses a \(16^{th}\) order Chebyshev polynomial and Markov chain to approximate the lifetime utility function. Ai reports a positive relation between the equity premium and the expected growth of technology.
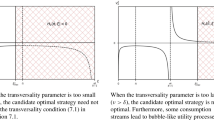
Schroder and Skiadas (2008) develop these arguments in the more complicated situations such as Poisson jumps to the investor’s opportunity set and trading costs.
Kaltenbrunner and Lochstoer (2010) show how the permanent and temporary shocks to technology interact with the elasticity of intertemporal substitution in the SDU to mimic the behavior of long-run risk. We demonstrate below that this occurs since Ai (2010) did not place a constraint on the second derivative of the polynomials. This constraint is implied by the original ODE.
These parameter’s are also used in Bansal et al. (2009).
See Chen et al. (2009) for details.
The standard deviation and quadratic variation are by-products of the stochastic process for consumption and Ito’s lemma. The expresssion for this standard deviation is derived below.
This functional form is chosen so that the scale invariant property of Schroder and Skiadas (2003) holds for the terminal utility.
As long as the means and variance are analytic functions, our procedure can be applied.
The stochastic process for the consumption is contained in the space of consumption plans considered by Schroder and Skiadas (2003) in their study of optimal consumption and portfolio decisions.
\(g(c(t), \psi (t))\) in Fisher and Gilles (1998) is given by \( (C^\alpha /\alpha ) g(x)^{\frac{\alpha }{\rho }} \). Note that they use \(\varphi (z)=(z^{\alpha }-1)/\alpha \) which does not effect our procedure.
We added the subscript \(K,\theta \) to Ai’s notation for this correlation so as to avoid confusion with the parameter in the lifetime utility function, \(\rho \).
Changing this value to \(\sigma _e = 0.01\) does not materially affect the ability to simulate the model. But it does lower the expected return on wealth by about 20 basis points.
We shift back to \(H(m)\) of Ai (2010), corresponding to the wealth-consumption ratio in his model, so that we can compare our results with his.
When \(\beta \) is increased in the simulation of Ai’s production economy, the accuracy of the solution does not change.
Ai used the wealth to consumption ratio to approximate the nonlinear term \(D_0/g(x)\) but the initial conditions are set by the solution to Ai’s approximate ODE.
This result is not effected by the change in \(\beta \).
Under certainty this term is exactly equal to \(-C_2\) at \(x=0\).
For both Ai’s approximate solution and the certainty case there is always a long run economic growth value low enough so that this effect arises.
See Chen et al. (2009) for details.
In the appendix, Ai’s approximation is applied to \(\alpha v(x) = g(x)^{\frac{\alpha }{\rho }}\).
See Hansen et al. (2008) for a further discussion of this point.
References
Abel, A. B. (1999). Risk premia and term premia in general equilibrium. Journal of Monetary Econonics, 43, 3–33.
Ai, H. (2010). Information quality and long-run risk: Asset pricing implications. Journal of Finance, 65, 1333–1367.
Ai, H., & Kiku, D. (2009). Growth to value: Option exercise and the cross-section of equity returns. Working paper Fuqua School of Business, Duke University.
Balvers, R. J., & Huang, D. (2007). Productivity-based asset pricing: Theory and evidence. Journal of Financial Economics, 86, 405–445.
Bansal, R., Kiku, D., Yaron, A. (2007). Risks for the long-run: Estimation and inference. Working paper Fuqua School of Business, Duke University.
Bansal, R., Kiku, D., & Yaron, A. (2009). An empirical evaluation of the long-run risks model for asset prices. Working paper Fuqua School of Business, Duke University.
Bansal, R., & Yaron, A. (2004). Risks for the long-run: A potential resolution of asset pricing puzzles. Journal of Finance, 59, 1481–1510.
Benzoni, L., Collin-Dufresne, P., & Goldstein, R. S. (2005). Can standard preferences explain the prices of out-of-the-money S &P 500 put options. NBER working paper 11861.
Bekaert, G., Engstrom, E., & Xing, Y. (2009). Risk, uncertainty and asset prices. Journal of Financial Economics, 91, 59–82.
Beeler, J. & Campbell, J. Y. (2009). The long-run risk model and aggregate asset prices: An empirical assessment. Working paper, Harvard University.
Bergstrom, A. R. (1984). Continuous time stochastic models and issues of aggregation over time. In Z. Griliches & M. D. Intriligator (Eds.), Handbook of econometrics (Vol. 2). Amsterdam: North-Holland.
Calin, O. L., Chen, Y., Cosimano, T. F., & Himonas, A. A. (2005). Solving asset pricing models when the price-dividend function is analytic. Econometrica, 73, 961–982.
Campbell, J. Y., Chacko, G., Rodrequez, J., & Viceira, L. (2004). Strategic asset allocation in a continuous-time VAR model. Journal of Econonmics Dynamics & Control, 28, 2195–2214.
Campbell, J. Y., & Kyle, A. S. (1993). Smart money, noise trading, and stock price behavior. Review of Economic Studies, 60, 1–34.
Chen, H. (2010). Macroeconomic conditions and the puzzles of credit spreads and capital structure. Journal of Finance, 65, 2171–2212.
Chen, Y., Cosimano, T. F., & Himonas, A. A. (2008). Analytic solving of asset pricing models: The by force of habit case. Journal of Economic Dynamics & Control, 32, 3631–3660.
Chen, Y., Cosimano, T. F., & Himonas, A. A. (2013). On formulating and solving portfolio decision and asset pricing problems. In K. Judd & K. Schmedders (Eds.), Handbook of Computational Economics. Amsterdam: Elsevier.
Chen, Y., Cosimano, T. F., & Himonas, A. A. (2010). Continuous time one-dimensional asset pricing models with analytic price-dividend functions. Economic Theory, 42, 461–503.
Chen, Y., Cosimano, T. F., Himonas, A. A., & Kelly, P. (2009). Asset pricing with long-run risk and stochastic differential utility: An analytic approach. www.nd.edu/~tcosiman.
Cochrane, J. H. (2005). Asset pricing (Rev. ed). Princeton, NJ: Princeton University Press.
Cochrane, J. H. (2008). Financial markets and the real economy (Chap. 7). In Handbook of the equity premium. Amsterdam: Elsevier.
Cochrane, J. H. (1991). Production-based asset pricing and the link between stock returns and economic fluctuations. The Journal of Finance, 46, 209–237.
Croce, M. M. (2010). Long-run productivity risk: A new hope for production-based asset pricing. Working paper Kenan-Flagler Business School, University of North Carolina.
Duffie, D. J. (2001). Dynamic asset pricing theory (3rd ed.). Princeton, NJ: Princeton University Press.
Duffie, D. J., & Epstein, L. G. (1992a). Stochastic differential utility. Econometrica, 60(353–39), 4.
Duffie, D. J., & Epstein, L. G. (1992b). Asset pricing with stochatic differential utility. Review of Financial Studies, 5, 411–436.
Duffie, D. J., Epstein, L. G., & Skiadas, C. (1992). Infinite horizon stochatic differential utility. Appendix to Duffie and Epstein 1992a. Econometrica, 60, 353–394.
Duffie, D. J., & Lions, P.-L. (1992). PDE solutions of stochastic differential utility. Journal of Mathematical Economics, 21, 577–606.
Duffie, D. J., Schroder, M., & Skiadas, C. (1997). A term structure model with preference for the timing of resolution of uncertainty. Economic Theory, 9, 3–22.
Duffie, D. J., & Skiadas, C. (1994). Continuous-time security pricing: A utility gradient approach. Journal of Mathematical Economics, 23, 107–131.
Epstein, L. G., & Zin, S. E. (1989). Substitution, risk aversion, and the temporal behavior of consumption and asset returns: A theoretical framework. Econometrica, 57, 937–969.
Epstein, L. G., & Zin, S. E. (1990). First-order risk aversion and the equity premium puzzle. Journal of Monetary Economics, 26, 387–407.
Epstein, L. G., & Zin, S. E. (1991). Substitution, risk aversion, and the temporal behavior of consumption and asset returns: An empirical analysis. Journal of Political Economy, 99, 263–286.
Fisher, M., & Gilles, C. (1998). Consumption and asset prices with recursive preferences. Working paper Federal Reserve Bank of Atlanta.
Hansen, L. P., Heaton, J. C., & Li, N. (2008). Consumption strikes back? Measuring long-run risk. Journal of Political Economy, 116, 260–302.
Hansen, L. P., & Scheinkman, J. A. (2012). Recursive utility in a Markov environment with stochastic growth. Working paper Becker Friedman Institute for Research in Economics.
Kaltenbrunner, G. K., & Lochstoer, L. A. (2010). Long-run risk through consumption smoothing. Review of Financial Studies, 23, 3190–3224.
Kreps, D., & Porteus, E. (1978). Temporal resolution of uncertainty and dynamic choice theory. Econometrica, 46, 185–200.
Malkhozov, A. (2009). Stochastic volatility and long-run risk in endowment and production economies. Working paper London School of Economics.
Schroder, M., & Skiadas, C. (1999). Optimal consumption and portfolio selection with stochastic differential utility. Journal of Economic Theory, 89, 68–126.
Schroder, M., & Skiadas, C. (2003). Optimal lifetime consumption-portfolio strategies under trading constraints and nontradeable income. Stochastic Processes and Their Applications, 155, 1–30.
Schroder, M., & Skiadas, C. (2008). Optimality and state pricing in constrained financial markets with recursive utility under continuous and discontinuous information. Mathematical Finance, 18, 199–238.
Skiadas, C. (2009). Asset pricing theory. Princeton, NJ: Princeton University Press.
Verdelhan, A. (2010). A habit-based explanation of the exchange rate risk premium. Journal of Finance, 65, 123–146.
Wachter, J. A. (2006). A consumption-based model of the term structure of interest rates. Journal of Financial Economics, 79, 365–399.
Weil, P. (1989). The equity premium puzzle and the risk-free rate puzzle. Journal of Monetary Economics, 24, 401–421.
Acknowledgments
We would like to thank the referee for thoughtful suggestions and Adam Speight for helpful discussions.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Derivation of Differential Equation for (14)
The lifetime utility \(V_t\) for a representative investor satisfies the stochastic differential equation (1)
where the aggregator is given by
The lifetime utility function satisfies the differential equation
Duffie and Epstein (1992b) and Schroder and Skiadas (1999, 2003) demonstrate that the solution to the differential equation (49) is of the separable form
Following an insight from Fisher and Gilles (1998), the differential equation can be simplified further by introducing the change of variable
By the stochastic process (8) and Ito’s lemma, we have
where \(\bar{C}=e^{\bar{c}}\) is the steady state level for consumption \(C_t\). The long-run risk variable \(x\) follows the stochastic process (9). Based on (9), (52), and the change of variable which leads to the equivalent aggregator (48), the lifetime utility follows the backward stochastic differential equation (49).
Duffie and Lions (1992) assume that \(V_t=V(C_t,x_t)\), where \(x\) is included in the lifetime utility function because it is a driving force of consumption.
By (49), we get the differential equation
Note that \(V(C,x)=(1/\alpha )C^\alpha v(x)\).
The differential equation (54) is equivalent to
Use the change of variable (51).
and
Substitute these results into differential equation (57) to get
After the change of variable leads to the ODE (27) its coefficients are
-
(i)
\(A_0 =(\rho -\alpha )/\rho \),
-
(ii)
\(B =\epsilon b\sigma _0\varphi _e\),
-
(iii)
\(B_0=-2\epsilon \alpha \sigma _0\rho _{xc}\),
-
(iv)
\(B_1=2\epsilon ^2a\kappa /(a+1), B_2=2\epsilon ^2\kappa /(a+1)\),
-
(v)
\(C_0=2\epsilon ^2a(\beta -\rho \bar{x})/(a+1)-\epsilon ^2\alpha \rho \sigma _0^2\),
-
(vi)
\(C_1=-2\epsilon ^3a\rho \sigma _0\varphi _e/(a+1)\),
-
(vii)
\(C_2=2\epsilon ^2(\beta -\rho \bar{x})/(a+1)\),
-
(viii)
\(C_3=-2\epsilon ^3\rho \sigma _0\varphi _e\),
-
(ix)
\(D_0=-2\epsilon ^2a\beta /(a+1)\), and
-
(x)
\(D_1=-2\epsilon ^2\beta /(a+1)\).
Following the procedure in Chen et al. (2010), the power series representations of \(g(x), g'(x)\), and \(g''(x)\) are substituted into (27). After equating the coefficients of the terms of degree \(n\), we find the recursive formula for \(g_k\), where \(k \ge 2\).
and if \(n \ge 1\), then
1.2 Derivation of Differential Equation (20) from Ai (2010)
Ai’s differential equation is (IA.3) in the appendix of Ai (2010).
Multiply the above equation by \(H(m)\).
To make it similar to (14), we introduce the change of variable
Then
and
The differential equation (64) becomes
This is the differential equation (20) when \(m = x + \bar{\theta }\).
Now introduce the change of variable \(m=\epsilon \sigma _m x+\bar{\theta }\) and set \(g(x)=h(m)\) so that the differential equation is in the form which is simulated.
Define the constants
So
1.3 Proof of Theorem 3.1
Define \(\tilde{g_n}=n^2L(g_n/g_0)\) for \(n \ge 1\), where \(L \ge 1\) is a constant to be determined later. For all \(n \ge 3\),
Lemma A.1
If \(a, b, c\), and \(d\) are integers such that \(a \ge 0, b \ge 0, a+c>0, b+d>0\), and \(c+d \ge 0\), then
where \(U_k=2[1+\ln (k+1)]/k\) for \(k=1,2,3,\ldots .\)
Proof
Note that \(\sum _{k=1}^n(1/k) \le 1+\ln (n+1)\) for \(n \ge 1\).
\(\square \)
Lemma A.2
Let \(B \ge 0\) be a real number. If \(b\) and \(d\) are integers such that \(b \ge 0, d \ge 0\), and \(b+d>0\), then
where \(U^B_k=[(1+2Be^B)+2Be^B\ln (k+1)]/k\) for \(k=1,2,3,\ldots .\)
Proof
By Lemma A.1, we have
\(\square \)
There exist a real number \(L \ge 1\) and an integer \(N \ge 3\) such that for all \(n \ge N\),
where
Pick a real number \(M_g \ge 1\) such that \(|\tilde{g}_n| \le M_g^n\) for \(1 \le n \le N+1\). Apply the following algorithm to construct a sequence \(\{G_n\}\) of nonnegative real numbers.
-
(i)
Use the recurrence relation (62) and \(g_0,\,g_1\) to calculate \(g_n\), where \(2 \le n \le N+1\).
-
(ii)
Calculate \(G_n=n^2L|g_n/g_0|\) for \(1 \le n \le N+1\).
-
(iii)
Calculate the remaining terms \(G_{n+2}\), with \(n \ge N\), by the recurrence relation:
Lemma A.3
Let \(M_g=\max \left\{ 1,\root n \of {n^2L|g_n/g_0|} \mid 1 \le n \le N+1\right\} \) and \(r_g=\epsilon \sigma _0\varphi _e/M_g\). For \(n \ge 1\),
Proof
Note that for any integer \(n \ge 3\), we have
and
The inequality follows from mathematical induction on \(n\) and the facts that \(M_g \ge 1\) and \(\mathcal B (n,L)<1\) for \(n \ge N\). \(\square \)
Applying the root test for convergence, the lifetime utility can be represented as a convergent power series in Theorem 3.1 is true. Suppose that \(|x| \le r_g\).
Suppose that \(|x| \leqslant \nu r_g\).
The proof is complete.
1.4 Derivation of the Stochastic Differential Equation for the State Price (44)
Given the lifetime utility of a representative investor, the stochastic process for the state price \(\Lambda _t\) can be found by using Duffie and Epstein (1992b) and Schroder and Skiadas (2003).
where \(d f_C(C_t, V_t)\) can be determined by using Ito’s Lemma. Then \(\Lambda _t\) can be computed by integrating (79).
where it is assumed that \(f_C(C_0, V_0)=\Lambda _0\).Footnote 31
The stochastic differential equation (44) follows from (79). Recall that
Then
and
Now take the partial derivatives of \(f_C(C,V)\) which will be used in the computation of \(d\Lambda \), and then evaluate using the functional form \(V(C,x)=C^\alpha v(x)\). The first order partial derivatives of \(f_C(C,V)\) are
The second order partial derivatives of \(f_C(C,V)\) are
We can apply Ito’s lemma to compute
Note that
The first and second partial derivatives of \(V\) are
By Ito’s Lemma, we get
By the stochastic processes (9) and (52), we get
Then (86) becomes
Substitute (87) into (83) to yield
Finally, substitute (91) and (92) into (79).
The differential equation (14) is used to remove \(g''(x_t)/g(x_t)\) from \(\mu _{\Lambda }(x_t)\).
Substitute this result into (93) to get a new expression for the instantaneous mean of \(d\Lambda _t/\Lambda _t\).
The rate of return for the risk-free bonds is determined by
This completes the derivation of the stochastic differential equation for the state price (44) and its mean (45).
1.5 Derivation of the Solution (43)
The equivalent differential equation in our model is Eq. (57).
Let the function be chosen to agree with Ai’s.
which is related to the wealth-consumption ratio. Find first order Taylor approximation of
Set
The first order approximation of (99) is
Substitute it back into the definition of \(z\).
Express (99) as
Set \(\kappa _1=1/y(0)\). In Ai (2010), he takes \(\kappa _1=\beta \) and \(\kappa _0=\kappa _1(1-\ln \kappa _1)\). Use (98) and (104) to yield
The differential equation (97) becomes
Following Ai (2010), we guess the solution to be of the form
Then
The differential equation (106) under this guess is
Set
If \(\sigma (x)=\sigma \) is constant, then
In this case, we have
So the initial conditions are
1.6 Solution to the Bansal and Yaron Model When \(\psi =1\)
To set the coefficients in (105), Ai uses the solution for the case when \(\psi = 1\). In this case, Ai uses
Let
Then
Recall that the differential equation (54) is
With the guess (115), we have
The differential equation becomes
Suppose that the differential equation has a solution of the form
Substituting it into the differential equation yields
Set
If \(\sigma (x)=\sigma \), is constant, then
This agrees with Ai (2010), since \(\kappa _0+\kappa _1\ln \beta =\beta \), when \(\kappa _1=\beta \).
1.7 Solution to Ai (2010) Under no Uncertainty
Consider the following first order linear differential equation for \(y=y(x)\)
where \(\nu , \zeta \) and \(\chi \) are real constants with
Note that the point \(x=0\) is regular singular for this equation. Here, we shall prove the following result for Eq. (125).
Theorem A.4
If \( \nu >0\), then Eq. (125) has the following general solution
and
where \(c\) is any real number. Furthermore, if \(\chi \ne 0\) then letting \(c=0\) we get the following particular solution \(y(x)=y_0(x)\)
and
Moreover, setting
makes the function \(y(x)\) defined by (129) and (130) continuous at \(x=0\).
Finally, setting
makes the function \(y(x)\) continuously differentiable at \(x=0\).
1.7.1 Solving Differential Equation (125)
Since equation (125) is singular at \(x=0\), we shall solve it for \(x>0\) and for \(x<0\) separately.
Solution for \(x>0\). Dividing both sides of (125) by \(x\) we write this equation in the normal form
Thus we find the integrating factor
Then multiplying both sides of (133) by the the integrating factor (134) we obtain the equation
which integrated gives
Thus, in this case the general solution of equation (125) is
where \(c\) is any real constant. Finally, setting \(c=0\) we obtain the following particular solutions.
Note, integral \(\int _0^x t^{\nu -1} e^{\zeta t}dt\) is finite for any \(x>0\) thanks to our assumption \(\nu >0\).
Solution for \(x<0\). Replacing \(x\) with \(-x\) changes our Eq. (125) for the function \(y=y(x), x<0\), into the following equation for the function \(u(x)=y(-x)\)
which has the normal form
Now, we observe that Eq. (137) can be obtained from Eq. (133) by replacing \(\zeta \) with \(-\zeta \). Thus, its general solution is obtained from (35) by replacing \(\zeta \) with \(-\zeta \). So, we get
and therefore
Furtheremore, making the change of variables \(t\mapsto -t\) gives
which is the general solution of Eq. (125) for \(x<0\). Finally, setting \(c=0\) gives
which is a particular solution of Eq. (125) for \(x<0\).
1.7.2 Proof of Conditions (39) and (132)
For \(x>0\) using the definition (129) and making the change of variables \(u=t/x\) we have
Now, we observe that as \(x\rightarrow 0^+\) the integrand \(u^{\nu -1} e^{\zeta x u}\) converges to \(u^{\nu -1}\). Therefore applying the dominated convergence theorem we get that
which is the desired limit. Similarly, for \(x<0\) using formula (130) we have
which goes to \({\chi }/{\nu }\) as \(x\rightarrow 0^-\).
This completes the proof of continuity condition (131).
Next, we prove condition (132). For \(x>0\) differentiating \(y(x)\) given by formula (129) gives
Now, letting \(x\rightarrow 0^+\) we see that the last term goes to zero and therefore we get
which gives the desired limit (132). Similarly working, for \(x<0\) we have
Now, proceeding as in the case \(x>0\) we obtain the desired limit (132). This completes the proof of the Theorem A.4.
Remark
Also, Eq. (125) can be solved by letting \(y(x)=|x|^ru(x)\) and reduce it to a simpler equation for \(u\). Finally, Eq. (125) can be solved by using power series. Since \(x=0\) is a regular singular point we look for solutions to Eq. (125) of the form
where \(c_0\ne 0\). We do this first for \(x>0\) and then for \(x<0\). In both case we substitute the above series into Eq. (125) and derive an equation for \(r\) and the corresponding recurrence relation for the coefficients \(c_n\).
1.8 The Equity Premium and its Variance from Ai (2010)
Considering wealth as an asset which pays the consumption level each period, its value is given by
Applying Ito’s lemma the change in wealth is given by
By (30) of Ai (2010) the stochastic process for \(x\) is
By (37) of Ai the stochastic process for consumption is
Here \(\mu _C(x)\) is an increasing function of \(x\).
Using (26) for the covariance between wealth and the long run risk variable, the variance of the return on wealth and its equity premium is given by
1.9 The Equity Premium on Wealth from Ai (2010)
We can calculate the return on wealth as on p. 1346 of Ai (2010). We already have the risk free interest rate
where
Because we have an endowment economy, the wealth is a claim on the consumption stream so that the changes in wealth and consumption are identical.
Following Cochrane (2005) Eq. (1.36) the expected return on an asset relative to the risk free rate is given by the covariance between the change in asset’s price, \(P_t\), and the pricing kernel.
Since wealth is the price of the claim on consumption, as in (34) of Duffie and Epstein (1992b), its change is given by (143), while the change in the pricing kernel is given by (142). As a result, the risk premium on aggregate wealth is
This corresponds to (48) in Ai’s case but with endowment model for consumption.
Rights and permissions
About this article
Cite this article
Chen, Y., Cosimano, T.F., Himonas, A.A. et al. An Analytic Approach for Stochastic Differential Utility for Endowment and Production Economies. Comput Econ 44, 397–443 (2014). https://doi.org/10.1007/s10614-013-9397-4
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10614-013-9397-4