OLG Life Cycle Model Transition Paths: Alternate Model Forecast Method

Abstract

The overlapping generations (OLG) model is an important framework for analyzing any type of question in which age cohorts are affected differently by exogenous shocks. However, as the dimensions and degree of heterogeneity in these models increase, the computational burden imposed by rational expectations solution methods for nonstationary equilibrium transition paths increases exponentially. As a result, these models have been limited in the scope of their use to a restricted set of applications and a relatively small group of researchers. In addition to providing a detailed description of the benchmark rational expectations computational method, this paper presents an alternative method for solving for equilibrium transition paths in OLG life cycle models that is new to this class of model. The key insight is that even naïve limited information forecasts within the model produce aggregate time series similar to full information rational expectations time series as long as the naïve forecasts are updated each period. We find that our alternate model forecast method reduces computation time by 85 percent, and the approximation error is small.

Appendices

Appendix 1: Description of Differences Between OLG and Infinite Horizon Models

In this section, we describe the difference between the OLG model with idiosyncratic uncertainty and no aggregate uncertainty and its infinite horizon counterpart. Chatterjee (1994) and Krusell and Ríos-Rull (1999) show that infinite horizon models with standard period utility functions and only idiosyncratic uncertainty with no aggregate uncertainty exhibit an aggregation theorem. That is, the law of motion for the aggregate capital stock, which is a function of the entire distribution of capital among idiosyncratically heterogeneous households, can be derived as a function solely of aggregate variables in the current information set.

This means that the infinite horizon analogue of our OLG model with idiosyncratic uncertainty has no need of adaptive expectations. Household beliefs about future interest rates and wages in the rational expectations infinite horizon model are simply a function of the aggregate capital stock in the current period. No alternate model forecast rule can be used here because the exact rational expectations law of motion can already be calculated with limited information.

For this reason, we only use our AMF approximation solution method for the OLG model with idiosyncratic uncertainty. The aggregation theorem does not hold in the OLG model with only idiosyncratic uncertainty, because each agent type within each generation cannot perfectly smooth consumption over its lifetime. This is the reason that the fundamental welfare theorems of economics do not hold in OLG models, in general. It is also the reason that the aggregation theorem does not hold, and forecasts of the aggregate capital stock remain a function of the entire distribution of capital rather than just a summary statistic (the aggregate capital stock) in the current information set.

For heterogeneous agent models with both idiosyncratic and aggregate uncertainty, other solution methods have been developed, such as Krusell and Smith (1998), Krueger and Kubler (2004), and Judd et al. (2011). But the OLG model with only idiosyncratic uncertainty remains important for answering many economic questions. Therefore, solution methods for this class of models are relevant.

Appendix 2: Computational Algorithm for Steady-State Equilibrium

The computation of the steady-state equilibrium described in Definition 1 requires the following steps. The MatLab code for this steady-state computation is available upon request.

• 1. Calibrate the exogenous parameters of the model $S, \beta , \sigma , \alpha , A, \delta$, the computation parameter $\rho$, the distribution of the ability shock $f_s(e)$, and the inelastic labor supply function as a function of age $n(s)$.

  • We chose the parameter values $[S,\beta ,\sigma ,\alpha ,\rho ,A,\delta ]=[60,0.96,3,0.35, 0.2,1,0]$.

  • The inelastic labor supply function of age $n(s)$ was calibrated to match the average labor supply by age reported in the CPS monthly survey, where the maximum average hours worked is normalized to unity.

    $$\begin{aligned} n(s) = {\left\{ \begin{array}{ll} \left[0.87,0.89,0.91,0.93,0.96,0.98\right] \quad \text{ for}\quad 1\le s\le 6 \\ 1 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,\text{ for}\quad 7\le s\le 40 \\ \bigl [0.95,0.89,0.84,0.79,0.73,0.68,0.63,0.57,0.52, \ldots \\ \quad 0.47,0.40,0.33,0.26,0.19,0.12,0.11,0.11,0.10,0.10,0.09\bigr ] \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,\,\,\text{ for}\quad 41\le s\le 60 \end{array}\right.} \end{aligned}$$

  • The discretized approximation of the ability shock is the following seven ability types $e_{s,t} \in \{0.1,0.5,0.8,1.0,1.2,1.5,1.9\}$ with a mass function $f_s(e) = \{0.04,0.09,0.20,0.34,0.20,0.09,0.04\}$ for all $s$. We could have just as easily made the probability distribution be conditional on $s$ but that does not increase the computation time.

• 2. Discretize the space of possible wealth levels into $B$ possible values such that $b\in \{b_1,b_2, \ldots b_B\}$, where $b_1=0$ and $b_B<\infty$.

  • We chose a discretized support of $B=350$ equally spaced points between $b_1=0$ and $b_B=15$.

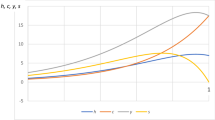
  • Note that we have to impose a savings maximum constraint due to there being some states in which the household wants to save more than their current wealth level. Setting $b_{max}=15$ is high enough to minimize the number of states in which the upper bound binds. The smoothness of Fig. 1 at its peak shows that the upper bound creates a minimal distortion.

• 3. Choose an arbitrary initial guess for the steady-state distribution of wealth $\bar{\Gamma }_0 = \bar{\gamma }_0(s,e,b)$ such that $\bar{\gamma }_0(s,e,b)\in [0,1]$ and $\sum _s\sum _e\sum _b\bar{\gamma }_0(s,e,b)=1$.

  • Our initial guess was simply the distribution across abilities by age spread across each possible wealth level $\gamma _0(s,e,b) = f_s(e)/\left[(S-1)B\right]$ for all $s, e$, and $b$.

• 4. Use $\bar{\Gamma }_0$ to calculate steady-state values for $\bar{K}_0, \bar{Y}_0, \bar{r}_0$ and $\bar{w}_0$ using Eqs. (2.11), (2.13), (2.14), (2.15), and (2.16).

• 5. Taking $\bar{r}_0$ and $\bar{w}_0$ as given each period, solve for the optimal policy rule of each agent $b^{\prime }=\phi (s,e,b|\Omega )$ by backward induction.

• 6. Use $b^{\prime }=\phi (s,e,b|\Omega )$ and $\bar{\Gamma }_0$ to calculate the distribution of wealth in the next period $\bar{\Gamma }^{\prime }_0$.

• 7. Generate a new guess for the steady-state distribution of wealth $\bar{\Gamma }_1$ as a convex combination of the two distributions from the previous step $\bar{\Gamma }_1 = \rho \bar{\Gamma }^{\prime }_0 + (1-\rho )\bar{\Gamma }_0$, where $\rho \in (0,1)$.

• 8. Repeat steps (4) through (7) until the distance between $\bar{\Gamma }_i$ and $\bar{\Gamma }^{\prime }_i$ is arbitrarily close to zero, where $i$ is the index of the iteration number. Let $|\cdot |$ be the sup norm and let $\varepsilon >0$ be some scalar arbitrarily close to zero. Then the steady state $\bar{\Gamma }$ is found when $\left|\bar{\Gamma }_i - \bar{\Gamma }^{\prime }_i\right| < \varepsilon$.

In our example, the computation of the steady-state equilibrium took 3 h, 5 min, and 25 s. Figure 1 shows the steady-state aggregate capital stock $\bar{K}$ and the average wealth $\bar{b}_s$ as a function of age $s$.

Appendix 3: Computational Algorithm for TPI Transition Path

The computation of the TPI transition path described in Sect. 3.1 requires the following steps. The MatLab code for this TPI transition path computation is available upon request.

• 1. Using the parameterization from the steady-state computation, and choose the value for $T$ at which the non-steady-state transition path should have converged to the steady state. We used $T=60$.

• 2. Choose an initial state of the aggregate capital stock $K_1$. Choose an initial distribution of capital $\Gamma _1$ consistent with $K_1$ according to (2.16).

  • We chose an initial capital stock of $K_1=5.45$, which is consistent with a simple initial distribution of wealth—the distribution of ability by age spread across all possible wealth levels $\gamma _1(s,e,b)= f_s(e)/\left[(S-1)B\right]$ for all $s, e$, and $b$.

• 3. Conjecture a transition path for the aggregate capital stock $\mathbf{K}^i=\{K^i_t\}_{t=1}^\infty$ where the only requirements are that $K^i_1=K_1$ is your initial state and that $K^i_t=\bar{K}$ for all $t\ge T$. The conjectured transition path of the aggregate capital stock $\mathbf{K}^i$, along with the exogenous aggregate labor supply from (2.15), implies specific transition paths for the real wage $\mathbf{w}^i=\{w^i_t\}_{t=1}^\infty$ and the real interest rate $\mathbf{r}^i=\{r^i_t\}_{t=1}^\infty$ through expressions (2.11), (2.13), and (2.14).

• 4. With the conjectured transition paths $\mathbf{w}^i$ and $\mathbf{r}^i$, one can solve for the lifetime policy functions of each household alive at time $t=1$ by backward induction using the Euler equations of the form (3.3). Rows 1 through 5 of Table 2 illustrate this process.

  • The first line is solving for the solution of the individual who is age $S-1$ at time $t=1$ obtaining $b_{2,2}=\phi _1(S-1,e,b)$ from Eq. (3.1).

  • Each subsequent row from Table 2 represents the solution of the lifetime savings policy functions of an individual with more years remaining in their life at time $t=1$, down the the person who is age $s=1$ at time $t=1$ and has the entire set of $S-1$ policy functions characterized by (3.3).

• 5. In similar fashion to step (4), solve for the lifetime policy functions by backward induction for the age $s=1$ household at times $2\le t \le T$. In Table 2, this means solving for the policy functions in the last two rows down to the age $s=1$ household at time $t=T$.

• 6. Each column in Table 2 represents a complete set of policy functions for the corresponding period. Using the initial distribution of wealth $\Gamma _1$ and all the period $t=1$ policy functions $\phi _1(s,e,b)$ for the households alive at time $t=1$, the next period distribution of wealth $\Gamma _2$ and the corresponding aggregate capital stock $K^{i^{\prime }}_2$ can be calculated. Consecutively repeat this procedure for each time period (column of Table 2) until a new transition path for the aggregate capital stock has been computed $\mathbf{K}^{i^{\prime }}=\{K^{i^{\prime }}_t\}_{t=1}^T$.

• 7. Generate a new guess for the transition path of the aggregate capital stock $\mathbf{K}^{i+1}$ as a convex combination of the initially conjectured transition path $\mathbf{K}^{i}$ and the newly generated transition path $\mathbf{K}^{i^{\prime }}$.

  $$\begin{aligned} \mathbf{K}^{i+1} = \rho \mathbf{K}^{i^{\prime }} + (1-\rho )\mathbf{K}^i \quad \text{ where}\quad \rho \in (0,1) \end{aligned}$$

• 8. Repeat steps (4) through (7) until the distance between $\mathbf{K}^{i^{\prime }}$ and $\mathbf{K}^{i}$ is arbitrarily close to zero, where $i$ is the index of the iteration number. Let $|\cdot |$ be the sup norm and let $\varepsilon >0$ be some scalar arbitrarily close to zero. Then the rational expectations equilibrium transition path of the economy is found when when $\left|\mathbf{K}^{i^{\prime }} - \mathbf{K}^i\right| < \varepsilon$.

Table 2 TPI backward induction policy function solution method

In our example, the computation of the TPI transition path took 31 h, 59 min, and 39 s. Figure 2 shows the transition path of the aggregate capital stock from its initial state at $K_1$ to the steady state $\bar{K}$. The aggregate capital stock arrived at its steady state in about 60 periods.

Appendix 4: Computational Algorithm for AMF Transition Path

The computation of the AMF transition path described in Definition 3 requires the following steps. The MatLab code for this AMF transition path computation is available upon request.

• 1. Conjecture an alternative model forecast method $\Omega _a.$

  • We use a linear trend from the current state $K_t$ to the steady state $\bar{K}.$

    $$\begin{aligned} K_{t+1} = \Omega _a\left(K_t\right) \Rightarrow K_{t+1} = K_t + \frac{\bar{K}-K_t}{T-t} \end{aligned}$$

    (3.7)

  • Our specific alternative model is written as a law of motion for the aggregate capital stock, but it implies a law of motion for the average wealth. From (2.16) we know that aggregate capital $K_t$ is just a function of the average wealth.

    $$\begin{aligned} K_t = \frac{S-1}{S}\bar{b}_t \end{aligned}$$

    (8.1)

    So the alternative model $\Omega _a$ implies a similar linear law of motion for the moments by combining (3.7) with (4.1).

    $$\begin{aligned} \bar{b}_{t+1} = \Omega _a\left(\bar{b}_t\right) \Rightarrow \bar{b}_{t+1} = \bar{b}_t + \frac{\bar{b}_{ss}-\bar{b}_t}{T-t} \end{aligned}$$

    (8.2)

• 2. Solve the lifetime savings policy functions $\phi (s,e,b)$ for each agent alive at time $t$ by backward induction using the alternate model forecast method (3.6) to obtain the forecasted series of prices over those lifetimes. (This step is the same as step 4 in Appendix 4.)

• 3. Use the complete set of policy functions for the current period in order to calculate the next period’s distribution of wealth $\Gamma _{t+1}$ and the corresponding aggregate capital stock $K_{t+1}$.

• 4. Repeat this process until the distribution of wealth $\Gamma _T$ and the aggregate capital stock $K_T$ have been computed for time $T.$ Make sure that $\Gamma _T = \bar{\Gamma }$ and $K_T = \bar{K}$.

In our example, the computation of the AMF transition path took 4 h, 50 min, and 9 s. Figure 3 shows the transition path of the aggregate capital stock from its initial state at $K_1$ to the steady state $\bar{K}$ as compared to the benchmark TPI transition path. The aggregate capital stock arrived at its steady state in about 60 periods.