Advance voting and political competition

Abstract

This paper appears to be the first to analyse political campaign incentives when the electorate vote at different moments before Election Day, a phenomenon known as early or advance voting. Many jurisdictions accommodate such voting by accepting mail-in ballots or by opening polling places before Election Day. Since politicians can thereby add campaign promises while citizens vote, they have an incentive to add promises valued by late-voting segments as Election Day approaches. This implies that early-voting segments of the electorate will pay higher taxes and receive lower transfers than had been announced when they voted. Late-voting segments benefit.

1 Introduction

Early voting is on the rise. Having been a peripheral activity in most advanced countries for the lion’s share of the twentieth century, early voting has in recent years accounted for around one-third of the votes in US elections (Biggers & Hanmer, 2015). The same trends can also be observed internationally, in countries ranging from Norway (where the share reached 30.2 per cent in the parliamentary election of 2013 according to Statistics Norway) to New Zealand (29.8 per cent in the general election of 2014, as reported by the New Zealand Electoral Commission).

Arranged in a variety of different ways across jurisdictions, voting prior to a scheduled election day is also known as advance voting, advance polling, pre-poll voting, or convenience voting. In jurisdictions with two or more of these terms in use, their referents may differ in details, but in this paper they will be treated as synonyms. Where sparseness of population necessitates remote ballot boxes, early votes may be cast a few days in advance since bad weather can cause voting to be difficult on the proper day, as happens in many coastal islands of the Republic of Ireland. Many other jurisdictions accept ballots starting much earlier, often well over a month ahead of Election Day.

This article deals with how the increased utilization of advance voting changes candidates’ incentives vis-á-vis their policy formulations during an election campaign. If certain identifiable (to politicians) segments of the electorate have already voted while time remains to try to attract new voters, candidates for public office have an incentive to build their platforms in a way to appeal to early voters first and successively add to their platform policies (including ways of financing them) which appeal to later voters as Election Day comes nearer.¹ It appears as though no article has hitherto explored these incentives, or even noted them.²

A variety of modelling approaches could yield this basic outcome but for simplicity the present paper focuses on imperfect voter recall; voters do not perfectly remember campaign platforms from past elections, nor their incarnations during a current campaign, but are forward-looking in the sense that they make inferences of future platform alterations from comparisons between current observations and memory. Beyond simplicity, this set-up has a number of advantages. It goes well with the traditional ‘rational-ignorance’ result (Becker, 1958; Downs, 1957), because if knowledge does not ‘pay’ then nor does recall. Imperfect recall would be more difficult to justify for higher-stakes situations, but for individual voters the stakes are virtually always low.

It may be useful to think of candidates as making promises over time with each promise having some probability of being honoured. Provided that promises made after early voters have cast their ballots are no less likely to be honoured than other promises, the finished platform will be one that relatively favours the later voters. This is because the later promises can always cancel earlier ones, as when general tax increases to finance transfers directed mainly at later-voting groups cancel out some of the benefits of some other policy which were previously promised to earlier voters. With large enough transfers and tax increases, any ‘pork’ promised to earlier-voting segments of the population can be effectively cancelled, even when both pork and transfers are implemented. Later-voting segments will therefore benefit at the expense of others provided that some positive fraction of campaign promises are kept.

Notice that individual voters cannot alter the timing of votes cast by their demographic segment by voting later, so any slight advantage to advance voting for the individual voter vitiates segment-wide coordination on Election-Day voting. For the same reason, individual voters have no incentive to improve their memory. Studies of voter recall also show that a large fraction of the electorate even fail to accurately identify the candidate or party for whom they voted in the most recent election (surely an easier task than is remembering particulars about their promises), underscoring the realism of the imperfect-recall assumption.³

A further factor that favours the imperfect-recall approach is that it allows a clear link between campaign promises and implemented policy since only past events are imperfectly recalled and post-election congruence between current policy and campaign programme (i.e. all the promises made by Election Day) may always be ascertained, thereby pressuring victorious politicians to at least attempt to keep their campaign promises. If voters had significantly greater cognitive shortcomings, policy would be relatively easier to impact through non-voting activities such as lobbying by pressure groups (Becker, 1983; Olson, 1965 – of course, pressure groups could push for (against) early voting because they expect to benefit (suffer) from it). On the other hand, mentally sharper voters will more easily detect platform alterations. Section 3 illustrates that other approaches can also work for analysing platform drift, but imperfect recall does provide an effective and realistic middle ground.

The rest of this paper proceeds as follows. Section 2 establishes that changes to policy proposals during an election will favour later voters as lfaong as the costs of making such changes are not prohibitively high (i.e. as long as voter recall is sufficiently imperfect). It also shows that the introduction of advance voting may nevertheless benefit earlier voters if advance voting attracts disproportionately more new voters who share preferences with previous early voters and the costs of changing policy promises are high enough. As the aforementioned literature on turnout and advance voting makes clear, this second proposition is empirically unlikely to apply, so that moves towards increased convenience voting are indeed apt to benefit Election Day voters.

Section 3 briefly sketches and compares alternative modelling set-ups, mainly taking cues from the aforementioned treatments of deviations from positions taken in party primaries when campaigning in a general election. The alternative set-ups are only roughly sketched, but the discussion illustrates how imperfect recall, though useful, is not necessary to establish incentives to alter platforms so that later voters gain during an election. Section 4 discusses the applicability of the basic model, using data on petrol taxes across US states for illustration, as petrol taxes are likely to divide rural (early) and urban (late) voters. Section 5 concludes.

2 A simple model

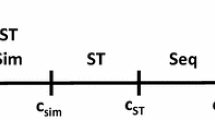
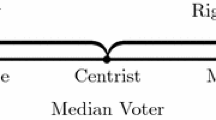
This section presents what is essentially an extended median-voter model (Black, 1948; Hotelling, 1929) in which $n$ citizens are located along a one-dimensional policy space and decide for whom of two candidates to vote. These two candidates position themselves on a policy axis with the purpose of gaining more votes than does their rival. The extension is that citizens belong to two different groups, early and late voters, and that these groups differ in average preferences over which point in policy space is optimal. This captures the facts that identifiable segments of the electorate tend to vote at different times due to different incentives to do so (e.g. polling-station proximity or difficulties getting out), and that identifiable segments of the electorate are apt to want different things. For simplicity, it is assumed that each type votes at one discrete time. Apart from this time segmentation, the analysis is exactly analogous to that of the Median Voter Theorem.

Voters have political preference characteristics according to $\alpha_{s}^{i}$, where $s$ refers to the stage at which the individual votes, i.e. either ‘early’ or ‘late’, and $i$ indexes voters. There are $k$ early voters and $l$ late ones. By the standard definition of single-crossing preferences (e.g. Persson & Guido, 2002, p. 23), if a voter with a given value of $\alpha_{s}^{i}$ prefers a point on the policy line $x$ to another point $y$, it implies that all voters with a preference parameter greater than or equal to $\alpha_{s}^{i}$ share the same preference. When this holds, the Median Voter Theorem can be applied. Voters with imperfect recall remember fractions of candidates’ prior platforms and make inferences about candidates based on their memories and the current platforms. Such recollections may stem from a previous election where a platform was amended after one’s (early) ballot had been cast.

A voter that observes a change in a politician’s platform may distrust that politician and infer that the less preferable platform is the one to be implemented. The rationale for this inference is that voters punish parties whose platforms they cannot trust. Voters may certainly behave in differently. The important point is that this is a conservative assumption on voter behaviour with respect to the present model, imposing a large cost on platform changes between elections; to the extent that voters may not punish candidates who shift their policy platforms, it will only strengthen the importance of the present model by encouraging shifting.

A voter $i$ recalls a past policy proposal with probability $p \in \left[ {0, 1} \right]$ and chooses candidate $A$ if $A$’s platform $\alpha^{A}$ is such that

$$\max \left\{ {\begin{array}{*{20}c} {\left( {\alpha_{t - 1}^{A} - \alpha^{i} } \right)^{2} {\text{ with probability }}p{ }} \\ {0{\text{ with probability }}1 - p} \\ \end{array} ,{ }\left( {\alpha_{t}^{A} - \alpha^{i} } \right)^{2} } \right\}$$

is lower than that of any other candidate (vote abstention is disregarded here, but could be incorporated by positing a maximum value beyond which no candidate gets a vote). The subscripts $t$ and $t - 1$ indicate the current time and the past, respectively. When voters are more likely to remember past platform incarnations, there is greater pressure on candidates not to deviate from them since the particular policy recalled by a voter might differ from the current platform.

Let $\alpha_{k}^{median}$ be the median preference among the $k$ early voters and $\alpha_{l}^{median}$ the corresponding preference among the $l$ late ones. The median preference among the entire set of voters may be denoted by $\alpha_{k + l}^{median}$, so that whenever $\alpha_{k}^{median} \ne \alpha_{l}^{median}$, $\alpha_{k + l}^{median}$ is closer to $\alpha_{k}^{median}$ the more strongly early voters outnumber late ones, and closer to $\alpha_{l}^{median}$ the more strongly late voters outnumber early ones. If early voters’ preferences are completely ignored as political candidates compete for the late voters, policy in the jurisdiction is fully determined by $\alpha_{l}^{median}$, so that the more distant are $\alpha_{l}^{median}$ from $\alpha_{k + l}^{median}$ and the smaller is $l$, the smaller is the minority whose preferences swing the election.

Apart from the risk of backfiring due to voter recall, incorporating time into the Median Voter Theorem also brings up costs since candidates must pay careful attention to timing and to which groups have already voted. Thus, platforms may not in the general case change completely to reflect the median preferences of the section of the electorate who vote late. In the presence of such ‘shifting costs’, the relative magnitudes of $l$ and $k$ will be important, since the candidates cannot hope to reach the median preference of both. The classic Median Voter Theorem is a special case of the present model when shifting costs are prohibitively large, since in this case candidates may only position themselves once to attempt to attract a majority of the votes.

Candidates choose $\alpha_{k}$ and $\alpha_{l}$ and derive utility purely from electoral success. If a $p$ is $0.2$, say, and a current platform has twenty per cent different material from an old one, voter $i$ will assume the less favourable one is to be implemented with a probability of four per cent ($0.2 \times 0.2$). Notice, however, that voters in the targeted electoral segment will have a higher $p$ than this, since the platform is changed precisely with the intention of attracting them. At this point, the candidate finds it worthwhile to amend his current platform further if the expected number of lost votes is lower than the expected number of gained ones, where the gain depends on closeness to the median later voter relative to the position of one’s opponent.

More generally, the marginal gain from a tiny amendment to one’s platform is the gross fraction $f$ of the late voters $l$ that one thereby attracts. The marginal cost is a function of $p$ and the fraction of the platform that has been amended, $\Delta \alpha$.. Consequently, as long as $\alpha^{A} \ne \alpha_{l}^{median} \ne \alpha_{k}^{median}$, Candidate A alters his platform if $f \times l > c\left( {p, \Delta \alpha^{A} , \mathop \sum \limits_{t = 0}^{\infty } \delta^{t + 1} k + \delta^{t} l; \Delta \alpha^{ - A} } \right)$, where $c\left( \cdot \right)$ is the cost function which depends positively on the recall probability, the magnitude of the platform change, and the losses of votes in the present election from late voters as well as discounted (captured by $\delta$) future losses of both early and late voters. Higher values of the non-choice variable $\Delta \alpha^{ - A}$ (changes in opponents’ platforms) lower $c$.

A number of things are immediately clear from this expression. Firstly, regardless of prior policy positions, sufficiently low values of $p$ imply that platform alterations will pay. In addition, the fewer late voters there are, the less likely a candidate is to touch his platform. If the candidates initially have the same off-median voter platform, $f$ means more voters than otherwise. Importantly, since voters choose between two candidates, a candidate may alter his platform with a greater probability of impunity if his opponent has also altered his: $\Delta \alpha^{A}$ and $\Delta \alpha^{ - A}$ are complements. To make at least a slight alteration to one’s platform is therefore almost surely going to be in a candidate’s interest as long as $p$ is not too high.

A practical formula for the winning policy platform in the present context is therefore given by

$$\left( {1 - c^{{\frac{k}{l + k}}} } \right)\alpha_{l}^{median} + c^{{\frac{k}{l + k}}} \alpha_{k + l}^{median}.$$

The cost of shifting $c\left( {p, \Delta \alpha^{A} , \mathop \sum \limits_{t = 0}^{\infty } \delta^{t + 1} k + \delta^{t} l; \Delta \alpha^{\neg A} } \right)$ is here written to $c \in \left[ {0, 1} \right]$ and is raised to the power of the fraction of voters who vote early, $\frac{k}{l + k}$, where $l$ and $k$ are both strictly positive. This cost function captures the essence of the treatment so far. The higher is the shifting cost, the more weight is given the full set of voters, early or late ($\frac{\partial }{\partial c} > 0$ when $\alpha_{k + l}^{median} > \alpha_{l}^{median}$, $\frac{\partial }{\partial c} \le 0$ when not). In the extreme case where $c = 0$, the wiing policy is $\alpha_{l}^{median}$ as long as there is but one late voter. In the opposite extreme, $c = 1$ implies that the median voter of both sets combined determines the election completely, no matter how many type-$l$ voters there are. This special case results in the traditional Median Voter Theorem.

For values of $c$ strictly between the extremes, a greater fraction of type-$k$ voters encourages positions away from $\alpha_{l}^{median}$ ($\frac{\partial }{\partial k} > 0$ when $\alpha_{k + l}^{median} > \alpha_{l}^{median}$, $\frac{\partial }{\partial k} \le 0$ when not). Intuitively, if platform alterations are not costless, $k$-types will be promised more the fewer $l$-types there are; if one candidate ignored this and positioned himself at a distance from $\alpha_{l}^{median}$ so that $\alpha_{l}^{median}$ is just reachable by $c$, the other candidate would gain an easy victory if he began the election by positioning himself a little bit closer to $\alpha_{k + l}^{median}$ than the first candidate, thus gaining most of the more numerous $k$-types and then moved towards $\alpha_{l}^{median}$ for the late stage of the campaign.

If an electoral reform introduces greater convenience for early voting, it may induce a rise in $k$ for two separate reasons; $\left( 1 \right)$ more Election-Day voters may decide to vote in advance, or $\left( 2 \right)$ previous abstainers may decide to vote. In either case, the share of voters who are of type $k$ will increase, but reason $\left( 1 \right)$ will affect both $\alpha_{l}^{median}$ and $\alpha_{k}^{median}$, while reason $\left( 2 \right)$ affects $\alpha_{k + l}^{median}$ and $\alpha_{k}^{median}$. If the additional type-$k$ voters are inclined to be more like the $k$-types before the reform, then $\left( 1 \right)$ implies that the distance between $\alpha_{l}^{median}$ and $\alpha_{k + l}^{median}$ increases, since the latter remains unchanged (no new voters), but only the $l$-types farthest away from the $k$-types remain late voters. When the reform attracts new voters, as in reason $\left( 2 \right)$, the distance between $\alpha_{k + l}^{median}$ and $\alpha_{k}^{median}$ is reduced when new and old late voters tend to be alike with respect to preferences.

Absent significant shifting costs, reason $\left( 1 \right)$ implies that policy comes to favour more ‘extreme’ $l$-types (in the sense that they are farther from $\alpha_{k + l}^{median}$ when only those voters most keen to vote late remain late voters), while $\left( 2 \right)$ does nothing since $\alpha_{l}^{median}$ remains unchanged. The more substantial are shifting costs, the more reason $\left( 2 \right)$ comes to favour early voters by making this group larger. Note that this is true even though advance voting always induces a shift of the victorious policy platform towards the late voters during the campaign; the outcome is still closer to the earlier voters when advance-voting reforms attract mainly new and early voters. Since reason $\left( 1 \right)$ leaves $\alpha_{k + l}^{median}$ unchanged, it would not imply the same advantage for early voters when $c\left( p \right)$ is significant.

The prediction is therefore that early voters can benefit when shifting costs are substantial and there is a major influx of former non-voters (that is, when the new early voters are not former late voters). However, in light of the empirical evidence on the backgrounds of early voters cited in Section 1, this effect is unlikely to be large since most estimates suggest no great influx. Consequently, early voting regimes will tend to favour the preferences of late voters.

3 Towards a general model of voting over time

It is evident from the foregoing discussion that imperfect voter recall is crucial for the present model, which would reduce to the traditional Median Voter Theorem under perfect recall, since any platform alteration would be made to attract later voters, who would remember the less palatable incarnations and infer that they are the true beliefs of the candidate. Thus, absent imperfect recall, whatever fraction of one’s platform is changed can only turn voters away.

However, imperfect recall is not a necessary assumption to capture the phenomenon that later-voting demographic segments gain from accommodating early voting. In her treatment of post-primary moderation effects, Agranov (2016) posits that voters do not observe a candidate’s full platform and that candidates may send signals of their platforms to voters at the primary and general-election stages. Voters are forward-looking and realize that candidates may alter their platforms between primaries and general elections. They trust signals more the more visible is a primary, since primary visibility makes later platform moderation more difficult.

In this set-up, imperfectly observed platforms make voters fail to realize that election promises are changing. Rather than positing imperfect recall, imperfect observability will yield equilibrium behaviour in which platforms shift to favour late voters closer to Election Day if candidates send strong enough signals and visibility is sufficiently low. Agranov shows that even if visibility is endogenous and may be increased by candidates in the primary, there will remain some pressure on winning candidates to moderate their positions between the primary and the general election.

By contrast, Hummel (2010) posits perfect observability and inference of unreliability from platform changes, but nevertheless reaches similar conclusions with respect to candidate drift towards more moderate positions. The problem with applying Hummel’s model to the present phenomenon is Hummel’s assumption that primary voters know that a drifting candidate will remain closer to their political positions than will a candidate from the other party’s primary. This is natural enough in Hummel’s setting (and in fact a somewhat weaker version of it actually suffices, as he notes on p. 1022n), but applied to competition during an election it is more difficult to justify.

The essential difficulty is that policy shifts would have to be no more displeasing to the voter when made by his preferred party than by the parties that do not get his vote. A potential replacement assumption would include different party ideologies such that one is known to favour earlier voters and the other to favour later ones. Something along these lines would be needed to model the present phenomena along the lines devised by Hummel to capture post-primary drift.

It should be emphasized that neither Agranov (2016), nor Hummel (2010) deals with platform drift during the period of voting, but the above should suffice to make it plausible that their modelling techniques could be fruitfully applied to the present phenomenon. Conversely, the present model based upon imperfect recall applies also to post-primary drift: voters who have cast their ballots in a primary may not remember months later all the positions that the politicians took in the primary. What is more, even if they infer that the less attractive positions are the politician’s actual ones, they are still likely to beat the positions taken at whatever time by his opponents.

Empirically, Agranov (2016) implies that signals of all the policies that transfer resources from early to late voters should be kept at a minimum until sufficiently many of the former group have voted. The challenge for this model is that when only observability and not recall is imperfect, voters will remember next election that signals appear in a time-biased way. Hummel (2010) implies that a candidate who favours early voters will do so less and less as Election Day becomes nigh, whereas a candidate who favours later voters will do so more and more. The challenge for this model is that parties are not in general distinguished by different attitudes to early and late voters.

In any event, candidates’ utterances would shift in a direction that is the same both in Hummel (2010) and Agranov (2016), as the one derived in this paper, although the present analysis may claim to be logically more seamless. Consequently, there are essentially three distinct models which can account for the phenomena of post-primary drift and incentives to change platforms during an election. In addition to the novelty of introducing the latter, two other contributions of the present paper are to widen – albeit with some challenges, as noted – the applicability of Agranov (2016) and Hummel (2010), as well as to provide an alternative to their approaches to post-primary drift.

4 Discussion

The article has so far been framed in terms to suggest that early and late voters are completely different with respect to policy preferences. Of course, both groups are realistically going to be very heterogeneous and likely to have overlapping policy preferences. Nonetheless, correlates in the literature on early voters suggest that certain distinct demographic groups are overrepresented among the ballots cast before Election Day. These groups are apt to share some preferences, and this section presents some statistics on early voting and a policy which early voters are prone to like.

To the extent that there is something to the present generalized median voter theorem, those groups that figure disproportionately prominently among the early voters should get less of what they want than do corresponding groups in jurisdictions that make lesser use of advance voting. To this end, Table 1 presents some panel data on early voting and policy changes in the USA. The policy is the state-level tax on petrol (or ‘gas’). The period is 1996–2012, 17 years in which early voting became widespread both in terms of accommodation by legislatures and in terms of utilization by the electorate.⁴

Table 1 Voting régimes and petrol taxes, 1996–2012

The significance of advance voting to the petrol tax is that people in the countryside have stronger incentives to vote early than do city-dwellers. Some of the correlates on this issue have already been cited in the introduction. For example, Dyck and Gimpel (2005) estimate that mail-in ballots are particularly popular among those living up to ten miles away from a polling station. In a study (which does not sample jurisdictions with advance voting), Haspel and Knotts (2005) find that distance to a polling station reduces the probability of voting generally.

Rural voters’ stronger incentives for advance voting are natural when considering the overall greater distances between individuals in the countryside. Absent an errand in the vicinity of the polling station on Election Day, mail-in ballots or early in-person voting become so much more convenient. Convenience and polling-station accessibility are also the top two reasons cited in Bliss’s (2010) survey of early voters. People in the countryside are also known to consume more petrol (e.g. Brownstone & Golob, 2009; Glaeser & Kahn, 2010), which is surely also due to greater distances outwith cities.

The states of Colorado, Oregon, and Washington are not sampled because they have largely done away with polling stations altogether (including them would yield results that are statistically indistinguishable from those in Table 1). Most voters there must therefore vote by post. It would seem that the rural population is still apt to vote earlier on account of living farther away from a post box, but for the sake of cleanliness the states are nevertheless not sampled. The state of Nebraska is not in the regressions (Panel (b)) in columns (3) to (6) because its unicameral and nonpartisan legislature precludes controls on the party in power. Among the other states, twelve allowed early voting at the start of the period. Of the 34 that did not, 18 allowed it at the period’s end.

There are three basic kinds of advance voting applicable to the sampled years: VBM (vote-by-mail), in which voters fill out their ballots and send them to the voting administration by post; EIP (early in-person voting), in which a polling station is set up that takes early votes; and no-excuse absentee voting, which is like VBM except that voters must generally request an absentee ballot (though they need not give an excuse). Apart from the excluded states, only two (Alaska and California) made use of VBM as a method of advance voting during the sampled period. Thus the table reports results only for the three methods together and for EIP and no-excuse absentee voting independently.

Panel (a) of Table 1 treats all forms of early voting as one category and presents summary statistics for changes in the petrol tax. The mean petrol tax changes are consistent with the hypothesis that politicians take advantage of early voters. Panel (b) shows that each day of advance voting is associated with an increase in the petrol tax by about three per cent of a cent. Thus, extending the period of early voting by 10 days would be associated with a 0.3 cent increase in the petrol tax per year. The correlations are statistically significant at very high levels; the t-statistics are almost always well above eight for the early voting measures. Column (4) interacts Fraction rural population with days of any early voting. Its positive sign indicates that, although more people in the countryside should strengthen support for low petrol taxes, these people’s tendency to vote early turns their relative advantage in numbers into a liability as there are more resources to transfer. Consistent with the studies showing a small or no effect of early voting on turnout, accommodating the rural (early) population cannot overturn the incentives to favour later voters.

There is a wealth of other potential sources of evidence that can also inform the present time-augmented median voter model. For instance, online campaigning is often likely to reach fewer elderly and rural individuals and should therefore relate straightforwardly to the present analysis. Online campaigning can also be targeted to specific voters far more easily than can traditional campaigns by using a person’s browsing history. Also interesting would be regional analyses of where electioneering takes place, as well as newspaper word frequencies to detect when politicians talk about what.

In addition to the above correlations, some qualitative evidence consistent with the present argument is that parties whose supporters make greater use of early voting, or whose values are more in tune with those of late voters will tend to favour advance voting whereas other parties will not. In the US, Blacks and Hispanics are more inclined to vote for the Democrats as well as to vote early, while the values of the Democratic Party are commonly seen to be more urban than rural. From this perspective, it makes sense that Democrats tend to be stronger proponents than Republicans of advance voting.

5 Conclusion

The foregoing discussion introduces a simple generalization of the median voter model to take into account the fact that persons’ voting early will incentivize politicians to promise more to those voting later as Election Day approaches. The outcome is quantitatively sensitive to the costs of making such policy adjustments. It is also qualitatively sensitive to the assumption of imperfect voter recall, although treatments of post-primary platform drift suggest alternative modelling frameworks which render unnecessary the assumption of imperfect recall.

Apart from being the first to analyse (and indeed even notice) the incentives for politicians to amend their platforms during the course of an election, this paper also provides a different way of modelling post-primary drift by imperfect recall. Although extant models of post-primary drift likewise apply to advance voting, they do so only at the cost of certain additional and sometimes quite challenging assumptions.

Empirical associations between advance voting and policy are consistent with the predictions of the paper. It should be emphasized that the practice of advance voting is still in its infancy and this paper’s petrol-tax illustration is but one of many potential policy consequences which may follow from more applied work. Wherever certain segments of the population may be identified as predominantly early voters, office seekers are incentivized to trick them.