Constitutional monarchy as power sharing

Abstract

In the transition to democracy some autocracies transformed to republics while others evolved to constitutional monarchies. The paper inquires how constitutional monarchy is established. It models a hereditary king and a liberal challenger who coexist over a succession of periods and fight for power which brings office rents and the right to decide one’s preferred policy. The outcome of the confrontation is uncertain and may vary from period to period. If the king wins, he establishes absolute monarchy, but if the liberal wins he establishes a republic. Instead of fighting they may agree on a constitutional monarchy and share office rents and policy making responsibilities. Whether constitutional monarchy is agreed depends on the marginal utilities from rents and policy preferences of the two actors, the sizes of the benefits from rents and policy, the rates by which they discount the future, and the probabilities of winning office. The contemporary European constitutional monarch as a ceremonial head of state who reigns but does not govern arises as a special case of the general model.

1 Introduction

Constitutional monarchy is a “system of government in which a monarch shares power with a constitutionally organized government. The monarch may be the de facto head of state or a purely ceremonial leader. The constitution allocates the rest of the government’s power to the legislature and judiciary.”¹ The question of why some democratic countries adopted constitutional monarchy rather than republic, has received only scant attention in political economy. Scholars have inquired the factors which led to democratization, but not whether the democracy which has emerged is headed by a hereditary king serving for life or an elected president serving for a limited term. The leading theories of the transition from autocracy to democracy equate autocratic rule to policy making by a privileged and wealthy elite, and democracy with government chosen in competitive elections. They focus on how and why the disenfranchised poorer classes of the population obtain the right to vote, but they leave unexplored the question of why the office of the head of the state may remain in the hands of a hereditary king. The purpose of this paper is to fill this gap.

Building on earlier work by Congleton (2011), who introduced the king as an explicit player in the democratic transition, the present work considers constitutional monarchy as a form of power sharing between the king and a liberal challenger to royal authority. The king and the liberal coexist over a succession of discrete periods. In each period one of the two governs. Governing confers two broad benefits. First, office rents, that is, monetary rewards, perks, patronage, glory, and personal satisfaction associated with occupying a public post; second, the right to pursue one’s favourite policy. When the king is in power, he governs as an absolute monarch²; he takes all office rents and chooses his preferred policy. If the liberal is in control, he abolishes the monarchy and introduces a republic³ where he takes all office rents and implements his most preferred policy. Who governs in each period is uncertain as the present winner of the conflict for power may retain or lose power in the future. Under constitutional monarchy the king and the liberal (a) share the rents from office and (b) implement a policy which combines their different policy preferences. Both the king and the liberal will choose the compromise solution of constitutional monarchy when each one of them derives a larger benefit than the product of the benefit conferred by his preferred pure form of government and the probability of success.

The paper explores whether there are values of the rent shares and the weights of policy preferences which, if chosen, will make the king and the liberal simultaneously better off in comparison to the pure forms of absolute monarchy or republic. The paper is structured as follows. Section 2 and the associated historical “Appendix 1” offer a brief account of the development of constitutional monarchy in pre-WWI European countries and its failure in others. Section 3 surveys the handful of studies which look at democratization and the retention or deposition of monarchy. Section 4 examines a formal model of constitutional monarchy as an institution of power sharing between the king and a liberal challenger; it identifies conditions for Nash, corner, and split-the-difference equilibriums, with various technical aspects of the model including attitudes to risk elaborated in “Appendices 2–4”. Section 5 concludes.

2 European constitutional monarchies

Contemporary European constitutional monarchies and republics emerged out of medieval monarchical orders. By 1905 nineteen out of the then twenty-one independent European states were constitutional monarchies: Belgium, Bulgaria, Denmark, Germany, Greece, Habsburg Empire (Austro-Hungarian Dual Monarchy), Italy, Luxembourg, Montenegro, The Netherlands, Norway, Ottoman Turkey, Portugal, Romania, Russia, Serbia, Spain, Sweden, and the United Kingdom; only France and Switzerland were republics.⁴ Despite constitutional limits, the early twentieth century European monarchs possessed important powers (Gilbert and Clay Large, 2002). “Appendix 1” sketches the timeline of major constitutional events in each one of the above countries and in Albania briefly ruled by a king. Today, only eight European monarchies remain: Belgium, Denmark, Luxembourg, The Netherlands, Norway, Spain, Sweden, and the United Kingdom. Their kings and queens serve as constitutional heads of state performing ceremonial functions without policy making powers.

The establishment of constitutional monarchy has been the cumulative result of introducing formal legal provisions and norms which replaced royal policy making power with representative government, and the king became a figurehead of the state. Over time and following negotiations, kings agreed to constitutions which limited royal powers, defined citizen rights, granted parliaments powers on domestic and foreign policy, and accepted that the cabinet of ministers must command a majority in parliament.⁵ More dramatically, and perhaps more traumatically, in countries where the king failed to keep within the limits imposed by the constitution and the expectations for political liberalization, the monarchy was overthrown. Neither the transformation to constitutional monarchy, nor the birth of republic were one-shot events or linear developments. That is, challengers to the monarch sometimes won gradual concessions, often in exchange for more funds for the royal household, while in other occasions, kings managed to claw back powers for themselves and implemented more authoritarian rule.

Historically, different countries followed different paths towards establishing constitutional monarchy; nevertheless, they also shared some broad common trends. During the nineteenth century, all European states founded after the Napoleonic wars were set up as kingdoms; in contrast all new European states emerging in the twentieth century after the two world wars were founded as republics. Newly independent European monarchical states which were parts of existing European monarchies, Belgium, Luxembourg, and Norway, have retained their monarchical order until today. On the other hand, European states which won their independence from the Ottoman Empire, Albania, Bulgaria, Greece, Montenegro, Romania, and Serbia, were founded as monarchies, but despite their differences regarding the existence of a domestic royal family,⁶ alliance with the victors of the two world wars,⁷ or religion,⁸ they all transitioned to republics.

In Spain and Greece, the swings between monarchy and republic and back have lasted until the third quarter of the twentieth century, as they both alternated between monarchy and republic and experienced bouts of military dictatorships (which were not controlled by their monarchs). Spain, where the institution of monarchy goes back to the medieval times, was briefly a republic during 1873–74, again in 1931–39 and was ruled dictatorially during 1939–75; the Bourbon dynasty was restored in 1975 and a constitutional monarchy was established. Greece started independent life as a monarchy in 1832. The monarchy was overthrown, and a republic prevailed during 1924–35. The monarchy was then restored, but the king was forced to leave the country after the 1967 military coup. Democracy was restored in 1974 and following a referendum the monarchy was abolished.⁹

3 A selective review of the literature on monarchy autocracy and democratization

Monarchical rule receives some attention in economic studies of dictatorship because autocracy is historically linked with monarchy. Tullock (1987: 1) writes “The difference between a dictatorship and a kingdom is … simply that the kingdoms tend to be hereditary … In actual government, however, there is not all that much difference between a hereditary ruler and a dictator … The word ‘autocracy’ encompasses both”.¹⁰ For Tullock, the main differences are that that dictatorships tend to be transitory, and succession becomes “an undignified squabble for power” (18; 136). On the other hand, longevity brings legitimacy (102; 105–107).¹¹ He considers support for an autocratic ruler as a function of time; the longer the ruler stays in power, the more legitimacy he has and the more likely he is to stay in power. Dictatorships then may survive by switching to hereditary control (17; 151).¹² A long-existing monarchy is therefore seen as legitimate simply because “it has always been there”. Extending this line of thought, Kurrild-Klitgaard (2000) shows that by setting a fixed and clear rule of the game for power, hereditary succession provides stability. When contestants know who will succeed in the throne, their payoffs from fighting change, which limits the number of potential coalitions and produces a structure-induced equilibrium of peaceful succession.¹³ In turn, long-run stability enhances the legitimacy of the regime.

Typically, studies of democratization, the transformation from autocracy to democracy, pay no attention to the institution of kingship. Acemoglu and Robinson (2006), Boix (2015), Ansell and Samuels (2014), North et al. (2009), and Stasavage (2020) among others equate democracy with government by majority rule and a fully enfranchised population. Their point of departure is autocratic rule by royal dynasties or dictators, as the case maybe, and focus on the reasons for the extension of the franchise to poorer classes of the population. However, these works say nothing about the survival of the institution of monarchy after the establishment of democracy.

Congleton (2007, 2011 and 2013) is a partial exception to this generalization. The starting point is Medieval Europe where “the monarch rules but he is surrounded by a circle of semi-independent noblemen, jealous of their privileges and able if necessary, to counterbalance the powers of the Crown…The king rules, but in council” (Finer, 1999: 56). Congleton then explicitly introduces the king as a player in the policy making game and develops the “king-and-council” template to study the game. In the king-and-council architecture, responsibilities for deciding policies are divided between a single person, the king, and a committee or council of noblemen, who advise the king and may have varying degrees of formal powers (advisory, veto or agenda-setting). The king-and-council form of governance emerges to exploit the benefits from specialization of labour when confronted with problems of information on public policy issues and succession (Congleton, 2013; Tridimas, 2018).

In the king-and-council template the shares of policy responsibilities between the king and the council are not rigid but vary over time. This reflects the ideas of thinkers like Locke and Montesquieu, who in the long European transition from autocracy to democracy, conceived constitutional monarchy as a form of governance where the king has executive and even some legislative powers balanced by a council-parliament. Congleton explains that the establishment of representative government involved two largely independent developments; first, a shift of policy making powers away from the king and towards the council-parliament, and second, the parliament becoming more representative of the population following the extension of the suffrage. The shift of policy making power involved a sequence of piecemeal and largely peaceful bargains between the king and the parliament, where the king trades policymaking authority to parliament in exchange for new tax revenues. Typically, new tax revenues are needed when the country goes to war. Further, “the importance of parliamentary majorities tended to increase as national budgets increased and more disciplined national parties emerged” (Congleton, 2011: 474). Constitutional exchanges are also most likely during changing circumstances as it was the case with the industrial revolution bringing rapid technological progress, new economic opportunities, and social trends. In the same vein of constitutional exchanges, and starting from the medieval constitutional order, Young (2021) explains that representation and limited government, and ultimately liberty, arose in Western Europe resulting from “exchanges of political property rights and changes in the rules of the game for governance.”¹⁴

Congleton (2011) shows that the developments of the constitutional monarchies of the UK, Sweden, the Netherlands, and, less obviously, of Germany up to and including the Weimar Republic, pre-WWII Japan, and the USA, are consistent with his theory of constitutional exchanges. However, Congleton does not examine the survival or demise of the institution of monarchy. One may nevertheless infer that in his account, the crown survives because the king has made sufficient concessions to the council-parliament which demands greater input into policy making. The present study expands and complements the work of Congleton.

Tridimas (2016) takes up the question of the causes of the overthrow of the monarchy distinguishing between proximate and fundamental causes. Historically, monarchies have been overthrown after war defeat, dissolution of the kingdom and decolonization (where new independent states repudiate the previous imperial order), revolution, and popular referendums, and often a combination of the above. However, these are only proximate causes for overthrowing the monarchy since the record is also full of cases where domestic conflict or military defeats did not end up with the removal of the monarchy. Proximate causes describe the sequence of events which lead to the fall of the monarchy and the rise of a republican order, which may be democratic or not, but the overthrow of the monarchy is attributed to fundamental causes which underpin the proximate ones. The institution of monarchy is fundamentally rejected if it loses its legitimacy, where legitimacy means that the monarchy is recognized to have the right to do what it does. The legitimacy of ancient monarchies was based on the divine status of the king. Medieval monarchies were “by the grace of god” too. With the transition to modernity following new scientific discoveries, rationalist thinking and the establishment of the nation-state, divine justification was replaced by the monarchy becoming a symbol of the unity and continuity of the community. In this setting, continuation and acceptance of the king rested on the lineage from the original monarch. However, if the monarchy loses its basis of acceptance, it is no longer legitimate. The monarchy may lose its legitimacy because of ethnic divisions, where a particular national group no longer recognizes the authority of the imperial ruler as legitimate; interference of the monarch in politics supporting a particular group or class, which destroys the role of the monarch as a unifying factor; corruption in the court which erodes the social cohesion role of the monarchy; and deep ideological shifts, like, for example, the virulent anti-royalist ideology of communism.¹⁵ However, loss of legitimacy is only a necessary condition. Those who no longer recognize the king as legitimate must also be able to solve their collective action problem, organise against the monarch and have enough strength to overthrow the institution.

4 A formal model of constitutional monarchy

4.1 Model set-up

The king and his challenger, where the latter according to Congleton (2011) and Tullock (1987) is in the council-parliament, engage in repeated interactions for controlling the government, which brings office rents and the right to set policy. Instead of fighting, they may compromise and establish constitutional monarchy which subjects them to constraints accepted by both. The gradual evolution towards representative government and constitutional monarchy reveals that there is a range of intermediate stages where the king and the liberal challenger possess different and changing shares of office rent and policy making power. It is these shares which are the focus of attention here.

The two opposing sides realise that open conflict produces only temporary winners. That is, after a confrontation, which may be violent and disruptive, one side emerges victorious and is in control for a period. It may be able to beat off several future attacks by the defeated side, but as circumstances change, the latter may grow stronger and at an opportune time it challenges successfully and wins power. The cycle is then repeated. The literature has shown that repeated interactions can generate compromises in the form of institutions of power sharing (Dixit, 2003; Rodrik, 2000; Tridimas, 2011). The power sharing arrangement means that the side which has won power gives up some of the benefits from office to the losing side, in exchange for the other side to reciprocate when in office. This trade off results in the side out of office suffering fewer losses in the long-run.

Thence, constitutional monarchy is modelled as a governance arrangement where the king and the liberal agree to share the rents from office and the authority over policy making. It is therefore a point in the two-dimension space of office rents and policy making. Nevertheless, the king and the liberal may have unequal shares and the king’s share of rents from office may differ from his share of input to policy making, as implied by the historical narrative. Since there is no higher authority to police the power sharing arrangement, it is viable only when it is a self-sustained equilibrium. That is, it makes both sides better off than the alternative of switching between absolute monarchy and republic. Contemporary European constitutional monarchies are therefore only one of the possible equilibrium points where, the king surrenders policy making powers and retains some rents from the office of the head of state, and the liberal challenger assumes policy making powers and consents to the king keeping the crown as head of state.

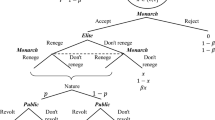
We assume a setting of two players stylistically called the king and the liberal challenger indexed by $K$ and $L$ respectively who coexist over an infinite succession of discrete periods. Each player is considered as a single actor abstracting from questions of the formation of coalitions (and division of spoils of power among their members; such issues are left for future research). In each period one of the two governs. As in Dixit (2003), we assume that if in one period the king prevails and governs as an absolute monarch there is a $\Pi$ probability that the monarchy survives in the next period and a $1-\Pi$ probability that the monarchy is overthrown and replaced by republic where the liberal governs. Similarly, under a republican order in one period, there is a $\Phi$ probability that the republic survives in the next period and a $1-\Phi$ probability that the republic is overthrown and replaced by monarchy. That is, the government types are characterized by a Markov process of fluctuation between a monarchical and a republican regime with fixed switching probabilities. The probabilities $\Pi$ and $\Phi$, depend on the military strengths of the king and the liberal, their financial resources and their legitimacy. For example, if the monarch is perceived as legitimate because of religious reasons, tradition, societal unity or simply a bulwark against political extremism, then $\Pi$ takes a high value. Throughout the main text we assume that both players are risk neutral as it is most often assumed in models of conflict (Garfinkel & Skaperdas, 2007). The technical “Appendix” 4 extends the analysis to risk aversion assuming that the utilities of the players are negatively affected by the variance of the uncertain constitutional outcome.

Let ${U}_{i}^{j}$ denote the static (period) utility and ${V}_{i}^{j}$ the expected present discounted utility of player $i=K, L$ under the constitutional order $j=M, R$. Let the discount factors of the king and the liberal be ${\delta }_{K}$ and ${\delta }_{L}$ respectively, where in general ${\delta }_{K}\ne {\delta }_{L}$.¹⁶ The expected discounted values of the utilities of the king and the liberal challenger can be expressed in the following recursive forms (Dixit, 2003; Rodrik, 2000).

$${\text{The\,king\,under\,absolute\,monarchy:}\quad{{V}_{K}^{M}={U}_{K}^{M}+\delta }_{K} \left(\Pi {V}_{K}^{M}+ \left(1-\Pi \right){V}_{K}^{R}\right)}$$

(1.1)

$${\text{The\,king\,under\,republic:}\quad {{V}_{K}^{R}={U}_{K}^{R}+\delta }_{K} \left(\Phi {V}_{K}^{R}+ \left(1-\Phi \right){V}_{K}^{M}\right)}$$

(1.2)

$${\text{The\,liberal\,under\,absolute\,monarchy:}\quad{{V}_{L}^{M}={U}_{L}^{M}+\delta }_{L} \left(\Pi {V}_{L}^{M}+ \left(1-\Pi \right){V}_{L}^{R}\right)}$$

(2.1)

$${\text{The\,liberal\,under\,republic:}\quad{{V}_{L}^{R}={U}_{K}^{R}+\delta }_{L} \left(\Phi {V}_{L}^{R}+ \left(1-\Phi \right){V}_{L}^{M}\right)}$$

(2.2)

Solving (1.1) and (1.2), we obtain the expected present discounted values of the utility of the king:

$${V}_{K}^{M}= \frac{\left(1-{\delta }_{K}\Phi \right){U}_{K}^{M}+{\delta }_{K}\left(1-\Pi \right){U}_{K}^{R} }{\left(1-{\delta }_{K}\right)\left(\left(1+{\delta }_{K}\left(1-\Pi -\Phi \right)\right)\right)} \mathrm{or} {V}_{K}^{M}= \frac{1}{1-{\delta }_{K}}\left({D}_{K\Phi }{U}_{K}^{M} + {D}_{K\Pi }{U}_{K}^{R}\right)$$

(1.3)

The expressions ${D}_{K\Phi }\equiv \frac{1-{\delta }_{K}\Phi }{1+{\delta }_{K}\left(1-\Pi -\Phi \right)}$ and ${D}_{K\Pi }\equiv \frac{{\delta }_{K}\left(1-\Pi \right)}{1+{\delta }_{K}\left(1-\Pi -\Phi \right)}$ show respectively the discounted probabilities of the king to continue controlling the government and the king staying out of office. Similarly, solving (2.1) and (2.2) we derive the expected present discounted values of the utility of the liberal

$${V}_{L}^{R}= \frac{\left(1-{\delta }_{L}\Pi \right){U}_{L}^{R}+{\delta }_{L}\left(1-\Phi \right){U}_{L}^{M} }{\left(1-{\delta }_{L}\right)\left(\left(1+{\delta }_{L}\left(1-\Pi -\Phi \right)\right)\right)} \mathrm{or} {V}_{L}^{R}=\frac{1}{1-{\delta }_{L}}\left({D}_{L\Pi }{U}_{L}^{R} + {D}_{L\Phi }{U}_{L}^{M}\right)$$

(2.3)

As before, the expressions ${D}_{L\Pi }\equiv \frac{1-{\delta }_{L}\Pi }{1+{\delta }_{L}\left(1-\Pi -\Phi \right)}$ and ${D}_{L\Phi }\equiv \frac{{\delta }_{L}\left(1-\Phi \right)}{1+{\delta }_{L}\left(1-\Pi -\Phi \right)}$ show respectively the discounted probabilities of the liberal to continue controlling the government and the liberal staying out of office. Note also $0<{D}_{K\Phi } , {D}_{L\Phi } , { D}_{K\Pi } {, D}_{L\Pi }<1$, and ${D}_{K\Phi }-{D}_{L\Phi }= {D}_{L\Pi }-{D}_{K\Pi }$ $= \frac{\left(1-{\delta }_{L}\right)\left(1-{\delta }_{K}\Phi \right)+{\delta }_{L}\left(1-{\delta }_{K}\right)\left(1-\Pi \right)}{\left(1+{\delta }_{K}\left(1-\Pi -\Phi \right)\right)\left(1+{\delta }_{L}\left(1-\Pi -\Phi \right)\right)} > 0$. The difference ${D}_{K\Phi }-{D}_{L\Phi }$ denotes the king’s discounted probability differential of staying in office. Similarly, the difference ${D}_{L\Pi }-{D}_{K\Pi }$ denotes the liberal’s discounted probability differential of staying in office.

The period utility of each player ${U}_{i}^{j}$ depends on the size of office rent $Y$ and the policy chosen $X$. Policy choices are modelled using the standard spatial model. That is, the king and the liberal are assumed to have ideal policy points ${K}^{*}$ and ${L}^{*}$ respectively and their utility losses increase the further away actual policy is from the ideal point; see Fig. 1.

Fig. 1

Policy under different constitutional orders

We assume ${{L}^{*}>K}^{*}$ with $A=\left|{L}^{*}-{K}^{*}\right|>0$. We may then write ${U}_{K}= \eta Y-\left(1-\eta \right)\left|{K}^{*}-X\right|$ and ${U}_{L}= \theta Y-\left(1-\theta \right)\left|{L}^{*}-X\right|$. The parameters $\eta$ and $-\left(1-\eta \right)$, and $\theta$ and $-\left(1-\theta \right)$, denote the marginal utility and marginal disutility of rent and policy losses of the king and respectively the liberal. It is differences in these marginal utilities which open the opportunity for mutually beneficial exchanges between the king and the challenger. For concreteness, we assume that the king’s marginal utility of rents is greater than that of the liberal, $\eta > \theta$, or equivalently, the liberal’s marginal utility of policy is greater than that of the king, $1-\theta >1-\eta$.¹⁷ The justification for this assumption is as follows. Kings seem to devote more time to their personal consumption and living standards than policy, partly because of their privileged upbringing and partly because they feel secure on the throne (Tullock (1987: 120). Indeed, historically, monarchs hardly separated the private wealth of the royal family from the wealth of the crown as an institution of governance, an observation which leads to the standard practice of modelling the stationary-bandit ruler as maximizing his consumption treating the public treasury as an extension of his private wealth (McGuire & Olson, 1996; Olson, 1993). Further, in the historical process of democratization, challengers to kings sought to influence public policy rather than confiscate the assets of the throne, alluding that for the liberal the marginal utility from policy making exceeds that of rents from office.

Under absolute monarchy the king takes the entire office rent $Y$ and sets policy at his ideal point $X{=K}^{*}$ so the utilities of the king and the liberal are written as ${U}_{K}^{M}=\eta Y$ and ${U}_{L}^{M}=-\left(1-\theta \right)A$. Under republic the liberal takes the office rent and sets policy at his ideal point $X{=K}^{*}$, so that the utilities of the king and the liberal are written as ${U}_{K}^{R}=-\left(1-\eta \right)A$ and ${U}_{L}^{R}=\theta Y$. Substituting these values into (3) and (4) we have the reduced forms:

$${V}_{K}^{M}= \frac{ 1}{1-{\delta }_{K}}\left(\eta Y{D}_{K\Phi }-\left(1-\eta \right)A{D}_{K\Pi }\right)$$

(3)

$${V}_{L}^{R}= \frac{1}{1-{\delta }_{L}}\left(\theta Y{D}_{L\Pi } +\left(1-\theta \right)A{D}_{L\Phi }\right)$$

(4)

Under constitutional monarchy, indexed by $C,$ the office rents are shared between the king and the liberal, while policy is set as a weighted average of their ideal points. The present values of their utilities are:

$${V}_{K}^{C}= \frac{{U}_{K}^{C} }{1-{\delta }_{K}}$$

(5)

$${V}_{L}^{C}= \frac{{U}_{L}^{C} }{1-{\delta }_{K}}$$

(6)

More specifically, (a) the king gets a $0\le \kappa \le 1$ share of office rents $Y,$ while the liberal takes the rest $1-\kappa$; and (b) policy is set as a weighted average of the two ideal points $X=\lambda {K}^{*}+\left(1-\lambda \right){L}^{*}$, where $0\le \lambda \le 1$ and $1-\lambda$ denote respectively the shares of the ideal policy points of the king and the liberal in the policy actually implemented. The instantaneous payoffs are then ${U}_{K}^{C}=\eta \kappa Y-\left(1-\eta \right)\left|{K}^{*}-X\right|$ and ${U}_{L}^{C}=\theta \left(1-\kappa \right)Y-\left(1-\theta \right)\left|{L}^{*}-X\right|$. From the definition of $X$ we have $\left|{K}^{*}-X\right|=\left(1-\lambda \right)A$ amd $\left|{L}^{*}-X\right|= \lambda A$. Substituting into (5) and (6) we obtain

$${V}_{K}^{C}= \frac{\eta \kappa Y-\left(1-\eta \right)\left(1-\lambda \right)A }{1-{\delta }_{K}}$$

(7)

$${V}_{L}^{C}= \frac{\left(1-\kappa \right)\theta Y-\left(1-\theta \right)\lambda A }{1-{\delta }_{L}}$$

(8)

Figure 2 summarises the constitutional outcomes.

Fig. 2

Timeline of constitutional outcomes

In sum, when compared to Congleton’s analysis, the model offers two innovations; first, it explicitly models the repeated interactions between the king and the challenger, and second it models two different benefits from controlling the government, office rents and policy.

4.2 Minimum acceptable loci of constitutional monarchy

Whether the king is better off with constitutional monarchy than absolute monarchy, and whether the liberal is better off with constitutional monarchy than republic depends on the difference between the payoffs under the two regimes, $\Delta K\equiv {V}_{K}^{C}-{V}_{K}^{M}$ and $\Delta L\equiv {V}_{L}^{C}-{V}_{L}^{R}$ respectively. Substituting from (7) and (3), and (8) and (4), and denoting ${\rm H}\equiv \eta Y+\left(1-\eta \right)A$ and $G\equiv \theta Y+\left(1-\theta \right)A$ the benefit of the king and the liberal from controlling the government, we have

$$\Delta K=\frac{1}{1-{\delta }_{K}}\left(\kappa \eta Y+\lambda \left(1-\eta \right)A-{\rm H}{D}_{K\Phi }\right)$$

(9)

$$\Delta L=\frac{1}{1-{\delta }_{L}}\left(G{D}_{L\Phi }-\kappa \theta Y-\lambda \left(1-\theta \right)A\right)$$

(10)

To avoid conflict whose outcome is uncertain, the two players may accept constitutional monarchy such that the shares of office rents and policy making simultaneously make them both better off, so that the resulting constitutional order is self-enforcing. This requires that the inequalities $\Delta K\ge 0$ and $\Delta L\ge 0$ hold simultaneously.¹⁸ Obviously, the king wishes for the highest possible $\kappa$ and $\lambda$ while the liberal aspires to the lowest possible $\kappa$ and $\lambda$. For parameter values such that $\Delta K<0$ the king chooses confrontation rather than compromise on the hope of establishing absolute monarchy. Similarly, for parameter values such that $\Delta L<0$ the liberal chooses conflict.

Solving $\Delta K=0$ we find the lowest values of $\kappa$ and $\lambda$ which lead the king to accept constitutional monarchy:

$$\lambda =\frac{1}{\left(1-\eta \right)A}\left(H{D}_{K\Phi }-\eta Y\kappa \right)$$

(9')

Graphically, the locus defined by (9') is shown by the line ${K}_{\lambda }{K}_{\kappa }$ in the $\left(\kappa , \lambda \right)$ space in Fig. 3 where ${K}_{\lambda }$ with coordinates $\left(0,\frac{H{D}_{K\Phi }}{\left(1-\eta \right)A}\right)$ and ${K}_{\kappa }$ with coordinates $\left(\frac{H{D}_{K\Phi }}{\eta Y}, 0\right)$ are respectively the vertical and horizontal intercepts of (9'). The line ${K}_{\lambda }{K}_{\kappa }$ depicts the minimum payoff the king demands for agreeing to constitutional monarchy. It represents the king’s lowest indifference curve in the $(\kappa ,\lambda )$ space. Points to the right of ${K}_{\lambda }{K}_{\kappa }$ indicate higher payoffs because the king enjoys higher shares of rent and input into policy making. Its negative slope indicates the trade-off between the share of the rent and the share of policy which the king demands to accept constitutional monarchy.

Fig. 3

Minimum payoffs and constitutional monarchy equilibrium

Similarly, solving $\Delta L=0$ we find the highest values of $\kappa$ and $\lambda$ which lead the liberal challenger to accept constitutional monarchy:

$$\lambda =\frac{1}{\left(1-\theta \right)A}\left(G{D}_{L\Phi }-\theta Y\kappa \right)$$

(10')

Graphically, the locus defined by (10') is shown by the line ${L}_{\lambda }{L}_{\kappa }$ in the $\left(\kappa , \lambda \right)$ space in Fig. 3, where ${L}_{\lambda }$ with coordinates $\left(0,\frac{G{D}_{L\Phi }}{\left(1-\theta \right)A}\right)$ and ${L}_{\kappa }$ with coordinates $\left(\frac{G{D}_{L\Phi }}{\theta Y},0\right)$ are respectively the vertical and horizontal intercepts of (10'). The line ${L}_{\lambda }{L}_{\kappa }$ depicts the minimum payoff the liberal demands for agreeing to constitutional monarchy. It represents the liberal’s lowest indifference curve in the $(\kappa ,\lambda )$ space, as it shows the maximum shares of rents and policy making prepared to grant to the king. Points to the left of ${L}_{\lambda }{L}_{\kappa }$ indicate higher payoffs, because the liberal gets a larger part of the rent and a larger input into policy making. Again, its negative slope reflects the trade-off between the share of the rent and the share of policy input which the liberal is prepared to grant to the king for agreeing to constitutional monarchy. Comparing (9') and (10') we have that since $\eta >\theta$ it also $\frac{\eta }{1-\eta }>\frac{\theta }{1-\theta }$, that is, the ${K}_{\lambda }{K}_{\kappa }$ line is steeper than the ${L}_{\lambda }{L}_{\kappa }$ line.

As already said, since a constitutional monarchy equilibrium must be acceptable to both the king and the liberal, it must be the case that $\Delta K\ge 0$ and $\Delta L\ge 0$ hold simultaneously; otherwise, one or both players expect higher payoffs from their exclusive control of the government and reject power sharing. In addition, the compromise solution must be in the first quadrant to guarantee non-negative $\kappa$ and $\lambda$ values and inside the set of points defined by the ${K}_{\lambda }{K}_{\kappa }$ and ${L}_{\lambda }{L}_{\kappa }$ lines. There are three possibilities to consider: (1) The ${K}_{\lambda }{K}_{\kappa }$ and ${L}_{\lambda }{L}_{\kappa }$ cross each other inside the first quadrant as shown in Fig. 3. (2) The ${K}_{\lambda }{K}_{\kappa }$ line lies below the ${L}_{\lambda }{L}_{\kappa }$ line as shown in Fig. 4 and their intersection occurring in the second quadrant. These two cases yield several constitutional monarchy equilibriums worthy of attention. (3) The ${K}_{\lambda }{K}_{\kappa }$ line is above the ${L}_{\lambda }{L}_{\kappa }$ line as shown in Fig. 5, with their intersection again in the second quadrant. In this case there is no constitutional monarchy equilibrium as the king and the liberal will never agree to any rent and policy power sharing arrangement.

Fig. 4

K_λK_κ lies below L_λL_κ: multiple Nash equilibriums. Split-the-difference equilibrium at DC

Fig. 5

K_λK_κ lies below L_λL_κ: a constitutional monarchy equilibrium does not exist

When the ${K}_{\lambda }{K}_{\kappa }$ and ${L}_{\lambda }{L}_{\kappa }$ cross each other inside the first quadrant at point $E$, as shown in Fig. 3, the constitutional monarchy equilibrium points are depicted by the shaded triangle $E{L}_{\kappa }{K}_{\kappa }$ formed by the intersection of the ${K}_{\lambda }{K}_{\kappa }$ and ${L}_{\lambda }{L}_{\kappa }$ lines and the horizontal $\kappa$ axis. Existence of equilibrium requires that ${K}_{\lambda }$, the vertical intercept of the ${K}_{\lambda }{K}_{\kappa }$, lies above ${L}_{\lambda }$, the vertical intercept of the ${L}_{\lambda }{L}_{\kappa }$, and simultaneously ${K}_{\kappa },$ the horizontal intercept of the ${K}_{\lambda }{K}_{\kappa }$, lies to the left of ${L}_{\kappa }$, the horizontal intercept of the ${L}_{\lambda }{L}_{\kappa }$.

Equations (9') and (10') imply that simultaneous satisfaction of these two conditions requires that

$$\frac{H}{G}\frac{{D}_{K\Phi }}{{D}_{L\Phi }}\frac{1-\eta }{1-\theta }>1>\frac{H}{G}\frac{{D}_{K\Phi }}{{D}_{L\Phi }}\frac{\theta }{\eta }$$

(11)

Since by assumption $\eta >\theta$ which yields $\frac{1-\eta }{1-\theta }<1$ and $\frac{\theta }{\eta }<1$, the necessary conditions for inequality (11) to hold are $\frac{H}{G}\frac{{D}_{K\Phi }}{{D}_{L\Phi }}>1$ and $\eta +\theta <1$. Further, for ${K}_{\lambda }\le 1$ and ${L}_{\kappa }\le 1$ it must be $H{D}_{K\Phi }\le \left(1-\eta \right)A$ and ${GD}_{L\Phi }\le \theta Y$ respectively which we assume that they also hold. The points of the $E{L}_{\kappa }{K}_{\kappa }$ triangle are all constitutional monarchy equilibrium points; they can be thought as the win-set of constitutional monarchy. They secure that for each side constitutional monarchy yields a higher payoff than the expected utility from the uncertain outcome of conflict and is therefore accepted by both sides. Hence, they render constitutional monarchy a self-enforcing equilibrium. Signing the constitutional document amounts to the two sides accepting to be bound by the agreed allocation of rents and policy weights.

Granting constitutions guaranteeing liberties, conceding policy powers and rents previously exclusively enjoyed by the king as described in the historical narrative, is represented as reaching points on or inside the $E{L}_{\kappa }{K}_{\kappa }$ triangle. The different constitutional arrangements agreed in different polities at various moments are represented by different points of the triangle. Clearly, there are several rent and policy inputs shares which may form a viable constitutional monarchy, although at this level of generality we cannot determine which equilibrium prevails, or how a given country travels from one equilibrium to another. However, there is a range of points of particular interest; specifically, the Nash equilibrium and the figurehead-king equilibrium.

4.3 Constitutional monarchy: rent and policy shares under Nash equilibrium

The intersection of ${K}_{\lambda }{K}_{\kappa }$ and ${L}_{\lambda }{L}_{\kappa }$, point $E$, depicts the Nash equilibrium obtained by solving the system of equations $\Delta K=0$ and $\Delta L=0$ for $\kappa$ and $\lambda .$ This is the same solution derived by assuming that the two players determine $\kappa$ and $\lambda$ in a Nash bargaining game, that is maximizing the function $W=ln(\Delta K\left(\kappa ,\lambda \right))+ln(\Delta L\left(\kappa ,\lambda \right))$. It corresponds to the solution of a non-cooperative game between the king and the liberal where each player takes the choices of the other as given. It shows the minimum shares simultaneously acceptable to both players. These are:

$${\kappa }^{*}= \frac{1}{\left(\eta -\theta \right) Y}\left({\left(1-\theta \right) H D}_{K\Phi } - \left(1-\eta \right) G{D}_{L\Phi }\right)$$

(12.1)

$${\lambda }^{*}=\frac{1}{\left(\eta -\theta \right) A}\left(\eta G {D}_{L\Phi }-\theta H {D}_{K\Phi }\right)$$

(12.2)

The comparative static properties of ${\kappa }^{*}$ and ${\lambda }^{*}$ are presented in “Appendix 3”. The corresponding equilibrium shares of the liberal under constitutional monarchy are:

$${1-\kappa }^{*}= {D}_{K\Pi }-\frac{1-\eta }{\eta -\theta } \frac{G}{Y} \left({D}_{K\Phi }- {D}_{L\Phi }\right)$$

(13.1)

$${1-\lambda }^{*}= {D}_{L\Pi }+\frac{\theta }{\eta -\theta } \frac{H}{A} \left({D}_{K\Phi }- {D}_{L\Phi }\right)$$

(13.2)

4.4 Rent shares under king-as-figurehead equilibrium

Obviously, the king would like a point to the right and further away from the $E{K}_{\kappa }$ side showing minimum acceptable shares. Similarly, the liberal would like a point to the left and further away from the $E{L}_{\kappa }$ side showing maximum shares to be granted. Thus, by choosing points inside the $E{L}_{\kappa }{K}_{\kappa }$ triangle away from $E$ towards the horizontal side of the triangle, the king and the liberal can be better off. This implies that any point of the horizontal segment ${L}_{\kappa }{K}_{\kappa }$ (excluding the vertices) represents a Pareto superior allocation for both players. But the coordinates of all points of the ${L}_{\kappa }{K}_{\kappa }$ side are $\left(\lambda =0,\kappa >0\right)$, that is, the king obtains a positive share of the rents but has no policy making power. This is the essence of European-style modern constitutional monarchy, where the king is a ceremonial head of state.¹⁹

If the constitutional monarchy equilibrium is at point ${K}_{\kappa }$ the king receives the minimum size of rents that he is prepared to accept, namely

$${\kappa }_{1}=\frac{H}{\eta Y}{D}_{K\Phi }$$

(14)

On the other hand, if the constitutional monarchy equilibrium is at point ${L}_{\kappa }$ the king receives the maximum size of rents that the liberal is prepared to accept, namely

$${\kappa }_{2}=\frac{G}{\theta Y}{D}_{L\Phi }$$

(15)

One may surmise that the larger the ${K}_{\kappa }{L}_{\kappa }$ distance the more likely that the king and the liberal will succeed in establishing a constitutional monarchy upon negotiation. This makes important to study the comparative static properties of the ${K}_{\kappa }$ and ${L}_{\kappa }$; they are shown in Table 1.

Table 1 Comparative static properties of minimum and maximum king’s rent

Analytically, when establishing a constitutional monarchy with the king as figurehead:

An increase in the size of office rents decreases the equilibrium share of rent accepted by the king, as the king is prepared to accept a smaller proportion of rents for the sake of securing a permanent stake of rents (row 1). On the contrary, an increase in the policy distance between the king and the liberal increases the equilibrium share of rent granted to the king to compensate for the removal of policy making power (row 2).

An increase in the king’s marginal utility of office rents decreases the minimum share of rent the king is prepared to accept, but leaves the maximum unaffected, since what matters for the king is rents (row 3). Analogously, an increase in the liberal’s marginal utility of office rents leaves the minimum rent accepted by the king unaffected but decreases the maximum rent for agreeing to constitutional monarchy (row 4).

An increase in the king’s discount factor, meaning that the king is more patient, decreases the king’s minimum share of rent but leaves the maximum unaffected (row 5). The opposite is true for an increase in the liberal's discount factor (row 6). That is, a more patient king accepts a smaller proportion of rents in exchange for rent certainty. The importance of this comparative static result becomes apparent when a person who was low in the line of succession to the throne and did not expect to become king or queen, after a fortunate turn of events finds himself or herself wearing the crown. It is also relevant to the case of a childless king who may have a different internal discount rate than a king with issue. Historically, parliamentary authority increases in the event of the king not having clear heirs and the agreement of the parliament is required to appoint a new sovereign. The 1689 accession of William III and Mary to the English throne is one of the best-known cases here; similar parliamentary assent was needed for the appointment of a foreign prince in the Balkan kingdoms previously ruled by the Ottoman Empire (see “Appendix 1”).

An increase in the probability that absolute monarchy continues increases the minimum and the maximum rent share of the king (row 7), but the opposite holds if the probability that the republic survives (row 8), as intuition suggests.

4.5 Split-the-difference cooperative constitutional monarchy equilibrium

When the king and the liberal are willing and able to coordinate, they may negotiate to split the difference between the maximum and minimum payoffs represented by ${K}_{\kappa }$ and ${L}_{\kappa }$, and agree the allocation represented by point $C$, the midpoint of the ${K}_{\kappa }{L}_{\kappa }$ segment. Since ${K}_{\kappa }C=C{L}_{\kappa }$, to the right of $C$, the king gets more utility at the expense of the liberal and vice versa to the left of $C$. The midpoint then emerges as the cooperative constitutional monarchy equilibrium securing the highest negotiated utility for each player. The share of the rent awarded to the king is

$${\kappa }_{C}=\frac{1}{2Y}\left(\frac{G}{\theta }{ D}_{L\Phi }-\frac{H}{\eta }{D}_{K\Phi }\right)$$

(16)

The comparative static properties of the equilibrium values of ${\kappa }_{C}$ mirror those of (15) and the negative of (14) causing some of the signs to be ambiguous; they are shown in “Appendix 3”.

To complete the analysis, we return to Fig. 4 where it is noted that when the ${K}_{\lambda }{K}_{\kappa }$ line of the minimum acceptable combinations of $\kappa$ and $\lambda$ lies below the ${L}_{\lambda }{L}_{\kappa }$ line of the liberal’s minimum concessions, the constitutional monarchy equilibrium is inside the quadrilateral ${K}_{\lambda }{L}_{\lambda }{L}_{\kappa }{K}_{\kappa }$. In this case there is no unique Nash equilibrium. As before, the segment ${K}_{\kappa }{L}_{\kappa }$ shows the equilibrium points where the king acts as head of state without policy powers, and $C$ the midpoint between the horizontal intercept ${K}_{\kappa }$ and ${L}_{\kappa }$ represents the cooperative split-the-difference equilibrium.

However, it is uncertain whether a self-sustained constitutional monarchy equilibrium always exists. If either, or both, of the relevant inequalities (11) are not satisfied, then the king and the liberal fail to agree on the power sharing agreement. As shown in Fig. 5, ex ante the two sides are better off by opting for open confrontation to establish their preferred constitutional order. This result formalizes the conflict between monarchy and republic and their changing fortunes over time.

5 Conclusions

The purpose of this study has been to examine how constitutional monarchy may emerge, if at all. Historically, the shift from a ruling king to a reigning king, or even complete abolition of monarchy, has been a gradual process involving a series of reversible steps, some of them bolder than others, towards limiting the policy making power of the monarch. Equally important, the timing and speed of the transformation have differed across different countries.

The inquiry started from the premise that a hereditary king and a liberal challenger fight for control in a game spanning over time. Holding power confers two types of benefits, office rents and the right to decide policy. Stylistically, under absolute monarchy (republic) the king (liberal) takes all rents and implements his most preferred policy. But the outcome of the confrontation between the king and the liberal in each period is uncertain; absolute monarchy may be succeeded by republic excluding the king from the spoils of office, or the republic may be overthrown by the royalist side. Constitutional monarchy is an institution of power sharing. In general, the compromise solution of power sharing involves the king obtaining a proportion of rents and having his ideal policy only partly reflected in the policy implemented, and similarly for the liberal challenger. The study set up a model of repeated interactions between the king and the liberal and identified conditions where the payoffs of both the king and the challenger under constitutional monarchy are higher than those from absolute monarchy for the king and republic for the liberal.

The formal investigation shows that there exists a range of parameter values where constitutional monarchy secures higher individual payoffs for both players than the alternative constitutional orders. The corresponding equilibrium shares depend on the marginal utilities from rents and policy preferences of the two actors, the sizes of the benefits from rents and the right to decide policy, the rates by which the future is discounted, and the probabilities of winning and retaining office. The comparative static properties showed how when circumstances change the shares awarded to the king and the liberal change. The modern Western European type of constitutional monarchy where the king is the head of state without policy powers emerges as a possible solution of the model, which under the conditions examined maximizes the expected payoffs of both the king and the liberal. However, the model also shows that there exist parameter values where either or both players are better off (in an expected sense) by rejecting the compromise solution and opting for conflict on the hope of gaining exclusive control of the government. It is therefore possible to claim that the model offers a sufficiently general explanation of how in the transition to democracy some European countries retained their monarchs as heads of state while others established republican orders.

Appendices

Appendix 1: Timeline of European monarchies and selected constitutional events

• Albania Monarchy: 1928–1939

  • 1913: Independence from Ottoman rule; William of Wied, a German prince, selected as Prince.

  • 1914: William of Wied expelled.

  • WWI: State collapses after invasion by Austria and then Italy & Serbia.

  • 1924: Ahmed Bey Zogu, a tribal chieftain, wins power.

  • 1928: President Zogu declares himself king Zog I.

  • 1939: Occupied by Italy; Albanian monarchy ended.

• Belgium Monarchy: 1830–

  • 1830: Independence from the Kingdom of Netherlands declared

  • 1831: Constitution adopted; Leopold of Saxe-Coburg-Saalfeld selected as King.

  • 1893: Constitutional reform

  • 1899: Revision of the Constitution

  • 1921: Revision of the Constitution

  • 1950: Referendum reaffirms constitutional monarchy.

• Bulgaria Monarchy: 1878–1946

  • 1878: autonomy from Ottoman rule; Alexander of Battenberg selected as Prince.

  • 1886: Alexander abdicates after pro-Russian coup; Ferdinand of Saxe-Coburg & Gotha selected as Prince (reigning dynasty until the end of monarchy)

  • 1908: Kingdom proclaimed.

  • WWI: Defeated; Ferdinand abdicates in favour of his son Boris.

  • 1935: King imposes dictatorship.

  • 1944: Red Army enters Bulgaria; Communists seize power.

  • 1946: Monarchy abolished after referendum.

• Denmark Monarchy: Medieval-

  • 1665: Constitution based on absolute monarchy and hereditary succession formalized

  • 1849: New constitution introduces constitutional monarchy and bicameral legislature

  • 1866: Constitutional revision enhances the powers of the monarch

  • 1915: Constitutional revision grants voting rights to women

  • 1953: Constitutional revision establishes unicameral legislature and basic human rights.

• France Monarchy: Medieval-1792; 1804–1848; 1852–1870

  • 1589: Henry IV Bourbon ascends to the throne (reigning dynasty until the end of monarchy)

  • 1789: French Revolution

  • 1791: Constitutional monarchy adopted.

  • 1792: King Louis XVI guillotined; Republic declared.

  • 1792: “Great Terror”

  • 1795: New constitution establishing government by the “Directory”

  • 1799: Napoleon overthrows Directory

  • 1804-1815: First Empire – Napoleon I

  • 1815-1848: Bourbon restoration

  • 1830: King Charles X abdicates after popular uprising; Louis-Philippe becomes King.

  • 1848: Revolution; Louis-Philippe abdicates; Republic declared.

  • 1852-1870: Second Empire - Napoleon III

  • 1870: Third Republic declared after defeat in the Franco-Prussian War

  • 1875: Republican constitution adopted.

• Germany Monarchy: 1861–1918

  • 1815: German Confederation founded (successor of the Holy Roman Empire, 962-1806); several German principalities adopt constitutions.

  • 1819: Karlsbad Decrees suppress liberal and nationalistic tendencies.

  • 1848–1849: Frankfurt Constitutional Convention fails to receive support for a unified Germany.

  • 1848: Prussia adopts constitution.

  • 1850: Prussian constitution revised.

  • 1866: North German Confederation founded under the control of Prussia.

  • 1871: Unification of Germany under Prussia; new Federal Constitution.

  • 1918: Kaiser Wilhelm II abdicates after WWI defeat; transition government formed.

  • 1919: Republican Constitution of Weimar approved.

• Greece Monarchy: 1832–1924; 1936–1967

  • 1832: Independence from Ottoman rule; Otto Wittelesbach, a Bavarian prince, selected as King.

  • 1843: Otto forced to grant constitution.

  • 1862: Otto deposed.

  • 1863: George Glucksburg, a Danish prince, selected as King (reigning dynasty until the end of monarchy).

  • 1864: New constitution proclaims constitutional monarchy.

  • 1911: Constitution revised (after 1909 military pronunciamento)

  • 1915–1917: National schism between Royalists and Liberals.

  • 1924: Republic proclaimed after defeat by the Turkey in the 1922 Asia Minor campaign

  • 1935: Monarchy restored.

  • 1946–1949: Civil War, Nationalist forces defeat Communists.

  • 1952: New authoritarian constitution.

  • 1967–1974: military dictatorship; 1967: King leaves Greece.

  • 1974: Democracy restored; Monarchy abolished after referendum.

• Habsburg Monarchy: Medieval-1918

• (Austria, Hungary, Czech lands, Slovakia).

  • 1526: Maximilian Habsburg succeeds Charles V Holy Roman Emperor

  • 1806: End of Holy Roman Empire

  • 1848: Revolution; Ferdinand I abdicates

  • 1849: Emperor Francis Joseph rejects constitutional document proposed by legislature.

  • 1862: First fundamental rights: Law on Personal Freedom; Law on the Right of the Home

  • 1867: Austria Empire transformed to Dual Monarchy of Austria-Hungary; December constitution; First Charta of fundamental Rights; State Basic Law on citizen rights

  • 1918: End of Austro-Hungarian Monarchy; proclamation of Republic.

• Italy Monarchy: 1862–1946

  • 1861: Constitution of Sardinia Piedmont (granted in 1848 by King Carlo Alberto) becomes the constitution of unified Italy under Victor Emanuel II of Savoy

  • 1922: Victor Emanuel III endorses fascist Mussolini as prime minister.

  • 1943: Victor Emanuel III dismisses Mussolini’s government, but Nazi Germany reinstates it.

  • 1946: Victor Emanuel III abdicates in favour of his son Umberto II.

  • 1946: Monarchy abolished after referendum.

• Luxembourg Monarchy: 1839-

  • 1815: Autonomous Grand Duchy

  • 1839: Fully sovereign and in personal union to the king of the Netherlands

  • 1867: Full independence gained.

  • 1868: Constitution adopted.

  • 1890: Dukedom passes to Adolph of the House of Nassau-Weilburg (reigning dynasty).

• Montenegro Monarchy: 1878–1918

  • 1878: Independence from Ottoman rule with Nikola Petrovic-Njegos as Prince.

  • 1905: Constitution granted.

  • 1910: Nikola proclaimed King.

  • 1918: Serbia annexes Montenegro and deposes Nikola (end of WWI); Montenegro becomes part of the Kingdom of Serbs, Croats, and Slovenes

• The Netherlands Monarchy: 1648-

  • 1581: Act of Abjuration of the Estates-General declaration of independence from Spain.

  • 1648: Independence of the Republic of United Provinces from Spain formalized.

  • 1814: Proclamation of Prince Frederic William as king (reigning dynasty). Foundation of the Kingdom of the Netherlands

  • 1815: Adoption of Constitution

  • 1840: Constitution reformed

  • 1848: Constitution reformed

  • 1917: Constitution reformed

  • 1983: Constitution thoroughly revised

• Norway Monarchy: 1905-

  • 1814: Constitution adopted, following the defeat of Napoleon.

  • 1851: Constitution amended.

  • 1884: Constitution amended: Establishment of Parliamentarism.

  • 1897: Constitution amended: Prohibition of Jesuits and Monastic orders abolished.

  • 1905: Independence from Sweden; constitutional monarchy adopted after referendum; Prince Carl of Denmark selected as King taking the name Haakon VII (reigning dynasty)

• Ottoman Turkey Monarchy: Medieval-1922

  • 1383: Ascendance of Osman dynasty to the throne (reigning dynasty until the end of monarchy)

  • 1876: Constitution granted by Sultan Abdul Hamid II bowing to domestic pressures.

  • 1878: Constitution suspended.

  • 1908: Young Turks revolution reactivates constitution.

  • 1922: End of Empire after WWI defeat

• Portugal Monarchy: Medieval-1910

  • 1640: Independence from Spain; John Braganza becomes King (reigning dynasty until the end of monarchy)

  • 1822: Constitution granted by John VI.

  • 1826: New constitution by Pedro IV

  • 1828-1834: Civil War over royal succession won by Queen Maria against Regent Miguel, her uncle.

  • 1834: Maria II restored to the throne

  • 1838: New constitution

  • 1908: King Carlos and his son and heir Luis Filipe assassinated by republicans

  • 1910: King Manuel II flees after republican military revolt.

• Romania Monarchy: 1871–1947

  • 1862: Autonomy from Ottoman Empire under Prince Alexandru Ioan Cuza

  • 1866: Cuza overthrown and replaced by Karl of Hohenzollern-Sigmaringen (reigning dynasty until the end of monarchy); Constitution granted

  • 1878: Fully independent

  • 1923: New democratic constitution coming to effect

  • 1938: New constitution introduces the personal dictatorship of King Carol II

  • 1947: Monarchy overthrown when the Communists took control

• Russia Monarchy: Medieval-1917

  • 1613: Michael Romanov becomes King (reigning dynasty until the end of monarchy)

  • 1825: Decembrist Revolt of army officers seeking constitutional government defeated

  • 1867: Abolition of serfdom

  • 1905: Tsar Nicholas II grants constitution after popular revolt, but government remains authoritarian

  • 1917-March: Tsar Nicholas II abdicates

  • 1917-November: Bolsheviks overthrow provisional government and establish Communist rule

  • 1918: Russia, defeated in WWI; royal family executed

• Serbia/Yugoslavia Monarchy: 1871–1945

  • 1817: Autonomy from Ottoman Empire; the domestic Houses of the Obrenovic and the Karadjordjevic fight each other and alternate on the throne.

  • 1835: Constitution granted by Milos Obrenovic.

  • 1838: New authoritarian constitution under Ottoman pressure.

  • 1869: New constitution upon regency of Milan Obrenovic.

  • 1878: Fully independent

  • 1888: New liberal constitution granted by Milan Obrenovic.

  • 1903: New liberal constitution granted by Peter I Karadjordjevic

  • 1918: Yugoslavia established as the Kingdom of Serbs, Croats, and Slovenes, under the Serbian king who also took the crown of Montenegro

  • 1929: King Alexander Karadjordjevic bans national political parties

  • 1945: Monarchy overthrown

• Spain Monarchy: Medieval-1873; 1874–1931; 1975-

  • 1526: Philip I Habsburg succeeds Charles V Holy Roman Emperor

  • 1812: Constitution granted by Jose Bonaparte.

  • 1814: Constitution revoked by Ferdinand VIII.

  • 1820: Constitution of 1812 reinstated.

  • 1824: Constitution revoked.

  • 1837: New liberal constitution granted by Isabella II.

  • 1868: Isabella deposed.

  • 1870-73: Amadeo Savoy King

  • 1873-1874: Republic

  • 1874: Monarchy restored; Alfonso XII, son of Isabella II, becomes King.

  • 1876: New constitution

  • 1931: King Alfonso XIII overthrown

  • 1931-1939: Republic

  • 1936-1939: Civil War; Nationalist forces defeat Republicans.

  • 1939-1975: Franco dictatorship

  • 1975: Monarchy restored, Juan Carlos, grandson of Alfonso XIII becomes King.

  • 1978: New constitution

• Sweden Monarchy: Medieval-

  • 1523: Sweden secedes from the Scandinavian Kalmar Union of Denmark, Sweden, and Norway; Gustav Vasa becomes king of Sweden.

  • 1544: Hereditary succession formalized.

  • 1594: Sovereign required to take oath of accession.

  • 1617: Formal establishment of four-chamber parliament

  • 1634: Constitution formalized (First instrument of government)

  • 1680: Revised instrument of government allows king Charles XI to claw back powers.

  • 1720: New liberal constitution

  • 1772: Constitutional reform shift authority back to the king

  • 1809: New constitutional revision re-establishes powers of the parliament.

  • 1866: Parliamentary reform establishing a two-chamber parliament.

  • 1969: Single-chamber parliament established.

  • 1975: Unification of fundamental constitutional laws

• Switzerland Independent Confederation: 1648-

• United Kingdom Monarchy: Medieval-

  • 1215: Magna Carta accepted by King John.

  • 1265: 2nd De Montfort parliament becomes the origin of the House of Commons.

  • 1414: House of Commons on equal footing with the House of Lords in passing legislation.

  • 1534: Act of Supremacy – split from Vatican and foundation of Anglican Church.

  • 1642-51: Civil War

  • 1649-1659: Commonwealth of England

  • 1660: Monarchy restored.

  • 1688: Glorious Revolution

  • 1689: English Bill of Rights; William III and Mary ascend to the throne.

  • 1701: Act of Settlement restricts succession to nearest Protestants.

  • 1714: George I, Elector of Hanoverian succeeds to the throne (reigning dynasty).

  • 1714–1911: Gradual shift of policy making from the king to parliament.

  • 1911: Veto power of the House of Lords ends.

Notes:

The Table lists European countries under monarchical rule which despite territorial changes are recognizable today.

The list excludes: (1) Poland because it ceased to exist after the 1795 third partition between Habsburg-Austria, Prussia, and Russia. (2) Baltic, German, Italian and Spanish kingdoms, Scotland and Ireland, duchies and other principalities ruled by hereditary aristocratic families which by the Nineteeth century had been unified in larger country formations. (3) The principalities of Monaco and Lichtenstein

“Medieval” signifies that the origins of a country’s monarchy are in the medieval times; see Young (2021) for the emergence of medieval kingships after the collapse of the Western Roman Empire

“Constitutional reform” indicates that the parliament takes policy powers from the king (unless otherwise specified), but description of suffrage reforms is omitted.

Source: Author’s compilation from the following: BBC timeline of Country profile, various countries; Congleton (2011); Encyclopedia Britannica, various countries; International Constitutional Law website: http://www.servat.unibe.ch/icl/; Wikipedia, various countries.

Appendix 2: When the king and the liberal have identical marginal utilities of rents $\eta =\theta$

In this case the loci of accepting constitutional monarchy of the king and the liberal are respectively

$$\lambda =\frac{1}{\left(1-\eta \right)A}\left(H{D}_{K\Phi }-\kappa \eta Y\right)$$

(9'')

$$\lambda =\frac{1}{\left(1-\eta \right)A}\left(H{D}_{L\Phi }-\kappa \eta Y\right)$$

(10'')

That is, they are parallel lines with different intercepts. Since ${D}_{K\Phi }-{D}_{L\Phi }>0$ [see the discussion following Eq. (2.3)], the ${K}_{\lambda }{K}_{\kappa }$ line is entirely above the ${L}_{\lambda }{L}_{\kappa }$ line implying that the two players will never agree to set up a constitutional monarchy.

Appendix 3: Comparative static properties of constitutional monarchy equilibriums

Notation:$\mathrm{\rm H}\equiv \eta Y+\left(1-\eta \right)A$;$\mathrm{G}\equiv \theta Y+\left(1-\theta \right)A$;${D}_{K\Phi }\equiv \frac{1-{\delta }_{K}\Phi }{1+{\delta }_{K}\left(1-\Pi -\Phi \right)}$; ${D}_{K\Pi }\equiv \frac{{\delta }_{K}\left(1-\Pi \right)}{1+{\delta }_{K}\left(1-\Pi -\Phi \right)}$;${D}_{L\Pi }\equiv \frac{1-{\delta }_{L}\Pi }{1+{\delta }_{L}\left(1-\Pi -\Phi \right)}$; ${D}_{L\Phi }\equiv \frac{{\delta }_{L}\left(1-\Phi \right)}{1+{\delta }_{L}\left(1-\Pi -\Phi \right)}$

• (1) Nash equilibrium:

  $${\kappa }^{*}= \frac{{\left(1-\theta \right) H D}_{K\Phi } - \left(1-\eta \right) G{D}_{L\Phi }}{\left(\eta -\theta \right) Y}$$

  (12.1)
  $${\lambda }^{*}=\frac{\eta G {D}_{L\Phi }-\theta H {D}_{K\Phi }}{\left(\eta -\theta \right) A}$$

  (12.2)
  $$\frac{{d\kappa }^{*}}{dY}=-\frac{\left(1-\eta \right)\left(1-\theta \right)}{\eta -\theta }\frac{A}{{Y}^{2}}\left({D}_{K\Phi }-{D}_{L\Phi }\right)<0 \; \frac{d{\lambda }^{*}}{dY}=-\frac{\eta \theta }{\eta -\theta }\frac{1}{A}\left({D}_{K\Phi }-{D}_{L\Phi }\right)<0$$
  $$\frac{d{\kappa }^{*}}{dA}=\frac{(1-\eta )(1-\theta )}{\eta -\theta }\frac{1}{Y}\left({D}_{K\Phi }-{D}_{L\Phi }\right)>0 \; \frac{d{\lambda }^{*}}{dA}=\frac{\theta }{\eta -\theta }\frac{Y}{{A}^{2}}\left({D}_{K\Phi }-{D}_{L\Phi }\right)>0$$
  $$\frac{{d\kappa }^{*}}{d\eta }=-\frac{1-\theta }{{\left(\eta -\theta \right)}^{2}}\frac{G}{Y}\left({D}_{K\Phi }-{D}_{L\Phi }\right)<0 \; \frac{d{\lambda }^{*}}{d\eta }=\frac{\theta }{{\left(\eta -\theta \right)}^{2}}\frac{G}{A}\left({D}_{K\Phi }-{D}_{L\Phi }\right)>0$$
  $$\frac{{d\kappa }^{*}}{d\theta }=\frac{1-\eta }{{\left(\eta -\theta \right)}^{2}}\frac{H}{Y}\left({D}_{K\Phi }-{D}_{L\Phi }\right)>0 \frac{d{\lambda }^{*}}{d\theta }=-\frac{\eta }{{\left(\eta -\theta \right)}^{2}}\frac{G}{A}\left({D}_{K\Phi } - {D}_{L\Phi }\right)<0$$
  $$\frac{d{\kappa }^{*}}{d{\delta }_{K}}=-\frac{1-\theta }{\eta -\theta }\frac{H}{ Y}\frac{1-\Pi }{{\left(1+{\delta }_{K}\left(1-\Pi -\Phi \right)\right)}^{2}}<0 \;\frac{d{\lambda }^{*}}{d{\delta }_{K}}=\frac{\theta }{\eta -\theta }\frac{H}{ A}\frac{1-\Pi }{\left(\eta -\theta \right) Y}>0$$
  $$\frac{d{\kappa }^{*}}{d{\delta }_{L}}=-\frac{1-\eta }{\eta -\theta }\frac{G}{Y}\frac{1-\Phi }{{\left(1+{\delta }_{K}\left(1-\Pi -\Phi \right)\right)}^{2}}<0 \;\frac{d{\lambda }^{*}}{d{\delta }_{L}}=\frac{\eta }{\eta -\theta }\frac{G}{A}\frac{1-\Phi }{{\left(1+{\delta }_{K}\left(1-\Pi -\Phi \right)\right)}^{2}}>0$$
  $$\frac{{d\kappa }^{*}}{d\Pi }=\frac{1}{\left(\eta -\theta \right)Y}\left(\frac{\left(1-\theta \right) H {\delta }_{K }{D}_{K\Phi }}{1+{\delta }_{K}\left(1-\Pi -\Phi \right)}-\frac{\left(1-\eta \right) G{ \delta }_{L}{D}_{L\Phi }}{1+{\delta }_{L}\left(1-\Pi -\Phi \right)}\right)>\left(<\right) 0 \; for \frac{ 1-\theta }{1-\eta }\frac{H}{G}\frac{ {\delta }_{K}}{{ \delta }_{L}}\frac{1+{\delta }_{L}\left(1-\Pi -\Phi \right)}{1+{\delta }_{K}\left(1-\Pi -\Phi \right)}>\left(<\right)\frac{{D}_{L\Phi }}{{D}_{K\Phi }}$$
  $$\frac{{d\kappa }^{*}}{d\Phi }=\frac{-1}{\left(\eta -\theta \right)Y}\left(\frac{\left(1-\theta \right) H {\delta }_{K }{D}_{K\Pi }}{1+{\delta }_{K}\left(1-\Pi -\Phi \right)}-\frac{\left(1-\eta \right) G{ \delta }_{L}{ D}_{L\Pi }}{1+{\delta }_{L}\left(1-\Pi -\Phi \right)}\right)>\left(<\right) 0 \;for \frac{ 1-\theta }{1-\eta }\frac{H}{G}\frac{ {\delta }_{K}}{{ \delta }_{L}}\frac{1+{\delta }_{L}\left(1-\Pi -\Phi \right)}{1+{\delta }_{K}\left(1-\Pi -\Phi \right)}<\left(>\right)\frac{{D}_{L\Pi }}{{D}_{K\Pi }}$$
  $$\frac{{d\lambda }^{*}}{d\Pi }=\frac{-1}{\left(\eta -\theta \right)A}\left(\frac{\theta H {\delta }_{K} {D}_{K\Phi }}{1+{\delta }_{K}\left(1-\Pi -\Phi \right)}-\frac{\eta G{ \delta }_{L} {D}_{L\Phi }}{1+{\delta }_{L}\left(1-\Pi -\Phi \right)}\right)>\left(<\right) 0 \;for \frac{ \theta }{\eta } \frac{H}{G}\frac{ {\delta }_{K}}{{ \delta }_{L}}\frac{1+{\delta }_{L}\left(1-\Pi -\Phi \right)}{1+{\delta }_{K}\left(1-\Pi -\Phi \right)}<\left(>\right)\frac{ {D}_{L\Phi }}{{D}_{K\Phi }}$$
  $$\frac{{d\lambda }^{*}}{d\Phi }=\frac{1}{\left(\eta -\theta \right)A}\left(\frac{\theta H {\delta }_{K} {D}_{K\Pi }}{1+{\delta }_{K}\left(1-\Pi -\Phi \right)}-\frac{\eta G{ \delta }_{L} {D}_{L\Pi }}{1+{\delta }_{L}\left(1-\Pi -\Phi \right)}\right)>\left(<\right) 0 \;for \frac{ \theta }{\eta } \frac{H}{G}\frac{ {\delta }_{K}}{{ \delta }_{L}}\frac{1+{\delta }_{L}\left(1-\Pi -\Phi \right)}{1+{\delta }_{K}\left(1-\Pi -\Phi \right)}>\left(<\right)\frac{ {D}_{L\Pi }}{{D}_{K\Pi }}$$

• (2) Split-the difference/cooperative equilibrium

  $${\kappa }_{C}=\frac{1}{2Y}\left(\frac{G}{\theta }{ D}_{L\Phi }-\frac{H}{\eta }{D}_{K\Phi }\right), \lambda =0$$

  (16)
  $$\frac{d{\kappa }_{C}}{dY}=\frac{A}{{Y}^{2}}\frac{\theta \left(1-\eta \right){D}_{K\Phi }-\eta {\left(1-\theta \right)D}_{L\Phi }}{2\eta \theta } >\left(<\right) 0 \;for \frac{\theta \left(1-\eta \right)}{\eta \left(1-\theta \right)}>(<)\frac{{ D}_{L\Phi }}{{D}_{K\Phi }}$$
  $$\frac{d{\kappa }_{C}}{dA}=-\frac{\theta {\left(1-\eta \right) D}_{K\Phi }-\eta \left(1-\theta \right){D}_{L\Phi }}{2\eta \theta Y}>\left(<\right) 0 \;for \frac{\theta \left(1-\eta \right)}{\eta \left(1-\theta \right)}<(>)\frac{{ D}_{L\Phi }}{{D}_{K\Phi }}$$
  $$\frac{d{\kappa }_{C}}{d\eta }=\frac{1}{{2\eta }^{2}}\frac{A}{Y}{D}_{K\Phi }>0$$
  $$\frac{d{\kappa }_{C}}{d\theta }=-\frac{1}{{2\theta }^{2}}\frac{A}{Y}{D}_{L\Phi }<0$$
  $$\frac{d{\kappa }_{C}}{d{\delta }_{K}}=\frac{H}{2\eta Y}\frac{1-\Pi }{{\left(1+{\delta }_{K}\left(1-\Pi -\Phi \right)\right)}^{2}}>0$$
  $$\frac{d{\kappa }_{C}}{d{\delta }_{L}}=\frac{G}{2\theta Y}\frac{1-\Phi }{{\left(1+{\delta }_{L}\left(1-\Pi -\Phi \right)\right)}^{2}}>0$$
  $$\frac{d{\kappa }_{C}}{d\Pi } =\frac{-1}{2\eta \theta Y}\left(\frac{\theta H{\delta }_{K}}{1+{\delta }_{K}\left(1-\Pi -\Phi \right)}{D}_{K\Phi }-\frac{\eta G{\delta }_{L}}{1+{\delta }_{L}\left(1-\Pi -\Phi \right)}{D}_{L\Phi }\right)>\left(<\right) 0 \; for \frac{\theta }{\eta }\frac{H}{G}\frac{{\delta }_{K}}{{\delta }_{L}}\frac{1+{\delta }_{L}\left(1-\Pi -\Phi \right)}{1+{\delta }_{K}\left(1-\Pi -\Phi \right)}<\left(>\right)\frac{{ D}_{L\Phi }}{{D}_{K\Phi }}$$
  $$\frac{d{\kappa }_{C}}{d\Phi }=\frac{1}{2\eta \theta Y}\left(\frac{\theta H{\delta }_{K}}{1+{\delta }_{K}\left(1-\Pi -\Phi \right)}{D}_{K\Pi }-\frac{\eta G{\delta }_{L}}{1+{\delta }_{L}\left(1-\Pi -\Phi \right)}{D}_{L\Pi }\right)>\left(<\right) 0 \;for \frac{\theta }{\eta }\frac{H}{G}\frac{{\delta }_{K}}{{\delta }_{L}}\frac{1+{\delta }_{L}\left(1-\Pi -\Phi \right)}{1+{\delta }_{K}\left(1-\Pi -\Phi \right)}>(<)\frac{{D}_{L\Pi }}{{D}_{K\Pi }}$$

Appendix 4: Introduction of risk aversion

We assume that the utility ${w}_{i}^{j}$ of player $i=K, L,$ under the constitutional order $j=M, R$, monarchy or republic, depends on the mean ${\mu }_{j}^{i}$ and the variance ${{\sigma }_{ij}}^{2}$ of the uncertain constitutional outcomes

$${w}_{i}^{j}={\mu }_{i}^{j}-{\gamma }_{i}{{\sigma }_{ij}}^{2};i=K, L; \,and \,j=M,R$$

The ${\gamma }_{i}$ parameter reflects risk aversion, that is, disutility from the variance of the constitutional outcome. The recursive forms of the expected discounted utilities are written as follows.

$${\text{The\,king\,under\,absolute\,monarchy:}\quad{V}_{K}^{M}={U}_{K}^{M}+{\delta }_{K}\left({\mu }_{K}^{M}-{\gamma }_{K} {{\sigma }_{KM}}^{2}\right)} $$

(17)

$${\text{The\,king\,under\,republic:}\quad {V}_{K}^{R}={U}_{K}^{R}+{\delta }_{K}\left({{\mu }_{K}^{R}-\gamma }_{K} {{\sigma }_{KR}}^{2}\right)} $$

(18)

$${\text{The\,liberal\,under\,absolute\,monarchy:}\quad {V}_{L}^{M}={U}_{L}^{M}+{\delta }_{L}\left({\mu }_{L}^{R}-{\gamma }_{L}{{\sigma }_{LM}}^{2}\right)}$$

(19)

$${\text{The\,liberal\,under\,republic:}\quad{V}_{L}^{R}={U}_{L}^{R}+{\delta }_{L}\left({\mu }_{L}^{R}-{\gamma }_{L}{{\sigma }_{LR}}^{2}\right)}$$

(20)

The mean of utility of the king with a $\Pi$ probability that the absolute monarchy survives is ${\mu }_{K}^{M}=\Pi {V}_{K}^{M}+ \left(1-\Pi \right){V}_{K}^{R} .$ The variance of the king’s utility under monarchy is ${{\sigma }_{KM}}^{2}={\Pi \left({V}_{K}^{M}-{\mu }_{K}^{M}\right)}^{2}+\left(1-\Pi \right){\left({V}_{K}^{R}-{\mu }_{K}^{M}\right)}^{2}$ which yields ${{\sigma }_{KM}}^{2}=\Pi \left(1-\Pi \right){\left({V}_{K}^{M}-{V}_{K}^{R}\right)}^{2}$. Working in a similar way we find ${{\sigma }_{KR}}^{2}=\Phi \left(1-\Phi \right){\left({V}_{K}^{M}-{V}_{K}^{R}\right)}^{2};$ ${{\sigma }_{LM}}^{2}=\Pi \left(1-\Pi \right){\left({V}_{L}^{M}-{V}_{L}^{R}\right)}^{2}$ and ${{\sigma }_{LR}}^{2}=\Phi \left(1-\Phi \right){\left({V}_{L}^{M}-{V}_{L}^{R}\right)}^{2}.$

Upon substituting and manipulating (17) and (18) yield

$$\left({V}_{K}^{M}-{V}_{K}^{R}\right)\left(1+{\delta }_{K}\left(1-\Pi -\Phi \right)\right)={U}_{K}^{M}-{U}_{K}^{R}-{\delta }_{K}{\gamma }_{K}\left(\Pi \left(1-\Pi \right)-\Phi \left(1-\Phi \right)\right) {\left({V}_{K}^{M}-{V}_{K}^{R}\right)}^{2}$$

Similarly (19) and (20) yield

$$\left({V}_{L}^{R}-{V}_{L}^{M}\right)\left(1+{\delta }_{L}\left(1-\Pi -\Phi \right)\right)={U}_{L}^{R}-{U}_{L}^{M}-{\delta }_{L}{\gamma }_{L}\left(\Phi \left(1-\Phi \right)-\Pi \left(1-\Pi \right)\right) {\left({V}_{L}^{M}-{V}_{L}^{R}\right)}^{2}$$

However, at this level of generality, the quadratic equations do not provide explicit solutions for the values of ${V}_{K}^{M}$ and ${V}_{L}^{R}$ required to compare the payoffs under absolute and constitutional monarchy. To proceed we assume that the probability of a constitutional order continuing is the same for the king and the liberal, so that $\Pi =\Phi =P$. Upon manipulating we obtain

$${V}_{K}^{M}= \frac{\eta Y\left(1-{\delta }_{K}\mathrm{P}\right)-\left(1-\eta \right)A{\delta }_{K}\left(1-P\right)}{\left(1-{\delta }_{K}\right)\left(1+{\delta }_{K}\left(1-2P\right)\right)}-\frac{{\delta }_{K}{\gamma }_{K}P(1-P)}{1-{\delta }_{K}}{\left(\frac{\eta Y+\left(1-\eta \right)A}{1+{\delta }_{K}\left(1-2P\right)}\right)}^{2}$$

(21)

$${V}_{L}^{R}= \frac{\theta Y\left(1-{\delta }_{L}\mathrm{P}\right)-\left(1-\theta \right)A{\delta }_{L}\left(1-P\right) }{\left(1-{\delta }_{L}\right)\left(1+{\delta }_{L}\left(1-2P\right)\right)}-\frac{{\delta }_{L}{\gamma }_{L}P(1-P)}{1-{\delta }_{L}}{\left(\frac{\theta Y+\left(1-\theta \right)A}{1+{\delta }_{L}\left(1-2P\right)}\right)}^{2}$$

(22)

Subtracting (21) and (22) from (7) and (8), the certain payoffs from constitutional monarchy respectively, we obtain the following loci of the king’s minimum acceptable trade-off between $\kappa$ and $\lambda$ and the liberal maximum concession trade-off between $\kappa$ and $\lambda$

$${\text{The\,king:}\quad \lambda = \frac{\left(1-{\delta }_{K}\mathrm{P}\right)\left(1+{\delta }_{K}\left(1-2P\right)\right)H-{\delta }_{K}{\gamma }_{K}P\left(1-P\right){H}^{2}}{\left(1-\eta \right)A{\left(1+{\delta }_{K}\left(1-2P\right)\right)}^{2}}-\frac{\eta }{1-\eta }\frac{Y}{A}\kappa }$$

(23)

$${\text{The\,liberal:}\quad\lambda =\frac{{\delta}_{L}{\left(1- \mathrm{P}\right)\left(1+{\delta }_{L}\left(1-2P\right)\right)G-\delta }_{L}{\gamma }_{L}P(1-P){G}^{2}}{\left(1-\theta \right)A{\left(1+{\delta }_{L}\left(1-2P\right)\right)}^{2}}-\frac{\theta }{1-\theta }\frac{Y}{A}\kappa} $$

(24)

It is clear from the above, that introduction of risk aversion decreases the values of the horizontal intercepts, points ${\kappa }_{1}$ and ${\kappa }_{2}$ of the Fig. 3. Although this has an ambiguous effect on the size of the region where constitutional monarchy, the inferences gained from the risk neutrality model remain the same.