Making exit costly but efficient: the political economy of exit clauses and secession

Abstract

This article presents a political economic analysis of exit from federations. After the federation has formed, members’ benefits from it may be different than expected. If a member ends up not benefitting, it may wish to secede i.e. exit the federation. Based on formal models, we show how state-contingent exit penalties can induce socially efficient exit decisions: they force the secessionist member to take into account the lost benefits of the federation for the other. Even if ex-ante specified exit penalties cannot be made state-contingent, they may still enhance social welfare by preventing forceful exit. Empirical evidence concerning Montenegro, Saint Kitts and Nevis, and the EU is compatible with these claims. In spite of the simplifications inherent to any modeling exercise, we hope that our results stimulate more research into exit clauses as a means to mitigate the problem of violent secessionism.

1 Introduction

Secessionism is on the rise (Griffiths 2016; Lake and O’Mahony 2004). Events in Catalonia gather global attention. This article develops a political economic model of secession and the potential role of exit clauses in making exit costly but efficient. Generally speaking, an exit clause specifies the conditions of exit or withdrawal from an agreement. Examples of exit clause conditions are the payment of a penalty or waiting out a notice period. In most types of international treaties, clauses regulating temporary escape or permanent withdrawal are relatively prevalent (Koremenos and Nau 2010; Rosendorff and Milner 2001). As an alternative way of ensuring flexibility, international agreements may be concluded for a limited duration (Koremenos 2005). This is not the case for federations, which some scholars even define on the basis of lacking legal exit options (Harbo 2008).

Indeed, true constitutional exit clauses are rare (Sorens 2012: 116). According to data from the Constitute Project (Elkins et al. 2009, 2014) among 192 constitutions currently in force, only 23 address the secession of territory. Among these, only 6 explicitly recognize some right to secede: Ethiopia, Liechtenstein, Saint Kitts and Nevis, Sudan, United Kingdom, and Uzbekistan.¹ It is generally accepted that the right to secede in Ethiopia does not amount to much in practice due to the autocratic nature of its government (Habtu 2005). Surprisingly, the microstate Liechtenstein allows for secession by each of its communes. The two-island federation of Saint Kitts and Nevis allows Nevis to secede by a two-thirds majority; in 1998, a referendum was organized but only 62% voted in favor (Veenendaal 2015). After the Comprehensive Peace Agreement of 2005, Sudan’s constitution allowed for secession by South Sudan after 6 years. In 2011, South Sudan exercised this option. The United Kingdom allows Northern Ireland to join a united Ireland. Like in Ethiopia, the right to secede of the Uzbek region of Karakalpakstan does not amount to much in practice (Roeder 2007: 67).

Historically, the Constitution of the Soviet Union allowed for secession—at least on paper (Sunstein 1991: 645–647). Another historical example is the 2003 State Union of Serbia and Montenegro, which allowed for secession after a 3 year waiting period; in 2006 Montenegro exercised the option after obtaining more than the requisite 55% in a referendum. Finally, the European Union (EU), which has many characteristics of a federation, has a withdrawal clause (Athanassiou 2009; Huysmans 2019): Article 50 of the Treaty on European Union specifies that any Member State may withdraw two years after notification.

Depending on how a secession takes place, it can be peaceful and swift, or painful and costly (Tir et al. 1998; Young 1994). According to Sorens (2012: 3), “since the 1980s, at least half of all ongoing civil wars in any given year have been secessionist”—see Cederman and Vogt (2017) for an overview of the civil war literature. If there is no exit clause in the federal constitution, exit from a federation requires an ex-post negotiated solution, i.e. consent from the remaining members. If a negotiated exit cannot be reached, embarking on a destructive secession war may be the only alternative for a member wishing to secede (Griffiths and Wasser 2019; Helfer 2005). Consistent with this logic, this article analyzes three modes of exit: exit based on an exit clause, forceful exit, and negotiated exit.

The idea that in some circumstances reneging on a prior agreement may be socially desirable is known as efficient breach (Goetz and Scott 1977). In theory, if exit from a federation is socially desirable those better off outside could offer an acceptable side-payment for exit and make everyone better off—an application of Coase (1960). In this light, Drèze, De Grauwe, and Edwards (1993) discuss a practical rule suggested by Drèze to ex-post reapportion national debt at the time of secession. However, as pointed out by De Grauwe, ex-post renegotiation may be very difficult politically. Hence ex-ante negotiated exit clauses may be necessary to enable efficient breach.

In spite of the potential benefits of exit clauses, the dominant position in the constitutionalist literature is that they should be avoided. This position was pioneered by Sunstein (1991), who sees constitutions as pre-commitment strategies in the presence of multiple equilibria.² Based on formal models, Chen and Ordeshook (1994) and Filippov, Ordeshook, and Shvetsova (2004) conclude that there should be a constitutional ban on exit, in order to coordinate on non-secession equilibria. However, the strength of this conclusion is limited by the underlying assumption that maintaining the federation is always efficient. While the two-period model of Bordignon and Brusco (2001) allows for shocks and the possibility of efficient breach, it introduces the restrictive assumption that countries are ex-ante identical.

Within the broader literature on secessionism, others have already zoomed in on potential information problems (Anesi 2012; Gradstein 2004; Olofsgård 2004). Hence we focus here on a setting with complete information, but with other theoretical innovations. Compared to Chen and Ordeshook (1994) and Bordignon and Brusco (2001), our contribution to the literature on the design of exit clauses is threefold. First, using a formal model of costly exit clauses, we show that appropriately costly exit clauses do not increase the likelihood of exit given the implicit option of forceful exit. This formalizes an argument made by Weinstock (2001). Second, our model allows for members of the union to be different ex-ante. Finally, reflecting the fact that benefits from the federation may change over time, we also present a continuous time model of exit.

Empirical evidence concerning Montenegro, Saint Kitts and Nevis, and the EU is shown to comport well with the predictions of these theoretical models, warranting further research into exit clauses.

The rest of this paper is organized as follows. First we present the basic two-period model of exit with costly exit clauses. Next we establish conditions for socially efficient exit and show how to achieve it in a decision-theoretical setting, with a continuous time model presented in “Appendix”. The subsequent sections present the game-theoretical setting, discuss the conclusion of the model and present some empirical plausibility probes. The final section concludes.

2 The model

The following model describes a union between two federated entities or members indexed by $i\in \{A,B\}$.³ For tractability, we assume that each entity is composed of identical inhabitants, and leave the analysis of within-entity heterogeneity for future work; see Weidmann (2009) and Gubler and Selway (2012) for empirical evidence regarding within-entity heterogeneity. The assumption of within-entity homogeneity means that each federal entity can be modeled as a unitary actor. For each such entity or member $i$, the net benefits of being in the federation versus outside depend on the rules of the federation and a member’s characteristics.

2.1 The net benefits of being in the federation versus outside

Consistent with the literature on the size of nations, we assume that the benefits and costs from being part of a federation comprise economies of scale, the internalization of externalities, fiscal transfers, and welfare losses from centralized decision-making in the presence of heterogeneity between the federated entities (Alesina and Spolaore 2003; Desmet et al. 2011; Haimanko et al. 2005; Hug 2005; Tullock 1969). Each of these components is determined by the substantive terms of the federation, such as the rules for computing fiscal transfers, and the characteristics of the entities, such as their average income. We denote an entity’s net expected benefits at the time of the creation of the federation by its type, ${\theta }_{i}$. A high type indicates high expected benefits from the union. Forcefully incorporated members of the federation may have a negative type. To simplify the exposition, we focus on the case ${\theta }_{i}>0$.

We start with the two-period model. The formation of the federation in the first period is taken as exogenous. A member’s ex-post benefits in the second period from being in the federation versus outside may be uncertain ex-ante because of changes in the state of the world. For instance, a member may become richer. While this may be good for the member per se, it may also decrease its benefits from the federation, because it will have to pay higher fiscal transfers. This may be the case for Catalonia in Spain and Flanders in Belgium. As another example, consider changes in heterogeneity: over time, the culture and preferences of people across the federated entities may diverge such that the benefits of the federation for each federated entity decrease. As a third example, global increases in free trade and peace decrease returns to scale (Alesina and Spolaore 2003). With more free trade the economies of scale from having a large internal market become less important. Likewise, the lower external military threats, the less important economies of scale in the provision of defense (Riker 1964).

In our basic model, we capture changes in the state of the world that are relevant for a member’s ex-post benefits of being in the federation versus outside by its second-period state ${x}_{i}$; later we present a continuous time extension. A high state means that a member enjoys the federation more than expected in the first period, and vice versa. We assume that the link between the state of the world and benefits is exogenous. Substantively, this assumption means that the terms of the union cannot be renegotiated, e.g. the rules for computing fiscal transfers cannot be changed. It also means that we do not consider decentralization as a means to appease separatist regions through partial exit (Cederman et al. 2015; Congleton et al. 2003; Sorens 2012). While this is a limitation, we leave a model with an endogenous state for future work.

To summarize, the net benefits for both members from being in the union versus outside depend on their types $({\theta }_{A},{\theta }_{B})$ and on the state of the world $x=\left({x}_{A},{x}_{B}\right)$. Concretely, member $i$’s payoff if the federation is maintained is

$${\pi }_{i}={\theta }_{i}+{x}_{i}$$

(1)

Given that the type ${\theta }_{i}$ captures the expected benefits, member $i$’s state is zero in expectation: $E\left({x}_{i}\right)=0$. For simplicity, assume that member $i$’s state ${x}_{i}$ has a discrete distribution and takes values ${-s}_{i}$ and ${s}_{i}$ with equal probabilities. The probability density function of ${x}_{i}$ is

$$f\left({x}_{i}\right)=0.5, \quad {x}_{i}\in \{-{s}_{i},{s}_{i}\}$$

(2)

Allowing for correlation $\rho \in \{-\mathrm{1,0},1\}$ between the members’ states, the joint probability distribution of $x=\left({x}_{A},{x}_{B}\right)$ is

$$\begin{array}{lll}\rho =1:&\quad f\left(x\right)=0.5&\quad \forall x\in \left\{\left(-{s}_{A},-{s}_{B}\right),\left({s}_{A},{s}_{B}\right)\right\}\\ \rho =0:&\quad f\left(x\right)=0.25 &\quad \forall x\in \left\{\left(-{s}_{A},-{s}_{B}\right),\left(-{s}_{A},{s}_{B}\right),\left({s}_{A},{-s}_{B}\right),\left({s}_{A},{s}_{B}\right)\right\}\\ \rho =-1:&\quad f\left(x\right)=0.5 &\quad \forall x\in \left\{\left(-{s}_{A},{s}_{B}\right),\left({s}_{A},{-s}_{B}\right)\right\}\end{array}$$

(3)

A positive correlation means that both members’ benefits tend to move together. A negative correlation means that changes in the state of the world tend to have an opposite effect on both members. For instance, if changes in the state of the world result predominantly in changes in fiscal transfers, then members’ states will be negatively correlated: if one member loses, the other member gains.

2.2 Exit clauses

Regarding exit clauses, we consider both exit penalties and one-off costs. An exit penalty consists of the payment of an amount ${c}_{i}$ by the exiting party $i$ to the remaining party $j$. It could be implemented in practice as an obligation to take on a disproportionate amount of the national debt. The amount may be negative in case of a bonus for exit. All other costs associated with exit are grouped in the one-off costs ${k}_{i}>0.$ This parameter comprises all non-transfer costs required for exit, such as the legal and administrative costs of creating a new state. The costs ${c}_{i}$ and ${k}_{i}$ have the same effect on $i$, but only ${c}_{i}$ will be received by $j$ as a compensation for exit. While we assume ${k}_{i}$ to be exogenous, ${c}_{i}$ can be freely specified.

Just as the entity that triggers an exit clause will incur one-off costs, the other entity will also face one-off costs in order to make the exit materialize. For simplicity, we assume that these costs are identical to those that an entity would have to incur had it called the clause itself. Hence by assumption, if $i$ calls the exit clause it will have to pay both ${c}_{i}$ and ${k}_{i}$. Conversely, if $j$ calls the exit clause, $i$ will receive ${c}_{j}$ but still pay ${k}_{i}$.

To conclude, member $i$’s payoff is

$${\pi }_{i}=\left\{\begin{array}{ll}{\theta }_{i}+{x}_{i}& \quad \text{if} \,\text{the federation is maintained}\\ -{c}_{i}-{k}_{i}& \quad \text{if }\,i\text{ calls the exit clause}\\ {c}_{j}-{k}_{i}&\quad \text{if }\,j\text{ calls the exit clause}\\ -{c}_{i}+{c}_{j}-{k}_{i}&\quad \text{if} \,\text{both call the exit clause}\end{array}\right.$$

(4)

2.3 Forceful exit

Exit clauses are not the only way for federations to end. Given that federal constitutions are not enforced by supranational courts, a member wishing to exit may do so forcefully. By forceful exit, we denote any unilateral exit which does not respect a pre-agreed exit clause or has not been negotiated. Such a forceful exit may take the form of a violent secession war. We model a forceful exit as a pair of costs $({f}_{i},{d}_{j}),$ where ${f}_{i}>0$ is the cost the exiting member $i$ would have to incur to make the secession materialize (including both the direct costs and the reputational costs) and ${d}_{j}>0$ is the corresponding damage to the remaining member $j$. Compared to clause-based exit, the one-off costs ${k}_{i}$ are assumed to be incorporated in the costs ${f}_{i}$ and ${d}_{i}$ so that ${f}_{i},{d}_{i}>{k}_{i}$.

The direct costs of a forceful exit depend on the relative ease of controlling a federal entity’s territory. The stronger the presence of a federal army within a federal entity, the more costly a forceful exit for that entity, since it may then have to take the form of a secession war. Geography also plays a role: overseas regions, regions on the outer border of a federation, or regions with rough terrain incur less costs in controlling their territory (Fearon and Laitin 2003; Sorens 2012).

The reputational costs of a forceful exit depend both on the international norm against unilateral exit and on the circumstances. For instance, regions with oppressed ethnic minorities generally incur low reputational costs, as they tend to be quickly welcomed by the international community, i.e. recognized by other countries, the UN and the WTO (Buchanan 1997; Sorens 2016). For an analysis of third countries’ recognition strategies, see Coggins (2011).

Note that the model assumes that both the costs of exit per an exit clause, ${c}_{i}+{k}_{i}$, and the cost of a forceful exit ${f}_{i}$ are certain. This assumption is not restrictive if the members of the federation are risk-neutral. If the members are not risk-neutral, the possible variance of the exit costs matters on top of their expected value. The bigger the uncertainty of the exit costs, the less attractive exit would become to risk-averse members (Nadeau et al. 1999). In practice, federal entities are likely to base their assessment of the costs of exit on past government behavior (Walter 2006) and on information provided by political leaders both from the center (Anesi 2012) and from the region attempting to secede (Olofsgård 2004).

2.4 Negotiated exit

The two previous sections discussed clause-based and forceful exit. A third mode of exit is through negotiation. As mentioned before, negotiations may also lead to a partial exit in the form of decentralization (Congleton et al. 2003), but we do not analyze this possibility here. In reality many obstacles may limit the scope for negotiating exit. Politicians or voters may be loss-averse, boundedly rational, or simply emotional and irrational. The importance of such impediments to a negotiated exit is ultimately an empirical matter. However, given the high prevalence of civil wars such barriers to negotiation clearly exist (Fearon and Laitin 2003). For the formal model presented here, we assume that barriers to renegotiation preclude ex-post negotiated exit. However, we do discuss the possibility of negotiated exit later on.

2.5 Anti-secession wars

We have argued that irrespective of an exit clause federations may be subject to a negotiated or a forceful exit. On the other hand, even if the federation includes an exit clause, a member trying to make legal use of this clause may be faced with an anti-secession war by the rump of the federation. Indeed, this is the expectation of what would have happened had Soviet Republics used Article 72 of the Constitution to declare their independence prior to the Gorbachev era (Suesse 2016).⁴ In the case of the 1861–1865 American Civil War, some Southerners claimed the union had an implicit secession right and that hence the North was conducting an illegal anti-secession war (Buchanan 1997: 36).

The more sensitive the central state is to reputational costs related to reneging on a constitutional exit clause, the less relevant the anti-secession war option. Clearly, for autocracies such as the Soviet Union, Ethiopia or Uzbekistan such reputational concerns are less important. In the remainder of the exposition we assume that anti-secession wars are not a relevant option, but we return to the issue later.

2.6 The exit game

To conclude the exposition of the model, we set up a game in which both players have the option to stay, to exit based on a clause or to exit forcefully. The players are assumed to move simultaneously to avoid building in artificial asymmetries related to which player would be assumed to move first. An example of such an artificial asymmetry is the following. In a setup with sequential moves and positive exit penalties, even if both players would prefer the federation to be dissolved, the first player would not exit. The reason is that he knows that the second player will exit anyway, and even pay a penalty for it to the first player. Reversing the assumed order of moves would reverse this conclusion, i.e. the order of moves would introduce an artificial asymmetry.

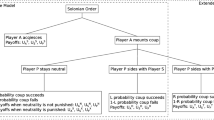
Table 1 presents the normal form of this game. The rows list the possible strategies for player $A$ and the columns for player $B$. Each cell gives the payoffs $({\pi }_{A},{\pi }_{B}$) for the strategy profile associated to that row and column. We use the letters S for “Stay”, C for “Exit Clause” and F for “Forceful Exit”. While the assumption of simultaneous moves avoids artificial asymmetries, it has the downside of allowing strategy profiles without a clear empirical referent. In particular, one may wonder what it would mean if both simultaneously opt for a forceful exit as in the strategy profile (F, F). However, as we show in the solution of the game, this strategy profile can never be an equilibrium. This confirms the intuition that the strategy profile, though theoretically conceivable, is not empirically relevant.

Table 1 Exit game

The payoffs in Table 1 for $A$ were derived as follows. In the first row A stays. If $B$ stays as well, $A$’s payoff is ${\theta }_{A}+{x}_{A}$ as defined in (4). If $B$ calls the clause, ${\pi }_{A}={c}_{B}-{k}_{A}$, again as defined in (4). If $B$ opts for forceful exit, $A$ suffers the damage ${d}_{A}$. In the second row $A$ calls the exit clause. For (C, S), ${\pi }_{A}=-{c}_{A}-{k}_{A}$ as defined in (4). For (C, C), we assume that each entity pays their agreed exit penalty to the other on top of the one-off costs. For $A$, that means paying ${c}_{A}$, receiving ${c}_{B},$ and paying ${k}_{A}$. For (C, F) we assume that $A$ pays ${c}_{A}$ as well as suffers ${d}_{A}$. In the third row, $A$ opts for a forceful exit. For (F, S), $A$ simply pays ${f}_{A}$. For (F, C), we assume that $A$ receives ${c}_{B}$ but pays ${f}_{A}$. For (F, F), $A$ pays ${f}_{A}$ and suffers ${d}_{A}$. The payoffs for $B$ are the mirror image of those for $A$, replacing the index $A$ by $B$ and vice versa.

3 Socially efficient exit

As pointed out in the introduction, exit clauses may be able to ex-ante enable efficient breach, i.e. dissolving the federation if it is socially efficient to do so. In order to assess this claim, a condition for socially efficient exit first needs to be established. The condition stipulates in which states of the world $({x}_{A},{x}_{B})$ the union should be dissolved when taking into account the payoffs of both players equally.

We present the derivation of the socially efficient exit state as stemming from a social planner who has as an objective function ${\pi }_{C}$, the combination of the members’ payoffs:

$${\pi }_{C}=\left\{\begin{array}{ll}{\theta }_{C}+{x}_{C}& \quad \text{if the federation is maintained}\\ -{k}_{C}& \quad \text{if the federation is dissolved peacefully}\\ -{f}_{i}-{d}_{j}& \quad\text{if }i\text{ dissolves the federation forcefully}\end{array}\right.$$

(5)

where ${\theta }_{C}={\theta }_{A}+{\theta }_{B}, {x}_{C}={x}_{A}+{x}_{B}, {k}_{c}={k}_{A}+{k}_{B}$. Using (3), the probability density function of ${x}_{C}$ depends on $\rho$ and is

$$\begin{array}{lll}\rho =1:&\quad f\left({x}_{C}\right)=0.5 &\quad \forall {x}_{C}\in \left\{-{s}_{A}-{s}_{B},{s}_{A}+{s}_{B}\right\}\\ \rho =0:&\quad f\left({x}_{C}\right)=0.25 &\quad \forall {x}_{C}\in \left\{-{s}_{A}-{s}_{B},{-{s}_{A}+{s}_{B},{s}_{A}-{s}_{B},s}_{A}+{s}_{B}\right\}\\ \rho =-1:&\quad f\left({x}_{C}\right)=0.5 &\quad \forall {x}_{C}\in \left\{-{s}_{A}+{s}_{B},{s}_{A}-{s}_{B}\right\}\end{array}$$

(6)

The social planner will dissolve the union peacefully if

$${\theta }_{C}+{x}_{C}\le -{k}_{C}\iff {x}_{A}+{x}_{B}\le -{(k}_{A}+{k}_{B})-({\theta }_{A}+{\theta }_{B})$$

(7)

Socially efficient exit requires taking into account the states of both members, as well as the total one-off costs of separation ${k}_{C}={k}_{i}+{k}_{j}$. If the combined state ${x}_{A}+{x}_{B}$ drops below the threshold specified in (7), dissolving the union is socially efficient. Consistent with the notion of efficient breach presented in the introduction, socially efficient exit may require hurting one member if this benefits the other member more. Note that since ${f}_{i},{d}_{i}>{k}_{i}$, dissolving the federation forcefully is never socially efficient. If the federation should be dissolved, it is more efficient to do so peacefully.

Substantively, the condition of a low joint state ${x}_{C}$ required for socially efficient exit can be fulfilled if heterogeneity has increased, or if the outside options of both players have improved simultaneously through an increase in free trade or peace. Elements that hurt one member while benefitting another, such as fiscal transfers, do not matter from this perspective. To see this, note that if $x$ is only determined by fiscal transfers, then $\rho =-1$ and ${s}_{A}={s}_{B}$ such that per (6) ${x}_{C}$ is 0 with probability 1. In this case, maintaining the union is ex post socially efficient as long as ${\theta }_{C}+{k}_{C}>0$, which is true provided that both members expected to benefit from it initially (${\theta }_{i}>0).$

Similarly, from the social planner’s point of view, exit penalties are internal transfers and do not matter. However, as the next section shows, for the individual members exit penalties do matter.

4 Optimal exit in a decision-theoretical setting

To analyze the consequences of exit clauses, this section solves a decision-theoretical version of the model, in which only one member can exit. It first discusses optimal exit with a fixed penalty $c$, assuming that any clause is fully binding. In the second subsection the possibility of forceful exit is incorporated. The third subsection shows how state-contingent exit penalties can enable socially efficient exit in the decision-theoretical setting. The fourth subsection discusses the continuous time version presented in the “Appendix”. The next section will show how state-contingent exit penalties can enable socially efficient exit in the game-theoretical setup.

4.1 Optimal exit with an exit clause specifying a penalty ${\varvec{c}}$

In the decision-theoretical version of the model, we assume that only one member can exit from the union. Hence for now we drop the index $i$ to lighten notation. When facing an exit penalty $c$, the total costs of exit are $c+k$. Leaving the federation is optimal if the net benefit from remaining is lower than from paying the exit costs: $\theta +x\le -(c+k)$. Rearranging this equation, the threshold state for exit is

$${x}^{e}=-\theta -(c+k)$$

(8)

The threshold state for exit consists of two components. The first one, $-\theta$, is the most intuitive. If $x$ reaches $-\theta$, the benefits from being in the federation drop to zero. The higher a member’s type $\theta$, the more negative the threshold state for exit: $\frac{\partial {x}^{e}}{\partial \theta }<0$. The second term, $-(k+c)$, reflects the deterring effect of exit costs since $\frac{\partial {x}^{e}}{\partial k}=\frac{\partial {x}^{e}}{\partial c}<0$. The benefit from being in the federation needs to drop to $-\left(k+c\right)$ to make exit worth considering.

In sum, rational exit decisions take into account the exit penalty $c$. The higher the penalty, the lower the threshold state for exit. This is intuitive: the costlier exit, the worse things need to be before exit becomes an optimal decision.

4.2 Optimal exit taking into account the possibility of forceful exit

Arguably, if a member of the federation has the choice between using an exit clause and engaging in a forceful exit, it will pick the option with the lowest cost. Hence exit clauses with costs $c+k$ above $f$ are ineffective as they cannot be enforced: the exit clause will never be used, but a forceful exit will occur if the state drops below ${x}^{e}\left(f\right)=-\theta -f$.

The higher $f$, the less relevant the forceful exit option and hence the less severe the enforcement problem. In particular, if $f>s-\theta$ then ${x}^{e}<-s$ and a forceful exit will not be attractive even in the low state. Conversely, if $f\le s-\theta$ a forceful exit will occur in the low state if $f<c+k$, resulting in an expected payoff of

$$E(\pi )=\left\{\begin{array}{ll}0.5\left(-f\right)+0.5(\theta +s)&\quad {\text{if} }\,\,c>f-k\\ 0.5\left(-c-k\right)+0.5(\theta +s)&\quad {\text{if}}\,-s-\theta -k<c\le f-k\\ -c-k&\quad {\text{if }}\,\,c\le -s-\theta -k\end{array}\right.$$

(9)

4.3 State-contingent exit penalties

In the previous subsection we temporarily reduced our two-player model to a one-player model. We now reintroduce the indices $i$ and $j$ to show that state-contingent exit penalties can induce socially efficient exit in the decision-theoretical setup.

Recall from (8) that $i$ exits if ${x}_{i}\le -{\theta }_{i}-({c}_{i}+{k}_{i})$. Rewriting condition (7), it says that exit is socially efficient if ${x}_{i}\le -({\theta }_{i}+{\theta }_{j})-{x}_{j}-{(k}_{i}+{k}_{j})$. In order to make this condition coincide with $i$’s private condition (8), it suffices to set ${c}_{i}={\theta }_{j}+{x}_{j}+{k}_{j}$, i.e. to make $i$’s penalty contingent on $j$’s state ${x}_{j}$. The intuition is as follows. The higher ${x}_{j}+{\theta }_{j}$, the more member $j$ is enjoying the union and hence the higher should be $i$’s penalty for ending the union. In addition, $i$ normally only cares about its private one-off costs ${k}_{i}$. However, if it exits, $j$ will also incur costs ${k}_{j}$. For socially efficient exit decisions, $i$ needs to be incentivized to take this into account.

Given the possibility of a forceful exit, a first best solution in which exit only happens under condition (7) is not attainable if ${f}_{i}\le {s}_{i}-{\theta }_{i}$, because a forceful exit would then occur if ${x}_{i}=-{s}_{i}$. In this case, the second best solution from a social welfare point of view would be to make sure that using the exit clause is always at least as attractive as exiting forcefully. Since the cost of using the exit clause is ${c}_{i}+{k}_{i}$, and the cost of a forceful exit is ${f}_{i}$, this can be achieved by making sure that ${c}_{i}+{k}_{i}\le {f}_{i}$, i.e. by setting

$${c}_{i}^{*}=Min\{{\theta }_{j}+{x}_{j}+{k}_{j},{f}_{i}-{k}_{i}\}$$

(10)

Setting the penalty for $i$ equal to this expression will result in the highest attainable likelihood of socially efficient exit decisions. If the exit clause were fully binding, a penalty of ${\theta }_{j}+{x}_{j}+{k}_{j}$ would be able to achieve maximal social welfare. However, given the possibility of forceful exit, if ${\theta }_{j}+{x}_{j}+{k}_{j}+{k}_{i}>{f}_{i}$, then states ${x}_{i}\le -{\theta }_{i}-{f}_{i}$ would result in value-destroying forceful exits with ${\pi }_{C}=-{f}_{i}-{d}_{j}$. In contrast, setting ${c}_{i}^{*}=Min\{{\theta }_{j}+{x}_{j}+{k}_{j},{f}_{i}-{k}_{i}\}$ will result in exit-clause based secession in those states, with ${\pi }_{C}=-{k}_{C}$. While it is not the first best solution to dissolve the federation in those cases, at least no additional value is destroyed in a forceful exit.

4.4 Optimal exit in continuous time

So far we have assumed that exit is a discrete time decision. However, in reality it is more natural to think about exit in continuous time: if you do not exit right now, you remain a member and you can exit at a later point. The “Appendix” develops a continuous time model consistent with this intuition.

The reason the rest of the paper focuses on the discrete time model, is tractability: the game-theoretical form of the continuous time model does not have closed form solutions. Also, comparing the decision-theoretical versions of the discrete time and continuous time models, the substantive conclusions are broadly similar. The main difference is that in the continuous time model, like in standard real options models (Dixit 1989), there is some hysteresis. If you are a member, you will remain a member for somewhat worse states than you would according to a non-dynamic model. There is an option logic at work: if you do not leave right now, you retain the option of leaving if the state becomes worse, but also of staying if the state improves again.

5 Optimal exit in a game-theoretical setting

Above we analyzed the case where only one member had an exit option. In this section, we analyze exit in a game-theoretical setting. If players are indifferent between two strategies, we assume that they choose S (stay) over C (clause) over F (forceful exit). Recall that Table 1 presents the normal form of the game, and that for $i\in \{A,B\}$: ${f}_{i},{d}_{i}>{k}_{i}>0$. For each potential realization of $x=({x}_{A},{x}_{B})$ and for each combination of exit penalties $({c}_{A},{c}_{B})$, the strategic nature of this game may be different. Hence giving an exhaustive overview of the potential equilibria is not desirable.

We now show that by introducing state-contingent exit penalties, socially efficient exit can be obtained in the game-theoretical setting as well. Social efficiency requires that the federation is dissolved peacefully if (7) holds, and maintained otherwise. This means that if (7) holds, the equilibrium should be (S, C) (C, S) or (C, C), and otherwise it should be (S, S). However, as discussed previously, given the possibility of forceful exit only a second best solution may be achievable, in which equilibria with C may occur if otherwise equilibria with F would result.

Irrespective of $({x}_{A},{x}_{B})$ and $({c}_{A},{c}_{B})$, if $i$ engages in a forceful exit, $j$ is always better off by staying than by also engaging in a forceful exit. This means (F, F) is always excluded as a Nash equilibrium. Consider making member $i$’s exit penalty conditional on $j$’s state as in (10): ${c}_{i}^{*}=Min\{{\theta }_{j}+{x}_{j}+{k}_{j},{f}_{i}-{k}_{i}\}$. Giving this value to ${c}_{i}$ for both $i\in \{A,B\}$ means that ${c}_{i}+{k}_{i}\le {f}_{i}$, so that F is weakly dominated by C, and only (S, S) (S, C) (C, S) and (C, C) remain as potential equilibria. Suppose $j$ stays, then $i$’s best response is to call the exit clause if $-Min\left\{{\theta }_{j}+{x}_{j}+{k}_{j},{f}_{i}-{k}_{i}\right\}-{k}_{i}\ge {\theta }_{i}+{x}_{i}$ and to stay otherwise. Suppose $j$ calls the clause, then $i$’s best response is to stay if ${c}_{A}>0$ and to call the clause otherwise.

Suppose that the costs of a forceful exit are prohibitive even in the low state, i.e. ${f}_{i}>{s}_{i}-{\theta }_{i}$, so that the first best is achievable. In this case ${c}_{A}^{*}={\theta }_{B}+{x}_{B}+{k}_{B}$ so that A’s best response if B stays is to call the clause if $-{\theta }_{B}-{x}_{B}-{k}_{B}-{k}_{A}\ge {\theta }_{A}+{x}_{A}$, and to stay otherwise. Notice that this condition is equivalent to condition (7) for socially efficient dissolution. If $A$ stays, the same condition results for $B$, who faces ${c}_{B}^{*}={\theta }_{A}+{x}_{A}+{k}_{A}$. Hence if the condition is not fulfilled, and exit is not socially efficient, the only equilibrium is (S, S).

Now observe the following. If (7) holds, ${c}_{A}^{*}+{c}_{B}^{*}={\theta }_{C}+{x}_{C}+{k}_{C}\le 0$. This means that ${c}_{A}$ and ${c}_{B}$ cannot both be positive. If both are negative, then (C, C) is the only equilibrium. If ${c}_{A}$ is positive and ${c}_{B}$ negative the equilibrium is (S, C), and if ${c}_{B}$ is positive and ${c}_{A}$ negative the equilibrium is (C, S). To conclude, if the costs of F are prohibitive, then with state-contingent exit penalties as in (10) socially efficient exit is guaranteed. If exit is not socially efficient, the only equilibrium is (S, S). If it is socially efficient, the equilibrium will be either (C, C) (S, C) or (C, S), so that the federation will be dissolved peacefully.

If the costs of a forceful exit are not prohibitive, i.e. ${f}_{i}\le {s}_{i}-{\theta }_{i}$, then the setting of ${c}_{i}^{*}=Min\left\{{\theta }_{j}+{x}_{j}+{k}_{j},{f}_{i}-{k}_{i}\right\}$ ensures that F is a weakly dominated strategy, so that (C, C) (S, C) or (C, S) will result instead of (S, F) and (F, S). Again, while it is not the first best solution to dissolve the federation in those cases, at least no additional value is destroyed in a forceful exit.

The preceding analysis assumed that exit clauses can be made contingent on players’ states $\left({x}_{A},{x}_{B}\right)$. It concluded that doing this appropriately results in second-best equilibria given the possibility of forceful exit. If $j$’s state is not directly observable by $i$, state-contingent exit penalties may not be feasible (Fearon 1995). However, even with states unobservable by others exit clauses can still be welfare enhancing. In particular, setting ${c}_{i}={f}_{i}-{k}_{i}$ makes F a weakly dominated strategy, hence avoiding socially inefficient forceful exit. These findings run counter to the dominant point of view in the constitutionalist literature that exit clauses should be avoided in federations.

6 Discussion and empirical support

We identified three potential modes of exit: ex-post negotiation, forceful exit, and exit based on an ex-ante agreed exit clause. If both members of a union are benefitting from it (are in a good state), neither will consider exit. Hence in states of the world $({x}_{i},{x}_{j})$ where both ${x}_{i}$ and ${x}_{j}$ are high the union continues.

The formal model solved above assumed that a negotiated exit is precluded. However, in the absence of obstacles to negotiating exit, if it is socially efficient those better off outside could offer an acceptable side-payment for exit and make everyone better off. Hence without obstacles to negotiation socially efficient exit would occur irrespective of a potential exit clause.

The formal model also did not incorporate the possibility of an anti-secession war. Intuitively, if $i$ triggers an exit clause, an anti-secession war may be attractive to $j$ if the lost benefits from the federation weigh up to the cost of such a war. However, the reputational cost of reneging on a constitutional exit right will likely be prohibitive, especially to democracies.

Combining the conclusions of our formal model with the discussion of negotiated exit and anti-secession wars, we conclude the following. If $i\in \{A,B\}$ is in a bad state (low ${x}_{i}$), its decision whether to exit depends on the exit costs of its cheapest mode of exit. If there is an exit clause, the associated costs consist of the penalty ${c}_{i}$ and the one-off costs ${k}_{i}$. If there are no barriers to ex-post negotiation exit occurs when it is socially efficient. If a negotiated exit is not possible because dissolving the union would not be efficient (i.e. $j$ is benefitting more from the union than $i$ is losing), or because of barriers to negotiation, then $i$ considers unilateral exit (clause-based or forceful). The costs of forceful exit are ${f}_{i}$. Since $i$ picks the cheapest option, the exit costs are equal to $Min\{{c}_{i}+{k}_{i},{f}_{i}\}$. The higher $i$’s exit costs, the lower the state ${x}_{i}$ can drop until exit becomes optimal for $i$. If $j$ has low reputational costs, it may start an anti-secession war if $i$ triggers an exit clause.

We have argued theoretically that exit clauses with state-contingent penalties can enable efficient breach from a federation. Since there are no real-world federal constitutions that ex-ante allow exit upon payment of a penalty, this claim cannot be evaluated empirically. However, below we discuss two relevant cases that may serve as plausibility probes: Montenegro and Saint Kitts and Nevis.

The case of Montenegro clearly supports the claim that constitutional exit clauses may enable peaceful secession. In 2006 Montenegro used the exit clause that was entered in the constitution of the State Union of Serbia and Montenegro in 2003. Serbia accepted the independence peacefully. The fact that the exit clause was called just shortly after the stipulated 3-year waiting period suggests that exit clauses really can play a binding role in enabling peaceful secession. This conclusion seems even stronger in the broader context of the Yugoslav breakup. There was no exit clause available to Slovenia, Croatia, Bosnia-Herzegovina, Macedonia or Kosovo, and so they all seceded forcefully—resulting in violence in Slovenia, Croatia, Bosnia-Herzegovina and Kosovo.⁵

While Nevis has had a right to secede from the two-island federation of Saint Kitts and Nevis since its creation in 1983, the federation is still intact. In 1998, a referendum was organized but the requisite two-thirds majority was not obtained. This shows that including conditions in the exit clause (be it in the form of an exit penalty or a supermajority) can allow exit without automatically making it liable to happen. In fact, the federation may precisely still be together because of the exit clause. With only three of the eleven seats in the federal parliament, Nevis is often not represented at all in the ruling federal coalitions (Veenendaal 2015). The fact that Nevis may secede gives an incentive to Kittitian politicians to take its welfare into account as well. This points to a second role for exit clauses, to be investigated in future work: they may function as safeguards protecting minorities against excessive centralization and unfavorable policy changes.

While we claim that constitutional exit clauses may be beneficial both on theoretical and empirical grounds, we do not claim that an exit clause is always a necessary condition for peaceful secession. In some cases, secession may be negotiated peacefully even in the absence of a clause. Examples that come to mind are the “velvet divorce” of Czechoslovakia in 1993, and the independence of Norway from Sweden in 1905. However, given the high frequency of civil wars over independence, it is clear that there are many barriers to ex-post negotiation. This is why we think that ex-ante negotiated exit clauses may improve outcomes. Given the possibility of stipulating fines or other conditions, they need not make secession more likely than under the implicit option of forceful exit.

The case of the EU illustrates the importance of including an exit penalty in the clause to obtain efficient exit. Most observers would agree that the UK leaving the EU is not efficient. A naïve conclusion would be that exit clauses increase the likelihood of (inefficient) exit. However, Article 50 does not provide for a penalty.⁶ An example of a penalty that could have been included explicitly—and that perhaps could have dissuaded the British public from voting to leave—would be the payment of a certain number of additional years of budget contribution without corresponding membership benefits, or the reimbursement of the EU’s administrative costs related to Brexit.

7 Conclusion

We presented a political economic analysis of secession and exit clauses in federations. In our model, a member’s benefits from a federation are determined by its type and its state. Because of changes in the state of the world, a member’s ex-post benefits may be higher or lower than expected. If a member’s ex-post benefits are negative, i.e. it is in a sufficiently low state, it may wish to exit if the exit costs are not prohibitive.

Exit costs depend on the mode of exit. If a federation has an exit clause, exit can occur on the basis of such a clause. Exit clauses can contain several conditions, among which we focused on exit penalties. If there is no exit clause, or the exit cost is high, exit may occur forcefully. The costs of such forceful exit consist of tangible costs (such as military expenses) and reputational costs (which depend on the international recognition of the exit). A third mode of exit is through ex-post negotiation, although this can be expected to be difficult because of barriers to renegotiation.

If there is an exit clause with a low penalty, and exit occurs while other members are benefitting a lot from the union, they may try to prevent exit forcefully through an anti-secession war. However, such attempted prevention of legal exit carries heavy reputational costs, especially for democracies.

When a member exits, the benefits for the other members of that member being in the union are also lost. From a social welfare perspective, exit should occur if and only if it generates value taking all members’ benefits into account: this is the principle of efficient breach. Based on a game-theoretical model, we showed that appropriate state-contingent exit penalties can ex-ante enable efficient breach. If exit penalties cannot be made state-contingent, fixed exit penalties can still increase social welfare by avoiding forceful exit. These findings run counter to the dominant point of view in the constitutionalist literature that exit clauses should be avoided in federations.

Our theoretical models are obviously simplified, and in no way definitive. However, we do hope that in light of the severity of the problem of secessionism and civil wars, our research at least prompts further investigation of the potential of ex-ante negotiated exit clauses.

An obvious question in light of our results is why exit clauses are not more prevalent in real-world federations. We tentatively advance two reasons. First, politicians negotiating federations may wish to tie their successors’ hands. In our model, we assumed that each federal entity could be represented as a unitary actor. In practice, each federal entity may be composed of a heterogeneous population. If that is the case, politicians whose electorate expect to benefit more from the federation may want to prevent exit in the future by not having an exit clause. Second, federations may not be rationally designed. This may be especially true for long-established federal countries. But even for modern federations there may be a norm against exit clauses because they are perceived as going against the spirit of collaboration. After all, who likes to talk about divorce on their wedding day (Weiler 1985)?

We leave for future research the negotiation of exit clauses. Given their distributional implications, the bargaining process will be important and socially efficient exit clauses are not guaranteed. However, to the extent that members are negotiating behind a veil of ignorance, their ex-ante preferences over exit clauses will be closer to the social optimum and ex-ante negotiations over a clause will be easier than ex-post negotiations over exit directly. In spite of potential information problems and strategic bargaining for concessions once exit clauses are in place (Anesi 2012; Olofsgård 2004), if ex-ante agreed exit clauses can reduce the incidence of secessionist violence they could do the world a great service. On the other hand, as the discussion of Brexit shows, if exit clauses are included, clear exit penalties or conditions are required to deter inefficient secession.

A second area for future research is to make members’ states endogenous. In the model presented here, the payoff-relevant state of the world is exogenous. In practice members may be able to change how the state of the world affects their payoffs by renegotiating the terms of the union. For instance, if at some point the prevailing transfers make the federation undesirable to a member, this member will likely try to renegotiate the laws affecting transfers before considering exit.

Appendix

We now set up and solve a decision-theoretical model of exit in continuous time. The model builds on Dixit (1989) and Dixit and Pindyck (1994), who study firms’ decisions to enter and exit markets with changing output prices. However, since output prices are normally positive, they focus on geometric Brownian motions. In contrast, the model presented here assumes a standard Brownian motion because the benefits from a federation can become negative.

In what follows, we assume for simplicity that exit is definitive and that there is no possibility of re-entering later. However, even if re-entry is free the qualitative conclusions from our model would still hold, but the solution process would be complicated as the optimal exit decisions and optimal entry decisions would be mutually interdependent.

First, assume that member $i$’s net benefit flow from being in the federation at time $t$ is given by

$${\pi }_{i}\left(t\right)={x}_{i}\left(t\right)+{\theta }_{i}$$

(11)

where ${x}_{i}(t)$ represents member $i$’s state at time $t$, and ${\theta }_{i}$ its type, as in the main text.

The state of the world captures the changes in benefits over time, which are uncertain. For simplicity, assume that member $i$’s state ${x}_{i}(t)$ evolves according to a Brownian motion without drift and with variance ${\sigma }_{i}^{2}$. A Brownian motion is a mathematical representation of a random process over time. Over any given time period $dt$, it can go up or down. The increments $d{x}_{i}$ have a normal distribution characterized by variance ${\sigma }_{i}^{2}$ (Mörters and Peres 2010). A higher variance ${\sigma }_{i}^{2}$ means that member $i$’s benefits are expected to fluctuate more. Formally, a Brownian motion is characterized by

$$d{x}_{i}={\sigma }_{i}{\epsilon }_{it}\sqrt{dt}$$

(12)

where ${\epsilon }_{it}$ has a standard normal distribution and is serially uncorrelated so that for all $t>0$

$$E\left[{\epsilon }_{it}\right]=0,\quad Var\left({\epsilon }_{it}\right)=E\left[{\epsilon }_{it}^{2}\right]=1,\quad E\left[{\epsilon }_{i{t}_{1}}{\epsilon }_{i{t}_{2}}\right]=0,\quad {t}_{1}\ne {t}_{2}$$

(13)

This implies that $E[d{x}_{i}]=0$ and $E[{(d{x}_{i})}^{2}]={\sigma }_{i}^{2}dt$: benefits are expected to remain the same, but have a variance of ${\sigma }_{i}^{2}$ per unit of time.

Without loss of generality, suppose that the union starts at $t=0$ and set ${x}_{i}\left(0\right)=0$. Since we have assumed no drift in the states ${x}_{i}$, their ex ante expected value is 0 for any future date $T$; mathematically, $E\left[{x}_{i}\left(T\right)\right]=0, \forall T>0$. Similarly, the expected value at time $t$ for a later time $T$ is simply the value at the time of the expectation: ${E}_{t}\left[{x}_{i}\left(T\right)\right]={x}_{i}(t)$. At time $t$ the probability density for time $T$ at state ${x}_{i}$ is

$${P}_{t}\left({x}_{i}\left(T\right)={x}_{i}\right)=\phi \left({x}_{i};{x}_{i}\left(t\right),{\sigma }_{i}^{2}(T-t)\right)=\phi \left(\frac{{x}_{i}-{x}_{i}\left(t\right)}{{\sigma }_{i}\sqrt{T-t}}\right)$$

(14)

where $\phi (x;\mu ,{\sigma }^{2})$ is the probability density function (pdf) of the normal distribution with mean $\mu$ and variance ${\sigma }^{2}$, and $\phi (x)$ is the pdf of the standard normal distribution. Substantively, this means that the expected change in ${x}_{i}$ over any time period $T-t$ is zero and that large changes are less likely than small changes. However, since the variance increases linearly with the time period $T-t$ the expected magnitude of changes increases with time.

Assume that the members have a common discount rate $r$, so that the expected discounted benefit from the union for member $i$ until time $T$ is $E\left[{\int }_{0}^{T}{\pi }_{i}\left(t\right){e}^{-rt}dt\right]$. The ex-ante expected value for member $i$ from a perpetual union is

$$E\left[{\int }_{0}^{+\infty }{\pi }_{i}\left(t\right){e}^{-rt}dt\right]= \underset{T\to +\infty }{\mathrm{l}\mathrm{i}\mathrm{m}}\left(\frac{{\theta }_{i}}{r}-\frac{{\theta }_{i}}{r}{e}^{-rT}\right)=\frac{{\theta }_{i}}{r}$$

(15)

In the decision-theoretical version of the model, we assume that only one member can exit from the union, and only consider that member. Hence we drop the index $i$ to lighten notation.

When thinking about exit in a continuous time set-up, a member compares the expected value of maintaining the union to the value of exiting right now. Assuming rationality, the expected value of maintaining the union right now should take as a given optimal exit behavior in the future. This is captured by the notion of continuation value: the continuation value $V(x)$ is the expected discounted benefit from maintaining the union when the current state is $x$, assuming optimal exit behavior in the future (Dixit and Pindyck 1994).

At any point in time, in order for a member to be willing to maintain the union for $dt$ longer, the expected change in the continuation value combined with the benefit flow (11) over $dt$ should add up to the normal return $rV\left(x\right)dt$:

$$E\left[dV\right]+\left(x+\theta \right)dt=rV\left(x\right)dt$$

(16)

Determining the continuation value is just like pricing a stock with expected appreciation $E[dV]$ and dividend flow $x+\theta$. By Ito’s lemma, $dV=\frac{\partial V}{\partial t}dt+\frac{\partial V}{\partial x}dx+\frac{1}{2}\frac{{\partial }^{2}V}{\partial {x}^{2}}{\left(dx\right)}^{2}$; see Øksendal (1991) for the theory of stochastic differential equations and a discussion of Ito’s lemma. The benefit flow does not depend on calendar time directly: $\frac{\partial V}{\partial t}=0$. Together with (12), $E\left[dx\right]=0$ and $E[{(d{x}_{i})}^{2}]={\sigma }_{i}^{2}dt$, this implies

$$dV={V}^{\prime}\left(x\right)dx+\frac{1}{2}{V}^{\prime \prime}\left(x\right){\sigma }^{2}{\epsilon }_{t}^{2}dt\Rightarrow E[dV]=\frac{1}{2}{V}^{\prime \prime}\left(x\right){\sigma }^{2}dt$$

(17)

By substituting (17) in (16), we find

$$\frac{1}{2}{\sigma }^{2}{V}^{\prime \prime}\left(x\right)-rV\left(x\right)=-x-\theta $$

(18)

This is a second order differential equation in $x$: we solve it by first identifying the solution ${V}_{h}(x)$ of the homogeneous equation $\frac{1}{2}{\sigma }^{2}{V}^{\prime \prime}\left(x\right)-rV\left(x\right)=0$. Next we identify a particular solution ${V}_{p}\left(x\right)$ which satisfies the equation $\frac{1}{2}{\sigma }^{2}{V}^{\prime \prime}\left(x\right)-rV\left(x\right)=-x-\theta$. The general solution is given by the particular solution plus any linear combination of solutions to the homogeneous equation. For the homogeneous part, we try a solution of the form $V\left(x\right)={e}^{\lambda x}$. This yields

$${V}_{h}\left(x\right)=A{e}^{\alpha x}+B{e}^{\beta x}, \quad \alpha =\sqrt{\frac{2r}{{\sigma }^{2}}}, \beta =-\sqrt{\frac{2r}{{\sigma }^{2}}}$$

(19)

with constants $A$ and $B$ to be identified. Note that $\alpha >0$ and $\beta =-\alpha <0$. For a particular solution, we try $V\left(x\right)=ax+b$. This yields the solution ${V}_{p}\left(x\right)=\frac{x+\theta }{r}$. This is the expected perpetuity value from the union starting from state $x$. Combining the particular solution with the homogeneous part, the general solution is

$$V\left(x\right)={V}_{p}\left(x\right)+{V}_{h}\left(x\right)=\frac{x+\theta }{r}+ A{e}^{\alpha x}+B{e}^{\beta x}$$

(20)

Since ${V}_{p}(x)$ represents the value from maintaining the union perpetually, ${V}_{h}\left(x\right)$ represents the option value of exit, which should be positive. As the state improves, the value of the exit option should converge to 0: the better the state, the higher the benefit flow and the less valuable the exit option. This implies that $A=0$ since $\alpha >0$. We now have an expression for the continuation value $V(x)$ up to the constant $B$.

$$V\left(x\right)=\frac{x+\theta }{r}+B{e}^{\beta x} , \quad \beta =-\sqrt{\frac{2r}{{\sigma }^{2}}}$$

(21)

The continuation value is the value of maintaining the union for now, assuming optimal behavior for the future. Hence the constant $B$ depends on the optimal exit state ${x}^{e}$. Two conditions are needed for optimal exit in a continuous time stochastic model (Dixit and Pindyck 1994). The first is Value Matching (VM): exit should occur when $V(x)$ drops to the value of the outside option. In our model, the outside option consists of paying the one-off costs and the penalty $c$, which corresponds to a value of $-k-c$. The second condition is Smooth Pasting (SP): optimal stopping requires that $V^{\prime}(x)$ be equal to the derivative of the value of being outside of the union—which is 0 in our case, since the exit value does not depend on the state.

Grouping the two conditions we obtain a system with two equations and two unknowns (${x}^{e},B){:}$

$$V\left({x}^{e}\right)=-k-c\iff \frac{{x}^{e}+\theta }{r}+B{e}^{\beta {x}^{e}}=-k-c \quad\quad{\varvec{V}}{\varvec{M}}$$

(22)

$${V}^{\prime}\left({x}^{e}\right)=0\iff \frac{1}{r}+\beta B{e}^{\beta {x}^{e}}=0 \quad\quad{\varvec{S}}{\varvec{P}}$$

(23)

The solutions for (${x}^{e},B)$ are.

$${x}^{e}=-\theta -r\left(k+c\right)+\frac{1}{\beta },\quad B=-\frac{{e}^{-\beta {x}^{e}}}{r\beta }$$

(24)

The optimal exit state consists of three components. The first one, $-\theta$, is the most intuitive. When $x$ reaches $-\theta$, the benefit flow drops to zero: $\pi \left(t|x\left(t\right)=-\theta \right)=-\theta +\theta =0$. The higher a member’s type $\theta$, the longer it is optimal to stay in the union, i.e. the more negative the optimal exit state: $\frac{\partial {x}^{e}}{\partial \theta }<0$. The second term, $-r(k+c)$, reflects the deterring effect of exit costs since $\frac{\partial {x}^{e}}{\partial k}=\frac{\partial {x}^{e}}{\partial c}<0$. The benefit flow needs to drop to $-r\left(k+c\right)$ to make exit worth considering, since the corresponding expected perpetuity value at that state would be equal to minus the exit costs $-(k+c)$.

The third term, $1/\beta$, is the least intuitive but can be interpreted as the optimal forbearance level. The equivalent of this term does not feature in the discrete time model presented in the main text. It reflects sophisticated rational behavior under the option logic: one should be willing to sustain some losses in the hope that the state improves again. Intuitively, the higher the variance of the benefits, the higher the possibility that a bad state turns around, and the more reluctant one should be to exit.