Abstract
Verification of programs using floating-point arithmetic is challenging on several accounts. One of the difficulties of reasoning about such programs is due to the peculiarities of floating-point arithmetic: rounding errors, infinities, non-numeric objects (NaNs), signed zeroes, denormal numbers, different rounding modes, etc. One possibility to reason about floating-point arithmetic is to model a program computation path by means of a set of ternary constraints of the form  and use constraint propagation techniques to infer new information on the variables’ possible values. In this setting, we define and prove the correctness of algorithms to precisely bound the value of one of the variables x, y or z, starting from the bounds known for the other two. We do this for each of the operations and for each rounding mode defined by the IEEE 754 binary floating-point standard, even in the case the rounding mode in effect is only partially known. This is the first time that such so-called filtering algorithms are defined and their correctness is formally proved. This is an important slab for paving the way to formal verification of programs that use floating-point arithmetics.
and use constraint propagation techniques to infer new information on the variables’ possible values. In this setting, we define and prove the correctness of algorithms to precisely bound the value of one of the variables x, y or z, starting from the bounds known for the other two. We do this for each of the operations and for each rounding mode defined by the IEEE 754 binary floating-point standard, even in the case the rounding mode in effect is only partially known. This is the first time that such so-called filtering algorithms are defined and their correctness is formally proved. This is an important slab for paving the way to formal verification of programs that use floating-point arithmetics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Programs using floating-point numbers are notoriously difficult to reason about [33]. Many factors complicate the task:
-
1.
compilers may transform the code in a way that does not preserve the semantics of floating-point computations;
-
2.
floating-point formats are an implementation-defined aspect of most programming languages;
-
3.
there are different, incompatible implementations of the operations for the same floating-point format;
-
4.
mathematical libraries often come with little or no guarantee about what is actually computed;
-
5.
programmers have a hard time predicting and avoiding phenomena caused by the limited range and precision of floating-point numbers (overflow, absorption, cancellation, underflow, etc.); moreover, devices that modern floating-point formats possess in order to support better handling of such phenomena (infinities, signed zeroes, denormal numbers, non-numeric objects a.k.a. NaNs) come with their share of issues;
-
6.
rounding is a source of confusion in itself; moreover, there are several possible rounding modes and programs can change the rounding mode any time.
As a result of these difficulties, the verification of floating-point programs in industry relies, almost exclusively, on informal methods, mainly testing, or on the evaluation of the numerical accuracy of computations, which only allows to determine conservative (but often too loose) bounds on the propagated error [19].
The satisfactory formal treatment of programs engaging in floating-point computations requires an equally satisfactory solution to the difficulties summarized in the above enumeration. Progress has been made, but more remains to be done. Let us review each point:
-
1.
Some compilers provide options to refrain from rearranging floating-point computations. When these are not available or cannot be used, the only possibility is to verify the generated machine code or some intermediate code whose semantics is guaranteed to be preserved by the compiler back-end.
-
2.
Even though the used floating-point formats are implementation-defined aspects of, say, C and C++Footnote 1 the wide adoption of the IEEE 754 standard for binary floating-point arithmetic [24] has improved things considerably.
-
3.
The IEEE 754 standard does provide some strong guarantees, e.g., that the results of individual additions, subtractions, multiplications, divisions and square roots are correctly rounded, that is, it is as if the results were computed in the reals and then rounded as per the rounding mode in effect. But it does not provide guarantees on the results of other operations and on other aspects, such as, e.g., when the underflow exception is signaled [17].Footnote 2
-
4.
A pragmatic, yet effective approach to support formal reasoning on commonly used implementation of mathematical functions has been recently proposed in [6]. The proposed techniques exploit the fact that the floating-point implementation of mathematical functions preserve, not completely but to a great extent, the piecewise monotonicity nature of the approximated functions over the reals.
-
5.
A static analysis for detecting floating-point exceptions based on abstract interpretation has been presented in [32]. A few attempts at this task have been made using other techniques [7, 38] but, as we argue in Sections 1.4 and 5, they present precision and soundness issues.
-
6.
Most verification approaches in the literature assume the round-to-nearest rounding mode [10], or over-approximate by always considering worst-case rounding modes [32]. Analyses based on SMT solvers [13] can treat each rounding mode precisely, but only if the rounding mode in use is known exactly. As we show in Section 5, some SMT solvers also suffer from soundness issues.
The contribution of this paper is in areas 5 and 6. In particular, concerning point 5, by defining and formally proving the correctness of constraint propagation algorithms for IEEE 754 arithmetic constraints, we enable the use of formal methods for a broad range of programs. Such methods, i.e., abstract interpretation and symbolic model checking, allow for proving that a number of generally unwanted phenomena (e.g., generation of NaNs and infinities, absorption, cancellation, instability, etc.) do not happen or, in case they do happen, allow the generation of a test vector to reproduce the issue. Regarding point 6, handling of all IEEE 754 rounding modes, and being resilient to uncertainty about the rounding mode in effect, is another original contribution of this paper.
While the round-to-nearest rounding mode is, by far, the most frequently used one, it must be taken into account that:
-
the possibility of programmatically changing the rounding mode is granted by IEEE 754 and is offered by most of its implementations (e.g., in the C programming language, via the fesetround() standard function);
-
such possibility is exploited by interval libraries and by numerical calculus algorithms (see, e.g., [35, 36]);
-
setting the rounding mode to something different from round-to-nearest can be done by third parties in a way that was not anticipated by programmers: this may cause unwanted non-determinism in video games [20] and there is nothing preventing the abuse of this feature for more malicious ends, denial-of-service being only the least dangerous in the range of possibilities. Leaving malware aside, there are graphic and printer drivers and sound libraries that are known to change the rounding mode and may fail to set it back [37].
As a possible way of tackling the difficulties described until now, and enabling sound formal verification of floating-point computations, this paper introduces new algorithms for the propagation of arithmetic constraints over floating-point numbers. These algorithms are called filtering algorithms as their purpose is to prune the domains of possible variable values by filtering out those values that cannot be part of the solution of a system of constraints. Algorithms of this kind must be employed in constraint solvers that are required in several different areas, such as automated test-case generation, exception detection or the detection of subnormal computations. In this paper we propose fully detailed, provably correct filtering algorithms for floating-point constraints. Such algorithms handle all values, including symbolic values (NaNs, infinities and signed zeros), and rounding modes defined by IEEE 754. Note that filtering techniques used in solvers over the reals do not preserve all solutions of constraints over floating-point numbers [30, 31], and therefore they cannot be used to prune floating-point variable domains reliably. This leads to the need of filtering algorithms such as those we hereby introduce.
The choice of the IEEE 754 Standard for floating-point numbers as the target representation for our algorithms is due to their ubiquity in modern computing platforms. Indeed, although some programming languages leave the floating-point format as an implementation-defined aspect, all widely-used hardware platforms —e.g., x86 [25] and ARM [3]—only implement the IEEE 754 Standard, while older formats are considered legacy.
Before defining our filtering algorithms in a detailed and formal way, we provide a more comprehensive context on the propagation of floating-point constraints and its practical applications (Sections 1.1 and 1.2), and justify their use in formal program analysis and verification (Section 1.3). We also give a more in-depth view of related work in Section 1.4, and clarify our contribution in Section 1.5.
1.1 From programs to floating-point constraints
Independently from the application, program analysis starts with parsing, the generation of an abstract syntax tree and the generation of various kinds of intermediate program representations. An important intermediate representation is called three-address code (TAC). In this representation, complex arithmetic expressions and assignments are decomposed into sequences of assignment instructions of the form
A further refinement is the computation of the static single assignment form (SSA) [2] whereby, labeling each assigned variable with a fresh name, assignments can be considered as if they were equality constraints. For example, the TAC form of the floating-point assignment := ∗ + is := ∗; := +, which in an SSA form becomes 1 := 1 ∗1;2 := 1 + 1. These, in turn, can be regarded as the conjunction of the constraints \(t_{1} = z_{1} \boxdot z_{1}\) and \(z_{2} = t_{1} \boxplus z_{1}\), where by \(\boxdot \) and \(\boxplus \) we denote the multiplication and addition operations on floating-point numbers, respectively. The Boolean comparison expressions that appear in the guards of if statements and loops can be translated into constraints similarly. This way, a C/C++ program translated into an SSA-based intermediate representation can be represented as a set of constraints on its variables. In particular, a constraint set arises form each execution path in the program. For this reason, this approach to program modeling can be viewed as symbolic execution [15, 26]. Constraints can be added or removed from such a set in order to obtain a constraint system that describes a particular behavior of the program (e.g., the execution of a certain instruction, the occurrence of an overflow in a computation, etc.). Once such a constraint system has been solved, the variable domains only contain values that cause the desired behavior. If one of the domains is empty, then that behavior can be ruled out. For more details on the symbolic execution of floating-point computations, we refer the reader to [4, 10].
1.2 Constraint propagation
Once constraints have been generated, they are amenable to constraint propagation: under this name goes any technique that entails considering a subset of the constraints at a time, explicitly removing elements from the set of values that are candidate to be assigned to the constrained variables. The values that can be removed are those that cannot possibly participate in a solution for the selected set of constraints. For instance, if a set of floating-point constraints contains the constraint \(x \boxdot x = x\), then any value outside the set \(\{ \text {NaN}, +0, 1, +\infty \}\) can be removed from further consideration. The degree up to which this removal can actually take place depends on the data-structure used to record the possible values for x, intervals and multi-intervals being typical choices for numerical constraints. For the example above, if intervals are used, the removal can only be partial (negative floating-point numbers are removed from the domain of x). With multi-intervals more precision is possible, but any approach based on multi-intervals must take measures to avoid combinatorial explosion.
In this paper, we only focus on interval-based constraint propagation: the algorithms we present for intervals can be rather easily generalized to the case of multi-intervals. We make the further assumption that the floating-point formats available to the analyzed program are also available to the analyzer: this is indeed quite common due to the wide adoption of the IEEE 754 formats.
Interval-based floating-point constraint propagation consists of iteratively narrowing the intervals associated to each variable: this process is called filtering. A projection is a function that, given a constraint and the intervals associated to two of the variables occurring in it, computes a possibly refined interval for the third variable (the projection is said to be over the third variable). Taking \(z_{2} = t_{1} \boxplus z_{1}\) as an example, the projection over z2 is called direct projection (it goes in the same sense of the TAC assignment it comes from), while the projections over t1 and z1 are called indirect projections.
1.3 Applications of constraint propagation to program analysis
When integrated in a complete program verification framework, the constraint propagation techniques presented in this paper enable activities such as abstract interpretation, automatic test-input generation and symbolic model checking. In particular, symbolic model checking means exhaustively proving that a certain property, called specification, is satisfied by the system in exam, which in this case is a computer program. A model checker can either prove that the given specification is satisfied, or provide a useful counterexample whenever it is not.
For programs involving floating-point computations, some of the most significant properties that can be checked consist of ruling out certain undesired exceptional behaviors such as overflows, underflows and the generation of NaNs, and numerical pitfalls such as absorption and cancellation. In more detail, we call a numeric-to-NaN transition a floating-point arithmetic computation that returns a NaN despite its operands being non-NaN. We call a finite-to-infinite transition the event of a floating-point operation returning an infinity when executed on finite operands, which occurs if the operation overflows. An underflow occurs when the output of a computation is too small to be represented in the machine floating-point format without a significant loss in accuracy. Specifically, we divide underflows into three categories, depending on their severity:
- Gradual underflow::
-
an operation performed on normalized numbers results in a subnormal number. In other words, a subnormal has been generated out of normalized numbers: enabling gradual underflow is indeed the very reason for the existence of subnormals in IEEE 754. However, as subnormals come with their share of problems, generating them is better avoided.
- Hard underflow::
-
an operation performed on normalized numbers results in a zero, whereas the result computed on the reals is nonzero. This is called hard because the relative error is 100%, gradual overflow does not help (the output is zero, not a subnormal), and, as neither input is a subnormal, this operation may constitute a problem per se.
- Soft underflow::
-
an operation with at least one subnormal operand results in a zero, whereas the result computed on the reals is nonzero. The relative error is still 100% but, as one of the operands is a subnormal, this operation may not be the root cause of the problem.
Absorption occurs when the result of an arithmetic operation is equal to one of the operands, even if the other one is not the neutral element of that operation. For example, absorption occurs when summing a number with another one that has a relatively very small exponent. If the precision of the floating-point format in use is not enough to represent them, the additional digits that would appear in the mantissa of the result are rounded out.
Definition 1 (Absorption)
Let \(x, y, z \in \mathbb {F}\) with \(y, z \in \mathbb {R}\), let  be any IEEE 754 floating-point operator, and let
be any IEEE 754 floating-point operator, and let  . Then
. Then  gives rise to absorption if
gives rise to absorption if
-
 and either x = y and z≠ 0, or x = z and y≠ 0;
and either x = y and z≠ 0, or x = z and y≠ 0; -
 and either x = y and z≠ 0, or x = −z and y≠ 0;
and either x = y and z≠ 0, or x = −z and y≠ 0; -
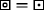 and either x = ±y and z≠ ± 1, or x = ±z and y≠ ± 1;
and either x = ±y and z≠ ± 1, or x = ±z and y≠ ± 1; -
 , x = ±y and z≠ ± 1.
, x = ±y and z≠ ± 1.
In this section, we show how symbolic model checking can be used to either rule out or pinpoint the presence of these run-time anomalies in a software program by means of a simple but meaningful practical example. Floating-point constraint propagation has been fully implemented with the techniques presented in this paper in the commercial tool ECLAIR,Footnote 3 developed and commercialized by BUGSENG. ECLAIR is a generic platform for the formal verification of C/C++ and Java source code, as well as Java bytecode. The filtering algorithms described in the present paper are used in the C/C++ modules of ECLAIR that are responsible for semantic analysis based on abstract interpretation [16], automatic generation of test-cases, and symbolic model checking. The latter two are based on symbolic execution and constraint satisfaction problems [22, 23], whose solution is based on multi-interval refinement and is driven by labeling and backtracking search. Indeed, the choice of ECLAIR as our target verification platform is mainly due to its use of constraint propagation for solving constraints generated by symbolic execution, which makes it easier to integrate the algorithms presented in this paper. However, such techniques are general, and could be used to solve the constraints generated by any symbolic execution engine.
Constraints arising from the use of mathematical functions provided by C/C++ standard libraries are also supported. Unfortunately, most implementations of such libraries are not correctly rounded, which makes the realization of filtering algorithms for them rather challenging. In ECLAIR, propagation for such constraints is performed by exploiting the piecewise monotonicity properties of those functions, which are partially retained by all implementations we know of [6].
To demonstrate the capabilities of the techniques presented in this paper, we applied them to the C code excerpt of Fig. 1. It is part of the implementation of the Bessel functions in the GNU Scientific Library,Footnote 4 a widely adopted library for numerical computations. In particular, it computes the scaled regular modified cylindrical Bessel function of first order, \(\exp (-|x|)I_{1}(x)\), where x is a purely imaginary argument. The function stores the computed result in the val field of the data structure result, together with an estimate of the absolute error (result->err). Additionally, the function returns an int status code, which reports to the user the occurrence of certain exceptional conditions, such as overflows and underflows. In particular, this function only reports an underflow when the argument is smaller than a constant. We analyzed this program fragment with ECLAIR’s symbolic model checking engine, setting it up to detect overflow (finite-to-infinite transitions), underflow and absorption events, and NaN generation (numeric-to-NaN transitions). Thus, we found out the underflow guarded against by the if statement of line 12 is by far not the only numerical anomaly affecting this function. In total, we found a numeric-to-NaN transition, two possible finite-to-infinite transitions, two hard underflows, 5 gradual underflows and 6 soft underflows. The code locations in which they occur are all reported in Fig. 1.
Function extracted from the GNU Scientific Library (GSL), version 2.5. The possible numerical exceptions detected by ECLAIR are marked by the raised letters next to the operators causing them. h, s and g stand for hard, soft and gradual underflow, respectively; a for absorption; i for finite-to-infinity; n for numeric-to-NaN
For each one of these events, ECLAIR yields an input value causing it. Also, it optionally produces an instrumented version of the original code, and runs it on every input it reports, checking whether it actually triggers the expected behavior or not. Hence, the produced input values are validated automatically. For example, the hard underflow of line 17 is triggered by the input = -0x1.8p-1021≈− 6.6752 × 10− 308. If the function is executed with = -0x1p + 1023≈− 8.9885 × 10307, the multiplication of line 29 yields a negative infinity. Since = ||, we know = 0x1p + 1023 would also cause the overflow. The same value of causes an overflow in line 30 as well. The division in the same line produces a NaN if the function is executed with \(\mathtt {x} = -\infty \).
The context in which the events we found occur determines whether they could cause significant issues. For example, even in the event of absorption, the output of the overall computation could be correctly rounded. Whether or not this is acceptable must be assessed depending on the application. Indeed, the capability of ECLAIR of detecting absorption can be a valuable tool to decide if a floating-point format with a higher precision is needed. Nevertheless, some of such events are certainly problematic. The structure of the function suggests that no underflow should occur if control flow reaches past the if guard of line 12. On the contrary, several underflows may occur afterwards, some of which are even hard. Moreover, the generation of infinities or NaNs should certainly either be avoided, or signaled by returning a suitable error code (and not GSL_SUCCESS). The input values reported by ECLAIR could be helpful for the developer in fixing the problems detected in the function of Fig. 1. Furthermore, the algorithms presented in this paper are provably correct. For this reason, it is possible to state that this code excerpt presents no other issues besides those we reported above. Notice, however, that due to the way the standard C mathematical library functions are treated, the results above only hold with respect to the implementation of the function in use. In particular, the machine we used for the analysis is equipped with the x86_64 version of EGLIBC 2.19, running on Ubuntu 14.04.1.
1.4 Related work
1.4.1 Filtering algorithms
In [30] C. Michel proposed a framework for filtering constraints over floating-point numbers. He considered monotonic functions over one argument and devised exact direct and correct indirect projections for each possible rounding mode. Extending this approach to binary arithmetic operators is not an easy task. In [10], the authors extended the approach of [30] by proposing filtering algorithms for the four basic binary arithmetic operators when only the round-to-nearest tails-to-even rounding mode is available. They also provided tables for indirect function projections when zeros and infinities are considered with this rounding mode. In our approach, we generalize the initial work of [10] by providing extended interval reasoning. The algorithms and tables we present in this paper consider all rounding modes, and contain all details and special cases, allowing the interested reader to write an implementation of interval-based filtering code.
Recently, [21] presented optimal inverse projections for addition under the round-to-nearest rounding mode. The proposed algorithms combine classical filtering based on the properties of addition with filtering based on the properties of subtraction constraints on floating-points as introduced by Marre and Michel [29]. The authors are able to prove the optimality of the lower bounds computed by their algorithms. However, [21] only covers addition in the round-to-nearest rounding mode, leaving other arithmetic operations (subtraction, multiplication and division) and rounding modes to future work. Special values (infinities and NaNs) are also not handled. Conversely, this paper presents filtering algorithms covering all such cases.
It is worth noting that the filtering algorithms on intervals presented in [29] have been corrected for addition/subtraction constraints and extended to multiplication and division under the round-to-nearest rounding mode by some of these authors (see [4, 5]). In this paper we discuss the cases in which the filtering algorithms in [4, 5, 29] should be used in combination with our filters for arithmetic constraints. However, the main aim of this paper is to provide an exhaustive and provably correct treatment of filtering algorithms supporting all special cases for all arithmetic constraints under all rounding modes.
1.4.2 SMT solvers
Satisfiability Modulo Theories (SMT) is the problem of deciding satisfiability of first-order logic formulas containing terms from different, pre-defined theories. Examples of such theories are integer or real arithmetic, bit-vectors, arrays and uninterpreted functions. Recently, SMT solvers have been widely employed as backends for different software verification techniques, such as model checking and symbolic execution [9]. The need for verifying floating-point programs lead to the introduction of a floating-point theory [13] in SMT-LIB, a library defining a common input language for SMT solvers. Since then, the theory has been implemented in different ways into several solvers. CVC4 [8, 12], MathSAT [14] and Z3 [18] use bit-blasting, i.e., they convert floating-point constraints to bit-vector formulae, which are then solved as Boolean SAT problems. Some tools, instead, use methods based on interval reasoning. MathSAT also supports Abstract Conflict Driven Learning (ACDL) for solving floating-point constraints based on interval domains [11]. Colibri [28] uses constraint programming techniques, with filtering algorithms such as those in [5, 10] and those presented in this paper. However, [28] does not report such filters in detail, nor proves their correctness. This leads to serious soundness issues, as we shall see in Section 5.2. An experimental comparison of such tools can be found in [12].
Note that SMT-LIB, the input language of all such tools, only allows to specify one single rounding mode for each floating-point operation. Thus, the only way of dealing with uncertainty of the rounding mode in use is to solve the same constraint system with all possible rounding mode combinations, which is quite unpractical. Our filtering algorithms are instead capable of working with a set of possible rounding modes, and retain soundness by always choosing the worst-case one.
1.4.3 Floating-point program verification
Several program analyses for automatic detection of floating-point exceptions were proposed in the literature.
Relational abstract domains for the analysis of floating-point computations through abstract interpretation have been presented in [32] and implemented in the tool Astrée.Footnote 5 Such domains, however, over-approximate rounding operations by always assuming worst cases, namely rounding toward plus and minus infinity, which may cause precision issues (i.e., false positives) if only round-to-nearest is used. Also, [32] does not offer a treatment of symbolic values (e.g., infinities) as exhaustive as the one we offer in this paper.
In [7] the authors proposed a symbolic execution system for detecting floating-point exceptions. It is based on the following steps: each numerical program is transformed to directly check each exception-triggering condition, the transformed program is symbolically-executed in real arithmetic to find a (real) candidate input that triggers the exception, the real candidate is converted into a floating-point number, which is finally tested against the original program. Since approximating floating-point arithmetic with real arithmetic does not preserve the feasibility of execution paths and outputs in any sense, they cannot guarantee that once a real candidate has been selected, a floating-point number raising the same exception can be found. Even more importantly, even if the transformed program over the reals is exception-free, the original program using floating-point arithmetic may not be actually exception-free.
Symbolic execution is also the basis of the analysis proposed in [38], that aims at detecting floating-point exceptions by combining it with value range analysis. The value range of each variable is updated with the appropriate path conditions by leveraging interval constraint-propagation techniques. Since the projections used in that paper have not been proved to yield correct approximations, it can be the case that the obtained value ranges do not contain all possible floating-point values for each variable. Indeed, valid values may be removed from value ranges, which leads to false negatives. In Section 6, the tool for floating-point exception detection presented in [38] is compared with the same analysis based on our propagation algorithms. As expected, no false positives were detected among the results of our analysis.
1.5 Contribution
This paper improves the state of the art in several directions:
-
1.
all rounding modes are treated and there is no assumption that the rounding mode in effect is known and unchangeable (increased generality);
-
2.
utilization, to a large extent, of machine floating-point arithmetic in the analyzer with few rounding mode changes (increased performance);
-
3.
accurate treatment of round half to even —the default rounding mode of IEEE 754— (increased precision);
-
4.
explicit and complete treatment of intervals containing symbolic values (i.e., infinities and signed zeros);
-
5.
application of floating-point constraint propagation techniques to enable detection of program anomalies such as overflows, underflows, absorption, generation of NaNs.
1.6 Plan of the paper
The rest of the paper is structured as follows: Section 2 recalls the required notions and introduces the notation used throughout the paper; Section 3 presents some results on the treatment of uncertainty on the rounding mode in effect and on the quantification of the rounding errors committed in floating-point arithmetic operations; Section 4 contains the complete treatment of addition and division constraints on intervals, by showing detailed special values tables and the refinement algorithms; Section 5 reports the results of experiments aimed at evaluating the soundness of existing tools. Section 6 concludes the main part of the paper. Appendix A contains the complete treatment of subtraction and multiplication constraints. The proofs of results not reported in the main text of the paper can be found in Appendix B.
2 Preliminaries
We will denote by \(\mathbb {R}_{+}\) and \(\mathbb {R}_{-}\) the sets of strictly positive and strictly negative real numbers, respectively. The set of affinely extended reals, \(\mathbb {R} \cup \{ -\infty , +\infty \}\), is denoted by \(\overline {\mathbb {R}}\).
Definition 2
(IEEE 754 binary floating-point numbers) A set of IEEE 754 binary floating-point numbers [24] is uniquely identified by: \(p \in \mathbb {N}\), the number of significant digits (precision); \(e_{\max \limits } \in \mathbb {N}\), the maximum exponent, the minimum exponent being \(e_{\min \limits } \overset {\text {def}}{=} 1 - e_{\max \limits }\). The set of binary floating-point numbers \(\mathbb {F}(p, e_{\max \limits }, e_{\min \limits })\) includes:
-
all signed zero and non-zero numbers of the form (− 1)s ⋅ 2e ⋅ m, where
-
s is the sign bit;
-
the exponent e is any integer such that \(e_{\min \limits } \leq e \leq e_{\max \limits }\);
-
the mantissa m, with 0 ≤ m < 2, is a number represented by a string of p binary digits with a “binary point” after the first digit:
$$ m = (d_{0} . d_{1} d_{2} {\dots} d_{p-1})_{2} = \sum\limits_{i = 0}^{p-1} d_{i} 2^{-i}; $$
-
-
the infinities \(+\infty \) and \(-\infty \); the NaNs: qNaN (quiet NaN) and sNaN (signaling NaN).
Numbers such that d0 = 1 are called normal. The smallest positive normal floating-point number is \(f^{\text {nor}}_{\min \limits }\overset {\text {def}}{=} 2^{e_{\min \limits }}\) and the largest is \(f_{\max \limits } \overset {\text {def}}{=} 2^{e_{\max \limits }}(2 - 2^{1-p})\). The non-zero floating-point numbers such that d0 = 0 are called subnormal: their absolute value is less than \(2^{e_{\min \limits }}\), and they always have fewer than p significant digits. Every finite floating-point number is an integral multiple of the smallest subnormal magnitude \(f_{\min \limits }\overset {\text {def}}{=} 2^{e_{\min \limits } + 1 - p}\). Note that the signed zeroes + 0 and − 0 are distinct floating-point numbers. For a non-zero number x, we will write even(x) (resp., odd(x)) to signify that the least significant digit of x’s mantissa, dp− 1, is 0 (resp., 1).
In the sequel we will only be concerned with IEEE 754 binary floating-point numbers and we will write simply \(\mathbb {F}\) for \(\mathbb {F}(p, e_{\max \limits }, e_{\min \limits })\) when there is no risk of confusion.
Definition 3
(Floating-point symbolic order) Let \(\mathbb {F}\) be any IEEE 754 floating-point format. The relation \(\prec \subseteq \mathbb {F}\times \mathbb {F}\) is such that, for each \(x, y \in \mathbb {F}\), x ≺ y if and only if both x and y are not NaNs and either: \(x = -\infty \) and \(y \neq -\infty \), or \(x \neq +\infty \) and \(y = +\infty \), or x = − 0 and \(y \in \{ +0 \} \cup \mathbb {R}_{+}\), or \(x \in \mathbb {R}_{-} \cup \{ -0 \}\) and y = + 0, or \(x, y \in \mathbb {R}\) and x < y. The partial order \(\preccurlyeq \subseteq \mathbb {F}\times {\mathbb {F}}\) is such that, for each \(x, y \in \mathbb {F}\), \(x \preccurlyeq y\) if and only if both x and y are not NaNs and either x ≺ y or x = y.
Note that \(\mathbb {F}\) without the NaNs is linearly ordered with respect to ‘≺’.
For \(x \in \mathbb {F}\) that is not a NaN, we will often abuse the notation by interchangeably using the floating-point number or the extended real number it represents. The floats − 0 and + 0 both correspond to the real number 0. Thus, when we write, e.g., x < y we mean that x is numerically less than y (for example, we have − 0 ≺ + 0 though \(-0 \nless +0\), but note that \(x \preccurlyeq y\) implies x ≤ y). Numerical equivalence will be denoted by ‘≡’ so that x ≡ 0, x ≡ + 0 and x ≡− 0 all denote (x = + 0) ∨ (x = − 0).
Definition 4
(Floating-point predecessors and successors) The partial function \(\mathbb {F}\rightarrowtail \mathbb {F}\) is such that, for each \(x \in \mathbb {F}\),
The partial function \(\mathbb {F}\rightarrowtail \mathbb {F}\) is defined by reversing the ordering, so that, for each \(x \in \mathbb {F}\), pred(x) = −succ(−x) whenever succ(x) is defined.
Let ∘∈{+,−,⋅,/} denote the usual arithmetic operations over the reals. Let \(R \overset {\text {def}}{=} \{ \downarrow ,\) 0,↑,n} denote the set of IEEE 754 rounding modes (rounding-direction attributes): round towards minus infinity (roundTowardNegative, ↓), round towards zero (roundTowardZero, 0), round towards plus infinity (roundTowardPositive, ↑), and round to nearest (roundTiesToEven, n). We will use the notation  , where
, where  and r ∈ R, to denote an IEEE 754 floating-point operation with rounding r.
and r ∈ R, to denote an IEEE 754 floating-point operation with rounding r.
The rounding functions are defined as follows. Note that they are not defined for 0: the IEEE 754 standard, in fact, for operations whose exact result is 0, bases the choice between + 0 and − 0 on the operation itself and on the sign of the arguments [24, Section 6.3].
Definition 5
(Rounding functions) The rounding functions defined by IEEE 754, \([\cdot ]_{\uparrow }:\mathbb {R}\backslash \{0\}\rightarrow \mathbb {F}\), \([\cdot ]_{\downarrow }:\mathbb {R}\backslash \{0\}\rightarrow \mathbb {F}\), \([\cdot ]_{0}:\mathbb {R}\backslash \{0\}\rightarrow \mathbb {F}\) and \([\cdot ]_{\mathrm {n}}:\mathbb {R}\backslash \{0\}\rightarrow \mathbb {F}\), are such that, for each \(x \in \mathbb {R}\setminus \{ 0 \}\),
Note that, when the result of an operation has magnitude lower than \(f^{\text {nor}}_{\min \limits }\), it is rounded to a subnormal number, by adjusting it to the form \((-1)^{s} \cdot 2^{e_{\min \limits }} \cdot m\), and truncating its mantissa m, which now starts with at least one 0, to the first p digits. This phenomenon is called gradual underflow, and while it is preferred to hard underflow, which truncates a number to 0, it still may cause precision issues due to the reduced number of significant digits of subnormal numbers.
The rounding modes ↓ and ↑ are the most “extreme”, while n and 0 are always contained between them. We formalize this observation as follows:
Proposition 1 (Properties of rounding functions)
Let \(x \in \mathbb {R} \setminus \{ 0 \}\). Then
Moreover,
In this paper, we use intervals of floating-point numbers in \(\mathbb {F}\) that are not NaNs.
Definition 6
(Floating-point intervals) Let \(\mathbb {F}\) be any IEEE 754 floating-point format. The set \({\mathscr{I}}_{\mathbb {F}}\) of floating-point intervals with boundaries in \(\mathbb {F}\) is given by
By [ℓ,u] we denote the set \(\{ x \in \mathbb {F} \mid \ell \preccurlyeq x \preccurlyeq u \}\). The set \({\mathscr{I}}_{\mathbb {F}}\) is a bounded meet-semilattice with least element ∅, greatest element \([-\infty , +\infty ]\), and the meet operation, which is induced by set-intersection, will be simply denoted by ∩.
Floating-point intervals with boundaries in \(\mathbb {F}\) allow to capture the extended numbers in \(\mathbb {F}\): NaNs should be tracked separately.
3 Rounding modes and rounding errors
The IEEE 754 standard for floating-point arithmetic introduces different rounding operators, among which the user can choose on compliant platforms. The rounding mode in use affects the results of the floating-point computations performed, and it must be therefore taken into account during constraint propagation. In this section, we present some abstractions aimed at facilitating the treatment of rounding modes in our constraint projection algorithms.
3.1 Dealing with uncertainty on the rounding mode in effect
Even if programs that change the rounding mode in effect are quite rare, whenever this happens, the rounding mode in effect at each program point cannot be known precisely. So, for a completely general treatment of the problem, such as the one we are proposing, our choice is to consider a set of possible rounding modes. To this aim, in this section we define two auxilliary functions that, given a set of rounding modes possibly in effect, select a worst-case rounding mode that ensures soundness of interval propagation. Soundness is guaranteed even if the rounding mode used in the actual computation differs from the one selected, as far as the former is contained in the set. Of course, if a program never changes the rounding mode, the set of possible rounding modes boils down to be a singleton.
The functions presented in the first definition select the rounding modes that can be used to compute the lower (function rℓ) and upper (function ru) bounds of an operation in case of direct projections.
Definition 7
(Rounding mode selectors for direct projections) Let \(\mathbb {F}\) be any IEEE 754 floating-point format and \(S \subseteq R\) be a set of rounding modes. Let also \(y, z \in \mathbb {F}\) and  be such that either
be such that either  .
.
Then

The following functions select the rounding modes that will be used for the lower (functions \(\bar {r}_{\ell }^{r}\) and \(\bar {r}_{\ell }^{\ell }\)) and upper (functions \(\bar {r}_{u}^{r}\) and \(\bar {r}_{u}^{\ell }\)) bounds of an operation when computing inverse projections. Note that there are different functions depending on which one of the two operands is being projected: \(\bar {r}_{\ell }^{r}\) and \(\bar {r}_{u}^{r}\) for the right one, \(\bar {r}_{\ell }^{\ell }\) and \(\bar {r}_{u}^{\ell }\) for the left one.
Definition 8
(Rounding mode selectors for inverse projections) Let \(\mathbb {F}\) be any IEEE 754 floating-point format and \(S \subseteq R\) be a set of rounding modes. Let also \(a, b \in \mathbb {F}\) and  First, we define
First, we define

Secondly, we define the following selectors:

The usefulness in interval propagation of the functions presented above will be clearer after considering Proposition 2. Moreover, it is worth noting that, if the set of possible rounding modes is composed by a unique rounding mode, then all the previously defined functions return such rounding mode itself. In that case, the claims of Proposition 2 trivially hold.
Proposition 2
Let \(\mathbb {F}\), S, y, z and ‘  ’ be as in Definition 7. Let also
’ be as in Definition 7. Let also  and
and  . Then, for each r ∈ S
. Then, for each r ∈ S

Moreover, there exist \(r^{\prime }, r^{\prime \prime } \in S\) such that

Now, consider  with \(x, z \in \mathbb {F}\) and r ∈ S. Let
with \(x, z \in \mathbb {F}\) and r ∈ S. Let  and
and  , according to Definition 8. Moreover, let \(\hat {y}^{\prime }\) be the minimum \(y^{\prime } \in \mathbb {F}\) such that
, according to Definition 8. Moreover, let \(\hat {y}^{\prime }\) be the minimum \(y^{\prime } \in \mathbb {F}\) such that  , and let \(\tilde {y}^{\prime \prime }\) be the maximum \(y^{\prime \prime } \in \mathbb {F}\) such that
, and let \(\tilde {y}^{\prime \prime }\) be the maximum \(y^{\prime \prime } \in \mathbb {F}\) such that  . Then, the following inequalities hold:
. Then, the following inequalities hold:
The same result holds if  , with
, with  and
and  .
.
Proof
Here we only prove the claims for direct projections (namely, (9) and (10)), leaving those concerning indirect projections, which are analogous, to Appendix B.2.
First, we observe that, for each \(x, y, z \in \mathbb {F}\), we have [y ∘ z]n = [y ∘ z]↓, or [y ∘ z]n = [y ∘ z]↑ or both. Then we prove that, for each \(x, y, z \in \mathbb {F}\), we have  We distinguish between the following cases, depending on y ∘ z:
We distinguish between the following cases, depending on y ∘ z:
- \(y \circ z = +\infty \lor y \circ z = -\infty :\) :
-
in this case we have
 and thus
and thus  holds.
holds. - \(y \circ z\leq -f_{\min \limits } \lor y \circ z\geq f_{\min \limits }:\) :
-
in this case we have, by Proposition 1,
 as
as  and
and  , the numerical order is reflected into the symbolic order to give
, the numerical order is reflected into the symbolic order to give 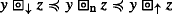 .
. - \(-f_{\min \limits } < y \circ z < 0:\) :
-
in this case we have
 by Definition 5; since either \([y \circ z]_{\mathrm {n}} = -f_{\min \limits }\) or [y ∘ z]n = − 0, we have [y ∘ z]n≠ + 0, thus
by Definition 5; since either \([y \circ z]_{\mathrm {n}} = -f_{\min \limits }\) or [y ∘ z]n = − 0, we have [y ∘ z]n≠ + 0, thus  .
. - \(0 < y \circ z<f_{\min \limits }:\) :
-
in this case we have
 by Definition 5; again, since either [y ∘ z]n = + 0 or \([y \circ z]_{\mathrm {n}} = f_{\min \limits }\) we know that [y ∘ z]n≠ − 0, and thus
by Definition 5; again, since either [y ∘ z]n = + 0 or \([y \circ z]_{\mathrm {n}} = f_{\min \limits }\) we know that [y ∘ z]n≠ − 0, and thus  .
. - y ∘ z = 0 ::
-
in this case, for multiplication and division the result is the same for all rounding modes, i.e., + 0 or − 0 depending on the sign of the arguments [24, Section 6.3]; for addition or subtraction we have
 while
while  ; hence, also in this case,
; hence, also in this case,  holds.
holds.
Note now that, by Definition 5, if y ∘ z > 0 then  whereas, if y ∘ z > 0, then
whereas, if y ∘ z > 0, then  . Therefore we can conclude that:
. Therefore we can conclude that:
-
if y ∘ z > 0, then
 while,
while, -
if y ∘ z < 0, then
 moreover,
moreover, -
if y ∘ z = 0 and ∘∉{+,−}, then
 while,
while, -
if y ∘ z = 0 and ∘∈{+,−}, then
 .
.
In order to prove inequality (9), it is now sufficient to consider all possible sets \(S \subseteq R\) and use the relations above.
For claim (10), observe that  for any combination of rounding modes in S except for one case: that is when y ∘ z > 0, and 0 ∈ S but ↓∉S. In this case, however, by Definition 5,
for any combination of rounding modes in S except for one case: that is when y ∘ z > 0, and 0 ∈ S but ↓∉S. In this case, however, by Definition 5,  . Similarly,
. Similarly,  except for the case when y ∘ z ≤ 0, 0 ∈ S but ↑∉S. First, assume that y ∘ z < 0: in this case, by Definition 5,
except for the case when y ∘ z ≤ 0, 0 ∈ S but ↑∉S. First, assume that y ∘ z < 0: in this case, by Definition 5,  . For the remaining case, that is y ∘ z = 0, we observe that for multiplication and division the result is the same for all rounding modes [24, Section 6.3], while for addition or subtraction we have
. For the remaining case, that is y ∘ z = 0, we observe that for multiplication and division the result is the same for all rounding modes [24, Section 6.3], while for addition or subtraction we have  . □
. □
Thanks to Proposition 2 we need not be concerned with sets of rounding modes, as any such set \(S \subseteq R\) can always be mapped to a pair of “worst-case rounding modes” which, in addition, are never round-to-zero. Therefore, projection functions can act as if the only possible rounding mode in effect was the one returned by the selection functions, greatly simplifying their logic. For example, consider the constraint  , meaning “x is obtained as the result of
, meaning “x is obtained as the result of  for some r ∈ S.” Of course,
for some r ∈ S.” Of course,  implies
implies  and
and  , which, by Proposition 2, imply
, which, by Proposition 2, imply  and
and  , where
, where  and
and  . The results obtained by projection functions that only consider rℓ and ru are consequently valid for any r ∈ S.
. The results obtained by projection functions that only consider rℓ and ru are consequently valid for any r ∈ S.
3.2 Rounding errors
For the precise treatment of all rounding modes it is useful to introduce a notation that expresses, for each floating-point number x, the maximum error that has been committed by approximating with x a real number under the different rounding modes (as shown in the previous section, we need not be concerned with round-to-zero).
Definition 9
(Rounding Error Functions) The partial functions \(\nabla ^{\uparrow }:\mathbb {F}\rightarrowtail \overline {\mathbb {R}}\), \(\nabla ^{\downarrow }:\mathbb {F}\rightarrowtail \overline {\mathbb {R}}\), \(\nabla ^{\mathrm {n}-}_{2}:\mathbb {F}\rightarrowtail \overline {\mathbb {R}}\) and \(\nabla ^{\mathrm {n}+}_{2}:\mathbb {F}\rightarrowtail \overline {\mathbb {R}}\) are defined as follows, for each \(x \in \mathbb {F}\) that is not a NaN:
An interesting observation is that the values of the functions introduced in Definition 9 are always representable in \(\mathbb {F}\) and thus their computation does not require extra-precision, something that, as we shall see, is exploited in the implementation. This is the reason why, for round-to-nearest, \(\nabla ^{\mathrm {n}-}_{2}\) and \(\nabla ^{\mathrm {n}+}_{2}\) have been defined as twice the approximation error bounds: the absolute value of the bounds themselves, being \(f_{\min \limits }/2\), is not representable in \(\mathbb {F}\) for each \(x \in \mathbb {F}\) such that \(|x| \leq f^{\text {nor}}_{\min \limits }\).
When the round-to-nearest rounding mode is in effect, Proposition 3 relates the bounds of a floating-point interval [xℓ,xu] with those of the corresponding interval of \(\overline {\mathbb {R}}\) it represents.
Proposition 3
Let \(x_{\ell }, x_{u} \in \mathbb {F}\cap \mathbb {R}\). Then
Proof
(sketch) To prove (15), we separately consider the two cases defined by (13).
If \(x_{\ell } = -f_{\max \limits }\), we prove that \(x_{\ell } + \nabla ^{\mathrm {n}-}_{2}(x_{\ell }) / 2 = -2^{e_{\max \limits }}(2 - 2^{-p})\), while for all xℓ < x ≤ xu we have \(x + \nabla ^{\mathrm {n}-}_{2}(x) / 2 = (x + \text {pred}(x)) / 2\). By monotonicity of ‘pred’, the minimum value of (x + pred(x))/2 occurs when \(x = \text {succ}(-f_{\max \limits })\), and
which proves (15) in this case.
If, instead, \(x_{\ell } > -f_{\max \limits }\), applying monotonicity of ‘pred’ suffices.
The full proof is in Appendix B.2, together with the one of (16), which is symmetric. □
3.3 Real approximations of floating-point constraints
In this section we show how inequalities of the form  and
and  , with r ∈{↓,↑,n} can be reflected on the reals. Indeed, it is possible to algebraically manipulate constraints on the reals so as to numerically bound the values of floating-point quantities. The results of this and of the next section will be useful in designing inverse projections.
, with r ∈{↓,↑,n} can be reflected on the reals. Indeed, it is possible to algebraically manipulate constraints on the reals so as to numerically bound the values of floating-point quantities. The results of this and of the next section will be useful in designing inverse projections.
Proposition 4
The following implications hold, for each \(x, y, z \in \mathbb {F}\) such that all the involved expressions do not evaluate to NaN, for each floating-point operation  and the corresponding extended real operation ∘∈{+,−,⋅,/}, where the entailed inequalities are to be interpreted over \(\overline {\mathbb {R}}\):
and the corresponding extended real operation ∘∈{+,−,⋅,/}, where the entailed inequalities are to be interpreted over \(\overline {\mathbb {R}}\):

moreover, if \(x \neq -\infty \),

conversely,

moreover, if \(x \neq +\infty \),

The proof of Proposition 4 is carried out by applying the inequalities of Proposition 1 to each rounded operation, resulting in a quite long case analysis. It can be found in Appendix B.2.
3.4 Floating-point approximations of constraints on the reals
In this section, we show how possibly complex constraints involving floating-point operations can be approximated directly using floating-point computations, without necessarily using infinite-precision arithmetic.
Without being too formal, let us consider the domain \(E_{\mathbb {F}}\) of abstract syntax trees with leafs labelled by constants in \(\mathbb {F}\) and internal nodes labeled with a symbol in {+,−,⋅,/} denoting an operation on the reals. While developing propagation algorithms, it is often necessary to deal with inequalities between real numbers and expressions described by such syntax trees. In order to successfully approximate them using the available floating-point arithmetic, we need two functions: \([\![\cdot ]\!]_{\downarrow }:E_{\mathbb {F}}\rightarrow \mathbb {F}\) and \([\![\cdot ]\!]_{\uparrow }:E_{\mathbb {F}}\rightarrow \mathbb {F}\). These functions provide an abstraction of evaluation algorithms that: (a) respect the indicated approximation direction; and (b) are as precise as practical. Point (a) can always be achieved by substituting the real operations with the corresponding floating-point operations rounded in the right direction. For point (b), maximum precision can trivially be achieved whenever the expression involves only one operation; generally speaking, the possibility of efficiently computing a maximally precise (i.e., correctly rounded) result depends on the form of the expression (see, e.g., [27]).
Definition 10
(Evaluation functions) The two partial functions \([\![\cdot ]\!]_{\downarrow }:{E_{\mathbb {F}}}{\mathbb {F}}\) and \([\![\cdot ]\!]_{\uparrow }:{E_{\mathbb {F}}}{\mathbb {F}}\) are such that, for each \(e \in \mathbb {F}\) that evaluates on \(\overline {\mathbb {R}}\) to a nonzero value,
Proposition 5
Let \(x \in \mathbb {F}\) be a non-NaN floating point number and \(e \in E_{\mathbb {F}}\) an expression that evaluates on \(\overline {\mathbb {R}}\) to a nonzero value. The following implications hold:
In addition, if \(\text {pred}\left ([[e]]_{\uparrow }\right ) < e\) (or, equivalently, [[e]]↑ = [e]↑) we also have
likewise, if \(\text {succ}\left ([[e]]\right ) > e\) (or, equivalently, [[e]]↓ = [e]↓) we have
The implications of Proposition 5 can be derived from Definition 10 and Proposition 1. Their proof is postponed to Appendix B.2.
4 Propagation for simple arithmetic constraints
In this section we present our propagation procedure for the solution of floating-point constraints obtained from the analysis of programs engaging in IEEE 754 computations.
The general propagation algorithm, which we already introduced in Section 1.2, consists in an iterative procedure that applies the direct and inverse filtering algorithms associated with each constraint, narrowing down the intervals associated with each variable. The process stops when fixed point is reached, i.e., when a further application of any filtering algorithm does not change the domain of any variable.
4.1 Propagation algorithms: definitions
Constraint propagation is a process that prunes the domains of program variables by deleting values that do not satisfy any of the constraints involving those variables. In this section, we will state these ideas more formally.
Let  and \(S \subseteq R\). Consider a constraint
and \(S \subseteq R\). Consider a constraint 
 with x ∈ X = [xℓ,xu], y ∈ Y = [yℓ,yu] and z ∈ Z = [zℓ,zu].
with x ∈ X = [xℓ,xu], y ∈ Y = [yℓ,yu] and z ∈ Z = [zℓ,zu].
Direct propagation aims at inferring a narrower interval for variable x, by considering the domains of y and z. It amounts to computing a possibly refined interval for x, \(X^{\prime } = [x^{\prime }_{\ell }, x^{\prime }_{u}] \subseteq X\), such that

Property (31) is known as the direct propagation correctness property.
Of course it is always possible to take \(X^{\prime } = X\), but the objective of constraint propagation is to compute a “small”, possibly the smallest \(X^{\prime }\) enjoying (31), compatibly with the available information. The smallest \(X^{\prime }\) that satisfies (31) is called optimal and is such that

Property (32) is called the direct propagation optimality property.
Inverse propagation, on the other hand, uses the domain of the result x to deduct new domains for the operands, y or z. For the same constraint,  , it means computing a possibly refined interval for y, \(Y^{\prime } = [y^{\prime }_{\ell }, y^{\prime }_{u}] \subseteq Y\), such that
, it means computing a possibly refined interval for y, \(Y^{\prime } = [y^{\prime }_{\ell }, y^{\prime }_{u}] \subseteq Y\), such that

Property (33) is known as the inverse propagation correctness property. Again, taking \(Y^{\prime } = Y\) is always possible and sometimes unavoidable. The best we can hope for is to be able to determine the smallest such set, i.e., satisfying

Property (34) is called the inverse propagation optimality property. Satisfying this last property can be very difficult.
4.2 The Boolean domain for NaN
From now on, we will consider floating-point intervals with boundaries in \(\mathbb {F}\). They allow for capturing the extended numbers in \(\mathbb {F}\) only: NaNs (quiet NaNs and signaling NaNs) should be tracked separately. To this purpose, a Boolean domain \({\mathscr{N}} \overset {\text {def}}{=} \{ \top , \bot \}\), where ⊤ stands for “may be NaN” and ⊥ means “cannot be NaN”, can be used and coupled with the arithmetic filtering algorithms.
Let be  an arithmetic constraint over floating-point numbers, and (X,NaNx), (Y,NaNy) and (Z,NaNz) be the variable domains of x, y and z respectively. In practice, the propagation process for such a constraint reaches a fixed point when the combination of refining domains \((X^{\prime }, \text {NaN}_{x}^{\prime })\), \((Y^{\prime }, \text {NaN}_{y}^{\prime })\) and \((Z^{\prime }, \text {NaN}_{z}^{\prime })\) remains the same obtained in the previous iteration. For each iteration of the algorithm we analyze the NaN domain of all the constraint variables in order to define the next propagator action.
an arithmetic constraint over floating-point numbers, and (X,NaNx), (Y,NaNy) and (Z,NaNz) be the variable domains of x, y and z respectively. In practice, the propagation process for such a constraint reaches a fixed point when the combination of refining domains \((X^{\prime }, \text {NaN}_{x}^{\prime })\), \((Y^{\prime }, \text {NaN}_{y}^{\prime })\) and \((Z^{\prime }, \text {NaN}_{z}^{\prime })\) remains the same obtained in the previous iteration. For each iteration of the algorithm we analyze the NaN domain of all the constraint variables in order to define the next propagator action.
The IEEE 754 Standard [24, Section 7.2] lists all combinations of operand values that yield a NaN result. For the arithmetic operations considered in this paper, NaN is returned if any of the operands is NaN. Moreover, addition and subtraction return NaN when infinities are subtracted (e.g., \(+\infty \boxplus -\infty \) or \(+\infty \boxminus +\infty \)), and also  ,
,  , and
, and 
Thus, direct projections are such that if NaNy = ⊤ or NaNz = ⊤, then also \(\text {NaN}_{x}^{\prime } = \top \); indirect projections yield \(\text {NaN}_{y}^{\prime } = \text {NaN}_{z}^{\prime } = \top \) if NaNx = ⊤. Moreover, e.g., if  , then the direct projection yields \(\text {NaN}_{x}^{\prime } = \top \) also if \(\pm \infty \in Y\) and \(\mp \infty \in Z\), and the indirect one allows for \(\pm \infty \) in \(Y^{\prime }\) and \(\mp \infty \) in \(Z^{\prime }\) only if NaNx = ⊤, and so on for the other operators.
, then the direct projection yields \(\text {NaN}_{x}^{\prime } = \top \) also if \(\pm \infty \in Y\) and \(\mp \infty \in Z\), and the indirect one allows for \(\pm \infty \) in \(Y^{\prime }\) and \(\mp \infty \) in \(Z^{\prime }\) only if NaNx = ⊤, and so on for the other operators.
4.3 Filtering algorithms for simple arithmetic constraints
Filtering algorithms for arithmetic constraints are the main focus of this paper. In the next sections, we will propose algorithms realizing optimal direct projections and correct inverse projections for the addition (\(\boxplus \)) and division (⍁) operations. The reader interested in implementing constraint propagation for all four operations can find the algorithms and results for the missing operations in Appendix A. We report the correctness proofs of the projections for addition in the main text, leaving those for the remaining operations to Appendix B.3.
The filtering algorithms we are about to present are capable of dealing with any set of rounding modes and are designed to distinguish between all different (special) cases in order to be as precise as possible, especially when the variable domains contain symbolic values. Much simpler projections can be designed whenever precision is not of particular concern. Indeed, the algorithms presented in this paper can be considered as the basis for finding a good trade-off between efficiency and the required precision.
4.3.1 Addition
Here we deal with constraints of the form \(x = y \boxplus _{S} z\) with \(S \subseteq R\). Let X = [xℓ,xu], Y = [yℓ,yu] and Z = [zℓ,zu].
Thanks to Proposition 2, any set of rounding modes \(S \subseteq R\) can be mapped to a pair of “worst-case rounding modes” which, in addition, are never round-to-zero. Therefore, the projection algorithms use the selectors presented in Definition 7 to choose the appropriate worst-case rounding mode, and then operate as if it was the only one in effect, yielding results implicitly valid for the entire set S.
Direct propagation
For direct propagation, i.e., the process that infers a new interval for x starting from the interval for y and z, we propose Algorithm 1 and functions daℓ and dau, as defined in Fig. 2. Functions daℓ and dau yield new bounds for interval X. In particular, function daℓ gives the new lower bound, while function dau provides the new upper bound of the interval. Functions daℓ and dau handle all rounding modes and, in order to be as precise as possible, they distinguish between several cases, depending on the values of the bounds of intervals Y and Z. These cases are infinities (\(-\infty \) and \(+\infty \)), zeroes (− 0 and + 0), negative values (\(\mathbb {R}_{-}\)) and positive values (\(\mathbb {R}_{+}\)).

It can be proved that Algorithm 1 computes a correct and optimal direct projection, as stated by its postconditions.
Theorem 1
Algorithm 1 satisfies its contract.
Proof
Given the constraint \(x = y \boxplus _{S} z\) with x ∈ X = [xℓ,xu], y ∈ Y = [yℓ,yu] and z ∈ Z = [zℓ,zu], Algorithm 1 sets \(X^{\prime } = [x^{\prime }_{\ell }, x^{\prime }_{u}] \cap X\); hence, we have \(X^{\prime } \subseteq X\). Moreover, by Proposition 2, for each y ∈ Y, z ∈ Z and r ∈ S, we have \(y \boxplus _{r_{\ell }} z \preccurlyeq y \boxplus _{r} z \preccurlyeq y \boxplus _{r_{u}} z\), and because \(a \preccurlyeq b\) implies a ≤ b for any \(a, b \in \mathbb {F}\) according to Definition 3, we know that \(y \boxplus _{r_{\ell }} z \leq y \boxplus _{r} z \leq y \boxplus _{r_{u}} z\). Thus, by monotonicity of \(\boxplus \), we have \( y_{\ell } \boxplus _{r_{\ell }} z_{\ell } \leq y \boxplus _{r_{\ell }} z \leq y \boxplus _{r} z \leq y \boxplus _{r_{u}} z \leq y_{u} \boxplus _{r_{u}} z_{u} \). Therefore, we can focus on finding a lower bound for \(y_{\ell } \boxplus _{r_{\ell }} z_{\ell }\) and an upper bound for \(y_{u} \boxplus _{r_{u}} z_{u}\).
Such bounds are given by the functions daℓ and dau of Fig. 2. Almost all of the cases reported in the tables can be trivially derived from the definition of the addition operation in the IEEE 754 Standard [24]; just two cases need further explanation. Concerning the entry of daℓ in which \(y_{\ell } = -\infty \) and \(z_{\ell } = +\infty \), note that \(z_{\ell } = +\infty \) implies \(z_{u} = +\infty \). Then for any \(y > y_{\ell } = -\infty \), \(y \boxplus +\infty = +\infty \). On the other hand, by the IEEE 754 Standard [24], \(-\infty \boxplus +\infty \) is an invalid operation. For the symmetric case, i.e., the entry of dau in which \(y_{u} = -\infty \) and \(z_{u} = +\infty \), we can reason dually.
We are now left to prove that \(\forall X^{\prime \prime } \subset X^{\prime } : \exists r \in S, y \in Y, z \in Z : y \boxplus _{r} z \not \in X^{\prime \prime }\). Let us focus on the lower bound \(x^{\prime }_{\ell }\), proving that there always exists a r ∈ S such that \(y_{\ell } \boxplus _{r} z_{\ell } = x^{\prime }_{\ell }\).
First, consider the cases in which \(y_{\ell } \not \in (\mathbb {R}_{-} \cup \mathbb {R}_{+})\) or \(z_{\ell } \not \in (\mathbb {R}_{-} \cup \mathbb {R}_{+})\). In these cases, a case analysis proves that daℓ(yℓ,zℓ,rℓ) is equal to \(y_{\ell } \boxplus _{r_{\ell }} z_{\ell }\). Indeed, if either of the operands (say yℓ) is \(-\infty \) and the other one (say zℓ) is not \(+\infty \), then according to the IEEE 754 Standard we have \(y_{\ell } \boxplus _{r} z_{\ell } = -\infty \) for any r ∈ R. Symmetrically, \(y_{\ell } \boxplus _{r} z_{\ell } = +\infty \) if one operand is \(+\infty \) and the other one is not \(-\infty \). If, w.l.o.g., \(y_{\ell } = +\infty \) and \(z_{\ell } = -\infty \), the set \(X^{\prime }\) is non-empty only if \(z_{u} \neq -\infty \), and \(y_{\ell } \boxplus _{r} z_{u} = +\infty \) for any r ∈ R.
For the cases in which \(y_{\ell } \in (\mathbb {R}_{-} \cup \mathbb {R}_{+})\) and \(z_{\ell } \in (\mathbb {R}_{-} \cup \mathbb {R}_{+})\) we have \(x^{\prime }_{\ell } = y_{\ell } \boxplus _{r_{\ell }} z_{\ell }\), by definition of daℓ of Fig. 2. Remember that, by Proposition 2, there exists r ∈ S such that \(y_{\ell } \boxplus _{\mathrm {r_{\ell }}} z_{\ell } = y_{\ell } \boxplus _{\mathrm {r}} z_{\ell }\). Since yℓ ∈ Y and zℓ ∈ Z, we can conclude that for any \(X^{\prime \prime } \subseteq X^{\prime }\), \(x^{\prime }_{\ell } \not \in X^{\prime \prime }\) implies \(y_{\ell } \boxplus _{\mathrm {r}} z_{\ell } \not \in X^{\prime \prime }\).
An analogous argument allows us to conclude that there exists an r ∈ S for which the following holds: for any \(X^{\prime \prime } \subseteq X^{\prime }\), \(x^{\prime }_{u} \not \in X^{\prime \prime }\) implies \(y_{u} \boxplus _{\mathrm {r}} z_{u} \not \in X^{\prime \prime }\). □
The following example will better illustrate how the tables in Fig. 2 should be used to compute functions daℓ and dau. All examples in this section refer to the IEEE 754 binary single precision format.
Example 1
Assume Y = [+ 0,5], Z = [− 0,8], and that the selected rounding mode is rℓ = ru =↓. In order to compute the lower bound \(x_{\ell }^{\prime }\) of \(X^{\prime }\), the new interval for x, function daℓ(+ 0,− 0,↓) is called. These arguments fall in case a1, which yields − 0 with rounding mode ↓. Indeed, when the rounding mode is ↓, the sum of − 0 and + 0 is − 0, which is clearly the lowest result that can be obtained with the current choice of Y and Z. For the upper bound \(x_{u}^{\prime }\), the algorithm calls dau(5,8,↓). This falls in the case in which both operands are positive numbers (\(y_{u}, z_{u} \in \mathbb {R}_{+}\)), and therefore \(x_{u} = y_{u} \boxplus _{r_{u}} z_{u} = 13\). In conclusion, the new interval for x is \(X^{\prime } = [-0, 13]\).
If any other rounding mode was selected (say, rℓ = ru = n), the new interval computed by the projection would have been \(X^{\prime \prime } = [+0, 13]\).
Inverse propagation
For inverse propagation, i.e., the process that infers a new interval for y (or for z) starting from the interval from x and z (x and y, resp.) we define Algorithm 2 and functions iaℓ in Fig. 3 and iau in Fig. 4, where ≡ indicates the syntactic substitution of expressions. Since the inverse operation of addition is subtraction, note that the values of x and z that minimize y are xℓ and zu; analogously, the values of x and z that maximize y are xu and zℓ.
When the round-to-nearest rounding mode is in effect, addition presents some nice properties. Indeed, several expressions for lower and upper bounds can be easily computed without approximations, using floating-point operations. In more detail, it can be shown (see the proof of Theorem 2) that when x is subnormal \(\nabla ^{\mathrm {n}+}_{2}(x)\) and \(\nabla ^{\mathrm {n}-}_{2}(x)\) are negligible. This allows us to define tight bounds in this case. On the contrary, when the terms \(\nabla ^{\mathrm {n}-}_{2}(x_{\ell })\) and \(\nabla ^{\mathrm {n}+}_{2}(x_{u})\) are non negligible, we need to approximate the values of expressions eℓ and eu. This can always be done with reasonable efficiency [27], but we leave this as an implementation choice, thus accounting for the case when the computation is exact ([[eℓ]]↓ = [eℓ] and [[eu]] = [eu]) as well as when it is not ([[eℓ]] > [eℓ] and [[eu]] < [eu]).

The next result assures us that our algorithm computes a correct inverse projection, as claimed by its postcondition.
Theorem 2
Algorithm 2 satisfies its contract.
Proof
Given the constraint \(x = y \boxplus _{S} z\) with x ∈ X = [xℓ,xu], y ∈ Y = [yℓ,yu] and z ∈ Z = [zℓ,zu], Algorithm 2 computes a new and refined domain \(Y^{\prime }\) for variable y.
First, observe that the newly computed interval \([y^{\prime }_{\ell }, y^{\prime }_{u}]\) is either intersected with the old domain Y, so that \(Y^{\prime } = [y^{\prime }_{\ell }, y^{\prime }_{u}] \cap Y\), or set to \(Y^{\prime } = \emptyset \). Hence, \(Y^{\prime } \subseteq Y\) holds.
Proposition 2 and the monotonicity of \(\boxplus \) allow us to find a lower bound for y by exploiting the constraint \(y \boxplus _{\bar {r}_{\ell }} z_{u} = x_{\ell }\), and an upper bound for y by exploiting the constraint \(y \boxplus _{\bar {r}_{u}} z_{\ell } = x_{u}\). We will now prove that the case analyses of functions iaℓ, described in Fig. 3, and iau, described in Fig. 4, express such bounds correctly.
Concerning the operand combinations in which iaℓ takes the value described by the case analysis a4, remember that, by the IEEE 754 Standard [24], whenever the sum of two operands with opposite sign is zero, the result of that sum is + 0 in all rounding-direction attributes except roundTowardNegative: in that case the result is − 0. Then, since \(z_{u} \boxplus _{\downarrow }(-z_{u}) = -0\), when \(\bar {r}_{\ell } = \downarrow \), yℓ can safely be set to succ(−zu).
As for the case in which iaℓ takes one of the values determined by a5, the IEEE 754 Standard [24] asserts that \(+0 \boxplus _{\downarrow } +0 = +0\), while \(-0 \boxplus _{\downarrow } +0 = -0\): the correct lower bound for y is \(y^{\prime }_{\ell } = +0\), in this case. As we already pointed out, for any other rounding-direction attribute \(+0 \boxplus -0 = +0\) holds, which allows us to include − 0 in the new domain.
Concerning cases of iaℓ that give the result described by the case analysis a6, we clearly must have \(y = +\infty \) if \(\bar {r}_{\ell } = \downarrow \); if \(\bar {r}_{\ell } = \uparrow \), it should be \(y + z_{u} > f_{\max \limits }\) and thus \(y > f_{\max \limits } - z_{u}\) and, by (28) of Proposition 5, \(y \succcurlyeq \text {succ}(f_{\max \limits } \boxminus _{\downarrow } z_{u})\). If \(\bar {r}_{\ell } = \mathrm {n}\), there are two cases:
- \(z_{u} < \nabla ^{\mathrm {n}+}_{2}(f_{\max \limits })/2\).:
-
In this case, y must be greater than \(f_{\max \limits }\), since \(f_{\max \limits }+ z_{u} < f_{\max \limits }+ \nabla ^{\mathrm {n}+}_{2}(f_{\max \limits })/2\) implies that \(f_{\max \limits } \boxplus _{\mathrm {n}} z_{u} = f_{\max \limits } < +\infty \). Note that in this case \(\nabla ^{\mathrm {n}+}_{2}(f_{\max \limits })/2 \boxminus _{\uparrow } z_{u} \geq f_{\min \limits }\), hence \(f_{\max \limits } \boxplus _{\uparrow } \left (\nabla ^{\mathrm {n}+}_{2}(f_{\max \limits })/2 \boxminus _{\uparrow } z_{u}\right ) = +\infty \).
- \(z_{u} \geq \nabla ^{\mathrm {n}+}_{2}(f_{\max \limits })/2\).:
-
Since \(\text {odd}(f_{\max \limits })\), for \(x_{\ell } = +\infty \) we need y to be greater than or equal to \(f_{\max \limits } + \nabla ^{\mathrm {n}+}_{2}(f_{\max \limits })/2 - z_{u}\). Note that \(y \geq f_{\max \limits } + \nabla ^{\mathrm {n}+}_{2}(f_{\max \limits })/2 - z_{u}\) together with
$$ \left[f_{\max} + \nabla^{\mathrm{n}+}_{2}(f_{\max})/2 - z_{u}\right]_{\uparrow} = f_{\max} \boxplus_{\uparrow} \left( \nabla^{\mathrm{n}+}_{2}(f_{\max})/2 \boxplus_{\uparrow} z_{u}\right) $$(35)allows us to apply (29) of Proposition 5, concluding \(y \succcurlyeq f_{\max \limits } \boxplus _{\uparrow } \left (\nabla ^{\mathrm {n}+}_{2}(f_{\max \limits })/2 \boxminus _{\uparrow } z_{u}\right )\). Equality (35) holds because either the application of ‘\({\boxminus _{\uparrow }}\)’ is exact or the application of ‘\({\boxplus _{\uparrow }}\)’ is exact. In fact, since \(z_{u} = m \cdot 2^{e} \geq \nabla ^{\mathrm {n}+}_{2}(f_{\max \limits })/2 = 2^{e_{\max \limits } -p}\), for some 1 ≤ m < 2, there are two cases: either \(e = e_{\max \limits }\) or \(e_{\max \limits } - p \leq e < e_{\max \limits }\).
Suppose first that \(e = e_{\max \limits }\): we have
$$ \begin{array}{@{}rcl@{}} \nabla^{\mathrm{n}+}_{2}(f_{\max})/2 - z_{u} &= 2^{e_{\max} -p} - m \cdot 2^{e_{\max}} \\ &= -2^{e_{\max}} (m - 2^{-p}), \end{array} $$and thus
$$ \nabla^{\mathrm{n}+}_{2}(f_{\max})/2 \boxminus_{\uparrow} z_{u} = \left\{\begin{array}{ll} -2^{e_{\max}} (m - 2^{1-p}), &\text{if} m > 1; \\ -2^{e_{\max} - 1}(2 - 2^{1-p}), &\text{if} m = 1. \end{array}\right. $$Since if \(e = e_{\max \limits }\) the application of ‘\({\boxminus _{\uparrow }}\)’ is not exact, we prove that the application of ‘\({\boxplus _{\uparrow }}\)’ is exact. Hence, if m > 1, we prove that
$$ \begin{array}{@{}rcl@{}} f_{\max} + (\nabla^{\mathrm{n}+}_{2}(f_{\max})/2 \boxminus_{\uparrow} z_{u}) &=& 2^{e_{\max}}(2 - 2^{1-p}) - 2^{e_{\max}}(m - 2^{1-p}) \\ &=& 2^{e_{\max}}(2 - 2^{1-p} - m + 2^{1-p}) \\ &=& 2^{e_{\max}}(2 - m) \\ &=& 2^{e_{\max} - k} \left( 2^{k} (2 - m)\right) \end{array} $$where \(k \overset {\text {def}}{=} -\bigl \lfloor \log _{2}(2-m)\bigr \rfloor \). It is worth noting that 2k(2 − m) can be represented by a normalized mantissa; moreover, since 1 ≤ k ≤ p − 1, \(e_{\min \limits } \leq e_{\max \limits } - k \leq e_{\max \limits }\), hence, \(f_{\max \limits } + (\nabla ^{\mathrm {n}+}_{2}(f_{\max \limits })/2 \boxminus _{\uparrow } z_{u}) \in \mathbb {F}\). If, instead, m = 1,
$$ \begin{array}{@{}rcl@{}} f_{\max} + (\nabla^{\mathrm{n}+}_{2}(f_{\max})/2 \boxminus_{\uparrow} z_{u}) &=& 2^{e_{\max}}(2 - 2^{1-p}) - 2^{e_{\max}-1}(2 - 2^{1-p}) \\ &=& (2^{e_{\max}} - 2^{e_{\max}-1})(2 - 2^{1-p}) \\ &=& 2^{e_{\max}-1}(2 - 2^{1-p}) \end{array} $$and, also in this case, \(f_{\max \limits } + (\nabla ^{\mathrm {n}+}_{2}(f_{\max \limits })/2 \boxminus _{\uparrow } z_{u}) \in \mathbb {F}\).
Suppose now that \(e_{\max \limits } - p \leq e < e_{\max \limits }\) and let \(h \overset {\text {def}}{=} e - e_{\max \limits } + p\) so that 0 ≤ h ≤ p − 1. In this case we show that the application of ‘\({\boxminus _{\uparrow }}\)’ is exact. Indeed, we have
$$ \begin{array}{@{}rcl@{}} \nabla^{\mathrm{n}+}_{2}(f_{\max})/2 - z_{u} &=& 2^{e_{\max} -p} - m \cdot 2^{e} \\ &=& -2^{e_{\max} - p} (m \cdot 2^{h} - 1) \\ &=& -2^{e_{\max} - p + h} (m - 2^{-h}). \end{array} $$If \(e = e_{\max \limits } - p\) and m = 1, then h = 0, m − 2−h = 0 and thus \(\nabla ^{\mathrm {n}+}_{2}(f_{\max \limits })/2 - z_{u} = 0\). Otherwise, let \(k \overset {\text {def}}{=} -\bigl \lfloor \log _{2}(m - 2^{-h})\bigr \rfloor \). We have
$$ \nabla^{\mathrm{n}+}_{2}(f_{\max})/2 - z_{u} = -2^{e_{\max} - p + h -k} \left( 2^{k} (m - 2^{-h})\right), $$which is an element of \(\mathbb {F}\).
Dual arguments w.r.t. the ones used to justify cases of iaℓ that give the result described by a4, a6 and a5 can be used to justify the cases of iau described by a9, a10 and a7.
We now tackle the entries of iaℓ described by a3, and those of iau described by a8. Exploiting \(x \preccurlyeq y \boxplus z\) and \(x \preccurlyeq y \boxplus z\), by Proposition 4, we have
The same case analysis gives us
We can now exploit the fact that x ∈ [xℓ,xu] and z ∈ [zℓ,zu] with \(x_{\ell }, x_{u}, z_{\ell }, z_{u} \in \mathbb {F}\) to obtain, using Proposition 3 and the monotonicity of ‘pred’ and ‘succ’:
We can now exploit Proposition 5 and obtain
In fact, if xℓ = zu, then, according to IEEE 754 [24, Section 6.3], for each non-NaN, nonzero and finite \(w \in \mathbb {F}\), − 0 is the least value for y that satisfies \(w = y \boxplus _{\downarrow } w\). If xℓ≠zu, then case (29) of Proposition 5 applies and we have \(y \succcurlyeq x_{\ell } \boxminus _{\uparrow } z_{u}\). Suppose now that pred(xℓ) = zu, then \(\text {pred}(x_{\ell }) \boxminus _{\downarrow } z_{u} \equiv 0\) and \(\text {succ}\left (\text {pred}(x_{\ell }) \boxminus _{\downarrow } z_{u}\right ) = f_{\min \limits }\), coherently with the fact that, for each non-NaN, nonzero and finite \(w \in \mathbb {F}\), \(f_{\min \limits }\) is the least value for y that satisfies \(w = y \boxplus _{\uparrow } \text {pred}(w)\). If pred(xℓ)≠zu, then case (26) of Proposition 5 applies and we have \(y \succcurlyeq \text {succ}\left (\text {pred}(x_{\ell }) \boxplus _{\downarrow } z_{u}\right )\). A symmetric argument justifies (39).
For the remaining cases, we first show that when \(\nabla ^{\mathrm {n}+}_{2}(x) = f_{\min \limits }\),
The previous equality has the following main consequences: we can perform the computation in \(\mathbb {F}\), that is, we do not need to compute \(\nabla ^{\mathrm {n}+}_{2}(x)/2\) and, since [xu − zℓ] = [[xu − zℓ]], we can apply (30) of Proposition 5, obtaining a tight bound for \(y_{u}^{\prime }\).
Let us prove (40). Suppose \(\nabla ^{\mathrm {n}+}_{2}(x_{u}) = f_{\min \limits }\), and assume xu≠zℓ. There are two cases:
- [xu − zℓ]↓ = xu − zℓ ::
-
then we have y ≤ [xu − zℓ]↓ = xu − zℓ since the addition of \(\nabla ^{\mathrm {n}+}_{2}(x_{u})/2 = f_{\min \limits }/2\) is insufficient to reach succ(xu − zℓ), whose distance from xu − zℓ is at least \(f_{\min \limits }\).
- [xu − zℓ]↓ < xu − zℓ < [xu − zℓ]↑ ::
-
since by Definition 2 every finite floating-point number is an integral multiple of \(f_{\min \limits }\), so are xu − zℓ and [xu − zℓ]↑. Therefore, again, y ≤ [xu − zℓ]↓, since the addition of \(\nabla ^{\mathrm {n}+}_{2}(x_{u})/2 = f_{\min \limits }/2\) xu − zℓ is insufficient to reach [xu − zℓ]↑, whose distance from xu − zℓ is at least \(f_{\min \limits }\).
In the case where xu = zℓ we have \([{x_{u} + \nabla ^{\mathrm {n}+}_{2}(x_{u})/2 - z_{\ell }}]_{\downarrow } = [{0 + f_{\min \limits }/2 }]_{\downarrow } = +0\), hence (40) holds. As we have already pointed out, this allows us to apply (30) of Proposition 5 to the case \(\nabla ^{\mathrm {n}+}_{2}(x_{u}) = f_{\min \limits }\), obtaining the bound \(y \preccurlyeq [{x_{u} - z_{\ell }}]_{\downarrow }\).
Similar arguments can be applied to \(\nabla ^{\mathrm {n}-}_{2}(x_{\ell })\) whenever \(\nabla ^{\mathrm {n}-}_{2}(x_{\ell }) = -f_{\min \limits }\) to prove that \([{x_{\ell } + \nabla ^{\mathrm {n}-}_{2}(x_{\ell })/2 - z_{u}}]_{\uparrow } = [{x_{\ell } - z_{u}}]_{\uparrow }\). Then, by (29) of Proposition 5, we obtain \(y \succcurlyeq [{x_{\ell } - z_{u}}]_{\uparrow }\).
When the terms \(\nabla ^{\mathrm {n}-}_{2}(x_{\ell })\) and \(\nabla ^{\mathrm {n}+}_{2}(x_{u})\) are non-negligible, we need to approximate the values of the expressions \(e_{\ell } \overset {\text {def}}{=} x_{\ell } + \nabla ^{\mathrm {n}-}_{2}(x_{\ell })/2 - z_{u}\) and \(e_{u} \overset {\text {def}}{=} x_{u} + \nabla ^{\mathrm {n}+}_{2}(x_{u})/2 - z_{\ell }\). Hence, we have the cases [[eℓ]]↑ = [eℓ]↑ and [[eu]]↓ = [eu]↓ as well as [[eℓ]]↑ > [eℓ]↑ and [[eu]]↓ < [eu]↓. Thus, when [[eu]]↓ < [eu]↓ by (37) and (27) of Proposition 5 we obtain \(y \preccurlyeq [[{e_{u}}]]_{\downarrow }\), while, when [[eℓ]]↓ > [eℓ]↓ by (37) and (25) of Proposition 5 we obtain \(y \succcurlyeq [[{e_{\ell }}]]\). Finally, when odd(xu), by (37) and (28) of Proposition 5, we obtain \(y \preccurlyeq \text {pred}\left ([[{e_{u}}]]_{\uparrow }\right )\). Dually, when odd(xℓ) by (36) and (26) of Proposition 5, we obtain \(y \succcurlyeq \text {succ}\left ([[{e_{\ell }}]]\right )\).
Thus, for the case \(\bar {r}_{\ell } = \mathrm {n}\) we have
whereas, for the case where \(\bar {r}_{u} = \mathrm {n}\), we have
□
Example 2
Let \(X = [+0, +\infty ]\) and \(Z = [-\infty , +\infty ]\). Regardless of the rounding mode, the calls to functions ia\(_{\ell }(+0, +\infty , \bar {r}_{\ell })\) and ia\(_{u}(+\infty , -\infty , \bar {r}_{u})\) yield \(Y^{\prime } = [-f_{\max \limits }, +\infty ]\). Note that \(-f_{\max \limits }\) is the lowest value that variable y could take, since there is no value for z ∈ Z that summed with \(-\infty \) gives a value in X. Indeed, if we take \(z = +f_{\max \limits }\), then we have \(-f_{\max \limits } \boxplus _{r} +f_{\max \limits } = +0 \in X\) for any r ∈ R. On the other hand, \(+\infty \) is clearly the highest value y could take, since \(+\infty \boxplus _{r} z = +\infty \in X\) for any value of \(z \in Z \backslash \{-\infty \}\). In this case, our projections yield a more refined result than the competing tool FPSE [10], which computes the wider interval \(Y^{\prime } = [-\infty , +\infty ]\).
Example 3
Consider also X = [1.0,2.0] and Z = [− 1.0 × 230,1.0 × 230] and S = {n}. With our inverse projection we obtain Y = [− 1.1⋯1 × 229,1.0 × 230] which is correct but not optimal. For example, pick y = 1.0 × 230: for z = − 1.0 × 230 we have \(y \boxplus _{S} z = 0\) and \(y \boxplus _{S} z^{+} = 64\). By monotonicity of \(\boxplus _{S}\), for no z ∈ [− 1.0 × 230,1.0 × 230] we can have \(y \boxplus _{S} z \in [1.0, 2.0]\).
One of the reasons the inverse projection for addition is not optimal is because floating point numbers present some peculiar properties that are not related in any way to those of real numbers. For interval-based consistency approaches, [29] identified a property of the representation of floating-point numbers and proposed to exploit it in filtering algorithms for addition and subtraction constraints. In [4, 5] some of these authors revised and corrected the Michel and Marre filtering algorithm on intervals for addition/subtraction constraints under the round to nearest rounding mode. A generalization of such algorithm to the all rounding modes should be used to enhance the precision of the classical inverse projection of addition. Indeed, classical and maximum ULP filtering [5] for addition are orthogonal: both should be applied in order to obtain optimal results. Therefore, inverse projections for addition, as the one proposed above, have to be intersected with a filter based on the Michel and Marre property in order to obtain more precise results.
Example 4
Assume, again, X = [1.0,2.0] and Z = [− 1.0 × 230,1.0 × 230] and S = {n}. By applying maximum ULP filtering [5, 29], we obtain the much tighter intervals Y,Z = [− 1.1⋯1 × 224,1.0 × 225]. These are actually optimal as \(-{1.1\cdots 1}\times 2^{24} \boxplus _{S} {1.0}\times 2^{25} = {1.0}\times 2^{25} \boxplus _{S} -{1.1\cdots 1}\times 2^{24} = 2.0\). This example shows that filtering by maximum ULP can be stronger than our interval-consistency based filtering. However, the opposite phenomenon is also possible. Consider again X = [1.0,2.0] and Z = [1.0,5.0]. Filtering by maximum ULP projection gives Z = [− 1.1⋯1 × 224,1.0 × 225]; in contrast, our inverse projection exploits the available information on Z to obtain Y = [− 4,1.0⋯01]. As we already stated, our filtering and maximum ULP filtering should both be applied in order to obtain precise results.
Exploiting the commutative property of addition, the refinement \(Z^{\prime }\) of Z can be defined analogously.
4.3.2 Division
In this section we deal with constraints of the form x = y ⍁Sz with \(S \subseteq R\).
Direct propagation
For direct propagation, interval Z is partitioned into the sign-homogeneous intervals \(Z_{-} \overset {\text {def}}{=} Z \cap [-\infty , -0]\) and \(Z_{+} \overset {\text {def}}{=} Z \cap [+0, +\infty ]\). This is needed because the sign of operand z determines the monotonicity with respect to y, and therefore the interval bounds to be used for propagation depend on it. Hence, once Z has been partitioned into sign-homogeneous intervals, we use the interval Y and W = Z−, to obtain the new interval \([x^{-}_{\ell }, x^{-}_{u}]\), and Y and W = Z+, to obtain \([x^{+}_{\ell }, x^{+}_{u}]\). The appropriate bounds for interval propagation are chosen by function τ of Fig. 5. Note that the sign of z is, by construction, constant over interval W. The selected values are then taken as arguments by functions ddℓ and ddu of Fig. 6, which return the correct bounds for the aforementioned new intervals for X. The intervals \(X \cap [x^{-}_{\ell }, x^{-}_{u}]\) and \(X \cap [x^{+}_{\ell }, x^{+}_{u}]\) are eventually joined using convex union, denoted by \(\biguplus \), to obtain the refining interval \(X^{\prime }\).

It can be proved that Algorithm 3 computes a correct and optimal direct projection, as ensured by its postconditions.
Theorem 3
Algorithm 3 satisfies its contract.
Example 5
Consider Y = [− 0,42], Z = [− 3,6] and any value of S. First, Z is split into Z− = [− 3,− 0] and Z+ = [+ 0,6]. For the negative interval, the third case of τ(− 0,42,− 3,− 0) applies, yielding (yL,yU,wL,wU) = (42,− 0,− 0,− 0). Then, the projection functions are invoked, and we have dd\(_{\ell }(42, -0, r_{\ell }) = -\infty \) and ddu(− 0,− 0,ru) = + 0, i.e., \([x^{-}_{\ell }, x^{-}_{u}] = [-\infty , +0]\). For the positive part, we have τ(− 0,42,+ 0,6) = (− 0,42,+ 0,+ 0) (sixth case). From the projections we obtain ddℓ(− 0,+ 0,rℓ) = − 0 and dd\(_{u}(42, +0, r_{u}) = +\infty \), and \([x^{+}_{\ell }, x^{+}_{u}] = [-0, +\infty ]\). Finally, \(X^{\prime } = [x^{-}_{\ell }, x^{-}_{u}] \biguplus [x^{+}_{\ell }, x^{+}_{u}] = [-\infty , +\infty ]\).
Inverse propagation first projection
The inverse projections of division must be handled separately for each operand. The projection on y is the first inverse projection. This case requires, as explained for Algorithm 3, to split Z into the sign-homogeneous intervals \(Z_{-} \overset {\text {def}}{=} Z \cap [-\infty , -0]\) and \(Z_{+} \overset {\text {def}}{=} Z \cap [+0, +\infty ]\). Then, in order to select the extrema that determine the appropriate lower and upper bound for y, function σ of Fig. 7 is applied. Finally, the functions defined in Figs. 8 and 9 are applied to such extrema.

Example 6
Suppose X = [− 42,+ 0], Z = [− 1.0 × 2100,− 0] and S = {n}. In this case, Z− = Z, and Z+ = ∅. We obtain σ(− 1.0 × 2100,− 0,− 42,+ 0) = (− 1.0 × 2100,− 1.0 × 2100,+ 0,− 42) from the sixth case of σ. Then, id\(^{f}_{\ell }(+0, -{1.0}\times 2^{100}, \mathrm {n}) = (f_{\min \limits } \boxdot _{\uparrow } (-{1.0}\times 2^{100}))/2 = -{1.0}\times 2^{-50}\), because the lowest value of yℓ is obtained when a division by − 1.0 × 2100 underflows. Moreover, id\(^{f}_{u}(-42, -{1.0}\times 2^{100}, \mathrm {n}) = {1.0101}\times 2^{105}\). Therefore, the projected interval is \(Y^{\prime } = [-{1.0}\times 2^{-50}, {1.0101}\times 2^{105}]\).
The following result assures us that Algorithm 4 computes a correct first inverse projection, as ensured by its postcondition.
Theorem 4
Algorithm 4 satisfies its contract.
Once again, in order to obtain more precise results in some cases, the first inverse projection for division has to be intersected with a filter based on an extension of the Michel and Marre property originally proposed in [29] and extended to multiplication and division in [5]. Indeed, when interval X does not contain zeroes and interval Z contains zeros and infinities, the proposed filtering by maximum ULP algorithm is able to derive more precise bounds than the ones obtained with the inverse projection we are proposing. Thus, for division (and for multiplication as well), the indirect projection and filtering by maximum ULP are mutually exclusive: one applies when the other cannot derive anything useful [5].
Example 7
Consider the IEEE 754 single-precision constraint x = y ⍁Sz with initial intervals X = [− 1.0 × 2− 110,− 1.0 × 2− 121] and \(Y = Z = [-\infty , +\infty ]\). When S = {n}, filtering by maximum ULP results in the possible refinement \(Y^{\prime } = [-{1.1 {\cdots } 1}\times 2^{17}, t{1.1 {\cdots } 1}\times 2^{17}]\), while Algorithm 4 would return the less precise \(Y^{\prime }=[-f_{\max \limits }, f_{\max \limits }]\), with any rounding mode.
Inverse propagation second projection
The second inverse projection for division computes a new interval for operand z. For this projection, we need to partition interval X into sign-homogeneous intervals \(X_{-} \overset {\text {def}}{=} X \cap [-\infty , -0]\) and \(X_{+} \overset {\text {def}}{=} X \cap [+0, +\infty ]\) since, in this case, it is the sign of X that matters for deriving correct bounds for Z. Once X has been partitioned, we use intervals X− and Y to obtain the interval \([z^{-}_{\ell }, z^{-}_{u}]\); intervals X+ and Y to obtain \([z^{+}_{\ell }, z^{+}_{u}]\). The new bounds for z are computed by functions id\(^{s}_{\ell }\) of Fig. 10 and id\(^{s}_{u}\) of Fig. 11, after the appropriate interval extrema of Y and V = X− (or V = X+) have been selected by function τ. The intervals \(Z \cap [z^{-}_{\ell }, z^{-}_{u}]\) and \(Z \cap [z^{+}_{\ell }, z^{+}_{u}]\) will be then joined with convex union to obtain \(Z^{\prime }\).

Our algorithm computes a correct second inverse projection.
Theorem 5
Algorithm 5 satisfies its contract.
Example 8
Consider \(X = [6, +\infty ]\), Y = [+ 0,42] and S = {n}. In this case, we only have X+ = X, and X− = ∅. With this input, \(\tau (+0, 42, 6, +\infty ) = (+0, 42, +\infty , 6)\) (case 5). Therefore, we obtain id\(^{s}_{\ell }(+0, +\infty , \mathrm {n}) = +0\), because any number in Y except + 0 yields \(+\infty \) when divided by + 0. If we compute intermediate values exactly, id\(^{s}_{u}(42, 6) = 7\) and the refined interval is \(Z^{\prime } = [+0, 7]\). If not, then \(z^{\prime }_{u} = {1.110 {\cdots } 01}\times 2^{2} = \text {succ}(7)\).
In order to obtain more precise results, the result of our second inverse projection can also be intersected with the interval obtained by the maximum ULP filter proposed in [5]. Indeed, when interval X does not contain zeros and interval Y contains zeros and infinities, the proposed filtering by maximum ULP algorithm is able to derive tighter bounds than those obtained with the inverse projection presented in this work.
Example 9
Consider the IEEE 754 single-precision division constraint x = y ⍁Sz with initial intervals x ∈ [1.0⋯010 × 2110,1.0 × 2121] and \(Y = Z = [-\infty , +\infty ]\). When S = {}, filtering by maximum ULP results in the possible refinement \(Z^{\prime } = [-{1.0}\times 2^{18}, {1.0}\times 2^{18}]\), while Algorithm 5 would compute \(Z^{\prime } = [-f_{\max \limits },f_{\max \limits }]\), regardless of the rounding mode.
5 Experimental evaluation
The main aim of this section is to motivate the need of provably correct filtering algorithms, by highlighting the issues caused by the unsoundness of most available implementations of similar methods.
5.1 Software verification
As we reported in Section 1.3, we implemented our work in the commercial tool ECLAIR. While the initial results on a wide range of self-developed tests looked very promising, we wanted to compare them with the competing tools presented in the literature, in order to better assess the strength of our approach with respect to the state of the art. Unfortunately, most of these tools were either unavailable, or not sufficiently equipped to analyze real-world C/C++ programs. We could, however, do a comparison with the results obtained in [38]. It presents a tool called seVR-fpe, for floating-point exception detection based on symbolic execution and value-range analysis. The same task can be carried out by the constraint-based symbolic model checker we included in ECLAIR. The authors of seVR-fpe tested their tool both on a self-developed benchmark suite and on real-world programs. Upon contacting them, they were unfortunately unable to provide us with more detailed data regarding their analysis of real world programs. This prevents us from doing an in-depth comparison of the tools, since we only know the total number of bugs found, but not their exact nature and location. Data with this level of detail was instead available for (most of) their self-developed benchmarks. The results obtained by running ECLAIR on them are reported in Table 1. ECLAIR could find a number of possible bugs significantly higher than seVR-fpe. As expected, due to the provable correctness of the algorithms employed in ECLAIR, no false positives were detected among the inputs it generated. This confirms the solid results obtainable by means of the algorithms presented in this paper.
5.2 SMT solvers
We compare ECLAIR with several SMT solvers that support floating-point arithmetic by executing them on a benchmark suite devised to test their floating-point theory for soundness. Since our aim is to evaluate filtering algorithms for floating-point addition, subtraction, multiplication and division, we only included tests that do not rely on other theories, such as arrays, bit-vectors and uninterpreted functions, as well as those containing quantifiers. Such features are typical of SMT, and are tackled by techniques which are out of the scope of this paper. The suite is made of a total of 151,432 tests, of which:
-
10,380 are randomly generated tests by Florian Schanda. (random directory from the benchmark suiteFootnote 6 used in [12]).
-
11,544 are randomly generated tests by Christoph M. Wintersteiger. (QF_FP/wintersteiger directory from the SMT-LIB benchmark repository.Footnote 7)
-
126,909 tests were generated from the IBM Test Suite for IEEE 754R ComplianceFootnote 8 created with FPgen [1].
The experiments were carried out on a high-end laptop with an x86_64 CPU (6 cores @2.20GHz) and 16 GB of RAM, running Ubuntu 20.04. Each solver’s version is reported in the table. MathSAT has been executed with the option -theory.fp.mode= 2, which enables the ACDL-based solver for the floating-point theory.
Results are reported in Table 2. The main observation we can make is that ECLAIR is the only tool based on interval reasoning to be completely sound. On the contrary, Colibri and MathSAT are unsound on numerous tests, even though they did not explicitly report any error. This hinders their use for program verification. On the other hand, bit-blasting based tools CVC4 and Z3 do not present such issues, because their bit-vector encodings for floating-point arithmetic are derived from solid and formally verified circuit designs such as [34]. This demonstrates that the provably-correct filters presented in this paper are needed to achieve reliable implementations of interval-based constraint solving methods.
The execution times seem to be mainly determined by implementation details such as the programming language used. In fact, Colibri and ECLAIR, the slowest tools, were written respectively in ECLiPSe PrologFootnote 9 and SWI Prolog,Footnote 10 while other tools were written in C++.
6 Discussion and conclusion
With the increasing use of floating-point computations in mission- and safety-critical settings, the issue of reliably verifying their correctness has risen to a point in which testing or other informal techniques are not acceptable any more. Indeed, this phenomenon has been fostered by the wide adoption of the IEEE 754 floating-point format, which has significantly simplified the use of floating-point numbers, by providing a precise, sound, and reasonably cross-platform specification of floating-point representations, operations and their semantics. The approach we propose in this paper exploits these solid foundations to enable a wide range of floating-point program verification techniques. It is based on the solution of constraint satisfaction problems by means of interval-based constraint propagation, which is enabled by the filtering algorithms we presented. These algorithms cover the whole range of possible floating-point values, including symbolic values, with respect to interval-based reasoning. Moreover, they not only support all IEEE 754 available rounding-modes, but they also allow to take care of uncertainty on the rounding-mode in use. Some important implementation aspects are also taken into account, by allowing both the use of machine floating-point arithmetic for all computations (for increased performance), and of extended-precision arithmetic (for better precision with the round-to-nearest rounding mode). In both cases, correctness is guaranteed, so that no valid solutions can erroneously be removed from the constraint system. This is supported by the extensive correctness proofs of all algorithms and tables, which allow us to claim that neither false positives, nor false negatives may be produced. The experimental evaluation of Section 5 shows that soundness is, indeed, a widespread issue in several floating-point verification tools. Our work provides solid foundations to soundly develop such kind of tools.
Several aspects of the constraint-based verification of floating-point programs remain, however, open problems, both from a theoretical and a practical perspective. As we showed throughout the paper, the filtering algorithms we presented are not optimal, i.e., they may not yield the tightest possible intervals containing all solutions to the constraint system. They must be interleaved with the filtering algorithms of [5], and they may require multiple passes before reaching the maximum degree of variable-domain pruning they are capable of. Therefore, the next possible advance in this direction would be conceiving optimal filtering algorithms, that reduce variable domains to intervals as tight as possible with a single application. This has been achieved in [21], but only for addition.
However, filtering algorithms only represent a significant, but to some extent limited, part of the constraint solving process. Indeed, even an optimally pruned interval may contain values that are not solutions to the constraint system, due to the possible non-linearity thereof. If the framework in use supports multi-intervals, this issue is dealt with by means of labeling techniques: when a constraint-solving process reaches quiescence, i.e., the application of filtering algorithms fails to prune variable domains any further, such intervals are split into two or more sub-intervals, and the process continues on each partition separately. In this context, the main issues are where to split intervals, and in how many parts. These issues are currently addressed with heuristic labeling strategies. Indeed, significant improvements to the constraint-propagation process could be achieved by investigating better labeling strategies. To this end, possible advancements would include the identification of objective criteria for the evaluation of labeling strategies on floating point-numbers, and the conception of labeling strategies tailored to the properties of constraint systems most commonly generated by numeric programs.
In conclusion, we believe the work presented in this paper can be an extensive reference for the readers interested in realizing applications for formal reasoning on floating-point computations, as well as a solid foundation for further improvements in the state of the art.
Notes
This is not relevant if one analyzes machine or sufficiently low-level intermediate code.
https://bugseng.com/eclair, last accessed on October 28th, 2021.
https://www.gnu.org/software/gsl/, last accessed on October 28th, 2021.
https://www.absint.com/astree/index.htm, last accessed on October 28th, 2021.
https://github.com/florianschanda/smtlib_schanda, last accessed on October 28th, 2021.
https://smtlib.cs.uiowa.edu/benchmarks.shtml, last accessed on October 28th, 2021.
https://www.research.ibm.com/haifa/projects/verification/fpgen/test_suite_download.shtml, last accessed on October 28th, 2021.
https://eclipseclp.org/, last accessed on October 28th, 2021.
https://www.swi-prolog.org/, last accessed on October 28th, 2021.
References
Aharoni, M., Asaf, S., Fournier, L., Koyfman, A., & Nagel, R. (2003). FPGen — a test generation framework for datapath floating-point verification. In Eighth IEEE international high-level design validation and test workshop. https://doi.org/10.1109/HLDVT.2003.1252469 (pp. 17–22). San Francisco: IEEE Computer Society.
Aho, A.V., Lam, M.S., Sethi, R., & Ullman, J.D. (2006). Compilers: principles, techniques, and tools, 2nd edn. Boston: Addison-Wesley Longman Publishing Co., Inc.
Arm Limited: Arm® Architecture Reference Manual, Armv8, for A-profile architecture edn. (2021). https://developer.arm.com/architectures/cpu-architecture/a-profile/docs. Last accessed on October 27th, 2021.
Bagnara, R., Carlier, M., Gori, R., & Gotlieb, A. (2013). Symbolic path-oriented test data generation for floating-point programs. In Proceedings of the 6th IEEE international conference on software testing, verification and validation. https://doi.org/10.1109/ICST.2013.17. Luxembourg City: IEEE Press.
Bagnara, R., Carlier, M., Gori, R., & Gotlieb, A. (2016). Exploiting binary floating-point representations for constraint propagation. INFORMS Journal on Computing, 28(1), 31–46. https://doi.org/10.1287/ijoc.2015.0663.
Bagnara, R., Chiari, M., Gori, R., & Bagnara, A. (2021). A practical approach to verification of floating-point C/C++ programs with math.h/cmath functions. ACM Transactions on Software Engineering and Methodology, 30(1), 9:1–9:53. https://doi.org/10.1145/3410875.
Barr, E.T., Vo, T., Le, V., & Su, Z. (2013). Automatic detection of floating-point exceptions. In The 40th annual ACM SIGPLAN-SIGACT symposium on principles of programming languages, POPL ’13, Rome, Italy - January 23 - 25, 2013. https://doi.org/10.1145/2429069.2429133 (pp. 549–560).
Barrett, C.W., Conway, C.L., Deters, M., Hadarean, L., Jovanovic, D., King, T., Reynolds, A., & Tinelli, C. (2011). CVC4. In Computer aided verification, proceedings of the 23rd international conference (CAV 2011), Lecture notes in computer science. https://doi.org/10.1007/978-3-642-22110-1_14, (Vol. 6806 pp. 171–177). Snowbird: Springer.
Barrett, C.W., & Tinelli, C. (2018). Satisfiability modulo theories. In E.M. Clarke, T.A. Henzinger, H. Veith, & R. Bloem (Eds.) Handbook of model checking. https://doi.org/10.1007/978-3-319-10575-8_11 (pp. 305–343). Springer.
Botella, B., Gotlieb, A., & Michel, C. (2006). Symbolic execution of floating-point computations. Software Testing, Verification and Reliability, 16(2), 97–121. https://doi.org/10.1002/stvr.333.
Brain, M., D’Silva, V., Griggio, A., Haller, L., & Kroening, D. (2014). Deciding floating-point logic with abstract conflict driven clause learning. Formal Methods in System Design, 45(2), 213–245. https://doi.org/10.1007/s10703-013-0203-7.
Brain, M., Schanda, F., & Sun, Y. (2019). Building better bit-blasting for floating-point problems. In Tools and algorithms for the construction and analysis of systems, proceedings of the 25th international conference (TACAS 2019), Part I, lecture notes in computer science. https://doi.org/10.1007/978-3-030-17462-0_5, (Vol. 11427 pp. 79–98). Springer.
Brain, M., Tinelli, C., & Rümmer, P. (2015). T-wahl: An automatable formal semantics for IEEE-754 floating-point arithmetic. In 22nd IEEE symposium on computer arithmetic (ARITH 2015). https://doi.org/10.1109/ARITH.2015.26 (pp. 160–167). Lyon: IEEE.
Cimatti, A., Griggio, A., Schaafsma, B.J., & Sebastiani, R. (2013). The mathSAT5 SMT solver. In Tools and algorithms for the construction and analysis of systems, proceedings of the 19th international conference (TACAS 2013), lecture notes in computer science. https://doi.org/10.1007/978-3-642-36742-7_7, (Vol. 7795 pp. 93–107). Springer.
Clarke, L.A., & Richardson, D.J. (1985). Applications of symbolic evaluation. Journal of Systems and Software, 5(1), 15–35. https://doi.org/10.1016/0164-1212(85)90004-4.
Cousot, P., & Cousot, R. (1977). Abstract interpretation: a unified lattice model for static analysis of programs by construction or approximation of fixpoints. In Proceedings of the fourth annual ACM symposium on principles of programming languages. https://doi.org/10.1145/512950.512973 (pp. 238–252). Los Angeles: ACM Press.
Cuyt, A., Kuterna, P., Verdonk, B., & Verschaeren, D. (2002). Underflow revisited. CALCOLO, 39(3), 169–179. https://doi.org/10.1007/s100920200003.
de Moura, L.M., & Bjørner, N. (2008). Z3: an efficient SMT solver. In Tools and algorithms for the construction and analysis of systems, proceedings of the 14th international conference (TACAS 2008), lecture notes in computer science. https://doi.org/10.1007/978-3-540-78800-3_24, (Vol. 4963 pp. 337–340). Springer.
Delmas, D., Goubault, E., Putot, S., Souyris, J., Tekkal, K., & Védrine, F. (2009). Towards an industrial use of FLUCTUAT on safety-critical avionics software. In Formal methods for industrial critical systems, proceedings of the 14th international workshop (FMICS 2009), lecture notes in computer science. https://doi.org/10.1007/978-3-642-04570-7_6, (Vol. 5825 pp. 53–69). Eindhoven: Springer.
Fiedler, G. (2021). Floating point determinism. Gaffer on games blog, February 24, 2019. https://gafferongames.com/post/floating_point_determinism/ (2010) Last accessed on October 28th.
Gallois-Wong, D., Boldo, S., & Cuoq, P. (2020). Optimal inverse projection of floating-point addition. Numerical Algorithms, 83(3), 957–986. https://doi.org/10.1007/s11075-019-00711-z.
Gotlieb, A., Botella, B., & Rueher, M. (1998). Automatic test data generation using constraint solving techniques. In Proceedings of the 1998 ACM SIGSOFT international symposium on software testing and analysis, ISSTA ’98. https://doi.org/10.1145/271771.271790 (pp. 53–62). New York: ACM.
Gotlieb, A., Botella, B., & Rueher, M. (2000). A CLP framework for computing structural test data. In Computational logic — CL 2000: first international conference london, UK, July 24–28, 2000 Proceedings. https://doi.org/10.1007/3-540-44957-4_27(pp. 399–413). Springer.
The Institute of Electrical and Electronics Engineers, Inc.: IEEE Standard for Floating-Point Arithmetic, IEEE Std 754-2008 (revision of IEEE Std 754-1985) edn. (2008). Available at http://ieeexplore.ieee.org/servlet/opac?punumber=4610933.
Intel Corporation. Intel® 64 and IA-32 Architectures Software Developer Manuals, 325462-075us edn. (2021). https://www.intel.com/content/www/us/en/developer/articles/technical/intel-sdm.html. Last accessed on October 27th, 2021.
King, J.C. (1976). Symbolic execution and program testing. Communications of the ACM, 19(7), 385–394. https://doi.org/10.1145/360248.360252.
Kornerup, P., Lefevre, V., Louvet, N., & Muller, J.M. (2009). On the computation of correctly-rounded sums. In Proceedings of the 19th IEEE symposium on computer arithmetic (ARITH 2009). https://doi.org/10.1109/ARITH.2009.16 (pp. 155–160). Portland.
Marre, B., Bobot, F., & Chihani, Z. (2017). Real behavior of floating point numbers. In Proceedings of the 15th international workshop on satisfiability modulo theories, CEUR workshop proceedings, (Vol. 1889 pp. 50–62).
Marre, B., & Michel, C. (2010). Improving the floating point addition and subtraction constraints. In D. Cohen (Ed.) Proceedings of the 16th international conference on principles and practice of constraint programming (CP 2010), lecture notes in computer science. https://doi.org/10.1007/978-3-642-15396-9_30, (Vol. 6308 pp. 360–367). St. Andrews: Springer.
Michel, C. (2002). Exact projection functions for floating point number constraints. In Proceedings of the 7th international symposium on artificial intelligence and mathematics. Fort Lauderdale.
Michel, C., Rueher, M., & Lebbah, Y. (2001). Solving constraints over floating-point numbers. In Principles and practice of constraint programming - CP 2001, 7th international conference, CP 2001, paphos, cyprus, november 26 - december 1, 2001, proceedings. https://doi.org/10.1007/3-540-45578-7_36 (pp. 524–538).
Miné, A. (2004). Relational abstract domains for the detection of floating-point run-time errors. In Programming languages and systems, proceedings of the 13th european symposium on programming (ESOP 2004), lecture notes in computer science. https://doi.org/10.1007/978-3-540-24725-8_2, (Vol. 2986 pp. 3–17). Barcelona: Springer.
Monniaux, D. (2008). The pitfalls of verifying floating-point computations. ACM Transactions on Programming Languages and Systems, 30(3), 12:1–12:41. https://doi.org/10.1145/1353445.1353446.
Müller, S.M., & Paul, W.J. (2000). Computer architecture - complexity and correctness springer. https://doi.org/10.1007/978-3-662-04267-0.
Rump, S.M. (2013). Accurate solution of dense linear systems, Part II: Algorithms using directed rounding. Journal of Computational and Applied Mathematics, 242, 185–212. https://doi.org/10.1016/j.cam.2012.09.024.
Rump, S.M., & Ogita, T. (2007). Super-fast validated solution of linear systems. Journal of Computational and Applied Mathematics, 199(2), 199–206. Special Issue on Scientific Computing, Computer Arithmetic, and Validated Numerics (SCAN 2004).
Watte, J. (2021). Floating point determinism. Gamedev.net Forum, June 30, 2008. https://www.gamedev.net/forums/topic/499435-floating-point-determinism/ (2008) Last accessed on October 28th.
Wu, X., Li, L., & Zhang, J. (2017). Symbolic execution with value-range analysis for floating-point exception detection. In 24th asia-pacific software engineering conference, APSEC 2017, Nanjing, China, December 4–8, 2017. https://doi.org/10.1109/APSEC.2017.6 (pp. 1–10).
Acknowledgements
The authors express their gratitude to Roberto Amadini, Isacco Cattabiani and Laura Savino for their careful reading of early versions of this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bagnara, R., Bagnara, A., Biselli, F. et al. Correct approximation of IEEE 754 floating-point arithmetic for program verification. Constraints 27, 29–69 (2022). https://doi.org/10.1007/s10601-021-09322-9
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10601-021-09322-9





 and either x = y and z≠ 0, or x = z and y≠ 0;
and either x = y and z≠ 0, or x = z and y≠ 0; and either x = y and z≠ 0, or x = −z and y≠ 0;
and either x = y and z≠ 0, or x = −z and y≠ 0;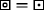 and either x = ±y and z≠ ± 1, or x = ±z and y≠ ± 1;
and either x = ±y and z≠ ± 1, or x = ±z and y≠ ± 1; , x = ±y and z≠ ± 1.
, x = ±y and z≠ ± 1.
 and thus
and thus  holds.
holds. as
as  and
and  , the numerical order is reflected into the symbolic order to give
, the numerical order is reflected into the symbolic order to give 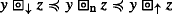 .
. by Definition 5; since either
by Definition 5; since either  .
. by Definition 5; again, since either [y ∘ z]n = + 0 or
by Definition 5; again, since either [y ∘ z]n = + 0 or  .
. while
while  ; hence, also in this case,
; hence, also in this case,  holds.
holds. while,
while, moreover,
moreover, while,
while, .
.








