Abstract
A well-known and powerful constraint model reformulation is to compute the solutions to a model part, say a custom constraint predicate, and tabulate them within an extensional constraint that replaces that model part. Despite the possibility of achieving higher solving performance, this tabling reformulation is often not tried, because it is tedious to perform; further, if successful, it obfuscates the original model. In order to encourage modellers to try tabling, we extend the MiniZinc toolchain to perform the automatic tabling of suitably annotated predicate definitions, without requiring any changes to solvers, thereby eliminating both the tedium and the obfuscation. Our experiments show that automated tabling yields the same tables as manual tabling, and that tabling is beneficial for solvers of several solving technologies.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
If poor propagation is achieved within part of a constraint programming (CP) model, then a common piece of advice is to table that model part. Tabling amounts to computing all solutions to that model part and replacing it by an extensional constraint requiring the variables of that model part to form one of these solutions. If there are not too many solutions, then the hope is that the increased propagation leads to faster solving. An example will be given shortly.
Extensional predicates abound and their efficient propagation to domain consistency is a topic of intense research over the last decade (see [14] for the state of the art): the  predicate takes the solutions in tabular form, whereas the
predicate takes the solutions in tabular form, whereas the  predicate [28] takes a compression of such a table into a finite automaton defining a regular language, and the
predicate [28] takes a compression of such a table into a finite automaton defining a regular language, and the  [8] and
[8] and  [9] predicates take a compression of such a table into a multi-valued decision diagram (MDD).
[9] predicates take a compression of such a table into a multi-valued decision diagram (MDD).
The tabling reformulation is however often not tried, because it is tedious to perform; further, it obfuscates the original model if it is actually performed.
Example 1
To illustrate the idea, consider the patience game Black Hole [27]. Before going into the details, let us first quote the rules as stated by the inventor:
- Layout :
-
Put the Ace of spades in the middle of the board as the base or “black hole”. Deal all the other cards face up in seventeen fans of three, orbiting the black hole.
- Object :
-
To build the whole pack into a single pile of 52 cards based on the black hole.
- Play :
-
The top (exposed) card of each fan is available for building on the centre pile. Build in ascending or descending sequence regardless of suit, going up or down ad lib and changing direction as often as necessary. Ranking is continuous between Ace and King.
Figure 1 shows an instance of the game and its solution, both taken from [17], whose authors studied symmetry breaking for this problem. A model and twenty instances of the game can be found in the MiniZinc benchmark suite.Footnote 1 In the model, the Ace of spades is encoded by 1, the King of spades by 13, the Ace of hearts by 14, and so on. The key variable is an array declared:

where x[j] gives the j th card in the pile. The Play rule involves a constraint:

where  can be expressed in several ways: see the first two variants in Fig. 2, where the reader should ignore the
can be expressed in several ways: see the first two variants in Fig. 2, where the reader should ignore the  annotation for now. Although declarative, the first formulation hinders propagation, because it does not yield domain consistency, and the second one is slow. For better propagation and speed,
annotation for now. Although declarative, the first formulation hinders propagation, because it does not yield domain consistency, and the second one is slow. For better propagation and speed,  is a natural candidate for tabling, and indeed in the MiniZinc model quoted above it has been converted by hand into a
is a natural candidate for tabling, and indeed in the MiniZinc model quoted above it has been converted by hand into a  constraint whose extension has 416 tuples: see the third variant in Fig. 2. Each of the tuples represents a solution to the
constraint whose extension has 416 tuples: see the third variant in Fig. 2. Each of the tuples represents a solution to the  predicate. Arguably, that extensional formulation is less declarative than the intensional ones, even though one can of course leave the original formulation nearby in comments. Further, the manual construction of the extension is error-prone.
predicate. Arguably, that extensional formulation is less declarative than the intensional ones, even though one can of course leave the original formulation nearby in comments. Further, the manual construction of the extension is error-prone.
Would it not be nice if the modeller could just add a  annotation to the head of the predicate definition whose solutions are to be computed and tabled, like in the first two variants of Fig. 2? Would it not be nice if the compilation and solving toolchain then performed this tabling, added the resulting
annotation to the head of the predicate definition whose solutions are to be computed and tabled, like in the first two variants of Fig. 2? Would it not be nice if the compilation and solving toolchain then performed this tabling, added the resulting  constraint to the model, and replaced each call to the annotated predicate definition by a call to the relevant
constraint to the model, and replaced each call to the annotated predicate definition by a call to the relevant  constraint?
constraint?
In this paper, our main contribution is to enable the scenario outlined by the preceding two questions: we extend the MiniZinc toolchain [26] to perform the automatic tabling of suitably annotated predicate definitions.
We see three advantages to our extension. First, the modeller is more likely to experiment with the well-known and powerful tabling reformulation if its tedium is eliminated by automation. Second, the original model is not obfuscated by tables, at the often negligible cost of computing them on-the-fly. Third, tabling is technology-neutral: our experiments in Section 2 show that tabling can be beneficial for CP backends, with or without lazy clause generation, constraint-based local search (CBLS) backends, Boolean satisfiability (SAT) backends, SAT modulo theory (SMT) backends, and hybrid backends; we have no evidence yet that a mixed-integer linear programming (MIP) backend to MiniZinc can benefit from tabling.
The organisation of the rest of this paper is as follows. In Section 2 we introduce our MiniZinc annotation and apply it on four case studies. In Section 3 we discuss the implementation issues of adding support for the discussed annotation to the MiniZinc toolchain, and we outline already implemented alternatives and future work. In Section 4 we discuss related work, and we conclude in Section 5.
2 Using the auto-tabling annotation
The MiniZinc toolchain first compiles, or flattens, a MiniZinc model into a sub-language called FlatZinc, using instantiations of all the model parameters and predicate definitions that are specific to the solver that is then invoked when interpreting the resulting FlatZinc model [26]. As part of this transformation, the MiniZinc compiler replaces all predicate calls by their definitions. We extend the compiler instead to replace each call to a predicate defined with our  annotation by a call to a
annotation by a call to a  constraint that has the same solutions (note that MiniZinc model annotations denote recommended but not imposed solving hints and do not affect the model semantics).
constraint that has the same solutions (note that MiniZinc model annotations denote recommended but not imposed solving hints and do not affect the model semantics).
To do this, the compiler needs to collect these solutions. This is done by creating and solving, during compilation, some smaller models, which we call submodels. Each submodel defines the annotated predicate and has a single constraint, which calls the annotated predicate with only variables as arguments. We consider three strategies that differ in how many submodels are created and presolved for each annotated predicate definition, and how their variable domains are defined.
We make four case studies with the instance-based strategy, where a single submodel is created for each annotated predicate definition, and the domain of each variable is the union of the domains of that variable across all the calls in the MiniZinc model to that predicate. We describe the two other strategies in Section 3.
We chose our four case studies among many potential ones (say within the model pool of the MiniZinc Challenge and MiniZinc distribution) as follows. The black-hole-patience model improvement (Section 2.1) is a famous textbook-level case and we wanted to show how easy it is to reproduce it now. The block party metacube problem (Section 2.2) is unknown within our community and we wanted to show how a straightforward model can be accelerated. The JP-encoding (Section 2.3) model was used in a MiniZinc Challenge and we wanted to show how easy it is now to improve it. The handball tournament (Section 2.4) model was also used in MiniZinc Challenges, and was refined in [7]. That last case study can be seen as a rational reconstruction of a fragment of the refined constraint model.
For each model, we carried out experiments using the following MiniZinc (MZN) backends:
-
Gecode [16], version 4.4.0, is a CP solver;
-
Chuffed [10], version a01c29e, is a CP solver with lazy clause generation;
-
or-tools [19], version 5.0, has a CP solver (or-tools/CP) and a SAT solver (or-tools/SAT);
-
MinisatID [11], version 3-11-0, is a hybrid solver combining ideas from CP, SAT, and SMT;
-
MZN/Yices2 [6], version 2-0-02, translates into an SMT model, solved by Yices2, version 2.5.1;
-
MZN/Gurobi [2], version 2.0.97, translates into a MIP model, solved by Gurobi Optimizer, version 6.5.2;
-
MZN/OscaR.cbls [5], version of December 2016, translates into a CBLS model and generates a black-box search procedure, run by OscaR.cbls [12], version of December 2016.
Other metrics than the solving times and the reported objective values (in the case of optimisation problems), such as CP backtracks, are not in common to all the solving technologies we apply here, hence we have not evaluated any technology-specific metrics.
All experiments were run on a single core of a Intel®; Xeon®; CPU E5520 @ 2.27 GHz with 16 cores and 24 GB RAM running Ubuntu 14.04 64 bits.
All models, instance data, and instance data generators used below are at https://github.com/Dekker1/MiniZinc-Auto-Tabling-Models.
2.1 The black-hole patience problem
We first revisit the black-hole patience problem of Section 1. We used the second intensional formulation of Fig. 2 because the first one contains the  function, which is not supported by all the MiniZinc backends we used; note that it does not matter which intensional formulation is used for auto-tabling, as the same extensional formulation (the one of Fig. 2) is generated, thereby yielding the published MiniZinc model with a
function, which is not supported by all the MiniZinc backends we used; note that it does not matter which intensional formulation is used for auto-tabling, as the same extensional formulation (the one of Fig. 2) is generated, thereby yielding the published MiniZinc model with a  constraint. When auto-tabling is not used, the second formulation is better for solvers: it creates a single
constraint. When auto-tabling is not used, the second formulation is better for solvers: it creates a single  constraint instead of three constraints (namely
constraint instead of three constraints (namely  ,
,  , and
, and  ).
).
The results in the upper-left plot of Fig. 3 are that auto-tabling generally yields some speedup for all solvers, with the exception of MinisatID, for which presolving has a negative effect, and MZN/Yices2, which seems unaffected. It is worth noting, for Gecode, that both the non-tabled and auto-tabled versions yield domain consistency, and that the speedup is only due to faster propagation rather than a smaller search tree. The presolving fraction for Gecode of the total solve time, for the instances that Gecode is able to solve or disprove without timing out, varies from 0.05% to 54%, with a median fraction of 7%. Actually, this high variation is mostly due to variations in actual solve time, as the presolve time never exceeds 20 ms.
Results on the black-hole patience problem (upper left), the block party metacube problem (upper right), the JP-encoding problem (lower left), and the handball tournament scheduling problem with 7 + 7 teams (lower right). A time limit of 10 minutes was used for all instances. Auto-tabling and flattening times were negligible throughout. All axes are logarithmic. A point at coordinates (x, y) corresponds to an instance solved with auto-tabling with performance x and without auto-tabling with performance y. Details: Black Hole (Section 2.1) The plot shows the time to find the first solution, or to prove unsatisfiability. MZN/Gurobi and MZN/OscaR.cbls timed out on all satisfiable instances. Block Party (Section 2.2) The plot shows the time to find the first solution. MZN/Gurobi and MZN/OscaR.cbls timed out on all instances, while the used version of or-tools/CP crashed on the non-tabled instances. JP-Encoding (Section 2.3) The plot shows the quantity 100 ⋅ o b j/o p t − 99 where opt is the global optimum and obj is the best solution found for the given instance, letting the solver run to the time limit or until it proves optimality. Handball (Section 2.4) The plot shows the time to prove optimality. Only Chuffed and Gecode were able to solve any instances.
2.2 The block party metacube problem
See Fig. 4: there are eight cubes in the block party metacube problem (BPMP, see http://w.3pxh.com); each corner of each side of each cube features an icon; each icon has three attributes — shape, colour, and pattern — with four possible values each. A party is made of four cubes placed in a 2 × 2 square such that the four icons in the centre of the visible side of the square have, for each of the three attributes, either all equal or all different values (e.g., four icons with a heart shape and a solid pattern, but in four different colours; or four icons with different shapes and different patterns, but all coloured black). A block party metacube is an arrangement of all eight cubes into a 2 × 2 × 2 metacube so that each of the six sides of the metacube forms a party. For example, in Fig. 4, only the top side of the metacube forms a party.
In our MiniZinc model, introduced in [13], the decision variables denote which cube is placed at each of the 8 metacube positions, and which icon is placed at each of the 24 centre positions of the six sides of the metacube. In addition to the party constraints, one must ensure that the cube in each metacube position and the icons in the three metacube centre positions of that cube are compatible with respect to one of the actual cubes. This is captured by the predicate defined in Fig. 5: it requires that there exists a rotation of the given cube such that the three given icons appear in their respective positions on that cube. The  parameter array encodes which icons appear where on the actual cubes, and the
parameter array encodes which icons appear where on the actual cubes, and the  parameter array maps each rotation to a triplet of positions in the data encoding, where the corners of the sides of each cube are numbered from 1 to 24 in some arbitrary order. For example, three of the lines in the
parameter array maps each rotation to a triplet of positions in the data encoding, where the corners of the sides of each cube are numbered from 1 to 24 in some arbitrary order. For example, three of the lines in the  array are
array are  ,
,  , and
, and  , corresponding to three rotations of the cube with the same three icons in the relevant positions.
, corresponding to three rotations of the cube with the same three icons in the relevant positions.
It is worth noting that this predicate introduces a local variable, namely  , which disappears when the predicate is tabled: as the predicate definition is not used anymore after the tabling, no extra variable is added to the FlatZinc model. This variable was used to express the relation in a succinct way, but is not necessary any more once the predicate is tabled.
, which disappears when the predicate is tabled: as the predicate definition is not used anymore after the tabling, no extra variable is added to the FlatZinc model. This variable was used to express the relation in a succinct way, but is not necessary any more once the predicate is tabled.
In order to obtain more than one problem instance, we generated the  array for 14 new satisfiable instances using a data-generating MiniZinc model producing sets of eight cubes similar to the original ones upon a randomised search procedure. The results, shown in the upper-right plot of Fig. 3, are very positive: the total runtime consistently drops by more than 10 times (and more instances are solved) for Chuffed, and by more than 5 times for Gecode. The results are more spread out for MinisatID and or-tools/SAT: auto-tabling increases the runtime for a few instances but it also decreases it by more than 20 times for some instances with MinisatID and allows us to solve more instances with or-tools/SAT. Note that MZN/Yices2 timed-out on all instances without auto-tabling but could solve 2 instances with it. The presolving fraction for Gecode of the total solve time, for the instances that Gecode is able to solve or disprove without timing out, is negligible and never exceeds 1%. The presolve time never exceeds 20 ms.
array for 14 new satisfiable instances using a data-generating MiniZinc model producing sets of eight cubes similar to the original ones upon a randomised search procedure. The results, shown in the upper-right plot of Fig. 3, are very positive: the total runtime consistently drops by more than 10 times (and more instances are solved) for Chuffed, and by more than 5 times for Gecode. The results are more spread out for MinisatID and or-tools/SAT: auto-tabling increases the runtime for a few instances but it also decreases it by more than 20 times for some instances with MinisatID and allows us to solve more instances with or-tools/SAT. Note that MZN/Yices2 timed-out on all instances without auto-tabling but could solve 2 instances with it. The presolving fraction for Gecode of the total solve time, for the instances that Gecode is able to solve or disprove without timing out, is negligible and never exceeds 1%. The presolve time never exceeds 20 ms.
2.3 The JP-encoding problem
The JP-encoding problem, introduced in the MiniZinc Challenge 2014,Footnote 2 is to recover the original encoding of a stream of Japanese text where several encodings might have been mixed, say by accident. The considered encodings are ASCII, EUC-JP, SJIS, and UTF-8. An array of bytes is given and the goal is to assign to each byte its encoding in order to maximise the sum of the likelihoods of each byte appearing in the assigned encoding. The encodings may use different numbers of bytes to represent a given character. For example, ASCII always uses one byte, but UTF-8 may use from one to four bytes depending on the encoded character. In addition, each encoding defines ranges of possible values for the byte of each position. For example, an ASCII byte can only have a value from 0 to 127, and a UTF-8 character on two bytes must have the first byte from 194 to 223 and the second byte from 128 to 191.
The published original MiniZinc model uses three arrays of variables having the same length as the input byte array, called  :
:
-
 is the status of
is the status of  , that is in which position of which variation of which encoding that byte is; the domain has 16 values, including one for an unknown status; for example, the value
, that is in which position of which variation of which encoding that byte is; the domain has 16 values, including one for an unknown status; for example, the value  states that the byte is in the second position of a four-byte UTF-8 encoding;
states that the byte is in the second position of a four-byte UTF-8 encoding; -
 is the encoding of
is the encoding of  ; the domain has 5 values, including one for an unknown encoding; for example, the value
; the domain has 5 values, including one for an unknown encoding; for example, the value  states that the byte is in the UTF-8 encoding;
states that the byte is in the UTF-8 encoding; -
 indicates whether
indicates whether  is the start of a character.
is the start of a character.
There are implications and disjunctions formulating the rules of the encodings and the functional dependency of each  and
and  on
on  . Let
. Let  be defined as a weighted sum of reified equalities, where the weight is given by the negative logarithm of the frequency of
be defined as a weighted sum of reified equalities, where the weight is given by the negative logarithm of the frequency of  in the corresponding encoding: see Fig. 6. A lower value for
in the corresponding encoding: see Fig. 6. A lower value for  indicates a higher likelihood
indicates a higher likelihood  of appearing in
of appearing in  . A byte of unknown encoding has a score of 1000. The objective function to be minimised is the sum of the
. A byte of unknown encoding has a score of 1000. The objective function to be minimised is the sum of the  variables.
variables.
Predicate defining the score of the JP-encoding of a byte. The identifiers starting with  are constants representing values in the domain of
are constants representing values in the domain of  . The arrays with identifiers ending with
. The arrays with identifiers ending with  are indexed from 0 to 255 and represent the score of each byte value in each encoding. If a byte is encoded in ASCII, then its score is zero, which is the best score
are indexed from 0 to 255 and represent the score of each byte value in each encoding. If a byte is encoded in ASCII, then its score is zero, which is the best score
In order to apply auto-tabling, we refactored the original model so as to introduce predicate definitions that we can annotate, thereby also giving more structure to the model. In particular, we introduced the following predicates:
-
 is used to restrict the status combinations for two given consecutive bytes; for example, value
is used to restrict the status combinations for two given consecutive bytes; for example, value  must be directly preceded by
must be directly preceded by  ;
; -
 is used to state the functional dependencies between the three variables for a given byte;
is used to state the functional dependencies between the three variables for a given byte; -
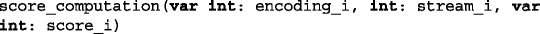 is used to state the functional dependency from the encoding and input stream to the score of a given byte.
is used to state the functional dependency from the encoding and input stream to the score of a given byte.
We added the  annotation to the definitions of these three predicates. The resulting
annotation to the definitions of these three predicates. The resulting  predicate is presented in Fig. 6. We do not show the other predicates here as each of them is several dozens of lines long.
predicate is presented in Fig. 6. We do not show the other predicates here as each of them is several dozens of lines long.
Many other changes can be made to the original model in order to improve it, and the problem can actually be solved more efficiently by dynamic programming. However, we refrained from making any major non-refactoring changes to the original model.
Our experiments were run on the five instances used in the MiniZinc Challenge 2014, which range from 100 to 1700 bytes in the  array. See the lower-left plot of Fig. 3: auto-tabling makes a huge difference. For all plotted solvers except MZN/Gurobi, it is possible to prove optimality on the smallest instance without timing out when auto-tabling is enabled, and the best found solution at time-out is the same or better with auto-tabling for all other instances. MZN/OscaR.cbls and MinisatID could not solve any instance without auto-tabling but could solve the smallest one with it. These improvements are not surprising given that our auto-tabling replaces a lot of small reified constraints with poor interaction by a few
array. See the lower-left plot of Fig. 3: auto-tabling makes a huge difference. For all plotted solvers except MZN/Gurobi, it is possible to prove optimality on the smallest instance without timing out when auto-tabling is enabled, and the best found solution at time-out is the same or better with auto-tabling for all other instances. MZN/OscaR.cbls and MinisatID could not solve any instance without auto-tabling but could solve the smallest one with it. These improvements are not surprising given that our auto-tabling replaces a lot of small reified constraints with poor interaction by a few  constraints that can be handled very efficiently by most solvers. This is however not the case for MZN/Gurobi: thanks to its own presolving capabilities, this solver is able to prove optimality of all instances without auto-tabling very fast; enabling the auto-tabling unfortunately makes MZN/Gurobi about 12 times slower. The presolving fraction for Gecode of the total solve time, for the instances that Gecode is able to solve or disprove without timing out, is negligible and never exceeds 1.5%. The presolve time never exceeds 70 ms.
constraints that can be handled very efficiently by most solvers. This is however not the case for MZN/Gurobi: thanks to its own presolving capabilities, this solver is able to prove optimality of all instances without auto-tabling very fast; enabling the auto-tabling unfortunately makes MZN/Gurobi about 12 times slower. The presolving fraction for Gecode of the total solve time, for the instances that Gecode is able to solve or disprove without timing out, is negligible and never exceeds 1.5%. The presolve time never exceeds 70 ms.
2.4 The handball tournament scheduling problem
Now, we study a sports scheduling problem that uses a tournament format that consists of two divisional round-robin tournaments run in parallel (Part I), followed by a full-league round-robin tournament (Part II). Elitserien, the top Swedish handball league, uses such a format for its league schedule, followed by Part II repeated but played in reverse order and swapping home and away games for all teams. The league consists of two divisions of n = 7 teams each. In this case study, we ignore the reversed Part II, but keep all other salient features.
A constraint model for this problem was presented in [22]. We will repeat a fragment of the model here, referring the reader to [22] for further details.
A partial solution to the problem is a home-away pattern, or H A P array, similar to the one shown in Fig. 7. Rows stand for teams, columns stand for time periods. The precise assignment of teams to rows is not fixed up front, but is part of the problem to be solved. However, the assignment of teams to divisions is given. H A P[r, p] = means that team r plays at home in period p, while H A P[r, p] = means that it plays away, and H A P[r, p] = means that it has a bye, i.e., it does not play in that period. In every row and column, the number of home games must match the number of away games. Also, at no point during the season can the number of home and away games played so far by any team differ by more than one. Every team is constrained to have exactly one bye during the divisional Part I and none during the full-league Part II.
A pair of grey-shaded H A P array elements denotes a break, i.e., the given team plays at home twice in a row or away twice in a row. It is a constraint of the problem that for any team there can be no break during Part I, at most one break during Part II, and that the number of breaks should be minimal. This number was shown in [21] to be 2n − 2 for leagues with odd division size n.
To make a solution complete, every H A P array element must be assigned the opponent team that will meet the given team in the given period. It is worth noting that not every partial solution can be extended to a complete solution.
Finally, every team prefers not to play at home during selected periods, for example because of venue unavailability. So we have a constrained optimisation problem with the objective of maximising the number of satisfied preferences.
Note that the problem is structurally very constrained. First, symmetry breaking allows us to completely fix Part I (divisional play) of the H A P array up front. Further, the valid combination of any row of the H A P array is functionally determined by the row number and the period in which its break occurs, if any. We now give a fragment of the constraint model.
Let n be the division size, let \(\mathcal {T} = \{1, \dots , 2n\}\) denote the set of teams, let \(\mathcal {P} = \{1, \dots , 3n-1\}\) denote the set of periods, and let \(\mathcal {B} = \{0\} \cup \{n+1, \dots , 3n-1\}\) denote the set of periods in which breaks can begin, plus the integer 0 denoting no break. Let σ denote a regular expression corresponding to the finite automaton shown in Fig. 8. Let the parameter N[t, p] = 1 if team t prefers not to play at home in period p, and 0 otherwise. The model has the following problem variables:
-
H A P[r, p] ∈{,,}, where the team in row r plays in period p.
-
H A P[r] is an abbreviation for the row \([\mathit {HAP}[r,p] \mid p \in \mathcal {P}]\).
-
\(B[r] \in \mathcal {B}\), the period in which the break for row r begins, or 0 if row r has no break in its schedule.
-
\(T[r] \in \mathcal {T}\), the team assigned to row r.
The constraints include (1) and (2) whereas (3) expresses the cost function to be minimised:

The full model was used in the MiniZinc Challenges 2014 and 2016.Footnote 3 It is worth noting that constraint (2) captures a conjunction of more basic requirements, and can be thought of as an example of tabling by hand. We now describe how we refactored that published MiniZinc model so as to improve it by presolving.
First, we applied auto-tabling to the conjunction of (1) and (2) and some symmetry-breaking constraints that allow us to completely fix Part I of the H
A
P array. This resulted in a  (r, b, p, x) constraint with x = H
A
P[r, p] functionally determined by r, b = B[r], and p. Let h(r, b, p) denote this function. This in itself did not result in a significant speedup, which did not come as a big surprise, since (2) was the bulk of the auto-tabled conjunction, and
(r, b, p, x) constraint with x = H
A
P[r, p] functionally determined by r, b = B[r], and p. Let h(r, b, p) denote this function. This in itself did not result in a significant speedup, which did not come as a big surprise, since (2) was the bulk of the auto-tabled conjunction, and  can be propagated to domain consistency on a CP solver.
can be propagated to domain consistency on a CP solver.
Next, we made the observation that the cost function is a sum over terms, each of which is a function of r, T[r], and H
A
P[r]. But since H
A
P[r] is a function of r and B[r], the cost function can be turned into a sum (5) over terms f(r, T[r],B[r]), where the f function, defined by (4), can also be obtained by auto-tabling, creating a  (r, t, b, y) constraint with y = f(r, t, b):
(r, t, b, y) constraint with y = f(r, t, b):
This transformation led to a significant performance improvement, as we now show. We generated 20 random instances of league size 7 + 7: the partitioning of teams into divisions was given, but the mapping of teams to rows, T[r], was left as part of the problem to solve; we let N[t, p] = 1 with probability 0.05, which is similar to the density of such preferences in Elitserien. As shown in the lower-right plot of Fig. 3, most of the instances were accelerated by auto-tabling, by up to 30 times. Chuffed solved all instances to optimality, whereas Gecode solved twelve of them. The presolving fraction for Gecode of the total solve time, for the instances that Gecode is able to solve or disprove without timing out, varies from 0.04% to 13%, with a median fraction of 1.5%. The presolve time never exceeds 170 ms. We also ran a similar experiment with league size 9 + 9: only Chuffed is able to solve those instances to optimality within 10 minutes. Finally, this case study can be seen as a rational reconstruction of a fragment of the refined constraint model in [7].
3 Tool support for auto-tabling
We now describe how we integrated auto-tabling into the MiniZinc toolchain.Footnote 4 For further details, see [13].
3.1 Design decisions and implementation
Our first two important design decisions were to auto-table predicate calls and to annotate predicate definitions. Indeed, there are other ways to define which subproblems should be presolved, as will be briefly surveyed in Section 5. Our decision to focus on predicates is mainly motivated by the facts that predicates offer a natural way to structure a model and that adding a single annotation to a predicate definition is the simplest way to enable auto-tabling. Using predicates as the basic building block has the additional benefit that any local variables introduced in a predicate definition disappear upon tabling, as seen in the case studies of Sections 2.2 and 2.4.
An apparent downside of using annotations to predicate definitions is that one may need to refactor a model in order to introduce the predicate definitions one wants to annotate, as seen in the case studies of Sections 2.3 and 2.4. However, one can also see this as an extra incentive for modellers to use predicates in the first place, as this is good modelling practice in the same way as it is good programming practice to break down procedural code into smaller units, such as functions or methods.
While MiniZinc annotations are usually targeted at the solvers, resolving annotations within the MiniZinc compiler is possible and has been done for other annotations in similar situations (for example,  is used when set variables are replaced by variables of other types during flattening). Adding our annotation to the MiniZinc language amounts simply to declaring it in the MiniZinc standard library: we will show with Fig. 10 how to do that, after a few additional considerations.
is used when set variables are replaced by variables of other types during flattening). Adding our annotation to the MiniZinc language amounts simply to declaring it in the MiniZinc standard library: we will show with Fig. 10 how to do that, after a few additional considerations.
An important advantage of our MiniZinc extension is that all changes are located within the compiler, so that no solver or other part of the toolchain needs to be changed. More precisely, our third important design decision was to add an extra compilation step into the MiniZinc compiler, namely after the type checking and before the actual flattening. This additional intermediate step provides all the presolving functionality. We chose to locate all code in this particular place in order to maintain the modular approach of the existing compiler.
The additional compiler step performs the following actions, for each predicate whose definition is annotated for presolving:
-
1.
Find the corresponding
 item and the calls to this predicate by walking through the parse tree.
item and the calls to this predicate by walking through the parse tree. -
2.
Construct a MiniZinc model, called a submodel, for finding the solutions to the predicate. The submodel comprises the predicate definition, decision variables of the types of the formal arguments of the predicate, a constraint calling the predicate on those decision variables, and a
 item in order to ask for satisfiability solving. The domain of each introduced variable is the union of the domains of the corresponding variables across all the calls in the original MiniZinc model to the annotated predicate definition.
item in order to ask for satisfiability solving. The domain of each introduced variable is the union of the domains of the corresponding variables across all the calls in the original MiniZinc model to the annotated predicate definition. -
3.
Search for all solutions to the constructed submodel by running the MiniZinc toolchain on the submodel: it is in turn flattened and given to a FlatZinc solver by asking for all solutions.
-
4.
Collect all the solutions into an array suitable for a
 constraint. While this is mostly straightforward, some care is needed when the arguments are of different types. Indeed, the MiniZinc language only defines the
constraint. While this is mostly straightforward, some care is needed when the arguments are of different types. Indeed, the MiniZinc language only defines the  constraint for all integer variables or all Boolean variables. Hence, one needs to cast Boolean variables into integer ones when they are mixed in a predicate. We currently do not support set and float variables.
constraint for all integer variables or all Boolean variables. Hence, one needs to cast Boolean variables into integer ones when they are mixed in a predicate. We currently do not support set and float variables. -
5.
Replace the body of the predicate definition in the original MiniZinc model by a call to a
 constraint with the obtained array of solutions. The subsequent flattening step will replace the calls to the predicate by this new body.
constraint with the obtained array of solutions. The subsequent flattening step will replace the calls to the predicate by this new body.
Note that any solver can be chosen for solving the constructed submodel, as long as it supports searching for all solutions. To avoid problems related to definitions of the MiniZinc library that may differ between solvers, it is generally a good idea to use the same solver for both solving and presolving, provided that it supports searching for all solutions.
We present in Fig. 9 a schematic view of the compilation and solving of a MiniZinc instance (that is, a MiniZinc model and instance data), including the new auto-tabling step.
Schematic view of how our compiler extension integrates into the existing MiniZinc toolchain. The rounded boxes represent processes and the rectangles represent their inputs and outputs. The dashed arrow corresponds to the previous dataflow, which is now replaced by the chain of double-shafted arrows
3.2 Two additional auto-tabling strategies
In order to accommodate other needs, we implemented two alternatives to the instance-based strategy, used throughout Section 2, which creates and solves a single submodel based on the calls in the MiniZinc model to the annotated predicate.
Under the call-based strategy, a separate submodel is created and solved for each call in the MiniZinc model to the annotated predicate: the domain of each variable in a submodel is the domain of that variable in the corresponding call. Compared to the instance-based strategy, this one may be more suitable when the domains of the calls do not overlap much, thereby creating smaller tables, at the cost of solving more submodels. This strategy must be used when the predicate is called with varying lengths for a variable-array argument: one cannot create a  constraint over a non-fixed number of variables, so each call must be handled separately. An example of such a problem is the Kakuro puzzle, where this strategy converts a highly readable model into the specialised model discussed in [30] and [16, Chapter 21].
constraint over a non-fixed number of variables, so each call must be handled separately. An example of such a problem is the Kakuro puzzle, where this strategy converts a highly readable model into the specialised model discussed in [30] and [16, Chapter 21].
Under the model-based strategy, a single, instance-independent submodel is created, and the domain of each variable is the domain of the corresponding formal argument in the annotated predicate definition of the MiniZinc model. This strategy is called model-based because it does not depend on the actual calls in the model to the predicate.
3.3 The new annotation
To give the choice between our auto-tabling strategies, we introduce an  annotation with one argument: see Fig. 10. Line 2 states that the instance-based strategy is the default one. We chose to encapsulate our
annotation with one argument: see Fig. 10. Line 2 states that the instance-based strategy is the default one. We chose to encapsulate our  annotation into a
annotation into a  one in order to pave the way for alternative predicate-based presolving ideas in the MiniZinc toolchain.
one in order to pave the way for alternative predicate-based presolving ideas in the MiniZinc toolchain.
Thanks to this set of annotations, it is easy now for the modeller, novice and expert alike, to make experiments. Indeed, it suffices to change the annotation keyword and measure the effect.
Not all strategies are applicable in all situations. If one tries to use the instance-based strategy when not all calls to the predicate can be aggregated into a single submodel because of, for example, a varying amount of variables in an argument array, then the compiler will issue an error. The same error arises if one tries to use the model-based strategy with a predicate having as formal argument an array of non-fixed length. The use of the call-based strategy is always safe and never leads to compilation errors.
3.4 Future work on the implementation
Future work includes new features for our implementation.
Under the model-based strategy, all solutions could be collected only once, provided the predicate does not make use of the instance data, and then cached for use by future runs of the model, even with different instances. Caching of the solutions can be used when presolving for every instance would be too time-consuming. This would however require extra care in the compiler to ensure that the predicate definition is indeed not dependent on instance-specific data to avoid producing invalid results. For example, caching can be used for the  predicate of Fig. 2, but not for the
predicate of Fig. 2, but not for the  predicate of Fig. 5 because the latter uses the instance-specific
predicate of Fig. 5 because the latter uses the instance-specific  array.
array.
A possible extension is to offer the modeller the option to augment the  constraints inserted into the presolved model with a backend-specific annotation, or even the choice of an alternative predicate to
constraints inserted into the presolved model with a backend-specific annotation, or even the choice of an alternative predicate to  . This relates to research into alternative implementations of
. This relates to research into alternative implementations of  and MiniZinc predicates that might perform better than the backend’s default. This is also related to adding to our implementation the support of MiniZinc features such as predicates on float and set variables or on mixed variable types.
and MiniZinc predicates that might perform better than the backend’s default. This is also related to adding to our implementation the support of MiniZinc features such as predicates on float and set variables or on mixed variable types.
A simple way to support float and set variables, optionally mixed with Boolean or integer variables, is to replace the  constraint by an
constraint by an  constraint for each column of the table, with all
constraint for each column of the table, with all  constraints sharing an index variable used to identify a row of the table. This reformulation is generally applicable, as MiniZinc has variants of the
constraints sharing an index variable used to identify a row of the table. This reformulation is generally applicable, as MiniZinc has variants of the  predicate on all variable types. However, it may lead to slower solving than using a single constraint.
predicate on all variable types. However, it may lead to slower solving than using a single constraint.
While the onus of internally using an MDD-based propagator for the  predicate is not on us but on the developers of CP backends to MiniZinc, it is important to understand why we currently do not compress the table of presolved tuples so as to use instead the
predicate is not on us but on the developers of CP backends to MiniZinc, it is important to understand why we currently do not compress the table of presolved tuples so as to use instead the  predicate of MiniZinc or an
predicate of MiniZinc or an  predicate (which does not belong to MiniZinc yet): before compressing the presolved tuples, they have to be generated in the first place. So even though a compressed extension can be generated incrementally, there is no way to avoid enumerating the presolved tuples. An exciting research question in solver design is how to generate sets or subsets of solutions intensionally, say in automaton or MDD form, for a given problem instance and for arbitrary submodels. A starting point would be the work described in [3].
predicate (which does not belong to MiniZinc yet): before compressing the presolved tuples, they have to be generated in the first place. So even though a compressed extension can be generated incrementally, there is no way to avoid enumerating the presolved tuples. An exciting research question in solver design is how to generate sets or subsets of solutions intensionally, say in automaton or MDD form, for a given problem instance and for arbitrary submodels. A starting point would be the work described in [3].
Other features might be added to help modellers. One could, for example, add a timeout parameter to presolving: if a predicate cannot be presolved within a set time limit, then the original definition of the predicate is used.
Further, one can investigate more advanced defaults for the choice of the presolving strategy and an automated choice of the solver to use for presolving, in order to match them better to the contents of the annotated predicate definition.
Finally, one can consider other strategies than the three already implemented ones. Notably, an alternative to the instance-based and call-based strategies would be to perform the tabling after the flattening, where more information about the actual variable domains and array lengths is available. This alternative implementation, which we are currently performing, has the further advantage of facilitating the support for reified calls to the annotated predicate, which are currently not supported.
4 Related work
In addition to the models for the Black Hole, Handball, and Kakuro problems discussed above, reformulation by tabling was used for the maximum-density still life problem in [9].
Auto-tabling has been studied for a long time in the constraint programming community. For example, in generalised propagation, as implemented in the Propia library [23] of ECLiPSe, all solutions to an appropriately annotated goal are precomputed and internally replaced by a table constraint. More recently, with IBM ILOG CPLEX CP Optimizer, one can post a strong constraint on a set of variables [20]: all solutions to the constraints involving those variables in the model are found and a corresponding table constraint is posted as an implied constraint on those variables. The main difference with those approaches is that our approach is solver-independent, and even technology-independent. Note also that using the strong predicate is less fine-grained than our approach, because it is at the variable level rather than the predicate level.
Another line of related work is the automated synthesis of propagators for arbitrary constraints. The goal is fundamentally the same as for our auto-tabling, namely to speed up the solving process by transforming a suitable part of a model into an efficient propagator. The generated propagators can take several forms, such as CHR rules [1], stateless C-code [18], multivalued decision diagrams [9], and extended indexicals [25]. Again, those approaches are very specific to a single technology or even to a particular solver. In our case, we generate table constraints, which can be used under various solvers and technologies.
Finally, it is important to mention that presolving in general is a well-known concept in mixed integer programming and SAT modulo theories: solvers may transform models, for example in order to eliminate variables, to tighten constraints and domains, or to isolate some special substructures [15]. While this is less common in constraint programming, a form of presolving by reformulation is implemented in the CP solver of Google or-tools [19]. It has also been shown recently that domain tightening can be integrated in the MiniZinc compiler and that it is beneficial to solvers of several technologies [24].
5 Conclusion
Tabling, that is replacing model parts by constraints with precomputed solution arrays, is a powerful yet laborious way to improve model performance. We proposed to automate this process by integrating it in the MiniZinc toolchain: a modeller enables auto-tabling simply by annotating the predicate definitions to table and the compiler takes care of the rest. Tabling is made easy to use and nonintrusive.
It is often said that modelling is an art that is difficult to master. Indeed, finding a model that is solved efficiently on at least one solver is often difficult. We argue that our auto-tabling annotation lowers the skill level required for designing a good model: while the way an auto-tabled predicate is defined still influences the presolving time, it has nearly no influence on the actual solving time (i.e., excluding the presolving time), as the same table will be generated, up to row ordering. Instead, the important modelling decisions for tabling are how to structure the model with predicates and which predicates to table.
While it is too early to extract general principles, our preliminary observations are that auto-tabling may make a huge difference when the tabled predicate exhibits some of the following characteristics: the predicate has few arguments; some argument is used more than once in the predicate definition; the predicate defines a variable that appears in the objective function; the predicate introduces local variables; or the predicate admits a moderate number of solutions.
Beside the tool-specific future work stated in Section 3.4, it would be interesting to study more closely whether those observations generalise and how much they depend on the use of the  predicate or a particular solver.
predicate or a particular solver.
In particular, while we showed good evidence that MiniZinc CP backends, with and without lazy clause generation, and SAT backends can benefit from auto-tabling, we have less evidence for the chosen solvers of the other selected technologies, probably because the chosen problems were not suited to those technologies (namely CBLS and hybrids) or, in the case of MZN/Yices2, because the FlatZinc-to-SMTlib conversion [6] is outdated. Auto-tabling may not be appropriate for MIP backends to MiniZinc: it is worth studying how one could improve the linearisation in [2] of the  predicate.
predicate.
Finally, lazily computing solutions to a model part is an interesting alternative to precomputing them, in a way similar to decomposition techniques in MIP, such as Benders decomposition or column generation, and to on-the-fly solution generation when enforcing CP-style domain consistency on part of a model [4]. However, this would require different architectural choices from the ones we made: in particular, we chose to make no modifications to solvers, which allowed us to perform experiments with a wide range of technologies and solvers, but an on-the-fly approach would require us to modify the solvers, probably including a tighter integration with the MiniZinc compiler; this might be doable on top of the MiniSearch extension [29] to the MiniZinc toolchain.
Notes
The source code of the extended MiniZinc compiler can currently be found at https://github.com/Dekker1/libminizinc in the feature/presolve branch. The version used in our experiments and described here is tagged cpaior.
References
Abdennadher, S., & Rigotti, C. (2004). Automatic generation of rule-based constraint solvers over finite domains. ACM Transactions on Computational Logic, 5(2), 177–205.
Belov, G., Stuckey, P.J., Tack, G., & Wallace, M. (2016). Improved linearization of constraint programming models. In Rueher, M. (Ed.), CP 2016, LNCS, (Vol. 9892 pp. 49–65): Springer.
Bergman, D., Cire, A.A., van Hoeve, W.J., & Hooker, J. (2016). Decision diagrams for optimization. Springer.
Bessière, C., & Régin, J.C. (1999). Enforcing arc consistency on global constraints by solving subproblems on the fly. In Jaffar, J. (Ed.), CP 1999, LNCS, (Vol. 1713 pp. 103–117): Springer.
Björdal, G., Monette, J.N., Flener, P., & Pearson, J. (2015). A constraint-based local search backend for MiniZinc. Constraints, 20(3), 325–345.
Bofill, M., Suy, J., & Villaret, M. (2010). A system for solving constraint satisfaction problems with SMT. In Strichman, O., & Szeider, S. (Eds.), SAT 2010, LNCS, (Vol. 6175 pp. 300–305): Springer.
Carlsson, M., Johansson, M., & Larson, J. (2017). Scheduling double round-robin tournaments with divisional play using constraint programming. European Journal of Operational Research, 259(3), 1180–1190.
Carlsson, M., Ottosson, G., & Carlson, B. (1997). An open-ended finite domain constraint solver. In Glaser, H., Hartel, P., & Kuchen, H. (Eds.), PLILP 1997, LNCS, (Vol. 1292 pp. 191–206): Springer.
Cheng, K.C.K., & Yap, R.H.C. (2008). Maintaining generalized arc consistency on ad hoc r-ary constraints. In Stuckey, P.J. (Ed.), CP 2008, LNCS, (Vol. 5202 pp. 509–523): Springer.
Chu, G. (2011). Improving combinatorial optimization. Ph.D. thesis, Department of Computing and Information Systems. Australia: University of Melbourne.
De Cat, B., Bogaerts, B., Devriendt, J., & Denecker, M. (2013). Model expansion in the presence of function symbols using constraint programming. In Brodsky, A. (Ed.), ICTAI 2013 (pp. 1068–1075): IEEE. The MinisatID solver is available from https://dtai.cs.kuleuven.be/software/minisatid.
De Landtsheer, R., & Ponsard, C. (2013). OscaR.cbls: An open source framework for constraint-based local search, ORBEL-27, the 27th annual conference of the Belgian Operational Research Society. Available at http://www.orbel.be/orbel27/pdf/abstract293.pdf; the OscaR.cbls solver is available from https://bitbucket.org/oscarlib/oscar/branch/CBLS.
Dekker, J.J. (2016). Sub-problem pre-solving in MiniZinc. Master’s thesis, Department of Information Technology, Uppsala University, Sweden. Available at http://urn.kb.se/resolve?urn=urn:nbn:se:uu:diva-307145.
Demeulenaere, J., Hartert, R., Lecoutre, C., Perez, G., Perron, L., Régin, J., & Schaus, P. (2016). Compact-table: Efficiently filtering table constraints with reversible sparse bit-sets. In Rueher, M. (Ed.), CP 2016, LNCS, (Vol. 9892 pp. 207–223): Springer.
Eén, N., & Biere, A. (2005). Effective preprocessing in SAT through variable and clause elimination. In Bacchus, F., & Walsh, T. (Eds.), SAT 2005, LNCS, (Vol. 3569 pp. 61–75): Springer.
Gecode Team (2016). Gecode: A generic constraint development environment. http://www.gecode.org.
Gent, I.P., Jefferson, C., Kelsey, T., Lynce, I., Miguel, I., Nightingale, P., Smith, B.M., & Tarim, S.A. (2007). Search in the patience game ’black hole’. AI Communications, 20(3), 211–226.
Gent, I.P., Jefferson, C., Linton, S., Miguel, I., & Nightingale, P. (2014). Generating custom propagators for arbitrary constraints. Artificial Intelligence, 211, 1–33.
Google Optimization Team (2016). or-tools: Google’s software suite for combinatorial optimization. https://developers.google.com/optimization.
IBM Knowledge Center. The strong constraint. http://www.ibm.com/support/knowledgecenter/SSSA5P_12.6.3/ilog.odms.ide.help/OPL_Studio/opllang_quickref/topics/tlr_oplsch_strong.html.
Larson, J., & Johansson, M. (2014). Constructing schedules for sports leagues with divisional and round-robin tournaments. Journal of Quantitative Analysis in Sports, 10 (2), 119–129.
Larson, J., Johansson, M., & Carlsson, M. (2014). An integrated constraint programming approach to scheduling sports leagues with divisional and round-robin tournaments. In Simonis, H. (Ed.), CPAIOR 2014, LNCS, (Vol. 8451 pp. 144–158): Springer.
Le Provost, T., & Wallace, M. (1992). Domain independent propagation, FGCS 1992, International conference on fifth generation computer systems (pp. 1004–1011): IOS Press.
Leo, K., & Tack, G. (2015). Multi-pass high-level presolving. In Yang, Q., & Wooldridge, M. (Eds.), IJCAI 2015 (pp. 346–352): AAAI Press.
Monette, J.N., Flener, P., & Pearson, J. (2015). Automated auxiliary variable elimination through on-the-fly propagator generation. In Pesant, G. (Ed.), CP 2015, LNCS, (Vol. 9255 pp. 313–329): Springer.
Nethercote, N., Stuckey, P.J., Becket, R., Brand, S., Duck, G.J., & Tack, G. (2007). MiniZinc: Towards a standard CP modelling language. In Bessière, C. (Ed.), CP 2007, LNCS. The MiniZinc toolchain is available at http://www.minizinc.org, (Vol. 4741 pp. 529–543): Springer.
Parlett, D. (Ed.) (1990). The Penguin Book of Patience. London: Penguin.
Pesant, G. (2004). A regular language membership constraint for finite sequences of variables. In Wallace, M. (Ed.), CP 2004, LNCS, (Vol. 3258 pp. 482–495): Springer.
Rendl, A., Guns, T., Stuckey, P.J., & Tack, G. (2015). MiniSearch: A solver-independent meta-search language for MiniZinc. In Pesant, G. (Ed.), CP 2015, LNCS, (Vol. 9255 pp. 376–392): Springer.
Simonis, H. (2008). Kakuro as a constraint problem. In Flener, P., & Simonis, H. (Eds.), ModRef 2018, the 7th International Workshop on Constraint Modelling and Reformulation. https://www.it.uu.se/research/group/astra/ModRef08/Simonis.pdf.
Acknowledgements
We thank Justin Pearson, Peter Stuckey, Guido Tack, Diego de Uña Gomez, and the anonymous referees for their helpful comments. Pierre Flener and Gustav Björdal are supported by the Swedish Research Council (VR) under grant 2015-4910.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article belongs to the Topical Collection: Integration of Artificial Intelligence and Operations Research Techniques in Constraint Programming
Guest Editors: Michele Lombardi and Domenico Salvagnin
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Dekker, J.J., Björdal, G., Carlsson, M. et al. Auto-tabling for subproblem presolving in MiniZinc. Constraints 22, 512–529 (2017). https://doi.org/10.1007/s10601-017-9270-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10601-017-9270-5










 is the status of
is the status of  , that is in which position of which variation of which encoding that byte is; the domain has 16 values, including one for an unknown status; for example, the value
, that is in which position of which variation of which encoding that byte is; the domain has 16 values, including one for an unknown status; for example, the value  states that the byte is in the second position of a four-byte UTF-8 encoding;
states that the byte is in the second position of a four-byte UTF-8 encoding; is the encoding of
is the encoding of  ; the domain has 5 values, including one for an unknown encoding; for example, the value
; the domain has 5 values, including one for an unknown encoding; for example, the value  states that the byte is in the UTF-8 encoding;
states that the byte is in the UTF-8 encoding; indicates whether
indicates whether  is the start of a character.
is the start of a character.
 is used to restrict the status combinations for two given consecutive bytes; for example, value
is used to restrict the status combinations for two given consecutive bytes; for example, value  must be directly preceded by
must be directly preceded by  ;
; is used to state the functional dependencies between the three variables for a given byte;
is used to state the functional dependencies between the three variables for a given byte;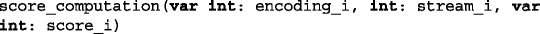 is used to state the functional dependency from the encoding and input stream to the score of a given byte.
is used to state the functional dependency from the encoding and input stream to the score of a given byte.

 item and the calls to this predicate by walking through the parse tree.
item and the calls to this predicate by walking through the parse tree. item in order to ask for satisfiability solving. The domain of each introduced variable is the union of the domains of the corresponding variables across all the calls in the original MiniZinc model to the annotated predicate definition.
item in order to ask for satisfiability solving. The domain of each introduced variable is the union of the domains of the corresponding variables across all the calls in the original MiniZinc model to the annotated predicate definition. constraint. While this is mostly straightforward, some care is needed when the arguments are of different types. Indeed, the MiniZinc language only defines the
constraint. While this is mostly straightforward, some care is needed when the arguments are of different types. Indeed, the MiniZinc language only defines the  constraint for all integer variables or all Boolean variables. Hence, one needs to cast Boolean variables into integer ones when they are mixed in a predicate. We currently do not support set and float variables.
constraint for all integer variables or all Boolean variables. Hence, one needs to cast Boolean variables into integer ones when they are mixed in a predicate. We currently do not support set and float variables. constraint with the obtained array of solutions. The subsequent flattening step will replace the calls to the predicate by this new body.
constraint with the obtained array of solutions. The subsequent flattening step will replace the calls to the predicate by this new body.
