Well-balanced central WENO schemes for the sediment transport model in shallow water

Abstract

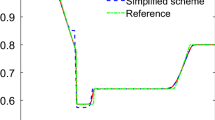
Sediment transport model in shallow water admits steady-state solutions in which the non-zero flux gradient is exactly balanced by the source term. In this paper, we develop high-order well-balanced central weighted essentially non-oscillatory schemes for the sediment transport model. In order to maintain the well-balanced property, we first reformulate the governing equations by an equivalent form and propose a novel reconstruction procedure for the Runge-Kutta flux. Rigorous theoretical analysis as well as extensive numerical examples all suggest that the present schemes preserve the well-balanced property. Moreover, the resulting schemes keep genuine high-order accuracy for general solutions.

Appendices

Appendix A: The WENO reconstruction for the cell averages

Based on ${\overline {U}_{j}^{n}}$, we introduce a polynomial reconstruction

$$P_{U}(x,t^{n}) = \sum\limits_{j} R_{j}(x) \chi_{j}, $$

here R _j (x) is a reconstruction polynomial on I _j and χ _j stands for a characteristic function on cell I _j . So the staggered cell average $\overline {U}_{j + 1/2}^{n}$ can be described by

$$\begin{array}{@{}rcl@{}} \overline{U}_{j + 1/2}^{n} &=& \frac{1}{\Delta x} {\int}_{x_{j}}^{x_{j + 1}} P_{_{U}}(x,t^{n}) \text{\, d}x = \frac{1}{\Delta x} \left[{\int}_{x_{j}}^{x_{j + 1/2}}R_{j}(x)\text{\, d}x\right.\\ &&+ \left. {\int}_{x_{j + 1/2}}^{x_{j + 1}}R_{j + 1}(x)\text{\, d}x \right]. \end{array} $$

(27)

To take conservation, high-order accuracy and non-oscillation into account, R _j (x) can be written as

$$ R_{j}(x) = \sum\limits_{k=-1}^{1} {w_{j}^{k}} P_{j+k}(x), $$

(28)

here P_{j + k}(x) is a polynomial of degree two on the stencil $\mathcal {P}_{j+k} = \bigcup \limits _{l=-1}^{1}I_{j+k+l}$ and satisfy the following requirement:

$$\frac{1}{\Delta x}{\int}_{I_{j+k-l}}P_{j+k}(x)\text{\, d}x = \overline{U}_{j+k-l}, \; l = -1, 0, 1. $$

The nonlinear weights ${w_{j}^{k}}$ in Eq. 28 can be computed as in [29]

$$ {w_{j}^{k}} = \frac{{\alpha_{j}^{k}}}{\sum\limits_{l=-1}^{1} {\alpha_{j}^{l}}}, \; \text{with} \; {\alpha_{j}^{k}} = \frac{C_{k}}{\left( \varepsilon + I{S_{j}^{k}}\right)^{2}}, $$

(29)

where C _k are linear weights in Table 1, ε is a small constant used here to avoid the denominator to be zero (we take ε as 10^− 6 in this paper), and $I{S_{j}^{k}}$ is the smoothness indicator used to measure the smoothness of P_{j + k}(x) on its corresponding stencil $\mathcal {P}_{j+k}$, and can be computed as in [29]

$$I{S_{j}^{k}} = \sum\limits_{l = 1}^{2}{\int}_{I_{j}} {\Delta} x^{2l} \left( P_{j+k}^{(l)}\right)^{2} \text{\, d}x. $$

Table 1 Linear weights for different purposes

Appendix B: The WENO reconstruction for K(x,U(x,t))

Herein, we write the reconstruction function for K(x,U(x,t)) denoted by T(x) on cell I _j as follows

$$ T(x) = \sum\limits_{k=-1}^{1} {w_{j}^{k}} P_{j+k}(x), $$

(30)

where P_{j + k}(x) is a reconstruction polynomial of degree two related to the corresponding stencils $\mathcal {S}_{j+k} = \bigcup \limits _{l=-1}^{1}\{x_{j+k+l}\}$, whose coefficients are determined by the following interpolation conditions

$$ P_{j+k}\left( x_{j+k+l}\right) = K \left( x_{j+k+l}, U_{j+k+l} \right), \;\; k=-1,0,1, \; l =-1, 0, 1. $$

(31)

The weight ${w_{j}^{k}}$ in Eq. 30 is computed as in Eq. 29, but the smoothness indicator $I{S_{j}^{k}}$ is resulted from the point values of K _j and linear weights C _k are from in Table 1.

Appendix C: The WENO reconstruction for ξ(x)

With ξ _j at hand, we can obtain a reconstruction function for ξ(x) denoted by M_j+ 1/2(x) of degree two on the staggered cell I_j+ 1/2. Then, the cell average of $\bar {\xi }_{j + 1/2}$ on cell I_j+ 1/2 can be expressed by

$$ \bar{\xi}_{j + 1/2} = \frac{1}{\Delta x}{\int}_{x_{j}}^{x_{j + 1}}M_{j + 1/2}(x)\text{\, d}x. $$

(32)

With a similar procedure as in the Appendix A and the Appendix B, we can write M_j+ 1/2(x) as follows:

$$M_{j + 1/2}(x) = \sum\limits_{m = 0}^{1} {w_{j}^{m}} N_{j+m}(x). $$

On the stencil $\mathcal {S}_{j+m} = \bigcup \limits _{l=-1}^{1} \{x_{j+m+l}\}$, N_{j + m}(x) has the following form

$$N_{j+m} = \tilde{\xi}_{j+m} + \tilde{\xi}_{j+m}^{\prime}\left( x-x_{j+m}\right) + \frac{1}{2}\tilde{\xi}_{j+m}^{\prime\prime}\left( x-x_{j+m}\right)^{2}, $$

with the coefficients being uniquely determined by the following interpolation requirements

$$N_{j+m}(x_{j+m+l}) = \xi_{j+m+l}, \; l=-1,0,1, $$

with

$$\begin{array}{lcl} \tilde{\xi}_{j+m} &=& \xi_{j+m}, \\ \tilde{\xi}_{j+m}^{\prime} &=& \frac{1}{2 {\Delta} x}\left( \xi_{j+m + 1} - \xi_{j+m-1}\right), \; m = 0,1, \\ \tilde{\xi}_{j+m}^{\prime\prime} &=& \frac{1}{({\Delta} x)^{2}}\left( \xi_{j+m + 1} - 2\xi_{j+m} + \xi_{j+m-1}\right). \end{array} $$

Moreover, the nonlinear weight ${w_{j}^{m}}$ has the following form

$${w_{j}^{m}} = \frac{{\alpha_{j}^{m}}}{\sum\limits_{l = 0}^{1} {\alpha_{j}^{l}}}, \; \text{with} \; {\alpha_{j}^{m}} = \frac{C_{m}}{(\varepsilon + I{S_{j}^{m}})^{2}}, $$

and the corresponding smoothness indicator $I{S_{j}^{m}}$ is described as follows

$$I{S_{j}^{m}} = \sum\limits_{l = 1}^{2}{\int}_{I_{j + 1/2}}{\Delta} x^{2l-1}\left( N_{j+m}^{(l)}\right)^{2} \text{\, d}x. $$

The linear weights C _m are also documented in Table 1.